Ultra-confined plasmons reveal moiré patterns in a twisted bilayer graphene–talc heterostructure

Abstract

This work investigates the plasmonic properties of a twisted bilayer graphene (TBG) and talc heterostructure. Talc, a naturally occurring phyllosilicate, promotes p-type charging of graphene, supporting high charge mobility and strong interaction between graphene plasmons and talc's phonon polaritons. This interaction results in the formation of surface plasmon–phonon polariton (SP³) modes, which are detected using infrared scattering-type scanning near-field optical microscopy (IR s-SNOM) at room temperature. Notably, without the need for electrostatic gating, our study reveals confinement of SP³ modes in a TBG–talc heterostructure and a transition from surface plasmonic waves to the emergence of moiré superlattices, characterized by reflections at domain walls. These findings provide fresh insights into the coupling mechanisms in hybrid materials and suggest promising applications in nanoscale optoelectronics.

---

André J. Chaves

André J. Chaves is a professor at the Aeronautics Institute of Technology (ITA). Dr Chaves holds a bachelor's degree in electronic engineering and a master's degree in physics from ITA, as well as a PhD in physics from the University of Minho. He has been a visiting researcher at the International Iberian Nanotechnology Laboratory (INL) and the Center for Polariton-driven Light–Matter Interactions (POLIMA) at the University of Southern Denmark (SDU). As a condensed matter physics theorist, Dr Chaves's main interest is the optical properties of two-dimensional (2D) materials, focusing on plasmons and excitons.

Ingrid D. Barcelos

Ingrid David Barcelos is an early-career scientist specializing in nanomaterials and optoelectronic devices, with a focus on polaritonic systems and their applications in THz and MIR technologies. She currently leads the Microscopic Sample Laboratory at the Brazilian Synchrotron Light Laboratory (LNLS), where she develops innovative approaches to explore the optical properties of 2D materials, such as semiconductor oxides and natural phyllosilicates, using advanced techniques like synchrotron infrared nanospectroscopy and s-SNOM. Recently recognized with the B-MRS Early Career Woman Scientist Prize, Dr Barcelos is also an Affiliate Member of the Brazilian Academy of Sciences (2025–2029). She is committed to advancing the understanding of low-dimensional materials while promoting diversity and inclusion in science.

---

Introduction

Since the experimental realization of graphene, studies on two-dimensional (2D) materials have uncovered properties that differ significantly from those of their bulk precursors,^1–3 stimulating advancements across fields such as optics,⁴ electronics,^5,6 catalysis,⁷ and energy storage.^8,9 Among these applications, graphene stands out in plasmonics^10–13 due to its ability to support highly confined surface plasmon polaritons, which can be finely tuned via electrostatic gating or chemical doping.^14,15 This tunability offers advantages for nanoscale light manipulation, enabling devices such as sensors,^16,17 modulators,¹⁸ and photodetectors.¹⁹ Despite these advancements, two major challenges hinder further development: intrinsic material losses and fabrication complexities.²⁰ Graphene's intrinsic losses, arising from electron–phonon interactions, vacancy defects, and scattering processes, notably reduce plasmon propagation lengths.^11,15,21 Even with intrinsic losses, nanoscale imaging using infrared through scattering-type scanning near-field optical microscopy enables the direct visualization of polaritonic standing waves in graphene,^14,22 highlighting the IR s-SNOM's potential for observing optical effects in high-mobility devices. Therefore, this technique provides new opportunities for studying many-body effects and complex phenomena.²⁰

Recently, it was shown that several properties of a graphene heterostructure can be tailored by selecting specific stacking materials³ and controlling the relative twist angle (θ) between them.²³ For example, when two graphene layers form twisted bilayer graphene, their lattices create a new periodic array, called the moiré pattern, introducing twist-angle-dependent features in the electronic, optical, and mechanical properties.²⁴ Remarkable phenomena occur when the twist angle is close to 1.1°, known as “magic angle”, at which the TBG turns into a strongly interacting system, revealing interesting phenomena such as enhanced many-body interactions, phase transitions from Mott insulators, metallic conductors, and unconventional superconductivity.^24–28 For TBG below the magic angle, the system undergoes a self-organized lattice reconstruction resulting in periodic triangular areas of alternating Bernal (AB and BA) stacking domains, separated by shear soliton regions (SP), with AA-stacked regions at the vertices of the triangles^29,30 (for further details on the TBG's reconstruction regime, refer to section S1 of the ESI†). At even lower angles, i.e. minimally twisted samples with θ < 0.5°, the band structure of the TBG is reconfigured activating very interesting physical phenomena such as topologically protected quantum valley Hall edge states,^31,32 moiré domain reconstruction³⁰ and topological transport in the network of domain boundaries.³³

TBG's moiré patterns and its reconstructed form can be investigated through various techniques, including transmission electron microscopy (TEM),³⁰ scanning microwave impedance microscopy (sMIM),^34,35 tip-enhanced Raman spectroscopy (TERS)²⁹ and infrared s-SNOM.³⁶ In plasmonics, the altered electronic structure due to TBG's moiré superlattices can enhance or tune plasmonic behavior, with plasmon wavelengths in TBG matching those of monolayer graphene but with reduced damping due to Fermi-velocity renormalization.²⁵ With the reduction of the twisting angle, enhanced layer interactions strengthen many-body effects, modifying plasmonic properties.^20,25 Moiré patterns modulate the electronic properties and significantly impact plasmonic wave dispersion and confinement.³⁷ Previous studies have imaged surface plasmon–phonon polaritons launched in graphene-based heterostructure devices, at low temperature²⁰ and by controlling their charge density through electrostatic gating.^20,38–40 High mobility pristine graphene requires doping to increase free-carrier density and enable SPP observation, achieved through substrate engineering or electrostatic gating.^20,38–40 However, IR s-SNOM systems with temperature control are rare and still under development, while electrostatic gating methods often involve complex fabrication steps that require delicate operation to avoid damage to the devices. This highlights the need to explore dielectric materials for graphene stacking to support plasmon–phonon polariton formation while addressing these limitations.

In that context, dielectric environments can modulate the plasmonic phenomena;^41–43 thus, understanding the behavior of polaritons at the substrate interface is crucial to unlock the potential of hybrid optoelectronic devices for modern applications. Talc, a naturally abundant phyllosilicate,^44,45 has shown intriguing properties when combined with graphene as a heterostructure,^46,47 including spontaneous p-type doping while preserving excellent charge mobility.⁴⁷ Additionally, a strong interaction between graphene plasmons and talc's phonon polaritons gives rise to hybrid modes,⁴⁶ specifically surface plasmon–phonon polaritons (SP³), resulting from the coupling between graphene's electron density oscillations and talc's lattice vibrations.⁴⁶ Here, we report SP³ modes in a twisted bilayer graphene–talc (TBG–talc) heterostructure observed using IR s-SNOM at room temperature without any back-gate voltage. We experimentally demonstrate the transition from SP³ waves on the surface of the TBG to the emergence of the TBG moiré pattern, evidenced by reflections at the superlattice domain walls. Analysis of the extracted SP³ wave's profiles unveils confinement factors of approximately 180, obtained by the equation:

f_con = λ_IR/λ_p, (1)

where λ_IR is the light wavelength in free space and λ_p is the SP³ propagation wavelength, surpassing the current state of the art.²⁰ Additionally, we image distinct double-line features centered at the reconstructed twisted bilayer graphene solitons, resulting from the coherent interference between propagating and reflected waves across domain boundaries.³⁶ This capability suggests new possibilities for hybrid optoelectronics whose operation can rely on the fine-tuning of moiré superlattices.

Methods

Our graphene and talc (Mg₃Si₄O₁₀(OH)₂) crystals were sourced from a graphite mine in Itapecerica, Brazil (Nacional de Grafite), and a soapstone mine in Ouro Preto, Brazil, respectively. Monolayer graphene and talc (approximately 25 nm thick) were obtained by the Scotch tape method⁴⁸ and deposited onto thermally oxidized silicon substrates. The TBG samples were fabricated using the tear-and-stack method with a polydimethylsiloxane pyramid stamp, as previously described.⁴⁹ Briefly, a transparent polycarbonate membrane was adhered to the pyramid stamp, aligned over half of the graphene flake and brought in contact with it while raising the sample temperature. After cooling, the pyramid stamp was retracted, lifting the first half of the graphene. The remaining half of the graphene was then rotated to the desired angle, and the procedure was repeated to pick up the other half using the same stamp. The completed TBG was deposited onto an atomically flat talc flake and subsequently characterized by IR s-SNOM at multiple laser frequencies.

The IR s-SNOM system is an atomic force microscope (AFM) operating in semicontact (tapping) mode, equipped with optics to focus and collect both incident and scattered light. The IR light illuminates the tip, which oscillates at its fundamental mechanical frequency Ω (∼250 kHz), inducing effective polarization of the tip that enhances light interaction with the sample. The near-field optical signal (S_m), originating from an area comparable to the tip radius (∼25 nm), is extracted from the detected back-scattered light by demodulating the signal at harmonics (m) of Ω, with m ≥ 2, with a lock-in amplifier, and the backscattered light interferes with the reference IR beam from a scanning mirror. The Fourier transform of the resultant interferogram yields the IR amplitude |S_m(ω)| and phase ϕ_m(ω) spectra of the complex optical near-field signal S_m(ω) = |S_m(ω)| × e^iΦ_m(ω). All nanoimages here are measured with third harmonic demodulation (m = 3) to yield S₃(ω) and ϕ₃(ω).

The IR s-SNOM measurements were conducted in the IMBUIA beamline at Sirius (LNLS, Campinas, Brazil) using a commercial s-SNOM instrument (neaSCOPE, neaspec/attocube systems AG). Nanoimaging was performed with a quantum cascade laser (QCL) model MirCat from Daylight Solutions, covering the spectral range of 930–1730 cm⁻¹, with a minimum frequency step of 1 cm⁻¹ and a pseudo-heterodyne detection scheme demodulated at the third harmonic. Post-processing of the nanoimages and s-SNOM profiles was carried out using the free software Gwyddion (https://gwyddion.net).

To obtain the plasmon–phonon polariton dispersion, we calculated the TBG–talc–SiO₂ heterostructure loss function, defined as L = −Im[r_p], where r_p is the Fresnel reflection coefficient for transverse magnetic (TM) polarized waves, calculated using the transfer matrix method.⁵⁰ For TBG, we considered a 2D optical conductivity obtained from the hydrodynamic model for graphene,⁵¹ as explained in sections S2 and S3 of the ESI.† We used the talc infrared dielectric function from a parallel work.⁵² For the SiO₂, we used the dielectric function of ref. 53. Details about the derivation of the hydrodynamic model and justification for the used approximations can be found in the ESI.†

Results and discussion

Fig. 1a depicts the optical micrograph of a TBG–talc heterostructure (see the Experimental section for details), showing the interface between a 25 nm thick talc crystal (outlined by the white dashed line) and the SiO₂ (300 nm)/Si substrate. The TBG regions are visible, with the upper graphene layer marked with an orange dashed line and the lower graphene layer outlined in blue, forming the characteristic moiré pattern of the heterostructure. Fig. 1b presents the AFM topography image of the heterostructure, highlighting the atomically flat surface of talc. The smooth and clean surface confirms the high quality of the sample preparation process. While some ripples appear along the TBG (white regions in Fig. 1b), due to the stacking procedure, the height variations offer a detailed view of the uniformity and thickness of the heterostructure. The yellow square region in Fig. 1b indicates the specific area selected for further investigation by the s-SNOM technique. Fig. 1c provides a schematic of our TBG–talc heterostructure, produced via the tear-and-stack method and characterized by IR s-SNOM. This schematic highlights the key features of the setup, including the moiré pattern and the spontaneous p-type doping,⁴⁷ indicated by the Fermi level position relative to the conduction band, which arises from the interaction between TBG and talc. Additionally, in this technique, IR radiation is focused on the apex of the metal-coated AFM tip that acts as an antenna, locally enhancing the electric field and producing a near-field interaction with the sample. This interaction excites polaritons along the material which backscatters at the sample edges, producing a standing wave of a well-defined wavelength

λ_p = 2π/q_p, (2)

where q_p is the SP³ momentum.

Fig. 1 One of the fabricated TBG samples deposited over a 25 nm thick talc flake observed by (a) optical microscopy and (b) AFM. (c) Schematic of our TBG–talc heterostructure produced through the tear-and-stack method and characterized by s-SNOM – the insets further highlight the moiré pattern, and the spontaneous p-type doping is indicated by the Fermi level position at the conduction band caused by the interaction of the TBG with talc. The characterization of the fabricated TBG–talc heterostructures by s-SNOM revealed (d) highly confined SP³ using a 940 cm⁻¹ laser frequency and (e) Moiré patterns for a 1021 cm⁻¹ laser frequency.

The TBG–talc heterostructure was investigated across a broad range of IR frequencies to probe SP³ modes and explore the impact of moiré patterns on plasmonic behavior. Fig. 1 shows a summary of the main phenomena observed, which will be described in detail in the following sections. Specifically, Fig. 1d and e show the IR s-SNOM nanoimages obtained at different laser frequencies. At a laser frequency of 940 cm⁻¹ (Fig. 1d), SP³ modes are visible, demonstrating the capability of the TBG–talc structure to support ultra-confined plasmonic waves, behaving coherently, at room temperature. On the other hand, at the laser frequency excitation of 1021 cm⁻¹ (Fig. 1e), moiré patterns emerge within the heterostructure, characterized by distinct reflections at the superlattice domain walls revealing a moiré period of approximately 150 nm, corresponding to a twist angle of 0.1°.

In an IR s-SNOM experiment, the SP³ propagation appears as interference fringes, resulting in periodic modulation of the near-field signal across the sample, as shown in Fig. 1d, for the 3^rd harmonic of the optical phase signal (ϕ₃(ω)). This modulation strongly depends on the density of charge in the material and on the frequency of the incident light.²⁰ Consequently, different frequencies produce fringes with varying wavelengths. To investigate the SP³ frequency dependency, we performed IR s-SNOM nanoimaging with excitation frequencies ranging from 920 cm⁻¹ up to 1060 cm⁻¹.

At 920 cm⁻¹, characteristic plasmonic interference fringes appear in the ϕ₃(ω) signal (Fig. 2a), showing minimal damping and indicating that the SP³ can propagate over several micrometers without losing coherence.⁵⁴ The dotted lines trace the line profiles of the confined SP³, allowing us to determine their wavelengths (λ_p) as a function of laser frequency. These line profiles demonstrate a decreased SP³ wavelength with increasing frequency, indicating strong frequency dependence of plasmon–phonon polariton confinement within the TBG–talc heterostructure. From the extracted profile, we measured a wavelength of 75 nm, corresponding to a confinement factor on the order of 145 (eqn (1)). We performed the same analysis for excitation frequencies of 940 cm⁻¹ (Fig. 2b), 960 cm⁻¹ (Fig. 2c) and 980 cm⁻¹ (Fig. 2d) obtaining wavelengths of 72 nm, 57 nm and 58 nm, respectively. These values yield confinement factors up to 180, establishing a new benchmark for polariton confinement in TBG samples at room temperature.²⁰ This high degree of confinement is attributed primarily to the spontaneous p-type doping induced by talc,⁴⁷ which enhances charge density and strengthens the coupling between graphene plasmons and talc phonon modes. This coupling is evidenced by the clear standing waves observed within the SP³ modes, as seen in the line profiles.

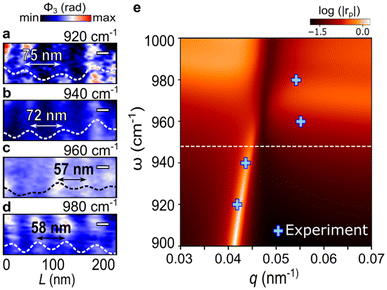Fig. 2 Near-field images of ϕ₃(ω) signals observed at selected frequencies: (a) 920 cm⁻¹, (b) 940 cm⁻¹, (c) 960 cm⁻¹ and (d) 980 cm⁻¹ revealing highly confined surface plasmon–phonon polaritons (SP³) – the dotted lines reveal the line profiles of the confined SP³ with its wavelength (λ_p) – scale bars: 25 nm. (e) Dispersion relation (ω(q)) for plasmon–phonon polariton in a TBG–talc–SiO₂ heterostructure obtained from the plot of the Fresnel reflection coefficient, calculated using the transfer matrix method (ESI section S2†), on a logarithmic scale (log|r_p|). The blue crosses were experimentally obtained from the measured λ_p by using eqn (2); the white dashed line marks the beginning of the talc's Reststrahlen band.⁵²

Fig. 2e presents the theoretical dispersion relation of the SP³ modes and experimental data (blue crosses) derived from the measured wavelengths (λ_p) in Fig. 2a–d. Below the frequency of 948 cm⁻¹, which corresponds to the talc z-polarized transverse optical phonons, the frequency of the plasmon–phonon branch increases with the wavenumber. Above this phonon frequency threshold, the peak of the loss function spreads out and approaches a horizontal line (see the ESI in sections S2 and S3†). This dispersion relation reveals key characteristics of SP³ propagation in TBG, where increasing frequency leads to a shorter wavelength and, thus, stronger confinement of the plasmon–phonon polaritons. Also, the observed dispersion behavior is consistent with theoretical models for SP³ modes in graphene–talc heterostructures,^25,55 where the moiré superlattice created by the twist angle modulates the electronic structure.^25,55 This modulation affects the momentum (q_p) and wavelength of SP³ modes, allowing for tunable dispersion properties. The frequency-dependent behavior observed in Fig. 2 demonstrates the potential for tuning SP³ propagation characteristics in TBG–talc systems through frequency adjustments, offering an additional layer of control for nanoscale optoelectronic applications. The ability to achieve ultra-confined SP³ modes at room temperature in TBG–talc, without the need for back-gating, opens new avenues for applications in nanoscale optics. The highly confined SP³ waves and their tunable dispersion make this heterostructure a promising candidate for use in plasmonic sensors, modulators, and photodetectors. By leveraging the natural p-type doping from talc and the moiré superlattice effect, it may be possible to create devices with fine control over plasmonic behavior at sub-wavelength scales.

Beyond 980 cm⁻¹, the SP³ propagation in the TBG–talc heterostructure largely vanishes, indicating plasmonic losses and a transition to the emergence of a distinct moiré pattern. This shift marks a transformation from surface plasmonic waves to the formation of hexagonal moiré patterns, which appear with periodicities that match those of the TBG superlattice, as revealed in Fig. 3. The visualization of these moiré patterns through IR s-SNOM highlights the power of this technique in probing local conductivity and optical modulation at the nanoscale. This approach has proven valuable in studying twisted bilayer graphene (TBG) and similar 2D systems.^32,56

Fig. 3 Near-field images of S₃(ω) signals observed at frequencies (a) 1000 cm⁻¹ and (b) 1021 cm⁻¹, revealing moiré patterns of the twisted bilayer graphene in the reconstruction regime, as depicted in (e). The inset in figure (a) is an AFM profile showing a thickness difference of approximately 1.5 nm between the left and right regions of the sample, which changes talc's vibrational modes,⁴⁶ impacting the SP³ formation. Figures (c) and (d) are zoomed-in images of the hexagonal superlattice shown in (a) and (b), respectively.

Fig. 3a presents S₃(ω) near-field images obtained at 1000 cm⁻¹, showing a moiré pattern on the right side of the sample, highlighted in the zoomed-in view in Fig. 3c. The observed superlattice shows a moiré period of approximately L_M = 150 nm, corresponding to a minimal twist angle of 0.1°, estimated from the expression θ = 2·arcsin(a_G/2·L_M), where a_G = 0.246 nm is the graphene's crystal lattice constant.⁵⁷ At this twist angle, the TBG enters the reconstruction regime,^29,30 as depicted in Fig. 3e. However, the expected triangular domains are less prominent in the S₃(ω) images obtained at 1000 cm⁻¹ than those obtained at 1021 cm⁻¹ (Fig. 3b and d).

At the excitation frequency of 1021 cm⁻¹ (Fig. 3b), a well-defined formation of the triangular Bernal stacking areas is observed on the right side of the sample, with an increase in the intensity of the amplitude signal at the soliton regions, indicating increased IR reflectivity at the domain walls. Additionally, a moiré pattern forms on the left side of the sample, which is absent at 1000 cm⁻¹ (Fig. 3a and c). A closer AFM examination of these regions reveals a difference in talc thickness of approximately 1.5 nm (inset in Fig. 3a), corresponding to about one monolayer of talc.⁵⁸ The thickness variation affects talc's vibrational modes,⁴⁶ impacting the SP³ formation. These results highlight the clear frequency dependence of SP³ coupling with the TBG superlattice and confirm the influence of talc's vibrational modes on SP³ behavior as a function of thickness, consistent with previous studies.⁴⁶

In TBG, solitons are sharp and localized changes in the stacking configuration that separate regions with different atomic alignments.³⁰ These soliton regions often form a network of domain walls in the moiré pattern, typically separating Bernal-stacked (AB/BA) domains. Solitons in TBG are particularly interesting because they give rise to unique electronic, optical, and plasmonic properties that can also be imaged by s-SNOM.³⁰Fig. 4a illustrates the mechanism underlying the double-line features observed in the ϕ₃(ω) images (Fig. 4b–d), specifically highlighting the interaction between SP³ and soliton boundaries in the reconstructed twisted bilayer graphene.

Fig. 4 (a) Schematic illustration of the TBG under IR excitation, depicting solitons that separate regions with different atomic alignments, specifically the Bernal-stacked AB and BA domains within the moiré pattern. These soliton boundaries act as reflective barriers, partially reflecting the forward-propagating SP³ wave and causing interference with the backward-propagating wave. This inference results in double-line features centered at the soliton domain walls, where destructive interference leads to a reduction in phase signal and lower IR absorption along these lines. Near-field images Φ₃(rad) observed at frequencies (b) 1000 cm⁻¹, (c) 1021 cm⁻¹ and (d) 1060 cm⁻¹ (scale bars: 50 nm). The separation between the double lines at different frequencies is shown in (e) 1000 cm⁻¹ and (f) 1021 cm⁻¹, where the observed separation distance is well below the expected resolution limit of the technique.

The phenomenon described above can be experimentally observed in the ϕ₃(ω) images in Fig. 4b–d, obtained at excitation frequencies of 1000 cm⁻¹, 1021 cm⁻¹, and 1060 cm⁻¹, respectively. These images provide a real-space view of the interference pattern, exhibiting double-line features aligned along the soliton boundaries. This behavior is consistent with previous studies,^30,56 which demonstrated that soliton boundaries in TBG alter local optical conductivity and act as plasmonic reflectors. The robustness of this effect across a range of frequencies is evident, as the double-line features remain visible at each frequency. However, the distance between the double lines varies with frequency, as shown in the line profiles for 1000 cm⁻¹ (Fig. 4e) and 1021 cm⁻¹ (Fig. 4f). This frequency-dependent separation suggests that the spacing between the lines is governed by the SP³ wavelength, which decreases as the excitation frequency increases. Consequently, at higher frequencies, the double-line separation narrows, reflecting the tunable plasmonic response within the TBG–talc heterostructure.

Conclusions

In summary, we investigated the plasmonic properties of minimally twisted TBG–talc heterostructures using infrared scattering-type scanning near-field optical microscopy (IR s-SNOM) at room temperature. By probing excitation frequencies between 920 cm⁻¹ and 1060 cm⁻¹, we observed ultra-confined hybrid SP³ modes on the TBG surface without the need for electrostatic gating. Our nanoimages revealed a frequency-dependent transition from SP³ waves to the emergence of the TBG moiré pattern. During SP³ propagation, we observed standing waves with wavelengths around 57 nm that maintain coherence over several micrometers, with confinement factors up to 180. This high degree of confinement arises from spontaneous p-type doping induced by talc, which enhances both the plasmonic activity in graphene as well as the coupling between graphene plasmons and talc phonon modes.

As the frequency exceeded 980 cm⁻¹, SP³ propagation largely vanishes due to plasmonic losses, revealing the underlying TBG moiré patterns. The observed superlattice exhibited distinct periodic triangular domains separated by shear soliton regions, characteristic of the TBG reconstruction regime, with moiré periods reaching up to 150 nm, corresponding to a minimal twist angle of 0.1°. Variations in the intensities of the S₃(ω) near field images were observed at the triangular domains, which were influenced by frequency and thickness variations within the talc flake. Additionally, the ϕ₃(ω) signal unveiled double-line features centered at the soliton boundaries in the reconstructed TBG structure, highlighting the coupling between SP³ modes and domain walls. These double lines indicate that soliton boundaries can act as reflective barriers, creating interference between forward- and backward-propagating SP³ waves, thereby modifying local optical conductivity.

Our findings underscore the utility of s-SNOM in exploring soliton-mediated plasmonic phenomena, emphasizing that solitonic boundaries in TBG can serve as frequency-dependent, reflective channels for SP³ modes. The moiré superlattice and soliton networks play a critical role in altering plasmonic wave dispersion and confinement, increasing the strength of plasmonic interactions and enhancing the control over plasmonic confinement and interference. These intricate plasmonic behaviors provide valuable insights into electron–plasmon interactions and offer exciting opportunities for nanoscale photonic and optoelectronic applications that leverage the fine-tuning of moiré superlattices and solitonic boundaries. Overall, our results position TBG–talc heterostructures as a promising platform for advancing nanoscale device technologies where precise control over plasmonic interactions is essential.

Author contributions

Conceptualization: Ingrid D. Barcelos, Tiago C. Barbosa and Leonardo C. Campos. Formal analysis: Tiago C. Barbosa. Theoretical model: André J. Chaves. Funding acquisition: Leonardo C. Campos, Ingrid D. Barcelos, and Raul O. Freitas. Investigation: Tiago C. Barbosa, Ingrid D. Barcelos and Raul O. Freitas. Project administration: Ingrid D. Barcelos. Resources: Raul O. Freitas and Leonardo C. Campos. Visualization: Tiago C. Barbosa and Ingrid D. Barcelos. Validation: Tiago C. Barbosa and Ingrid D. Barcelos. Writing – original draft: Tiago C. Barbosa and Ingrid D. Barcelos. Writing – review & editing: Tiago C. Barbosa, Ingrid D. Barcelos, André J. Chaves, Leonardo C. Campos and Raul O. Freitas.

Data availability

All data that support the findings of this study are included within the article and in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

All Brazilian authors acknowledge the financial support from CNPq, CAPES, FAPEMIG, Rede 2D FAPEMIG, and the Brazilian Nanocarbon Institute of Science and Technology (INCT/Nanomateriais de Carbono). The authors also thank the UFMG-Laboratory of Characterization and Processing of Nanomaterials (LCPNano), Sisteman Nacional de Laboratórios em Nanotecnologias (SisNANO), the Brazilian Synchrotron Light Source (LNLS), part of the Brazilian Centre for Research in Energy and Materials (CNPEM), a private non-profit organization under the supervision of the Brazilian Ministry of Science, Technology, and Innovations (MCTI). The authors thank LAM and IMBUIA (Proposal: 20232660) for sample preparation and characterization. I. D. B. acknowledges the L'ORÉAL-UNESCO-ABC For Women in Science Prize – Brazil (2021 edition) and financial support from FAPESP (Grant No. 2022/02901-4). I. D. B., A. J. C. and R. O. F. also acknowledge support from CNPq through research grants 306170/2023-0, 315408/2021-9 and 309946/2021-2. I. D. B. and A. J. C. also acknowledge CNPq grant 408144/2022-0. A. J. C. also acknowledges CNPq grant 423423/2021-5. Finally, support from FAPESP through the Young Investigator Grant (Grant No. 2019/14017-9) is gratefully acknowledged.

References

1. A. K. Geim, Science, 2009, 324, 1530–1534.
2. A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425.
3. P. Ajayan, P. Kim and K. Banerjee, Phys. Today, 2016, 69, 38–44.
4. R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres and A. K. Geim, Science, 2008, 320, 1308–1308.
5. Q. Bao and K. P. Loh, ACS Nano, 2012, 6, 3677–3694.
6. J. R. Williams, D. A. Abanin, L. Dicarlo, L. S. Levitov and C. M. Marcus, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–7.
7. Y. Yan, W. I. Shin, H. Chen, S.-M. Lee, S. Manickam, S. Hanson, H. Zhao, E. Lester, T. Wu and C. H. Pang, Carbon Lett., 2021, 31, 177–199.
8. Y. Sun, Q. Wu and G. Shi, Energy Environ. Sci., 2011, 4, 1113.
9. N. G. Sahoo, Y. Pan, L. Li and S. H. Chan, Adv. Mater., 2012, 24, 4203–4210.
10. S. Xiao, X. Zhu, B.-H. Li and N. A. Mortensen, Front. Phys., 2016, 11, 117801.
11. X. Luo, T. Qiu, W. Lu and Z. Ni, Mater. Sci. Eng., R, 2013, 74, 351–376.
12. F. J. García de Abajo, ACS Photonics, 2014, 1, 135–152.
13. A. N. Grigorenko, M. Polini and K. S. Novoselov, Nat. Photonics, 2012, 6, 749–758.
14. Z. Fei, A. S. Rodin, G. O. Andreev, W. Bao, A. S. McLeod, M. Wagner, L. M. Zhang, Z. Zhao, M. Thiemens, G. Dominguez, M. M. Fogler, A. H. C. Neto, C. N. Lau, F. Keilmann and D. N. Basov, Nature, 2012, 487, 82–85.
15. Z. Fei, G. O. Andreev, W. Bao, L. M. Zhang, A. S. McLeod, C. Wang, M. K. Stewart, Z. Zhao, G. Dominguez, M. Thiemens, M. M. Fogler, M. J. Tauber, A. H. Castro-Neto, C. N. Lau, F. Keilmann and D. N. Basov, Nano Lett., 2011, 11, 4701–4705.
16. S. Ogawa, S. Fukushima and M. Shimatani, Sensors, 2020, 20, 1–21.
17. L. Wu, H. S. Chu, W. S. Koh and E. P. Li, Opt. Express, 2010, 18, 14395.
18. F. Zhou and W. Du, Appl. Opt., 2018, 57, 6645–6650.
19. S. Castilla, I. Vangelidis, V.-V. Pusapati, J. Goldstein, M. Autore, T. Slipchenko, K. Rajendran, S. Kim, K. Watanabe, T. Taniguchi, L. Martín-Moreno, D. Englund, K.-J. Tielrooij, R. Hillenbrand, E. Lidorikis and F. H. L. Koppens, Nat. Commun., 2020, 11, 4872.
20. G. X. Ni, A. S. McLeod, Z. Sun, L. Wang, L. Xiong, K. W. Post, S. S. Sunku, B.-Y. Jiang, J. Hone, C. R. Dean, M. M. Fogler and D. N. Basov, Nature, 2018, 557, 530–533.
21. M. Jablan, M. Soljacic and H. Buljan, Proc. IEEE, 2013, 101, 1689–1704.
22. J. Chen, M. Badioli, P. Alonso-González, S. Thongrattanasiri, F. Huth, J. Osmond, M. Spasenović, A. Centeno, A. Pesquera, P. Godignon, A. Zurutuza Elorza, N. Camara, F. J. García, R. Hillenbrand and F. H. L. Koppens, Nature, 2012, 487, 77–81.
23. S. Carr, D. Massatt, S. Fang, P. Cazeaux, M. Luskin and E. Kaxiras, Phys. Rev. B, 2017, 95, 1–6.
24. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50.
25. R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12233–12237.
26. X. Lu, P. Stepanov, W. Yang, M. Xie, M. A. Aamir, I. Das, C. Urgell, K. Watanabe, T. Taniguchi, G. Zhang, A. Bachtold, A. H. MacDonald and D. K. Efetov, Nature, 2019, 574, 653–657.
27. M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young and C. R. Dean, Science, 2019, 363, 1059–1064.
28. E. Suárez Morell, J. D. Correa, P. Vargas, M. Pacheco and Z. Barticevic, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 121407.
29. A. C. Gadelha, D. A. A. Ohlberg, C. Rabelo, E. G. S. Neto, T. L. Vasconcelos, J. L. Campos, J. S. Lemos, V. Ornelas, D. Miranda, R. Nadas, F. C. Santana, K. Watanabe, T. Taniguchi, B. van Troeye, M. Lamparski, V. Meunier, V.-H. Nguyen, D. Paszko, J.-C. Charlier, L. C. Campos, L. G. Cançado, G. Medeiros-Ribeiro and A. Jorio, Nature, 2021, 590, 405–409.
30. H. Yoo, R. Engelke, S. Carr, S. Fang, K. Zhang, P. Cazeaux, S. H. Sung, R. Hovden, A. W. Tsen, T. Taniguchi, K. Watanabe, G. C. Yi, M. Kim, M. Luskin, E. B. Tadmor, E. Kaxiras and P. Kim, Nat. Mater., 2019, 18, 448–453.
31. F. Zhang, A. H. MacDonald and E. J. Mele, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10546–10551.
32. L. Ju, Z. Shi, N. Nair, Y. Lv, C. Jin, J. Velasco, C. Ojeda-Aristizabal, H. A. Bechtel, M. C. Martin, A. Zettl, J. Analytis and F. Wang, Nature, 2015, 520, 650–655.
33. P. Rickhaus, J. Wallbank, S. Slizovskiy, R. Pisoni, H. Overweg, Y. Lee, M. Eich, M.-H. Liu, K. Watanabe, T. Taniguchi, T. Ihn and K. Ensslin, Nano Lett., 2018, 18, 6725–6730.
34. D. A. A. Ohlberg, D. Tami, A. C. Gadelha, E. G. S. Neto, F. C. Santana, D. Miranda, W. Avelino, K. Watanabe, T. Taniguchi, L. C. Campos, J. C. Ramirez, C. G. do Rego, A. Jorio and G. Medeiros-Ribeiro, Nat. Commun., 2021, 12, 2980.
35. G. Bargas, D. A. A. Ohlberg, K. Watanabe, T. Taniguchi, L. C. Campos and G. Medeiros-Ribeiro, Phys. Status Solidi B, 2024, 2400548.
36. Y. Luo, R. Engelke, M. Mattheakis, M. Tamagnone, S. Carr, K. Watanabe, T. Taniguchi, E. Kaxiras, P. Kim and W. L. Wilson, Nat. Commun., 2020, 11, 1–7.
37. D. N. Basov, M. M. Fogler and F. J. García de Abajo, Science, 2016, 354, aag1992.
38. S. Dai, Q. Ma, M. K. Liu, T. Andersen, Z. Fei, M. D. Goldflam, M. Wagner, K. Watanabe, T. Taniguchi, M. Thiemens, F. Keilmann, G. C. A. M. Janssen, S. E. Zhu, P. Jarillo-Herrero, M. M. Fogler and D. N. Basov, Nat. Nanotechnol., 2015, 10, 682–686.
39. V. W. Brar, M. S. Jang, M. Sherrott, S. Kim, J. J. Lopez, L. B. Kim, M. Choi and H. Atwater, Nano Lett., 2014, 14, 3876–3880.
40. S. S. Sunku, G. X. Ni, B. Y. Jiang, H. Yoo, A. Sternbach, A. S. McLeod, T. Stauber, L. Xiong, T. Taniguchi, K. Watanabe, P. Kim, M. M. Fogler and D. N. Basov, Science, 2018, 362, 1153–1156.
41. C. Busse, S. Baud, G. Bihlmayer, C. Polop, T. Michely and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 201401.
42. X. Luo and T. Ishihara, Appl. Phys. Lett., 2004, 84, 4780–4782.
43. R. Laha, P. Malar, T. Osipowicz and S. Kasiviswanathan, J. Nanopart. Res., 2017, 19, 302.
44. R. Longuinhos, A. R. Cadore, H. A. Bechtel, C. J. S. De Matos, R. O. Freitas, J. Ribeiro-Soares and I. D. Barcelos, J. Phys. Chem. C, 2023, 12, 5876–5885.
45. R. Frisenda, Y. Niu, P. Gant, M. Muñoz and A. Castellanos-Gomez, npj 2D Mater. Appl., 2020, 4, 1–13.
46. I. D. Barcelos, A. R. Cadore, A. B. Alencar, F. C. B. Maia, E. Mania, R. F. Oliveira, C. C. B. Bufon, Â. Malachias, R. O. Freitas, R. L. Moreira and H. Chacham, ACS Photonics, 2018, 5, 1912–1918.
47. E. Mania, A. B. Alencar, A. R. Cadore, B. R. Carvalho, K. Watanabe, T. Taniguchi, B. R. A. Neves, H. Chacham and L. C. Campos, 2D Mater., 2017, 4, 031008.
48. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
49. A. C. Gadelha, D. A. A. Ohlberg, F. C. Santana, G. S. N. Eliel, J. S. Lemos, V. Ornelas, D. Miranda, R. B. Nadas, K. Watanabe, T. Taniguchi, C. Rabelo, P. P. D. M. Venezuela, G. Medeiros-Ribeiro, A. Jorio, L. G. Cançado and L. C. Campos, ACS Appl. Nano Mater., 2021, 4, 1858–1866.
50. P. Markos and C. M. Soukoulis, Wave Propagation: From Electrons to Photonic Crystals and Left-Handed Materials, Princeton University Press, 2008.
51. A. J. Chaves, N. M. R. Peres, G. Smirnov and N. A. Mortensen, Phys. Rev. B, 2017, 96, 195438.
52. F. H. Feres, F. C. B. Maia, S. Chen, R. A. Mayer, M. Obst, O. Hatem, L. Wehmeier, T. Nörenberg, M. S. Queiroz, V. Mazzotti, J. M. Klopf, S. C. Kehr, L. M. Eng, A. R. Cadore, R. Hillenbrand, R. O. Freitas and I. D. Barcelos, arXiv, 2025, 1–8.
53. I. J. Luxmoore, C. H. Gan, P. Q. Liu, F. Valmorra, P. Li, J. Faist and G. R. Nash, ACS Photonics, 2014, 1, 1151–1155.
54. H. Alnatah, Q. Yao, J. Beaumariage, S. Mukherjee, M. C. Tam, Z. Wasilewski, K. West, K. Baldwin, L. N. Pfeiffer and D. W. Snoke, Sci. Adv., 2024, 10, eadk6960.
55. V. Hung Nguyen, D. Paszko, M. Lamparski, B. Van Troeye, V. Meunier and J.-C. Charlier, 2D Mater., 2021, 8, 035046.
56. L. Jiang, Z. Shi, B. Zeng, S. Wang, J. H. Kang, T. Joshi, C. Jin, L. Ju, J. Kim, T. Lyu, Y. R. Shen, M. Crommie, H. J. Gao and F. Wang, Nat. Mater., 2016, 15, 840–844.
57. H. Beyer, M. Müller and T. Schimmel, Appl. Phys. A: Mater. Sci. Process., 1999, 68, 163–166.
58. A. B. Alencar, A. P. M. Barboza, B. S. Archanjo, H. Chacham and B. R. A. Neves, 2D Mater., 2015, 2, 015004.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04532g

---