Impact of processing atmosphere on nanoscale properties of highly efficient Cs_0.05MA_0.05FA_0.9PbI₃ perovskite solar cells

Abstract

The fabrication process of triple-cation-halide organic inorganic perovskites must be tightly controlled to make high-efficiency solar cells. After precursor deposition, the amount of oxygen and moisture during the annealing process is important but not always well-monitored and understood. In this study, Cs_0.05MA_0.05FA_0.9PbI₃ perovskite films were annealed in different environments, namely N₂, O₂ and air, to systematically explore the relationship between the evolution of PbI₂, the grain boundary band bending and the optoelectronic properties. We find higher amounts of PbI₂ after air annealing, accompanied by an increased number of grain boundaries that show downward band bending. Photoluminescence measurements showed that absorbers annealed in the absence of air or O₂ (i.e. N₂ environment) exhibit the best optoelectronic properties, which however did not translate to the highest V_OC of the devices. Drift-diffusion simulations show that the interface between the perovskite and the Spiro-OMeTAD is very sensitive to the defect density. Consequently, the higher amount of PbI₂ is likely to passivate some of the interface defects, which means better translation of the opto-electronic absorber quality into open-circuit voltage. Although this strategy was adequate for the perovskite/Spiro-OMeTAD solar cell architecture that was used in this study, our results show that an even better way would be to grow perovskites without intentional incorporation of air or oxygen, which reduces PbI₂ and grain boundary band bending, allowing higher quasi Fermi-level splitting. This layer would need to be combined with an optimized hole extraction layer with improved band alignment.

---

Organic–inorganic halide perovskites are among the most promising candidates for topcells in next-generation tandem solar cells. The tunability of the bandgap, the low production costs, and the easy manufacturing^1,2 have allowed the researchers to push the record power conversion efficiency beyond all traditional thin film technologies in only a couple of years, now reaching 26.7% for single junction devices and 34.2% for perovskite/Si tandems.³

The formation and stabilization of the perovskite structure is of key importance to meet the high-stability demand for commercialization. It is well known that methylammonium (MA)-based absorbers are too unstable.^4,5 Therefore, formamidinium (FA)-based perovskites (FAPI) are nowadays preferred,⁶ which often include small amounts of Cs and MA to achieve a stable α-phase,^7–12 due to a better Goldschmidt tolerance factor.¹³

FAPI perovskites must be prepared in a controlled environment to maximize stability and power conversion efficiencies (PCE).^14,15 Several studies suggest that incorporating a small amount of water or moisture within the precursor solution or during the annealing process leads to a modulation of the crystal orientation and phase distribution, recrystallization, or healing of defects in the perovskite film, which ultimately leads to higher PCEs.^16–22

In addition to changes in the perovskite lattice and defects, changes of the PbI₂ secondary phase need to be considered.^23–25 The PbI₂ possesses a relatively large band gap (E_g ≈ 2.3 eV (ref. 26)) that is not suitable for photovoltaic applications.²⁷ In addition, light-induced degradation of PbI₂ is also considered detrimental to the overall stability and performance of the device.^28,29 However, some reports also discuss the potential benefits of excess PbI₂ in solar cell absorbers. Possible reasons include type I band alignment between the PbI₂ layer and the transport layer, creating a barrier for electrons toward the hole transport layer (HTL) and passivation of the grain boundaries, which reduces band bending at the grain boundaries.^30–39

A detailed microscopic picture of how different annealing atmospheres impact the surface properties and grain boundaries of perovskite absorbers and their interaction with the PbI₂ secondary phase is not available. In the following study, perovskite absorbers annealed in three different environments (N₂, O₂, and air) will be discussed. We focus on the annealing process directly after the spin coating, where solvent evaporation and recrystallization takes place.

In this work, we will show how different atmospheres change the amount of excess PbI₂ on the surface. We will discuss changes at grain boundaries and correlate the microscopic analysis, carried out by atomic force microscopy and secondary ion mass spectrometry, with photoluminescence-based techniques. This will allow us to link the changes at the surface to the carrier lifetimes, photoluminescence quantum yields, and absorber doping. Finally, the absorber properties will be compared with the device efficiencies, and we will use drift diffusion simulations to better understand the results.

We show that changes in grain boundary band bending are not likely to be responsible for the changes in power conversion efficiency. However, the amount of PbI₂ varied. We found the best optoelectronic quality for the lowest amount of PbI₂ in the perovskite absorbers. However, devices with more PbI₂ perform slightly better. We relate this to changes in the interface quality between the hole extraction layer and the perovskite. This will be discussed with the help of drift-diffusion simulations.

1 Experimental methods

The device with an architecture of FTO glass/compact TiO₂ layer (c-TiO₂)/compact SnO₂ layer (c-SnO₂)/Cs_0.05MA_0.05FA_0.9PbI₃ (PVK)/spiro-OMeTAD (HTM)/Au structure was fabricated. The patterned FTO substrate (Asahi FTO glass, 12–13 Ω per square) was sequentially cleaned with detergent (5% Hellmanex in water), deionized water, acetone and isopropanol in an ultrasonic bath for 30 min each. The FTO substrate was then further cleaned with ultraviolet-ozone surface treatment for 15 min. The compact TiO₂ layer (c-TiO₂) and the SnO₂ layer were sequentially deposited on the clean FTO substrate by the chemical bath deposition (CBD) method.⁴⁰ The substrate was annealed on a hotplate at 190 °C for 60 min.

The perovskite precursor solution (1.4 M) was prepared by adding 645.4 mg of PbI₂, 216.7 mg of formamidium iodide (FAI), 11.1 mg of methylammonium iodide (MAI), 11.8 mg of CsCl, and 33.1 mg of MACl into 200 μL of N,N′-dimethylsulfoxide (DMSO) and 800 μL of dimethylformamide (DMF) mixture. After UV ozone treatment of the substrates for 15 min, the perovskite precursor solution was spin coated on the surface of the FTO/c-TiO₂/c-SnO₂ substrate at 1000 rpm for 10 s, accelerated to 5000 rpm for 5 s, and maintained at this speed for 20 s. This process was carried out in an N₂-filled glovebox. The substrate was then placed on home-made rapid vacuum drying equipment, as previously reported.⁴¹ After pumping for 20 s, a brown, transparent perovskite film with a mirror-like surface was obtained. The fresh perovskite layer was annealed at 100 °C for 1 h and then at 150 °C for 10 min in N₂, O₂, or air atmosphere. Afterwards, 60 μL of PEAI solution (5 mg mL⁻¹ in isopropanol) was spin-coated on the perovskite film at 5000 rpm for 30 s. A hole transport layer was deposited on the perovskite film by depositing a doped spiro-OMeTAD solution at 3000 rpm for 30 s. The doped spiro-OMeTAD solution was prepared by dissolving 105 mg of spiro-OMeTAD and 41 μL of 4-tert-butylpyridine in 1343 μL of chlorobenzene with an additional 25 μL of bis(trifluoromethane)sulfonimide lithium salt solution (517 mg mL⁻¹ in acetonitrile) and 19 μL of cobalt-complex solution (376 mg mL⁻¹ in acetonitrile). Finally, a ∼70 nm-thick gold layer was evaporated on the spiro-OMeTAD layer as the back electrode.

The characterization of the grain structure and the grain boundaries was performed with an atomic force microscope. The topography was acquired in amplitude modulation (AM-mode) while the KPFM was performed using frequency modulation (FM-mode, side band excitation) based on reports from the literature showing that FM-KPFM yield more reliable results.^42,43 The topography and work function maps were acquired in a single-pass mode. To translate the contact potential difference between the tip and the sample into a work function, the tip work function was calibrated with a reference sample (highly oriented pyrolytic graphite, work function: 4.6 eV). All measurements were performed under ambient pressure in a nitrogen-filled box. During the measurements or the transfer process, the samples were not exposed to ambient conditions.

The nanometric distribution of elements on the surface of perovskite was determined by using a Helium Ion Microscope (HIM) coupled with a Secondary Ion Mass Spectrometer (SIMS).⁴⁴ HIM-SIMS analyzes were performed using a 25 keV neon beam with a current of 4 pA to scan a surface area of 8 × 8 μm², achieving a spatial resolution below 20 nm. Positive and negative ions were successively recorded in a 512 × 512 pixel matrix with a dwell time of 1.5 ms per pixel (≈6 minutes per acquisition). The SIMS images are used to determine the homogeneity in composition within the grains and grain boundaries, including the depletion or excess of the signal intensity of ions of interest.

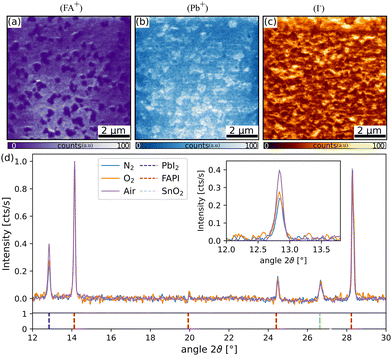
To study the crystalline structure of the films and confirm the presence of secondary phases, X-ray diffraction (XRD) measurements were performed in a Bruker D8 diffractometer with a θ–2θ Bragg–Brentano configuration. The CuK_α X-ray source was set to 40 kV and 40 mA with a 8 mm fixed slit. The integration time was 1 s with a step size of 2θ = 0.02θ.

Absolute Photoluminescence (PL) measurements were conducted at room temperature (here 295 K) under ∼1 sun incident photon flux density. The temperature was independently measured with a thermometer. A blue laser with a wavelength of 405 nm and a beam diameter of ∼1.5 mm was used to excite the samples. The PL signal was collected using two off-axis parabolic mirrors and then directed through optical fiber into a spectrometer where it was detected by a Si detector. Subsequently, a commercially available halogen lamp with a known spectrum was employed to spectrally correct the PL spectrum.

The quasi-Fermi level splitting (QFLs) of the absorbers was deduced from the measured photoluminescence quantum yield (Q^lum_e) defined as the ratio of emitted photon flux over incident photon flux (considering the assumption that the absorbance is 1). The QFLs and Q^lum_e are related via:

QFLs = QFLs^rad + k_BT ln(Q^lum_e) (1)

Here QFLs^rad is the radiative limit of the semiconductor, k_B the Boltzmann constant, and T the temperature. In the idealised case where the solar cell shows the step-like absorptance (A(E)) spectrum, the QFLS^rad is equal to the Shockley–Queisser (SQ) voltage limit (qV^SQ_OC). However, real solar cells do not exhibit a step-like A(E) spectrum, leading to a QFLS^rad that is lower than the qV^SQ_OC.

Generally, the extraction of QFLS^rad requires exact knowledge of the A(E) spectrum. Nevertheless, one can use the maximum photoluminescence (PL) emission energy as a radiative band gap in simplified cases. The QFLS^rad can then be estimated with the SQ limit (qV^SQ_OC) of the corresponding radiative band gap. For the present case, this approach was well justified, since the broadening of the absorption onset was around 30 meV. More details are explained in ref. 45. All three absorber types exhibited low Urbach energies (≈12 meV), indicating low sub-bandgap absorption. The Urbach energies and the broadening of the absorption onset can be found in ESI Fig. 8.†

Finally, drift-diffusion simulations were performed with the SCAPS⁴⁶ version (3.3.11). All parameters relevant to the simulations are described in the main body of the manuscript or can be found in Table 1 in the ESI.†

2 Results and discussion

Fig. 1 shows the AFM and KPFM measurements obtained from the different types of samples, namely N₂ annealed samples (Fig. 1(a and b)), O₂ annealed samples (Fig. 1(c and d)) and air annealed samples (Fig. 1(e and f)). All three annealing routines resulted in absorbers with grain sizes in the micrometer range. Slightly enlarged grains for the case of air annealing compared to the other two cases were measured. The grains in the air-annealed sample averaged 738 ± 148 nm, while the O₂-annealed and N₂-annealed samples averaged 625 ± 146 nm and 596 ± 106 nm, respectively. The air annealed samples showed slightly enlarged roughness compared to the other two sample types (RMS roughness; air annealing: 36 nm, O₂ annealing: 27 nm and N₂ annealing: 29 nm).

Fig. 1 (a), (c) and (e) AFM topography images of the three absorbers annealed in N₂, O₂ and air. (b), (d) and (f) Work function maps of the same absorbers at the identical positions shown in (a), (c) and (e). The absolute scales vary but the range (0.3 eV) is identical for the three cases. (g) Work function distributions deduced from the three images presented in (b), (d) and (f). Dashed lines show a fit to the main and secondary work function. Inset: mean work function value of the main and secondary work function. (h) Surface coverage in % of secondary phase measured in multiple AFM and KPFM images. (i) Grain boundary band bending measured for the three different absorber types. The band bending is always relative to the mean value of the adjacent grains.

Work function maps acquired on the three different sample types show significant differences. For the N₂ and O₂ cases, regions of reduced work functions (dark spots in Fig. 1(b and d)) were observed. These regions were linked to specific grains in the topography images (see ESI Fig. 1,† which shows an overlay of some low work function regions with the sample topography). The situation was different for the air annealed case, where most of the low work function areas were gone and a lot of high work function areas could be found.

Work function distributions of the three sample types are presented in Fig. 1(g). The first observation was that the average work function of the three samples was different. An average work function of 4.55 eV was measured for the N₂ case, 4.7 eV for the O₂ annealed case, and 4.9 eV for the air annealed case. The error bar is estimated to be ±100 meV.⁴⁷

In all three cases, an additional prominent work function was detected as a shoulder in the histograms, which was consistent with the KPFM images. The work function of this secondary phase was lower than the average perovskite value for the N₂ and O₂ cases and higher for the air annealing, as shown in the inset of Fig. 1(g).

In that sense, the three different sample types showed at least one secondary phase, whose chemical nature is still to be determined. Previously, high-work function areas were assigned to PbI₂,^29,48 which is known to have a high work function value.⁴⁹ The strongly reduced values of the secondary phase for O₂ and N₂ annealed samples were puzzling, and a straightforward allocation to PbI₂ must be well justified and will be addressed in the following.

In addition to the secondary phase, the work function of the perovskite also changed. The lowest value was measured for the samples that did not see oxygen or air. In the literature, oxygen incorporation has been reported to lead to p-doping in methylammonium triiodide, which could be reduced again by prolonged vacuum exposure.⁵⁰ In that study, the perovskite films that did not contain oxygen behaved like intrinsic semiconductors. Consequently, for the present case, higher values of the work function for the air and oxygen cases could be expected because of oxygen-induced p-doping, which shifts the Fermi level closer to the valence band. The magnitude of the shift in work function would be determined by the amount of oxygen incorporated. From the KPFM measurements, one could infer that the doping increase was greater for the air-annealed case compared to the O₂ case. As will be discussed later, the increase was very similar. Furthermore, the oxygen and air annealed samples changed the secondary phase in a different way. There are two possibilities to interpret the results. Either the secondary phase was different for air compared to oxygen and N₂ or the moisture changes the properties of the secondary phase, which led to a different work function.

In the following, the total surface coverage of the secondary phase was measured with the help of the KPFM images, independent of whether the work functions were lower or higher. The results are shown for the three types of samples in Fig. 1(h) and the highest amount of secondary phase was present on the surface of the air-annealed sample, while the minimum values were derived for the N₂ samples. This amount will be compared with SIMS mapping results in the following paragraphs to make an unambiguous assignment. Importantly, Fig. 1(h) showed that despite the identical composition of the precursor, the amount of the secondary phase was different for the different annealing routines.

Finally, the band bending at the grain boundaries was analyzed (ESI Fig. 2† for a detailed explanation) for the three different cases (Fig. 1(i)). In all three cases, low band bending values were measured that spread between +40 meV and −50 meV. The average values in all three cases were below the thermal energy (≈26 meV) and unchanged within the error bar. Any band bending values below 10 meV were considered a neutral GB, as this falls within the limitations of the KPFM measurements. The results were in agreement with previous measurements carried out in ultra-high vacuum.⁴⁸ The distributions of the upward, downward and neutral GBs were different for the three cases. Most grain boundaries showed negligible band bending for the N₂ case and the O₂ annealed samples, as evident from the share of neutral grain boundaries given for each case in (Fig. 1(i)). The air annealed samples exhibited a large number of grain boundaries with downward band bending. The small changes in the band bending values needed to be treated with care as they were close to the resolution limit of the techniques (±10 meV).⁵¹ The only trend that could be trusted was the higher fraction of grain boundaries with small downward bending for the air-annealed case compared to the two other sample types.

Simulations have shown that band bending at the grain boundaries is not beneficial to device performance.^52,53 Although downward band bending would favor electron accumulation and hole repulsion at the grain boundaries, leading to higher current densities, the open-circuit voltage would be reduced. In the present case, the absolute values of the band bending are too small to be relevant to the performance of the device at room temperature. We therefore conclude that changes in grain boundary properties are not important in the present study.

To shed more light on the chemical nature and evolution of the secondary phases, HIM-SIMS measurements were performed for the three types of samples. In Fig. 2(a–c) nanometer-resolved SIMS maps of an air-annealed sample are depicted, while the results for the other two sample types can be found in the ESI Fig. 3.† In Fig. 2(a) the lateral variation in FA is shown. Fig. 2(b) (blue) shows the distribution map of Pb and in Fig. 2(c) (orange) the variation in iodine is shown. The color coding of each image is normalized, since we discuss changes in relative intensity across the surface only. The FA and Pb signals were strongly anticorrelated (ESI Fig. 5†), which meant that regions with FA depletion showed a lot of Pb. The same anticorrelation was found for Cs and Pb (ESI Fig. 4†). In agreement with previous reports,^29,48 the lack of FA or Cs combined with an increase in Pb is a strong hint at PbI₂. When the three different sample types were compared, no indication of other phases could be detected. The samples annealed in N₂ or O₂ exhibited very similar distribution maps as presented in Fig. 2. In all cases, an anticorrelation of FA and Pb was found. The lateral variations in the iodine signal were difficult to interpret and no correlation was found. The only change observed was a decrease in the signal for the air-annealed sample, compared to N₂. This hinted at a more iodine-depleted surface region. However, since SIMS is not quantitative, these measurements can only be considered indicative. The oxygen signal was close to the resolution limit for all three samples.

Fig. 2 Elemental variations on the surface of an air annealed sample, acquired with HIM-SIMS. (a) Elemental distribution of FA⁺ ions, (b) Pb⁺ ions, and (c) I⁻. (d) XRD spectra of the three different sample types. Dashed blue lines correspond to PbI₂ reflections, dashed red corresponds to FAPI reflections and green corresponds to the SnO₂ substrate. The XRD spectra are normalized to the highest FAPI peak. The inset shows the changes in the PbI₂ (001) peak intensity.

For the SIMS data, we could conclude that the secondary phase was PbI₂ in all three cases since we did not observe FA and Cs ions in the regions of the highest Pb. The surface coverage of secondary phases (PbI₂) can be calculated from SIMS and can then be compared to the measurements done with the KPFM. The surface coverage of PbI₂ deduced from SIMS increased from N₂ to O₂ to air, which was in agreement with the AFM and KPFM data presented in Fig. 1(h) where the coverage of the secondary phases increased from N₂ to O₂ and reached a maximum for the air-annealed samples. The good correlation between SIMS and KPFM allowed us to conclude that the secondary phase was PbI₂ in all three cases although the work functions were different for the three different annealings. The increase in PbI₂ for the air-annealed sample would also be in line with higher losses of iodine, as suggested by the SIMS maps of I⁻.

XRD measurements were performed for the three different types of samples and the results are shown in Fig. 2(d). All peaks could be assigned to FAPI (ICDD: 01-073-1752), PbI₂ (ICDD: 07-0235) or the substrate (fluorine-doped SnO₂ ⁵⁴). The only difference between the samples was the height of the PbI₂ peak at a 2θ = 12.8θ with respect to FAPI reflections. This finding was in agreement with the AFM and SIMS measurements, which suggested lower amounts of PbI₂ for N₂ and a higher amount of PbI₂ for the air annealed case. No peak shifts in the perovskite or in the height of the substrate signal were observed, which showed that the different annealing environments did not induce differences in the perovskite composition or crystal quality.

The SIMS maps and the XRD peaks corroborated the existence of PbI₂ and especially the high-resolution chemical mapping did not show any other secondary phase. Consequently, the different work functions, found for the secondary phase in KPFM shown in Fig. 1 could all be assigned to PbI₂. However, the different annealing conditions did change the PbI₂ to a certain degree, since different work functions were measured. A possible explanation could be that oxidation or the nature and quantity of iodine vacancies can shift the Fermi level, which can directly impact the work function of perovskite/PbI₂.⁴⁹

In the next step, the optical properties were measured via steady-state photoluminescence, and time-resolved photoluminescence. In Fig. 3(a) steady-state absolute photoluminescence spectra are depicted for the three different sample types. The curves displayed are averages of six different spots chosen randomly on one absorber. The samples annealed in N₂ exhibited the highest PL yield, while the oxygen annealed one was approximately a factor of two lower. The PL yield of the air-annealed sample was in between the two other sample types. PL spectra were used to derive the quasi-Fermi level spitting of the three absorbers,⁵⁶ which are shown in Fig. 3(b). Values close to 1.16 eV were measured for the N₂ case, while the oxygen values were approximately 20 meV lower. The air annealed sample exhibited values close to 1.15 eV. The QFLs values were compared to the measured V_OC of the devices (JV-curves of the devices can be found in the ESI Fig. 9†). Open circuit voltages of 1.12 eV were measured for the N₂ case, which were approximately 40 meV lower than the QFLs. The difference between QFLs and V_OC was reduced for the O₂ case, whereas it was within the error bar for air annealed samples. This showed that the sample with the best optoelectronic quality, namely the one annealed in N₂ did not lead to the best devices and there was another active recombination channel, which reduced V_OC.^55,57

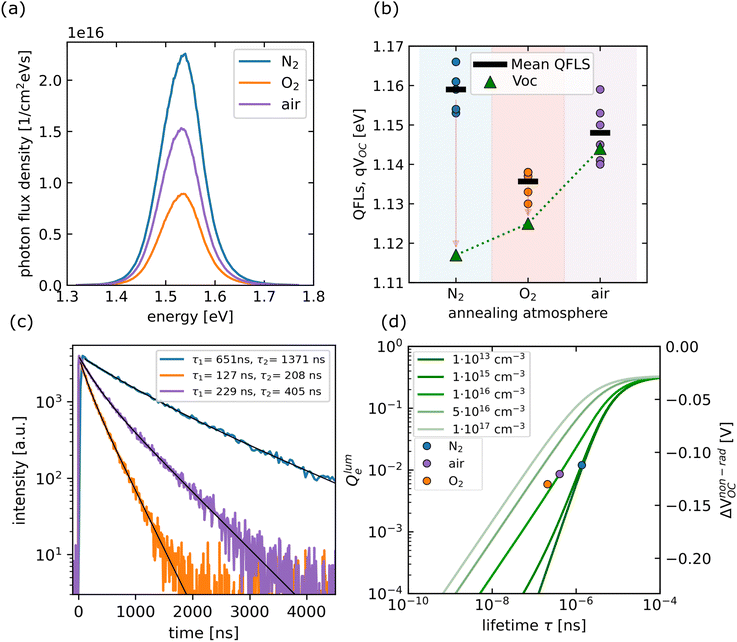Fig. 3 (a) Absolute Photoluminescence measurements for the three sample types denoted as N₂, O₂, and air (the spectra are averages of six different spots). (b) Quasi-Fermi level splitting of the absorber layers and a comparison to the measured V_OCs of the devices. The arrows indicate the losses from the absorber to the final devices. (c) Time-resolved photoluminescence measurements were carried out on the three absorbers (black line is fitted) representing τ₁ and τ₂ lifetime values (ns) in the legend. (d) Doping level deduced from the TRPL lifetime values with the formalism discussed in ref. 55. Green lines represent doping densities, with lighter shades indicating higher densities and vice versa. The N₂ annealed samples could be considered as intrinsic whereas the air and O₂ annealed absorbers exhibited a doping level in the order of 10¹⁶ cm⁻³.

The three sample types were further analyzed with TRPL to better understand the carrier dynamics in the films. For the three cases, the transients could be fitted with bi-exponential decays as shown in Fig. 3(c). A detailed comparison of bi-exponential and single exponential decay can be found in ESI Fig. 7 and eqn (3).† The longest decay times were measured on samples annealed in N₂, while the fastest decays were found for the O₂ case, in agreement with the steady-state PL results. In analogy to steady-state measurements (Fig. 3(a)), the data for the air-annealed samples were between the two other cases.

In the following, the values of τ₂ are used as they are closer to the characteristic SRH minority carrier lifetime.⁵⁸ As discussed in ESI Fig. 6 and eqn (1), (2),† the decay times deduced from TRPL measurements are always a convolution of bulk- and surface-related recombination rates. The deduced decay time is therefore an effective lifetime, which accounts for both terms. For the N₂ annealed case, where a τ₂ value of approximately 1.3 μs was measured the surface recombination velocity must be less than 1 cm s⁻¹, assuming that only the exposed surface contributes to the recombination.

The values for the oxygen-annealed samples were six times lower than those of the air-annealed case. Since QFLs and decay times are linked via the doping level, as discussed in⁵⁵ the same method was used to compare the PL quantum yields, the decay times and non-radiative losses of the three types of absorbers (eqn (4) and (6) in ESI†). From this analysis, the doping level increased from N₂ to air to O₂. This is shown in Fig. 3(d) where the measured lifetime values are plotted against the measured Q^lum_e-values on a double logarithmic plot. The green lines show how the two quantities are linked with the doping level (varying from 1 × 10¹³ cm⁻³ to 1 × 10¹⁷ cm⁻³). The plot clearly shows that the samples annealed in oxygen and air exhibit a higher doping level than those annealed in N₂.

The plot also shows that the doping level for the N₂ annealed films was subject to large error bars (darker green lines are overlapping in Fig. 3(d) although the doping level changed by two orders of magnitude). The important point of this analysis was that the doping level of the perovskite absorbers was affected by the annealing atmosphere and the lowest background doping (probably intrinsic) was found for the case of N₂. Shin et al.⁵⁹ conducted a study in which perovskite absorbers were exposed to two different environments: N₂ and air. The study concluded that the absorber prepared in an inert N₂ atmosphere exhibited a very low intrinsic doping level and a negligible surface state density. In contrast, the sample prepared under ambient conditions showed a strong p-type character. DFT calculations revealed that the observed increase in p-doping was due to native iodine vacancies⁶⁰ being replaced by oxygen molecules. This substitution led to a rise in the sample's work function as the Fermi level shifted towards the valence band. Additionally, oxygen incorporation irreversibly reduces metallic lead-related surface states, thus facilitating surface defect passivation. Oxygen also removes secondary phases or surface states associated with metallic lead, further aiding in surface defect passivation. The doping level variations in this study were in accordance with the results of the AFM/KPFM data discussed previously where an increase in work function was found for O₂ and air annealed samples compared to the N₂ annealed ones. The optical analysis was therefore qualitatively in agreement with the KPFM data. However, as already stated, the work function was also influenced by other factors, and therefore a quantitative comparison between the doping level increase and the changes in work function is not necessarily meaningful. In the present case, the doping level analysis would suggest that the work function of O₂ and air would be very similar. However, we found a higher value for air compared to O₂. The exact reason is not yet clear. One possible explanation could be the different concentrations of iodine that were measured by SIMS, which would certainly have an impact on the charge distribution on the surface and thereby also on the work function.

Combining the results of AFM/KPFM, HIM-SIMS, and PL showed that an increase in PbI₂ was not beneficial for the absorber properties. The samples with the lowest amount of secondary phase (the N₂ annealed one) exhibited the highest QFLs and the longest PL decay times. This showed that the oxygen free perovskite bulk and/or surface had the lowest defect density. However, after device fabrication, the high QFLs values could not be retained and a reduced V_OC was found. The cause of this decrease had to be linked to the interface of the extraction layer on top of the perovskite. In particular, air-annealed samples did not show a drop of V_OC compared to QFLs, which meant that in that case the quality of the interface was preserved. A possible explanation could be that the deposition of Spiro-OMeTAD deteriorated the interface for the N₂ case, while it affected the surface of the air annealed samples in a less drastic manner.

In order to see whether the solar cell parameters can be reproduced with a slightly worse interface in the case of N₂ annealed vs. air annealed, drift diffusion simulations were carried out with the “SCAPS” program.⁴⁶ In the following, the most important parameter variations will be discussed. All parameters used in the simulations can be found in the ESI.†

Fig. 4(a) shows the band diagram (at V_OC) of the perovskite solar cell structure used in the study. A comparison of the band diagram under illumination and under dark conditions can be found in ESI Fig. 11.† The electron extraction layer was FTO and Spiro-OMeTAD was used as a hole extraction layer. The band alignment is dictated by the electron affinities E_A and the interface band gaps of the materials. For the perovskite absorber E_A = 3.9 eV (ref. 61) and E_g = 1.54 eV (from PL peak position and ref. 48) were used while for the Spiro-OMeTAD E_A = 2.2 eV and E_g = 2.9 eV (ref. 62 and 63) were introduced as starting parameters. As discussed in⁶² the Spiro-OMeTAD properties depend on the processing conditions and doping. As a consequence, the values in the literature scatter significantly, and a variation of E_A will be discussed in the next paragraphs. The FTO and perovskite conduction bands were aligned, which meant that E_A,FTO = E_A,pero.

Fig. 4 (a) Simulated band diagram of the perovskite solar cell used in this study. The diagram shown was acquired at V_OC. (b) Simulated V_OCversus surface recombination velocity at the perovskite/Spiro-OMeTAD interface (blue). The J_SC is not impacted by the variation. (c) V_OC as a function of the Spiro-OMeTAD electron affinity, for a constant interface recombination velocity.

In Fig. 4(a) the blue and red curves depict the electron and hole quasi-Fermi levels. For the chosen parameters, the valence band position of the perovskite and the HOMO level of the Spiro-OMeTAD resulted in a cliff-like offset (no barrier for holes), which is known to make the interface very sensitive to defects.⁶⁴

Fig. 4(b) illustrates how a cliff-like offset at the interface between the perovskite and Spiro-OMeTAD affected V_OC and J_SC. The bulk properties of the perovskite were fixed (minority carrier lifetime: 1300 ns, as for the N₂ case). The highest V_OC achieved for this set of simulations was 1.14 eV. To achieve such values in the simulation, the interface recombination velocity for electrons and holes S_n,p at the Spiro-OMeTAD/perovskite had to be set to approximately 1 cm s⁻¹. These values are in agreement with other reported perovskite values⁶⁵ and with the estimation of S_n,p from our TRPL measurements (see Fig. 7 in the ESI†). Varying S_n,p by only a factor of two changed V_OC by more than 20 mV, which highlighted that small changes at the interface were sufficient to reproduce the results of the solar cells observed in this study. The J_SC values did not change for this set of simulations, which is expected since there was no barrier for holes at the hole extraction layer and no barrier for electrons at the electron extraction layer. A comparison between the dependence of V_OC and QFLs for a larger range of S_n,p can be found in the ESI Fig. 10.†

In addition to the strong dependence of V_OC on S_n,p, the electron affinity of the Spiro-OMeTAD was important. Reduction of E_A,spiro with respect to E_A,pero further deteriorated V_OC as shown in Fig. 4(b and c) On the other hand, an increase in E_A,spiro, was beneficial to device properties. As soon as the cliff-like offset in the valence band was removed, the properties of the device became independent of S_n,p, which is very beneficial for the devices.

The impact of doping was checked because the combination of PLQY and TRPL suggested that air and oxygen annealing increased doping from intrinsic to approximately 1 × 10¹⁶ cm⁻³. Consistent with⁵⁵ the increase in bulk doping did not lead to a significant variation in simulated V_OC to values of 5 × 10¹⁵ cm⁻³. Beyond this point, a slight increase for p-doping was observed, whereas n-doping reduced V_OC. For a p-doping of 1 × 10¹⁶ cm⁻³, the increase compared to an intrinsic semiconductor was only 5 mV in V_OC, which was too low to explain the changes observed experimentally, which meant that absorber doping was most probably not the dominant effect. The bulk lifetime of the perovskite absorber was also not responsible for the observed changes, as the values were largest for the N₂ case, which exhibited the lowest V_OC.

The simulations then showed that for the device structure used in this study, the surface recombination velocity at the Spiro-OMeTAD/perovskite was the most crucial parameter because of the cliff-like valence band offset for the holes. The AFM and SIMS measurements showed that the amount of PbI₂ increased for the case of air-annealed samples. Since PbI₂ is known to form spikes in the conduction band and valence band, leading to blocking of both the electron and hole in the hole extraction layer,^38,66,67 an increase in the amount of PbI₂ may explain the results presented here very well. The area covered with PbI₂ would be inactive for additional recombinations, which would reduce the effective defect density. As a consequence, V_OC would slightly increase for the PbI₂ rich film, compared to the PbI₂ poor film. The current density is likely not to be affected by the PbI₂ since these regions are only several hundred nanometers in size, which allows carriers to diffuse to regions where the surface was not covered with PbI₂.

3 Conclusions

In summary, the study shows that better solar cell performance is not always a result of better absorber properties. The perovskite films produced via an air annealing step resulted in solar cells exceeding 25%, while the absorbers annealed in N₂ and O₂ showed lower efficiencies. We found that the excess PbI₂ was the highest for air-annealed samples. However, optical analysis showed that this was not beneficial for the perovskite absorber itself, as lower QFLs and faster decay times were measured.

In a solar cell, the absorbers are in contact with the extraction layers. It turns out for the present case where Spiro-OMeTAD was used as a hole extraction layer that the surface recombination velocity was the most important parameter that dictated the V_OC. A increased amount of PbI₂ reduces the effective defect density and therefore solar cells become more efficient. However, it should be taken into account that PbI₂ will reduce the long-term stability of the devices, which nullifies the short-term beneficial effect.²⁹

In literature, different annealing atmospheres are often linked to changes in grain boundaries. Despite the fact that we do see subtle changes in grain boundary band bending, it seems unlikely that these changes are responsible for the better performance of air annealed samples. Especially since we find slightly more band bending for air-annealed compared to the other sample types. The grain size did not change much, which rules out that this may have a significant impact on the device properties.

This work clearly shows that the path to even higher performance is to minimize the PbI₂ segregation while maintaining high absorber quality and low surface defect densities.²⁹ The hole extraction layer needs to be fine-tuned to exhibit a small spike for the holes at the valence band. This value needs to be high enough to reduce interface recombination but low enough to allow thermionic emission of the holes into the extraction layer.

Author contributions

M.U.F.: writing original draft, editing, methodology, AFM/KPFM, analysis and compiling of the data, review. S.G.: PL investigation, analysis and writing. D.Y.: absorber/device fabrication, device characterization, writing, review. J.F.M: XRD acquisition, analysis, writing, review. J.N.A.: HIM-SIMS analysis & writing, review. T.W.: writing – review. M.K.N.: writing – review. S.S.: PL, writing – review & editing. A.R.: writing, review, programming for PL/TRPL/doping densities, SCAPS, writing original draft.

Data availability

All the data can be found in either the main or ESI.† Additional raw data can be provided upon request to the author.

Conflicts of interest

The author/co-authors show no conflict of interest.

Acknowledgements

Financial support from the Fonds National de la Recherche (FNR) in the framework of the projects C20/MS/14735144 and INTER/DFG/18/13390539 are acknowledged. For the purpose of open access, the author has applied a Creative Commons Attribution 4.0 International (CC BY 4.0) license to any Author Accepted Manuscript version arising from this submission. The authors acknowledge technical support by B. Uder, U. Siegel, and R. Himelrick. Useful discussions with E. M. Lanzoni are acknowledged.

References

1. H. Wang and D. H. Kim, Chem. Soc. Rev., 2017, 46, 5204–5236.
2. N. Pellet, P. Gao, G. Gregori, T.-Y. Yang, M. K. Nazeeruddin, J. Maier and M. Grätzel, Angew. Chem., Int. Ed., 2014, 53, 3151–3157.
3. M. A. Green, E. D. Dunlop, M. Yoshita, N. Kopidakis, K. Bothe, G. Siefer, D. Hinken, M. Rauer, J. Hohl-Ebinger and X. Hao, Prog. Photovoltaics: Res. Appl., 2024, 32, 425–441.
4. E. J. Juarez-Perez, Z. Hawash, S. R. Raga, L. K. Ono and Y. Qi, Energy Environ. Sci., 2016, 9, 3406–3410.
5. J. Yang, B. D. Siempelkamp, D. Liu and T. L. Kelly, ACS Nano, 2015, 9, 1955–1963.
6. E. Smecca, Y. Numata, I. Deretzis, G. Pellegrino, S. Boninelli, T. Miyasaka, A. La Magna and A. Alberti, Phys. Chem. Chem. Phys., 2016, 18, 13413–13422.
7. N. Zhou, Y. Shen, Y. Zhang, Z. Xu, G. Zheng, L. Li, Q. Chen and H. Zhou, Small, 2017, 13, 1700484.
8. T. Duong, Y. Wu, H. Shen, J. Peng, X. Fu, D. Jacobs, E.-C. Wang, T. C. Kho, K. C. Fong and M. Stocks, et al. , Adv. Energy Mater., 2017, 7, 1700228.
9. J.-W. Lee, D.-H. Kim, H.-S. Kim, S.-W. Seo, S. M. Cho and N.-G. Park, Adv. Energy Mater., 2015, 5, 1501310.
10. M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate and A. Hagfeldt, et al. , Energy Environ. Sci., 2016, 9, 1989–1997.
11. C. Wang, C. Zhang, S. Wang, G. Liu, H. Xia, S. Tong, J. He, D. Niu, C. Zhou and K. Ding, et al. , Sol. RRL, 2018, 2, 1700209.
12. T. Singh and T. Miyasaka, Adv. Energy Mater., 2018, 8, 1700677.
13. Z. Li, M. Yang, J.-S. Park, S.-H. Wei, J. J. Berry and K. Zhu, Chem. Mater., 2016, 28, 284–292.
14. Y. Zhang, S. Seo, S. Y. Lim, Y. Kim, S.-G. Kim, D.-K. Lee, S.-H. Lee, H. Shin, H. Cheong and N.-G. Park, ACS Energy Lett., 2020, 5, 360–366.
15. G. Kim, H. Min, K. S. Lee, D. Y. Lee, S. M. Yoon and S. I. Seok, Science, 2020, 370, 108–112.
16. X. Zhou, C. Xin, F. Hou, B. Shi, S. Pan, S. Hou, J. Zhang, P. Wang, H. Ren and Y. Zhao, et al. , ACS Sustainable Chem. Eng., 2019, 7, 17691–17696.
17. K. Meng, C. Wang, Z. Qiao, Y. Zhai, R. Yu, N. Liu, R. Gao, B. Chen, L. Pan and M. Xiao, et al. , Small, 2021, 17, 2104165.
18. K. Sveinbjörnsson, N. K. K. Thein, Z. Saki, S. Svanström, W. Yang, U. B. Cappel, H. Rensmo, G. Boschloo, K. Aitola and E. M. Johansson, Sustainable Energy Fuels, 2018, 2, 606–615.
19. X. Li, G. Wu, M. Wang, B. Yu, J. Zhou, B. Wang, X. Zhang, H. Xia, S. Yue and K. Wang, et al. , Adv. Energy Mater., 2020, 10, 2001832.
20. W. Zhang, J. Xiong, J. Li and W. A. Daoud, ACS Appl. Mater. Interfaces, 2019, 11, 12699–12708.
21. J. M. Howard, K. J. Palm, Q. Wang, E. Lee, A. Abate, J. N. Munday and M. S. Leite, Adv. Opt. Mater., 2021, 9, 2100710.
22. K. Liu, Y. Luo, Y. Jin, T. Liu, Y. Liang, L. Yang, P. Song, Z. Liu, C. Tian and L. Xie, et al. , Nat. Commun., 2022, 13, 4891.
23. K. Ho, M. Wei, E. H. Sargent and G. C. Walker, ACS Energy Lett., 2021, 6, 934–940.
24. S. J. Yoon, M. Kuno and P. V. Kamat, ACS Energy Lett., 2017, 2, 1507–1514.
25. J. Hidalgo, C. A. Perini, A.-F. Castro-Mendez, D. Jones, H. Koler, B. Lai, R. Li, S. Sun, A. Abate and J.-P. Correa-Baena, ACS Energy Lett., 2020, 5, 3526–3534.
26. A. F. D. Silva, N. Veissid, C. Y. An, I. Pepe, N. B. D. Oliveira and A. V. B. D. Silva, Appl. Phys. Lett., 1996, 69, 1930–1932.
27. A. P. Amalathas, L. Abelová, B. Conrad, B. Dzurňák, M. Ledinskýb and J. Holovský, 35th European Photovoltaic Solar Energy Conference and Exhibition, 2018, pp. 856–859.
28. Z. Hu, Q. An, H. Xiang, L. Aigouy, B. Sun, Y. Vaynzof and Z. Chen, ACS Appl. Mater. Interfaces, 2020, 12, 54824–54832.
29. J. Hieulle, A. Krishna, A. Boziki, J. N. Audinot, M. U. Farooq, J. F. Machado, M. Mladenović, H. Phirke, A. Singh, T. Wirtz, A. Tkatchenko, M. Graetzel, A. Hagfeldt and A. Redinger, Energy Environ. Sci., 2023, 17, 284–295.
30. J. Barbé, M. Newman, S. Lilliu, V. Kumar, H. K. H. Lee, C. Charbonneau, C. Rodenburg, D. Lidzey and W. C. Tsoi, J. Mater. Chem. A, 2018, 6, 23010–23018.
31. Y. Gao, H. Raza, Z. Zhang, W. Chen and Z. Liu, Adv. Funct. Mater., 2023, 2215171.
32. Q. Jiang, Z. Chu, P. Wang, X. Yang, H. Liu, Y. Wang, Z. Yin, J. Wu, X. Zhang and J. You, Adv. Mater., 2017, 29, 1703852.
33. C. Luo, Y. Zhao, X. Wang, F. Gao and Q. Zhao, Adv. Mater., 2021, 33, 2103231.
34. H.-Y. Wang, M.-Y. Hao, J. Han, M. Yu, Y. Qin, P. Zhang, Z.-X. Guo, X.-C. Ai and J.-P. Zhang, Chem. – Eur. J., 2017, 23, 3986–3992.
35. S. Wang, W. Dong, X. Fang, Q. Zhang, S. Zhou, Z. Deng, R. Tao, J. Shao, R. Xia and C. Song, et al. , Nanoscale, 2016, 8, 6600–6608.
36. D. H. Cao, C. C. Stoumpos, C. D. Malliakas, M. J. Katz, O. K. Farha, J. T. Hupp and M. G. Kanatzidis, APL Mater., 2014, 2, 091101.
37. F. Jiang, Y. Rong, H. Liu, T. Liu, L. Mao, W. Meng, F. Qin, Y. Jiang, B. Luo and S. Xiong, et al. , Adv. Funct. Mater., 2016, 26, 8119–8127.
38. T. J. Jacobsson, J.-P. Correa-Baena, E. Halvani Anaraki, B. Philippe, S. D. Stranks, M. E. Bouduban, W. Tress, K. Schenk, J. Teuscher and J.-E. Moser, et al. , J. Am. Chem. Soc., 2016, 138, 10331–10343.
39. Y. Chen, Q. Meng, Y. Xiao, X. Zhang, J. Sun, C. B. Han, H. Gao, Y. Zhang, Y. Lu and H. Yan, ACS Appl. Mater. Interfaces, 2019, 11, 44101–44108.
40. B. Ding, S.-Y. Huang, Q.-Q. Chu, Y. Li, C.-X. Li, C.-J. Li and G.-J. Yang, J. Mater. Chem. A, 2018, 6, 10233–10242.
41. L.-L. Gao, L.-S. Liang, X.-X. Song, B. Ding, G.-J. Yang, B. Fan, C.-X. Li and C.-J. Li, J. Mater. Chem. A, 2016, 4, 3704–3710.
42. A. Axt, I. M. Hermes, V. W. Bergmann, N. Tausendpfund and S. A. Weber, Beilstein J. Nanotechnol., 2018, 9, 1809–1919.
43. E. M. Lanzoni, T. Gallet, C. Spindler, O. Ramírez, C. K. Boumenou, S. Siebentritt and A. Redinger, Nano Energy, 2021, 88, 106270.
44. J.-N. Audinot, P. Philipp, O. De Castro, A. Biesemeier, Q. H. Hoang and T. Wirtz, Rep. Prog. Phys., 2021, 84, 105901.
45. S. Siebentritt, U. Rau, S. Gharabeiki, T. P. Weiss, A. Prot, T. Wang, D. Adeleye, M. Drahem and A. Singh, Faraday Discuss., 2022, 239, 112–129.
46. M. Burgelman, P. Nollet and S. Degrave, Thin Solid Films, 2000, 361, 527–532.
47. M. M. Beerbom, B. Lägel, A. J. Cascio, B. V. Doran and R. Schlaf, J. Electron Spectrosc. Relat. Phenom., 2006, 152, 12–17.
48. Y. Ding, B. Ding, H. Kanda, O. J. Usiobo, T. Gallet, Z. Yang, Y. Liu, H. Huang, J. Sheng, C. Liu, Y. Yang, V. I. E. Queloz, X. Zhang, J. N. Audinot, A. Redinger, W. Dang, E. Mosconic, W. Luo, F. D. Angelis, M. Wang, P. Dörflinger, M. Armer, V. Schmid, R. Wang, K. G. Brooks, J. Wu, V. Dyakonov, G. Yang, S. Dai, P. J. Dyson and M. K. Nazeeruddin, Nat. Nanotechnol., 2022, 17, 598–605.
49. H. Chen, H. Yan and Y. Cai, Chem. Mater., 2022, 34, 1020–1029.
50. D. Shin, F. Zu, A. V. Cohen, Y. Yi, L. Kronik and N. Koch, Adv. Mater., 2021, 33, 2100211.
51. W. Melitz, J. Shen, A. C. Kummel and S. Lee, Surf. Sci. Rep., 2011, 66, 1–27.
52. M. Gloeckler, J. R. Sites and W. K. Metzger, J. Appl. Phys., 2005, 98, 113704.
53. K. Taretto and U. Rau, J. Appl. Phys., 2008, 103, 094523.
54. W. H. Baur, Über die Verfeinerung der Kristallstrukturbestimmung einiger Vertreter des Rutiltyps: TiO₂, SnO₂, GeO₂ und MgF₂, 1956.
55. T. Kirchartz, J. A. Márquez, M. Stolterfoht and T. Unold, Adv. Energy Mater., 2020, 10, 1904134.
56. D. Abou-Ras, T. Kirchartz and U. Rau, Advanced Characterization Techniques for Thin Film Solar Cells, Wiley-VCH, 2016.
57. M. Sood, A. Urbaniak, C. Kameni Boumenou, T. P. Weiss, H. Elanzeery, F. Babbe, F. Werner, M. Melchiorre and S. Siebentritt, Prog. Photovoltaics: Res. Appl., 2022, 30, 263–275.
58. R. K. Ahrenkiel and M. S. Lundstrom, in Minority-Carrier Lifetime in 111-V Semiconductors, 1993, vol. 39, pp. 39–150.
59. D. Shin, F. Zu, A. V. Cohen, Y. Yi, L. Kronik and N. Koch, Adv. Mater., 2021, 33, 2100211.
60. A. Senocrate and J. Maier, J. Am. Chem. Soc., 2019, 141, 8382–8396.
61. S. Prathapani, P. Bhargava and S. Mallick, Appl. Phys. Lett., 2018, 112, 092104.
62. Z. Hawash, L. K. Ono and Y. Qi, Recent Advances in Spiro-MeOTAD Hole Transport Material and Its Applications in Organic–Inorganic Halide Perovskite Solar Cells, 2018.
63. S. Karthick, S. Velumani and J. Bouclé, Sol. Energy, 2020, 205, 349–357.
64. M. Stolterfoht, P. Caprioglio, C. M. Wolff, J. A. Márquez, J. Nordmann, S. Zhang, D. Rothhardt, U. Hörmann, Y. Amir, A. Redinger, L. Kegelmann, F. Zu, S. Albrecht, N. Koch, T. Kirchartz, M. Saliba, T. Unold and D. Neher, Energy Environ. Sci., 2019, 12, 2778–2788.
65. F. Staub, H. Hempel, J.-C. Hebig, J. Mock, U. W. Paetzold, U. Rau, T. Unold and T. Kirchartz, Phys. Rev. Appl., 2016, 6, 044017.
66. Q. Chen, H. Zhou, T.-B. Song, S. Luo, Z. Hong, H.-S. Duan, L. Dou, Y. Liu and Y. Yang, Nano Lett., 2014, 14, 4158–4163.
67. H. Chen, H. Yan and Y. Cai, Chem. Mater., 2022, 34, 1020–1029.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04205k

---