Single atom alloys aggregation in the presence of ligands

Abstract

Single atom alloys (SAAs) have gained tremendous attention as promising materials with unique physicochemical properties, particularly in catalysis. The stability of SAAs relies on the formation of a single active dopant on the surface of a metal host, quantified by the surface segregation and aggregation energy. Previous studies have investigated the surface segregation of non-ligated and ligated SAAs to reveal the driving forces underlying such phenomena. In this work we address another key factor dictating the stability in non-ligated and ligated SAAs: the aggregation energy (E_agg) of dopants. Specifically, we examine how thiols and amines, commonly found ligands in colloidal bimetallic nanoparticle synthesis, affect the aggregation of dopants (forming dimers and trimers) on the surface of a metal host. Utilizing Density Functional Theory (DFT) and machine learning (ML), we explore the stability patterns of SAAs through the energetics of low-index surfaces, such as (111) and (100), consisting of d⁸-(Pt, Pd, Ni) and d⁹-(Ag, Au, Cu) metals, both in the presence and absence of ligands. Collecting rich and accurate DFT data, we developed a four-feature support vector regression using the radial basis function (SVR RBF) to predict the E_agg. The model revealed important and easily accessible (tabulated) thermodynamic stability features that drive metal aggregation in SAAs, such as the bulk cohesive energy of the metal considering the exposed coordination environment on the surface, the charge transfer represented by the difference in electron affinities of metals and the radii of the metals describing strain effects. Additional incorporated features include adsorbate properties, such as the binding energy of the ligand on a single atom considering the coordination environment of the adsorbate. Through our study, we have revealed that stable SAAs are formed in Ni-, Pd-, Pt-based SAAs in the presence of ligands, while Ag-, Au-, Cu- doped with Ni-, Pd-, Pt- lead to aggregation. Finally, we tested our model against several experimental studies and demonstrated its robustness in predicting the formation of SAAs, enabling rapid screening across the vast materials space of SAAs. Additionally, we suggest criteria for stabilization of SAAs, guiding experimental efforts. Overall, our study advances the understanding of thermodynamic stability of colloidal SAAs, paving the way for rational SAA design.

---

Introduction

Over the years, metal alloys have gained prominence in many applications,^1,2 particularly in catalysis, owing to their unique stability and catalytic activity and selectivity performance.³ Furthermore, due to the synergistic effect arising from the different metals, metal alloys have shown enhanced catalytic efficiency in a wide range of chemical reactions.⁴ As an example, a bimetallic AuPd catalyst was utilized in the synthesis of vinyl acetate. Pd served as the active component, while the inclusion of Au improved the stability of the catalyst by preventing sintering.⁵ However, traditional metal alloys suffer from inefficient atomic utilization as well as increased complexity due to the presence of multiple active sites.⁶ To tackle this challenge, there has been a transition to single-site catalysts due to their well-defined active sites.

Single atom alloys (SAAs), a class of single-site catalysts, merge the favorable characteristics of traditional alloys and single atom catalysts due to the presence of a more active atom doped on a more selective metal host, making them highly active in many catalytic reactions.^7,8 For instance, Kyriakou et al. observed that the presence of an isolated Pd dopant atom allowed for enhanced activity, while the presence of Cu led to higher selectivity towards the hydrogenation of styrene and acetylene.⁷ Another study demonstrated that the inclusion of Ru in Ni host improved both the activity and selectivity of 4-nitrostyrene hydrogenation to 4-aminostyrene.⁹ As a result, SAAs have emerged as promising catalytic architectures for a wide range of reactions.

The mixing behavior in SAAs is a crucial factor determined by the interaction between the host and dopant metals, which in turn affects their stability.⁸ Moreover, the stability of SAAs is described by the formation of a single dopant atom on the surface of the host metal. This is quantified by two energetic descriptors, the segregation and aggregation energy. Dopant segregation, which is the thermodynamic tendency of the dopant to reside on the surface of the catalyst, is influenced by several factors including, but not limited to, the radius, temperature, surface energy/cohesive energy, and the presence of adsorbates.^8,10 Furthermore, the binding strength between an adsorbate and the dopant can induce dopant segregation, reversing segregation behavior under vacuum conditions. For instance, reverse segregation has been observed in the cases of Pt-, Pd-, and Ni- doped on Ag, Au, and Cu metals when CO is introduced.^11,12 Conversely, segregation of Pt on Ag and Au (100) and (111) is not observed in the presence of hydrogen.¹³ Hence, understanding adsorbate-dopant interactions critical for efficient catalyst design.

Another factor affecting the stability of SAAs is the aggregation of dopants. It is the thermodynamic tendency to form a single dopant on the surface, as opposed to ensembles (such as dimers, trimers, or islands), which is described by the aggregation energy (E_agg).^11,12 Dopants that avoid aggregation in SAAs and form well-defined active sites can prevent the formation of coking. For instance, in the case of PtCu SAA, the Pt active site is responsible for activating C–H bond, while the Cu host metal facilitates the C–C coupling.¹⁴ Li et al. found that dispersed atoms enhanced the charge redistribution on the surface, thereby improving the catalytic performance in CO₂ to methanol conversion.¹⁵ Conversely, SAAs can show poor catalytic performance compared to nanostructures where the dopants form ensembles on the catalyst surface. For example, the activation barrier for O₂ dissociation on Pd ensembles is significantly lower, whereas achieving O₂ dissociation is challenging in the presence of isolated active sites.¹⁶ Therefore, understanding the aggregation behavior in SAAs is critical in determining their catalytic application.

Methods such as Density Functional Theory (DFT)^10–12,17 and tight-binding^18,19 are implemented to gain insight into the segregation behavior of non-ligated (absence of adsorbates) and ligated (presence of adsorbates) SAAs. Given the computational cost of DFT and the need for accelerated materials discovery, alternative approaches should be considered for accurately (and rapidly) screening through the vast materials space of SAAs. There is a growing interest in applying machine learning (ML) to understand the physicochemical properties that drive segregation and aggregation in SAAs. Recently, Salem et al. developed a 2^nd order polynomial kernel ridge regression (KRR) model to predict segregation energy (E_seg) of the non-ligated (111), (100), (110), and (210) surfaces on platinum-group metal-based SAAs.²⁰ The model includes tabulated features, including terms inspired by the Bond-Centric Model,²¹ such as the ratio of the difference in bulk cohesive energy to the coordination number of the dopant (ΔCE_bulk/CN). Other incorporated tabulated features encompass the atomic radius of the dopant, the electronegativity of the host, and disparities in electron affinity and first ionization potential of the dopant. Although the model was trained using DFT on periodic surfaces, it successfully captured trends in E_seg for nanoparticles, demonstrating robust generalization across various material scales. To extend this study and understand the effect of commonly used ligands in colloidal nanoparticle synthesis on the segregation behavior, DFT and ML was implemented to develop an accurate neural network model to predict E_seg on (111) and (100) surfaces of d⁸ (Ni, Pd, Pt) and d⁹ (Ag, Au, Cu) metals.²² These ML-based models revealed the physics underlying the segregation behavior in SAAs in non-ligated and ligated systems, allowing for rapid and efficient screening of different SAA systems.

Similar methods can also be applied to investigate the aggregation behavior of non-ligated SAAs, in addition to Monte Carlo simulations.^11,12,23,24 ML techniques have been implemented to build an understanding on the effect of adsorbates (and their absence) on the aggregation behavior. Rao et al. leveraged ML to predict the formation energy (i.e., stability) of different SAAs with surface, subsurface, dimer, and adatom dopants on multiple surfaces such as FCC (111), BCC (110), and HCP (0001).²⁵ Another study carried by Lu and co-workers developed Gaussian process regression model to predict the E_agg in Cu(111)-based SAAs in the absence and presence of oxygen.²⁶ Although these models were able to capture E_agg trends, current studies are limited to commonly used catalytic adsorbates such as CO, O, and H.

In this work, we first unravel what drives aggregation in non-ligated SAA systems using DFT. Next, we aim to understand how the presence of commonly used thiol and amine ligands in colloidal nanoparticle synthesis, R-S and R-NH, affects the aggregation behavior in SAAs. Additionally, the latter, radical amines (R-NH), are found as reaction intermediates on SAA surfaces in reactions such as ammonia dehydrogenation²⁷ and ammonia formation from dinitrogen.²⁸ In both the non-ligated and ligated metal surfaces, we investigate the formation of dopant dimers and trimers. Specifically, we focused on the effect of H₃C-NH (binding in a bridge adsorption configuration) on dopant dimer formation and H₃C-S (binding in a hollow adsorption configuration) on dopant trimer formation. This analysis includes metal combinations of Ag, Au, Cu, Ni, Pd, and Pt (36 different metal combinations) on low-index surfaces such as (100) and (111). Although E_agg provides useful thermodynamic trends, the final structural characteristics of the dopants, including the ensembles they form and dopant segregation, will ultimately be determined by minimizing the Gibbs free energy of the system in the presence of adsorbates.^23,29 Lastly, we applied ML to develop a model that captures E_agg in non-ligated and ligated systems across different metal combinations and facets. This work, in addition to demonstrating a method for accelerated prediction of thermodynamically stable colloidal SAAs, it reveals the physicochemical parameters that control metal aggregation.

Methodology

Density functional theory

DFT calculations on non-ligated and ligated slabs were performed using CP2K.³⁰ The PBE functional³¹ was used in conjunction with Grimme's D3 dispersion correction.³¹ Goedecker, Teter, and Hutter (GTH) pseudopotentials³² were used with DZVP (double-zeta valence polarized) basis set at 600-Rydberg cutoff.³³ Spin polarization was implemented in all calculations, as considering magnetic effects is crucial for accurately capturing the thermodynamic stability of SAAs, as shown in previous work.^10,34 Self-consistent field cycles were performed with a convergence criterion of 10⁻⁷ Ha. Geometry relaxations were performed using the Broyden–Fletcher–Goldfarb–Shanno minimization algorithm until the forces converged to 4.0 × 10⁻⁴ Ha Bohr⁻¹. We use a 6 × 6 × 6 cell to model the (111) and (100) surface. We allow the first three layers to relax, while fixing the bottom three layers. Metal combinations of d⁸ (Ni, Pd, Pt) and d⁹ (Ag, Au, Cu) are considered in this study. Additionally, the adsorbates H₃C-NH and H₃C-S are used. For the non-ligated surface, we investigated ensembles of dimers and trimers, while for the ligated systems, we investigated the dimers for H₃C-NH and trimers for H₃C-S, due to the bridge and hollow adsorption configuration of the amine and thiol, respectively. Our study included a total of 240 different systems. To compute the E_agg of non-ligated systems¹¹ with a cluster of n dopant atoms (E_tot(n)) with respect to the pure host material (E_tot(host)), and the SAA (E_tot(SAA)), we use eqn (1):

E_agg = E_tot(n) + (n − 1)E_tot(host) – nE_tot(SAA). (1)

The equivalent structures for different facets and adsorbates are shown in Fig. 1 and S1(a–c).† Based on this formulation, E_agg < 0 indicates that the dopant atoms prefer to form aggregates (dimers or trimers) on the surface, while E_agg > 0, SAAs.^11,12

Fig. 1 Top view of the (111) surface of the metal host with (a) a single dopant (SAA), (b) a dopant dimer, (c) a dopant trimer, (d) a H₃C-NH bridge adsorption on SAA, (e) a H₃C-NH bridge adsorption on the dopant dimer, and (f) a H₃C-S hollow adsorption on the dopant trimer.

The adsorbate-induced aggregation energy (E^m×ads_agg) is calculated using eqn (2).^11,12 The most stable configuration was considered in this study, i.e. hollow-site for the thiolate ligand and bridge site for the amine, as illustrated in Fig. 1 and S1(d–f).†

where E_agg is the aggregation energy under vacuum conditions, m is the number of adsorbates (in our work, m = 1), and E^SAA_ads and E^n-mer_ads are the adsorption energies of the adsorbates on the isolated dopant in the SAA and n-mer dopant island, respectively.

Machine learning implementation

We used ML to develop an accurate E_agg model. Similar to our previous work, we use tabulated elemental features³⁵ such as the radius, coordination number, first ionization potential, and electron affinity, along with the binding energy of the adsorbate on a single atom and bulk cohesive energy (Table S1†). A full list of the features (Table S2†) used can be found in section 2 of the ESI.† We specifically picked these descriptors as they have appeared in our E_seg models.^20,22 These features capture structural effects, electronic effects, as well as thermodynamic stability. In each of these features, we consider the host property, dopant property, and the difference between the host and dopant property. As a result of taking the difference, negative values are possible. For instance, if the dopant has a larger radius than the host metal, then the change in the radii would be a negative value. The features were standardized by transforming the inputs in a manner that the distribution has a mean of 0 and a standard deviation of 1, ensuring equal contribution of the different features. We use 85/15% train/test split and apply 5-fold Cross Validation to obtain the train and validation errors for the entire dataset (240 datapoints). For the non-ligated systems, we use Leave-One-Out Cross Validation. Additionally, we evaluate the accuracy of the test (unseen) data using mean absolute error (MAE) and root mean squared error (RMSE) (eqn (3) and (4), respectively). To select the features for the ML models, we employ variable importance³⁶ plot based on the random forest regression. This aids in determining which features contribute more to predicting E_agg in both the ligated and non-ligated surfaces. Next, we tune the hyperparameters present in KRR (2^nd order polynomial, radial basis function (RBF), laplacian),³⁷ support vector regressor (SVR: 2^nd and 3^rd order polynomial and RBF),³⁸ LASSO,³⁹ and linear regression (OLS) using GridSearchCV⁴⁰ by minimizing the MAE of the validation data set in Scikit-Learn Python package.⁴¹ To ensure that the model is not over-fitting, we applied bootstrapping.

In eqn (3) and (4), y is the actual output value, ŷ is the predicted output value, and x is the total number of data points.

Results and discussion

DFT calculated aggregation trends of non-ligated systems

In this analysis, we investigate the effect of the coordination environment on the E_agg as a function of the number of dopants (dimers vs. trimers). In the dimer cases, we find that regardless of the host and dopant combination (i.e., d⁸_hostd⁸_dopant, d⁹_hostd⁹_dopant, d⁹_hostd⁸_dopant, d⁸_hostd⁹_dopant), the SAA phase is majorly favored as denoted by the positive sign in most of the data presented in Fig. 2a. However, we do find cases where dimer formation is favored, these include, Pt(100)-based systems, Cu doped on Ni(111)/(100), Ni and Pt doped on Ag(111), Ni doped on Cu(111) and Pt doped on Au(111) (Fig. 2a). Focusing on how the coordination environment influences E_agg ((100) facet corresponds to coordination number 8, while the (111) facet represents coordination number 9), we observe that both facets follow similar E_agg trends (almost parallel lines) in each metal host.

Fig. 2 E _agg for the formation of (a) dimers and (b) trimers relative to SAAs in d⁸ and d⁹ metal combinations. Blue and red colors represent the (111) and (100) facets, respectively. Circle and star markers represent the dimers and trimers, respectively. A positive E_agg indicates a preference for forming SAAs, while a negative E_agg suggests that aggregates (dimers/trimers) are favored.

Additionally, we find that the (100) results in more positive E_agg values compared to the (111) facet in the d⁹_hostd⁸_dopant combination, as denoted by the red line in Fig. 2a. Notably, in the Pt host, the (100) facet displays opposite E_agg trends compared to the (111) facet. This is because Pt has a relatively higher surface energy compared to other metals,^42,43 particularly on the less stable (100) facet, making it more prone to aggregation when dopants are introduced. Overall, the impact of the coordination environment on dimer formation is not significant (all within ∼0.1 eV change). This could be because the difference in coordination environment, going from 8 to 9, is not large enough to cause changes in E_agg behavior.

Moving on to the trimer cases, there is a wide E_agg range, and the effect of the coordination number becomes more prominent compared to the dimer cases (as illustrated in Fig. 2b). The (111) facet generally results in more negative E_agg values compared to the (100), indicating that the formation of trimers is thermodynamically more favored on the (111) facet. This could be due to the more compact alignment of the trimers on the (111) facet, where they form an isosceles triangle, compared to the (100) facet, where they form an orthogonal triangle, resulting in a more negative E_agg for the (111) case. For example, Ni(111)Cu_trimer produced an E_agg of ∼−0.1 eV, while Ni(100)Cu_trimer resulted in an E_agg of −0.002 eV. The exception is the Pt host, where, similar to the dimer cases, trimers are also more favored on the (100) facet compared to the (111) facet. The cases of favorable trimer aggregation involve Ni and Pt doped on Ag(111), Pt doped on Au(111), Cu doped on Ni(111) and Ni(100), Ni doped on Cu(111), Ag and Au doped on Pt(111), Pt doped on Pd(100), and Pt(100)-based systems. We find that in most of the Pt and Ni dopant cases, they tend to be more stable as ensembles compared to SAA, as Pt–Pt and Ni–Ni bonds are particularly strong, with bond dissociation energies of 3.93 eV and 4.33 eV, respectively. These metals are also the ones with the highest cohesion among the ones studied. As a result, these bonds are harder to break compared to other metals, making cluster formation more favorable.

Both trimer and dimer cases showed relatively similar aggregation behavior between the (100) and (111). However, when comparing the values obtained from the dimer and trimer cases, trimer formation proves to be more stable, as indicated by the more negative E_agg values. For instance, Ag(111)Ni_trimer resulted in an E_agg of −0.192 eV, whereas Ag(111)Ni_dimer gave −0.045 eV. Similarly, for the (100) facet, although the E_agg of trimers is more negative, the difference is not as pronounced. For example, Pt(100)Ag_trimer yielded an E_agg of −0.154 eV, while dimer formation led to −0.106 eV. Overall, dopant trimer formation is more stable than dimers.

E _agg model in non-ligated systems

We applied ML techniques to develop an understanding of what drives aggregation in non-ligated systems. To achieve this, we conducted a variable importance analysis using the data from Fig. 2. Our findings revealed that there are two top features playing a crucial role in capturing E_agg trends. These key features are the change in the radii of the metals and a combined term, which is the difference in the bulk cohesive energy of the host and dopant multiplied by the change in the number of the dopants, divided by the coordination number of the dopant (ΔnCE_bulk/CN). The change in the radius is instrumental in capturing strain effects, while the second term represents the stability of SAAs and considers the different facets as well as the number of dopants on the surface. These findings align with our previous analysis on metal segregation on SAAs,^20,22 emphasizing the significance of these features in understanding the stability in SAAs, captured in both E_seg and E_agg. We have previously developed two E_seg models: (1) non-ligated SAA systems²⁰ and (2) ligated SAA systems.²² The ΔCE_bulk/CN, radius of the metals, and electron affinity are common features in both E_seg models. The ΔnCE_bulk/CN was inspired from the ΔCE_bulk/CN used in the previous E_seg models. Furthermore, the main difference between the two features is the Δn term. Based on the Farsi and Deskins E_seg equation,¹⁰ the systems involved in the DFT E_seg are the host and SAA based systems; thus, applying the Δn term would just be 1, since the dopants present in the pure host systems are 0 and the dopant in the SAA is 1 (1–0 = 1); hence, the ΔnCE_bulk/CN is essentially the same as the ΔCE_bulk/CN. Additionally, in our DFT E_agg calculations, the SAA system was used as a reference. For consistency, we take our reference to be the SAA (single dopant) in the ΔnCE_bulk/CN term; hence, the Δn was incorporated. We then utilized these two features (Δr and ΔnCE_bulk/CN) in various ML models (SVR (2^nd and 3^rd order polynomial and RBF), KRR (2^nd order polynomial, RBF, and laplacian), LASSO, and OLS) and tuned their respective hyperparameters accordingly (Table S3†). We found that a second order polynomial KRR E_agg model (Fig. S2 and Table S4†) outperformed all other models, resulting in a test MAE of 0.084 eV and a RMSE of 0.112 eV.

We then aim to determine the regions where dopant aggregation is expected. Before doing so, we need to investigate how the same two features impact dopant segregation in non-ligated systems since the dopant must reside on the surface of a SAA for any catalytic (and beyond) application. A stable SAA is quantified by having a negative E_seg and positive E_agg. Our findings indicate that dopant segregation occurs (indicated by negative E_seg) under the conditions where Δr* < 0.9 and ΔnCE_bulk/CN* < 0, displayed as green points in Fig. S3a,† while data outside these conditions represent the anti-segregation behavior (red points). However, we note that there is a discrepancy in the Au(100)Ag case where the criteria predicts that the dopant will segregate, contrary to our DFT E_seg calculations (all DFT E_seg data used in this analysis are obtained from a previous work of our lab at the same level of theory²²). Based on the criteria, the dopants in Ni(111)Pt_dopant and Pt(100)Cu_dopant will not segregate, while DFT E_seg findings point at a mildly exothermic SAA phase-preference, as shown in Fig. S3† (E_seg DFT values for these cases are −0.060 and −0.037 eV, respectively). This discrepancy could be attributed to the charge transfer (captured through the ΔEA term) occurring between the host and dopant metals that is missing in the criteria (incorporated later on), which is another feature that is critical in describing surface segregation in SAAs.^20,22

Next, we filtered our results based on the E_seg criteria, focusing only on cases where segregation occurred, as indicated by the green points in Fig. S3.† The main aim is to identify the conditions (Δr* and ΔnCE_bulk/CN*) under which aggregation happens (and should be avoided to form SAAs) among points that ensure segregation (i.e. presence of dopant on the surface). In the E_agg data shown in Fig. 4a, we marked the metal combinations in black to denote systems where segregation did not occur and thus not considered. We established that dopant aggregation (blue points) is likely to happen when Δr* > 0 and ΔnCE_bulk/CN* < −0.55, illustrated in Fig. 4b. We also utilized the E_agg model to predict the E_agg in non-ligated systems and applied the criteria (Δr* > 0 and ΔnCE_bulk/CN* < −0.55) to identify cases where aggregation will occur, illustrated in Fig. S4† and showed similar trends as Fig. 4b. When Δr* > 0, it indicates that the atomic radius of the dopant is smaller than that of the host metal. A smaller dopant size allows the dopant to fit more comfortably within the host bulk structure, which affects atomic interactions. Additionally, when ΔnCE_bulk/CN < −0.55, it suggests stronger interactions between the dopant and the host atoms. This is due to a more negative change in bulk cohesive energy, amplified by the number of dopants on the surface relative to the coordination number, implying that stronger bonding interactions facilitate the formation of aggregates.

Fig. 3 Variable importance based on random forest regression on the non-ligated systems. Asterisks indicate that the features are standardized.

Fig. 4 3D plot of the DFT E_aggversus the top two features (Δr* and ). In (a), data points are colored based on the actual DFT energetics (negative E_seg and positive E_agg refers to formation of SAA), while in (b) datapoints are colored based on the criteria of Δr* > 0 and ΔnCE_bulk/CN* < −0.55 (excluding the black points from (a)). The blue points refer to the formation of aggregates (dimer and trimer clusters), green points represent the SAA phase, and black points correspond to anti-segregation behavior based on Fig. S3.†

Comparing these findings to DFT E_seg and E_agg data directly, we observed that the specified criteria accurately capture the DFT data trends, shown in Fig. 4. However, there were exceptions with Pd(100)Ag_dopant/dimer, Pt(111)Au_dopant/dimer, and Pt(111)Pd_{dopant/trimer} where the criteria suggested dopant segregation and aggregation, while the DFT E_seg and E_agg revealed that the dopant will segregate but has a mild tendency to form a SAA phase instead. Through this analysis, we introduce a more robust approach to identify the different behaviors (anti-segregation vs. segregation and aggregates vs. SAA). Furthermore, we found that these conditions effectively capture the overall stability of non-ligated systems in SAAs.

DFT calculated aggregation trends in ligated systems: H₃C-NH

In this analysis, we examined the influence of H₃C-NH on E_agg. Fig. 5a and b reveal that both (100) and (111) facets exhibit similar E_agg trends across different host metals. Interestingly, Ag- and Au-based host metals exhibit similar aggregation trends with varying dopant. On the other hand, Ag- and Au-metal dopants prefer to form SAAs compared to other dopants, regardless of the metal host and facet. Notably, the formation of the SAA phase is more thermodynamically favorable relative to the dimer phase when d⁸-host metals are doped with d⁹ metals in the presence of H₃C-NH, irrespective of the facet. In these cases, the introduction of H₃C-NH produced more positive E_agg compared to the non-ligated systems. This effect is more pronounced when transitioning from (100) to (111) facets. Prior to the introduction of the adsorbate, almost all the cases favored the SAA phase. However, upon the addition of H₃C-NH, there is a shift from the SAA phase to aggregation (11 cases for the (111) and 12 cases for the (100) facet). This is because H₃C-NH interacts strongly with the dopants (Table S5†) and forms a bridge site on the dopant atoms, making them more susceptible to aggregation. It is important to note that the large E_agg(111) values stem from the configuration changes that occurred in the adsorbate-XNi (where X is the dopant and Ni is the host) during geometry optimization calculations. In these instances, the adsorbate-host bond is stronger than the adsorbate-dopant bond, leading to a new configuration. As a result, during geometry optimization, the bond between the adsorbate and the dopant breaks, and the adsorbate forms a bond with the host metal instead. In this analysis, we find that this has occurred in Ni(111)Ag, Pt(111)Ag, and Pt(111)Au cases, illustrated in Fig. S5a.† Moreover, the new configuration occurred in the SAA case. In the optimized dopant dimer surface calculation in the presence of H₃C-NH, the ligand does not move away, but rather forms two bonds with the two metal dopants. This explains why we still observe changes in aggregation behavior between the non-ligated and ligated systems.

Fig. 5 E _agg for the formation of dimers in non-ligated and ligated systems on (a) (100) and (b) (111) surfaces relative to SAAs in d⁸ and d⁹ metal combination. Blue and red colors represent the (111) and (100) facets in non-ligated systems, respectively, while green represents the systems in the presence of H₃C-NH. A positive E_agg indicates a preference for forming SAAs, while a negative E_agg suggests that dimers are favored. Asterisks represent the systems that formed a new configuration during geometry optimization.

DFT calculated aggregation trends in ligated systems: H₃C-S

Moving on to the second adsorbate, methylthiolate, we compare the trends across the different facets and metal combinations. Similar to the H₃C-NH case, both facets exhibit similar E_agg trends across the different host metals. Across both facets, we observe that when d⁹ metals are doped onto d⁸ metals, they tend to prefer the SAA phase rather than forming trimers, as shown in Fig. 6. As a dopant, Ni has greater tendency to form trimers. This could trace back to the strong binding strength between Ni (dopant) and the methylthiolate relative to the other metals (except Pt, they have similar binding energies), as demonstrated in Table S6.† When comparing the two facets, (111) displays a broader range of E_agg values compared to the (100) and generally has a larger E_agg in the presence of H₃C-NH compared to the non-ligated case. Similar to the H₃C-NH case, due to the formation of a new configuration during geometry optimization (shown in Fig. S5b†), we find a wide E_agg range arising in a few thiolate cases. These cases include Ni(111)Ag, Ni(111)Au, Ni(111)Pd, Pd(111)Ag, Pd(111)Au, and Cu(111)Ag. Within these metal combinations, the largest deviation in the E_agg in the presence of methylthiolate appears for Ni-host systems (Ni(111)Ag, Ni(111)Au, Ni(111)Pd) and less for the others (Pd(111)Ag, Pd(111)Au, and Cu(111)Ag), making a pronounced impact on the E_agg. This is because the methylthiolate binds strongly to Ni (Table S6†) driving this configurational change. Furthermore, analyzing the difference in binding energies of single atoms to methylthiolate between the host and dopant metals reveals that Ni shows in the largest difference (Ni(111)Ag = ∼−1.63 eV, while Cu(111)Ag = ∼−0.617 eV), highlighting the strong interaction between the Ni and methylthiolate compared to other metals. Additionally, we found that only 7 cases led to aggregation in pristine (100), whereas 12 cases exhibited aggregation in the presence of H₃C-S. As for the (111) facet, 7 cases led to aggregation in the absence of the adsorbate, while the presence of H₃C-S resulted in 13 aggregation cases. We further emphasize that the adsorption energies between the dopant and host dictates the aggregation behavior in ligated SAAs, as illustrated in Fig. S9.† Therefore, our analysis suggests that the presence of H₃C-S promotes aggregation due to the strong interaction of thiolate with metals, which traps the dopants as aggregates.

Fig. 6 E _agg for the formation of trimers in non-ligated and ligated systems in (a) (100) and (b) (111) relative to SAAs in d⁸ and d⁹ metal combination. Blue and red colors represent the (111) and (100) facets in non-ligated systems, respectively, while green represents the systems in the presence of H₃C-S. A positive E_agg indicates a preference for forming SAAs, while a negative E_agg suggests that trimers are favored. Asterisks represent the systems that formed a new configuration during geometry optimization.

Generalized E_agg model development

We have combined all 240 DFT-calculated E_agg data points, covering non-ligated (dimers and trimers) and ligated systems (H₃C-NH forming dimers and H₃C-S forming trimers). We aim to develop an accurate and unbiased model (including cases where the ligand moved away from the dopant) that captures E_agg trends across various metal combinations, facets, and adsorbates. ML models like the one developed here, have the potential to significantly accelerate materials discovery while revealing the physics governing aggregation on bimetallic structures. To identify the top features for predicting E_agg, we employed variable importance analysis. Based on Fig. 7, the top four features include the difference in the bulk cohesive energy of the host and dopant times the change in the number of dopants divided by the coordination number of the dopant (ΔnCE_bulk/CN), the difference in the binding energy of the adsorbate on a single atom of the host and dopant, divided by the coordination number of the adsorbate on the surface (ΔBE/CN_ads), the difference in the electron affinity of the host and dopant (ΔEA), and the difference in the radius of the host and dopant (Δr). We stopped at the fourth feature, as the fifth and third feature correlate highly with each other (Pearson correlation coefficient of 0.78, as shown in Fig. S6†). It is noteworthy that two of these features were used in our previous analysis of the non-ligated systems (Fig. 3), proving their significance in capturing the stability of SAAs. The complete dataset used in this study, along with the features, is available on our GitHub (https://github.com/mpourmpakis/EaggModel).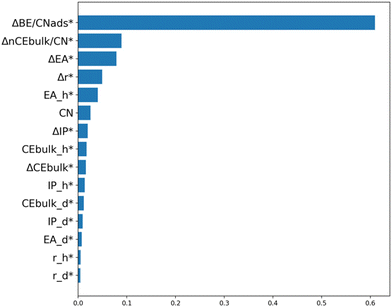

Fig. 7 Variable importance based on random forest regression on the non-ligated and ligated systems. Asterisks indicate that the features are standardized.

We then tuned the hyperparameters in the models and assessed their performance, shown in Tables S7 and S8.† Furthermore, we compared different models to identify the one with the lowest validation MAE and the smallest difference between validation and training MAE (Table S8†). We found that LASSO, OLS, SVR (2nd and 3rd order polynomial), and KRR (2nd order polynomial) produced higher validation MAE compared to SVR (RBF) and KRR (Laplacian and RBF). Additionally, SVR (RBF) showed the smallest difference between validation and training MAE, indicating that it is the top-performing model. Our results show that SVR (RBF) achieved a test MAE of 0.161 eV and an RMSE of 0.239 eV (illustrated in Fig. 8 and Fig. S7†). Additionally, the model consistently produced similar MAEs across the training, validation, and test datasets (Table S8†). We conducted bootstrapping over 100 iterations, obtaining comparable MAEs across the different datasets (displayed in Fig. S8†), indicating that the model is not over-fitting. Even in cases involving H₃C-S (denoted by blue edge color), where larger deviations were observed, our model effectively captured aggregation behavior, reaffirming its significance. We do note that ML models struggle with extrapolation,⁴⁴ so while it is possible to test them on different ligands or metals, additional training with new data will likely be necessary.

Fig. 8 Parity plot between the SVR RBF kernel predictions and DFT E_agg of the test set (36 datapoints). Color indicates the different metal hosts, the marker type indicates the different metal dopants, and edge color represents the adsorbates.

To further affirm the reliability of the model's predictions, we assess its performance by comparing it to 7 experimental observations, as demonstrated in Table S9.† We specifically compare the thermodynamic tendency of aggregation (E_agg) to what final structures (e.g. SAAs or aggregates) have been observed in experiments. The experimental studies include PtAu-thiol,⁴⁵ AuPt-thiol,⁴⁵ CuNi-thiol,⁴⁶ PdAu,⁴⁷ CuPd,⁴⁸ AuCu,⁴⁹ and AuPd.⁴⁷ Our findings reveal that the model accurately reproduces the experimental observations of the 7 SAA cases. This experimental validation underscores the considerable potential of our model, enabling accelerated screening across diverse SAAs in the presence and absence of ligands. It is worth highlighting that our model stands out by utilizing features that capture E_agg behavior in the presence of various adsorbates (with different binding groups and adsorption configurations) and different metal combinations, demonstrating its versatility.

The importance of this model is mainly attributed to the features used. Each of these features represent a critical factor in capturing the underlying physics dictating the stability (in terms of aggregation) in SAAs. The first term, ΔBE/CN_ads, describes the adsorbate binding affinity to the metals and the corresponding adsorption configuration (i.e. how many bonds the ligands form with the surface). The second term, ΔnCE_bulk/CN, represents the cohesion of SAAs, while taking into consideration the coordination number of the facet and the number of dopants. This term is derived from the BCM, which was previously found to accurately capture the stability of bimetallic nanoparticles.²¹ Through this, the model can distinguish between SAA or dopant ensembles and the facet type. The third term, ΔEA, quantifies the charge transfer between the metal host and dopant. Lastly, the final term, Δr, captures strain effects. We would like to note that these four features were also instrumental in our previous work on E_seg in the presence of adsorbates.²² Additionally, three of these features (r, ΔCE_bulk/CN, ΔEA) were also top contributors to segregation behavior of SAAs in the absence of adsorbates.²⁰ This proves how critical these features are in describing SAA in the absence and presence of adsorbates.

Conclusions

In this work, we investigated the aggregation energy behavior (E_agg) of d⁸ (Ni, Pd, Pt) and d⁹ (Ag, Au, Cu)-based SAAs in the absence and presence of adsorbates (H₃C-NH and H₃C-S), considering different low-index facets, different ligand adsorption configurations, and dopant dimer and trimer aggregates. Furthermore, we compared the non-ligated SAAs to the dopant dimers and trimers formed in the presence of H₃C-NH (bridge binding configuration) and H₃C-S (hollow binding configuration) ligands. We found that, regardless of the facet, similar E_agg trends were observed across different metal combinations, with the Pt-host showing a stronger preference for aggregation on the (100) facet compared to the (111) facet. In the absence of adsorbates, the formation of SAA is more thermodynamically stable compared to dimers. Furthermore, there were more cases where the formation of trimers was more favorable compared to the dimers in the absence of ligands. We then employed ML techniques to develop a robust approach for accurately predicting the aggregation behavior of non-ligated systems, based on the change in radius (Δr* > 0) and change in the bulk cohesive energy divided by the coordination number (ΔnCE_bulk/CN < −0.55) as our criteria. We provided specific feature values as design criteria that promote surface segregation of the dopant and the creation of SAAs instead of aggregates. We also investigated the effect of adsorbate on E_agg behavior. A wider E_agg range is observed when adsorbates are introduced due to their adsorption configurations. Due to the adsorption configuration of H₃C-NH (bridge) and H₃C-S (hollow), the ligands trap the dopants in place, promoting the formation of aggregates. As a result, an increase in the ensemble (dimers and trimers) formation cases was observed as opposed to the SAA cases. Finally, we collected DFT E_agg values of the non-ligated and ligated systems and conducted variable importance analysis. The top features identified were ΔBE/CN_ads, ΔnCE_bulk/CN, ΔEA, and Δr. Each of these features represent critical driving forces that capture E_agg: adsorbate effects, thermodynamic stability of formed sites, charge transfer between host and dopants, as well as strain effects. Similar features were observed from our previous work that focused on SAA stability in terms of segregation energy analysis.^20,22 A stable SAA forms when well-dispersed dopants (i.e., single dopants) are present on the surface, characterized quantitively by negative E_seg and positive E_agg values, factors that are reflected on the selected features (which can be found tabulated) as design parameters. Our SVR RBF model accurately captures the aggregation behavior across the different adsorbates, metal combinations, facets and aggregates (dimers/trimers) and our predictions were compared against experimental literature demonstrating the model's accurate prediction performance. First-principles-based ML models like the ones presented in this work, enable rapid prediction of SAA stabilization in colloidal bimetallic systems, accelerating nanomaterials discovery while guiding experimental synthesis work.^20,22

Author contributions

Maya Salem: methodology (DFT calculations and Machine learning), formal analysis, data curation, visualization, writing (original draft). Giannis Mpourmpakis: supervision, project administration, conceptualization, writing (review & editing), funding acquisition.

Data availability

Data for this article, including datasets and codes are available at the Mpourmpakis lab Github at https://github.com/mpourmpakis/EaggModel. Additional data supporting this article have been included as part of the ESI.†

Conflicts of interest

The corresponding author states that there is no conflict of interest.

Acknowledgements

This work has been supported by the National Science Foundation (NSF, CBET-CAREER program) under Grant No. 1652694. The authors would like to acknowledge computational support from the Center for Research Computing at the University of Pittsburgh, RRID: SCR_022735, through the resources provided. Specifically, this work used the H2P cluster, which is supported by NSF award number OAC-2117681. Additional computational resources are acknowledged provided by the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS), which is supported by the NSF (ACI-1053575).

References

1. R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910.
2. J. Han, M. C. Freyman, E. Feigenbaum and T. Yong-Jin Han, ACS Photonics, 2018, 5, 1343–1350.
3. S. C. Purdy, R. R. Seemakurthi, G. M. Mitchell, M. Davidson, B. A. Lauderback, S. Deshpande, Z. Wu, E. C. Wegener, J. Greeley and J. T. Miller, Chem. Sci., 2020, 11, 5066–5081.
4. A. K. Singh and Q. Xu, ChemCatChem, 2013, 5, 652–676.
5. N. Macleod, J. M. Keel and R. M. Lambert, Appl. Catal., A, 2004, 261, 37–46.
6. J. Mao, J. Yin, J. Pei, D. Wang and Y. Li, Nano Today, 2020, 34, 100917.
7. G. Kyriakou, M. B. Boucher, A. D. Jewell, E. A. Lewis, T. J. Lawton, A. E. Baber, H. L. Tierney, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Science, 2012, 335, 1209–1212.
8. R. T. Hannagan, G. Giannakakis, M. Flytzani-Stephanopoulos and E. C. H. Sykes, Chem. Rev., 2020, 120, 12044–12088.
9. W. Liu, H. Feng, Y. Yang, Y. Niu, L. Wang, P. Yin, S. Hong, B. Zhang, X. Zhang and M. Wei, Nat. Commun., 2022, 13, 3188.
10. L. Farsi and N. A. Deskins, Phys. Chem. Chem. Phys., 2019, 21, 23626–23637.
11. K. G. Papanikolaou, M. T. Darby and M. Stamatakis, J. Phys. Chem. C, 2019, 123, 9128–9138.
12. M. T. Darby, E. C. H. Sykes, A. Michaelides and M. Stamatakis, Top. Catal., 2018, 61, 428–438.
13. Q. Wang, B. Zhu, F. Tielens, D. Tichit and H. Guesmi, Appl. Surf. Sci., 2021, 548, 149217.
14. M. D. Marcinkowski, M. T. Darby, J. Liu, J. M. Wimble, F. R. Lucci, S. Lee, A. Michaelides, M. Flytzani-Stephanopoulos, M. Stamatakis and E. C. H. Sykes, Nat. Chem., 2018, 10, 325–332.
15. M. Li, B. Hua, L. C. Wang, Z. Zhou, K. J. Stowers and D. Ding, Catal. Today, 2022, 388–389, 403–409.
16. H. C. Ham, J. A. Stephens, G. S. Hwang, J. Han, S. W. Nam and T. H. Lim, J. Phys. Chem. Lett., 2012, 3, 566–570.
17. Z.-K. Han, D. Sarker, R. Ouyang, A. Mazheika, Y. Gao and S. V. Levchenko, Nat. Commun., 2021, 12, 1833.
18. L.-L. Wang and D. D. Johnson, J. Am. Chem. Soc., 2009, 131, 14023–14029.
19. G. Tréglia, B. Legrand and F. Ducastelle, Europhys. Lett., 1988, 7, 575–580.
20. M. Salem, M. J. Cowan and G. Mpourmpakis, ACS Omega, 2022, 7, 4471–4481.
21. Z. Yan, M. G. Taylor, A. Mascareno and G. Mpourmpakis, Nano Lett., 2018, 18, 2696–2704.
22. M. Salem, D. J. Loevlie and G. Mpourmpakis, J. Phys. Chem. C, 2023, 127, 22790–22798.
23. K. G. Papanikolaou, M. T. Darby and M. Stamatakis, ACS Catal., 2020, 10, 1224–1236.
24. J. R. Michalka and J. D. Gezelter, J. Phys. Chem. C, 2015, 119, 14239–14247.
25. K. K. Rao, Q. K. Do, K. Pham, D. Maiti and L. C. Grabow, Top. Catal., 2020, 63, 728–741.
26. Z. Lu, S. Yadav and C. V. Singh, Catal. Sci. Technol., 2020, 10, 86–98.
27. D. Chattaraj and C. Majumder, Phys. Chem. Chem. Phys., 2024, 26, 524–532.
28. G. Zheng, Y. Li, X. Qian, G. Yao, Z. Tian, X. Zhang and L. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 16336–16344.
29. B. C. Han, A. Van der Ven, G. Ceder and B.-J. Hwang, Phys. Rev. B:Condens. Matter Mater. Phys., 2005, 72, 205409.
30. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
31. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
32. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
33. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
34. Q. Yin, F. Ma, Y. Zhou, Z.-J. Sui, X.-G. Zhou, D. Chen and Y.-A. Zhu, J. Phys. Chem. C, 2019, 123, 18417–18424.
35. L. M. Mentel, 2014, preprint.
36. B. Gregorutti, B. Michel and P. Saint-Pierre, Comput. Stat., 2017, 27, 659–678.
37. V. Vovk, in Empirical Inference: Festschrift in Honor of Vladimir N. Vapnik, ed. B. Schölkopf, Z. Luo and V. Vovk, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 105–116.
38. M. Awad and R. Khanna, Efficient Learning Machines – Theories, Concepts, and Applications for Engineers and System Designers, in Support Vector Regression, 2015, pp. 67-80.
39. J. Ranstam and J. A. Cook, Br. J. Surg., 2018, 105, 1348–1348.
40. D. Paper, in Hands-on Scikit-Learn for Machine Learning Applications, Apress, Berkeley, CA, 2020, pp. 137–163.
41. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, J. Mach. Learn. Res., 2011, 12, 2825–2830.
42. A. V. Ruban, H. L. Skriver and J. K. Nørskov, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 15990–16000.
43. L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202.
44. Towards Integrative Machine Learning and Knowledge Extraction, ed. A. Holzinger, R. Goebel, M. Ferri and V. Palade, Springer International Publishing, Cham, 2017, vol. 10344.
45. L. J. Torres-Pacheco, A. De Leon-Rodriguez, L. Álvarez-Contreras, M. Guerra-Balcázar and N. Arjona, Electrochim. Acta, 2020, 353, 136593.
46. L. Chen, H. Xu, H. Cui, H. Zhou, H. Wan and J. Chen, Particuology, 2017, 34, 89–96.
47. N. Takehiro, P. Liu, A. Bergbreiter, J. K. Nørskov and R. J. Behm, Phys. Chem. Chem. Phys., 2014, 16, 23930–23943.
48. F. Xing, J. Jeon, T. Toyao, K. Shimizu and S. Furukawa, Chem. Sci., 2019, 10, 8292–8298.
49. H. Wang, D. Liu and C. Xu, Catal. Sci. Technol., 2016, 6, 7137–7150.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr04202f

---