Small-rotation-angle moiré structures of 2H TaSe₂ monolayers on Au(111)

Abstract

Direct synthesis of two-dimensional (2D) materials with moiré patterns can provide 2D moiré structures with a clean interface and be useful for future electronics applications. However, the synthesis of moiré structures with small rotation angles is challenging since such structures possess the tendency to untwist during high temperature synthesis. Here, we study the moiré structures formed by epitaxially grown 2H TaSe₂ monolayers on Au(111). By resolving atomic configurations using scanning tunneling microscopy (STM), we reveal the as-grown TaSe₂ monolayers demonstrate small rotation angles between 0° to 3° with respect to the underlying Au lattices. We demonstrate that the deposition sequence of Se and Ta during growth can make an important difference: first depositing Se on Au predominantly gives small rotation angles, while first depositing Ta on Au predominantly results in perfectly aligned lattices. Further, we unveil that defects, including hole and line defects, are closely related to the changing orientations of moiré superlattices. Our work provides important insights for the synthesis of small-twist-angle moiré structures and will facilitate future studies of TaSe₂ and moiré physics and devices in general.

---

Moiré patterns are superlattice patterns, formed for example when a two-dimensional (2D) layer is stacked on another lattice with lattice mismatch or a twist angle. The large periodicity (compared to that of the original lattice) moiré potential not only affects atomic structures, but also changes electronic bands. Recently, a variety of fascinating quantum states and phenomena has been reported in 2D van der Waals (vdW) moiré structures, including for example unconventional superconductivity and Mott insulating states in magic-angle (special twist angles typically smaller than 2° in twisted multilayer graphene¹) graphene superlattices,^2,3 quantum trapped excitons^4,5 and fractional topological states in twisted transition metal dichalcogenides (TMDCs) bilayers^6–9 and moiré magnetism in twisted 2D magnets.^10–12

Moiré patterns in 2D vdW structures can be prepared by artificially stacking the mechanically exfoliated 2D layer on another with a twist angle, which can be controlled by a tunable experimental transfer stage. With this approach, one can in principle produce any twist angles and thus fabricate different designed moiré superstructures. However, the interlayer contamination, as well as lack of mass production and twist angle precision of this method hinder further applications of 2D vdW moiré structures in future twistronics. Direct synthesis of moiré structures can produce a clean interface and hold the potential of scalable synthesis, thus overcoming the limitations of mechanical exfoliation. By lattice mismatch engineering, hetero-site nucleation or using pre-rotated substrates, twisted 2D TMDCs and bilayer graphene have been synthesized.^13–17 However, controllable synthesis of moiré superlattices with small twist angles is difficult. The ability to achieve small twist angles is of special interest, for example, in magic-angle graphene systems and other twisted structures when a relatively large moiré periodicity is desired for electronic state engineering or device applications.^2,10

Previous studies of 2D materials grown on single crystals have shown occasional growth of moiré superlattices with small rotation angles.^18–20 Factors such as interaction strength, strain and interfacial adlayers have been widely discussed and demonstrated to play crucial roles in the final patterns and rotation angles.^21–23 These results highlight the potential of growing 2D materials on single-crystalline lattices, for the achievement of controllable growth of small-rotation-angle moiré structures.

Here we explore the moiré structures formed by epitaxially grown 2H TaSe₂ monolayers on Au(111). TaSe₂ in its 2H phase is a well-known metallic layered/2D material with interesting physical properties ranging from charge density wave (CDW) to superconductivity.^24–28 We resolve the topographic and atomic structures of the moiré patterns by scanning tunneling microscopy (STM) and confirm the 2H phase of as-grown TaSe₂ by an ultrahigh vacuum (UHV) multiprobe surface analysis system, including STM, X-ray photoelectron spectroscopy (XPS) and high-resolution electron energy loss spectroscopy (HREELS). We reveal that the as-grown 2H TaSe₂ flakes demonstrate a variety of small rotation angles spanning from 0° to 3°, which may result from thermal fluctuation induced by Se at the interface of TaSe₂ and Au. Further analysis shows that defects are associated with changing moiré orientations. Changing the deposition sequence to first depositing Ta (instead of Se) on Au gives predominantly alighted lattices (instead of small twisting angles). Our work opens up an avenue for the synthesis of moiré patterns with small twist angles and may facilitate the future exploration of moiré physics and devices.

TaSe₂ monolayer flakes were synthesized on Au(111) in an UHV environment. Se and Ta were deposited sequentially on a freshly cleaned Au surface by thermal and sputtering deposition, respectively. After annealing at 400 °C in protective Se flux, TaSe₂ triangular islands were epitaxially grown on the Au surface (Fig. 1(a), see growth details in the ESI Fig. S1 and S2†). The samples were then characterized by STM at room temperature, at which one does not expect to observe CDW phases^24–26 (typically occurring below 120 K) of 2H TaSe₂. In the magnified STM topographic image, a big TaSe₂ island (constructed by a few triangular TaSe₂ flakes joined together) displays a hexagonal periodic pattern with a relatively large periodicity of 16.0 ± 0.3 Å (Fig. S3a,† where error is the standard deviation from different measurements at different positions). This large-periodicity hexagonal pattern, as discussed below, is the moiré pattern formed between TaSe₂ monolayer and underlying Au (111). The height of the flake is ∼2.2 Å (Fig. S3b†), comparable with the height of monolayer TMDCs grown on Au(111).¹⁹ This height is smaller than the interlayer distance in bulk TaSe₂ (∼6.1 Å),²⁹ possibly due to the strong interaction between TaSe₂ and Au(111) or a reduced tip–sample tunneling conductance.¹⁹ Further, atomic resolution STM was carried out to understand the moiré pattern. In Fig. 1(b), except for the large pattern, hexagonal atom arrays with the periodicity of 3.44 ± 0.14 Å were observed, consistent with the lattice constants of TaSe₂.²⁹ Meanwhile, it is clearly seen that the lattices of moiré and TaSe₂ are not aligned perfectly, but with a rotation angle of φ = 6.0° ± 0.9° between them, which was also distinguished in the 2D fast Fourier transform (FFT) image (Fig. 1(c)). 2D FFT demonstrates two sets of hexagonal patterns, representing the reciprocal lattices of moiré and TaSe₂. The angle between the two lattice vectors k_moiré and k_TaSe2 is 5.8° ± 0.6°, close to the rotation angle observed in the real space STM image (Fig. 1(c), φ = 6.0 ± 0.9°). The epitaxial relation among the TaSe₂ overlayer lattice, underlying Au(111) lattice and moiré superlattice can be demonstrated by the following equation of reciprocal lattice vectors: k_moiré = k_TaSe2 − k_Au(111) (inset of Fig. 1(c)). Since the magnitude of reciprocal space vector for a hexagonal lattice k is (a is the lattice constant in real space), one can calculate the rotation angle θ = 1.0° ± 0.1° between the TaSe₂ and underlying Au(111) by using measured a_moiré = 16.0 ± 0.3 Å, a_TaSe2 = 3.44 ± 0.14 Å and φ = 5.8° ± 0.6°. Note the lattice constant of Au(111) was not involved in the calculation for rotation angle θ. With the above method, we obtained a calculated lattice constant for Au of 2.84 ± 0.04 Å, in reasonable agreement with the known lattice constant of Au(111) of 2.88 Å.³⁰

Fig. 1 Epitaxially grown TaSe₂ monolayer flakes on Au(111). (a and b) STM images of topographic and atomic structures of the as-grown TaSe₂ monolayer flakes. The white and red rhombuses indicate the moiré and TaSe₂ unit cells, respectively. The white and red arrows are the lattice vectors of moiré and TaSe₂ lattices, respectively. The rotation angle between moiré and TaSe₂ lattice vectors is φ. (c) A 2D FFT image of Fig. S4,† which is a bigger-area STM image taken on the same TaSe₂ flake as that in (b). The red arrows represent reciprocal lattice vectors of moiré and TaSe₂ lattices. Inset: the relation between reciprocal lattice vectors of moiré, TaSe₂ and Au(111) lattices. φ and θ represent the rotation angle between lattices of moiré and TaSe₂, and between TaSe₂ and Au(111), respectively. STM measurement conditions: V_b = −0.5 V, I_t = 1.0 nA.

Since TaSe₂ can present both 2H and 1 T phases and they exhibit different atomic configurations,²⁹ XPS and HREELS were further conducted to confirm the phase of the as-grown TaSe₂. Core-levels of Ta measured by XPS show one set of peaks at the binding energies of 23.5 eV and 25.4 eV (Fig. 2(a)), corresponding to Ta 4f_7/2 and 4f_5/2 orbitals in 2H TaSe₂, respectively³¹ (different from those of 1T TaSe₂ at 22.6 eV and 24.4 eV³²). Meanwhile, XPS spectra of Se 3d exhibit two sets of peaks. The peaks at lower binding energies of 53.7 eV and 54.6 eV (Fig. 2(b)) are close to those of 2H TaSe₂ at 53.6 eV and 54.5 eV³¹ (different from those of 1T TaSe₂ at 53.3 eV and 54.1 eV³²). In addition, we also observed a minor set of Se components at the binding energies of 55.4 eV and 56.3 eV, close to those of elemental Se (55.6 eV and 56.5 eV).³³ Interestingly, these components were absent when we switched the deposition sequence of Se and Ta during growth (i.e., depositing Ta before Se, detailed discussions of growth with different deposition sequences could be found in the following text). The minor set of Se peaks could be possibly attributed to elemental Se at the interface between TaSe₂ and Au(111). Moreover, two electron energy loss signals were detected at 26 meV and 31 meV (Fig. 2(c)) by HREELS, in fair agreement with the characteristic E_2g and A_1g phonon modes³⁴ (215 cm⁻¹ and 233 cm⁻¹, equal to ∼27 meV and ∼29 meV, respectively) of monolayer 2H TaSe₂ previously measured by Raman spectroscopy and significantly different from those of 1T TaSe₂ at ∼185 cm⁻¹ (∼23 meV) and ∼105 cm⁻¹ (∼13 meV),³² confirming the 2H phase of the as-grown TaSe₂.

Fig. 2 XPS and HREELS spectra of the as-grown TaSe₂ monolayers. (a and b) XPS core-level spectra of Ta and Se, respectively. Dark blue lines and black circles denote the fitted and raw data, respectively. Black lines are backgrounds. Purple peaks in (a) represent the fitted components for Ta. Yellow and green peaks in (b) represent the fitted components for Se. The light blue peak in (b) represents the Au 5p_3/2 peak. Fitting details are shown in the ESI Table S1.† (c) HREELS spectra of the as-grown TaSe₂ monolayers. Inset: a zoomed-in spectrum of (c) after background subtraction.

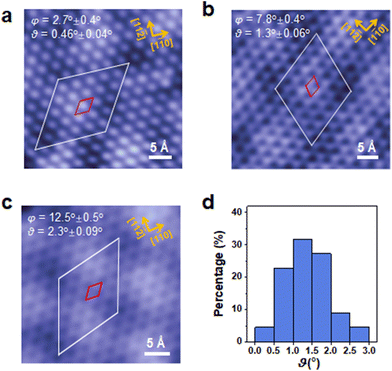
To understand the moiré structures of 2H TaSe₂ monolayers on Au(111), we analyzed 51 TaSe₂ flakes based on three experimental batches and obtained the statistical distribution of the rotation angles between the as-grown TaSe₂ and Au(111). It should be noted that, to ensure high quality STM images, typical sizes of the analyzed flakes are above ∼8 nm. Fig. 3(a)–(c) display three representative moiré patterns. Although they all present hexagonal moiré patterns, it can be seen that the orientations between the lattice of moiré and TaSe₂ are different. Detailed analysis confirms that the rotation angles (θ) between TaSe₂ and Au(111) in these three cases are 0.46° ± 0.04°, 1.3° ± 0.06° and 2.3° ± 0.09° (Fig. 3(a)–(c), respectively). All the analyzed angles are found to range from 0° to 3° and their distribution is shown in Fig. 3(d). TaSe₂ flakes with rotation angles between 1.0° and 1.5° occupy the biggest population (∼32%), and ∼82% of the as-grown flakes exhibit rotations between 0.5° and 2.0°.

Fig. 3 Different moiré orientations of 2H TaSe₂ monolayers on Au(111). (a–c) Atomic scale STM images of the moiré structures on three different TaSe₂ flakes. V_b = −1.0 V, I_t = 1.0 nA. The angle between moiré and TaSe₂ lattices is represented by φ. The rotation angle between TaSe₂ and Au(111) lattices is represented by θ. The white and red rhombuses indicate the moiré and TaSe₂ unit cells, respectively. Note the crystal orientations of Au(111) are different in (a–c) (indicated by the yellow arrows). It is because (a–c) are results from different experimental batches and the Au(111) crystal was remounted a few times during the experiment. (d) Distribution of the rotation angle θ based on the analyzed 51 TaSe₂ flakes.

Further, we investigated the origin of the small rotation angles. We observed that the overall lattice rotations of the as-grown TaSe₂ exhibit strong dependence on the deposition sequence of Se and Ta in the growth. When Se was first deposited on Au, TaSe₂ is likely to present various small rotation angles (schematically depicted in Fig. 4(a)) as discussed above. In contrast, when Ta was first deposited on Au, TaSe₂ mostly demonstrates perfectly aligned lattices (schematically depicted in Fig. 4(b)). Topographic and atomic resolution moiré structures of TaSe₂ grown by first depositing Ta on Au are shown in Fig. 4(c) and (d), respectively (more details in Fig. S5†). It can be seen that the orientations of moiré superlattice and TaSe₂ lattice are perfectly aligned with each other, suggesting a 0° rotation relation between TaSe₂ and underlying Au lattice. The periodicity of the moiré superlattice is 16.2 ± 0.1 Å. Further analysis (Fig. 4(e)) of 47 TaSe₂ flakes shows that θ = 0° dominates the rotation angles, accounting for ∼88% of the analyzed flakes, dramatically different from the case when Se was deposited first on Au. We attribute this intriguing difference to the interfacial fluctuation induced by Se at the interface of TaSe₂ and Au(111). Since it is known that interfacial intercalation can trigger twisting in 2D layers,³⁵ when Se is first deposited on Au, it is possible that interfacial Se forms on Au(111) upon annealing,^23,36 generating thermal fluctuations and resulting in the growth of TaSe₂ with small rotation angles. In contrast, when Ta is first deposited on Au, no interfacial Se exists between TaSe₂ and Au (Fig. 4(f), compared with Fig. 2(b), only Se XPS peaks corresponding to 2H TaSe₂, at the binding energies of 53.7 eV and 54.6 eV, were observed). Therefore, TaSe₂ prefers the perfectly aligned lattices on Au(111). To confirm the existence/lack of interfacial Se, further characterizations by other surface-sensitive and high-resolution techniques such as synchrotron XPS^37,38 and X-ray standing wave (XSW)^37,38 are worth considering in future studies.

Fig. 4 Moiré structures of 2H TaSe₂ on Au with different deposition sequences. (a and b) Schematic illustrations of moiré structures of 2H TaSe₂ on Au when changing the deposition sequence of Se and Ta, respectively. (c and d) Topographic and atomic structures images of the perfectly aligned TaSe₂ lattices on Au, respectively. V_b = −1.0 V, I_t = 1.0 nA. The white and red rhombuses in (c) and (d) indicate the moiré and TaSe₂ unit cells, respectively. The white and red arrows in (d) are the lattice vectors of moiré and TaSe₂ lattices, respectively. (e) Distribution of the rotation angle θ based on the analyzed 47 TaSe₂ flakes grown by depositing Ta first on Au in the growth. (f) Se 3d XPS spectra on a sample grown by depositing Ta first on Au(111). Black circles and dark blue curves represent raw and fitted curves, respectively. Yellow components are Se in TaSe₂. The light blue component is the Au 5p_3/2 peak.

We also observed that changes in the orientations of moiré superlattices appeared along with defects formed during the growth. Fig. 5(a) shows the continuity of the moiré superlattice is disrupted by a hole defect in the TaSe₂ flake. With the hole defect in the center, an area within ∼8 nm from the defect is obviously distorted. Moiré orientations could also be affected by line defects (e.g. edges and grain boundaries). The orientation of the moiré superlattice in Fig. 5(b) demonstrates a sudden rotation of 20° inside a single triangular flake, indicating two lattice orientations in this flake. This is unusual for a single synthesized triangular TMDC flake because it typically exhibits single crystallinity within the entire flake.^39,40 The different lattice orientations could possibly be attributed to strain induced during growth from the edges.⁴¹ This phenomenon was also observed when two TaSe₂ flakes are connected by a grain boundary. In Fig. 5(c), two moiré superlattices exhibit an angle of 9° between them, separated by a grain boundary that makes a change in the orientations of the two moiré superlattices.

Fig. 5 Moiré orientations near defects. (a) Moiré structures affected by a hole defect. The black dashed circle approximately outlines the area of moiré lattices that are disturbed. (b and c) Moiré orientations affected by line defects. The two black arrows in (b) point to the edges of the flake (and another flake at lower left). Dashed white lines in (b) and (c) are guides for eyes for the orientations of moiré superlattices. Black dashed lines in (b) and (c) approximately indicate the boundaries where moiré patterns change orientations. V_b = −0.5 V, I_t = 1.0 nA.

It has been well-known that defects in 2D materials are actively involved in triggering local atomic reconstruction,⁴² creating novel atomic structures,⁴³ inducing atomic movement and phase transitions.^42,44 Here, defects may play a role in inducing local atomic migration and strain field,^45,46 thus contributing to lattice rotations. To further clarify the role of defects in moiré formation, atomic-scale dynamic imaging approaches, such as transmission electron microscopy (TEM), could be conducted in future. With electron beam irradiation during imaging, real-time defect formation and its role in disturbing moiré patterns could be further studied.

Conclusions

In summary, we demonstrated the epitaxial growth of TaSe₂ monolayers on Au(111) and the moiré structures formed by the two lattices. The 2H phase of the as-grown TaSe₂ was confirmed by the observation of characteristic binding energies in XPS and phonon modes in HREELS spectra. Further, by resolving atomic structures characterized using STM, we observed different rotation angles between the as-grown TaSe₂ lattices and the moiré superlattices. Statistical analysis showed that the TaSe₂ lattices exhibited small rotation angles with respect to the underlying Au(111) lattices, ranging from 0° to 3°, with most rotation angles between 1.0° and 1.5°. More importantly, we illustrated that the small-rotation-angle moiré structures were likely to grow when Se was first deposited on Au. Depositing Ta first leads to the dominant growth of perfectly aligned TaSe₂ lattices. This difference may result from interfacial Se which disturbs lattice alignment and weakens sample-substrate interaction during growth. An interesting comparison may be made with, for example, the role of a 2D material in remote epitaxy,^47,48 where interfacial interactions are also weakened. Our approach and findings (such as the deposition order of different elements may lead to different alignments) may offer new insights to enhance the control of other methods of 2D materials growth (such as remote epitaxy), thereby facilitating the fabrication of advanced semiconductors and oxide films for future electronics. In addition, we demonstrated that defects, including hole and line defects, can be associated with changing orientations of moiré superlattices. Our work sheds new light on the understanding of synthesized moiré structures. Future studies, such as using a 2D single crystal substrate or proper interfacial engineering, can be conducted for the general synthesis of 2D moiré vdW structures particularly with small rotation angles, thus promoting both their fundamental studies and twistronic applications.

Author contributions

L.L. conceived the idea and designed the experiments. L.L. and D.Y.Z. performed the experiments and data analysis, with advice from Y.P.C. All authors co-wrote the paper and gave approval of the final version.

Data availability

Data related to this paper are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This experimental work was supported by the U.S. Department of Energy (Office of Basic Energy Sciences) under Award No. DE-SC0019215 and Multidisciplinary University Research Initiatives (MURI) Program under Award No. FA9550-20-1-0322. We also acknowledge the Villum Investigator program (Grant No. 25931) for supporting the data analysis.

References

1. E. Khalaf, A. J. Kruchkov, G. Tarnopolsky and A. Vishwanath, Phys. Rev. B, 2019, 100, 085109.
2. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50.
3. Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras, R. C. Ashoori and P. Jarillo-Herrero, Nature, 2018, 556, 80–84.
4. K. Tran, G. Moody, F. Wu, X. Lu, J. Choi, K. Kim, A. Rai, D. A. Sanchez, J. Quan, A. Singh, J. Embley, A. Zepeda, M. Campbell, T. Autry, T. Taniguchi, K. Watanabe, N. Lu, S. K. Banerjee, K. L. Silverman, S. Kim, E. Tutuc, L. Yang, A. H. MacDonald and X. Li, Nature, 2019, 567, 71–75.
5. K. L. Seyler, P. Rivera, H. Yu, N. P. Wilson, E. L. Ray, D. G. Mandrus, J. Yan, W. Yao and X. Xu, Nature, 2019, 567, 66–70.
6. J. Cai, E. Anderson, C. Wang, X. Zhang, X. Liu, W. Holtzmann, Y. Zhang, F. Fan, T. Taniguchi, K. Watanabe, Y. Ran, T. Cao, L. Fu, D. Xiao, W. Yao and X. Xu, Nature, 2023, 622, 63–68.
7. H. Park, J. Cai, E. Anderson, Y. Zhang, J. Zhu, X. Liu, C. Wang, W. Holtzmann, C. Hu, Z. Liu, T. Taniguchi, K. Watanabe, J. H. Chu, T. Cao, L. Fu, W. Yao, C. Z. Chang, D. Cobden, D. Xiao and X. Xu, Nature, 2023, 622, 74–79.
8. F. Xu, Z. Sun, T. Jia, C. Liu, C. Xu, C. Li, Y. Gu, K. Watanabe, T. Taniguchi, B. Tong, J. Jia, Z. Shi, S. Jiang, Y. Zhang, X. Liu and T. Li, Phys. Rev. X, 2023, 13, 031037.
9. Y. Zeng, Z. Xia, K. Kang, J. Zhu, P. Knuppel, C. Vaswani, K. Watanabe, T. Taniguchi, K. F. Mak and J. Shan, Nature, 2023, 622, 69–73.
10. G. H. Cheng, M. M. Rahman, A. L. Allcca, A. Rustagi, X. T. Liu, L. N. Liu, L. Fu, Y. L. Zhu, Z. Q. Mao, K. Watanabe, T. Taniguchi, P. Upadhyaya and Y. P. Chen, Nat. Electron., 2023, 6, 434–442.
11. Y. Xu, A. Ray, Y. T. Shao, S. Jiang, K. Lee, D. Weber, J. E. Goldberger, K. Watanabe, T. Taniguchi, D. A. Muller, K. F. Mak and J. Shan, Nat. Nanotechnol., 2022, 17, 143–147.
12. H. Xie, X. Luo, G. Ye, Z. Ye, H. Ge, S. H. Sung, E. Rennich, S. Yan, Y. Fu, S. Tian, H. Lei, R. Hovden, K. Sun, R. He and L. Zhao, Nat. Phys., 2021, 18, 30–36.
13. M. Fortin-Deschenes, K. Watanabe, T. Taniguchi and F. Xia, Nat. Mater., 2024, 23, 339–346.
14. W. M. Zhao, L. Zhu, Z. Nie, Q. Y. Li, Q. W. Wang, L. G. Dou, J. G. Hu, L. Xian, S. Meng and S. C. Li, Nat. Mater., 2022, 21, 284–289.
15. L. Sun, Z. Wang, Y. Wang, L. Zhao, Y. Li, B. Chen, S. Huang, S. Zhang, W. Wang, D. Pei, H. Fang, S. Zhong, H. Liu, J. Zhang, L. Tong, Y. Chen, Z. Li, M. H. Rummeli, K. S. Novoselov, H. Peng, L. Lin and Z. Liu, Nat. Commun., 2021, 12, 2391.
16. C. Liu, Z. Li, R. Qiao, Q. Wang, Z. Zhang, F. Liu, Z. Zhou, N. Shang, H. Fang, M. Wang, Z. Liu, Z. Feng, Y. Cheng, H. Wu, D. Gong, S. Liu, Z. Zhang, D. Zou, Y. Fu, J. He, H. Hong, M. Wu, P. Gao, P. H. Tan, X. Wang, D. Yu, E. Wang, Z. J. Wang and K. Liu, Nat. Mater., 2022, 21, 1263–1268.
17. R. He, T. F. Chung, C. Delaney, C. Keiser, L. A. Jauregui, P. M. Shand, C. C. Chancey, Y. Wang, J. Bao and Y. P. Chen, Nano Lett., 2013, 13, 3594–3601.
18. S. G. Sorensen, H. G. Fuchtbauer, A. K. Tuxen, A. S. Walton and J. V. Lauritsen, ACS Nano, 2014, 8, 6788–6796.
19. F. Tumino, C. S. Casari, M. Passoni, V. Russo and A. L. Bassi, Nanoscale Adv., 2019, 1, 643–655.
20. M. Gao, Y. Pan, L. Huang, H. Hu, L. Z. Zhang, H. M. Guo, S. X. Du and H. J. Gao, Appl. Phys. Lett., 2011, 98, 033101.
21. P. Zeller and S. Günther, New J. Phys., 2014, 16, 083028.
22. P. Merino, M. Svec, A. L. Pinardi, G. Otero and J. A. Martin-Gago, ACS Nano, 2011, 5, 5627–5634.
23. F. Cheng, Z. Hu, H. Xu, Y. Shao, J. Su, Z. Chen, W. Ji and K. P. Loh, ACS Nano, 2019, 13, 2316–2323.
24. D. E. Moncton, J. D. Axe and F. J. DiSalvo, Phys. Rev. Lett., 1975, 34, 734–737.
25. R. M. Fleming, D. E. Moncton, D. B. McWhan and F. J. DiSalvo, Phys. Rev. Lett., 1980, 45, 576–579.
26. H. Ryu, Y. Chen, H. Kim, H. Z. Tsai, S. Tang, J. Jiang, F. Liou, S. Kahn, C. Jia, A. A. Omrani, J. H. Shim, Z. Hussain, Z. X. Shen, K. Kim, B. I. Min, C. Hwang, M. F. Crommie and S. K. Mo, Nano Lett., 2018, 18, 689–694.
27. K. Yokota, G. Kurata, T. Matsui and H. Fukuyama, Phys. B, 2000, 284–288, 551–552.
28. T. Kumakura, H. Tan, T. Handa, M. Morishita and H. Fukuyama, Czech. J. Phys., 1996, 46, 2611–2612.
29. J. A. Yan, M. A. D. Cruz, B. Cook and K. Varga, Sci. Rep., 2015, 5, 16646.
30. A. Maeland and T. B. Flanagan, Can. J. Phys., 1964, 42, 2364.
31. M. L. Adam, I. B. Garba, A. A. Bala, A. A. Suleiman, S. M. Gana and F. L. Adam, Phys. Rev. B, 2023, 107, 104510.
32. H. Wang, Y. Chen, C. Zhu, X. Wang, H. Zhang, S. H. Tsang, H. Li, J. Lin, T. Yu, Z. Liu and E. H. T. Teo, Adv. Funct. Mater., 2020, 30, 2001903.
33. J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, Perkin-Elmer Corporation, Physical Electronics Division, Eden Prairie, Minnesota, USA, 1992.
34. P. Hajiyev, C. Cong, C. Qiu and T. Yu, Sci. Rep., 2013, 3, 2593.
35. B. Li, J. Wei, C. Jin, K. Si, L. Meng, X. Wang, Y. Jia, Q. He, P. Zhang, J. Wang and Y. Gong, Nano Lett., 2023, 23, 5475–5481.
36. B. Liu, Y. Zhuang, Y. D. Que, C. Q. Xu and X. D. Xiao, Chin. Phys. B, 2020, 29, 056801.
37. C. C. Silva, D. Dombrowski, N. Atodiresei, W. Jolie, F. F. zum Hagen, J. Q. Cai, P. T. P. Ryan, P. K. Thakur, V. Caciuc, S. Blügel, D. A. Duncan, T. Michely, T. L. Lee and C. Busse, 2D Mater., 2022, 9, 025003.
38. C. C. Silva, D. Dombrowski, A. Samad, J. Q. Cai, W. Jolie, J. Hall, P. T. P. Ryan, P. K. Thakur, D. A. Duncan, T. L. Lee, U. Schwingenschlögl and C. Busse, Phys. Rev. B, 2021, 104, 205414.
39. L. Liu, H. Qiu, J. Wang, G. Xu and L. Jiao, Nanoscale, 2016, 8, 4486–4490.
40. S. Zhou, L. Liu, S. Cui, X. Ping, D. Hu and L. Jiao, Nano Res., 2020, 14, 1659–1662.
41. S. E. Krasavin and V. A. Osipov, Sci. Rep., 2022, 12, 14553.
42. Y. C. Lin, D. O. Dumcenco, Y. S. Huang and K. Suenaga, Nat. Nanotechnol., 2014, 9, 391–396.
43. J. Kotakoski, A. V. Krasheninnikov, U. Kaiser and J. C. Meyer, Phys. Rev. Lett., 2011, 106, 105505.
44. S. Cho, S. Kim, J. H. Kim, J. Zhao, J. Seok, D. H. Keum, J. Baik, D. H. Choe, K. J. Chang, K. Suenaga, S. W. Kim, Y. H. Lee and H. Yang, Science, 2015, 349, 625–628.
45. K. Parto, S. I. Azzam, K. Banerjee and G. Moody, Nat. Commun., 2021, 12, 3585.
46. K. Burns, A. M. Z. Tan, H. Gordon, T. Y. Wang, A. Gabriel, L. Shao, R. G. Hennig and A. Aitkaliyeva, Phys. Rev. B, 2020, 102, 085421.
47. B. I. Park, J. Kim, K. Lu, X. Zhang, S. Lee, J. M. Suh, D. H. Kim, H. Kim and J. Kim, Nano Lett., 2024, 24, 2939–2952.
48. Y. Kim, S. S. Cruz, K. Lee, B. O. Alawode, C. Choi, Y. Song, J. M. Johnson, C. Heidelberger, W. Kong, S. Choi, K. Qiao, I. Almansouri, E. A. Fitzgerald, J. Kong, A. M. Kolpak, J. Hwang and J. Kim, Nature, 2017, 544, 340–343.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03398a

---