Open Access Article
Open Access ArticleAtomic-level mechanisms of abnormal activation in NRAS oncogenes from two-dimensional free energy landscapes†
Zheyao
Hu‡
 and
Jordi
Martí‡
and
Jordi
Martí‡
 *
*
Department of Physics, Polytechnic University of Catalonia-Barcelona Tech, B5-209 Northern Campus, Jordi Girona 1-3, 08034 Barcelona, Catalonia, Spain. E-mail: jordi.marti@upc.edu; Fax: +3493 4017100; Tel: +34 93 4017184
First published on 23rd December 2024
Abstract
The NRAS-mutant subset of melanoma is one of the most aggressive and lethal types associated with poor overall survival. Unfortunately, a low understanding of the NRAS-mutant dynamic behavior has led to the lack of clinically approved therapeutic agents able to directly target NRAS oncogenes. In this work, accurate local structures of NRAS and its mutants have been fully explored through the corresponding free energy surfaces obtained by microsecond scale well-tempered metadynamics simulations. Free energy calculations are crucial to reveal the precise mechanisms of Q61 mutations at the atomic level. Considering specific atom–atom distances d and angles ϕ as appropriate reaction coordinates we have obtained free energy surfaces revealing local and global minima together with their main transition states, unveiling the mechanisms of abnormal NRAS activation from the atomic-level and quantitatively analyzing the corresponding stable states. This will help in advancing our understanding of the basic mechanisms of NRAS mutations, offering new opportunities for the design of potential inhibitors.
1 Introduction
RAS families play a central role in a variety of cellular processes such as signaling, survival, apoptosis or membrane trafficking.1–3 They function like “binary switches” cycling between active (GTP-bound)4,5 and inactive (GDP-bound) states.6 When activated, they can interact with effector proteins that control fundamental biological processes such as EGFR,7–9 MAPK10,11 or PI3K.12 However, excessive activation of RAS will eventually lead to cancers, such as melanoma, colorectal, lung and, especially, pancreatic cancer.13,14 Mutations of RAS key residues such as G12, G13 and G61, are found in more than 30% of human tumors.15 Given its importance, the RAS family of oncogenes has been extensively studied from long ago, in computational and theoretical works16–19 and also by experimental methods such as NMR,20 X-ray21 and Fourier transform infrared spectroscopy.22,23 Specifically, the neuroblastoma RAS viral (v-ras) oncogene homolog (NRAS) is one of the most important RAS isoforms, with the typical mutated codon occurring at residue 61,14,24 so that the excessive activation of NRAS is highly associated with malignant melanoma. The NRAS Q61-mutant subset of melanoma shows aggressive clinical behavior, poor prognosis and low overall survival, annually causing the largest number of deaths.25–28It has been observed that NRAS mutations tend to stay in their active GTP-bound state as their most predominant conformation,29 mainly because the mutations are codon 61 impairing the intrinsic enzymatic activity of NRAS to hydrolyze GTP to GDP. This makes the task of drugging NRAS very difficult. Although several studies30–35 have been focused on the most relevant NRAS mutations and some immunotherapies are available to patients with cancers related to NRAS oncogenes,26 there is still a significant lack of knowledge on the detailed atomic level structure of NRAS and, especially, of efficient strategies capable of directly targeting NRAS.36–38 For instance, some inhibitors such as the potential inhibitor HM-387 have been recently designed in silico, in order to target the NRAS-Q61 positively charged mutant R61, inducing the GTP-bound NRAS-Q61 oncogenic mutations to an “off-like” state.35 However, its effectiveness still needs to be verified in a wet lab and in clinical practice. Therefore, the detailed conformation and local structure of NRAS still require a significant increase of knowledge, in order to be used for locating potential targeting pockets that may facilitate the discovery and improvement of potential drug-like compounds.
Detailed information on atomic interactions and local structures at the all-atom level of NRAS is of crucial importance in inhibitor development,39 given the difficulty to access nanoscale length and time in experimental measurements. In a previous work, the impact of NRAS-Q61 mutations on its structural characteristics was qualitatively investigated35 by means of microsecond time-scale molecular dynamics simulations. In this regard, quantitative properties such as free energy barriers associated with Q61 mutations and multidimensional free energy (hyper)surfaces (FES) of NRAS and their mutations in solution still remain to be revealed. Moreover, the choice of appropriate collective variables (CV) to accurately describe the dynamic behavior of NRAS remains unclear. To move forward in this direction, we report in the present work two high-quality CVs, which will be one cornerstone of the present and future RAS investigations.40–42 Overall, combined with well-tempered metadynamics (WTM) simulations, we report in the present work a series of FESs obtained in aqueous solution for the GTP-bound wild-type NRAS and its mutations, helping to foster subsequent medicinal development in wet lab experiments and in clinical tests.
2 Methods
2.1 System preparation and setups
In the present work we conducted WTM simulations of 5 NRAS isoforms with the same sequences represented as in a previous work.35 Each system contained one isoform of the GTP or GDP bound NRAS complex fully solvated by TIP3P water molecules43 in potassium chloride (0.15 M) and magnesium chloride (0.03 M) solution. The detailed numbers of particles in the simulation boxes are listed in Table 1. All WTM inputs were generated by means of the CHARMM-GUI solution builder44–46 assuming the CHARMM36m force field.47 All bonds involving hydrogens were set to fixed lengths, allowing fluctuations of bond distances and angles for the remaining atoms. The crystal structures of GDP-bound NRAS and GTP-bound NRAS were downloaded from RCSB PDB Protein Data Bank,48 namely file names “6zio” and “5uhv”. The sets of NRAS proteins (wild type, Q61R, Q61K and Q61L) were solvated in a water box, and all systems were energy minimized and well equilibrated (NVT ensemble) before generating the WTM simulations.| Species | WT | WT-GDP | R61 | K61 | L61 |
|---|---|---|---|---|---|
| Water | 5732 | 5695 | 5742 | 5738 | 5736 |
| K+ | 25 | 21 | 24 | 24 | 25 |
| Mg2+ | 4 | 4 | 4 | 4 | 4 |
| Cl− | 22 | 22 | 22 | 22 | 22 |
| Total atoms | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911 911 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884 884 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947 947 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 933 933 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 925 925 |
The GROMACS/2021 package (version released on January 28th, 2021) was employed49 for the system minimization and equilibration steps. The system was minimized with steepest descents and a conjugate-gradient step every 10 steps until convergence to Fmax 1000 kJ mol−1. After energy minimization, a time step of 1 fs was used in all equilibration simulations and the particle mesh Ewald method with a Coulomb radius of 1.2 nm was employed to compute long-ranged electrostatic interactions. The cutoff for Lennard-Jones interactions was set to 1.2 nm. The system was equilibrated for 1.25 μs with the Nosé–Hoover thermostat at 310.15 K in the NVT ensemble. Periodic boundary conditions in three directions of space have been taken.
2.2 Well-tempered metadynamics
A wide variety of methods has been proposed to handle the complex problem of computing free energy landscapes in multidimensional systems.50–54 In this work we have employed WTM, a method able to efficiently explore free energy surfaces of complex systems using multiple reaction coordinates, very successful for a wide variety of complex systems.40,55–59 The main advantage of WTM is its suitability for a wide variety of systems, including model cell membrane systems with attached small-molecules and proteins,60–63 recently developed in our group.After equilibration, we switched to running WTM simulations for each system in order to perform Gibbs free energy calculations, starting from the last configuration of MD simulations with the Nosé–Hoover thermostat at 310.15 K and the Parrinello–Rahman barostat at 1 atm in the NPT ensemble. Long well-tempered metadynamics simulations were performed using the joint GROMACS/2022.5-plumed-2.9.0 tool.64,65 Periodic boundary conditions in the three directions of space were also considered. The set of CVs adopted in the WTM simulations will be discussed in detail below (see section 3.1). We should point out that determining and using more than two CVs in a WTM simulation are hard challenges from the computational point of view and would produce a four-dimensional FES, unsuitable to deal with. A very usual choice is to consider one or two CVs.66 From our experience, the use of two CVs produces a complete enough description of the FES and it is the optimal way to proceed. It is a usual procedure to project the free energies onto one single coordinate, integrating out the contribution of the second CV. The values of the parameters taken for the two sets of WTM simulations67 are listed in Tables 2 and 3.
| Parameter | WT | WT-GDP | R61 | K61 | L61 |
|---|---|---|---|---|---|
| Gaussian width of d [nm] | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Gaussian width of ϕ [rad] | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Gaussian hill [kJ mol−1] | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 |
| Deposition stride [ps] | 1 | 1 | 1 | 1 | 1 |
| Biasfactor | 10 | 10 | 15 | 15 | 10 |
| Simulation time [μs] | 3 | 3 | 3 | 3 | 3 |
| Parameter | WT | R61 |
|---|---|---|
| Gaussian width of ψ [rad] | 0.5 | 0.5 |
| Gaussian hill [kJ mol−1] | 1.2 | 1.2 |
| Deposition stride [ps] | 1 | 1 |
| Biasfactor | 4 | 4 |
| Simulation time [μs] | 1 | 1 |
2.3 Data analysis and visualization
The R-package metadynminer was used to analyze the WTM results, such as calculating the free energy surface, finding minima and analyzing transition pathways between stable states (minimum free energy paths) in order to locate the transition states of the system.68 The software VMD69 was used for visualization purposes.3 Results
In a previous report,35 the effect of Q61 mutations on the microscopic configurations of NRAS was revealed at the atomic level. In the case of GTP-bound NRAS, we found that the positively charged mutations Q61R and Q61K maintain stable conformations comparable to wild-type NRAS and that the mutated residues R61 and K61 showed significant interaction properties with guanosine triphosphate (GTP) whereas, in a fully qualitatively different fashion, the mutation NRAS-Q61L (with the non-polar residue L61) can be captured by a hydrophobic pocket. Limited by unbiased simulations, the free energy barriers of these interactions cannot be accurately measured. Besides, the FESs of NRAS have not been reported yet. This information would be of crucial importance in order to fully understand the signaling of NRAS and the impact of Q61 mutations on it, as well as for subsequent pharmaceutical research and development. In order to access a clear and well defined FES, it is of paramount importance to know the best reaction coordinates or CV, to be employed in precise calculations. In the present work, we will evaluate the best CV candidates for NRAS and its mutations in aqueous ionic solution, and evaluate their reliability by computing the FES in each case. Moreover, the physical meaning of the results will be discussed and the proof of convergence of the WTM simulations will be reported in the ESI.†3.1 Well-tempered metadynamics simulations: collective variables
The enhanced sampling method WTM applies a time-dependent biasing potential along a set of CVs by adding a Gaussian additional bias potential to the total potential in order to overcome barriers larger than kBT, with kB being Boltzmann's constant and T the temperature. In the method, sampling is performed on a selected number of degrees of freedom (si), i.e. a chosen set of CVs. For each degree of freedom, the biased potential V(sit) is a dynamic function constructed as the sum of Gaussian functions:67,70,71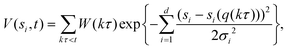 | (1) |
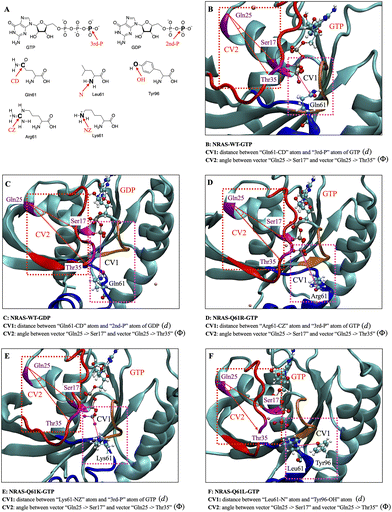
The conformational dynamics and biological effects of RAS families are mainly reflected by the structures of Switch-I (SW-I, residues 27–37) and Switch-II (SW-II, residues 58–64).19,35,73,74 So the CVs chosen in this work are directly related to SW-I and SW-II and they will help to fully describe all intermediate states of NRAS and its mutants.
After a thorough selection from a variety of distances and angular coordinates, the two CVs selected to perform the 2D WTM calculations are (see Fig. 1): (1) distances (CV1 d) between the 61st amino acid residue of NRAS and the terminal phosphate group of GTP/GDP. In the case of NRAS-Q61L, considering that the non-polar hydrophobic amino acid Leu61 cannot form stable interaction with the negatively charged phosphate group, we instead used the distance between Leu61 and Tyr96 as CV1 and (2) the angles between two vectors (CV2 ϕi) formed by the vector “GIn25-Cα → Ser17-Cα” and vector “GIn25-Cα → Thr35-Cα” in all cases. Among them, CV1 (d) characterizes the biological function of Q61 and the impact of Q61 mutations on the intrinsic GTPase function of NRAS and CV2 (ϕ) represents well the “on/off” status of switch-I. Detailed information for each CV is provided in Fig. 1. The averaged results for each CV are reported in the following sections 3.2 and 3.4. In addition, considering that the conformation of residue Tyr32 has a significant effect on the interaction between RAS and GAPs or effectors,75 we performed additional one-dimensional WTM simulations with the torsion angle of Tyr32 (ψ) as the collective variable, as seen in Table 3. For the sake of brevity, we will not make a separate figure for the CV (ψ) and instead it will be sketched together with the one-dimensional free energy profiles of ψ.
3.2 The two-dimensional free energy landscapes of NRAS wild-type and its main Q61 mutations
Two dimensional (2D) free energy landscapes of NRAS and its mutations are presented in Fig. 2 for the two selected CVs. We can observe that several main basins (minima such as A, B…) and their corresponding molecular conformations are well defined in all cases. We have only indicated the basins which are clearly seen from the FES, assuming that even with well converged runs the clearest definition of the FES would require a huge amount of statistics of the order of 20 μs, for each WTM simulation, out of the standard available ranges. The coordinates of the representative basins (minima) corresponding to Fig. 2 are reported in Table 4, whereas the detailed coordinates of minima are reported in ESI-Tables 1–5.† | ||
| Fig. 2 The 2D free energy landscape F(d,ϕ) (kJ mol−1) for wild-type NRAS and its Q61 mutations. Basins “A”, “B”, “C”, “D”, “E”, “F”, “G”, “H” and “I” are the stable states (minima) and are indicated in white. The conformations corresponding to the representative basins are listed on the right side of the 2D free energy landscape. The detailed complete Ras protein conformations corresponding to the representative basins are listed in the ESI.† | ||
| System | Basins | d [nm] | ϕ [rad] | Free energy [kJ mol−1] |
|---|---|---|---|---|
| WT-GTP | A | 0.7 | 2.1 | 0.0 |
| D | 0.7 | 0.5 | 2.4 | |
| E | 0.5 | 1.8 | 2.7 | |
| WT-GDP | A | 1.2 | 2.3 | 0.0 |
| B | 0.7 | 2.3 | 0.0 | |
| D | 1.0 | 0.4 | 14.2 | |
| R61-GTP | A | 0.4 | 1.1 | 0.0 |
| B | 0.4 | 0.4 | 2.7 | |
| C | 1.4 | 0.5 | 3.1 | |
| K61-GTP | A | 0.4 | 0.5 | 0.0 |
| B | 1.4 | 0.7 | 3.5 | |
| C | 1.4 | 2.1 | 7.7 | |
| L61-GTP | A | 0.3 | 0.8 | 0.0 |
| B | 1.5 | 1.1 | 9.1 | |
| C | 1.0 | 1.1 | 12.9 |
As a general concept, the basins in the FES indicate the most probable configurations of the system in equilibrium. As a matter of fact, WTM is able to reveal those stable configurations in such a way that the free energy barriers that the system needs to overcome to shift between stable states can be estimated with a high degree of accuracy. In this work, we can distinguish several basins for each simulation system proposed. In the case of GTP-bound wild-type NRAS, several stable states can be clearly observed (see Fig. 2A). GTP-bound wild-type NRAS is responsible for the normal biological signal transduction. The corresponding FES indicates that the conformation of wild-type NRAS is evenly distributed and that the free energy barriers required to switch between several stable states are of low magnitude. The most stable conformation is distributed between minima A, B and C. The representative conformation minimum A holds the SW-I half open, while SW-II remains compact. The residue Q61 stabilizes the water molecules around γ-phosphate through hydrogen-bond interactions (HB) and it is therefore responsible for the intrinsic GTP hydrolysis activity of NRAS. In the meta-stable state D, SW-I is closed and SW-II (especially residue Q61) shows a similar fashion with its configuration in minimum A. The above results indicate that Q61 can stabilize water molecules around γ-phosphate of GTP through HB. This is fully consistent with previously reported mechanisms indicating that residue Q61 participates in the intrinsic GTP hydrolysis activity of NRAS by stabilizing transient hydronium ions around the γ-phosphate,30–35 although unbiased classical MD simulations rather than QM/MM simulations were used in those investigations.
From our results we observe that in the GDP-bound wild-type NRAS case, both SW-I and SW-II are kept open, with a free energy difference between basins A, B and D of approximately 14.2 kJ mol−1, as shown on Fig. 2B and Table 4. In general, the release of the γ-phosphate after GTP hydrolysis allows the two switch regions to relax into a more “open” state, which is in good agreement with the so called “GDP-specific conformation”.6,19,76,77
Mutations in NRAS Q61 significantly reduce the intrinsic GTPase activity, leading to abnormal activation and ultimately causing cancer.78–81 In a previous work,35 we revealed the effect of Q61 mutations on the conformational characteristics of GTP/GDP-bound NRAS, while the global FES and the precise free energy barriers were estimated.35 In the GTP-bound NRAS Q61 positively charged mutations (Q61R and Q61K), the FES shows significant differences compared to GTP-bound wild-type NRAS, Fig. 2C and D. The positively charged Q61 mutations show a marked tendency to maintain the SW-I/II regions in a compact conformation. In the GTP-bound NRAS-Q61R case, the basins A and B at the FES correspond to the same distance d (0.4 nm) and two different angles (1.1, 0.4 rad), and this in good agreement with the previous results obtained from unbiased MD simulations.35
Furthermore, large free energy barriers of the system are explored by WTM so that an additional undiscovered meta-stable state can be found. For instance, the minimum C at the FES corresponds to the distance d = 1.4 nm and angle ϕ = 0.5 rad. In the case of GTP-bound NRAS-Q61K, due to the similar chemical structures and charge properties between R61 and K61, their FESs are quite similar. The basin A at the FES corresponds to the distance d = 0.4 nm and angle = 0.5 rad, whereas the meta-stable state B corresponds to the distance d = 1.4 nm and angle ϕ = 0.7 rad. In addition, since the side chain length of K61 is slightly smaller than that of R61, the interaction strength between K61 and GTP is slightly smaller than that of R61, making the largely opened conformation of NRAS-Q61K easier to reach in comparison with NRAS-Q61R, providing a stable basin C with the coordinates (1.4 nm, 2.1 rad). Finally, for the non-polar mutation Q61L, hydrophobic interactions of L61 with the hydrophobic pocket composed of D92, L95, Y96 and Q9935 can be also detected in the FES stable basin A with the coordinates (0.3 nm, 0.8 rad) (see Fig. 2E). Moreover, benefiting from the WTM, an unknown meta-stable state B (1.5 nm, 1.1 rad) corresponding to the dissociation of L61 from the hydrophobic pocket has also been identified.
3.3 The conformational transitions of GTP-bound NRAS wild-type, NRAS-Q61R and NRAS-Q61L
The barriers between stable state basins indicate the amount of free energy required for NRAS to exchange its conformation between stable configurations. Using the metadynminer method,68 we have been able to trace the minimum free energy path (MFEP) and calculate the energy barriers ΔF with high accuracy. Metadynminer tracks the MFEP by iteratively refining the path connecting stable states, which converges to the minimum free energy trajectory between them. Furthermore, the transition states (TS) between two selected stable states can also be determined from the knowledge of MFEP. To characterize the conformational change differences in FESs reported in Fig. 2, we have used the MFEP to explore the transition between different conformation changes of NRAS and its mutants. By means of comparing the effects of Q61 mutations on the local structures of the well-established potential binding pockets (SW-I/II), we may provide initial global structural differences that might help design anti-cancer drugs targeting the (meta)stable states reported in this work. The MFEP of GTP-bound NRAS and the corresponding main TS are reported in Fig. 3.The FES minima of GTP-bound wild-type NRAS were discussed in the above section 3.2. The two large free energy basins are mainly composed of minima A, B, and C and minima D and F, respectively. Consequently, minima A and D have been selected to represent the two stable states of GTP-bound wild-type NRAS and employed to calculate the MFEP between them (see Fig. 3A). The free energy differences between basins A and D have been estimated to be 2.4 kJ mol−1. Along the MFEP depicted in Fig. 3A, we identified free energy barriers ΔFTS–A from “A” to “TS” of 9.4 kJ mol−1, ΔFTS–B from “B” to “TS” of 8.0 kJ mol−1 and ΔFTS–D from “D” to “TS” of 7.0 kJ mol−1. From the MFEP and the screenshots of TS, the conformational changes of GTP-bound wild-type NRAS are mainly reflected in the “on/off” states of SW-I, while Q61 continues to stabilize the water molecules around γ-phosphate, again in good agreement with the hydrolysis mechanism of GTP.30–35
Considering the similarities between the NRAS positively charged mutations (R61 and K61), GTP-bound NRAS-Q61R will be taken as an example to introduce the effect of positively charged Q61 mutations on the conformational transitions. In the GTP-bound NRAS-Q61R case, at least three stable states (minima A, B and C) can be clearly detected. The free energy difference between basins B and C has been estimated to be 0.4 kJ mol−1 (see Table 4), so two MFEPs have been calculated to characterize the GTP-bound NRAS-Q61R conformational changes, namely MFEPA–B and MFEPA–C (see Fig. 3B). Along the MFEPA–B, the free energy barrier ΔFTS1–A from “A” to “TS1” is 27.0 kJ mol−1 and ΔFTS1–B from “B” to “TS1” is 24.3 kJ mol−1, so that the conformational TS1 is mainly correlated with the “on/off” state of SW-I. Correspondingly, along the MFEPA–C, the free energy barrier ΔFTS2–A from “A” to “TS2” is 30.3 kJ mol−1 and ΔFTS2–C from “C” to “TS2” is 27.3 kJ mol−1, so that the conformational TS2 is related to both SW-I and SW-II. Moreover, due to the significantly high TS free energy barriers ΔF, NRAS is “locked” in a small conformational region.
Our findings are in good qualitative agreement with the replica exchange simulation of Li et al.,75 who observed three clear minima in their computed FESs, mainly related to the proximity of the Switch-I region (represented by residue Tyr32) to the γ-phosphate tail of GTP. In addition, in a NMR study of Ras complexed to the GTPγS analogue, Spoerner et al.82 obtained activation free-energies around 40 kJ mol−1 for the binding of Ras (mutated residue 35) to the γ-phosphate of GTP, related to two main equilibrium basins. When RAS was bound to the effector RAF-RBD, the Gibbs free-energy for Tyr35S bound to γ-GTP was found to be about 30 kJ mol−1. Despite the fact that in the present work we considered the Q61 mutated site instead of T35, the similarity of the estimated binding affinities to GTP is quite remarkable. In comparison with other computational works, Chen et al.83 found barriers of KRAS-G12 and GTP binding between 3 and 6 kcal mol−1 using multiple replica-Gaussian accelerated molecular dynamics. The values reported by us (Fig. 3B and C) are slightly larger (around 24–27 kJ mol−1) but in reasonable qualitative agreement. Glennon et al.16 computed empirical valence bond differences in activation energies of free HRAS and catalysis by GAP and found values of 4 kcal mol−1 (wild-type) and 7 kcal mol−1 (GAP bound), respectively. The experimental values84 are of 4.5 and 6.5 kcal mol−1. We observed again, for the wild-type case, a reasonable qualitative agreement with the value of 7–9 kJ mol−1 reported in the present work (Fig. 3A).
Conversely, the GTP-bound NRAS-Q61L case is much simpler than the previous one, with three stable states (minima A, B and C) to be considered for the calculation of the MFEP (see Fig. 3C). Basin A is the most stable state, with free energy differences with basins B and C of 9.1 kJ mol−1 and 12.9 kJ mol−1, respectively (see Table 4), significantly larger than that in the previous R61 case. Along the MFEPA–C, the free energy barriers are: ΔFTS1–A from “A” to “TS1” of 25.1 kJ mol−1 and ΔFTS1–C from “C” to “TS1” of 12.3 kJ mol−1. Moreover, along the MFEPB–C, the free energy barriers are moderately smaller: ΔFTS2–B from “B” to “TS2” is 5.8 kJ mol−1 and ΔFTS2–C from “C” to “TS2” is 2.0 kJ mol−1. The physical meaning of MFEP between minima A, C and B relies on the binding and dissociation states of L61 with the hydrophobic pocket.
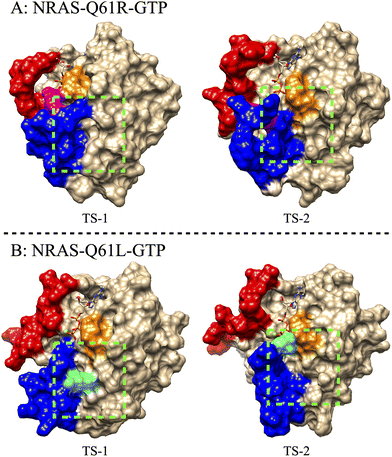
The intermediate conformational states related to TS configurations may be relevant for inhibitor designing. We show snapshots of such TS structures in Fig. 4, especially the TS of NRAS-Q61R and NRAS-Q61L. In the NRAS-Q61R-GTP case, “TS-1” and “TS-2” correspond to different intermediate states of NRAS-Q61R, whereas in “TS-1” the R61 residue maintains a tight interaction with the γ-phosphate of GTP, and in “TS-2” the interaction between R61 and γ-phosphate is interrupted. However, the targetable pocket between Switch-II and α-helix 335 still exists. This further demonstrates the feasibility of targeting NRAS-Q61R-GTP. As for the NRAS-Q61L-GTP case, in the “TS-1” state the L61 was captured by the hydrophobic pocket located on the α-helix 3 (composed of D92, L95, Y96 and Q99), and the targetable pocket between switch-II and α-helix 3 is blocked. L61 was released from the hydrophobic pocket in the “TS-2” state, so that the vacant hydrophobic pocket can become a potential binding site, for instance for the inhibitor “LIG1”, recently proposed by Lu et al.85
3.4 One-dimensional free energy profiles
From the 2D free energy landscapes and minimum free energy paths obtained from WTM simulations (Fig. 2 and 3) it is possible to obtain a one-dimensional (1D) free energy profile where one single CV is considered and the second one has been integrated out. This calculation along one single CV (si, i = 1, 2) allows us to directly compare free energy barriers to experimental findings, as pointed out by Jämbeck et al.86 These authors pointed out that a direct route to connect FESs to experiments is normally cumbersome, since information about binding modes in solutes obtained from experiments is normally not available. Then, it is possible to use standard binding free energies ΔGbind determined from experiments as an indirect measurement of the accuracy of computed free energy barriers. In the present work, 1D free energy profiles F(s1) (equivalent to the ΔGbind mentioned above) can be obtained as:86,87 | (2) |
 | ||
| Fig. 5 1D free energy profiles for two CVs (d,ϕ). Top row corresponds to: (A) the comparison of 1D free energy profiles between GTP-bound wild-type NRAS and GDP-bound wild-type NRAS; the second row corresponds to: (B) the comparison of 1D free energy profiles between GTP-bound wild-type NRAS and GTP-bound NRAS-Q61R/K; and the last row corresponds to: (C) the comparison of 1D free energy profiles between GTP-bound wild-type NRAS and GTP-bound NRAS-Q61L. In each row, the left column corresponds to the distances CV d, whereas the right column corresponds to the angles CV ϕ defined in Fig. 1 for each NRAS. In order to directly compute the height of free energy barriers, each absolute minimum has been set equal to zero. | ||
As a general fact, both angles ϕ and distances d characterize well the movement of the corresponding NRAS functional regions SW-I/II. The barriers for the free energies dependent on angles ϕ and distances d are in the range of 9 kJ mol−1, the largest in the GTP-bound wild-type NRAS case, and the free energies of distances d minimum tend to be located at the coordinate 0.7 nm, where Q61 plays the role of stabilizing the water molecules around γ-phosphate. When GTP is hydrolyzed to GDP, the coordinates corresponding to the free energy minima of ϕ and d both increased to 2.3 rad and 1.2 nm, respectively (see Fig. 5A). The barriers for the free energies dependent on ϕ are in the range of 22 kJ mol−1, which is the largest.
The GTP-bound NRAS-Q61 mutations show the opposite trend in comparison with the wild-type NRAS, as reported in Fig. 5B and C. The barriers for the free energies dependent on angles ϕ are similar to those obtained from wild-type NRAS, say around 6 to 13 kJ mol−1, while the free energy minimum coordinates are located at a smaller coordinate position: 0.5 rad for NRAS-Q61R, 0.7 rad for NRAS-Q61K and 0.8 rad for NRAS-Q61L. As for the distances d, there exist higher free energy barriers that force the system to remain at the smaller coordinate position. The free energy barriers for the R61/K61 interaction with γ-phosphate are 32 kJ mol−1 and 25 kJ mol−1, respectively, and the free energy barrier for the L61 interaction with the hydrophobic pocket on the α-helix 3 is 18 kJ mol−1. These values should be compared with the low barrier obtained in the Q61 case, of only 7 kJ mol−1 (Fig. 3A), indicating the difficulty of the mutated species in transferring from a “bound” to an “unbound” state. The difference can be attributed to the fact that the conformational changes in the wild-type species are mainly due to orientational changes, whereas in oncogenic species they are due to translational changes, as is clearly seen in the L61 case (Fig. 3C).
Moreover, it has been observed that the conformation of residue T32 has a significant impact on the binding of RAS to effector proteins. “T32in” is conducive to the combination of Ras and Raf, while “T32out” is conducive to the combination of Ras and GAPs, as described by Li et al.75 Following this idea, we have run additional one-dimensional WTM simulations using the specific torsion angle associated with residue T32 as the collective variable (CV, ψ). In this 1D free energy profile of ψ (Fig. 6), we have located “T32in/T32out” positions and a free energy difference between “T32in” and “T32out” (ΔFin–out = 5 kJ mol−1) for wild-type NRAS, which is in very good agreement with the values reported by Li et al.75 This fact also demonstrates the delicate balance between GTP hydrolysis and signaling in wild-type NRAS proteins. Furthermore, in the mutated NRAS-Q61R case, the free energy difference “T32in/T32out” is greatly enhanced (ΔFin–out ∼ 23 kJ mol−1). Regarding the TS, in the NRAS-Q61R case ΔFTS–R61–in = 35 kJ mol−1, compared to ΔFTS–R61–out = 11 kJ mol−1. This means that the GTP hydrolysis of NRAS-Q61R is inhibited (does not readily bind to GAPs) and is activated abnormally (tends to remain bound to RAF). These findings should be combined with the 2D WTM simulations (CVs, d and ϕ) from section 3.2, which revealed that the Q61 mutation will damage the intrinsic GTPase activity of NRAS. These results explain well the rarity of GDP-bound NRAS species in NRAS mutations and the fact that NRAS mutations can lead to overactivation of NRAS and ultimately cause cancer.
4 Conclusions
NRAS are small GTPases with the ability to regulate cell growth, differentiation and survival. The mutated NRAS shows a strong association with the malignant melanoma, which has an aggressive clinical behavior and poor prognosis, as well as a low overall survival rate. Several efforts have been focused on the structural and pharmaceutical aspects of NRAS-Q61 mutations, but validated inhibitors are still missing. There is also a lack of accurate FESs of NRAS and its mutants. The present study is an extension of previous investigations,35 where the WTM has been employed to evaluate the FES of NRAS and its Q61 mutations in detail. Their conformational differences in solution will help us understand the impact of the NRAS Q61 mutations and further promote the inhibitor design. In this work, we have conducted WTM simulations of five NRAS systems and obtained the corresponding FES, considering in all cases a specific pair of reaction coordinates or collective variables. Our simulations reached the scale of 3.0 μs, for a total of 15.0 μs. In all cases the convergence of the WTM simulations has been clearly proved. With the help of well-tempered metadynamics simulations we have calculated 2D FES and the 1D profiles after integrating out one CV. All conformationally accessible regions of NRAS and its mutations have been fully explored. We observed that each system has several stable states, which are the signature of the equilibrium configurations for each system. The two selected CVs are: (1) the distance d between the 61st amino acid residue of NRAS and the terminal phosphate group of GTP/GDP and (2) the angle ϕ between the two vectors defined by “GIn25-Cα → Ser17-Cα” and “GIn25-Cα → Thr35-Cα”.In the 2D FES of GTP-bound wild-type NRAS, a series of minima (“A” to “I”) were detected with conformations evenly distributed within the low free energy barriers. The main feature of the conformations corresponding to minima A, B and D is the existence of “bridge water”, which is stabilized between Q61 and γ-phosphate by hydrogen bonding interactions with them. This is well consistent with the reported intrinsic GTP hydrolysis mechanism of wild-type NRAS.30–35 A subsequent analysis of 1D free energy profiles revealed that the barriers for the free energies dependent on ϕ and d are in the range of 8 to 9 kJ mol−1. When GTP is hydrolyzed, accompanied by the dissociation of γ-phosphate, GDP-bound wild-type NRAS enters a so called “GDP-specific conformation” state,6,19,76,77 with the SW-I/II region largely opened. The free energy barrier to maintain this “GDP-specific conformation” state is approximately 22 kJ mol−1, around 3 times larger than that in the GTP-bound wild-type NRAS case. The NRAS Q61 mutation showed obvious differences in conformational changes compared with the wild type case. The most noticeable difference is related to the distance d, although the angles ϕ for the mutated species also tend to show smaller values in comparison with those of the wild-type case NRAS. For the positively charged mutations Q61R and Q61K, there exist large free energy barriers of 32 kJ mol−1 and 25 kJ mol−1, respectively, which correspond to the strong HBs between positively charged R61 (K61) and negatively charged γ-phosphate. In a previous work,35 we estimated by unbiased simulations the overall barriers of HBs between GDP-NRAS-R61(K61) and aqueous solutions to be 8.9 kBT (23 kJ mol−1) and 5.4 kBT (14 kJ mol−1), respectively. This indicates that in the case of GDP-bound NRAS-Q61R(K),35 SW-II can be separated from the protein surfaces, meanwhile the “GTP-bound” will maintain tight conformations in unbiased simulations.
In summary, benefiting from WTM simulations, we evaluated the FES of each NRAS case (rare GDP-bound NRAS-Q61 mutation cases are excluded) and accurately assessed the free energy barriers for the NRAS conformational changes and the effect of Q61 mutations on it. Meanwhile, through the WTM, we also calculated the free energy barriers for the interactions of R61(K61)-GTP and L61 with the hydrophobic pocket located on α-helix3 (approximately 18 kJ mol−1), which could not be accurately evaluated by the unbiased simulations. Furthermore, the knowledge of stable and transition states obtained from 2D (CVs d,ϕ) and 1D (CV ψ) WTM simulations for the RAS family, represented in the present work on the NRAS sub-species, is crucial for a deep understanding of how mutations affect RAS signal transduction. The NRAS-Q61 mutations can keep NRAS continuously activated by destroying its intrinsic GTPase activity and weakening its interaction with GAPs. In addition, the NRAS-Q61 mutation causes NRAS to maintain a dominant conformation (“T32in”) for binding to Raf, promoting the continuous activation of downstream signaling pathways and ultimately leading to cancer. On the other hand, a detailed study of SOS1–KRAS interactions at the atomic level has been recently published.88 The latter will provide another perspective on mutations leading to abnormal activation of RAS. We can conclude that the methodology and results presented here can be useful tools to provide detailed atomic-level structural information for the development/optimization of specific inhibitors for NRAS-Q61 mutations in the further investigation.
Author contributions
Zheyao Hu: data curation, formal analysis, writing – original draft preparation, visualization, investigation, software, and validation. Jordi Martí: conceptualization, writing – reviewing and editing, resources, supervision, and funding acquisition.Data availability
The crystal structure files and MD simulation files (input files, parameter files, topology files, plumed files etc.) are all available on the website https://github.com/Zheyao-Hu/NRAS-plumed. Moreover, all software (free to use) mentioned in the text is the official release version without any modification.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We are thankful for the financial support provided by the Spanish Ministry of Science, Innovation and Universities (funds MCIU/AEI/FEDER, EU). This publication is a part of the I + D + i project number PID2021-124297NB-C32, funded by MCIN/AEI/10.13039/501100011033/ and “FEDER Una manera de hacer Europa”. Zheyao Hu is a Ph.D. fellow from the Chinese Scholarship Council (grant 202006230070). J. M. thanks the Generalitat de Catalunya for the support through the grant Grup de Recerca SGR-Cat2021 Condensed, Complex and Quantum Matter Group reference 2021SGR-01411 and the Polytechnic University of Catalonia-Barcelona Tech through the funding AGRUPS. Computational resources awarded by the Barcelona Supercomputing Center-Spanish Supercomputing Network (grant BCV-2024-2-0005 “Simulation and modeling of biosystems with applications to medicine (1): drug design for the treatment of cancers of the RAS family”) are also acknowledged.References
- J. Cherfils and M. Zeghouf, Physiol. Rev., 2013, 93, 269–309 CrossRef CAS.
- J. M. Ostrem and K. M. Shokat, Nat. Rev. Drug Discovery, 2016, 15, 771–785 CrossRef CAS.
- W. Kolch, D. Berta and E. Rosta, Biochem. J., 2023, 480, 1–23 Search PubMed.
- G. Li and X. C. Zhang, J. Mol. Biol., 2004, 340, 921–932 CrossRef CAS.
- M. Spoerner, C. Hozsa, J. A. Poetzl, K. Reiss, P. Ganser, M. Geyer and H. R. Kalbitzer, J. Biol. Chem., 2010, 285, 39768–39778 CrossRef CAS.
- I. R. Vetter and A. Wittinghofer, Science, 2001, 294, 1299–1304 CrossRef CAS PubMed.
- N. Normanno, S. Tejpar, F. Morgillo, A. De Luca, E. Van Cutsem and F. Ciardiello, Nat. Rev. Clin. Oncol., 2009, 6, 519–527 CrossRef CAS PubMed.
- C. M. Ardito, B. M. Grüner, K. K. Takeuchi, C. Lubeseder-Martellato, N. Teichmann, P. K. Mazur, K. E. DelGiorno, E. S. Carpenter, C. J. Halbrook and J. C. Hall, et al. , Cancer Cell, 2012, 22, 304–317 CrossRef CAS PubMed.
- C. Navas, I. Hernández-Porras, A. J. Schuhmacher, M. Sibilia, C. Guerra and M. Barbacid, Cancer Cell, 2012, 22, 318–330 CrossRef CAS.
- K. W. Wood, C. Sarnecki, T. M. Roberts and J. Blenis, Cell, 1992, 68, 1041–1050 CrossRef CAS.
- L. R. Howe, S. J. Leevers, N. Gómez, S. Nakielny, P. Cohen and C. J. Marshall, Cell, 1992, 71, 335–342 Search PubMed.
- P. Rodriguez-Viciana, P. H. Warne, R. Dhand, B. Vanhaesebroeck, I. Gout, M. J. Fry, M. D. Waterfield and J. Downward, Nature, 1994, 370, 527–532 CrossRef CAS PubMed.
- S. Li, A. Balmain and C. M. Counter, Nat. Rev. Cancer, 2018, 18, 767–777 CrossRef CAS.
- A. R. Moore, S. C. Rosenberg, F. McCormick and S. Malek, Nat. Rev. Drug Discovery, 2020, 19, 533–552 Search PubMed.
- Y. Pylayeva-Gupta, E. Grabocka and D. Bar-Sagi, Nat. Rev. Cancer, 2011, 11, 761–774 CrossRef CAS PubMed.
- T. M. Glennon, J. Villa and A. Warshel, Biochemistry, 2000, 39, 9641–9651 CrossRef CAS.
- N. Futatsugi and M. Tsuda, Biophys. J., 2001, 81, 3483–3488 CrossRef CAS.
- M. Klähn, J. Schlitter and K. Gerwert, Biophys. J., 2005, 88, 3829–3844 CrossRef PubMed.
- Z. Hu and J. Marti, Int. J. Mol. Sci., 2022, 23, 13865 CrossRef CAS PubMed.
- M. Spoerner, C. Herrmann, I. R. Vetter, H. R. Kalbitzer and A. Wittinghofer, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 4944–4949 CrossRef CAS PubMed.
- K. Scheffzek, M. R. Ahmadian, W. Kabsch, L. Wiesmuller, A. Lautwein, F. Schmitz and A. Wittinghofer, Science, 1997, 277, 333–339 CrossRef CAS.
- C. Allin, M. R. Ahmadian, A. Wittinghofer and K. Gerwert, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7754–7759 CrossRef CAS.
- C. Kötting, M. Blessenohl, Y. Suveyzdis, R. S. Goody, A. Wittinghofer and K. Gerwert, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13911–13916 CrossRef.
- I. A. Prior, F. E. Hood and J. L. Hartley, Cancer Res., 2020, 80, 2969–2974 CrossRef.
- D. B. Johnson and I. Puzanov, Curr. Treat. Options Oncol., 2015, 16, 1–12 CrossRef PubMed.
- T. Randic, I. Kozar, C. Margue, J. Utikal and S. Kreis, Cancer Treat. Rev., 2021, 99, 102238 CrossRef PubMed.
- D. Schadendorf, A. C. Van Akkooi, C. Berking, K. G. Griewank, R. Gutzmer, A. Hauschild, A. Stang, A. Roesch and S. Ugurel, Lancet, 2018, 392, 971–984 CrossRef PubMed.
- P. Nagarajan, M. M. Asgari, A. C. Green, S. M. Guhan, S. T. Arron, C. M. Proby, D. E. Rollison, C. A. Harwood and A. E. Toland, Clin. Cancer Res., 2019, 25, 2379–2391 CrossRef PubMed.
- C. Posch and S. Ortiz-Urda, Oncotarget, 2013, 4, 494 CrossRef PubMed.
- M. Frech, T. Darden, L. Pedersen, C. Foley, P. Charifson, M. Anderson and A. Wittinghofer, Biochemistry, 1994, 33, 3237–3244 CrossRef PubMed.
- R. H. Tichauer, G. Favre, S. Cabantous, G. Landa, A. Hemeryck and M. Brut, Biophys. J., 2018, 115, 1417–1430 CrossRef PubMed.
- E. T. Novelli, J. T. First and L. J. Webb, Biochemistry, 2018, 57, 6356–6366 CrossRef PubMed.
- R. H. Tichauer, G. Favre, S. Cabantous and M. Brut, J. Phys. Chem. B, 2019, 123, 3935–3944 CrossRef PubMed.
- K. A. Maegley, S. J. Admiraal and D. Herschlag, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8160–8166 CrossRef PubMed.
- Z. Hu and J. Martí, Computational and structural biotechnology journal, 2024 Search PubMed.
- I. V. Fedorenko, G. T. Gibney and K. S. Smalley, Oncogene, 2013, 32, 3009–3018 CrossRef.
- D. B. Johnson, C. M. Lovly, M. Flavin, K. S. Panageas, G. D. Ayers, Z. Zhao, W. T. Iams, M. Colgan, S. DeNoble and C. R. Terry, et al. , Cancer Immunol. Res., 2015, 3, 288–295 CrossRef PubMed.
- L. E. Davis, S. C. Shalin and A. J. Tackett, Cancer Biol. Ther., 2019, 20, 1366–1379 CrossRef.
- D. Liu, Y. Mao, X. Gu, Y. Zhou and D. Long, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2024725118 CrossRef.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 Search PubMed.
- G. Bussi and A. Laio, Nat. Rev. Phys., 2020, 2, 200–212 CrossRef.
- J. McCarty and M. Parrinello, J. Chem. Phys., 2017, 147, 204109 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef PubMed.
- B. R. Brooks, C. L. Brooks III, A. D. Mackerell Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels and S. Boresch, et al. , J. Comput. Chem., 2009, 30, 1545–1614 CrossRef PubMed.
- J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong and Y. E. A. Qi, J. Chem. Theory Comput., 2016, 12, 405–413 CrossRef.
- J. Huang and A. D. MacKerell Jr., J. Comput. Chem., 2013, 34, 2135–2145 CrossRef PubMed.
- A. Kouranov, L. Xie, J. de la Cruz, L. Chen, J. Westbrook, P. E. Bourne and H. M. Berman, Nucleic Acids Res., 2006, 34, D302–D305 CrossRef PubMed.
- H. J. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef.
- H. M. Senn and W. Thiel, Atomistic approaches in modern biology, Springer, 2006, pp. 173–290 Search PubMed.
- P. L. Geissler, C. Dellago, D. Chandler, J. Hutter and M. Parrinello, Science, 2001, 291, 2121–2124 CrossRef.
- C. Dellago, P. G. Bolhuis and P. L. Geissler, Adv. Chem. Phys., 2002, 123, 1–78 CrossRef.
- J. Henin, G. Fiorin, C. Chipot and M. L. Klein, J. Chem. Theory Comput., 2009, 6, 35–47 CrossRef PubMed.
- C. Bartels and M. Karplus, J. Comput. Chem., 1997, 18, 1450–1462 CrossRef.
- G. Bussi, F. L. Gervasio, A. Laio and M. Parrinello, J. Am. Chem. Soc., 2006, 128, 13435–13441 CrossRef.
- M. Deighan, M. Bonomi and J. Pfaendtner, J. Chem. Theory Comput., 2012, 8, 2189–2192 CrossRef PubMed.
- J. C. Palmer, R. Car and P. G. Debenedetti, Faraday Discuss., 2013, 167, 77–94 RSC.
- S. Haldar, P. Kührová, P. Banáš, V. Spiwok, J. Sponer, P. Hobza and M. Otyepka, J. Chem. Theory Comput., 2015, 11, 3866–3877 CrossRef PubMed.
- J. Martí, Mol. Simul., 2018, 44, 1136–1146 CrossRef.
- H. Lu and J. Marti, Sci. Rep., 2020, 10, 9235 CrossRef CAS.
- H. Lu and J. Marti, J. Phys. Chem. Lett., 2020, 11, 9938–9945 CrossRef CAS PubMed.
- J. Martí and H. Lu, Int. J. Mol. Sci., 2021, 22, 2842 CrossRef.
- Z. Hu and J. Marti, Mol. Phys., 2024, e2316883 CrossRef.
- M. Bonomi, D. Branduardi, G. Bussi, C. Camilloni, D. Provasi, P. Raiteri, D. Donadio, F. Marinelli, F. Pietrucci and R. A. E. A. Broglia, Comput. Phys. Commun., 2009, 180, 1961–1972 CrossRef.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613 CrossRef.
- G. Bussi and D. Branduardi, et al. , Rev. Comput. Chem., 2015, 28, 1–49 Search PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- P. Hošek and V. Spiwok, Comput. Phys. Commun., 2016, 198, 222–229 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef.
- G. Bussi, A. Laio and M. Parrinello, Phys. Rev. Lett., 2006, 96, 090601 CrossRef.
- M. Bonomi, C. Camilloni and M. Vendruscolo, Sci. Rep., 2016, 6, 31232 CrossRef PubMed.
- H. Lu and J. Marti, Membranes, 2020, 10, 364 CrossRef PubMed.
- R. Nussinov, C.-J. Tsai and H. Jang, Cancer Res., 2018, 78, 593–602 CrossRef CAS PubMed.
- A. R. Moore, S. C. Rosenberg, F. McCormick and S. Malek, Nat. Rev. Drug Discovery, 2020, 19, 533–552 CrossRef CAS.
- Y. Li, Y. Zhang, F. Großeruschkamp, S. Stephan, Q. Cui, C. Kotting, F. Xia and K. Gerwert, J. Phys. Chem. Lett., 2018, 9, 1312–1317 CrossRef CAS PubMed.
- P. Grudzien, H. Jang, N. Leschinsky, R. Nussinov and V. Gaponenko, J. Mol. Biol., 2022, 434, 167695 CrossRef CAS PubMed.
- S. Lu, H. Jang, S. Muratcioglu, A. Gursoy, O. Keskin, R. Nussinov and J. Zhang, Chem. Rev., 2016, 116, 6607–6665 CrossRef CAS.
- J. P. McGrath, D. J. Capon, D. V. Goeddel and A. D. Levinson, Nature, 1984, 310, 644–649 CrossRef.
- R. W. Sweet, S. Yokoyama, T. Kamata, J. R. Feramisco, M. Rosenberg and M. Gross, Nature, 1984, 311, 273–275 CrossRef PubMed.
- M. Trahey and F. McCormick, Science, 1987, 238, 542–545 CrossRef PubMed.
- H. Adari, D. R. Lowy, B. M. Willumsen, C. J. Der and F. McCormick, Science, 1988, 240, 518–521 CrossRef.
- M. Spoerner, A. Nuehs, C. Herrmann, G. Steiner and H. R. Kalbitzer, FEBS J., 2007, 274, 1419–1433 CrossRef PubMed.
- J. Chen, S. Zhang, Q. Zeng, W. Wang, Q. Zhang and X. Liu, Front. Mol. Biosci., 2022, 9, 912518 CrossRef PubMed.
- P. Prakash and A. A. Gorfe, Mol. Simul., 2014, 40, 839–847 CrossRef PubMed.
- H. Lu, Z. Hu, J. Faraudo and J. Martí, Nanoscale, 2023, 15, 19359–19368 RSC.
- J. P. Jämbeck and A. P. Lyubartsev, J. Phys. Chem. Lett., 2013, 4, 1781–1787 CrossRef.
- B. Roux, Biophys. J., 1999, 77, 139–153 CrossRef.
- Z. Hu and J. Martí, Comput. Biol. Med., 2025, 186, 109599 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03372h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |