 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of magnetic convection on separation efficiency in magnetophoretic microfluidic processes: a combined simulation and experimental study†
Leonie
Wittmann‡
 a,
Emily
Krucker-Velasquez‡
a,
Emily
Krucker-Velasquez‡
 b,
Julia
Schaupp
a,
Laura
Westphal
a,
James W.
Swan§
b,
Julia
Schaupp
a,
Laura
Westphal
a,
James W.
Swan§
 b,
Alfredo
Alexander-Katz
b,
Alfredo
Alexander-Katz
 c,
Martin Z.
Bazant
c,
Martin Z.
Bazant
 b,
Sebastian P.
Schwaminger
b,
Sebastian P.
Schwaminger
 *ade and
Sonja
Berensmeier
*ade and
Sonja
Berensmeier
 af
af
aTechnical University of Munich, TUM School of Engineering and Design, Chair of Bioseparation Engineering, Boltzmannstr. 15, 85748 Garching, Germany. E-mail: s.schwaminger@tum.de
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
cDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA
dMedical University Graz, Otto-Loewi Research Center, Division of Medicinal Chemistry, Neue Stiftingtalstr. 6, 8010 Graz, Austria. E-mail: sebastian.schwaminger@medunigraz.at
eBioTechMed-Graz, Mozartgasse 12, 8010 Graz, Austria
fTechnical University of Munich, Munich Institute of Integrated Materials, Energy and Process Engineering, Lichtenberstr. 4a, 85748 Garching, Germany
First published on 4th November 2024
Abstract
This work explores the complex hydrodynamics in magnetophoretic microfluidic processes, focusing on the interplay of forces and particle concentrations. The study employs a combined simulation and experimental approach to investigate the impact of magnetophoresis on magneto-responsive nanoparticles (MNPs) and their environment, including non-magneto-responsive nanoparticles (non-MNPs) in a microfluidic system. Our findings reveal that the motion of MNPs induces a hydrodynamic convective motion of non-MNPs, significantly affecting the separation efficiency and purity of the particles. The separation efficiency of MNPs increases with the Péclet number, reflecting the increase in the magnetophoretic force, but decreases with lower concentrations. Conversely, non-MNPs exhibit high and constant separation efficiency with increasing Péclet number, independent of the magnetophoretic force. In a mixture, the separation efficiency of non-MNPs decreases, suggesting that non-MNPs drag along MNPs. The Mason number, representing the ratio between shear and magnetophoretic force, also plays a crucial role in the separation process. The results underscore the need for careful control and optimization of the Péclet and Mason numbers, as well as particle concentrations, for efficient magnetophoretic microfluidic processes. This study provides valuable information on the underlying principles of magnetophoresis in microfluidic applications, with implications for biochemistry, biomedicine, and biotechnology.
1 Introduction
In recent years, the development of lab-on-a-chip platforms has garnered significant attention in the field of biomedical research, including disease diagnosis, drug development, and personalized medicine. These miniaturized analytical devices offer a range of advantages over traditional laboratory techniques, including reduced sample volumes, faster analysis times, and improved sensitivity and selectivity.1,2The basic principle of a lab-on-a-chip platform involves the integration of multiple laboratory functions onto a single microchip, allowing the parallel processing of multiple samples having a high degree of controllability and optimization. This integration is achieved through the use of microfluidics, which enables manipulation at the microscale level2,3 and precise control of fluid flow with low Reynolds numbers4 ranging from 10–6 to 10. Using microfluidic technology, lab-on-a-chip platforms are capable of performing a range of functions, including magnetophoresis-based cell sorting and detection,5 DNA sequencing,6 and protein analysis.7 The potential impact of lab-on-a-chip platforms in biomedical research is huge. For example, using them for point-of-care diagnostics could greatly improve access to medical care in low-resource settings, where traditional laboratory techniques are often prohibitively expensive or logistically challenging.8,9 Similarly, performing high-throughput drug screening on a microfluidic platform could greatly accelerate the drug development process, leading to more efficient and cost-effective drug discovery.1
In transport processes, the Péclet number describes the ratio of convective to diffusive forces. Controlling the Péclet number is crucial in microfluidic devices to optimize either a sorting process or to achieve efficient mixing in reaction processes.4,10 In magnetophoresis-based processes, one key challenge is the need for a comprehensive theory for predicting and understanding the dynamic behavior of magneto-responsive nanoparticles (MNPs).11–13 These magneto-responsive nanoparticles can be engineered with different surface coatings and functionalizations to serve as carriers for a particular substance or to specifically target cells.14–17 Moreover, the presence of magnetic fields can lead to complex emergent behavior; such as spontaneous pattern formation and self-assembly.18 When this magnetic field varies in space, MNPs will experience a force that causes them to migrate. This phenomenon is commonly referred to as magnetophoresis, which, similar to its analogous “electrophoresis” for charged nanoparticles,19 has frequently been modeled via mean-field approximations.20 Nonetheless, thermal fluctuations and discrete particle interactions are essential at the mesoscale, making classic mean-field theories poorly equipped to accurately simulate and predict the transport and equilibrium properties of magnetic colloidal suspensions. Particle-based simulations, such as molecular or Brownian dynamics simulations, can provide a picture of the underlying physical phenomena present in colloidal suspensions. However, due to the long-ranged and many-bodied nature of the hydrodynamic and magnetic forces present in magnetophoretic processes, previous computational work has only considered magnetic species and mainly focused on the aggregation kinetics of magnetic agglomerates.16,21
This study aims to explore the transport mechanisms in colloidal dispersions of MNPs and non-MNPs in the presence of a spatially varying magnetic field, particle concentration, and particle solution flow and their effect on the separation efficiency (schematically shown in Fig. 1). Notably, the influence of magnetic convection in a hydrodynamic system comprising magnetic and non-magneto-responsive entities in a microfluidic or millifluidic chip has yet to be previously investigated.3,22,23 We compliment and support our findings with large-scale Brownian dynamics simulations coupled to the magnetic equivalent of Poisson's equation to solve for the magnetostatic field of a mixture of magneto-responsive and non-magneto-responsive nanoparticles in the presence of a magnetic field gradient. The hydrodynamic forces between colloidal particles are computed using a positively split Ewald method24 and the magnetostatic potential is computed using a spectral Ewald method.25,26 We present a combined simulation and experimental approach to demonstrate that convection motion is an underappreciated effect in magnetohydrodynamic systems.
2 Theory and numerical methods
2.1 Brownian dynamics simulation
We model the mixture of MNP and non-MNP as a suspension of charged, hard, spherical particles of radius a. We assume that these particles are suspended in a continuum Newtonian fluid such that the colloids interact with the solvent only via stochastic Brownian forces from fluctuations in the thermal energy or fluctuating hydrodynamics due to the momentum relaxation of the solvent molecules.27 Under these assumptions we can start with Langevin's equation to derive our equations of motion: | (1) |
| 〈FB(t)〉 = 0; 〈FB(t)FB(t + τ)〉 = 2kBT(MH)−1δ(τ) | (2) |
A more mathematically rigorous formulation states that the Brownian force, consistent with the distribution in the second term of eqn (2), is sampled from a collection of independent Wiener processes, W(t), expressed as
 | (3) |
Here, the square root of the inverse of the mobility matrix, (MH)−1/2, satisfies the relation (MH)−1/2 · (MH)−1/2† = (MH)−1, where † denotes the adjoint (or conjugate transpose).
At the colloidal scale, inertial relaxation occurs on time scales orders of magnitude smaller than those governing colloidal motion. Consequently, any perturbation to the particle's momentum dissipates almost instantaneously. Rigorous integration of eqn (1) results in a set of stochastic differential-algebraic equations (SDAE) that faithfully capture the overdamped Langevin dynamics:
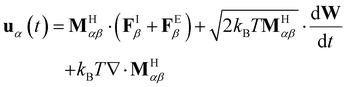 | (4) |
The final term in eqn (4), often referred to as the Brownian or thermal drift, emerges from integrating out the inertial degrees of freedom in eqn (1). Physically, this drift introduces an additional flux that actively displaces particles from regions of low mobility,29 preventing their accumulation and ensuring a uniform exploration of the system's phase space.
Good agreement between experimental measurements and simulation results for a suspension of colloidal particles (including concentrated ones) can be achieved with a relatively coarse approximation for the interparticle hydrodynamic interactions. The fields generated by beads in a Newtonian fluid can be approximated as the superposition of the field generated by a point particle and a point quadrupole.24 When all colloidal particles are of the same size, the hydrodynamic fields are given by the Rotne–Prager–Yamakawa mobility tensor:19
 | (5) |
Naive evaluation of the mobility tensor involves computational operations scaling as O(N2), while its inversion, necessary for calculating the Brownian displacements in eqn (2), incurs a complexity of O(N3). This computational burden often limits the feasibility of simulating large-scale systems. However, a substantial reduction in numerical complexity can be achieved by recognizing that the mobility tensor is positive-definite.30
This positive-definiteness allows for fast algorithms, such as those yielding O(N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) scaling for evaluating particle velocities from applied forces.24 Furthermore, the Positively Split Ewald (PSE) method, introduced by Fiore, Swan, and colleagues, enables linear scaling in the sampling of Brownian displacements.31
N) scaling for evaluating particle velocities from applied forces.24 Furthermore, the Positively Split Ewald (PSE) method, introduced by Fiore, Swan, and colleagues, enables linear scaling in the sampling of Brownian displacements.31
In periodic systems, the mobility tensor in eqn (5) exhibits translational invariance, making it divergence-free and resulting in a zero Brownian drift term in eqn (4). In this case, the trajectories over time can be numerically solved via a forward Euler–Maruyama integration scheme:
| xα(t + Δt) = xα(t) + uα(t)Δt | (6) |
Forces arising from conservative interactions among colloidal particles are represented as the gradient of a potential energy  , which is a function of the coordinates of all ions
, which is a function of the coordinates of all ions  ,
,
 | (7) |
| ∇·B = 0, B = μH | (8) |
Paramagnetic particles of magnetic permeability μp in a solvent of permeability μs. By defining a magnetic scalar potential ψ, the problem reduces to Laplace's equation:
| ∇2ψ = 0 | (9) |
 | (10) |
 | (11) |
 | (12) |
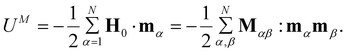 | (13) |
Similarly, the resulting magnetic force acting on the αth particle is
 | (14) |
We simulate a mixture of MNPs and non-MNPs of the equal radius, α ≈ 47 nm, in water a room temperature. We assume that the solvent behaves as a Newtonian fluid, with a viscosity of μ = 1 cp, constant magnetic permeability, μf ≈ 1.25 × 103 H nm−1, and constant permittivity εf = 80. Furthermore, the colloidal particles are electrostatically stabilized in a binary electrolyte, such as NaCl, which is simulated implicitly. The concentration of the implicit ions is estimated using Graham's equation38 based on the experimental zeta potential of ζMNP = −24.26 mV and ζnon-MNP = −43.48 mV.
2.2 Characterization of the magneto-responsive suspension using Péclet and Mason number
The displacement of the magneto-responsive particles results in a perturbation of the microstructure of the suspension which can be characterized by the Péclet number.39 This non-dimensional number expresses the importance of the external force deforming the system, Fext, with respect to the restoration of entropic spring forces from Brownian motion,30,40,41 | (15) |
 direction.
direction.
For paramagnetic particles, the magnetic dipole is induced by the field and assumed to be perfectly aligned with the field. Moreover, in our simulations, the magnetic field only varies in the direction of the applied field,  . Then, the only non-zero components of the field gradient 2-tensor ∇H are those in the
. Then, the only non-zero components of the field gradient 2-tensor ∇H are those in the  direction. To facilitate our analysis, we define a gradient vector containing the gradient direction and field magnitude,
direction. To facilitate our analysis, we define a gradient vector containing the gradient direction and field magnitude, 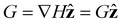 . By definition,
. By definition,  , where μf is the fluid permittivity, and χ = 3(μp/μf − 1)/(μp/μf + 2) is the susceptibility, with μp being the particle's permittivity. Then, this magnetic Péclet number is given by Pe = (4πa3μfχ∇|H|2)/3kBT ∼ (a4μfχGH0)/kBT, where G is the field gradient magnitude. This equation tells us that in the limit of very small Péclet numbers, the deformation of the particle arrangement within the suspension, and consequently the local polarization density, due to the externally imposed magnetic gradient is easily restored by the Brownian bath. On the other hand, high Péclet numbers indicate that the arrangement of particles and thus the macroscopic properties of the suspension are defined by the magnetophoretic process.
, where μf is the fluid permittivity, and χ = 3(μp/μf − 1)/(μp/μf + 2) is the susceptibility, with μp being the particle's permittivity. Then, this magnetic Péclet number is given by Pe = (4πa3μfχ∇|H|2)/3kBT ∼ (a4μfχGH0)/kBT, where G is the field gradient magnitude. This equation tells us that in the limit of very small Péclet numbers, the deformation of the particle arrangement within the suspension, and consequently the local polarization density, due to the externally imposed magnetic gradient is easily restored by the Brownian bath. On the other hand, high Péclet numbers indicate that the arrangement of particles and thus the macroscopic properties of the suspension are defined by the magnetophoretic process.
In our experimental set-up, the presence of no-slip boundary conditions in a Newtonian fluid results in an additional tangential force due to momentum transfer (a shear force), which further deforms the suspension. Assuming that the shear force is orthogonal to the magnetic gradient, as in our experimental set-up, this deformation will be opposed in the simplest of cases by the dipole–dipole interactions of the magnetic particles. The competition of both forces is given by a Mason number,42,43 defined as
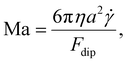 | (16) |
 is the shear rate and Fdip is obtained by taking the gradient of the potential energy with respect to the distance between a pair of magnetic interacting dipoles.44 In the context of microfluidic devices employed for separation processes, performance evaluation revolves around two key metrics: Purity and separation efficiency. The purity, P, of the outlet streams is quantified, where the ratio of concentration to velocity serves as the defining factor for mass flux
is the shear rate and Fdip is obtained by taking the gradient of the potential energy with respect to the distance between a pair of magnetic interacting dipoles.44 In the context of microfluidic devices employed for separation processes, performance evaluation revolves around two key metrics: Purity and separation efficiency. The purity, P, of the outlet streams is quantified, where the ratio of concentration to velocity serves as the defining factor for mass flux  of components A and B:
of components A and B:  . The separation efficiency S is defined as
. The separation efficiency S is defined as  .
.
3 Experimental methods
3.1 Microfluidic platform
The microfluidic chip was designed in SolidWorks 2021 and printed by a FormLabs 3B + printer using clear resin (Formlabs, RS-F2-GPCL-04). The chip was placed horizontally and twisted in every direction to facilitate the later washing process. When the print was finished, the uncured resin was flushed out with 100% 2-propanol via a syringe. Then, the chip was washed for 15 min in a 2-propanol bath and cured by UV light at 60 °C for 20 min. Finally, the supporting structures were removed, and the printed M5 threads were drilled into the in- and outlets, enabling the connection of the silicon tubes (1.3 mm, VWR) via Luer lock tubing adapters (male, 1.6 mm, Reichelt Chemie Technik GmbH & Co.).The experiments were performed at a viscosity η of 2.2274 mPa s, increasing the colloidal stability of the nanoparticles.45 Therefore, the nanoparticles are dissolved in 24 wt% D(+)-sucrose (Carl Roth) at pH 7. The concentration stayed the same for the mixture experiments as for the single experiments per particle species. This means the overall particle mass flux for a mixture experiment was twice the one of the single experiment 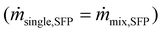 . The density for the particles is 2650 for the non-magneto-responsive and 4870 kg m−3 for the MNPs, respectively. For the experimental set-up, the chip and the neodymium iron boron magnet (4 × 0.5 × 1.5 cm, N40, supermagnete) were placed in the holder, and the tubes were connected. The sample was pumped at 52 μL min−1 (u = 0.00107 m s−1) by a syringe pump (kdScientific), the buffer via a peristaltic pump (ISMATEC) with 37% (u = 0.00425 m s−1), and the outlet samples were removed with 229 μL min−1 by a self-made multi-syringe adapter for a syringe pump (Krüss, Havard Apparatus) as presented in Fig. 2 and in the ESI section.† The flow of the viscous solution should be higher than the sample flow to minimize the transverse diffusional migration of the nanoparticles. For running the experiments, the chip was first slowly filled with the viscous solution, then the sample was connected, avoiding bubble formation. After 30 s of equilibration time, the outlet tubes were connected, and each experiment was run for 4 min in triplicates (n = 3, error bars presenting the standard deviation). The outlets A/B and C/D are combined to calculate the process purity and selectivity.
. The density for the particles is 2650 for the non-magneto-responsive and 4870 kg m−3 for the MNPs, respectively. For the experimental set-up, the chip and the neodymium iron boron magnet (4 × 0.5 × 1.5 cm, N40, supermagnete) were placed in the holder, and the tubes were connected. The sample was pumped at 52 μL min−1 (u = 0.00107 m s−1) by a syringe pump (kdScientific), the buffer via a peristaltic pump (ISMATEC) with 37% (u = 0.00425 m s−1), and the outlet samples were removed with 229 μL min−1 by a self-made multi-syringe adapter for a syringe pump (Krüss, Havard Apparatus) as presented in Fig. 2 and in the ESI section.† The flow of the viscous solution should be higher than the sample flow to minimize the transverse diffusional migration of the nanoparticles. For running the experiments, the chip was first slowly filled with the viscous solution, then the sample was connected, avoiding bubble formation. After 30 s of equilibration time, the outlet tubes were connected, and each experiment was run for 4 min in triplicates (n = 3, error bars presenting the standard deviation). The outlets A/B and C/D are combined to calculate the process purity and selectivity.
The nanoparticle concentration was analyzed in triplicates via UV absorbance at 400 nm and fluorescent measurement (excitation wavelength 488 nm, emission wavelength 520 nm) in a plate reader (Tecan Infinite M200 Microplate Reader). They were compared to standard calibration curves; if necessary, the samples were centrifugally concentrated and resuspended in an ultrasonication bath (132 kHz, Sonorex) for 15 min.
The details of nanoparticle synthesis are provided in the ESI section.†
4 Results
4.1 Exploring the dependence of magnetophoresis on magnetic field and nanoparticle concentration
The separation efficiencies and purities for separating non-MNPs from MNPs are investigated using a magnetophoretic microfluidic platform as presented in Fig. 1 and in the ESI section,† characterized by a laminar flow with a Reynold's number of 0.53. A detailed characterization of the nanoparticles used is given in the ESI section.†Fig. 3 depicts the separation efficiency of the MNPs over varying Péclet numbers. For the lower concentration of ϕ = 0.01, the separation efficiency is S = 0.11 ± 0.10 for Pe = 2.85 × 10–3. By increasing the Péclet number from Pe = 3.35 × 10−3 to Pe = 3.6 × 10−3, the separation efficiency increases from S = 0.38 ± 0.15 to S = 0.94 ± 0.04. However, the results show that for a higher concentration, only a lower Péclet number is required to achieve higher separation efficiencies. Here, for ϕ = 0.02, a separation efficiency of S = 0.94 ± 0.10 is already reached at a Péclet number of Pe = 2.85 × 10−3. Elevated particle concentrations promote dipole–dipole particle interactions, leading to aggregation and, therefore, an increased magnetic moment. Consequently, these clusters experience an augmented magnetic force, which drives them towards regions of higher magnetic field intensity.
 | ||
| Fig. 3 The separation efficiency of soley MNPs determined with microfluidic experiments is presented as a function of the Péclet number for two different concentrations, namely ϕ = 0.02 and ϕ = 0.01. | ||
Fig. 4 compares the separation efficiencies (a and e) and purities (b and f) for varying Péclet numbers achieved by using only one particle species versus a mixture of both in the microfluidic chip. Fig. 4(a) refers to the separation efficiency for the non-MNPs, and Fig. 4(e) shows the separation efficiency for the magneto-responsive ones. The separation efficiency for the non-magneto-responsive particles varies little for the applied Péclet numbers but increases from S = 0.75 ± 0.13 to S = 0.86 ± 0.05 by halving the concentration from ϕ = 0.02 to ϕ = 0.01 (shaded). However, being within a mixture of both particle species, the separation efficiency decreases from S = 0.57 ± 0.13 to S = 0.24 ± 0.01 as the Péclet number increases. In contrast to the MNPs, it evolves for the non-MNPs that a lower concentration favors a higher separation efficiency at a constant Péclet number. For ϕ = 0.01 (shaded), the separation efficiency reaches S = 0.59 ± 0.1, compared to S = 0.24 ± 0.01 for ϕ = 0.02, both at Pe = 3.39 × 10−3. As the separation efficiency decreases with increasing Péclet numbers for ϕ = 0.02, the purity of the non-MNPs rises from P = 0.51 ± 0.13 to 0.88 ± 0.1. For the lower concentration of ϕ = 0.01, it decreases to a purity of P = 0.52 ± 0.1.
From the perspective of the MNPs (Fig. 4e), independent of being present in a particle mixture or not, their separation efficiencies show a similar trend. As the Péclet number rises, signifying an increase in the magnetophoretic force, a notable enhancement in the separation efficiency is observed from S = 0.44 ± 0.07 for Pe = 2.31 × 10−3 to S = 0.97 ± 0.02 for Pe = 3.39 × 10−3 for the particles in the mixture. But again, by decreasing the concentration at a Péclet number of Pe = 3.39 × 10−3, the separation efficiency decreases from S = 0.97 ± 0.02 (ϕ = 0.02) to S = 0.46 ± 0.1 (ϕ = 0.01). For separating a mixture with both particle species, the purity (Fig. 4f) is approximately 0.5 for all applied Péclet numbers. This finding aligns with the outcomes observed for non-MNPs, as their separation efficiency diminishes with increasing Péclet numbers. Conversely, higher Péclet numbers exhibit enhanced separation capabilities for the MNPs. This implies that these non-MNPs tend to migrate alongside their magneto-responsive counterparts, consequently compromising the purity of the MNPs. As the magnetic field gradient induces the movement of the MNPs, a hydrodynamic instability appears, generating a convective flow. This flow also instigates a hydrodynamic force on non-MNPs in the direction of the moving MNPs.
4.2 The impact of hydrodynamic forces on magnetic particle interactions
The influence of varying Mason numbers on separation efficiency and purities is depicted in Fig. 4, where it serves as a metric for the ratio of shear to magnetic forces. It evolves that for the non-MNPs in Fig. 4(c), the separation efficiency is around 0.7 for all applied Mason numbers. However, when being present in a mixture with MNPs, it is S = 0.24 ± 0.01 at Ma = 3.62 × 10−2, but increases to S = 0.58 ± 0.04 at Ma = 1.06 × 10−1. At the same time, the purity of the non-MNPs fraction decreases from P = 0.88 ± 0.08 to P = 0.51 ± 0.05.Since the shear force prevails the magnetophoretic force, the separation efficiency for the magneto-responsive nanoparticles decreases from S = 0.97 ± 0.02 at Ma = 3.62 × 10−2 to S = 0.45 ± 0.07 at Ma = 1.06 × 10−1, depicted in Fig. 4(g) and (h). This decline is observed irrespective of whether the particles are in a mixture with non-magneto-responsive entities or not, the same as for the variation of the Péclet number. Even if the separation efficiency for Ma = 3.62 × 10−2 is high, the purity is P = 0.56 ± 0.01. The observed reduction in separation efficiency for non-MNPs, presented in Fig. 4(c), implies their tendency to be concurrently entrained with MNPs, which is indicative of the resultant low purity in the separation process. Under increased shear conditions, represented by the highest Mason number (Ma = 1.06 × 10−1), it is noteworthy that although the MNPs in the mixture exhibit a lower separation efficiency (S = 0.45 ± 0.07), the non-MNPs align their movement with the MNPs again. Consequently, this leads to a purity level of only P = 0.52 ± 0.07, which is comparable to the purity achieved at the lowest Mason number (Fig. 4(d)).
To further investigate the hydrodynamically induced transport of non-MNPs alongside MNPs, as suggested by the experimental observations, we employ large-scale Brownian dynamic simulations. They are designed to analyze the interplay between the nanoparticles depending on the magnetophoretic forces that contribute to the co-transport phenomenon.
4.3 Hydrodynamically induced transport of undesired species: large-scale Brownian dynamic simulations
Fig. 5(e) shows a snapshot of the simulation box in the absence of shear for a mixture of MNPs (in blue, magneto-responsive nanoparticles) and non-MNPs (in gray, non-magneto-responsive nanoparticles). Such a simple simulation, is similar to the flow present at the geometric symmetric axis along the developing convective flow . The applied magnetic field in the z direction (outward page) is
. The applied magnetic field in the z direction (outward page) is  , and the gradient G = 0.02. The gradient in units of
, and the gradient G = 0.02. The gradient in units of 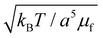 .
.
 | ||
| Fig. 5 (a) and (b) Simulated average particle velocity in the direction of the applied field, uz, and (c) and (d) orthogonal, ux, to the field as a function of the Péclet number. (a) and (c) Correspond to the average velocities of the non-magnetic particles and (b) and (d) to the magnetic particles, respectively. The concentrations of ϕmag = 0.01 (ϕnon-mag = 0.022), ϕmag = 0.02 (ϕnon-mag = 0.044), ϕmag = 0.05 (ϕnon-mag = 0.111), and ϕmag = 0.08 (ϕnon-mag = 0.178) are colored as dark gray, light gray, blue, and red respectively. The circled, squared, triangled and starred markers correspond to field gradients of |∇H|/H0 = 0.01, |∇H|/H0, |∇H|/H0, and |∇H|/H0, respectively. (e) Snapshot of a slice of the xy plane simulated mixture of MNP and non-MNPs in the absence of shear. Non- and magneto-responsive nanoparticles are shown in gray and blue, respectively. Snapshot corresponds to simulation of filling fraction ϕmag = 0.05 (ϕnon-mag = 0.111), field H0 = 0.4kBT/a3μf in the z direction, with constant gradient in z given by |∇H|/H0 = 0.02. (f) zz component of the mobility matrix, Mzz, for the magnetoresponsive particles, computed using eqn (17) (g) zz component of the mobility matrix, Mzz, for the non-magnetoresponsive particles, computed using eqn (17) of the MNPs as a function of the Péclet number. Concentrations of ϕmag = 0.01 (ϕnon-mag = 0.022), ϕmag = 0.02 (ϕnon-mag = 0.044), ϕmag = 0.05 (ϕnon-mag = 0.111), and ϕmag = 0.08 (ϕnon-mag = 0.178) are shown in blue, orange, green, and red, respectively. Circled, squared, triangle, and starred markers correspond to field gradients of |∇H|/H0=0.01, |∇H|/H0 = 0.02, |∇H|/H0 = 0.10, and |∇H|/H0 = 0.20 respectively. | ||
The motion of MNPs in the presence of a nonuniform magnetic field is known as magnetophoresis. While this topic is a meticulously studied field of study, see ref. 20 and 46 here we are interested on the importance of hydrodynamically induced transport of potentially undesired species (non-magnetic particles) in microfluidic devices. If the components of the applied field gradient ∇H0 are small compared to H0/a, the steady-state structure of the dispersion is only weakly perturbed by the magnetophoretic forces. Under these assumptions, the magnetophoretic force felt by the αth colloid is equal to FαP = (∇H0) · mα ≡ G(Ĥ0 · mα), where G = ∇H0 and Ĥ0 = H0/H0. Similar to our magnetic Péclet number estimation, we do not need to consider the field gradient tensor, which has both the field and the gradient directions, but rather the field gradient vector, G. This would not be the case if there is there was any permanent magnetization, for which we would need the complete tensorial expression for the force.
The velocities of the magneto-responsive particles depend on the magnetophoretic forces on the colloids,  , where
, where  is a list containing the induced dipole moments, and magnetophoretic mobility,
is a list containing the induced dipole moments, and magnetophoretic mobility,  . The average magnetophoretic velocity will then be given by
. The average magnetophoretic velocity will then be given by  , where uα is the velocity of the αth colloid.
, where uα is the velocity of the αth colloid.
The first two Fig. 5(a) and (b), show the average colloid velocity of the non-MNPs and MNPs in the direction of the field as a function of the Péclet number. Concentrations vary from ϕmag = 0.01 (ϕnon-mag = 0.022) to ϕmag = 0.08 (ϕnon-mag = 0.178) and field gradient magnitude from |∇H|/H0 = 0.01 to |∇H|/H0 = 0.20. The field strength increases with the Péclet number and is varied from O(10–6) to O(10–2). As expected, the velocity of the magneto-responsive particles in the direction of the field (Fig. 5d) increases with the magnetophoretic force (proportional to the Péclet number). Non-MNPs do not show any clear displacement for values of Péclet numbers less than  , that is, at low-field and/or low-field gradients. The increase in the velocity of the non-MNPs, subpanel (a), with values of Péclet numbers greater than
, that is, at low-field and/or low-field gradients. The increase in the velocity of the non-MNPs, subpanel (a), with values of Péclet numbers greater than  suggests the existence of motion induced by the hydrodynamic interactions between particles in the direction of the field. In consistency with what has been found in magnetophoretic separations,20Fig. 5(a) suggests low field gradients are more efficient at reducing the transport of unwanted species (represented by the non-magnetic nanoparticles). In contrast, the orthogonal component of the velocity, as shown in Fig. 5(c) and (d) for the non-MNPs and MNPs, respectively, display no dependence on the applied field or the field gradients and the average velocities of both species are negligible.
suggests the existence of motion induced by the hydrodynamic interactions between particles in the direction of the field. In consistency with what has been found in magnetophoretic separations,20Fig. 5(a) suggests low field gradients are more efficient at reducing the transport of unwanted species (represented by the non-magnetic nanoparticles). In contrast, the orthogonal component of the velocity, as shown in Fig. 5(c) and (d) for the non-MNPs and MNPs, respectively, display no dependence on the applied field or the field gradients and the average velocities of both species are negligible.
From the average velocity, we can compute the approximate magnetophoretic mobility by introducing a summation tensor, Σ;47 we find
 | (17) |
5 Discussion
The hydrodynamics in magnetophoretic microfluidic separation processes are characterized by a complex interplay of forces that influence the overall process efficiency. Our experimental results show high and constant separation efficiencies for solely non-magneto-responsive nanoparticles with increasing Péclet number, indicating that their separation is independent of the magnetic force when no magneto-responsive entities are present. But, keeping a constant Péclet number, a higher separation selectivity is achieved for lower concentrations due to the reduction of diffusive effects.10,48 Conversely, at low concentrations of magneto-responsive nanoparticles, the separation efficiency is reduced. When a magnetic field is applied at low Péclet numbers, the separation efficiency of MNPs initially remains limited due to the predominance of thermal fluctuations over magnetic forces. However, as the Péclet number increases, enhanced dipole–dipole interactions lead to aggregation, amplifying the magnetic moment and enabling more efficient separation by the magnetic field gradient. Also, raising their concentration amplifies their total magnetic moment. These aggregates, larger in size and showing reduced Brownian motion, are more effectively moved by the magnetic field gradient towards areas of higher magnetic field intensity, resulting in improved separation.22,49In a mixture of both particle species, the presence of non-magneto-responsive nanoparticles does not influence the separation efficiency of the magneto-responsive ones with rising magnetic field strength. However, the reverse is not true. The separation efficiency of non-MNPs decreases with increasing magnetic field strength (increasing Péclet number). The process purities of the MNPs are constant even though the separation efficiency of MNPs improves with increasing Péclet number, suggesting that non-MNPs drag along MNPs. That happens as the magneto-responsive nanoparticles induce a hydrodynamic force acting on the non-magneto-responsive entities, influencing the separation process significantly.23,50 The simulation integrates and extends beyond the experimentally tested parameters of magnetic field strength and concentration, showing that this convective motion is an intrinsic aspect of the system's dynamics. Focusing on the direct interplay of the magneto-responsive entities and the non-magneto-responsive ones, the simulation confirms that the magnetic field gradient primarily induces the motion of the MNPs, as the orthogonal velocity to the field is constant for both particle species. However, the influence of magneto-responsive particles on their non-magneto-responsive counterparts is significant. Although the motion of non-MNPs is an order of magnitude smaller, it is evident that the movement of the magneto-responsive entities leads to a hydrodynamic convective motion that entrains the non-magneto-responsive particles. Since experimental measurements could only be performed offline, after the magnetophoretic process, direct experimental observation of this interaction within the magnetic field is challenging. Simulations are thus essential for capturing and analyzing the underlying dynamics comprehensively. The simulations allowed us to directly investigate the dynamic behavior within the magnetic field, providing valuable insights into parameter regimes that are costly to explore experimentally. Across all simulated particle concentrations and magnetic field gradients the hydrodynamic effect remains consistent. Exceeding the experimentally tested parameters, the average velocity of the non-magneto responsive particle in the direction of the field can be minimized by decreasing the magnetic field gradient. However, this will lead to a reduced responsiveness (velocity) of the magneto-responsive ones as well, resulting in a lower separation efficiency.22 Experimentally, increasing the shear by increasing the volumetric buffer flow leads to an improved separation efficiency and fewer diffusive effects of the non-MNPs.10,48 But again, in a mixture where both particle species are present, the purity of MNPs is reduced. Due to the increased shear counteracting the magnetophoretic force, the magneto-responsive nanoparticles are less attracted toward higher magnetic fields.11
Magnetic separation techniques are widely used in biochemistry, biomedicine, and biotechnology. Applications range from the purification of biomolecules51 to targeted drug delivery.52 These techniques rely on applying a magnetic field to manipulate magneto-responsive particles, most commonly superparamagnetic particles, in a non-magnetic environment. In this study, we evaluate the impact of magnetophoresis on magneto-responsive entities, which are nanoparticles in our case but can be modified for other purposes, for instance, through drug functionalization. This happens in a non-magneto-responsive environment, which is represented by non-magneto-responsive particles in a microfluidic system. The magnetic-induced convective motion is a promising technique for nanoparticle manipulation due to its simple and effective separation mechanism.49,50,53 However, the induced hydrodynamic force acting on the non-magneto-responsive entities has to be considered when it comes to a lab-on-a-chip separation process or application in biomedicine.25,54 For targeted processes, e.g., drug delivery, mixing motion should be avoided, allowing effective delivery and localization in the body.55,56
Given the complexity of the hydrodynamics in magnetophoretic microfluidic processes, it is crucial to consider strategies that could enhance the separation efficiency and purity of the particles. In the study of Solsona et al., a 3D-printed magnetophoretic chip was developed to sort catalyst particles by their magnetic moment; however, they could not see a difference in the magnetic susceptibility between the different fractions. Besides their discussion that the formation of nano-clusters agglomerates accounts for this observation, the induced convective motion reduced the purity of their fractions.57 As investigated by Robert et al., the separation efficiency could be improved by an increased flow and a decrease in magneto-responsive entities. Their study successfully differentiated between non-magnetic monocytes and magnetic macrophages; however, they noted that during the separation process, fractions may tend to overlap due to the convective motion engendering mixing and generation of a current.5 In another approach, the purity of a microfluidic separation process of red (non-magnetic) and white (magnetically labeled) blood cells decreased with a higher flow as the hydrodynamic drag force prevails the magnetophoretic force. Therefore, Lin et al. implemented a two-stage cell separation strategy in their chip, preventing the undesired motion of the red blood cells along with the white ones.25
6 Conclusion
In conclusion, our experimental and simulative results highlight that the motion of magneto-responsive nanoparticles induces a hydrodynamic motion that entrains the non-magneto-responsive ones. This interaction significantly influences the separation efficiency and purity of both nanoparticle species in the microfluidic system. The simulations directly investigated these dynamic behaviors within the magnetic field and provided insights that are difficult to obtain experimentally. Besides the careful control of the Péclet and Mason number, a practical approach to minimize the unavoidable magnetic-induced convection of non-magneto-responsive entities may include a multi-step process. Here, a prior static batch separation reduces the concentration of non-magneto-responsive nanoparticles in the system, thereby enhancing the overall separation efficiency and purity.Author contributions
L.W., E.K., M.B., J.W.S., and S.S. conceptualization, methodology; L.W., J.S., La.W. and E.K. data curation, investigation; L.W. and E.K. formal analysis, visualization; M.B., A.A., S.S. and S.B. writing – review and editing, supervision, project administration; L.W. and E.K. writing – original draft.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare. All data is available upon request.Acknowledgements
The authors would like to thank Matthias Opel for the SQUID measurement and Carsten Peters for his support with the TEM imaging. This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 441672360, and by the TUM Global Incentive Fund, MIT's Global Seed Fund, MISTI 2116645, and NASA Grant No. 80NSSC18K0162.References
- S. Gupta, K. Ramesh, S. Ahmed and V. Kakkar, Int. J. Bio-Sci. Bio-Technol., 2016, 8, 311–322 CrossRef.
- G. Gharib, İ. Bütün, Z. Muganl, G. Kozalak, İ. Naml, S. S. Sarraf, V. E. Ahmadi, E. Toyran, A. J. van Wijnen and A. Koşar, Biosensors, 2022, 12, 1–60 CrossRef PubMed.
- W. H. Chong, S. S. Leong and J. K. Lim, Electrophoresis, 2021, 42, 2303–2328 CrossRef CAS PubMed.
- T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977–1026 CrossRef CAS.
- D. Robert, N. Pamme, H. Conjeaud, F. Gazeau, A. Iles and C. Wilhelm, Lab Chip, 2011, 11, 1902–1910 RSC.
- Y. Zhao, D. Chen, H. Yue, J. B. French, J. Rufo, S. J. Benkovic and T. J. Huang, Lab Chip, 2013, 13, 2183–2198 RSC.
- A. Thiha and F. Ibrahim, Sensors, 2015, 15, 11431–11441 CrossRef CAS PubMed.
- R. Augustine, A. Hasan, S. Das, R. Ahmed, Y. Mori, T. Notomi, B. D. Kevadiya and A. S. Thakor, Biology, 2020, 9, 1–17 CrossRef PubMed.
- E. K. Theel and S. P. Schwaminger, Int. J. Mol. Sci., 2022, 23, 1–22 CrossRef PubMed.
- R. F. Ismagilov, A. D. Stroock, P. J. Kenis, G. Whitesides and H. A. Stone, Appl. Phys. Lett., 2000, 76, 2376–2378 CrossRef CAS.
- Y. W. Tan, S. S. Leong, J. K. Lim, W. M. Yeoh and P. Y. Toh, Electrophoresis, 2022, 43, 2234–2249 CrossRef CAS PubMed.
- E. P. Furlani, J. Appl. Phys., 2006, 99, 1–35 CrossRef.
- A. O. Ayansiji, A. V. Dighe, A. A. Linninger and M. R. Singh, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 30208–30214 CrossRef CAS PubMed.
- R. K. Singh, T. H. Kim, K. D. Patel, J. C. Knowles and H. W. Kim, J. Biomed. Mater. Res., Part A, 2012, 100 A, 1734–1742 CrossRef PubMed.
- J. P. Steimel, J. L. Aragones and A. Alexander-Katz, Phys. Rev. Lett., 2014, 113, 178101 CrossRef PubMed.
- S. E. Favela-Camacho, E. J. Samaniego-Benítez, A. Godínez-García, L. M. Avilés-Arellano and J. F. Pérez-Robles, Colloids Surf., A, 2019, 574, 29–35 CrossRef CAS.
- M. Eigenfeld, L. Wittmann, R. Kerpes, S. P. Schwaminger and T. Becker, Biotechnol. J., 2023, 18, 1–11 Search PubMed.
- S. A. Majetich, T. Wen and R. A. Booth, ACS Nano, 2011, 5, 6081–6084 CrossRef CAS PubMed.
- D. Saville, W. Russel and R. William, Colloidal Dispersions, Cambridge University Press, 1989 Search PubMed.
- T. B. Jones, Electromechanics of Particles, Cambridge University Press, 1st edn, 1995 Search PubMed.
- R. G. Gontijo and F. R. Cunha, Phys. Fluids, 2017, 29, 062004 CrossRef.
- S. S. Leong, Z. Ahmad, S. C. Low, J. Camacho, J. Faraudo and J. K. Lim, Langmuir, 2020, 36, 8033–8055 CrossRef CAS PubMed.
- G. Kitenbergs and A. Cēbers, J. Magn. Magn. Mater., 2020, 498, 166247 CrossRef CAS.
- J. W. Swan and G. Wang, Phys. Fluids, 2016, 28, 011902 CrossRef.
- S. Lin, X. Zhi, D. Chen, F. Xia, Y. Shen, J. Niu, S. Huang, J. Song, J. Miao, D. Cui and X. Ding, Biosens. Bioelectron., 2019, 129, 175–181 CrossRef CAS PubMed.
- E. S. Krucker-Velasquez, Z. Sherman and J. W. Swan, Immersed Boundary Method for Dynamic Simulation of Polarizable Colloids of Arbitrary Shape in Explicit Ion Electrolytes, Ssrn preprint, 2023.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic Press, 2002 Search PubMed.
- Z. Sherman, PhD Thesis, Massachusets Institute of Technology, 2019.
- A. M. Fiore and J. W. Swan, J. Fluid Mech., 2019, 878, 544–597 CrossRef.
- S. Kim and S. J. Karrila, Microhydrodynamics: principles and selected applications, Dover Publications, Mineola, N.Y, 2005 Search PubMed.
- A. M. Fiore, F. B. Usabiaga, A. Donev and J. W. Swan, J. Chem. Phys., 2017, 146, 124116 CrossRef PubMed.
- A. Gubbiotti, M. Chinappi and C. M. Casciola, Phys. Rev. E, 2019, 100, 053307 CrossRef CAS PubMed.
- S. Delong, F. B. Usabiaga, R. Delgado-Buscalioni, B. E. Griffith and A. Donev, J. Chem. Phys., 2014, 140, 134110 CrossRef PubMed.
- S. Delong, F. Balboa Usabiaga and A. Donev, J. Chem. Phys., 2015, 143, 144107 CrossRef PubMed.
- E. E. Keaveny, J. Comput. Phys., 2014, 269, 61–79 CrossRef.
- A. M. Fiore and J. W. Swan, J. Chem. Phys., 2018, 148, 044114 CrossRef PubMed.
- A. W. C. Lau and T. C. Lubensky, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 76, 011123 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press London, San Diego, 2nd edn, 1991 Search PubMed.
- P. Moritz, A. Gonon, T. Blon, N. Ratel-Ramond, F. Mathieu, P. Farger, J. M. Asensio-Revert, S. Cayez, D. Bourrier, D. Saya, L. Nicu, G. Viau, T. Leïchlé and L. M. Lacroix, ACS Nano, 2021, 15, 5096–5108 CrossRef CAS PubMed.
- R. Zwanzig, Nonequilibrium statistical mechanics, Oxford University Press, Oxford, New York, 2001 Search PubMed.
- J. W. Swan, R. N. Zia and J. F. Brady, J. Rheol., 2014, 58, 1–41 CrossRef CAS.
- G. Bossis, O. Volkova, S. Lacis and A. Meunier, Magnetorheology: Fluids, Sturcutres and Rheology, Springer-Verlag Berlin Heidelberg, 2002, vol. 594, pp. 202–233 Search PubMed.
- Z. Varga, V. Grenard, S. Pecorario, N. Taberlet, V. Dolique, S. Manneville, T. Divoux, G. H. McKinley and J. W. Swan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 12193–12198 CrossRef CAS PubMed.
- J. D. Jackson, Classical electrodynamics, John Wiley I& Sons, 1999 Search PubMed.
- L. Wittmann, C. Turrina and S. P. Schwaminger, Magnetochemistry, 2021, 7, 80 CrossRef CAS.
- R. Cobos and A. S. Khair, J. Fluid Mech., 2023, 968, A14 CrossRef CAS.
- E. Krucker-Velasquez and J. W. Swan, J. Chem. Phys., 2021, 155, 134903 CrossRef CAS PubMed.
- P. Agnihotri, Microfluid. Nanofluid., 2023, 27, 1–15 CrossRef.
- M. Fratzl, S. Delshadi, T. Devillers, F. Bruckert, O. Cugat, N. M. Dempsey and G. Blaire, Soft Matter, 2018, 14, 2671–2681 RSC.
- J. G. Lee, V. Porter, W. A. Shelton and B. Bharti, Langmuir, 2018, 34, 15416–15424 CrossRef CAS PubMed.
- A. Shiriny and M. Bayareh, Meccanica, 2020, 55, 1903–1916 CrossRef.
- T. Vangijzegem, D. Stanicki and S. Laurent, Expert Opin. Drug Delivery, 2019, 16, 69–78 CrossRef CAS PubMed.
- S. Schuerle, A. P. Soleimany, T. Yeh, G. M. Anand, M. Häberli, H. E. Fleming, N. Mirkhani, F. Qiu, S. Hauert, X. Wang, B. J. Nelson and S. N. Bhatia, Sci. Adv., 2019, 5, 1–10 Search PubMed.
- S. S. Leong, S. P. Yeap and J. Lim, Interface Focus, 2016, 6, 1–20 CrossRef PubMed.
- X. Li, W. Li, M. Wang and Z. Liao, J. Controlled Release, 2021, 335, 437–448 CrossRef CAS PubMed.
- P. M. Martins, A. C. Lima, S. Ribeiro, S. Lanceros-Mendez and P. Martins, ACS Appl. Bio Mater., 2021, 4, 5839–5870 CrossRef CAS PubMed.
- M. Solsona, A. E. Nieuwelink, F. Meirer, L. Abelmann, M. Odijk, W. Olthuis, B. M. Weckhuysen and A. van den Berg, Angew. Chem., Int. Ed., 2018, 57, 10589–10594 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02225d |
| ‡ These authors contributed equally to this work. |
| § Deceased author. |
| This journal is © The Royal Society of Chemistry 2025 |



