Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetically controlled cluster formation/dissociation in high-moment nanoparticle-based ferrofluids†
Marianna Vasilakaki a,
Dino Fioranib,
Davide Peddis
a,
Dino Fioranib,
Davide Peddis bc and
Kalliopi N. Trohidou
bc and
Kalliopi N. Trohidou *a
*a
aInstitute of Nanoscience and Nanotechnology, NCSR “Demokritos”, Aghia Paraskevi, Attiki, 153 10, Greece. E-mail: k.trohidou@inn.demokritos.gr
bIstituto di Struttura della Materia, CNR, Monterotondo Scalo, 00015, Rome, Italy
cDepartment of Chemistry and Industrial Chemistry (DCIC), University of Genova, Genova, 16126, Italy
First published on 23rd June 2025
Abstract
Ferrofluids (FFs) based on high-moment nanoparticles have emerged as an important class of smart nanomaterials, because of their fast response to moderate strength magnetic fields. Understanding the mechanism of cluster formation stimulated by external magnetic fields, followed by cluster dissociation, is pivotal for FFs’ magnetic manipulation. A new strategy is proposed here, using the diffusion limited cluster aggregation (DLCA) model, to investigate the characteristics and the optimum conditions for the formation of field-driven high-moment structures in a fluid at room temperature. The conditions for fast cluster dissociation after removing the field, studied for the first time, suggest a completely reversible process, resulting in the initial FF structures; therefore, the FFs can be reused. Two representative cases of high-moment material-based FFs are investigated: (1) the CoFe2O4 multicore particle-based FFs and (2) the FeCo alloy nanoparticle-based FFs. In both cases, each particle inside the fluid is covered with an organic surfactant shell. The numerical simulations demonstrate that (a) high magnetic moment plays a significant role in the cluster aggregation rate in the presence of the field and (b) steric interactions from the surfactant coating result in complete reversibility of the cluster process. The results open new perspectives for novel FF-based applications.
New conceptsFerrofluids (FFs) based on high-moment nanoparticles are an important class of smart nanomaterials, because of their fast response to magnetic fields of moderate strength. Our work provides a new insight into the mechanism of cluster formation driven by an external magnetic field and for the first time investigates the factors that contribute to complete cluster dissociation at room temperature, which is pivotal for green ferrofluid based applications, since it results in energy saving and reduced material consumption. A complete model of the FF energy profile is developed for the first time including structural and magnetic particle parameters and it is applied in two representative cases of high-moment material-based FFs experimentally synthesized, i.e. CoFe2O4 multicore particle-based FFs and FeCo alloy ones. Our results of the time evolution of these FFs, obtained employing the diffusion limited cluster aggregation method, reveal the optimum conditions for fast cluster dissociation resulting in the initial FF structures. Importantly, our study lays the foundation for investigating FFs which can be reused. |
1. Introduction
Ferrofluids (FFs) are synthesized fluids, which are produced by dispersing magnetic particles (MPs) in a liquid medium (carrier).1–3 The magnetic particles can vary in size (from a few nanometers to tens of microns), in internal structure (single-domain ferro- or ferrimagnetic and antiferromagnetic) and in shape/morphology (e.g., quasi-spherical, cubic, nanodisks, nanorods, nanoplatelets, nanoflowers/multicore particles). The morphology and properties of FFs can be controlled by an external magnetic field4–6 and this is very attractive for applications in industry and nanomedicine. Indeed recently, FFs have been used in a large number of innovative applications such as in micro/nano-robots, swimmers for minimally invasive surgery, biopsy, biofilm disruption/eradication, imaging-guided drug delivery/therapy/surgery, magnetic hyperthermia, tissue engineering scaffolds, pollution removal for environmental remediation, ferrofluid cooling systems, magnetic lubricants, mechanical dampers and actuators.7–11 A key factor for the colloidal stability of FFs has been proven to be a surfactant layer surrounding each particle inside the fluid.12 In its absence, the attractive inter-particle interactions may lead to MPs’ sedimentation.13 The surfactant layer also offers multiple advantages, such as narrow size and shape distribution of the MPs during their synthesis, chemical and structural protection, protection from toxicity, dispersibility in specific solvents (e.g. water or ionic liquids), and functionalization for specific applications.14 Furthermore, several studies have demonstrated that surface coatings can modify the magnetic properties of the nanoparticles and their assemblies.15–19 The effect of the coating depends on the type of the magnetic particles and the type of the coating. In addition, the presence of a surfactant minimizes the direct surface-to-surface exchange interactions and can affect both the strength of the dipolar interactions, since it modifies the inter-particle distances, and the morphology of the assembly, contributing to the synthesis of self-assembled secondary structures.6,20–22There are a variety of particle-based simulation techniques to investigate the aggregation process and rheological properties of magnetic particles inside a fluid, depending on the length scale of the interactions. These techniques include molecular dynamics (Newton's equations of motion are solved for interacting particles),23,24 Brownian dynamics (the magnetic moments’ orientation changes, due to the forces and the torques acting on the particles inside the fluid, cause the Brown relaxation mechanism),25 and Langevin dynamics (Newtonian dynamics including Brownian motion).26,27 In the majority of the above dynamics simulations, a colloidal suspension is treated as an assembly of magnetic point dipoles, which interact via long-range dipolar forces and short-range repulsive forces.25,27 Short-range attractive van der Waals interactions have also been included.26 The stochastic simulation approach of the Monte Carlo (MC) method with the implementation of the Metropolis algorithm is an alternative powerful technique used to investigate the thermal relaxation characteristics of the magnetic particles during the aggregation process.28–31 The magnetic moments relax under the influence of thermal fluctuations (not related to the particle motion) and the interaction fields. In this way, the induced thermal relaxation of the magnetic moments also affects the aggregation process, by modifying the magnetic energy of the FFs. More sophisticated algorithms have been developed to describe more efficiently the aggregation process, i.e. diffusion limited cluster aggregation (DLCA).28,29 The advantage of this method is that it takes into account both the spin relaxation phenomena and the energy-driven motion of particles in the fluid at finite temperature with the implementation of the Metropolis Monte Carlo algorithm. In the simulations, the dipolar energy terms, the Zeeman energy term and the repulsive either electrostatic32 or steric interaction potential energy terms33 have been included for the investigation of the aggregation process. In the literature, there are also studies in which a different type of electrostatic potential has been added to account for the ionic species in the solvent.30,31 In most of these MC studies, the Brownian phenomena are ignored because of the energy driven motion of the magnetic nanoparticles, especially in the case of high moment materials.34 However, Okada and Satoh35 proposed that Brownian dynamics should be included in the case of a system containing rod-like nanoparticles since the rod-like shape of the nanoparticles affects the magneto-rheological behavior. The short-range van der Waals interactions are excluded from numerical calculations when the steric shell exceeds 2 nm in size, because strong repulsive forces exist inhibiting their attractive effect.3 In all the above cases, the magnetic anisotropy is neglected.36
Up to now, both dynamic and MC approaches have been used to study the cluster formation process and the resulting configurations including the role of dipolar interactions and either steric or electrostatic forces in iron-oxide nanoparticles.25,33 The results showed that in the presence of steric interactions, without applying a magnetic field, chain-like agglomerates are formed and their length and linearity depend on the strength of the dipolar interactions. On applying an external magnetic field, the agglomerates become elongated and orient themselves parallel to the field lines. In the case of the absence of steric interactions, fractal structures are obtained.27,28,32 Recently, the spontaneous cluster formation has been investigated in electrostatically stabilized core/shell CoFe2O4@γ-Fe2O3 (ref. 30) and sterically stabilized Fe3C,26 in both cases in the absence of a magnetic field. Chen et al. also used a simplified worm-like chain model, taking into account only the dipolar energy term, to describe the dynamic chain growth in large cubic FeCo nanoparticles of 140 nm edge length in the absence of a magnetic field.5
The present study focuses on the cluster formation process and for the first time it demonstrates how cluster dissociation can be achieved in two representative cases of FFs consisting of high-moment spherical magnetic particles at 300 K. High-moment materials are considered because of their fast response to an applied magnetic field. The first FF consists of OA coated multicore iso-oriented Co ferrite nanoparticles of ∼60 nm size,37 which are very interesting because they consist of nanoparticles that show magnetic ordering across the neighboring surfaces.38 These iso-oriented structures enhance the total magnetic moment of each multicore structure, increasing the efficiency of their remote magnetic manipulation. The second FF contains high moment FeCo alloy nanoparticles of 10 nm size,39 with further enhancement of their saturation magnetization when they are coated with oleic acid (OA).40
Our model includes all the necessary ingredients to describe efficiently the interactions inside the FFs with and without the application of a magnetic field. We take into account both the electrostatic interactions for the ionic species in the solvent and the steric interactions between particles. As we have demonstrated in our previous studies,41,42 the magnetic anisotropy that influences the magnetic moments’ orientation affects the magnetothermal and magnetorheological behavior of a FF; therefore the magnetic particle anisotropy energy term in the Hamiltonian is also included. Here, the van der Waals interactions are ignored, because the surfactant shell is considered to be thick enough.3 In our calculations, since the ratio of dipolar energy to thermal energy is large enough (ED/kBT ≫ 1), the spherical particles aggregate fast due to energy-driven motion,28 and thus the Brownian effects on the particle kinetics and cluster formation are also ignored.34
Recently, the ability to control remotely the cluster formation process in FFs on surfaces, by using magnetic fields or trapping the nanoparticles with field gradients, in order to form large agglomerates or surface patterns,9,43–45 has opened new perspectives for advanced technological applications. In addition, the ideas of high degree of reconfigurability (change of shape or re-arrangement), programmability, recyclability and versatility of nanomagnetic elements in the fluid suggest great advances and breakthroughs such as in logic applications and targeted cargo delivery.46,47 In this context, we take a step forward and we study the cluster formation by switching on the magnetic field and consequently the cluster dissociation by switching off the field or by applying an out-of-plane magnetic field. Understanding the mechanism, under which the reversibility of the cluster formation/dissociation process is succeeded, is pivotal for sustainable FF applications. Therefore, we investigate for the first time the optimum conditions for achieving cluster formation/dissociation for two representative systems of FFs based on high-moment particles. The intriguing role of the surfactant layer and the field directions, under which the reversibility of the cluster formation/dissociation process emerges, are investigated thoroughly by mapping particle positions.
2. Model and numerical simulations of the magnetic particles’ kinetics
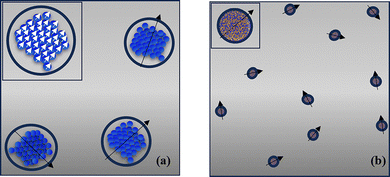
Two different dilute assemblies of high-moment particles in a fluid are modelled (Fig. 1). The first one, denoted as FF1, is composed of CoFe2O4 (CFO) multicore particles, and the second one, denoted as FF2, is composed of FeCo alloy nanoparticles. Both types of particles are coated with oleic acid (OA) of shell thickness 2 nm.A CFO multicore particle of diameter d = 60 nm is defined as a spherical nanoporous aggregate of single-domain nanocrystalline particles of 7 nm size, as described in the experimental works in ref. 38 and 48. Because of the intra-cluster interactions, a multicore particle exhibits collective magnetic order state characteristics (see the inset in Fig. 1(a)) with higher magnetization and thermal stability at room temperature compared to a single CFO particle.20,21,49 Each multicore particle i possesses a three-dimensional magnetic moment ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) i (Fig. 1(a)) and a magnetic volume 27% smaller than the physical volume, because of the nanopores that exist among the nanoparticles, as observed in TEM images.50
i (Fig. 1(a)) and a magnetic volume 27% smaller than the physical volume, because of the nanopores that exist among the nanoparticles, as observed in TEM images.50
In the second system, single-domain high-moment FeCo alloy nanoparticles with diameter d = 10 nm are considered39 (Fig. 1(b)). In this case also, a three-dimensional magnetic moment ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) i is assigned to each nanoparticle i.
i is assigned to each nanoparticle i.
In the model, the coated magnetic particles are dispersed randomly at the nodes of a triangular lattice and undergo energy-driven motion inside the fluid, since they experience competing forces.
Each of the N particles in the assembly is described as a point magnetic dipole with magnetic moment ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) i = mŝi, where ŝi is the three-dimensional classical unit spin vector with i = 1,…,N and the magnitude of the magnetic moment is defined as m = MsVm, where Ms is the saturation magnetization and Vm = πd3/6 is the volume of the ith particle. The dipolar interaction energy between particles in the system is
i = mŝi, where ŝi is the three-dimensional classical unit spin vector with i = 1,…,N and the magnitude of the magnetic moment is defined as m = MsVm, where Ms is the saturation magnetization and Vm = πd3/6 is the volume of the ith particle. The dipolar interaction energy between particles in the system is
 | (1) |
In eqn (1), ŝi and ŝj are the classical unit spin vectors, rij is the center-to-center distance between particles i and j, measured in units of particle diameter, and ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij is the unit vector along the distance vector
ij is the unit vector along the distance vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij. Our simulations are performed at temperature T = 300 K. The energy parameters in our calculations have been normalized to the thermal energy kBT at T = 300 K, where kB is the Boltzmann constant, so we use reduced (dimensionless) units. We define the reduced dipolar strength g = m2/d3kBT. For the case of CFO multicore particles, we consider a 40% decrease from the Ms reported value at T = 5 K.48 This decrease is attributed to the temperature effect and the OA coverage effect, as demonstrated in ref. 15, so we set Ms (300 K) = 213 kA m−1 and m = 1.75 × 10−17 A m2, which gives g = 33.26. In the case of FeCo alloy nanoparticles, we set Ms (300 K) = 1910 kA m−1 (ref. 39) and m = 10−18 A m2, which gives g = 24.75. Therefore, despite the big difference in size between the CFO multicore particles and the FeCo alloy particles, their dipolar strengths are comparable.
ij. Our simulations are performed at temperature T = 300 K. The energy parameters in our calculations have been normalized to the thermal energy kBT at T = 300 K, where kB is the Boltzmann constant, so we use reduced (dimensionless) units. We define the reduced dipolar strength g = m2/d3kBT. For the case of CFO multicore particles, we consider a 40% decrease from the Ms reported value at T = 5 K.48 This decrease is attributed to the temperature effect and the OA coverage effect, as demonstrated in ref. 15, so we set Ms (300 K) = 213 kA m−1 and m = 1.75 × 10−17 A m2, which gives g = 33.26. In the case of FeCo alloy nanoparticles, we set Ms (300 K) = 1910 kA m−1 (ref. 39) and m = 10−18 A m2, which gives g = 24.75. Therefore, despite the big difference in size between the CFO multicore particles and the FeCo alloy particles, their dipolar strengths are comparable.
When an external magnetic field is applied, the Zeeman energy term between magnetic particles’ moment and the applied field H is given by the expression
 | (2) |
Here, the unit vector êh is the direction of the magnetic field. The field strength is defined in reduced units as h = mH/kBT.
The magnetic particle anisotropy energy of the system is
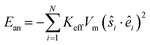 | (3) |
In eqn (3), êi is the random anisotropy easy-axis direction and Keff is the effective anisotropy energy density which includes the magneto-crystalline anisotropy of the material and the surface anisotropy of the particle of volume Vm. The reduced effective anisotropy strength of each particle is defined as k = KeffVm/kBT. The magnetic anisotropy strength is temperature dependent,51 and it is considered to be relatively low when the system approaches the superparamagnetic regime, as in the case of the reported nanoparticle systems.39,48 We calculate the reduced effective anisotropy strength for FeCo alloy nanoparticles as k = 2.53, from the bulk magnetocrystalline anisotropy of the soft FeCo Kbulk = 2 × 104 J m−1 (ref. 52) at 300 K and the particle volume of 5 × 10−25 m3. The experimental findings38,39,48,50 demonstrate similar coercivities at 300 K for both FeCo alloy nanoparticles and multicore CFO particles, and these findings allow us to consider similar effective anisotropy strengths for both systems.
The magnetic nanoparticles are charged particles and the surfactant molecules, attached at their surface, also contribute to their effective surface charge in an electrolyte solution. Therefore, the electrostatic interaction energy between all considered pairs of charged particles i and j in a carrier liquid is calculated from the approximate expression given in eqn (4), which is based on the electrostatic double layer repulsion theory (in the case where the Debye length is larger than 0.1 × d).53
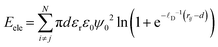 | (4) |
In eqn (4), the surface charge ψ0 is analogous to the zeta potential ζ of particles and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) D−1 is the Debye reciprocal length.31 The latter depends on the effective ionic charge concentration induced by the surfactant concentration31 and the ionic strength of the carrier liquid; εr is the dielectric constant of the carrier liquid (since we have considered water as the carrier liquid here, εr = 78.4)54 and ε0 is the permittivity of vacuum (= 8.85 × 10−12 C V−1 m−1). In our calculations, we set an intermediate value of ζ = 35 mV, commonly found in the literature for colloidally stable magnetic nanoparticles55 in a carrier medium of low ionic strength as the one considered here, I = 0.001 M. The reduced electrostatic strength is defined as λele = πdεrε0ψ02/kBT.
D−1 is the Debye reciprocal length.31 The latter depends on the effective ionic charge concentration induced by the surfactant concentration31 and the ionic strength of the carrier liquid; εr is the dielectric constant of the carrier liquid (since we have considered water as the carrier liquid here, εr = 78.4)54 and ε0 is the permittivity of vacuum (= 8.85 × 10−12 C V−1 m−1). In our calculations, we set an intermediate value of ζ = 35 mV, commonly found in the literature for colloidally stable magnetic nanoparticles55 in a carrier medium of low ionic strength as the one considered here, I = 0.001 M. The reduced electrostatic strength is defined as λele = πdεrε0ψ02/kBT.
In the presence of a surfactant coating, the steric repulsion potential energy in all considered pairs of particles at a distance smaller than twice the surfactant thickness is given by the expression31
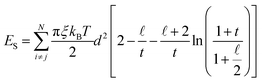 | (5) |
In eqn (5), ξ is the grafting density, i.e. surface density of molecules adsorbed on the particle, rij − d is the distance between the particles’ surfaces, δ is the surfactant layer width,  and
and  . The grafting value depends on the way of synthesis and usually ranges from 1 × 1016 mol m−2 to 1 × 1019 mol m−2.56 In our calculations, we consider a dense surfactant layer of ξ = 5 × 1018 mol m−2 and layer thickness δ = 2 nm, which usually corresponds to surfactant characteristics of oleic acid.18 The reduced strength of the steric interactions is defined as
. The grafting value depends on the way of synthesis and usually ranges from 1 × 1016 mol m−2 to 1 × 1019 mol m−2.56 In our calculations, we consider a dense surfactant layer of ξ = 5 × 1018 mol m−2 and layer thickness δ = 2 nm, which usually corresponds to surfactant characteristics of oleic acid.18 The reduced strength of the steric interactions is defined as  .
.
The total energy of the system of N coated particles suspended in a liquid is
| Etot = ED + EZ + Ean + Eele + Es | (6) |
In Table 1, the reduced dimensionless energy parameters for the two systems at 300 K are summarized. From Table 1, we observe that the steric interactions are the dominant interactions for both systems, with the CFO multicore particles having 36 times larger steric strength, because they have larger diameter than the FeCo alloy nanoparticles.
| Ferrofluids | Particle volume concentration (%) | Steric strength | Electrostatic strength | Anisotropy strength | Dipolar strength |
|---|---|---|---|---|---|
| CFO multicore particles (FF1) | 0.18 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
41 | 2.53 | 33.26 |
| FeCo alloy nanoparticles (FF2) | 0.18 | 785 | 8 | 2.53 | 24.75 |
In order to study the various contributions to the motion of the particles inside the fluid, the energy terms of the electrostatic Eele, the steric Es and the dipolar ED for a pair of particles and the corresponding total interaction energy are calculated as a function of the pair distance. The results are shown in Fig. 2 for multicore CFO particles (solid lines) and the FeCo alloy nanoparticles (dashed lines) inside the fluid. These calculations show that the ratio of the steric energy to the dipolar energy is Es/ED ∼ 5 for a pair of FeCo alloy nanoparticles at direct contact (r/d = 1), whereas it is four times higher (Es/ED ∼ 20) for the multicore CFO particles. In addition, as shown in Fig. 2 (inset), the total energy minimum shows that colloidally stable agglomerates of both coated particles’ assemblies are expected to be formed at r = 1.5 × d, where dipolar interactions dominate. Therefore, the dipolar interactions in the studied systems play a major role in the shape and length of the formed clusters.
Dilute assemblies with a very low particle volume concentration of p = 0.18% are considered. N = 116 particles are randomly placed at the sites of a triangular lattice of length L = 287d that resembles the off-lattice model,28 since we have 6 neighboring movements instead of 4 of a square lattice. The DLCA model28 is employed for the numerical simulations of the cluster aggregation inside the fluid. Also, the particles and the clusters are allowed to rotate by 60° instead of 90° of a tetragonal lattice. In our model, we allow the particles to touch but not overlap. Each particle is selected randomly and can move to one of the six neighboring lattice sites of the triangular lattice. In the case where during their motion/rotation particles are on neighboring nodes, they stick and define clusters. A cluster size-dependent diffusion coefficient is also introduced. Diffusive rotations, by 60° around the center of mass of a cluster, are also incorporated in the simulations. Free boundary conditions are used, so that particles are moving back when reaching the edges of the lattice. The Metropolis Monte Carlo algorithm57 is used for energy minimization. At each Monte Carlo step (MCS), a random movement (translation and/or rotation) of a cluster is assumed and if it is accepted, then a thermal relaxation of all the magnetic moments is performed with the Metropolis algorithm where the magnetic moments are free to reorient over three dimensions. In this way, the energy of the system is minimized and a thermal equilibrium configuration is found for the whole system.
The simulation scheme of the cluster formation process under a magnetic field is as follows: (1) the particles are let to diffuse in the absence of a magnetic field for time t = 200 MCS, (2) the final particle configuration is selected and the magnetic field is applied (stage 1), and (3) we let the system to evolve with time for t = 106 MCS until well defined clusters (composed of more than 5 nanoparticles) are formed. Next, the final particle configuration is selected and the magnetic field (stage 2) is either turned off (h = 0) or switched to a vertical direction.
We must note here that the particles of both FFs are initially randomly dispersed on the surface when the field is zero, and because of their very low density (0.18%), there is a very small probability that very few of them will create small clusters of 2 or maximum 3 nanoparticles (see Section S1 in ESI,† Fig. S1 for the time evolution of the Co ferrite multicore based FF without magnetic field at t = 0 MCS, t = 200 MCS and t = 1000 MCS, ESI†).
We have to add here that since the Monte Carlo simulation method does not include true dynamics, the MCS time unit cannot be related to any real time unit.58 The time evolution of the system does not come from any deterministic equation for the magnetization or kinetics. The obtained dynamics is intrinsic to the MC method. However, MC simulations can give reliable results on the time rate of the dynamic effects.58 Indeed, in the literature, there are a lot of examples of good qualitative agreement between experimental and Monte Carlo simulation data for magnetic relaxation processes on nanoparticles and thin films59,60 or for cluster aggregation processes.29 Since the time rate of the system evolution depends on its characteristics and the external conditions which our model explicitly takes into account (energy barriers, size of the clusters, applied magnetic field, temperature), the resulting particle configurations presented here can show qualitatively how slow or how fast the cluster formation/dissociation process occurs and the system parameters that influence this rate. Therefore, the MC method can provide reliable qualitative information on the kinetics and factors that affect the structural evolution of ferrofluids.
3. Results and discussion
Here, we present our Monte Carlo simulation results for the study of the clustering/dissociation process in these two different FFs. The simulation scheme follows the time evolution of FF1 and FF2 under the application of a magnetic field (stage 1), and when the magnetic field is switched off or the field direction is perpendicular to the plain (stage 2). In order to gain a deeper insight into the mechanism of the nanoparticle aggregation process and the factors that affect it, we study step-by-step graphically the aggregation process during the simulations. In addition, the visual dissociation of clusters is provided in order to reveal the conditions under which the whole process becomes reversible. We must note here that the study is focused on the low field regime (<100 Oe), since the advantage of high-moment materials with high magnetic susceptibility is their fast response to low magnetic fields at 300 K, resulting in energy saving. The reversibility of the process, resulting in the initial FF configuration, is a key feature which avoids material waste, since the ferrofluid can be reused. Therefore, these FF structures can be characterized as materials for green surface patterning.In Fig. 3, snapshots of only a part of the ferrofluid FF1 that includes representative cluster structures are given. We have chosen this part only, because the sample is very big. In this way, we have a clear picture of particle clustering.
Starting from an initial random configuration, where the multicore CFO particles are dispersed in the liquid (Fig. 3(a)), the dynamic evolution of the magnetic particles leading to the formation of agglomerates is presented in Fig. 3(b) under the application of an in-plane field of strength hX = 2.9. In terms of real units, this field is in the range of a few Oe (∼7 Oe). Note that the strength of the field is comparable to the particles’ anisotropy strength k = 2.53. On applying the magnetic field, the aggregation process is accelerated. We let the system to evolve in time for t = 106 Monte Carlo Steps (MCS), creating several clusters of at least 5 particles and larger and then we switch it off. As we can see in Fig. 3, when the magnetic field is turned on (Fig. 3(b)), the magnetic moments tend to be oriented along the magnetic field. This enhances the strength of the dipolar interactions and increases the tendency of linear chain formation, with nose-to-tail spin arrangement. When the field is switched off (hX = 0) the clusters are dissociated gradually as the time evolves until the system is back to its initial random configuration (Fig. 3(c) and (d)). Indeed, the magnetic moments tend to misalign, the thermal fluctuations weaken the dipolar forces and the steric interaction energy dominates over the other energy terms at short distances (see Section 2). Thus, the steric potentials drive the kinetics of the system; consequently the formed clusters break up and particles tend to quickly redisperse as monomers in the fluid. We observe that the longer chains are dissociated slower at around t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080
080![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS. In Fig. 3, the corresponding spin configurations are also shown with the black arrows. The whole process from t = 200 MCS to t = 1
000 MCS. In Fig. 3, the corresponding spin configurations are also shown with the black arrows. The whole process from t = 200 MCS to t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS when the field is applied and then from t = 1
000 MCS when the field is applied and then from t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS to t = 1
000 MCS to t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS with the field switched off is clearly presented in Movie_FF1_1.
000 MCS with the field switched off is clearly presented in Movie_FF1_1.
The MC simulations have been also repeated for different initial spin configurations and different random seeds, giving similar results to those of Fig. 3. In our simulations we have seen that in the case that the system evolves for a longer time above t = 106 MCS in the presence of the field, the particle agglomeration continues, but the structure of the clusters does not change significantly; upon removing the field, the clusters again dissociate fast (see ESI,† Section S2 and the corresponding Fig. S2).
In the literature,27,32 it has been demonstrated that if the magnetic field is applied perpendicular to the plane, then the cluster morphology is different. This is also confirmed in our study (see ESI,† Section S3) when a magnetic field of the same strength is applied out-of-plane and consequently it is removed (Fig. S3, ESI†). Interestingly, MC simulations demonstrate that in this case no agglomeration occurs. This is attributed to the competition between the dipolar interactions, which favor the in-plane nose-to-tail spin configurations, and the magnetic field, which tends to orient the magnetic moments out-of-plane.
Furthermore, it has been shown experimentally in ref. 61 that switching the magnetic field successively towards different anisotropic orientations influences the clustering process in particle assemblies. To this end, we study the cluster formation with the in-plane field as before (Fig. 3(a) and (b)) and consequently we apply an out-of-plane field (Fig. 3(e) and (f)) instead of removing it as previously (Fig. 3(c) and (d)). The whole process from t = 200 MCS to t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS applying the field and then from t = 1
000 MCS applying the field and then from t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS to t = 1
000 MCS to t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS turning the field out-of-plane is also presented in Movie_FF1_2.
000 MCS turning the field out-of-plane is also presented in Movie_FF1_2.
As we can see from Fig. 3(e), the clusters dissociate faster (t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020
020![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) when applying an out-of-plane field (see Movie_FF1_2) compared to the case of removing the field (Fig. 3(c)). Therefore, our results reveal that the proposed methodology succeeds in the fast cluster dissociation, by switching the magnetic field out-of-plane.
000) when applying an out-of-plane field (see Movie_FF1_2) compared to the case of removing the field (Fig. 3(c)). Therefore, our results reveal that the proposed methodology succeeds in the fast cluster dissociation, by switching the magnetic field out-of-plane.
The same investigation has been carried out on the cluster formation/dissociation process of FF2 based on FeCo alloy nanoparticles with particle size d = 10 nm. As we can see in Fig. 4, the FeCo alloy nanoparticles initially are dispersed randomly in the fluid (Fig. 4(a)), then clusters are formed under an in-plane magnetic field hX = 2.9 (which in this case corresponds to ∼100 Oe) (Fig. 4(b)) and then the dissociation process follows upon removing the field (Fig. 4(c) and (d)). Spin configurations (black arrows) are also included. The whole process is also presented in Movie_FF2_1.
In this case, as discussed in Section 2, because of the smaller size and the higher Ms of the FeCo alloy nanoparticles, the calculated dipolar interaction strength is slightly smaller than that of the multicore CFO particles. The calculated steric interaction strength is significantly lower than that of the corresponding Co ferrite particles. Consequently, the steric interactions of FeCo alloy nanoparticles are only 5 times stronger than the dipolar interactions (see Section 2).
In shown in Fig. 4(b), the dipolar interactions lead to the creation of quasi-linear chains with nose-to-tail spin configurations in the presence of the surfactant coating. We observe that a smaller number of chains is created compared to FF1 at t = 106 MCS (Fig. 3(b)) because of the smaller dipolar strength. Thus, their dissociation is faster than that of the Co ferrite case, as observed at t = 1.020 × 106 MCS (see Movie_FF2_1). When the field is applied perpendicular to the plane (Fig. 4(e) and (f)), the cluster dissociation is even faster (see the whole process in Movie_FF2_2) than the corresponding one of Fig. 4(c) when the field is turned off, as in the case of FF1 (Fig. 3).
The role of the magnetic particle anisotropy in the structural evolution and the field response of high-moment ferrofluids can be clearly observed in Fig. 3(b) and 4(b). When the magnetic field is applied, the magnetic moments of both the chains and the monomers are not fully aligned, as expected, along the field direction because of the random anisotropy contribution. In order to demonstrate further the significant role of the anisotropy in the cluster aggregation process, we have performed Monte Carlo simulations for CFO multicore nanoparticles with 1.7 times higher reduced anisotropy (k = 5) than the present one (k = 2.53). In this case, the MC simulation results (see ESI,† Section S4) show that the number and size of the formed clusters are smaller for hX = 2.9 at t = 106 MCS compared to the case of k = 2.53 (Fig. 3(b)). This is attributed to the higher random anisotropy energy barrier which delays the rotation of the magnetic moments towards the field direction and consequently weakens the dipolar strength contribution. These smaller formed clusters dissociate easily when the field is switched off or is turned out-of-plane.
In order to evaluate the structural evolution of the two ferrofluids with time, we have calculated the time dependence of the mean cluster size  ,29 where ns(t) is the number of clusters and s(t) is the number of particles in these clusters at time t. The sums are taken over all clusters shown in the snapshots of Fig. 3 and 4.
,29 where ns(t) is the number of clusters and s(t) is the number of particles in these clusters at time t. The sums are taken over all clusters shown in the snapshots of Fig. 3 and 4.
As can been seen in Fig. 5, up to t = 5 × 105 MCS the mean cluster size evolves in time with the same rate for both FF1 (black squares) and FF2 (black triangles) and dimers are formed on average. At t = 106 MCS, larger clusters are formed in the case of multicore CFO particles (FF1) (squares) compared to FeCo alloy nanoparticles (FF2) (triangles) due to higher dipolar strength. Therefore, when the field is removed, the FeCo alloy nanoparticle clusters dissociate faster (red triangles) than the clusters of the multicore CFO particles (red squares). In the case of consequently applying out of plane (blue symbols) instead of removing it, the cluster dissociation is faster for both FFs because of the energy competition between the in-plane dipolar field and the out-of-plane magnetic field contributions.
The calculated in-plane magnetization MX during the cluster formation/dissociation process is studied as a function of time for both ferrofluids (Fig. 6). MX is the mean value of the particles’ magnetization along the x-axis, which is defined as the sum of the x components of all magnetic particle moments over the saturation magnetization. As we can see in Fig. 6, when the in-plane field is applied, the magnetization saturates at 105 MCS indicating the formation of well-aligned spin configurations (nose-to-tail spin configurations). When the field is removed (red symbols), the in-plane mean magnetization of the system vanishes, since the thermal fluctuations disorient the magnetic moments of the particles. Upon applying the field out of the x–y plane (blue circles), the energy competition between the out-of-plane Zeeman energy and the in-plane dipolar energy results in tilting of the magnetic component. As a result, MX decreases faster than in the case of removing the field and consequently the cluster dissociation is faster, confirming the observed behaviour in Fig. 3 and 4.
In what follows, we examine the role of the organic coating and the induced steric interactions in the reversibility of the cluster formation/dissociation process (see Section S5 in ESI†). In the literature, it is stated that the type of the particle and its magnetic moment and the type and the thickness of the organic coating play an important role in the shape of the formed clusters.26 The organic coating prevents surface-to-surface contact and consequently the development of strong short range exchange interactions. In the case of a very thin surfactant layer or in the absence of a capping ligand, van der Waals interactions play an important role in the cluster formation process. This is confirmed here, where MC simulations on the uncoated multicore CFO particle system are performed by removing from eqn (6) the energy term of steric interactions (Es = 0) and adding the energy term of van der Waals interactions (eqn (S1) in the ESI†) in eqn (6). In this case, the particles come closer and the attractive van der Waals forces result in fast clustering. In Fig. 7(a) and (b), starting from a state of randomly dispersed particles with hX = 0, where cluster formation is not observed because of their very low density (0.18%) as we discussed in Section 2, we show the cluster formation process under an in-plane field of strength hX = 2.9 and consequently the process when the field is turned off (Fig. 7(c) and (d)) or the field is applied out-of-plane hZ = 2.9 (Fig. 7(e) and (f)), even for times larger than t = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MCS.
000 MCS.
The Monte Carlo results demonstrate the formation of large aggregates of irregular shape for the same time of observation as for the coated particles (see Fig. 3) under an in-plane magnetic field. Then, the applied field (hX = 2.9) is switched off (Fig. 7(c) and (d)) or is applied out-of-plane hZ = 2.9 (Fig. 7(e) and (f)) and the particle aggregation further evolves. This is attributed to the fact that in the majority of the clusters of irregular shape, the nearest neighbours have more than two particles; thus the intra-cluster dipolar interactions are very strong preventing the cluster dissociation.
The same behaviour is observed in the case of FeCo alloy nanoparticle-based FF, when the steric interactions are switched off and the van der Waals interactions are included in the calculations (see ESI,† Section S5 and Fig. S5). For the uncoated FeCo alloy nanoparticles, when the magnetic field is applied in-plane hX = 2.9 large aggregates are formed (Fig. S5(b), ESI†) and then if the applied magnetic field is turned off (Fig. S5(c) and (d), ESI†) or turned out-of-plane hZ = 2.9 (Fig. S5(e) and (f), ESI†) the aggregates continue to develop.
Therefore, in the case that the studied FFs are based on uncoated high-moment particles, the strong attractive interactions do not permit their cluster dissociation. This highlights the importance of the organic coating in the chain formation and the reversibility of the process under investigation.
4. Conclusions
Diluted FFs based on surfactant coated high-moment particles show fast response to a moderate in-plane applied magnetic field at room temperature. Our simulations have demonstrated that a moderate field, comparable in strength to the particles’ anisotropy, can create chain-like structures and that the dipolar strength and the anisotropy play the most important role in the cluster formation process. Reversibility of the cluster formation process, by removing the field, can only be achieved when the particles are coated with a surfactant, because of the contribution of the steric interaction potential. An important finding of our work is that the interplay between in-plane and out-of-plane field can result in fast cluster dissociation and thus can act as a monitoring mechanism for the achievement of the preferable type of cluster formation and its density in liquids.The numerical results look very promising for the development of environmentally sustainable FFs, which are easy to manipulate with the application of a field and can be used in novel green technologies at room temperature. New perspectives are opening up for breakthroughs in microelectronics, nano/biotechnology and photonics. In addition, the proposed strategy can be a solution to the important issue of redispersion of nanoparticles after magnetic separation for reusing them in environmental and biomedical applications.
Conflicts of interest
There are no conflicts to declare.Data availability
Data for the article cannot be made available due to on-going work in the framework of the European Union's Horizon Europe EIC Pathfinder Open Programme REMAP (Reusable Mask Patterning), under grant agreement no. 101046909.Acknowledgements
This work has been supported by the European Union's Horizon Europe EIC Pathfinder Open Programme REMAP (Reusable Mask Patterning) under grant agreement no. 101046909. https://re-map.eu. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or European Innovation Council and SME Executive Agency (EISMEA). Neither the European Union nor the granting authority can be held responsible for them. Computational time was granted from the Greek Research & Technology Network (GRNET) in the National HPC facility ARIS (https://hpc.grnet.gr).References
- O. Oehlsen, S. I. Cervantes-Ramírez, P. Cervantes-Avilés and I. A. Medina-Velo, ACS Omega, 2022, 7, 3134–3150 CrossRef CAS PubMed.
- P. Ryapolov, A. Vasilyeva, D. Kalyuzhnaya, A. Churaev, E. Sokolov and E. Shel’deshova, Nanomaterials, 2024, 14, 222 CrossRef CAS PubMed.
- P. Ilg and S. Odenbach, Lect. Notes Phys., 2009, 763, 249–325 CrossRef CAS PubMed.
- K. Butter, P. H. H. Bomans, P. M. Frederik, G. J. Vroege and A. P. Philipse, Nat. Mater., 2003, 2, 88–91 CrossRef CAS PubMed.
- Y. Chen, H. A. Zhang and A. El-Ghazaly, Nanoscale, 2024, 16, 8868–8879 RSC.
- M. Khelfallah, C. Carvallo, V. Dupuis, S. Neveu, D. Taverna, Y. Guyodo, J. M. Guigner, E. Bertuit, L. Michot, W. Baaziz, O. Ersen, I. M. Andersen, E. Snoeck, C. Gatel and A. Juhin, J. Phys. Chem. C, 2024, 128, 13162–13176 CrossRef CAS.
- X. Z. Chen, M. Hoop, F. Mushtaq, E. Siringil, C. Hu, B. J. Nelson and S. Pané, Appl. Mater. Today, 2017, 9, 37–48 CrossRef.
- V. Socoliuc, M. V. Avdeev, V. Kuncser, R. Turcu, E. Tombácz and L. Vékás, Nanoscale, 2022, 14, 4786–4886 RSC.
- Z. Yang, M. Wei, O. Voznyy, P. Todorovic, M. Liu, R. Quintero-Bermudez, P. Chen, J. Z. Fan, A. H. Proppe, L. N. Quan, G. Walters, H. Tan, J. W. Chang, U. S. Jeng, S. O. Kelley and E. H. Sargent, J. Am. Chem. Soc., 2020, 141, 8296–8305 CrossRef PubMed.
- M. Sun, B. Hao, S. Yang, X. Wang, C. Majidi and Z. Li, Nat. Commun., 2022, 13, 7919 CrossRef CAS PubMed.
- N. Li, Y. Tu, K. Wang, D. Huang, Q. Shen, W. Chen, J. Zhou, Q. Ma and M. Liu, Chem. Eng. J., 2021, 421, 129940 CrossRef CAS.
- A. Heuer-Jungemann, N. Feliu, I. Bakaimi, M. Hamaly, A. Alkilany, I. Chakraborty, A. Masood, M. F. Casula, A. Kostopoulou, E. Oh, K. Susumu, M. H. Stewart, I. L. Medintz, E. Stratakis, W. J. Parak and A. G. Kanaras, Chem. Rev., 2019, 119, 4819 CrossRef CAS PubMed.
- A. Shokuhfar and S. S. S. Afghahi, Nanoscale Res. Lett., 2013, 8, 540 CrossRef PubMed.
- M. Abdolrahimi, M. Vasilakaki, S. Slimani, N. Ntallis, G. Varvaro, S. Laureti, C. Meneghini, K. N. Trohidou, D. Fiorani and D. Peddis, Nanomaterials, 2021, 11, 1787 CrossRef CAS PubMed.
- M. Vasilakaki, N. Ntallis and K. N. Trohidou, J. Phys. Chem. Solids, 2023, 180, 111424 CrossRef CAS.
- M. Vasilakaki, N. Ntallis, D. Fiorani, D. Peddis and K. N. Trohidou, Nanoscale Adv., 2022, 4, 4366–4372 RSC.
- M. Vasilakaki, N. Ntallis, M. Bellusci, F. Varsano, R. Mathieu, D. Fiorani, D. Peddis and K. N. Trohidou, Nanotechnology, 2020, 31, 025707 CrossRef CAS PubMed.
- M. Vasilakaki, N. Ntallis, N. Yaacoub, G. Muscas, D. Peddis and K. N. Trohidou, Nanoscale, 2018, 10, 21244–24253 RSC.
- M. Vasilakaki, F. Gemenetzi, E. Devlin, D. K. Yi, S. N. Riduan, S. S. Lee, J. Y. Ying, G. C. Papaefthymiou and K. N. Trohidou, J. Magn. Magn. Mater., 2020, 522, 167570 CrossRef.
- A. Kostopoulou, K. Brintakis, M. Vasilakaki, K. N. Trohidou, A. P. Douvalis, A. Lascialfari, L. Manna and A. Lappas, Nanoscale, 2014, 6, 3764–3776 RSC.
- P. Bender, D. Honecker and L. Fernandez Barquin, Appl. Phys. Lett., 2019, 115, 132406 CrossRef.
- M. S. Chowdhury, D. A. Esteban, R. Amin, C. Rom, E. Laureen, M. Etzkorn, M. Schilling, F. Ludwig, S. Bals, V. Salguerino and A. Lak, Chem. Mater., 2024, 36, 6865 CrossRef CAS PubMed.
- E. Myrovali, N. Maniotis, A. Makridis, A. Terzopoulou, V. Ntomprougkidis, K. Simeonidis, D. Sakellari, O. Kalogirou, T. Samaras, R. Salikhov, M. Spasova, M. Farle, U. Wiedwald and M. Angelakeris, Sci. Rep., 2016, 6, 37934 CrossRef CAS PubMed.
- D. A. Rozhkov, E. S. Pyanzina, E. V. Novak, J. J. Cerdà, T. Sintes, M. Ronti, P. A. Sanchez and S. S. Kantorovich, Mol. Simul., 2018, 44, 507 CrossRef CAS.
- G. Meriguet, M. Jardat and P. Turq, J. Chem. Phys., 2004, 121, 6078–6085 CrossRef CAS PubMed.
- F. L. Durhuus, L. H. Wandall, M. H. Boisen, M. Kure, M. Beleggia and C. Frandsen, Nanoscale, 2021, 13, 1970–1981 RSC.
- M. Biersack, A. Lakkis, R. Richter, O. Bilous, P. A. Sánchez and S. S. Kantorovich, Phys. Rev. E, 2023, 108, 054905 CrossRef CAS PubMed.
- K. N. Trohidou and J. A. Blackman, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 11521–11526 CrossRef CAS PubMed.
- G. Helgesen, A. T. Skjeltorp, P. M. Mors, R. Botet and R. Jullien, Phys. Rev. Lett., 1988, 61, 1736–1739 CrossRef PubMed.
- F. L. O. Paula, L. L. Castro, T. S. A. Cassiano, S. G. dos Santos, G. Gomide, J. Depeyrot and A. F. C. Campos, Colloids Surf., A, 2023, 658, 130578 CrossRef CAS.
- A. F. Bakuzis, L. C. Branquinho, L. Luiz, E. Castro, M. T. De Amaral, E. Eloi and R. Miotto, Adv. Colloid Interface Sci., 2013, 191–192, 1–21 CrossRef CAS PubMed.
- A. Ghazali and J.-C. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 064409 CrossRef.
- T. Kruse, A. Spanoudaki and R. Pelster, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 054208 CrossRef.
- G. Bossis, L. Iskakova, V. Kostenko and A. Zubarev, Physica A, 2011, 390, 2655–2663 CrossRef CAS.
- K. Okada and A. Satoh, J. Magn. Magn. Mater., 2017, 437, 29–41 CrossRef CAS.
- S. Menear, A. Bradbury and R. W. Chantrell, J. Magn. Magn. Mater., 1984, 43, 166–176 CrossRef.
- C. Cannas, A. Musinu, G. Piccaluga, D. Fiorani, D. Peddis, H. K. Rasmussen and S. Mørup, J. Chem. Phys., 2006, 125, 164714 CrossRef CAS PubMed.
- S. Laureti, G. Varvaro, A. M. Testa, D. Fiorani, E. Agostinelli, G. Piccaluga, A. Musinu, A. Ardu and D. Peddis, Nanotechnology, 2010, 21, 315701 CrossRef CAS PubMed.
- A. Omelyanchik, G. Varvaro, P. Maltoni, V. Rodionova, J. P. M. Murillo, F. Locardi, M. Ferretti, C. Sangregorio, F. Canepa, P. Chernavsky, N. Perov and D. Peddis, Appl. Sci., 2022, 12, 1899 CrossRef CAS.
- G. S. Chaubey, C. Barcena, N. Poudyal, C. Rong, J. Gao, S. Sun and J. P. Liu, JACS Au, 2007, 129, 7214–7215 CrossRef CAS PubMed.
- M. Vasilakaki, I. Chikina, V. B. Shikin, N. Ntallis, D. Peddis, A. A. Varlamov and K. N. Trohidou, Appl. Mater. Today, 2020, 19, 100587 CrossRef.
- N. Daffé, J. Zecevic, K. N. Trohidou, M. Sikora, M. Rovezzi, C. Carvallo, M. Vasilakaki, S. Neveu, J. D. Meeldijk, N. Bouldi, V. Gavrilov, Y. Guyodo, F. Choueikani, V. Dupuis, D. Taverna, P. Sainctavit and A. Juhin, Nanoscale, 2020, 12, 11222–11231 RSC.
- A. R. Mohtasebzadeh, J. C. Davidson, K. L. Livesey and T. M. Crawford, Adv. Mater. Interfaces, 2022, 9, 2201056 CrossRef.
- Y. W. Tan, P. F. E. Gunn, W. M. Ng, S. S. Leong, P. Y. Toh, J. Camacho, J. Faraudo and J. K. Lim, Chem. Eng. Process., 2024, 199, 109768 CrossRef CAS.
- S. S. Leong, Z. Ahmad, S. C. Low, J. Camacho, J. Faraudo and J. Lim, Langmuir, 2020, 36, 8033–8055 CrossRef CAS PubMed.
- X. Fan, M. Sun, L. Sun and H. Xie, Adv. Funct. Mater., 2020, 30, 2000138 CrossRef CAS.
- A. Haldar and A. O. Adeyeye, ACS Nano, 2016, 10, 1690–1698 CrossRef CAS PubMed.
- C. Cannas, A. Ardu, A. Musinu, D. Peddis and G. Piccaluga, Chem. Mater., 2008, 20, 6364–6371 CrossRef CAS.
- L. Lartigue, P. Hugounenq, D. Alloyeau, S. P. Clarke, M. Lévy, J. C. Bacri, R. Bazzi, D. F. Brougham, C. Wilhelm and F. Gazeau, ACS Nano, 2012, 6, 10935–10949 CrossRef CAS PubMed.
- C. Cannas, A. Ardu, D. Peddis, C. Sangregorio, G. Piccaluga and A. Musinu, J. Colloid Interface Sci., 2010, 343, 415–422 CrossRef CAS PubMed.
- C. De Julián Fernández, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 054438 CrossRef.
- J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge University Press, NY, 2010 Search PubMed.
- Z. He and P. Alexandridis, Phys. Chem. Chem. Phys., 2015, 17, 18238–18261 RSC.
- C. G. Malmberg and A. A. Maryott, J. Res. Natl. Bur. Stand., 1934, 1956(56), 2641 Search PubMed.
- S. Munjal, N. Khare, C. Nehate and V. Koul, J. Magn. Magn. Mater., 2016, 404, 166–169 CrossRef CAS.
- L. L. Castro, G. R. R. Gonçalves, K. S. Neto, P. C. Morais, A. F. Bakuzis and R. Miotto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061507 CrossRef CAS PubMed.
- K. Trohidou and M. Vasilakaki, in Applications of Monte Carlo Method in Science and Engineering, ed. P. S. Mordechai, InTech, Croatia, 2011, pp. 513–538 Search PubMed.
- D. P. Landau and K. Binder, A Guide to Monte Carlo Simulations in Statistical Physics, Cambridge University Press, Cambridge, 2014 Search PubMed.
- J. M. González, O. A. Chubykalo and R. Smirnov Rueda, J. Magn. Magn. Mater., 1999, 203, 18–22 CrossRef.
- K. N. Trohidou, M. Vasilakaki, L. Del Bianco, D. Fiorani and A. M. Testa, J. Magn. Magn. Mater., 2007, 316, e82–e85 CrossRef CAS.
- Y. T. Xu, A. J. Ackroyd, A. Momeni, M. Oudah and M. J. MacLachlan, Nanoscale Horiz., 2024, 9, 317–323 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Time evolution of the initially randomly dispersed Co ferrite multicore particles in a fluid in the absence of a magnetic field. Cluster formation/dissociation of the Co ferrite multicore based FF under the applied magnetic field at longer times. The effect of the cluster formation/dissociation process by applying the magnetic field out-of-plane for the FF based on the Co ferrite multicore particles. The role of the magnetic particle anisotropy in the cluster formation/dissociation process for the Co ferrite multicore particle based FF. The role of the surfactant layer in the cluster formation/dissociation process for Co ferrite multicore particles and FeCo alloy nanoparticles in a fluid. Movie_FF1_1, Movie_FF1_2, Movie_FF2_1, and Movie_FF2_2. See DOI: https://doi.org/10.1039/d5nh00235d |
| This journal is © The Royal Society of Chemistry 2025 |