Open Access Article
Open Access ArticleDiffusiophoresis in porous media saturated with a mixture of electrolytes
Siddharth
Sambamoorthy
 a and
Henry C. W.
Chu
a and
Henry C. W.
Chu
 *b
*b
aDepartment of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA
bDepartment of Chemical Engineering and Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA. E-mail: h.chu@ufl.edu
First published on 12th February 2025
Abstract
Current theories of diffusiophoresis in porous media are limited to a porous medium saturated with a valence symmetric electrolyte. A predictive model for diffusiophoresis in porous media saturated with a valence asymmetric electrolyte, or a general mixture of valence symmetric and asymmetric electrolytes, is lacking. To close this knowledge gap, in this work we develop a mathematical model, based upon the regular perturbation method and numerical integration, to compute the diffusiophoretic mobility of a colloid in porous media saturated with a general mixture of electrolytes. We model the electrokinetics using the Poisson–Nernst–Planck equations and the fluid transport in porous media using the Brinkman equation with an electric body force. We report three novel key findings. First, we demonstrate that, in the same electrolyte concentration gradient, lowering the permeability of the porous medium can significantly weaken the colloid diffusiophoretic motion. Second, we show that, surprisingly, by using a valence asymmetric electrolyte the colloid diffusiophoretic motion in a denser porous medium can be stronger than that in a less dense porous medium saturated with a symmetric electrolyte. Third, we demonstrate that varying the composition of an electrolyte mixture does not only change the strength of the colloid diffusiophoretic motion drastically, but also qualitatively its direction. The model developed from this work can be used to understand and predict natural phenomena such as intracellular transport, as well as design technological applications such as enhanced oil recovery, nanoparticle drug delivery, and colloidal species separation.
1 Introduction
Diffusiophoresis is the deterministic motion of a colloid induced by a surrounding solute concentration gradient.1–7 Diffusiophoresis in an ionic solute concentration gradient comprises the chemiphoretic and electrophoretic transport: the chemiphoretic transport is driven by an osmotic pressure gradient and the electrophoretic transport is driven by an electric field; both the osmotic pressure gradient and the electric field are induced by the solute concentration gradient. Diffusiophoresis is pivotal in natural settings such as intracellular transport8–11 and is increasingly utilized in applications such as enhanced oil recovery,12–15 nanoparticle drug delivery,16,17 and colloidal species separation.18–41 The diffusiophoretic velocity follows u = M∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n, where n is the ion number density and M is the diffusiophoretic mobility. A positive (negative) M corresponds to a colloid driven up or down the solute concentration gradient. The mobility is the key to quantify diffusiophoresis and encompasses physical properties of the colloid and the surrounding media. The objective of this article is to develop a predictive model of diffusiophoresis that accounts for the surrounding porous media and a mixture of valence symmetric and asymmetric electrolytes, thereby uncovering and predicting their impacts on diffusiophoresis.
n, where n is the ion number density and M is the diffusiophoretic mobility. A positive (negative) M corresponds to a colloid driven up or down the solute concentration gradient. The mobility is the key to quantify diffusiophoresis and encompasses physical properties of the colloid and the surrounding media. The objective of this article is to develop a predictive model of diffusiophoresis that accounts for the surrounding porous media and a mixture of valence symmetric and asymmetric electrolytes, thereby uncovering and predicting their impacts on diffusiophoresis.
Current theories of diffusiophoresis in a valence asymmetric electrolyte and a mixture of valence symmetric and asymmetric electrolytes have ignored the presence of porous media. Pawar et al.42 developed the first theory of diffusiophoresis in a valence asymmetric electrolyte, where the colloid electric double layer thickness κ−1 is infinitesimally thin relative to the colloid radius a, i.e., κa ≫ 1. Bhattacharyya et al.43,44 derived a general model that accounts for arbitrary values of the colloid surface potential ζ and κa. Wilson et al.45 measured the colloid diffusiophoretic mobility in a valence asymmetric electrolyte in experiments and obtained good agreement with prior theories. Chiang and Velegol46 developed the first theory of diffusiophoresis in a mixture of electrolytes. Their theory assumes that κa ≫ 1 and ζ is low compared to the thermal voltage kT/e, where k is the Boltzmann constant, T is the absolute temperature, and e is the proton charge. Shi et al.19 derived a more general expression for the diffusiophoretic mobility, by relaxing the assumption of ζ ≪ kT/e. Gupta et al.47 and Ohshima48 presented approximate expressions for the mobility in the limit of ζ ≪ 1, ζ ≫ 1, and κa ≥ 50. Samanta et al.49 derived a general model that accounts for κa ≥ 50 and arbitrary values of ζ.
Current theories of diffusiophoresis in porous media are not applicable to a valence asymmetric electrolyte nor a mixture of electrolytes, and are limited to a valence symmetric electrolyte, i.e., two ionic species with valence z1 = −z2 = z. Recently, our group pioneered a theory for diffusiophoresis in porous media.50 The theory models the hydrodynamic interactions between the colloid and the porous media, which act to dampen the colloid motion as the porous medium permeability decreases. The model accurately captures diffusiophoresis experiments by Doan et al.17 with no adjustable parameters, where collagen gels are used as the porous media. Bhaskar and Bhattacharyya51 incorporated the effect of ion size into the theory, showing quantitatively different predictions. Somasundar et al.52 demonstrated the feasibility of diffusiophoresis in another porous medium, by driving colloids through porous bacterial films using a concentration gradient of a valence symmetric electrolyte. Jotkar et al.53,54 and Alipour et al.55 conducted pore-scale simulations and microfluidic experiments to examine the effect of diffusiophoresis on the hydrodynamic dispersion in porous media with different degrees of water saturation and geometric disorder. However, currently it is lacking a model that can simulate diffusiophoresis in porous media saturated with a valence asymmetric electrolyte or a general mixture of valence symmetric and asymmetric electrolytes.
In this work, we develop a mathematical model to predict the colloid diffusiophoretic mobility in a porous medium saturated with a general mixture of valence symmetric and asymmetric electrolytes. We employ the Poisson–Nernst–Planck equations to model the ion transport and electric potential distribution, and the Brinkman equation with an electric body force to model the fluid transport in a porous medium. We solve the equations using a combination of the regular perturbation method and numerical integration. We report three novel key findings that highlight the coupled effects of porous media and electrolyte mixtures on diffusiophoresis. First, we show that in the same electrolyte concentration gradient the colloid diffusiophoretic motion is significantly weaker in a less permeable porous medium. This is consistent with the fundamental nature of porous media in dampening hydrodynamics,56,57 and generalizes the same conclusion that was made in prior work for a valence symmetric electrolyte17,50–55 to a valence asymmetric electrolyte and a general mixture of electrolytes. Second, we show that by using a valence asymmetric electrolyte, surprisingly, diffusiophoresis in a denser porous medium can be stronger than that in a less dense porous medium filled with a valence symmetric electrolyte. This demonstrates the competition between electrokinetics and hydrodynamics, and offers new insights to generate strong diffusiophoresis in porous media using a valence asymmetric electrolyte. Third, we show that, in a mixture of electrolytes, not just the magnitude of the colloid diffusiophoretic motion but qualitatively its direction can change by varying the mixture composition. This highlights the novelty of the present work to leverage valence asymmetric electrolyte and electrolyte mixtures to generate a richer set of diffusiophoresis responses.
The rest of this article is structured as follows. In Section 2, we present the problem formulation for the electrokinetic equations and the diffusiophoretic mobility. In Section 3, we present the results and discussion that elucidate the above-mentioned three key findings. In Section 4, we conclude this study.
2 Problem formulation
Consider a non-conducting colloid of radius a and a constant surface charge density q (or a constant surface potential ζ) in a static porous medium with a constant permeability l2 and screening length l, subject to a constant concentration gradient of an electrolyte mixture ∇ni∞ with i = 1, 2, …, N (Fig. 1). By symmetry, the colloid translates with a constant diffusiophoretic velocity U parallel to ∇ni∞ along the z-direction, where U is to be determined. A reference frame moving with U is adopted.At steady state, ionic species conservation requires that58
 | (1) |
 | (2) |
| ∇·u = 0 and 0 = −∇p + η∇2u − ρ∇ϕ − ηl−2(u + U), | (3) |
Eqn (1)–(3) are specified by the following boundary conditions. At the colloid surface at r = a, no slip and no penetration of the solvent prescribe u = 0. No penetration of the ionic species prescribes n·ji = 0, where n is the unit normal vector pointing away from the colloid surface. The colloid surface charge density q or surface potential ζ could be specified as −n·ε∇ϕ = q or ϕ = ζ. Far from the colloid at r → ∞, u → −U and p → p∞, where p∞ is a reference constant pressure. The ion number densities and their imposed gradients are represented by ni → ni∞ + ∇ni∞·r, where ni∞ is the constant bulk electrolyte concentration and the position vector r is anchored at the centroid of the colloid. To main bulk electroneutrality, the electrolyte concentration gradient induces an electric field E = −∇ϕ = (kT/e)βG,1–3 where G = (∇n1∞)/n1∞ = …=(∇nN∞)/nN∞ and  . The ion diffusivity ratio β controls the magnitude of E and thus the electrophoretic contribution in diffusiophoresis.
. The ion diffusivity ratio β controls the magnitude of E and thus the electrophoretic contribution in diffusiophoresis.
In typical diffusiophoresis,1–3,5,6 the electrolyte concentration gradient at the size of the colloid is much smaller than the background concentration, α = |G|a ≪ 1. Using the regular perturbation method, we expand the dependent variables in α as
 | (4) |
 is twice the ionic strength of the mixture, and quantities with a superscript 0 (and 1) are associated with the equilibrium (and nonequilibrium) state, where an electrolyte concentration gradient and diffusiophoresis are absent (and present). Quantities with carets are dimensionless. We non-dimensionalize lengths by the colloid radius a and the surface charge density by εkT/(ea). Substituting eqn (4) into the governing equations and boundary conditions yield a set of differential equations at different orders of α. Below we present the O(1) perturbation equations and the O(α) perturbation equations for computing the diffusiophoretic velocity and mobility.
is twice the ionic strength of the mixture, and quantities with a superscript 0 (and 1) are associated with the equilibrium (and nonequilibrium) state, where an electrolyte concentration gradient and diffusiophoresis are absent (and present). Quantities with carets are dimensionless. We non-dimensionalize lengths by the colloid radius a and the surface charge density by εkT/(ea). Substituting eqn (4) into the governing equations and boundary conditions yield a set of differential equations at different orders of α. Below we present the O(1) perturbation equations and the O(α) perturbation equations for computing the diffusiophoretic velocity and mobility.
2.1 O(1) perturbation equations
The O(1) equations pertains to the equilibrium state where there is no electrolyte concentration gradient and fluid flow, u0 = 0. The ionic species conservation and Poisson equation are | (5) |
 | (6) |
![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = κa with κ−1 = (εkT/e2n∞)1/2 being the Debye length. The boundary condition at the colloid surface at
= κa with κ−1 = (εkT/e2n∞)1/2 being the Debye length. The boundary condition at the colloid surface at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 1 is
= 1 is  or
or ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) 0 =
0 = ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) . The far-field boundary condition at
. The far-field boundary condition at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) → ∞ are
→ ∞ are ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0i →
0i → ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i∞ and
i∞ and ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) 0 → 0. Integrating eqn (5) with the boundary condition at
0 → 0. Integrating eqn (5) with the boundary condition at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) → ∞ gives the Boltzmann distribution of the ionic species
→ ∞ gives the Boltzmann distribution of the ionic species ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0i =
0i = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i∞
i∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−zi
exp(−zi![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) 0). Substituting this result into eqn (6) gives the Poisson–Boltzmann equation58
0). Substituting this result into eqn (6) gives the Poisson–Boltzmann equation58 | (7) |
To solve eqn (7) in a finite computational domain, we consider a sphere of radius ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) that is concentric to and encloses the colloid.50,63–65 At a sufficiently large
that is concentric to and encloses the colloid.50,63–65 At a sufficiently large ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) = 1 + 20/
= 1 + 20/![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) as in this work, the electric potential decays to zero asymptotically as (1/
as in this work, the electric potential decays to zero asymptotically as (1/![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) )exp(−
)exp(−![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif)
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ). The far-field boundary conditions that were at
). The far-field boundary conditions that were at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) → ∞ are transformed to d
→ ∞ are transformed to d![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) 0/d
0/d![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) + (
+ (![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) + 1/
+ 1/![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) )
)![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) 0 = 0 at
0 = 0 at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) =
= ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) . Eqn (7) is solved using the standard shooting method with the boundary condition at
. Eqn (7) is solved using the standard shooting method with the boundary condition at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 1 and the transformed far-field boundary condition.
= 1 and the transformed far-field boundary condition.
2.2 O(α) perturbation equations
The O(α) equations pertains to the nonequilibrium state. We convert the O(α) equations to a set of ordinary differential equations by introducing the![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1 potential,
i1 potential, ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) i1 = −zi
i1 = −zi![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 0i(
0i(![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1 +
i1 + ![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) 1),50,63,64 and writing the dependent variables as û
1),50,63,64 and writing the dependent variables as û![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1(
1(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) , θ) = −(2/
, θ) = −(2/![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) )ĥ
)ĥ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, ûθ1(
θ, ûθ1(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) , θ) = (1/
, θ) = (1/![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) )[d(
)[d(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ĥ)/d
ĥ)/d![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ]sin
]sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, and
θ, and ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1(
i1(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) , θ) =
, θ) = ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1
i1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where û
θ, where û![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 1 and ûθ1 are the radial and angular components of û1, respectively. The O(α) equations now reduce to solving for ĥ = ĥ(
1 and ûθ1 are the radial and angular components of û1, respectively. The O(α) equations now reduce to solving for ĥ = ĥ(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ) and
) and ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1 =
i1 = ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1(
i1(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ), which are governed by
), which are governed by | (8) |
 | (9) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 1 are d
= 1 are d![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1/d
i1/d![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 0, ĥ = 0, and dĥ/d
= 0, ĥ = 0, and dĥ/d![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 0. The far-field boundary conditions at
= 0. The far-field boundary conditions at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) → ∞ are
→ ∞ are ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1 → (β − 1/zi)
i1 → (β − 1/zi)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) and ĥ →
and ĥ → ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif)
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) /2. The non-dimensionalized diffusiophoretic mobility
/2. The non-dimensionalized diffusiophoretic mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) relates to the dimensional diffusiophoretic mobility M via
relates to the dimensional diffusiophoretic mobility M via | (10) |
To solve eqn (8) and (9) in a finite computational domain, it again requires transforming the far-field boundary conditions at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) → ∞ to ones at
→ ∞ to ones at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) =
= ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) . First, in the asymptotic limit of a vanishing electric potential at a sufficiently large
. First, in the asymptotic limit of a vanishing electric potential at a sufficiently large ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) , the far-field boundary condition for
, the far-field boundary condition for ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1 that was at
i1 that was at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) → ∞ is transformed to be
→ ∞ is transformed to be
 | (11) |
Second, the net hydrodynamic and electric forces are zero on the large sphere of radius ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) that encloses a freely suspended colloid. A sufficiently large
that encloses a freely suspended colloid. A sufficiently large ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) guarantees that the sphere is electric force-free.50,63–65 Thus, the constraint reduces to that the sphere is hydrodynamic force-free:
guarantees that the sphere is electric force-free.50,63–65 Thus, the constraint reduces to that the sphere is hydrodynamic force-free:  , where
, where  is the Newtonian stress tensor and I is the identity tensor. Rearranging eqn (9) at
is the Newtonian stress tensor and I is the identity tensor. Rearranging eqn (9) at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) =
= ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) with the hydrodynamic force-free condition yields
with the hydrodynamic force-free condition yields
 | (12) |
 | (13) |
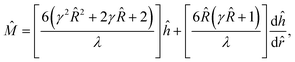 | (14) |
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 3 + 9γ
3 + 9γ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) 2 + 9
2 + 9![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) . In sum, we solve eqn (8) and (9) for ĥ and
. In sum, we solve eqn (8) and (9) for ĥ and ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1 subject to the boundary conditions d
i1 subject to the boundary conditions d![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) i1/d
i1/d![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 0, ĥ = 0, and dĥ/d
= 0, ĥ = 0, and dĥ/d![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 0 at
= 0 at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) = 1, in addition to the boundary conditions (11) to (13) at
= 1, in addition to the boundary conditions (11) to (13) at ![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) =
= ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) , using the solver NDSolve in Wolfram Mathematica and the solver bvp4c in MATLAB. We obtain the diffusiophoretic mobility from eqn (14). We have validated the present model by recovering results from prior work. Details are presented in Appendix A.
, using the solver NDSolve in Wolfram Mathematica and the solver bvp4c in MATLAB. We obtain the diffusiophoretic mobility from eqn (14). We have validated the present model by recovering results from prior work. Details are presented in Appendix A.
3 Results and discussion
Current knowledge of diffusiophoresis in porous media is limited to porous media saturated with a valence symmetric electrolyte.17,50–55 In this section, we compute and discuss novel results diffusiophoresis in porous media saturated with a valence asymmetric electrolyte, in addition to a mixture of valence symmetric and asymmetric electrolytes. Model inputs taken from typical experiments are listed in Table 1. The zeta potential ζ ∈ [−100, 100] mV corresponds to![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) ∈ [−4, 4]. The porous medium pore diameter is at least about 1.5 times the colloid diameter, which allows the passage of the colloid. In Section 3.1, we demonstrate the first and the second key findings of this work. Namely, in the same electrolyte, lowering the permeability of the porous medium significantly weakens the colloid diffusiophoretic motion. Also, surprisingly, in an valence asymmetric electrolyte, diffusiophoresis in a denser porous medium can be stronger than that in a less dense porous medium saturated with a valence symmetric electrolyte. In Section 3.2, we demonstrate the third key finding of this work. Namely, in a mixture of electrolytes, not just the magnitude but also the direction of the colloid motion can change by varying the mixture composition.
∈ [−4, 4]. The porous medium pore diameter is at least about 1.5 times the colloid diameter, which allows the passage of the colloid. In Section 3.1, we demonstrate the first and the second key findings of this work. Namely, in the same electrolyte, lowering the permeability of the porous medium significantly weakens the colloid diffusiophoretic motion. Also, surprisingly, in an valence asymmetric electrolyte, diffusiophoresis in a denser porous medium can be stronger than that in a less dense porous medium saturated with a valence symmetric electrolyte. In Section 3.2, we demonstrate the third key finding of this work. Namely, in a mixture of electrolytes, not just the magnitude but also the direction of the colloid motion can change by varying the mixture composition.
| Parameters | Values | Ion diffusivities66 | Values |
|---|---|---|---|
| Colloid radius (a)17,20,52 | 100 nm | Potassium (DK+) | 1.96 × 10−9 m2 s−1 |
| Ionic strength (I)17,20 | [0.25, 1] mM | Sodium (DNa+) | 1.33 × 10−9 m2 s−1 |
| Screening length (l)17,20,67,68 | ≥50 nm | Barium (DBa2+) | 0.847 × 10−9 m2 s−1 |
| Temperature (T) | 298 K | Magnesium (DMg2+) | 0.706 × 10−9 m2 s−1 |
| Permittivity (ε) | 6.95 × 10−10 F m−1 | Aluminum (DAl3+) | 0.541 × 10−9 m2 s−1 |
| Dynamic viscosity (η) | 0.891 × 10−3 kg m−1 s−1 | Lanthanum (DLa3+) | 0.619 × 10−9 m2 s−1 |
| Surface potential (ζ)17,20,52,58,69–73 | [−100, 100] mV | Chloride (DCl−) | 2.03 × 10−9 m2 s−1 |
3.1 Diffusiophoresis in porous media saturated with a valence asymmetric electrolyte
Let us first examine diffusiophoresis in porous media saturated with a AlCl3 solution. Fig. 2(a) shows the non-dimensionalized diffusiophoretic mobility![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus the non-dimensionalized colloid surface potential
versus the non-dimensionalized colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) . The ionic strength of the solution is I = 0.25 mM. Let us first focus on the black line with l/a ≫ 1, which corresponds to an infinitely permeable porous media, i.e., an electrolyte solution in the absence of porous media. Here, the first observation is that for a negatively charged colloid
. The ionic strength of the solution is I = 0.25 mM. Let us first focus on the black line with l/a ≫ 1, which corresponds to an infinitely permeable porous media, i.e., an electrolyte solution in the absence of porous media. Here, the first observation is that for a negatively charged colloid ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is positive, whereas for a positively charged colloid
is positive, whereas for a positively charged colloid ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is negative. This is consistent with the classical understanding of diffusiophoresis as follows.1–4 Let us first consider a negatively charged colloid as shown in Fig. 2(b). A negative β implies that the induced electric field E is pointing in the negative z-direction. The field E drives positive counterions to the left and generates an electroosmotic flow in the same direction, causing the colloid to undergo electrophoresis to the right. Meanwhile, the osmotic pressure gradient induced by the electrolyte concentration gradient generates a chemiosmotic flow to the left, causing the colloid to undergo chemiphoresis to the right. Since diffusiophoresis is the sum of electrophoresis and chemiphoresis, diffusiophoresis acts in the positive z-direction and
is negative. This is consistent with the classical understanding of diffusiophoresis as follows.1–4 Let us first consider a negatively charged colloid as shown in Fig. 2(b). A negative β implies that the induced electric field E is pointing in the negative z-direction. The field E drives positive counterions to the left and generates an electroosmotic flow in the same direction, causing the colloid to undergo electrophoresis to the right. Meanwhile, the osmotic pressure gradient induced by the electrolyte concentration gradient generates a chemiosmotic flow to the left, causing the colloid to undergo chemiphoresis to the right. Since diffusiophoresis is the sum of electrophoresis and chemiphoresis, diffusiophoresis acts in the positive z-direction and ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is positive. In contrast, for a positively charged colloid as shown in Fig. 2(c), electrophoresis which acts to the left outweighs chemiphoresis which acts to the right. This results in diffusiophoresis acting in the negative z-direction and
is positive. In contrast, for a positively charged colloid as shown in Fig. 2(c), electrophoresis which acts to the left outweighs chemiphoresis which acts to the right. This results in diffusiophoresis acting in the negative z-direction and ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is negative.
is negative.
The second observation of the black line in Fig. 2(a) is that for a negatively charged colloid the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) experiences a decay at
experiences a decay at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) ≤ 1, whereas for a positively charged colloid the magnitude of
≤ 1, whereas for a positively charged colloid the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is monotonically increasing. This can be understood by examining the ionic transport between the two cases. Let us first consider a negatively charged colloid by referring to Fig. 2(b). Both the electroosmotic and chemiosmotic flow are transporting positive counterions downstream to the colloid to the left. Due to coulombic attraction, these counterions will slow down the colloid motion that is to the right.4,63 The stronger the colloid's charge, the stronger this slowing-down effect to the colloid. Therefore,
is monotonically increasing. This can be understood by examining the ionic transport between the two cases. Let us first consider a negatively charged colloid by referring to Fig. 2(b). Both the electroosmotic and chemiosmotic flow are transporting positive counterions downstream to the colloid to the left. Due to coulombic attraction, these counterions will slow down the colloid motion that is to the right.4,63 The stronger the colloid's charge, the stronger this slowing-down effect to the colloid. Therefore, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) decays as
decays as ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) becomes more negative. Next, let us consider a positively charged colloid by referring to Fig. 2(c). In contrast to Fig. 2(b), in Fig. 2(c) only the electroosmotic flow is transporting negative counterions downstream to the colloid to the right, whereas the chemiosmotic flow is transporting counterions upstream to the colloid to the left. As a result, the slowing-down effect to the colloid due to coulombic attraction between the counterions and the colloid is weak. Therefore, the magnitude of
becomes more negative. Next, let us consider a positively charged colloid by referring to Fig. 2(c). In contrast to Fig. 2(b), in Fig. 2(c) only the electroosmotic flow is transporting negative counterions downstream to the colloid to the right, whereas the chemiosmotic flow is transporting counterions upstream to the colloid to the left. As a result, the slowing-down effect to the colloid due to coulombic attraction between the counterions and the colloid is weak. Therefore, the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) does not experience a decay but grows monotonically.
does not experience a decay but grows monotonically.
The first key finding of this work arises from an overview of Fig. 2(a), where decreasing l/a decreases the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) significantly. For example, at
significantly. For example, at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 2, decreasing l/a (from black to green line) decreases the magnitude of
= 2, decreasing l/a (from black to green line) decreases the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) from 0.459 to 0.298. Physically, decreasing l/a implies decreasing the permeability of the porous medium to the transport of the electrolyte and the colloid. That is, the presence of porous media is to weaken the magnitude of diffusioosmosis (and its constituting electroosmosis and chemiosmosis), and therefore the magnitude of the resulting diffusiophoresis (and its constituting electrophoresis and chemiphoresis). As the permeability decreases, the hydrodynamic drag to the electrolyte and the colloid increases, and therefore
from 0.459 to 0.298. Physically, decreasing l/a implies decreasing the permeability of the porous medium to the transport of the electrolyte and the colloid. That is, the presence of porous media is to weaken the magnitude of diffusioosmosis (and its constituting electroosmosis and chemiosmosis), and therefore the magnitude of the resulting diffusiophoresis (and its constituting electrophoresis and chemiphoresis). As the permeability decreases, the hydrodynamic drag to the electrolyte and the colloid increases, and therefore ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) decreases. This key finding is consistent with the fundamental nature of porous media in weakening hydrodynamics.56,57 Also, this key finding and the two observations in the previous paragraphs hold in a lower valence, valence asymmetric electrolyte BaCl2 as shown in Fig. 2(d) and in a valence symmetric electrolyte NaCl as shown in Fig. 2(e).
decreases. This key finding is consistent with the fundamental nature of porous media in weakening hydrodynamics.56,57 Also, this key finding and the two observations in the previous paragraphs hold in a lower valence, valence asymmetric electrolyte BaCl2 as shown in Fig. 2(d) and in a valence symmetric electrolyte NaCl as shown in Fig. 2(e).
Next, let us turn to Fig. 3. We consider a porous medium with l = 75 nm. In three difference cases, the porous medium is saturated with three different electrolyte solutions, AlCl3, BaCl2, and NaCl. The ionic strength of the three solutions are the same as I = 0.25 mM. The third observation is that, for a negatively charged colloid, the decay in the diffusiophoretic mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) occurs at a lower colloid surface potential
occurs at a lower colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in a higher valence electrolyte than in a lower valence electrolyte. For example, the decay in
in a higher valence electrolyte than in a lower valence electrolyte. For example, the decay in ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) for AlCl3 (black line) occurs at
for AlCl3 (black line) occurs at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) ≤ −1, whereas the decay for NaCl (green line) occurs at
≤ −1, whereas the decay for NaCl (green line) occurs at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) ≤ −3.5. This can be understood by recalling the explanation for the second observation. Specifically, the decay is due to the coulombic attraction between the colloid and the downstream counterions. For AlCl3, the counterions are Al3+, which have a higher charge density than the counterions Na+ of NaCl. Hence, at the same
≤ −3.5. This can be understood by recalling the explanation for the second observation. Specifically, the decay is due to the coulombic attraction between the colloid and the downstream counterions. For AlCl3, the counterions are Al3+, which have a higher charge density than the counterions Na+ of NaCl. Hence, at the same ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) , the coulombic attraction between the colloid and Al3+ is stronger than that between the colloid and Na+. As a result, the decay in
, the coulombic attraction between the colloid and Al3+ is stronger than that between the colloid and Na+. As a result, the decay in ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) occurs at a weaker
occurs at a weaker ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) for AlCl3.
for AlCl3.
The fourth observation is from the range of a positive ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in Fig. 3, where
in Fig. 3, where ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) can be increasingly enhanced by a more valence asymmetric electrolyte. The enhancement in
can be increasingly enhanced by a more valence asymmetric electrolyte. The enhancement in ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is significant. For example, at
is significant. For example, at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 2,
= 2, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) for NaCl is −0.137 (green line). In a BaCl2 solution,
for NaCl is −0.137 (green line). In a BaCl2 solution, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) has a 86% increase and equals −0.254 (blue line). In a AlCl3 solution,
has a 86% increase and equals −0.254 (blue line). In a AlCl3 solution, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) has a 158% increase and equals −0.354 (black line). As noted in the first observation, the electrophoretic component of diffusiophoresis dominates for a positively charged colloid. The driving force for electrophoresis is the induced electric field E = (kT/e)βG, which is proportional to the ion diffusivity ratio β. Thus, as the magnitude of β increases from |β| = 0.207 (NaCl) to |β| = 0.318 (BaCl2) and |β| = 0.408 (AlCl3), the magnitude of
has a 158% increase and equals −0.354 (black line). As noted in the first observation, the electrophoretic component of diffusiophoresis dominates for a positively charged colloid. The driving force for electrophoresis is the induced electric field E = (kT/e)βG, which is proportional to the ion diffusivity ratio β. Thus, as the magnitude of β increases from |β| = 0.207 (NaCl) to |β| = 0.318 (BaCl2) and |β| = 0.408 (AlCl3), the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) increases.
increases.
Next, let us turn to Fig. 4. The black line denotes a denser porous medium (l/a = 0.5) saturated with a AlCl3 solution and the blue line denotes a less dense porous medium (l/a = 0.75) saturated with a NaCl solution. The solution ionic strength I = 0.25 mM is the same in the two cases. Here, the second key finding of this work is that the magnitude of the diffusiophoretic mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) in a denser porous medium can be stronger than that in a less dense porous medium. For example, for a positive colloid surface potential
in a denser porous medium can be stronger than that in a less dense porous medium. For example, for a positive colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) , the magnitude of the black line is larger than that of the blue line. This is a rather surprising and non-intuitive result, as one may expect that the colloid movement in a denser porous medium is always weaker than that in a less dense porous medium due to the stronger hydrodynamic drag to the fluid and the colloid. However, results here show that, by employing a valence asymmetric electrolyte, diffusiophoresis in a denser porous medium can be much stronger than that in a less dense porous medium saturated with a valence symmetric electrolyte. Physically, this is because the enhancement to the electrophoretic component of diffusiophoresis by the valence asymmetric electrolyte outweighs the hydrodynamic drag due to the porous media. This finding offers new insights into using valence asymmetric electrolyte to generate strong diffusiophoresis in porous media.
, the magnitude of the black line is larger than that of the blue line. This is a rather surprising and non-intuitive result, as one may expect that the colloid movement in a denser porous medium is always weaker than that in a less dense porous medium due to the stronger hydrodynamic drag to the fluid and the colloid. However, results here show that, by employing a valence asymmetric electrolyte, diffusiophoresis in a denser porous medium can be much stronger than that in a less dense porous medium saturated with a valence symmetric electrolyte. Physically, this is because the enhancement to the electrophoretic component of diffusiophoresis by the valence asymmetric electrolyte outweighs the hydrodynamic drag due to the porous media. This finding offers new insights into using valence asymmetric electrolyte to generate strong diffusiophoresis in porous media.
3.2 Diffusiophoresis in porous media saturated with a mixture of valence symmetric and asymmetric electrolytes
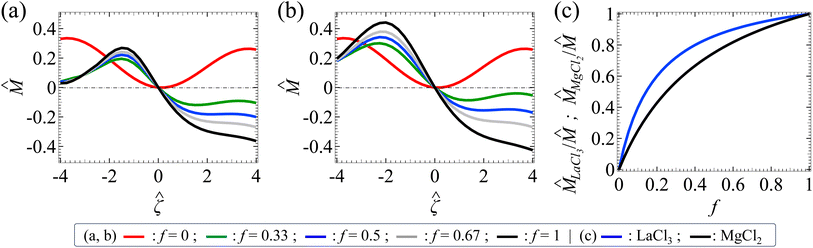
Let us examine diffusiophoresis in porous media saturated with solution mixtures of p molar of KCl and q molar of LaCl3 with different compositions f = q/(p + q), where f ∈ [0, 1] with f = 0 and f = 1 representing a pure KCl solution and a pure LaCl3 solution, respectively. Fig. 5(a) shows the diffusiophoretic mobility![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus the colloid surface potential
versus the colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) . The screening length is l = 75 nm and the ionic strength of the solution is I = 1 mM. Let us first focus on the black and the red line with f = 1 and f = 0, respectively. The first observation is that the variation of
. The screening length is l = 75 nm and the ionic strength of the solution is I = 1 mM. Let us first focus on the black and the red line with f = 1 and f = 0, respectively. The first observation is that the variation of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus
versus ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in a pure LaCl3 solution (f = 1; black line) is qualitatively different from that in a pure KCl solution (f = 0; red line). Specifically, in a pure LaCl3 solution,
in a pure LaCl3 solution (f = 1; black line) is qualitatively different from that in a pure KCl solution (f = 0; red line). Specifically, in a pure LaCl3 solution, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is positive for a negative
is positive for a negative ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) and is negative for a positive
and is negative for a positive ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) . This follows the same trend and explanation as for AlCl3 in the first observation in Section 3.1 and is not repeated here. In contrast, in a pure KCl solution,
. This follows the same trend and explanation as for AlCl3 in the first observation in Section 3.1 and is not repeated here. In contrast, in a pure KCl solution, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is positive regardless of the sign of
is positive regardless of the sign of ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) . This is understood by noting the very small value β = −0.0188, which reflects the negligibly small electrophoretic contribution in diffusiophoresis. Hence, the colloid undergoes diffusiophoresis chiefly due to chemiphoresis that drives the colloid in the positive z-direction and thus
. This is understood by noting the very small value β = −0.0188, which reflects the negligibly small electrophoretic contribution in diffusiophoresis. Hence, the colloid undergoes diffusiophoresis chiefly due to chemiphoresis that drives the colloid in the positive z-direction and thus ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is positive.
is positive.
The third key finding of this work is that varying the mixture composition f can change not just the magnitude of the colloid diffusiophoretic motion drastically, but also qualitatively its direction; the latter is reflected from the sign change of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) for a fixed positive
for a fixed positive ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) as f increases. In a mixture of electrolytes,
as f increases. In a mixture of electrolytes, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is not simply the superposition nor the weighted average of the contributions from its individual electrolyte. For example, in Fig. 5(a) at
is not simply the superposition nor the weighted average of the contributions from its individual electrolyte. For example, in Fig. 5(a) at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = 3,
= 3, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f=0 = 0.240 (red line) and
f=0 = 0.240 (red line) and ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f=1 = −0.328 (black line), but
f=1 = −0.328 (black line), but ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f=0.5 = −0.179 (blue line) ≠ (
f=0.5 = −0.179 (blue line) ≠ (![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f = 0 +
f = 0 + ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f=1)/2. In fact,
f=1)/2. In fact, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) depends nonlinearly on f. This is because
depends nonlinearly on f. This is because ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) is a result of the nonlinearly coupled Poisson–Nernst–Planck and Brinkman eqn (1)–(3). Because of this intricate coupling,
is a result of the nonlinearly coupled Poisson–Nernst–Planck and Brinkman eqn (1)–(3). Because of this intricate coupling, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) can vary non-monotonically with f. For example, at
can vary non-monotonically with f. For example, at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −2.8,
= −2.8, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f=0 = 0.283 (red line); as f increases,
f=0 = 0.283 (red line); as f increases, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) first decreases and then increases. In the special case at
first decreases and then increases. In the special case at ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) = −2.4,
= −2.4, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f=0 (red line) can even be identical to
f=0 (red line) can even be identical to ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) f=1 (black line), meaning that a colloid undergoes the same diffusiophoretic motion regardless of the electrolyte identity. These observations are not restricted to a KCl/LaCl3 mixture but is general to other electrolyte mixtures. For example, Fig. 5(b) shows a similar set of diffusiophoretic response in a KCl/MgCl2 mixture as in Fig. 5(a). These observations underline the importance of this work to solve the coupled Poisson–Nernst–Planck–Brinkman equations to predict diffusiophoresis.
f=1 (black line), meaning that a colloid undergoes the same diffusiophoretic motion regardless of the electrolyte identity. These observations are not restricted to a KCl/LaCl3 mixture but is general to other electrolyte mixtures. For example, Fig. 5(b) shows a similar set of diffusiophoretic response in a KCl/MgCl2 mixture as in Fig. 5(a). These observations underline the importance of this work to solve the coupled Poisson–Nernst–Planck–Brinkman equations to predict diffusiophoresis.
A scaling analysis illustrates that the nonlinearity between ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and f depends on the ion valence z. First, referring to the far-field boundary condition below eqn (9),
and f depends on the ion valence z. First, referring to the far-field boundary condition below eqn (9), ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) ∼ ĥ. Further, from eqn (9),
∼ ĥ. Further, from eqn (9),  , where Î is the non-dimensionalized mixture ionic strength. Combining these relations,
, where Î is the non-dimensionalized mixture ionic strength. Combining these relations, ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) ∼ Î. Second, recall that f = q/(p + q). Stoichiometry requires that the ionic strength of KCl is IKCl = (1/2)(zK+2p + zCl−2p) M = p M, with zK+ = −zCl− = 1. The ionic strength of LaCl3 is ILaCl3 = (1/2)(zLa3+2q + zCl−2q) M = 6q M, with zLa3+ = 3 and zCl− = −1. Note that ILaCl3 increases nonlinearly with an increase in the ion valence zLa3+2. Thus, I = IKCl + ILaCl3 = p + 6q M. Upon non-dimensionalization, ÎLaCl3 = 6
∼ Î. Second, recall that f = q/(p + q). Stoichiometry requires that the ionic strength of KCl is IKCl = (1/2)(zK+2p + zCl−2p) M = p M, with zK+ = −zCl− = 1. The ionic strength of LaCl3 is ILaCl3 = (1/2)(zLa3+2q + zCl−2q) M = 6q M, with zLa3+ = 3 and zCl− = −1. Note that ILaCl3 increases nonlinearly with an increase in the ion valence zLa3+2. Thus, I = IKCl + ILaCl3 = p + 6q M. Upon non-dimensionalization, ÎLaCl3 = 6![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) and Î =
and Î = ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) (5f + 1)/f. Recall that
(5f + 1)/f. Recall that ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) ∼ Î, thus
∼ Î, thus ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) LaCl3 ∼ ÎLaCl3, where
LaCl3 ∼ ÎLaCl3, where ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) LaCl3 is the contribution of LaCl3 to the mobility of the mixture
LaCl3 is the contribution of LaCl3 to the mobility of the mixture ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) . Thus, it is established that
. Thus, it is established that
 | (15) |
 | (16) |
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) LaCl3/
LaCl3/![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) and
and ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) MgCl2/
MgCl2/![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) to f. Note that
to f. Note that ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) LaCl3/
LaCl3/![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) (blue line) shows a stronger increase than
(blue line) shows a stronger increase than ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) MgCl2/
MgCl2/![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) (black line) at the same f. This is because the nonlinearity in the ion valence for zLa3+2 = 9 is stronger than that for zMg2+2 = 4. This explains why in Fig. 5(a) and (b) the sensitivity of
(black line) at the same f. This is because the nonlinearity in the ion valence for zLa3+2 = 9 is stronger than that for zMg2+2 = 4. This explains why in Fig. 5(a) and (b) the sensitivity of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) to a change in f in a KCl/LaCl3 mixture is stronger than that in a KCl/MgCl2 mixture.
to a change in f in a KCl/LaCl3 mixture is stronger than that in a KCl/MgCl2 mixture.
Before closing, we demonstrate the generality of the first two key findings of this work, which were demonstrated in Section 3.1 with a valence asymmetric electrolyte, in an electrolyte mixture. First, recall the first key finding that the magnitude of diffusiophoresis weakens significantly as the porous medium permeability decreases. Fig. 6(a) shows the diffusiophoretic mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus the colloid surface potential
versus the colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in different porous media saturated with a KCl/LaCl3 mixture of composition f = 0.5. The first key finding is confirmed that the magnitude of
in different porous media saturated with a KCl/LaCl3 mixture of composition f = 0.5. The first key finding is confirmed that the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) decreases substantially as l/a decreases (from black to green line). In fact, the first key finding holds not just in a mixture of two electrolytes. Fig. 6(b) shows
decreases substantially as l/a decreases (from black to green line). In fact, the first key finding holds not just in a mixture of two electrolytes. Fig. 6(b) shows ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus
versus ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in different porous media saturated with a phosphate-buffered saline (PBS) solution, which is a mixture of NaCl, KCl, Na2HPO4, and KH2PO4. The detailed ionic composition of the PBS solution is given in Appendix B. Again, the first key finding is confirmed by the decreasing magnitude of
in different porous media saturated with a phosphate-buffered saline (PBS) solution, which is a mixture of NaCl, KCl, Na2HPO4, and KH2PO4. The detailed ionic composition of the PBS solution is given in Appendix B. Again, the first key finding is confirmed by the decreasing magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) with decreasing l/a (from black to green line).
with decreasing l/a (from black to green line).
Lastly, recall the second key finding that, with a valence asymmetric electrolyte, diffusiophoresis in a denser porous medium can be stronger than diffusiophoresis in a less dense porous medium saturated with a valence symmetric electrolyte. Fig. 6(c) shows ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus
versus ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in different porous media saturated with different KCl/LaCl3 mixtures. The black line corresponds to a denser porous medium (l/a = 0.5) saturated with a mixture with a higher fraction of LaCl3 (f = 1), whereas the blue line corresponds to a less dense porous medium (l/a = 0.75) saturated with a mixture with a lower fraction of LaCl3 (f = 0.33). The second key finding is confirmed by observing that for positive
in different porous media saturated with different KCl/LaCl3 mixtures. The black line corresponds to a denser porous medium (l/a = 0.5) saturated with a mixture with a higher fraction of LaCl3 (f = 1), whereas the blue line corresponds to a less dense porous medium (l/a = 0.75) saturated with a mixture with a lower fraction of LaCl3 (f = 0.33). The second key finding is confirmed by observing that for positive ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) the magnitude of
the magnitude of ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) of the black line can indeed be larger than that of the blue line. In sum, these results underline the novelty of this work and the importance of leveraging valence asymmetric electrolytes and electrolyte mixtures to achieve richer responses in diffusiophoresis in porous media.
of the black line can indeed be larger than that of the blue line. In sum, these results underline the novelty of this work and the importance of leveraging valence asymmetric electrolytes and electrolyte mixtures to achieve richer responses in diffusiophoresis in porous media.
4 Conclusions
In this work, we have developed a predictive model for diffusiophoresis in porous media saturated with a general mixture of electrolytes. Prior models have focused either on diffusiophoresis in a mixture of electrolytes in the absence of porous media,19,42–44,46–49 or diffusiophoresis in porous media saturated with a valence symmetric electrolyte.17,50–55 The present model is novel in that it accounts for the coupled effects of porous media and electrolyte mixtures. We have computed the diffusiophoretic mobilities in porous media saturated with a valence asymmetric electrolyte as well as in porous media saturated with a mixture of valence symmetric and asymmetric electrolytes. We summarize the three key findings below.The first key finding of this work is that, in the same electrolyte solution, decreasing the porous medium permeability weakens the colloid diffusiophoretic motion significantly. This is consistent with the fundamental nature of porous media which provides a larger hydrodynamic hindrance to the colloid and the suspending fluid, and thus, weakens diffusiophoresis. This key finding is consistent with the same conclusion drawn in prior work for diffusiophoresis in porous media saturated with a valence symmetric electrolyte.17,50–52 Here, we have generalized this key finding to diffusiophoresis in porous media saturated with a valence asymmetric electrolyte and a general mixture of electrolytes.
The second key finding is that, by utilizing a valence asymmetric electrolyte, diffusiophoresis in a denser porous medium can be stronger than that in a less dense porous medium saturated with a valence symmetric electrolyte. This is contrary to what one might expect that diffusiophoresis in a denser porous medium is always weaker. In fact, this surprising result is due to the fact that valence asymmetric electrolyte can generate a stronger electrophoretic motion of the colloid, which outweighs the hydrodynamic drag due to the porous medium. We have further generalized this key finding by showing that diffusiophoresis in a denser porous medium saturated with a mixture of higher fraction of asymmetric electrolyte can be stronger than that in a less dense porous medium saturated with a mixture of lower fraction of asymmetric electrolyte.
The third key finding is that varying the mixture composition can change not only the magnitude of the diffusiophoretic motion significantly, but also qualitatively its direction. The diffusiophoretic mobility in an electrolyte mixture is not simply the superposition nor the weighted average of the contributions from its individual electrolyte. This is because diffusiophoresis is governed by the nonlinearly coupled Poisson–Nernst–Planck–Brinkman equations. This underlines the value of the present work to determine the colloid diffusiophoretic motion by solving the coupled governing equations. Together, the present model and these key findings will enable fundamental understanding of diffusiophoresis in porous media and predict a richer set of diffusiophoresis responses in the presence of an electrolyte mixture.
Data availability
All data that supports this study is included in this article.Conflicts of interest
There are no conflicts of interest to declare.Appendices
Appendix A: Model validations
We validate the present model by recovering results from prior work. First, Fig. 7 shows that the present model recovers Fig. 4 in Sambamoorthy and Chu,50 for diffusiophoresis in different porous media saturated with a NaCl solution. Second, Fig. 8 shows that the present model recovers Fig. 3 in Gupta et al.,47 for diffusiophoresis in different valence asymmetric electrolyte solutions in the limit of a thin electric double layer and in the absence of porous media. Here, the diffusiophoresis results have the same magnitude and an opposite sign as the diffusioosmosis results in Gupta et al.,47 since diffusiophoresis is the exact opposite of diffusioosmosis in the limit of a thin electric double layer. Third, Fig. 9 shows that the present model recovers Fig. 9 in Prieve and Roman,65 for diffusiophoresis in a NaCl solution in the absence of porous media. Lastly, Fig. 10 shows that the present model recovers Fig. 4 in Prieve et al.,1 for diffusiophoresis in different valence symmetric electrolyte solutions in the limit of a thin electric double layer and in the absence of porous media. | ||
Fig. 7 The non-dimensionalized diffusiophoretic mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus the non-dimensionalized colloid surface potential versus the non-dimensionalized colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in different porous media saturated with a NaCl solution with the Debye–Huckel approximation. Lines: predictions by the present model. Symbols: predictions by Sambamoorthy and Chu.50 Black: the ratio of the screening length to the colloid radius l/a ≫ 1. Grey: l/a = 4. Blue: l/a = 1. Green: l/a = 0.1. Orange: l/a = 0.02. in different porous media saturated with a NaCl solution with the Debye–Huckel approximation. Lines: predictions by the present model. Symbols: predictions by Sambamoorthy and Chu.50 Black: the ratio of the screening length to the colloid radius l/a ≫ 1. Grey: l/a = 4. Blue: l/a = 1. Green: l/a = 0.1. Orange: l/a = 0.02. | ||
 | ||
Fig. 8 The non-dimensionalized diffusiophoretic mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus the non-dimensionalized colloid surface potential versus the non-dimensionalized colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in different valence asymmetric electrolyte solutions in the limit of a thin electric double layer (the ratio of the colloid radius to the Debye length in different valence asymmetric electrolyte solutions in the limit of a thin electric double layer (the ratio of the colloid radius to the Debye length ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) ≫ 1) and in the absence of porous media (the ratio of the screening length to the colloid radius l/a ≫ 1). Lines: predictions by the present model. Symbols: predictions by Gupta et al.47 Black: H2SO4. Blue: Na2SO4. Green: CaCl2. Orange: Mg(HCO3)2. ≫ 1) and in the absence of porous media (the ratio of the screening length to the colloid radius l/a ≫ 1). Lines: predictions by the present model. Symbols: predictions by Gupta et al.47 Black: H2SO4. Blue: Na2SO4. Green: CaCl2. Orange: Mg(HCO3)2. | ||
 | ||
Fig. 9 The non-dimensionalized diffusiophoretic mobility (3/2)![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus the non-dimensionalized colloid surface potential versus the non-dimensionalized colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in a NaCl solution in the absence of porous media (the ratio of the screening length to the colloid radius l/a ≫ 1). Lines: predictions by the present model. Symbols: predictions by Prieve and Roman.65 Black: the ratio of the colloid radius to the Debye length in a NaCl solution in the absence of porous media (the ratio of the screening length to the colloid radius l/a ≫ 1). Lines: predictions by the present model. Symbols: predictions by Prieve and Roman.65 Black: the ratio of the colloid radius to the Debye length ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) ≫ 1. Grey: ≫ 1. Grey: ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = 1000. Purple: = 1000. Purple: ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = 100. Blue: = 100. Blue: ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = 10. Cyan: = 10. Cyan: ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = 1. Green: = 1. Green: ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = 0.1. Orange: = 0.1. Orange: ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) = 0. = 0. | ||
 | ||
Fig. 10 The non-dimensionalized diffusiophoretic mobility 2![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) versus the non-dimensionalized colloid surface potential versus the non-dimensionalized colloid surface potential ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) in different valence symmetric electrolyte solutions in the limit of a thin electric double layer (the ratio of the colloid radius to the Debye length in different valence symmetric electrolyte solutions in the limit of a thin electric double layer (the ratio of the colloid radius to the Debye length ![[small kappa, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e109.gif) ≫ 1) and in the absence of porous media (the ratio of the screening length to the colloid radius l/a ≫ 1). Lines: predictions by the present model. Symbols: predictions by Prieve et al.1 Black: NaCl. Blue: KCl. Green: NH4F. ≫ 1) and in the absence of porous media (the ratio of the screening length to the colloid radius l/a ≫ 1). Lines: predictions by the present model. Symbols: predictions by Prieve et al.1 Black: NaCl. Blue: KCl. Green: NH4F. | ||
Appendix B: Ionic composition of phosphate-buffered saline solution
A 1× phosphate-buffered saline (PBS) solution comprises 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, and 1.8 mM KH2PO4. From dissociation, there are 157 mM Na+, 139.7 mM Cl−, 4.5 mM K+, 10 mM HPO42−, and 1.8 mM H2PO4−. Dihydrogen phosphate ion H2PO4− and monohydrogen phosphate ions HPO42− have a chemical equilibrium, H2PO4− ⇌ H+ + HPO42−, with an equilibrium constant of 10−4.21 mM and diffusivities DHPO42− = 0.439 × 10−9 m2 s−1 and DH2PO4− = 0.879 × 10−9 m2 s−1.66,74 Thus, there is 1.11 × 10−5 mM H+, which is negligible compared to the five dominant species, namely, Na+, K+, Cl−, HPO42−, and H2PO4−. To obtain the concentrations of the five dominant species at I = 1 mM as in Fig. 6(b), we first obtain the ratios of the concentrations of the five species to the ionic strength of the mixture as | (17) |
The above ratios remain unchanged for PBS solutions at other ionic strengths. Thus, the concentrations of the five dominant species at I = 1 mM can be obtained by multiplying the above ratios to I = 1 mM, giving 0.915 mM Na+, 0.0262 mM K+, 0.815 mM Cl−, 0.0583 mM HPO42−, and 0.0105 mM H2PO4−.
Acknowledgements
H. C. W. Chu acknowledges the funding support from University of Florida. This work was supported by the donors of ACS Petroleum Research Fund under Doctoral New Investigator Grant 66915-DNI9. H. C. W. C served as Principal Investigator on ACS PRF 66915-DNI9 that provided support for S. S. The authors acknowledge the fruitful discussion with Professor Anthony J. C. Ladd.References
- D. C. Prieve, J. L. Anderson, J. P. Ebel and M. E. Lowell, J. Fluid Mech., 1984, 148, 247–269 CrossRef CAS.
- D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703 RSC.
- H. J. Keh, Curr. Opin. Colloid Interface Sci., 2016, 24, 13–22 CrossRef CAS.
- E. Lee, Theory of Electrophoresis and Diffusiophoresis of Highly Charged Colloidal Particles, Elsevier, New York, 2018 Search PubMed.
- S. Shin, Phys. Fluids, 2020, 32, 101302 CrossRef CAS.
- S. Shim, Chem. Rev., 2022, 122, 6986–7009 CrossRef CAS PubMed.
- J. T. Ault and S. Shin, Annu. Rev. Fluid. Mech., 2024, 57, 227–255 CrossRef.
- M. Loose, E. Fischer-Friedrich, J. Ries, K. Kruse and P. Schwille, Science, 2008, 320, 789–792 CrossRef CAS PubMed.
- J. Lutkenhaus, Science, 2008, 320, 755–756 CrossRef CAS PubMed.
- R. P. Sear, Phys. Rev. Lett., 2019, 122, 128101 CrossRef CAS PubMed.
- B. Ramm, A. Goychuk, A. Khmelinskaia, P. Blumhardt, H. Eto, K. A. Ganzinger, E. Frey and P. Schwille, Nat. Phys., 2021, 17, 850–858 Search PubMed.
- A. Kar, T. Chiang, I. O. Rivera, A. Sen and D. Velegol, ACS Nano, 2015, 9, 746–753 CrossRef CAS PubMed.
- S. W. Park, J. Lee, H. Yoon and S. Shin, Energy Fuels, 2021, 35, 4885–4892 CrossRef CAS.
- N. Shi and A. Abdel-Fattah, Phys. Rev. Fluids, 2021, 6, 053103 CrossRef.
- H. Tan, A. Banejee, N. Shi, X. Tang, A. Abdel-Fattah and T. M. Squires, Sci. Adv., 2021, 7, eabh0638 CrossRef CAS PubMed.
- S. Shin, V. S. Doan and J. Feng, Phys. Rev. Appl., 2019, 12, 024014 CrossRef CAS.
- V. S. Doan, S. Chun, J. Feng and S. Shin, Nano Lett., 2021, 21, 7625–7630 CrossRef CAS.
- C. Lee, C. Cottin-Bizonne, A. L. Biance, P. Joseph, L. Bocquet and C. Ybert, Phys. Rev. Lett., 2014, 112, 244501 CrossRef CAS PubMed.
- N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah and T. M. Squires, Phys. Rev. Lett., 2016, 117, 258001 CrossRef PubMed.
- S. Shin, E. Um, B. Sabass, J. T. Ault, M. Rahimi, P. B. Warren and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 257–261 CrossRef CAS PubMed.
- S. Zhai and H. Zhao, Phys. Rev. E, 2016, 93, 052409 CrossRef PubMed.
- S. Shin, J. T. Ault, P. B. Warren and H. A. Stone, Phys. Rev. X, 2017, 4, 041038 Search PubMed.
- F. Raynal, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and R. Volk, J. Fluid Mech., 2018, 847, 228–243 CrossRef CAS.
- F. Raynal and R. Volk, J. Fluid Mech., 2019, 876, 818–829 CrossRef CAS.
- J. T. Ault, S. Shin and H. A. Stone, Soft Matter, 2019, 15, 1582–1596 RSC.
- A. McMullen, G. Araujo, M. Winter and D. Stein, Sci. Rep., 2019, 9, 15065 CrossRef PubMed.
- D. Ha, S. Seo, K. Lee and T. Kim, ACS Nano, 2019, 13, 12939–12948 CrossRef CAS PubMed.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2020, 16, 238–246 RSC.
- M. K. Rasmussen, J. N. Pedersen and R. Marie, Nat. Commun., 2020, 11, 2337 CrossRef CAS PubMed.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, J. Fluid Mech., 2021, 917, A52 CrossRef CAS.
- N. Singh, G. T. Vladisavljevic, F. Nadal, C. Cottin-Bizonne, C. Pirat and G. Bolognesi, Phys. Rev. Lett., 2020, 125, 248002 CrossRef CAS PubMed.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2022, 18, 1896–1910 RSC.
- B. M. Alessio, S. Shim, A. Gupta and H. A. Stone, J. Fluid Mech., 2022, 942, A23 CrossRef CAS.
- B. E. McKenzie, H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, J. Fluid Mech., 2022, 949, A17 CrossRef CAS.
- R. Volk, M. Bourgoin, C. Brehier and F. Raynal, J. Fluid Mech., 2022, 948, A42 CrossRef CAS.
- J. Xu, Z. Wang and H. C. W. Chu, RSC Adv., 2023, 13, 9247–9259 RSC.
- B. Akdeniz, J. A. Wood and R. G. H. Lammertink, Langmuir, 2023, 39, 2322–2332 CrossRef CAS PubMed.
- S. Zhang and H. C. W. Chu, Nanoscale, 2024, 16, 9367–9381 RSC.
- J. Teng, B. Rallabandi and J. T. Ault, J. Fluid Mech., 2023, 977, A5 CrossRef CAS.
- S. Zhang and H. C. W. Chu, Chem. Sci., 2024, 15, 18476–18489 RSC.
- H. Liu and A. A. Pahlavan, Solute-mediated colloidal vortex in a microfluidic T-junction, arXiv, 2025, preprint, arXiv:2409.01594, DOI:10.48550/arXiv.2409.01594.
- Y. Pawar, Y. E. Solomentsev and J. L. Anderson, J. Colloid Interface Sci., 1993, 155, 488–498 CrossRef CAS.
- S. Majhi and S. Bhattacharyya, Colloids Surf., A, 2022, 648, 129272 CrossRef CAS.
- B. Bhaskar and S. Bhattacharyya, Phys. Fluids, 2023, 35, 062012 CrossRef CAS.
- J. L. Wilson, S. Shim, Y. E. Yu, A. Gupta and H. A. Stone, Langmuir, 2020, 36, 7014–7020 CrossRef CAS PubMed.
- T. Chiang and D. Velegol, J. Colloid Interface Sci., 2014, 424, 120–123 CrossRef CAS PubMed.
- A. Gupta, B. Rallabandi and H. A. Stone, Phys. Rev. Fluids, 2019, 4, 043702 CrossRef.
- H. Ohshima, Colloid Polym. Sci., 2021, 299, 1877–1884 CrossRef CAS.
- S. Samanta, P. Mahapatra, H. Ohshima and P. P. Gopmandal, Phys. Fluids, 2023, 35, 032006 CrossRef CAS.
- S. Sambamoorthy and H. C. W. Chu, Soft Matter, 2023, 19, 1131–1143 Search PubMed.
- B. Bhaskar and S. Bhattacharyya, Phys. Fluids, 2023, 35, 102023 CrossRef CAS.
- A. Somasundar, B. Qin, S. Shim, B. L. Bassler and H. A. Stone, ACS Appl. Mater. Interfaces, 2023, 15, 33263–33272 CrossRef CAS PubMed.
- M. Jotkar, P. de Anna, M. Dentz and L. Cueto-Felgueroso, J. Fluid Mech., 2024, 991, A8 CrossRef CAS.
- M. Jotkar, I. Ben-Noah, J. J. Hidalgo and M. Dentz, Adv. Water Resour., 2024, 193, 104828 CrossRef CAS.
- M. Alipour, Y. Li, H. Liu and A. A. Pahlavan, Diffusiophoretic transport of colloids in porous media, arXiv, 2025, preprint, arXiv:2411.14712, DOI:10.48550/arXiv.2411.14712.
- H. C. Brinkman, Appl. Sci. Res., 1949, 1, 27–34 Search PubMed.
- J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics, Springer, New York, 1983 Search PubMed.
- R. J. Hunter, Zeta Potential in Colloid Science, Academic Press, New York, 1981 Search PubMed.
- S. A. Allison, Y. Xin and H. Pei, J. Colloid Interface Sci., 2007, 313, 328–337 CrossRef CAS PubMed.
- P. Tsai and E. Lee, Soft Matter, 2011, 7, 5789–5798 RSC.
- J. P. Hsu, C. Huang and S. Tseng, Chem. Eng. Sci., 2012, 84, 574–579 CrossRef CAS.
- R. J. Hill, Soft Matter, 2016, 12, 8030–8048 RSC.
- R. W. O'Brien and L. R. White, J. Chem. Soc. Faraday Trans. II, 1978, 74, 1607–1626 RSC.
- R. W. O'Brien and R. J. Hunter, Can. J. Chem., 1981, 81, 1878–1887 CrossRef.
- D. C. Prieve and R. Roman, J. Chem. Soc. Faraday Trans. II, 1987, 83, 1287–1306 RSC.
- J. H. Dane and G. C. Topp, Methods of Soil Analysis Part 4 Physical Methods, Soil Science Society of America Inc., Madison Wisconsin, 2002 Search PubMed.
- P. G. Righetti and C. Gelfi, J. Chromatogr. B, 1996, 699, 63–75 CrossRef PubMed.
- A. Pluen, P. A. Netti, R. K. Jain and D. A. Berk, Biophys. J., 1999, 77, 542–552 CrossRef CAS PubMed.
- L. Ramirez, S. R. Gentile, S. Zimmermann and S. Stoll, J. Colloid Sci. Biotechnol., 2016, 5, 1–9 CrossRef.
- Y. Chang, Y. Wang and W. Cheng, Colloid Polym. Sci., 2009, 287, 659–670 CrossRef CAS.
- A. Kotera, K. Furusawa and Y. Takeda, Kolloid-Z. Z. Polym., 1970, 239, 677–681 CrossRef CAS.
- K. Bere, X. Xiong, S. Saringer, G. Douglas and I. Szilagyi, J. Mol. Liq., 2023, 384, 122285 CrossRef CAS.
- H. Ono, F. Sato, E. Jidai and K. Shibayama, Colloid Polym. Sci., 1975, 253, 538–543 CrossRef CAS.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC press, Boca Raton, FL, 2014 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |