 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Novel auxetic semiconductors with high carrier mobility: first principles prediction of Janus Ge2XY (X/Y = S, Se, Te) monolayers
Vo Q.
Nha
a,
Nguyen Q.
San
a,
Huynh T. T.
Linh
a,
Tuan V.
Vu
 bc and
Nguyen D.
Hien
bc and
Nguyen D.
Hien
 *de
*de
aSchool of Engineering and Technology, Hue University, Hue, Vietnam
bLaboratory for Computational Physics, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: tuan.vu@vlu.edu.vn
cFaculty of Mechanical - Electrical and Computer Engineering, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam
dInstitute of Research and Development, Duy Tan University, Da Nang, Vietnam. E-mail: nguyendinhhien2@duytan.edu.vn
eSchool of Engineering & Technology, Duy Tan University, Da Nang, Vietnam
First published on 21st February 2025
Abstract
Recently, auxetic materials have attracted attention due to their unusual behavior and multifunctional applications. A negative Poisson's ratio has been found in some two-dimensional (2D) asymmetric layered materials. In this work, we predict a new class of 2D auxetic materials with the chemical formula Ge2XY (X/Y = S, Se, Te) using ab initio calculations. We construct the crystal structure and evaluate the stability of Janus Ge2XY monolayers under ambient conditions. Phonon dispersion spectra, cohesive energy calculations, and molecular dynamics simulations confirm the high structural stability of Ge2XY. At the ground state, Ge2XY monolayers are semiconductors with narrow band gaps ranging from 0.11 to 1.09 eV. We also calculate the mechanical properties, including elastic constants, Young's modulus, and Poisson's ratio. Importantly, the Ge2XY monolayers represent ideal auxetic materials with a large negative Poisson's ratio. All three Ge2XY systems possess Poisson's ratio values of around −0.2 along the x-axis. Moreover, Ge2XY monolayers are predicted to have high electron mobility up to 10.92 × 103 cm2 V−1 s−1 (Ge2STe). The combination of ideal auxetic behavior and tunable transport properties makes the Janus Ge2XY structures promising materials for nanoelectronic and mechanical applications.
1 Introduction
One of the important parameters for determining a material's mechanical characteristics is Poisson's ratio. Auxetic materials, which possess a negative Poisson's ratio (NPR), have several unique and beneficial properties, such as high indentation resistance,1 improved toughness,2 and superior sound absorption.3 These enhanced features could lead to uses in protector devices,4 healthcare,5 and industry.6 Previous reports have shown that bulk, two-dimensional (2D), and even one-dimensional (1D) materials exhibit NPR effects. For example, 1D carbon nanostructures named diamond nanothreads show auxetic behavior.7 The NPR phenomena were also observed in poly[5]asterane,8 which is known to be a 1D nanostructure with mechanical and chemical stability. 3D structures, such as composites,9 microporous polymers,10 and cubic metals,11 also exhibit NPR effects. Like bulk and 1D materials, auxetic behavior is also present in many 2D nanostructures. Jiang and Park observed that the first 2D material to possess the NPR phenomenon was black phosphorus.12 However, the effect in black phosphorus is small, with a Poisson's ratio value of −0.027. Other 2D structures, such as δ-phosphorene,13 borophene,14 and penta-graphene,15 are auxetic materials. According to earlier results, the NPR behavior originates from the unusual geometrical structures of the materials, such as re-entrant or puckered crystal structures.Very recently, the NPR phenomenon has also been observed in van der Waals heterostructures. Li and co-workers predicted that the graphene/hexagonal boron nitride (G/h-BN) superlattice in various stacking modes possesses NPR values of around −0.1.16 Interestingly, the authors showed that the auxetic behavior in the G/h-BN superlattice originates from the interaction of pz orbitals between the interfacial layers. The strength of this interaction depends on the distance-dependent hopping integral, which is considered a parameter related to the electronic band structure. This study has contributed to enriching the family of auxetic materials. In addition, it has been shown that the NPR phenomenon is present in 2D Janus asymmetric materials. It is well known that the mirror symmetry structure is lost when we add a third element to the binary compound, forming an asymmetric configuration in the vertical direction. The symmetry breaking in Janus structures has given rise to many unusual and interesting properties compared to their symmetric counterparts.17–19 Therefore, 2D Janus structures have introduced a new class of materials with diverse applications in different fields.20–24 In recent studies, auxetic behavior has been found in Janus systems, further enriching the exotic properties of this class of materials. For example, Hiep et al. theoretically predicted that Janus Si2XY (X/Y = S, Se, Te) monolayers are stable structures possessing NPR effects along both in-plane directions.25 The Si2SSe monolayers exhibit the highest auxetic behavior, possessing a Poisson's ratio value of −0.131 along the x-axis. In addition, Si2OS and Si2OSe semiconductors have both been predicted to exhibit Poisson's ratio with large negative values.26 Amazingly, the NPR effect in Janus Si2OS monolayers is superior, up to −0.234 along the x-direction. The advantages of superior electronic properties and NPR effects make these Janus structures promising for applications in various fields. To date, few studies have explored the NPR effect in Janus structures, so it is worth searching for new auxetic materials belonging to the family of Janus materials.
Group 2D IV–VI compounds are known as representative materials in the family of 2D nanostructures because of their unique structure and physical properties.27,28 Yang et al. assumed that the Pma2-SiS semiconductor has a moderate bandgap.29 Remarkably, compared to 2D α-SiS and β-SiS, the smaller formation energy suggests that the 2D Pma2-SiS structure is more structurally stable. Furthermore, because of its appealing ZT values at medium-high temperatures, the 2D Pma2-SiSe monolayer has recently been suggested as a potential thermoelectric material.30 Previously, the first-principles technique revealed the mechanical and electrical characteristics of 2D SiS, SiSe, and Si2SSe.31 It has been predicted that these structures are good candidates for auxetic materials due to their high negative Poisson's ratio values. In particular, the SiS monolayer possesses a high NPR value of −0.19 in the x-axis.31
In addition to the auxetic behavior, 2D IV–VI structures possess high anisotropic carrier mobility and strain-tunable band gap energy, making them promising in optoelectronic and nanomechanical applications. The NPR phenomenon was also observed in GeS monolayers by using first-principles calculations.32 Also, piezoelectricity was enhanced in GeS compared to transition metal dichalcogenide and hexagonal BN monolayers. Intrigued by the diverse and outstanding physical properties of group IV–VI materials, herein, we investigate the structural, mechanical, electronic, and transport features of three 2D Janus Ge2XY (X/Y = S, Se, Te) monolayers employing ab initio calculations. The combination of remarkable transport properties and exotic auxetic behavior makes this family of materials a potential candidate for multifunctional applications.
2 Computational details and methodology
In the present manuscript, all simulations were carried out by density functional theory (DFT) via the Vienna ab initio simulation package (VASP)33,34 in conjunction with the projector augmented wave approach.33 We used the generalized-gradient approximation formulated by Perdew–Burke–Ernzerhof (PBE)35 to treat the electronic exchange–correlation energy. Further, the Heyd–Scuseria–Ernzerhof hybrid functional (HSE06) was used to achieve an accurate band structure.36 A k-points grid of (15 × 15 × 1) was adopted for integration over the Brillouin zone using the Monkhorst–Pack scheme.37 For the plane-wave expansion, a kinetic cutoff energy of 500 eV was applied. The convergence criteria of energy and forces on each atom are set to be 10−6 eV and 10−3 eV Å−1, respectively. A vacuum region of 20 Å was adopted in the z direction to reduce the interaction between neighboring slabs. Ab initio molecular dynamics (AIMD) simulations were employed to examine the thermal stability of structures.38 We recorded the phonon dispersion spectra by using the finite displacement technique via the PHONOPY code.39 Carrier mobility in the proposed materials is calculated based on deformation potential (DP) theory.403 Results and discussion
3.1 Crystal structure, structural stability, and mechanical features
We first examine the crystal structures of Janus Ge2XY monolayers and their structural stability. Fig. 1(a) reveals the optimized structure of the Janus Ge2XY monolayers from various views. Notably, Ge2XY has an orthorhombic structure. Indeed, there are eight atoms in the unit cell: two X, two Y, and four Ge atoms. We can obtain the asymmetric Ge2XY structure from its symmetric counterpart GeX by replacing one layer of X atoms with one layer of Y atoms. We calculate the structural parameters of Ge2XY crystals and summarize them in Table 1. Our results reveal that Janus Ge2SSe, Ge2STe, and Ge2SeTe monolayers have lattice constants a (b) of 6.98 Å (4.11 Å), 7.12 Å (4.14 Å), and 7.40 Å (4.17 Å), respectively. The increasing trend of the lattice constant is consistent with the increasing atomic radius of the chalcogen element in the periodic table. At the same time, the bond length between two neighboring Ge atoms is almost unchanged in all three predicted structures. Meanwhile, the Ge–X and Ge–Y bond lengths depend on the atomic radius of the chalcogen element, similar to the changing trend of the lattice constant.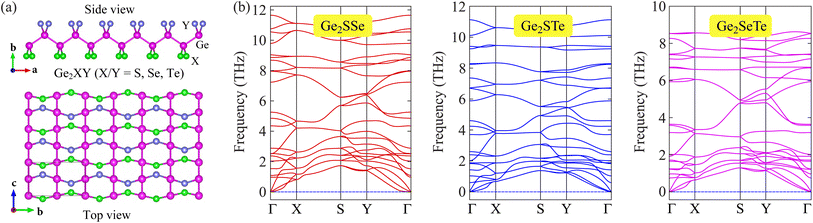 | ||
| Fig. 1 Crystal structures (a) and phonon dispersions (b) of Janus Ge2XY (X/Y = S, Se, and Te; X ≠ Y) monolayers. | ||
| a (Å) | b (Å) | d Ge–X (Å) | d Ge–Y (Å) | d Ge–Ge (Å) | E c (eV per atom) | C 11 (N m−1) | C 12 (N m−1) | C 22 (N m−1) | C 66 (N m−1) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ge2SSe | 6.98 | 4.11 | 2.26 | 2.38 | 2.48 | 4.47 | 61.03 | −9.01 | 47.22 | 6.57 |
| Ge2STe | 7.12 | 4.14 | 2.28 | 2.60 | 2.50 | 4.28 | 45.39 | −8.84 | 43.12 | 6.40 |
| Ge2SeTe | 7.40 | 4.17 | 2.42 | 2.60 | 2.50 | 4.14 | 42.85 | −8.96 | 42.73 | 5.83 |
Next, we examine the stability of the proposed structures. We first calculate the cohesive energies of the proposed structures to evaluate the strength of their chemical bond lengths. The cohesive per atom Ec of Janus Ge2XY can be calculated as41
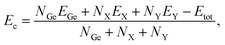 | (1) |
To confirm the dynamical stability of the Janus Ge2XY structures, we recorded their phonon dispersion spectra along the high symmetry points in the Brillouin zone (BZ), as shown in Fig. 1(b). We can observe that the vibrational branches are all positive in the BZ for our three considered monolayers. It suggests that the Janus Ge2XY structures possess high dynamical stability. Fig. 1(b) reveals that the phonon spectrum contains 24 vibrational modes, including three acoustic and 21 optical branches. It is attributed to the presence of eight atoms in the unit cell.
Along with the dynamical stability, we further consider the thermal stability of the Janus Ge2XY monolayers by performing AIMD simulations at room temperature within 8 ps. Fig. 2 plots the total energy fluctuations with the simulation time of Janus Ge2XY at room temperature. We note that the energy fluctuations occur only over a small range. The crystal structures of the calculated monolayers remain stable within 8 ps of the AIMD test. We observe no structural phase transitions or bond breaking in these monolayers after test. These results indicate the high thermal stability of the three Ge2XY structures.
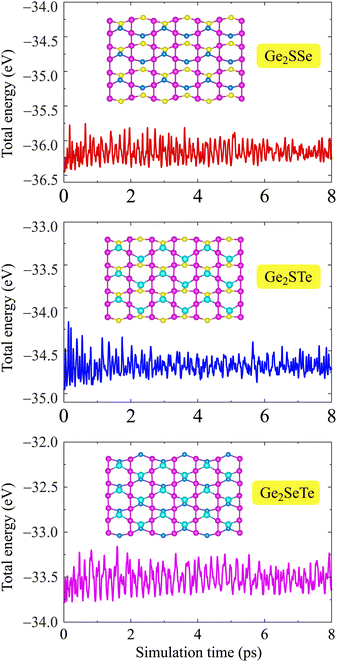 | ||
| Fig. 2 Time dependence of the total energies of Ge2XY from AIMD simulations at room temperature. Insets show the crystal structures of Ge2XY at 8 ps. | ||
Next, we explore the mechanical features of the Ge2XY structures, including the elastic constant Cij, Young's modulus Y2D, and Poisson's ratio  . For Ge2XY structures, there are four coefficients, including C11, C12, C22, and C66, as listed in Table 1. Our calculated results demonstrate that C12 has a negative value as revealed in Table 1. The presence of a negative value for C12 may lead to the auxetic behavior. Importantly, the obtained results satisfy the conditions of C66 > 0 and C11C22 − C122 > 0, confirming the mechanical stability of Janus Ge2XY structures according to the Born–Huang criteria.43,44 Our calculated results demonstrated that Janus Ge2XY monolayers are dynamically, thermally, energetically, and mechanically stable. This supports the hypothesis that the proposed monolayers can be fabricated by conventional experimental methods.
. For Ge2XY structures, there are four coefficients, including C11, C12, C22, and C66, as listed in Table 1. Our calculated results demonstrate that C12 has a negative value as revealed in Table 1. The presence of a negative value for C12 may lead to the auxetic behavior. Importantly, the obtained results satisfy the conditions of C66 > 0 and C11C22 − C122 > 0, confirming the mechanical stability of Janus Ge2XY structures according to the Born–Huang criteria.43,44 Our calculated results demonstrated that Janus Ge2XY monolayers are dynamically, thermally, energetically, and mechanically stable. This supports the hypothesis that the proposed monolayers can be fabricated by conventional experimental methods.
The angle-dependent Young's modulus Y2D(θ) and Poisson's ratio  are determined as follows:45,46
are determined as follows:45,46
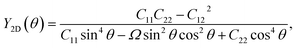 | (2) |
 | (3) |
Fig. 3(a) demonstrates the angle-dependent Y2D(θ) of the 2D Janus Ge2XY systems. As can be seen, Young's modulus exhibits a highly anisotropic character, consistent with the in-plane anisotropy of the crystal structure in the predicted monolayers. For all Ge2XY monolayers, Y2D reaches its maximum value at θ = 0° and then decreases to a minimum value at θ = 45°. For example, the Ge2SeTe monolayer has a maximum Y2D of 40.97 N m−1 at θ = 0° and a minimum Y2D of 17.34 N m−1 at θ = 45°. This leads us to conclude that, for Janus Ge2XY materials, they will be stiffest along the zigzag direction (θ = 0°) and that they will be softest corresponding to θ = 45° and θ = 135°. In addition, the obtained value of Young's modulus decreases in the order from Ge2SSe to Ge2STe to Ge2SeTe. These calculated results can be explained by the fact that the shorter the interatomic bond length, the stronger the bond, and the higher the in-plane stiffness. Compared with other 2D structures, such as γ-GeS (73.25 N m−1),41 WS2 (137 N m−1)47 or graphene (336 N m−1)48 monolayer, the Young's modulus value of the 2D Ge2XY monolayer is much smaller. It implies that our predicted systems withstand applied strain better than other 2D systems.
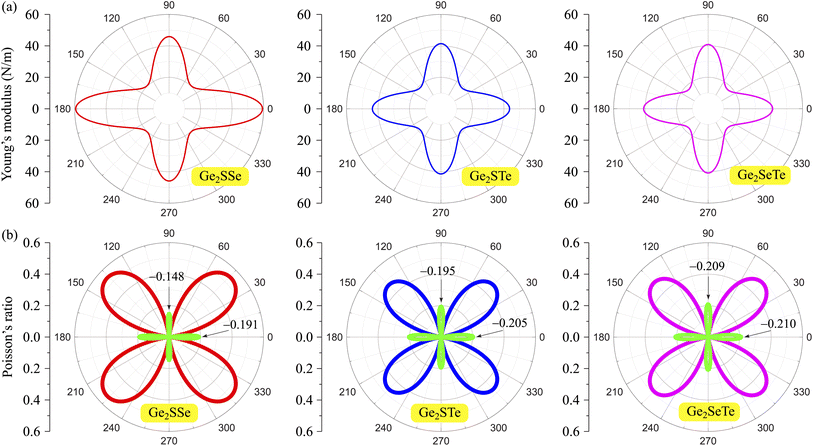 | ||
| Fig. 3 Young's moduli (a) and Poisson's ratios (b) of Janus Ge2XY monolayers. Negative values of Poisson's ratio in (b) are indicated in green. | ||
Fig. 3(b) depicts the angle dependence of Poisson's ratio for the Janus Ge2XY systems. Like Young's modulus, Poisson's ratios of Ge2XY structures exhibit a highly anisotropic feature. As shown in Fig. 3(b), the angle-dependent 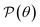 plots of all three materials are similar. The maximum values of
plots of all three materials are similar. The maximum values of  for Ge2XY monolayers correspond to θ = 45° and θ = 135°. The maximum values of
for Ge2XY monolayers correspond to θ = 45° and θ = 135°. The maximum values of 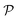 for Ge2SSe, Ge2STe, and Ge2SeTe are calculated to be 0.54, 0.47, and 0.49, respectively. Importantly, we found the NPR along the two in-plane axes x and y in the polar diagrams of
for Ge2SSe, Ge2STe, and Ge2SeTe are calculated to be 0.54, 0.47, and 0.49, respectively. Importantly, we found the NPR along the two in-plane axes x and y in the polar diagrams of 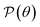 of Ge2XY materials. It is indicated that Janus Ge2SeTe possesses the largest NPR of −2.10 along the x direction, as revealed in Fig. 3. The value of NPR along the y direction for Ge2SeTe is found to be −2.09. The NPR values along the x(y) direction are found to be −0.191(−0.148) and −0.205(−0.195) for Ge2SSe and Ge2STe, respectively. The negative Poisson's ratio behavior in Janus Ge2XY is closely related to its hinge-like structure. This hinge-like structure is a necessary condition for the negative Poisson's ratio. This has also been shown in phosphorene with a high negative Poisson's ratio.49 Possessing a high negative Poisson's ratio value, Janus Ge2XY monolayers exhibit a much stronger auxetic effect than other 2D auxetic structures, such as SiS (−0.19),31 borophene (−0.053),49 phosphorene (−0.027),50 or GeS monolayer (−0.137).32 The superior mechanical properties of Janus Ge2XY monolayers may lead to many nanomechanical applications.
of Ge2XY materials. It is indicated that Janus Ge2SeTe possesses the largest NPR of −2.10 along the x direction, as revealed in Fig. 3. The value of NPR along the y direction for Ge2SeTe is found to be −2.09. The NPR values along the x(y) direction are found to be −0.191(−0.148) and −0.205(−0.195) for Ge2SSe and Ge2STe, respectively. The negative Poisson's ratio behavior in Janus Ge2XY is closely related to its hinge-like structure. This hinge-like structure is a necessary condition for the negative Poisson's ratio. This has also been shown in phosphorene with a high negative Poisson's ratio.49 Possessing a high negative Poisson's ratio value, Janus Ge2XY monolayers exhibit a much stronger auxetic effect than other 2D auxetic structures, such as SiS (−0.19),31 borophene (−0.053),49 phosphorene (−0.027),50 or GeS monolayer (−0.137).32 The superior mechanical properties of Janus Ge2XY monolayers may lead to many nanomechanical applications.
3.2 Electronic characteristics
In the following, we explore the electronic features of 2D Janus Ge2XY monolayers to suggest them for suitable applications. We use different functionals, namely PBE and HSE06, to calculate the electronic energy band structure of Ge2XY as illustrated in Fig. 4. Both methods reveal that the 2D Ge2XY systems are all semiconductors with small bandgaps. Compared to the PBE method, the HSE06 method provides higher bandgap values. Among all the proposed monolayers, the Ge2SSe monolayer possesses the widest bandgap energy of 1.09 eV at the HSE06 level. The other two monolayers have narrower HSE06 bandgaps, which are 0.32 eV and 0.11 eV for Ge2STe and Ge2SeTe, respectively. The obtained bandgap energies of Ge2XY are smaller than those of the Janus Si2SSe monolayer (1.51 eV) at the HSE06 level.31Table 2 summaries the obtained PBE and HSE06 bandgaps of Janus Ge2XY structures.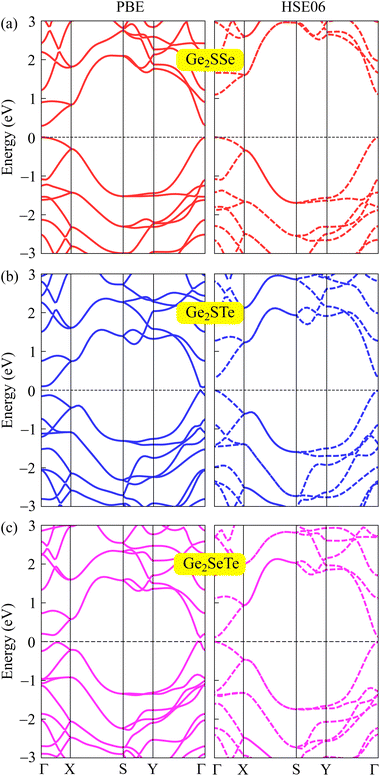 | ||
| Fig. 4 The computed band structures of Ge2SSe (a), Ge2STe (b), and Ge2SeTe (c) materials at the PBE (left) and HSE06 (right) theoretical levels. | ||
| E PBEg (eV) | E HSE06g (eV) | Φ X (eV) | Φ Y (eV) | ΔΦ (eV) | |
|---|---|---|---|---|---|
| Ge2SSe | 0.29 | 1.09 | 5.24 | 4.84 | 0.40 |
| Ge2STe | 0.07 | 0.32 | 5.46 | 4.57 | 0.89 |
| Ge2SeTe | 0.10 | 0.11 | 4.88 | 4.39 | 0.49 |
In addition to the band structures, we calculate the electrostatic potentials and the work functions of Janus Ge2XY monolayers. The value of the work function reflects the energy required for electrons to escape from the crystal surface. The work function Φ is related to the Fermi level EF and the vacuum level Evac through the expression Φ = Evac − EF. For the studied compounds, the two faces are made up of various chalcogen elements, whose electronegativities are different, giving rise to an out-of-plane dipole moment. The magnitude of this dipole moment depends on the electronegativity difference between the two faces of the material. Therefore, it is necessary to add the dipole correction when evaluating the electrostatic potentials in asymmetric structures.51Fig. 5 shows the electrostatic potentials of Janus Ge2XY monolayers with dipole corrections. The computed results reveal that the vacuum levels on the two faces of the structure are different, and the shape of the electrostatic potential is asymmetric. That is attributed to the lack of vertical mirror symmetry in the Janus structure. The values of the work function Φ and the vacuum level differences ΔΦ at the Ge2XY surfaces are listed in Table 2. For Ge2XY monolayers, the work functions at the X surface vary from 4.88 to 5.46 eV, while those at the Y surface range from 4.39 to 4.84 eV. Our results reflect that the energy required for electrons to escape from the Y surface is lower than that of the X surface. In addition, Table 2 also reveals that the Ge2STe monolayer has the highest vacuum level difference ΔΦ compared to the other monolayers. This result is consistent with the fact that the higher the electronegativity difference between the elements, the higher the vacuum level difference between the surfaces.
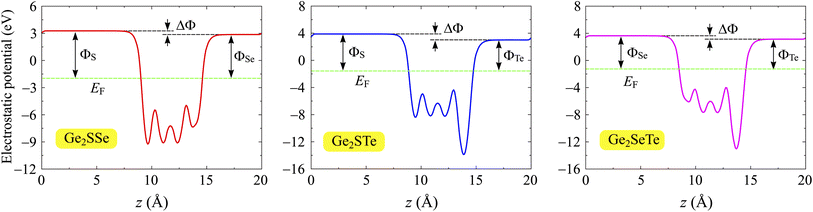 | ||
| Fig. 5 Electrostatic potentials of Ge2SSe, Ge2STe, and Ge2SeTe monolayers. The dashed horizontal lines indicate the Fermi level EF. The potential difference between the sides is labeled with ΔΦ. | ||
3.3 Transport features and carrier mobility
In the last part, we explore the fundamentals of the proposed Janus Ge2XY monolayers. Transport parameters, particularly carrier mobility, play a critical role in the performance and efficiency of electronic devices. It is necessary to investigate electron mobility because it strongly affects the efficiency, speed, and behavior of electronic devices. Here, we use deformation potential (DP) theory to explore the carrier mobility of the proposed structures.40The carrier mobility in the framework of DP for 2D nanostructures is given by52
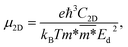 | (4) |
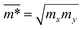 , and Ed is the DP constant.
, and Ed is the DP constant.
The transport parameters can be calculated based on the DFT method via the following equations:
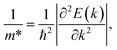 | (5) |
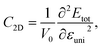 | (6) |
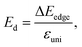 | (7) |
The effective mass of charge carriers (holes and electrons) plays a fundamental role in determining carrier mobility in semiconductors. The effective mass is a concept that arises from the band structure and strongly affected by the curvature of the sub-band at the band-edges. From eqn (5), we can see that a flat curvature (large radius) indicates a large effective mass, while a steep curvature leads to a smaller effective mass. The calculated results for m* along the x and y axes are listed in Table 3. It can be seen that Janus Ge2XY monolayers exhibit very low electron-effective mass. Further, the effective mass of carriers exhibits highly directional anisotropy along the two transport directions x and y. For example, the calculated values of mx and my for Janus Ge2SSe are calculated to be 0.67m0 and 0.13m0 (m0 refers to the mass of the free electron), respectively. We can obtain the C2D and Ed by fitting the uniaxial strain dependence of the total energy and band-edge positions as shown in Fig. 6. In these procedures, a small uniaxial strain εx/yuni ranging from −0.4 to 0.4% is applied along the x/y axis. The computed values of C2D, Ed, and corresponding μx/y2D are listed in Table 3. We can see that the transport parameters of Ge2XY monolayers exhibit highly directional anisotropic characteristics. This is consistent with the anisotropy in the crystal structures of Ge2XY monolayers. It is demonstrated that Ge2XY monolayers have high electron mobility, as shown in Table 3. The electron mobility along the x (μx2D) and y (μy2D) directions for Ge2SSe is 417.79 and 266.44 cm2 V−1 s−1, respectively. The Janus Ge2SeTe possesses a higher electron mobility with μx2D = 5.57 × 103 cm2 V−1 s−1 and μy2D = 501.38 cm2 V−1 s−1. Particularly, ultra-high electron mobility up to 10.92 × 103 cm2 V−1 s−1 is found along the x axis in the Janus Ge2STe monolayer as presented in Table 3. With high electron mobility, Janus Ge2XY monolayers are suitable for applications in flexible nanoelectronics.
| m x | m y | C x 2D | C y 2D | E x d | E y d | μ x 2D | μ y 2D | ||
|---|---|---|---|---|---|---|---|---|---|
| Electron | Ge2SSe | 0.67 | 0.13 | 124.42 | 73.30 | −5.66 | −12.35 | 417.79 | 266.44 |
| Ge2STe | 0.10 | 0.07 | 106.23 | 66.91 | −5.01 | −8.31 | 10.92 × 103 | 3.68 × 103 | |
| Ge2SeTe | 0.11 | 0.26 | 97.32 | 61.77 | −4.47 | −7.72 | 5.57 × 103 | 501.38 | |
| Hole | Ge2SSe | 2.70 | 0.31 | 124.42 | 73.30 | −3.62 | −6.18 | 81.75 | 143.94 |
| Ge2STe | 0.17 | 0.18 | 106.23 | 66.91 | −5.02 | −7.84 | 3.02 × 103 | 735.37 | |
| Ge2SeTe | 0.09 | 0.07 | 97.32 | 61.77 | −4.43 | −8.30 | 14.50 × 103 | 3.97 × 103 | |
 | ||
| Fig. 6 The uniaxial strain dependence of (a) the total energy shifts and (b) band-edge positions of Ge2XY structures. | ||
4 Conclusion
In conclusion, a new class of 2D auxetic materials Ge2XY (X/Y = S, Se, Te) has been predicted by employing ab initio calculations. Janus Ge2XY monolayers have been predicted to be stable crystalline semiconductors. They are materials with great mechanical flexibility due to their small Young's coefficient. Due to the anisotropic crystalline structure, the mechanical properties of Ge2XY are highly anisotropic. In particular, they possess auxetic behaviors with large negative Poisson's ratios, up to −0.210 (Ge2SeTe monolayer). We found that the auxetic effect along the x-axis is the strongest. The transport characteristics of Ge2XY monolayers also exhibit strong anisotropic characteristics. The carrier mobility along the x-axis is computed to be larger than that along the y-axis. With their large carrier mobility and outstanding mechanical properties, 2D Janus Ge2XY monolayers have great prospects for applications in flexible nanoelectromechanical devices. Our findings broaden the range of auxetic materials and provide insight into the physical characteristics of 2D Ge2XY structures.Data availability
All data that support the findings of this study are included within the article.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This study was funded by Hue University under project number DHH2024-18-03.References
- A. Alderson and K. L. Alderson, Proc. Inst. Mech. Eng., Part G, 2007, 221, 565–575 CrossRef.
- J. B. Choi and R. S. Lakes, Int. J. Fract., 1996, 80, 73–83 CrossRef.
- W. Yang, Z.-M. Li, W. Shi, B.-H. Xie and M.-B. Yang, J. Mater. Sci., 2004, 39, 3269–3279 CrossRef.
- M. Sanami, N. Ravirala, K. Alderson and A. Alderson, Procedia Eng., 2014, 72, 453–458 CrossRef.
- F. Scarpa, IEEE Signal Process. Mag., 2008, 25, 128 Search PubMed.
- C. Huang and L. Chen, Adv. Mater., 2016, 28, 8079–8096 CrossRef PubMed.
- J. F. Silveira and A. R. Muniz, Carbon, 2017, 113, 260–265 CrossRef.
- B. Saha, S. M. Pratik and A. Datta, Chem.–Eur. J., 2017, 23, 12917–12923 CrossRef PubMed.
- G. W. Milton, J. Mech. Phys. Solids, 1992, 40, 1105–1137 Search PubMed.
- B. D. Caddock and K. E. Evans, J. Phys. D:Appl. Phys., 1989, 22, 1877 Search PubMed.
- F. Milstein and K. Huang, Phys. Rev. B:Condens. Matter Mater. Phys., 1979, 19, 2030–2033 Search PubMed.
- J.-W. Jiang and H. S. Park, Nat. Commun., 2014, 5, 4727 Search PubMed.
- H. Wang, X. Li, P. Li and J. Yang, Nanoscale, 2017, 9, 850–855 Search PubMed.
- A. J. Mannix, X.-F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516 Search PubMed.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377 Search PubMed.
- X. Li, X. Qiang, Z. Gong, Y. Zhang, P. Gong and L. Chen, Research, 2021, 2021, 1904839 Search PubMed.
- T. V. Vu, C. V. Nguyen, H. V. Phuc, A. A. Lavrentyev, O. Y. Khyzhun, N. V. Hieu, M. M. Obeid, D. P. Rai, H. D. Tong and N. N. Hieu, Phys. Rev. B, 2021, 103, 085422 Search PubMed.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Phys. Rev. B, 2021, 104, 115410 Search PubMed.
- T. V. Vu, N. T. Hiep, H. V. Phuc, B. D. Hoi, A. I. Kartamyshev and N. N. Hieu, Phys. Rev. B, 2024, 110, 235403 CrossRef.
- T. V. Vu, V. T. T. Vi, C. V. Nguyen, H. V. Phuc and N. N. Hieu, J. Phys. D: Appl. Phys., 2020, 53, 455302 CrossRef.
- T. V. Vu, V. T. T. Vi, H. V. Phuc, C. V. Nguyen, N. A. Poklonski, C. A. Duque, D. P. Rai, B. D. Hoi and N. N. Hieu, J. Phys.: Condens. Matter, 2021, 33, 225503 Search PubMed.
- L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242–8248 CrossRef PubMed.
- A. Mogulkoc, Y. Mogulkoc, S. Jahangirov and E. Durgun, J. Phys. Chem. C, 2019, 123, 29922–29931 CrossRef.
- X. Yan, X. Cui, B. Wang, H. Yan, Y. Cai and Q. Ke, Iscience, 2023, 26, 106731 CrossRef PubMed.
- N. T. Hiep, C. Q. Nguyen and N. N. Hieu, Appl. Phys. Lett., 2023, 123, 092102 CrossRef.
- N. P. Q. Anh, N. A. Poklonski, V. T. T. Vi, C. Q. Nguyen and N. N. Hieu, RSC Adv., 2024, 14, 4966–4974 Search PubMed.
- T. V. Vu, H. V. Phuc, L. C. Nhan, A. I. Kartamyshev and N. N. Hieu, J. Phys. D: Appl. Phys., 2023, 56, 135302 CrossRef.
- T. V. Vu, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, Appl. Phys. Lett., 2023, 122, 061601 CrossRef.
- J.-H. Yang, Y. Zhang, W.-J. Yin, X. G. Gong, B. I. Yakobson and S.-H. Wei, Nano Lett., 2016, 16, 1110–1117 CrossRef PubMed.
- J.-H. Yang, Q. Yuan, H. Deng, S.-H. Wei and B. I. Yakobson, J. Phys. Chem. C, 2017, 121, 123–128 CrossRef.
- T. Jing, D. Liang, M. Deng and S. Cai, J. Mater. Chem. C, 2020, 8, 10382–10389 RSC.
- L. C. Gomes, A. Carvalho and A. H. Castro Neto, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 214103 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188–5192 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511 CrossRef.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72 CrossRef.
- M. J. Varjovi, S. Ershadrad and B. Sanyal, Phys. Rev. B, 2023, 107, 195421 CrossRef.
- T. V. Vu, N. P. Anh, H. V. Phuc, A. I. Kartamyshev and N. N. Hieu, New J. Chem., 2023, 47, 11660–11668 RSC.
- M. Born and K. Huang, Am. J. Phys., 1955, 23, 474 CrossRef.
- T. Jing, D. Liang, M. Deng and S. Cai, J. Mater. Chem. C, 2020, 8, 10382–10389 RSC.
- N. T. Hung, A. R. T. Nugraha and R. Saito, J. Phys. D: Appl. Phys., 2018, 51, 075306 CrossRef.
- P. Xiang, S. Sharma, Z. M. Wang, J. Wu and U. Schwingenschlögl, ACS Appl. Mater. Interfaces, 2020, 12, 30731 CrossRef PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033 CrossRef PubMed.
- E. Cadelano, P. L. Palla, S. Giordano and L. Colombo, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 82, 235414 CrossRef.
- L. Kou, Y. Ma, C. Tang, Z. Sun, A. Du and C. Chen, Nano Lett., 2016, 16, 7910–7914 CrossRef PubMed.
- H. Wang, X. Li, P. Li and J. Yang, Nanoscale, 2017, 9, 850–855 RSC.
- C.-F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18, 6312–6317 CrossRef PubMed.
- W. Wan, S. Zhao, Y. Ge and Y. Liu, J. Phys.: Condens. Matter, 2019, 31, 435501 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2025 |
