Dual-band flexible large-area ultrasonic energy conveying via elastic chiral Landau levels

Abstract

While conventional topological metamaterials offer promising avenues for manipulating elastic waves, energy capacities are commonly restricted from narrow structural boundaries or domain walls. The emergence of the chiral Landau level via introducing synthetic pseudomagnetic fields has been demonstrated to support unique bulk states, thereby spurring versatile wave controls. However, existing research primarily implements the chiral Landau level in a single frequency regime, impeding the applications of multiband functional devices. In this study, we realize the ultrasonic chiral Landau level of elastic waves in two separated frequency regions based on integrated topological valley phononic crystals. We demonstrate the chiral Landau level-induced dual-band bulk transport of ultrasonic waves with exceptional robustness against geometric perturbation, by numerical simulations and experiments. Remarkably, we achieve flexible ultrasonic energy manipulation including wave steering along an arbitrary route and energy splitting, through strategically tailoring the synthetic pseudomagnetic field in valley topological metamaterials. The developed topological elastic metamaterials with the dual-band chiral Landau levels functioning as extraordinary bulk states can find potential applications in multiband and multidirectional ultrasonic signal processing and energy management.

---

New concepts

This work achieves a dual-band chiral Landau level (CLL) based on a compact topological elastic metamaterial. The CLL is a groundbreaking concept originating from condensed matter physics that has attracted attention in recent years, and which gives rise to unique bulk states enabling the desirable large-area energy transport. In particular, when incorporated into artificial topological metamaterials, the CLL brings about a series of exotic wave manipulations that are unattainable in traditional metamaterials. However, the previously reported CLLs almost all emerge in a single frequency regime, restricting their applications in multiband communications. Moreover, experimental demonstrations of CLL-induced intriguing wave functionalities are rarely reported in practical mechanical systems. In recognition of this insufficiency, this work achieves breakthroughs in two main aspects: (a) dual-band elastic CLLs observed in a small-scale topological metamaterial, which greatly enhance the energy capacities of bulk propagative states of ultrasonic waves compared with those in conventional topological metamaterials. (b) CLL-induced flexible ultrasonic wave manipulations including wave steering along arbitrary routes and beam splitting, which are challenging to realize in conventional topological metamaterials. The proposed topological metamaterial with dual-band CLLs greatly enhances the wave control capabilities of multi-frequency mechanical functional devices.

1. Introduction

Manipulating elastic waves using topological metamaterials^1–3 has gained considerable research interest over the past decade. With attractive features including robust energy transport and high-quality-factor wave localization, topological elastic metamaterials spawn a wide spectrum of practical applications, e.g., high-capability energy harvesting,^4–7 enhanced sensing,^8,9 and signal demultiplexing.^10–12 In this context, phononic crystals (PCs)^13–16 and locally resonant metamaterials¹⁷ offer suitable avenues for observing nontrivial topological states of elastic waves in solids, involving edge states and corner states featuring profound energy concentration. Within the realm of topological elastic metamaterials, PCs based on pseudospin^18–22 and valley Hall physics^23–28 have garnered significant attention. A common practice is endowing PCs with demanded crystalline symmetries, such as C₃,²⁶ C₄,²⁹ C₆^20–22 and glide symmetries,^30–32 which significantly facilitates their fabrication and practical implementation.

In general, high-intensity elastic energies in conventional topological metamaterials are tightly concentrated at PC boundaries or narrow domain walls between two topologically distinct PCs. For example, topological valley PCs commonly hold topological valley states at narrow interfaces between two PC domains with contrast valley physics.^23–28 Hence, it is perceived that energy conveying fluxes in conventional topological devices are heavily limited. Realizing large-area topological states can facilitate a series of potential applications such as robust multi-position energy harvesting⁷ and guided wave-based material characterization,^33,34 which require high spatial efficiency. In recognition of this challenge, several new mechanisms have been exploited to enhance the energy capacities of topological metamaterials. Typically, topological heterostructures^35,36 and Dirac semimetals^37,38 are proposed, both allowing for large-area energy transport. However, it should be noted that elastic wave manipulation based on the above-mentioned topological devices still suffers from several limitations, e.g., wave propagation pathways are constrained by the inherent crystalline symmetry of PCs. Therefore, there is a call for a new mechanism enabling more flexible controls of large-area topological elastic waves.

Recently, introducing a synthetic in-plane pseudomagnetic field (PMF) into topological metamaterials has greatly advanced the understanding of topological states, known as the chiral Landau level (CLL).^39–42 The CLL gives rise to unique bulk states, enabling the desirable large-area energy transport. Motivated by this, experimental investigations have been conducted in valley Hall physics-based electromagnetic metamaterials^43–45 and acoustic crystals.⁴⁶ Meanwhile, Li et al.⁴⁷ presented theoretical and numerical evidence of the elastic CLL based on valley truss structures. In addition to unique bulk states, the synthetic PMF brings about an extra degree of freedom, thereby leading to more flexible wave manipulation. Nevertheless, the previously reported CLLs mostly arise in a single frequency regime,^47–49 restricting their applications in multiband communications. Meanwhile, experimental verifications of CLL-induced intriguing wave functionalities are rarely reported in mechanical systems. It is therefore expected that dual-band or multiband CLLs can enable novel multi-frequency elastic functional devices, particularly desirable for miniaturized PCs towards multiband signal processing or analog computational applications using high-frequency ultrasonic waves.

To fill this gap, we herein achieve dual-band CLLs through introducing the synthetic PMF in topological valley PCs. In particular, dual-frequency Dirac cones at 165 kHz and 365 kHz are leveraged in the proposed compact PCs, given that ultrasonic waves within such frequency ranges have broad applications in non-destructive testing, structural health monitoring, and material characterization.^33,34 Carefully modulating the hole sizes in PCs allows for the creation of position-dependent Dirac mass, which in turn synthesizes the in-plane PMF and introduces the zeroth CLLs. We observe the CLL-induced bulk energy transport of ultrasonic waves and validate the robustness of the transport against geometrical perturbation at dual frequency regimes. Significantly, we experimentally demonstrate intriguing ultrasound manipulation functions via tailoring CLLs, including wave steering along an arbitrary route and energy splitting, which are challenging to realize in conventional topological metamaterials. The developed prototypes open up new possibilities for manufacturing high-capability multiband topological ultrasonic devices and integrating them into on-chip systems.

2. Results

We first construct the topological valley PC on planar elastic plates (thickness h = 0.5 mm), the unit cell of which is sketched in Fig. 1(a). A split-ring resonator with C₃ rotational symmetry is perforated on the plate, which possesses superior manufacturability, compactness, and scalability. In particular, such split-ring resonators can lead to multiband topological band gaps owing to unique multimodal resonant characteristics^32,50,51 (see the ESI† for details). The lattice constant a = 5 mm, while other geometric parameters t = 0.4 mm, r = 2.2 mm, and e = 1 mm. In particular, throughout this research, only the out-of-plane flexural waves in the elastic plates are investigated. The rotation angle θ with respect to the x direction, as the only degree of freedom, can be rotated to change the band structures of the flexural waves. When θ = 0°, dual Dirac cones are formed at the K(K′) valleys of the 7th and 8th bands (Dirac cone I), and of the 13th and 14th bands (Dirac cone II), as indicated by the dash lines in Fig. 1(b). In such a two-dimensional (2D) system, the Hamiltonian around each Dirac cone can be described as H_D = v_D (k̂_xσ_x + k̂_yσ_y), where v_D is the group velocity, k̂ = (k̂_x,k̂_y) = k − k_K/K′ being the wave vector with respect to the Dirac point vector k_K/K′, and σ_i (i = x, y) denotes the Pauli matrix. By rotating the θ, the Dirac cone can be lifted, causing an omnidirectional band gap due to the broken space inversion symmetry,²³ and an effective Dirac mass m is introduced into the H_D. In particular, generating a synthetic PMF requires spatial linearly-varying Dirac mass.^46–49 To do so, we linearly alter the rotation angle θ from −12° to 12° (variation step Δθ = 2°) from the bottom to the top of the PC plate while maintaining translational invariance along the horizontal direction, as indicated in Fig. 1(a). Consequently, dual Dirac cones are opened and the gap sizes are position-dependent. Evolutions of the upper and lower bound frequencies of the dual band gaps as θ varies from −12° to 12° are recorded in Fig. 1(d). Note that both band gaps experience the process of ‘open–close–reopen’. During this process, the chirality of the phase distributions of the eigenmodes at K/K′ valleys is inverted at Dirac cone frequencies, which corresponds to a topological phase transition.^23,25,27 While two unit cells with opposite θ share identical band gaps, they carry distinct topological properties. For instance, when θ = ±12° (solid lines in Fig. 1(b)), there exist two omnidirectional band gaps with the frequency window of [113.5, 134.8] kHz and [347.9, 372.7] kHz, respectively. However, the phase distributions of the eigenmodes at K and K′ valleys show the reversed chirality (Fig. 1(c)). More importantly, the Dirac mass m = Δω/2 (Δω = ω₊ − ω₋), where ω₊ and ω₋ denote the eigenfrequencies of eigenmodes with clockwise (red) and anticlockwise (blue) phase distributions. This means that unit cells with opposite θ have opposite Dirac mass.

Fig. 1 (a) Topological valley PC with a graded distribution (along y direction) of the rotation angle θ, where the arrow B signifies the PMF and the dashed box denotes the supercell. The lower panel shows the unit cell including the 3D view and top view. (b) Band structures of the unit cell when θ = 12° (solid lines) and when θ = 0° (dash lines). Blue and red lines represent the eigenmodes with opposite chirality. (c) Phase fields at labeled positions in (b), where green arrows denote the chirality. (d) Bound frequencies of the band gaps as a function of the rotation angle θ for the Dirac cone I (left) and Dirac cone II (right). Background colors represent the position-dependent Dirac mass. (e) Projected dispersions around CLL I (left) and CLL II (right). (f) Displacement fields at labeled positions in (e).

This graded pattern causes the nearly linearly-varied Dirac mass with respect to the y direction, namely m = γy, indicated by the gradient background colors in Fig. 1(d). As such, the Hamiltonian of this inhomogeneous PC system with position-dependent Dirac mass becomes H^m_D = v_D(ηk̂_xσ_x + k̂_yσ_y) + mσ_z, where η = ±1 corresponding to the K and K′ valleys. The effective mass term m can be interpreted as an out-of-plane gauge potential A_z = γy. Consequently, an in-plane pseudomagnetic field B_x = ∂_yA_z = γ, indicated by the black arrow B in Fig. 1(a), is synthetized along the x direction. The energy levels (i.e., Landau levels) of H^m_D can be obtained as

where the chirality η = ±1 corresponding to the K and K′ valleys and n represents the order of the Landau levels. In this paper, we only focus on the zeroth CLLs. Fig. 1(e) illustrates the projected dispersions (white circles) along the k_x direction, numerically calculated in a supercell (dashed box in Fig. 1(a)). One can notice the zeroth CLL emerging within both band gaps, referred to as CLL I and CLL II. The energy distributions of the out-of-plane elastic waves are depicted in Fig. 1(f). We can find that elastic energies are mainly concentrated around the central unit cells with zero Dirac mass, with larger energy volumes compared to those of conventional edge states.

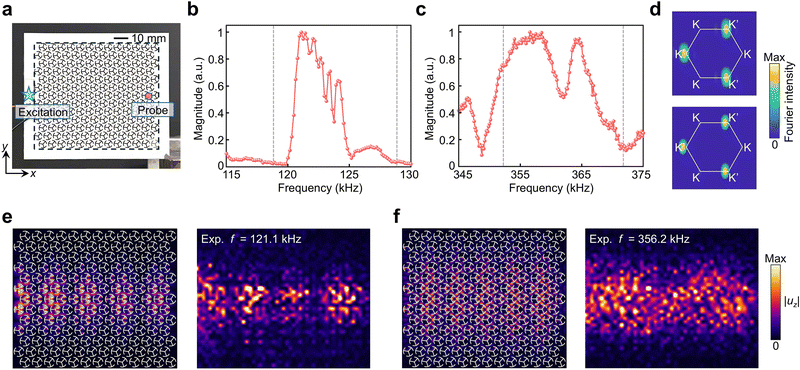
After revealing the dual-band CLLs in simulations, we construct a 2D finite PC plate and experimentally measure the CLL-induced bulk wave transport. The PC plate contains thirteen supercells in the horizontal direction, as viewed in Fig. 2(a). We first plot the experimentally measured dual-band CLLs via extracting phase information along the middle line of the PC plate and performing the Fourier transformation. The background colors in Fig. 1(e) represent the experimentally obtained Fourier intensity spectra of the band structures, which keep good alignment with the numerically calculated band dispersions (white circles). Meanwhile, we also extract the response spectra at the end (see the probe in Fig. 2(a)) of the bulk waveguide, as shown in Fig. 2(b) and (c). One can notice the strong response within the frequency ranges of CLLs I and II (bound by the gray dash lines). Furthermore, scanned wave fields along with simulated ones (see Fig. 2(e) and (f)) at peak frequencies (121.1 kHz for CLL I and 356.2 kHz for CLL II) clearly reveal the large-area energy transport along the horizontal direction. Besides, the measured 2D Fourier intensity spectra confirm that these propagative bulk states exhibit the valley-locked characteristic in the momentum space, as shown in Fig. 2(d).

Fig. 2 (a) Photograph of the fabricated sample, where the excitation and the probe are labeled. The dashed box denotes the laser-scanned region. (b) and (c) Measured response spectra around (b) CLL I and (c) CLL II. Gray dashed lines represent the bound frequencies of the CLLs. (d) Measured 2D fast Fourier transform (FFT) result of bulk waves at respective peak frequencies. (e) and (f) Simulated (left) and laser-scanned (right) wave fields at the peak frequency (e) 121.1 kHz and (f) 356.2 kHz.

Now we proceed to examine the robustness of CLL-induced bulk energy transport against geometric perturbations. First, we deliberately introduce a defect (by removing a unit cell) and disorder (by randomly rotating several holes) in the waveguide, as indicated by the red boxes in Fig. 3(a) and (b). Under the same excitation and measurement conditions, we scan the whole wave field of two PC plates in the presence of these perturbations. The obtained spectra, as viewed in Fig. 3(c) and (d), still exhibit remarkable peaks in the frequency ranges of dual-band CLLs. Moreover, scanned wave fields at the corresponding peak frequencies are shown in Fig. 3(e) and (f). It is evident that propagative bulk waves still concentrate around the central unit cells, almost unaffected by the presence of the defects and disorder. These experimental results confirm the strong robustness of CLL-induced bulk energy transport against different geometric perturbations.

Fig. 3 (a) and (b) Fabricated samples of perturbed structures with (a) defects and (b) disorder, where geometric perturbations are marked by red boxes. (c) and (d) Measured response spectra on the perturbed structures around the frequency range of (c) the CLL I and (d) the CLL II. Gray dashed lines represent the bound frequencies of the CLLs. (e) and (f) Laser-scanned wave fields at respective peak frequencies on the perturbed structure with a defect (left) and disorder (right).

In previous cases, the propagation pathway of the CLLs is fixed to be straight as the PC plate contains horizontally periodic supercells in the x direction. In other words, the CLLs are solely exerted along the straight middle line of the PC plate. Here, we show that the wave propagation pathway can be customized through strategically engineering the positions of combined supercells. For illustration, Fig. 4(a) displays the schematic of the target PC region with a designated pathway, which is constructed by shifting up/down eight pairs of PC blocks, each consisting of four supercells in the horizontal direction. Note that each supercell is the same as the one in Fig. 1(a), where the central unit cells with zero Dirac mass are labeled by purple dashed lines. As discussed before, the CLLs are concentrated around the central unit cells of each supercell. Hence, CLL-induced bulk energy transport in each block can be coupled to convey elastic energy from the left to the right of the structure. To confirm this, the sample supporting a curved propagation pathway is fabricated, as displayed in Fig. 4(b). Notably, in the fabricated sample, the whole target PC region (colored region) is surrounded by a series of unit cells (outside of the colored region) with the largest band gap (θ = −12°/12°) to eliminate the influence of wave reflections from plate boundaries. In the experiment, the excitation (green star in Fig. 4(b)) is imposed at the left center of the sample. Correspondingly, the response spectra are extracted at the end of the prescribed pathway, as marked by the probe in Fig. 4(b). It is noted that the measured spectra in Fig. 4(c) exhibit an evident peak within the frequency ranges of both CLLs. Moreover, as seen in Fig. 4(d) and (e), laser-scanned wave fields at 122.7 kHz and 359.8 kHz unravel that flexural waves propagate along the designated pathway as expected, showing excellent agreement with the simulated displacement fields. This result underscores a new promising method to realize elastic energy conveying along user-customized pathways. Apart from the specific pathway illustrated above, more diverse propagation pathways of CLLs are achievable in different ways of combining supercells, which is expected to realize topological waveguides with arbitrary propagation pathways, a truly remarkable feature difficult to realize using conventional topological states.

Fig. 4 (a) Schematic of the customized waveguide by shifting up/down a set of PC blocks, where dashed lines denote the central unit cells with zero Dirac mass. (b) Top view of the fabricated sample, where the green region signifies the target PC region and the remaining part is filled with unit cells with the largest band gap (θ = −12°/12°). The excitation source and probe are marked. (c) Measured response spectra around the CLL I (left) and II (right). Gray dashed lines represent the bound frequencies of the CLLs. (d) and (e) Simulated and laser-scanned wave fields at (d) 122.7 kHz and (e) 359.8 kHz. The blue dashed box represents the laser-scanned region in the PC plate.

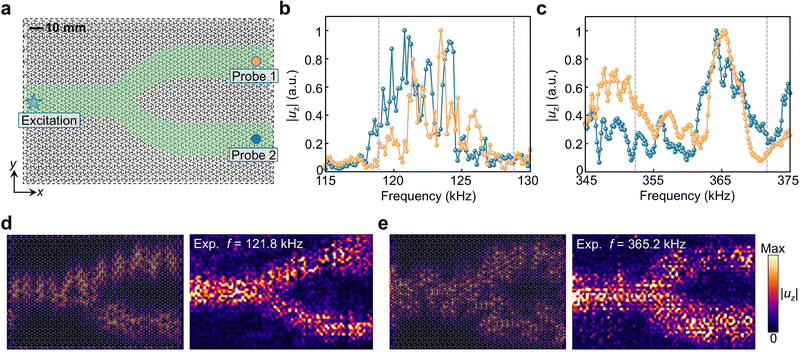
Furthermore, we explore another interesting wave functionality via engineering PMFs in the valley PC, that is, the energy splitting. The whole sample of the designed energy splitter is schematically illustrated in Fig. 5(a), where the propagation pathways of elastic waves are shaded in green. Initially, unit cells with zero Dirac mass are located at the horizontal middle line of the PC plate, and then slowly separate up/down, and finally reside at two well-separated positions (see the ESI† for details). As a result, the elastic energies of propagative CLLs are expected to be initially concentrated around the middle line of the sample and then gradually split, and eventually become confined at two well-separated positions. It is noteworthy that, different from previous examples, the variation step Δθ in the vertical direction is 1° while it is 0.5° in the horizontal direction, to more clearly observe the wave splitting phenomenon (see the ESI†). In the experiment, we impose the excitation at the left center of the sample, and then observe the resulting flexural wave propagation. Fig. 5(b) and (c) present the response spectra extracted at the two output ports (see probes 1 and 2 in Fig. 5(a)) around the frequency regions of the CLL 1 (Fig. 5(b)) and CLL 2 (Fig. 5(c)), respectively, where response peaks can be observed. More importantly, the energy splitting phenomenon can be clearly observed in simulated and laser-scanned wave fields at two selected frequencies of 121.8 kHz and 365.2 kHz. The above results confirm the flexible control capability on energy flows via tailoring PMFs in topological valley PCs. This new mechanism of constructing energy splitters exhibits great potential for advanced mechanical signal processing.

Fig. 5 (a) Schematic of the fabricated sample for energy splitting, where the propagation pathways of flexural waves are highlighted in green. Green star represents the excitation position while orange and blue dots denote two probes. (b) and (c) Measured response spectra at the upper (probe 1) and lower (probe 2) output port, around the frequency region of (b) CLL I and (c) CLL II. The gray dashed lines denote the bound frequencies of the CLLs. (d) and (e) Simulated (left) and laser-scanned (right) wave fields at (d) 121.8 kHz and (e) 365.2 kHz.

3. Conclusions

To conclude, we have demonstrated dual-band elastic CLLs based on topological valley PCs and observed the unique large-area bulk energy transport of ultrasonic waves mediated by these CLLs. Through simply varying the rotation angle of perforated holes on the PC plates, dual-frequency Dirac cones are opened and the gap sizes are controllable. By properly tuning the position-dependent Dirac mass that induces the synthetic PMF, the dual-band zeroth CLLs of ultrasound are achieved. We have revealed in simulations and experiments the large-area energy transport of ultrasonic waves in dual frequency regions, and verified the exceptional robustness of the transport against geometric perturbation. Then, we showcase diverse ultrasonic wave manipulations via modulating the PMF in the proposed valley PCs. It has been demonstrated that the propagation pathways of ultrasonic waves can be customized by strategically engineering the positions of combined supercells, desirable for constructing topological waveguides with arbitrary propagation pathways. Besides, an energy splitter has been designed and tested, where the splitting phenomenon of propagative ultrasound has been well observed in experiments and simulations. This study expands the scope of topological elastic metamaterials and greatly enhances the manipulative capabilities of ultrasonic waves for multi-frequency mechanical functional devices.

4. Methods

4.1. Sample fabrication and experimental procedure

The sample is fabricated by high-precision laser cutting technology with the precision of 0.2 μm, which guarantees the demanded variation of θ. In the measurement, the damping layers (Blu tack) are glued at plate boundaries to suppress unwanted wave reflections. A piezoelectric ceramic patch (PZT-5H, 20 × 5 × 2 mm) is used for exciting ultrasonic waves. The out-of-plane displacement field |u_z| is obtained by scanning the whole PC plate (dash box) using a laser vibrometer (Polytec, PSV-500). In experimental measurements, the up-chirp signal from the PSV-500 controller is sent to a power amplifier (Aigtek, ATA-2021H) to drive piezoelectric ceramics. The time-domain signals measured using the vibrometer are processed via FFT to obtain the frequency spectra, with the sampling rate of 1.28 MHz.

4.2. Numerical simulations

The numerical simulations throughout the paper are performed using the commercial finite element software COMSOL Multiphysics 5.6. In particular, 2D plate elements in COMSOL are used, given the planar surfaces of the designed PC plates. The presented dispersion curves in all figures only contain the out-of-plane vibration modes. In the simulations, the used material is aluminum with the Young's modulus E = 70 GPa, density ρ = 2700 kg m⁻³, and Poisson's ratio v = 0.33.

Author contributions

L. Fan: methodology, formal analysis, investigation, and writing – original draft. Z. Lan: methodology, writing – review and editing. Y. Chen: conceptualization, methodology, supervision, formal analysis, writing – review and editing. J. Zhu: conceptualization, supervision, funding acquisition, writing – review and editing. Z. Su: conceptualization, supervision, funding acquisition, writing – review and editing.

Data availability

The main data and models supporting the findings of this study are available within the paper. Further information is available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No.: 92263208, 12102134), the Research Grants Council of Hong Kong SAR (No.: AoE/P-502/20, 15214323, 15200922 and N_PolyU597/24), and Innovation and Technology Commission Hong Kong SAR (No.: ITS/005/24SC and KBBY1).

References

1. G. Ma, M. Xiao and C. T. Chan, Nat. Rev. Phys., 2019, 1, 281.
2. X. Li, S. Yu, H. Liu, M. Lu and Y. Chen, Curr. Opin. Solid State Mater. Sci., 2020, 24, 100853.
3. X. Ni, S. Yves, A. Krasnok and A. Alu, Chem. Rev., 2023, 123, 7585.
4. G. J. Chaplain, J. M. De Ponti, G. Aguzzi, A. Colombi and R. V. Craster, Phys. Rev. Appl., 2020, 14, 054035.
5. Y. Chen, L. Fan, J. Zhu and Z. Su, Adv. Funct. Mater., 2025, 35, 2413285.
6. T. X. Ma, Q. S. Fan, C. Zhang and Y. S. Wang, Extreme Mech. Lett., 2022, 50, 101578.
7. Y. Chen, L. Fan, J. Zhu, L. An and Z. Su, Nano Energy, 2024, 127, 109722.
8. G. Duan, S. Zheng, Z. Cheng, H. Wu and B. Xia, Adv. Funct. Mater., 2025, 2425815.
9. D. Lee, B. Oh, J. Park, S. W. Moon, K. Shin, S. M. Kim and J. Rho, Nat. Commun., 2024, 15, 3044.
10. F. Zangeneh-Nejad and R. Fleury, Adv. Mater., 2020, 32, 2001034.
11. Y. Chen, L. Fan, J. Zhu and Z. Su, Adv. Sci., 2025, 12, 2411398.
12. S. Zhao, Z. Tian, C. Shen, S. Yang, J. Xia, T. Li, Z. Xie, P. Zhang, L. P. Lee, S. A. Cummer and T. J. Huang, Nat. Mater., 2025, 24, 707–715.
13. D.-S. Kim, W. Choi, S.-W. Kim, E.-J. Kim, S. Nahm and M. Kim, Mater. Horiz., 2023, 10, 149–159.
14. M. Oudich, N. J. Gerard, Y. Deng and Y. Jing, Adv. Funct. Mater., 2023, 33, 2206309.
15. B. Wu, W. Jiang, J. Jiang, Z. Zhao, Y. Tang, W. Zhou and W. Chen, Adv. Funct. Mater., 2024, 34, 2316745.
16. B. Oh, K. Kim, D. Lee and J. Rho, Mater. Today Phys., 2023, 39, 101273.
17. Y. Jang, S. Kim, E. Kim and J. Rho, Sci. Bull., 2025, 70, 1080–1086.
18. S. H. Mousavi, A. B. Khanikaev and Z. Wang, Nat. Commun., 2015, 6, 8682.
19. S. Y. Yu, C. He, Z. Wang, F. K. Liu, X. C. Sun, Z. Li, H. Z. Lu, M. H. Lu and Y. F. Chen, Nat. Commun., 2018, 9, 3072.
20. M. Miniaci, P. K. Pal, B. Morvan and M. Ruzzene, Phys. Rev. X, 2018, 8, 031074.
21. H. Fan, B. Xia, L. Tong, S. Zheng and D. Yu, Phys. Rev. Lett., 2019, 122, 204301.
22. Y. Huang, C. Yang, W. Yuan, Y. Zhang, Y. Pan, F. Yang, Z. Zhong, J. Zhao, O. B. Wright and J. Ren, Adv. Sci., 2024, 11, 2404839.
23. M. Yan, J. Lu, F. Li, W. Deng, X. Huang, J. Ma and Z. Liu, Nat. Mater., 2018, 17, 993.
24. M. Miniaci, R. K. Pal, R. Manna and M. Ruzzene, Phys. Rev. B, 2019, 100, 024304.
25. N. Gao, S. Qu, L. Si, J. Wang and W. Chen, Appl. Phys. Lett., 2020, 118, 063502.
26. Z. Du, H. Chen and G. Huang, J. Mech. Phys. Solids, 2020, 135, 103784.
27. L. Fan, Y. Chen, J. Zhu and Z. Su, Int. J. Mech. Sci., 2024, 266, 108916.
28. P. Dorin, M. Khan and K. W. Wang, Adv. Sci., 2023, 10, 2304793.
29. L. Fan, Y. Chen, S. An, T. Liu, H. Fan, J. Zhu and Z. Su, Phys. Rev. Appl., 2023, 19, 034065.
30. Y. Wu, M. Yan, Z. K. Lin, H. X. Wang, F. Li and J. H. Jiang, Sci. Bull., 2021, 66, 1959.
31. Y. Liu, B. Lei, P. Yu, L. Zhong, K. Yu and Y. Wu, Mech. Syst. Signal Process., 2023, 198, 110433.
32. L. Fan, Y. Chen, J. Zhu and Z. Su, J. Sound Vib., 2025, 595, 118795.
33. Z. Su, L. Ye and Y. Lu, J. Sound Vib., 2006, 295, 753.
34. A. De Luca, F. Caputo, Z. S. Khodaei and M. H. Aliabadi, Compos. B Eng., 2018, 138, 168–180.
35. Z. Lan, M. L. N. Chen, J. W. You and W. E. I. Sha, Phys. Rev. A, 2023, 107, L041501.
36. Y. Chen, X. Wen, Y. Lu, Z. Lan, L. Fan, H. S. Park, Z. Gu, J. Zhu and Z. Su, Compos. Struct., 2025, 352, 118669.
37. M. Wang, Q. Ma, S. Liu, R.-Y. Zhang, L. Zhang, M. Ke, Z. Liu and C. T. Chan, Nat. Commun., 2022, 13, 5916.
38. Z.-D. Zhang, M.-H. Lu and Y.-F. Chen, Phys. Rev. Lett., 2024, 132, 086302.
39. Z. Yang, F. Gao, Y. Yang and B. Zhang, Phys. Rev. Lett., 2017, 118, 194301.
40. H. Abbaszadeh, A. Souslov, J. Paulose, H. Schomerus and V. Vitelli, Phys. Rev. Lett., 2017, 119, 195502.
41. X. Wen, C. Qiu, Y. Qi, L. Ye, M. Ke, F. Zhang and Z. Liu, Nat. Phys., 2019, 15, 352.
42. M. Yan, W. Deng, X. Huang, Y. Wu, Y. Yang, J. Lu, F. Li and Z. Liu, Phys. Rev. Lett., 2021, 127, 136401.
43. H. Jia, M. Wang, S. Ma, R.-Y. Zhang, J. Hu, D. Wang and C. T. Chan, Light: Sci. Appl., 2023, 12, 165.
44. R. Barczyk, L. Kuipers and E. Verhagen, Nat. Photonics, 2024, 18, 574.
45. M. Barsukova, F. Grise, Z. Zhang, S. Vaidya, J. Guglielmon, M. I. Weinstein, L. He, B. Zhen, R. McEntaffer and M. C. Rechtsman, Nat. Photonics, 2024, 18, 580.
46. Y. Liu, K. Li, W. Liu, Z. Zhang, Y. Cheng and X. Liu, Quantum Front., 2024, 3, 1.
47. S. Li, P. G. Kevrekidis and J. Yang, Phys. Rev. B, 2024, 109, 184109.
48. Z. Cui, C. Wu, Q. Wei, M. Yan and G. Chen, Phys. Rev. Lett., 2024, 133, 256602.
49. Y. Chen, Z. Lan, L. Fan, S. Liang, L. An, J. Zhu and Z. Su, Phys. Rev. B, 2025, 111, 184303.
50. Z. Huang, J. Wu, C. Wang, S. Yang and F. Ma, Phys. Rev. B, 2021, 104, 094110.
51. Z. Huang, J. H. Wu, Y. Lei, C. Liu and F. Ma, Mater. Today Phys., 2022, 27, 100793.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5mh00662g

---