Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermoelectric transport and the role of different scattering processes in the half-Heusler NbFeSb
Bhawna
Sahni
 *a,
Yao
Zhao
*a,
Yao
Zhao
 a,
Zhen
Li
a,
Zhen
Li
 b,
Rajeev
Dutt
b,
Rajeev
Dutt
 a,
Patrizio
Graziosi
a,
Patrizio
Graziosi
 c and
Neophytos
Neophytou
c and
Neophytos
Neophytou
 a
a
aSchool of Engineering, University of Warwick, Coventry, CV4 7AL, UK. E-mail: Bhawna.Sahni@warwick.ac.uk
bSchool of Materials Science and Engineering, Beihang University, Beijing 100191, China
cInstitute of Nanostructured Materials, CNR, Bologna, Italy
First published on 20th August 2025
Abstract
We perform an ab initio computational investigation of the electronic and thermoelectric transport properties of one of the best performance half-Heusler (HH) alloys, NbFeSb. We use Boltzmann Transport equation while taking into account the full energy/momentum/band dependence of all relevant electronic scattering rates, i.e. with acoustic phonons, non-polar optical phonons (intra- and inter-valley), polar optical phonons (POP), and ionized impurity scattering (IIS). We use a highly efficient and accurate computational approach, where the scattering rates are derived using only a few ab initio extracted matrix elements, while we account fully for intra-/inter valley/band transitions, screening from both electrons and holes, and bipolar transport effects. Our computed thermoelectric power-factor (PF) values show good agreement with experiments across densities and temperatures, while they indicate the upper limit of PF performance for this material. We show that the polar optical phonon and ionized impurity scattering (importantly including screening), influence significantly the transport properties, whereas the computationally expensive non-polar phonon scattering part (acoustic and non-polar optical) is somewhat weaker, especially for electrons, and at lower to intermediate temperatures. This insight is relevant in the study of half-Heusler and other polar thermoelectric materials in general. Although we use NbFeSb as an example, the method we employ is material agnostic and can be broadly applied efficiently for electronic and thermoelectric materials in general, with more than 10× reduction in computational cost compared to fully ab initio methods, while retaining ab initio accuracy.
New conceptsModern thermoelectric materials have complex electronic structures with multiple bands and valleys. Evaluating their electronic transport is challenging due to intricate scattering mechanisms often requiring first principles evaluation, which is computationally expensive and non-scalable. Simplifications are often made, which reduce accuracy and our understanding of internal processes which are crucial for determining transport. We develop and employ a novel method offering ab initio accuracy with 10×–100× computational savings and providing detailed scattering process descriptions for full understanding of the material transport properties. We apply this method to one of the most prominent half-Heusler thermoelectric materials, NbFeSb, as an example, first demonstrating good agreement with experiments, and revealing key insights: that ionized impurity and polar optical phonon scattering significantly influence transport (especially for n-type carriers and lower to intermediate temperatures); that intra-valley processes dominate; that carrier screening is important; and that the power factor could be up to 2× higher than current experiments. This method enables first principles accuracy and comprehensive understanding of thermoelectric transport, applicable broadly for performance optimization in complex materials. |
1 Introduction
In the last few decades, a new paradigm in materials science has been initiated by the widespread use of first-principles electronic structure calculations, coupled with the continuously growing power and accessibility of massively parallel supercomputers.1–4 This has allowed the detailed study of material properties in a large variety of areas, as well as accurate predictions that are subsequently verified by experiment. With regards to computational studies of thermoelectric materials, and the thermoelectric power factor in particular, the electronic structure calculations are coupled to electronic transport solvers. Transport is governed by the semi-classical Boltzmann transport theory and the solution of the Boltzmann transport equation (BTE). However, this still presents significant computational challenges, making such studies impractical for realistic material systems. The difficulty lies in obtaining the charge carrier relaxation times, which are essential inputs to the BTE and are not easily obtained using current computational methods. Because of this difficulty, for electronic transport, the constant relaxation time approximation (CRTA) has typically been used to solve the BTE.5,6 However, this assumption is very crude since the relaxation time typically depends on energy, momentum, band, temperature, among others, and the CRTA leads to quantitative and qualitative errors.7,8One way to address this challenge is by utilizing scattering rate expressions based on deformation potentials. In 1950, Bardeen and Shockley initially suggested the deformation potential method due to acoustic phonons in the long wavelength limit, and it has since had a considerable impact on the modelling of semiconductor devices.9–11 AMSET is a recently developed program that obtains rough estimates of a ‘global’ deformation potential derived from the change in band energy due to lattice deformation (induced by phonons).12 Further advancements in density functional theory (DFT) and density-functional perturbation theory (DFPT) have enabled first-principles computations of electron–phonon interactions,13 which can be used for ab initio scattering rate extraction. However, such methods are computationally very expensive. They typically require the computation and further post-processing of millions of matrix elements and need a very fine sampling of the electron and phonon momentum spaces,14–16 making scaling quite challenging and impractical. In order to maintain high accuracy while reducing computational costs, various methods based on the DFPT + Wannier approach have been developed, which include averaging or integrating matrix elements across the entire Brillouin zone, such as EPA17 and EPICSTAR.18 EPA takes an average over electron–phonon coupling matrix elements as well as phonon energies and thus, requires only a sparse grid. EPICSTAR also employs a sparse grid of matrix elements and adjusts them according to their phonon frequency to create a more uniform matrix element distribution. In both cases, the results are subject to the mesh discretization while convergence tests are also expensive. These are computationally efficient methods which provide improvement over the CRTA, although they hide detailed transport physics, especially related to intra/inter-valley/band scattering transitions. The latter is essential in band alignment strategies for TE performance improvements in multi-band/valley materials.19 In this work, we also use an efficient formalism to compute the electronic transport properties by employing the DFPT + Wannier method and extract a limited, yet highly relevant set of matrix elements to obtain deformation potentials and determine electron–phonon scattering rates. We distinguish between all scattering processes, which allows for a complete understanding of the internal effects that determine electronic transport. We then employ our Boltzmann Transport Equation (BTE) code ElecTra,20 which can account for all scattering processes individually.
We extract the TE electronic transport properties of NbFeSb, one of the more prominent TE half-Heusler materials. We find that its transport properties are strongly influenced by electron-POP and electron-IIS scattering. At 300 K, the POP + IIS scattering mechanisms are around twice as strong in determining σ and PF compared to ADP + ODP for p-type carriers, and five times as strong for n-type carriers, but this strength reduces with temperature. We find that the TE power factor in the p-type case peaks at 11.45 mW m−1 K−2, whereas for the n-type case at 5.92 mW m−1 K−2, which can even be achieved for an order of magnitude less density (at 6.27 × 1019 cm−3) compared to the p-type material. Compared to experiments, we find that the calculated conductivity is around three times higher, while the Seebeck coefficient is somewhat lower, suggesting the possible presence of significant defects in experiments that lower conductivity. With regards to the PF, however, we find reasonably good agreement with existing p-type measured data, with the computational data being around two times higher. As our approach provides valuable insights into the contribution of individual scattering mechanisms (acoustic, optical, intra- and inter-valley), it provides a way to hierarchise the scattering processes based on their strengths. Thus, we are able to provide deep understanding regarding the internal processes, and finally derive even more generalized conclusions that can be broadly applied to other half-Heusler materials and beyond.
The paper is organized as follows: In Section 2 we present the results obtained starting from the discussion of the crystal structure of NbFeSb, its electronic and phonon dispersion, the method for the extraction of deformation potentials using matrix elements obtained for p-type and n-type NbFeSb, then moving to the scattering rates and thermoelectric coefficients in Section 3. In Section 4, we conclude and summarise our findings. In Section 5, we present the methods used for our transport simulation.
2 Results
Fig. 1(a) shows the cubic structure of NbFeSb, which belongs to the family of half-Heusler alloys having chemical composition XYZ, where X and Y are transition metal elements and Z is a p-block element. Half-Heusler (HH) thermoelectric (TE) materials have gathered significant research attention in the past few decades due to their thermal stability, mechanical robustness, and reasonable TE figure of merit (ZT) values. ZT is the dimensionless figure of merit that quantifies the efficiency of the energy conversion process. It is defined as ZT = (σS2)/(κe + κL), where σ is electrical conductivity, S is Seebeck coefficient, and κe and κL are the electronic and lattice thermal conductivities, respectively. The quantity σS2 is called the power factor (PF). HHs are promising TE materials for use in medium to high temperature applications, which aligns well with the temperature range of many industrial waste heat sources.21,22 NbFeSb is one of the high-performance thermoelectric materials with a p-type TE figure of merit ZT > 1,23 which corresponds to approximately 10% of the Carnot efficiency, and it compares with the best performing materials.24–26 The investigation and clear understanding of the electronic structure and strength of the scattering mechanisms in this material, can pave the way for future optimization of TE properties in this group of materials in general. Indeed, the high TE performance of this type of materials originates mostly from their PF, which is around 3–6 mW m−1 K−2, and is comparable to some of the best such values across materials and operating temperatures.27–34 On the other hand, although its p-type performance is well established, very little is known about its n-type performance with only few reports available.35–372.1 Electronic and phonon band structure
The electronic band structure of NbFeSb is shown in Fig. 1(b). The impact of spin–orbit coupling on the band structure of these materials has been investigated in the past and found to be negligible.38 Thus, we proceed with the band structure without spin–orbit coupling in our calculations. Our calculations show a band gap of Eg = 0.51 eV which is in agreement with previous reports.29,33,39 The atom-projected density of states of NbFeSb is shown in Fig. S1 (SI). The conduction bands show major contribution from Nb d-orbitals only, while the valence bands show major contribution from Fe d-orbitals, followed by Nb d-orbitals and Sb p-orbitals. There is a hybridization between Nb d-orbitals and Sb p-orbitals in the energy range of 0 to −1 eV. The valence band maximum is located at the L high symmetry point and is doubly degenerate, while the conduction band minimum is at the X high symmetry point. The valence bands are flatter as compared to the conduction bands indicating higher effective masses, as noted in Fig. 1. We have extracted the density of states effective mass (mDOS) and conductivity effective mass (mcond) for both holes and electrons using the method described in ref. 40 and 41 from our EMAF code.42 This band structure asymmetry will have some effect on the transport properties, which will be discussed in a later section.Since NbFeSb has 3 atoms in its primitive unit cell, the phonon spectrum has 9 phonon branches/modes, as shown in Fig. 1(c). The atom-projected phonon density of states is shown in Fig. S2 which shows the major contribution of Sb atoms in low frequency regions, followed by contributions from Nb and Fe atoms. The high frequency (longitudinal optical phonon) modes show dominant contribution from Fe atoms. The highlighted green and blue regions in Fig. 1(c) roughly show the acoustic and optical phonon mode regions considered in extracting the deformation potentials. These are regions that satisfy momentum/energy conservation to facilitate the electronic transitions. For intra-valley scattering (scattering of a carrier within its own valley), small values of wave-vector |q| (the zone-centre phonons) participate, which can be found in either the acoustic or optical phonon modes. For inter-valley scattering (scattering of a carrier from one valley to another), a large value of |q| (near zone-edge phonons) are involved due to a substantial change in momentum. The modes responsible for inter-valley scattering can also be found in both the acoustic and optical branches, but they both resemble optical modes since these modes are away from the Γ point and are thus high in energy. Even in the case of acoustic branches participating, at those wave-vector regions they are flattened out and resemble optical modes. Schematics for the inter-valley scattering between the six conduction band minima valleys at the X point and the eight valence band maxima valleys at the L point are shown in Fig. 1(d) and (e). Fig. 1(f) and (g) show the 2D cross section view for the Brillouin zone of electrons (transparent) and phonons (cyan), showing the CBM and VBM valleys with blue and grey ellipsoids respectively. The phonon wave vector q involved in the transition between equivalent CBM valleys and VBM valleys is along the Γ–X direction and thus the modes responsible for inter-valley scattering are shown by the highlighted region near the X-point in Fig. 1(c). Note that this participating phonon vector direction holds for the cases of both the valence (L–L) and conduction band (X–X) transitions. In the case of the VB this is geometrically easy to identify as shown in Fig. 1(g). For the CB, however, the vector from an X to another X-valley in the perpendicular direction is longer than the half of the Brillouin zone (the BZ for phonons), thus, we consider the equivalent final X-valley in the second electronic BZ, which happens to be in the Γ–X direction as shown in Fig. 1(f).
2.2 Deformation potential extraction method
For acoustic phonons (in the long wavelength limit, i.e. small wave-vector |q|), the atomic displacements can cause the crystal to deform. Such deformations alter the electronic energies at various locations inside the Brillouin zone. Deformation potentials are the parameters that characterise these changes in electronic energies, brought on by static distortions of the lattice.9 The deformation potentials can be more accurately determined by calculating the electron–phonon coupling matrix elements, from which we can determine the electron–phonon coupling strength, and using Fermi's Golden rule determine the scattering rates. The scattering matrix elements are the probability amplitude for scattering from an initial state |ψnk〉 to a final state |ψmk+q〉 due to a perturbing potential δqνV associated with a phonon on branch ν, frequency ωqν and wave vector q, are defined as:43–45| Mmnν(k,q) = 〈ψnk|δqνV|ψmk+q〉 | (1) |
The acoustic deformation potential (ADP) can be calculated by taking the slope of the matrix elements with respect to the phonon wave vector, DADP = (Mmnν(k,q))/(|q|).46 The optical phonons on the other hand, give rise to microscopic distortions which can be regarded as an internal strain within the unit cell. The optical deformation potential (ODP) is the value of the matrix element itself, DODP = (Mmnν(k,q)). The acoustic and optical deformation potential scattering mechanisms are of short-range in nature, and they do not depend explicitly on the phonon wave-vector q.
In the case of polar crystals, the long wavelength (small |q|) longitudinal optical phonon modes (LO) induce an oscillating polarization, generating a macroscopic electric field.47 This electric field couples with the carriers and is known as the Frohlich interaction,48 which is long-range in nature. The Fröhlich interaction becomes stronger for smaller |q| and it diverges as |q| becomes zero. The long-range component of the electron–phonon coupling matrix elements due to the Fröhlich interaction is defined as:48
 | (2) |
 is the Born effective charge tensor. A polar phonon mode can include both, a short-range (deformation potential) part, and a long-range (POP) part.49 The long-range component needs to be separated from the short-range component to deal with the polar singularity as the wave vector approaches zero. For calculating acoustic and optical deformation potentials for polar materials, the long-range part of the matrix elements is subtracted from the total matrix elements to get the short-range part of the matrix elements.50 The short-range component of matrix elements is then used to calculate DADP and DODP.
is the Born effective charge tensor. A polar phonon mode can include both, a short-range (deformation potential) part, and a long-range (POP) part.49 The long-range component needs to be separated from the short-range component to deal with the polar singularity as the wave vector approaches zero. For calculating acoustic and optical deformation potentials for polar materials, the long-range part of the matrix elements is subtracted from the total matrix elements to get the short-range part of the matrix elements.50 The short-range component of matrix elements is then used to calculate DADP and DODP.
The overall DADP value is calculated after averaging the longitudinal and transverse acoustic deformation potentials as:
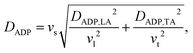 | (3) |
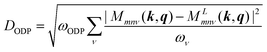 | (4) |
We follow this process of subtracting the long-range part of the matrix elements from the total matrix element to obtain the short-range part for all modes for generality in the computational approach. Of course, we know that only two of the modes are polar and include long-range parts.51 In the other modes, the long-range part is zero, but it is more convenient for the numerical automation of the process, since we do not identify which ones are polar to begin with. The POP scattering rate itself, is then computed using the Frohlich formula for POP scattering including screening, as described in the methods section, whereas the average mode frequency is used for the interaction.
For inter-valley scattering, as discussed earlier, phonons with large wave-vectors |q|, scatter electrons from one valley to another valley of the same or different band. The zone-edge phonons away from the Γ point are the ones which mediate these scattering events. The inter-valley deformation potential is obtained again by considering the contribution from all the modes and taking an average as51:
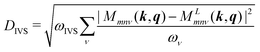 | (5) |
2.3 Matrix elements for NbFeSb
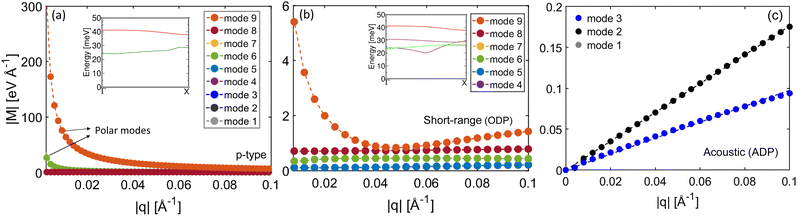
The first step for the calculation of the deformation potentials is identifying the band extrema and all different possible transitions (intra/inter-band/valley) from the electronic band structure of the material. Using the wavevectors that facilitate those transitions, the participating phonon modes that satisfy energy/momentum conservation are identified and then the electron–phonon coupling matrix elements for all of them are computed. In this section, we first compute the deformation potentials for transitions in the valence band (VB) of NbFeSb and afterwards in the conduction band (CB).Fig. 2(a) shows the scattering matrix elements for intra-valley transitions (small q-vector) for B1 → B1 along the Γ–X direction (see Fig. S5 for the matrix elements in the other directions, which are of similar trend and amplitude). There are two polar modes due to the two longitudinal optical phonon modes (mode 6 and 9) as shown in Fig. 2(a), recognised by their 1/|q| trend. The rest of the matrix elements are much lower in amplitude. The inset of Fig. 2(a) shows the frequencies of these two polar modes along the same direction. The average value of the polar optical phonon energy is calculated along various high-symmetry directions. Then those values from all polar modes are averaged to extract a single dominant frequency for the overall polar optical phonon scattering process. This is determined to be ħω = 32 meV here, and that is used in the equation for the Frohlich interaction (see methods). The short-range part of these matrix elements for the six optical modes is shown in Fig. 2(b) after the long-range part is subtracted out. The average optical phonon energy is determined to be ħω = 29 meV.
The acoustic modes in Fig. 2(c) shows the short-range part of the matrix elements corresponding to the longitudinal and transverse acoustic modes. The intra-valley deformation potentials for all four scattering processes (between the two bands) along different high-symmetry directions are listed in Table S1. The calculated ADP and ODP values along different high-symmetry directions are shown in Table 1. The overall ODP and ADP values for holes turn out to be DODP = 2.8 eV−1 (with an overall phonon energy of ħω = 29 meV) and DADP = 2.5 eV, respectively. The overall deformation potentials are calculated as:
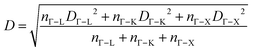 | (6) |
| Holes | ||||
|---|---|---|---|---|
| Γ–L | Γ–X | Γ–K | Γ–W | |
| D ADP (eV) | 2.38 | 2.16 | 2.76 | 2.5 |
| D ODP (eV Å−1) | 2.58 | 2.13 | 3.11 | 2.87 |
The number of the equivalent crystallographic orientations for a face-centered cubic (FCC) lattice are nΓ–L = 8, nΓ–X = 6, and nΓ–K = 12. Note that we used sampling along the 〈111〉, 〈100〉 and 〈110〉 crystal directions. This covers the majority of the volume of the BZ (ending up on the hexagonal and square surfaces on the BZ, and the edges around those surfaces, respectively – see Fig. S4 in the SI). We have also computed the deformation potentials along the path between Γ and W, which is also towards the edge of the BZ in between the hexagonal and square surfaces. This gives similar values as the Γ and K direction (which is towards the edges as well). We exclude this direction from the sampling, as is covered by the Γ and K and as it is not one of crystal directions.
Next, we consider the inter-valley scattering processes. Since the VBM resides on the L high-symmetry point, the Fermi surface of holes contains eight half L-valleys in the first Brillouin zone (BZ). Due to the cubic crystal symmetry, only one unique type of inter-valley transition from any given initial VBM valley to other equivalent VBM valley can be identified, as shown by the solid black arrow in the BZ of Fig. 3. The other equivalent transitions are shown by the dashed grey color arrows. Fig. 3 shows the matrix elements from all phonon modes for that transition, identified by different colors for different phonon modes. We considered a few points in the vicinity of the band extrema (∼5 points on each final valley – from which we take the average value) and thus, there are 45 points from 9 phonon modes in Fig. 3, corresponding to transition from one valley to another. The brown square in Fig. 3 shows the overall inter-valley matrix element (and deformation potential) value for these transitions for VBM (B1). Note that the energies at which the different points appear, correlated very well from the energy of the phonon bands under the highlighted regions in the phonon spectrum of Fig. 1. The DIVS value (average of B1 → B1 (0.48), B1 → B2 (0.56)) is 0.52 eV Å−1 as computed using eqn (6) including all nine modes (one averaged value for each mode) with the average frequency value ħω ∼ 24 meV.
| Electrons | ||||
|---|---|---|---|---|
| Γ–L | Γ–X | Γ–K | Γ–W | |
| D ADP (eV) | 1.93 | 2.56 | 6.51 | 6.3 |
| D ODP (eV−1) | 3.7 | 3.88 | 2.51 | 1.61 |
For inter-valley scattering, the CBM is at the X high-symmetry point, so the Fermi surface of electrons contains six half X-valleys in the first Brillouin zone (BZ). One unique type of inter-valley transitions from any given initial CBM valley to other equivalent CBM valleys can be identified, as shown by the solid black arrow in the BZ of Fig. 5. The other equivalent transitions are shown by the dashed grey color arrows. The matrix elements for the transitions facilitated by all phonon modes are shown in Fig. 5, where each color corresponds to a different mode. Again, we consider 5 points in the vicinity of each of the band extrema, resulting in 45 points in Fig. 5 for transitions from one valley to another. The brown square shows the overall inter-valley deformation potential value for this transition. The DIVS values are computed to be DIVS = 0.22 Å−1 with the average frequency value of ħω ∼ 24 meV (as computed above for the VB as well).
3 Scattering rates and thermoelectric transport
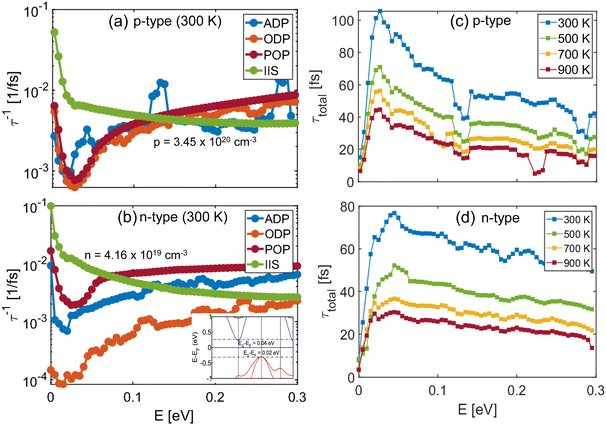
The transport calculations are performed using our open-source Boltzmann Transport Equation solver (BTE) code ElecTra.20 The expressions for individual scattering rates are described in the computational methods section below. The BTE simulator takes the deformation potentials and the dominant frequency for polar optical phonons as inputs for the electronic transport calculations. Table S2 (in the SI) lists the other required input parameters, such as dielectric constants and mass densities, which are also obtained through first-principles calculations. In the calculation we do not separate p-type and n-type transport, but treat the entire band structure as one entity, including bipolar effects, and full treatment of screening, i.e. both electrons and holes contribute to screening, irrespective of the Fermi level position.53 Thus, the calculations are performed under the assumption of a complete bipolar transport, integrating the complete transport distribution function TDF (see methods) across the entire energy range. Note that although it is computationally more convenient and easier to perform unipolar transport calculations and afterwards combine the two parts, in the presence of IIS this is not possible, and the full bipolar computation needs to be performed in order to capture the impurity density and screening correctly.53Fig. 6(a) and (b) show the individual scattering rates for p-type and n-type NbFeSb at 300 K when the Fermi level is placed in the vicinity of the respective band edge, as shown in the inset of Fig. 6(a); this is the region where the PF peaks, as we show later on. For p-type, the ADP, ODP and POP scattering rates are comparable, while IIS is the dominant scattering mechanism. For n-type, ADP and ODP scattering rates are lower while POP and IIS are the dominant scattering mechanisms. The total relaxation time values obtained by Matthiessen's rule (explained in the methods section), for both holes and electrons for various temperatures, are shown in Fig. 6(c) and (d) respectively, again when the Fermi level is placed at the vicinity of the band edges. The relaxation time values vary with energy and temperature and differ from the constant value of τC = 10 fs as often assumed in the constant relaxation time approximation (CRTA).54,55 The variation of individual scattering processes with energy and temperature are also shown in Fig. S5 and S6 for p-type and n-type, respectively (SI).
3.1 Thermoelectric (TE) coefficients
Next, we present the TE coefficients with respect to the Fermi level's relative position, EF, which correlates directly with doping density. Here, EF is set to 0 eV at the intrinsic Fermi level in the bandgap (typically not the midgap level due to VB/CB asymmetry) while the midgap is at Emid = −0.037 eV. The CB minima is placed at EC = 0.22 eV whereas the VB maxima at EV = −0.29 eV. All the relevant scattering mechanisms such as ADP and ODP (intra and inter-valley), POP and IIS are considered.The comprehensive computed electronic transport properties (S, σ and σS2) versus the relative position of Fermi-level EF (left panel), as well as versus the doping density (right-panel) for p-type and n-type NbFeSb for different temperatures, are shown in Fig. 7. With the black, blue and red vertical lines, we indicate the position of the intrinsic Fermi level, the VB edge and the CB edge, respectively. Due to the asymmetry between the masses in the VB and CB, the zero crossing of the Seebeck coefficient is shifted from the charge neutrality point towards the VB, as the Seebeck coefficient becomes zero at the point of equal conduction between the VB and the CB (more evident in Fig. 7(b)). Note that the effective mass of holes is significantly greater than that of electrons, resulting in lower mobility for holes compared to that for electrons (see Fig. S13 in SI). Thus, the point of equal conductivity between holes and electrons is shifted towards the lower conductivity band (VB).53
The peak power factor for p-type is obtained to be around 10.44 mW m−1 K−2 at 300 K, while it peaks to 11.45 mW m−1 K−2 at 500 K at a carrier concentration of p = 8.4 × 1020 cm−3. For n-type, the computed peak power-factor is 5.28 mW m−1 K−2 at 300 K, while it peaks to 5.92 mW m−1 K−2 at 900 K at a carrier concentration of n = 6.27 × 1019 cm−3. Thus, the n-type peak can be obtained at a doping density an order of magnitude lower than that for p-type NbFeSb, a consequence of the higher effective mass (mDOS of holes as compared to that of electrons, as shown in Fig. 7(b). In general, for n-type the PF peak for the various temperatures is achieved when EF is placed somewhat more into the bands compared to p-type (in the case of T = 300 K the n-type PF peak is achieved when EF is placed 0.04 eV into the CB, whereas for p-type when EF is 0.02 eV into the VB).
At high temperatures, the minority carriers can be thermally generated. In the case where the Fermi level is placed in the bandgap, the absence of doping can lead to intrinsic phonon-limited carrier mobility. In addition, the asymmetry between the transport in the VB and CB, which leads to an asymmetric zero Seebeck crossing, can provide finite Seebeck coefficients, which together with phonon-limited conductivity, can lead to high power-factor values around the intrinsic ηF = 0 eV region.56 As shown in Fig. 7(f), the PF remains around 1–2 mW m−1 K−2 at 700–900 K for a large range of carrier concentrations for the case where the Fermi level is in the bandgap (region between the blue dashed lines). Note that much higher values of PFs can be obtained in this low carrier density region under different conditions. As we have shown in ref. 56, asymmetric band structures with regards to the CB and VB can allow for very high bipolar PFs compared to their unipolar ones, in materials in which the intrinsic phonon conductivity is high in the bandgap regions where the Seebeck is finite, assisted by the absence of the strong IIS mechanism.
With regards to the accuracy of the simulations, in Fig. 8, we compare our results with the previously experimentally reported transport coefficient values for p-type NbFeSb. The power-factor values calculated using our method agree well with previous experimental reports. Most of the reported data points are in the region where the optimal carrier concentration is obtained. In most experimental reports, the peak PF value is around PF = 2–10.5 mW m−1 K−2 in the temperature range from 400–900 K and the carrier concentration is around p = 6.3× 1020–1.5 × 1021 cm−3. Our peak PF of around 11.5 mW m−1 K−2 at 500 K at carrier concentration of 8.4 × 1020 cm−3 is somewhat higher. However, it is expected that the theoretical values are generally higher than the experimental values, because of various factors such as the presence of defects, dislocations, alloying etc. in the measured structures, which are not accounted for in simulations. These factors almost certainly reduce the electrical conductivity and mobility significantly. Overall, the electrical conductivity of the experimental data is around a factor of three lower compared to our computed results, as shown in Fig. 8(b). On the other hand, the measured Seebeck coefficient is larger compared to the computed Seebeck coefficient, following the well-expected adverse trend compared to the electrical conductivity, as shown in Fig. 8(a). The electrical conductivity suffers much more in experiment compared to the improvements in the Seebeck coefficient (compared to the simulated data), such that the PF is overall lower the experiment (especially for higher temperatures).
 | ||
| Fig. 8 Comparison with experimental values: our calculations for: (a) Seebeck coefficient, (b) electrical conductivity, and (c) power factor for p-type NbFeSb versus doping concentration for various temperatures. The diamond, star, hexagram, and square markers correspond to experimentally reported values from ref. 23 and 27–34. | ||
3.2 The effect of screening
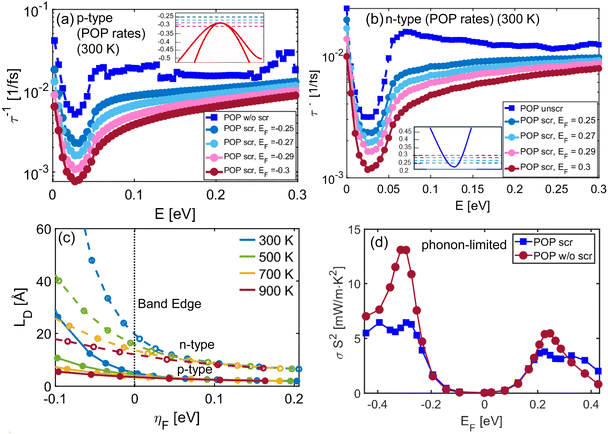
An important consideration for POP and IIS is the effect of screening. In the case of IIS, the free charge carriers can shield the dopant ions and mitigate the scattering rates. Similarly, screening also weakens the POP scattering mechanism and needs to be accounted for. In this case the scattering rates are reduced due to screening of the POP dipole electric field by free carriers. Considering screening is computationally much more expensive, because the scattering rates are not only energy dependent alone, but are also Fermi level dependent. Thus, they need to be computed separately for every EF position. Screening considerations, however, are quite important to accurately compute the electronic transport properties.In Fig. 9(a) and (b) we show the POP rates up to ηF values of −0.3 and 0.3 for p-type and n-type respectively, covering the region where the power-factors peak in each case (see insets for the actual positions of the Fermi level). The POP scattering rates for both p-type and n-type decrease with the increase in carrier concentration, a consequence of increased screening. The POP rates for the unscreened case (blue lines) are larger for p-type as compared to n-type. This is due to the presence of two degenerate valence bands, which introduces inter-band scattering, in addition to the intra-band scattering between the heavy mass p-type bands (see eqn (9) in methods). In fact, a single heavier band mass (as in the VB) will result in larger exchange vectors and reduce the POP and IIS rates. However, having a second heavier band overlapping at the same k-space region, enables small exchange vector transitions between them (from geometrical considerations), which increases the scattering rates (and makes the overall exchange vector smaller – note that inter-valley transitions involve large exchange vectors, but these scattering rates are small and do not affect the overall scattering significantly). When screening is considered, the p-type POP rates decrease more with increasing carrier concentration as compared to the n-type rates. The reason behind this behavior can be explained by examining the generalized screening term for POP rates, defined as 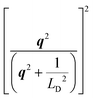 . Here q is the momentum exchange vector,
. Here q is the momentum exchange vector, 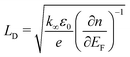 is the screening length, EF is the Fermi level and n is the carrier density. The screening length LD for holes and electrons is shown by the solid and dashed lines, respectively, for different temperatures in Fig. 9(c) at the same reduced Fermi levels (the band edge for both cases is noted and placed at ηF = 0 eV). In general, it decreases with EF (and density) indicating reduction in the scattering rates, and it is lower for holes compared to electrons (solid lines are lower compared to the dashed lines), indicating lower scattering rates for holes (note that low LD means that the scattering interaction is screened at very small length and the scattering rate is thus low). The reason for this behavior is the larger density of states (DOS) for holes, which reduces LD since it involves the
is the screening length, EF is the Fermi level and n is the carrier density. The screening length LD for holes and electrons is shown by the solid and dashed lines, respectively, for different temperatures in Fig. 9(c) at the same reduced Fermi levels (the band edge for both cases is noted and placed at ηF = 0 eV). In general, it decreases with EF (and density) indicating reduction in the scattering rates, and it is lower for holes compared to electrons (solid lines are lower compared to the dashed lines), indicating lower scattering rates for holes (note that low LD means that the scattering interaction is screened at very small length and the scattering rate is thus low). The reason for this behavior is the larger density of states (DOS) for holes, which reduces LD since it involves the 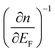 term, which decreases as the DOS increases. Thus, around the energy regions at which the PF peaks, the holes scattering rates are becoming weaker, approaching similar values as those for electrons. Note that the screening length under simplifications is proportional to
term, which decreases as the DOS increases. Thus, around the energy regions at which the PF peaks, the holes scattering rates are becoming weaker, approaching similar values as those for electrons. Note that the screening length under simplifications is proportional to  . Here, since we compare at the same ηF, the density increases with temperature as well (more than linearly), which makes the LD seem to reduce with T, rather than increase.
. Here, since we compare at the same ηF, the density increases with temperature as well (more than linearly), which makes the LD seem to reduce with T, rather than increase.
The phonon-limited PF values with and without considering POP screening show large differences especially for p-type transport, as shown in Fig. 9(d). This signifies that screening needs to be considered, despite the fact that the entire computation is now in addition Fermi level dependent. This is more important with materials with large density of states and elongated, dispersive bands (p-type here), rather than materials with smaller effective masses and narrow bands (n-type here). We stress, however, this is specifically the case for NbFeSb. In our calculations for different half-Heusler materials, these conclusions could vary.
3.3 Intra- versus inter-valley transition strength
It is also important to highlight the significance of intra- versus inter-valley transitions, since this is crucial information for studying band alignment in TE materials.19,57 For this, the scattering rates from Fig. 10 were averaged in the energy range of E = 0–0.1 eV, to provide an estimate of the relative strength of these processes. The deformation potential interaction can be both intra-valley and inter-valley, whereas the polar optical scattering is mostly intra-valley because of its long-range nature (|q|−1). The inter-valley scattering is essentially the IVS non-polar optical processes, whose strength is very small (shown in red in Fig. 10(a and b)) for both the p-type and n-type NbFeSb cases. Thus, the intra-valley processes dominate in this material. We expect this to be the case broadly in the family of polar half-Heusler materials, but also in other polar TE materials as is in the case of Mg3Sb2 as well.51 Note that it is not just inter-valley scattering that is detrimental for band alignment strategies, but also intra-band scattering, which can be strong in the case where the valleys of the aligned and base bands are at the same position in the Brillouin zone (as in the VB of NbFeSb here, although these two bands are actually aligned).583.4 Influence of scattering mechanisms in transport
Since IIS in p-type and POP and IIS in n-type are the strongest scattering mechanisms, we now compute how much of the PF these mechanisms determine. For this, we compute the PF considering only the POP and IIS scattering mechanisms and compare this with the overall PF values (considering all scattering mechanisms). The two calculations are shown in Fig. 10(c) and (d) for σ and S2σ, respectively. The ratio of the σ values taking into account POP + IIS to those calculated by taking into account all scattering mechanisms is shown in the inset of Fig. 10(c). Using resistance combination consideration, a ratio of 2 signifies equal strength between IIS + POP and the non-polar ADP + ODP, while a ratio of 1 shows that IIS + POP has full dominance over ADP + ODP. At 300 K (blue line), this ratio is around 1.5 and 1.2 at the valence and conduction band edges, respectively. This indicates that the POP + IIS scattering mechanisms are around twice as strong in determining σ compared to ADP + ODP for p-type, and five times as strong for n-type (again using resistance combination considerations). For p-type the discrepancy is somewhat larger due to the fact that the non-polar scattering rates are higher compared to the rates in the n-type case (see Fig. 6(a), and also the smaller screening lengths in the heavier VB, which weaken the POP and IIS rates). Fig. 10(d) shows that the conductivity differences are almost entirely transferred to the PF, as the Seebeck coefficient (inset of Fig. 10(d)) is almost identical between the two simulation cases (at 300 K).Note, however, that this comparison is shown for 300 K. At higher temperatures, the comparative strengths would change in favor of the non-polar ADP + ODP mechanisms – our calculations show that the influence of POP + IIS scattering compared to ADP + ODP in determining σ is approximately halved (compared to their influence at 300 K) with doubling the temperature. In general, the ratio in the inset of Fig. 10(c) increases with T. In the case of p-type, at 900 K, the strength of the coulombic and non-polar mechanisms becomes equal. For n-type, even at high T, the coulombic IIS + POP are still much stronger. Thus, even in polar materials such as this one, accurate computation of the non-polar scattering component could be important for the PF, especially for high T. An inaccurate computation of the acoustic and optical deformation potential scattering can lead to significant quantitative error in the transport properties.
3.5 Computational performance
In this subsection, we highlight the major computational efficiencies provided by our approach, specifically compared to the full DFPT + Wannier methods, as for example in EPW.59 The overall computation can be split into two steps. The first involves calculating electron–phonon matrix elements via the DFT and DFPT methods. The second pertains to the transport computation. The first step, which identifies the transitions and extracts the selected matrix elements for those transitions is the same in our case as in the DFPT + Wannier methods. For the first step, we used a k-mesh of 12 × 12 × 12 for DFT and a q-mesh of 6 × 6 × 6 for DFPT. This step is the most time-consuming part of the calculation, requiring around 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CPU hours.
000 CPU hours.
The second step, involving the transport calculation, is computationally significantly less expensive in comparison to DFPT + Wannier based approaches. Full DFPT + Wannier approaches require a fairly dense post-interpolation mesh and the consideration of millions of matrix elements contributing to transport, in order to obtain convergent results.60 This could lead to computational challenges, such as the requirement of higher memory nodes as well as more core hours, especially in case of complex systems with large unit cells and low symmetry.51 In our method, the transport simulation step requires only 6300 CPU hours for both electrons and holes which is significantly lower compared to what DFPT + Wannier methods demand. The transport computation from DFPT + Wannier method is expected to require around 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CPU hours or even more, depending on convergence, for only one type of carrier, as elaborated on in our previous works.51 Thus, effectively, we can reduce the overall computational cost by around 20 times for full bipolar transport using our approach compared to the full DFPT + Wannier method.51,52 (We would like to note that we tried substantially to simulate this material (NbFeSb) using EPW in order to compare with our results. However, achieving quantitative convergence with EPW proved very difficult due to the extremely fine Brillouin-zone sampling needed.) In ElecTra, although we extract just a limited number of matrix elements and converting them into deformation potentials, we intentionally concentrate on the critical transport areas, leading to a locally concentrated grid of matrix elements. This approach might be more beneficial than choosing matrix elements on a sparse grid throughout the entire Brillouin zone.59 More developments in this area could lead to considerable reduction in computational costs making it feasible to compute accurate deformation potentials for large number of systems and even bigger with respect to unit cell size and complexity. We also performed AMSET12 calculations for NbFeSb and compared the result to our ElecTra computations. We found that for this material, the two results differ in some cases, with AMSET predicting higher power factor compared to the ElecTra results. AMSET derives a global deformation potential value for the non-polar electron–phonon scattering contributions based on the band shifts when straining the material, and thus does not make distinction between ADP and non-polar ODP scattering. However, in certain cases, for example if we exclude the non-polar optical deformation potential scattering and screening due to POP, the values obtained from AMSET and ElecTra are in very good agreement.
000 CPU hours or even more, depending on convergence, for only one type of carrier, as elaborated on in our previous works.51 Thus, effectively, we can reduce the overall computational cost by around 20 times for full bipolar transport using our approach compared to the full DFPT + Wannier method.51,52 (We would like to note that we tried substantially to simulate this material (NbFeSb) using EPW in order to compare with our results. However, achieving quantitative convergence with EPW proved very difficult due to the extremely fine Brillouin-zone sampling needed.) In ElecTra, although we extract just a limited number of matrix elements and converting them into deformation potentials, we intentionally concentrate on the critical transport areas, leading to a locally concentrated grid of matrix elements. This approach might be more beneficial than choosing matrix elements on a sparse grid throughout the entire Brillouin zone.59 More developments in this area could lead to considerable reduction in computational costs making it feasible to compute accurate deformation potentials for large number of systems and even bigger with respect to unit cell size and complexity. We also performed AMSET12 calculations for NbFeSb and compared the result to our ElecTra computations. We found that for this material, the two results differ in some cases, with AMSET predicting higher power factor compared to the ElecTra results. AMSET derives a global deformation potential value for the non-polar electron–phonon scattering contributions based on the band shifts when straining the material, and thus does not make distinction between ADP and non-polar ODP scattering. However, in certain cases, for example if we exclude the non-polar optical deformation potential scattering and screening due to POP, the values obtained from AMSET and ElecTra are in very good agreement.
4 Conclusions
In summary, we have studied with ab initio simulations the thermoelectric transport properties and the role of the different scattering processes in the high-performance thermoelectric (TE) material NbFeSb. Our computation shows that at 300 K, the POP + IIS scattering mechanisms are around twice as strong in determining σ and the PF compared to ADP + ODP for p-type carriers, while for n-type carrier POP + IIS is five times stronger compared to scattering from the non-polar ADP + ODP mechanisms, although these numbers reduce as the temperature increases. Our calculations also suggest that the intra-valley processes dominate in this material, owing to the strength of IIS, POP, ADP, ODP over IVS (see Fig. 10). Screening weakens POP and IIS for the larger DOS valence band more compared to the lower DOS conduction band, but they still remain strong to determine the PF (especially for n-type). We show that the peak PF for p-type is 11.45 mW m−1 K−2 with very good agreement with multiple experiments. We also show that the peak PF for the very less explored experimentally n-type case, is lower at 5.9 mW m−1 K−2. For n-type the PF peak is reached at densities around n = 6.27 × 1019 cm−3, which are almost an order of magnitude lower compared to where the peak of the PF in the p-type case is reached. Still, however, although the calculated PF values are somewhat close with the experimental values, we show that the electrical conductivity in experiment is three times lower compared to our calculations, while the experimental Seebeck coefficients are somewhat higher. This suggests that better crystallinity and reduced defects could allow even up to doubling the PFs in certain cases. This information offers guidance of performance optimization through selection of appropriate doping levels.Regarding our method, we have used an approach which involves the extraction of deformation potentials ab initio, to calculate scattering rates to be used in a BTE simulator. Our method uses a limited number of matrix elements near specific q-vectors related to intra/inter-valley scattering, which can be chosen on a fine mesh. Crucially, by considering each q-vector and phonon branch individually, we gain insight into the underlying fundamental physical processes, including intra- versus inter-valley transitions and the strengths of each mechanism separately. Our approach achieves ab initio accuracy, at significant computational cost reductions compared to fully ab initio DFPT + Wannier techniques by at least 20 times due to the significantly fewer matrix elements needed. Thus, we believe that our approach can be extremely useful for understanding transport properties, but can also be scalable to provide high quality training data for further machine learning related research.
5 Methods
The electronic band structure, phonon dispersion, and electron–phonon coupling matrix elements are determined using DFT and DFPT through the Quantum ESPRESSO package.61 The calculations employ optimized norm-conserving Vanderbilt (ONCV) pseudopotentials within the framework of the generalized gradient approximation (GGA) utilizing the Perdew–Burke–Ernzerhof (PBE) functional. The EPW package59 is utilized to carry out Wannier function interpolation for the electron–phonon coupling matrix elements.For transport calculations for NbFeSb (having 3 atoms per unit cell), a k-mesh of 81 × 81 × 81 was used. We use our BTE simulator ElecTra for calculating the transport properties.20 The scattering rate expressions for different scattering processes used are as follows. For ADP:
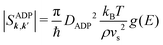 | (7) |
 | (8) |
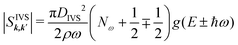 | (9) |
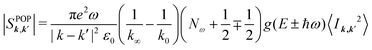 | (10) |
 is the overlap integral which is given by:
is the overlap integral which is given by:Imn(k,k + q)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = 〈um,k+q|un,k〉, = 〈um,k+q|un,k〉, | (11) |
 | (12) |
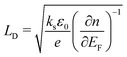 , where EF is the Fermi-level and n is the carrier density. The overall transition rate,
, where EF is the Fermi-level and n is the carrier density. The overall transition rate, , is calculated by combining the strength of all scattering mechanisms using Matthiessen's rule as:
, is calculated by combining the strength of all scattering mechanisms using Matthiessen's rule as: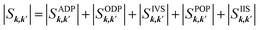 | (13) |
After calculating the scattering rates, the thermoelectric coefficients, namely the electrical conductivity, σ, and Seebeck coefficient, S are calculated as:
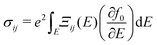 | (14) |
 | (15) |
Here, f0 is the equilibrium Fermi–Dirac distribution function, Ξij(E) is transport distribution function (TDF) defined as:
 | (16) |
 is the relaxation time (inversely proportional to the transition rates), v(E) is the bandstructure velocity, g(E) stands for the density of states at energy E, and i, j are the Cartesian coordinate indexes, for which we set i = j = x).
is the relaxation time (inversely proportional to the transition rates), v(E) is the bandstructure velocity, g(E) stands for the density of states at energy E, and i, j are the Cartesian coordinate indexes, for which we set i = j = x).
Author contributions
BS, ZL and NN conceived the project. BS performed the calculations, analyzed the results and drafted the manuscript. BS and YZ computed interband and intraband overlap integrals. NN supervised the work, analysed the results and helped in drafting the manuscript. PG helped in TE calculations using the ElecTra code. YZ, ZL, PG and RD helped in editing and finalizing the draft.Conflicts of interest
There are no conflicts to declare.Data availability
The ElecTra code (for calculating thermoelectric properties) can be found at: https://github.com/PatrizioGraziosi/ELECTRA ElecTra (v1.4) was used for calculations. The EMAF code (for computing effective masses) can be found at: https://github.com/PatrizioGraziosi/EMAF-code. Quantum espresso (v6.8) was used for DFT, DFPT and matrix elements calculations. The input files and codes for calculating deformation potentials can be found at https://github.com/Computational-Nanotechnology-Lab/Deformation-potential-extraction. Part of the data supporting this article has been included in the SI. Larger data files can be provided upon request. Supplementary information: Atom-projected electron and phonon density of states, intravalley electron–phonon matrix elements for electrons and holes in different crystallographic directions, overlap integrals calculation formalism BTE input parameters, variation of electron–phonon scattering rates with temperature and mobility of electrons and holes at different temperatures. See DOI: https://doi.org/10.1039/d5mh00228aAcknowledgements
This work has received funding from the UK Research and Innovation fund (project reference EP/X02346X/1). The calculations were performed using the Sulis Tier 2 HPC platform hosted by the Scientific Computing Research Technology Platform at the University of Warwick. Sulis is funded by EPSRC Grant EP/T022108/1 and the HPC Midlands+ consortium. The computing facilities were provided by the Scientific Computing Research Technology Platform of the University of Warwick.References
- G. Ceder, Y.-M. Chiang, D. Sadoway, M. Aydinol, Y.-I. Jang and B. Huang, Nature, 1998, 392, 694–696 CrossRef CAS.
- J. Hafner, C. Wolverton and G. Ceder, MRS Bull., 2006, 31, 659–668 CrossRef.
- G. Hautier, A. Jain and S. P. Ong, J. Mater. Sci., 2012, 47, 7317–7340 CrossRef CAS.
- A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 1–13 Search PubMed.
- G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- P. Graziosi, C. Kumarasinghe and N. Neophytou, ACS Appl. Energy Mater., 2020, 3, 5913–5926 CrossRef CAS.
- P. Graziosi, C. Kumarasinghe and N. Neophytou, J. Appl. Phys., 2019, 126, 155701 Search PubMed.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72 CrossRef CAS.
- M. V. Fischetti and S. E. Laux, J. Appl. Phys., 1996, 80, 2234–2252 Search PubMed.
- A. Hong, L. Li, R. He, J. Gong, Z. Yan, K. Wang, J.-M. Liu and Z. Ren, Sci. Rep., 2016, 6, 22778 CrossRef CAS PubMed.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222 CrossRef CAS PubMed.
- S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- T. Bazhirov, J. Noffsinger and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 184509 CrossRef.
- S. Poncé, E. R. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133 CrossRef.
- J.-J. Zhou, J. Park, I.-T. Lu, I. Maliyov, X. Tong and M. Bernardi, Comput. Phys. Commun., 2021, 264, 107970 CrossRef CAS.
- G. Samsonidze and B. Kozinsky, Adv. Energy Mater., 2018, 8, 1800246 CrossRef.
- T. Deng, G. Wu, M. B. Sullivan, Z. M. Wong, K. Hippalgaonkar, J.-S. Wang and S.-W. Yang, npj Comput. Mater., 2020, 6, 46 CrossRef CAS.
- C. Kumarasinghe and N. Neophytou, Phys. Rev. B, 2019, 99, 195202 CrossRef CAS.
- P. Graziosi, Z. Li and N. Neophytou, Comput. Phys. Commun., 2023, 287, 108670 CrossRef CAS.
- T. Zhu, C. Fu, H. Xie, Y. Liu and X. Zhao, Adv. Energy Mater., 2015, 5, 1500588 CrossRef.
- D. Zillmann, A. Waag, E. Peiner, M.-H. Feyand and A. Wolyniec, J. Electron. Mater., 2018, 47, 1546–1554 CrossRef CAS.
- R. He, D. Kraemer, J. Mao, L. Zeng, Q. Jie, Y. Lan, C. Li, J. Shuai, H. S. Kim and Y. Liu, et al. , Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13576–13581 CrossRef CAS PubMed.
- R. J. Quinn and J.-W. G. Bos, Mater. Adv., 2021, 2, 6246–6266 RSC.
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Chem. Rev., 2016, 116, 12123–12149 Search PubMed.
- M. Martin-Gonzalez, K. Lohani and N. Neophytou, Energy Mater., 2025, 5, 500121 Search PubMed.
- C. Fu, T. Zhu, Y. Pei, H. Xie, H. Wang, G. J. Snyder, Y. Liu, Y. Liu and X. Zhao, Adv. Energy Mater., 2014, 4, 1400600 CrossRef.
- J. Yu, C. Fu, Y. Liu, K. Xia, U. Aydemir, T. C. Chasapis, G. J. Snyder, X. Zhao and T. Zhu, Adv. Energy Mater., 2018, 8, 1701313 CrossRef.
- C. Fu, H. Wu, Y. Liu, J. He, X. Zhao and T. Zhu, Adv. Sci., 2016, 3, 1600035 Search PubMed.
- W. Ren, H. Zhu, Q. Zhu, U. Saparamadu, R. He, Z. Liu, J. Mao, C. Wang, K. Nielsch and Z. Wang, et al. , Adv. Sci., 2018, 5, 1800278 Search PubMed.
- G. Joshi, R. He, M. Engber, G. Samsonidze, T. Pantha, E. Dahal, K. Dahal, J. Yang, Y. Lan and B. Kozinsky, et al. , Energy Environ. Sci., 2014, 7, 4070–4076 RSC.
- C. Fu, T. Zhu, Y. Liu, H. Xie and X. Zhao, Energy Environ. Sci., 2015, 8, 216–220 RSC.
- J. N. Kahiu, U. S. Shenoy, S. K. Kihoi, H. Kim, S. Yi, D. K. Bhat and H. S. Lee, J. Alloys Compd., 2022, 891, 162033 CrossRef CAS.
- C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Nat. Commun., 2015, 6, 8144 CrossRef PubMed.
- J. Li, J. Zhu, Z. Ti, W. Zhai, L. Wei, C. Zhang, P.-F. Liu and Y. Zhang, J. Mater. Chem. A, 2022, 10, 24598–24610 RSC.
- J. Shen, L. Fan, C. Hu, T. Zhu, J. Xin, T. Fu, D. Zhao and X. Zhao, Mater. Today Phys., 2019, 8, 62–70 Search PubMed.
- D. Hobbis, R. P. Hermann, H. Wang, D. S. Parker, T. Pandey, J. Martin, K. Page and G. S. Nolas, Inorg. Chem., 2019, 58, 1826–1833 CrossRef CAS PubMed.
- J. Zhou, H. Zhu, T.-H. Liu, Q. Song, R. He, J. Mao, Z. Liu, W. Ren, B. Liao and D. J. Singh, et al. , Nat. Commun., 2018, 9, 1721 CrossRef PubMed.
- T. Fang, S. Zheng, H. Chen, H. Cheng, L. Wang and P. Zhang, RSC Adv., 2016, 6, 10507–10512 Search PubMed.
- P. Graziosi and N. Neophytou, arXiv, preprint, 2019, arXiv:1912.10924 DOI:10.48550/arXiv.1912.10924.
- N. Neophytou and H. Kosina, Nano Lett., 2010, 10, 4913–4919 Search PubMed.
- https://github.com/PatrizioGraziosi/EMAF-code .
- S. Y. Savrasov, D. Y. Savrasov and O. Andersen, Phys. Rev. Lett., 1994, 72, 372 CrossRef CAS PubMed.
- A. Y. Liu and A. A. Quong, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, R7575 CrossRef CAS PubMed.
- F. S. Khan and P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 3341–3349 CrossRef.
- M. Lundstrom, Meas. Sci. Technol., 2002, 13, 230 CrossRef.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Oxford University Press, 1996 Search PubMed.
- H. Fröhlich, Adv. Phys., 1954, 3, 325–361 CrossRef.
- J. Park, J.-J. Zhou, V. A. Jhalani, C. E. Dreyer and M. Bernardi, Phys. Rev. B, 2020, 102, 125203 CrossRef CAS.
- C. Verdi and F. Giustino, Phys. Rev. Lett., 2015, 115, 176401 CrossRef PubMed.
- Z. Li, P. Graziosi and N. Neophytou, npj Comput. Mater., 2024, 10, 8 CrossRef CAS.
- Z. Li, P. Graziosi and N. Neophytou, Phys. Rev. B, 2021, 104, 195201 CrossRef CAS.
- P. Graziosi and N. Neophytou, J. Phys. Chem. C, 2020, 124, 18462–18473 CrossRef CAS.
- B. Sahni, Vikram, J. Kangsabanik and A. Alam, J. Phys. Chem. Lett., 2020, 11, 6364–6372 CrossRef CAS PubMed.
- Vikram, B. Sahni, C. Barman and A. Alam, J. Phys. Chem. C, 2019, 123, 7074–7080 CrossRef CAS.
- P. Graziosi, Z. Li and N. Neophytou, Appl. Phys. Lett., 2022, 120, 072102 CrossRef CAS.
- S. E. A. Akhtar and N. Neophytou, ACS Appl. Energy Mater., 2025, 8, 1609–1619 CrossRef CAS PubMed.
- J. Park, M. Dylla, Y. Xia, M. Wood, G. J. Snyder and A. Jain, Nat. Commun., 2021, 12, 3425 CrossRef CAS PubMed.
- H. Lee, S. Poncé, K. Bushick, S. Hajinazar, J. Lafuente-Bartolome, J. Leveillee, C. Lian, J.-M. Lihm, F. Macheda and H. Mori, et al. , npj Comput. Mater., 2023, 9, 156 CrossRef CAS.
- S. Poncé, E. R. Margine and F. Giustino, Phys. Rev. B, 2018, 97, 121201 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2025 |