Boosting the energy storage performance of BCZT-based capacitors by constructing a Schottky contact

Abstract

Multilayer thin films composed of dielectric Ba_0.7Ca_0.3Zr_0.2Ti_0.8O₃ (BCZT) and oxygen-deficient BCZT (BCZT-OD) were fabricated on (001)-oriented NSTO substrates using the pulsed laser deposition (PLD) technique. Unlike conventional approaches to energy storage capacitors, which primarily focus on compositional or structural modifications, this study explored the influence of the layer sequence and periodicity. The interface between the NSTO substrate and the BCZT-OD layer forms a Schottky barrier, resulting in electric field redistribution across the sublayers of the BCZT/BCZT-OD//(1P) thin film. This redistribution delays the breakdown of the BCZT layer, significantly enhancing the film's electric breakdown strength. Furthermore, mathematical analysis reveals that the electric field redistribution amplifies dipole polarization, with BCZT-OD-initiated multilayers exhibiting superior polarization compared to those with equivalent periodicity but different starting layers. Consequently, the BCZT/BCZT-OD//(1P) multilayer achieves an exceptional recoverable energy density (W_rec) of 150.22 J cm⁻³ and an energy efficiency (η) of 83.07%, surpassing typical performance benchmarks for BCZT-based thin films. These findings are corroborated by comprehensive structural characterization studies, performance evaluations, and finite element simulations, which further validate the role of the Schottky barrier in enhancing voltage endurance. Analogous to “Tian Ji's Strategy for Horse Racing”, this work achieved high W_rec by sacrificing the ferroelectricity of the negative side of the P–E loop, introducing an innovative paradigm for designing and developing next-generation electronic devices.

---

New concepts

Inspired by the Chinese traditional philosophy story “Tian Ji's Strategy for Horse Racing”, which teaches us to sacrifice the secondary factors for the ultimate success, this study proposed a novel layer-sequence design strategy for enhancing energy storage performance in dielectric capacitors, which is different from the commonly used domain engineering and interface engineering. Multilayer thin films of Ba_0.7Ca_0.3Zr_0.2Ti_0.8O₃ (BCZT) and oxygen-deficient BCZT (BCZT-OD) are fabricated via the pulsed laser deposition technique. By constructing the Schottky barrier in the interface between the BCZT-OD layer and the NSTO substrate, the voltage endurance of the BCZT/BCZT-OD//(1P) thin film was enhanced by optimizing the voltage distribution, and simultaneously, P_max was also increased by enhancing the dipole polarization. Ultimately, a W_rec of 150.22 J cm⁻³ with an η of 83.07% was achieved in the BCZT/BCZT-OD//(1P) thin film, providing a new idea for designing high-performance capacitors.

1. Introduction

The ancient Chinese philosophical story, “Tian Ji's Strategy for Horse Racing,” has deeply influenced Chinese culture and resonates with people worldwide. Its lessons continue to inspire modern research across various fields. The story is set during the Spring Autumn and Warring States periods in China, where King Wei of Qi frequently competed in horse races against General Tian Ji. Each race comprised three rounds, with horses classified into fast, medium, and slow categories, as shown in Fig. 1(a1). King Wei's horses would race against Tian Ji's corresponding horses, and due to a disparity in quality, Tian Ji consistently lost. One day, Tian Ji's friend, the strategist Sun Bin, proposed a clever solution. Sun suggested Tian Ji to alter his racing strategy, as illustrated in Fig. 1(a2). Rather than matching horses by speed, Tian Ji should race his slow horse against the king's fastest in the first round, then race his fast and medium horses against the king's medium and slow horses in the subsequent rounds. While Tian Ji would sacrifice the first race, he would likely win the remaining two, securing an overall victory. The lesson of “Tian Ji's Strategy for Horse Racing” illustrates that sacrificing secondary factors can lead to ultimate success—a principle applicable far beyond horse racing. In fact, this strategy finds relevance in modern research, such as in the quest to achieve higher energy storage density in dielectric capacitors. By prioritizing strategic trade-offs, as Tian Ji did, researchers can unlock innovative solutions to complex challenges.

Fig. 1 The sketch to show (a1) the 1st round; (2) the 2nd round of the horse racing of Tian Ji's strategy; (b) the sketch to show W_rec in different kinds of P–E loops. The story of “Tian Ji's Strategy for Horse Racing” tells us the principle of reaching the final match by sacrificing unimportant factors, which is thought to be the slow horse in the story, as circled with a green dashed line, and the unimportant factor in a P–E loop is the negative side, also marked with a green dashed line.

Compared to Li-ion batteries, widely used in electric vehicles but suffer from drawbacks such as long charging times, dielectric capacitors offer significant advantages, particularly in their fast charge–discharge capabilities. As a result, they have garnered increasing attention in recent years.^1–5 Among various material forms, epitaxial thin films exhibit superior energy storage capabilities compared to ceramic bulks and ceramic–polymer composite films. This is due to their higher electric breakdown strength (E_b) and greater maximum polarization (P_max), which arise from size effects and anisotropy, respectively.^6–8 Moreover, specific regulation techniques, such as stress engineering and superlattice engineering, are more effective and, in some cases, exclusively applicable to epitaxial thin films.^9,10 For instance, in 2017, the author demonstrated that fabricating BCT/BZT superlattices significantly enhances the energy storage density (W_rec) of thin films. This improvement was attributed to enhanced voltage endurance, which resulted from the blocking effect of accumulated charge at the interface, preventing current spread. Additionally, the critical thickness of the films was determined in the following study.^11,12 In 2022, Minh D. N. and colleagues conducted a more in-depth investigation into the effects of interfacial strain on the energy storage performance of layered films. Their model revealed that inter-diffusion between PZ and PLZT layers not only inhibits the formation of electrical conduction paths but also increases maximum polarization (P_max) while reducing total hysteresis. These effects were attributed to polarization coupling between adjacent PZ and PLZT layers.¹³ As a result, an impressive W_rec of up to 128.4 J cm⁻³ was achieved in the PZ/PLZT multilayer. In addition to structural design, elemental doping is also an effective strategy for enhancing the energy storage performance. For instance, stabilized by interphase strain, super-T polar clusters with a tetragonality of approximately 1.25 were found to be dispersed along the entire c-axis of BNBT thin films. This led to a remarkably high W_rec of over 86 J cm⁻³ at a relatively low electric field of 1.7 MV cm⁻¹, providing valuable insights for the development of low-energy-consumption capacitors.¹⁴ Notably, this approach is also applicable to ceramic bulks.¹⁵

Whether through structural design or elemental doping, the studies mentioned above primarily focus on the films themselves. However, electrodes or substrates can significantly influence the behavior of thin films, though their impact is often overlooked in the energy storage field. Shifting attention to semiconductors, certain phenomena at the film/electrode or film/substrate interfaces could provide valuable insights. Since this work focuses on (relaxor) ferroelectric thin films, the following examples will be confined to ferroelectric semiconductors. BaTiO₃ (BTO) is a typical ferroelectric material, but when sufficient oxygen vacancies are introduced into its lattice, the films exhibit n-type semiconductor behavior, with two distinct resistance states under positive and negative bias. This effect is believed to result from the coupling between carrier trapping (primarily electrons) and ferroelectric polarization.^16–18 Similar behavior was observed in the author's previous research, where controlling the 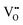concentration by adjusting the annealing time resulted in a resistive switching (RS) ratio of 1916, meaning that compared to the negative side, the positive side of the BTO thin film shows quite higher resistivity. This effect was attributed to the ferroelectric domain-modulated built-in potential between the BTO and LSMO in the heterostructure.¹⁹ As expressed in the ESI,† the W_rec of a dielectric capacitor is highly dependent on its E_b, and voltage endurance also influences its conductive behavior. Considering this, the E_b of thin films can be modulated by creating a built-in potential at the interface between the film and the electrodes or substrates. However, when the current on one side is reduced, resulting in an enhanced E_b, the opposite side inevitably experiences reduced voltage endurance. In the story of Tian Ji's Strategy for Horse Racing, success was achieved not by attempting to win every individual race, but by strategically sacrificing one match to secure victory in the overall competition. Similarly, for dielectric materials, the calculation of W_rec typically focuses on the positive-side P–E loops. Inspired by this strategy, our approach leverages the trade-off between the positive and negative voltage endurance in dielectric thin films. By deliberately sacrificing the negative side's voltage endurance, we optimize and enhance W_rec on the positive side, achieving overall superior performance. This concept is illustrated in Fig. 1(b), where the green dashed lines in Fig. 1(a1) and (b) highlight the factors that can be deliberately traded off to maximize the desired outcome. Just as Tian Ji strategically deployed his slow horse to turn the tide in his favor, we utilize this sacrifice as a calculated move to elevate the energy storage performance of dielectric thin films.

In this work, periodic-structured thin films composed of regular dielectric Ba_0.7Ca_0.3Zr_0.2Ti_0.8O₃ (BCZT) and oxygen-deficient BCZT (BCZT-OD) were grown on (001)-oriented NSTO substrates using the pulsed laser deposition (PLD) technique. By simultaneously adjusting the periodicity and deposition sequence, a Schottky barrier was formed, which helped the BCZT/BCZT-OD//(1P) thin film achieve an ultra-high W_rec by optimizing the electric field distribution.

2. Experimental section

Details of this part are provided in the ESI.†

3. Results and discussion

3.1 Phase and structure characterization

As shown in Fig. 2(a), the films were designed to be deposited with varying periodicities and sequences. For all multilayers, the total thickness of the BCZT and BCZT-OD layers was 450 nm and 150 nm, respectively, resulting in an overall film thickness of approximately 600 nm. Additionally, pristine BCZT and BCZT-OD single layers of the same thickness were grown as a control group. Fig. S1 (ESI†) presents the X-ray diffraction (XRD) 2Theta-ω-scans from 15° to 75° for all films, with only (00l) planes observed, confirming their (001)-oriented cubic-on-cubic growth. The enlarged view from 42° to 48°, shown in Fig. 2(b), indicates that the (002) peaks for BCZT, BCZT-OD/BCZT//(1P), and BCZT-OD/BCZT//(2P) are symmetric, while those of the other three films are not. Furthermore, from the bottom to the top of the figure, the peaks shift toward lower angles before returning to higher angles. To gain further insights into the phase characteristics, we applied the Gaussian–Lorentz cross function, as detailed in the ESI,† to fit the (002) peaks of BCZT-OD and BCZT/BCZT-OD(1P) using Origin 9.0. The fitting results are presented in Fig. 2(c). Notably, the BCZT-OD film consists of two distinct layers, represented by a main peak and a strained peak. The strained peak, which appears at a lower angle, results from strain induced by the substrate, as previously reported by the authors.¹⁹ A similar phenomenon is observed in the BCZT/BCZT-OD//(1P) film, though the strained peak is significantly less pronounced. To further examine the interaction between the main layer, strained layer, and the NSTO substrate, reciprocal space mappings (RSMs) around the (204) plane of BCZT-OD and BCZT/BCZT-OD//(1P) are measured and shown in Fig. 2(d1) and (d2), respectively. As anticipated, both films exhibit mappings that can be divided into two distinct regions, which correspond to orthorhombic (O) and tetragonal (T) phases based on their lattice parameters. The RSMs of the (204) planes for all films, along with their corresponding (002) plane mappings, are provided in Fig. S2 (ESI†). The lattice parameters of all the films, calculated from those mappings, are summarized in Fig. 2(e). Interestingly, (1) films with a periodicity of 1 exhibit a larger in-plane lattice parameter (a) and a smaller out-of-plane lattice parameter (c) than their counterparts with a periodicity of 2; (2) films that start with the BCZT layer have larger tetragonality (that is the c/a ratio) than those that start with BCZT-OD layers. Considering that the NSTO substrate shows smaller a with larger c when compared to the films and offers compressive stress to them, the 1st observation can be attributed to the fact that thinner sublayers experience greater interfacial stress from the substrates than the thicker sublayers, and strain is more easily transferred in films with more periodicities, as previously reported by the authors.^12,20 The 2nd observation is more difficult to explain at this stage; therefore, cross-sectional scanning transmission electron microscopy (STEM) images of BCZT-OD/BCZT//(1P) and BCZT/BCZT-OD//(1P) were obtained, as shown in Fig. 2(f1) and (f2). As seen in the images, the thickness of all sublayers matches our predictions. Unexpectedly, the BCZT layer appears highly dense, while the BCZT-OD layers exhibit a columnar structure. This columnar morphology is consistent with literature reports, which is attributed to reduced atomic collisions during transport towards the substrate surface.²¹ This finding provides insight into the 2nd observation mentioned above: the compressive stress from the NSTO substrates relaxes more easily in the columnar BCZT-OD layer than in the denser BCZT layer. As a result, the BCZT layer in the BCZT/BCZT-OD(1P) and BCZT/BCZT-OD//(2P) films experiences significantly less compressive stress, leading to a larger a and a smaller c compared to the BCZT layer in the BCZT-OD/BCZT//(1P) and BCZT-OD/BCZT//(2P) thin films. As a result, based on the average lattice parameter, Fig. 2(e) is divided into three distinct regions corresponding to the O-phase, T-phase, and O-phase. Based on this trend, it can be predicted that, compared to the other films, the BCZT-OD/BCZT//(1P) and BCZT-OD/BCZT//(2P) thin films should exhibit higher spontaneous polarization (P_s). The ball-and-stick model of the red dashed region in Fig. 2(f2) is presented in Fig. 2(f3).

Fig. 2 (a) The sketch of the thin films in this work, and all the films have the same thickness; (b) the 2Theta-ω-scans of all the films from 42° to 48°; (c) the fitting result of the 2Theta-ω-scans of all the films around the (002) plane; the RSMs of the (d1) BCZT-OD//(1P); (d2) BCZT/BCZT-OD//(1P) around the (204) plane; (e) the lattice parameter of all the films in this work; the cross-sectional STEM images of the (f1) BCZT-OD/BCZT//(1P); (f2) BCZT/BCZT-OD//(1P); (f3) the ball-and-stick model of the red dashed area in (f2).

Fig. S3(a) (ESI†) provides an enlarged view of the red dashed area in Fig. 2(f2). As shown, there is no distinct interface between the BCZT-OD layer and the BCZT layer, suggesting that BCZT nucleates easily on columnar-structured BCZT-OD at high oxygen pressure. To gain further insights, the red dashed area in Fig. S3(a) (ESI†) was again zoomed in and is displayed in Fig. S3(b) (ESI†), where a neat atomic arrangement and coherent growth of BCZT on BCZT-OD can be seen. Fig. S3(c) (ESI†) presents an atomic-scale image of the dashed area in Fig. S3(b) (ESI†). By examining the displacement of B-site atoms (weaker contrast for Ti and Zr) relative to the center of the surrounding four A-site atoms (stronger contrast for Ba and Ca), the P_s orientation in the BCZT-xBZT ceramics’ lattice can be confirmed.^22,23 More importantly, the coexistence of two phases (T-phase and O-phase) is directly observed, which agrees well with the results from the RSMs. The T-phase tends to exist in the lower regions, which experience greater compressive stress, while the stress relaxation toward the top allows more O-phase to form in the upper regions.

3.2 Energy storage performance

The Weibull method, as detailed in ESI,† was used to calculate the E_b for all six thin films, as shown in Fig. 3(a1). The relationship between E_b and the film structure is plotted in Fig. 3(a2), revealing three key observations: (1) the BCZT single layer exhibits significantly better voltage endurance than the BCZT-OD single layer; (2) the E_b values of BCZT/BCZT-OD//(1P) and BCZT/BCZT-OD//(2P) are higher than those of BCZT-OD/BCZT//(1P) and BCZT-OD/BCZT//(2P), indicating that films with a BCZT-OD starting layer have a higher E_b compared to their counterparts that start with BCZT; (3) for films with the same composition, higher periodicity does not always correspond to a higher E_b, which contrasts with the previous conclusion.^11–13 The 1st observation will be revealed in Section 3.3 and the explanation of the following two can be found in Section 3.4. Before that, the energy storage performance of these thin films should be known, so their polarization–electric field (P–E) loops at their respective E_b values are shown in Fig. 3(b). Unlike typical studies that focus on simply adjusting the composition or periodicity, the variation in the loop shape observed here appears irregular. A more detailed explanation of this behavior is provided in the following section. All unipolar P–E loops at different applied electric fields are presented in Fig. S4 (ESI†). By integrating these loops, the relationships between energy storage performance, including W_rec and energy storage efficiency (η), and the applied electric field are plotted in Fig. 3(c). The highest W_rec of 150.22 J cm⁻³, with an η of 83.07%, is achieved in the BCZT/BCZT-OD(1P) film. As expressed in eqn (S1)–(S3) (ESI†), the W_rec of a dielectric capacitor is strongly influenced by the difference between the P_max and remanent polarization (P_r), and the E_b. When compared to previous works of BCZT-based capacitors on various material systems—including thin films, ceramic bulk, and polymers—the BCZT/BCZT-OD(1P) film in this study demonstrates a significant advantage in achieving high W_rec, as illustrated in Fig. 3(d).^{11,20,24–51} Additionally, since polymer-based materials inherently exhibit excellent voltage endurance, and the E_b of the BCZT/BCZT-OD//(1P) film surpasses that of most polymer materials, its impressive energy storage performance is attributed more to its voltage endurance than to its polarization. However, some BCZT-based thin films exhibit even higher E_b values but display inferior W_rec, indicating that the BCZT/BCZT-OD(1P) thin film likely also exhibits favorable polarization properties. Overall, the excellent energy storage performance of the BCZT/BCZT-OD//(1P) thin film in this work should be attributed to both the high E_b and P_max, a combination that has traditionally been considered a paradox in energy storage dielectrics,^52–54 which gives more research significance to this work. Therefore, the polarization and E_b of the thin films in this work will be discussed separately.

Fig. 3 The result of the Weibull distribution of (a1) all the films; (a2) pristine BCZT and BCZT-OD thin films; (b) the P–E loops of all the films near their E_b; (c) the variation between W_rec, η, and applied field; (d) the comparison between the BCZT/BCZT-OD//(1P) film in this work and previous works of BCZT-based capacitors on various material systems—including thin films, ceramic bulk, and polymers; (e) the PFM amplitude image of BCZT/BCZT-OD//(1P) below 200 V, and the corresponding phase and amplitude loops are inserted in it; (f) the variation between the P_max at different electric fields, ΔP_max and the thin film's structure; (g) the J–E curve to show its three different components; (h1) the ABF-STEM image of the (h1) BCZT layer; (h2) BCZT-OD layer in the BCZT/BCZT-OD//(1P) thin film; (i1) and (i2) the intensity profiles of the white dotted regions in (h1) and (h2), respectively.

Before that, the piezoresponse force microscopy (PFM), with its testing principle illustrated in Fig. S5 (ESI†), needed to be performed on the BCZT/BCZT-OD//(1P) film to further confirm its ferroelectricity. The amplitude image, along with the amplitude–voltage and phase–voltage loops, is shown in Fig. 3(e) following the application of −200 V bias over a 2 × 2 μm² area and +200 V bias over a 1 × 1 μm² area. The boundary between the different switching regions in the amplitude image, typically attributed to the canceling effect of opposite domain walls, is sharp and well-defined. Combined with the observed hysteretic loops, as illustrated in the bottom left corner, these features confirm the film's characteristic ferroelectricity.^55,56

3.3 Polarization

To assess the effect of polarization on the energy storage performance of the thin films, the unipolar P–E loops of all films at both low (1.0 MV cm⁻¹) and high fields (3.0 MV cm⁻¹) are compared, as shown in Fig. S6(a1) and (a2) (ESI†). The P_max at both fields, along with the polarization difference (ΔP), is defined as:

ΔP = P_max-3.0 − P_max-1.0 (1)

as summarized in Fig. 3(f). The red and blue dashed lines represent the average P_max based on the value and proportion of pristine BCZT and BCZT-OD layers at both fields, respectively. These values were calculated using the following equation:where P_max-ave is the average P_max of BCZT and BCZT-OD single layers, P_max-BCZT and P_max-BCZT-OD are the P_max values of BCZT and BCZT-OD, and d_-BCZT and d_-BCZT-OD are their respective thicknesses. From this figure, three key conclusions can be drawn: (1) the P_max of all multilayer films is higher than the calculated P_max-ave at both fields; (2) at 1.0 MV cm⁻¹, multilayers starting with the BCZT layer exhibit a higher P_max than those starting with BCZT-OD, whereas, at 3.0 MV cm⁻¹, this trend is reversed; and (3) the highest ΔP value, 41.19 μC cm⁻³, is observed in BCZT/BCZT-OD//(2P), followed by BCZT/BCZT-OD//(1P) with a ΔP of 28.96 μC cm⁻³. The 1st conclusion suggests that multilayers containing both BCZT and BCZT-OD exhibit a higher P_max than the linear sum of their individual layers. As reported in previous studies, this additional polarization is related to charge accumulation and lattice distortion at the interfaces between adjacent sublayers.^13,57 Regarding the 2nd point, the higher P_max observed in BCZT-OD/BCZT//(1P) and BCZT-OD/BCZT//(2P) at lower fields is attributed to their higher P_s, as discussed in Section 3.1. However, the reason behind the higher P_max in BCZT/BCZT-OD//(1P) and BCZT/BCZT-OD//(2P) at higher fields is unclear at this stage. To investigate this, we measured the J–E curves, which display the relationship between switching polarization current and electric field and provide additional information beyond the P–E loops, as shown in Fig. S7 (ESI†). According to previous studies, the J–E curve can be divided into three regions, corresponding to dielectric displacement, electrical conductivity, and domain switching, as illustrated in Fig. 3(g).⁵⁸ Upon comparison, it is evident that electrical conductivity plays a significant role in the current density of BCZT/BCZT-OD(2P), particularly at higher electric fields. Therefore, their higher P_max is likely driven by dipole polarization. To gain a deeper understanding of the underlying mechanisms behind dipole polarization and the microstructural differences between the BCZT and BCZT-OD layers, angular bright-field STEM (ABF-STEM) images of these two regions of BCZT-OD/BCZT(1P) were captured and are shown in Fig. 3(h1) and (h2), respectively. In the BCZT layer, the oxygen atoms, which appear with lower contrast compared to the metal atoms, are arranged in an orderly fashion. In contrast, the BCZT-OD layer exhibits a notable presence of , leading to some degree of lattice distortion. The intensity profiles of the white dotted regions in Fig. 3(h1) and (h2) are presented in Fig. 3(i1) and (i2). In Fig. 3(i1), distinct deep and shallow valleys, corresponding to Ti and O atoms, are clearly visible. In Fig. 3(i2), the deep valleys representing Ti atoms remain identifiable, but some shallow valleys are missing, confirming the existence of .^59,60 To understand the cations that neutralize V_O, a multiple test that includes X-ray photoelectron spectroscopy (XPS) and electron paramagnetic resonance (EPR) measurement was employed. Fig. 4(a1) and (a2) show the XPS for O of BCZT/BCZT-OD//(1P) and BCZT-OD/BCZT//(1P), respectively, and because the photoelectron hit the surface of the films and the detection depth is around 5 nm, they reflect the information of the BCZT layer in BCZT/BCZT-OD//(1P) and the BCZT-OD layer in BCZT-OD/BCZT//(1P), respectively. As expected, two peaks, which are caused by the lattice-O and lattice-O near V_O, are observed at around 529 eV and 532 eV, respectively, in both films, and the peak for lattice-O near V_O in the BCZT-OD layer in BCZT-OD/BCZT//(1P) is much higher. Due to the test philosophy, the EPR can not only be carried out on the specific part of the films but the measurement is performed on pristine BCZT and BCZT-OD thin films, and the spectrum is shown in Fig. 4(b). The g factor of the result was calculated according to the following equation:where h, μ_B, ν, and B are the Planck constant, Bohr magneton, applied microwave frequency, and the resonance magnetic field, respectively.⁶¹ The peak for g = 2.001 appears in both BCZT and BCZT-OD, and of course, that of the latter is much higher than the former. The peaks for g = 1.980 and 1.968 are caused by Ti³⁺ and Zr³⁺, respectively, which have been reported previously.^62,63 The EPR result not only verifies the above-mentioned deduction, but also definitizes the formation of the defect dipoles of and , which can be expressed below:

Fig. 4 The XPS for O of the (a1) BCZT/BCZT-OD//(1P); (a2) BCZT-OD/BCZT//(1P); (b) the EPR of the BCZT/BCZT-OD//(1P) and BCZT-OD/BCZT//(1P) from 310 mT to 350 mT; (c) the ε–f curves of all the thin films; (d) the mapping that illustrates the relationship among T, f, and ε; (e1)–(e3) the relationship between the logarithm of current and the applied electric field of all the thin films; (f1) and (f2) the fitting result of (e4) and (e5) according to the Schottky emission mode; (g) the band diagram, which can be defined as the MSD structure, of the BCZT/BCZT-OD//(1P) under forward bias; (h1)–(h4) the result of the simulation on the current spread of the four multilayers.

Although the form of the defect dipole has been confirmed, the underlying reason for its differing effects on the polarization of thin films with varying layer sequences remains unclear. For instance, while BCZT/BCZT-OD//(1P) and BCZT-OD/BCZT//(1P) contain the same quantity of defect dipoles—given that the thickness of the BCZT-OD layer is identical—their corresponding “ΔP” values differ significantly. Based on the mathematical derivation provided in the ESI,† when all other factors are constant, dipole polarization (P_dn) shows a positive correlation with the applied electric field. Since the total voltage applied to both BCZT/BCZT-OD//(1P) and BCZT-OD/BCZT//(1P) is equal, the differing partial voltages across layers could explain this discrepancy. This aspect will be explored in detail in the following section. Additionally, the first observation in Section 3.2 can now be rationalized: the lower E_b of the pristine BCZT-OD layer compared to the pristine BCZT layer is attributed to the higher concentration of in the former.

To investigate the influence of defect dipoles, the frequency dependence of the dielectric constant (ε–f curve) at room temperature for all films is presented in Fig. 4(c). For all samples, ε exhibits a monotonous decrease with an increase in frequency, indicative of typical ferroelectric behavior.⁶⁴ Notably, each film displays a region where ε decreases sharply, suggesting the diminishing contribution of dipole polarization to ε. Among the samples, BCZT-OD, which contains a significant quantity of defect dipoles, demonstrates the highest ε at frequencies below 10⁴ Hz. Fig. S8 (ESI†) illustrates the ε–f curves for all thin films across a temperature range of 25 °C to 200 °C, where a characteristic frequency dispersion is observed. By extracting ε at various temperatures, the temperature dependence of ε (ε–T curve) at different frequencies can be plotted, as shown in each figure. It is observed that the temperature corresponding to the maximum ε (T_m) is relatively insensitive to the film structures, varying between approximately 100 °C and 130 °C. This T_m value is notably higher than that of bulk ceramics with the same composition, a phenomenon previously attributed by the authors to the clamping effect exerted by the substrates.^39,65 Furthermore, due to its lower concentration of defect dipoles, BCZT exhibits a comparatively narrower relaxer peak than the other samples. The shift in T_m and the broadening of the phase transition peak are anticipated to enhance the thermal stability of energy storage in the films, a topic that will be discussed in detail in the following section. To visually represent the dielectric behavior of BCZT/BCZT-OD//(1P), a mapping illustrating the relationship among T, f, and ε is presented in Fig. 4(d). The color coding indicates that dispersion occurs around 8 × 10³ Hz. As indicated by the arrow, T_m increases with an increase in f.

3.4 Electric breakdown behavior

In addition to polarization, the electric breakdown behavior of a dielectric significantly also influences its energy storage performance. As mentioned earlier, this study diverges from typical investigations focused on compositions and structural adjustments. The results shown in Fig. 3(a) reveal irregular changes in E_b. Furthermore, the unipolar P–E loops do not provide sufficient insights, prompting the measurement of the bipolar loops for all films, and such loops measured at 3.0 MV cm⁻¹ are illustrated in Fig. S9(a1)–(a6) (ESI†). Symmetric loops are observed for BCZT, BCZT-OD/BCZT//(1P), BCZT-OD/BCZT//(2P), and BCZT/BCZT-OD//(2P), although the last loop appears somewhat “fat”. What puzzles the authors is the evident asymmetry in the loops of BCZT/BCZT-OD//(1P) and BCZT-OD//, where the positive side displays typical hysteresis, as highlighted in the enlarged view of the dashed rectangle area in Fig. S9(a5) and (a6) (ESI†), while the negative side exhibits significant leakage. To investigate this further, the corresponding J–E curves were measured and are presented in Fig. S9(b1)–(b6) (ESI†). As observed in Fig. S9(b5) and (b6) (ESI†), the current density on the negative side of the loops is significantly high, particularly for BCZT-OD. According to their research experience, the authors note that the shape of this curve resembles the I–V characteristics of semiconductors, although the loop remains observable on the positive side, as highlighted in the enlarged view of the dashed rectangle area in Fig. S9(b6) (ESI†). In light of these observations, we measured the I–V characteristics of all the films at 3.0 MV cm⁻¹, as shown in Fig. S9(c1)–(c6) (ESI†). As anticipated, the I–V characteristics of BCZT-OD closely resemble the shape of its J–E curve; meanwhile, the I–V characteristics of BCZT/BCZT-OD//(1P) also exhibit a similar form. To elucidate the conduction mechanisms of the films, the relationship between the logarithm of current and the applied electric field is illustrated in Fig. 4(e1)–(e6). For BCZT-OD and BCZT/BCZT-OD//(1P), the relationship is expected to be asymmetric, whereas the others demonstrate symmetry. We subsequently fitted these results based on the physical descriptions of various conducting mechanisms, including Ohmic conduction (which encompasses the space charge limited current (SCLC) mode), the Schottky emission mode, the Poole–Frenkel (P–F) mode, and the Fowler–Nordheim (F–N) tunneling mode. Our analysis revealed that the positive sides of Fig. 4(e4) and (e5) both align with the Schottky emission mode, which can be expressed as follows:⁶⁶Here, A*, k, q, ε₀, and ε_r represent the effective Richardson constant, Boltzmann's constant, electronic charge, vacuum dielectric constant, and relative dielectric constant, respectively, all of which are held constant. The variables J, Φ_s, E, and T denote the current density, Schottky barrier potential, electric field across the material, and absolute temperature, respectively. (Since no reasonable results were obtained when fitting according to the other mechanisms, their corresponding physical expressions will not be discussed here.). The fitting result of Fig. 4(e4) and (e5) is plotted in Fig. 4(f1) and (f2), with slope values of 2.1 and 5.8, respectively. For all the multilayers in this work, the BCZT/BCZT-OD//(1P) shows the highest E_b, which is considered to be one of the key factors in achieving its outstanding W_rec the authors would like to use the band theory to dig out further information.

Based on the results obtained above, it appears that BCZT and BCZT-OD exhibit characteristics of a typical dielectric and semiconductor, respectively. To confirm this, we measured the electric field dependence of the dielectric constant (ε–V curve, also known as the C–V curve), as shown in Fig. S10(a) (ESI†). As expected, BCZT displays a characteristic butterfly-shaped C–V curve typical of dielectrics, featuring two broadened peaks. In contrast, the C–V curve for BCZT-OD is asymmetric, showing a single sharp peak and a near-zero ε value on the negative side, consistent with typical semiconductor behavior.^67,68 Consequently, the band diagram of the BCZT/BCZT-OD//(1P) under forward bias, identified as a metal–semiconductor–dielectric (MSD) structure, is illustrated in Fig. 4(g). As discussed in the ESI,† the NSTO/BCZT-OD interface in this MSD structure can be interpreted as a metal–semiconductor contact. Due to the formation of a depletion layer (R_d), the resistivity (ρ) of the BCZT-OD layer in BCZT/BCZT-OD//(1P) is expected to increase, making it higher than that in BCZT-OD/BCZT//(1P). As shown in the equations below:

σ = ωε₀ε tan δ (7)

where ε₀ is the vacuum permittivity, with a constant value of 8.9 × 10⁻¹² F m⁻¹, and σ and ρ represent the conductivity and resistivity, respectively.^68,69 The ε of a dielectric is inversely proportional to its ρ. Consequently, the ε of the BCZT-OD layer in BCZT/BCZT-OD(1P) should be lower than that in BCZT-OD/BCZT(1P). As illustrated in Fig. S10(c) (ESI†), both BCZT/BCZT-OD(1P) and BCZT-OD/BCZT(1P) structures can be modeled as double-layer dielectrics, following the equation:where U_BCZT and U_BCZT-OD are voltages, E_BCZT and E_BCZT-OD are the electric fields, and ε_BCZT and ε_BCZT-OD are the ε of the BCZT and BCZT-OD layers in both BCZT/BCZT-OD//(1P) and BCZT-OD/BCZT//(1P), respectively. Based on the C–V curves, the ε values of the pristine BCZT and BCZT-OD layers are approximately 148.6 and 53.5, respectively. This results in an ε ratio of ε_-BCZT/ε_-BCZT-OD = 1/2.78 and an electric field ratio of E_BCZT/E_BCZT-OD = 2.78/1 at an applied voltage. Given that the E_b ratio of E_b-BCZT/E_b-BCZT-OD is approximately 2.35/1, as the applied voltage increases, the BCZT layer will ideally reach its breakdown field before the BCZT-OD layer, leading to an earlier breakdown in the BCZT layer. This phenomenon is observed in the BCZT-OD/BCZT//(1P) structure. In the BCZT/BCZT-OD//(1P) structure, however, the situation differs slightly. As inferred, the ε of the BCZT-OD layer in BCZT/BCZT-OD//(1P) is lower than that in BCZT-OD/BCZT//(1P), which results in a higher partial voltage being applied across the BCZT-OD layer. Given that both BCZT-OD/BCZT//(1P) and BCZT/BCZT-OD//(1P) have the same thickness, the partial voltage across the BCZT layer in BCZT/BCZT-OD//(1P) is consequently lower than in BCZT-OD/BCZT//(1P). This indicates that in BCZT/BCZT-OD//(1P), the BCZT layer is effectively protected, delaying the breakdown behavior of the entire thin film. This difference in voltage endurance explains why BCZT/BCZT-OD//(1P) demonstrates superior voltage resistance compared to BCZT-OD/BCZT//(1P), despite having the same overall thickness. For BCZT/BCZT-OD//(2P) and BCZT-OD/BCZT//(2P), a similar phenomenon occurs, and the 2nd observation is Section 3.2 is explained. As to the 3rd observation, it can be explained as follows: for the enhanced voltage endurance in multilayers with larger periodicity in previous work, such an enhancement is attributed to the optimization of voltage distribution or the blocking behavior of the accumulated charges in the interfaces between adjacent sublayers.^11–13,45 Due to a certain amount of oxygen vacancies, in this work, the behavior of voltage distribution's optimization and the accumulated charges’ blocking are both weakened, leading to close E_b between BCZT-OD/BCZT//(1P) and BCZT-OD/BCZT//(2P), BCZT/BCZT-OD//(1P) and BCZT/BCZT-OD//(2P). In other words, by constructing a Schottky contact between the film and the electrode, the ferroelectricity on the negative side of the P–E loop was sacrificed. However, this trade-off significantly enhanced the E_b on the positive side, a critical factor in calculating W_rec. This approach mirrors the principle in the story of “Tian Ji's Strategy for Horse Racing:” sacrificing a secondary factor to secure the ultimate victory.

To validate this observation, the finite element method (FEM) was applied to simulate the electric breakdown process of these two structures by linking the COMSOL Multiphysics6.0 and Matlab5.2. Fig. 4(h1)–(h4) depicts the current distribution across each multilayered structure after a prolonged application of a 6.0 MV cm⁻¹ electric field. As shown, current flows through all thin films except the BCZT/BCZT-OD//(1P) structure, consistent with the experimental findings. To further analyze how structure influences breakdown behavior, Fig. S11 (ESI†) presents the current distribution over time after voltage activation for each multilayer. In the BCZT-OD/BCZT//(1P) configuration, the current begins at the top BCZT-OD layer, and notably, the current flow appears in the BCZT layer even before the BCZT-OD layer undergoes breakdown. This early breakdown in the BCZT layer is attributed to the applied electric field exceeding its voltage endurance. Similar behavior is observed in the BCZT-OD/BCZT//(2P) structure, where the breakdown occurs first in the BCZT layers. Once these layers fail, the entire voltage load transfers to the BCZT-OD layers, resulting in overall structural failure. In contrast, the BCZT/BCZT-OD//(2P) structure demonstrates a sequential current spread from top to bottom, with interfaces between adjacent layers acting as barriers to current propagation. The simulation parameters, based on experimental data detailed in the ESI,† closely match the experimental results, underscoring the reliability of the simulation.

3.5 Energy storage stability

Instead of solely focusing on maximizing the performance of energy storage capacitors, enhancing their stability across diverse environmental conditions is more crucial. Fig. S12(a) and (b) (ESI†) show the unipolar P–E loops and J–E curves of the BCZT/BCZT-OD(1P) thin film subjected to polarization fatigue, measured from the 1st to the 10⁶th cycle under an applied field of 5.0 MV cm⁻¹. The corresponding energy storage performance of the BCZT/BCZT-OD(1P) ceramic during this process is summarized in Fig. 5(a1), where the changes in W_rec and η are remarkably low, at only 1.0% and 5.62%, respectively. To see this change more intuitively, the variation of polarization and switching current with both electric field and cycling number were summarized in mappings, as displayed in Fig. 5(a2) and (a3), respectively. As the cycling number increases, the current peak decreases, as seen in Fig. 5(a3), while the parallel stripes can still be observed in Fig. 5(a2), demonstrating its excellent fatigue endurance. The P–E loops and J–E curves measured from 20 °C to 250 °C at 5.0 MV cm⁻¹ are shown in Fig. S13(a) and (b) (ESI†), respectively, and the corresponding energy storage performance is plotted in Fig. 5(b1). The BCZT/BCZT-OD(1P) shows quite good energy storage thermal stability before 140 °C, and both W_rec and η decrease sharply as the temperature further increases. From the red area in the top right corner of Fig. 5(b2), we can infer that the polarization's huge increment ocurrs under the combined effect of high temperature and high electric field, which indicates that the ionic conductance plays a dominant role. The highest W_rec in this temperature range, which was calculated to be 97.38 J cm⁻³ with an η of 79.75%, is located at 80 °C. In addition, the fading of the switching current in Fig. 5(b3) indicates the decline of the ferroelectricity with an increase in temperature. Thus, the energy storage performance's decrement of BCZT/BCZT-OD//(1P) after 140 °C is caused by the combined effect of the defect dipoles and the loss of ferroelectricity. Interestingly, 140 °C is a key temperature to provide the possibility of application of dielectric capacitors on the hybrid electrical vehicle.⁷⁰ Fig. S14(a) and (b) (ESI†) show unipolar P–E loops and J–E curves of the BCZT/BCZT-OD//(1P) measured from 10 Hz to 5000 Hz under 5.0 MV cm⁻¹ at room temperature, respectively. After integration, the variation between the energy storage performance and applied frequency is plotted in Fig. 5(c1), and as expected, both the W_rec and η increase with an increase in f and then decrease. The mappings that are composed of polarization and switching current with both the electric field and frequency are displayed in Fig. 5(c2) and (c3), respectively. In the former, vertical stripes, which indicate the stability of ferroelectric polarization, can be seen. In the latter, however, a red area in the top left corner indicates a huge increment of switching current at f over 1000 Hz, and according to Fig. 3(g), the domain switching, electrical conductivity, and dielectric displacement all affect it. Thus, the inferior energy storage performance of BCZT/BCZT-OD(1P) at low frequency is thought to be caused by the high leakage current inside the film.

Fig. 5 (a1) The variation between W_rec, η, and cycling number from 1st to 10⁶th at room temperature and at 5.0 MV cm⁻¹ of the BCZT/BCZT-OD//(1P) thin film; the corresponding mapping of the variation between (a2) polarization; (a3) switching current, electric field and cycling number; (b1) the variation between W_rec, η, and temperature from 25 °C to 250 °C at 5.0 MV cm⁻¹ of the BCZT/BCZT-OD//(1P) thin film; the corresponding mapping of the variation between (b2) polarization; (b3) switching current, electric field and temperature; (c1) the variation between W_rec, η, and frequency from 10 Hz to 5000 Hz at 5.0 MV cm⁻¹ of the BCZT/BCZT-OD//(1P) thin film; the corresponding mapping of the variation between (c2) polarization; (c3) switching current, electric field and frequency.

3.6 Charge–discharge properties

For most studies on energy storage capacitors, the charge–discharge measurement, which reflects their discharge power in the practical dynamic electric field, is always necessary.^71–74 Regrettably, after many attempts, in this work, no reasonable data on the charge–discharge property can be obtained in the BCZT/BCZT-OD//(1P) thin film. The authors are yet to find out the reason, and it might be caused by the irregular structure.

4. Conclusions

By altering the layer sequence and periodicity in multilayered structures composed of regular BCZT and oxygen-deficient BCZT (BCZT-OD), the influence of the Schottky barrier—formed at the interface between the BCZT-OD layer and the NSTO substrate in the BCZT/BCZT-OD//(1P) thin film—on the multilayers' energy storage performance was elucidated. Enhanced resistivity in the BCZT-OD layer optimized electric field redistribution, resulting in notably high voltage endurance for the BCZT/BCZT-OD//(1P) thin film. Additionally, the extra electric field across the BCZT-OD layer in this configuration induced defect dipoles, especially and , to contribute more significantly to dipole polarization, yielding a higher P_max than the BCZT-OD/BCZT//(1P) thin film, which has an identical composition but a different starting layer. Consequently, the BCZT/BCZT-OD//(1P) thin film achieved a W_rec of 150.22 J cm⁻³ with an η of 83.07%, along with strong energy storage reliability. Similar to the strategic approach in the tale of “Tian Ji's Strategy for Horse Racing”, this work introduces a novel design strategy for high-performance dielectric capacitors: optimizing the positive side of the P–E loop by adjusting the configuration, even at the expense of the negative side, to achieve higher W_rec.

Author contributions

Zixiong Sun: conceptualization (lead), project administration (lead), and writing – review & editing (lead). Haoyang Xin: data curation (equal). Liming Diwu: data curation (equal). Zhanhua Wang: project administration (equal). Ye Tian: writing – original draft (equal). Hongmie Jing: data curation (equal). Xiuli Wang: writing – original draft (equal). Wanbiao Hu: writing – original draft (equal). Yongming Hu: project administration (equal) and writing – original draft (equal). Zhuo Wang: writing – original draft (equal).

Data availability

The data supporting this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

This work was financed by the National Natural Science Foundation of China (52472132, U24A20203); the Opening Project of State Key Laboratory of Polymer Materials Engineering (Sichuan University) (Grant No. sklpme2024-1-24); the Opening Project of Engineering Research Center of Eco-friendly Polymeric Materials, Ministry of Education (Sichuan University) (EFP-KF2403)); and the Project of the Yunnan Key Laboratory of Electromagnetic Materials and Devices, Yunnan University (ZZ2024004).

References

1. H. Zubairi, Z. L. Lu, Y. B. Zhu, I. M. Reaney and G. Wang, Chem. Soc. Rev., 2024, 53, 10761–10790.
2. Z. Wang, B. Zhou, Y. Li, Z. Shen and J. H. Wang, Polym. Rev., 2024, 1–21.
3. Z. X. Sun, Y. H. Bai, J. Q. Liu, G. Jian, C. Guo, L. Zhang and Y. P. Pu, J. Alloys Compd., 2022, 909, 29.
4. X. H. Fan, J. Wang, H. Yuan, Z. H. Zheng, J. Zhang and K. J. Zhu, J. Adv. Ceram., 2023, 12, 649–680.
5. Y. T. Jiao, J. Dai, Z. H. Fan, J. Y. Cheng, G. P. Zheng, L. Grema, J. W. Zhong, H. F. Li and D. W. Wang, Mater. Today, 2024, 77, 92–117.
6. Z. X. Sun, Z. Wang, Y. Tian, G. Wang, W. Wang, M. D. Yang, X. Y. Wang, F. H. Zhang and Y. P. Pu, Adv. Electron. Mater., 2020, 6, 34.
7. W. Abbas, M. S. Ibrahim, M. Waseem, C. Lu, H. H. Lee, S. Fazal, K. H. Loo and A. Pramanick, Chem. Eng. J., 2024, 482, 28.
8. T. D. Zhang, H. Sun, C. Yin, Y. H. Jung, S. W. Min, Y. Zhang, C. H. Zhang, Q. G. Chen, K. J. Lee and Q. G. Chi, Prog. Mater. Sci., 2023, 140, 58.
9. H. Pan, F. Li, Y. Liu, Q. H. Zhang, M. Wang, S. Lan, Y. P. Zheng, J. Ma, L. Gu, Y. Shen, P. Yu, S. J. Zhang, L. Q. Chen, Y. H. Lin and C. W. Nan, Science, 2019, 365, 578–582.
10. S. Q. Xu, X. M. Shi, H. Pan, R. Z. Gao, J. Wang, Y. H. Lin and H. B. Huang, Adv. Theory Simul., 2022, 5, 7.
11. Z. X. Sun, C. R. Ma, M. Liu, J. Cui, L. Lu, J. B. Lu, X. J. Lou, L. Jin, H. Wang and C. L. Jia, Adv. Mater., 2017, 29, 6.
12. Z. X. Sun, L. X. Wang, M. Liu, C. R. Ma, Z. S. Liang, Q. L. Fan, L. Lu, X. J. Lou, H. Wang and C. L. Jia, J. Mater. Chem. A, 2018, 6, 1858–1864.
13. M. D. Nguyen, Y. A. Birkhölzer, E. P. Houwman, G. Koster and G. Rijnders, Adv. Energy Mater., 2022, 12, 14.
14. Y. L. Sun, L. Zhang, Q. W. Huang, Z. B. Chen, D. Wang, M. M. Seyfouri, S. L. Y. Chang, Y. Wang, Q. Zhang, X. Z. Liao, S. A. Li, S. J. Zhang and D. Y. Wang, Adv. Sci., 2022, 9, 10.
15. Z. X. Sun, Y. H. Bai, H. M. Jing, T. Y. Hu, K. Du, Q. Guo, P. Gao, Y. Tian, C. R. Ma, M. Liu and Y. P. Pu, Mater. Horiz., 2024, 11, 3330–3344.
16. A. P. Chen, W. R. Zhang, L. R. Dedon, D. Chen, F. Khatkhatay, J. L. MacManus-Driscoll, H. Y. Wang, D. Yarotski, J. Chen, X. S. Gao, L. W. Martin, A. Roelofs and Q. X. Jia, Adv. Funct. Mater., 2020, 30, 9.
17. A. Gómez, J. M. Vila-Fungueiriño, R. Moalla, G. Saint-Girons, J. Gázquez, M. Varela, R. Bachelet, M. Gich, F. Rivadulla and A. Carretero-Genevrier, Small, 2017, 13, 10.
18. J. X. Yao, M. Ye, Y. W. Sun, Y. Yuan, H. Fan, Y. Zhang, C. Chen, C. Liu, K. Qu, G. K. Zhong, T. T. Jia, Z. Fan, S. M. Ke, Y. Zhao, C. G. Duan, P. Gao and J. Y. Li, Acta Mater., 2020, 188, 23–29.
19. S. Z. Huang, W. X. Zhu, Y. A. Birkhoelzer, R. A. Avila, H. B. Huang, X. J. Lou, E. P. Houwman, M. D. Nguyen, G. Koster and G. Rijnders, APL Mater., 2023, 11, 8.
20. Z. X. Sun, X. X. Tian, L. Shang, X. D. Hao, G. X. Wang, Y. Shi and Y. P. Pu, Appl. Surf. Sci., 2021, 559, 10.
21. A. P. Chen, F. Khatkhatay, W. Zhang, C. Jacob, L. Jiao and H. Wang, J. Appl. Phys., 2013, 114, 6.
22. H. Pan, S. Lan, S. Xu, Q. Zhang, H. Yao, Y. Liu, F. Meng, E.-J. Guo, L. Gu and D. Yi, Science, 2021, 374, 100–104.
23. A. Yadav, C. Nelson, S. Hsu, Z. Hong, J. Clarkson, C. Schlepütz, A. Damodaran, P. Shafer, E. Arenholz and L. Dedon, Nature, 2016, 530, 198–201.
24. V. S. Puli, D. K. Pradhan, B. C. Riggs, D. B. Chrisey and R. S. Katiyar, Integr. Ferroelectr., 2014, 157, 139–146.
25. X. M. Fan, P. Li, J. A. Du, C. Chen, P. Fu, J. G. Hao, Z. X. Yue and W. Li, J. Mater. Sci.:Mater. Electron., 2020, 31, 9974–9981.
26. M. K. Bilal, J. Wang, R. Bashir, H. Liu, S. U. Asif, J. Y. Xie and W. B. Hu, J. Am. Ceram. Soc., 2021, 104, 3982–3991.
27. Y. H. Wang, S. Y. Gao, T. Wang, J. Q. Liu, D. Li, H. B. Yang, G. L. Hu, L. Kong, F. Wang and G. Liu, Ceram. Int., 2020, 46, 12080–12087.
28. B. Tai, Y. Jin, J. F. Wang, F. D. Peng, X. Li, X. Y. Peng and Y. Yao, Ceram. Int., 2022, 48, 17046–17052.
29. Z. X. Sun, Y. H. Bai, T. Ouyang, Q. Guo, Y. T. Ning, J. Q. Liu, H. S. Wei, K. Du, H. M. Jing, Y. Tian and Y. P. Pu, Appl. Phys. Lett., 2023, 122, 8.
30. Y. Yang, P. Liu, Y. J. Zhang, K. R. Kandula, J. W. Xu, G. Z. Zhang and S. L. Jiang, Ceram. Int., 2020, 46, 18106–18113.
31. Q. G. Chi, T. Ma, Y. Zhang, Y. Cui, C. H. Zhang, J. Q. Lin, X. Wang and Q. Q. Lei, J. Mater. Chem. A, 2017, 5, 16757–16766.
32. Q. G. Chi, T. Ma, Y. Zhang, Q. G. Chen, C. H. Zhang, Y. Cui, T. D. Zhang, J. Q. Lin, X. Wang and Q. Q. Lei, ACS Sustainable Chem. Eng., 2018, 6, 403–412.
33. Y. X. Ding, W. M. Zhang, X. X. Zou and Z. M. Wang, J. Appl. Polym. Sci., 2023, 140, 13.
34. C. Chen, T. D. Zhang, C. H. Zhang, Y. Feng, Y. Q. Zhang, Y. Zhang, Q. G. Chi, X. Wang and Q. Q. Lei, ACS Appl. Energy Mater., 2021, 4, 11726–11734.
35. S. H. Liu, S. X. Xue, S. M. Xiu, B. Shen and J. W. Zhai, Sci. Rep., 2016, 6, 11.
36. Y. Wang, H. Wang, K. Xu, B. Y. Wang, F. Wang, C. L. Li, C. L. Diao, H. B. Huang and H. W. Zheng, Ceram. Int., 2022, 48, 16114–16122.
37. H. X. Liu, W. X. Zhu, Q. Mao, B. Peng, Y. W. Xu, G. H. Dong, B. H. Chen, R. B. Peng, Y. A. Zhao, Z. Y. Zhou, S. Yang, H. B. Huang and M. Liu, Adv. Mater., 2023, 35, 9.
38. A. P. Sharma, D. K. Pradhan, S. K. Pradhan and M. Bahoura, Sci. Rep., 2019, 9, 8.
39. Z. X. Sun, C. R. Ma, X. Wang, M. Liu, L. Lu, M. Wu, X. J. Lou, H. Wang and C. L. Jia, ACS Appl. Mater. Interfaces, 2017, 9, 17097–17102.
40. V. S. Puli, D. K. Pradhan, I. Coondoo, N. Panwar, S. Adireddy, S. J. Luo, R. S. Katiyar and D. B. Chrisey, J. Phys. D:Appl. Phys., 2019, 52, 10.
41. M. D. Nguyen, Mater. Res. Bull., 2021, 133, 8.
42. J. Qian, G. H. Li, K. Zhu, G. L. Ge, C. Shi, Y. Liu, F. Yan, Y. X. Li, B. Shen, J. W. Zhai and Z. X. Cheng, ACS Appl. Mater. Interfaces, 2022, 14, 54012–54020.
43. Y. H. Ren, H. B. Cheng, J. Ouyang, O. Kurt, J. J. Wang, Q. H. Zhang, Y. Y. Zhao, L. Gu and L. Q. Chen, Energy Storage Mater., 2022, 48, 306–313.
44. K. Wang, J. Ouyang, M. Wuttig, Y. Y. Zhao, H. B. Cheng, Y. Zhang, R. X. Su, J. Yan, X. L. Zhong and F. Zeng, Adv. Energy Mater., 2020, 10, 8.
45. Z. S. Liang, C. R. Ma, L. K. Shen, L. Lu, X. L. Lu, X. J. Lou, M. Liu and C. L. Jia, Nano Energy, 2019, 57, 519–527.
46. Z. S. Liang, M. Liu, C. R. Ma, L. K. Shen, L. Lu and C. L. Jia, J. Mater. Chem. A, 2018, 6, 12291–12297.
47. F. Zhao, J. Jin, G. L. Hu, C. R. Ma, L. Lu, T. Y. Hu, Y. P. Liu, D. W. Hu, M. Liu and C. L. Jia, Chem. Eng. J., 2022, 450, 10.
48. K. Wang, H. F. Zhu, J. Ouyang, Y. Tian, S. X. Wang, Q. Li, Y. Y. Zhao, H. B. Cheng and X. Zhai, Appl. Surf. Sci., 2022, 581, 8.
49. Q. L. Fan, C. R. Ma, Y. Li, Z. S. Liang, S. Cheng, M. Y. Guo, Y. Z. Dai, C. S. Ma, L. Lu, W. Wang, L. H. Wang, X. J. Lou, M. Liu, H. Wang and C. L. Jia, Nano Energy, 2019, 62, 725–733.
50. K. Wang, Y. Zhang, S. X. Wang, Y. Y. Zhao, H. B. Cheng, Q. Li, X. L. Zhong and J. Ouyang, ACS Appl. Mater. Interfaces, 2021, 13, 22717–22727.
51. H. B. Cheng, J. Ouyang, Y. X. Zhang, D. Ascienzo, Y. Li, Y. Y. Zhao and Y. H. Ren, Nat. Commun., 2017, 8, 7.
52. M. Z. Yang, W. B. Ren, M. F. Guo and Y. Shen, Small, 2022, 18, 23.
53. M. R. Zhang, B. F. Zhu, X. Zhang, Z. X. Liu, X. Y. Wei and Z. C. Zhang, Mater. Horiz., 2023, 10, 2455–2463.
54. M. J. Feng, Y. Feng, C. H. Zhang, T. D. Zhang, Q. G. Chen and Q. G. Chi, Mater. Horiz., 2022, 9, 3002–3012.
55. Y. Ivry, D. P. Chu, J. F. Scott and C. Durkan, Phys. Rev. Lett., 2010, 104, 4.
56. N. Balke, P. Maksymovych, S. Jesse, A. Herklotz, A. Tselev, C. B. Eom, I. I. Kravchenko, P. Yu and S. V. Kalinin, ACS Nano, 2015, 9, 6484–6492.
57. Z. X. Sun, H. S. Wei, S. B. Zhao, Q. Guo, Y. H. Bai, S. T. Wang, P. Y. Sun, K. Du, Y. T. Ning, Y. Tian, X. H. Zhang, H. M. Jing, Y. P. Pu and S. F. Zhang, J. Mater. Chem. A, 2023, 12, 128–143.
58. E. Brown, C. Ma, J. Acharya, B. Ma, J. Wu and J. Li, ACS Appl. Mater. Interfaces, 2014, 6, 22417–22422.
59. O. L. Krivanek, M. F. Chisholm, V. Nicolosi, T. J. Pennycook, G. J. Corbin, N. Dellby, M. F. Murfitt, C. S. Own, Z. S. Szilagyi, M. P. Oxley, S. T. Pantelides and S. J. Pennycook, Nature, 2010, 464, 571–574.
60. Z. Sun, Y. G. Zhao, M. He, L. Gu, C. Ma, K. J. Jin, D. Y. Zhao, N. N. Luo, Q. H. Zhang, N. Wang, W. H. Duan and C. W. Nan, ACS Appl. Mater. Interfaces, 2016, 8, 11583–11591.
61. G. J. Wang, J. Zheng, H. Bi, S. T. Wang, J. Wang, J. Sun, Y. F. Guo and C. C. Wang, Scr. Mater., 2019, 162, 28–32.
62. W. M. Ding, X. M. Li, S. D. Su, Z. Y. Liu, Y. Cao, L. H. Meng, S. B. Yuan, W. H. Wei and M. Luo, Nanoscale, 2023, 15, 4014–4021.
63. S. B. Wang, L. Pan, J. J. Song, W. B. Mi, J. J. Zou, L. Wang and X. W. Zhang, J. Am. Chem. Soc., 2015, 137, 2975–2983.
64. S. Saha and T. Sinha, Phys. Rev. B, 2002, 65, 134103.
65. Z. X. Sun, Y. P. Pu, Z. J. Dong, Y. Hu, X. Y. Liu and P. K. Wang, Ceram. Int., 2014, 40, 3589–3594.
66. F. Chiu, Adv. Mater. Sci. Eng., 2014, 2014, 927358.
67. J. Werner, A. F. J. Levi, R. T. Tung, M. Anzlowar and M. Pinto, Phys. Rev. Lett., 1988, 60, 53–56.
68. Z. X. Sun, E. P. Houwman, S. T. Wang, M. D. Nguyen, G. Koster and G. Rijnders, J. Alloys Compd., 2024, 981, 8.
69. P. A. Shaikh, D. Shi, J. R. D. Retamal, A. D. Sheikh, M. A. Haque, C. F. Kang, H. He, O. M. Bakr and T. Wu, J. Mater. Chem. C, 2016, 4, 8304–8312.
70. D. Tan, L. L. Zhang, Q. Chen and P. Irwin, J. Electron. Mater., 2014, 43, 4569–4575.
71. L. Y. Zhang, R. Y. Jing, Y. Y. Huang, Y. L. Yang, Y. Li, M. Y. Tang, S. Y. Cao, Z. B. Chen, F. Gao, Y. X. Du, S. Y. Zhou, J. W. Zhao, S. Y. Liu, D. W. Wang, S. J. Zhang and L. Jin, Adv. Mater., 2024, 36, 11.
72. Y. Song, M. Zhang, S. Lan, B. B. Yang, Y. Q. Liu, C. W. Nan and Y. H. Lin, J. Adv. Ceram., 2024, 13, 1498–1504.
73. Z. L. Chang, L. Lei, L. W. Zhu, Y. Quan, Z. L. Ren, Y. H. Qian, D. Dastan and Z. C. Shi, Mater. Horiz., 2024, 9,  10.1039/d4mh01305k.
74. J. Xiong, G. X. Zhang, S. B. Tan, H. H. Gong, Y. C. Xie, X. Zhang and Z. C. Zhang, Mater. Horiz., 2024, 8,  10.1039/d4mh01225a.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01651c

‡ Z. Sun, H. Xin, and L. Diwu contributed equally to this work.

---