Liquid ferrofluid synapses for spike-based neuromorphic learning

Abstract

Solid-state memory devices have emerged as promising synapses for neuromorphic engineering and computing. However, features such as limited endurance, static sensitivity, and lower ON/OFF ratios, as well as the need for peculiar conditions including current compliance and forming, still make their adoption challenging. Here we report a liquid state neuromorphic device based on a ferrofluid that exhibits short-term plasticity featuring extraordinary properties: a lower dynamic range, a high endurance, a fault tolerance capability, a deterministic resistance switching behavior, and no need for prerequisites such as a forming procedure and compliance current requirements. We also show how to stabilize nanoparticles using oleic acid as the surfactant, resulting in a yield increase and a smaller resistance variance. Additionally, we propose a low-power inference system on such a liquid synapse by applying the minimal magnitude of read biases, which are only affected to about 10% by the offset, gain errors, and noise of the system. Finally, we show the liquid synapse's feature to scale down the size and the capability to classify digits using a spike-based unsupervised learning method.

---

New concepts

This work pioneers the concept of liquid ferrofluid-based synapses for spike-based neuromorphic learning, via introducing liquid robotics into the realm of neuromorphic hardware. Moving beyond conventional solid-state memristive devices, in which challenges like limited endurance, stochastic switching, and vulnerability to electrostatic discharge are encountered, our ferrofluid synapse achieves deterministic resistance switching, exceptional fault tolerance, and endurance surpassing 10 million cycles—without the need for forming procedures or current compliance. By stabilizing magnetic colloids with oleic acid, we enhance device stability and enable ultra-low-power operation, applying read biases as low as 14 mV, advancing the frontier of low-energy computing. Beyond the memory functionality, these liquid-state synapses embody reconfigurable, adaptive material behavior that synergizes with liquid robotics concepts, opening pathways for self-healing, deformable, and scalable computational units. Supporting spike-timing dependent plasticity (STDP), our system learns patterns and classifies digits at the materials level, uniting soft matter physics, colloidal chemistry, and neuromorphic engineering. This work offers transformative insights for materials science, establishing ferrofluids not just as passive media but as active, scalable elements for unconventional computing architectures poised for integration in flexible electronics, soft robotics, and sustainable, beyond-Moore information processing systems.

1 Introduction

The word ‘unconventional’ computing¹ was coined, when Calude and Casti first predicted the decay of Moore's law² in the mid-1990s. The ardent developments in unconventional computing in the next two decades took the computational world by storm by motivating radical rethinking of possible futuristic information processors, architectures, learning techniques, and supporting technologies.^3,4 ‘Beyond Moore’ further nurtured the exploration of alternate processing devices (such as nanowire FETs, spinFETs, tunneling transistors, memristors, etc.), information processing architectures, and learning approaches inclined with nature.^5–8 ‘Neuromorphic computing’ is one such approach that traces back to the late 1980s when Mead first proposed the idea of morphing biological neurons on custom silicon.⁹ Memristive neural networks are being used to classify patterns, cluster data, recognize patterns and edges, etc. using different learning rules like the perceptron, Sanger's rule, spike time dependent plasticity (STDP), etc.^10–14 An overview of STDP and an illustrative comparison of biological and neuromorphic vision systems are presented in Section S1 of the ESI.† The von Neumann bottleneck, in other words the latency between the memory and processor, still represents an issue,¹⁵ as well as reliability in connection to emerging memory technologies. These setbacks justify the research for new possible paradigms and materials for memories: colloids that allow us to rethink the way memories exist and store information. The colloidal form of magnetite is one potential candidate that stores information and outsmarts emerging memory technologies. An illustrative comparison of the device structure of the solid-state memories with the LiRAM (liquid random access memory), ferrofluid in the form of an 1T1R synapse, is shown in Fig. 1(b).

Fig. 1 (a) A fully connected memristive crossbar and (b) ferrofluid LiRAM (liquid random access memory) device structure compared with its solid state counterparts.^16–20

Magnetite (Fe₃O₄) was used in ancient days (as a ‘lodestone’) to magnetize the soft iron wire in a mariner's compass. Its high Néel temperature (described in Section S9 (2) of ESI†) makes it suitable for room-temperature spintronic applications. Nanosized magnetite particles have interesting features, and incorporation of such materials can enable a magnetic response in polymeric materials,^21,22 or stabilization in liquid carriers results in globally homogeneous fluids responsive to magnetic fields,²³ also known as ferrofluids. Colloids comprising nano-sized magnetite particles suspended in a liquid medium date back to the 1960s, when Steve Papell invented it for pumping liquid fuel in a zero-gravity environment using magnetic fluid.²⁴ Ferrofluids have been widely used in applications like magnetic seals for pumps and mixers,²⁵ inertial and viscous damping for loudspeakers and stepper motors,²⁶ bearings,²⁷ lubricants,²⁸ heat transfers,²⁹ and soft-robots.^30–32

We have investigated the potential of in-memory computing in a ferrofluid,³³ and we have demonstrated that a volume of it can be seen as a system, that is, a reservoir of computing nodes, capable of showing complex features. Here, we focus on the use of a ferrofluid as a single device in direct replacement of a two-terminal solid-state memristor device, in compliance with its standard parameters and performance metrics. We are reporting its DC switching characteristics using a custom-made setup, whose characterization results are excellent when compared to its solid-state memory counterparts. Ferrofluid, in its liquid form, combines the advantages of several memory technologies. Firstly, the ferrofluid is tolerant towards damages due to accidental electrostatic discharge (ESD), which most solid-state memories intrinsically lack (ESD effects on solid state memories are elaborated with other reliability issues in Section S2 of the ESI†). Using this system also paves tolerance to liquid loss and stability to liquid injection (volumetric changes of the functional liquid). Other comparable results include a high endurance, lower dynamic range, and no stochastic switching behaviors.

Here we show the switching characteristics of a liquid synapse between a high resistance state (HRS) and a low resistance state (LRS), which is retained for a short time thereby proving short term plasticity (STP), both by DC sweep experiments and by applying dynamic pulses. An experimental improvement in yield and reduction in variation of LRS and HRS values was obtained when stabilizing the colloid with oleic acid. The liquid synapse was proven to be compliant with low-power operation during inference whose results are only influenced by the DC offset, gain errors, and noise of the set-up. We also experimentally validate the scalability feature of the ferrofluid synaptic system by reducing the volume and distance between the conducting electrodes, which enables the possible integration with silicon. Lastly, we simulated the ferrofluid's STP capabilities at the circuit and systems level to classify patterns through an unsupervised spike-based learning mechanism.

2 Physico-chemical properties of ferrofluids

This work has employed two commercial water-based magnetites (or ferrofluids), purchased from Ferrotech (U.S.A.), the EMG 601p,³⁴ and from PlasmaChem (Germany), the PL-M-Fe₃O₄.³⁵ We will refer to them as EMG and PL, respectively, in the following text. UV-Vis absorption spectra of the materials in solution are recorded using a single-beam diode-array spectrophotometer (Agilent 8453, USA) in 1 cm quartz cells. Fig. 2(a) depicts UV-Vis spectra of the two ferrofluids functionalized with different surfactants. The higher concentration of dodecyl sulfate as the surfactant in PL compared to ammonium sulfate or carboxylate in EMG (see further XPS analyses) results in a better dispersion and a steeper slope in the absorption spectrum, and suggests smaller particles. A higher absorbance in the PL is found, which is composed of two peaks: magnetite, Fe₃O₄ with a band comprised between 300 and 400 nm, and hematite, Fe₂O₃ with absorption in the range 450 to 500 nm. The ATR-FTIR spectra of powder samples on a diamond crystal are recorded using a Bruker TENSOR II spectrometer in the 350–4000 cm⁻¹ range (Fig. 2(b)).

Fig. 2 UV-Visible absorption spectra of the ferrofluids: (a) PL spectrum, (b) EMG spectrum, ATR-FTIR spectra of the ferrofluids, (c) PL spectrum, and (d) EMG spectrum.

The measurements, with a resolution of 1 cm⁻¹, are based on 16 scans. The ATR-FTIR spectra of the two samples after evaporation of solvent under vacuum at room temperature shows distinct peaks corresponding to different functional groups and bonding interactions. In the case of PL, the sharp peak observed around 2900–3000 cm⁻¹ suggests the presence of C–H stretching vibrations, likely from the alkyl chains of the surfactant, oleic acid. The absence of a broad peak near 3400 cm⁻¹ confirms the removal of water, as this region typically corresponds to O–H stretching vibrations. Peaks in the range of 1000–1200 cm⁻¹ can be attributed to sulfate (SO₄²⁻) symmetric and asymmetric stretching modes, indicating the presence of a sulfate-based surfactant used for ferrofluid stabilization, like sodium dodecyl sulphate. Additionally, two peaks below 560 cm⁻¹ and 370 cm⁻¹ correspond to Fe–O stretching vibrations, confirming the presence of iron oxide nanoparticles such as Fe₃O₄ (magnetite) or γ-Fe₂O₃ (maghemite). The bands in the 1400–1600 cm⁻¹ region could be related to C–H bending or possible carboxylate (COO⁻) stretching of a carboxyl-based stabilizer. In the EMG sample, Fe–O stretching vibrations can be observed. However, the peaks before 3000 cm⁻¹ related to the alkyl group in sulfate-based surfactant can be ignored, suggesting the absence of this stabilizing agent. The carboxylate (COO⁻) group presents two characteristic peaks in the 1500–1650 cm⁻¹ and 1300–1450 cm⁻¹ regions that correspond to asymmetric and symmetric stretching vibrations. The morphology, homogeneity of the particles and size distribution are investigated using scanning electron microscopy (SEM), energy-dispersive X-ray spectroscopy (EDX) and transmission electron microscopy (TEM). SEM images are obtained using a Helios 5 PFIB CXe ultra-high-resolution scanning electron microscope (Thermo Fisher Scientific), equipped with a Schottky field emission gun. Imaging is performed at 25 kV, with a beam current of 0.8 nA and a working distance of 5 mm. A 20 μL ferrofluid aliquot was drop-cast onto a Si wafer. EDX is carried out using an Ultim MAX 60 EDX detector (Oxford Instruments) at 25 keV beam energy and 1.6 nA beam current. TEM images are acquired using a Tecnai TF 20 X-TWIN (Thermo Fisher Scientific, formerly FEI), equipped with a field emission gun, at an acceleration voltage of 200 kV. A 20 μL ferrofluid aliquot is drop-cast onto a 3 nm C-coated Au TEM holey grid. Selected area diffraction was conducted using a 200 nm aperture. Data analysis was performed using CrystBox.³⁶ SEM images of samples prepared from diluted solutions which are dispersed on silicon wafer and dried under vacuum are shown in Fig. 3(a) and (b).

Fig. 3 SEM images of ferrofluids drop-cast onto a Si wafer: (a) PL nanoparticles, (b) EMG nanoparticles, TEM images of dried nanoparticles, with size histograms in the insets: (c) PL nanoparticles, and (d) EMG nanoparticles.

After evaporation of the solvent, both samples show a distribution of the residual solid which is highly inhomogeneous, featuring both chain-like and fractal particle alignments (see Fig. S3, ESI†). Due to such inhomogeneity, a quantitative analysis by EDX is not possible; nevertheless, the presence of characteristic peaks for a given element is represented in Fig. S4 (ESI†). Fig. 3(c) and (d) displays the TEM images. The size distribution (as an inset image) shows that PL particles have an average size of less than 9 nm, with a more uniform size distribution. In contrast, EMG features larger particles, exhibiting a size range comprised between 8 and 24 nm, with an average size of slightly less than 15 nm. Both materials have similar XRD and SAED patterns in Fig. S5 (ESI†), and the composition of both materials appears as a mixture of maghemite and magnetite iron oxides. The size of the particles and the d-spacing are represented in Fig. S5 (ESI†), panels (c) and (d). HRTEM images are displayed in Fig. S6 (ESI†).

XPS analyses are performed using a PHI VersaProbeII scanning XPS system, employing monochromatic Al Kα (1486.6 eV) X-rays focused on a 100 μm spot. The photoelectron take-off angle was set to 45°, with a pass energy of 117.50 eV for survey scans and 46.95 eV for high-resolution spectra. A dual-beam charge compensation system, utilizing 7 eV Ar⁺ ions and 1 eV electrons, is employed to maintain a constant sample surface potential, regardless of sample conductivity. All XPS spectra are calibrated to the unfunctionalized, saturated carbon (C–C) C 1s peak at 285.0 eV. The analysis chamber pressure is maintained below 3 × 10⁻⁹ mbar. Spectral deconvolution was performed using PHI MultiPak software (v.9.9.3), and the Shirley method was applied to subtract the background. The macroscopic feature of PL is its viscous, foaming liquid with a dark brown color, whereas EMG has a less viscous consistency and black color. These differences in appearance arise from the distinct compositions of the two samples. To investigate further, XPS spectroscopy is used to identify the surface composition and characteristic elements at the microscopic level, and the results are presented in Table 1. Wide survey spectra are shown in Fig. S7 (ESI†) and high-resolution spectra of both samples are represented in Fig. 4.

Table 1 Surface composition (atomic %) of the two ferrofluid samples after XPS analyses

	Fe	C				N		O			S	Cl	Na
Binding energy [eV]	708.9	248.6	285.0	286.3	288.4	400.1	401.8	530.1	531.8	533.3	168.4	198.2	1071.7
Oxidation state	Fe^2 +/Fe^3+	C=C	C–C	C–O,C–N	O–C=O	–NH2	–NH4^+	O–Fe	O–Fe,O=C	O–C,O–H	SO4^2−	Cl^−	Na^+
PL sample	2.7	26.0	36.7	3.6	1.2	0.0	0.0	7.4	13.1	1.5	2.4	0.0	5.4
EMG sample	5.1	9.6	27.3	14.9	2.6	5.3	3.9	14.8	11.1	2.9	1.0	1.4	0.2

---

Fig. 4 XPS high resolution spectra of the two colloidal samples: from (a)–(f): EMG sample. From (g)–(k): PL sample.

In the Fe 2p_3/2 region, the spectra are fitted with five components (see Fig. 4(a) and (g)). The first peak at 708.9 eV suggests a low concentration of Fe²⁺, while the second peak at 710.4 eV corresponds to Fe³⁺. The three additional peaks between 711 and 715 eV result from multiplet splitting.^37,38 Due to this splitting, which causes the Fe 2p line to be described by four to five components for each oxidation state, it is difficult to precisely determine the concentration of individual species without risking over-interpretation. The ratio of Fe²⁺ to Fe³⁺ shows that sample PL has more Fe³⁺ than sample EMG. The C 1s spectra are fitted with four components (see Fig. 4(b) and (h)). The first peak at 284.6 eV corresponds to C=C sp² bonds, the second peak at 285.0 eV is attributed to aliphatic C–C sp³ bonds, the third peak at 286.3 eV indicates C–O–C, C=O, and/or C–NH bonds, and the fourth peak at 288.4 eV is associated with O–C=O bonds.^39,40

In the N 1s region, two peaks are observed (see Fig. 4(c)). The first, at 400.1 eV, originates from amine C–NH₂ bonds, while the second, at 401.8 eV, attributes to ammonium NH₄⁺ which is present only in the EMG sample. The O 1s spectra are fitted with up to four components (see Fig. 4(d) and (i)). The first peak at 530.1 eV indicates O–Fe and/or O–S bonds, while the second peak at 531.8 eV is attributed to O=C and/or O–Fe defective bonds. The third peak at 533.3 eV is associated with –OH and/or O–C bonds and some contribution from the Auger Na KLL line. The fourth peak at 536.2 eV is solely attributed to the Auger Na KLL line. The S 2p spectra (see Fig. 4(e) and (j)) are fitted with a doublet structure, with a separation of 1.18 eV between the p_3/2 and p_1/2 peaks. The p_3/2 peak at 168.4 eV indicates the presence of SO₄²⁻ ions. The Cl 2p spectra (see Fig. 4(f)) are found in sample EMG only and are fitted with a doublet structure, with a separation of 1.6 eV. The main peak at 198.2 eV is indicative of Cl⁻ ions in chlorides such as NaNH₄. The Na 1s spectrum (see Fig. 4(k)) is found in the PL sample only and was fitted with a single peak at 1071.7 eV, indicating the Na⁺ oxidation state, primarily found in Na₂SO₄.

3 Experimental setup

The hardware design is shown in Fig. 6(a) for emulating the resistance states of the ferrofluid.³⁴ In this design, two OpAmps are connected to a vial (containing <5 mL of ferrofluid) using shielded RF cables. The design details of the vial is described in Section S4 of the ESI.† OpampA is in a buffer configuration while OpampB facilitates different feedback loops for various characterization tasks which mainly include establishing a read, a programming, and an idle path. The read path enables inferring the internal state of the ferrofluid. The programming path is used to apply programming biases (both write and erase biases) across the vial while the idle path is chosen to keep both the terminals of the vial at a similar virtual ground levels. A MicroPython board⁴¹ is used to apply analog biases (Vin_A and Vin_B) through its 8-bit digital to analog converters (DACs), save the analog values of the nodes – A, B and C through its 12-bit analog to digital converters (ADCs) and digitally control the switches to pick the feedback paths of OpampB using a multiplexer. A computer is used to send commands and save data via the USB cable that connects the MicroPython board. Fig. 5 shows the illustration of the experimental setup.

Fig. 5 Setup used for implementing the liquid synapse. On the right, a polymeric vial with open lid, showing the black ferrofluid inside, has been adapted to host the two SMA connectors. RF cables connect the reservoir with a test PCB (middle left of the image) hosting the OpAmps and MUX. On top left, the MicroPython board is shown which renders digital controls and analog input sources to the liquid synapse.

4 Electronic characterization methods

DC sweep experiment

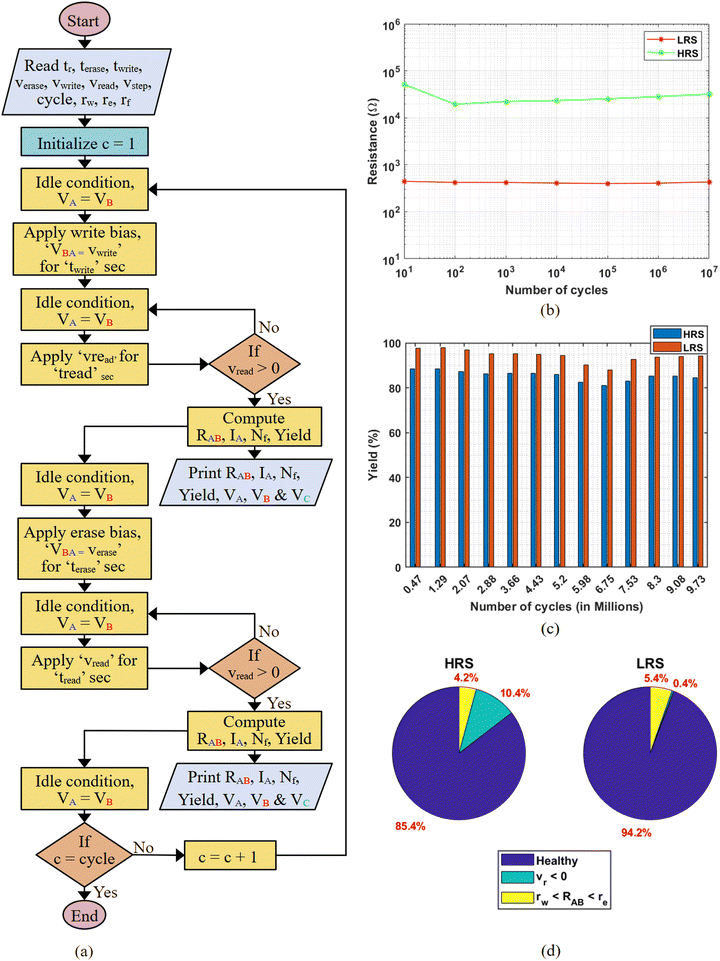
Fig. 6(b) shows the proposed flowchart for carrying out the DC sweep experiments to plot the IV curves of the ferrofluid. Initially, the values of the read time (t_r), erase time (t_e), write time (t_w), read voltage (v_r), sweep voltage for erasing (vs_e), sweep voltage for writing (vs_w), step voltage (v_s) (described in Section S9 (3) of ESI†), number of cycles (cycle), threshold post-write resistance (r_w), threshold post-erase resistance (r_e), and feedback resistance (r_f) are fed to the system. The number of positive voltage steps (n_w), the number of negative voltage steps (n_e), and the number of cycles (c) are initiated. The write biases are applied across the terminals of the vial, B and A for t_w s with incremental magnitude starting from 0 V to vs_w in v_s step voltage. Following each write bias a read bias of magnitude v_r is applied for t_r s and the analog values (V_A, V_B and V_C) of the nodes – A, B, and C are collected through the MicroPython board's ADCs. Due to the ferrofluid's STP, the approach to target a particular sample during ‘read’ is carried out and this is explained in Section S5 of the ESI.†

Fig. 6 (a) Proposed system architecture, (b) flowchart for carrying out the IV characteristic experiment of the ferrofluid, and (c) IV characteristics of the ferrofluid for 30 full cycles of switching between the erase and write cycles.

Applying write biases is carried out in incremental steps of v_step until the observed resistance (R_AB) reaches the threshold resistance, r_w. After attaining r_w, a train of read biases is applied in numbers similar to the numbers of v_step needed to reach r_w. Similarly, erase biases are applied in decremental steps of v_s until the observed resistance (R_AB) reaches below r_e and when this is attained, a train of read biases is applied in numbers similar to the number of v_ss needed to reach r_e. In this way, both the alternate positive and negative DC sweeps are carried out for the desired cycle(s) until the corresponding threshold resistance values are reached. N_f refers to the total number of incremental/decremental v_s needed or the accumulated n_w or n_e to reach corresponding threshold resistances.

The ferrofluid's resistance R_AB and the current flowing through it, I_A, are determined as follows:

When a positive voltage sweep is performed from 0 to vs_w, at a certain voltage (called as v_set) the current increases with a superlinear trend. This corresponds to a ‘set’ or ‘write’, where the change of resistance from HRS to LRS occurs. When a negative voltage sweep is performed from 0 to –vs_e, at a certain voltage (called as v_reset) the current drops and this corresponds to ‘reset’ or ‘erase’ where the change of resistance from LRS to HRS occurs. The IV characteristics of the ferrofluid for 30 full cycles of switching between the erase and write cycles are shown in Fig. 6(c).

Colloids, having characteristic lengths on the order of hundreds to thousands of nm, exhibit Reynolds numbers that are significantly lower than 1 (Re ≪ 1). This indicates a regime of creeping motion where inertial forces are negligible compared to viscous forces. For colloids solvated in water, the fluid behaves as viscous as molasses does to humans. A key consequence of such low Reynolds numbers is articulated using the scallop theorem,⁴² which states that no momentum can be accumulated while moving in the fluid. Therefore, the dissipation of any structure resulting from the ordering, eventually anisotropic effects, induced by applied fields is not instantaneous, emphasizing the memory of the colloidal arrangements. We have found several other colloidal systems enabling memory, namely a suspension of polyaniline nanorods,⁴³ graphitic carbon nitride,⁴⁴ zinc oxide nanoparticles⁴⁵ and several others. In the case of polyaniline, the involved mechanism is based on the fact that polyaniline can be considered as a polyelectrolyte: a macromolecule characterized by several charges. When exposed to apolar and/or aprotic solvents, positive and negative ions associate in the chains forming ion pairs that favor a coil conformation of the molecular chain. In contrast, in the presence of polar and/or protic solvents (e.g., water) the enhanced solvation of the charges lead to a more open and expanded molecular conformation (tail-like). Any effect that enhances the distance between positive and negative charges causes the expansion of the polymeric chain conformation and an increase in conductivity. Here, the application of an electric stimulus can be considered responsible for the polarization of polymeric chains enhancing the distance between positive and negative charges with a beneficial effect on the materials conductivity. Once the polarization drops, the electrical equilibrium of the system is restored by Brownian motion in some seconds, but the morphological changes remain for a longer time scale, providing an increased DC resistance. This memory effect lasts for longer times and provides the observed learning. In the case of carbon nitride, another relevant property is found to provide a memory effect: the mechanisms of oxidation and reduction present in the aqueous suspension of g-C₃N₄ are not symmetrical, resulting in a non-symmetric hysteresis loop, and in the appearance of a mem-fractive behaviour, or a memory effect that involves resistance, inductance and capacitance in this complex colloid. In the case of ZnO, the conductive network generation upon the application of a voltage stimulus is time dependent, leading to the development of a concept known as dynamic percolation. The time of dropping resistance depends on the length of stimulation, linearly. The resistance increases slowly during 120 h after stopping stimulation indicating memory existence in the colloid.⁴⁵ To conclude with the case of ferrofluids, we have already demonstrated that a water-based system containing magnetite nanoparticles can provide a slowly fading memory, which can also be profitably used to implement computational schemes, such as reservoir computing.³³ One further note is about the negative differential resistance (NDR) seen in the low voltage regime, first quadrant of Fig. 6(c). This particular behaviour is observed in materials where residual charge is stored in surface defects and Coulomb repulsion opposes to a growing voltage stimulus, resulting in lower currents instead of higher.⁴⁶ FF nanoparticles act as electron scavengers and become negatively charged particles, slowing the carrier speed. In our case, surface charges may diffuse in the surfactant layer and be trapped or released depending on the voltage, screened by the same molecules. In order to better link the algorithmic description of Fig. 2 to the physical properties of the materials, let us analyse in detail the four phases of the write/erase procedure. The writing phase occurs in the first quadrant of Fig. 6(c), with a first brief phase experiencing NDR due to trapped charges. When the ferrofluid dissipates such charges, a steady behaviour is found with positive differential resistance, until the current reaches a plateau and the “write” state is achieved. Now reducing the voltage brings the material to a slightly different impedance state, until zero bias conditions. The measured current is positive by definition, therefore in Fig. 6(c) we are not able to see the third quadrant. By bringing the system to negative voltages, we experience an abrupt change in the current, that reaches higher values and a steeper descent. This is due to the inductive component of the ferrofluid impedance,⁴⁷ bringing higher currents when the system is characterized at lower frequencies (remember that the time constant for the erase phase is 66.6 μs, while for the write phase it is 20 μs, see Table S2, ESI†). Once the minimum negative voltage has been reached, the erase phase is complete, and the voltage gradually moves to zero. The curve does not close perfectly because of the nano-battery effect,⁴⁸ in this case disregarded, but alternatively a useful property that can also be programmed to store information.⁴⁹ The bias conditions for the DC sweep experiment are shown in Table S1 of the ESI.†

Switching in pulse mode

We experimentally characterize the ferrofluids in pulse mode where switching between resistances is carried out using a short programming pulse followed by a read pulse of lower magnitude, thereby opening doors to low-power inference, whose measurements are only affected by gain and offset errors of the DAC, the DC offset voltages across the read path, and noise in the system. For this, we take advantage of the DACs in the MicroPython board for setting the tiniest magnitude of the read pulses and implement an additional check for the read magnitude to be a positive value. This additional check is carried out because the dominant factors – DC offset voltages, gain errors, and high frequency noise can cause negative read voltages when attempting to apply the mean read pulses of magnitude of about 14 mV. A similar ‘read’ approach of targeting a particular sample as done in the DC sweep experiment is carried out here during ‘read’. The bias conditions for the resistance switching are shown in Table S2 of the ESI.† Fig. 7(a) illustrates the flowchart for switching the EMG ferrofluid's resistances in dynamic pulse mode. An endurance test has been carried out, whose average results of every decade for 10 million cycles using a mean read voltage of 14 mV is shown in Fig. 7(b). Unlike IV characteristics (shown in Fig. 6(c)), the switching characterization using pulse mode has a higher ON/OFF ratio due to the applied optimal switching conditions as listed in Table S1 of the ESI.† Furthermore, in analog computing and neuromorphic systems, memristors often operate in a continuum of resistance states rather than binary states. This allows them to emulate synaptic weights with gradual changes, making a high ON/OFF ratio less essential.⁵⁰ The endurance characterization of all 10 million cycles, the statistical distribution of the HRS and LRS values, and the applied read voltages are shown in Fig. S11(a)–(d) of the ESI.† The reason for restricting the measurements to 10 million endurance cycles is explained in Section S9 (4) of the ESI.†

Fig. 7 (a) Flowchart for switching the EMG ferrofluid's resistance between HRS and LRS in pulse mode, (b) endurance test results of 10 million switching cycles between the LRS and HRS using a mean read voltage of 14 mV, (c) yield distribution of the HRS and LRS values for 10 million cycles using a mean read voltage of 14 mV, (d) factors affecting the yield of the HRS and LRS values.

To determine the robustness of our system for resistance switching in dynamic pulse mode, we carried out yield estimation for all 10 million characterization cycles. Our yield is mainly affected by two factors – a possible negative read voltage (v_r < 0) and the post-programming resistances are out of range of the threshold resistances (r_e > R_AB > r_w). Fig. 7(c) shows the average yield (in %) of the HRS and LRS values for about every 1 million characterization cycles of the EMG ferrofluid. As a similar number of samples are targeted during ‘read’ after ‘write’ and ‘erase’, the negative read voltage affects more the HRS values when compared to the LRS values. This is mainly due to the transient signal, V_B which takes a few milliseconds time to settle during ‘read’ of the HRS value. Fig. 7(d) shows contributing factors that affect the yield for determining the HRS and LRS values, where we can see an average yield of 85% and 94% for the HRS and LRS values respectively. Interestingly, the ferrofluid's resistance, R_AB reaching beyond the threshold resistance limits is dominant when reading LRS while the impact of negative read voltage, v_r is dominant when reading HRS. The memory fades exponentially within a few milliseconds (please refer to labels Sw_i with i = 1 : 10 in Fig. S10 of the ESI†), particularly for the LRS value. Considering these experimental values, retention is comparatively low (in the range of a few milliseconds), due to the STP property. This low retention also exists in solid-state memories that have STP. To overcome the STP, we pick a particular sample uniformly in the visible LRS region throughout the experiments.

An improvement in the yield is noticed when replacing the water-soluble surfactant of the ferrofluid (EMG) with a capping layer of oleic acid surrounding the nanoparticles (PL), which provides increased stability of the particles. The IV characteristics of this PL ferrofluid for 30 DC sweep cycles are shown in Fig. 8(a), where a higher reset voltage is observed. Its corresponding resistance (R_AB) is plotted in Fig. S13 of the ESI.† A 10 million endurance cycle test using dynamic programming pulses is also carried out, where it is found that the programming window needed for the PL ferrofluid is only 4.4 μs, whereas, for EMG ferrofluid, it is 11 μs. We know that the electrodynamics of the system reflects its impedance versus frequency behaviour: oleic acid acts as an insulator, while water soluble surfactants might be more conductive and dissipate higher currents, negatively affecting the duration of the measures and optimal timings. In addition to this, a reduction in error when reading HRS and LRS values is also observed. Fig. 8(b) and (c) show the comparison of error between the two categories of ferrofluids when reading HRS and LRS values. The oleic acid cap layer reduces the negative read voltage error by half and the error due to increased post-write resistance by 35% when reading LRS values. Also, when reading HRS values there is a slight reduction of error due to negative read voltage. Surprisingly, the nano battery effects are also minimized due to the stabilization of oleic acid whose results can be compared from Fig. 6(c) and 8(a). The high-performance colloid's 100 million endurance characterization switching cycles, the statistical distribution of the HRS and LRS values, and the applied read voltages are shown in Fig. S12(a)–(d) of the ESI.† The increased stability of nanoparticles in the ferrofluid with oleic acid has also led to the reduction of variation (3σ) to about 46% in the LRS and HRS values whose differences are observed in Fig. S12 and S13 of the ESI.† Considering the resolution of the output of the 8-bit DAC in the MicroPython board and the applied read voltage across the ferrofluid, we experimentally determined the value of the dominant factors – DC offset, gain errors, and noise (v_o), whose mean value is about 1.2 mV and its statistical spread is shown in Fig. 8(d).

Fig. 8 (a) IV characteristics of PL ferrofluid for 30 full cycles of switching between the erase and write cycles, (b) comparison of error (in %) due to negative read voltage and post-erase resistance reaching below threshold post-erase resistance when reading HRS values, (c) comparison of error (in %) due to negative read voltage and post-write resistance reaching above threshold post-write resistance when reading LRS value, (d) statistical spread of the DC offset, gain errors, and noise across the read path of the characterization set-up.

Table S3 (ESI†), presented in Section S7 of the ESI† compares the specifications of the proposed liquid-based memory with its solid-state counterparts. The magnetite (Fe₃O₄) based liquid synapse combines the advantages of FERAM and ReRAM by having high endurance cycles and lower dynamic range. We also applied a low-power read operation in pulse mode by applying read voltages of about 14 mV amplitude, which are only influenced by DC offset, gain errors, and noise. The high frequency noise resulting mainly due to the setup gets averaged and passes through when we apply read pulses.⁵¹ Resistance switching in liquid-based memories (such as ferrofluid) is also quite deterministic, unlike solid-state memories where intrinsic stochasticity is inherent. The fault-tolerant capability of the ferrofluid-based liquid memories does not age or die out like the conventional solid-state memories, which are highly vulnerable to ESD (electrostatic discharge) and accidental damages. The primary reason to apply the least magnitude of read bias is to make a low-power inference at the system level when classifying patterns, etc., and by doing so, we join the group of specific memory technologies where read biases of less than 100 mV are applied and this comparison along with the ON/OFF ratio is shown in Fig. S15 of the ESI.† The feature of scaling down the size of ferrofluid synapse is experimentally validated by minimizing the distance between the electrodes and the volume of the ferrofluid using a newly designed vial with adjustable volume (as detailed in Section S4.2 of the ESI†). The results of these experiments are shown in Fig. S16 of the ESI,† which prove the capability of scaling down the ferrofluid synapses thereby obtaining higher electric field similar to nanoscale solid state memories. This opens a new era of possibility of monolithic integration of ferrofluid synapses with technologies such as thin film transistors⁵² in the future.

5 Pattern recognition using spike-based unsupervised learning

To evaluate the capabilities of the ferrofluid, a circuit-level simulation is carried out to learn patterns and digits in the Simulink environment of MATLAB® using the experimental resistance switching characteristics of the ferrofluid and other behavioral circuits and components. Unlike conventional digital approaches in computational neuroscience, the ANN is simulated at the circuit and system level to give an insight into the analog in-memory computing perspective. The considered patterns and the numbering of the pixels are shown in Fig. 9(a). The scheme of the 4 × 4 synaptic crossbar is shown in Fig. 9(b) where four pre-synaptic drivers, pre_{a,b,c,d} are fully connected to the four post-synaptic neurons, pos_{a,b,c,d} with sixteen liquid synapses, s_{1,2,…,16}, whose switching characteristics are equivalent to the ferrofluid characterized earlier. A switch is used in series with each synapse to avoid sneak path currents,⁵³ provided our preliminary characterization experiments (explained in Section 4) reveal – the ferrofluid does not require any compliance currents for ‘erase’ or ‘write’ tasks. This aspect marks a gap in comparison to solid-state memories, where delimiting switches are needed for healthy resistance switching. The switches in the crossbar also facilitate selecting a synapse and applying the desired bias without disturbing the states of the other synapses. A spike processor control block is implemented where the STDP learning rule is carried out. It collects and compares the time of occurrence of the digital output spikes, tpos_{a,b,c,d} from the post-synaptic neurons and the time of occurrence of the incoming pre-synaptic spikes, tpre_{a,b,c,d} whose inputs are the pixels of the patterns in the form of read pulses fed to the system within the time frame.

Fig. 9 (a) Numbering of the 2 × 2 pixel and different patterns considered for learning, (b) scheme of the 4 × 4 synaptic crossbar where the patterns are applied as read pulses across the rows, (c) scheme of the pre-synaptic drivers and post-synaptic neurons with their digital control signals, and (d) flowchart for carrying out spike-based unsupervised learning for pattern recognition.

The scheme of the pre-synaptic drivers, post-synaptic neurons, and the digital control for the switch inputs (g_{a,b,c,d}) is shown in Fig. 9(c), which primarily has OpAmps and two sets of switches connected in combination so that one set of switch connections is used to select the synaptic task (like ‘read’, ‘erase’, ‘write’, ‘idle’, and ‘reset’), while the other is used to choose a synapse in the 4 × 4 synaptic array. ‘idle’ condition is applying similar biases at the terminals of the synapse without changing its state whereas, the ‘reset’ of the post-synaptic drivers is carried out after every pixel input. The pre-synaptic driver's OpAmps are connected in buffer configuration, while one of these post-synaptic OpAmps is used to establish different feedback loops to implement specific synaptic tasks, and during ‘read’ the integrated (using the capacitor, c_int) outputs are compared with a reference bias, v_c using the comparator OpAmps. During on-chip implementation attenuation of inference current is carried out by implementing circuits like Gilbert's current normalizer,⁵⁴ MOS-ladder,⁵⁵ and modified current normalizer (MCN)⁵⁶ to minimize the size of the integrating capacitor (c_int), particularly when reading the post-write resistance. The digital nodes, A and B are used to pick the desired synaptic task, while R_A, R_B, C_A and C_B are used to choose a synapse in the array. As the same feedback loops are used for ‘erase’, ‘write’, ‘idle’, and ‘reset’, it further reduces the number of switches.

The analog biases applied on the crossbar terminals are categorized into ‘active’ and ‘default’ biases. When a synapse is chosen, active biases are applied across its terminal whereas the unselected synaptic terminals are applied with default biases. The active biases applied at the top of the synapse are – v_tra (for ‘read’), v_twa (for ‘write’), v_tea (for ‘erase’) and v_tia (for ‘idle’), while its default biases are – v_trd (for ‘read’), v_twd (for ‘write’), v_ted (for ‘erase’) and v_tid (for ‘idle’). Similarly, the nomenclature of the names of the active and default biases applied at the bottom of the synapse are replaced with ‘b’ in the above eight biases (for example – v_bra, v_bwa, v_bea, and so on). The biasing conditions and values of the components, used in the pre-synaptic drivers, post-synaptic neurons, and control for the switches (near synapses) are listed in Table S4 of the ESI.† The switch condition (either open or closed) shown in Fig. 9(c) is when the digital input, ‘reset’ is activated. For example – if we want to choose the synapse, s₇ and apply ‘erase’, the digital signals applied are – reset = LOW, A = HIGH, B = LOW, R_A = LOW, R_A = HIGH, C_A = LOW, and C_A = HIGH. In this way, an ‘erase’ is carried out across s₇ thereby leaving other rows, r_{a,c,d} and columns, c_{a,c,d} being biased with default biases to leave unchanged the state of other unselected synapses.

Pattern recognition using the STDP learning algorithm is based on – updating the weights of the synapses using the STDP rule i.e. by determining the time of occurrence of the pre-synaptic and post-synaptic pulses. When the post-synaptic pulse spikes after the pre-synaptic pulse, the weight of the corresponding synapse is strengthened, and when the pre-synaptic pulse spikes after the post-synaptic pulse or when there is no pre-synaptic pulse, the weight of the corresponding synapse is weakened. Fig. 9(d) shows the flowchart for carrying out the STDP learning for pattern recognition where the indicated variables – ‘m’ and ‘n’ are the number of rows and the number of patterns considered. The times of occurrence of tpos_{a,b,c,d} and tpre_{a,b,c,d} pulses are stored in a memory array for each pixel throughout the simulation. Hence, we will have four values of times of occurrence for each post-synaptic pulse when the whole pattern is fed into the system. The internally stored time of occurrence of tpos_{a,b,c,d} is compared with the time of occurrence of its corresponding tpre_{a,b,c,d} and the appropriate synaptic weight s_{1,2,…,16} is updated using the spike processor control based on the STDP learning rule and an additional condition. The condition is – when two or more post-synaptic pulses spike at the same time, priority for weight update is given to the contributing neuron with a ‘minimum index’ number and the one that hasn’t learned any pattern yet. The STDP binary weight update is done in steps for the synapses in the crossbar such that the weights evolve from ‘random values’ to reach ‘learned values’, which results in each post-synaptic neuron learning an individual pattern. In this combination of using STDP learning rule and using integrate and fire neurons as post-synaptic neurons, the neuron that learns has to fire faster, thereby correlating with an applied particular pattern and the STDP weight updates continue until all neurons distinctly learn an input pattern. Also, after learning, the final results of pattern recognition using the unsupervised STDP learning rule differ for different initial weights. Fig. S17 of the ESI† shows the waveforms of the applied pre-synaptic pulse, the output waveforms of the post-synaptic neurons, the output of the integrators of the post-synaptic neurons, the binary weights updates, reset signal, cycle, etc. for a randomly assigned initial weight of the 4 × 4 synaptic crossbar. Fig. S18 of the ESI† shows how the weights evolve from four different random weights to become learned weights thereby making different neurons in all four cases learn uniquely the applied patterns. The approach is extended to classify digits, 0 to 9 in a 3 × 3 image pixel using STDP learning rule and by implementing an additional condition, which is – the synapses of the neurons that have already learned do not take part in the future weight updates. This is done to keep the number of weight updates uniform in the learning process for all random initial weights. Note that each digit corresponds to a unique combination of serialized bits. A 9 × 10 synaptic crossbar is used to realize the learning results. Fig. 10(a) shows the numbering of the 3 × 3 pixel and the pixel arrangements for digits from 0 to 9, which our neural network classifies. Fig. 10(b) shows how the weight evolves from four different initial weights to become learned weights thereby making the post-synaptic neurons learn the digits uniquely for different initial weights. For example – in the first case the first post-synaptic neuron learns digit 1 whereas in the second case, the same neuron learns digit 7, and so on.

Fig. 10 (a) Numbering of the 3 × 3 pixel and pixel arrangement of digits (0 to 9) considered for learning, (b) STDP weight updates applied on four random initial weights to achieve learned weights for learning digits, 0 to 9. The weights of the post-synaptic neurons that faced STDP weight updates are highlighted at every weight update.

6 Conclusions

In this work, we show the features of a ferrofluid-based neuromorphic liquid synapse that has excellent resistance switching properties, including high endurance, lower dynamic range, deterministic switching behavior and exhibits short term plasticity (STP). It does not require either forming or current compliance requirements. We experimentally observe the improvement in yield and reduction in variation of the resistance values by stabilizing the PL ferrofluid with oleic acid, instead of polar surfactants as in EMG one. The entire setup is based on low-cost components, and read biases feature low magnitudes, thereby paving the way for a low-power inference system, whose results are only affected by offset, gain errors, and noise of the system. Ferrofluid volumes are taken as small aliquots from a batch size of up to 1 L volume. In an industrial production chain, device-to-device variability can be avoided by properly sizing the amount of raw materials needed and stored as homogeneous reservoir, partitioned and dispensed in the smaller volumes necessary for production. This represents a competitive advantage of the liquid electronic devices over conventional solid state ones. We finally validate the feature for scaling down the size of the ferrofluid synapse and extend the characterization results to verify the capabilities of the ferrofluid used as neuromorphic liquid synapses matrix in artificial neural networks to classify digits from 0 to 9 in a 3 × 3 image pixel by applying the spike-based learning rule. The experimental DC characterization results, verification of short term plasticity, and capability of scaling down the size of the neuromorphic liquid synapse make it a promising futuristic candidate for CMOS integration in realizing ANNs for analog in-memory computing.

Author contributions

C. M. conceived the idea, designed the experiments, interpreted the data, performed the memristive simulations, and wrote the manuscript; M. C. and A. C. co-wrote the manuscript, assisted and oversaw the experimental measurements, and contributed to data discussion and interpretation; D. D. designed and fabricated both the vials for the experiment including their assembly; A. A. assisted in writing the manuscript and contributed to data discussion and interpretation; G. A. and A. S. performed physico-chemical analyses and related data analyses; A. C. performed LTP measurements.

Data availability

Data will be available from the corresponding author upon request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has received funding from the European Innovation Council and SMEs Executive Agency (EISMEA) under grant agreement No. 964388. We would like to thank Alessandro Barcellona, Francesco Diotalevi and Claudio Lorini for helping in making the PCB. We also thank Carsten Jost and Alexei Antipov (from PlasmaChem) for synthesizing the ferrofluid with the oleic acid surfactant.

References

1. C. S. Calude, J. Casti and M. J. Dinneen, Unconventional Models of Computation, Springer, Singapore, 1998.
2. G. E. Moore, Cramming More Components onto Integrated Circuits, Electronics, 1965, 38, 114–117.
3. A. Adamatzky, Unconventional Computing, Springer, New York, 2018.
4. A. Adamatzky, Handbook of Unconventional Computing, World Scientific, Singapore, p. 2021.
5. R. K. Cavin, P. Lugli and V. V. Zhirnov, Science and Engineering Beyond Moore's Law, Proc. IEEE, 2012, 100, 1720–1749.
6. S. Ji, The cell as the smallest DNA/based molecular computer, BioSystems, 1999, 52, 123–133.
7. A. Danchin, Bacteria as computers making computers, FEMS Microbiol. Rev., 2008, 33, 3–26.
8. C. T. Fernando, A. M. L. Liekens, L. E. H. Bingle, C. Beck, T. Lenser, D. J. Stekel and J. E. Rowe, Molecular circuits for associative learning in single-celled organisms, J. R. Soc. Interface, 2009, 6, 463–469.
9. C. Mead, Analog VLSI and Neural Systems, Addison Wesley, 1989.
10. F. Alibart, E. Zamanidoost and D. B. Strukov, Pattern classification by memristive crossbar circuits using ex-situ and in situ training, Nat. Commun., 2013, 4, 2072.
11. S. Choi, P. Sheridan and W. D. Lu, Data Clustering using Memristor Networks, Sci. Rep., 2015, 5, 10492.
12. S. Duan, X. Hu, Z. Dong, L. Wang and P. Mazumder, Memristor-based cellular nonlinear/neural network: design, analysis, and applications, IEEE Trans. Neural Network Learn. Syst., 2015, 26, 1202–1213.
13. J. Moon, W. Ma, J. H. Shin, F. Cai, C. Du, S. H. Lee and W. D. Lu, Temporal data classification and forecasting using a memristor-based reservoir computing system, Nat. Electron., 2019, 2, 480–487.
14. F. Cai, J. M. Correll, S. H. Lee, Y. Lim, V. Bothra, Z. Zhang, M. P. Flynn and W. D. Lu, A fully integrated reprogrammable memristor-CMOS system for efficient multiply-accumulate operations, Nat. Electron., 2019, 2, 290–299.
15. J. von Neumann, The Computer and the Brain, Yale University Press, New Haven/London, 1958.
16. M. Hosomi, H. Yamagishi, T. Yamamoto, K. Bessho, Y. Higo, K. Yamane, H. Yamada, M. Sholi, H. Hachino, C. Fukumoto, H. Nagao and H. Kano, IEEE International Electron Devices Meeting, Washington DC, USA, 2005.
17. F. Pellizzer, A. Pirovano, F. Ottogalli, M. Magistretti, M. Scaravaggi, P. Zuliani, M. Tosi, A. Benvenuti, P. Besana, S. Cadeo, T. Marangon, R. Morandi, R. Piva, A. Spandre, R. Zonca, A. Modelli, E. Varesi, T. Lowrey, A. Lacaita, G. Casagrande, P. Cappelletti and R. Bez, Digest of Technical Papers, Symposium on VLSI Technology, 2004, pp. 18–19.
18. D. Garbin, E. Vianello, O. Bicher, Q. Rafhay, C. Gamrat, G. Ghibaudo, B. DeSalvo and L. Perniola, HfO₂ -based OxRAM Devices as Synapses for Convolution Neural Networks, IEEE Trans. Electron Devices, 2015, 62, 2494–2501.
19. S. Dietrich, M. Angerbauer, M. Ivanov, D. Gogl, H. Hoenigschmid, M. Kund, C. Liaw, M. Markert, R. Symanczyk, L. Altimime, S. Bournat and G. Mueller, A Nonvolatile 2-Mbit CBRAM Memory Core Featuring Advanced Read and Program Control, IEEE, J. Solid State Circ., 2007, 42, 839–845.
20. J. Okuno, T. Kunihiro, M. Konishi, K. Materano, T. Ali, K. Kuehnel, K. Seidel, T. Mikolajick, U. Schroeder, M. Tsukamoto and T. Umebayashi, 1T1C FeRAM Memory Array Based on Ferroelectric HZO With Capacitor Under Bitline, IEEE J. Electron Devices Soc., 2021, 10, 29–34.
21. M. Sangermano, L. Vescovo, N. Pepino, A. Chiolerio, P. Allia, P. Tiberto, M. Coïsson, L. Suber and G. Marchegiani, Photoinitiator-free UV-cured acrylic coatings containing magnetite nanoparticles, Macromol. Chem. Phys., 2010, 211, 2530–2535.
22. P. Allia, P. Tiberto, M. Coïsson, A. Chiolerio, F. Celegato, F. Vinai, M. Sangermano, L. Suber and G. Marchegiani, Evidence for magnetic interactions among magnetite nanoparticles dispersed in photoreticulated PEGDA-600 matrix, J. Nanopart. Res., 2011, 13, 5615–5626.
23. L. Cecchini and A. Chiolerio, The magnetic body force in ferrofluids, J. Phys. D:Appl. Phys., 2021, 54, 355002.
24. S. S. Papell, Low viscosity magnetic uid obtained by the colloidal suspension of magnetic particles, US Pat., US3215572 A, 1965.
25. W. Ochoński, Z. Szydlo and B. Zachara, Paper presented at The Tribology conference, 7-12 June, Nagasaki, Japan, 2000.
26. W. Bottenberg, L. Melillo and K. Raj, The dependence of loudspeaker design parameters on the properties of magnetic fluids, J. Audio Eng. Soc., 1980, 28, 17–25.
27. S. Y. Huang, L. M. Jiang, H. X. Qian, X. M. Shen, D. C. Sun, Y. F. Tang and Y. M. Wen, On the Magnetic Sealing Capability of Ferrofluid-Lubricated Journal Bearings, Proc. R. Soc. London, Ser. A, 1986, 404, 69–88.
28. A. K. Deysarkar and B. H. Clampitt, Evaluation of ferrofluids as lubricants, J. Synth. Lubr., 1988, 5, 105–114.
29. H. Zhu, C. Zhang, S. Liu, Y. Tang and Y. Yin, Effects of nanoparticle clustering and alignment on thermal conductivities of Fe₃O₄ aqueous nanofluids, Appl. Phys. Lett., 2006, 89, 023123.
30. X. Fan, M. Sun, L. Sun and H. Xie, Ferrofluid Droplets as Liquid Microrobots with Multiple Deformabilities, Adv. Funct. Mater., 2020, 30, 2000138.
31. J. V. I. Timonen, M. Latikka, L. Leibler, R. H. A. Ras and O. Ikkala, Switchable Static and Dynamic Self-Assembly of Magnetic Droplets on Superhydrophobic Surfaces, Science, 2013, 341, 253–257.
32. X. Fan, X. Dong, A. C. Karacakol, H. Xie and M. Sitti, Reconfigurable multifunctional ferrofluid droplet robots, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 27916–27926.
33. M. Crepaldi, C. Mohan, E. Garofalo, A. Adamatzky, K. Szaciłowski and A. Chiolerio, Experimental Demonstration of In-Memory Computing in a Ferrofluid System, Adv. Mater., 2023, 35, 2211406.
34. EMG 600P Series – 601P, 603P, 605P, 607P, 608P Ferrofluid, https://ferrofluid.ferrotec.com/wp-content/uploads/sites/3/emg600psds.pdf, Accessed: 2023-11-03.
35. Ferrofluid stabilized with oleic acid, https://shop.plasmachem.com/oxide-nanoparticles/121-664-magnetic-fluid-fe3o4-ca7v-aqsusp-stabilized-with-oleic-acid.html#/41-volume-10ml, Accessed: 2023-11-03.
36. M. Klinger, More features, more tools, more CrysTBox, J. Appl. Crystallogr., 2017, 50, 1226–1234.
37. A. P. Grosvenor, B. A. Kobe, M. C. Biesinger and N. S. McIntyre, Investigation of multiplet splitting of Fe 2p XPS spectra and bonding in iron compounds, Surf. Interface Anal., 2004, 36, 1564–1574.
38. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. Lau, A. R. Gerson and R. S. Smart, Resolving surface chemical states in XPS analysis of first row transition metals, oxides and hydroxides: Cr, Mn, Fe, Co and Ni, Appl. Surf. Sci., 2011, 257, 2717–2730.
39. A. Naumkin, A. Kraut-Vass and S. Gaarenstroom, Photoelectron, C. P. N. X.-r. Spectroscopy Database, 2023.
40. G. Beamson, High Relution XPS of Organic Polymers. The Scienta ESCA 300 Database. ICIplc, 1992.
41. MicroPython Pyboard v1.1, https://store.micropython.org/product/PYBv1.1, Accessed: 2023-07-27.
42. E. M. Purcell, Life at low Reynolds number, Am. J. Phys., 1977, 45, 3–11.
43. A. Chiolerio, E. Garofalo, N. Phillips, E. Falletta, R. de Oliveira and A. Adamatzky, Learning in colloidal polyaniline nanorods, Results Phys., 2024, 58, 107501.
44. R. Fortulan, N. R. Kheirabadi, N. Raeisi-Kheirabadi, A. Nezamzadeh-Ejhieh, A. Chiolerio and A. Adamatzky, Fractional-order memristive dynamics in colloidal graphitic carbon nitride systems, Phys. Rev. E, 2024, 110, 034607.
45. N. R. Kheirabadi, A. Chiolerio, N. Phillips and A. Adamatzky, Learning in colloids: Synapse-like zno+ dmso colloid, Neurocomputing, 2023, 557, 126710.
46. B. K. Ridley, in Negative Differential Resistance: A Brief History and Review, ed. N. Balkan, B. K. Ridley and A. J. Vickers, Springer US, Boston, MA, 1993, pp. 1–21.
47. E. Garofalo, M. Bevione, L. Cecchini and A. Chiolerio, On the Pyroelectric and Triboelectric Phenomena in Ferrofluids, Adv. Mater. Technol., 2022, 7, 2200127.
48. I. Valov, E. Linn, S. Tappertzhofen, S. Schmelzer, J. van den Hurk, F. Lentz and R. Waser, Nanobatteries in redox-based resistive switches require extension of memristor theory, Nat. Commun., 2013, 4, 1771.
49. A. Chiolerio, S. Bocchini, K. Bejtka and C. F. Pirri, Bridging electrochemical and electron devices: fast resistive switching based on polyaniline from one pot synthesis using FeCl3 as oxidant and co-doping agent, Synth. Met., 2022, 229, 72–81.
50. F. Liu, C. H. Chang, J. Shen and B. B. Pant, Characteristics of Electrostatic Discharge Induced Damage on Magnetic Tunnel, IEEE Trans. Magn., 2006, 42, 2447–2449.
51. C. Mohan, L. A. Camuñas-Mesa, J. M. de la Rosa, E. Vianello, T. Serrano-Gotarredona and B. Linares-Barranco, Neuromorphic Low-Power Inference on Memristive Crossbars With On-Chip Offset Calibration, IEEE Access, 2021, 9, 38043–38061.
52. FLexIC Foundry of Pragmatic, https://www.pragmaticsemi.com/flexible-ics/custom-ics, Accessed: 2023-12–13.
53. Y. Cassuto, S. Kvatinsky and E. Yaakobi, 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 2013.
54. B. Gilbert, in Analogue IC design: the current-mode approach, ed. C. Toumazou, F. J. Lidgey and D. G. Haigh, Peter Peregnirus, London, 1990.
55. K. Bult and G. J. G. M. Geelen, An inherently linear and compact MOST-only current division technique, IEEE, J. Solid State Circ., 1992, 27, 1730–1735.
56. C. Mohan, J. M. de la Rosa, E. Vianello, L. Perniola, C. Reita, T. Serrano-Gotarredona and B. Linares-Barranco, IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 2019.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01592d

---