Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simulating open quantum systems with molecular spin qudits†
Sebastián
Roca-Jerat
 ae,
Emilio
Macaluso
ae,
Emilio
Macaluso
 b,
Alessandro
Chiesa
b,
Alessandro
Chiesa
 bcd,
Paolo
Santini
bcd,
Paolo
Santini
 bcd and
Stefano
Carretta
bcd and
Stefano
Carretta
 *bcd
*bcd
aInstituto de Nanociencia y Materiales de Aragón (INMA), CSIC-Universidad de Zaragoza, Zaragoza 50009, Spain
bUniversità di Parma, Dipartimento di Scienze Matematiche, Fisiche e Informatiche, 43124 Parma, Italy. E-mail: stefano.carretta@unipr.it
cGruppo Collegato di Parma, INFN-Sezione Milano-Bicocca, I-43124 Parma, Italy
dUdR Parma, INSTM, I-43124 Parma, Italy
eDepartamento de Física de la Materia Condensada, Universidad de Zaragoza, Zaragoza 50009, Spain
First published on 19th March 2025
Abstract
Noise affecting quantum processors still limits quantum simulations to a small number of units and operations. This is especially true for the simulation of open quantum systems, which involve additional units and operations to map environmental degrees of freedom. Hence, finding efficient approaches for the simulation of open quantum systems is an open issue. In this work, we demonstrate how using units with d > 2 levels (qudits) results in a reduction of up to two orders of magnitude in the number of operations (gates) required to implement state-of-the-art algorithms. We explore two conceptually distinct families of these algorithms that were initially designed for qubits and discuss the gate complexity scaling that different platforms (qubit-based vs. qudit-based) offer. Additionally, we present realistic simulations of an experimental platform based on molecular spin qudits coupled to superconducting resonators, where the main hardware error sources are included. We show that, in all cases considered, the use of qudits leads to a remarkable reduction in circuit complexity and that molecular nanomagnets are ideal qudit hosts.
New conceptsWe propose a new point of view about the digital quantum simulation of open quantum systems (OQS) by showcasing the potential of units with more than two logical levels (qudits). Efficiently simulating OQS is important for designing novel quantum technologies. We demonstrate that qudits reduce the number of gates needed for incoherent (but controlled) dynamics by nearly two orders of magnitude using state-of-the-art algorithms originally conceived for qubits. This improvement helps to bridge the gap between circuit execution times and decoherence times in current noisy devices. We show that molecular nanomagnets coupled to superconducting resonators are ideal materials to implement this novel approach to quantum simulations, exploiting the chemical tunability of molecular spin qudits combined with the ability of superconducting resonators to wire and control them. This work opens the door for an efficient use of molecular qudits to circumvent the poor scaling in the number of non-local gates required to simulate OQS exhibited thus far by qubit-based platforms and promotes the synthesis of new molecular materials designed to provide the required number of levels and optimal connectivity for faster circuit execution. |
1 Introduction
The ever-growing development of quantum computers recently allowed for public accessibility to noisy intermediate-scale quantum (NISQ) computers.1 Now, great efforts of conceptualization and implementation of efficient quantum simulations is bringing closer the future envisioned by Feynman2 in which we are finally able to tackle quantum phenomena which go beyond classical computation.3 However, interaction with the environment typical of open quantum systems (OQS) represents a double-edged sword in such applications. On the one hand, it is the primary cause of the “noisy” nature of nowadays quantum simulators, limiting the computational power of algorithms developed on such platforms. On the other hand, since most quantum systems of relevant interest are effectively OQS, quantum simulators are faced with the problem of simulating non-unitary time evolution together with the coherent Hamiltonian dynamics. This represents a significant challenge, since in the digital computing paradigm the controlled dynamics simulated by quantum computers is limited to unitary quantum gates. This challenge has been met with considerable theoretical developments over the last two decades,4–15 resulting in initial experimental demonstrations on multiple qubit-based systems.16–23 In all these algorithms, an auxiliary system, or ancilla, serves as an artificial environment with which the target system interacts. We distinguish two main families of techniques. The first comprises algorithms based on Stinespring's dilation theorem,24 where the dimension of the ancilla system increases with the complexity of the environment being simulated,7,10,19,21,23,25 offering a more straightforward implementation at the cost of a larger ancilla system. The second calls for usually more sophisticated circuits but maintains the advantage of a small and constant ancilla register dimension regardless of problem size.6,8,18,22,26–31In this work, we demonstrate how the use of units with d > 2 levels (qudits) can significantly decrease the circuit complexity for both classes of algorithms. The use of qudits to simulate OQS was already proposed in ref. 32 to encode the degrees of freedom of the system, but not for the environment. Here, we show a more general study on how the use of qudits can be crucial for hosting both the target system and the ancilla in a wide variety of scenarios. We present a detailed implementation proposal for simulating OQS on a real platform based entirely on molecular spin qudits.33,34 These systems exhibit promising features for quantum computing, including long coherence times even at high temperatures35–39 and efficient implementation of single- and multi-qubit gates via microwave or radio-frequency pulses.40,41 The high degree of chemical control over their synthesis allows tailoring energy levels for specific applications42,43 and limiting decoherence.35,44 This chemical engineerability facilitates scalability of multi-qubit systems with switchable interactions, achievable through molecular spins alone34,42,43 or by integrating them with superconducting resonators.45–49 Importantly, molecular spin qudits—derived from individual spin S > 1/2 ions or low-energy multiplets of strongly coupled magnetic ions—can reduce the number of computational units and required gates for a given algorithm, potentially offering computational bases more resilient to decoherence.34 The versatility offered by molecular systems can benefit other applications such as quantum error correction50–52 and quantum simulation of closed systems.43,53,54
Here, we demonstrate that molecular spin qudits also provide an efficient platform for simulating OQS. For both families of algorithms mentioned above, we demonstrate a remarkable reduction of circuit complexity (up to two orders of magnitude) by replacing multiple qubits with d > 2 qudits. Specifically, complexity is measured by the number of required single- and two-body gates.55,56 This reduction is especially pronounced when the target of the simulation involves multi-level systems (e.g. spins S > 1/2). We perform numerical simulations for the combined coherent and incoherent dynamics of target one- and two-qubit systems, using both algorithms, finding very good results. These simulations are based on the blueprint of a molecular-spin quantum processor consisting of molecular spin qudits strongly coupled to superconducting resonators45 and include the most significant errors related to dissipation and decoherence. These results open the door for the integration of qudits into quantum digital computation, enabling the efficient tackling of complex problems where the use of qubits is inefficient.
2 Results
2.1 Qubits vs. qudits for simulating open quantum systems
We start by taking as a practical example a spin-3/2 particle interacting with a Markovian bath. The dynamics of such an OQS can be described by the Lindblad equation: | (1) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) and Lk do not depend explicitly on time, eqn (1) can be directly integrated as |ρ(t)〉 = e
and Lk do not depend explicitly on time, eqn (1) can be directly integrated as |ρ(t)〉 = e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) t|ρ(t = 0)〉, where |ρ〉 is the unraveled density operator in the vector form and
t|ρ(t = 0)〉, where |ρ〉 is the unraveled density operator in the vector form and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) is the related super-operator.57 The Lindblad equation relies on the Born (weak system–bath interaction), Markov (no memory of the bath) and secular approximations.58,59 Some of the above assumptions can fail in describing decoherence in relatively small molecules. For instance, the Markov approximation is not fulfilled where the nuclear spin bath is of limited size. Nonetheless, the Lindblad description represents one of the simplest and most widely used formalisms to model decoherence and hence is an optimal starting point for investigating algorithms on the quantum simulation of open systems. We also note that the presented approaches could be extended also to more complex forms of the system–bath interaction, which are not captured by the Lindblad formalism.
is the related super-operator.57 The Lindblad equation relies on the Born (weak system–bath interaction), Markov (no memory of the bath) and secular approximations.58,59 Some of the above assumptions can fail in describing decoherence in relatively small molecules. For instance, the Markov approximation is not fulfilled where the nuclear spin bath is of limited size. Nonetheless, the Lindblad description represents one of the simplest and most widely used formalisms to model decoherence and hence is an optimal starting point for investigating algorithms on the quantum simulation of open systems. We also note that the presented approaches could be extended also to more complex forms of the system–bath interaction, which are not captured by the Lindblad formalism.
The evolution given by M(t) = e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) t commonly consists of several non-commuting terms which are implemented through a series of subsequent unitary gates on the hardware. For instance, one could split
t commonly consists of several non-commuting terms which are implemented through a series of subsequent unitary gates on the hardware. For instance, one could split ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) into the coherent and incoherent dynamics,
into the coherent and incoherent dynamics, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) =
= ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) c +
c + ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) inc. The Suzuki–Trotter approximation allows for a simple solution to this problem by replacing the time-evolution operator M(t) = e
inc. The Suzuki–Trotter approximation allows for a simple solution to this problem by replacing the time-evolution operator M(t) = e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) t with multiple operators Mi(t/NT) = e
t with multiple operators Mi(t/NT) = e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) it/NT which can all be translated into quantum gates. This can be written as:
it/NT which can all be translated into quantum gates. This can be written as:
 | (2) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) i are non-commuting terms of
i are non-commuting terms of 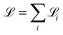 , Δt = t/NT and NT is the number of Trotter steps. The larger the NT, the smaller the error introduced by this approximation (a.k.a. digital error), which scales as
, Δt = t/NT and NT is the number of Trotter steps. The larger the NT, the smaller the error introduced by this approximation (a.k.a. digital error), which scales as ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (t2/NT2).60 However, in NISQ devices each gate involves an error (due, e.g., to decoherence or imperfections in the implementation) and hence increasing NT yields a detrimental error accumulation. The choice of NT is therefore associated to a trade-off between digital and implementation errors. For a more comprehensive discussion on the possible errors one may encounter in NISQ devices, we refer the reader to ref. 23.
(t2/NT2).60 However, in NISQ devices each gate involves an error (due, e.g., to decoherence or imperfections in the implementation) and hence increasing NT yields a detrimental error accumulation. The choice of NT is therefore associated to a trade-off between digital and implementation errors. For a more comprehensive discussion on the possible errors one may encounter in NISQ devices, we refer the reader to ref. 23.
Alternatively, the dynamics of the OQS can be computed at discrete time steps through the dynamical map:
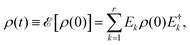 | (3) |
 , and r is the Kraus rank or Choi rank, such that r ≤ ds2, ds being the dimension of the Hilbert space. This description is usually employed by algorithms in which the ancilla mimics the environment, and its effect on the target system is divided into the successive application of the different operators Ek.19
, and r is the Kraus rank or Choi rank, such that r ≤ ds2, ds being the dimension of the Hilbert space. This description is usually employed by algorithms in which the ancilla mimics the environment, and its effect on the target system is divided into the successive application of the different operators Ek.19
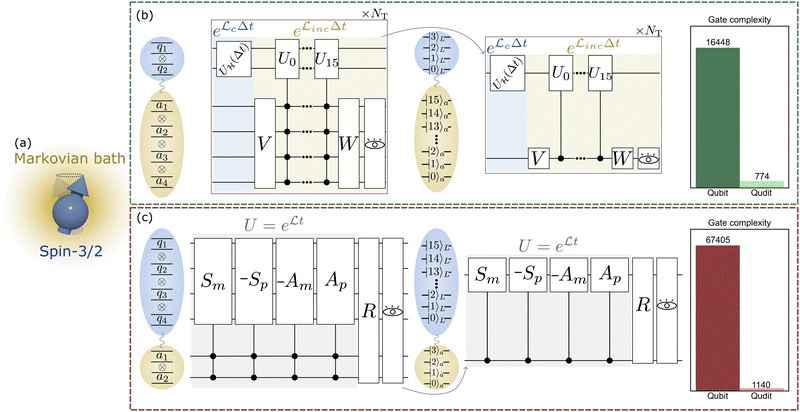
The first algorithm we consider belongs to this family of algorithms, in which two registers are required. The first one contains the degrees of freedom of the target system (for instance, the spin-3/2 with ds = 4). The second one is an ancilla which mimics the environment and whose size grows with the rank of the Kraus map in eqn (3). The joint coherent and incoherent evolution (driven, respectively, by U![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (Δt) = exp [− i
(Δt) = exp [− i![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) Δt] and by eqn (3)) can be implemented by exploiting a Suzuki–Trotter decomposition [eqn (2)] of the associated super-operator. The quantum circuit accomplishing this is presented in Fig. 1(b). On the left side, the circuit originally proposed for qubits is shown. Two qubits are needed to represent the target spin-3/2 system, and up to 4 qubits as the ancilla to represent the most general scenario, where the Kraus rank is maximum, r = ds2 = 16. The block labeled e
Δt] and by eqn (3)) can be implemented by exploiting a Suzuki–Trotter decomposition [eqn (2)] of the associated super-operator. The quantum circuit accomplishing this is presented in Fig. 1(b). On the left side, the circuit originally proposed for qubits is shown. Two qubits are needed to represent the target spin-3/2 system, and up to 4 qubits as the ancilla to represent the most general scenario, where the Kraus rank is maximum, r = ds2 = 16. The block labeled e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) incΔt represents the interaction between the environment and the spin-3/2 system. The set of Kraus operators is represented in a basis of unitary operations, {Ui}i=0,15, such as the Pauli matrices, which are the conditional operations applied to the target system. The weights corresponding to each Kraus operator are encoded in the V and W operations, fulfilling the condition
incΔt represents the interaction between the environment and the spin-3/2 system. The set of Kraus operators is represented in a basis of unitary operations, {Ui}i=0,15, such as the Pauli matrices, which are the conditional operations applied to the target system. The weights corresponding to each Kraus operator are encoded in the V and W operations, fulfilling the condition 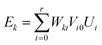 . Finally, a projective measurement on the ancilla traces out the environment's degrees of freedom, effectively applying the incoherent channel over the target system.
. Finally, a projective measurement on the ancilla traces out the environment's degrees of freedom, effectively applying the incoherent channel over the target system.
The number of single- and two-qubit gates required to implement the incoherent part of the dynamics is substantial, as shown in the histogram of Fig. 1(b), mainly due to the necessity of performing gates on the system qubits controlled by the state of all the environment qubits (generalized Toffoli gates; see the ESI†). These non-local operations are required to mimic the entanglement of the environment to the system and represent the main bottleneck of a qubit-based approach. This problem is effectively overcome by using a circuit composed of only two qudits, where a ququart acts as the target system and a 16-level qudit acts as an artificial bath. In this scenario, entangling gates are performed between two physical units, removing the need for non-local operations and causing a staggering reduction in gate complexity: from ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (16
(16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) gates to
000) gates to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (800). Note that this only takes into account the block corresponding to the incoherent part and a single Trotter step. Therefore, this reduction becomes even more remarkable when considering the full time evolution.
(800). Note that this only takes into account the block corresponding to the incoherent part and a single Trotter step. Therefore, this reduction becomes even more remarkable when considering the full time evolution.
The second algorithm we consider is shown in Fig. 1(c). It is based on the implementation of the operator M = e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) t in a single block by dilating the Hilbert space with a 4-level ancilla,27,28 regardless of the dimensionality of
t in a single block by dilating the Hilbert space with a 4-level ancilla,27,28 regardless of the dimensionality of ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) . Note that, since the super-operator M acts on the space of the vectorized density matrix, the register that stores the degrees of freedom of the target system must have ds2 levels. We begin by expressing this M as a sum of four unitary operators according to the following Taylor expansion:
. Note that, since the super-operator M acts on the space of the vectorized density matrix, the register that stores the degrees of freedom of the target system must have ds2 levels. We begin by expressing this M as a sum of four unitary operators according to the following Taylor expansion:
 | (4) |
| RU|ρ(0) ⊕ ρ(0) ⊕ ρ(0) ⊕ ρ(0)〉 = |ρ(t) ⊕ v1 ⊕ v2 ⊕ v3〉, | (5) |
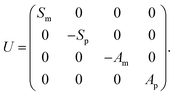 | (6) |
Once again, we present the circuit that implements this algorithm on both a qubit-based platform and a qudit-based platform in Fig. 1(c). Note that the dimensionality of the registers is reversed compared to the previous method [cf.Fig. 1(b)]. Now the gate complexity is even greater than before. This is because both coherent and incoherent dynamics are fully included in the operation U and the matrices Sm, Sp, Am, and Ap have a much more complex internal structure than the matrices Ui of the previous algorithm. However, qudits enable the realization of such operations as controlled gates between two physical units, inducing an even more pronounced decrease in gate complexity with respect to the first algorithm, reaching a factor of ∼60. All information regarding the derivation of the gate complexity in each scenario, as well as a more detailed description of each algorithm, can be found in the ESI.†
Consequently, a qudit approach not only achieves an obvious reduction in the number of physical units in the circuit, but dramatically cuts down the number of single- and two-body gates required for implementation, leading to a substantial increase in efficiency and scalability. In light of this potential, researchers using different platforms are exploring ways to extend control over their units beyond two levels. Examples include transmons,61 trapped ions62,63 or magnetic molecules.34 The latter could offer greater versatility in hosting qudits, due to their ability to accommodate and coherently control many levels, which can also offer a very high mutual connectivity. A clear example of this is the vanadyl porphyrin molecule,64 which hosts an S = 1/2 electronic spin coupled to an I = 7/2 nuclear spin and could be a suitable candidate for the 16-level qudit proposed in Fig. 1.
2.2 Molecular nanomagnets as qudits
Having established that the use of qudits presents a remarkable advantage, we now show that these algorithms can be efficiently implemented on a platform based on molecular spin qudits. Molecular nanomagnets offer a broad catalog of qudit candidates, from complexes with electronic spin to complexes that combine them with nuclear spins, naturally more protected from interaction with the environment. Progress has been made in recent years to produce systems with longer and longer coherence times even scratching the millisecond scale.35 Here we mention a few notable examples and refer the reader to ref. 65 for a more detailed review on the subject. The Cr7Ni polynuclear ring with ground state S = 1/2 is a very good qubit candidate for its remarkable chemical tunability. In particular, Ni2+ can be replaced with another divalent ion (such as Mn2+ or Zn2+), thus changing the total spin of the ground multiplet from 1/2 to 1 or 3/2 and making the resulting ring a potential qudit. In addition, engineering the ligands enabled the reduction of low-energy vibrations and the increase of the coherence time from a few μs to 15 μs.44 Even more importantly, several rings can be combined together into complex supramolecular structures with tailored interactions42,66,67 which can fulfill specific requirements for implementing quantum algorithms. This point is important for the scheme we propose below and will be discussed further.Mononuclear systems based on transition metal ions are also promising qudit candidates. For instance, the [Cr3+(C2O4)3]3− (ref. 68) complex shows an electronic spin S = 3/2 and coherence times of a few μs.
Moreover, molecules consisting of an (effective) electronic spin 1/2 coupled by a strong hyperfine interaction with a nuclear spin I ≥ 3/2 can encode nuclear spin qudits more robust against noise. Examples are represented by Ln-based mononuclear complexes such as Yb(trensal) (S = 1/2, I = 5/2)69 or TbPc2 (I = 3/2)70 and by VO compounds such as VO(TPP) (S = 1/2, I = 7/2), which stands out for its remarkable coherence times of up to 64 μs. VO ions have already been combined into dimers for two-qubit gates71,72 and have demonstrated resilience to decoherence even at high temperatures.37
As a first case study, we consider the case of a single spin-1/2 coupled to a depolarizing channel (DEP). This channel can be described either through the jump operators  , (Si = σi/2 and σi are the Pauli matrices) with γ = 1/TDEP, or by the set of Kraus operators
, (Si = σi/2 and σi are the Pauli matrices) with γ = 1/TDEP, or by the set of Kraus operators 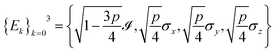 with p(t) = 1 − exp[4t/TDEP]. This channel drives the system towards the maximally mixed state with probability p(t): ρ(t) = [1 − p(t)]
with p(t) = 1 − exp[4t/TDEP]. This channel drives the system towards the maximally mixed state with probability p(t): ρ(t) = [1 − p(t)]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ(0) + p(t)
ρ(0) + p(t)![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) /2.
/2.
We begin by applying the algorithm described in Fig. 1(b). As discussed in the previous section, we need a two-level system to act as our spin-1/2 and a ququart to incorporate the degrees of freedom of the Kraus map. The coherent part of the evolution is driven by U![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (Δt) = e−i
(Δt) = e−i![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) Δt, where
Δt, where  . This Hamiltonian in conjunction with the DEP channel gives rise to damped Rabi oscillations. The block of operations that implements the DEP channel, labeled as e
. This Hamiltonian in conjunction with the DEP channel gives rise to damped Rabi oscillations. The block of operations that implements the DEP channel, labeled as e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) incΔt in Fig. 1(b), is constructed from the decomposition of the Kraus operators into unitary operators. In this case, the process is straightforward. The controlled operations Uj correspond to the Pauli operators, {Ui} = {I,σx,σy,σz}, while the matrices V and W adjust the weights associated with each operator. In this case,
incΔt in Fig. 1(b), is constructed from the decomposition of the Kraus operators into unitary operators. In this case, the process is straightforward. The controlled operations Uj correspond to the Pauli operators, {Ui} = {I,σx,σy,σz}, while the matrices V and W adjust the weights associated with each operator. In this case,  and W =
and W = ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) . Note that in this algorithm the ancilla register always starts and ends in the ground state |0〉a, so only the first column of the matrix V is of interest. The remaining columns can be completed arbitrarily as long as the unitarity condition is satisfied (for more details on the algorithm see the ESI†).
. Note that in this algorithm the ancilla register always starts and ends in the ground state |0〉a, so only the first column of the matrix V is of interest. The remaining columns can be completed arbitrarily as long as the unitarity condition is satisfied (for more details on the algorithm see the ESI†).
As a molecular system to implement this algorithm, we propose the complex schematized in the inset of Fig. 2(a). It consists of two spins (A,B) which encode the degrees of freedom of both the system and environment, respectively. Both are coupled to an antiferromagnetic dimer (M, SM1 = SM2 = 1/2) which provides a switch of the effective A–B interaction.43 For the here-examined case of a single-qubit system subject to the depolarizing channel, we can choose SA = 1/2 and SB = 3/2. This molecular complex is described by the spin Hamiltonian (ħ = 1):
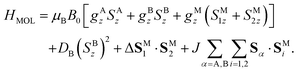 | (7) |
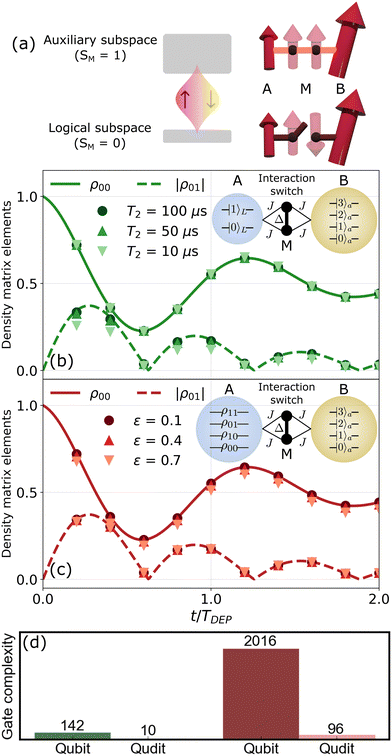 | ||
| Fig. 2 (a) Scheme of how the intermediate antiferromagnetic dimer operates as an interaction switch. The A and B units only interact with each other when the M dimer is in its SM = 1 excited state. (b) Dynamics of the density matrix elements of a spin-1/2 particle coupled to a depolarizing bath, simulated with the algorithm depicted in Fig. 1(b), for different natural dephasing times T2. (c) Dynamics of the density matrix elements of a spin-1/2 particle coupled to a depolarizing bath, simulated with the algorithm depicted in Fig. 1(c), for different values of the expansion parameter ε in eqn (4). In both panels (b) and (c), a small inset schematically shows the molecular complex proposed for each algorithm. (d) Gate complexity required for the implementation of the same quantum simulation between a molecular qudit-based and a superconducting qubit-based platform for both algorithms (green bars correspond to panel (b) and red bars correspond to panel (c)). | ||
Based on the brief review of possible candidates for spin molecular qudits at the beginning of the section, a possible realization of this architecture could be a supramolecule in which A is a Cr7Ni ring, B is a Cr3+ in an approximately octahedral crystal field environment and the switch is a Cu2 dimer, similar to what was proposed in ref. 66. In Hamiltonian (7), gAz = 1.84, gBz = 1.98, are typical gyromagnetic ratios for Cr7Ni and Cr3+, B0 is the external magnetic field and DB/2π = 5.2 GHz is a typical axial zero-field splitting of Cr3+,73 which ensures that all qudit energy gaps are well separated in energy and hence individually addressable by microwave pulses of different frequencies. Note that the zero-field splitting anisotropy term in eqn (7) is important to make the qudit spectrum anharmonic (i.e. with all energy gaps different) and hence allow for a universal control of the qudit. In particular, increasing anisotropy helps to mitigate leakage problems during coherent control by faster pulse sequences. However, increasing the gap between levels too much can lead to an increase in the relaxation rates.74 The isotropic exchange interaction within the Cu2 dimer and between the computational and switch units is parameterized by Δ and J, respectively. We consider a regime in which Δ > 0 is much larger than both |gAz − gBz|μBB0 and J, such that the eigenstates of the switch are factorized from those of the computational units A and B. The former practically correspond to a ground state singlet and an excited triplet (split by the Zeeman interaction with the external field), and the latter to the eigenstates of SAz (|mA〉) and SBz (|mB〉). To fulfill these conditions, we consider Δ/2π = 30 GHz, J/2π = 0.2 GHz, and B0 = 700 mT. We also assume a difference in the component of the g-factors along the direction of the microwave pulses ΔgCu,x = 0.2, as could be obtained with orthogonal orientations of Cu2+, while gMz = 2.1. Note the value for Δ/2π was chosen to keep the pulses needed to implement two-qudit gates in the microwave regime, although it can be considered rather small for some experimental realizations of the Cu2 dimer.66 With this choice, we define the computational subspace within the singlet ground state of the switch. As long as the switch is frozen in this subspace, the two units A and B are effectively decoupled. Then, entangling gates between A and B can be performed simply by exciting a transition of the dimer M conditioned on the states of the other spins. A basic scheme of this process is shown in Fig. 2(a). The idea is to apply two consecutive π pulses between the logic subspace (corresponding to the ground state of the dimer with SM = 0) and the auxiliary subspace (excited state of the dimer with SM = 1) for only a specific state of A and B. This generates entanglement between the A and B units equivalent to the application of a Cφ gate (see ref. 43 and the ESI† for details). The phase φ is controlled by the phase difference between the two pulses.
For the projective measurements required on the ancilla, we consider the coupling of the molecular complex to a superconducting resonator, described by Hr = ωra†a, with a† (a) being the bosonic creation (annihilation) operator for the photons and ωr its resonant frequency. The full Hamiltonian that accounts for the physical hardware reads
 | (8) |
The last term in eqn (8) accounts for the coupling between the two molecules acting as registers in the algorithm and the resonator. The origin of this coupling lies in the Zeeman effect between the magnetic field generated by the resonator (assuming its relevant component is along the X-axis, perpendicular to the quantization axis Z) and the angular momentum of each spin. The bare coupling G is expected to reach values up to G = 100 kHz making use of nanoconstrictions in the inductor line in order to confine and increase the photon magnetic field,75,76 whereas the effective coupling (including the matrix element of the spin excitation) can be further enhanced with molecular engineering to take advantage of high spin systems.45
Projective measurements are conducted by bringing the resonator (initialized in its vacuum state with no photons) into resonance with a transition of the molecule and detecting a possible photon emission. The emission of a photon indicates that the system was in the excited state of the corresponding transition.45 Photons can also be exploited to mediate the interaction between distant molecules, thus implementing switchable qubit–qubit entangling gates and hence granting scalability. In particular, an efficient implementation of the molecular-spin quantum processor focused in the simulation of OQS includes local units composed by a system and an environment qudit, whose interaction can be rapidly turned on and off by an interposed molecular switch (such as the dimer). The effective coupling between these units is then mediated by the resonator (see the simulations discussed below).
Fig. 2(a) shows the results of the simulations made for this implementation. These are obtained by numerically integrating the Lindblad equation for the hardware density matrix (see the ESI†), including the sequence of pulses needed to implement the gates, as well as the main sources of errors. These are represented by pure dephasing of the molecular spins, parameterized by time T2, and photon loss of the resonator, with a rate of ωr/2πQ, with Q being the quality factor of the resonator. We plot the evolution of the ground state population, ρ00, as well as the coherence, |ρ01|, of the two-level system as a function of the relative time t/TDEP for different values of the natural decoherence time of the molecules, T2. The total pulse sequence lasts between 1.8 μs (t/TDEP = 0.25) and 2.58 μs (t/TDEP = 2.0), and hence even a short T2 = 10 μs gives reliable results. Note that in this particular example, due to the symmetry of the problem, NT = 1 suffices to exactly reproduce the joint dynamics. As can be seen from Fig. 2(c), even in the simpler case of simulating the dynamics of a spin-1/2, the reduction in gate complexity compared to a qubit-based architecture remains significant. For a 3-superconducting-qubit circuit, the application of 142 ± 4 native operations (RZ, SX, X, CNOT) is required, according to Qiskit's transpiler at its highest optimization level.77 In contrast, our proposed platform allows the implementation of the exact same dynamics with just 10 microwave pulses (see the ESI†).
We now demonstrate the versatility offered by the molecular design with the implementation of the second algorithm presented in the previous section, shown in Fig. 1(c). Once again, we consider the dynamics of a single-qubit Hamiltonian, 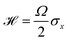 , under the effect of a DEP channel. To implement both the degrees of freedom of the target system's density matrix and the auxiliary ancilla, we use two ququarts. Consequently, we opted to utilize the same molecular hardware described by Hamiltonian (7), where the spin-1/2 of unit A is replaced by another spin-3/2. The only parameters that differ from the previous implementation are gAz = 1.96, gBz = 2.00, B0 = 600 mT, DA/2π = 3 GHz, and DB/2π = 5.2 GHz. In Fig. 2(b), we show the results for the simulated dynamics as a function of different values for the ε parameter. This parameter has important consequences for the physical implementation of the algorithm. On the one hand, a large ε value leads to an erroneous approximation. On the other hand, small values of ε require a high precision in the readout, because the final state populations have to be re-scaled by a factor 1/2ε [cf.eqn (4) and the ESI† for more details]. For that reason, in order to assess the resilience of the algorithm to different values of ε, we have not considered the presence of decoherence in the molecules for these simulations (T2 → ∞). Remarkably, we find that the validity of the approximation for the e
, under the effect of a DEP channel. To implement both the degrees of freedom of the target system's density matrix and the auxiliary ancilla, we use two ququarts. Consequently, we opted to utilize the same molecular hardware described by Hamiltonian (7), where the spin-1/2 of unit A is replaced by another spin-3/2. The only parameters that differ from the previous implementation are gAz = 1.96, gBz = 2.00, B0 = 600 mT, DA/2π = 3 GHz, and DB/2π = 5.2 GHz. In Fig. 2(b), we show the results for the simulated dynamics as a function of different values for the ε parameter. This parameter has important consequences for the physical implementation of the algorithm. On the one hand, a large ε value leads to an erroneous approximation. On the other hand, small values of ε require a high precision in the readout, because the final state populations have to be re-scaled by a factor 1/2ε [cf.eqn (4) and the ESI† for more details]. For that reason, in order to assess the resilience of the algorithm to different values of ε, we have not considered the presence of decoherence in the molecules for these simulations (T2 → ∞). Remarkably, we find that the validity of the approximation for the e![[script L]](https://www.rsc.org/images/entities/char_e144.gif) t operator remains acceptable up to values of ε = 0.4.
t operator remains acceptable up to values of ε = 0.4.
Although the scaling in the ancilla register for this algorithm is favorable compared to the other shown in Fig. 1(b), the main bottleneck lies in the implementation of the Sm, Sp, Am and Ap unitaries. To implement the 2-ququart gates, we have followed the decomposition algorithm of ref. 61, making use of the natural controlled-Rz gate implemented in our hardware (see the ESI†). The implementation of these 4 operations in our case requires a total of 96 microwave pulses, which compares very favorably with 2016 native operations for a circuit composed of 4 superconducting qubits, according to Qiskit's transpiler (see the ESI†). Additionally, 96 pulses are still sensibly less than the 142 operations required to implement the previous algorithm on a qubit-based quantum simulator (Fig. 2(c)). Although this method requires almost ten times more pulses than the other to simulate the same dynamics on molecular qudits, keep in mind that here there is no need for Trotter decomposition, which could give an advantage for cases requiring a large number of Trotter steps. In contrast, this second algorithm is limited by scalability. Indeed, to simulate the dynamics of N particles with spin S, we would need to implement 4 unitary operations acting on the entire ds2-dimensional Hilbert space conditioned by the state of the ancilla ququart, being ds = (2S + 1)N. This could introduce a significant overhead in the number of operations, despite having a smaller ancilla dimension, since it requires an all-to-all connectivity between the units of the circuit. Still, since the size 4ds2 of the whole needed space rapidly grows with the size ds of the target system, this method greatly benefits by incorporating additional levels through molecular qudits.
At this point, it should be emphasized that there are simpler molecular complexes which could substitute the proposed qudit–dimer–qudit structure at the expense of more complex pulse sequences. For instance, replacing the dimer with a single spin would result in a less efficient switch (leading to a residual second-order qudit–qudit coupling even when the switch is “off”) but simpler on the synthetic side, with examples already available.78 On the other hand, there are other schemes exploiting a different type of switch, such as a redox-active unit that can change its spin state upon oxidation.79 Finally, the simplest option from a chemical synthesis point of view would be that of molecular nanomagnets consisting of permanently coupled A–B dimers (i.e., without the interposed switch). This structure could already fit the proposed implementation for both algorithms. For the present scheme, in which scalability of the register is ensured by coupling individual units with resonators, this would only require ≈2–4 times more parallel pulses for single qudit gates, whereas A–B entangling gates would reduce to a single pulse.80 As a result, no significant change is expected in the overall duration of the circuit. Suitable spin qudit dimers already exist,81–83 thus bringing our scheme closer to an experimental implementation.
2.3 Scaling
To conclude, we simulate the dynamics of a dimer composed of two interacting spin-1/2 particles, each coupled to a DEP channel, demonstrating the favourable scaling to higher-dimensionality problems of our platform based on molecular spin qudits coupled to superconducting resonators. The interaction considered follows the transverse-field Ising (TFI) model, described by the target Hamiltonian![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = Jsz1sz2 + hx(sx1 + sx2), = Jsz1sz2 + hx(sx1 + sx2), | (9) |
 | ||
Fig. 3 (a) Schematic design of the physical hardware to simulate the dynamics of two spins A1 and A2 coupled to artificial environments B1 and B2. The resonator, characterized by a bare frequency ωr, enables entanglement between units A1 and A2, as well as performing projective measurements on ancillas B1 and B2. The SQUID loop allows for shifts Δωr in the bare ωr to address the different excitation frequencies required. (b) Quantum circuit to simulate the transverse field Ising model in the presence of a DEP channel for two 1/2-spins. (c) Simulation results for different characteristic times of the DEP channel and decoherence times of the molecular hardware. The time evolution for the total magnetization is shown in (c.1) and (c.2) and that of the two-body correlator in (c.3) and (c.4). Different lines show the numerical solutions considering the Trotter decomposition (black line with open dots), absence of the environment (grey solid line) and exact solution of the joint dynamics (dashed line). Different markers represent different decoherence times T2 and resonator quality factors Q. The gray vertical line in panels (c.1) and (c.3) indicates the operating point for which the fidelity in the next panel has been calculated. (d) Fidelity ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) calculated using eqn (10) between the density matrix obtained after our pulse sequence and the expected one after the exact Trotter evolution for hxt = 2.5 and TDEP = 15, plotted as a function of T2 and Q. calculated using eqn (10) between the density matrix obtained after our pulse sequence and the expected one after the exact Trotter evolution for hxt = 2.5 and TDEP = 15, plotted as a function of T2 and Q. | ||
Fig. 3(c.1–4) show the results obtained for several values of the different parameters. The Hamiltonian parameters J and hx have been set to J = −2hx, hx = 1 (where the Trotter approximation is more critical). Moreover, to show the validity of the proposed physical implementation, both the molecular decoherence time T2 and the resonator quality factor Q have been fixed to values compatible with real devices [cf. ref. 45]. Finally, results are presented for two different intensity regimes of the DEP channel. Panels (c.1) and (c.3) illustrate the dynamics of the total magnetization, 〈sz1 + sz2〉, and the correlation function, 〈sz1sz2〉, over a characteristic time of TDEP = 15. In contrast, panels (c.2) and (c.4) show the behavior of the same observables at TDEP = 5, reflecting a stronger interaction between the system and the environment. We note that satisfactory results are obtained from T2 ≥ 50 μs and Q ≥ 106. A more exhaustive analysis of the effect of noise on our simulations is reported in Fig. 3(d). We studied the fidelity ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) between the density matrices produced by our protocol, ρsim, and that expected by the exact Trotter evolution (black solid lines in panels (c.1–4) of Fig. 3), ρth, for hxt = 2.5 (gray line in panels (c.1) and (c.3) of Fig. 3) and TDEP = 15. This metric is defined as
between the density matrices produced by our protocol, ρsim, and that expected by the exact Trotter evolution (black solid lines in panels (c.1–4) of Fig. 3), ρth, for hxt = 2.5 (gray line in panels (c.1) and (c.3) of Fig. 3) and TDEP = 15. This metric is defined as
 | (10) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ≤ 1.84 The dependence of
≤ 1.84 The dependence of ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) on T2 and Q is shown in Fig. 3(d). We note that T2 limits much more than Q the maximum fidelity attainable, but reasonable values of both parameters ensure a good fidelity. It can be seen that for T2 > 40 μs and Q > 2 × 105 a fidelity higher than 0.95 is systematically obtained. We finally note that the effective spin–photon coupling considered for the simulations presented in Fig. 3(c) and (d) is 1 MHz. This can be achieved34,45 starting from a bare coupling of 100 kHz and encoding of the two logical levels needed for the spin-1/2 target particle in the two lowest |m| states of an S = 10 molecule (such as Fe8 or Mn12), which would provide a further enhancement of one order of magnitude.
on T2 and Q is shown in Fig. 3(d). We note that T2 limits much more than Q the maximum fidelity attainable, but reasonable values of both parameters ensure a good fidelity. It can be seen that for T2 > 40 μs and Q > 2 × 105 a fidelity higher than 0.95 is systematically obtained. We finally note that the effective spin–photon coupling considered for the simulations presented in Fig. 3(c) and (d) is 1 MHz. This can be achieved34,45 starting from a bare coupling of 100 kHz and encoding of the two logical levels needed for the spin-1/2 target particle in the two lowest |m| states of an S = 10 molecule (such as Fe8 or Mn12), which would provide a further enhancement of one order of magnitude.
As a last note, we estimate that the simulation of these same dynamics using the second algorithm would result in a pulse sequence incompatible with the available decoherence rates and photon loss in our experimental platform, as well as beyond the computational resources at our current reach.
3 Conclusion
In summary, we have investigated two conceptually distinct algorithms that align with the current state of the art in the field and extended them to a qudit-based architecture. In this context, it has been analyzed how, in the current era of noisy devices, algorithms that prioritize the use of additional units in exchange for shallower circuits (as in Fig. 1(b)) may be more advantageous. This is in contrast to more sophisticated algorithms that require deeper circuits (as in Fig. 1(c)), which often exceed the available coherence times in current systems but will become crucial in the fault-tolerant era. We have demonstrated that the use of systems with d > 2 levels largely narrows the gap between circuit execution times and system decoherence times. This is achieved by reducing the number of required operations to be implemented in all considered cases, reaching a reduction of almost two orders of magnitude in some scenarios. To this end, we have shown through realistic simulations that molecular spin qudits are ideal candidates for the implementation of qudit-based codes due to their natural ability to host many accessible levels and their chemical engineerability. In Section 2.2, we have shown that even the simulation of a simple spin-1/2 OQS can benefit greatly from the use of qudits, reducing the gate complexity by a factor of 10. Moreover, with execution times of less than 3 μs, we consider that the first experimental proofs of concept could be realized in the near future. Furthermore, in Section 2.3, we have explored the next steps to be taken in order to simulate more than a single particle by exploiting the scalability offered by superconducting circuits. Through detailed simulations (see Fig. 3(d)), we have shown that the prevailing noise levels needed to obtain satisfactory results even for these advanced quantum circuits are not beyond the scope of what should be expected in the near future for these platforms (spin decoherence times T2 > 40 μs and photon loss through the resonator quality factor Q > 2 × 105).45 However, work still lies ahead to find compounds that meet the coherence and control requirements outlined in this work.Nonetheless, the results regarding the reduction of the gate complexity presented in this work are applicable to any platform capable of implementing and coherently controlling systems with more than two levels. Similarly, we consider that the use of qudits can be beneficial for any OQS simulation algorithm, such as the one presented in ref. 23, where the ancilla grows with the number of jump operators, or the Sz.-Nagy algorithm,22,30 where the action of each Kraus operator is simulated in parallel and combined classically in the post-processing. In the latter case, although the required ancilla is a single two-level system, the use of qudits can reduce the number of non-local operations to be implemented by using fewer units to store the same amount of logical levels.
As a final note, we believe that this work serves as a call to join efforts between the physics and the materials science community towards the design of devices that allow for the implementation of advanced quantum algorithms to efficiently study crucial phenomena such as the dynamics of open quantum systems.
Author contributions
Conceptualization: A. C. and S. C.; methodology: S. R.-J., E. M. and A. C.; investigation: S. R.-J. and E. M.; software: S. R.-J.; writing – original draft: S. R.-J. and E. M.; writing – review and editing: A. C., P. S. and S. C.; supervision: P. S. and S. C.; funding acquisition: S. C.; project administration: S. C.Data availability
All the data shown in the figures of the article are available on Zenodo at DOI: https://doi.org/10.5281/zenodo.14833902.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We warmly thank D. Zueco and F. Luis for useful and stimulating discussions. The work received funding from the European Union – NextGenerationEU, PNRR MUR project PE0000023-NQSTI, from Novo Nordisk foundation under grant NNF21OC0070832 in the call “Exploratory Interdisciplinary Synergy Programme 2021”, and from MCIN/AEI/10.13039/501100011033 through grants CEX2023-001286-S and TED2021-131447B-C21. S. R.-J. acknowledges financial support from Gobierno de Aragón through a doctoral fellowship and from Fundación Ibercaja-CAI through grant CB 7/23. S. R.-J. also acknowledges the Gobierno de Aragón (Grant No. E09-17R Q-MAD), Quantum Spain and the CSIC Quantum Technologies Platform PTI-001.Notes and references
- J. Preskill, Quantum, 2018, 2, 79 CrossRef.
- R. P. Feynman, Int. J. Theor. Phys., 1982, 21, 467–488 CrossRef.
- F. Arute, et al. , Nature, 2019, 574, 505 CrossRef CAS PubMed.
- S. Lloyd, Science, 1996, 273, 1073–1078 CrossRef CAS PubMed.
- D. Bacon, A. M. Childs, I. L. Chuang, J. Kempe, D. W. Leung and X. Zhou, Phys. Rev. A:At., Mol., Opt. Phys., 2001, 64, 062302 CrossRef.
- S. Lloyd and L. Viola, Phys. Rev. A:At., Mol., Opt. Phys., 2001, 65, 010101 CrossRef.
- L. Gui-Lu, Commun. Theor. Phys., 2006, 45, 825 CrossRef.
- E. Andersson and D. K. L. Oi, Phys. Rev. A:At., Mol., Opt. Phys., 2008, 77, 052104 CrossRef.
- M. Kliesch, T. Barthel, C. Gogolin, M. Kastoryano and J. Eisert, Phys. Rev. Lett., 2011, 107, 120501 CrossRef CAS PubMed.
- H. Wang, S. Ashhab and F. Nori, Phys. Rev. A:At., Mol., Opt. Phys., 2011, 83, 062317 CrossRef.
- R. Sweke, I. Sinayskiy, D. Bernard and F. Petruccione, Phys. Rev. A:At., Mol., Opt. Phys., 2015, 91, 062308 CrossRef.
- A. Chenu, M. Beau, J. Cao and A. del Campo, Phys. Rev. Lett., 2017, 118, 140403 CrossRef CAS PubMed.
- R. Cleve and C. Wang, 44th International Colloquium on Automata, Languages, and Programming (ICALP 2017), Dagstuhl, Germany, 2017, pp. 17:1–17:14.
- R. Iten, R. Colbeck and M. Christandl, Phys. Rev. A, 2017, 95, 052316 CrossRef.
- F. Ticozzi and L. Viola, Quantum Sci. Technol., 2017, 2, 034001 Search PubMed.
- J. T. Barreiro, M. Müller, P. Schindler, D. Nigg, T. Monz, M. Chwalla, M. Hennrich, C. F. Roos, P. Zoller and R. Blatt, Nature, 2011, 470, 486–491 CAS.
- H. Lu, C. Liu, D.-S. Wang, L.-K. Chen, Z.-D. Li, X.-C. Yao, L. Li, N.-L. Liu, C.-Z. Peng, B. C. Sanders, Y.-A. Chen and J.-W. Pan, Phys. Rev. A, 2017, 95, 042310 Search PubMed.
- C. Shen, K. Noh, V. V. Albert, S. Krastanov, M. H. Devoret, R. J. Schoelkopf, S. M. Girvin and L. Jiang, Phys. Rev. B, 2017, 95, 134501 CrossRef.
- T. Xin, S. J. Wei, J. S. Pedernales, E. Solano and G. L. Long, Phys. Rev. A, 2017, 96, 022302 CrossRef.
- L. Hu, X. Mu, W. Cai, Y. Ma, Y. Xu, H. Wang, Y. Song, C. L. Zou and L. Sun, Sci. Bull., 2018, 63, 1551–1557 CrossRef PubMed.
- J. Han, W. Cai, L. Hu, X. Mu, Y. Ma, Y. Xu, W. Wang, H. Wang, Y. P. Song, C. L. Zou and L. Sun, Phys. Rev. Lett., 2021, 127, 020504 CrossRef CAS PubMed.
- A. Gaikwad, Arvind and K. Dorai, Phys. Rev. A, 2022, 106, 022424 CrossRef CAS.
- M. Cattaneo, M. A. Rossi, G. García-Pérez, R. Zambrini and S. Maniscalco, PRX Quantum, 2023, 4, 010324 CrossRef.
- W. F. Stinespring, Proc. Am. Math. Soc., 1955, 6, 211–216 Search PubMed.
- H. Kamakari, S. N. Sun, M. Motta and A. J. Minnich, PRX Quantum, 2022, 3, 010320 CrossRef.
- Z. Hu, R. Xia and S. Kais, Sci. Rep., 2020, 10, 3301 CrossRef CAS PubMed.
- A. W. Schlimgen, K. Head-Marsden, L. M. Sager, P. Narang and D. A. Mazziotti, Phys. Rev. Lett., 2021, 127, 270503 CrossRef CAS PubMed.
- A. W. Schlimgen, K. Head-Marsden, L. A. M. Sager-Smith, P. Narang and D. A. Mazziotti, Phys. Rev. A, 2022, 106, 022414 CrossRef CAS.
- A. W. Schlimgen, K. Head-Marsden, L. A. M. Sager, P. Narang and D. A. Mazziotti, Phys. Rev. Res., 2022, 4, 023216 CrossRef CAS.
- N. Suri, J. Barreto, S. Hadfield, N. Wiebe, F. Wudarski and J. Marshall, Quantum, 2023, 7, 1002 CrossRef.
- Y. Wang, E. Mulvihill, Z. Hu, N. Lyu, S. Shivpuje, Y. Liu, M. B. Soley, E. Geva, V. S. Batista and S. Kais, J. Chem. Theory Comput., 2023, 19, 4851–4862 CrossRef CAS PubMed.
- W. Cai, J. Han, L. Hu, Y. Ma, X. Mu, W. Wang, Y. Xu, Z. Hua, H. Wang, Y. P. Song, J.-N. Zhang, C.-L. Zou and L. Sun, Phys. Rev. Lett., 2021, 127, 090504 CrossRef CAS PubMed.
- S. Carretta, D. Zueco, A. Chiesa, A. Gómez-León and F. Luis, Appl. Phys. Lett., 2021, 118, 240501 CrossRef CAS.
- A. Chiesa, P. Santini, E. Garlatti, F. Luis and S. Carretta, Rep. Prog. Phys., 2024, 87, 034501 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492 CrossRef CAS PubMed.
- K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 3623–3626 RSC.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS PubMed.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341 CrossRef CAS PubMed.
- D. Aguilà, D. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. Alonso, J. Sesé, S. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215 Search PubMed.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Inf., 2015, 1, 15012 CrossRef.
- J. Ferrando-Soria, E. Moreno-Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. Vitorica-Yrezabal, F. Tuna, E. J. L. McInness and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed.
- P. Santini, S. Carretta, F. Troiani and G. Amoretti, Phys. Rev. Lett., 2011, 107, 230502 CrossRef CAS PubMed.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- A. Chiesa, S. Roca, S. Chicco, M. de Ory, A. Gómez-León, A. Gomez, D. Zueco, F. Luis and S. Carretta, Phys. Rev. Appl., 2023, 19, 064060 CrossRef CAS.
- A. Urtizberea, E. Natividad, P. J. Alonso, L. Pérez-Martínez, M. A. Andrés, I. Gascón, I. Gimeno, F. Luis and O. Roubeau, Mater. Horiz., 2020, 7, 885–897 RSC.
- A. Ghirri, C. Bonizzoni, F. Troiani, N. Buccheri, L. Beverina, A. Cassinese and M. Affronte, Phys. Rev. A, 2016, 93, 063855 CrossRef.
- S. Carretta, A. Chiesa, F. Troiani, D. Gerace, G. Amoretti and P. Santini, Phys. Rev. Lett., 2013, 111, 110501 CrossRef CAS PubMed.
- A. Chiesa, P. Santini, D. Gerace, J. Raftery, A. A. Houck and S. Carretta, Sci. Rep., 2015, 5, 16036 CrossRef PubMed.
- A. Chiesa, E. Macaluso, F. Petiziol, S. Wimberger, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2020, 11, 8610–8615 CrossRef CAS PubMed.
- M. Chizzini, L. Crippa, L. Zaccardi, E. Macaluso, S. Carretta, A. Chiesa and P. Santini, Phys. Chem. Chem. Phys., 2022, 24, 20030 RSC.
- M. Mezzadri, A. Chiesa, L. Lepori and S. Carretta, Mater. Horiz., 2024, 11, 4961–4969 RSC.
- F. Tacchino, A. Chiesa, R. Sessoli, I. Tavernelli and S. Carretta, J. Mater. Chem. C, 2021, 9, 10266–10275 RSC.
- S. Chicco, G. Allodi, A. Chiesa, E. Garlatti, C. D. Buch, P. Santini, R. De Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2024, 146, 1053–1061 CrossRef CAS PubMed.
- M. A. Nielsen, M. R. Dowling, M. Gu and A. C. Doherty, Science, 2006, 311, 1133–1135 CrossRef CAS PubMed.
- S. Roca-Jerat, T. Sancho-Lorente, J. Román-Roche and D. Zueco, SciPost Phys., 2023, 15, 186 CrossRef.
- T. F. Havel, J. Math. Phys., 2003, 44, 534–557 CrossRef.
- H.-P. Breuer and F. Petruccione, The theory of open quantum systems, Oxford University Press, USA, 2002 Search PubMed.
- D. Tupkary, A. Dhar, M. Kulkarni and A. Purkayastha, Phys. Rev. A, 2022, 105, 032208 CrossRef CAS.
- N. Hatano and M. Suzuki, Finding Exponential Product Formulas of Higher Orders, Springer, Berlin, Heidelberg, 2005, pp. 37–68 Search PubMed.
- L. E. Fischer, A. Chiesa, F. Tacchino, D. J. Egger, S. Carretta and I. Tavernelli, PRX Quantum, 2023, 4, 030327 Search PubMed.
- M. Ringbauer, M. Meth, L. Postler, R. Stricker, R. Blatt, P. Schindler and T. Monz, Nat. Phys., 2022, 18, 1053–1057 Search PubMed.
- P. Hrmo, B. Wilhelm, L. Gerster, M. W. van Mourik, M. Huber, R. Blatt, P. Schindler, T. Monz and M. Ringbauer, Nat. Commun., 2023, 14, 2242 Search PubMed.
- I. Gimeno, A. Urtizberea, J. Román-Roche, D. Zueco, A. Camón, P. J. Alonso, O. Roubeau and F. Luis, Chem. Sci., 2021, 12, 5621–5630 CAS.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CAS.
- G. A. Timco, S. Carretta, F. Troiani, F. Tuna, R. J. Pritchard, C. A. Muryn, E. J. L. McInnes, A. Ghirri, A. Candini, P. Santini, G. Amoretti, M. Affronte and R. E. P. Winpenny, Nat. Nanotechnol., 2009, 4, 173–178 CrossRef CAS PubMed.
- S. J. Lockyer, A. Chiesa, A. Brookfield, G. A. Timco, G. F. S. Whitehead, E. J. L. McInnes, S. Carretta and R. E. P. Winpenny, J. Am. Chem. Soc., 2022, 144, 16086–16092 CrossRef CAS PubMed.
- M. J. Graham, J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 7623–7626 CrossRef CAS PubMed.
- V. Rollano, M. C. de Ory, C. D. Buch, M. Rubn-Osanz, D. Zueco, C. Sánchez-Azqueta, A. Chiesa, D. Granados, S. Carretta, A. Gomez, S. Piligkos and F. Luis, Commun. Phys., 2022, 5, 246 CrossRef.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS PubMed.
- M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183 RSC.
- D. Ranieri, F. Santanni, A. Privitera, A. Albino, E. Salvadori, M. Chiesa, F. Totti, L. Sorace and R. Sessoli, Chem. Sci., 2023, 14, 61–69 RSC.
- A. Abragam and B. Bleaney, Electron paramagnetic resonance of transition ions, OUP, Oxford, 2012 Search PubMed.
- P. C. E. Stamp and I. S. Tupitsyn, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 69, 014401 CrossRef.
- M. D. Jenkins, U. Naether, M. Ciria, J. Sesé, J. Atkinson, C. Sánchez-Azqueta, E. D. Barco, J. Majer, D. Zueco and F. Luis, Appl. Phys. Lett., 2014, 105, 162601 CrossRef.
- I. Gimeno, W. Kersten, M. C. Pallarés, P. Hermosilla, M. J. Martnez-Pérez, M. D. Jenkins, A. Angerer, C. Sánchez-Azqueta, D. Zueco, J. Majer, A. Lostao and F. Luis, ACS Nano, 2020, 14, 8707–8715 CrossRef CAS PubMed.
- Qiskit contributors, Qiskit: An Open-source Framework for Quantum Computing, 2023.
- A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423 CrossRef CAS PubMed.
- J. Lehmann, A. Gaita-Arino, E. Coronado and D. Loss, Nat. Nanotechnol., 2007, 2, 312–317 CrossRef CAS PubMed.
- F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, J. Sesé, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203 CrossRef CAS PubMed.
- T. Sanada, T. Suzuki, T. Yoshida and S. Kaizaki, Inorg. Chem., 1998, 37, 4712–4717 CrossRef CAS PubMed.
- F. Luis, P. J. Alonso, O. Roubeau, V. Velasco, D. Zueco, D. Aguilà, J. I. Martínez, L. A. Barrios and G. Aromí, Commun. Chem., 2020, 3, 176 CAS.
- H. Biard, E. Moreno-Pineda, M. Ruben, E. Bonet, W. Wernsdorfer and F. Balestro, Nat. Commun., 2021, 12, 4443 CrossRef CAS PubMed.
- M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information, Cambridge University Press, 2010 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details on the numerical simulations, on both algorithms (with circuit decompositions into qubit-based and qudit-based platforms of the dynamical map into elementary one- and two-qudit gates and their implementation on the molecular spin quantum hardware), and on the simulation of an open system of two qubits (super-operator formalism and entangling gates mediated by the resonator). See DOI: https://doi.org/10.1039/d4mh01512f |
| This journal is © The Royal Society of Chemistry 2025 |