Accelerated design of solid bio-based foams for plastics substitutes

Abstract

Biobased substitutes for plastics are a future necessity. However, the design of substitute materials with similar or improved properties is a known challenge. Here we show an example case of optimizing the mechanical properties of a fully biobased methylcellulose-fiber composite material. We tackle the process–structure–property paradigm using Bayesian optimization with Gaussian process regression to map the processed material composition to the final mechanical properties of new bio-based solid foams. We exploited the fast-to-measure rheological properties of the liquid biofiber suspensions processed into foams to show how these collapse to an auxiliary sub-space of low dimensionality for design. The optimal compositions for methylcellulose-fiber foams shown here correspond to two distinct cases: high methylcellulose content for the formation of strong closed-cell foams, and high fiber contents with approximately equal amounts of methylcellulose for the formation of methylcellulose-bound fiber networks. The novel approach is transferable to other biobased foam compositions with different fibers and additives. This new approach allows the rational design of bio-based plastics replacements by encompassing desired final material properties, descriptors of materials processed, and knowledge of the process.

---

New concepts

We demonstrate a novel framework of dimensionality reduction and Bayesian optimization (BO) to map the properties of a material from the liquid state to the solid state. The fast measurements in the liquid state are first reduced to a two-dimensional auxiliary sub-space with principal component analysis (PCA) and again to mechanical properties of the solidified material with BO. The proposed process enables the use of small data in multidimensional input spaces by capturing the hidden correlations between measurables not captured by simplified physical models. The dimensionality reduction results in a geometrically interpretable view of the property space, instead of a black-box function. As a practical application, we use the method to optimize the yield stress of a bio-based plastic replacement foam material using rheological measurements in the liquid state as surrogate experiments, minimizing the labour and time compared to mechanical compression experiments after aerating and drying the foam. The framework would also be transferable to other clustering and machine learning algorithms, not just PCA or BO that are used here.

1. Introduction

Plastics are lightweight, mechanically resilient, and inexpensive.¹ However, they have severe negative impacts on the environment, and plastic pollution is a growing problem worldwide.^2,3 The most viable solution to this problem—finding replacements for these plastics—is a crucial part of the green transition² and meeting the United Nations sustainable development goals.³ The manufacturing methods should be industrially viable⁴ and follow circular principles to decouple manufacturing from the sole use of natural resources. To achieve this goal, data-driven approaches⁵ explore and exploit the material design spaces and learn the process–structure–property relationships. The candidates for biodegradable plastics substitutes usually comprise several bio-based constituents from widely varying sources, as when circular economy raw material sources are utilized, making them complex systems to model.¹

A natural solution to this problem is machine learning by Bayesian methods, where prior knowledge is utilized in combination with the data to arrive at a posterior estimate in the form of a probability distribution with naturally quantified uncertainty in the form of Bayesian optimization (BO).^6–14 BO consists of two components: a surrogate model and a utility function. Good models for new materials often do not exist, so a simple choice for the surrogate model is a Gaussian process (GP), which approximates the expensive “black box” functions associated with composition–structure–property relationships.^9,15–17 Compared to an alternative for BO—a Bayesian neural network¹⁸—GPs require far fewer hyperparameters and are thus computationally cheaper, while retaining the ability to represent functional relationships with widely varying shapes. A utility function is then used to implement active learning,^{7,9,16,19–22} where the extremum of the utility function gives the choice of the next sampling point.

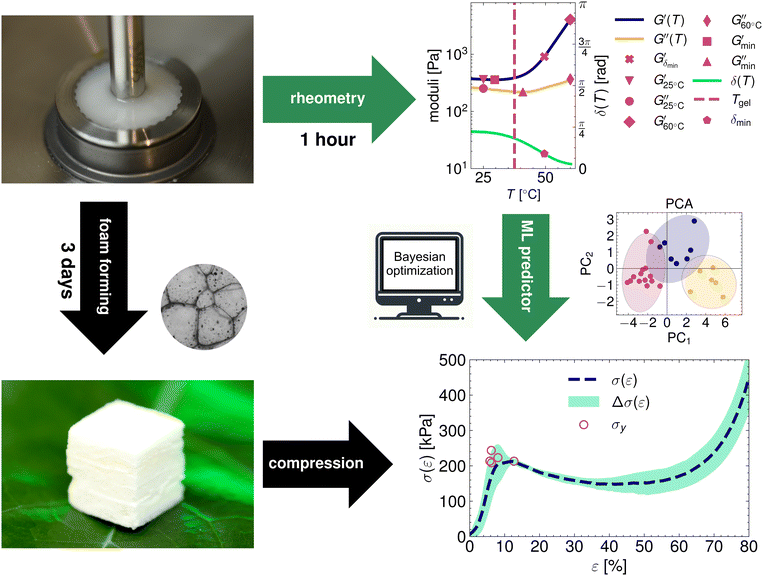
Packaging materials are an important industry where new and efficient replacements are needed, as in Europe, 19% of packaging waste is plastic packaging.²³ Cellulose-based materials^24–29 are a promising alternative to petrochemical-based packaging that comprises mostly polystyrene foams. We developed hierarchically structured biodegradable foams made from forest-derived materials.^12,24,25,30 These foams have mechanical properties that are well-suited for packaging applications (orthotropic strength, making the material strong in one direction and soft in another), and they can be manufactured in a scalable, continuous manner. The manufacturing process consists of preparing an aqueous suspension of methylcellulose and cellulose fibers, wet-foaming the suspension, 3D printing the liquid foam, and evaporating the water to obtain a solid foam material.

The iterative experimentation of material compositions through foam manufacture is slow, so ideally, the properties of the solid foam should be optimized by choices made before the foam manufacturing process.^12,31–33 The suspension rheology of a viscoelastic material is fast to measure and has been suggested to describe the properties of the material when it takes a viscoelastic solid conformation.³⁴ This sets up a composition–process–structure–property path with a constant manufacturing process where the structure is inferred from the viscoelastic properties of the liquid suspension.

Here, we show how biodegradable foams can be designed as plastic substitutes in packaging by optimizing the mechanical properties of a biobased foam material using a simple BO approach. We used Gaussian process regression (GPR) to map the composition–process–structure–property path from the constituent materials to the mechanical properties via the structure-determining rheological properties. Using an auxiliary rheology space enables the transferability of the results to extended and optimized raw material design spaces.

2. Results

2.1. Machine learning predictor

The input data used by the machine learning predictor consists of compositions and rheological observables for suspensions with varying concentrations of MC and fibers, as well as output data of the mechanical testing results of the corresponding solid foams. The composition of the suspension and the solid foam can be thought of as a vector in the composition space (where the components are the concentrations c in the wet suspension) . Here, we use MC and one type of fiber, so our composition space [capital script C] is 2-dimensional.

The rheological measurements then determine the vectors residing in the rheology space [scr R, script letter R]. The space is set up by the 11 rheological observables (described in more detail in the Methods section), thus 11-dimensional. However, these 11 observables are not independent, and principal component analysis (PCA) can be used for dimensionality reduction.^35–37 This maps from the rheology space [scr R, script letter R] to the principal component space [scr P, script letter P] based on the experimentally measured points. Alternative dimensionality reduction techniques, such as t-distributed stochastic neighbor embedding³⁸ (t-SNE) or uniform manifold approximation and projection³⁹ (UMAP), require hyperparameters and can arrive at different local optima with different initializations. These methods might be more appropriate with highly nonlinear data, but PCA has the advantage of being unique and free of hyperparameters.

Finally, we have the mechanical properties of the solid foams. Here, we have only used the yield stress σ_y ∈ [scr M, script letter M] (as it well characterizes the mechanical behavior of the material⁴⁰), so the space of mechanical properties [scr M, script letter M] is one-dimensional, but other choices could easily be made. As several measurements of the yield stress are made for each composition, these are all added to the dataset, corresponding to the same point in the PCA reduced rheology space. This enables the GPR to learn the inherent sample-to-sample variability in the data.

The machine learning predictor was used to circumvent the laborious iterative experimentation through foam forming and mechanical testing. Instead, the fast-to-measure rheology was used to infer the mechanical properties using the predictor. See Fig. 1 for a description of this workflow.

Fig. 1 A workflow with slow iterative experimentation and fast Bayesian optimization. Solid foams can be produced from a wet foam using foam forming and probing the mechanical properties using compression tests. Alternatively, the rheology of the wet foams can be measured and then use the ML methods presented in this paper to predict the mechanical properties. The rheometry figure in the top-right corner shows the different rheological observables extracted from the experiments. The compression curve in the bottom-right corner shows the yield stress point used to optimize the mechanical quantity. The different yield stress points correspond to different experiments, illustrating the sample-to-sample variation.

The predictor comprises two steps. The first step is to find a mapping from [capital script C] to [scr R, script letter R] (or to the dimensionally reduced version [scr P, script letter P]). This is initially done by the fast rheology measurements, and then we used GPR to define a direct mapping f: [capital script C] → [scr P, script letter P] where f was a GP. The second step was to define another mapping g: [scr P, script letter P] → [scr M, script letter M] where g was again a GP. A more detailed description of the GPR can be found in the ESI.†

2.2. Mapping the composition to the rheology

To construct the initial dataset, we made suspensions of wet foam with varying concentrations of MC and fibers, measured the rheology, made a solid foam, and did compression tests on the solid foam to determine the yield stress (Fig. 1). The suspensions in the initial dataset were composed of a grid-like set of compositions, as depicted in Fig. 2a–c.

Fig. 2 Mapping from composition space to the rheology space. (a) The compositions of fiber and MC in the suspensions of the initial dataset as blue points. The contours represent the first principal component derived from the GPR mapping f to the PCA reduced rheology space. (b) As panel a but for the second principal component. (c) The combined standard deviation of the mapping f. (d) The mapping of the rheology observables into the PCA space, where the shaded area represents the whole composition space (fiber content between 0 and 2.0 wt%, MC content between 0.6 and 2.0 wt%) and the points the actual measured points. The vectors shown are the unit vectors of the rheology space mapped to the PCA space, scaled for clarity of visual presentation. The inset shows the explained value ratio as a function of the number of PCA components and our chosen number of principal components n = 2 (dashed line). (e) The goodness-of-fit of the GPR mapping f for both of the principal components.

The rheology observables had strong correlations, and therefore, the dimension of the rheology space [capital script C] was reduced using PCA to yield points in the 2D space (Fig. 2d). In two main directions, the unit vectors related to temperature observables map to vectors almost perpendicular to the other rheology observables (Fig. 2d). This was also seen in the explained variance ratio (EVR) of the PCA, which was over 90% with just two components (inset of Fig. 2d).

The studied concentrations set up a domain of feasible rheologies achievable from this material combination. They are the result of mapping all the concentrations in the considered region (0.6% < c_MC ≤ 2.0% and 0%< c_fiber ≤ 2.0%) to the PCA reduced rheology space (shaded region in Fig. 2d). The mapping f has very reasonable accuracy (Fig. 2e). Furthermore, in Fig. 2a and b, we visualize how the mapping f behaves in the composition space; this aids in understanding the unit vectors and the effect of composition on the magnitude of the PCA components (Fig. 2d). Lastly, Fig. 2c depicts the combined standard deviation of the principal components as a function of the composition.

2.3. Mapping the rheology to the mechanical properties

This method allowed the prediction of the yield stress of the solid foams by using GPR to determine the mapping g from the PCA reduced rheology space to the space of mechanical properties (Fig. 3). This mapping worked very well (Fig. 3a), and it is noteworthy that there is a lot of scatter in the yield stress values for different samples made using the same suspension. The yield stress had a highly nontrivial landscape in the rheology space (Fig. 3b). Such rugged landscape could be the result of overfitting, but by using a portion of the data as a test dataset we have checked that this is not the case.

Fig. 3 Mapping from the rheology space to the space of mechanical properties and exploiting this mapping. (a) The goodness-of-fit of the GPR mapping g from the (PCA reduced) rheology space to the space of mechanical properties. The blue points are the original dataset, the purple ones are the test set, and the yellow ones are the extended dataset, including additives. (b) The mean GPR prediction of the yield stress plotted in the PCA reduced rheology space. The colors of the points are as in panel (a). (c) The EI computed using the GPR prediction of the yield stress in the PCA reduced rheology space.

The yield stress has a multimodal character, with two very clear peaks at differing values of the first principal component of the rheology space (Fig. 3b). We computed a utility function—the expected improvement (EI)—in the rheology space to exploit this new mapping approach. EI was chosen among the many utility functions for its simplicity and as it is hyperparameter-free and balances data exploitation and exploration (see ESI† for more details on the choice of utility function). The EI has clear peaks at specific points in the rheology space (Fig. 3c) where the surrogate function can be expected to improve over the current optimum. These two cases correspond to high moduli G at medium characteristic temperatures T, and high characteristic temperatures at medium moduli. Based on Fig. 2a and b, we can identify two distinct rheological behaviors linked to different foam compositions that increase the yield stress. The first approach involves maximizing the MC content in the foams, while the second entails a strategic combination of MC and fibers.

Maximizing the MC content yields closed-cell foam structures,²⁴ where the small amounts of fiber only serve to reinforce the structure. These compositions have high gelation temperatures. On the other hand, starting from a high fiber concentration forms a structure which is a matrix of fibers and the addition of MC then binds the fibers to each other. The high fiber content also reduces the gelation temperature due to the enhanced connectivity of the gel matrix.¹² Additionally, fibers also reduce the thermal softening of the suspension, observed by a smaller gap between the moduli at the room temperature and the gelation temperature. The worst compositions—the ones far from the EI peaks—have high energy dissipation (high δ values), which means that the ratios of MC and fiber are unfavorable for developing elastic gel matrices.

The two EI peaks are in the domain of feasible rheologies given by our mapping from the composition space to the rheology space. Therefore, we made a test set of two measurements using the compositions that would give us the rheologies pointed out by these locations of maximum expected improvement. One of the resulting solid foams had a yield stress of 150 kPa, which is among the strongest in our dataset, and it is composed of 1.8 wt% MC and 0.0 wt% fibers, achieving an improvement of 70 kPa over the mean yield stress of the dataset. The other sample in the test set corresponded to an equal ratio of MC and fibers (1.5 wt%). Thus, our approach demonstrates that BO can be used to exploit the information gathered to design stronger materials.

Finally, to demonstrate the transferability of the results, we extended the dataset by conducting two additional experiments: one using a different type of fiber in the suspension and one incorporating lignin into the suspension as an additive. The yield stress results obtained for these new measurements agree well with the GPR, which predicted, for example, a yield stress of 90 kPa for the lignin foam (Fig. 3a). This shows the exploitability of the auxiliary rheology space to predict the mechanical properties when the observed rheologies of the new measurement points are in the same region as the training data (Fig. 3b). With just these few additional measurement points we have shown that the method is transferable to extended composition spaces without any knowledge of the mechanical properties for any of the points in the extended composition space. Thus, using an auxiliary rheology space becomes a valuable tool that allows a rheologist to favor either a strong or soft mechanical response in the foams with additives.

To compare our foams with other packaging materials, we have compared the yield stress vs. density characteristics of different types of materials in Fig. 4. Our material achieves strength comparable to high-strength flexible polymer foams with similar or lower densities. The strength is also close to the strength of rigid polymer foams or cork, with similar or lower density. Our optimized foams also have yield stress comparable to low-density expanded polystyrene⁴¹ (commonly known as Styrofoam).

Fig. 4 Comparison between our material and other packaging materials. The Ashby plot of density vs. yield stress shows how our material (blue points and grey background) performs when comparing to other materials such as rigid polymer foams (blue), flexible polymer foams (green), and cork (orange). The red point corresponds to the optimal sample in our dataset.

3. Discussion

Here we have shown how plastic substitutes made from cellulose-derived ingredients can be designed to have optimized properties—such as mechanical strength—for practical applications including packaging. We use the material composition and the measured rheology of the resulting suspension to predict the mechanical properties of the solid foam, without resorting to slow iterative experimentation. The predictor used—BO with GPR on a dimensionally reduced space—is a simple machine learning method to tackle the process–structure–property paradigm.

Including the auxiliary rheology space has two advantages over predicting the mechanical properties directly from the composition. Firstly, the rheology of viscoelastic suspensions infers the properties of the solid foams and is essentially the structure part in the process–structure–property path. Secondly, it enables the transferability of the results to extended design spaces. We show this by extending the composition space to different types of fibers and adding lignin—an additive not at all present in the training set—to the suspensions. The use of additives—such as plasticizers, hydrophobizers, and fire retardants—is a common practice in polymer processing. The additives increase the dimensionality of the composition space but using the methods described here, the composition space can essentially be ignored in favor of using only the observed rheology of the new suspensions. The general idea of our new concept—using auxiliary spaces and dimensionality reduction to obtain additional information for prediction—is easily transferable to other systems.

The observed optimal rheologies correspond to two distinct cases: high MC content, and having high contents of both MC and fibers. This nontrivial result can be understood by considering the resulting structures, where high MC content provides a strong closed-cell foam, and having high fiber content forms a fiber network, which needs binding through high amounts of MC. Compositions far from these MC-fiber ratios are unfavorable for elastic gel matrix development.

To search for even better mechanical strength, one can vary e.g. the fiber type and use the methods developed here to exploit the fast-to-measure rheology to find the optimal composition with the new foam constituents. When circular economy raw material sources are considered, the deciding factor in fiber selection is often the availability of the raw material rather than the optimal performance, so we have here not explored the effect of fiber type further.

A rheology expert might interpret the measurements and make a good choice of 2–3 key rheology observables that do not have the problem of being correlated and needing dimensionality reduction. However, our method obviates the need for such expertise and automates the design of biofoams to better identify suitable space using dimensionality reduction. Methods such as anisotropic distance kernels could also be used to similar effect. We have checked that our results are not very sensitive to the number of observables used.

In our case we have just standardized the observables to zero mean and unit variance. In cases where nonlinear behavior with more widely varying observables is encountered, either the nonlinear dimensionality reduction methods mentioned previously (such as t-SNE or UMAP) or some linearizing transformations might be more appropriate. In the case of rheology this might be log-transformation, as many of the quantities behave in exponential or power-law fashion. Similarly our method assumes homoscedastic sample-to-sample variation, and in more complicated cases heteroscedastic variants of GPR⁴² might be needed.

These types of machine learning methods are usually good at interpolating between the points in the training data but less useful for extrapolation. This is also true here, as using stationary kernels in the GPR means that the predictions for rheologies far from the ones measured in the training set (around one kernel lengthscale away) tend to the mean value. Here we do not encounter this problem, as the test set and the additional tests with different fibers and additives have rheologies sufficiently close to the mapped part of the search space. When rheologies far from the training sets are encountered, the training data should be amended in this region.

A direction for further work would be to utilize high-throughput experimental methods such as an automated rheometry setup¹ to probe the composition and rheology spaces. Using this type of blind brute-force approach would enable the exploration of truly vast regions of possible material compositions.

In practical scenarios one might also be interested in other properties of the foams, e.g. their water resistance.^43,44 One can then utilize the method shown here for any number of these properties and using standard multitarget optimization methods, such as expected hypervolume improvement,⁴⁵ proceed to find a Pareto front.

Similarly, in our case the composition space searched was chosen so that the compositions explored are all foamable and show a gelling transition, enabling the formation of dry foams. Also the measurement points suggested by the expected improvement were in this domain of feasible rheologies. In cases where this is not true, the use of feasibility aware optimization methods^46,47 might be necessary.

4. Methods

4.1. Materials

We make wet foam suspensions out of methylcellulose, water, and fibers. Three different fibers were used. The foams are dried into a solid 3D configuration using previously reported methodologies.^12,24,25 Five samples were made for each composition. The initial training set consists of 26 compositions with fiber content between 0 and 2.0 wt% and MC content between 0.6 and 2.0 wt%. These ranges were chosen so that the resulting suspensions are foamable, show a gelling transition, and can therefore be used to make dry foams. Two compositions were then made as a test set, as well as two compositions to show the transferability of the results to different fibers and additives. Further details on the materials used and the foam manufacture can be found in the ESI.†

The densities of the foams are measured simply by weighing them and dividing this by the outer dimensions of the tested foam block. The comparison data for other materials in Fig. 4 is gathered from the Ansys GRANTA EduPack software.⁴⁸

4.2. Experimental methods

The rheological properties of the suspensions were characterized using dynamic mechanical thermal analysis (DMTA). In a Couette geometry we apply a sinusoidal strain γ to the suspension with an amplitude of 1.0% and a constant angular frequency ω = 6.28 s⁻¹, while heating the sample at a rate of 1 °C min⁻¹ from 15 to 60 °C. The viscoelastic response of the sample is characterized by recording the storage modulus G′ and the loss modulus G′′ as a function of the temperature T. Additionally we observe the phase shift angle δ = arctan(G′′/G′). A more detailed description of the rheometry methods can be found in the ESI.†

For the GPR we record 11 rheological observables. These are the phase shift angle at the minimum of its gradient with respect to temperature when the material exhibits the sol-to-gel transition δ_min, the storage modulus corresponding to this angle , the storage modulus at 25 °C temperature , the storage modulus at 60 °C temperature (high temperature), the minimum value of the storage modulus 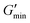, the loss modulus at room temperature 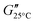, the loss modulus at high temperature 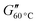, the minimum value of the loss modulus , the minimum storage modulus temperature the minimum loss modulus temperature , and the sol-to-gel transition temperature T_gel.

We test the mechanical properties of the solid foams by performing compression tests. The experiments consist of compressing the samples with a constant engineering strain rate of 0.033 s⁻¹, and recording the force F and displacement d. From these the engineering stress σ = F/A (where A is the initial cross-sectional area of the sample) and engineering strain ε = d/h (where h is the initial height of the sample) are calculated.

For the GPR we determine the yield point of the sample, and characterize the strength of the material by the value of the yield stress σ_y. A more detailed explanation of the compression test methods can be found in the ESI.†

Author contributions

Isaac Y. Miranda-Valdez: methodology, software, formal analysis, visualization, investigation, data curation, writing – original draft, and writing – review & editing. Tero Mäkinen: methodology, software, formal analysis, visualization, investigation, data curation, writing – original draft, and writing – review & editing. Sebastian Coffeng: investigation and methodology. Axel Päivänsalo: methodology and data curation. Luisa Jannuzzi: investigation and methodology. Leevi Viitanen: methodology and data curation. Juha Koivisto: supervision, validation, writing – review & editing, funding acquisition. Mikko J. Alava: supervision, validation, conceptualization, writing – review & editing, funding acquisition, project administration.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. J. A. and J. K. acknowledge funding from FinnCERES flagship (151830423), Business Finland (211835), and Future Makers programs. M. J. A., T. M., J. K. and I. M. V. acknowledge funding from Business Finland (211909, 211989). M. J. A. acknowledges funding from the Finnish Cultural Foundation. I. M. V. and L. V. acknowledge the Vilho, Yrjö and Kalle Väisälä Foundation of the Finnish Academy of Science and Letters for personal funding. Aalto Science-IT project is acknowledged for computational resources.

Notes and references

1. T. Chen, Z. Pang, S. He, Y. Li, S. Shrestha, J. M. Little, H. Yang, T.-C. Chung, J. Sun, H. C. Whitley, I.-C. Lee, T. J. Woehl, T. Li, L. Hu and P.-Y. Chen, Nat. Nanotechnol., 2024, 1–10.
2. M. MacLeod, H. P. H. Arp, M. B. Tekman and A. Jahnke, Science, 2021, 373, 61–65.
3. S. H. Ali, Nat. Mater., 2018, 17, 1052–1053.
4. L. Hultman, S. Mazur, C. Ankarcrona, A. Palmqvist, M. Abrahamsson, M.-L. Antti, M. Baltzar, L. Bergström, P. de Laval, L. Edman, P. Erhart, L. Kloo, M. W. Lundberg, A. Mikkelsen, E. Moons, C. Persson, H. Rensmo, J. Rosén, C. Rudén, M. Selleby, J.-E. Sundgren, K. D. Thelander, K. Tybrandt, P. Weihed, X. Zou, M. Åstrand, C. P. Björkman, J. M. Schneider, O. Eriksson and M. Berggren, Nat. Mater., 2024, 23, 160–161.
5. R. Pollice, G. Dos Passos Gomes, M. Aldeghi, R. J. Hickman, M. Krenn, C. Lavigne, M. Lindner-DAddario, A. Nigam, C. T. Ser, Z. Yao and A. Aspuru-Guzik, Acc. Chem. Res., 2021, 54, 849–860.
6. S. Diwale, M. K. Eisner, C. Carpenter, W. Sun, G. C. Rutledge and R. D. Braatz, Mol. Syst. Des. Eng., 2022, 7, 622–636.
7. Y. Zhang, D. W. Apley and W. Chen, Sci. Rep., 2020, 10, 4924.
8. M. Todorović, M. U. Gutmann, J. Corander and P. Rinke, npj Comput. Mater., 2019, 5, 5.
9. S. Greenhill, S. Rana, S. Gupta, P. Vellanki and S. Venkatesh, IEEE Access, 2020, 8, 13937–13948.
10. C. Li, D. Rubín De Celis Leal, S. Rana, S. Gupta, A. Sutti, S. Greenhill, T. Slezak, M. Height and S. Venkatesh, Sci. Rep., 2017, 7, 5683.
11. L. Bassman Oftelie, P. Rajak, R. K. Kalia, A. Nakano, F. Sha, J. Sun, D. J. Singh, M. Aykol, P. Huck, K. Persson and P. Vashishta, npj Comput. Mater., 2018, 4, 74.
12. I. Y. Miranda-Valdez, L. Viitanen, J. Mac Intyre, A. Puisto, J. Koivisto and M. Alava, Carbohydr. Polym., 2022, 298, 119921.
13. G. Hautier, C. C. Fischer, A. Jain, T. Mueller and G. Ceder, Chem. Mater., 2010, 22, 3762–3767.
14. V. Torsti, T. Mäkinen, S. Bonfanti, J. Koivisto and M. J. Alava, APL Mach. Learn., 2024, 2, 016119.
15. C. E. Rasmussen and C. K. I. Williams, Regression, The MIT Press, 2005, ch. 2.
16. A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. Decost, S. Sarker, C. Oses, C. Toher, S. Curtarolo, A. V. Davydov, R. Agarwal, L. A. Bendersky, M. Li, A. Mehta and I. Takeuchi, Nat. Commun., 2020, 11, 5966.
17. M. Ziatdinov, Y. Liu, K. Kelley, R. Vasudevan and S. V. Kalinin, ACS Nano, 2022, 16, 13492–13512.
18. L. V. Jospin, H. Laga, F. Boussaid, W. Buntine and M. Bennamoun, IEEE Comput. Intell. Mag., 2022, 17, 29–48.
19. B. Lei, T. Q. Kirk, A. Bhattacharya, D. Pati, X. Qian, R. Arroyave and B. K. Mallick, npj Comput. Mater., 2021, 7, 194.
20. Y. Tian, D. Xue, R. Yuan, Y. Zhou, X. Ding, J. Sun and T. Lookman, Phys. Rev. Mater., 2021, 5, 013802.
21. T. Lookman, P. V. Balachandran, D. Xue and R. Yuan, npj Comput. Mater., 2019, 5, 21.
22. M. Stricker, L. Banko, N. Sarazin, N. Siemer, J. Neugebauer and A. Ludwig, arXiv, 2022, preprint, arXiv:2212.04804,  DOI:10.48550/arXiv.2212.04804.
23. K. Helanto, L. Matikainen, R. Talja and O. J. Rojas, BioResources, 2019, 14, 4902–4951.
24. M. Reichler, S. Rabensteiner, L. Törnblom, S. Coffeng, L. Viitanen, L. Jannuzzi, T. Mäkinen, J. R. Mac Intyre, J. Koivisto, A. Puisto and M. J. Alava, Sci. Rep., 2021, 11, 1–11.
25. I. Y. Miranda-Valdez, S. Coffeng, Y. Zhou, L. Viitanen, X. Hu, L. Jannuzzi, A. Puisto, M. A. Kostiainen, T. Mäkinen, J. Koivisto and M. Alava, Cellulose, 2023, 1–14.
26. C. Chen, Y. Zhou, W. Xie, T. Meng, X. Zhao, Z. Pang, Q. Chen, D. Liu, R. Wang, V. Yang, H. Zhang, H. Xie, U. H. Leiste, W. L. Fourney, S. He, Z. Cai, Z. Ma, T. Li and L. Hu, Adv. Funct. Mater., 2022, 2204219.
27. C. Wang, Y. Zhang, B. Zhang and J. Yang, Adv. Funct. Mater., 2022, 2205537.
28. B. Wicklein, A. Kocjan, G. Salazar-Alvarez, F. Carosio, G. Camino, M. Antonietti and L. Bergström, Nat. Nanotechnol., 2015, 10, 277–283.
29. E. S. Ferreira, E. Dobrzanski, P. Tiwary, P. Agrawal, R. Chen and E. Cranston, Mater. Adv., 2023, 641–650.
30. I. Y. Miranda-Valdez, M. R. Yazdani, T. Mäkinen, S. Coffeng, L. Viitanen, J. Koivisto and M. J. Alava, J. Energy Storage, 2023, 73, 109036.
31. Q. Liang, A. E. Gongora, Z. Ren, A. Tiihonen, Z. Liu, S. Sun, J. R. Deneault, D. Bash, F. Mekki-Berrada, S. A. Khan, K. Hippalgaonkar, B. Maruyama, K. A. Brown, J. Fisher and T. Buonassisi, npj Comput. Mater., 2021, 7, 1–10.
32. G. Lo Dico, B. Muõoz, V. Carcelén and M. Haranczyk, Ind. Eng. Chem. Res., 2022, 61, 11455–11463.
33. G. L. Dico, Á. P. Nuñez, V. Carcelén and M. Haranczyk, Chem. Sci., 2021, 12, 9309–9317.
34. M. Sun, H. Sun, Y. Wang, M. Sánchez-Soto and D. Schiraldi, Gels, 2018, 4, 33.
35. R. Moriconi, M. P. Deisenroth and K. Sesh Kumar, Mach. Learn., 2020, 109, 1925–1943.
36. E. Raponi, H. Wang, M. Bujny, S. Boria and C. Doerr, Parallel Problem Solving from Nature-PPSN XVI: 16th International Conference Proceedings, 2020, pp. 169–183.
37. Z. Chen, Y. Wu, Y. Xie, K. Sattari and J. Lin, Mater. Horiz., 2024, 6028–6039.
38. L. Van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 1.
39. L. McInnes, J. Healy and J. Melville, arXiv, 2018, preprint, arXiv:1802.03426,  DOI:10.48550/arXiv.1802.03426.
40. I. Cheddadi, P. Saramito, B. Dollet, C. Raufaste and F. Graner, Eur. Phys. J. E, 2011, 34, 1.
41. K. S. Seo, J. C. Lee, K. S. Bang, H. S. Han, S. H. Chung, B. I. Choi and J. H. Ha, 4th International Symposium on the Packaging and Paper, 2004, 240.
42. M. Binois, R. B. Gramacy and M. Ludkovski, J. Comput. Graph. Stat., 2018, 27, 808–821.
43. K. Mobredi, I. Y. Miranda-Valdez, T. Mäkinen, J. Koivisto and M. J. Alava, Soft Matter, 2024, 20, 5607–5615.
44. I. Y. Miranda-Valdez, T. Mäkinen, X. Hu, J. Lejon, M. Elamir, L. Viitanen, L. Jannuzzi, J. Koivisto and M. J. Alava, Adv. Eng. Mater., 2024, 26, 2400233.
45. S. Daulton, M. Balandat and E. Bakshy, Adv. Neur. Inform. Process. Syst., 2020, 33, 9851–9864.
46. R. Arróyave, D. Khatamsaz, B. Vela, R. Couperthwaite, A. Molkeri, P. Singh, D. D. Johnson, X. Qian, A. Srivastava and D. Allaire, MRS Commun., 2022, 12, 1037–1049.
47. R. Hickman, M. Aldeghi and A. Aspuru-Guzik, chemRxiv, 2023, 1–28 , preprint10.26434/chemrxiv-2023-s5qnw.
48. ANSYS Inc., Ansys GRANTA EduPack, https://www.ansys.com/materials, 2019.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01464b

---