Discerning order from chaos: characterising the surface structure of liquid gallium

Abstract

Liquid metal (LM) technologies are rapidly advancing in modern materials science, with low melting point metals playing a pivotal role in emerging applications. Recent studies reveal that doped liquid gallium systems form spectacular and diverse surface structures during cooling, [Tang et al., Nat. Nanotechnol., 2021, 16, 431–439] sparking renewed interest in the possible geometric structuring at the surface of pure liquid gallium. Distinct from the known increase in surface density, this lateral surface order has long been hinted at experimentally and theoretically but has remained enigmatic. Here, we quantitatively characterise the depth and nature of this surface ordering for the first time, using highly accurate and large scale molecular dynamics simulations coupled with machine learning analysis techniques. We also quantify the enhanced structural order introduced by the addition of a gallium oxide film as well as the disruption due to a dopant (bismuth).

---

New concepts

We demonstrate geometric ordering parallel to the surface of liquid gallium, distinct from the well-known surface density increase. We prove this decades-old conjecture by providing a detailed geometric description of the surface structure of liquid gallium. Through the development of a highly accurate first-principles machine learning force field, we perform simulations of liquid gallium with both liquid–vacuum and liquid–oxide interfaces at an unprecedented scale. Applying newly-designed machine learning-based analytical methods, we establish for the first time properties of foundational importance to liquid metal research and broad interest to materials science: the depth of surface ordering, a minimum depth for a true bulk liquid environment, the enhanced structuring introduced by an oxide film, and the disruption caused by a dopant. These findings offer valuable insights that will shape future research on liquid metals and are key to emerging gallium-based liquid metal technologies. Furthermore, the adaptable analytical methods presented here can be applied to the study of any liquid surface or bulk system, broadening the impact of this work across materials science.

“We adore chaos because we love to produce order” (M.C. Escher, n.d.). While “chaos” might be a strong term for the atomic disorder of a liquid, this phase of matter is literally defined by ever-changing, dynamic and largely random displacements of atoms. However, this isn’t quite the whole story. Look a little closer and you see that many liquids, particularly metals, exhibit some degree of short-range order^1,2 based on an energetically preferred, though temperature-broadened, first nearest neighbour distance. In certain liquids, such as liquid crystals, a unique type of longer-range order exists.³ In others, such as liquid gallium, experiments have hinted at an enigmatic geometric structuring without surface freezing,^4–8 which may play a role in the spectacular structures emerging from doped liquid gallium systems.^9–13 While the order in liquid crystals has been at least broadly characterised, the structuring of the liquid gallium surface has remained speculative and qualitative.

Experimentally, the difficulty in characterising any liquid surface structuring arises from both the dynamic nature of the liquid and the opacity of gallium to both light and electrons.¹² Theoretical explorations have been hindered by limits on the simulation size that have significant consequences for accurately modelling important material properties, such as the predicted melting temperature.¹⁴ Density functional theory (DFT) imposes a relatively small limit on simulation size, but force fields that enable larger scale simulations have been historically inaccurate for gallium.^15–17 The theoretical limitations have recently been eliminated by the emergence of highly accurate first-principles machine learning force fields (DFT-MLFF).^18–24 This coincides with the increased interest in these methods due to the emergence of liquid gallium as a solvent in many emerging liquid metal (LM) technologies. The possible advancements offered by liquid gallium-based systems include increased catalytic yield and selectivity,^25–29 solar thermoelectric generation,³⁰ medical applications,³¹ improved battery technologies,³² and enhanced gas-sensing performance.³³ Furthermore, interfacing liquid gallium with its native oxide has recently shown utility in novel electronic applications,³⁴ such as transparent and flexible conductors,³⁵ and its presence dramatically lowers interfacial tension, positioning it as a potential new class of surfactant.³⁶ Clearly, further investigation into the existence and characterisation of surface structuring in liquid gallium is strongly justified. But the question still remains: Is it even possible to discern order from apparent chaos? If there is order, can we detect or even quantify modifications to that structuring that might be introduced with the addition of a dopant or oxide layer? Armed with the tools of statistics and machine learning algorithms, our answer to all these questions is a resounding “yes!”

In this work, we utilise the support vector classification (SVC)^37–42 and k-means cluster analysis^41,43–45 machine learning (ML) algorithms to address an open question in materials science: Is there geometric ordering at the surface of liquid gallium beyond a simple increase in density and, if so, what is its structure? We explore the depth and nature of surface ordering in pure liquid gallium through ML analysis of DFT-MLFF molecular dynamics (MD) simulations, benchmarked against pure first-principles MD simulations. We further investigate the geometric changes to the surface layers of liquid gallium with the introduction of a surface oxide film, as well as the disruption due to the addition of a dopant atom (bismuth). Determining the depth and nature of the atomic scale structure at the surface of liquid gallium is of significant importance to our current body of work on LM systems^{9–11,46–49} and LM catalysis.^27,28,50 This study builds on our recent work on bulk liquid gallium, which demonstrated an unexpected increase in covalency with rising temperature and resolved decades of debate about bulk liquid structure.⁵¹ Here, we shift the focus to surface structure through the introduction of an interface (vacuum or oxide). While this work specifically focuses on gallium, we anticipate that our methods will be broadly applicable to other liquid systems.

The paper is organised in three tiers of detail. In Section 1, we give an overview of all key results without technical detail, intended for the broadest range of scientific specialists. In Section 2, we provide additional details on methods and evidence leading to our key findings. The third tier is the ESI† where detail is provided at the level of reproducibility. ESI† is extensively referenced in Section 2 as section and figure references with a leading ‘S’.

1 Summary of key results

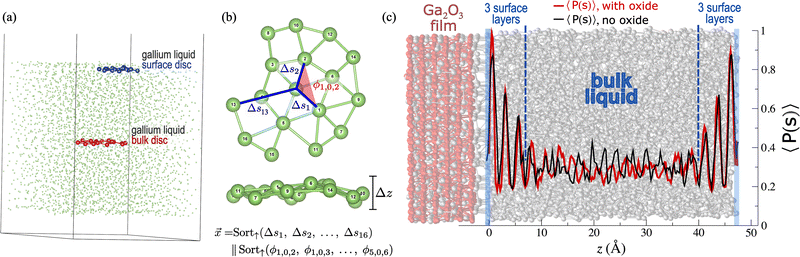
Using thin atomic discs of 17 atoms with faces parallel to the liquid surface, extracted from MD snapshots (Fig. 1a), we capture local structural environments of liquid gallium and investigate liquid surface structuring using two ML analysis methods: SVC binary classification and k-means clustering. For binary classification, the geometry of each disc is represented by a vector that characterises distances and angles between the disc atoms (Fig. 1b). For k-means clustering, the disc geometry is represented by a graph which better captures connectivity (Fig. S12 and Section S4, ESI†).

Fig. 1 (a) A snapshot of the pure liquid gallium MD supercell, highlighting two thin atomic discs used for training the classification (SVC) model: one representing the liquid surface (blue) and the other representing the bulk liquid (red). Note that all atoms shown are gallium atoms, with the colours used only to differentiate the discs. (b) Top and side views of an example atomic disc are given, along with a graphical depiction representing how the disc is transformed into a vector (x⃑) of geometric measures for use in SVC. The disc is constructed as a central atom (labeled 0), and a set of n nearest neighbours that lie within ±Δz/2 of that central atom's z coordinate. The vector x⃑ is a combination of distances and angles, e.g., Δs₁ (distance between atoms 0 and 1) and ϕ_1,0,2 (angle between atoms 1 and 2, with atom 0 as the vertex). The side view exemplifies the disc height Δz. (c) The SVC classification probability that a disc is from the surface class, P(s), indicates the extent to which the disc's geometry resembles a surface structure. Tracking each disc's depth (z) and averaging the surface probabilities over thousands of MD snapshots (〈P(s)〉), we obtain a curve showing how deeply the surface structuring extends. Here, 〈P(s)〉 as a function of depth is shown for both the gallium liquid + oxide (red) and the pure gallium liquid (black), overlaid on an opaque background giving a side view of the liquid + oxide supercell. The liquid surfaces for both simulations are highlighted with blue rectangles, with the finite width of the rectangle reflecting the approximate variation in the liquid's depth over the course of the MD simulations. The three geometrically structured surface layers lie in the regions between the blue rectangles and the dashed lines. The true bulk liquid structure exists only between the two dashed lines.

Using SVC, we demonstrate that discs from the liquid surface can be statistically distinguished from those of the bulk to a high degree of accuracy (84%). Tracking each disc's depth and including a classification probability analysis, we find that higher-than-average surface-like character persists for 3 distinct surface layers in pure liquid gallium (Fig. 1c, black line), in excellent agreement with experimental findings.^4–8 We show that bulk liquid geometries do not statistically dominate until 8.5 Å from the surface, meaning that a system with two liquid–vacuum interfaces requires a depth that exceeds 17 Å for any part of the system to represent a true bulk liquid environment. This explains the atypical melting temperatures observed for 2D multilayer gallenene slabs with depths ranging from ∼5–13 Å.^14,52 To confirm that these results are not influenced by surface freezing, we also conduct a mobility analysis verifying that the surface remains fully liquid (Section S3, ESI†).

Applying k-means clustering and subsequent statistical analyses, we find a high degree of geometric order in the surface discs, which is characterised by 2 concentric shells of atoms (at 3 Å and ∼5.4 Å) surrounding a central atom, with approximate hexagonal angular symmetry and most frequent nearest neighbour angles of 40 and 50° (Fig. 2a, red). In stark contrast, the bulk local environment is entirely disordered (Fig. 2a, blue).

Fig. 2 The frequency distribution analyses for the (top) most common interatomic distances and (bottom) angles of various subsets of geometric discs: (a) (red) the discs most representative of surface geometries compared to (blue) those most representative of bulk from the pure gallium liquid simulation (Section S5.2, ESI†); (b) shallow-depth discs (z < 1.5 Å) from (red-dashed) the pure liquid gallium simulation compared to (orange) those from the liquid gallium + oxide simulation (Section S5.3, ESI†); and (c) the discs most representative of surface geometries from (red-dashed) the pure liquid gallium simulation compared to those (purple) with a surface bismuth central atom from the liquid + Bi dopant simulation (Section S5.4, ESI†). The height of the disc, Δz, varies for different analyses and is explicitly given in each plot. Note that the terms nodes, node-distance, and node-angle are detailed in Section 2.3.

We also demonstrate that the addition of a gallium oxide film alters only the surface layer closest to oxide (Fig. 1c, red), enhancing the surface-like features of that single atomic layer. The statistical analysis of k-means results confirms that the oxide layer increases the degree of surface geometric order through a significant contraction (0.3 Å) and finer resolution of nearest neighbour distances, as well as an increased angular symmetry in the first shell of atoms around the central atom (Fig. 2b).

Finally, we show that the addition of a bismuth dopant entirely destroys the 2-shell structure and disrupts the angular symmetry of the surface geometries (Fig. 2c). Using k-means analysis to compare between discs from different environments (surface, bulk, oxide-adjacent and bismuth-disrupted), we find that the disorder introduced by a bismuth dopant at the surface creates a local environment more similar to the disordered bulk liquid than the geometrically ordered liquid surface (Fig. 3).

Fig. 3 K-means results (K = 4) for the concatenated set of graphs, derived from geometric discs representing the gallium liquid surface (circles), gallium liquid bulk (triangles), gallium liquid at oxide interface (cross) and bismuth-disrupted gallium liquid surface (square), as outlined in the main text. A K-means analysis groups data into clusters by minimizing the variance within each cluster, effectively grouping similar data points together. Here, the grouping of the bismuth-doped surface discs with the disordered bulk liquid discs emphasizes the disruption introduced by a single dopant atom. Note that for this analysis, the graphs are derived from geometric discs with a height of Δz = 2.0 Å.

2 Methods and additional detail

2.1 Simulations

The structures analysed in this work are derived from the trajectories of four different density functional-based MD simulations completed using the Vienna Ab Initio Simulation Package (VASP) version 6.2.4.^53–56 We employ the Perdew–Becke–Ernzerhof for solids (PBEsol) exchange–correlation functional⁵⁷ and the projector augmented wave (PAW) method^58,59 for density functional calculations. Each simulation utilises periodic boundary conditions with at least 29 Å of vacuum padding in the z-dimension, resulting in two liquid–vacuum interfaces perpendicular to the z⃑-axis. All simulations are thermostatted to 450 K and tested to ensure a fully liquid state. Three of the four simulations utilise an MLFF generated using the on-the-fly ML algorithm as implemented in VASP.^22–24 Section S1 (ESI†) gives details of testing, settings and force field training, with top and side view snapshots of all simulation unit cells in Fig. S1 (ESI†).

The four simulations are as follows: (1) a pure liquid gallium system with 320 gallium atoms where the forces between the atoms at each time step are calculated by first-principles but the time-evolution is governed by the classical equations of motion (labeled GaLiq_dft, Fig. S1a, ESI†); (2) an MLFF simulation of pure liquid gallium with 3608 gallium atoms (labeled GaLiq, Fig. S1b, ESI†); (3) an MLFF simulation of liquid gallium with an oxide film, having the same 3608 liquid gallium atoms and adding a six-monolayer gallium oxide (Ga₂O₃) film to one surface (labeled GaLiq + Ox, Fig. S1c, ESI†); and (4) an MLFF simulation of bismuth-doped liquid gallium, with 3606 gallium atoms, one bismuth atom seeded in the upmost surface layer and a second bismuth seeded in the z-centre of the liquid (labeled GaLiq + Bi, Fig. S1d, ESI†). Note that the surface bismuth atom remains within 3.5 Å of the simulation surface for the entirety of the simulation, despite being unconstrained.

2.2 Support vector classification

SVC is a type of support vector machine, which is a widely-used supervised ML algorithm most commonly associated with spam e-mail filtering. Supervised ML algorithms require a set of feature vectors with corresponding labels in order to train the model. A feature vector represents the attributes or properties of the data, while the label indicates the category (class) to which the data belongs. In this work, we would like to capture geometric differences between the surface and bulk environments, therefore our feature vector will be comprised of geometric descriptors and our labels will be surface and bulk (Section S2.1, ESI†).

We capture the surface and bulk environments through the geometric discs shown in Fig. 1a and b. The disc construction was based on experimental results indicating that surface ordering in liquid gallium is largely lateral (parallel to the surface), persisting only ∼3 atomic layers below the surface.^4–6 Therefore, the face of each disc is parallel to the liquid–vacuum interface, and the effective radius of the disc's face is approximately an order of magnitude larger than its height (Δz), as illustrated by the example disc in Fig. 1b. Each disc is constructed around a central atom (labeled 0) by selecting the nearest n neighbour atoms that fall within ±Δz/2 of the central atom (NN_Δz). The set of NN_Δz atoms are labeled according to distance from the central atom (1 is nearest, n is farthest). Example surface and bulk discs are shown in the simulation cell in Fig. 1a and Fig. S3 (ESI†).

Each disc is then geometrically characterised by a vector (feature vector in the language of ML) comprised of: the distances from the central atom to each of the other disc atoms; and all unique angles less than 180° with a vertex on the central atom and endpoints on the 6 nearest NN_Δz. Using the labelling shown in Fig. 1b, the feature vector will be: x⃑ = Sort_↑(Δs₁,Δs₂,…,Δs_n)‖Sort_↑(ϕ_1,0,2,ϕ_1,0,3,…,ϕ_5,0,6). Here, Δs₁ is defined as the distance between atoms 0 and 1, while ϕ_1,0,2 designates the angle between atoms 1 and 2, with atom 0 as the vertex. By carefully distinguishing surface from bulk discs, we train a supervised SVC model to distinguish bulk from surface geometries. The maximum SVC model accuracy of 84% was obtained using training and test data from the GaLiq simulation, Δz = 1.2 Å and n = 16. Sections S2.1 and S2.2 (ESI†) give details of the SVC model training, testing and feature vector construction. We note that while we have selected SVC, five other ML binary classifiers have been tested yielding similar, but slightly lower, accuracies (Section S2.3, ESI†).

The trained SVC model is primarily used to determine a probability score⁶⁰ which indicates the likelihood that a given feature vector belongs to the surface or bulk class, P(s) or P(b), respectively. Calculating the shortest distance between a disc and the liquid surface (depth, z), binning the discs by depth and averaging P(s) for each bin over all MD snapshots, we can determine the average probability that a disc has surface-like geometric features, 〈P(s)〉, as a function of z (Section S2.4, ESI†). Fig. 1c gives the results of this analysis for both the GaLiq (black line) and GaLiq + Ox (red line) simulations, clearly illustrating the increased surface character introduced by the gallium oxide film with the notably higher 〈P(s)〉 for the GaLiq + Ox result nearest the oxide–liquid interface. Note that this probability analysis is completed with the SVC model trained on the GaLiq dataset, meaning that feature vectors from the GaLiq + Ox simulation are statistically compared with those from the GaLiq simulation (Section S2.5, ESI†).

There is no statistically significant difference in 〈P(s)〉 as a function of depth between the GaLiq + Bi and pure GaLiq simulations. As previously mentioned, the surface-seeded bismuth atom remains within 3.5 Å of the surface throughout the simulation. However, despite the limited z-range of that bismuth dopant, gallium-centered discs vastly outnumber bismuth-centered discs by at least two orders of magnitude, effectively diluting any impact that the bismuth atom might have on 〈P(s)〉.

For comparison and benchmarking, the same probability and depth analysis is completed for the GaLiq_dft simulation. Again, the feature vectors from the pure DFT simulation are statistically compared with the SVC training set from the GaLiq MLFF simulation. Apart from minor deviations, the 〈P(s)〉 as a function of depth is identical between the GaLiq and GaLiq_dft simulations (Fig. S8, ESI†), validating that the MLFF has been well-trained.

Finally, the probability scores can also be used to determine which geometric features differentiate discs with high P(s) from those with high P(b). Using discs from the GaLiq simulation with a very high (>99%) P(s) and P(b) score, the average feature vector of each class is calculated (Section S2.6, ESI†), with the result given in Fig. S10 (ESI†). The largest difference arises from the notably shorter distances of the high-P(s) vectors. Remembering that these distances represent the bond lengths between the disc's central atom and each of the NN_Δz, we note that the statistical differentiation of the surface geometries might arise from the known increase in surface density of many LMs.^61–63 In order to investigate whether geometric structuring might also play a role in distinguishing the surface discs, we require a geometric descriptor that includes connectivity: a graph.

2.3 Graph construction

In order to better capture the geometric connectivity of the local environment discs, the geometric descriptor is changed from a distance-angle vector to a graph. Graphs consist of a set of nodes and edges, each of which can have multiple features. A simple example of a graph is a transportation network, where the cities are represented as nodes (example features: population size or geographic area) and the roads connecting them are represented as edges (example features: distance or speed limit).

Here, graphs will be constructed from the same geometric discs used for SVC, which contain a central atom and 16 NN_Δz. Graph features are selected from the following geometric measures. For each atom i in the disc, the distances to the 6 nearest NN_Δz atoms are labeled as Δr_i,j (where j is associated with a second atom in the disc, i ≠ j). The 6 smallest angles between the 6 nearest NN_Δz centred on atom i are labeled θ_i,n (n = [1,6]). Finally, the distance between the geometric centre of the disc to each of the 17 atoms is calculated (ΔR_cent,i). The graphs are then constructed as:

• Nodes: each of the 17 atoms in the disc becomes a node in the graph;

• Node features: one distance (ΔR_cent,i) and 6 angles (θ_i,n);

• Edges: pairwise (unidirectional) connections between all atoms in the disc (total of 256 edges);

• Edge features: one distance (Δr_i,j), which is set to 0 beyond the 6 nearest NN_Δz distances of atom i.

The nodes are numbered according to the ascending distance from the central atom: zero for the central atom and 16 for the farthest atom. For each node, the 6 angles are sorted in ascending order. By setting node and edge features using only the 6 nearest NN_Δz atoms and using more node-angles than node-distances, the graph focuses on local environment connectivity, which is emphasised over interatomic distances. Section S4 (ESI†) provides more detail, including an example graph with representative node and edge features in Fig. S12 and Section S4.1 (ESI†).

2.4 K-means clustering

K-means clustering^41,43–45 is an unsupervised ML algorithm that partitions the data into a specified number of clusters (K) by grouping data points. In overview, this grouping is done through an iterative process of choosing K centroids, assigning data points to the nearest centroid based on a chosen distance metric (e.g., Euclidean distance), and recalculating each clusters centroid. This process repeats until the centroids stabilise. For k-means analysis, the geometric descriptor is the previously-described graph. K-means analysis is employed for two primary purposes: (1) to discern whether the connectivity patterns of different sets of discs can be statistically differentiated by an unsupervised model (i.e., without training or labels) and (2) to use the clustering statistics to summarise the most representative patterns of a given set of discs (Section S5, ESI†).

To discern connectivity patterns between surface and bulk discs of the GaLiq simulation, a combined set of graphs is created from two subsets of discs: (1) those within the first two surface layers of the liquid with a >97% P(s) and (2) discs located near the liquid's midpoint with a >97% P(b). For interest, we added 12 graphs constructed from the non-thermalised gallium 2D bilayer (gallenene),⁶⁴ which serves as an excellent reference system since it is in solid form. In total, >3000 graphs are analysed using a k-means model configured with 3 clusters (K = 3). More information and settings are given in Section S5.1 (ESI†).

The results are graphically illustrated in ESI,† Fig. S13, using the first two principal components of a principal component analysis (PCA) transformation for ease of visual representation. The model identifies two distinct main clusters, showing that the connectivity patterns can be statistically differentiated between bulk and surface discs. Benchmarking against our known labels showed that the clustering was ≫99% accurate (Table S2, ESI†), which is excellent for the highly fluxional liquid environment. Despite configuring k-means to identify three distinct clusters, the solid gallenene graphs are assigned to the same cluster as the high P(s) graphs, indicating the high degree of similarity between the gallium bilayer and the liquid surface structuring.

The connectivity of each group can then be statistically compared. We identify the ‘most representative’ graphs as the 100 graphs that are nearest (Euclidean distance) to the the centroid (mean) of each subset of graphs, then calculate distance and angle frequency distribution plots for these representative graphs (Section S5.2, ESI†). We also calculate the average of these representative graphs (Fig. S15, ESI†).

The average node distances for the 100 representative graphs (Fig. S15b, ESI†) shows that surface graphs have one clear shell of 6 NN_Δz atoms, with a second shell of 6 NN_Δz also discernible. This two-shell structuring of the surface discs is also supported by the node-distance distributions (Fig. 2a, top), with one distance peak at ∼3 Å and another broader peak from 4.8–6 Å. The node-angle distributions are given in Fig. 2a (bottom) for the inner shell of atoms. The surface graphs again show a high degree of angular symmetry, with peaks at 40° and 50°. Node distance and angle distributions for the bulk discs show nothing but diffuse noise. Edge-distance and outer node-angular distributions are given in Fig. S14a and b (ESI†), also showing the increased geometric order of the surface discs.

In summary, Fig. 2a and Fig. S15 (ESI†) demonstrate a clear structuring of the localised geometric environments lateral to the gallium liquid surface. This structuring is characterised by a central atom surrounded by two distinct shells of atoms, each consisting of 6 atoms. Additionally, the angular distribution for the first shell of atoms is narrowly peaked at 40° and 50°, indicating a high-degree of angular symmetry. The bulk distance and angle distributions show only geometric disorder.

A k-means analysis is also completed for the GaLiq + Ox simulation (Section S5.3, ESI†). Here, the discs are limited to shallow-depth (z < 1.5 Å), in order to focus on only the upper surface layer which demonstrated the greatest oxide-induced modification (Fig. 1c). Graphs are created for these shallow depth discs for both the GaLiq + Ox and GaLiq simulations, and compared using a k-means analysis (K = 2). While the results show partially overlapping clusters (Fig. S16, ESI†), the GaLiq + Ox discs are still distinguished from those of the GaLiq simulation with 75–78% accuracy. A more detailed picture emerges from an analysis of the most representative graphs. The node-distance distribution for the first two shells of atoms shows that the first shell contracts significantly from 3 Å to 2.7 Å once the oxide film is added (Fig. 2b, top). Additionally, the two split peaks in the angular distribution of the GaLiq results become one finer peak from 50–55° (Fig. 2b, bottom).

Taken together with the SVC analysis (Fig. 1c), these results demonstrate that the oxide layer does, in fact, increase the structuring in the topmost layer of the gallium liquid surface. The change induced by the oxide is a significant contraction and an increased order within the distances and angles of the first shell of atoms. These results are consistent with experimental results indicating that the oxide layer stabilises and ‘smooths’ the liquid gallium surface.^65,66

Finally, we complete a k-means analysis for discs centred on the surface bismuth atom in the GaLiq + Bi simulation compared to GaLiq high-P(s) discs (Section S5.4, ESI†), where both subsets of discs are required to meet the surface criteria (depth < 6 Å). Extensive testing showed that the k-means statistical differentiation between the two datasets was maximised when the height (Δz) of each geometric disc was increased from 1.2 Å (as used in previous analyses) to 2.8 Å. This result itself is intriguing as it suggests that the bismuth atom disrupts the liquid surface structure both parallel and orthogonal to the surface. Additionally, the graphs yielding the greatest cluster distinction contain only node features (no edges), indicating that the substantive difference between the two sets of discs does not arise from the local pairwise interatomic distances.

The 2-cluster k-means analysis yields well-separated groups (Fig. S17, ESI†) with a 95% accuracy, illustrating the clear difference in connectivity for the bismuth-centred discs compared to the undisrupted gallium surface graphs. Fig. 2c gives the distance and angle frequency distributions for the 100 most representative graphs of each subset. The discs with bismuth central atoms (purple) are entirely disordered, in stark contrast to the GaLiq surface results which have three narrow, distinct peaks at 2.7, 3.1 and 4.9 Å. Note that these results differ from the previous GaLiq results as Δz has more than doubled. The angular distribution of the inner shell of atoms peaks at 50° for both subsets of graphs; however, the GaLiq + Bi results show a disorder-induced broadening and lowering of the main peak.

Taken together, the bismuth atom completely disturbs the surface order in liquid gallium by expanding and disrupting the surface bond networks and the inner-node angular symmetry of the disc. These results are consistent with the findings of our previous work,⁴⁶ where the bismuth atom was found to have disturbed the surface layer of a small bismuth doped gallium nanoparticle. Here, the larger geometric size and non-curved liquid surface has allowed us to better quantify that disturbance.

2.5 Comparing all sets of discs

As a final question, we address whether k-means can yield additional information from a combined analysis of graphs derived from all different types of geometric environments. To be statistically sound, all graphs need to be created using the same disc constraints. Setting Δz = 2.8 Å optimises the k-means differentiation for GaLiq + Bi, while Δz = 1.2 Å yielded the clearest cluster distinction for the other 3 analyses. Here, the analysis is completed with a ‘middle ground’ Δz = 2.0 Å, keeping n = 16. To account for the changed disc height, a new SVC training and classification with probability analysis is performed on the discs from the GaLiq simulation, resulting in the SVC probabilities P(s)_2.0 and P(b)_2.0, which indicate the likelihood that a disc originates from a surface or bulk environment, respectively (Section S5.5, ESI†).

Subsequently, two new subsets of graphs are created: one created from discs with P(s)_2.0 > 95% and a depth < 6 Å and one created from discs with P(b)_2.0 > 95% and a depth within ±1 Å of the liquid's midpoint along the z-axis. Two additional graph subsets are also added: one created from GaLiq + Ox discs that have a central atom at a shallow depth of <1.5 Å, and a fourth consisting of all discs from the GaLiq + Bi simulation that have a surface bismuth central atom. This provides us with one large set of graphs derived from four physically relevant datasets, characterised as:

– gallium liquid surface

• all discs from the GaLiq simulation with high P(s)_2.0 and a depth < 6 Å;

– gallium liquid bulk

• all discs from the GaLiq simulation with high P(b)_2.0 and a depth within ±1 Å of the liquid midpoint along the z-axis;

– gallium liquid at oxide interface

• all discs from the GaLiq + Ox simulation with a shallow depth < 1.5 Å; and

– bismuth-disrupted gallium liquid surface

• all discs from the GaLiq + Bi simulation that have the surface bismuth atom as a central atom (z < 6 Å).

Fig. 3 gives the results of a k-means analysis (K = 4) on the concatenated set of graphs, where once again, only the node-features are included in the analysis (edges are excluded). Summarising these results accounting for each subset of graphs:

(1) 94% of the gallium liquid surface graphs are grouped in cluster 4 (red);

(2) 98% of the gallium liquid at oxide interface graphs are also grouped in cluster 4 (red);

(3) 95% of the gallium liquid bulk graphs are grouped in a combined cluster 1 + 2 (blue and green);

(4) 36% of the bismuth-disrupted gallium liquid surface graphs are grouped in cluster 3 (purple), while 48% are in the combined cluster 1 + 2.

This analysis reveals a number of things about how surface ordering is altered or enhanced with the introduction of new elements. First, while 36% of the bismuth-disrupted surface graphs are clustered in a unique group (cluster 3), nearly 50% of the bismuth-disrupted surface graphs are clustered with the gallium liquid bulk graphs (clusters 1 + 2). Since previous analysis showed that the bulk graphs have considerably higher disorder (Fig. 2a and Fig. S14, ESI†), this clustering indicates the significant disruption caused by the single Bi dopant atom: the gallium networks surrounding a bismuth central atom become more disordered and bulk-like. Secondly, even with an allowance for four cluster centres, k-means clusters the gallium liquid surface graphs together with the gallium liquid at oxide interface graphs (cluster 4), further indicating the geometric similarity of these two subsets. Lastly, an analysis of the subset components of cluster 4 revealed that, compared to the gallium liquid surface graphs, the gallium liquid at oxide interface graphs are farther (Euclidean distance) from the disordered discs (gallium liquid bulk and bismuth-disrupted), giving additional evidence that the oxide layer enhances the surface ordering in liquid gallium.

3 Next steps

Looking forward, while we have applied these statistical analysis techniques to investigate geometric ordering in liquid gallium, the methods outlined here are highly generalisable. The geometric representations (vectors and graphs) are inherently flexible and can be straightforwardly applied to any atomic liquid system. Even in the absence of surface ordering, these methods can assess the depth of surface modification or the structural impact of any interface, such as in interfacial templating.

One particularly impactful application could be determining the extent and nature of surface layering in liquid alkali metals, which has direct relevance to high-temperature battery technologies.⁶⁷ With the addition of orientational measures, we anticipate that these methods could also be readily extended to molecular liquids. Future work in our group will explore structural changes introduced by variations in liquid metal solvents and solutes. Here, it has been a particular pleasure to dive into (and swim a bit in) the chaos of liquid gallium, only to emerge at the surface to find order. We believe M.C. Escher would approve.

Data availability

The datasets and code generated in this study are not publicly available due to the large size and volume of the files. However, they can be made available by the authors upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors wish to acknowledge the use of New Zealand eScience Infrastructure (NeSI) high performance computing facilities. New Zealands national facilities are provided by NeSI and funded jointly by NeSIs collaborator institutions and through the Ministry of Business, Innovation and Employments Research Infrastructure programme, https://www.nesi.org.nz. This work is supported by the Marsden Fund Council from Government funding, managed by Royal Society Te Apārangi (21-UOA-179).

Notes and references

1. J. Hafner and G. Kahl, J. Phys. F: Met. Phys., 1984, 14, 2259–2278.
2. N. W. Ashcroft, Nuovo Cimento D, 1990, 12, 597–618.
3. P.-G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 2nd edn, 1993.
4. M. J. Regan, E. H. Kawamoto, S. Lee, P. S. Pershan, N. Maskil, M. Deutsch, O. M. Magnussen, B. M. Ocko and L. E. Berman, Phys. Rev. Lett., 1995, 75, 2498–2501.
5. M. J. Regan, P. S. Pershan, O. M. Magnussen, B. M. Ocko, M. Deutsch and L. E. Berman, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 9730–9733.
6. M. J. Regan, P. S. Pershan, O. M. Magnussen, B. M. Ocko, M. Deutsch and L. E. Berman, Phys. Rev. B:Condens. Matter Mater. Phys., 1997, 55, 15874–15884.
7. J. E. Northrup, J. Neugebauer, R. M. Feenstra and A. R. Smith, Phys. Rev. B:Condens. Matter Mater. Phys., 2000, 61, 9932–9935.
8. L. E. González and D. J. González, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 064202.
9. J. Tang, S. Lambie, N. Meftahi, A. J. Christofferson, J. Yang, M. B. Ghasemian, J. Han, F.-M. Allioux, M. A. Rahim, M. Mayyas, T. Daeneke, C. F. McConville, K. G. Steenbergen, R. B. Kaner, S. P. Russo, N. Gaston and K. Kalantar-Zadeh, Nat. Nanotechnol., 2021, 16, 431–439.
10. S. A. Idrus-Saidi, J. Tang, S. Lambie, J. Han, M. Mayyas, M. B. Ghasemian, F.-M. Allioux, S. Cai, P. Koshy, P. Mostaghimi, K. G. Steenbergen, A. S. Barnard, T. Daeneke, N. Gaston and K. Kalantar-Zadeh, Science, 2022, 378, 1118–1124.
11. J. Tang, S. Lambie, N. Meftahi, A. J. Christofferson, J. Yang, J. Han, M. A. Rahim, M. Mayyas, M. B. Ghasemian, F.-M. Allioux, Z. Cao, T. Daeneke, C. F. McConville, K. G. Steenbergen, R. B. Kaner, S. P. Russo, N. Gaston and K. Kalantar-Zadeh, Nat. Synth., 2022, 1, 158–169.
12. K. Kalantar-Zadeh, T. Daeneke and J. Tang, Science, 2024, 385, 372–373.
13. F.-M. Allioux, M. B. Ghasemian, W. Xie, A. P. O’Mullane, T. Daeneke, M. D. Dickey and K. Kalantar-Zadeh, Nanoscale Horiz., 2022, 7, 141–167.
14. S. Lambie, K. G. Steenbergen and N. Gaston, Nanoscale Adv., 2021, 3, 499–507.
15. M. I. Baskes, S. P. Chen and F. J. Cherne, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 66, 104107.
16. J. Nord, K. Albe, P. Erhart and K. Nordlund, J. Phys.: Condens. Matter, 2003, 15, 5649.
17. K. Albe, K. Nordlund, J. Nord and A. Kuronen, Phys. Rev. B:Condens. Matter Mater. Phys., 2002, 66, 035205.
18. O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Chem. Rev., 2021, 121, 10142–10186.
19. H. Niu, L. Bonati, P. M. Piaggi and M. Parrinello, Nat. Commun., 2020, 11, 2654.
20. C. Zeni, K. Rossi, A. Glielmo and F. Baletto, Adv. Phys.:X, 2019, 4, 1654919.
21. C. Zeni, K. Rossi, T. Pavloudis, J. Kioseoglou, S. D. Gironcoli, R. E. Palmer and F. Baletto, Nat. Commun., 2021, 12, 6056.
22. R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701.
23. R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105.
24. R. Jinnouchi, F. Karsai, C. Verdi, R. Asahi and G. Kresse, J. Chem. Phys., 2020, 152, 234102.
25. M. A. Rahim, J. Tang, A. J. Christofferson, P. V. Kumar, N. Meftahi, F. Centurion, Z. Cao, J. Tang, M. Baharfar, M. Mayyas, F.-M. Allioux, P. Koshy, T. Daeneke, C. F. McConville, R. B. Kaner, S. P. Russo and K. Kalantar-Zadeh, Nat. Chem., 2022, 14, 935–941.
26. J. Tang, A. J. Christofferson, J. Sun, Q. Zhai, P. V. Kumar, J. A. Yuwono, M. Tajik, N. Meftahi, J. Tang, L. Dai, G. Mao, S. P. Russo, R. B. Kaner, M. A. Rahim and K. Kalantar-Zadeh, Nat. Nanotechnol., 2023, 1–5.
27. C. Ruffman, K. G. Steenbergen, A. L. Garden and N. Gaston, Chem. Sci., 2023, 15, 185–194.
28. C. Ruffman, K. G. Steenbergen and N. Gaston, Angew. Chem., Int. Ed., 2024, e202407124.
29. N. Taccardi, M. Grabau, J. Debuschewitz, M. Distaso, M. Brandl, R. Hock, F. Maier, C. Papp, J. Erhard, C. Neiss, W. Peukert, A. Görling, H.-P. Steinrück and P. Wasserscheid, Nat. Chem., 2017, 9, 862–867.
30. N. Flores, F. Centurion, J. Zheng, M. Baharfar, M. Kilani, M. B. Ghasemian, F. Allioux, J. Tang, J. Tang, K. Kalantar-Zadeh and M. A. Rahim, Adv. Mater., 2024, 36, e2308346.
31. C. Zhang, B. Yang, J. M. Biazik, R. F. Webster, W. Xie, J. Tang, F.-M. Allioux, R. Abbasi, M. Mousavi, E. M. Goldys, K. A. Kilian, R. Chandrawati, D. Esrafilzadeh and K. Kalantar-Zadeh, ACS Nano, 2022, 16, 8891–8903.
32. S. Zhang, Y. Liu, Q. Fan, C. Zhang, T. Zhou, K. Kalantar-Zadeh and Z. Guo, Energy Environ. Sci., 2021, 14, 4177–4202.
33. Y. Chi, J. Han, J. Zheng, J. Yang, Z. Cao, M. B. Ghasemian, M. A. Rahim, K. Kalantar-Zadeh, P. Kumar and J. Tang, ACS Appl. Mater. Interfaces, 2022, 14, 30112–30123.
34. K. Kalantar-Zadeh, J. Tang, T. Daeneke, A. P. O’Mullane, L. A. Stewart, J. Liu, C. Majidi, R. S. Ruoff, P. S. Weiss and M. D. Dickey, ACS Nano, 2019, 13, 7388–7395.
35. W. Jung, M. H. Vong, K. Kwon, J. U. Kim, S. J. Kwon, T. Kim and M. D. Dickey, Adv. Mater., 2024, e2406783.
36. M. Kong, M. H. Vong, M. Kwak, I. Lim, Y. Lee, S.-H. Lee, I. You, O. Awartani, J. Kwon, T. J. Shin, U. Jeong and M. D. Dickey, Science, 2024, 385, 731–737.
37. V. N. Vapnik, The Nature of Statistical Learning Theory, Springer, 1995.
38. C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297.
39. B. Schölkopf and A. J. Smola, Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond, MIT Press, 2002.
40. C.-C. Chang and C.-J. Lin, ACM Trans. Intell. Syst. Technol., 2011, 2, 1–27.
41. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and V. Dubourg, et al. , J. Mach. Learn. Res., 2011, 12, 2825–2830.
42. C. J. Burges, Data Mining and Knowledge Discovery, 1998, vol. 2, pp. 121–167.
43. J. B. MacQueen, Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, 1967, pp. 281–297.
44. S. Lloyd, IEEE Trans. Inf. Theory, 1982, 28, 129–137.
45. J. A. Hartigan and M. A. Wong, J. R. Stat. Soc. C, 1979, 28, 100–108.
46. S. Lambie, K. G. Steenbergen and N. Gaston, Phys. Chem. Chem. Phys., 2021, 23, 14383–14390.
47. S. Lambie, K. G. Steenbergen and N. Gaston, Chem. Commun., 2022, 58, 13771–13774.
48. S. Lambie, K. G. Steenbergen and N. Gaston, Angew. Chem., Int. Ed., 2023, 62, e202219009.
49. C. Ruffman, S. Lambie, K. G. Steenbergen and N. Gaston, Phys. Chem. Chem. Phys., 2023, 25, 1236–1247.
50. C. Ruffman, S. R. B. Case, T. Grayson and N. Gaston, Adv. Mater. Interfaces, 2024, 2400456.
51. S. Lambie, K. G. Steenbergen and N. Gaston, Mater. Horiz., 2024, 11, 4201–4206.
52. K. G. Steenbergen and N. Gaston, Chem. Commun., 2019, 55, 8872–8875.
53. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561.
54. G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
55. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
56. G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
57. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
58. P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
59. G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
60. J. Platt, Advances in large margin classifiers, MIT Press, 1999, pp. 61–74.
61. B. G. Walker, N. Marzari and C. Molteni, J. Phys.: Condens. Matter, 2006, 18, L269–L275.
62. Y. Kang and I.-H. Jung, Metall. Mater. Trans. B, 2024, 1–13.
63. T. Iida and R. I. L. Guthrie, The Physical Properties of Liquid Metals, Oxford University Press, Oxford, 1988.
64. V. Kochat, A. Samanta, Y. Zhang, S. Bhowmick, P. Manimunda, S. A. S. Asif, A. S. Stender, R. Vajtai, A. K. Singh, C. S. Tiwary and P. M. Ajayan, Sci. Adv., 2018, 4, e1701373.
65. M. J. Regan, H. Tostmann and P. S. Pershan, Phys. Rev. B:Condens. Matter Mater. Phys., 1997, 55, 10786–10790.
66. P. H. A. Vaillant, V. Krishnamurthi, C. J. Parker, R. Kariuki, S. P. Russo, A. J. Christofferson, T. Daeneke and A. Elbourne, Adv. Funct. Mater., 2023, 2310147.
67. G. Nikiforidis, M. C. M. V. D. Sanden and M. N. Tsampas, RSC Adv., 2019, 9, 5649–5673.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01415d

---