Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simulation of perovskite thin layer crystallization with varying evaporation rates†
M.
Majewski‡
 a,
S.
Qiu‡
a,
S.
Qiu‡
 b,
O.
Ronsin
b,
O.
Ronsin
 *a,
L.
Lüer
*a,
L.
Lüer
 b,
V. M.
Le Corre
b,
V. M.
Le Corre
 b,
T.
Du
b,
T.
Du
 *bc,
C. J.
Brabec
*bc,
C. J.
Brabec
 bc,
H.-J.
Egelhaaf
bc,
H.-J.
Egelhaaf
 bc and
J.
Harting
bc and
J.
Harting
 ad
ad
aHelmholtz Institute Erlangen-Nürnberg for Renewable Energy (HIERN), Forschungszentrum Jülich, Fürther Straße 248, 90429 Nürnberg, Germany. E-mail: o.ronsin@fz-juelich.de
bInstitute of Materials for Electronics and Energy Technology (i-MEET), Department of Materials Science and Engineering, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany. E-mail: tian.du@fau.de
cHelmholtz Institute Erlangen-Nürnberg for Renewable Energy (HIERN), Forschungszentrum Jülich, Immerwahrstraße 2, 91058 Erlangen, Germany
dDepartment of Chemical and Biological Engineering and Department of Physics, Friedrich-Alexander-Universität Erlangen-Nürnberg, Fürther Straße 248, 90429 Nürnberg, Germany
First published on 21st October 2024
Abstract
Perovskite solar cells (PSC) are promising potential competitors to established photovoltaic technologies due to their superior efficiency and low-cost solution processability. However, the limited understanding of the crystallization behaviour hinders the technological transition from lab-scale cells to modules. In this work, advanced phase field (PF) simulations of solution-based film formation are used for the first time to obtain mechanistic and morphological information that is experimentally challenging to access. The well-known transition from a film with many pinholes, for a low evaporation rate, to a smooth film, for high evaporation rates, is recovered in simulation and experiment. The simulation results provide us with an unprecedented understanding of the crystallization process. They show that supersaturation and crystallization confinement effects determine the final morphology. The ratio of evaporation to crystallization rates turns out to be the key parameter driving the final morphology. Increasing this ratio is a robust design rule for obtaining high-quality films, which we expect to be valid independently of the material type.
New conceptsPerovskite photovoltaics (PV) has the potential to become a key PV technology. An essential challenge for high-throughput production is to deposit high-quality, homogeneous, smooth perovskite films. Many papers have, therefore, attempted to understand the mechanisms of film formation, mainly by chemical considerations on crystal nucleation and growth. We present a novel approach to tackle the film formation problem. It uses not only in situ monitoring, but also a coupled fluid mechanics/phase field simulation framework in order to model film formation during processing. It is the first time such an advanced theoretical approach has been applied to improve the fabrication of perovskite layers. The simulation results provide us with an unprecedented understanding of the crystallization process. They show that supersaturation and crystallization confinement effects drive the morphology built-up. The ratio of evaporation to crystallization rates turns out to be the key parameter determining the final morphology. Increasing this ratio for obtaining high-quality films is found to be a robust, general design rule, which we expect to be valid for any perovskite material or even beyond. This new unified framework can help understand the process–structure relationship of perovskite films, thus devising robust processing routes for efficient perovskite solar cells. |
Introduction
Perovskite solar cells have become a very promising option for the 3rd generation of photovoltaics.1 Single-layer solar cells with perovskites as the absorber layer have now reached astonishing power conversion efficiencies (PCE) of over 26%.2 These efficiencies can be reached due to the excellent optoelectronic properties of this class of materials, which include a high absorption coefficient, high carrier diffusion lengths, tunability of the band gap, and high defect tolerance.3 A prominent issue that hinders the upscaling of perovskite photovoltaics is the efficiency gap between lab-scale solar cells and modules.4 One reason is the poor control of the morphology of the active layer which strongly impacts the device performance,5 owing to a deficiency in the comprehensive understanding of its morphology formation. Even for the most investigated system, methylammonium lead triiodide (MAPbI3), the interplay of the physical mechanisms involved in the crystallization process for one-step solution processing, including evaporation, nucleation, growth, and mass transport, remains poorly understood.6 The goal is therefore to gain a better understanding of the processes taking place in a drying film, notably for deposition techniques that can be used for large-scale production and roll-to-roll processing to exploit the potential of fully printed perovskite solar cells at industrial scale.7It has been established that drying in ambient conditions of the precursor solution is usually not sufficient to get a high-quality film.8 A widely employed route to improve film quality is to increase the evaporation rate. This can be achieved by several methods like gas quenching,8 anti-solvents,9 or vacuum drying.10 The morphology information measured on the final film using scanning electron microscopy (SEM),11 X-ray diffraction (XRD),12 or photoluminescence (PL)13 helps to judge the quality of the film. However, these techniques are insufficient to understand how the film has formed, which is needed and indispensable to rationally control the film formation and therefore its quality. The crystallization process can be investigated in situ by grazing-incidence wide-angle X-ray scattering (GIWAXS),14,15 UV-vis absorption,16,17 white light reflectance spectroscopy (WLR),18 and PL.16,17 These techniques help to understand the chemical transition from the solution to the crystalline perovskite film. However, the information gained on the evolution of grain sizes, crystallinity, and crystal arrangement is rarely reported.19 For MAPbI3 the picture looks as follows: lead (II) iodide and methylammonium Iodide are dissolved in polar solvents. For strongly coordinating solvents such as DMSO20 the formation of solid-state intermediates (SSI) is observed during drying, which can result in a needle-like structure in the final state.21 For weakly binding solvents, like 2-ME,22 direct conversion, without SSI, is also reported.5,14
To obtain a qualitative description of the crystallization of the perovskite films, one can refer to nucleation and growth models, including the Lamer model,23–25 the Johnson–Mehl–Avrami–Kolmogorov (JMAK) model,12,22 classical nucleation theory,24 Volmer–Weber growth and Frank-van der Merwe growth6 or the evolution of Voronoi cells.26 However, all the aforementioned models are not able to predict the spatial organization of the crystalline film, namely the roughness of the dry film, the stacking of the crystals, and the amount of uncovered substrate, which all have a strong impact on device performance.27 As a result, to the best of our knowledge, no coherent description of the formation pathway of solution-processed perovskite films based on physical phenomena can be found in the existing literature. Therefore, a theoretical framework is needed that can explain the process–structure relationship in more detail. This can be achieved by phase field (PF) simulations, a powerful tool used to investigate the kinetics of thermodynamic phase transitions based on a continuum description with diffuse interfaces. The thermodynamics is described using a free energy functional, and the kinetic evolution is usually governed by the Allen–Cahn and Cahn–Hilliard equations. PF simulations can describe the phase change between liquid to solid28,29 and/or spinodal decomposition30 in multicomponent mixtures. The effects of evaporation31 and hydrodynamics32 can be included as well. PF simulations for printable photovoltaic systems were presented by Wodo33,34 in the case of amorphous organic photovoltaic blends and by Michels35 for crystallizing films. We recently developed a PF framework taking into account liquid–liquid demixing, crystallization, and hydrodynamic effects in drying films.36 This allowed us to successfully simulate the bulk-heterojunction formation in printed organic solar cells featuring crystalline materials.37 For OPV, important features of the film bulk-heterojunction morphology is the relative size of the donor and acceptor domains, might they be due to crystallization and/or liquid–liquid phase demixing. The picture for perovskite material is different, and the solar cell performance is related notably to roughness, pinholes, as well as crystal sizes and orientation. Now, a decisive, unique advantage of our theoretical framework regarding its application to perovskites is precisely the possibility to investigate the fundamental problems of pinholes and surface roughness of the dried film by tracking the displacement and deformation of the film–vapour interface.36
In this paper, we use PF simulations coupled to in situ and ex situ measurements in order to understand the formation mechanisms of solution-processed perovskite films. We focus on MAPbI3 layers cast from a 2ME-NMP solution using blade coating, a well-established model process for upscaling. Model parameters in the simulation are kept generic on purpose in order to obtain results that are valid not only for the specific material system and solution deposition technique investigated in the current work but also for other perovskite materials. The impact of the solvent evaporation rate (varied by gas quenching) on the final film morphology and its formation pathway is investigated experimentally. In parallel, our phase field model is used to simulate the morphology formation process. The roughness, the vertical stacking of the crystals, the occurrence of pinholes in the film, the time-dependent crystallinity, and the crystal sizes are extracted from the simulation data. The PF simulations are validated extensively against experiments. Then, the simulations are used to gain deep insights into the film formation process. For the first time, the precise film formation pathway is established, explaining the large variations in morphology for solution-processed perovskite depending on the process parameters. This proves that our framework can be used to understand the impact of processing conditions on the final morphology, making use of a sound physical basis. As a result, fully printed perovskite solar cells with improved performance were fabricated. Their JV curves are fitted with an open-source drift-diffusion model.38 From the drift-diffusion simulations, the main reasons for the observed changes in performance are extracted and correlated to the observed changes in morphology. We believe this methodology can be useful for minimizing the morphological gap and the efficiency gap from lab to fab.
The structure of the work is as follows: first, the simulation technique, the time-dependent evolution of the drying film during a typical simulation, and the experimental methods are described. Second, the results are presented in the main part of the paper: to start with, the model is validated using extensive comparison with experimental data. Then, the mechanisms driving the morphology formation are described and discussed in detail based on both in situ measurements and simulation results. Afterwards, evidence is given that the ratio of evaporation to growth rate is the determining factor for the formation of different morphologies. Finally, the performance of the fully printed solar cells is presented, and the relationship with film morphology is discussed. Third, the work is summarized, and future research directions are proposed in the conclusion.
Simulation procedure and experimental approach
The phase field model used here is a adaption of the Cahn–Hilliard Allen–Cahn Navier–Stokes multi-component model presented in.36 The system is modelled with three volume fractions (see ESI,† 1): one field variable for the solute (φ1, perovskite material), one for the solvents (φ2), and one for the air (φ3), which is a buffer material compensating solvent removal due to evaporation.36 Additionally, two order parameters define regions of crystalline perovskite (ϕc) and vapor (ϕair) phases. Finally, two additional fields ν and P allow for tracking the velocity and pressure in the film, respectively. Using a single solute and a single crystalline phase to represent the perovskite formation is a strong simplification since the crystallization of perovskite involves sophisticated chemistry with the formation of several ion complexes and sometimes colloidal aggregates and/or solid-state precursor crystals.22 However, our focus is on the physics of nucleation and growth and their impact on the morphology formation. For this, we will show that we can gain very useful insights without considering the details of the solution chemistry. Note that in the presently investigated system, it has been shown that direct perovskite crystallization is dominant.22,39The Gibbs free energy Gν accounts for the entropic mixing and enthalpic molecular interactions as described in the Flory–Huggins theory, surface energy for all the considered interfaces, and an energy of phase change from the liquid to the solid state featuring an energy barrier. The chosen form of the free energy ensures that crystallization can only take place through a nucleation and growth process (see ESI,† 1.1 and 2.1).
The evolution of the volume fraction fields φi is given by the advective Cahn Hilliard equation
 | (1) |
This is the generalized form of the advection-diffusion equation, where Λij are the symmetric Onsager mobility coefficients, which depend themselves on the composition and the phase state. μj − μ3 is the exchange chemical potential evaluated from the functional derivatives of the free energy Gν, R is the gas constant, ν0 is the molar volume of a lattice size as defined in the Flory–Huggins theory, and T is the temperature.
The evolution of the crystalline order parameter ϕc is given by the stochastic advective Allen Cahn equation
 | (2) |
The velocity field v is obtained by solving the fluid mechanics equations, whereby the convective flows are due to the capillary forces arising from the liquid–solid and liquid–vapor interfaces, which can be derived from the phase fields. Advection is responsible for the solid particle transport, but it has been checked that it has no impact on the nucleation and growth process itself, and therefore the final morphologies are quite insensitive to the solution viscosity (see ESI,† 1.4). This allows to use a damped kinetics for convective transport, which is necessary to have tractable simulation times.
To handle the evaporation of the solvent the top of the simulation box is initialized with a layer of air above the drying film. During the simulation, an outflux jz = zmax of solvent is applied at the top of the simulation box (z = zmax):
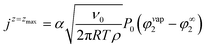 | (3) |
This expression corresponds to the Hertz–Knudsen theory, where α is the evaporation-condensation coefficient, P0 is a reference pressure, and φ∞2 = P∞2/P0, with P∞2 being the solvent pressure in the environment. φvap2 is the calculated volume fraction in the vapor resulting from the local liquid–vapor equilibrium at the film surface. The displacement of the film–vapor interface is described with an additional Allen–Cahn equation.
2D cross-sections of the film are simulated. Initially, the fluid film is assumed to be fully amorphous and perfectly mixed, and initialized with 20% volume fraction of solute. This corresponds roughly to 1.3 M MAPbI3 and is well below the volume fraction needed for crystallization (‘crystallization threshold’, φcrit, see ESI,† 2.2).
Two sets of simulations are performed. Simulations of the first set solely differ in the evaporation rate of the solvent. In the second set only the crystallization rate is varied. While the evaporation rate is modified by adjusting the evaporation-condensation coefficient α (see eqn (3)), the crystallization rate can be adjusted by modifying the Allen–Cahn mobility Mc (see eqn (2)). The effect of the annealing step in the experiment is mimicked by increasing the evaporation rate. A full list of parameters can be found in the ESI,† 1.5. For each condition, five simulation runs are performed.
The behaviour of a typical simulation with a low evaporation rate is shown in Fig. 1. The time increases from left to right and top to bottom. Initially, the condensed film is fully homogenous (Fig. 1(a)). When the volume fraction of solute exceeds φcrit first nuclei form (Fig. 1(b)). In the supersaturation regime nuclei keep appearing and all nuclei grow continuously (Fig. 1(c)). In this example, the volume fraction of solute decreases in the liquid phase due to material consumption by crystallization. Below φcrit no further nucleation happens, and only growth proceeds (Fig. 1(d)). When the amorphous phase reaches the thermodynamic equilibrium volume fraction of solute (saturation concentration), crystal growth terminates and the crystals coarsen (Fig. 1(e)). Finally, the remaining solvent evaporates, and the substrate falls dry (Fig. 1(f)).
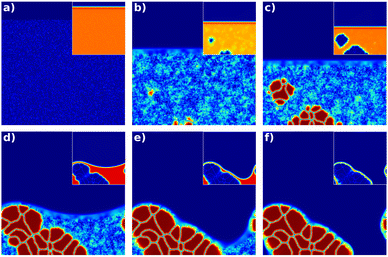 | ||
| Fig. 1 Time series of the simulated film drying for a low evaporation rate. The crystalline order parameter is shown as well as the volume fraction of the solvent (inset). The time increases from left to right and from top to bottom. (a) Initially, there is a homogenous, amorphous film without any crystals and a thin layer of air on top. (b) after some time, some solvent has evaporated, the height of the film is smaller and first nuclei appear. (c) In the supersaturation regime further nuclei appear. (d) When the volume fraction of solute decreases below the critical concentration φcrit no further nucleation can happen and only crystal growth takes place. (e) At a certain point, all the solute is consumed by the crystals, and only coarsening happens (note that the central crystal on the substrate is consumed by its neighbors from (d) to (e)). (f) Finally, the liquid film breaks, leaving pinholes. The full set of fields for this simulation is shown in ESI,† 2.3. | ||
Fig. 2 shows a sketch of the experimental fabrication and characterization process. The precursors MAI and PbI2, are dissolved in a solvent mixture of 2-methoxyethanol (2-ME) and N-methylpyrrolidone (NMP). The solution is blade-coated onto an ITO substrate in ambient atmosphere. Gas quenching is applied at various air pressures immediately after deposition. The advantage of gas quenching is that we only change the evaporation rate of the solvent, in contrast to temperature or solvent changes, which might also affect nucleation and growth kinetics and/or mechanisms. During gas quenching, in situ PL and UV-vis, and WLR are recorded in parallel experiments using the same processing conditions. XRD diffractograms are taken on the dry film. Afterwards, the film is annealed on a hot plate. SEM and confocal images, as well as haze measurements, are performed after annealing to gain insight into the dry film morphology. The detailed descriptions of the setup, materials, and experimental procedures are reported in ESI,† 2.4.
Results
Impact of the drying rate on the morphology and model validation
The evaporation rate of a PbI2/MAI/2-ME/NMP film is controlled experimentally using gas quenching by varying the gas pressure from 0 to 2 bar. The evolution of the scaled film height h/hfin depending on the scaled time t/τ, as measured by WLR, is shown in Fig. 3 for three of the six tested gas pressures. Thereby, hfin is the expected average final film height and τ is the evaporation time for the fastest evaporation rate. In the simulations, the evaporation-condensation coefficient α is adjusted accordingly, such that there is a qualitative agreement of the evaporation rate variations between the simulations and the experiments (Fig. 3(a) and (b)).For all the evaporation rates the film height decreases at a constant evaporation rate through the drying process. For high evaporation rates, the solvent fully evaporates. At the end of the drying, the film has crystallized directly into MAPbI3 as confirmed by the XRD spectra (Fig. 3(c)). All films exhibit the perovskite phase originating from a diffraction peak located at 14.1°. For the 0 bar, the evaporation stops at a higher film height. This indicates that not all solvent is evaporated, but is trapped in the film (this hypothesis is supported by infrared reflectometry spectra, see ESI,† 3.1). In the simulations, a similar behaviour is observed for low evaporation rates. There might be two reasons for solvent trapping in the film. First, it might be involved in SSI. Diffraction peaks located below 10° are present, which indicates that a second crystalline phase has formed. Note that this effect has not been taken into account in the simulation approach which focuses on direct crystallization only. Second, solvent might be trapped in small spaces in between or underneath the crystals, as evidenced in the simulations (see ESI,† 3.2). In such a case, annealing enables further solvent removal (see ESI,† 3.3).
A comparison of the simulated and experimentally observed morphologies after annealing is shown in Fig. 4 and 5. The amount of uncovered area of the sample and the final crystal sizes can be estimated from the SEM top view (Fig. 4(j)–(l)). The vertical stacking of the crystals and the roughness of the sample can be obtained from the cross-section image (Fig. 4(m)–(o)). For the simulation, these quantities can be calculated directly from the simulated fields in Fig. 4(g)–(i), (see ESI,† 3.4). Note that for the quantification of pinholes and crystal sizes, data from simulation cross sections have been compared to data SEM top views (more statistics available): it is clear from the SEM observations that the deviations between crystal sizes and uncovered areas from cross sections and from top views are minimal, which allows such a comparison with minimal bias. The film morphologies after drying and annealing in the experiment and for five different simulation runs of each drying rate are shown in ESI,† 3.5 and 3.6. The mechanisms of morphology formation will be discussed in detail, later in the manuscript.
 | ||
| Fig. 4 Crystalline order parameter and volume fraction of solvent (inset) for a low evaporation rate (a), (d), (g), a medium evaporation rate (b), (e), (h) and a high evaporation rate (c), (f), (i). The onset of crystallization (a), (b), (c), snapshot during drying with a similar crystallinity for all evaporation rates (d), (e), (f), and the morphology of the dry film ((g), (h), (i), without annealing) are shown. SEM images for dry films before annealing obtained at different evaporation rates (j)–(l) top view, (m)–(o) cross-section. The snapshots correspond to the evaporation rates shown in Fig. 3: (a), (d), (g), (j), (m) 0 bar and low vevap, (b), (e), (h), (k), (n) 0.2 bar and medium vevap, (c), (f), (i), (l), (o) 2 bar and high vevap. | ||
The morphological variations show excellent agreement between experiments and simulations: the roughness (Fig. 5(a) and (b)) of the film, the size of the crystals (Fig. 5(c) and (d)), and the fraction of uncovered substrate (Fig. 5(e) and (f)) decrease with increasing evaporation rate in both experiment and simulation. Furthermore, the order of magnitude of the scaled roughness of the film is comparable in the experiments and the simulations for all evaporation rates and Haze measurements (see ESI,† 3.8) confirm the decreasing roughness of the samples. The trend of decreasing crystal sizes with increasing drying rate is recovered nicely in the simulations, although the values differ. The only exception to that is the slightly lower crystal size for naturally dried films, which is not recovered in the simulations. This might be due to the existence of the SSP phase for natural drying (see XRD spectra in Fig. 3), which is not accounted for in the simulations.
 | ||
| Fig. 5 Different morphological properties of the perovskite films after annealing depending on the evaporation rate, obtained from experiment (left column) and simulation (right column). Evaporation rates for experiment and simulation are represented by the gas pressure of the air gun and the evaporation-condensation coefficient α, respectively. From top to bottom: film roughness RQ normalized to the final film height hfin (a) and (b), mean crystal sizes normalized to the final film height (c) and (d), fraction of uncovered substrate (e) and (f). One standard deviation from the mean value is indicated as the shaded area. The encircled crosses are the experiments/simulations shown in Fig. 3 and 4 (a comparison between these morphological descriptors at the end of drying and after annealing in the simulation is shown in ESI,† 3.7). | ||
The fraction of uncovered substrate reaches its maximum value of roughly 25% for low evaporation rates for both experiment and simulation. Additionally, the relatively constant fraction of uncovered substrate and roughness for medium to high evaporation rates matches in simulation and experiment.
Overall, the observations in the experiments are very well captured by the simulation, including dramatic variations of the morphology features (roughness, coverage, crystal size increase) for very low evaporation rates and high-quality morphology (fully covered smooth films, stable crystal size) beyond a certain evaporation rate.
Mechanisms driving the morphology formation
In the following, the impact of the solvent evaporation rate on the crystallization pathway is analysed in detail with the help of the PF simulations and in situ experimental data. The grain sizes calculated from in situ PL data, the crystal sizes evaluated from the simulation, the UV/vis data together with the crystallinity curves from the simulations, and the simulated LaMer curves are shown in Fig. 6. Since the simulated crystals rather correspond to the grains observed in SEM images, their size evolution differs from the crystallite sizes derived from the PL peak positions (see ESI,† 3.9). Nevertheless, the time it takes for the crystals to appear can be compared between experiment and simulation. The trend of earlier crystallization onset for a higher evaporation rate is recovered in the simulations (Fig. 6(b)). Regarding the crystallization rates, the trend of a higher crystallization rate for a higher evaporation rate is clearly visible in the simulations as well as from the UV-vis measurements (Fig. 6(d) and (e)). | ||
| Fig. 6 (a) Evolution of grain sizes during drying as calculated from PL spectra (see ESI,† 3.9) (b) Evolution of relative grain sizes r/hfin as obtained from simulations. (c) Absorbance, measured at 750 nm, as a measure of the overall crystallinity of the film (see ESI,† 3.9). (d) Crystallinity calculated from the simulations. (e) Simulated Lamer graphs: the volume fraction φ1,liq of solute in the condensed liquid film for the three selected evaporation rates is shown as a function of the evaporation time. The crystallization onset φcrit, expected from the binary blend simulations, and the thermodynamic equilibrium volume fraction in the fluid phase φsat (see ESI,† 2.2) are also indicated (the evolution of the crystallinity, including annealing, is displayed in ESI,† 3.3). | ||
The reason for the different crystallization onset times is straightforward: initially the volume fraction is below the volume fraction for the onset of crystallization φcrit (Fig. 6(e)). The time required to reach that concentration is longer for a lower evaporation rate, so that crystallization starts later.
Once this critical concentration is reached, the decisive phase for the formation of the final morphology starts. From there, two distinct physical mechanisms drive the morphology formation in the simulations. A high evaporation rate leads to a high supersaturation and to a significant confinement of the space available for the crystals to grow and nucleate. This is drastically different for a low evaporation rate, where only a low supersaturation level is reached and where the crystals are allowed to evolve in a thick wet film with looser spatial constraints. The variations in the morphology when changing the evaporation rate can be explained by taking both effects into account.
We first focus on the supersaturation effect: after the saturation concentration is reached, nucleation is not instantaneous, so that a higher evaporation rate results in a higher supersaturation at the onset of crystallization. The level of attainable supersaturation for the different evaporation rates can be seen in Fig. 6(e), considering the maximum value reached by the solute volume fraction in the liquid φ1,liq. The curves for low and medium evaporation rates are fully in line with the qualitative LaMer description in literature. Note that for a higher evaporation rate, crystallization is not fast enough to generate a solute sink term in the liquid film that is large enough to overcome the source term due to evaporation. As a result, the volume fraction of solute increases monotonously until the film has fully dried. In any case, for higher supersaturation, nucleation of the crystals is favored over crystal growth, which results in a larger number of smaller crystals in the final morphology.
We now turn to the confinement effect: the space where the crystals can grow is more limited for high evaporation rates. This can be understood as follows: first, at the onset of crystallization (Fig. 4(a)–(c)), the height of the liquid film is lower for higher evaporation rates, due to the delay between crossing the critical concentration φcrit and nucleation (see Fig. 6(e)). During the whole process this trend persists for comparable amounts of crystallization (Fig. 4(d)–(f)). Here again, for comparable amounts of crystalline materials, the film is thinner for higher evaporation rates. As a result, clusters with a size larger than the mean dry film height can only form for low evaporation rates (Fig. 4(d)), while this is not possible when the evaporation rate is higher (Fig. 4(e) and (f)). As a result, the dried film originating from a low evaporation rate shows a large roughness and pinholes (Fig. 4(g)) whereas the films processed with a higher evaporation rate are smoother and pinhole-free (Fig. 4(h) and (i)).
The ratio of evaporation to crystallization rate determines the final film morphology
We hypothesize that the effects of supersaturation and confinement on film morphology depend only on the balance between the rates of crystallization and evaporation. The natural and most simple descriptor for this balance is the ratio of both characteristic rates vevap/vcryst. To illustrate this, we vary the crystallization rate at fixed evaporation rate, by changing only the mobility Mc in the Allen–Cahn equation (see eqn (2)). The corresponding dry film morphologies are shown in Fig. 7. For a low crystallization rate (Fig. 7(a)), a smooth film without pinholes is observed. The roughness increases with the crystallization rate and pinholes appear for the highest crystallization rate (Fig. 7(b) and (c)). | ||
| Fig. 7 Film morphology after drying at fixed evaporation rate. (a) Slow crystallization rate. (b) Medium crystallization rate. (c) Fast crystallization rate. The film morphology in (c) is similar to a film with a slow evaporation rate regarding pinhole density, roughness, and crystal sizes. The morphology in (b) is like the one obtained for a medium evaporation rate and the one in (a) to a fast evaporation rate (see Fig. 4). (d) LaMer curves of the simulations with variable crystallization rates at fixed evaporation rate (represented as crosses) and for simulations with variable evaporation rate at fixed growth rate (represented as lines, time scaled by the simulation input parameter α). The LaMer curves for similar ratios of evaporation to growth rate collapse to the same curves, which proves, that the ratio of these two quantities is the determining factor. | ||
This behaviour is analogous to the morphology changes upon varying evaporation rate variation at fixed crystallization rate. Decreasing the crystallization rate has the same effect as increasing the evaporation rate. This is further illustrated in Fig. 7(d), where the LaMer curves obtained from crystallization rate variations (crosses) and evaporation rate variations (lines) are plotted together. This proves our hypothesis that dominantly the ratio of crystallization to evaporation rate controls the final film morphology.
The fact that fast evaporation is generally beneficial for perovskite film formation, independent of precursor composition and solvent system, further supports the hypothesis that it is mainly the ratio of both characteristic rates vevap/vcryst which defines the film morphology, regardless of the atomistic, molecular, or chemical detail of the crystallization process. The good agreement between the experiments and the simulations presented in this work is also a strong indication that, except for very low evaporation rates (see Fig. 3), intermediate species do not play a decisive role in perovskite film formation, at least for the solvent system used in our investigations.
From a more general perspective, this means that for any crystallizing material in a drying film, this effect is expected to be active as soon as the drying time and the crystallization time become comparable. A transition from smooth, pinhole-free films to rough films with incomplete substrate coverage should be experienced around vevap ∼ vcryst. This can in principle be encountered for any fast-crystallizing material or even for slow-crystallizing materials if the process conditions are appropriate (very slow drying speed). Following this argument, we suggest that for any application experiencing rough films and/or pinholes, adjusting the processing condition by increasing vevap/vcryst might lead to changes in the film morphology similar to the ones observed for perovskites.
Dependence of the device performance on film morphology
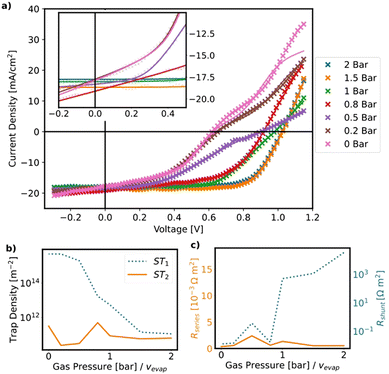
In this section, the relationship between the performance of the solar cells and the film morphology of the active layer is analyzed. For each evaporation rate, 20 fully printed solar cells with the layer stack glass/ITO/SnO2/MAPbI3/P3HT/carbon are produced. Details on the stack can be found in the ESI,† 2.4.Guided by the PF simulations, the optimal performance can be achieved at an evaporation rate of 2 bar. Fig. 8(b) shows the current density–voltage (J–V) curves of the best solar cell processed at 2 bar, which gives an efficiency of 19.34% with JSC of 23.10 mA cm−2, VOC of 1.06 V and FF of 79% obtained from the reverse scan but with a non-negligible hysteresis effect. To understand the impact of hysteresis, we measured the stabilized current and PCE. Thus, a stabilized PCE of 19.0% at maximum power point is achieved (see ESI,† 4.1). The JV characteristics evaluated from the reverse scan are shown in Fig. 8. While Voc, FF, and PCE decrease significantly for lower evaporation rates, Jsc decreases only slightly. For gas pressures of 0.5 bar and less, the JV-curves feature an S-shape. It should be noted that the yield of these devices follows the same trends: higher evaporation rates lead to higher yields (see ESI,† 4.2).
To gain a deeper understanding of this behaviour, the JV curves are fitted with an open-source drift-diffusion model (see Fig. 9 and ESI,† 4.3).38 The fits indicate a decrease in shunt resistance and an increase in interfacial trap density along with a slight increase in series resistance upon decreasing the evaporation rate (see Fig. 9(c)). The decrease of the shunt resistance is assigned to the increasing pinhole density as quantified by the fraction of the uncovered substrate area (see Fig. 5), which leads to direct electrical contact between the hole and electron transport layers.
The increase of interface trap density obtained from the fits of the JV-curves is corroborated by the steady-state and time-resolved PL (TRPL) measurements, which indicate a substantial decrease of charge carrier lifetime with decreasing evaporation rate (see ESI,† 4.4), caused by the increasing rate of nonradiative charge carrier recombination at the interfaces between perovskite film and charge transport layer. We tentatively ascribe the increase of interface trap density to the higher film roughness, which leads to larger interface areas, along with the deteriorated crystal quality as evidenced by the XRD spectra in Fig. 3(c) and the SEM cross sections in Fig. 4. Therefore, the deterioration of device performance with decreasing evaporation rate can be nicely understood from the trends in film morphology reported in the previous section.
Conclusions
We investigated the effect of changing the solvent evaporation rate on the morphology formation of perovskite layers. MAPbI3 cast from the solvent blend 2ME/NMP was used as a model system. The film height and the formation of the crystals were measured in situ and the roughness, pinhole density, and crystal sizes of the final film were quantified. The evaporation rate was varied independently of any other effect using gas quenching. To gain insights into the morphology formation pathway, a recently developed simulation framework was used, and the simulations were successfully validated against experiments. A change from a rough film with many pinholes for low evaporation rates to a smooth, fully covered film, for high evaporation rates was observed. Furthermore, the change from larger crystal sizes at lower evaporation rates to smaller crystals at higher evaporation rates could be recovered with the simulations. A similar transition from smooth to pinhole-prone films was observed when changing the crystallization rate at a fixed evaporation rate. This indicates that the ratio of both rates is the main factor defining the final film morphology.Our simulations allow to assign these changes to two effects: first, a high evaporation rate leads to high supersaturation and a high crystal density. Second, for a high supersaturation, these crystals nucleate at higher solute concentration, therefore in a thinner film, and thus in a much more confined space, leading to a smoother film. This is a purely geometrical effect. Both effects are expected to be valid independently of the specific chemical transitions involved. This transition from a rough film with many pinholes to a smooth, fully covered film is expected to occur in any crystallizing system where the evaporation rate and the crystallization rate are comparable independently of the atomic/molecular mechanisms responsible for the crystallization. The JV curves of the solar cells prepared from the different perovskite layers were fitted with a drift-diffusion model. The simulations suggest that shunts and interfacial trap density increase for decreasing evaporation rates.
Based on PF simulations of the fabrication process combined with device physics simulations, process–structure–property relationships can be established: in the present case, we provide the mechanistic explanation for the well-known fact that fast drying is necessary to get a pinhole-free film with low roughness, thus limiting trap state density and shunting, which is a prerequisite for achieving high PCE. Our simulations, thus, provide a so far unprecedented insight into the interplay between the drying and crystallization processes. They show that the key parameter determining the film morphology is the ratio of evaporation to crystallization rates. We expect this result to be valid for a wide range of materials, even beyond metal halide perovskites, as soon both rates lie in the same range.
In the future, we plan to understand and find the limits of the processing windows for high-quality perovskite films by varying the relevant process and material parameters. Adjusting, for example, the growth rate compared to the nucleation rate of the crystals is expected to allow the control of crystal sizes of the final film. In addition, the influence of the substrate on the film formation and the role of intermediate phases/solid state precursors can be investigated.
Data availability
The simulation data and the scripts used to process it are publicly available at DOI: 10.5281/zenodo.10974044. The remaining data that support the findings of this study are included in the ESI† or available from the corresponding authors upon reasonable request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors thank Maxime Siber for helpful discussions. They acknowledge the financial support from the Deutsche Forschungsgemeinschaft (DFG) via the Perovskite SPP2196 programme (project no. 506698391, HA 4382/16-1 & DU_2323_1), the European Commission (H2020 Program, project 101008701/EMERGE), the Helmholtz Association (SolarTAP Innovation Platform), ITRG 2495 (DFG), and the ‘Solar Factory of the Future’ as part of the Energy Campus Nürnberg (EnCN), which is supported by the Bavarian State Government (FKZ 20.2-3410.5-4-5). V. M. L. C. acknowledge funding from the German Federal Ministry of Education and Research (BMBF) for the Solar TAP innovation platform under the Helmholtz Innovation Platforms funding line.Notes and references
- P. Zhu, C. Chen, J. Dai, Y. Zhang, R. Mao and S. Chen, et al., Toward the Commercialization of Perovskite Solar Modules, Adv. Mater., 2024, 36(15), 2307357 CrossRef CAS PubMed.
- NREL Best Research-Cell Efficiency Chart [Internet]. [cited 2023 Oct 24]. Available from: https://www.nrel.gov/pv/cell-efficiency.html.
- L. Schmidt-Mende, V. Dyakonov, S. Olthof, F. Ünlü, K. M. T. Lê and S. Mathur, et al., Roadmap on organic–inorganic hybrid perovskite semiconductors and devices, APL Mater., 2021, 9(10), 109202 CrossRef CAS.
- B. Parida, A. Singh, A. K. Kalathil Soopy, S. Sangaraju, M. Sundaray and S. Mishra, et al., Recent Developments in Upscalable Printing Techniques for Perovskite Solar Cells, Adv. Sci., 2022, 9(14), 2200308 CrossRef.
- X. Dai, Y. Deng, C. H. Van Brackle and J. Huang, Meniscus fabrication of halide perovskite thin films at high throughput for large area and low-cost solar panels, Int. J. Extreme Manuf., 2019, 1(2), 022004 CrossRef CAS.
- W. A. Dunlap-Shohl, Y. Zhou, N. P. Padture and D. B. Mitzi, Synthetic Approaches for Halide Perovskite Thin Films, Chem. Rev., 2019, 119(5), 3193–3295 CrossRef CAS.
- Z. Saki, M. Malekshahi Byranvand, N. Taghavinia, M. Kedia and M. Saliba, Solution-processed perovskite thin-films: the journey from lab- to large-scale solar cells, Energy Environ. Sci., 2021, 14(11), 5690–5722 RSC.
- S. Ternes, J. Mohacsi, N. Lüdtke, H. M. Pham, M. Arslan and P. Scharfer, et al., Drying and Coating of Perovskite Thin Films: How to Control the Thin Film Morphology in Scalable Dynamic Coating Systems, ACS Appl. Mater. Interfaces, 2022, 14(9), 11300–11312 CrossRef CAS.
- O. Telschow, N. Scheffczyk, A. Hinderhofer, L. Merten, E. Kneschaurek and F. Bertram, et al., Elucidating Structure Formation in Highly Oriented Triple Cation Perovskite Films, Adv. Sci., 2023, 2206325 CrossRef CAS.
- X. Li, D. Bi, C. Yi, J. D. Décoppet, J. Luo and S. M. Zakeeruddin, et al., A vacuum flash–assisted solution process for high-efficiency large-area perovskite solar cells, Science, 2016, 353(6294), 58–62 CrossRef CAS.
- X. Xie, S. Zeng, C. Zhou and S. Xiao, Fabrication strategies for high quality halide perovskite films in solar cells, Mater. Chem. Front., 2023, 7, 5309–5332 RSC.
- K. Suchan, J. Just, P. L. Becker, E. Unger and T. Unold, Optical in situ monitoring during the synthesis of halide perovskite solar cells reveals formation kinetics and evolution of optoelectronic properties, J. Mater. Chem. A, 2020, 8(20), 10439–10449 RSC.
- C. Witt, K. Schötz, M. Kuhn, N. Leupold, S. Biberger and P. Ramming, et al., Orientation and Grain Size in MAPbI3 Thin Films: Influence on Phase Transition, Disorder, and Defects, J. Phys. Chem. C, 2023, 127(22), 10563–10573 CrossRef CAS.
- Y. Zhong, R. Munir, J. Li, M. C. Tang, M. R. Niazi and D. M. Smilgies, et al., Blade-Coated Hybrid Perovskite Solar Cells with Efficiency >17%: An In Situ Investigation, ACS Energy Lett., 2018, 3(5), 1078–1085 CrossRef CAS.
- C. Y. Chang, Y. C. Huang, C. S. Tsao and W. F. Su, Formation Mechanism and Control of Perovskite Films from Solution to Crystalline Phase Studied by in Situ Synchrotron Scattering, ACS Appl. Mater. Interfaces, 2016, 8(40), 26712–26721 CrossRef CAS.
- F. Babbe and C. M. Sutter-Fella, Optical Absorption-Based In Situ Characterization of Halide Perovskites, Adv. Energy Mater., 2020, 10(26), 1903587 CrossRef CAS.
- M. Chauhan, Y. Zhong, K. Schötz, B. Tripathi, A. Köhler and S. Huettner, et al., Investigating two-step MAPbI 3 thin film formation during spin coating by simultaneous in situ absorption and photoluminescence spectroscopy, J. Mater. Chem. A, 2020, 8(10), 5086–5094 RSC.
- N. S. Güldal, T. Kassar, M. Berlinghof, T. Unruh and C. J. Brabec, In situ characterization methods for evaluating microstructure formation and drying kinetics of solution-processed organic bulk-heterojunction films, J. Mater. Res., 2017, 32(10), 1855–1879 CrossRef.
- P. Wang, Y. Wu, B. Cai, Q. Ma, X. Zheng and W. H. Zhang, Solution-Processable Perovskite Solar Cells toward Commercialization: Progress and Challenges, Adv. Funct. Mater., 2019, 29(47), 1807661 CAS.
- A. M. Valencia, O. Shargaieva, R. Schier, E. Unger and C. Cocchi, Optical Fingerprints of Polynuclear Complexes in Lead Halide Perovskite Precursor Solutions, J. Phys. Chem. Lett., 2021, 12(9), 2299–2305 CAS.
- K. Yan, M. Long, T. Zhang, Z. Wei, H. Chen and S. Yang, et al., Hybrid Halide Perovskite Solar Cell Precursors: Colloidal Chemistry and Coordination Engineering behind Device Processing for High Efficiency, J. Am. Chem. Soc., 2015, 137(13), 4460–4468 CAS.
- O. Shargaieva, H. Näsström, J. Li, D. M. Többens and E. L. Unger, Temperature-Dependent Crystallization Mechanisms of Methylammonium Lead Iodide Perovskite From Different Solvents, Front. Energy Res., 2021, 9 Search PubMed.
- B. Ding, Y. Li, S. Y. Huang, Q. Q. Chu, C. X. Li and C. J. Li, et al., Material nucleation/growth competition tuning towards highly reproducible planar perovskite solar cells with efficiency exceeding 20%, J. Mater. Chem. A, 2017, 5(15), 6840–6848 RSC.
- J. Jiao, C. Yang, Z. Wang, C. Yan and C. Fang, Solvent engineering for the formation of high-quality perovskite films:a review, Results Eng., 2023, 18, 101158 CrossRef CAS.
- Q. Liu, W. Cai, W. Wang, H. Wang, Y. Zhong and K. Zhao, Controlling Phase Transition toward Future Low-Cost and Eco-friendly Printing of Perovskite Solar Cells, J. Phys. Chem. Lett., 2022, 6503–6513 CrossRef CAS.
- M. He, B. Li, X. Cui, B. Jiang, Y. He and Y. Chen, et al., Meniscus-assisted solution printing of large-grained perovskite films for high-efficiency solar cells, Nat. Commun., 2017, 8, 16045 CrossRef CAS PubMed.
- W. Li, S. K. Yadavalli, D. Lizarazo-Ferro, M. Chen, Y. Zhou and N. P. Padture, et al., Subgrain Special Boundaries in Halide Perovskite Thin Films Restrict Carrier Diffusion, ACS Energy Lett., 2018, 3(11), 2669–2670 CrossRef CAS.
- J. A. Warren, R. Kobayashi, A. E. Lobkovsky and W. Craig Carter, Extending phase field models of solidification to polycrystalline materials, Acta Mater., 2003, 51(20), 6035–6058 CrossRef CAS.
- L. Gránásy, G. I. Tóth, J. A. Warren, F. Podmaniczky, G. Tegze and L. Rátkai, et al., Phase-field modeling of crystal nucleation in undercooled liquids – A review, Prog. Mater. Sci., 2019, 106, 100569 CrossRef.
- F. Wang, P. Altschuh, L. Ratke, H. Zhang, M. Selzer and B. Nestler, Progress Report on Phase Separation in Polymer Solutions, Adv. Mater., 2019, 31(26), 1806733 CrossRef.
- D. M. Saylor, C. Forrey, C. S. Kim and J. A. Warren, Diffuse Interface Methods for Modeling Drug-Eluting Stent Coatings, Ann. Biomed. Eng., 2016, 44(2), 548–559 CrossRef.
- B. Nestler, A. A. Wheeler, L. Ratke and C. Stöcker, Phase-field model for solidification of a monotectic alloy with convection, Phys. D, 2000, 141(1–2), 133–154 CrossRef.
- V. Negi, O. Wodo, J. J. van Franeker, R. A. J. Janssen and P. A. Bobbert, Simulating Phase Separation during Spin Coating of a Polymer–Fullerene Blend: A Joint Computational and Experimental Investigation, ACS Appl. Energy Mater., 2018, 1(2), 725–735 CrossRef CAS.
- O. Wodo and B. Ganapathysubramanian, Modeling morphology evolution during solvent-based fabrication of organic solar cells, Comput. Mater. Sci., 2012, 55, 113–126 CrossRef CAS.
- J. J. Michels, K. Zhang, P. Wucher, P. M. Beaujuge, W. Pisula and T. Marszalek, Predictive modelling of structure formation in semiconductor films produced by meniscus-guided coating, Nat. Mater., 2021, 20(1), 68–75 CrossRef CAS.
- O. J. J. Ronsin and J. Harting, Phase-Field Simulations of the Morphology Formation in Evaporating Crystalline Multicomponent Films, Adv. Theory Simul., 2022, 2200286 CrossRef CAS.
- O. J. J. Ronsin and J. Harting, Formation of Crystalline Bulk Heterojunctions in Organic Solar Cells: Insights from Phase-Field Simulations, ACS Appl. Mater. Interfaces, 2022, 14(44), 49785–49800 CrossRef CAS.
- M. Koopmans, V. M. L. Corre and L. J. A. Koster, ‘SIMsalabim’: An open-source drift-diffusion simulator for semiconductor devices, J. Open Source Softw., 2022, 7(70), 3727 CrossRef.
- Y. Deng, C. H. Van Brackle, X. Dai, J. Zhao, B. Chen and J. Huang, Tailoring solvent coordination for high-speed, room-temperature blading of perovskite photovoltaic films, Sci. Adv., 2019, 5(12), eaax7537 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00957f |
| ‡ Co-first author. |
| This journal is © The Royal Society of Chemistry 2025 |