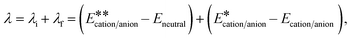Elucidating the role of charge transfer on semiconductor properties in a new donor–acceptor cocrystal 1,5-dihydroxynaphthalene : TCNQ

Abstract

In this work, we have investigated the semiconducting properties of an unprecedented 1 : 1 π-stacked donor–acceptor cocrystal of 1,5-dihydroxynaphthalene (DHN) as the π-donor (D) with 7,7′,8,8′-tetracyanoquinodimethane (TCNQ) as the π-acceptor (A). Molecular semiconductors with electron dominant transport, narrow bandgap, solution processing ability, air-stability are highly sought-after for application in n-channel organic field effect transistors. The DHN : TCNQ cocrystal shows n-type semiconductor nature with a narrow bandgap of around 1 eV, and a low LUMO energy level (−3.8 eV) making it less prone to areal degradation. The electron dominant transport in this cocrystal is described by assuming that electron and hole hop via a super-exchange mechanism along the mixed ⋯D–A⋯ π-stack direction. The participation of bridging molecular orbitals other than donor HOMO make a significant contribution to the super-exchange electron transfer, thus resulting in electron hopping from acceptor to acceptor which is four times larger than the value of hole hopping from donor to donor. Detailed analysis of crystal packing and electronic properties demonstrate that the super-exchange charge carrier transport is facilitated by strong π⋯π stacking interaction between the donor and acceptor, and prominent charge transfer.

---

Design, System, Application

The n-channel field effect transistors (FETs) containing n-type semiconductor as active layer materials have emerged as indispensable part of multiple electronic circuits because the n-channel transistors often provide better performance than p-channel FETs. Organic molecular crystals have drawn attention as semiconductor materials in FETs due to novel properties like high crystallinity which reduces electric leakage in circuits, and low molecular weight and flexibility ideal for micro-electronic circuits. However organic semiconductors are predominantly reported as hole transport materials, hence n-type organic semiconductors are in huge demand. Cocrystallization of π-donor and π-acceptor coformers leads to the formation of ambipolar or n-type semiconductor cocrystals. The semiconductor properties in such donor–acceptor cocrystals depend on the strength of π⋯π stacking interaction between the coformers, and the electronic features of the donor and acceptor. Strong charge transfer from the donor to the acceptor, and robust π⋯π stacking favour higher charge carrier mobilities in the cocrystals. On the other hand, lower value of intermolecular interaction energy results in high charge carrier mobility values. In this work, we studied the semiconductor property of two structurally analogous donor–acceptor cocrystals to elucidate the role of charge transfer, intermolecular interactions and reorganization energy in dictating charge carrier motilities.

1. Introduction

Organic molecular materials are emerging as non-hazardous and non-toxic alternatives to lead halide perovskites semiconductor materials capable of solution processing under mild conditions.^1,2 These non-toxic organic molecular semiconductors can be fabricated into flexible large area thin films suitable for flexible electronic circuits viz. wearable sensors and flexible displays.^3,4 Moreover, the organic molecular materials can challenge silicon or metal oxide based inorganic semiconductors in terms of efficient, low cost thin film processing at ambient conditions.⁵

While inorganic semiconductors are predominantly n-type, organic molecular semiconductors are mainly of p-type nature⁶ and with low charge carrier mobility.⁷ Low mobility can be overcome by improvement of crystallinity and consequently the reduction of grain boundaries.⁸ In contrast, the electron dominant or ambipolar (i.e., balanced electron and hole transport) transport are rare in organic molecular semiconductors. However, electron dominant transport is crucial for applications in field effect transistors, diodes, and bi-layer heterojunction solar cells. Only a handful of intrinsic n-type organic molecular semiconductors with air stability have been reported to date.^9,10 This list includes 7,7′,8,8′-tetracyanoquinodimethane (TCNQ) and its fluorinated derivatives, naphthalene diimides, perylene diimides, and fullerenes. Hence, realization of new organic crystalline materials for electron dominant transport with high electron mobility, air stability, and room temperature solution processing are necessary to develop organic field effect transistors, organic light emitting diodes, and solar cells.

In the last decade, organic ‘push–pull’ copolymers comprising alternative electron rich π-donor (D) and electron deficient π-acceptor (A) units have attracted wide attention for their electron dominant transport, and room temperature solution processing to produce highly crystalline thin films.¹¹ Organic donor–acceptor cocrystals with electron rich and electron deficient π-molecular backbones have been recognized as promising alternatives to D–A copolymers.^12,13 This is because it is in general much easier to synthesize D–A cocrystals in highly crystalline pure form at room temperature. A number of recent reports show that face to face alternating π-stacked D–A cocrystals possess myriads of intriguing properties including ambipolar/n-type semiconductor properties,¹⁴ thermally activated delayed fluorescence,¹⁵ room temperature phosphorescence,¹⁶ photoconduction,¹⁷ photovoltaic properties,¹⁸ optical waveguide property,¹⁹ solid state lasing property,²⁰ photo-detection,²¹ photo-thermal conversion²²etc. originating from their intrinsic charge transfer nature. Organic donor–acceptor charge transfer cocrystals have recently found a niche in molecular ambipolar or n-type semiconductors,^23,24 and this created an upsurge of interest to explore new D–A cocrystals for this purpose.

In the present study, we have explored a cocrystal comprising 1,5-dihydroxynaphthalene (DHN) as the donor and TCNQ as the acceptor (Fig. 1a). Naphthalene has a π-electron rich aromatic core (Fig. 1b) and HOMO energy (≈ −5.8 eV) that is slightly higher for serving as a π-donor for air stable donor–acceptor cocrystals.²⁵ Di-substitution of the naphthalene moiety by electron donating substituents has proven to be an effective strategy to increase the HOMO energy suitable for acting as the π-donors for semiconductor cocrystals.²⁶ The TCNQ is known as the n-type semiconductors with significant electron mobility values,²⁷ and also serve as the π-acceptor for multiple ambipolar or n-type D–A charge transfer cocrystals.²⁸ The TCNQ molecule has LUMO energy level ≈ −4.8 eV and a highly electron depleted π-core (Fig. 1c), and therefore is a popular choice for semiconductor D–A cocrystals. The energy difference between the HOMO (−5.18 eV) of DHN and the LUMO (−4.82 eV) of TCNQ being small, indicates the possibility of strong charge transfer from the DHN to the TCNQ moiety (Fig. 1c). In addition, the complementarity of a deep π-hole²⁹ in the quinonoid core of TCNQ and the electron rich aromatic core of DHN favor strong face to face π⋯π stacking between these molecules. Recently, a structurally analogous cocrystal of 1,5-diaminonaphthalene (DAN) donor and TCNQ acceptor was reported to possess n-type semiconductor property, and theoretical calculation shows a significant electron transfer integral value for this cocrystal system.^26b Hence, we have dedicated the current study for theoretical modeling of charge carrier transport properties of the DHN : TCNQ cocrystal, and also investigated similar properties in DAN : TCNQ cocrystal for comparison.

Fig. 1 (a) Donor (DHN) and acceptor (TCNQ) moieties used in the present study; (b) molecular electrostatic potential (MEP) for donor and acceptor, MEP of 1,5-diaminonaphthalene (DAN) is shown for comparison; (c) HOMO/LUMO energies of our studied donor and acceptor and 1,5-diaminonaphthalene donor.

The charge carrier transport in D–A cocrystals has been mostly explained by small polaron hopping similar to the majority of reported low mobility organic semiconductors.³⁰ In a mixed stack D–A cocrystal, the transfer of electron or hole occurs via a ‘super-exchange’ mechanism along the infinite ⋯D⋯A⋯D⋯A⋯ π-stacked array.^30b,c In super-exchange mechanism, an electron hops from one acceptor moiety to the nearest neighbouring acceptor moiety via the bridging donor moiety, and a hole hops from one donor to the nearest donor via the bridging acceptor moiety. The present study will focus on the supramolecular features, electronic and spectroscopic properties, as well as modeling of electron/hole transport of the 1 : 1 cocrystal of 1,5-dihydroxynaphthalene and TCNQ. The charge carrier transport mechanism in this system will be studied atomistically (DFT) using a polaron hopping model via super-exchange pathway along the mixed –D–A– stack, and also by the band conduction model using periodic DFT.³⁰

2. Methods

Materials

1,5-Dihydoxynaphthalene (97% purity), 7,7′,8,8′-tetracyanoquinodiemthane (98% purity), KBr (99% purity), tetrahydrofuran and toluene solvents were purchased from Sigma Aldrich and used as received without further purification.

Synthesis of DHN : TCNQ cocrystal

The DHN : TCNQ cocrystal was synthesized by solvent assisted mechanochemical grinding³¹ of a 1 : 1 mixture of DHN and TCNQ with few drops of tetrahydrofuran as the solvent added at regular five minute intervals for an hour (Fig. S1 in ESI†). Instantaneous color change from brown to dark green was observed with the addition of tetrahydrofuran solvent. Flat needle shaped dark green crystals were grown from 2 : 1 mixture of tetrahydrofuran and toluene. The formation of a new DHN : TCNQ cocrystal phase was confirmed from the powder XRD pattern of the green powder obtained after solvent assisted mechanochemical grinding, which is significantly different from PXRD patterns observed in DHN and TCNQ coformers (Fig. S2 in ESI†).

Single crystal and powder X-ray diffraction

Single crystal X-ray diffraction (XRD) data were collected with Mo Kα radiation (wavelength 0.71073 Å). The structure was solved by direct methods using SHEXL. The non-hydrogen atoms were refined anisotropically with full matrix least squares on F². Coordinates were refined for the hydroxylic hydrogen atom of DHN; other H atoms were positioned with idealized geometry, with fixed C–H bond-length = 0.93 Å. The U_iso(H) values were set at 1.2U_eq of the carrier atom or at 1.5U_eq for the hydroxyl group. Crystallographic and refinement parameters are summarized in Table S1,† an ORTEP diagram is shown in Fig. S3.† The structure has been deposited in the Cambridge Structural Database, CCDC number 2402657. Powder XRD data of the coformers and the cocrystal were collected with Cu Kα radiation (wavelength 1.5406 Å).

Spectroscopic studies

Absorbance data was acquired from diffuse reflectance measurements using the Kubelka–Munk method,³² which was measured using a Shimadzu UV-3600 UV-vis-NIR spectrophotometer, equipped with an integrating sphere attachment (ISR-603, Shimadzu). Spectra were collected in the wavelength range of 250–900 nm with a resolution of 0.2 nm. Measurement was acquired on samples diluted in BaSO₄ at ratio of 1 : 10 w/w. Pressed BaSO₄ was used as white reference. The FTIR spectra of TCNQ and cocrystal DHN : TCNQ were collected as powders diluted in pellets of KBr using a Bruker Vertex70 FTIR spectrometer. A scan resolution of 1 cm⁻¹ was used with 64 scans averaged for each sample and a DTGS detector.

Computational methods

Theoretical estimation of intermolecular interaction energies. The binding energy between the donor and acceptor in gas phase was calculated at the crystal structure geometry using meta hybrid-GGA functional M06-2X³³ with 6-31G(d,p) basis set, and the counterpoise method was used to correct the basis set superposition error (BSSE).³⁴ The M06-2X functional with 54% Hartree–Fock exchange is ideal to account for the dispersive nature of π⋯π stacking and weak hydrogen bonding interactions.³²

The intermolecular interactions are presented by the parameter d_norm in Hirshfeld surface analysis. The d_norm distance is defined by the expression [(d_i − r^vdW_i/r^vdW_i) + (d_i − r^vdW_e/r^vdW_e)]; where, r^vdW_i and r^vdW_e are the vdW radii of the appropriate atoms internal and external to the surface, respectively. The distance from Hirshfeld surface to the nearest molecule inside the surface is defined by d_i (internal), and the distance between the surface and the nearest molecule outside the surface is denoted by d_e (external).³⁵ The d_norm distance is presented by red-blue-white color scheme; red indicates strong intermolecular interaction with the distance between two interacting atoms much smaller than the sum of their van der Waals radii. The interactions with distance between two interacting atoms at the sum of van der Waals radii are denoted by white region, while interactions at distance greater than the sum of van der Waals radii are presented by blue region. The contribution of different intermolecular interactions on crystal packing were estimated by 2D fingerprint plots. The energy components of π⋯π stacking and hydrogen bonding interactions were calculated using B3LYP/6-31G(d,p) level of theory using CrystalExplorer.³⁵

Theoretical prediction of opto-electronic properties at molecular level. The Gaussian 16 program package was used for all calculations at molecular level. The HOMO/LUMO energies and molecular electrostatic potential surfaces of the donor and acceptor coformers were calculated at the B3LYP/6-31G(d,p) level. The HOMO/LUMO energies of D–A dimer, tetramer and hexamer were calculated with Coulomb attenuated B3LYP i.e., CAM-B3LYP functional and the 6-31G(d,p) basis set using coordinates extracted from experimental geometry. The hybrid exchange–correlation functional CAM-B3LYP with 65% Hartree–Fock exchange at long-range takes account of long range electron–electron coupling effect.³⁶ Natural bond orbital (NBO) analysis of the π-stacked D–A dimer was performed at the M06-2X/6-31G(d,p) level of theory to estimate the degree of charge transfer.³⁷ The strength of donor to acceptor charge transfer is estimated from the second order perturbation (E²) energy values, and NBO charges.³⁸

Time dependent DFT (TD-DFT) calculation on the D–A dimer was performed using crystal coordinates. The CAM-B3LYP functional was used for TD-DFT calculation, and spin allowed singlet-singlet transitions were considered to get the excited state. Hybrid CAM-B3LYP functional can take care of electron–electron coupling effects in non-covalently bonded molecular systems to produce reliable transition energy values for the π-stacked systems.³⁹

Modelling of charge carrier transfer. Non-adiabatic internal hole/electron reorganization energy (λ_int) of molecules were calculated at B3LYP/6-31G(d,p) level by adding up the reorganization energy at ground (λ_i) and excited (λ_f) states of cation/anion. A four point energy model⁴⁰ (Fig. S5 in ESI†) was used to obtain the value of internal reorganization energy (λ_int)

The E_neutral and indicate the energy of optimized geometry of neutral molecule and the single point energy of neutral molecule with the optimized geometry of cation/anion state, respectively. Similarly, the E_cation/anion and refer to energy of optimized geometry of cation/anion and the single point energy of the cation/anion having optimized geometry of the neutral state, respectively.

Super-exchange hole/electron integrals are measured from the energy splitting of HOMO or LUMO of the mixed D–A–D or A–D–A molecular triads, respectively.⁴¹ The value of the electron transfer integral is derived from the energy difference between the LUMO+1 and LUMO of A–D–A triad; while the hole transfer integral is calculated from the energy difference of the HOMO and HOMO−1 of D–A–D triad.⁴¹ The direct electron transfer integral is calculated from the energy difference of the LUMO+1 and LUMO of the A–A dimer, and the direct hole transfer is calculated from the energy difference between the HOMO and HOMO−1 of D–D dimer. The coordinates of molecular trimers and dimers were extracted from the crystal geometry. The transfer integrals were calculated at the CAM-B3LYP/6-31G(d,p) level of theory. Long range corrected CAM-B3LYP functional is ideal for the transfer integral calculation as the frontier molecular orbitals in diads/triads are distributed on two different moieties, hence long range correction is required for MO energy calculation of molecular diads/triads. The electron–hole distribution of S₁/S₂ excited states were obtained from the TD-DFT calculation results. Multiwfn software⁴² was used for plotting excited state electron–hole distribution maps.

Band structure calculation. The band structure calculation for DHN : TCNQ cocrystal was performed on optimized crystal geometry using Vienna ab initio simulation package (VASP). The geometry optimization was performed using the PBE functional with Grimme's D2 dispersion correction to account for the dispersive nature of π⋯π stacking interaction dominating the crystal packing.⁴³ A Γ-centered 2 × 1 × 2 mesh and an energy cut-off of 600 eV were used for unit cell geometry optimization. A strict convergence criterion of 10⁻⁸ eV Å⁻¹ was applied to attain energetic convergence. Both the positions of atoms and the unit cell were allowed to relax during geometry optimization. The parameters of DFT optimized and experimental unit cell geometries are given in Table S2 (in ESI†). The band structure calculation of the optimized crystal geometry was performed with an energy cut-off of 500 eV and a convergence criterion of 10⁻⁷ eV Å⁻¹ were applied for the hybrid functional HSE06.⁴⁴ A Gaussian smearing scheme with a smearing width 0.05 eV was used for both the geometry optimization and band structure calculations.

3. Results and discussion

Crystal packing of DHN : TCNQ cocrystal

The 1 : 1 DHN : TCNQ cocrystal (1) crystallizes in the centrosymmetric monoclinic P2₁/n space group. The asymmetric unit contains half a molecule of the TCNQ acceptor and half a molecule of the DHN donor (Fig. S3 in ESI†). The second half of each of these can be generated by inversion symmetry. The TCNQ and DHN moieties are bonded into infinite alternative face to face donor–acceptor π⋯π stacks along the crystallographic a axis (Fig. 2a). The strength of π⋯π stacking is estimated from the distance between the centroids (Cg) and the planes of naphthalene ring of DHN and quinonoid ring of TCNQ. The Cg⋯Cg distance between naphthalene and quinonoid ring is 3.565 Å, which is in the range of the sum of the van der Waals radii of carbon atoms (3.40 Å). In addition, the angle between the planes of these rings is 1.62° (Fig. 2b), and the slip distances between the DHN and TCNQ moieties vary in between 1.28–1.32 Å (Fig. S4 in ESI†) indicating moderately strong interaction. These –D–A–D–A– infinite π-stacks are tethered by strong O–H⋯N hydrogen bonds (O⋯N, 2.925(4) Å; and O–H⋯N, 174.0(3)°) along the cell diagonals (Fig. 2a, Table S3 in ESI†). The DHN molecules form a hydrogen bonded ribbons via weak C–H⋯O hydrogen bonds (C⋯O, 3.432(5) Å; and C–H⋯O, 145.1°) along the c axis, similarly TCNQ molecules form H-bonded ribbons (Fig. 2c, Table S4 in ESI†) via weak C–H⋯N bonds (C⋯N, 3.538(4) Å; and C–H⋯N, 154.4°).

Fig. 2 (a) The π⋯π stacking and O–H⋯N hydrogen bonding interactions in 1 : 1 DHN : TCNQ cocrystal; (b) binding energy and crystallographic parameters of π⋯π stacking interaction between DHN and TCNQ; (c) the C–H⋯N and C–H⋯O hydrogen bonded ribbons in crystal packing.

Strength and nature of non-covalent interactions in DHN : TCNQ cocrystal

The charge carrier transport pathways in an organic molecular crystal are strongly dependent on the crystal packing as the charge carriers move between the nearest molecular pairs. Hence, it is of paramount importance to understand the nature of intermolecular interactions to identify the plausible charge carrier pathways in a molecular crystal system.⁴⁵ The intermolecular interaction energies sustaining the crystal packing have been quantitatively estimated by two ways: (a) calculation of binding energies from the gas phase molecular dimers extracted from the crystal; (b) Hirshfeld surface analysis and calculation of pairwise interaction energies in the solid phase.

The gas phase binding energy between donor and acceptor moieties is −11.6 kcal mol⁻¹ indicating moderately strong π⋯π stacking interactions. The calculated gas phase binding energy between DAN and TCNQ in the reported DAN : TCNQ cocrystal is −14.11 kcal mol⁻¹, which is more negative than the value of −11.6 kcal mol⁻¹ observed for our system. We have also calculated the strength and nature of other intermolecular interactions in DHN : TCNQ in order to find out if there is any other electron/hole transfer pathways other than that in the mixed stacking direction. The binding energy of O–H⋯N hydrogen bond adjoining the mixed π-stacks calculated is −3.05 kcal mol⁻¹. On the other hand, the binding energy for doubly C–H⋯N hydrogen bonded dimer is −2.19 kcal mol⁻¹ and the doubly C–H⋯O hydrogen bonded dimer is −0.50 kcal mol⁻¹ (Fig. 3) indicating weak nature of these interactions. We can conclude that the charge carrier transport can take place along these hydrogen bonded chains in addition to π⋯π stacking direction.

Fig. 3 Binding energies of various hydrogen bonded motifs calculated at B3LYP/6-31G(d,p) level by CrystalExplorer.

The strength of the π⋯π stacking and hydrogen bonding interactions have been further estimated by decomposing the energetic contributions of the total binding energies of the molecular dimers in the solid phase.³⁵ The electrostatic and dispersive forces are the major components of π⋯π stacking interaction (Table 1). The energetic components of π⋯π stacking interaction in reported analogous cocrystal of 1,5-diaminonaphthalene (DAN) and TCNQ have been calculated by comparing the strength of π⋯π stacking in both the cocrystals. The values of electrostatic and dispersive components observed in DAN : TCNQ cocrystal are larger than the values obtained for our studied DHN : TCNQ cocrystal (Table 1). Therefore, the face to face π⋯π stacking interaction in the previously reported DAN : TCNQ is slightly stronger than that calculated for our studied DHN : TCNQ cocrystal, while the electrostatic component is significant in both the cocrystals indicating substantial charge transfer nature of π⋯π stacking interaction in both systems.

Table 1 Energy components of different intermolecular interaction (kcal mol⁻¹) in DHN : TCNQ and DAN : TCNQ cocrystals calculated at B3LYP/6-31G(d,p) level using CrystalExplorer^a

Cocrystal	Intermolecular interaction	Electrostatic energy (Eele)	Polarization energy (Epol)	Dispersion energy (Edis)	van der Waals repulsion energy (Erep)	Total energy (Etot)
a Scaling factor used for the energy component analysis: kele = 1.057, kpol = 0.740, kdis = 0.871, krep = 0.618. Etot = keleEele + kpolEpol + kdisEdis + krepErep.
DHN : TCNQ	π⋯π stacking	−4.93	−1.36	−14.07	9.71	−12.45
DAN : TCNQ	π⋯π stacking	−6.88	−1.95	−17.02	15.48	−14.05
DHN : TCNQ	N–H⋯O	−11.02	−2.16	−2.48	13.50	−7.09
DHN : TCNQ	C–H⋯N	−2.52	−1.69	−5.28	4.96	−5.43
DHN : TCNQ	C–H⋯O	−1.02	−0.51	−4.61	4.33	−2.76

---

Hirshfeld surface analysis was performed to gain more insights on the nature and contributions of the intermolecular interactions, and 2D fingerprint plots were plotted to quantify these interactions. The d_norm surfaces of DHN and TCNQ molecules were mapped over a range of 0.8 to 3.8 Å (Fig. S6 in ESI†). The light red spots on Hirshfeld surface indicate weak C–H⋯N hydrogen bond, on the other hand, the π⋯π stacking and C–H⋯O hydrogen bonds are presented by the white regions implying that these are primarily van der Waals interaction (Fig. S6 in ESI†). The 2D fingerprint plots demonstrate that the O⋯H interaction (i.e., N–H⋯O + C–H⋯O bonds) comprise 21.5% of Hirshfeld surface and appear as a very sharp spike with the lowest contact distance d_i = 1.2 Å and d_e = 0.8 Å. The N⋯H interaction (i.e., C–H⋯N bond) constitute 3.5% of total Hirshfeld surface and is shown by a blunt spike at a contact distance d_i = 1.4 Å, and d_e = 1.1 Å. The π⋯π stacking interaction though having a significant contribution (10%) on total Hirshfeld surface, appears at d_i + d_e = 4 Å (Fig. S6 in ESI†).

Electronic features of 1 : 1 DHN : TCNQ cocrystal

Frontier molecular orbital analysis of D–A dimer shows that dimer HOMO (−7.17 eV) is predominantly localized on the donor moiety, while the dimer LUMO (−3.79 eV) is localized on the acceptor (Fig. 4). The molecular offset of dimer HOMO and LUMO (ΔE = 3.38 eV) confirms intermolecular charge transfer nature of DHN : TCNQ cocrystal. The dimer HOMO-n orbitals (n = 1, 2) are also primarily concentrated on the donor moiety, however, the LUMO+1 orbital is spread over both the donor and acceptor (Fig. 4). We have also mapped the frontier molecular orbitals of D–A tetramer and hexamer, and found the similar HOMO/LUMO offset on donor and acceptor moieties, respectively. The HOMO/LUMO energy gap in the D–A tetramer and hexamer are −3.2 and −3.15 eV, respectively (Fig. S7 and S8 in ESI†), thus the HOMO/LUMO difference are decreasing with increasing size of the π-stacked unit. The HOMO/LUMO energy gap in D–A dimer of reported n-type semiconductor cocrystal of 1,5-diaminonaphthalene and TCNQ is 2.93 eV which is smaller than calculated in our studied system (Fig. S9 in ESI†).

Fig. 4 Frontier molecular orbitals of D–A dimer of DHN : TCNQ cocrystal calculated at M06-2X/6-31G(d,p) level at crystal geometry.

Natural bond orbital (NBO) analysis confirm moderate values of second order perturbation energy (E²) corresponding to the charge transfer from DHN to TCNQ moiety (Fig. 5a). The second order perturbation energy values corresponding to a donor-π to acceptor-π* orbital transfer are less than that observed for reported n-type semiconductor cocrystal of 1,5-diaminonaphthalene and TCNQ (Fig. 5b).^26b The Mulliken and NBO charge analyses were performed to understand the degree of ionicity ρ in the DHN : TCNQ cocrystal (D^ρ˙⁺A^ρ˙⁻) at the ground state. The degree of ionicity calculated by Mulliken and NBO charge analyses are 0.055 and 0.067 respectively, confirming the charge transfer of the DHN : TCNQ cocrystal. The degree of ionicity by Mulliken and NBO methods are 0.070 and 0.084 respectively in analogous DAN : TCNQ cocrystal, and the values are higher than observed in the DHN : TCNQ system. Hence, it can be concluded that higher degree of ionicity values result in lower HOMO–LUMO energy gap in D–A cocrystals.

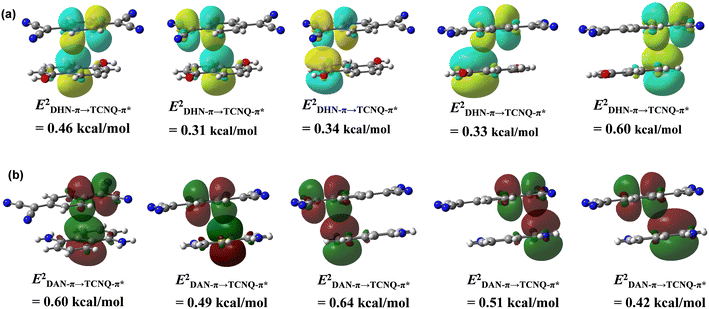Fig. 5 (a) NBO analysis at M06-2X/6-31G(d,p) level to show charge transfer from DHN to TCNQ moiety; (b) NBO analysis to show charge transfer from DAN to TCNQ moiety in DAN : TCNQ.

Spectroscopic signatures of DHN : TCNQ cocrystal

The vibrational spectroscopy provides additional support of charge transfer from DHN to TCNQ. The C≡N stretching frequencies observed in the cocrystal are 2221 and 2226 cm⁻¹, while the corresponding frequencies are 2222 and 2232 cm⁻¹ in pristine TCNQ indicating charge transfer towards C=N⁻ formation (Fig. 6a, Table 2). However, the minute decrease in the values of C≡N stretching frequencies shows that the degree of ionization in the DHN : TCNQ cocrystal is low as confirmed from Mulliken/NBO charge analysis. This is also supported by very small changes in the C≡N, C=C and C–C bond lengths in TCNQ (Table S4 in ESI†) upon cocrystallization.

Fig. 6 (a) FTIR spectra of TCNQ and the DHN : TCNQ cocrystal show no significant change in the C≡N stretching frequency due to charge transfer; (b) absorption spectrum of the DHN : TCNQ cocrystal showing broad charge transfer band (450–750 nm); (c) charge transfer origin of S₁ and S₂ states shown by time-dependent DFT calculation.

Table 2 TD-DFT calculated wavelength, oscillator strength and orbital contributions for S₁–S₆ excited states

State	Calculated wavelength (nm)	Excitation energy (eV)	Oscillator strength (f)	Orbital contribution
S1	741	1.67	0.0236	HOMO → LUMO, 100%
S2	417	2.97	0.2553	HOMO−1 → LUMO, 4%
				HOMO−2 → LUMO, 40%
				HOMO−3 → LUMO, 56%
S3	393	3.15	0.1853	HOMO−3 → LUMO, 31%
				HOMO−2 → LUMO, 50%
				HOMO−1 → LUMO, 19%
S4	367	3.38	0.4581	HOMO−3 → LUMO, 65%
				HOMO−2 → LUMO, 11%
				HOMO−1 → LUMO, 24%
S5	326	3.80	0.0126	HOMO−6 → LUMO, 3%
				HOMO−4 → LUMO, 97%
S6	269	4.62	0.0126	HOMO−2 → LUMO+2, 3%
				HOMO−2 → LUMO+1, 2%
				HOMO−2 → LUMO+3, 9%
				HOMO → LUMO+1, 29%
				HOMO → LUMO+2, 6%
				HOMO → LUMO+3, 5%
				HOMO → LUMO+4, 45%

---

The absorption spectrum of the DHN : TCNQ cocrystal shows a broad band in the range from 450 to 750 nm indicating a charge transfer from DHN to TCNQ moiety in the excited state (Fig. 6b). Time dependent DFT calculation on the D–A dimer was carried out to understand the origin of this broad absorption band. The relatively dark S₁ state (λ = 741 nm, f = 0.0236) is solely due to charge transfer from DHN to TCNQ moiety, while the bright S₂ (λ = 417 nm, f = 0.2553) and S₃ (λ = 353 nm, f = 0.1853) states have predominant charge transfer character but also minor contributions from local excitation (Fig. 6c and Table 2, Fig. S10 in ESI†). In addition to the broad CT band, absorptions with prominent local excitation nature i.e., corresponding to S₀ → S₄, S₀ → S₅, S₀ → S₆ transitions (Fig. S10,†Table 2) are also observed. It is pertinent to mention that the local excitation is not visible in the UV-vis spectrum without dilution of the sample by BaSO₄.

The charge transfer nature of the excited states were further confirmed by the electron–hole distribution of the first three excited states. The first three excited states are characterized with electron distribution on the TCNQ and hole distribution on the DHN showing excited state charge transfer (Fig. 7).

Fig. 7 Electron (green) and hole (blue) distribution map in S₁, S₂ and S₃ excited states responsible for charge transfer absorption in DHN : TCNQ cocrystal (drawn at an iso-surface = 0.002 Hartree).

Charge carrier transport in the DHN : TCNQ cocrystal

The electron and hole transport in organic semiconductors with low charge carrier mobility values is frequently described using a hopping model where the charge carriers viz. electron/hole are assumed to hop between nearest neighbouring molecules.⁴⁶ The rate of charge carrier transfer in can be explained by semi-classical Marcus–Hush theory.⁴⁷ The rate of charge carrier transport (k_CT):
In this equation, h and ΔG° denote Planck's constant and the free energy for electron transfer from donor to acceptor, respectively. The free energy of charge transfer is calculated from energies of neutral DHN/TCNQ molecules and DHN˙⁺ cation/TCNQ˙⁻ anion. The value of ΔG⁰ for electron transfer from DHN to TCNQ (i.e., DHN + TCNQ → DHN˙⁺ + TCNQ˙⁻ process) is −1.93 eV indicating an energetically favorable process.

The pivotal factors responsible for charge carrier transfer are the transfer integral (t) and reorganization energy (λ).⁴⁷ The transfer integral measures the strength of electron and hole coupling between the nearest acceptor and donor molecular pair.⁴⁷ The reorganization energy term represents the energy prerequisite when a molecule accepts or ejects an electron (i.e., hole formation). This term λ is a sum of internal reorganization energy (λ_int) and external reorganization energy (λ_ext).⁴⁸ The internal reorganization energy term arises from the energy required for the molecular geometry change when a particular molecule accepts or ejects an electron, while the external reorganization term takes into account of the energy change accompanying the change in geometry of the surrounding molecules.⁴⁹ The term λ_ext is often ignored in the calculation as the geometry change of surrounding molecules is much less prominent in a solid state crystalline system rendering λ_int ≫ λ_ext.⁵⁰

The electron/hole transport in a π⋯π stacked D–A cocrystal takes place by the super-exchange mechanism along the mixed ⋯DADADA⋯ stacking direction (Fig. 8).⁵¹ In the super-exchange path, the electron hops between two acceptor molecules in a mixed stack via a donor molecule and the hole hops between two donor molecules in a mixed stack via an acceptor molecule. The super-exchange charge transfer integral is estimated from the coupling between two closest donors/acceptors along the π⋯π stacking (Fig. 8). However, all the D–A pairs along the stacking direction are equivalent in the DHN : TCNQ cocrystal. Hence, the super-exchange electron/hole transfer integrals were calculated by ‘energy splitting’ method using the molecular orbital energies of D–A–D/A–D–A triads.⁴¹

Fig. 8 (a) Super-exchange, and (b) direct electron/hole transfer integrals along different crystallographic directions in DHN : TCNQ cocrystal.

The calculated super-exchange electron transfer integral value of the DHN : TCNQ cocrystal is 12.4 meV and the hole transfer integral value is 48.2 meV (Fig. 9b and c). The transfer integral values indicate that DHN : TCNQ cocrystal is a n-type semiconductor. The super-exchange electron and hole transfer in structurally similar reported 1 : 1 DAN : TCNQ cocrystal are 65.4 and 28.5 meV respectively (Fig. S11 in ESI†), as aligned with the experimentally observed n-type semiconductor nature of this cocrystal. Comparison of DHN : TCNQ and DAN : TCNQ cocrystals demonstrates that the super-exchange transfer integral values are directly proportional to the degree of ground state charge transfer and strength of π⋯π stacking interaction between D and A. It is pertinent to note that the electron transfer integral value for DAN : TCNQ is similar to the value of the cocrystal of sulphur bridged annulene and TCNQ with a reported electron mobility value 0.24 cm² V⁻¹ s⁻¹ measured from the OFET device with I_on/I_off ratio being 1.5 × 10³.⁵² On the other hand, the electron mobility value of DAN : TCNQ cocrystal is 2.5 × 10⁻⁸ cm² V⁻¹ s⁻¹ measured from the OFET device with I_on/I_off ratio ≈ 1, indicating device parameters are as important as transfer integrals.^26b

Fig. 9 (a) Symmetry and energy of the frontier molecular orbitals on donor and acceptor available for super-exchange hole transfer in DHN : TCNQ cocrystal; (b) frontier MOs involved in super-exchange electron transfer; (c) super-exchange hole transfer integral calculated from D–A–D triad; (c) super-exchange electron transfer integral from A–D–A triad.

Super-exchange mechanism of charge transfer is largely dependent on nodal symmetry and the energy of the frontier MOs.⁵³ The electron dominant transport by super-exchange mechanism in these cocrystals should have originated from the nodal symmetry and energies of the participating orbitals. The hole transfer between donor HOMOs (−5.18 eV) takes place via bridging acceptor LUMO (−4.82 eV), and not the LUMO+1 orbital (−1.75 eV) as it is too high in energy to take part as a bridging orbital in the super-exchange hole transfer (Fig. 9a). The LUMO of TCNQ shows diagonal asymmetry (ungerade), while the HOMO of DHN possesses diagonal symmetry (gerade) (Fig. 8a). On the other hand, the electron transfer between two acceptor LUMOs cannot take place by both bridging donor HOMO and HOMO−1 orbital (−6.53 eV) as these orbitals possess diagonal symmetry in contrast to the diagonal asymmetry of LUMO of TCNQ (Fig. 9a). The HOMO−2 orbital (−6.54 eV), however, is suitable as a bridging orbital for having diagonal asymmetry similar to the TCNQ LUMO, and whereas the HOMO−3 orbital (−8.45 eV) of DHN is not energetically suitable to act as the bridging orbital. The absence of suitable bridging orbital for hole transfer explains the value of super-exchange hole transfer integral being smaller than the electron transfer integral. However, the energy difference (1.73 eV) between TCNQ LUMOs participating in super-exchange electron transfer and the bridging DHN HOMO−2 orbital is not insignificant, and this explains the moderate value of electron transfer integral.

We have also checked the super-exchange electron and hole transfer integral values along the O–H⋯N hydrogen bonded chain of DHN and TCNQ molecules (Fig. 8, Table 3) following super-exchange model. However, both the electron and hole transfer integral values are less than 1 meV indicating very little transfer along this direction. The very low values of electron/hole transfer integrals along the hydrogen bonded chain is the consequence of poor geometric overlap between the donor and acceptor. On the other hand, direct electron transfer among TCNQ molecules along the C–H⋯N hydrogen bonded ribbon, and direct hole transfer between DHN molecules along the C–H⋯O hydrogen bonded ribbon should also be considered as potential charge carrier transfer pathways. The direct electron transfer integral between the TCNQ molecules is 8.0 meV, and the direct hole transfer between the DHN molecules is 12.1 meV (Fig. S12 in ESI†). However the direct transfer integral values are significantly smaller in comparison to super-exchange electron transfer integral, hence a dominant n-type semiconductor nature of DHN : TCNQ cocrystal is expected.

Table 3 Direct and super-exchange transfer integral values along different directions

Type of transfer	Molecular diads/triads	Direction	Transfer integral value (meV)
Direct electron transfer	TCNQ diad	c-Axis	8.0
Direct hole transfer	DHN diad	c-Axis	12.1
Super-exchange hole transfer	TCNQ : DHN π–π stacked triad	a-Axis	12.4
Super-exchange electron transfer	TCNQ : DHN π–π stacked triad	a-Axis	48.2
Super-exchange hole transfer	TCNQ : DHN hydrogen bonded triad	c-Axis	0.2
Super-exchange electron transfer	TCNQ : DHN hydrogen bonded triad	c-Axis	0.8

---

The reorganization energy term plays an important role in deciding the charge carrier transfer rate. The internal hole reorganization energy (i.e., energy required to produce DHN˙⁺ cation from neutral DHN) of 1,5-dihydroxynaphthalene is 486 meV. The high value of hole reorganization energy in DHN arises due to the small size of naphthalene molecular backbone. On the other hand, the value of electron reorganization energy of TCNQ (energy required to produce TCNQ˙⁻ anion from neutral TCNQ) is 356 meV. The λ_int values for DHN and TCNQ moieties indicate electron dominant transport as the hole reorganization energy of DHN is not favorable for hole transport.

Band structure analysis

The band structure of DHN : TCNQ cocrystal were computed at PBE level of theory with Grimme's dispersion correction (PBE-D3), and using the HSE06 hybrid functional at the optimized unit cell geometry. The band structures were plotted along the high symmetry points of first Brillouin zone. The DHN : TCNQ cocrystal is an indirect bandgap semiconductor with the valence bond maxima (VBM) at the B point (0, 0, 0.5), and the conduction band minima (CBM) at the Γ point (0, 0, 0). The bandgap calculated using dispersion corrected PBE functional is 0.39 eV (Fig. S13 in ESI†), which is considerably lower than the experimentally observed bandgap of 0.94 eV from the Tauc plot (Fig. 10a). However, the generalized gradient approximation (GGA) functionals like PBE reportedly underestimate the bandgap values of molecular semiconductors.⁵⁴ The band gap calculated using HSE06 functional is slightly higher 0.54 eV (Fig. 10b and c).

Fig. 10 (a) Bandgap energy of DHN : TCNQ cocrystal estimated by Tauc plot; (b) band structure calculated with hybrid HSE06 functional with Γ-centered 4 × 1 × 4 mesh and 500 eV energy cut-off; (c) two highest valence bands and two lowest conduction bands are shown, calculated at hybrid HSE06 functional with Γ-centered 4 × 1 × 4 mesh.

The greatest curvature of the conduction band is observed along the B → A direction, which is equivalent to the crystallographic a axis i.e., the direction of super-exchange electron transfer via π⋯π stacking (Fig. 10c and S14b in ESI†). It is pertinent to notice the curvatures of both the valence and conduction band along the E → C direction, which coincides with the crystallographic c axis (Fig. 10c). This corresponds to the direct hole and electron transfer via the hydrogen bonded ribbons of DHN and TCNQ molecules. We have also calculated the band structure on experimental geometry with hybrid HSE06 functional and Γ-centered 4 × 1 × 4 mesh for the comparison. The calculated bandgap at the experimental geometry is 0.93 eV, which matches well with the experimentally observed bandgap value (Fig. S14 in ESI†). The difference in the bandgap value calculated at experimental and optimized unit cells can arise from the difference in the geometries especially the parameters of π⋯π stacking interaction (Table S2 in ESI†).

Additionally, we have calculated the bandgap of structurally analogous DAN : TCNQ cocrystal at HSE06 level of theory using the experimental geometry and Γ-centered 4 × 1 × 4 mesh. The DAN : TCNQ system possesses an indirect bandgap with value 0.60 eV, with the maxima of valence bond located at high symmetry point D (0, 0.5, 0.5) and the conduction band maxima at Γ point (0, 0, 0) (Fig. S15 and S16 in ESI†). Comparison of the bandgap values in the cocrystals shows that higher degree of charge transfer and stronger π⋯π stacking interaction lower the bandgap value; similar to the trend observed for the super-exchange electron/hole transfer integrals (Table 4).

Table 4 Bandgap of DHN : TCNQ at different geometries, k-mesh and theory level

Functional	k-Mesh	Geometry	Bandgap (eV)
PBE-D3	Γ-Centered 4 × 1 × 4	DFT-D2 optimized geometry	0.39
HSE06	Γ-Centered 4 × 1 × 4	DFT-D2 optimized geometry	0.54
HSE06	Γ-Centered 4 × 1 × 4	Experimental geometry	0.93

---

4. Conclusion

We have studied the electronic properties of a π-stacked donor–acceptor cocrystal based on π-donor 1,5-dihydroxynapthalene (DHN) and π-acceptor 7,7′,8,8′-tetracyanoquinodimethane (TCNQ). We have investigated the charge transfer and semiconducting features of this cocrystal using a combination of structural, spectroscopic and DFT studies. The experimentally observed narrow bandgap of the cocrystal (0.94 eV) is in good agreement with that found by periodic DFT calculations. The narrow bandgap value of the DHN : TCNQ cocrystal with a suitable LUMO energy level (−3.8 eV) corresponds to the potential application for air stable and high mobility n-channel organic field effect transistors. The super-exchange electron and hole transfer integral values along the π⋯π stacking direction confirms the n-type semiconductor nature of the DHN : TCNQ system. A closer look in the crystal packing features reveals that stronger intermolecular interactions result in higher values of transfer integrals. The comparison of two structurally analogous cocrystals π-stacked DHN : TCNQ and DAN : TCNQ show that the super-exchange transfer integrals are proportional to the strength of π⋯π stacking interaction and the degree of charge transfer. Organic semiconductors with electron dominant transport, ultra-narrow bandgap (<1 eV), solution processing ability, and appropriate LUMO energy (−3.8 eV) suitable for air stability are very rare. This donor–acceptor cocrystal is a step towards filling this void and finding potential application in fabricating n-channel organic field effect transistors.

Data availability

The following is the supplementary data related to this article: CCDC 2402657 contains the supplementary crystallographic data for the cocrystal DHN : TCNQ. Information of powder X-ray diffraction data, crystallographic and refined parameters, bond length and hydrogen bonding parameters, and computational details can be obtained in the ESI† section of online version of the article.

Author contributions

AM: conceptualizing the project, structural and DFT studies, writing the main draft, acquiring funding; CEM: band structure calculation, conceptualizing, editing manuscript; CHG: supervision of the single crystal XRD experiments and contribution to describing the molecular structure; MR: acquiring optical characterization data; ON: aiding optical characterization and commenting on manuscript draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project has received funding from the European Union's Horizon Europe research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101106582. Computational resources have been available from the Norwegian infrastructure for high-performance computing (NOTUR) through a grant of computing time (grant number NN2916K). AM and CEM are thankful to Prof. Caterina Cocchi (at Carl von Ossiezetzky Universitat Oldenburg) for helpful suggestions.

References

1. (a) A. W. Hains, Z. Liang, M. A. Woodhouse and B. A. Gregg, Molecular semiconductors in organic photovoltaic cells, Chem. Rev., 2010, 110, 6689–6735; (b) C. Ruiz, E. M. García-Frutos, G. Hennrich and B. Gómez-Lor, Effects of morphology on the functionality of organic electronic devices, J. Phys. Chem. Lett., 2012, 3, 1428–1436.
2. (a) G. Schweicher, G. Garbay, R. Jouclas, F. Vibert, F. Devaux and Y. H. Geerts, Molecular semiconductors for logic operations: Dead-end or bright future?, Adv. Mater., 2020, 32, 1905909; (b) T. Minari, C. Liu, M. Kano and K. Tsukagoshi, Controlled self-Assembly of organic semiconductors for solution-based fabrication of organic field-effect transistors, Adv. Mater., 2012, 24, 299–306; (c) S. Wang, L. Peng, H. Sun and W. Huang, The future of solution processing toward organic semiconductor devices: a substrate and integration perspective, J. Mater. Chem. C, 2022, 10, 12468–12486.
3. (a) M. Y. Lee, H. R. Lee, C. H. Park, S. G. Han and J. H. Oh, Organic transistor-based chemical sensors for wearable bioelectronics, Acc. Chem. Res., 2018, 51, 2829–2838; (b) P. C. Y. Chow and T. Someya, Organic photodetectors for next-generation wearable electronics, Adv. Mater., 2020, 32, 1902045; (c) I. Manunza, A. Sulis and A. Bonfiglio, Organic semiconductor field effect transistors for unconventional applications: flexible sensors and wearable devices, International Workshop on Wearable and Implantable Body Sensor Networks (BSN'06), Cambridge, MA, USA, 2006, pp. 4–211.
4. (a) Y. Wang, L. Sun, C. Wang, F. Yang, X. Ren, X. Zhang, H. Dong and W. Hu, Organic crystalline materials in flexible electronics, Chem. Soc. Rev., 2019, 48, 1492–1530; (b) I. Kymissis, C. D. Dimitrakopoulos and S. Purushothaman, Patterning pentacene organic thin film transistors, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2002, 20, 956.
5. (a) S. K. Gupta, P. Jha, A. Singh, M. M. Chehimi and D. K. Aswal, Flexible organic semiconductor thin films, J. Mater. Chem. C, 2015, 3, 8468–8479; (b) H. Zhu, E. S. Shin, A. Liu, D. Ji, Y. Xu and Y. Y. Noh, Printable semiconductors for backplane TFTs of flexible OLED displays, Adv. Funct. Mater., 2020, 30, 1904588; (c) Y. Qian, X. Zhang, L. Xie, D. Qi, B. K. Chandran, X. Chen and W. Huang, Stretchable organic semiconductor devices, Adv. Mater., 2016, 28, 9243–9265.
6. (a) W. Jiang, Y. Li and Z. Wang, Heteroarenes as high performance organic semiconductors, Chem. Soc. Rev., 2013, 42, 6113–6119; (b) T. Okamoto, C. P. Yu, C. Mitsui, M. Yamagishi, H. Ishii and J. Takeya, Bent-shaped p-type small-molecule organic semiconductors: A molecular design Strategy for next-generation practical applications, J. Am. Chem. Soc., 2020, 142, 9083–9096; (c) T. Takahashi, T. Takenobu, J. Takeya and Y. Iwasa, Ambipolar organic field-effect transistors based on rubrene single crystals, Appl. Phys. Lett., 2006, 88, 033505; (d) B. A. Jones, A. Facchetti, M. R. Wasielewski and T. J. Marks, Effects of arylene diimide thin film growth conditions on n-channel OFET performance, Adv. Funct. Mater., 2008, 18, 1329.
7. (a) P. Friederich, V. Meded, A. Poschlad, T. Neumann, V. Rodin, V. Stehr, F. Symalla, D. Danilov, G. Lüdemann, R. F. Fink, I. Kondov, F. von Wrochem and W. Wenzel, Molecular origin of the charge carrier mobility in small molecule organic semiconductors, Adv. Funct. Mater., 2016, 26, 5757–5763; (b) G. Schweicher, Y. Olivier, V. Lemaur and Y. H. Geerts, What currently limits charge carrier mobility in crystals of molecular semiconductors?, Isr. J. Chem., 2014, 54, 595–620.
8. (a) I. Vladimirov, M. Kühn, T. Geßner, F. May and R. T. Weitz, Energy barriers at grain boundaries dominate charge carrier transport in an electron-conductive organic semiconductor, Sci. Rep., 2018, 8, 14868; (b) J. Rivnay, L. H. Jimison, J. E. Northrup, M. F. Toney, R. Noriega, S. Lu, T. J. Marks, A. Facchetti and A. Salleo, Large modulation of carrier transport by grain-boundary molecular packing and microstructure in organic thin films, Nat. Mater., 2009, 8, 952; (c) T. Meier, H. Bässler and A. Köhler, The impact of grain boundaries on charge transport in polycrystalline organic field-effect transistors, Adv. Opt. Mater., 2021, 9, 2100115.
9. (a) S. Mondal, W. H. Lin, Y. C. Chen, S. H. Huang, R. Yang, B. H. Chen, T. F. Yang, S. W. Mao and M. Y. Kuo, Solution-processed single-crystal perylene diimide transistors with high electron mobility, Org. Electron., 2015, 23, 64; (b) X. Gao and Y. Hu, Development of n-type organic semiconductors for thin film transistors: a viewpoint of molecular design, J. Mater. Chem. C, 2014, 2, 3099–3117; (c) B. A. Jones, A. Facchetti, M. R. Wasielewski and T. J. Marks, Tuning orbital energetics in arylene diimide semiconductors: Materials design for ambient stability of n-type charge transport, J. Am. Chem. Soc., 2007, 129, 15259–15278.
10. (a) X. Zhan, A. Facchetti, S. Barlow, T. J. Marks, M. A. Ratner, M. R. Wasielewski and S. R. Marder, Rylene and related diimides for organic electronics, Adv. Mater., 2011, 23, 268–284; (b) C. C. Kao, P. Lin, Y. Y. Shen, J. Y. Yan, J. C. Ho and C. C. Lee, Solid-state structure of the naphthalene-based n-type semiconductor, and performance improved with Mo-based source/drain electrodes, Synth. Met., 2008, 158, 299–305; (c) K. Namsheer and C. S. Rout, Conducting polymers: a comprehensive review on recent advances in synthesis, properties and applications, RSC Adv., 2021, 11, 57–70.
11. (a) Z. Chen, M. J. Lee, R. S. Ashraf, Y. Gu, S. A. Seifried, M. M. Nielsen, B. Schroeder, T. D. Anthopoulos, M. Heeney, I. McCulloch and H. Sirringhaus, High-performance ambipolar diketopyrrolopyrrole-thieno[3,2-b]thiophene copolymer field-effect transistors with balanced hole and electron mobilities, Adv. Mater., 2012, 24, 647–652; (b) K. Singh, A. A. Mohapatra, D. Giri, C. Gangadharappa, S. Jhulki, S. Barlow, S. R. Marder, A. Ghosh, S. Patil and N. Chauhan, Ambipolar doping in π-conjugated polymers, ACS Appl. Electron. Mater., 2023, 5, 6765–6777.
12. (a) P. Yu, Y. Li, H. Zhao, L. Zhu, Y. Wang, W. Xu, Y. Zhen, X. Wang, H. Dong, D. Zhu and W. Hu, 1D Mixed-stack cocrystals based on perylene diimide toward ambipolar charge transport, Small, 2021, 17, 2006574; (b) J. Zhang, W. Xu, P. Sheng, G. Zhao and D. Zhu, Organic donor–acceptor complexes as novel organic semiconductors, Acc. Chem. Res., 2017, 50, 1654–1662.
13. (a) T. Zou, J. Chang, Q. Chen, Z. Nie, L. Duan, T. Guo, Y. Song, W. Wu and H. Wang, Novel strategy for organic cocrystals of n-type and p-type organic semiconductors with advanced optoelectronic properties, ACS Omega, 2020, 5, 12067–12072; (b) W. R. Bodlos, S. K. Park, B. Kunert, S. Y. Park and R. Resel, Thin film growth of a charge transfer cocrystal (DCS/TFPA) for ambipolar thin film transistors, ACS Appl. Electron. Mater., 2021, 3, 2783–2789.
14. (a) J. Zhang, J. Jin, H. Xu, Q. Zhang and W. Huang, Recent progress on organic donor–acceptor complexes as active elements in organic field-effect transistors, J. Mater. Chem. C, 2018, 6, 3485–3498; (b) N. Yee, A. Dadvand and D. F. Perepichka, Band gap engineering of donor–acceptor co-crystals by complementary two-point hydrogen bonding, Mater. Chem. Front., 2020, 4, 3669–3677; (c) R. Sato, T. Kawamoto and T. Mori, Asymmetrical hole/electron transport in donor–acceptor mixed-stack cocrystals, J. Mater. Chem. C, 2019, 7, 567–577; (d) L. Sun, W. Zhu, F. Yang, B. Li, X. Ren, X. Zhang and W. Hu, Molecular cocrystals: design, charge-transfer and optoelectronic functionality, Phys. Chem. Chem. Phys., 2018, 20, 6009–6023.
15. (a) L. Sun, W. Hua, Y. Liu, G. Tian, M. Chen, M. Chen, F. Yang, S. Wang, X. Zhang, Y. Luo and W. Hu, Thermally activated delayed fluorescence in an organic cocrystal: narrowing the singlet–triplet energy gap via charge transfer, Angew. Chem., 2019, 131, 11433–11438; (b) X. Zhang, J. De, H. Liu, Q. Liao, S. T. Zhang, C. Zhou, H. Fu and B. Yang, Cis-Trans Isomerism Inducing Cocrystal Polymorphism with Thermally Activated Delayed Fluorescence and Two-Photon Absorption, Adv. Opt. Mater., 2022, 10, 2200286.
16. Y. Wen, S. Zhao, Z. Yang, Z. Feng, Z. Yang, S. T. Zhang, H. Liu and B. Yang, Transforming Thermally Activated Delayed Fluorescence to Room-Temperature Phosphorescence through Modulation of the Donor in Charge-Transfer Cocrystals, J. Phys. Chem. Lett., 2024, 15, 2690–2696.
17. (a) S. Singha, R. Jana, R. Mondal, P. P. Ray, P. P. Bag, K. Gupta, N. Pakhira, C. Rizzoli and A. Mallick, Photo-responsive Schottky diode behavior of a donor–acceptor co-crystal with violet blue light emission, CrystEngComm, 2021, 23, 3510–3523; (b) W. Zhu, R. Zheng, Y. Zhen, Z. Yu, H. Dong, H. Fu, Q. Shi and W. Hu, Rational design of charge-transfer interactions in halogen-bonded co-crystals toward versatile solid-state optoelectronics, J. Am. Chem. Soc., 2015, 137, 11038–11046.
18. H. Zhang, L. Jiang, Y. Zhen, J. Zhang, G. Han, X. Zhang, X. Fu, Y. Yi, W. Xu, H. Dong, W. Chen, W. Hu and D. Zhu, Organic cocrystal photovoltaic behavior: A model system to study charge recombination of C₆₀ and C₇₀ at the molecular level, Adv. Electron. Mater., 2016, 2, 1500423.
19. J. Wang, S. Xu, A. Li, L. Chen, W. Xu and H. Zhang, Polymorphism-based luminescence and morphology-dependent optical waveguide properties in 1: 1 charge transfer cocrystals, Mater. Chem. Front., 2021, 5, 1477–1485.
20. Y. Yu, Z. Z. Li, J. J. Wu, G. Q. Wei, Y. C. Tao, M. L. Pan, X. D. Wang and L. S. Liao, Transformation from nonlasing to lasing in organic solid-state through the cocrystal engineering, ACS Photonics, 2019, 6, 1798–1803.
21. Y. Wang, H. Wu, W. Zhu, X. Zhang, Z. Liu, Y. Wu, C. Feng, Y. Dang, H. Dong, H. Fu and W. Hu, Cocrystal engineering: toward solution-processed near-infrared 2D organic cocrystals for broadband photodetection, Angew. Chem., Int. Ed., 2021, 60, 6344–6350.
22. Q. Huang, X. Ye, W. Chen, X. Song, Y. Chen, X. Wen, M. Zhang, Y. Wang, S. L. Chen, L. Dang and M. D. Li, Boosting photo-thermo-electric conversion via a donor–acceptor organic cocrystal strategy, ACS Energy Lett., 2023, 8, 4179–4185.
23. (a) C. Mathur, R. Gupta and R. K. Bansal, Organic donor-acceptor complexes as potential semiconducting materials, Chem. – Eur. J., 2024, 30, e202304139; (b) L. Zhu, Y. Yi, A. Fonari, N. S. Corbin, V. Coropceanu and J. L. Brédas, Electronic properties of mixed-stack organic charge-transfer crystals, J. Phys. Chem. C, 2014, 118(26), 14150–14156; (c) A. Mandal, A. Choudhury, S. Sau, P. K. Iyer and P. Mal, Exploring ambipolar semiconductor nature of binary and ternary charge-transfer cocrystals of triphenylene, pyrene, and TCNQ, J. Phys. Chem. C, 2020, 124, 6544–6553.
24. R. R. Dasari, X. Wang, R. A. Wiscons, H. F. Haneef, A. Ashokan, Y. Zhang, M. S. Fonari, S. Barlow, V. Coropceanu, T. V. Timofeeva, O. D. Jurchescu, J. L. Brédas, A. J. Matzger and S. R. Marder, Charge-transport properties of F₆TNAP-based charge-transfer cocrystals, Adv. Funct. Mater., 2019, 29, 1904858.
25. T. Higashino and T. Mori, Small-molecule ambipolar transistors, Phys. Chem. Chem. Phys., 2022, 24, 9770–9806.
26. (a) R. K. Behera, N. R. Goud, A. J. Matzger, J. L. Brédas and V. Coropceanu, Electronic properties of 1, 5-diaminonaphthalene: Tetrahalo-1, 4-benzoquinone donor–acceptor cocrystals, J. Phys. Chem. C, 2017, 121, 23633–23641; (b) N. R. Mallela, T. Kawamoto and T. Mori, Charge polarity control in organic transistors of mixed and segregated complexes based on diaminonaphthalene and pyrene, ACS Appl. Mater. Interfaces, 2023, 15, 45201–45211.
27. (a) S. Hiroma, H. Kuroda and H. Akamatu, Semiconductivity and photoconductivity of TCNQ crystal, Bull. Chem. Soc. Jpn., 1971, 44(4), 974–977; (b) N. T. Johnson, M. R. Probert and P. G. Waddell, Structural investigations into a new polymorph of F4TCNQ: towards enhanced semiconductor properties, Acta Crystallogr., Sect. C: Struct. Chem., 2021, 77(7), 426–434.
28. (a) A. Ashokan, C. Hanson, N. Corbin, J. L. Brédas and V. Coropceanu, Mater. Chem. Front., 2020, 4, 3623–3631; (b) J. Zhang, H. Geng, T. S. Virk, Y. Zhao, J. Tan, C. Di, W. Xu, K. Singh, W. Hu, Z. Shuai, Y. Liu and D. Zhu, Sulfur-bridged annulene-TCNQ co-Crystal: A self-assembled “molecular level heterojunction” with air stable ambipolar charge transport behavior, Adv. Mater., 2012, 24, 2603–2607; (c) Z. Wang, R. Li, K. Zhao, F. Yu, J. Zhao, Y. Zhen and Q. Zhang, A co-crystallization strategy toward high-performance n-type organic semiconductors through charge transport switching from p-type planar azaacene derivatives, J. Mater. Chem. C, 2022, 10, 2757–2762; (d) Z. Ding, Q. Mu, J. Ren, Y. Li, Q. Shen, L. Zhang and S. Zhang, The impact of polymorphism on charge transport properties for pyrene-FxTCNQ cocrystals, J. Phys.: Conf. Ser., 2023, 2610, 012054.
29. P. Politzer, J. S. Murray and T. Clark, The π-hole revisited, Phys. Chem. Chem. Phys., 2021, 23, 16458–16468.
30. (a) S. Melis, S. Hung, C. Bagade, Y. Chung, E. Hughes, X. Zhang, P. Barbara, P. Han, T. Li, D. McCusker, R. Hartsmith, J. Bertke, P. Dev, I. Stone, J. Joshi, P. Vora and E. V. Keuren, Charge transport through superexchange in phenothiazine–7, 7, 8, 8-tetracyanoquinodimethane (PTZ–TCNQ) cocrystal microribbon FETs grown using evaporative alignment, ACS Appl. Electron. Mater., 2022, 4, 5973–5983; (b) H. Geng, L. Zhu, Y. Yi, D. Zhu and Z. Shuai, Superexchange induced charge transport in organic donor–acceptor cocrystals and copolymers: a theoretical perspective, Chem. Mater., 2019, 31, 6424–6434; (c) H. Geng, X. Zheng, Z. Shuai, L. Zhu and Y. Yi, Understanding the charge transport and polarities in organic donor-acceptor mixed-stack crystals: molecular insights from the super-exchange couplings, Adv. Mater., 2015, 27, 1443–1449; (d) M. Guerrini, A. M. Valencia and C. Cocchi, Long-range order promotes charge-transfer excitations in donor/acceptor co-crystals, J. Phys. Chem. C, 2021, 125(38), 20821–20830; (e) K. A. Ivshin, K. Metlushka, A. Fedonin, S. K. Latypov, V. V. Khrizanforova, Y. H. Budnikova, A. E. Vandyukov, A. G. Kiiamov, A. Laskin, S. M. Avdoshenko, M. Knupfer and O. Kataeva, Substituent controllable assembly of anthracene donors and TCNQ acceptors in charge transfer cocrystals, Cryst. Growth Des., 2023, 23, 954–964.
31. Y. Xiao, C. Wu, X. Hu, K. Chen, L. Qi, P. Cui, L. Zhou and Q. Yin, Mechanochemical synthesis of cocrystal: From mechanism to application, Cryst. Growth Des., 2023, 23, 4680–4700.
32. R. Alcaraz de la Osa, I. Iparragirre and D. Ortiz, et al., The extended Kubelka–Munk theory and its application to spectroscopy, ChemTexts, 2020, 6, 2.
33. (a) D. Josa, J. R. Otero, E. M. C. Lago and M. R. Piñeiro, Analysis of the performance of DFT-D, M05-2X and M06-2X functionals for studying π⋯ π interactions, Chem. Phys. Lett., 2013, 557, 170–175; (b) N. Marom, A. Tkatchenko, M. Rossi, V. V. Gobre, O. Hod, M. Scheffler and L. Kronik, Dispersion interactions with density-functional theory: Benchmarking semiempirical and interatomic pairwise corrected density functionals, J. Chem. Theory Comput., 2011, 7, 3944–3951; (c) M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, Performance of M06, M06-2X, and M06-HF density functionals for conformationally flexible anionic clusters: M06 functionals perform better than B3LYP for a model system with dispersion and ionic hydrogen bonding interactions, J. Phys. Chem. A, 2013, 117(47), 12590–12600.
34. (a) N. X. Wang, K. Venkatesh and A. K. Wilson, Behavior of density functionals with respect to basis set. 3. Basis set superposition error, J. Phys. Chem. A, 2006, 110, 779–784; (b) S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566.
35. (a) M. A. Spackman and D. Jayatilaka, Hirshfeld surface analysis, CrystEngComm, 2009, 11, 19–32; (b) J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces, Chem. Commun., 2007, 3814–3816; (c) A. Parkin, G. Barr, W. Dong, C. J. Gilmore, D. Jayatilaka, J. J. McKinnon, M. A. Spackman and C. C. Wilson, Comparing entire crystal structures: structural genetic fingerprinting, CrystEngComm, 2007, 9, 648–652; (d) M. J. Turner, S. Grabowsky, D. Jayatilaka and M. A. Spackman, Accurate and efficient model energies for exploring intermolecular interactions in molecular crystals, J. Phys. Chem. Lett., 2014, 5(24), 4249–4255.
36. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
37. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, Performance of M06, M06-2X, and M06-HF density functionals for conformationally flexible anionic clusters: M06 functionals perform better than B3LYP for a model system with dispersion and ionic hydrogen-bonding interactions, J. Phys. Chem. A, 2013, 117(47), 12590–12600.
38. F. Weinhold, Natural bond orbital analysis: A critical overview of relationships to alternative bonding perspectives, J. Comput. Chem., 2012, 33, 2363–2379.
39. (a) D. Hall, J. C. Sancho-García, A. Pershin, D. Beljonne, E. Z. Colman and Y. Olivier, Benchmarking DFT functionals for excited-state calculations of donor–acceptor TADF emitters: insights on the key parameters determining reverse inter-system crossing, J. Phys. Chem. A, 2023, 127(21), 4743–4757; (b) B. Mahato and A. N. Panda, Assessing the performance of DFT functionals for excited-state properties of pyridine-thiophene oligomers, J. Phys. Chem. A, 2021, 125(1), 115–125.
40. O. L. Estrada, H. G. Laguna, C. B. Flores and C. A. Bedolla, Reassessment of the four-point approach to the electron-transfer Marcus–Hush theory, ACS Omega, 2018, 3(2), 2130–2140.
41. L. Zhu, Y. Yi, Y. Li, E.-G. Kim, V. Coropceanu and J.-L. Brédas, Prediction of remarkable ambipolar charge-transport characteristics in organic mixed-stack charge-transfer crystals, J. Am. Chem. Soc., 2012, 134, 2340.
42. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
43. (a) S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799; (b) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
44. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106.
45. G. R. Hutchison, M. A. Ratner and T. J. Marks, Intermolecular charge transfer between heterocyclic oligomers. Effects of heteroatom and molecular packing on hopping transport in organic semiconductors, J. Am. Chem. Soc., 2005, 127, 16866–16881.
46. (a) J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Organic semiconductors: A theoretical characterization of the basic parameters governing charge transport, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809; (b) V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J. L. Brédas, Charge transport in organic semiconductors, Chem. Rev., 2007, 107, 926–952.
47. (a) A. V. Szeghalmi, M. Erdmann, V. Engel, M. Schmitt, S. Amthor, V. Kriegisch, G. Nöll, R. Stahl, C. Lambert, D. Leusser, D. Stalke, M. Zabel and J. Popp, How delocalized Is N,N,N',N'-tetraphenylphenylenediamine radical cation? An experimental and transistor properties of Charge-transfer complexes – combined requirements from energy levels and orbital symmetry, theoretical study on the electronic and molecular structure, J. Am. Chem. Soc., 2004, 126(25), 7834–7845; (b) B. S. Brunschwig, C. Creutz and N. Sutin, Optical transitions of symmetrical mixed-valence systems in the Class II–III transition regime, Chem. Soc. Rev., 2002, 31, 168–184.
48. E. F. Valeev, V. Coropceanu, D. A. da Silva Filho, S. Salman and J. L. Brédas, Effect of electronic polarization on charge-transport parameters in molecular organic semiconductors, J. Am. Chem. Soc., 2006, 128(30), 9882–9886.
49. (a) N. Metri, X. Sallenave, C. Plesse, L. Beouch, P. H. Aubert, F. Goubard, C. Chevrot and G. Sini, Processable star-shaped molecules with triphenylamine core as hole-transporting materials: Experimental and theoretical approach, J. Phys. Chem. C, 2012, 116(5), 3765–3772; (b) M. E. Köse and K. S. Schanze, Prediction of internal reorganization energy in photoinduced electron transfer processes of molecular dyads, J. Phys. Chem. A, 2020, 124(45), 9478–9486.
50. D. P. McMahon and A. Troisi, Evaluation of the external reorganization energy of polyacenes, J. Phys. Chem. Lett., 2010, 1(6), 941–946.
51. (a) H. Geng, L. Zhu, Y. Yi, D. Zhu and Z. Shuai, Superexchange induced charge transport in organic donor–acceptor cocrystals and copolymers: A theoretical perspective, Chem. Mater., 2019, 31(17), 6424–6434; (b) X. Chen, H. Wang, B. Wang, Y. Wang, X. Jin and F. Q. Bai, Charge transport properties in organic DA mixed-stack complexes based on corannulene and sumanene derivatives-a theoretical study, Org. Electron., 2019, 68, 35–44; (c) C. Cheng, H. Geng, Y. Yi and Z. Shuai, Super-exchange-induced high performance charge transport in donor–acceptor copolymers, J. Mater. Chem. C, 2017, 5, 3247–3253; (d) C. Lambert, C. Risko, V. Coropceanu, J. Schelter, S. Amthor, N. E. Gruhn, J. C. Durivage and J. L. Brédas, Electronic coupling in tetraanisylarylenediamine mixed-valence systems: the interplay between bridge energy and geometric factors, J. Am. Chem. Soc., 2005, 127(23), 8508–8516; (e) B. Liu, S. Fan, R. Huang, T. Kawamoto and T. Mori, Transistor properties of charge-transfer complexes – combined requirements from energy levels and orbital Symmetry, J. Phys. Chem. C, 2023, 127(10), 5125–5133.
52. Y. Qin, J. Zhang, X. Zheng, H. Geng, G. Zhao, W. Xu, W. Hu, Z. Shuai and D. Zhu, Adv. Mater., 2014, 26, 4093.
53. (a) B. Liu, S. Fan, R. Huang, T. Kawamoto and T. Mori, Transistor properties of charge-transfer complexes-combined requirements from energy levels and orbital symmetry, J. Phys. Chem. C, 2023, 127(10), 5125–5133; (b) K. Iijima, R. Sanada, D. Yoo, R. Sato, T. Kawamoto and T. Mori, Carrier charge polarity in mixed-stack charge-transfer crystals containing dithienobenzodithiophene, ACS Appl. Mater. Interfaces, 2018, 10(12), 10262–10269.
54. (a) Z. Wan, Q. D. Wang, D. Liu and J. Liang, Effectively improving the accuracy of PBE functional in calculating the solid band gap via machine learning, Comput. Mater. Sci., 2021, 198, 110699; (b) X. K. Chen, Y. T. Fu, H. Li and J. L. Bredas, Electronic structure at the interface between rubrene and perylenediimide single crystals: Impact of interfacial charge transfer and its modulation, Adv. Mater. Interfaces, 2014, 1, 1400362.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2402657. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5me00033e

---