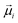Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Origins of curvature in meso-tetra(4-sulfonatophenyl) porphine aggregation: molecular dynamics and electronic spectroscopy†
Laura
Baliulyte
 *a,
Eimantas
Urniezius
*a,
Eimantas
Urniezius
 a,
Vytautas
Bubilaitis
a,
Vytautas
Bubilaitis
 a,
Mindaugas
Macernis
a,
Mindaugas
Macernis
 a,
Lorenzo
Cupellini
a,
Lorenzo
Cupellini
 b and
Darius
Abramavicius
b and
Darius
Abramavicius
 a
a
aInstitute of Chemical Physics, Faculty of Physics, Vilnius University, Sauletekio av. 9, LT-10222 Vilnius, Lithuania. E-mail: laura.baliulyte@ff.vu.lt
bDepartment of Chemistry and Industrial Chemistry, University of Pisa, 56124, Pisa, Italy
First published on 9th June 2025
Abstract
meso-Tetra(4-sulfonatophenyl) porphine (TPPS4) is a significant theranostic agent for photodynamic therapy (PDT) and a model system of molecular nanowires. The zwitterionic forms of TPPS4 tend to form large chiral nanotubes in acidic conditions at pH ≈1. However, it is still not clear how these aggregates are structured at the molecular level. We describe a computational strategy to model the TPPS4 aggregation of small clusters using a molecular dynamics (MD) approach. Two possible forms of zwitterionic TPPS4 tetramers were considered, and their absorption and circular dichroism (CD) spectra were calculated using the Frenkel exciton model. Possible molecular packing is suggested as a candidate for the formation of large aggregates.
Design, System, ApplicationSynthetic tubular porphyrin nano-aggregates are potential candidates for quantum energy wiring as well as drug-driving components in photodynamic therapy in cancer treatment. Only small molecular systems, mostly dimers, can be optimized by, e.g., density functional approach with sufficient accuracy. To consider large numbers of molecules in various designs, we used the classical molecular mechanics (MM) approach, which is computationally much less expensive. The general Amber force field (GAFF) has parameters for most organic molecules; however, the parameters must be revised due to the conjugation of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in porphyrins. Reparameterization of the zwitterionic TPPS4 porphyrins is performed (leading to extension of GAFF force field parameters for porphyrin macrocycles), then tetramers are designed, solvated in a box of water. MD simulation was performed and a room temperature trajectory is obtained, which shows the emergence of global tetramer structure curling. This demonstrates the origin of tubular structure formation. Tetramer absorption and circular dichroism spectra were calculated using the Frenkel exciton model and peak positions in absorption spectra are similar to peak positions in experimentally measured spectra. From this information we can learn about various artificial chiral molecular aggregate formation for specific applications. C bonds in porphyrins. Reparameterization of the zwitterionic TPPS4 porphyrins is performed (leading to extension of GAFF force field parameters for porphyrin macrocycles), then tetramers are designed, solvated in a box of water. MD simulation was performed and a room temperature trajectory is obtained, which shows the emergence of global tetramer structure curling. This demonstrates the origin of tubular structure formation. Tetramer absorption and circular dichroism spectra were calculated using the Frenkel exciton model and peak positions in absorption spectra are similar to peak positions in experimentally measured spectra. From this information we can learn about various artificial chiral molecular aggregate formation for specific applications.
|
Introduction
In the past few decades, aggregates of molecular pigments have been extensively investigated as potential light harvesters1 and light energy concentrators.2 Water-soluble, metal-free, highly stable aggregates are additionally important as possible theranostic agents for photoacoustic imaging (PAI) and photodynamic therapy (PDT) due to the intense light absorption in the phototherapeutic window.3 A graphical representation of the curved TPPS4 tetramer in a water box, illustrating light absorption and the generation of optical spectra, is shown in Fig. 1.PDT is an innovative and non-invasive form of treatment of oncological diseases. PDT is also well tolerated by patients because it has high selectivity for neoplastic tissues.4 In contrast, many cancer patients who undergo chemotherapy5 and radiotherapy6 experience side effects. 5,10,15,20-Tetrakis(4-sulfonatophenyl) porphyrin (TPPS4) molecules absorb light and may initiate the activation processes leading to the death of tumor cells, hence could be used in PDT.3 PDT treatment success might be related to aggregation and spectroscopic characteristics. However, the structural details of TPPS4 aggregation are still not completely understood.
The prevalent protonation state of TPPS4 molecules depends on the pH of the solvent: H8TPPS42+ (dicationic form) is prevalent at extremely low pH (<0), H6TPPS40 (zwitterionic form) appears to dominate at pH ≈1, whereas H4TPPS42− (diacid form) dominates in the pH ≈3 to 4 range, and H2TPPS44− (tetra-anion form) dominates in neutral (pH ≈7) and alkaline (pH ≈12) solutions.7,8 The monomers of TPPS4 spontaneously associate into tubular structures – J-aggregates (side by side) and/or H-aggregates (face to face) – in the host solution, depending on the pH value of the aqueous medium and on the concentration of TPPS4 molecules.9,10 The structures of TPPS4 could be helical,11 flat or flocculated,12 but there is still little knowledge about the explicit molecular packing.
J-type aggregates are formed when monomers concentrate with respect to each other in a direction approximately parallel to the molecular plane, while H-aggregates are formed when the monomers are placed on top of each other.13 The self-organization state of molecules can be deduced from the changes in spectral properties of the solution samples. J-aggregates are characterized by a bathochromic (red-shifted) absorption band, whereas H-aggregates possess a hypsochromic (blue-shifted) absorption band in relation to the monomer absorption band.14 It has been experimentally confirmed that the zwitterionic TPPS4 aggregates spectroscopically feature absorption bands of J-aggregates at low pH value (the intermolecular electrostatic repulsion being weakened among the molecules due to the acidic medium) specifically in the B-band (400–500 nm) region.15
Tubular and stripelike structures of TPPS4 aggregates have been suggested, assuming that the zwitterionic TPPS4 molecules self-assemble into a bent thread that can contain approximately 60–70 monomers in a loop.12,16 The structures on silicon substrates were analysed with atomic force microscopy (AFM). It was determined that the size of the separate stripes varies from 4.5 nm × 40 nm × 200 nm to 4.5 nm × 40 nm × 1000 nm (height × width × length).12
Pleckaitis et al. published two possible structural models of TPPS4 molecular nanotubes. In a face-exposed structure, TPPS4 molecules have “adjacent” sulfonate (SO3−) groups and these molecules oriented with the planar side towards the porphyrin nanotube surface, whereas in an edge-exposed structure, molecules have “opposite” SO3− groups and these molecules are put together with the edge exposed to the TPPS4 nanotube surface.17
However, such microscopic-level information is not available in experiments. Additionally, only small molecular systems, mainly dimers, can be modeled with sufficient accuracy to describe ground and excited states by ab initio quantum chemistry methods, e.g. density functional theory (DFT).18–20 Ishii et al. used DFT with Becke's three-parameter hybrid functional applying the non-local correlation provided by the Lee, Yang, and Parr (B3LYP) method along with the Pople 6-31G* basis set for modelling similar types of H4TPPS1 J-dimers. Right-handed helical, left-handed helical, or parallel structures have been found.20 In our previous study, 5 different monomers and 10 dimers of TPPS4, differing by protonation pattern, were determined using DFT with the Coulomb-attenuating B3LYP functional (CAM-B3LYP) and Pople 6-31G(d,p) basis set. The influence of water (solvent) was also approximately evaluated with the polarizable continuum model (PCM). It has been shown that the dimers are dominant at pH 1.0, while the monomeric forms dominate at pH 12.1 to 3.0 and at pH −1.0. However, the calculations showed that zwitterionic TPPS4 molecules and their dimers do not show curvature (or bending) and the proposed tubular aggregation remains inconsistent with the DFT-implied planar type of TPPS4 molecular structure.21
Larger molecular aggregates may be necessary to address in order to expose the structural bending, influence of water molecules and thermal effects, which might demonstrate the accumulation effect. The classical molecular dynamics (MD) approach, based on classical equations of motion and using effective molecular mechanics (MM) intermolecular interactions, could be used for this purpose due to lower computational cost in comparison to quantum chemistry. MD simulations allow for finite temperature dynamical corrections due to the anharmonicity of interaction potentials. MD simulations provide a toolkit to study static and dynamical processes in larger systems consisting of tens of thousands of atoms.22,23
In a previous study, the chiral self-organization of diacid TPPS4 (H4TPPS42−) tetramers was theoretically simulated. Despite the progress of porphyrin chiral self-organization investigations,24 very little is known about the zwitterionic TPPS4 (H6TPPS40) form aggregation. In this study, starting from quantum mechanical (QM) calculation of H6TPPS40 monomers Z1 and Z2 (see Fig. 2(a–c) inside the blue rectangles), the molecular structures were parametrized for MM optimization and MD simulations leading to an updated force field (FF). A fluctuating exciton model based on the MD trajectory was constructed. Linear absorption and circular dichroism (CD) spectra, which are very sensitive to the molecular organization,25,26 were calculated for the obtained chiral tetramers. Correlation between the modelled and the experimentally measured21 spectra was used to suggest the favourable aggregation type of the TPPS4 aggregates.
Results and discussion
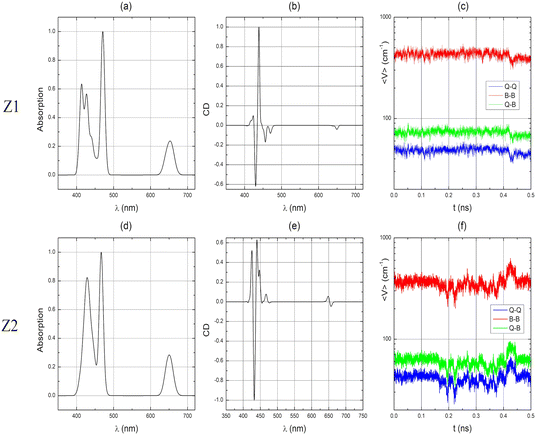
The QM optimized TPPS4 structures of Z1 and Z2 monomers are shown in Fig. 3(a) and (b), respectively. As these forms of the porphyrin molecule are charge-neutral, we have shown by quantum mechanical calculations that they tend to form dimers.21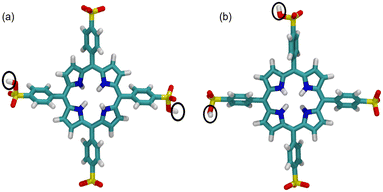 | ||
| Fig. 3 QM optimized structures of TPPS4 monomers. (a) Z1 monomer, (b) Z2 monomer. Hydrogens of SO3H groups are surrounded by a black oval. | ||
These structures are very similar to those used in our previous publication.21 However, in the present study, we obtained the Z1 and Z2 monomers using B3LYP with the Pople 6-311G(d,p) basis set, whereas in ref. 21, we used CAM-B3LYP with the Pople 6-31G(d,p) basis set. In this study, the B3LYP method was used because we calculated separate molecules (monomers) and in this case long-range Coulomb interaction is not important. Therefore, these structures are not equivalent. B3LYP calculations were not used for larger structures. Here we point out that the Z1 monomer has almost perfect C2 symmetry, unlike Z2. Additionally, the side rings (of benzene) are much more twisted in Z2. Apparently, the symmetry of the molecule significantly affects the electron distribution in the porphyrin ring, which affects the twisting of the side rings. These structures and their mechanical properties are used to parameterize classical force fields specifically for these molecules.
The MM optimized geometries of the TPPS4 Z1 and Z2 monomers with the numbers of carbon and nitrogen atoms used in this paper are presented in Fig. 4(a) and (b), respectively.
It was observed that phenyl groups with non-protonated sulfonate groups (SO3−) in para positions are more twisted than phenyl groups with protonated sulfonate groups (SO3H) in para positions in both the Z1 and Z2 monomers (Fig. 4(a) and (b)). Atom types of these monomers were assigned automatically with the Antechamber program27 and revised upon visual inspection. The overlap of the TPPS4 Z1 and Z2 monomer structures optimized with B3LYP/6-311G(d,p) and MM optimized structures with marked atom types, which were changed, are depicted in Fig. 4(c) and (d), respectively. Other atom types were not changed. Technical information on MM optimized Z1 and Z2 monomers is presented in the ESI.†
A comparison of parameters (bond lengths, valence angles and dihedral angles) between TPPS4 Z1 and Z2 monomer structures optimized with QM vs. MM is presented in Tables 1–3. Table 1 presents only bonds with lengths that differ the most between QM and MM structures, i.e. absolute length difference equal to 0.02 Å.
| Bond lengths (Å) | Z1 monomer | |
|---|---|---|
| QM | MM | |
| C23–C22 | 1.40 | 1.42 |
| C13–C12 | 1.40 | 1.42 |
| Z2 monomer | ||
|---|---|---|
| QM | MM | |
| N1–C1 | 1.38 | 1.40 |
| C6–C43 | 1.40 | 1.42 |
| C5–C42 | 1.40 | 1.42 |
| Valence angles (°) | Z1 monomer | |
|---|---|---|
| QM | MM | |
| C26–C7–C8 | 126.47 | 129.33 |
| C23–C22–C21 | 125.42 | 125.08 |
| C14–C17–C18 | 126.46 | 129.37 |
| C11–C12–C13 | 125.42 | 126.08 |
| Z2 monomer | ||
|---|---|---|
| QM | MM | |
| C5–C42–C14 | 125.54 | 127.07 |
| C10–C41–C13 | 126.47 | 127.38 |
| C1–C43–C6 | 127.15 | 127.38 |
| C2–C44–C9 | 124.66 | 128.04 |
| Dihedral angles (°) | Z1 monomer | |
|---|---|---|
| QM | MM | |
| C13–C12–C39–C44 | −120.67 | −123.88 |
| C14–C17–C33–C34 | −117.12 | −103.85 |
| C26–C7–C4–C3 | 117.19 | 107.67 |
| C23–C22–C27–C32 | 120.64 | 122.00 |
| Z2 monomer | ||
|---|---|---|
| QM | MM | |
| C1–C43–C35–C37 | −109.99 | −121.44 |
| C2–C44–C17–C18 | −125.61 | −109.78 |
| C14–C42–C29–C30 | 118.59 | 118.59 |
| C13–C41–C23–C25 | 118.11 | 110.65 |
This shows that the reparameterization resulted in very good FF representation (note that the difference in bond lengths in the other tetrapyrrole (pheophytin a) structure is up to 0.15 Å between QM and MM structures in a previous study28).
The valence and dihedral angles of TPPS4 monomer macrocycles (see Tables 2 and 3) were also compared between QM and MM structures. It was noticed that the largest differences are 3.38° (Z2 monomer, C2–C44–C9), 13.27° (Z1 monomer, C14–C17–C33–C34) and 15.83° (Z2 monomer, C2–C44–C17–C18). Hence, structures of the Z2 monomer with “adjacent” SO3H groups differ more than those of the Z1 monomer with “opposite” SO3H groups at QM and MM level. Conversely, in the pheophytin a structure,28 the largest valence angle difference is equal to 8.3° (larger than in our structures).
Despite the fact that the MM Z2 monomer (Fig. 4b) is deformed compared to the QM Z2 monomer (Fig. 3b), as shown in Fig. 4(c) and (d), the QM and MM optimized structures of our monomers (including both Z1 and Z2) are very similar. The tetramers were constructed gradually to keep the simulation stable as described in section Computational details. 100 ns MD simulation was performed for solvated tetramers.
In order to know whether TPPS4 Z1 and Z2 tetramers form some type of curved structure, the Z1 and Z2 tetramer global structures were inspected by introducing an intermolecular curvature angle, which is recorded along the MD trajectory (see Fig. 5(c) and (d), respectively). The molecules were numbered 1 to 4 in a row. A first vector, ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) 12, is drawn between the porphyrin ring centres of the first and second TPPS4 (these are mass centres defined by the corresponding four nitrogen atoms of the four molecules). A second vector,
12, is drawn between the porphyrin ring centres of the first and second TPPS4 (these are mass centres defined by the corresponding four nitrogen atoms of the four molecules). A second vector, ![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) 34, is drawn between the porphyrin rings of the third and fourth TPPS4 molecules. Then the angle between these two vectors (by using the dot product definition) is given by:
34, is drawn between the porphyrin rings of the third and fourth TPPS4 molecules. Then the angle between these two vectors (by using the dot product definition) is given by:
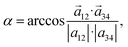 | (1) |
The results, reported in Fig. 5(c) and (d) show that the molecules form a curved structure having permanent curve angle α = ∼30°. Structures with the smallest/largest α are depicted in Fig. 5(e) and (f) for the Z1 tetramer, and in Fig. 5(g) and (h) for the Z2 tetramer. The largest curvature for Z1 (α = 96°) is found at 92 ns, while in Z2 a larger maximum angle (α = 121°) is found at around 19.2 ns. It is also noticed that in the Z2 tetramer after simulation (Fig. 5(g)), the second and fourth TPPS4 residues were rotated by ∼270° compared with the initial Z2 tetramer (Fig. 5(b)). Hence, our results show that TPPS4 forms a curved structure. Meanwhile, El-Hachemi et al.29 determined by X-ray and electron diffraction methods that H4TPPS4−2 forms sheets along the [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01] plane direction. According to their results, each porphyrin molecule is slightly rotated. Moreover, the porphyrin macrocycle is almost perpendicular to this plane. It causes a decrease in the symmetry in the structure on the plane mentioned above. Due to these reasons, parallel dimers are arranged as π-stacks. However, we cannot compare these results directly because we use different protonation patterns of TPPS4 (our porphyrin is electrically neutral, while the authors investigated the diacid form). Moreover, these authors investigated the crystal architecture of TPPS4, while we simulated TPPS4 tetramers solvated with a water box.
01] plane direction. According to their results, each porphyrin molecule is slightly rotated. Moreover, the porphyrin macrocycle is almost perpendicular to this plane. It causes a decrease in the symmetry in the structure on the plane mentioned above. Due to these reasons, parallel dimers are arranged as π-stacks. However, we cannot compare these results directly because we use different protonation patterns of TPPS4 (our porphyrin is electrically neutral, while the authors investigated the diacid form). Moreover, these authors investigated the crystal architecture of TPPS4, while we simulated TPPS4 tetramers solvated with a water box.
In order to qualitatively assess whether this permanently curved and fluctuating structure is feasible, we performed absorption spectra calculation using the Frenkel exciton model, which has been successfully used for calculating absorption and CD.30
Due to its structural symmetry, TPPS4 has two degenerate optical transitions for each absorption band. Two absorption bands are mostly considered for this type of molecules,21 thus leading to four transitions per molecule.
The TPPS4 molecule would have C4 symmetry if hydrogen atoms were ignored. Only the electrons of the porphyrin ring are optically active. Hence, the protonation state of distant SO3 groups should not affect significantly the optical transitions. For such symmetry all electronic excitations are doubly degenerate with perpendicular, e.g.x and y, transition dipoles in the symmetry plane. The exact orientation of these dipoles is irrelevant, because for degenerate transformation the two quantum basis states could be used to construct equivalent “twisted” basis functions as their two linear superpositions. The two basic transitions can be conveniently placed along the four nitrogen atoms.
However, the Z1 and Z2 forms of the TPPS4 molecule have reduced symmetry since, during the MD run, the molecular geometry fluctuates. Thus, an arbitrary transition dipole placement does not hold, so we have considered two models for dipole configurations. Consider a single molecule. Considering two absorption bands (Q and B), two transitions per single absorption band, there are four transitions per molecule with four transition dipoles. The two dipoles of the Q band are perpendicular, while the other two dipoles of the B band are also perpendicular, and the orientation of the Q dipole with respect to the B dipole is not defined. Perpendicular transition dipoles can be placed along lines connecting opposite nitrogen atoms (giving two perpendicular directions). Additionally, we can consider directions which are diagonal to the lines connecting the nitrogen molecules. Consequently, for the two absorption bands we can consider two models for transition dipole orientations, as shown in Fig. 6: two of them are perpendicular to the other two. In both models the transition dipoles of the Q band are perpendicular, and the transition dipoles of the B band are perpendicular. However, in model I transition dipoles of the B band make a 45° angle with transition dipoles of the Q band, while in model II transition dipoles of the B band have the same directions as transition dipoles of the Q band. As the molecules fluctuate along the trajectory, the transition dipole orientations (and angles between them) slightly fluctuate, making these two models not equivalent.
The given set of dipole vectors of a single molecule (model I and model II) are used for all four molecules in the tetramers. Note that all parameters except the molecular transition energies and transition dipole amplitudes are fluctuating along the MD trajectory. Consequently, the resonant couplings fluctuate along with the transition dipole orientations and intermolecular distance fluctuations.
The calculated absorption and CD spectra are averaged along the MD trajectory. For reference, in Fig. 7 and 8(c and f) we present the calculated nearest-neighbour coupling constants, averaged across the Hamiltonian matrix for the same kind of interactions: we thus have three types: Q–Q, mixed Q–B and B–B couplings. It can be observed that average values can be established for Z1 monomers and relative fluctuations for all types of couplings are the same. Z2 monomers show a slightly larger variation of the couplings. The dynamics of the average strength of the intermolecular couplings of the Q–Q, B–B and mixed Q–B bands in Fig. 7 and 8(c and f) correlate with the change in both the Z1 and Z2 tetramer's curvature α angles (Fig. 5c and d).
Absorption and CD spectra for both Z1 and Z2 tetramers, for two dipole models (in Fig. 6), are shown in Fig. 7 and 8(a, b, d and e) and are summarized in Table 4. Both models show almost identical absorption with splitting of the B band with a strong peak at ∼470 nm. Another peak is at 428 nm for the Z2 type tetramer, while this feature further splits in the Z1 tetramer. The molecular transition is at 435 nm (see model parameters below, eqn (2)). The 470 nm band in the spectra is often denoted as the J band, while the 425 nm feature is the H band.
| Absorption spectra | CD spectra | ||||
|---|---|---|---|---|---|
| Modela | Tetramer | B (nm) | Q (nm) | B (nm) | Q (nm) |
| a Model by orientation of the optical transition dipole vectors (see Fig. 6). b Boldface denotes the strongest spectral peaks. c “—” denotes a spectral peak with no intersect with y = 0. | |||||
| I | Z1 | 413, 428, 440, 470b | 652 | 425, 434, 448 | —c |
| Z2 | 428, 466b | 650 | 428, 437, 475, 480 | 653 | |
| II | Z1 | 413, 428, 440, 470b | 652 | 425, 434, 448 | —c |
| Z2 | 428, 466b | 650 | 421, 428, 437, 461 | 652 | |
The Q band has a much simpler profile (the fine sub-peaks are not resolved with the given linewidth) showing a single peak at ∼650 nm which is red-shifted from molecular transition at 646 nm (see model parameters below, eqn (2)). Most notably, there is a difference between Z1 and Z2 tetramers in absorption only in the B band region.
CD spectra are much more sensitive to fine structure fluctuations, which is confirmed by the calculated result: fine variations of the spectral line incomplete convergence with respect to fluctuations; however, the spectral variations are small and the trend is clear. The Z1 tetramer in B band demonstrates a − + pattern for model I and a + − + pattern for model II (from blue to red spectral region). Only a negative feature is observed for both models in the Q band. The Z2 tetramer demonstrates a + − + pattern for model I dipole configuration and a − + − pattern for model II dipole configuration in the B region, whereas this tetramer demonstrates a + − obvious pattern for both models in the Q band. The crossing points of the zero amplitude line are listed in Table 4.
TPPS4 molecules in acidic conditions are known to self-organize into extended cylindrical structures as confirmed by experiments. In our previous study we used quantum mechanical optimization of molecular dimers to sort out possible structures which are stable and can grow into larger structures. However, the quantum mechanical optimization can hardly be extended to large structures. As a result, here we switch to classical molecular dynamics.
Using MD simulations, we seek to reveal the main molecular building blocks which lead to formation of the structures. MD relies on classical force fields, which are parameterized for specific molecular bonding and intermolecular interactions. The force field has been extensively parameterized for molecular short-range properties (bond lengths, valence angles, …).28,31 However, optically active molecular chromophores usually contain extended conjugated structures, which have unique electronic configurations. Accordingly, the force field has to be adjusted for the given chromophores.
TPPS4 molecules possess intricate cyclic structures. Structurally, a porphyrin molecule comprises four pyrrole rings. Each of these rings contains one nitrogen and four carbon atoms connected by –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) linkages. The center of the porphyrin ring in TPPS4 binds protons. Symmetric configuration of bonds leads to formation of cyclic 18 π-electron ring system, which connects the four pyrrole rings and their linkers. According to our calculations, direct application of general Amber force field (GAFF) leads to a molecular structure which significantly deviates from the quantum chemistry optimized result. Hence, reparametrization has been performed. Molecular geometry optimization using classical force fields leads to an almost perfect match of the molecular optimal geometry.
linkages. The center of the porphyrin ring in TPPS4 binds protons. Symmetric configuration of bonds leads to formation of cyclic 18 π-electron ring system, which connects the four pyrrole rings and their linkers. According to our calculations, direct application of general Amber force field (GAFF) leads to a molecular structure which significantly deviates from the quantum chemistry optimized result. Hence, reparametrization has been performed. Molecular geometry optimization using classical force fields leads to an almost perfect match of the molecular optimal geometry.
Linear Z1 and Z2 tetramers were constructed and the tetramer structures were optimized in an explicit water box. This leads to a specific structure; however, the structure cannot be understood as necessarily the most optimal. It is merely one possibility because at room temperature the solvent has sufficient thermal energy to shift the molecule out of the potential minimum and a variable structure becomes a better representative of the typical structure.
A global structure parameter becomes necessary to introduce for fluctuating structure characterization. Schifino et al. used a tilting angle between TPPS4 porphyrin rings.24 We thus use a similar parameter – the curvature α angle; however, it covers more extended geometrical information. The tilting angle in Schifino et al.'s study of Rac-H4TPPS42− tetramer varies more than our α angle (and structures) of Z1 and Z2 tetramers. However, we cannot compare these results directly because we performed plain molecular dynamics simulations, while Schifino et al. performed enhanced sampling simulations with parallel bias metadynamics.24 Moreover, our structures have a different protonation pattern (our chromophore is electrically neutral). Their main result is that axial chirality affects the chiral self-assembly of the H4TPPS42− porphyrin in larger supramolecular structures. On the other hand, our Z1 and Z2 tetramers are “racemic”, i.e. they have 2 positive and 2 negative dihedral angles and one tetramer, which as determined by the above-mentioned authors is also racemic.
Our previous calculations based on dimers did not reveal any tilt between neighbouring molecules. We thus find that larger molecular structures in explicit water are necessary to reveal structural curvature. The important result here is that such curvature remains conserved at room temperature in the presence of extensive fluctuations. Such formation hence could be behind the formation of cylindrical structures when the number of molecules increases. As was mentioned above, TPPS4 tetramers form structures with a permanent curve angle (α) of approximately 30°. Longer aggregates would tend to curve into a ring. A full ring of the nanotube structure spans 360°. Therefore, if four molecules correspond to ∼30°, then 48 molecules will correspond to 360°, indicating that the nanotube ring should contain approximately 48 TPPS4 molecules. This result aligns well with literature data, which suggest that aggregates typically contain 60–70 monomers in a ring, as determined by comparing experimentally measured and theoretically calculated results.12,16 However, at least two-dimensional larger structures may be necessary to characterize.
The most direct correlation to experiment can be performed by considering spectra of molecular structures. Indeed the spectroscopic properties significantly depend on intermolecular resonant interactions. This forms the basis of the Frenkel exciton model, which assumes different molecules interacting only electrostatically and electron exchange is not included. The model allows calculating the spectra with such restrictions, which usually yield sufficiently accurate results.
Using MD variation of the structure yields variation of the spectra. The trajectory thus has to be sufficiently long so that the calculated spectra cover the most probable structure variations and shows the converged result. We have checked the convergence of the spectra by inspecting the variation of the spectra with the number of frames included. In Fig. 9 we show that the number of frames included in our calculations only slightly affects the intensity of the spectral peaks in the B band (the Q band remains constant). We can see in Fig. 10 that the number of frames that we use in our theoretically calculations only slightly changes the intensity of the B band in the CD spectrum as well. This confirmation of CD is very important as the CD spectrum is very tightly related to molecular structure variations as it is directly induced by structural chirality. As independent molecules in the dipole approximation are assumed to be non-chiral, the CD spectrum becomes induced by global properties of the tetramer. Hence, the CD spectrum directly indicates the effect of the chiral curvature of the structure.
 | ||
| Fig. 9 Calculated B band of the Z1 tetramer of model I averaged over different numbers of frames. For definitions of the models, see Fig. 6. | ||
 | ||
| Fig. 10 Calculated B band CD spectra of the Z1 aggregate of model I averaged over different numbers of frames. For definitions of the models, see Fig. 6. | ||
One of the targets is related to defining the most probable zwitterionic structure by comparing to experimental data. In our previous study, we determined that the theoretically calculated results for the monomers and dimers support the experimentally observed spectral shift when the pH values decrease from pH 7.1 to pH 1.0 (ref. 21) (on the other hand, the spectral shift obtained by quantum chemical methods does not coincide with experimentally measured data when the pH decreases from 1.0 to −1.0). Our previous studies revealed that the J(0)3 dimer (which forms from the Z2 monomer) is the most likely initial structure to form larger structures at pH 1 (ref. 21) (see corresponding dimer scheme in Fig. 2(b) inside the orange rectangle). In our present calculations in Fig. 5(c and d) we find that the Z1 tetramers are slightly more compact than Z2 – the variation of the curvature angle of the Z1 tetramer is smaller and the angle itself is smaller, hence the Z2 tetramer is more curved. As the result the intermolecular interactions (e.g. B–B type in Fig. 7(c and f)) in the Z2 tetramer are slightly smaller compared to that in the Z1 tetramer. The difference in interactions results in a slightly distinct B band between the Z1 and the Z2 tetramers: the B band of the Z1 tetramer shows four distinct peaks (with the strongest peak at 470 nm), while only two peaks are resolved in the case of the Z2 tetramer. Our present calculations of absorption spectra of Z1 and Z2 tetramers, corresponding to pH 1.0, show that the peaks in the B and Q regions become red-shifted (Table 4) compared to that of the monomers (Table 1 (ref. 21)). These results very well coincide with literature data.14 Eventually, the difference between absorption of Z1 and Z2 tetramers is quite small; however, the larger red-shift of the Z1 tetramer better represents the experiment, where the aggregate-related peak (B band) was identified at 490 nm. This does not rule out the significance of the Z2 form. However, more research on this topic needs to be undertaken in order to know whether Z1 or Z2 TPPS4 forms are more probable candidates to form large aggregates, or whether mixed Z1–Z2 aggregation is also possible.
In many of the spectra of J-aggregated TPPS4 porphyrins reported so far in the literature (see e.g. ref. 32 and 33), the spectral features at 490–492 nm are rather sharp and are often used as aggregate markers. The aggregate-related peak in ref. 21 is broad and relatively small. We can easily show that this broad linewidth is related to variation of the intermolecular couplings or to different levels of aggregation. As an example, we have used our MD trajectory and calculated spectra including only dimers and trimers by neglecting other chromophores. We can see that when we decrease the number of molecules in our model, the gap between the most pronounced peaks of the B band decreases and becomes closer to the shape expected in a monomer. Even when considering a dimer, the splitting of the B band is still very pronounced (Fig. 11). If the large J-aggregates have a peak at 490 nm, the smaller ones should be somewhat more blue-shifted. However, from Fig. 11, the tetramer already shows a significantly red-shifted band compared with monomers (and dimers). As such, it may be that the majority of the red shift is already present at the level of the tetramer. We also note that the spectra of ref. 21 were done at small concentrations. Spectroscopic characteristics and changes with respect to the number of molecules (Fig. 11) are the same for Z1 and Z2.
 | ||
| Fig. 11 Calculated absorption spectra of a monomer, dimer and tetramer of Z1 aggregate model I. For definitions of the models, see Fig. 6. | ||
The most sensitive spectroscopic structure probable is the CD spectrum. The CD spectra are difficult to compare to experimental results as the TPPS4 tetramers may exist only at very low concentrations, too low for quality CD measurements. Hence, we did not find quality experimental CD spectra of TPPS4 at very low concentrations. Additionally, the CD spectra are dependent not only on the solute but also on the solution environment, and induced dichroism is often obtained,34,35 which has been observed for TPPS4-type J-aggregates when the pH of the solution is about 1.36 On the other hand, this does not mean that J-aggregates under these conditions are not chiral. Most probably the solution involves racemic mixtures of chiral aggregate molecules and their CD signals compensate for each other. For this reason, the calculated CD spectra are presented as the reference spectra, which can be used for future studies.
The racemization phenomenon of TPPS4 was investigated experimentally by D'Urso et al.37 They determined that the intensity and sign of the CD signal in H2TPPS4−4 and H4TPPS4−2 spectra dynamically depend on mechanical stirring direction (clockwise and counterclockwise). Hence, the equilibrium of a racemic TPPS4 mixture shifts by stirring. Moreover, the chirality also depends not only on mechanical stirring but also on the reagent mixing order, i.e., whether porphyrin is added as the first or as the last reagent in the solution.38 Furthermore, it was determined that counter-anions probably influence the precursor (initial dimer) formation and the stabilization of the oligomeric structures of TPPS4. The sign and intensity of the CD signal also depend on the hydrogen bonding ability of the various anions.39
It must also be taken into consideration that our Hamiltonian calculation approach is approximate – we include only dipole–dipole interactions. Higher-level intermolecular coupling calculation can be performed using the Poisson-TrEsp approach,40 which has higher accuracy at small intermolecular distances, i.e. for nearest-neighbour molecules in the aggregates. Additionally, the description of the dielectric environment is improved by self-consistent solution of the Poisson equation, which may be relevant for our system since molecules have non-uniform charge distribution. However, these developments for TPPS4 aggregates would be important for direct comparison with experiments, while here we present the qualitative estimations.
All in all, this study employs MD simulations for modelling molecular aggregation, which is a nontrivial computation problem. MD simulations still lack reliability for extrapolating and predicting structures or processes. Our study is thus tightly correlated with experimental observations and therefore provides the missing molecular-level link towards formation of TPPS4 nanotubes. For this purpose, the highly symmetric metal-free porphyrin macrocycle was parametrized, i.e. GAFF parameters for TPPS4 were determined. A curvature angle α was introduced for global structure characterization. Such analysis could help to analyse larger chromatophore (TPPS4 and similar) aggregates.
Regarding the reliability, the results were correlated with experimental observations: not only absorption and CD spectra but also dynamics of the average strength of the intermolecular couplings of the Q–Q, B–B and mixed Q–B bands improve the prediction of aggregate spectroscopic characteristics, which could be related with quantum energy wiring efficiency. Our complex approach to the problem of molecular cooperative quantum response is a solid step towards bottom-up approach molecular aggregation.
Computational details
The zwitterionic form of TPPS4 (H6TPPS40) dominates at a pH ≈1.8,21,41 There are two types of zwitterionic monomers: the “opposite” zwitterion, where SO3H groups are opposite (which we denote as Z1, as we did in our previous article21), and the “adjacent” zwitterion, where SO3H groups are adjacent (denoted as Z2 (ref. 21)). The initial TPPS4 structures were constructed by hand using the GaussView 6.1 software package.42Ab initio QM geometry optimization of the zwitterionic TPPS4 Z1 and Z2 monomers (see Fig. 2(a–c) inside blue rectangles) was performed to determine the molecular configuration using the DFT B3LYP method along with the Pople 6-311G(d,p) basis set. The polarizable continuum model (PCM) was used to evaluate the influence of water (solvent).43 All QM calculations were performed using the Gaussian 16 software package.44The MM and MD methods are based on optimized inter-atom interaction potentials, commonly referred to as an atomic force field. Classical FF, including one of the most widespread GAFF, characterizes two types of interactions: chemically bonded and non-bonded. Parameters of bonded interactions characterize bond lengths, bond angles, and dihedrals (torsional) angles. Hence, covalent bond stretching and valence angle bending are parameterized using the harmonic models, while a harmonic function is used for dihedral twisting energy. The non-bonded interactions are characterized by electrostatic and van der Waals terms.45,46
GAFF has parameters for most organic molecules made of C, N, O, H, S, P, F, Cl, Br and I.47 However, for some molecular systems, the parameters must be revised due to the extended conjugation of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds in pigments.48 Since TPPS4 has a complex electron delocalization it is necessary to adjust the FF parameters. There is little published data about tetrapyrroles parametrization. To date, only naturally found tetrapyrrole- like pigments have been parametrized for MM: Guerra et al. performed chlorophyll a and pheophytin a FF parametrization,28 while Zhang et al. developed new FF parameters for metalloporphyrin heme b.31 However, these parameters do not apply to TPPS4 since chlorophylls have different macrocycles and symmetry. There is no published FF for synthetic tetrapyrroles such as TPPS4, which is structurally more symmetric than, e.g. chlorophylls (especially the Z1 form). In the present case several atom types, bond lengths, valence angles and dihedral angles were adjusted for bonded interactions for both Z1 and Z2 zwitterions. The obtained set of parameters is combined in the ESI.† Atomic partial charges of TPPS4 were derived by fitting the electrostatic potential (ESP) of the molecule using the restrained electrostatic potential (RESP) model.47,48 All parametrization and MM calculations were performed with AMBER 22 software package.49
C bonds in pigments.48 Since TPPS4 has a complex electron delocalization it is necessary to adjust the FF parameters. There is little published data about tetrapyrroles parametrization. To date, only naturally found tetrapyrrole- like pigments have been parametrized for MM: Guerra et al. performed chlorophyll a and pheophytin a FF parametrization,28 while Zhang et al. developed new FF parameters for metalloporphyrin heme b.31 However, these parameters do not apply to TPPS4 since chlorophylls have different macrocycles and symmetry. There is no published FF for synthetic tetrapyrroles such as TPPS4, which is structurally more symmetric than, e.g. chlorophylls (especially the Z1 form). In the present case several atom types, bond lengths, valence angles and dihedral angles were adjusted for bonded interactions for both Z1 and Z2 zwitterions. The obtained set of parameters is combined in the ESI.† Atomic partial charges of TPPS4 were derived by fitting the electrostatic potential (ESP) of the molecule using the restrained electrostatic potential (RESP) model.47,48 All parametrization and MM calculations were performed with AMBER 22 software package.49
Next, the dimers (see Fig. 2(a–c) inside orange rectangles, respectively) were constructed from TPPS4 Z1 or Z2 monomers (see Fig. 2(a–c) inside blue rectangles, respectively). Each dimer was solvated in a truncated octahedral box of water (one dimer in one box) with a 3-charge, 4-point rigid water model (OPC) with a distance of 10 Å between the solute and the edges of the box.50
The solvated structures were first optimized using 500 steps of steepest descent (SD) followed by 1500 steps of conjugate gradient (CG). TPPS4 aggregation experiments are usually performed at room temperature.3,51,52 Due to this reason, after minimization, the molecular systems were heated to 298.15 K for 50 ps constant-volume, constant-temperature (NVT) ensemble simulations. Positional restraints (4 kcal mol−1 A−2) were applied to all non-hydrogen atoms of the TPPS4 dimers (and also tetramers). Next, a 1000 ps constant-pressure, constant-temperature (NPT) ensemble equilibration at 298.15 K was performed applying the same constraints on the structures. Finally, a production step of 100 ns at 298.15 K in the NPT ensemble was performed. A time step of 2 fs was used in combination with the SHAKE algorithm. Temperature and pressure were controlled with a Langevin thermostat and a Monte Carlo barostat as implemented in AMBER 22. Particle-mesh Ewald algorithm (PME) electrostatics with a short-range cutoff of 10 Å were used for all simulations.53 Asymmetrical flat-bottom distance restraints were employed to limit the configurational space available to the tetramers. Specifically, these restraints were applied between the H(N) atoms of the porphyrin ring and the oxygen atoms of the sulphonic groups. The potential was left unchanged for distances below 9 Å to allow for a rearrangement of the tetramer structure while avoiding a complete dissociation of monomers (this was never observed for stable initial configurations).
The tetramers were constructed based on the structures extracted from dimer simulations (see Fig. 2(a) and (b)). Two linear Z1 and Z2 tetramers (see Fig. 5(a) and (b)) were constructed from the dimers and their MD simulation was performed. In the Z1 tetramer due to C2 symmetry, both negative sulfonate groups can be positioned to interact with the positively charged porphyrin ring of its neighbour (see Fig. 5(a)), while in the Z2 tetramer only one negative sulfonate group can be interacting with the positively charged porphyrin ring (see Fig. 5(b)). The Z1 and Z2 tetramers were solvated in a truncated octahedral box of water before MD simulation. At least 12 Å were kept between the TPPS4 tetramers and the edges of the box. The simulation was run using the same conditions as for the dimers.
MD analysis was performed by using the CPPTRAJ54 module of AmberTools. For trajectory visualization the Visual Molecular Dynamics (VMD) software was employed.55 Typical obtained structures are shown in Fig. 5.
The two transitions are responsible for the Q band (600–700 nm), while the other two are related to the B (Soret) band (400–500 nm).56 Consequently, the electronic Hamiltonian (unique for each MD frame) is given by
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 cm−1 → 646 nm (Q band) and E3,4 = 22
485 cm−1 → 646 nm (Q band) and E3,4 = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 cm−1 → 435 nm (B band). These transition energies were chosen to match peaks in the experiment at low concentrations (c = 3 × 10−6 mol L−1) at pH 1,21 when monomers are expected to dominate the spectra.
987 cm−1 → 435 nm (B band). These transition energies were chosen to match peaks in the experiment at low concentrations (c = 3 × 10−6 mol L−1) at pH 1,21 when monomers are expected to dominate the spectra.
Dipole–dipole intermolecular interaction was assumed for off-diagonal elements of the Hamiltonian between different molecules:
 | (3) |
The matrix of transition dipoles forms the aggregate polarization operator, which can be written in the following form:
 | (4) |
The exciton states are calculated by solving the Hamiltonian eigenvalue equation:
| Ĥψ = εψ, | (5) |
 | (6) |
 is the exciton transition dipole, where ψni,e is the eigenvector component of excitonic state e. Similarly, the CD spectrum25,26 is given by:
is the exciton transition dipole, where ψni,e is the eigenvector component of excitonic state e. Similarly, the CD spectrum25,26 is given by: | (7) |
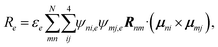 | (8) |
Conclusions
We performed QM and MM optimization of the TPPS4 zwitterionic form (Z1 and Z2) monomers. The GAFF description of these monomers was revised. Several parameters – atom types, bond lengths, valence angles and dihedral angles – were adjusted to improve the description of the Z1 and Z2 structures. Two linear TPPS4 Z1 and Z2 tetramers were constructed and their MD simulation was performed. Absorption and CD spectra of these tetramers were also calculated. It was determined that both Z1 and Z2 tetramers form on average a curved chiral structure, i.e. the four monomers in tetramers (both Z1 and Z2) do not stay on a perfect line. According to our results, the ring should contain 48 molecules of TPPS4 in the cylindrical structures. The Z1-based structure is more straight and more compact. Accordingly, intermolecular couplings in the Z1 tetramer are larger. A comparison was performed of Z1 and Z2 tetramers' absorption spectra with the measured spectra from a previous published article. Our analysis of results demonstrates that the larger peak shifts of the Z1 tetramer's spectra are more similar to the experimental data; however, other configurations can be possible as well.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Laura Baliulyte: writing – original draft (lead); writing – review & editing (equal); visualization (equal); methodology (equal); investigation (equal); formal analysis (equal); conceptualization (equal). Eimantas Urniezius: writing – original draft (equal); visualization (equal); methodology (equal); investigation (equal); formal analysis (equal). Vytautas Bubilaitis: methodology (supporting); formal analysis (supporting). Mindaugas Macernis: writing – review & editing (supporting). Lorenzo Cupellini: supervision (equal); writing – review & editing (lead); visualization (supporting); methodology (equal); conceptualization (equal). Darius Abramavicius: supervision (lead); writing – original draft (equal), writing – review & editing (lead); methodology (equal); conceptualization (equal); funding acquisition (lead); project administration (lead).Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
LB has been partly supported under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme and the computer resources and technical support provided by CINECA. LB, VB, MM and DA were supported by the Research Council of Lithuania (Grant No. S-MIP-23-48). Most computations were performed using resources at the supercomputer “VU HPC” Sauletekis of Vilnius University at the Faculty of Physics.Notes and references
- B. Hemavathi, V. Jayadev, S. C. Pradhan, G. Gokul, K. Jagadish, G. K. Chandrashekara, P. C. Ramamurthy, R. K. Pai, K. N. N. Unni, T. N. Ahipa, S. Soman and R. G. Balakrishna, Sol. Energy, 2018, 174, 1085–1096 CrossRef CAS.
- J. L. Banal, B. Zhang, D. J. Jones, K. P. Ghiggino and W. W. H. Wong, Acc. Chem. Res., 2017, 50(1), 49–57 CrossRef CAS PubMed.
- G. G. Parra, D. S. Correa, E. Silveira-Alves, L. M. Almeida, M. A. R. Souza, L. De Boni, L. Misoguti, C. R. Mendonça, S. C. Zílio, N. M. B. Neto, I. E. Borissevitch and P. J. Gonçalves, Spectrochim. Acta, Part A, 2021, 261, 120063 CrossRef CAS PubMed.
- S. Kwiatkowski, B. Knap, D. Przystupski, J. Saczko, E. Kędzierska, K. Knap-Czop, J. Kotlińska, O. Michel, K. Kotowski and J. Kulbacka, Biomed. Pharmacother., 2018, 106, 1098–1107 CrossRef PubMed.
- Y. Ferro, S. Maurotti, M. G. Tarsitano, O. Lodari, R. Pujia, E. Mazza, L. Lascala, R. Russo, A. Pujia and T. Montalcini, Nutrients, 2023, 15, 2666 CrossRef CAS PubMed.
- L. Barazzuol, R. P. Coppes and P. van Luijk, Mol. Oncol., 2020, 14(7), 1538–1554 CrossRef PubMed.
- M. A. Castriciano, A. Romeo, V. Villari, N. Micali and L. M. Scolaro, J. Phys. Chem. B, 2003, 107(34), 8765–8771 CrossRef CAS.
- T. Kim, S. Ham, S. H. Lee, Y. Hong and D. Kim, Nanoscale, 2018, 10(35), 16438–16446 RSC.
- L. P. F. Aggarwal and I. E. Borissevitch, Spectrochim. Acta, Part A, 2006, 63(1), 227–233 CrossRef.
- I. G. Occhiuto, R. Zagami, M. Trapani, M. A. Castriciano, A. Romeo and L. M. Scolaro, Molecules, 2020, 25(23), 5742 CrossRef CAS PubMed.
- J. M. Short, J. A. Berriman, C. Kübel, Z. El-Hachemi, J. V. Naubron and T. S. Balaban, ChemPhysChem, 2013, 14(14), 3209–3214 CrossRef CAS PubMed.
- R. Rotomskis, R. Augulis, V. Snitka, R. Valiokas and B. Liedberg, Hierarchical structure of TPPS4 J-aggregates on substrate revealed by atomic force microscopy, J. Phys. Chem. B, 2004, 108(9), 2833–2838 CrossRef CAS.
- G. Pescitelli, L. Di Bari and N. Berova, Chem. Soc. Rev., 2014, 43, 5211–5233 RSC.
- T. Kobayashi, J-Aggregates, World Scientific Publishing Company, Singapore, 1996 Search PubMed.
- Y. Xiu, X. Zhang, Y. Feng, R. Wei, S. Wang, Y. Xia, M. Cao and S. Wang, Nanoscale, 2020, 12(28), 15201–15208 RSC.
- R. Augulis, J. Tamuliene, A. Tamulis and R. Rotomskis, Solid State Phenom., 2004, 97, 225–228 Search PubMed.
- M. Pleckaitis, F. Habach, L. Kontenis, G. Steinbach, G. Jarockyte, A. Kalnaityte, I. Domonkos, P. Akhtar, M. Alizadeh, S. Bagdonas, V. Karabanovas, G. Garab, R. Rotomskis and V. Barzda, Nano Res., 2022, 15(6), 5527–5537 CrossRef CAS.
- F. Sabuzi, M. Stefanelli, D. Monti, V. Conte and P. Galloni, Molecules, 2019, 5(1), 133 CrossRef.
- G. G. B. Alves, F. C. Lavarda, C. F. O. Graeff and A. Batagin-Neto, J. Mol. Graphics Modell., 2020, 98, 107609 CrossRef CAS PubMed.
- K. Ishii, S. Hattori and Y. Kitagawa, Photochem. Photobiol. Sci., 2020, 19(1), 8–19 CrossRef CAS.
- L. Baliulyte, D. Abramavicius, S. Bagdonas, A. Kalnaityte, V. Poderys, R. Rotomskis and V. Barzda, AIP Adv., 2023, 13(10), 105011 CrossRef CAS.
- S. Bottaro and K. Lindorff-Larsen, Science, 2018, 361, 355–360 CrossRef CAS PubMed.
- S. Maity and U. Kleinekathöfer, Photosynth. Res., 2023, 156(1), 147–162 CrossRef CAS PubMed.
- G. Schifino, M. Fortino, L. M. Scolaro and A. Pietropaolo, Mol. Syst. Des. Eng., 2023, 8(12), 1512–1519 RSC.
- F. Bertocchi, C. Sissa and A. Painelli, Chirality, 2023, 35(10), 681–691 CrossRef CAS PubMed.
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, 2004 Search PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 2001, 222, 2001 Search PubMed.
- F. Guerra, S. Adam and A. N. Bondar, J. Mol. Graphics Modell., 2015, 58, 30–39 CrossRef CAS.
- Z. El-Hachemi, C. Escudero, F. Acosta-Reyes, M. T. Casas, V. Altoe, S. Aloni, G. Oncins, A. Sorrenti, J. Crusats, J. L. Campos and J. M. Ribó, J. Mater. Chem. C, 2013, 1(20), 3337–3346 RSC.
- S. M. Vlaming, R. Augulis, M. C. A. Stuart, J. Knoester and P. H. M. Van Loosdrecht, J. Phys. Chem. B, 2009, 113(8), 2273–2283 CrossRef CAS PubMed.
- L. Zhang, D. A. Silva, Y. Yan and X. Huang, J. Comput. Chem., 2012, 33(25), 1969–1980 CrossRef CAS.
- O. Ohno, Y. Kaizu and H. Kobayashi, J. Chem. Phys., 1993, 99(5), 4128–4139 CrossRef CAS.
- A. S. R. Koti, J. Taneja and N. Periasamy, Chem. Phys. Lett., 2003, 375(1–2), 171–176 CrossRef CAS.
- R. Randazzo, M. Gaeta, C. M. A. Gangemi, M. E. Fragalà, R. Purrello and A. D'Urso, Molecules, 2019, 24(1), 84 CrossRef.
- M. A. Castriciano, D. Gentili, A. Romeo, M. Cavallini and L. M. Scolaro, Sci. Rep., 2017, 7, 44094 CrossRef CAS.
- L. Zeng, Y. He, Z. Dai, J. Wang, Q. Cao and Y. Zhang, ChemPhysChem, 2009, 10(6), 954–962 CrossRef CAS PubMed.
- A. D'Urso, R. Randazzo, L. L. Faro and R. Purrello, Angew. Chem., Int. Ed., 2010, 49(1), 108–112 CrossRef PubMed.
- A. Romeo, M. A. Castriciano, I. Occhiuto, R. Zagami, R. F. Pasternack and L. M. Scolaro, J. Am. Chem. Soc., 2014, 136(1), 40–43 CrossRef CAS PubMed.
- G. Occhiuto, R. Zagami, M. Trapani, L. Bolzonello, A. Romeo, M. A. Castriciano, E. Collini and L. M. Scolaro, Chem. Commun., 2016, 52(77), 11520–11523 RSC.
- T. Renger and F. Müh, Photosynth. Res., 2012, 111, 47–52 CrossRef CAS.
- U. Mazur and K. W. Hipps, J. Phys. Chem. C, 2018, 122(40), 22803–22820 CrossRef CAS.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- R. E. Skyner, J. L. McDonagh, C. R. Groom, T. van Mourik and J. B. O. Mitchell, Phys. Chem. Chem. Phys., 2015, 17(9), 6174–6191 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C. 01, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25(9), 1157–1174 CrossRef CAS.
- M. A. González, Force fields and molecular dynamics simulations, Collection SFN, 2011, 12, 169–200 CrossRef.
- C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97(40), 10269–10280 CrossRef CAS.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25(2), 247–260 CrossRef CAS PubMed.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, J. T. Berryman, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. A. Izmailov, K. Kasavajhala, M. C. Kaymak, E. King, A. Kovalenko, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, V. Man, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O'Hearn, A. Onufriev, F. Pan, S. Pantano, R. Qi, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, J. Wang, H. Wei, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York, S. Zhao and P. A. Kollman, Amber 2022, University of California, San Francisco, 2022 Search PubMed.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5(21), 3863–3871 CrossRef CAS PubMed.
- R. Augulis, V. Snitka and R. Rotomskis, Solid State Phenom., 2004, 97, 191–194 Search PubMed.
- V. Snitka, M. Rackaitis and R. Rodaite, Sens. Actuators, B, 2005, 109(1), 159–166 CrossRef CAS.
- T. Darden, L. Perera, L. Li and P. Lee, Structure, 1999, 7(3), R55–R60 CrossRef CAS.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9(7), 3084–3095 CrossRef CAS.
- W. Humphrey, D. Andrew and S. Klaus, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed.
- J. M. Ribó, J. M. Bofill, J. Crusats and R. Rubires, Chem. – Eur. J., 2001, 7(13), 2733–2737 CrossRef.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, New York, 1995 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5me00010f |
| This journal is © The Royal Society of Chemistry 2025 |