Computational screening analysis of iron zeolites for selectively capturing NO_x and CO over H₂O and CO₂

Abstract

This work aims at shedding light on the capture mechanisms of toxic atmospheric pollutants by zeolites. A comprehensive computational investigation has been conducted to evaluate the interaction energies of NO, NO₂, CO, CO₂, and H₂O with Fe²⁺ supporting both chabazite and mordenite zeolites using periodic density functional theory calculations. Si/Al ratio sets of {11, 5, 3} and {23, 11, 5} have been respectively chosen for chabazite and mordenite. Our findings show that both systems exhibit a thermodynamic preference for bonding NO and NO₂ over H₂O and CO₂. Moreover, ab initio molecular dynamics simulations at 300 K for the Fe-chabazite system with Si/Al = 3 confirm the adsorption of NO, NO₂ and CO even in the presence of H₂O molecules, and the radial distribution function was employed to understand how steam affects NO, NO₂ and CO bonding. CO₂ co-adsorption was eventually neglected in our study due to its low interaction energy. Finally, Bader charges and charge density differences were calculated to analyze bond elongation after adsorption and account for the regeneration of the substrate. Results show that low Si/Al ratios enhance the affinity for NO and NO₂ and favour the regenerability of the adsorbent. This study demonstrates that the utilization of zeolites containing iron as the compensating cation presents promising potential as effective adsorbents for capturing NO_x and CO in the presence of H₂O and CO₂ originating from diesel engine emissions within confined work environments.

---

Design, System, Application

Zeolites are widely recognized for their affordability and effectiveness as sorbents in various applications. In confined work environments, the emission of diesel exhaust gases poses significant health and safety risks due to exposure to nitrogen oxides and carbon monoxide. Removal of these pollutants from exhaust gas calls for engineering of an optimum sorbent for the selective trapping of NO, NO₂, and CO in the presence of H₂O and CO₂. To address this challenge, we computationally investigated several iron-based zeolites (with chabazite and mordenite structures) at varying Si/Al ratios to identify the most suitable candidate.

1. Introduction

Nitrogen oxides (NO_x), including nitrogen dioxide (NO₂) and nitric oxide (NO), and carbon monoxide (CO) are toxic air pollutants involved in climate change and production of photochemical smog, acid rain, and tropospheric ozone. These pollutants are also responsible for human health issues including asthma development, cardiovascular disease and cancer.^1–7 Among the sources of NO_x and CO, diesel engine vehicles^8,9 operating in building sites constitute a major threat for workers, especially in confined spaces lacking ventilation. In order to mitigate this significant issue, it is imperative to restrict the emissions of NO_x and CO to enhance the quality of working conditions for individuals.

Moreover, regulations established for example by the European Union (EU) aim to decrease the limit of NO_x and CO emissions, encouraging the adoption of sustainable technologies in vehicles. For environmental protection, according to Euro 6/VI (implemented in September 2014) vehicle emission standards, NO_x fumes from diesel vehicles cannot surpass the limit of 80 mg km⁻¹, a decrease of 56% with respect to Euro 5 adopted in September 2009.^10,11 In occupational settings, EU directive 2017/164 limits NO and NO₂ exposures per 8 hours (a full-time working day) to 2 and 0.5 ppm, respectively.¹² To meet these restrictions, several technologies have been proposed.

Catalytic treatment is the main method to reduce NO_x emissions. The two major representatives are NO_x storage reduction (NSR)^13,14 and selective catalytic reduction (SCR).^15,16 At maximum efficiency, SCR can reach almost 100% NO_x conversion to harmless N₂. However, high catalytic performances demand a temperature higher than 473 K.¹⁷ Since vehicles operating in construction sites work discontinuously throughout the day, they are subjected to many cold starts. In a gasoline engine, a three-way catalyst component located close to the engine-out position reaches its operating temperature quite quickly. In contrast, diesel engines produce lower-temperature exhaust gases showing extended cold starts, thus jeopardizing the low-temperature NO_x removal process.^18–20

The solution to low temperature de-NO_x consists in using materials capable of low temperature NO_x adsorption, based on thermodynamic selectivity. Two major categories of materials have been used for this purpose. The first one comprises passive NO_x adsorbers (PNAs), positioned upstream of the catalytic reactors for trapping NO_x and CO at low temperatures. Then, once the PNA is hot, gases are released, to be treated by catalysis.^21–25 The second one comprises cold start concept (CSC) catalysts, which catalyse NO_x conversion during capture, further enhancing the performance of the system.^26–28 Successful candidates include oxides such as CeO₂, ZrO₂, and WO₃. Their combinations achieved even greater physicochemical properties, not possible by a pure oxide.^21,22 These materials were used as transition metal promoters, with Pt and Pd being the most prominent metals for the application. They are highly efficient for low temperature NO_x reduction, even in the presence of steam, a strong NO_x inhibitor²¹ (with an NO_x concentration of 350–1000 ppm and H₂O content of about 10% (ref. 26 and 29)). However, these oxide-based materials are notoriously sensitive to sulphur poisoning due to the presence of sulphur oxides in the diesel exhaust gases, which degrades the catalysts. In addition, the MXene Y-doped Ti₂CO₂ was recently theoretically identified to be promising to remove N₂O and CO simultaneously.³⁰ Also, the adsorption energy of CO and CO₂ on Hf-doped Ti₂CO₂ were found to be equal to −1.447 eV (−139.6 kJ mol⁻¹) and −1.377 eV (−132.9 kJ mol⁻¹), respectively, with CO being strongly adsorbed.

Zeolites not only have been employed to address this issue with great efficiency, but also have shown excellent behaviour as Pd/Pt promoters for the low-temperature NO_x removal. Under realistic conditions, zeolites display high storage efficiencies combined with significant resistance to sulphur poisoning.^24,31,32 Furthermore, studies have assessed the efficiency of zeolites with various cationic loadings.^31,33–36 Indeed, measuring the Pt-group-cation/NO_x occupation ratio revealed that loadings <1 wt% perform far more cost-efficiently. However, transition metals belonging to other groups may even perform better at higher loadings. Furthermore, the stabilization of divalent cations in zeolites requires low Si/Al ratios,³⁷ resulting in much higher loadings. Hence, the increased cation-linked cost requires the exploration of cheap substitutes for Pd and Pt.

Besides NO_x, CO is one major environmental pollutant present in exhaust gases due to incomplete fuel combustion. Using a catalytic converter, not only carbon monoxide, but also hydrocarbons, volatile organic compounds, and methane in engine exhaust gases are removed by reaction with oxygen. However, as with SCR, the converter temperature must be high enough to handle these chemical species.³⁸ Therefore, investigations are required to find the best adsorbent to trap the gases at low temperature before the catalytic treatment of exhaust gases.³⁹

Recent theoretical studies on cation exchanged zeolites have identified some promising low-cost candidates for low temperature selective NO_x and CO removal in the presence of water.^40–42 By performing density functional theory (DFT) to study the thermodynamic selectivity and regenerability of faujasite with Si/Al = 47, Hessou et al.⁴⁰ proposed Cu^I as a valid choice for the three pollutants concerned with H₂O and CO₂. Extending this computational exploration to divalent cations, Daouli et al.⁴¹ found that Pt²⁺ and Pd²⁺ supporting faujasite, with Si/Al = 23, exhibit much higher affinity for NO_x than for H₂O. More recently, it has been predicted by DFT that Fe^II Y zeolites could be promising for this application.⁴² Iron appears as a promising candidate for selective removal of NO_x since it is much cheaper than platinum or palladium. Fe²⁺ exchanged zeolites have been used in the past for various applications. Sun et al.⁴³ used Fe exchanged ZSM-5 for the catalytic decomposition of N₂O. They identified various ferrous species with cationic or oligomeric nature, but high Fe²⁺ concentration was observed after a high temperature treatment in He at 1173 K. Panov et al.⁴⁴ used Fe-ZSM-5 for the room-temperature oxidation of hydrocarbons. Iron exchange is perfectly feasible as demonstrated by SCR of NO_x with a variety of zeolites such as mordenite (MOR), BEA, chabazite (CHA), and ZSM-5.^45–48

The present work aims at assessing the performances of MOR and CHA zeolites supporting divalent iron for low temperature NO_x and CO adsorption, versus water and CO₂. Si/Al ratios of 23, 11 and 5, as well as 11, 5 and 3, were selected for mordenite and chabazite respectively, in order to investigate at the DFT level the key microscopic phenomena affecting the adsorption process at 0 K. Ab initio molecular dynamics (AIMD) were finally performed on the most favourable structure at room temperature on the one hand, to harvest those microscopic details under operando conditions and on the other hand, to compare computational results with experiments carried out under dynamic conditions, in the future.

2. Methods and models

2.1 Computational details

Periodic DFT calculations were implemented through the Vienna ab initio simulation package (VASP)^49–53 with the projected augmented wave (PAW) method. Perdew–Burke–Ernzerhof (PBE) functional⁵⁴ – a particularly efficient representative of the generalized gradient approximation (GGA) – was chosen for the simulations. Grimme D2 (ref. 55–58) long-range dispersion correction was employed as a complement to GGA.^59,60 In particular, it was validated by Hessou et al.⁴⁰ over systems akin to ours. The dispersion contributions, which account for a small percentage of the interaction energy, range from 15 to 30 kJ mol⁻¹ (see ESI† data).

The Kohn–Sham equations were solved self-consistently until the energy difference between two consecutive cycles was less than 10⁻⁷ eV. For fixed cell parameters, as in similar systems,^40,61–63 the plane wave energy cut-off was set at 450 eV. The latter was raised to 1000 eV when the cell parameters were treated as dynamical variables. The reciprocal space was modelled with one k-point at the gamma point of the Brillouin zone. A Gaussian smearing of σ = 0.1 eV was applied to the band occupations to improve the total energy convergence. The atomic positions were optimized until the force differences between ionic steps were within 0.02 eV Å⁻¹ per atom.

GGA is the lowest acceptable level of DFT to describe the electron structure of systems with chemical bonds.⁶⁴ Its adequacy is severely challenged during the modelling of strongly correlated d and f orbitals of transition metals. Hubbard's on-site potential (U) is introduced to treat the overstabilization of the electrons occupying these orbitals.^65,66 In this work, we have applied the linear response method to calculate optimal U values for adequately sparse transition metals in chabazite and mordenite structures. The values obtained were 3.0 eV and 3.5 eV for mordenite and chabazite respectively and were adopted for all the calculations on the Fe atom. U in the VASP was set-up with LDAUTYPE = 3, setting J = 1. The single configuration interaction energy between gas and zeolite was computed as follows (eqn (1)):

ΔE_int = E_zeo-X − E_zeo − E_X (1)

where E_zeo-X expresses the energy of the adsorption of the gas with the zeolite, E_zeo, the energy of the bare zeolite, and E_X the energy of the gas.⁵⁹ Correspondingly, utilization of molecular dynamics (MD) for the calculation of interaction energy was performed by replacing the variables into relation (1) with their averages over a time interval of 50 ps after an equilibration period of 20 ps (eqn (2)). A time step of 1 fs was used.

ΔE_int = 〈E_zeo-X〉 − 〈E_zeo〉 − 〈E_X〉 (2)

A key point to account for the regeneration of the material is based on the intramolecular bond elongations of the gases due to their adsorption. These elongations are rationalized by their association with induced Bader charge transfer^67–71 and charge density differences. Bader charges were first calculated for the relaxed complex (Q_zeo-X), the zeolite omitting the gas, (Q_zeo), and the gas omitting the zeolite (Q_X), and their subtraction gave the charge difference due to adsorption ΔQ as (eqn (3)):

ΔQ = Q_zeo-X − Q_zeo − Q_X (3)

due to the corresponding adsorptions. Likewise, the electron density difference Δρ is defined as (eqn (4)):

Δρ = ρ_zeo-X − ρ_zeo − ρ_X (4)

2.2 Structures

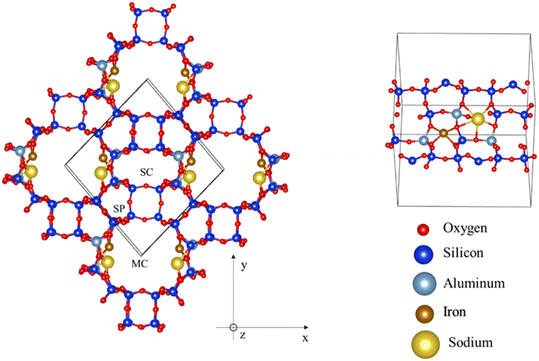
Zeolites are aluminosilicate porous materials comprising 4-coordinated Si and Al atoms bridged with 2-coordinated oxygens, forming solids with various ring-like arrangements. The aperture sizes of the rings are typically described by the number of tetrahedrally coordinated (T-atoms) Si and Al belonging in it. For instance, a ring composed of 4 T-atoms (and hence 4 O atoms too), is described as a 4-membered ring (4MR). Zeolites are classified according to their maximum aperture size into small – (≤8 MR), medium – (≤10 MR), large – (≤12 MR) and ultra large-pore ones. The introduction of Al atoms in the framework is accompanied by one electron deficit, which will be covered by a cation. This way, the appearance of 2 Al atoms in a close distance can be neutralized by the electron donation that an iron atom will introduce, appearing as an Fe²⁺ species.

Chabazite and mordenite zeolitic models were built by replacing Si with Al atoms in a manner that the Lowenstein rule is respected (two Al atoms cannot be bridged by only an O atom). Al atoms were close enough to iron cations, so that the latter exist in the form Fe²⁺.³⁷ Thus, the adsorptions sites are characterized by the nature of the cation, the shape and size of the pore, and the Al distribution around the cation.

The unit cells used were taken from the studies of Bučko et al.⁷² and Rey et al.⁷³ A low Si/Al ratio favours the presence of divalent-Fe in the framework of operando systems.³¹ Al distributions with high stability were implemented on the zeolites. The Si/Al ratios that have been considered for the purely Fe-supporting chabazite are 11, 5 and 3 giving rise to loadings of 3.7, 7.2 and 11.0 wt%, respectively. Regarding mordenite, the achievable Si/Al ratios of 23, 11 and 5 were explored,^37,74,75 with the first two structures carrying solely Fe, and the last one promoting Na too, giving the possibility for further testing. These formulations led to the loadings of 1.9, 3.7 and 3.7 wt%.

2.2.1 Chabazite. Chabazite is a naturally abundant small-pore zeolite. It consists of double 6-membered rings (D6R), forming prisms, which are themselves connected by 8MRs as shown in Fig. 1. Large volume spaces are formed, called supercages, which are of utter importance to this application, due to the accessibility they offer to the gases, through the sufficiently wide 8MR. Two locations are adopted for the localization of cations in chabazite throughout this study. They are based on the combination of high stability and availability offered: the first one in the middle of the six membered ring with at least 2 Al atoms in the ring, called site-II, and the second one in the 8MR, called site-IV. The unit cells used have a rhombohedral symmetry with a ≈ b ≈ c ≈ 13 Å and α ≈ β ≈ γ ≈ 60°.

Fig. 1 A representation of chabazite with Si/Al = 11. The names of the basic structural units are provided on-site.

2.2.2 Mordenite. Mordenite is an abundant material belonging to the category of large-pore zeolites. Its channel-based structure is composed of three fundamental units: an 8MR elliptical ring, which, when extended transversely, gives rise to the side channel (SC), a 5MR generating the side pocket (SP) in a similar way to SC, and – the most important part – a 12MR generating the main channel (MC) (Fig. 2). The main channel, being the most spacious channel hosts the majority of the gas stream,⁷⁶ and is consequently the most interesting for our investigation. The cations are hosted on ellipsoid 6MRs that offer the highest stability between the available choices^63,77 (Fig. 2). The Si/Al ratio of 23 considers only one cation on a ring with the most stable possible Al distribution, where the Al atoms retain a minimum distance of 3 T-atoms (configuration 1–4). 11 and 5, additionally to the adsorption site of 23, contain a ring with Al atoms staying at a minimum distance of 2 T-atoms (configuration 1–3, Fig. 2). According to our findings, a minor decrease in stability results in a slight increase of the interaction energy between the gas and the cation. The unit cells used for mordenite are slightly distorted tetragonal, with a ≈ b ≈ 13.6 Å, c ≈ 15 Å and α ≈ β ≈ 90°, γ ≈ 83°.

Fig. 2 A representation of mordenite with Si/Al = 5, with the channels denoted with labels is presented on the left side, from an x–y plane perspective. Three different channels are available: SC, with an opening of 8 tetrahedral atoms, SP with 5 and MC with 12, being the most spacious, thus the most interesting for us. The smaller figure on the right side depicts the inner part of the main channel, highlighting iron in a 6MR, 1–3 configuration.

NO₂ requires special treatment due to its large size compared to the other gases. Certainly, proximity of two cations enables the simultaneous adsorption of NO₂ by both entities, a phenomenon which we define as cross-adsorption. Cross-adsorption occurs in the cases of MOR with Si/Al = 5, and CHA, with Si/Al = 5 and 3. Furthermore, when CHA with Si/Al = 3 is considered, two kinds of cross-adsorption can occur: 1) between a site-II and a site-IV Fe, and 2) between two site-IV cations.

3. Results and discussion

3.1 Adsorption screening for mordenite

The thermodynamic selectivity of MOR structures with Si/Al of 23, 11 and 5 has been assessed for NO_x and CO over H₂O and CO₂. Aluminium 1–3 and 1–4 configurations have also been assessed (see § 2.2 Structures).

Interaction energies of gases with mordenite are presented in Table SI† and Fig. 3. Interaction patterns are as follows: 1) the preferred adsorbate is always NO; 2) the second one is NO₂ except for Si/Al = 23, where water is more tightly adsorbed than NO₂; 3) close adsorption energies are observed for CO and H₂O, except for Si/Al = 23 and Si/Al = 5 with Al distributions 1–4 and 4), the weakest adsorption deals with CO₂. The interaction energies of CO₂ are very low; consequently the study of the influence of this chemical species on the material selectivity has been excluded, and this work focused on H₂O only. Indeed, NO_x is preferred over water for all geometries apart from the one where Si/Al = 23. Considering the 1–4 configuration, Si/Al = 11 showed positive results, with NO and NO₂ surpassing water's interaction energy by 104.1 and 29.2 kJ mol⁻¹ respectively, while CO remained barely below water by 1.1 kJ mol⁻¹ for the 1–3 configuration (Si/Al = 11) (These values are in the range of chemical accuracy, which means we can effectively consider them equal). Likewise, regarding Si/Al = 5, NO and NO₂ overcome water by 89.8 and 33.4 kJ mol⁻¹ respectively, while CO remained behind by 28.3 kJ mol⁻¹ (Table SI,† Fig. 3). NO₂ showed increased affinities for Si/Al = 5, compared to the other cells by ≈20 kJ mol⁻¹. This difference is attributed to the cross-adsorption between Fe and Na cations. For reference, the adsorption energies of CO and CO₂ have been explored by Gholizadeh et al.⁷⁸ over Si- and Se-doped graphene using DFT. The adsorption energy of CO was found to be equal to 18.4 and 17.0 kJ mol⁻¹ for Si and Se-doped graphene, respectively, while for CO₂, it was found to be equal to 17.8 and 20.5 kJ mol⁻¹. In addition, Li et al.⁷⁹ calculated the adsorption energies of CO and CO₂ on WO₃ and found the values of 4.1 and 4.5 kJ mol⁻¹ respectively. Although these materials are not optimized for PNA applications, this comparison illustrates not only the potential of Fe-exchanged MOR and CHA on CO adsorption capabilities, but also their superior selectivity.

Fig. 3 Interaction energies computed at the PBE + D2 + U level of theory of NO, NO₂, CO, H₂O and CO₂ on Fe-MOR. The adsorption sites considered are characterized by Si/Al = {23, 11, 5}, 6MR topology, and Al distributions 1–3 and 1–4.

3.2 Adsorption screening for chabazite

Three structures have been considered for chabazite, corresponding to the Si/Al ratios of 11, 5 and 3. For each of these unit cells, adsorptions of NO, NO₂, CO, H₂O and CO₂ have been performed, and the interaction energy has been calculated according to eqn (1). The size of NO₂ is large enough to allow adsorption between two cations at the same time, calling for special treatment for structures with Si/Al ratios of 5 and 3.

The interaction energies are presented in Table SII† and Fig. 4. The most obvious patterns are the following: 1) NO is always the most preferred; 2) CO₂ is the least preferred; 3) CO is the last but CO₂ and 4) NO₂ is the second most preferred on site II but H₂O takes its place while site-IV is considered. Adsorption between two different cations enables NO₂ to enhance its affinity towards the zeolite, even overcoming water in the case of adsorption between two site-IV located cations. For the remaining discussion, CO₂ will be neglected because of its low interaction energy, compared to the other gases.

Fig. 4 Interaction energies computed at the PBE + D2 + U level of theory of NO, NO₂, CO, H₂O and CO₂ on divalent iron embedded CHA, considering cations on site-II (denoted as II), site-IV (denoted as IV) and areas between the two of them (denoted as II–IV and IV–IV).

For Si/Al = 11, both NO and NO₂ adsorb with a higher interaction energy than water by 87.2 kJ mol⁻¹ and 11.6 kJ mol⁻¹ respectively. CO, on the other hand, adsorbs less tightly than water by 24.2 kJ mol⁻¹. For Si/Al = 5, in regard to site-II, the findings follow the same trend as before, with NO and NO₂ remaining at 93.5 and 11.1 kJ mol⁻¹ over water and for CO, it is13.2 kJ mol⁻¹ lower (the differences are depicted as absolute values). In the case of site-IV, only NO remains higher than water by 38.5 kJ mol⁻¹, NO₂ and CO remaining lower by 46.3 kJ mol⁻¹ and 67.9 kJ mol⁻¹. One can observe that in comparison to site II, the differences have globally moved by approximately 50 kJ mol⁻¹, in favour of water. Finally, for Si/Al = 3, the same trends hold. For site-II, NO and NO₂ overcame the interaction of water by 83.6 and 17.3 kJ mol⁻¹, respectively while CO remained lower by 24.3 kJ mol⁻¹. For site-IV, NO was once again the only one to overcome water by 27.3 kJ mol⁻¹, leaving NO₂ and CO lower than H₂O by 58.0 and 73.6 kJ mol⁻¹.

Cross-adsorption enabled a sharper adsorption of NO₂ with respect to water. The structure with Si/Al = 5 contains two Fe atoms close to each other (one on site-II and one on site-IV), and Si/Al = 3 contains three, giving rise to two new different adsorption configurations for NO₂: bridged 1) between site-II and site-IV (cross-II–IV) and 2) between two different site-IV (cross-IV–IV). In the case of Si/Al = 5, only cross-II–IV is possible, which presented higher interaction energy than the corresponding site-II by 57.7 kJ mol⁻¹ and lower for site-IV by 20.7 kJ mol⁻¹. As for Si/Al = 3, cross-II–IV appeared again with an interaction energy higher than both site-II and site-IV by 28.7 and 6.6 kJ mol⁻¹, respectively. In contrast, cross-IV–IV adsorption energy quite increased compared to site-IV. This configuration surpassed even water in adsorption energy by 5.3 kJ mol⁻¹.

3.3 Co-adsorption investigation by AIMD

Ab initio molecular dynamics (AIMD) have been employed to shed light on the impact of steam on the trapping efficiency. We have selected the chabazite with a Si/Al ratio of 3 to simulate the co-adsorption of water with the three pollutants, CO, NO and NO₂, taken individually. Indeed, low Si/Al ratios are more interesting for low-temperature NO_x adsorption, as they contain more cations and higher chances for Al atoms to be close to each other, permitting the stabilization of Fe²⁺. The choice of chabazite is more related to the low computational cost with this structure compared in comparison with mordenite. The initial positions of the gases were on site-II. This guess was made, because, if the gases were placed randomly, they would adsorb on site-IV, due to the stronger interaction. In contrast, placing them on site-II may reveal whether the gases will spontaneously migrate to site-IV.

The mean distance between the cation and adsorbed gas was calculated using a radial distribution function (RDF). As point of reference for the location of the gas, the locations of C for CO, N for NO and N for NO₂ have been used. This distance was also calculated in the presence of n = 0, 1, 2, 3 and 4 H₂O molecules according to Fig. 5.

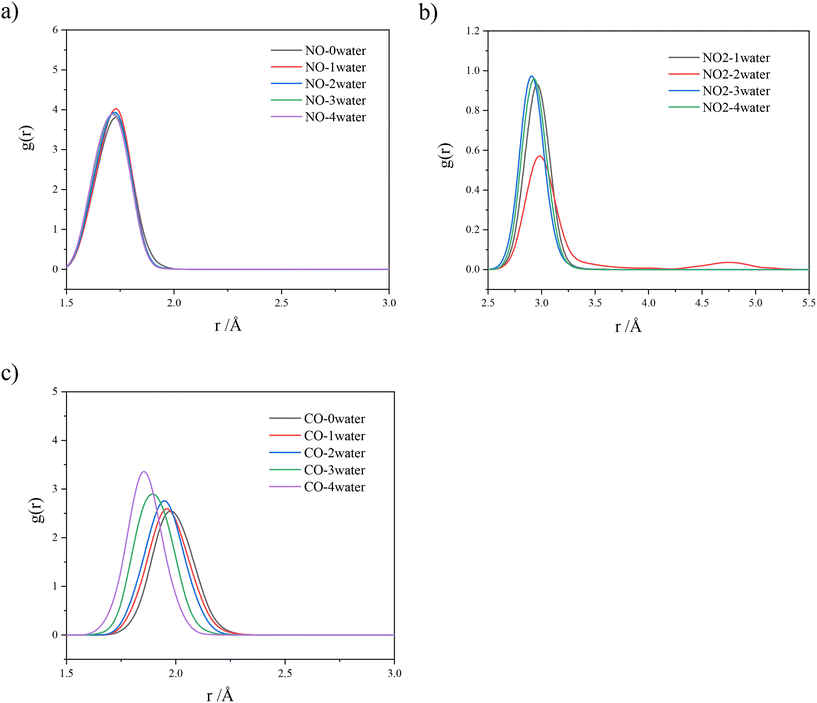Fig. 5 RDFs between site-II Fe and {a) NO, b) NO₂, and c) CO} respectively, in the presence of n = 0, 1, 2, 3 and 4 H₂O molecules. Isolated NO₂ RDF is omitted as it escapes site-II Fe.

RDFs illustrate that the presence of steam does not affect the adsorptions of NO and CO. The peaks exhibit similar shape and height independent of the number of water molecules involved. An exception is observed in the case of NO₂, when two water molecules were considered. In this case, a secondary peak is depicted owing to a short-termed migration of NO₂ from site-II to site-IV.

The RDF of NO₂ is not present when n = 0, as the gas escaped the bond barrier, impelled by the attraction of the cations on site-IV. The presence of water does not repel NO₂ away from site-II. In contrast, water molecules screen the attractive potential of site-IV, due to their presence around the cations, forcing NO₂ to stay on site-II.

The interaction energies obtained with molecular dynamics, which are gathered in Table 1, agree with the ones obtained with certain single configuration DFT calculations, proving the latter's worth. Dealing with CO, an interaction energy of −72.4 kJ mol⁻¹ has been found, in close agreement with the interaction energy on site-II. For H₂O, −189.0 kJ mol⁻¹ has been found, which agrees with site-IV adsorption. For NO, the interaction energy of −172.6 kJ mol⁻¹ suggests that DFT gives a slight overestimation, though agrees with site-II adsorption. Finally, NO₂ adsorption energy agrees with the cross-IV–IV value.

Table 1 The interaction energies, ΔE_in (kJ mol⁻¹), calculated by AIMD, for the isolated gases at 298 K (at the corresponding site) – chabazite with Si/Al = 3

Gas	ΔEint
NO	−172.6 (site-II)
NO2	−201.8 (cross-IV–IV)
CO	−72.4 (site-II)
H2O	−189.0 (site IV)

---

3.4 Thermodynamic assessment

The thermodynamic separation criterion is fulfilled by most of the cases considered above. Regarding CHA, site-II Fe exhibits stronger affinity for NO_x than for H₂O. Moreover, two closely located Fe²⁺, which occupy site-IV can cross adsorb NO₂, leading once again to stronger adsorption than water. Overall, NO is always preferred over water. Similar trends were found for MOR. NO is always preferred over water and NO₂ in all cases but only for Si/Al = 23, configuration 1–3. It needs to be pointed out that the high affinity for NO is itself an excellent finding of ours. The concentration of NO_x in the SCR section of the exhaust gas diesel during a cold start is mainly NO. Moreover, CO reduces NO₂ to NO, further shifting their chemical equilibrium. Because of that, several experimental studies have used only NO in the gas stream for the evaluation of PNAs.^26,28,32,35

Mordenite with Si/Al = 23 shows a high affinity relatively to the cells with Si/Al = 11 and 5. This excessive hydrophilicity of 23 is attributed to the H-bond that H₂O forms with the O atoms of the cell. This H-bond formation is prohibited in the other cells because of the deformation that the extra cations apply on the channel. Moreover, the introduction of Na atoms, close to Fe, strongly enhanced the selectivity of MOR towards NO₂.

Despite molecular dynamics calculations not being performed for mordenite, because of their high computational cost, chabazite gave strong evidence that our static DFT results are trustworthy. The RDFs further support the idea that NO_x resist water's competition for the adsorption sites, at least when there are several cations in the vicinity, which is expected in low-silica solids.

3.5 Zeolitic aspects and bonding analysis

To illustrate the impact of the topology and Si/Al ratios on the adsorption, we plotted the interaction energy of each gas, for the structures of MOR_1–3 and CHA_sII, with different Si/Al ratios in Fig. SVII.† We kept only one Al distribution to represent MOR (1–3) for simplicity and left MOR_1–4 behind. This choice cannot harm the objectivity of the conclusions, as changing the Al distribution leaves the adsorption energy practically unchanged, at least in our case, where there are always two Al atoms in the vicinity of the extraframework Fe.

By careful analysis of Fig. SVII,† we observe a slight tendency for increase of the interaction energy when decreasing the Si/Al ratio. However, this tendency is very slight, and we can conclude that decreasing Si/Al does not directly affect the adsorption behaviour. However, it increases the cationic exchange rate, hence the saturation limit of the zeolites. In addition, it offers the possibility for cross adsorption, highly benefiting NO₂ selective adsorption.

The topology of CHA and MOR plays a crucial role in the adsorption behaviour. Firstly, there is no doubt that all the adsorptions on site-IV of CHA are far stronger than the ones on site-II, or on MOR. Secondly, according to Fig. SVII,† the adsorptions on site-II CHA are slightly stronger than the ones on MOR. The nature of this effect lies on the stability of the extra-framework Fe(II). Higher coordination numbers, shorter bonds with the framework, and better alignment of the orbitals of Fe(II) with those of O, lead to more stable Fe(II). And as the stability of the cation increases, the adsorption of the gas becomes weaker. This is a known effect in the context of zeolites. Site IV adsorptions are generally much stronger than the rest, because the coordination number of Fe is equal to 3, whereas in site-II CHA and MOR, it is equal to 4 (Fig. 6). Furthermore, when we try to compare the stability of Fe(II) on site-II CHA and MOR, there are two conflicting factors. As we see in Fig. 6 of the manuscript, the coordination bonds (Fe–O) are shorter in the case of CHA than MOR, which favours the stability of CHA. On the other hand, Fig. 6 illustrates that the oxygen atoms that take part in the coordination of Fe fall very close to the edges of a square with Fe as the centre, which does not happen in the case of CHA. Consequently, there is much better orbital alignment between Fe and the O atoms of MOR than of CHA. This favours MOR over CHA regarding the stability. This discussion summarizes the variety of adsorption energies on the frameworks.

Fig. 6 Fe placed a) on the 6MR of CHA-3, b) on the 6MR of MOR, c) and d) on the 8MR of CHA-3. Two figures are given for the 8-MR to illustrate the slightly perturbed plane.

Finally, to understand how Fe(II) interacts with the gases, we have performed Bader charge analysis and bond elongation analysis and generated charge density difference plots.

3.5.1 CO₂. The adsorption of CO₂ on Fe(II) is performed through one of the O atoms. According to Table SI and SII,† the adsorption energies range between 39.2 and 54.6 kJ mol⁻¹ for MOR, from −34.6 to −40.5 kJ mol⁻¹, for CHA site II and from −66.5 to −80.0 kJ mol⁻¹ for CHA site IV. The adsorption lengths between Fe(II) and O remain above 2.08 Å (Fig. SI–SVI†), which is quite higher than the sum of the covalent radii of O (63 pm) and Fe (116 pm).⁸⁰ The low intensity of the interaction between CO₂ and Fe(II) as well as their nearest distance, suggests a weak physisorption, driven by electrostatic interactions, due to the large quadrupole moment of CO₂ (ref. 81) and the positively charged Fe(II).

3.5.2 CO. The length of the bond Fe–C during adsorption ranges from 1.94 Å to 1.97 Å (Fig. SI–SVI†). The sum of the covalent radii of C (75 pm) and Fe (116 pm) is barely below these lengths; thus we can infer that the covalent character is low. Bader charge transfer equal to 0.05 from MOR to CO and 0.02e (Table 3), as well as the absence of C–O bond elongation during adsorption (Table 2), suggests that π-backdonation is limited. Electrostatic interactions are also not so important in this case, as CO has very low dipole moment, and much lower quadrupole moment than CO₂. The interaction energy with MOR was computed as −92.8 kJ mol⁻¹ while for CHA −76.4 kJ mol⁻¹. Inspection of the charge density difference plots of MOR (Fig. 7) and CHA (Fig. 8) reveals charge accumulation in the area between Fe(II) and C, coming from the d_z² of Fe(II). Based on the above, we suggest the occurrence of chemisorption of CO with minor contribution of its LUMO (due to the absence of C–O elongation). Induction effects arising from the polarization of CO (ref. 82) by Fe(II)'s strong electric field stabilize the adsorption.

Table 2 Bond elongations due to adsorption are reported for NO_x, CO and H₂O over both MOR and CHA with Si/Al equal to 5 and 3, respectively. The configurations treated for MOR are always over Fe with Al distributions 1–4, and for CHA, the ones obtained from MD calculations

Gas species concerned	NO	NO2		CO	H2O
Bond	N–O	O1–NO	O2–NO	C–O	H1–OH	H2–OH
Initial length (Å)	1.17	1.21	1.21	1.144	0.97	0.97
Fe^(II) MOR-5 (Å)	0.00 (0%)	0.14 (12%)	0.00 (0%)	0.00 (0%)	0.00 (0%)	0.01 (1%)
Fe^(II) CHA-3 (Å)	0.00 (0%)	0.07 (6%)	0.07 (6%)	0.00 (0%)	0.07 (7%)	0.01 (1%)

---

Fig. 7 The charge density differences that occurred during the adsorption on FeMOR-5, of a) NO, b) NO₂, c) CO and d) H₂O. The isosurfaces have a density of 0.002 e Å⁻³.

Fig. 8 The charge density differences that occurred during the adsorption on FeCHA-3, of a) NO, b) NO₂, c) CO, and d) H₂O. The isosurfaces have a density of 0.002 e/ų.

3.5.3 NO. The length of the bond Fe–N during adsorption ranges from 1.69 Å to 1.71 Å (Fig. SI–SVI†) which is much lower than the sum of the covalent radii of N (71 pm) and Fe (116 pm). Bader charges show transfers of 0.13e from MOR to NO and 0.11e (Table 3), from CHA to NO. Interaction energies of −211.4 kJ mol⁻¹ and −184.3 kJ mol⁻¹ are associated with the adsorption on MOR and on CHA site II, respectively. All of these are arguments in favour of a strong chemisorption of NO on Fe(II), with strong π-backdonation. The absence of N–O bond elongation in both cases, despite the π-backdonation, is attributed to counterbalancing with donation to its HOMO as well.

Table 3 Bader charge differences attributed to the adsorption of the gases on MOR with Si/Al = 5 on the left, and CHA with Si/Al = 3 on the right. The adsorptions for MOR have been performed on the 1–4 site for all cases, but for CHA the locations are the same as for the MD calculations

Mordenite	Atom	Charge difference	Chabazite	Atom	Charge difference
Fe–NO	O	0.12	Fe–NO	O	0.09
	N	−0.25		N	−0.20
	Fe	0.00		Fe	0.09
Fe–NO2	O1	−0.24	Fe–NO2	O1	−0.27
	O2	−0.19		O2	−0.25
	N	−0.04		N	−0.05
	Fe	0.05		Fe1	0.16
				Fe2	0.19
Fe–CO	O	0.07	Fe–CO	O	0.06
	C	−0.12		C	−0.09
	Fe	0.02		Fe	0.01
Fe–H2O	O	−0.03	Fe–H2O	O	−0.11
	H1	0.04		H1	0.10
	H2	0.05		H2	0.09
	Fe	−0.02		Fe	0.05

---

3.5.4 NO₂. This gas adsorbs in a multitude of ways, through O, through N, or both at the same time. Due to its relatively big size, it adsorbs by two cations simultaneously, when they are available. It is thus more complicated to draw conclusions about the nature of the interactions, and we would have to treat each case separately. However, the minimum distances between Fe and NO₂ shown in Fig. SI–SVI† are smaller compared to the sum of the covalent radii, suggesting the existence of covalent bonding. Also, there is strong π-backdonation according to Bader charge analysis and the density difference plots, which is confirmed by significant elongation of the N–O bonds in both CHA and MOR cases. Taken together, these findings point to a chemisorption mechanism for NO₂ that is strongly governed by π-backdonation.

3.5.5 H₂O. Finally, the adsorption of water is performed through O. The Fe–O bond length ranges between 2.04 and 2.10 Å in all cases except site IV, where we even observe lengths of 1.93 Å. These values are much higher than the sum of the covalent radii of Fe and O (1.79 Å). Bader charges reveal charge transfer equal to 0.06e from water to MOR and 0.08e from water to CHA. Charge difference plots reveal charge accumulation between water and Fe(II) in both cases. Chemisorption is apparent in both cases, and they are verified by large interaction energies of −101.6 and −197.1 kJ mol⁻¹ (this value is so high because it refers to the adsorption at site IV). However, the adsorptions are strongly supported by electrostatic interactions arising from H₂O's dipole moment⁸³ and the positively charged Fe.

Conclusions

To sum up, we provided promising results with Fe²⁺ – supporting chabazite and mordenite as passive NO_x adsorbers (PNAs). This study is based on static PBE + D2 + U at 0 K and state of the art ab initio molecular dynamics at 300 K. U values have been calculated for CHA and MOR using the linear response method. The selectivity of several structures for CO, NO and NO₂ is checked by the comparison of their adsorption energies with that of CO₂ and H₂O, at 0 K. The suitability of the most promising structure has been cross evaluated performing ab initio molecular dynamics calculations. Excellent agreement was found between static density functional theory and molecular dynamics regarding the adsorption energies of the gases, validating the adequacy of the first, for the gases under study. The radial distribution function of gas–metal bond length evolutions has been plotted for CHA with Si/Al = 3. Fe²⁺ embedded CHA with Si/Al = 3, was found, not only to prefer NO_x over the rest of the gases, but also not to cause extensive bond elongation to the gases.

The bond elongations were further studied by Bader charge population analysis, accompanied with density difference figures, for the visualization of the charge transfer during the adsorptions. For most of the gases, the charge transfer is relatively low and the elongations too. In the past it was predicted that adsorption of NO₂ on Fe²⁺ promoting Y zeolite causes serious N–O1 activation. Therefore, the extended bond stretching is prevented even for NO₂ in the cases of cross-adsorption. This is a very consequential finding, which restores the interest in Fe²⁺ promoting zeolites. The low-price of the studied zeolites as well as of Fe might render these materials worthy substitutes for the up to now best, but nonetheless extremely expensive Pt²⁺ and Pd²⁺. The current findings call for the synthesis of these materials and their studies: characterization, isotherm and dynamic experiments using a mixture of NO_x, CO and water have to be carried out to validate these numerical investigations. Indeed, exhaust gas contains a lot of water (close to 10 vol%) and if all adsorption sites are occupied by water molecules, it could be difficult to trap NO_x and CO. Otherwise, oxygen (8 vol%) and water can lead to the formation of undesirable by-products. Finally, materials have to be thermally stable because in the exhaust line they can reach very high temperatures. Therefore, further experimental investigations are required to choose the best industrial media.

Data availability

Part of the data supporting this article have been included as part of the ESI.† Optimized structures will be shared with the community as cif or xyz files at the revision stage.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was granted access to the HPC resources of TGCC under the allocations 2023-A0140810433 and 2024-A0160810433 made by GENCI. This work is partially funded by the French National Research Agency NOA Project (ANR-20-CE08-0024).

References

1. A. M. Radwan and M. C. Paul, Int. J. Hydrogen Energy, 2024, 52, 819–833.
2. S. Muhammad Farhan, W. Pan, C. Zhijian and Y. JianJun, Fuel, 2024, 355, 129364.
3. A. K. Jain, Z. Tao, X. Yang and C. Gillespie, J. Geophys. Res.: Atmos., 2006, 111(D6) DOI:10.1029/2005JD006237.
4. L. Jaeglé, L. Steinberger, R. V. Martin and K. Chance, Faraday Discuss., 2005, 130, 407.
5. M. Amann, D. Derwent, B. Forsberg, O. Hänninen, F. Hurley, M. Krzyzanowski, F. de Leeuw, S. J. Liu, C. Mandin, J. Schneider, P. Schwarze and D. Simpson, Health Risks of Ozone from Long-Range Transboundary Air Pollution, WHO Regional Office for Europe: DK-2100 Copenhagen Ø, Denmark, 2008.
6. V. Strand, M. Svartengren, S. Rak, C. Barck and G. Bylin, Eur. Respir. J., 1998, 12, 6–12.
7. R. W. Atkinson, I. M. Carey, A. J. Kent, T. P. van Staa, H. R. Anderson and D. G. Cook, Epidemiology, 2013, 24, 44.
8. I. W. G. in the E. of C. R. to Humans, Diesel and Gasoline Engine Exhausts and Some Nitroarenes, International Agency for Research on Cancer, 2014.
9. X. Wang, D. Westerdahl, J. Hu, Y. Wu, H. Yin, X. Pan and K. M. Zhang, Atmos. Environ., 2012, 46, 45.
10. A technical summary of Euro 6/VI vehicle emission standards, https://theicct.org/publication/a-technical-summary-of-euro-6-vi-vehicle-emission-standards/, (accessed May 20, 2025).
11. Directive-2017/164 - EN-EUR-Lex, https://eur-lex.europa.eu/eli/dir/2017/164/oj/eng, (accessed May 20, 2025).
12. Commission Directive (EU) 2017/164 of 31 January 2017 establishing a fourth list of indicative occupational exposure limit values pursuant to Council Directive 98/24/EC, and amending Commission Directives 91/322/EEC, 2000/39/EC and 2009/161/EU (Text with EEA relevance.), 2017, vol. 027.
13. L. Castoldi, L. Lietti, R. Bonzi, N. Artioli, P. Forzatti, S. Morandi and G. Ghiotti, J. Phys. Chem. C, 2011, 115, 1277–1286.
14. R. Büchel, R. Strobel, A. Baiker and S. E. Pratsinis, Top. Catal., 2009, 52, 1799–1802.
15. Steam: its generation and use, ed. J. B. Kitto, Babcock & Wilcox, Barberton, Ohio, 41st edn, 2005.
16. H. S. Latha, K. V. Prakash, M. Veerangouda, D. Maski and K. T. Ramappa, Int. J. Curr. Microbiol. Appl. Sci., 2019, 8, 1553–1559.
17. T. Lee, J. Park, S. Kwon, J. Lee and J. Kim, Sci. Total Environ., 2013, 461–462, 377–385.
18. D. Ball, M. Zammit, J. Wuttke and C. Buitrago, SAE Int. J. Fuels Lubr., 2011, 4, 1–8.
19. F. Millo and D. Vezza, Characterization of a New Advanced Diesel Oxidation Catalyst with Low Temperature NO _x Storage Capability for LD Diesel, 2012, 2012-01-0373,  DOI:10.4271/2012-01-0373.
20. C. Henry, D. Langenderfer, A. Yezerets, M. Ruth, H.-Y. Chen, H. Hess and M. Naseri, Passive Catalytic Approach to Low Temperature NOx Emission Abatement, 2011, p. 12.
21. Y. Ji, D. Xu, S. Bai, U. Graham, M. Crocker, B. Chen, C. Shi, D. Harris, D. Scapens and J. Darab, Ind. Eng. Chem. Res., 2017, 56, 111–125.
22. Y. Ji, S. Bai, D. Xu, D. Qian, Z. Wu, Y. Song, R. Pace, M. Crocker, K. Wilson, A. Lee, D. Harris and D. Scapens, Appl. Catal., B, 2020, 264, 118499.
23. Y. Ji, S. Bai and M. Crocker, Appl. Catal., B, 2015, 170–171, 283–292.
24. H.-Y. Chen, J. E. Collier, D. Liu, L. Mantarosie, D. Durán-Martín, V. Novák, R. R. Rajaram and D. Thompsett, Catal. Lett., 2016, 146, 1706–1711.
25. Y. Ryou, J. Lee, H. Lee, C. H. Kim and D. H. Kim, Catal. Today, 2017, 297, 53–59.
26. H.-Y. Chen, S. Mulla, E. Weigert, K. Camm, T. Ballinger, J. Cox and P. Blakeman, SAE Int. J. Fuels Lubr., 2013, 6, 372–381.
27. R. R. Rajaram, H.-Y. Chen and D. Liu, Cold Start Catalyst and Its Use in Exhaust Systems, US20150158023A1, 2015, https://patents.google.com/patent/US20150158023A1/en, (accessed 2023-03-03).
28. Y. Gu and W. S. Epling, Appl. Catal., A, 2019, 570, 1–14.
29. J. Kašpar, P. Fornasiero and N. Hickey, Catal. Today, 2003, 31.
30. Y.-X. Yu, J. Colloid Interface Sci., 2025, 695, 137799.
31. Y. Ryou, J. Lee, S. J. Cho, H. Lee, C. H. Kim and D. H. Kim, Appl. Catal., B, 2017, 212, 140–149.
32. H.-Y. Chen, J. E. Collier, D. Liu, L. Mantarosie, D. Durán-Martín, V. Novák, R. R. Rajaram and D. Thompsett, Catal. Lett., 2016, 146, 1706–1711.
33. J. Lee, Y. Ryou, S. J. Cho, H. Lee, C. H. Kim and D. H. Kim, Appl. Catal., B, 2018, 226, 71–82.
34. Y. Ryou, J. Lee, H. Lee, C. H. Kim and D. H. Kim, Catal. Today, 2019, 320, 175–180.
35. Y. Zheng, L. Kovarik, M. H. Engelhard, Y. Wang, Y. Wang, F. Gao and J. Szanyi, J. Phys. Chem. C, 2017, 121, 15793–15803.
36. S. Jones, Y. Ji and M. Crocker, Catal. Lett., 2016, 146(5), 909–917.
37. J. Dědeček, Z. Sobalík and B. Wichterlová, Catal. Rev.: Sci. Eng., 2012, 54, 135–223.
38. E. Kritsanaviparkporn, F. M. Baena-Moreno and T. R. Reina, Chemistry, 2021, 3, 630–646.
39. S. Dey and G. C. Dhal, Mater. Sci. Energy Technol., 2020, 3, 6–24.
40. E. P. Hessou, W. G. Kanhounnon, D. Rocca, H. Monnier, C. Vallières, S. Lebègue and M. Badawi, Theor. Chem. Acc., 2018, 137, 161.
41. A. Daouli, E. P. Hessou, H. Monnier, M.-A. Dziurla, A. Hasnaoui, G. Maurin and M. Badawi, Phys. Chem. Chem. Phys., 2022, 24, 15565–15578.
42. I. Karamanis, A. Daouli, H. Monnier, M.-A. Dziurla, G. Maurin and M. Badawi, Mol. Syst. Des. Eng., 2023, 8, 1165–1181.
43. K. Sun, H. Xia, E. Hensen, R. Vansanten and C. Li, J. Catal., 2006, 238, 186–195.
44. M. A. Rodkin, V. I. Sobolev, K. A. Dubkov, N. H. Watkins and G. I. Panov, in Studies in Surface Science and Catalysis, Elsevier, 2000, vol. 130, pp. 875–880.
45. X. Feng and W. Keith Hall, J. Catal., 1997, 166, 368–376.
46. C. He, Y. Wang, Y. Cheng, C. K. Lambert and R. T. Yang, Appl. Catal., A, 2009, 368, 121–126.
47. H. I. Hamoud, V. Valtchev and M. Daturi, Appl. Catal., B, 2019, 250, 419–428.
48. F. Gao, Y. Zheng, R. K. Kukkadapu, Y. Wang, E. D. Walter, B. Schwenzer, J. Szanyi and C. H. F. Peden, ACS Catal., 2016, 6, 2939–2954.
49. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
50. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
51. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
52. G. Kresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245.
53. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
54. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
55. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
56. T. Bučko, J. Hafner, S. Lebègue and J. G. Ángyán, J. Phys. Chem. A, 2010, 114, 11814–11824.
57. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
58. T. Kerber, M. Sierka and J. Sauer, J. Comput. Chem., 2008, 29, 2088–2097.
59. A. J. Stone, The Theory of Intermolecular Forces, Clarendon Press, 1997.
60. M. D. Strømsheim, N. Kumar, S. Coriani, E. Sagvolden, A. M. Teale and T. Helgaker, J. Chem. Phys., 2011, 135, 194109.
61. A. Daouli, E. P. Hessou, H. Monnier, M.-A. Dziurla, A. Hasnaoui, G. Maurin and M. Badawi, Phys. Chem. Chem. Phys., 2022, 24(25), 15565–15578.
62. T. Ayadi, S. Lebègue and M. Badawi, Phys. Chem. Chem. Phys., 2022, 24, 24992–24998.
63. T. Ayadi, M. Badawi, L. Cantrel and S. Lebègue, Mol. Syst. Des. Eng., 2022, 7, 422–433.
64. F. Jensen, Introduction to computational chemistry, John Wiley & Sons, Chichester, England, Hoboken, NJ, 2nd edn, 2007.
65. M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
66. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
67. R. F. W. Bader, Acc. Chem. Res., 1985, 18, 7.
68. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
69. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908.
70. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
71. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111.
72. T. Bučko and J. Hafner, J. Catal., 2015, 329, 32–48.
73. J. Rey, A. Gomez, P. Raybaud, C. Chizallet and T. Bučko, J. Catal., 2019, 373, 361–373.
74. T. M. Nenoff, M. A. Rodriguez, N. R. Soelberg and K. W. Chapman, Microporous Mesoporous Mater., 2014, 200, 297–303.
75. V. E. Borisenko, S. V. Gaponenko, V. S. Gurin and A. B. Filonov, Physics, Chemistry And Application Of Nanostructures: Reviews And Short Notes To Nanomeeting '99, World Scientific, 1999.
76. S. Chibani, M. Chebbi, S. Lebègue, L. Cantrel and M. Badawi, Phys. Chem. Chem. Phys., 2016, 18, 25574–25581.
77. S. Chibani, I. Medlej, S. Lebègue, J. G. Ángyán, L. Cantrel and M. Badawi, ChemPhysChem, 2017, 18, 1642–1652.
78. R. Gholizadeh and Y.-X. Yu, Appl. Surf. Sci., 2015, 357, 1187–1195.
79. J.-H. Li, J. Wu and Y.-X. Yu, Appl. Surf. Sci., 2021, 546, 149104.
80. P. Pyykkö and M. Atsumi, Chem. – Eur. J., 2009, 15, 186–197.
81. A. D. Buckingham and R. L. Disch, Proc. R. Soc. London, Ser. A, 1963, 273(1353) DOI:10.1098/rspa.1963.0088.
82. G. Maroulis, J. Phys. Chem., 1996, 100, 13466–13473.
83. S. A. Clough, Y. Beers, G. P. Klein and L. S. Rothman, J. Chem. Phys., 1973, 59, 2254–2259.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5me00003c

---