Open Access Article
Open Access ArticleMethods for kinetic evaluation of reversible covalent inhibitors from time-dependent IC50 data†
Lavleen K.
Mader
 and
Jeffrey W.
Keillor
and
Jeffrey W.
Keillor
 *
*
Department of Chemistry and Biomolecular Sciences, University of Ottawa, Ottawa, Ontario K1N 6N5, Canada. E-mail: jkeillor@uottawa.ca
First published on 20th March 2025
Abstract
Potent reversible covalent inhibitors are often slow in establishing their covalent modification equilibrium, resulting in time-dependent inhibition. While these inhibitors are commonly assessed using IC50 values, there are no methods available to analyze their time-dependent IC50 data to provide their inhibition (Ki and  ) and covalent modification rate (k5 and k6) constants, leading to difficulty in accurately ranking drug candidates. Herein, we present an implicit equation that can estimate these constants from incubation time-dependent IC50 values and a numerical modelling method, EPIC-CoRe, that can fit these kinetic parameters from pre-incubation time-dependent IC50 data. The application of these new methods is demonstrated by the evaluation of a known inhibitor, saxagliptin, providing results consistent with those obtained by other known methods. This work introduces two new practical methods of evaluation for time-dependent reversible covalent inhibitors, allowing for rigorous characterization to enable the fine-tuning of their binding and reactivity.
) and covalent modification rate (k5 and k6) constants, leading to difficulty in accurately ranking drug candidates. Herein, we present an implicit equation that can estimate these constants from incubation time-dependent IC50 values and a numerical modelling method, EPIC-CoRe, that can fit these kinetic parameters from pre-incubation time-dependent IC50 data. The application of these new methods is demonstrated by the evaluation of a known inhibitor, saxagliptin, providing results consistent with those obtained by other known methods. This work introduces two new practical methods of evaluation for time-dependent reversible covalent inhibitors, allowing for rigorous characterization to enable the fine-tuning of their binding and reactivity.
Introduction
Reversible covalent inhibitors are a subset of targeted covalent inhibitors (TCIs). These compounds follow a two-step inhibition mechanism (Scheme 1, blue) featuring an initial non-covalent binding event, whose equilibrium is described by the inhibition constant Ki, followed by a reversible covalent reaction between the protein target and the inhibitor's electrophilic ‘warhead’. | ||
Scheme 1 Kinetic scheme of reversible covalent inhibition, where Ki = k4/k3 and  = Ki/1 + (k5/k6). This figure was adapted from ref. 1. = Ki/1 + (k5/k6). This figure was adapted from ref. 1. | ||
The entire equilibrium from free enzyme E to covalently bound enzyme E–I is described by the inhibition constant  , which can be calculated from Ki, k5, and k6.2–5 Many warheads are known to display such reversible reactivity, including α-cyanoacrylamides, α-ketoamides, nitriles, and boronic acids.4,6–12 While our understanding and development of reversible TCIs is still relatively new, some inhibitors of this class have shown clinical potential, and others are already on the market.13–15 Reversible covalent inhibitors have been proposed to offer lower toxicity profiles compared to irreversible inhibitors, due to reversible off-target protein modification, while still providing the increased residence time and affinity afforded by a covalent interaction.6,16 Interestingly, all FDA-approved drugs of this type also display time-dependent inhibition,13,17–21 where the final equilibrium between free enzyme and covalently bound enzyme is slow to establish. This time-dependent behaviour is almost always due to the breakdown of the covalent inhibitor-enzyme complex being very slow compared to covalent bond formation (k6 ≪ k5), often due to the intrinsic stability of the covalent bond, or steric hindrance introduced by either the scaffold itself or the surrounding protein microenvironment.22 This behaviour serves to enhance on-target residence times and apparent affinity even further, and can also be tuned based on the intrinsic reactivity of the warhead or the steric environment around it (i.e. increase or decrease k5 and/or k6), as first demonstrated by Taunton et al.8,22 Therefore, complete characterization of all relevant binding and rate constants is crucial to optimizing overall on- and off-rates for both on-target and off-target proteins, in order to ensure potency while minimizing off-target side effects. Recently, this strategy has been particularly relevant in achieving selectivity among kinases, which have very similar binding sites.23,24
, which can be calculated from Ki, k5, and k6.2–5 Many warheads are known to display such reversible reactivity, including α-cyanoacrylamides, α-ketoamides, nitriles, and boronic acids.4,6–12 While our understanding and development of reversible TCIs is still relatively new, some inhibitors of this class have shown clinical potential, and others are already on the market.13–15 Reversible covalent inhibitors have been proposed to offer lower toxicity profiles compared to irreversible inhibitors, due to reversible off-target protein modification, while still providing the increased residence time and affinity afforded by a covalent interaction.6,16 Interestingly, all FDA-approved drugs of this type also display time-dependent inhibition,13,17–21 where the final equilibrium between free enzyme and covalently bound enzyme is slow to establish. This time-dependent behaviour is almost always due to the breakdown of the covalent inhibitor-enzyme complex being very slow compared to covalent bond formation (k6 ≪ k5), often due to the intrinsic stability of the covalent bond, or steric hindrance introduced by either the scaffold itself or the surrounding protein microenvironment.22 This behaviour serves to enhance on-target residence times and apparent affinity even further, and can also be tuned based on the intrinsic reactivity of the warhead or the steric environment around it (i.e. increase or decrease k5 and/or k6), as first demonstrated by Taunton et al.8,22 Therefore, complete characterization of all relevant binding and rate constants is crucial to optimizing overall on- and off-rates for both on-target and off-target proteins, in order to ensure potency while minimizing off-target side effects. Recently, this strategy has been particularly relevant in achieving selectivity among kinases, which have very similar binding sites.23,24
While the kinetic behaviour of fast-binding and fast-reacting reversible covalent inhibitors is difficult to distinguish from that of traditional non-covalent reversible inhibitors (i.e., instantaneous and uniform decrease in activity, showing no time-dependence), slow-binding and/or slow-reacting covalent inhibitors display time-dependent kinetics, which allow their individual rate and inhibition constants to be measured. This time-dependence can be seen clearly in continuous assays, where product formation over time resembles a ‘curve’ rather than a straight line.2,3 These ‘curves’ feature an initial linear phase representative of non-covalent binding (described by Ki) which slowly transitions to a final linear phase once the final covalent equilibrium has also been established (described by  ). Progress curves from continuous assays can be used to evaluate time-dependent reversible inhibitors and derive all of their binding and rate constants. However, the fitting of data from this method is error prone, especially for the typically small k6 values.3 Additionally, if a continuous assay is not available, attempting to mimic continuous monitoring by taking many time-based aliquots of an enzymatic reaction can be very labour- and time-intensive to perform. It has also recently been shown that these kinetic parameters can be estimated in a substrate-free manner by strategically monitoring binding kinetics at assumed pre- and post-equilibrium periods using surface plasmon-resonance, followed by complex modelling using fixed k3 and k4 (Scheme 1) values.24 This is a clever approach, but this type of analysis requires not only specialized instrumentation but also advanced knowledge of mathematics and modelling.
). Progress curves from continuous assays can be used to evaluate time-dependent reversible inhibitors and derive all of their binding and rate constants. However, the fitting of data from this method is error prone, especially for the typically small k6 values.3 Additionally, if a continuous assay is not available, attempting to mimic continuous monitoring by taking many time-based aliquots of an enzymatic reaction can be very labour- and time-intensive to perform. It has also recently been shown that these kinetic parameters can be estimated in a substrate-free manner by strategically monitoring binding kinetics at assumed pre- and post-equilibrium periods using surface plasmon-resonance, followed by complex modelling using fixed k3 and k4 (Scheme 1) values.24 This is a clever approach, but this type of analysis requires not only specialized instrumentation but also advanced knowledge of mathematics and modelling.
In practice, the time-dependence of reversible covalent inhibitors is often probed by time-dependent IC50 assays that are performed by varying either the duration of the ‘pre-incubation’ phase, when the enzyme is incubated with inhibitor alone, or the ‘incubation phase’, when substrate is added (Scheme 1, yellow).25,26 A shift to lower IC50 values with increasing assay times confirms the time-dependence of covalent addition, while the reversibility must be established otherwise.27,28 However, no fitting methods are available to analyze this kind of time-dependent IC50 data and derive all relevant inhibition and rate constants, perhaps due to the mathematical difficulty the additional rate constant (k6) imposes. Instead, many researchers simply report a single IC50 value at a single time point. While this single value may be useful for screening compounds within the same library using the exact same assay, it is difficult to discern whether such an IC50 value is reporting on the initial linear phase (i.e., pre-equilibrium), the transitionary period, or the final linear phase (i.e., equilibrium) of the reaction. Hence, information about the forward and reversible covalent reaction steps (related to k5 and k6) and the overall affinity (related to  ) may be missed, causing researchers to overlook promising candidates.2
) may be missed, causing researchers to overlook promising candidates.2
Herein, we report, for the first time, two new methods to analyze time-dependent IC50 data from reversible covalent inhibitors in order to derive the inhibition constants Ki and  , and the covalent reaction rate constants k5 and k6. The first method is an implicit equation that relates incubation time-dependent IC50 values (obtained without pre-incubation) to these constants. The second method is an empirical global fitting method that models pre-incubation time-dependent IC50 data to estimate the same constants. To demonstrate the performance of our methods and consensus with established evaluation procedures, we also present the characterization of a known, clinically relevant, time-dependent reversible covalent di-peptidyl peptidase IV (DPPIV) inhibitor, saxagliptin.14 All relevant equations, derivations thereof, differential equations and embodying code relating to these methods of evaluation have been provided in the ESI,† with key fitting equations included in the Experimental section.
, and the covalent reaction rate constants k5 and k6. The first method is an implicit equation that relates incubation time-dependent IC50 values (obtained without pre-incubation) to these constants. The second method is an empirical global fitting method that models pre-incubation time-dependent IC50 data to estimate the same constants. To demonstrate the performance of our methods and consensus with established evaluation procedures, we also present the characterization of a known, clinically relevant, time-dependent reversible covalent di-peptidyl peptidase IV (DPPIV) inhibitor, saxagliptin.14 All relevant equations, derivations thereof, differential equations and embodying code relating to these methods of evaluation have been provided in the ESI,† with key fitting equations included in the Experimental section.
Results and discussion
While the recent general resurgence in interest in covalent inhibitors has led to the development of many clever methods to evaluate irreversible binders,1,17,29,30 introduction of a reversible reaction step (i.e., corresponding to rate constant k6 in Scheme 1) results in much more nuance to the mathematical models that describe the kinetics of reversible covalent modulators. For a fast-binding and fast-reacting reversible covalent inhibitor there are no practical means for kinetically distinguishing it from a fast-binding (traditional) reversible non-covalent inhibitor, using activity assay-based methods. This means only its overall affinity, related to the inhibition constant , can be measured, giving no information about the reactivity of the compound with its protein target. However, reversible covalent inhibitors that react more slowly with their targets display time-dependent kinetics, which allows their initial non-covalent binding and subsequent covalent reaction to be dissected to provide individual inhibition and rate constants.2 The basic mathematical principles that form the foundation of all previous methods, and the new methods described herein for evaluation of these inhibitors, are identical to those previously derived for slow-binding reversible non-covalent inhibitors that display an ‘induced fit’ mechanism, as summarized by Copeland.2 The only difference between the induced fit slow-binding mechanism and that of slow-reacting reversible covalent modification is that a covalent bond is formed (and broken) in the reversible step described by rate constants k5 (and k6) (Scheme 1). Recognition of this similarity allows for the application of eqn (S12) and (S13) in continuous, progress curve analysis for these inhibitors, as described in the ESI:†
, can be measured, giving no information about the reactivity of the compound with its protein target. However, reversible covalent inhibitors that react more slowly with their targets display time-dependent kinetics, which allows their initial non-covalent binding and subsequent covalent reaction to be dissected to provide individual inhibition and rate constants.2 The basic mathematical principles that form the foundation of all previous methods, and the new methods described herein for evaluation of these inhibitors, are identical to those previously derived for slow-binding reversible non-covalent inhibitors that display an ‘induced fit’ mechanism, as summarized by Copeland.2 The only difference between the induced fit slow-binding mechanism and that of slow-reacting reversible covalent modification is that a covalent bond is formed (and broken) in the reversible step described by rate constants k5 (and k6) (Scheme 1). Recognition of this similarity allows for the application of eqn (S12) and (S13) in continuous, progress curve analysis for these inhibitors, as described in the ESI:† | (S12) |
 | (S13) |
However, despite the growing attention given to this class of inhibitors, there is much confusion in the literature about the application and interpretation of this fitting method.22,24 Continuous assays for these types of inhibitors typically require optimization for long assay times in order to observe and capture the steady state equilibrium in the fitting. Moreover, the fitting procedures for the resulting data cannot account for substrate depletion and/or enzyme degradation (i.e., the uninhibited control must be perfectly linear, since no mathematical correction can be applied in the way that it can be for an irreversible inhibitor) and often lead to high errors in the fitted parameters.3
Perhaps for these reasons, these inhibitors are more often evaluated using IC50 experiments, where time-dependency is simply demonstrated by a decrease in IC50 values with increasing times of either assay incubation or enzyme-inhibitor pre-incubation.13,22 Prior to this work, this type of data could only be used to confirm time-dependent behaviour, before selecting a given time-point and ranking inhibitors based on their IC50 at that time, with no knowledge of whether the final equilibrium has been reached. This poses the obvious problem of grossly misleading structure–activity relationship data, as well as limited information about how to tune binding and reactivity, preventing researchers from harnessing the true potential of such inhibitors. Not too long ago, irreversible inhibitors were also plagued by this very issue, which has since been resolved by equations and modelling methods for irreversible binding.1,29 Recognizing this disconnect and drawing on our own expertise in the methodologies for evaluating irreversible covalent inhibitors,1,31–33 we have developed two new methods that allow for time-dependent IC50 data to be analyzed to provide values for Ki, k5, and k6, and subsequently calculate  , for time-dependent reversible covalent inhibitors. For the sake of clarity, in the main body of this article we will only describe the elements of method development that relate to implementation, assay design, and drug properties, in the simplest terms possible. The detailed derivation of equations is provided in the ESI.†
, for time-dependent reversible covalent inhibitors. For the sake of clarity, in the main body of this article we will only describe the elements of method development that relate to implementation, assay design, and drug properties, in the simplest terms possible. The detailed derivation of equations is provided in the ESI.†
Development of implicit equation for time-dependent IC50 values
First, we took an approach similar to that of Krippendorff et al.28,29 in recognizing the central relationship between continuous product formation (as described by eqn (S13)) and IC50 values measured at different incubation times, in an assay where enzyme, inhibitor, and substrate are all combined at the same time. We will refer to this as an incubation time-dependent IC50 experiment (Scheme 1, yellow). Functionally, an IC50 value at any given time is simply the inhibitor concentration that results in 50% of the uninhibited response, where the uninhibited response (i.e. product formation) is described by Michaelis–Menten kinetics ([P] = v0·t, where v0 is given by the Michaelis–Menten equation). At any given assay time, half of this response (½v0·t = [P]IC50), is observed in an inhibited reaction when [I] = IC50(t) (see ESI,† eqn (S16)). Understanding the derivation of eqn (S16),† and the definitions of the parameters within, allows for algebraic manipulation (shown in the ESI†) to arrive at an implicit equation (eqn (S18)) that relates a discontinuous IC50 value determined at time t to parameters Kappi, k5, and k6: | (S18) |
 | (S19) |
Eqn (S18) is an implicit equation in that the dependent parameter (i.e., IC50(t)) appears on both sides of the equation. However, if many discontinuous IC50 values are measured at different times (Fig. 1A), a curve can be generated by plotting IC50(t)vs. time (Fig. 1B) which can be fitted to eqn (S18) by non-linear regression, allowing for Kappi, k6, and k5 to be solved. Note that Ki is calculated from Kiapp using eqn (S4).†
 | ||
| Fig. 1 Fitting of incubation time-dependent IC50 values to implicit eqn (S18). A) Simulated IC50 curves for the reaction of 1 nM enzyme (kcat = 1000 min−1) with 500 μM substrate (KM = 100 μM) in the presence of varying concentrations (1–500 nM) of a reversible covalent inhibitor (k5 = 0.5 min−1, k6 = 0.005 min−1, Ki = 0.10 μM), measured after incubation times ranging from 8–80 min. B) Fitting of IC50 values resulting from (A) to implicit eqn (S18). | ||
It is also instructive to consider the limits of eqn (S18), at vanishingly small or infinite incubation times. As shown in the ESI,† the limit of IC50(t) as time approaches zero is equal to Kappi (see eqn (S22)†). Intuitively, this makes sense as it describes the initial rapid-binding equilibrium, before covalent modification has taken place. Alternatively, at infinite incubation time, the limit of IC50(t) is equal to  (see eqn (S24)†). This reflects the final inhibition equilibrium that is definitively established after infinite incubation time.
(see eqn (S24)†). This reflects the final inhibition equilibrium that is definitively established after infinite incubation time.
Eqn (S18) can also be compared to the ‘Krippendorff equation’, which was derived for two-step irreversible inhibition (see eqn (S25)†).1,29 Interestingly, if k6 is set to zero, which would simplify the kinetic scheme shown in Scheme 1 to that of irreversible inhibition, eqn (S18) does indeed simplify to the Krippendorff equation (see eqn (S27)†). Likewise, setting k6 to zero in eqn (S19) results in a simplified equation (eqn (S28)†) that is equivalent to what is observed for irreversible inhibition. These comparisons serve to validate eqn (S18) and (S19), but they also demonstrate that the Krippendorff equation can be thought of as a simplified version of eqn (S18), for the special case where k6 is equal to zero. Thus, the equation derived here (i.e.eqn (S18)) is all-encompassing for all types of covalent inhibitors that show time-dependence.
Despite the apparent complexity of eqn (S18) at first glance, it allows for fitting through non-linear regression, using any standard graphing software (e.g., GraphPad Prism). In the ESI† we provide a plain-text version that can be copied and pasted as a user-defined equation in any desired software and used to fit experimental data.
Development of EPIC-CoRe
In the equally, if not more common case where a pre-incubation time-dependent IC50 experiment is performed, by first incubating the enzyme with inhibitor for varying times (Scheme 1, blue), before adding substrate and measuring product formation after a defined incubation period (Scheme 1, yellow), no implicit equation can be derived to describe the variation of IC50 with time. This is due to the biphasic nature of such an experiment, where enzyme is differentially inhibited, in the first phase rapidly by inhibitor alone, and in the second phase more slowly due to partial protection by a competitive substrate (Fig. 2A). The IC50 is then measured, based on product formation at a fixed end-point time in the second (assay incubation) phase (Fig. 2B).Similar to an incubation time-dependent IC50 experiment, IC50 values also decrease with increasing pre-incubation times (Fig. 2B); however, in this case, it is impossible to embody both phases in any one equation to fit kinetic parameters. We recently noted the absence of tools available to characterize irreversible inhibitors in this way as well – that is, to derive KI and kinact values from pre-incubation time-dependent IC50 data. This led us to develop a numerical modelling method, EPIC-Fit, to accomplish this important task.1 Here, we describe a similar empirical approach, developed for time-dependent reversible covalent inhibitors, that we call EPIC-CoRe (![[E with combining low line]](https://www.rsc.org/images/entities/b_char_0045_0332.gif) ndpoint
ndpoint ![[P with combining low line]](https://www.rsc.org/images/entities/b_char_0050_0332.gif) re-incubation
re-incubation ![[I with combining low line]](https://www.rsc.org/images/entities/b_char_0049_0332.gif)
![[C with combining low line]](https://www.rsc.org/images/entities/b_char_0043_0332.gif) 50-
50-![[C with combining low line]](https://www.rsc.org/images/entities/b_char_0043_0332.gif)
![[o with combining low line]](https://www.rsc.org/images/entities/b_char_006f_0332.gif) valent
valent ![[R with combining low line]](https://www.rsc.org/images/entities/b_char_0052_0332.gif)
![[e with combining low line]](https://www.rsc.org/images/entities/b_char_0065_0332.gif) versible).
versible).
This method employs code that uses differential equations to describe instantaneous changes in enzyme, inhibitor, substrate, and product concentrations, from the beginning of the pre-incubation phase to the end of the assay incubation phase, ultimately predicting the end-point signal (e.g. product concentration) that would be observed for a given set of inhibition parameters (Ki, k5, and k6) in a pre-incubation IC50 experiment. This calculation is performed for every inhibitor concentration, at a given pre-incubation and assay measurement time, for a competitive inhibitor/substrate pair, to generate a predicted IC50 at that time. Thus, experimental parameters of the activity assay must also be known, including initial enzyme and substrate concentrations, the kcat and KM values, and the dilution of enzyme and inhibitor resulting from addition of substrate to initiate the incubation phase. When experimental IC50 datasets (comprising product signal values measured at different inhibitor concentrations) are entered at many different pre-incubation times, and initial estimates for k5, k6 and Ki are provided (see below for practical considerations), the difference between each observed endpoint value recorded in the global dataset and the endpoint concentration predicted according to initial estimates are reported as “residuals”. Least squares regression can then be performed to arrive at k5, k6 and Ki values that provide a global minimum to the sum of the squares of these residuals (i.e., where the predicted signal values match the experimental signal values as closely as possible) for all data points.
This method can be implemented using any spreadsheet or modelling software that allows user code to be inputted. We have chosen to use Microsoft Excel, as it offers readily accessible spreadsheet calculations, user-defined code input (in visual basic for applications (VBA)) for rapid iterative calculations, and least-squares fitting using the Solver add-in, to create a functional embodiment of this method. Our spreadsheet contains cells to input values of the experimental parameters of the assay, as well as predicted and experimental IC50 plots from all the pre-incubation time-dependent datasets that are updated in real-time as data is entered. It also presents a column of predicted endpoint values, the calculated residual of each data point, and the residual sum of squares (RSS). The VBA code used for the numerical modelling calculations is also presented in the Supporting Information, showing how differential equations are used iteratively to arrive at the predicted end-point concentrations. The Solver add-in included in Excel has been set up such that the cells containing the values of k5, k6 and Ki contain initial estimates and are subsequently optimized by least square regression, using Generalized Reduced Gradient (GRG2) code.34 We have also included a cell that calculates  , based on fitted parameters. A fully functional EPIC-CoRe spreadsheet that includes all aforementioned features, as well as instructions and formatting to guide user data input, is freely available upon request.
, based on fitted parameters. A fully functional EPIC-CoRe spreadsheet that includes all aforementioned features, as well as instructions and formatting to guide user data input, is freely available upon request.
Evaluation of saxagliptin
To demonstrate the application of the new methodologies reported herein, we evaluated the well-known DPPIV inhibitor, saxagliptin, which bears a reversibly reactive nitrile warhead (Fig. 3).14 We chose to evaluate saxagliptin because it is one of the very few inhibitors that has been previously shown to exhibit time-dependent, reversible covalent inhibition and for which a chromogenic continuous activity assay has already been developed, in the form of a commercially available kit. This makes saxagliptin nearly uniquely amenable to independent evaluation according to all of the methods discussed above, allowing us to validate our two new methods against the existing one. The fitted kinetic parameters determined by each method are summarized in Table 1. The enzymatic assay follows the chromogenic DPPIV-mediated hydrolysis of substrate glycine-proline-para-nitroanilide (Gly-Pro-pNA), which releases the coloured product para-nitroaniline (Scheme 2).14,35,36 We used this assay in both continuous (real-time monitoring) and discontinuous (end-point) mode, depending on the method of evaluation, for demonstration purposes. Since each of the methods described here employs a substrate that is competitive with inhibitor, a KM value is required for each method, and a kcat value is required for analysis by EPIC-CoRe, as discussed above. Using standard Michaelis–Menten kinetic analysis (Fig. S3†) we obtained values of KM = 70.7 ± 6.0 μM and kcat = 17.6 ± 0.5 s−1 (or roughly 1056 min−1), which are consistent with literature values.14 These values were used for subsequent inhibitor characterization.| Assay | Fitting method | k 5 (min−1) | k 6 (min−1) | K i (nM) | (nM) |
|---|---|---|---|---|---|
a Errors in parameters shown for this method are from the fitting of saturation kinetic data (kobsvs. [I]).
b Errors in parameters shown for this method are from the fitting of IC50 values vs. incubation time, according to implicit equation eqn (S18).
c Errors in parameters shown for this method are from the standard deviation of duplicate values determined from the global fitting of pre-incubation time-dependent IC50 data.
d
 was calculated using eqn (S11). was calculated using eqn (S11).
|
|||||
| Continuous assay | Saturationa | 0.54 ± 0.03 | 0.0033 ± 0.0031 | 81 ± 7 | 0.49 ± 0.41 |
| IC50 from initial slopes | — | — | 89 ± 6 | — | |
| IC50 from final slopes | — | — | — | 0.74 ± 0.18 | |
| Incubation time-dependent IC50 | Implicit equationb | 0.85 ± 0.15 | 0.0042 ± 0.0015 | 120 ± 15 | 0.52 ± 0.20 |
| EPIC-CoRec | 0.63 ± 0.14 | 0.0028 ± 0.0009 | 83 ± 17 | 0.35 ± 0.12 | |
| Pre-incubation time-dependent IC50 | EPIC-CoRe | 0.64 ± 0.05 | 0.0045 ± 0.0015 | 141 ± 8 | 0.99 ± 0.35 |
Firstly, we evaluated saxagliptin in a continuous assay fashion (Scheme 1, yellow) to obtain progress curves at different inhibitor concentrations. This type of reaction, initiated in the presence of both inhibitor and substrate, can be described by the explicit equation for time-dependent product formation, eqn (S13). Incubation of 12 different concentrations of saxagliptin with DPPIV in the presence of Gly-Pro-pNA, in an experiment where enzyme is added to initiate the reaction, resulted in biphasic ‘curves’ of absorbance vs. time, representing time-dependent inhibition (Fig. 4A). These curves were monitored over 80 minutes to allow sufficient time for steady state slopes to be reached, and were fitted to eqn (S13) to give kobs values for the transition phase at each concentration.14 These rate constants were then plotted against inhibitor concentrations (corrected for competition with substrate), and then fitted to hyperbolic eqn (S12), representative of saturation kinetics, taking care not to constrain the y-intercept to zero (Fig. 4B). This analysis provided values of k5 = 0.54 ± 0.03 min−1, k6 = 0.0033 ± 0.0031 min−1, Ki = 81 ± 9 nM, and 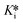 = 0.49 ± 0.41 nM. Note that the rather large relative error in k6 and consequently in
= 0.49 ± 0.41 nM. Note that the rather large relative error in k6 and consequently in  are typical for this method of analysis.3
are typical for this method of analysis.3
 | ||
| Fig. 4 Continuous activity assay with saxagliptin, DPPIV, and Gly-Pro-pNA. (A) kobs values were fitted from reaction progress curves of absorbance vs. time at different concentrations of saxagliptin using eqn (S12). (B) Saturation fitting of these kobs values according to eqn (4) provided values for k5, k6, and Ki. | ||
The fitting of these reaction progress curves to eqn (S12) also provides initial and steady state slopes of inhibition, vi and vs, respectively. As previously shown,3 these slopes can be normalized as a percentage of the uninhibited slope and plotted against the inhibitor concentration to provide an IC50 plot. The IC50 values obtained from analysis of vi and vs are equivalent to Ki and  , respectively, when competition from substrate is accounted for.2,3 However, this analysis cannot provide individual rate constants k5 and/or k6. For saxagliptin, these IC50 plots provided values of Ki = 89 ± 6 nM (Fig. 5A) and
, respectively, when competition from substrate is accounted for.2,3 However, this analysis cannot provide individual rate constants k5 and/or k6. For saxagliptin, these IC50 plots provided values of Ki = 89 ± 6 nM (Fig. 5A) and  = 0.74 ± 0.18 nM (Fig. 5B). Interestingly, although this type of IC50 analysis cannot provide individual reaction rate constants, it is the recommended method of analysis of progress curves due the lower error it typically provides in
= 0.74 ± 0.18 nM (Fig. 5B). Interestingly, although this type of IC50 analysis cannot provide individual reaction rate constants, it is the recommended method of analysis of progress curves due the lower error it typically provides in  values.3 Moreover, it is still possible to analyze the ratio of the rate constants as k5/k6 = (Ki/
values.3 Moreover, it is still possible to analyze the ratio of the rate constants as k5/k6 = (Ki/ ) − 1 (≈ 120 in the case of saxagliptin analyzed in this way), which may provide useful insight and distinction into how much the forward reaction is favoured compared to the reverse reaction, within a library of inhibitors.
) − 1 (≈ 120 in the case of saxagliptin analyzed in this way), which may provide useful insight and distinction into how much the forward reaction is favoured compared to the reverse reaction, within a library of inhibitors.
Next, we carried out an incubation time-dependent IC50 experiment, which is performed essentially in the same way as the continuous assay method, except that one absorbance value (related to product concentration) is measured at a final end-point at a pre-determined time for each inhibitor concentration, from which an IC50 plot is generated. This is then repeated at different assay incubation times to generate many time-dependent IC50 curves (Fig. 6A). IC50 values decrease with increasing incubation time (i.e., apparent potency increases) as the inhibitor is allowed more time to establish the final equilibrium with the covalently bound enzyme. These IC50 values change dramatically at short incubation times, but very little at long incubations times, as the steady state-equilibrium is approached. IC50 values for saxagliptin were determined at 10 different time points up to 80 minutes, then were plotted against assay incubation time and fitted to implicit eqn (S18) (Fig. 6B) to obtain the kinetic parameter values k5 = 0.85 ± 0.15 min−1, k6 = 0.0042 ± 0.0015 min−1, Ki = 120 ± 15 nM, and  = 0.52 ± 0.20 nM, showing excellent agreement with the values determined by progress curve analysis (above).
= 0.52 ± 0.20 nM, showing excellent agreement with the values determined by progress curve analysis (above).
 | ||
| Fig. 6 Incubation time-dependent IC50 experiment with saxagliptin, DPPIV, and Gly-Pro-pNA. (A) IC50 value decreases with increasing incubation time. (B) Fitting of time-dependent IC50 values to implicit eqn (S18) provides k5, k6, and Kiapp. | ||
Interestingly, the IC50 curves obtained from this incubation time-dependent IC50 experiment can also be analyzed using our EPIC-CoRe spreadsheet (Fig. S4†), by setting the dilution factor to 1 and a pre-incubation time to zero. Global fitting of the same data by this method provided values of k5 = 0.63 ± 0.14 min−1, k6 = 0.0028 ± 0.0009 min−1, Ki = 83 ± 17 nM, and  = 0.35 ± 0.12 nM, with an average correlation of R2 = 0.99, and RMSE = 1.2, very similar to those obtained by fitting to implicit eqn (S18). This suggests that either fitting procedure would be suitable for analysis of incubation time-dependent IC50 datasets.
= 0.35 ± 0.12 nM, with an average correlation of R2 = 0.99, and RMSE = 1.2, very similar to those obtained by fitting to implicit eqn (S18). This suggests that either fitting procedure would be suitable for analysis of incubation time-dependent IC50 datasets.
Finally, a pre-incubation experiment was performed by incubating 10 different concentrations of inhibitor with enzyme alone, for six different pre-incubation times up to 60 minutes, before initiating the assay by addition of substrate. An end-point absorbance was then measured after 20 minutes of running the activity assay. The endpoint data were used to generate IC50 curves at each pre-incubation time. These IC50 values decrease with increasing pre-incubation time (Fig. 7), phenomenologically similar to the incubation experiment above. However, since no equation exists to fit these pre-incubation IC50 datasets, they can only be analyzed by global fitting using EPIC-CoRe (Fig. 8). This fitting provided values of k5 = 0.64 ± 0.05 min−1, k6 = 0.0045 ± 0.0015 min−1, Ki = 141 ± 8 nM, and 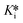 = 0.99 ± 0.35 nM, with an average correlation of R2 = 0.98, and RMSE = 4.4.
= 0.99 ± 0.35 nM, with an average correlation of R2 = 0.98, and RMSE = 4.4.
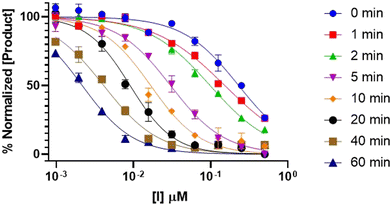 | ||
| Fig. 7 Time-dependent IC50 curves for the inhibition of DPPIV with saxagliptin, showing decreasing IC50 values with increasing pre-incubation times. | ||
Evaluation of the reaction rate constants and inhibition constants describing the time-dependent reversible covalent inhibition of DPPIV by saxagliptin using the known progress curve analysis method, as well as the new time-dependent IC50 analysis methods presented herein, allows for direct comparison of the precision and congruency of each method. We have confirmed that saturation fitting from progress curves produces the largest relative error in k6 and  , with errors essentially as large as the fitted values, providing little confidence in the fitting, even though the values do match reasonably with the other methods. All methods provided a k5 value of around 0.5–1.0 min−1, which is consistent with typical forward covalent reaction rate constants for a nitrile warhead (i.e., analogous to kinact for an irreversible inhibitor).7,37,38 Values for k6 ranged from roughly 0.003–0.005 min−1, around 200-fold less than k5, which is consistent with the manifestation of time-dependent inhibition that almost resembles irreversibility due to the reverse reaction being very slow (Fig. 4A). This value is also consistent with the observed off-rate constant (koff) that approximates k6, as painstakingly determined by Kim et al. in an independent jump-dilution experiment.14 In their experiment, the recovery of enzymatic activity was monitored, to measure koff ≈ k6 ≈ 0.0030 ± 0.0002 min−1, as the slowest, rate-determining step of inhibitor dissociation.14,39 Our Ki values ranged from ∼80–140 nM and were an order of magnitude higher than our calculated
, with errors essentially as large as the fitted values, providing little confidence in the fitting, even though the values do match reasonably with the other methods. All methods provided a k5 value of around 0.5–1.0 min−1, which is consistent with typical forward covalent reaction rate constants for a nitrile warhead (i.e., analogous to kinact for an irreversible inhibitor).7,37,38 Values for k6 ranged from roughly 0.003–0.005 min−1, around 200-fold less than k5, which is consistent with the manifestation of time-dependent inhibition that almost resembles irreversibility due to the reverse reaction being very slow (Fig. 4A). This value is also consistent with the observed off-rate constant (koff) that approximates k6, as painstakingly determined by Kim et al. in an independent jump-dilution experiment.14 In their experiment, the recovery of enzymatic activity was monitored, to measure koff ≈ k6 ≈ 0.0030 ± 0.0002 min−1, as the slowest, rate-determining step of inhibitor dissociation.14,39 Our Ki values ranged from ∼80–140 nM and were an order of magnitude higher than our calculated 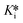 values (∼0.4–1 nM), highlighting the importance of taking time-dependency into account to evaluate true affinity. Again, this is consistent with the value of
values (∼0.4–1 nM), highlighting the importance of taking time-dependency into account to evaluate true affinity. Again, this is consistent with the value of  ≈ 0.35 nM determined by Kim et al., using continuous progress curve fitting and subsequent calculations.14 Overall, all methods produced reasonably consistent results with each other and literature sources,14 generally within 1–2 standard deviations. This analysis provides confidence in the use of our new implicit equation, as well as our EPIC-CoRe method, for the robust evaluation of independent values of k5, k6, Ki, and
≈ 0.35 nM determined by Kim et al., using continuous progress curve fitting and subsequent calculations.14 Overall, all methods produced reasonably consistent results with each other and literature sources,14 generally within 1–2 standard deviations. This analysis provides confidence in the use of our new implicit equation, as well as our EPIC-CoRe method, for the robust evaluation of independent values of k5, k6, Ki, and 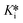 for time-dependent reversible covalent inhibition from commonly acquired time-dependent IC50 data.
for time-dependent reversible covalent inhibition from commonly acquired time-dependent IC50 data.
Practical considerations
From an assay design perspective, continuous methods are generally the most powerful for kinetic characterization. They require relatively little material and are easy to implement, while providing nearly instantaneous information. For irreversible inhibitors, continuous assay methods are indeed the most robust option not only for assay implementation but also subsequent kinetic analysis and fitting.33 However, in the case of a time-dependent reversible inhibitor, these types of assays can be particularly difficult to optimize and analyze, if they are available at all. Generally, long incubation times on the course of hours are required to fully observe steady state equilibria, and over this period the uninhibited control must be strictly linear, as no algebraic correction can be applied to account for substrate depletion and/or enzyme degradation.3 This requires considerable optimization of the concentrations of enzyme, substrate, and inhibitor. It also requires that the enzyme itself must be stable over this extended time period. Even when these requirements are met, progress curve fitting may result in high relative error in k6, as this value is typically very small and sensitive to any non-linearity in the uninhibited control. This then leads to high errors in the calculated value. In a model system, such as the one demonstrated by our evaluation of saxagliptin, this fitting method worked well and provided reasonable values of kinetic parameters. However, for researchers studying new inhibitors and/or new targets it can be quite cumbersome to perform,14 especially to extract k5 and k6 values. It may be easier to use vi and vs values to arrive at a ratio of k5/k6, as shown above, but dissection and subsequent tuning of the forward and reverse reactions is not possible.
value. In a model system, such as the one demonstrated by our evaluation of saxagliptin, this fitting method worked well and provided reasonable values of kinetic parameters. However, for researchers studying new inhibitors and/or new targets it can be quite cumbersome to perform,14 especially to extract k5 and k6 values. It may be easier to use vi and vs values to arrive at a ratio of k5/k6, as shown above, but dissection and subsequent tuning of the forward and reverse reactions is not possible.
For the same amount of effort and material, an incubation time-dependent IC50 experiment can be performed, with the added benefit that substrate depletion or degradation of enzyme can be accounted for by normalizing against the uninhibited control reaction. The major consideration for this method is selecting time-points at which to measure IC50 values. Time points that encompass the initial vi phase, the transitionary phase, and the final vs phase provide the most robust fitting of all parameters, of which the final phase is the most crucial for fitting of k6. The times at which these phases occur will depend on the specific inhibitor/substrate/target combination. Generally, it is recommended to run the experiment out to >5 half-lives of the slowest transition phase, in order to allow the final equilibrium to be observed completely. The slowest transition, at the lowest concentration of inhibitor, may be approximated roughly by a kobs of ∼0.1 × k5 (see eqn (S19)), corresponding to a recommended experiment duration of ∼35/k5.
While fitting to the implicit equation with the saxagliptin model system worked well, we noted that 10 data points and long incubation times were still required to provide precise fitting. Interestingly, we have found that for this type of experiment using EPIC-CoRe requires fewer time points overall to arrive at similar solutions to the implicit equation. For the sake of demonstration, the results shown above include 6 time-points up to 80 minutes; however, similar results were obtained by monitoring for up to only 40 minutes with 4 data sets (see ESI,† Fig. S5), cutting the assay time in half. This is likely due to the robustness provided by global fitting of entire datasets rather than fitting the variance of IC50 values. Although this was not our original intended application, we note that EPIC-CoRe may be better suited for estimation of kinetic parameters from incubation time-dependent IC50 datasets that contain more error or noise.
While a pre-incubation time-dependent IC50 experiment does require more material (particularly more enzyme) to perform, it is commonly employed in industry as it lends itself well to automated assay procedures where end-point observations are taken at a pre-defined time into the activity assay. Similar to its utility in incubation time-dependent IC50 experiments, we have found that fewer time-points (i.e., at least 4) and shorter assay times are required for robust fitting (see ESI,† Fig. S6). With a pre-incubation phase included, the final steady state equilibrium is reached much faster than in a single-phase incubation experiment, allowing shorter subsequent (incubation phase) assay times to provide sufficient information for fitting. We generally recommend using a broad range of pre-incubation times, such as zero, 1/k5, 2/k5, and 5/k5, which would normally ensure broad variation of IC50 dataset values and robust fitting.1
For both methods, successful fitting requires datasets that show broad variance of end-point signal with respect to both inhibitor concentration and time, such that the dynamic range and inflection point of each IC50 curve is well-defined and time-dependence is clear between the different data sets. These methods do not account for more complex inhibition behaviour that result in binding isotherms with atypical Hill slopes (i.e., nH ≠ 1). In our experience, EPIC-CoRe provides robust fitting from initial estimates that may be orders of magnitude different from optimized values, whereas the implicit equation requires more accurate initial estimates for k5 and k6. However, given that time-dependent reversible inhibition generally results when k6 is at least an order of magnitude less than k5, and k5 is analogous to well-catalogued kinact values for a broad range of irreversible warheads,1 initial estimates of 0.1–1.0 min−1 for k5 and 0.001–0.010 min−1 for k6 are appropriate for a broad range of inhibitors. We recommend constraining k6 < k5 during fitting, as this must be true for time-dependent inhibition to be observed (where vs < vi). Initial estimates for Ki require less accuracy, and a value of 0.1–1.0 μM is generally suitable. Further guidance for an initial estimate for Ki can be obtained from the IC50 value measured at the shortest incubation or pre-incubation time, as the Ki value will be higher than this.1 For this reason, we also recommend including a pre-incubation time of zero among the pre-incubation data sets. It is also important to note that inhibitors must show appreciable reversibility to allow k6 to be fitted. As k6 gets smaller, inhibition becomes effectively irreversible, and the fitting methods discussed in this work will result in a fitted value of k6 approaching zero. For these inhibitors it may be more expedient to treat them as irreversible and to fit the data sets as described previously.1
If IC50 values or global datasets do not demonstrate sufficient predictable variance of signal as a function of time, fitting by implicit equation or EPIC-CoRe may not converge to a unique solution. In this case, it may be necessary to include additional datasets covering a larger time frame, as recommended above. It is also possible to fix one parameter (i.e., fix Ki to a value larger than the one obtained from the shortest incubation/pre-incubation time, or fix k5 based on known values for similar warheads), fit the rest of the parameters, and then fix those parameters and re-fit the first. This will also allow one to confirm convergence to a global minimum over a local minimum. In the spreadsheet we have developed for EPIC-CoRe, real-time visual comparison of the experimental data and predicted values allow the user to gauge how well their initial estimates of fitted parameters describe the data sets. It is therefore possible to manually adjust Ki, k5, and k6 values to arrive at reasonable estimates prior to Solver-powered fitting. Adjustment of Ki will largely shift the inflection points of all of the predicted IC50 curves along the x-axis, while the adjustment of k5 and k6 will more prominently alter the degree of their time-dependence. This provides a user-friendly and intuitive way to guide the fitting procedure.
Drug design optimized for strong on-target interaction and weak off-target reactivity/binding is generally best guided by tuning overall koff values (for drug release) rather than kon values (for drug binding).39 This is because the in vivo rate of association and actual concentration of drug reaching the target is heavily influenced by pharmacokinetics. Additionally, diffusion, desolvation, and orientation effects are difficult to predict. However, the rate of dissociation is almost entirely dependent on specific drug-target interactions alone, and can be tuned systematically by structure-based design.16,39 Time-dependent reversible covalent inhibitors provide a unique avenue to do this, as the overall koff value and therefore drug-target residence time will be most influenced by k6 (note that koff and residence time are actually a collection of rate constants).39 Knowledge of on- and off-target protein microenvironments and the mechanism of the reverse covalent reaction allows for fine-tuning of warhead structure to alter k6 values to lower values for the target protein and to higher values for off-targets, providing additional potency and selectivity.22,24 From a practical standpoint, reversibility is only relevant in vivo if the drug dissociates from a protein faster than its rate of degradation. In some cases, residence times of reversible covalent inhibitors can be so long that the inhibitor does not dissociate before the protein is degraded; effectively, this is equivalent to irreversible modification.22 However, a reversible inhibitor may be able to recapture newly synthesized protein, once the original to which it was bound has been degraded. If the residence time with off-targets is much lower, this provides the advantage of fewer side effects while maintaining prolonged desired target engagement.23 For these reasons, it is highly recommended to fully characterize these inhibitors with k6 values for rational drug design, which is now possible from IC50 experiments, using the methods reported in this work.
Finally, it is relevant to discuss the limitations of the scope of these new methods, which illustrates possible directions for future work. First, it is important to reiterate that all of the methods discussed herein are only applicable to assays that employ competitive inhibitor-substrate pairs. While this is currently the most common application for covalent inhibition, we acknowledge that it would be possible to design covalent inhibitors that operate at an allosteric site and are non-competitive in modality.40 Neither our EPIC-CoRe spreadsheet nor implicit eqn (S18) account for this mode of inhibition. Furthermore, if the E·S·I complex from a non-competitive inhibition scheme can lead to (slower) product formation, it would be possible to observe a non-zero lower plateau in experimental IC50 datasets. Our numerical modelling does not account for this pathway for product formation, and both eqn (S18) and Krippendorff's equation were derived on the assumption that saturation with inhibitor leads to zero product formation (see eqn (S15)†).29 It is also important to clarify that our work focuses on truly reversible covalent inhibitors, and does not account for covalent inhibitors that may be slowly consumed by the enzyme as a pseudo-substrate.41,42 Finally, apart from these very unusual cases where a covalent inhibitor may be non-competitive or undergo enzyme-mediated degradation, it is possible that an optimised covalent inhibitor may be bound very tightly, such that its Kappi value approaches the concentration of enzyme used in the assay. Eqn (S18), like Krippendorff's equation, was derived using the free ligand approximation (see eqn (S4)†) and does not account for tight binding. Experimentally, the use of low enzyme concentrations and high competing substrate (such that Kappi ≥ [Enz]) would extend the range of applicability of these implicit equations. However, the numerical modelling embodied in EPIC-CoRe uses Morrison's quadratic equation to calculate the fraction of E·I,43 which means it is uniquely appropriate to be applied to the evaluation of tight-binding reversible covalent inhibitors, as well.
Conclusions
In recent years there has been an emerging interest in reversible covalent inhibitors that provide enhanced covalent affinity without permanent off-target modifications. Time-dependent inhibitors of this type that dissociate slowly from their target, due to the reverse covalent reaction rate constant (k6) being small, are particularly notable, as they allow for fine-tuning of residence time based on warhead structure and protein microenvironment. The goal is to modulate k5 and k6 to allow for a moderately fast on-target addition reaction and slow dissociation from the desired target, but relatively rapid dissociation from any off-target reactive proteins. This strategy has proven successful for many kinases and growth receptors. Best practice to achieve this sort of fine-tuning requires individual characterization of all relevant inhibition and rate constants (k5, k6, Ki, and ) for this complex kinetic scheme, by taking time-dependency into account. Previously, the only practical way to achieve this was through progress curve analysis, which requires the availability of a convenient continuous assay and often results in high errors. Recognizing that these inhibitors are often assessed more practically using discontinuous (end-point) IC50 experiments, we developed two methods that allow for time-dependent IC50 data from time-dependent reversible covalent inhibitors to be analyzed, to provide all aforementioned constants. For incubation IC50 experiments, we present an implicit equation that can be used to fit IC50 value vs. time data to arrive at these constants. For pre-incubation IC50 experiments, we have developed EPIC-CoRe, a numerical modelling method that relates the global fitting of IC50 data sets to all relevant parameters. EPIC-CoRe features versatility that allows it to be used for incubation IC50 data sets (i.e., obtained with no pre-incubation phase) as well, providing an alternative to the complex implicit equation. These methods can be implemented quite easily by any practicing medicinal chemist as they only require common fitting (e.g., GraphPad Prism) or spreadsheet (e.g., Microsoft Excel) software. Both methods were shown to provide values that are consistent with other known methods of evaluation, as demonstrated here for the DPPIV inhibitor, saxagliptin, confirming their robustness and utility. To the best of our knowledge, this is the first demonstration of approaches that allow discontinuous IC50 data to be used to separately derive inhibition and rate constants of a time-dependent reversible covalent inhibitor. This is critical to drug design and optimization, allowing chemists to discern and improve overall on-target affinity
) for this complex kinetic scheme, by taking time-dependency into account. Previously, the only practical way to achieve this was through progress curve analysis, which requires the availability of a convenient continuous assay and often results in high errors. Recognizing that these inhibitors are often assessed more practically using discontinuous (end-point) IC50 experiments, we developed two methods that allow for time-dependent IC50 data from time-dependent reversible covalent inhibitors to be analyzed, to provide all aforementioned constants. For incubation IC50 experiments, we present an implicit equation that can be used to fit IC50 value vs. time data to arrive at these constants. For pre-incubation IC50 experiments, we have developed EPIC-CoRe, a numerical modelling method that relates the global fitting of IC50 data sets to all relevant parameters. EPIC-CoRe features versatility that allows it to be used for incubation IC50 data sets (i.e., obtained with no pre-incubation phase) as well, providing an alternative to the complex implicit equation. These methods can be implemented quite easily by any practicing medicinal chemist as they only require common fitting (e.g., GraphPad Prism) or spreadsheet (e.g., Microsoft Excel) software. Both methods were shown to provide values that are consistent with other known methods of evaluation, as demonstrated here for the DPPIV inhibitor, saxagliptin, confirming their robustness and utility. To the best of our knowledge, this is the first demonstration of approaches that allow discontinuous IC50 data to be used to separately derive inhibition and rate constants of a time-dependent reversible covalent inhibitor. This is critical to drug design and optimization, allowing chemists to discern and improve overall on-target affinity  and reactivity (k5 and k6), while maintaining intrinsic and off-target stability. Our methods serve to bridge the gap between the most commonly used assay methods for reversible covalent inhibitors, namely discontinuous IC50 experiments, and the most powerful kinetic characterization required for the fine-tuning of effective inhibitors of this type.
and reactivity (k5 and k6), while maintaining intrinsic and off-target stability. Our methods serve to bridge the gap between the most commonly used assay methods for reversible covalent inhibitors, namely discontinuous IC50 experiments, and the most powerful kinetic characterization required for the fine-tuning of effective inhibitors of this type.
Experimental section
General
No unexpected, new, or significant hazards/risks were encountered in any of the experimental procedures. All commercially available chemicals, enzymes, and solvents were used without further purification. Saxagliptin hydrochloride (item no. 23697) and Gly-Pro-pNA hydrochloride (item no. 21244) were purchased from Cayman Chemical with a reported purity of >95% as determined by HPLC analysis. Active recombinant, and untagged, DPPIV was purchased from Enzo Life Sciences Inc. as part of a commercial activity assay kit (BML-AK499-0001). The provided stock enzyme concentration was 0.071 mg mL−1 with an activity of 0.867 U mL−1. Biochemical assays were conducted directly in standard sterile 96-well plates and absorbance readings were taken in either continuous or discontinuous fashion using a BioTek Synergy 4 plate reader at 405 nm at 25 °C. Raw and/or processed readout data were analyzed by either GraphPad Prism or our EPIC-CoRe (Microsoft Excel) spreadsheet. All experiments were performed in at least duplicate. Derivations of all equations are provided in the Supporting Information, as well as commentary on how these relate to the differential equations used to develop EPIC-CoRe.Determination of KM and kcat of Gly-Pro-pNA with DPPIV
Buffered solutions of 50 mM TRIS (pH 7.5) and various concentrations of Gly-Pro-pNA (from 10–500 μM in the final assay solution, representing roughly 0.1–5 × KM) were prepared in 96-well plates. To initiate the enzymatic reactions, a solution of DPPIV was added to the wells, ensuring that the final concentration was 2.5 nM (2.6 mU mL−1), and additional buffer was added to the blank. The final well volume was 100 μL. Stock solutions of Gly-Pro-pNA were prepared by diluting a 10 mM DMSO stock in assay buffer, ensuring that the final concentration of DMSO did not exceed 2.5% v/v. The enzyme stock solution was prepared by dilution in assay buffer. The formation of the hydrolysis product, para-nitroaniline (pNA) was monitored at 405 nm for 80 min. No background hydrolysis was observed over this time period. Initial rates were calculated over 10% of substrate conversion (Fig. S1†). A standard curve was generated (Fig. S2†) for product pNA by taking an absorbance reading of solutions of concentrations varying from 10–500 μM, in assay buffer. Stock solutions of pNA were prepared using a 10 mM DMSO stock and diluting in assay buffer. A blank absorbance reading with assay buffer alone was subtracted from the readings. Absorbance readings were plotted against [pNA] and the slope of this line (representing the experimental extinction coefficient) was used to convert the initial rates from Abs/s to μM s−1. These initial rates were then plotted against [Gly-Pro-pNA] to generate a saturation plot (Fig. S3†) that was fitted by non-linear regression to the Michaelis–Menten equation (eqn (1), cf. eqn (S1)†) to obtain KM and Vmax. The value of kcat was then calculated using eqn (2). | (1) |
 | (2) |
Continuous activity assay
Enzymatic assays were run according to a modified procedure reported by Kim et al.,14 in the presence of final concentrations of 500 μM (≈7 × KM) Gly-Pro-pNA and 0.64 nM (0.65 mU mL−1) DPPIV. These concentrations were chosen to ensure a significant and linear signal in the uninhibited positive control over the 80 minute assay. Buffered solutions of 50 mM TRIS (pH 7.5), 500 μM Gly-Pro-pNA, and various concentrations of saxagliptin (2.4–5000 nM in the final assay well, 12 2-fold serial dilutions, representing roughly 0.01–10 × Kappi) were prepared in a 96-well plate. Saxagliptin stocks were prepared by dilution of a 10 mM stock in assay buffer, ensuring that the concentration of DMSO did not excess 2.5% v/v in the final assay well. To initiate the enzymatic reactions, DPPIV was added to a final concentration of 0.64 nM (0.65 mU mL−1) and additional buffer was added to the blank. The final well volume was 100 μL. Formation of pNA was followed at 405 nm for 80 minutes. No background reaction was observed. Observed pseudo-first order rate constants of inactivation (kobs), initial inhibited rates vi, and final inhibited rates vs, were obtained by fitting the resulting progress curves to eqn (3) (cf.eqn (S13)). | (3) |
Fitted kobs values were plotted against inhibitor concentrations corrected for the presence of substrate ([I]/α) by dividing inhibitor concentrations by (α = 1 + [S]/KM = 8.14). The resulting hyperbolic curve was fitted to eqn (4) (cf.eqn (S12)) to obtain values for k5, k6, and Ki. A value for  was subsequently calculated using eqn (S11).
was subsequently calculated using eqn (S11).
 | (4) |
 | (S11) |
Alternatively, the fitted vi and vs values were normalized with respect to the uninhibited control by dividing by the slope of the control (note the slope of the control should be the same throughout the assay, i.e., vi,0 = vs,0) and multiplying by 100. The resulting % inhibition values were plotted against [I]/α on a logarithmic scale and IC50 values were determined using four-parameter fitting according to eqn (5) (the upper plateau (top) can be fixed at 100, the lower plateau (bottom) can be fixed at 0, and a Hill slope can be fixed at 1 if needed). The IC50 value obtained from analysis of initial slopes is equal to Ki and the IC50 value obtained from analysis of steady state slopes is equal to 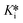 .
.
 | (5) |
Incubation time-dependent IC50 assay
Enzymatic assays were run under the same conditions as the continuous activity assay described above. An absorbance reading at 405 nm was taken from each reaction with different saxagliptin concentrations at 8, 16, 24, 32, 40, 48, 56, 64, 72, and 80 min observation times. No background reaction was observed. The absorbance reading of each inhibited reaction was divided by the absorbance reading taken from the uninhibited control at the same time to give a percent relative absorbance according to the following equation (eqn (6)):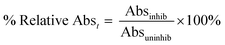 | (6) |
These percent relative absorbance values for each time point were plotted against the inhibitor concentration on a logarithmic scale to generate IC50 curves. IC50 values at each time point were determined using four-parameter fitting as described above (eqn (5)). These IC50 values were then plotted against their corresponding observation times to generate a curve that was fitted to user-defined implicit eqn (S18) using initial estimates of k5 = 0.1 min−1, k6 = 0.01 min−1, and Ki = 0.1 μM to obtain k5, k6, and Kappi; then Ki was calculated from the Cheng–Prusoff equation (eqn (S4)†) and 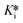 was calculated using eqn (S11).
was calculated using eqn (S11).
 | (S18) |
 | (S19) |
Alternatively, the percent relative absorbance values were entered into our EPIC-CoRe Excel sheet, using pre-incubation times of zero and incubation times of 8, 24, 40, 56, 72, and 80 min for the corresponding datasets. The response coefficient for each data set (which corresponds to the signal sensitivity and normalisation) was adjusted to give a value of approximately 100% in the presence of ‘zero’ inhibitor. The substrate and enzyme concentrations were 500 μM and 0.64 nM, respectively. The kcat value used was 1056 min−1 and KM was 70.7 μM, as measured herein (see above). The pre-incubation and incubation volumes were both set as 100 μL, representing a dilution factor of 1 (i.e. no dilution). Initial estimates of k5 = 0.1 min−1, k6 = 0.01 min−1, and Ki = 0.1 μM were entered before fitting these values using Solver. The value of  was automatically calculated within the spreadsheet according to eqn (S11). This fitting procedure was repeated on each individual dataset, as well as on a dataset of averaged endpoint values, to generate a standard deviation reflective of experimental error, as well as R2 and RMSE values to assess goodness of fit.
was automatically calculated within the spreadsheet according to eqn (S11). This fitting procedure was repeated on each individual dataset, as well as on a dataset of averaged endpoint values, to generate a standard deviation reflective of experimental error, as well as R2 and RMSE values to assess goodness of fit.
Pre-incubation time-dependent IC50 assay
A 96-well microplate was set up with 12 different reactions, in duplicate, representing an uninhibited control, 10 different saxagliptin concentrations (2-fold serial dilutions starting from 1 μM), and a blank, each to an initial volume of 35 μL in assay buffer (50 mM TRIS, pH 7.5). Then, 15 μL of a 0.0043 μM (4.3 mU mL−1) solution of DPPIV in assay buffer was added to each well using a multi-channel pipette. This gave a final concentration of 0.0013 μM (1.3 mU mL−1) of DPPIV and 2-fold dilutions of saxagliptin starting from 0.5 μM in the pre-incubation phase. After pre-incubation, 50 μL of a 1 mM stock solution of Gly-Pro-pNA in assay buffer (prepared from a 20 mM DMSO stock) was added to each well using a multi-channel pipette to initiate the activity assay, giving a final concentration of 500 μM Gly-Pro-pNA in the assay and approximately 2.5% DMSO v/v fixed in each well, with the final well volume being 100 μL. After a 20 min assay incubation period, an absorbance reading at 405 nm was taken from each well. This was repeated, in duplicate, for pre-incubation times of 0, 1, 2, 5, 10, and 20 min. No background reaction was observed.The absorbance reading of each inhibited reaction was divided by the absorbance reading taken from the uninhibited control to give a percent relative absorbance (eqn (6)). The percent relative absorbance values were entered into our EPIC-CoRe Excel sheet with the pre-incubation times set to 0, 1, 2, 5, 10, and 20 min and an incubation time of 20 min for the corresponding datasets. The response coefficient for each data set was adjusted to give a value of approximately 100% in the presence of ‘zero’ inhibitor. The substrate and enzyme concentrations were entered as 500 and 0.0013 μM, respectively. The kcat was entered as 1056 min−1 and KM as 70.7 μM, as determined herein (see above). The pre-incubation volume was set to 50 μL and incubation volume was set to 100 μL, representing a dilution factor of 0.5. Initial estimates of k5 = 0.1 min−1, k6 = 0.01 min−1, and Ki = 0.1 μM were entered before fitting these values using Solver. The value of  was automatically calculated within the spreadsheet according to eqn (S11). This fitting procedure was repeated on each individual dataset, as well as an averaged data set to generate a standard deviation reflective of experimental error, as well as R2 and RMSE values to assess goodness of fit.
was automatically calculated within the spreadsheet according to eqn (S11). This fitting procedure was repeated on each individual dataset, as well as an averaged data set to generate a standard deviation reflective of experimental error, as well as R2 and RMSE values to assess goodness of fit.
List of abbreviations
| TCI | Targeted covalent inhibitor |
| EPIC-CoRe | ![[E with combining low line]](https://www.rsc.org/images/entities/char_0045_0332.gif) ndpoint ndpoint ![[P with combining low line]](https://www.rsc.org/images/entities/char_0050_0332.gif) re-Incubation re-Incubation ![[I with combining low line]](https://www.rsc.org/images/entities/char_0049_0332.gif) ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) 50 fitting- 50 fitting-![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[o with combining low line]](https://www.rsc.org/images/entities/char_006f_0332.gif) valent valent ![[R with combining low line]](https://www.rsc.org/images/entities/char_0052_0332.gif) ![[e with combining low line]](https://www.rsc.org/images/entities/char_0065_0332.gif) versible versible |
| Gly-Pro-pNA | Glycine-proline-para-nitroanilide |
| DMSO | Dimethyl sulfoxide |
| DPPIV | Dipeptidyl peptidase 4 |
| RMSE | Root mean squared error |
| VBA | Visual basic for applications |
| RSS | Residual sum of squares |
| TRIS | Tris(hydroxymethyl)aminomethane |
Data availability
The data supporting this article have been included as part of the ESI.† The code for the fitting spreadsheet can be found at https://github.com/JeffreyKeillor/JeffreyKeillor. The version of the code employed for this study is version 1.1.Author contributions
Conceptualization: J. W. K. and L. K. M.; funding acquisition: J. W. K.; supervision: J. W. K.; investigation and methodology: J. W. K. (method development), L. K. M. (characterization and enzymatic assays), writing – original draft: L. K. M.; reviewing and editing: L. K. M. and J. W. K.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
J. W. K. thanks the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Canadian Institutes of Health Research (CIHR) for funding. L. K. M. thanks NSERC for a CGS-D Award.References
- L. K. Mader and J. W. Keillor, Fitting of kinact and KI Values from Endpoint Pre-incubation IC50 Data, ACS Med. Chem. Lett., 2024, 15, 731–738 CAS.
- R. A. Copeland, Slow Binding Inhibitors, Evaluation of Enzyme Inhibitors in Drug Discovery, John Wiley & Sons, 2013, pp. 203–244 Search PubMed.
- E. Mons, S. Roet, R. Q. Kim and M. P. C. Mulder, A Comprehensive Guide for Assessing Covalent Inhibition in Enzymatic Assays Illustrated with Kinetic Simulations, Curr. Protoc., 2022, 2(6), e419 CAS.
- D. Patel, Z. E. Huma and D. Duncan, Reversible Covalent Inhibition–Desired Covalent Adduct Formation by Mass Action, ACS Chem. Biol., 2024, 19(4), 824–838 CAS.
- J. F. Morrison and C. T. Walsh, The behavior and significance of slow-binding enzyme inhibitors, Adv. Enzymol. Relat. Areas Mol. Biol., 1988, 61, 201–301 CAS.
- A. Bandyopadhyay and J. Gao, Targeting biomolecules with reversible covalent chemistry, Curr. Opin. Chem. Biol., 2016, 34, 110–116 CrossRef CAS.
- L. Hillebrand, X. J. Liang, R. A. M. Serafim and M. Gehringer, Emerging and Re-emerging Warheads for Targeted Covalent Inhibitors: An Update, J. Med. Chem., 2024, 67(10), 7668–7758 CrossRef CAS PubMed.
- I. M. Serafimova, M. A. Pufall, S. Krishnan, K. Duda, M. S. Cohen, R. L. Maglathlin, J. M. McFarland, R. M. Miller, M. Frödin and J. Taunton, Reversible targeting of noncatalytic cysteines with chemically tuned electrophiles, Nat. Chem. Biol., 2012, 8(5), 471–476 CrossRef CAS.
- P. Ábrányi-Balogh and G. M. Keserű, Warheads for designing covalent inhibitors and chemical probes, Advances in Chemical Proteomics, Elsevier, 2022, pp. 47–73 Search PubMed.
- S. P. De Visser, M. G. Quesne and R. A. Ward, Cysteine protease inhibition by nitrile-based inhibitors: a computational study, Front. Chem., 2013, 1, 39 Search PubMed.
- J. Plescia and N. Moitessier, Design and discovery of boronic acid drugs, Eur. J. Med. Chem., 2020, 195, 112270 CrossRef CAS PubMed.
- L. Zhang, D. Lin, Y. Kusov, Y. Nian, Q. Ma, J. Wang, A. von Brunn, P. Leyssen, K. Lanko, J. Neyts, A. de Wilde, E. J. Snijder, H. Liu and R. Hilgenfeld, α-Ketoamides as Broad-Spectrum Inhibitors of Coronavirus and Enterovirus Replication: Structure-Based Design, Synthesis, and Activity Assessment, J. Med. Chem., 2020, 63(9), 4562–4578 CrossRef CAS.
- Faridoon, R. Ng, G. Zhang and J. J. Li, An update on the discovery and development of reversible covalent inhibitors, Med. Chem. Res., 2023, 32(6), 1039–1062 CrossRef CAS PubMed.
- Y. B. Kim, L. M. Kopcho, M. S. Kirby, L. G. Hamann, C. A. Weigelt, W. J. Metzler and J. Marcinkeviciene, Mechanism of Gly-Pro-pNA cleavage catalyzed by dipeptidyl peptidase-IV and its inhibition by saxagliptin (BMS-477118), Arch. Biochem. Biophys., 2006, 445(1), 9–18 CrossRef CAS PubMed.
- P. F. Smith, J. Krishnarajah, P. A. Nunn, R. J. Hill, D. Karr, D. Tam, M. Masjedizadeh, J. O. Funk and S. G. Gourlay, A phase I trial of PRN1008, a novel reversible covalent inhibitor of Bruton's tyrosine kinase, in healthy volunteers, Br. J. Clin. Pharmacol., 2017, 83(11), 2367–2376 CrossRef CAS PubMed.
- R. A. Copeland, The drug–target residence time model: a 10-year retrospective, Nat. Rev. Drug Discovery, 2016, 15(2), 87–95 CrossRef CAS PubMed.
- J. Singh, R. C. Petter, T. A. Baillie and A. Whitty, The resurgence of covalent drugs, Nat. Rev. Drug Discovery, 2011, 10(4), 307–317 CrossRef CAS PubMed.
- A. Wang, C. Dorso, L. Kopcho, G. Locke, R. Langish, E. Harstad, P. Shipkova, J. Marcinkeviciene, L. Hamann and M. S. Kirby, Potency, selectivity and prolonged binding of saxagliptin to DPP4: maintenance of DPP4 inhibition by saxagliptin in vitro and ex vivo when compared to a rapidly-dissociating DPP4 inhibitor, BMC Pharmacol., 2012, 12(1), 2 CrossRef CAS PubMed.
- J. Gao and V. Nobile, Chemistry perspectives of reversible covalent drugs, Annual Reports in Medicinal Chemistry, Academic Press, 2021, vol. 56, pp. 75–94 Search PubMed.
- D. E. Ehmann, H. Jahić, P. L. Ross, R. F. Gu, J. Hu, G. Kern, G. K. Walkup and S. L. Fisher, Avibactam is a covalent, reversible, non-β-lactam β-lactamase inhibitor, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(29), 11663–11668 CrossRef CAS.
- Y. R. Alugubelli, Z. Z. Geng, K. S. Yang, N. Shaabani, K. Khatua, X. R. Ma, E. C. Vatansever, C. C. Cho, Y. Ma, J. Xiao, L. R. Blankenship, G. Yu, B. Sankaran, P. Li, R. Allen, H. Ji, S. Xu and W. R. Liu, A systematic exploration of boceprevir-based main protease inhibitors as SARS-CoV-2 antivirals, Eur. J. Med. Chem., 2022, 240, 114596 CrossRef CAS.
- J. M. Bradshaw, J. M. McFarland, V. O. Paavilainen, A. Bisconte, D. Tam, V. T. Phan, S. Romanov, D. Finkle, J. Shu, V. Patel, T. Ton, X. Li, D. G. Loughhead, P. A. Nunn, D. E. Karr, M. E. Gerritsen, J. O. Funk, T. D. Owens, E. Verner, K. A. Brameld, R. J. Hill, D. M. Goldstein and J. Taunton, Prolonged and tunable residence time using reversible covalent kinase inhibitors, Nat. Chem. Biol., 2015, 11(7), 525–531 CrossRef CAS.
- T. D. Owens, K. A. Brameld, E. J. Verner, T. Ton, X. Li, J. Zhu, M. R. Masjedizadeh, J. M. Bradshaw, R. J. Hill, D. Tam, A. Bisconte, E. O. Kim, M. Francesco, Y. Xing, J. Shu, D. Karr, J. LaStant, D. Finkle, N. Loewenstein, H. Haberstock-Debic, M. J. Taylor, P. Nunn, C. L. Langrish and D. M. Goldstein, Discovery of Reversible Covalent Bruton's Tyrosine Kinase Inhibitors PRN473 and PRN1008 (Rilzabrutinib), J. Med. Chem., 2022, 65(7), 5300–5316 CrossRef CAS PubMed.
- D. Bálint, Á. L. Póti, A. Alexa, P. Sok, K. Albert, L. Torda, D. Földesi-Nagy, D. Csókás, G. Turczel, T. Imre, E. Szarka, F. Fekete, I. Bento, M. Bojtár, R. Palkó, P. Szabó, K. Monostory, I. Pápai, T. Soós and A. Reményi, Reversible covalent c-Jun N-terminal kinase inhibitors targeting a specific cysteine by precision-guided Michael-acceptor warheads, Nat. Commun., 2024, 15(1), 8606 CrossRef PubMed.
- P. J. Tonge, Quantifying the Interactions between Biomolecules: Guidelines for Assay Design and Data Analysis, ACS Infect. Dis., 2019, 5(6), 796–808 CrossRef PubMed.
- R. A. Copeland, Assay Considerations for Compound Library Screening, Evaluation of Enzyme Inhibitors in Drug Discovery, John Wiley & Sons, 2013, pp. 123–168 Search PubMed.
- R. A. Copeland, A. Basavapathruni, M. Moyer and M. P. Scott, Impact of enzyme concentration and residence time on apparent activity recovery in jump dilution analysis, Anal. Biochem., 2011, 416(2), 206–210 CrossRef CAS PubMed.
- T. S. Maurer, M. A. Tabrizi-Fard and H. L. Fung, Impact of mechanism-based enzyme inactivation on inhibitor potency: implications for rational drug discovery, J. Pharm. Sci., 2000, 89(11), 1404–1414 CrossRef CAS PubMed.
- B. F. Krippendorff, R. Neuhaus, P. Lienau, A. Reichel and W. Huisinga, Mechanism-based inhibition: deriving K(I) and k(inact) directly from time-dependent IC(50) values, J. Biomol. Screening, 2009, 14(8), 913–923 CrossRef CAS.
- R. Kitz and I. B. Wilson, Esters of Methanesulfonic Acid as Irreversible Inhibitors of Acetylcholinesterase, J. Biol. Chem., 1962, 237(10), 3245–3249 CrossRef CAS.
- L. Mader, S. K. I. Watt, H. R. Iyer, L. Nguyen, H. Kaur and J. W. Keillor, The war on hTG2: warhead optimization in small molecule human tissue transglutaminase inhibitors, RSC Med. Chem., 2023, 14(2), 277–298 RSC.
- J. W. Keillor, N. Chabot, I. Roy, A. Mulani, O. Leogane and C. Pardin, Irreversible inhibitors of tissue transglutaminase, Adv. Enzymol. Relat. Areas Mol. Biol., 2011, 78, 415–447 CrossRef CAS.
- L. K. Mader, J. E. Borean and J. W. Keillor, A practical guide for the assay-dependent characterisation of irreversible inhibitors, RSC Med. Chem., 2025, 16, 63–76 RSC.
- L. S. Lasdon, A. D. Waren, A. Jain and M. Ratner, Design and Testing of a Generalized Reduced Gradient Code for Nonlinear Programming, ACM Trans. Math. Softw., 1978, 4, 34–50 CrossRef.
- L. M. Kopcho, Y. B. Kim, A. Wang, M. A. Liu, M. S. Kirby and J. Marcinkeviciene, Probing prime substrate binding sites of human dipeptidyl peptidase-IV using competitive substrate approach, Arch. Biochem. Biophys., 2005, 436(2), 367–376 CrossRef CAS.
- V. Matheeussen, A.-M. Lambeir, W. Jungraithmayr, N. Gomez, K. Mc Entee, P. Van der Veken, S. Scharpé and I. De Meester, Method comparison of dipeptidyl peptidase IV activity assays and their application in biological samples containing reversible inhibitors, Clin. Chim. Acta, 2012, 413(3), 456–462 CrossRef CAS PubMed.
- L. M. Mihalovits, G. G. Ferenczy and G. M. Keserű, Free Energy Calculations in Covalent Drug Design, Computational Drug Discovery, John Wiley & Sons, 2024, pp. 561–578 Search PubMed.
- P. A. MacFaul, A. D. Morley and J. J. Crawford, A simple in vitro assay for assessing the reactivity of nitrile containing compounds, Bioorg. Med. Chem. Lett., 2009, 19(4), 1136–1138 CrossRef CAS.
- R. A. Copeland, D. L. Pompliano and T. D. Meek, Drug–target residence time and its implications for lead optimization, Nat. Rev. Drug Discovery, 2006, 5(9), 730–739 CrossRef CAS PubMed.
- H. Tao, B. Yang, A. Farhangian, K. Xu, T. Li, Z.-Y. Zhang and J. Li, Covalent-Allosteric Inhibitors: Do We Get the Best of Both Worlds?, J. Med. Chem., 2025, 68(4), 4040–4052 CAS.
- A. Tuley and W. Fast, The Taxonomy of Covalent Inhibitors, Biochemistry, 2018, 57(24), 3326–3337 CrossRef CAS PubMed.
- D. E. Ehmann, H. Jahić, P. L. Ross, R.-F. Gu, J. Hu, G. Kern, G. K. Walkup and S. L. Fisher, Avibactam Is a Covalent, Reversible, Non–β-Lactam β-Lactamase Inhibitor, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(29), 11663–11668 CAS.
- R. A. Copeland, Tight Binding Inhibition, Evaluation of Enzyme Inhibitors in Drug Discovery, John Wiley & Sons, 2013, pp. 245–285 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Derivations of all kinetic equations, table of differential equations, code for numerical modelling and kinetic data for Gly-Pro-pNA KM and kcat determination (pdf). See DOI: https://doi.org/10.1039/d5md00050e |
| This journal is © The Royal Society of Chemistry 2025 |