 Open Access Article
Open Access ArticleSimulation and machine learning driven optimization of Rb2SnBr6-based lead-free perovskite solar cells using diverse ETLs for enhanced photovoltaic performance
Md. Selim
Reza
a,
Avijit
Ghosh
 *a,
Asadul Islam
Shimul
*a,
Asadul Islam
Shimul
 b,
Saeed Hasan
Nabil
c,
Manjuara
Akter
d,
Aijaz Rasool
Chaudhry
b,
Saeed Hasan
Nabil
c,
Manjuara
Akter
d,
Aijaz Rasool
Chaudhry
 e,
Dipongkar Ray
Sobuj
e,
Dipongkar Ray
Sobuj
 f,
Yedluri
Anil Kumar
f,
Yedluri
Anil Kumar
 g,
Shaikat
Biswas
h,
Khorshed
Alam
i and
Maida
Maqsood
j
g,
Shaikat
Biswas
h,
Khorshed
Alam
i and
Maida
Maqsood
j
aDepartment of Electrical and Electronic Engineering, Begum Rokeya University, Rangpur-5400, Bangladesh. E-mail: avijitghosheee@gmail.com
bDepartment of Electrical and Electronic Engineering, Gopalganj Science and Technology University, Gopalganj 8100, Bangladesh
cDepartment of Electrical and Computer Engineering, Lamar University, Beaumont, TX 77710, USA
dDepartment of Computer Science Engineering, The University of Asia Pacific, Dhaka, Bangladesh
eDepartment of Physics, College of Science, University of Bisha, P.O. Box 551, Bisha 61922, Saudi Arabia
fGraduate Research Assistant, Department of Chemistry and Biochemistry, Lamar University, Beaumont, TX 77710, USA
gDepartment of Condensed Matter Physics, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, SIMATS, Chennai 602105, India
hDepartment of Computer Science, Troy University, Troy, USA
iDepartment of Industrial and Systems Engineering, Lamar University, Beaumont, 77710 Texas, USA
jCollege of International Studies, Shenzhen University, Nanhai Ave. 3688, Shenzhen 518060, China
First published on 10th October 2025
Abstract
In this work, n–i–p planar heterojunction perovskite solar cells (PSCs) were simulated using SCAPS-1D, employing Rb2SnBr6 as a lead-free, stable, and cost-effective absorber. Fluorine-doped tin oxide (FTO) served as the transparent substrate, with gold (Au) as the rear contact, and three electron transport layers (ETLs) – ZnSe, In2S3, and CdZnSe – were evaluated. Device I (ZnSe) achieved the best performance with a PCE of 28.73%, VOC of 0.868 V, JSC of 38.09 mA cm−2, and FF of 86.86%. Device II (In2S3) and device III (CdZnSe) exhibited lower efficiencies of 26.62% and 24.04%, respectively. To further analyze performance, a random forest (RF) machine learning model was applied, with SHAP values identifying the most influential parameters. The RF model demonstrated high accuracy (R2 = 0.8825) and strong agreement between predicted and actual efficiencies. These results highlight the potential of Rb2SnBr6, particularly with a ZnSe ETL, for developing high-efficiency, eco-friendly PSCs.
1. Introduction
One of the primary areas of research in energy harvesting (EH) focuses on capturing ambient energy from the surroundings and converting it into electrical energy. This accumulated energy can be used to charge batteries or directly power electronic devices. Power generation in the nanowatt (nW) to milliwatt (mW) range is made possible by harnessing various external energy sources, including solar radiation, thermal gradients, radio frequency (RF) signals, mechanical motion, and environmental vibrations.1 The rising global demand for electricity is compelling scientists to explore alternatives to traditional energy sources. Meanwhile, the enhancing need for eco-friendly energy solutions has become more urgent, driven by the limited availability of non-renewable resources and their harmful environmental impacts, high costs, and significant logistical challenges.2 Among various sustainable energy sources, sun-derived power is widely regarded as one of the most efficient and practical alternatives. Silicon (Si) has become the material of choice for the commercialization of photovoltaic cells due to its numerous advantages, including high power conversion efficiency (PCE), durability, and strong resistance to radiation.3 The development of traditional photocells, incorporating silicon (Si), has been obstructed by inherent limitations like silicon's indirect and suboptimal energy gap, as well as the high costs associated with its production.4 Since 2009, certain hybrid inorganic–organic lead halide perovskite (OILHP) components have emerged as promising substances for solar cells.5–8 Their notable features have garnered significant interest for potential use in solar energy applications. These features include high power conversion efficiency (PCE), an optimal bandgap, a strong absorption coefficient, exceptional mobility of charge carriers, and excellent resistance to defects.4,9 The PCE of absorber photocells has seen remarkable growth in recent years. Starting at 3.8% in 2009, the PCE has made significant advancements, reaching an impressive 26% by 2021.10,11 F. Rahman et al. replicated Rb2SnBr6 in 2025 using the one-dimensional solar cell capacitance simulator (SCAPS-1D), achieving a conceptual peak PCE of 27.25%.12 These remarkable advancements underscore the rapid progress in perovskite solar cell technology and its exceptional energy conversion efficiency. However, the limited stability and the harmful effects associated with the presence of lead (Pb) pose significant challenges to the widespread adoption and further development of perovskite solar cells.13–15 Despite ongoing researches to develop lead-free perovskite materials, it is still exceedingly challenging to obtain the identical layers of surroundings durability and PCE as lead-based solar cells.12 Therefore, research into PV components that are both greatly effective and lead-free and appropriate for commercial use is immensely needed in the photocell sector.16,17 X2SnBr6 (where X represents elements such as Cs, Rb, K, and Na) is a member of the X2BA6 family of compounds. In this family, X denotes cations like Cs+, Rb+, K+, and Na+, B represents cations such as Si2+, Ge2+, Sn2+, and Pb2+,18 and A signifies anions, for example, F, Cl, Br, and I. Within the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, X2SnBr6 exhibits a high-symmetry structure akin to that of a cubic halide solar cell.19,20 The authorized transitions in band-edge conditions, facilitated by parity, observed in X2SnBr6 materials suggest their promising potential for next-generation solar cell utilization.21 The energy gap of a substance plays an essential role in calculating the PCE of photo-cells, as it immediately impacts generation and solar absorption. Therefore, optimizing the bandgap is essential for improving photocell efficiency. According to the Shockley–Queisser limit, perovskite photocells could gain a maximum PCE of up to 33% if the material's energy gap is carefully tuned between 1.2 and 1.4 eV.22 ZnSe, In2S3, CdZnSe, and Rb2SnS3 have garnered significant attention for their potential functions in photocells and optoelectronics. ZnSe, with its hexagonal crystal structure and wide bandgap of 1.8 eV, holds promise for photovoltaic applications. However, its relatively low carrier mobility limits its overall efficiency, presenting a challenge for further optimization.23 Research is ongoing to enhance its performance using doping and hybridization techniques. In2S3, with an energy gap limit from 2.0 to 2.4 eV, is known for its high optical transparency and conductivity, making it ideal for use in thin-film solar cells and transparent electronics.24,25 ZnSe, In2S3, and CdZnSe are promising components for electron transport layers (ETLs) in photocells and optoelectronics. ZnSe, with an energy gap of 1.8 eV, offers high electron mobility and transparency, making it suitable for thin-film and perovskite solar cells, though it can face adhesion issues. In2S3, with a 2.1 eV bandgap, provides good transparency and moderate electron mobility but suffers from low carrier mobility, limiting efficiency. CdZnSe, a ternary compound with an energy gap of 2.7–2.8 eV, offers elevated electron mobility and transparency, ideal for transparent and adaptable electronics, but faces obstacles related to long-term stability and expandability for large-area applications.26 Rb2SnBr6 is selected as the absorber layer due to its lead-free composition, making it an eco-friendly and non-toxic replacement for traditional lead-based perovskites. As an all-inorganic, vacancy-ordered double perovskite, it offers superior thermal and moisture stability, enhancing device longevity and reliability compared to organic–inorganic hybrids. With a suitable band gap (1.0–1.3 eV), strong light absorption, good charge transport properties, and intrinsic defect tolerance, Rb2SnBr6 is well-suited for high-performance photovoltaic applications. It is also compatible with inorganic electron transport layers like ZnSe, further improving efficiency and stability. Recent studies have shown promising efficiencies and operational stability of Rb2SnBr6-based devices, supporting their potential for scalable, eco-friendly solar technologies. Ongoing research continues to advance its charge transport and interface properties, bringing it closer to commercial viability as a robust absorber material.12,27,28 However, its low carrier mobility is a major limitation in its use for high-performance solar cells. All these materials share common challenges, primarily related to low carrier mobility, which affects their efficiency in photovoltaic devices. Ongoing research aims to overcome these challenges through doping, hybridization, and advanced deposition techniques. While ZnSe and Rb2SnBr6 show promise as absorber layers in thin-film solar cells, In2S3 and CdZnSe are more commonly used as buffer or transparent conducting oxide layers.29 Each material offers unique advantages, but further optimization is required to improve their performance and stability. The integration of these materials into tandem solar cells could potentially enhance their efficiency.30 Au (gold) and Al (aluminum) are used as metal contacts due to their suitable electrical properties and energy level alignment with adjacent layers. Gold, with its high work function (5.47 eV), forms an efficient ohmic contact with the valence band of Rb2SnBr6, facilitating effective hole extraction. Additionally, Au is chemically stable and resistant to oxidation, ensuring long-term interface stability. On the other hand, aluminum has a lower work function (4.2 eV), making it well-suited for forming an ohmic contact with the conduction band of ZnSe, thereby enabling efficient electron extraction. Al is also cost-effective and highly conductive, which supports scalable and efficient device fabrication. Altogether, these metal contacts are carefully chosen to refine charge collection, reduce recombination losses, and boost overall model performance.31,32 Continued research and development are necessary to fully exploit their potential in next-generation solar cells and optoelectronic devices. By addressing their limitations, these materials could become key components in sustainable, high-efficiency solar technology. The future of solar cell technology depends largely on the development of materials that offer a combination of high efficiency, long-term stability, and ease of fabrication. Materials such as ZnSe, In2S3, CdZnSe, and Rb2SnBr6 each present unique merits in terms of optical attributes, charge carrier mobility, and material stability. However, to fully understand their
capability in solar energy applications, these materials must overcome significant challenges related to performance, scalability, and integration with other components. Ongoing research into doping strategies, material hybridization, and advanced fabrication techniques will be essential in advancing these materials toward commercial viability and widespread adoption in next-generation solar cells and optoelectronic devices.
m space group, X2SnBr6 exhibits a high-symmetry structure akin to that of a cubic halide solar cell.19,20 The authorized transitions in band-edge conditions, facilitated by parity, observed in X2SnBr6 materials suggest their promising potential for next-generation solar cell utilization.21 The energy gap of a substance plays an essential role in calculating the PCE of photo-cells, as it immediately impacts generation and solar absorption. Therefore, optimizing the bandgap is essential for improving photocell efficiency. According to the Shockley–Queisser limit, perovskite photocells could gain a maximum PCE of up to 33% if the material's energy gap is carefully tuned between 1.2 and 1.4 eV.22 ZnSe, In2S3, CdZnSe, and Rb2SnS3 have garnered significant attention for their potential functions in photocells and optoelectronics. ZnSe, with its hexagonal crystal structure and wide bandgap of 1.8 eV, holds promise for photovoltaic applications. However, its relatively low carrier mobility limits its overall efficiency, presenting a challenge for further optimization.23 Research is ongoing to enhance its performance using doping and hybridization techniques. In2S3, with an energy gap limit from 2.0 to 2.4 eV, is known for its high optical transparency and conductivity, making it ideal for use in thin-film solar cells and transparent electronics.24,25 ZnSe, In2S3, and CdZnSe are promising components for electron transport layers (ETLs) in photocells and optoelectronics. ZnSe, with an energy gap of 1.8 eV, offers high electron mobility and transparency, making it suitable for thin-film and perovskite solar cells, though it can face adhesion issues. In2S3, with a 2.1 eV bandgap, provides good transparency and moderate electron mobility but suffers from low carrier mobility, limiting efficiency. CdZnSe, a ternary compound with an energy gap of 2.7–2.8 eV, offers elevated electron mobility and transparency, ideal for transparent and adaptable electronics, but faces obstacles related to long-term stability and expandability for large-area applications.26 Rb2SnBr6 is selected as the absorber layer due to its lead-free composition, making it an eco-friendly and non-toxic replacement for traditional lead-based perovskites. As an all-inorganic, vacancy-ordered double perovskite, it offers superior thermal and moisture stability, enhancing device longevity and reliability compared to organic–inorganic hybrids. With a suitable band gap (1.0–1.3 eV), strong light absorption, good charge transport properties, and intrinsic defect tolerance, Rb2SnBr6 is well-suited for high-performance photovoltaic applications. It is also compatible with inorganic electron transport layers like ZnSe, further improving efficiency and stability. Recent studies have shown promising efficiencies and operational stability of Rb2SnBr6-based devices, supporting their potential for scalable, eco-friendly solar technologies. Ongoing research continues to advance its charge transport and interface properties, bringing it closer to commercial viability as a robust absorber material.12,27,28 However, its low carrier mobility is a major limitation in its use for high-performance solar cells. All these materials share common challenges, primarily related to low carrier mobility, which affects their efficiency in photovoltaic devices. Ongoing research aims to overcome these challenges through doping, hybridization, and advanced deposition techniques. While ZnSe and Rb2SnBr6 show promise as absorber layers in thin-film solar cells, In2S3 and CdZnSe are more commonly used as buffer or transparent conducting oxide layers.29 Each material offers unique advantages, but further optimization is required to improve their performance and stability. The integration of these materials into tandem solar cells could potentially enhance their efficiency.30 Au (gold) and Al (aluminum) are used as metal contacts due to their suitable electrical properties and energy level alignment with adjacent layers. Gold, with its high work function (5.47 eV), forms an efficient ohmic contact with the valence band of Rb2SnBr6, facilitating effective hole extraction. Additionally, Au is chemically stable and resistant to oxidation, ensuring long-term interface stability. On the other hand, aluminum has a lower work function (4.2 eV), making it well-suited for forming an ohmic contact with the conduction band of ZnSe, thereby enabling efficient electron extraction. Al is also cost-effective and highly conductive, which supports scalable and efficient device fabrication. Altogether, these metal contacts are carefully chosen to refine charge collection, reduce recombination losses, and boost overall model performance.31,32 Continued research and development are necessary to fully exploit their potential in next-generation solar cells and optoelectronic devices. By addressing their limitations, these materials could become key components in sustainable, high-efficiency solar technology. The future of solar cell technology depends largely on the development of materials that offer a combination of high efficiency, long-term stability, and ease of fabrication. Materials such as ZnSe, In2S3, CdZnSe, and Rb2SnBr6 each present unique merits in terms of optical attributes, charge carrier mobility, and material stability. However, to fully understand their
capability in solar energy applications, these materials must overcome significant challenges related to performance, scalability, and integration with other components. Ongoing research into doping strategies, material hybridization, and advanced fabrication techniques will be essential in advancing these materials toward commercial viability and widespread adoption in next-generation solar cells and optoelectronic devices.
This study investigates the potential of Rb2SnBr6-based perovskite solar cells by evaluating various electron transport layers (ETLs) to propose an optimized device configuration. The novelty of this work lies in the integrated simulation and machine learning approach: multiple ETLs (ZnSe, In2S3, and CdZnSe) were systematically assessed, identifying ZnSe as the optimal candidate with a superior simulated PCE of 28.73%. A random forest model with SHAP analysis was employed to quantify the relative impact of key device parameters, providing interpretable insights and predictive guidance, an approach not previously applied to Rb2SnBr6-based PSCs. While prior SCAPS-based studies have reported efficiency estimates, a systematic ETL comparison combined with ML-driven analysis has not been explored. This study addresses that gap by offering both optimized device design and actionable design insights for future experimental development.
Building on previous research, this study analyzed key factors affecting performance, including operating temperature, metal contact work function, series and shunt resistances, electron surface recombination, charge carrier density, and layer thickness and defect density in both the absorber and ETL. Device performance was evaluated using current–voltage (J–V) characteristics and quantum efficiency (QE), and the results were compared with prior studies to highlight technological improvements. These analyses provide comprehensive guidance for designing high-efficiency, stable, and scalable Rb2SnBr6-based perovskite solar cells.
2. In simulation techniques, models are employed and band structures are aligned
2.1 Computation using SCAPS-1D
The numerical structure of PSCs can be replicated using a single-dimensional simulator called SCAPS-1D, which was produced at the University of Gent in Belgium.33 Key parameters such as layer depth, bandgap, defect density, and doping concentration are critically tuned to elevate the efficiency of photocell systems.34,35 This mathematical analysis depends on two basic equations: the Poisson equation (eqn (1)) and the continuity equations (eqn (2) and (3)). The Poisson equation relates the electrostatic field E(x), the material's permittivity, and the total charge concentration. Meanwhile, the continuity equations describe the transport and behavior of charge carriers within the device: eqn (2) for electrons and eqn (3) for holes, capturing their generation, recombination, and flow under varying conditions.36 | (1) |
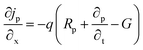 | (2) |
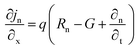 | (3) |
The density of electron pair recombination, density of hole pair recombination, and density of generation are denoted by the symbols Rn, Rp, and G, respectively. The formula J = jp + jn presents the overall density of current. On the other hand, the symbols jp and jn, respectively, represent the current concentrations for charge carriers (holes and electrons). Eqn (4) and (5) illustrate the development of a drift-diffusion formula for determining the electron and hole flow densities.
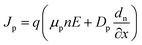 | (4) |
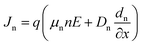 | (5) |
 | (6) |
The mass diffusivity, diffusion length, and minority carrier lifetime are denoted by the icons D(n,p), L(n,p), and T(n,p), respectively. SCAPS-1D computes the coefficient of absorption, which characterizes the connection between photons and the perovskite layer, in accordance with what are known as the “Tauc laws,” using eqn (7).
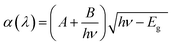 | (7) |
2.2 The form of the Rb2SnBr6 photocell
Fig. 1(a) illustrates the n–i–p junction model of the Rb2SnBr6-based photocell, which forms the core focus of this study. The n, i, and p regions represent the ETL, the intrinsic absorber layer, and the HTL, respectively. In the numerical model, the device architecture includes three ETLs, an absorber layer, a front contact, and a rear (back) contact. Within this configuration, when excitons are generated in the perovskite layer, the ETL plays a crucial role by facilitating the transport of electrons while acting as a barrier to hole movement. This selective charge transport enhances carrier separation and minimizes recombination, contributing to improved device efficiency. The band alignments for the (Au/Rb2SnBr6/ETLs/FTO/Al) configurations are shown in Fig. 1(b). Notably, gold (Au), which has been the subject of several previous studies, exhibits the highest work function, exceeding 5.47 eV.37,38 Due to the high work function of gold (Au), constructing a solar cell with this material effectively forms a Schottky barrier that facilitates electron collection. Its optimal alignment with the ZnSe electron band ensures efficient hole transit, thereby minimizing recombination losses. This model increases the overall conductivity, stability, and efficiency of the solar cell. Similarly, with Al also exhibiting a high work function, constructing an (Au/Rb2SnBr6/ETL (ZnSe, In2S3, CdZnSe)/FTO/Al) solar cell creates a Schottky barrier to effectively collect electrons.The excellent alignment between Al and the ZnSe electron band further contributes to improved cell performance and stability.39 A well-known application of the quarter-wavelength (λ/4) principle is in enhancing solar cell performance by optimizing layer thickness to the highest optical surface and minimizing reflection. When a level has a thickness equal to an odd factor of λ/4, where λ is the shortest wavelength of light within the material, harmful obstruction is reduced, thereby decreasing reflection and enhancing light propagation and absorption. Specifically, adjusting the thickness of the FTO (fluorine-doped tin oxide) layer to approximately λ/4 improves sunlight penetration and optical clarity, particularly within the critical 500–700 nm wavelength range, where solar irradiance is most intense. To maximize light absorption and minimize reflection, similar quarter-wavelength (λ/4) thickness adjustments should be applied to the ZnSe, In2S3, CdZnSe, and Rb2SnBr6 layers. This study investigates three distinct device configurations without an HTL, aiming to identify the optimal ETL for enhanced performance. Each setup is analyzed in detail, and the configuration yielding the best efficiency is selected. Throughout the investigation, the composition of the absorber layer, Rb2SnBr6, remains constant to ensure consistency and isolate the effects of ETL variation. After optimizing the model, the roles of temperature, density of defects (Nt), series-shunt resistance, and other key parameters are analyzed. These include characteristics such as thickness (t) and (donor (ND) and acceptor (NA)) density. The initial components, including the effective density of the conduction band (NC), energy gap (Eg), mobility of electrons (μn), insulator permittivity (εr), effective density of the valence band (NV), electron affinity (χ), hole mobility (μp), and various ETLs, FTO, and absorber materials, are listed in Table 1. The SCAPS-1D simulation is performed under AM1.5 solar spectrum conditions with an illumination intensity of 100 mW cm−2 to evaluate the performance of the device.
| Factors | Rb2SnBr612 | ZnSe40 | In2S341 | CdZnSe42 | FTO43 |
|---|---|---|---|---|---|
| t (nm) | 1000 | 50 | 50 | 50 | 50 |
| E g (eV) | 1.208 | 1.8 | 2.1 | 2.8 | 3.6 |
| χ (eV) | 4.25 | 4.55 | 4.65 | 3.8 | 4.5 |
| εr | 4.208 | 5.54 | 13.5 | 10 | 10 |
| N C (cm−3) | 1.842 × 1018 | 1 × 1018 | 1.8 × 1019 | 1 × 1018 | 2 × 1018 |
| N V (cm−3) | 1.273 × 1019 | 1 × 1018 | 4 × 1013 | 1 × 1018 | 1.8 × 1019 |
| μ n (cm2 V−1 s−1) | 100 | 100 | 400 | 100 | 100 |
| μ h (cm2 V−1 s−1) | 250 | 50 | 210 | 25 | 20 |
| N D (cm−3) | 0 | 1 × 1019 | 1 × 1019 | 1 × 1019 | 1 × 1018 |
| N t (cm−3) | 1 × 1013 | 1 × 1013 | 1 × 1013 | 1 × 1013 | 1 × 1014 |
| N A (cm−3) | 1 × 1017 | 0 | 0 | 0 | 0 |
The increase in efficiency may be readily seen by calculating the lattice mismatch between the perovskite and ETL layers using eqn (8).
 | (8) |
The lattice constants for the substrate, lattice misfit, and epitaxial thin film are as, ae, and δ, respectively. The lattice properties are an additional important consideration in the development and design of heterojunction models. Table 2 presents the lattice parameters and percentage of lattice mismatch for devices based on Rb2SnBr6 with various reported ETLs. The lattice mismatch between Rb2SnBr6 and ZnSe was the lowest at 51.08%, while mismatches with other ETLs were substantially higher. Although these values are relatively large (>50%), the simulations assume ideal, defect-free interfaces. This allows the model to predict theoretical upper-limit performance, which explains the excellent PCE observed for device I in Table 3. In practical devices, such high mismatches would likely introduce interface defects and degrade performance. Therefore, interface engineering, passivation layers, or alternative ETLs with better lattice compatibility would be essential to achieve comparable efficiencies experimentally. This clarification emphasizes that the simulation results should be interpreted as performance trends and design guidance rather than direct fabrication predictions. Table 3 summarizes the simulated performance parameters for the Al/FTO/ETL/Rb2SnBr6/Au structures using the three ETL components.
| Layers | Lattice parameters | Lattice mismatch (%) | ||
|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | ||
| Rb2SnBr6 | 11.01 | 11.01 | 11.01 | — |
| ZnSe | 3.98 | 3.98 | 6.53 | 51.08 |
| In2S3 | 7.621 | 7.621 | 32.053 | 97.73 |
| CdZnSe | 5.858 | — | — | 61.08 |
| Model | V OC (V) | J SC (mA cm−2) | FF (%) | PCE (%) |
|---|---|---|---|---|
| Al/FTO/ZnSe/Rb2SnBr6/Au | 0.868 | 38.094 | 86.86 | 28.73 |
| Al/FTO/In2S3/Rb2SnBr6/Au | 0.843 | 38.087 | 82.93 | 26.62 |
| Al/FTO/CdZnSe/Rb2SnBr6/Au | 0.869 | 38.093 | 72.60 | 24.04 |
3. Results and discussion
3.1 The factor of absorption for each single layer
The absorption coefficient of each material layer, as determined using the SCAPS-1D simulator, plays a vital role in defining the amount of photoenergy absorbed. This, in turn, meaningfully influences the PCE of the solar cell. High absorption in the first layers of photocells is essential since it shows which light wavelengths the components can absorb.30,44 The solar cell (SC) architecture used in all three device configurations consists of multiple material layers, including ZnSe, In2S3, CdZnSe, and Rb2SnBr6, each selected for their favorable optical and electronic properties. FTO (fluorine-doped tin oxide) serves as the transparent front contact, while the remaining layers function as buffer or absorber materials. Fig. 2 illustrates the wavelength-dependent absorption coefficients for FTO, ZnSe, In2S3, CdZnSe, and Rb2SnBr6. FTO shows its zenith absorption at 172.21 nm, primarily within the deep ultraviolet (UV) region. In comparison, ZnSe, In2S3, CdZnSe, and Rb2SnBr6 demonstrate significant absorption peaks around 200 nm, indicating their effectiveness in the UV-visible spectrum. The maximum absorption coefficients (in cm−1) for these materials are as follows: Rb2SnBr6 (202![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260.602), ZnSe (156
260.602), ZnSe (156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 345.149), In2S3 (139
345.149), In2S3 (139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 725.667), CdZnSe (110
725.667), CdZnSe (110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.769), and FTO (100
192.769), and FTO (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000). These high absorption values are critical for efficient photon harvesting, directly impacting the PCE of the photocells. Among the studied components, Rb2SnBr6 shows the highest absorption, making it a strong candidate for the active perovskite layer. The combination of these materials supports broad-spectrum light absorption, effective charge carrier generation, and optimized solar cell performance.
000). These high absorption values are critical for efficient photon harvesting, directly impacting the PCE of the photocells. Among the studied components, Rb2SnBr6 shows the highest absorption, making it a strong candidate for the active perovskite layer. The combination of these materials supports broad-spectrum light absorption, effective charge carrier generation, and optimized solar cell performance.
3.2 Correlation between the work function and solar cell efficiency
For solar panels to function and be effective overall, the left contact is crucial for solar energy.45 The back contact, an essential part of the electrical structure from which resources show origination, should have the lowest ohmic losses possible in order to improve solar cell performance. A poor contact model could result in elevated opposition in series, which reduces charge movement.To provide endurance, the back contact can also offer strong adhesion and limited combined communication with the semiconductor. A tiny active zone, less photon absorption, and obscuring can all be consequences of suboptimal contact designs. Well-designed left contacts boost charge carrier buildup and reduce recombination losses, increasing the photo module's overall efficiency and dependability. The reason for choosing ideal metals for the right and left contacts, respectively, is their work functions being restricted to 4.20 eV to 4.95 eV and 5.0 eV to 5.47 eV. Fig. 3(a)–(d) displays the PV properties of structures I, II, and III with various left vs. right connections. We have observed that devices I, II, and III function optimally when gold (Au) is utilized as the back contact. However, the same value is observed for all materials with the appropriate contacts (Al, Fe, Ru, and Tc).
Although it may create an oxide layer, aluminum (Al) is the most economical option among those suitable connections because of its high conductivity and low cost. Al is frequently used in solar cells because it offers a good balance between cost and performance, making it the most practical option for contacts in this application. Although different left contacts provide similar results to Al, Au is employed in Rb2SnBr6 perovskites due to its high work function, which aligns well with the valence band, and its chemical inertness that ensures stable hole extraction. Unlike Ni, Cu, and Ge, Au does not oxidize or react with halides, thereby providing superior long-term stability and reproducibility. With Au and Al used as the back and front contacts, respectively, the devices achieved the highest performance, with a PCE of 28.23%, FF of 86.765%, JSC of 37.343 mA cm−2, and VOC of 0.871 V when ZnSe was employed as the ETL.
3.3 Electronic band diagram of Rb2SnBr6
The refined energy band gaps for PSCs incorporating Rb2SnBr6 as the perovskite layer are presented in Fig. 4(a)–(c). The selection of the ETL plays an important role in finding the conduction and valence band offsets, which represent the power rank mismatches between the absorber and bordering transport layers. In this configuration, zinc selenide (ZnSe) is employed as the ETL in conjunction with Rb2SnBr6 as the light-absorbing material. The arrangement of power levels at the interfaces, particularly between the ETL and absorber, is essential for efficient carrier separation, minimized recombination reduction, and enhanced total device performance. Proper band alignment facilitates the smooth transfer of photogenerated charge carriers, reducing potential energy barriers that hinder charge flow. In this structure, photogenerated electrons are extracted through the right contact (Al), where holes are collected at the left metallic electrode (Au), enabling efficient carrier separation and current flow. This optimized energy band configuration demonstrates the importance of interfacial engineering in PSCs, highlighting how careful selection and alignment of materials significantly influence power conversion efficiency. Device performance can be greatly influenced by improper energy band alignment at the interface between the ETL and Rb2SnBr6 absorber. Such misalignment could lead to increased interfacial recombination, which is primarily determined by the surface properties of the contacting layers. Fine-tuning the electrical characteristics of the ETL is crucial for efficient electron extraction in Rb2SnBr6-based devices. The ETL must possess a higher ionization energy than the absorber to ensure proper energy-level alignment, which promotes smooth electron transfer, suppresses recombination, and improves device efficiency.In ideal models, the Fermi level lies near the band of conduction, as shown in Fig. 4(a), with ZnSe as the ETL. Similar performance is also observed with In2S3 and CdZnSe (Fig. 4(b) and (c)), confirming that effective alignment can be achieved with multiple ETLs. The corresponding device architectures are: device-I (Al/FTO/ZnSe/Rb2SnBr6/Au), device-II (Al/FTO/In2S3/Rb2SnBr6/Au), and device-III (Al/FTO/CdZnSe/Rb2SnBr6/Au), as illustrated in Fig. 4(a)–(c).
Cell performance largely depends on the conduction band offset (CBO) and valence band offset (VBO). A spike-like CBO (0–0.2 eV) is typically ideal, as it forms a small barrier at the ETL/absorber interface that suppresses electron backflow while maintaining efficient electron transport, thereby reducing interfacial recombination and enhancing VOC. A large positive CBO (>0.4 eV) hinders current flow, while a negative (cliff-like) CBO can increase recombination. Similarly, a spike-like VBO—where the absorber's valence band maximum (VBM) lies slightly below the HTL—improves hole transport and VOC, whereas a cliff-like VBO reduces performance.
In our devices, ZnSe, In2S3, and CdZnSe act as n-type ETLs with strong electron affinity, while Rb2SnBr6, being intrinsic or slightly p-type, provides efficient light absorption, charge generation, and hole transport. The small CBM difference (∼0.2 eV) between ZnSe (1.8 eV) and Rb2SnBr6 (1.208 eV) forms a shallow barrier that blocks hole back-transfer without impeding electron flow, ensuring effective charge separation and minimal recombination losses. Although the calculated CBOs for ZnSe (−0.3 eV) and In2S3 (−0.4 eV) are slightly cliff-like, the cliffs are shallow, and the ETLs’ high electron affinity and conductivity enable rapid electron extraction. The favorable VBO further ensures efficient hole transport toward the HTL. Altogether, these factors minimize interfacial recombination and allow high FF and PCE, demonstrating that device performance is determined not solely by the CBO magnitude but by the combined effect of electron and hole transport at the interfaces.
Fig. 4 illustrates the various cliff and spike shapes that have a direct effect on this photocell's efficiency. We’re aware that
| VBO = {χ(ETL/HTL) − Eg(Absorber) + Eg(ETL/HTL) − χ(Absorber)} | (9) |
| CBO = χAbsorber − χ(ETL/HTL) | (10) |
Eqn (9) and (10) were used to find out the CBO and VBO.46 For the absorber and ETLs, the CBO and VBO is:
For the ZnSe ETL
| CBO = χAbsorber − χETL = 4.25 − 4.55 = −0.3 eV |
| VBO = χETL − χAbsorber + Eg(ETL) − Eg(Absorber) = 4.55 − 4.25 + 1.8 − 1.208 = 0.892 eV |
For the In2S3 ETL
| CBO = χAbsorber − χETL = 4.25 − 4.65 = −0.4 eV |
| VBO = χETL − χAbsorber + Eg(ETL) − Eg(Absorber) = 4.65 − 4.25 + 2.1 − 1.208 = 1.292 eV |
For the CdZnSe ETL
| CBO = χAbsorber − χETL = 4.25 − 3.8 = 0.45 eV |
| VBO = χETL − χAbsorber + Eg(ETL) − Eg(Absorber) = 3.8 − 4.25 + 2.8 − 1.208 = 1.142 eV |
3.4 Impact of thickness of both the ETL and absorber layer
The thickness of the ETL plays a vital role in the overall efficiency of PSCs by affecting carrier mobility and facilitating effective electron extraction from the perovskite layer. As illustrated in Fig. 5(a), the effect of varying ETL thickness from 25 nm to 400 nm was analyzed for ZnSe, In2S3, and CdZnSe-based devices. The results indicate that changes in ETL thickness within this limit have a minimal role in the PCE of the devices, demonstrating that performance remains relatively stable regardless of the ETL used. However, in devices utilizing CdZnSe, reducing the ETL thickness from 50 nm to 25 nm caused a notable drop in VOC from 0.93 V to 0.872 V, even though slight improvements in PCE, JSC, and FF were observed when increasing the thickness from 25 nm to 50 nm. For devices incorporating ZnSe and In2S3 as ETLs, all photovoltaic parameters remained nearly constant, except for ZnSe, which showed a slight increase in JSC with increasing thickness. Although similar performance was recorded at both 25 nm and 50 nm during simulation, a thickness of 50 nm was selected as optimal, as very thin layers (e.g., 25 nm) may introduce challenges in experimental reproducibility and device fabrication. At the optimized ETL thickness of 50 nm, the devices demonstrated the following performance metrics: device-I ZnSe achieved an efficiency of 28.40%, a VOC of 0.898 V, a FF of 87.86%, and a JSC of 37.08 mA cm−2; device-II (In2S3) showed an efficiency of 26.40%, a VOC of 0.848 V, an FF of 82.86%, and a JSC of 38.08 mA cm−2; and device-III (CdZnSe) showed an efficiency of 24.04%, a VOC of 0.898 V, an FF of 87.86%, and a JSC of 37.08 mA cm−2. | ||
| Fig. 5 Effect of PV factors considering the variation in the thickness of the (a) ETL layer and (b) absorber layer on efficiency, VOC, JSC, and FF. | ||
These findings confirm that a 50 nm ETL thickness offers optimal performance while maintaining practical feasibility for further investigations.
Fig. 5(b) demonstrates the effect of varying perovskite layer thickness from 200 nm to 2000 nm on the performance of the reported devices, keeping all other factors from Table 1 stable. Enhancing the thickness of the perovskite absorber layer is crucial to achieving high device efficiency, as it directly influences photon absorption, charge generation, and recombination dynamics. The goal is to determine an optimal thickness that maximizes performance while minimizing material usage, thereby reducing production costs. The simulation results show that increasing the absorber thickness from 200 nm to 1000 nm significantly improves device performance across all configurations. Specifically, for device-I, the efficiency, VOC, and short circuit current increased from 22.59% to 28.73%, 0.842 V to 0.868 V, and 29.52 to 38.094 mA cm−2, respectively. Similarly, device-II exhibited improvements from 19.25% to 26.62% in PCE, 0.833 V to 0.843 V in VOC, and 29.52 to 38.087 mA cm−2 in JSC. Device-III showed a PCE increase from 16.94% to 24.04%, VOC slightly varied from 0.872 to 0.869 V, and JSC rose from 29.52 to 38.092 mA cm−2. Beyond a thickness of 1000 nm, these performance metrics plateaued, indicating no further gains with additional material. Throughout the thickness range, the FF remained constant at 86.86%, 82.93%, and 72.60% for devices-I, -II, and -III, respectively. As the absorber layer becomes thicker, both carrier generation and recombination rates increase; thus, an optimal balance must be achieved. Based on these findings, a thickness of 1000 nm is selected as the optimal value, offering the best trade-off between performance enhancement and material efficiency.
3.5 Impact of density of doping of the perovskite layer and ETL layer
Optimizing the acceptor doping concentration (NA) in the perovskite layer is pivotal for enhancing solar cell efficiency. Proper doping improves charge carrier concentration, strengthens the built-in solar field at the p–n junction, and enhances charge separation and extraction, thereby boosting total model performance. However, excessive doping can lead to enhanced recombination rates, altered charge transport mechanisms, and the formation of defects, which reduce the VOC and efficiency. On the other hand, insufficient doping results in weak electric fields and poor carrier separation. Moreover, achieving the optimal doping level adds complexity to the fabrication process and can affect charge carrier mobility. Therefore, precise control of doping concentration is essential to balance enhanced performance with manufacturability, less recombination, and secure efficient carrier transport in high-performance solar cells. In our simulations, the NA of the absorber layer was systematically varied from 1014 to 1021 cm−3 to determine the optimal value for device performance. As shown in Fig. 6(a), the VOC and JSC remain relatively constant up to a doping level of 1016 cm−3. Beyond this point, VOC began to increase with higher NA values. This upward trend is attributed to a reduction in recombination losses and improved hole collection efficiency resulting from the enhanced doping. The increase in NA strengthens the internal electric field, facilitating more efficient charge separation and transport, thereby contributing to the observed rise in VOC. The JSC remained largely unaffected by changes in the NA until it reached 1018 cm−3, after which a noticeable decline was observed. This reduction in JSC was particularly significant in devices utilizing In2S3 and ZnSe as electron transport layers, while the decrease was slightly less pronounced in devices employing CdZnSe. The drop in JSC at higher doping levels is primarily attributed to the increased presence of impurities and defects within the absorber layer, which act as non-radiative recombination centers. | ||
| Fig. 6 Effect of PV factors considering the variation in the acceptor density of (a) the perovskite layer and donor density of (b) the ETL layer on PCE, VOC, JSC, and FF. | ||
These defects shorten the carrier lifetime and reduce the number of photogenerated charge carriers that can be effectively collected, ultimately diminishing the device's current output. The FF exhibited a gradual increase with rising NA, peaking at 1016 cm−3, beyond which it remained relatively constant even as NA exceeded 1018 cm−3. This behavior reflects the sensitivity of FF to internal recombination dynamics within the device. At higher doping levels, increased defect densities lead to elevated recombination rates, thereby hindering efficient charge collection at the interfaces. Similarly, the PCE remained stable up to an NA of 1016 cm−3 followed by a modest rise before beginning to decline after 1017 cm−3.47
This drop is primarily assigned to the compounded effects of intensified recombination and disrupted charge transport pathways at excessively high doping levels. These simulation results underscore the important impact of NA in shaping the performance of perovskite solar cells. Achieving an optimal doping concentration is essential for enhancing carrier density, suppressing recombination losses, and promoting effective charge transport. Based on our findings, an NA of 1018 cm−3 represents the optimal value, offering the best balance between efficiency and device stability. Fig. 6(b) further investigates the impact of donor concentration (ND) on the ETL, spanning the limit of 1014 cm−3 to 1021 cm−3. The findings demonstrate that as the donor concentration rose to 1018 cm−3, the photovoltaic properties of In2S3 and CdZnSe stabilized. However, a plateau was then achieved, suggesting a minor drop in performance. On the other hand, ZnSe stability kept becoming a little better until it reached a donor concentration of 1019 cm−3. This pattern is consistent with earlier research findings.47 This implies that increased donor concentrations improve PCE by facilitating charge carrier extraction and transfer at the ETL/perovskite interface. However, an increase in series resistance happens when the ND is too high, which has a detrimental impact on the model's total performance. To enhance device performance, an ND of 1017 cm−3 was selected for additional adjustment.
3.6 Effects of a Rb2SnBr6 absorber and ETL's defect density Nt fluctuations on the photovoltaic performance of device-I
The effect of defect density (Nt) in both the Rb2SnBr6 perovskite and ZnSe ETL on the PV operation of device-I was investigated over a wide range of values, from 1010 to 1015 cm−3. This analysis is crucial, as defect states in these layers play an important role in finding the total efficiency and stability of the model. As presented in Fig. 7(a)–(d), when the density of defects of the Rb2SnBr6 perovskite increases from 1010 to 1016 cm−3, the performance parameters, namely PCE, JSC, and FF, exhibit a gradual but consistent decline. The efficiency drops slightly from 28.73% to 28.54%, the short-circuit current decreases from 38.09 to 38.078 mA cm−2, and the fill factor falls from 86.86% to 86.75%. These changes, though minimal, indicate that up to a density of defects of 1014 cm−3, the perovskite layer can still support effective charge transport and extraction, with only minor losses due to recombination. Yet, once the absorber defect density surpasses 1014 cm−3 a more pronounced deterioration in device performance is observed. This is attributed to the increase in non-radiative recombination centers, trapping charge carriers and reducing the overall carrier lifetime, leading to substantial losses in both voltage and current generation.48 Such defect-related losses are particularly detrimental in materials like Rb2SnBr6, where the defect tolerance is lower compared to other halide-based semiconductors. In contrast, the variation of defect density in the ZnSe ETL, across the same range from 1010 to 1014 cm−3, shows a negligible impact on all the evaluated photovoltaic parameters. | ||
| Fig. 7 Role of PV factors considering the modification in the defect density of the ETL vs. the perovskite layer for device-I: (a) efficiency, (b) VOC, (c) JSC, and (d) FF. | ||
Throughout this range, the efficiency, JSC, and FF remain essentially unchanged, indicating that the device is largely insensitive to the presence of traps or imperfections in the ETL.
This suggests that ZnSe offers favorable energy band alignment and efficient electron transport, which minimizes the impact of intrinsic or extrinsic defects within the layer. Based on these outcomes, it is evident that the performance of device-I is far more sensitive to defect states in the absorber than in the ETL. Consequently, for optimized device performance and to minimize recombination-related losses, a density of defects of 1013 cm−3 is identified as the optimum for both the Rb2SnBr6 absorber and the ZnSe ETL. This value offers a balance between realistic material quality and high efficiency, making it a suitable benchmark for further simulation and experimental studies aimed at enhancing device stability and performance.
3.7 Effects of a Rb2SnBr6 absorber and ETL's defect density Nt fluctuations on the photovoltaic performance of device-II
The effect of density of defect (Nt) fluctuations in the Rb2SnBr6 absorber and In2S3 ETL on the photovoltaic performance of device-II was evaluated by varying Nt from 1010 to 1016 cm−3 for both layers. As drawn in Fig. 8(a)–(d), when the density of defects in the absorber increases across this entire range, the key performance parameters remain remarkably stable. Specifically, the device maintains a PCE of 26.62%, a VOC of 0.843 V, a JSC of 38.089 mA cm−2, and an FF of 82.91%. This consistency indicates a high degree of defect tolerance in the absorber layer of device-II, with a negligible impact on charge transport and recombination even at high defect concentrations. However, a different trend is observed when increasing the defect density in the In2S3 ETL. While performance remains largely unaffected up to a density of defects of 1016 cm−3, beyond this threshold, slight but noticeable declines in several parameters are observed. As displayed in Fig. 8(a), PCE decreases modestly from 26.62% to 26.25%. Similarly, in Fig. 8(b), VOC drops from 0.843 V to 0.825 V, and in Fig. 8(c), JSC falls from 38.089 to 37.968 mA cm−2. Interestingly, as seen in Fig. 8(d), FF exhibits a slight increase, rising from 82.91% to 83.78%, potentially due to improved charge extraction dynamics compensating for minor losses in current and voltage. These findings suggest that device-II exhibits stable and efficient operation across a wide limit of absorber defect densities, with only minimal sensitivity to ETL defect fluctuations, particularly beyond 1014 cm−3. Based on these results, a defect density of 1013 cm−3 is identified as the optimal value for both the absorber and the ETL. This choice ensures a favorable balance between performance and material quality and is selected for further optimization and device development. | ||
| Fig. 8 Role of PV factors considering the modification in the defect density of the ETL vs. absorber layer for device-II: (a) efficiency, (b) VOC, (c) JSC, and (d) FF. | ||
3.8 Effects of a Rb2SnBr6 absorber and ETL's defect density Nt fluctuations on the photovoltaic performance of device-III
The influence of defect density (Nt) in the Rb2SnBr6 absorber and CdZnSe ETL on the efficiency of device-III was analyzed over a range from 1010 to 1016 cm−3. As displayed in Fig. 9(a)–(d), increasing the absorber's density of defects up to 1014 cm−3 causes only slight reduction in power conversion efficiency (24.06% to 24.04%), short-circuit current (38.09 to 38.082 mA cm−2), and fill factor (72.63% to 70.92%). The observed relationship between absorber layer defect density and VOC suggests that as defect density increases, performance tends to decline due to enhanced non-radiative recombination. However, when defect levels are low, the absorber layer exhibits higher efficiency and improved VOC, primarily because reduced defect states minimize recombination losses and facilitate better charge carrier lifetimes49. | ||
| Fig. 9 Role of PV considering the variation in the defect density of the ETL vs. absorber layer for device-III: (a) PCE, (b) VOC, (c) JSC, and (d) FF. | ||
However, beyond 1013 cm−3, a more significant decline occurs due to enhanced non-radiative recombination. In contrast, variations in CdZnSe ETL defect density show a minimal effect on performance, indicating strong defect tolerance and efficient charge transport. Based on these findings, an optimal density of defects of 1013 cm−3 is suggested for both layers, offering a balance between device efficiency and material quality for further development.
3.9 Evaluation of JV and QE features in Rb2SnBr6
Understanding the density of current, representing the electric current generated area density, is pivotal for evaluating the efficiency of photocells, as it directly reflects their efficiency.The J–V properties of a structure with the configuration Al/FTO/ETLs/Rb2SnBr6/Au, incorporating three different ETLs and measured across a voltage limit of 0 to 0.90 V, are presented in Fig. 10(a). All three configurations exhibit similar photocurrent responses, demonstrating consistent behavior and stable current output throughout the entire voltage limit, from 0.0 to 0.90 V. Yet, a noticeable diminution in photocurrent takes place in all PSCs in the 0.70–0.90 V operating voltage range. In the initial optimization stage, the ETLs based on ZnSe, In2S3, and CdZnSe showed increased J–V efficiency, especially under conditions of JSC and VOC, relative to those based on ZnSe and In2S3. Particularly, the PSCs using devices I, II, and III attained a JSC of roughly 38.09 mA cm−2. Furthermore, when the input voltage increased, the electricity of light in all models considerably diminished. Fig. 10(b) demonstrates the connection between quantum efficiency (QE) and formula wave interval for PSCs that utilize models I, II, and III, including the wave interval limit of 300–1000 nm. The QE ranges matching each configuration are illustrated in Fig. 10(b). At a spectrum wave interval of 300 nm, PSCs using ZnSe, In2S3, and CdZnSe ETLs gained a maximum QE of 100% and less at 1000 nm. The decline in QE observed in most solar cells is primarily attributed to recombination processes that hinder carriers from reaching the external outer circuit. Various factors, including modifications to the front surface that affect carrier collection probability, also play a role in influencing QE. Moreover, for longer wavelengths, a further decrease in QE may result from the absorption of free carriers in strongly doped front surface layers.50 After achieving their maximum values, the quantum efficiency (QE) of all device designs showed a progressive decrease with increasing wavelength. The decreased absorption of longer-wavelength photons is the cause of this trend. QE is often improved by thickening the absorber layer because a fatter absorber can capture more incident photons, which increases carrier production.51
3.10 Examining how interface flaws and temperature affect PV efficiency
The efficiency of PSCs is significantly swayed by recombination losses at the interfaces between Rb2SnBr6 and the ETL. The main cause of these losses is defects that trap charge carriers, decreasing their mobility and raising the chance of recombination. We changed the defect density (Nt) in Fig. 11(a) from 109 to 1015 cm−2 in order to evaluate its effect at the Rb2SnBr6/ETL interface. The findings demonstrate that the PCE of the Rb2SnBr6/ZnSe and Rb2SnBr6/In2S3 interfaces stayed relatively stable up to an Nt of 1012 cm−2. However, it decreased for the Rb2SnBr6/CdZnSe interface. Beyond this point, though, the PCE dramatically dropped for every device configuration. The ZnSe-based structure maintained the maximum PCE of 28.75% as Nt rose, whereas the CdZnSe-based structure showed the lowest PCE of 24.06%. Additionally, a PCE value of 26.62% is assigned to the In2S3-based structure. Up to an Nt of 1012 cm−2, the VOC and FF of the ZnSe- and In2S3-based structures stayed constant. However, as Nt was above this cutoff, both metrics saw notable decline. The decline in PCE was mirrored by a decreased trend in both VOC and FF for the CdZnSe-based structure as Nt increased. However, up to an Nt of 1015 cm−2, the JSC of the ZnSe, In2S3, and CdZnSe-based structures stayed stable. The buildup of trap states and recombination, obstructing the flow and collection of carriers and reducing the solar cells’ total performance, is the cause of the performance decline at higher Nt values.52 This phenomenon is measured by the higher rate of transport production and recombination on the device's front side, where light enters through the ETL. Finding the optimal Nt at the Rb2SnBr6/ETL interface at 1010 cm−2 reduced recombination losses and improved the model's total performance.53Temperature has a crucial role in the efficiency of photocells, primarily leading to a reduction in total performance. As temperature increases, the band gap of the absorber material slightly decreases, which may cause a minor increase in JSC. However, this is usually outweighed by a more substantial reduction in VOC, as higher temperatures increase carrier recombination and the reverse saturation current. This leads to a decline in VOC and, consequently, a drop in power conversion efficiency. Additionally, elevated temperatures can increase recombination losses and negatively affect the fill factor. In materials like perovskites, high temperatures can also accelerate degradation processes such as ion migration, thermal decomposition, and interface instability, further reducing device performance and long-term stability. Therefore, effective thermal management is crucial to maintain the efficiency and durability of photocells. Within a moderate temperature range, a slight increase can lead to a small rise in current due to bandgap narrowing, but this is usually outweighed by a reduction in open-circuit voltage (VOC), resulting in decreased overall efficiency. Typically, efficiency drops by 0.3% to 0.5% per °C for many solar cell types. Under extreme temperature conditions, the device may experience severe performance degradation due to increased carrier recombination, thermal instability, and material degradation, especially in perovskite-based devices. High temperatures can accelerate ion migration, phase changes, and interfacial breakdown, leading to permanent efficiency loss and reduced lifespan. Therefore, thermal stability is a key factor in reliable PV device design and material selection.
As illustrated in Fig. 11(b), increasing the temperature from 250 K to 400 K leads to a decline in VOC, PCE, and FF, while JSC shows a slight increase. Temperature variations have different impacts on the carrier layers, helping transit charge carriers. This fluctuation is attributed to distinctions in conductivity, particular temperature, and density within the components used.54 Similar patterns are shown for FF, JSC, and PCE, and the decrease in VOC becomes more pronounced as the temperature rises.
Eqn (8) is given to help clarify how temperature affects solar cell performance.55 This behavior is explained by eqn (11):
 | (11) |
3.11 The function of carrier concentration and generation–recombination rates
As illustrated in Fig. 12, the area of the solar cell in the apparatus impacts the pace of recombination and production of the charge carrier combination, determining cell efficiency. When a solar cell is triggered, excitons are generated inside. When electrons shift from the valence band to the conduction band, electron–hole pairs are made. SCAPS-1D uses incident photon flux to calculate the generation of charge carriers. Eqn (12) contains Nphot(λ,χ), which is applied to calculate the production of the G(x), which is known as an electron–hole pair.| G(λ,χ) = α(λ,χ)·Nphot(λ,χ) | (12) |
 | ||
| Fig. 12 The effect of the absorber layer's depth on (a) total generation and (b) recombination rates, (c) density of electrons, and (d) density of holes. | ||
Fig. 12(a) and (b) depict the generation and recombination rates for all construction diagrams of large sites. Rb2SnBr6 emits electrons and holes through carrier formation. When an electron shifts from the hole in the valence band (VB) to the conduction band (CB), it forms couples of electrons and holes. Significantly, this transportation results in an increase in carriers for all devices, with devices I, II, and III producing an inferior value at approximately 0 μm and the largest at approximately 1.05 μm, respectively.
Recombination rate values for every component range from 0 μm at the lowest to 1.05 μm at the highest. Changes in hole and electron configurations occur in the photosystem's energy band. In strong and enhanced SCs, the recombination rates are mostly calculated using the density and endurance of these negatively charged fragments. The defect states present in each stratum are a significant factor affecting SC recombination. When the energy barrier is breached, further electrons from the conduction spectrum make contact with holes in the valence band. The power values linked to this shift also affect the rates of electron and hole recombination.
Fig. 12(c) and (d) exemplify the transitions in the ZnSe, In2S3, and CdZnSe ETLs and how they affect the electron and hole carrier concentrations. These indicate how deep the Rb2SnBr6 perovskite layer is. These changes in perovskite depth affect the hole concentration in the Rb2SnBr6 perovskite because of the influence of various densities of states (DOS) inside the valence electron bands.56 Greater concentrations of carriers are more significant, notably when they align with parallel densities of electrons and holes. According to this work, the performance of the absorber substances may be enhanced by employing ZnSe as the ETL in conjunction with Rb2SnBr6 to reduce hole–electron recombination and increase carrier generation. This technology could potentially enable the creation of highly profitable SCs.
3.12 Effects of series and shunt resistances on photocell performance
The use of series resistance (Rs) and shunt resistance (Rsh) in the solar cell device is investigated in Fig. 13. The resistance of the front and back conductive interfaces, the circuit resistance, and the incremental resistance work together to determine a photocell's Rs. Higher Rsh and minimum Rs are crucial for the SC to run more optimally.57,58 The outcomes of these impedances also change the JSC and VOC. Rs is assessed between 0 and 5 Ω cm2, while Rsh is assessed between 10 and 107 Ω cm2, and the efficacy of the recommended and traditional SCs is observed using SCAPS-1D. VOC is significantly impacted by Rsh. With an increase in Rsh from 10 to 103 Ω cm2, the value of VOC rises from 0.38 to 0.87 V. Raising the Rs by itself remains constant at the VOC from 0 to 5 Ω cm2 when Rsh is 0 Ω cm2 as displayed in Fig. 13(b). Fig. 13(c) depicts the highest JSC at 0 Ω cm2Rs and 0–107 Ω cm2Rsh. This Rs mainly reduces the FF and stops it from increasing. As depicted in Fig. 13, when Rs rises from 0 to 6 Ω cm2 and Rsh varies from 10 to 107 Ω cm2, the VOC, JSC, FF (Fig. 13(d)), and PCE (Fig. 13(a)) shift from 0.38 V to 0.87 V, 25.79 to 38.09 mA cm−2, 25.00 to 86.67% and 2.42 to 28.71%, respectively. According to the study, to increase Rsh and decrease Rs, ideal outputs should be gained. | ||
| Fig. 13 Impact of the change in series vs. shunt impedance on PV parameters: optimum device-I values for (a) efficiency, (b) VOC, (c) JSC, and (d) FF. | ||
3.13 Enhanced apparatus when contrasted to earlier studies
According to scientists studying Rb2SnBr6-based solar cells today, using ZnSe as the ETL at first led to subpar performance. Nevertheless, further investigation has generated a necessary discovery: at the beginning of this year, a peak efficiency of 27.25% was seen.12 This value suggests that photo-systems based on Rb2SnBr6 have been functioning more productively each year. This work on the optimum device model, as displayed in Fig. 14, unexpectedly discovered an amazing 28.73% largest PCE for Rb2SnBr6-based solar cells, with an FF of 86.86%, a JSC of 38.094 mA cm−2, and a VOC of 0.868 V. A correlation between the output metrics from this research and those from previous research is shown in Table 4.| Structure | V OC (V) | J SC (mA cm−2) | FF (%) | PCE (%) | Ref. |
|---|---|---|---|---|---|
| Device-I | 0.8682 | 38.094 | 86.86 | 28.73 | This work |
| Device-II | 0.8427 | 38.087 | 82.93 | 26.62 | This work |
| Device-III | 0.8693 | 38.093 | 72.60 | 24.04 | This work |
| FTO/TiO2/Rb2SnBr6 | 0.87 | 36.72 | 85.18 | 27.25 | 12 |
| TiO2/CsPbI3/CBTS | 0.99 | 21.07 | 85.21 | 17.9% | 59 |
| CuSCN/CsGeI3/C60 | 1.0169 | 19.653 | 88.13 | 17.61 | 60 |
| ZnO/CsSnI3/NiOx | 1.05 | 28.02 | 81.22 | 23.84 | 61 |
| CuSCN/FASnI3/Zn | 1.0859 | 28.12 | 84.96 | 25.94 | 62 |
| CuI//KSnI3/ZnO/FTO | 1.44 | 17.06 | 85.24 | 20.99 | 63 |
| WS2/Cs4CuSb2Cl12/CuSbS2 | 1.16 | 29.27 | 83.33 | 23.10 | 48 |
| ZnMgO/CsSnI3/GO | 0.62 | 35.61 | 78.21 | 17.37 | 64 |
| FTO/SnS2/RbSnI3 | 0.83 | 51.83 | 81.44 | 26.38 | 65 |
To improve the reliability and validity of simulation outcomes, as summarized in Table 4, future experimental investigations should adopt a comprehensive approach that encompasses material combination, depiction, device manufacturing, performance evaluation, and durability testing.
Although experimental reports on Rb2SnBr6-based PSCs are limited, our simulations show that device I (Au/Rb2SnBr6/ZnSe/FTO/Al) achieves a PCE of 28.73%, slightly higher than the 27.25% reported for FTO/TiO2/Rb2SnBr6 devices.12 This improvement can be attributed to optimized ETL selection, which enhances charge transport and reduces recombination losses. Device II (In2S3) and device III (CdZnSe) exhibit lower PCEs (26.62% and 24.04%, respectively), highlighting the critical role of ETL choice. As summarized in Table 4, device I not only outperforms previous Rb2SnBr6-based PSCs, but also demonstrates superior PCE compared with other lead-free perovskites, such as CsSnI3−, FASnI3−, and Cs4CuSb2Cl12-based devices, indicating its competitive efficiency and favorable optoelectronic properties. Moreover, the random forest model with SHAP analysis identifies layer thickness, defect density, and doping concentration as the most influential parameters, providing interpretable guidance for experimental optimization and interface engineering. These insights bridge the gap between theoretical predictions and practical device design, highlighting the effectiveness of optimized ETL selection and the predictive value of the simulation-ML framework in guiding high-performance, lead-free PSC development.
4. Employing machine learning to forecast and improve PSC performance
The incorporation of artificial intelligence (AI) in renewable energy has facilitated significant advancements in materials discovery, device optimization, and performance prediction. In this context, machine learning (ML) has demonstrated significant efficacy in PSC research, as the complex interactions between materials and devices complicate performance optimization via traditional experimental and simulation methods.66,67 Utilizing machine learning models allows for the capture of complex relationships among physical parameters, facilitating precise predictions of photovoltaic behavior and markedly decreasing both computational and experimental expenses. This study constructed a dataset from 1000 SCAPS-1D simulations, systematically varying the properties of the absorber, ETL, and HTL within practical ranges of interest. Key variables included absorber thickness, defect density, doping concentration, and material parameters, all of which influence photovoltaic performance. The simulations generated output parameters, including VOC, JSC, FF, and PCE, which formed a structured dataset appropriate for supervised learning. The large dataset provided adequate variability for the ML model to effectively capture nonlinear dependencies between material properties and device output. The dataset was randomly divided into an 80:20 split, allocating 800 samples for training and 200 for independent testing to ensure thorough model evaluation. This method is commonly employed to evaluate generalization ability, mitigating the risk of overfitting to the training dataset. A 10-fold cross-validation procedure was conducted solely on the training subset to further assess the model's robustness beyond the initial partitioning. In this procedure, the training data were systematically partitioned into ten folds, utilizing nine folds for training and one-fold for validation in each iteration, thereby ensuring that each data point contributed to both model training and validation. This strategy reduced the likelihood of random bias in train-test partitioning and yielded a dependable estimate of predictive accuracy.The random forest (RF) algorithm was chosen for predictive modeling due to its ability to manage nonlinearities, intricate feature interactions, and diverse data distributions without requiring extensive preprocessing.68 In contrast to deep neural networks, which can add unnecessary complexity when data are limited, random forests maintain a balance among accuracy, interpretability, and computational efficiency.69,70 Additionally, the ensemble-based learning approach mitigates the risk of overfitting by averaging the outputs of several decorrelated decision trees. The random forest was configured with 1000 estimators, each trained on bootstrap samples of the training dataset, which ensured diversity among the trees and enhanced generalization. Hyperparameters were optimized using a comprehensive grid search process, evaluating various candidate values for maximum depth, minimum samples per split, and the number of features considered at each split. The optimized configuration comprised a maximum tree depth of 25 nodes, a minimum of two samples per split, and square-root feature selection at each branching step. This configuration achieved an ideal equilibrium between capturing intricate interactions and avoiding excessive complexity in individual trees. Validation results demonstrated consistent predictive performance across folds, with root mean square error (RMSE) values under 0.02 for normalized outputs and coefficients of determination (R2 > 0.8825) for all photovoltaic parameters. Scatter plots analysis indicated a swift convergence of training and validation errors, with no divergence observed, thereby confirming the lack of high-variance overfitting. Parity plots provided additional support, demonstrating that predicted and actual values closely aligned along the diagonal, highlighting the reliability of the RF model. In addition to prediction accuracy, interpretability improved via feature importance analysis, which measured the relative contribution of each input parameter to the model's decision-making process. This interpretability validated the physical soundness of the machine learning predictions and provided actionable insights into the relationships between material properties and performance, thereby guiding future experimental optimization.
4.1 Synopsis of the RF algorithm
This study utilized the RF algorithm due to its exceptional capacity for producing precise forecasts while ensuring interpretability and robustness. As an ensemble learning method, RF produces several regression trees, each constructed from casually appointed subsets of data and features. The ultimate output is obtained by consolidating the findings of these several trees either via majority vote for classification jobs or averaging for regression issues. This collaborative decision-making process improves the model's stability and generalization capabilities, rendering it suitable for intricate scientific applications like PV performance prediction. A primary benefit of RF is its ability to identify complex, non-linear correlations between material properties and PV operational variable relationships that frequently elude simpler statistical methods.71,72 By amalgamating numerous decision trees, RF circumvents dependence on a solitary model and attains equilibrium between predictive efficacy and robustness.The primary advantages of the RF method in this situation can be listed as follows:
Modeling complex interactions: RF adeptly captures non-linear relationships between component features and PV metrics, facilitating a more accurate simulation of real-world behavior.
Overfitting mitigation: by averaging predictions from many decision trees, the model's variance is diminished, hence reducing the likelihood of overfitting, a prevalent drawback of singular decision trees.
Feature significance evaluation: RF delivers significance scores for each input variable, thereby determining which features have the most significant impact on PSC efficiency. This facilitates both scientific analysis and the prioritization of experiments.
Hyperparameter tuning: various parameters were meticulously tuned to enhance performance. These encompass:
• Quantity of trees (T): set at 100 to optimize operational efficiency and prediction precision.
• Tree depth: limited to avoid undue complexity and overfitting.
• Minimum samples per leaf node: established at two, guaranteeing generalizable forecasts devoid of bias from excessively minor splits.
• Bootstrap sampling: utilized to provide varied training subsets, enhancing robustness.
• Feature subsampling: randomly picking features at each split mitigates the dominance of variables and guarantees equitable representation of all input parameters.
A feature selection technique was applied to improve model accuracy and interpretability. This investigation indicated that only a limited number of variables significantly influenced PV characteristics. Fig. 15 demonstrates that among the eleven most significant features, bandgap, left contact, and temperature exhibited the greatest influence on PSC efficiency. Secondary considerations encompassed interface defect density, contact integrity, layer thickness, doping concentration, carrier mobilities (both electron and hole), and dielectric permittivity, all of which exhibited comparatively minor impact. A refined RF model was created by concentrating solely on the most crucial parameters. This streamlined version attained roughly equivalent prediction performance to the full-feature model while substantially decreasing processing requirements. The integration of ensemble learning with systematic feature selection enhanced prediction reliability and offered deeper scientific understanding of the critical aspects influencing PSC performance.
 | ||
| Fig. 15 The integration of ML enables the identification of critical design parameters that significantly influence and enhance the PCE of Au/Rb2SnBr6/ZnSe/FTO/Al solar cells. | ||
4.2 Disclosing feature importance in predictive models through SHAP values
This study addresses a significant challenge in applying machine learning to photovoltaic research: achieving high predictive accuracy while ensuring transparent reasoning for model outputs. This was accomplished through the integration of Shapley additive explanations (SHAP). SHAP, based on cooperative game theory, provides a robust and model-agnostic framework for interpretability that quantifies the contribution of each feature to the predictive outcome. This approach ensures fairness, transparency, and reproducibility, offering both global and local perspectives.73 The SHAP summary plot (Fig. 16) indicated that contact layers (left and right) and hole mobility had the most significant positive impact on PCE, with increased values consistently improving device performance. Conversely, increased defect density, interface defects, and the dielectric constant negatively impacted performance, aligning with their contribution to recombination losses and diminished carrier lifetime. The bandgap and doping density demonstrated nonlinear effects, with both excessively high and low values leading to reduced efficiency. This underscores the necessity of maintaining optimal ranges for band alignment and charge balance. Electron mobility, absorber thickness, and operating temperature exhibited moderate, context-dependent effects, with their advantages reliant on the concurrent regulation of additional parameters, including the reduction of defect density and the optimization of hole mobility. The distribution of SHAP values revealed that certain parameters, like contact quality, exerted consistently strong effects across the majority of samples, while others, such as bandgap, exhibited varied and occasionally opposing influences based on their magnitude and interactions with other features. This analysis highlights that the efficiency of PSC is determined by the complex and nonlinear interactions among various material and structural variables, rather than by a single dominant factor. This study integrates SHAP into the modeling framework, illustrating how explainable AI can both validate predictive reliability and generate physically meaningful insights. This approach offers a scientifically grounded method for directing material design, defect engineering, and optimization strategies in next-generation perovskite solar cells. | ||
| Fig. 16 The impact of individual variables on PCE was systematically evaluated using SHAP values, with rankings derived from their importance in the RF regression model. | ||
4.3 Analysis of the correlation heatmap
Fig. 17 illustrates the correlation heatmap for the eleven input features utilized in the ML-assisted solar cell design: thickness, dielectric constant, defect density, doping density, bandgap, electron mobility, hole mobility, interface defect, temperature, left contact, and right contact. The diagonal value of 1.00 indicates self-correlation, whereas the off-diagonal entries demonstrate the extent of pairwise linear correlations, varying from −1 (strong negative correlation) to +1 (strong positive correlation).74 Most correlation coefficients are near 0, signifying that the bulk of variables exhibit weak correlations and are mostly independent. This benefits the ML framework by reducing multicollinearity and ensuring that each parameter provides distinct information to the predictive model. Minor correlations were noted, including a slight negative association between electron mobility and hole mobility (−0.08), indicating a subtle trade-off in charge transport properties. Electron mobility and dielectric constant (0.07) demonstrated a slight positive correlation, indicating a possible relationship between dielectric characteristics and carrier mobility. All other feature pairings, including thickness, bandgap, and defect-related characteristics, exhibited minimal correlation values. The comprehensive dispersion of correlations validates the appropriateness of the chosen variables for ML research, as they jointly offer varied and independent descriptions of the solar cell system. This improves the interpretability and robustness of the RF model in assessing feature significance and optimizing PV performance. | ||
| Fig. 17 Correlation heatmap of the proposed solar cell structure showing relationships among different variable parameters. | ||
4.4 Metrics and outcomes of performance assessment
A thorough evaluation framework was built to examine the predictive capabilities of the RF model in forecasting key performance characteristics of PV systems. The structure was experimented with 1100 estimators, ensuring that the ensemble accurately represented the intricate interactions between material attributes and PV efficiency measures. Upon completion of training, the structure generated predictions for several PV components, which were later matched to simulation data to assess performance reliability. The precision of predictions was illustrated using scatter plots (Fig. 18), in which the expected outcomes were compared to actual values. These plots offer a clear assessment of model accuracy, with a closer alignment of dots along the reference line (y = x) signifying enhanced prediction performance. | ||
| Fig. 18 Assessment of model prediction accuracy through comparison of ML-predicted and simulation-derived parameters for Au/Rb2SnBr6/ZnSe/FTO/Al solar cells: (a) PCE, (b) VOC, (c) JSC, and (d) FF. | ||
The predictive accuracy of the RF model was further assessed using established statistical metrics:
Coefficient of determination (R2): this statistic assesses the extent of concordance between expected and actual values. Elevated R2 values indicate superior model fit. In this analysis, the RF model attained significant results: VOC = 0.91, PCE = 0.88, JSC = 0.89, and FF = 0.85, all indicating robust predictive concordance.
Root mean square error (RMSE): calculated the size of squared prediction errors, assigning higher significance to larger discrepancies and emphasizing cases of model underperformance.
Mean absolute error (MAE): quantifies the average absolute deviation between predictions and actual values, providing a clear indication of overall accuracy.
The results collectively demonstrated a prediction accuracy of 88.25%, affirming the efficacy of the RF algorithm in correlating material properties with PV performance outcomes. The incorporation of feature selection optimized the model by diminishing dimensionality, therefore enhancing computational efficiency while maintaining accuracy. Fig. 18(a)–(d) illustrates that the dense aggregation of data points along the optimal fit line visually substantiates the model's reliability. These findings highlight the RF model's capacity to provide dependable predictions while facilitating a more profound comprehension of the complex interdependencies that influence PV device performance. Fig. 19(a) displays regression graphs juxtaposing projected values with actual data, providing compelling proof of the model's robust generalization capability. The strong correlation between predicted and observed values in both training and testing datasets indicates that the RF model attains an accurate fit while preventing overfitting, thereby maintaining high performance on unseen samples.75 In accordance with statistical principles, as the R2 nears 1, the reliability and validity of the model's predictions increase.
 | ||
| Fig. 19 Performance evaluation of the proposed solar cell structure illustrated through (a) the parity plot and (b) the confusion matrix. | ||
In addition to regression performance, the model's classification abilities were evaluated using the confusion matrix depicted in Fig. 19(b). Of 220 data points, the RF model accurately identified 96 instances as class 0 and 122 as class 1, with only one mistake in each group. This exceptional outcome achieved an overall accuracy of 99.09%, further corroborated by robust precision and recall metrics. Collectively, these results underscore the RF algorithm's exceptional reliability and versatility. It not only reduces prediction errors but also exhibits remarkable efficacy in class distinction, positioning it as a robust instrument for both regression and classification tasks in solar system analysis. Although the methodology outlined in this paper exhibits considerable prediction accuracy, there is significant potential for enhancement. Future research may concentrate on amalgamating larger and more heterogeneous datasets, enhancing model generalizability across various device architectures and operational situations. Moreover, integrating ML with experimental validation could produce hybrid methodologies that connect computational predictions with practical applications.
This paper establishes a robust basis for integrating ML into solar cell research and design. By facilitating more efficient, stable, and economically viable PV solutions, ML serves as a revolutionary instrument for the forthcoming generation of sustainable energy technology.
5. Conclusion
This study demonstrates the potential of Rb2SnBr6 as a lead-free, stable, and high-performance absorber material for perovskite solar cells. Among the three simulated device structures with different electron transport layers (ETLs), device I (Au/Rb2SnBr6/ZnSe/FTO/Al) exhibited the highest performance, achieving a PCE of 28.73%, VOC of 0.8682 V, JSC of 38.094 mA cm−2, and FF of 86.86%. Device II (In2S3) and device III (CdZnSe) showed lower efficiencies of 26.62% and 24.04%, respectively, highlighting the critical role of ETL selection in enhancing charge transport and minimizing recombination losses. In addition to SCAPS-based simulations, a random forest model with SHAP analysis was applied to quantify the relative impact of device parameters. The analysis identified layer thickness, defect density, and doping concentration as the most influential factors affecting PCE, providing interpretable design insights that extend beyond conventional simulation optimization. It should be noted that the reported PCE of 28.73% represents a theoretical upper limit under idealized SCAPS simulation conditions. When assessing the performance metrics of these cells with ML, the model's accuracy was 88.25%. In practical devices, interface defects, material non-uniformity, and environmental degradation are likely to reduce efficiency. Therefore, these results should be interpreted as guidance for optimized device design rather than guaranteed experimental performance. Overall, this work delivers a dual contribution: an optimized Rb2SnBr6-based device structure (device I) and a predictive, interpretable machine learning framework to guide future experimental design, highlighting pathways toward high-efficiency, scalable, and sustainable perovskite photovoltaics. Future studies should focus on experimental validation, interface engineering, and operational stability to translate these findings into practical devices.Ethical approval
All the authors declare that the manuscript does not have studies on human subjects, human data or tissue, or animals.Author contributions
Md. Selim Reza and Avijit Ghosh: conceptualization, methodology, software, validation, formal analysis, visualization, investigation, data curation, supervision, writing – original draft, and review and editing; Asadul Islam Shimul, Manjuara Akter, Saeed Hasan Nabil, Aijaz Rasool Chaudhry, Dipongkar Ray Sobuj, Yedluri Anil Kumar, Shaikat Biswas, Khorshed Alam, and Maida Maqsood: software, validation, formal analysis, writing – original draft, and review and editing.Conflicts of interest
The authors have no conflicts of interest.Abbreviations
| Rb2SnBr6 | Rubidium tin hexabromide |
| PCE | Power conversion efficiency |
| FF | Fill factor |
| PV cell | Photo-voltaic cell |
| J SC | Short circuit voltage |
| VBO | Valence band offset |
| SC | Solar cell |
| HPSCs | Hybrid perovskite solar cells |
| ETL | Electron transport layer |
| Pb | Lead |
| PSCs | Perovskite solar cells |
| V OC | Open circuit voltage |
| HTL | Hole transport layer |
| CBO | Conduction band offset |
| QE | Quantum efficiency |
| DOS | Density of states |
Data availability
Data will be made available upon reasonable request.Acknowledgements
The authors are thankful to the Deanship of Graduate Studies and Scientific Research at the University of Bisha for supporting this work through the Fast-Track Research Support Program.References
- M. E. Kiziroglou and E. M. Yeatman, Materials and techniques for energy harvesting, Functional Materials for Sustainable Energy Applications, Elsevier, 2012, pp. 541–572 DOI:10.1533/9780857096371.4.539.
- R. Yao, S. Ji, T. Zhou, C. Quan, W. Liu and X. Li, Self-energy correction and numerical simulation for efficient lead-free double perovskite solar cells, Phys. Chem. Chem. Phys., 2024, 26(6), 5253–5261, 10.1039/D3CP03639A.
- T. W. Kelley, et al., Recent Progress in Organic Electronics: Materials, Devices, and Processes, Chem. Mater., 2004, 16(23), 4413–4422, DOI:10.1021/cm049614j.
- H. Shirai, T. Ariyoshi, J. Hanna and I. Shimizu, Stability and hole-transport in a-Si:H prepared by ‘Chemical Annealing, J. Non-Cryst. Solids, 1991, 137–138, 693–696, DOI:10.1016/S0022-3093(05)80215-7.
- A. Mujtaba, M. I. Khan, M. Aslam, B. S. Almutairi and S. Ezzine, Improving the performance of mixed halide perovskite solar cells through crystal engineering and the alignment of energy band edges, New J. Chem., 2025, 49(22), 9233–9242, 10.1039/D5NJ01233C.
- A. Mujtaba, M. I. Khan, M. Amami and D. O. Alshahrani, Enhancing perovskite solar cell efficiency: ZnO–WO3 as an electron transport layer to minimize recombination losses, RSC Adv., 2025, 15(31), 25019–25029, 10.1039/D5RA03446A.
- M. I. Khan, A. Mujtaba, M. Fatima, R. Marzouki, S. Hussain and T. Anwar, Impact of Ce doping on the optoelectronic and structural properties of a CsPbIBr2 perovskite solar cell, Phys. Chem. Chem. Phys., 2025 10.1039/D5CP02196K.
- A. Mujtaba, et al., Tailoring the morphological, optical, structural, and electrochemical properties of MnVO3 perovskite for ideal energy storage applications, Mater. Sci. Eng., B, 2025, 320, 118455, DOI:10.1016/j.mseb.2025.118455.
- M. K. A. Mohammed, et al., Designing a Novel Hole-Transporting Layer for FAPbI3-Based Perovskite Solar Cells, Energy Fuels, 2023, 37(24), 19870–19881, DOI:10.1021/acs.energyfuels.3c03526.
- M. K. Hossain, et al., Numerical Analysis in DFT and SCAPS-1D on the Influence of Different Charge Transport Layers of CsPbBr3 Perovskite Solar Cells, Energy Fuels, 2023, 37(8), 6078–6098, DOI:10.1021/acs.energyfuels.3c00035.
- M. K. Hossain, et al., Design Insights into La2NiMnO6-Based Perovskite Solar Cells Employing Different Charge Transport Layers: DFT and SCAPS-1D Frameworks, Energy Fuels, 2023, 37(17), 13377–13396, DOI:10.1021/acs.energyfuels.3c02361.
- M. F. Rahman, et al., Achieving efficiency above 30% with new inorganic cubic perovskites X2SnBr6 (X = Cs, Rb, K, Na) via DFT and SCAPS-1D, Phys. Chem. Chem. Phys., 2025, 27(2), 1155–1170, 10.1039/D4CP01883D.
- S. R. Raga, E. M. Barea and F. Fabregat-Santiago, Analysis of the Origin of Open Circuit Voltage in Dye Solar Cells, J. Phys. Chem. Lett., 2012, 3(12), 1629–1634, DOI:10.1021/jz3005464.
- S. Roy and P. Bermel, Electronic and optical properties of ultra-thin 2D tungsten disulfide for photovoltaic applications, Sol. Energy Mater. Sol. Cells, 2018, 174, 370–379, DOI:10.1016/j.solmat.2017.09.011.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Lead-free solid-state organic–inorganic halide perovskite solar cells, Nat. Photonics, 2014, 8(6), 489–494, DOI:10.1038/nphoton.2014.82.
- W. Zhou, et al., Light-Independent Ionic Transport in Inorganic Perovskite and Ultrastable Cs-Based Perovskite Solar Cells, J. Phys. Chem. Lett., 2017, 8(17), 4122–4128, DOI:10.1021/acs.jpclett.7b01851.
- I. Alam, R. Mollick and M. A. Ashraf, Numerical simulation of Cs2AgBiBr6-based perovskite solar cell with ZnO nanorod and P3HT as the charge transport layers, Phys. B, 2021, 618, 413187, DOI:10.1016/j.physb.2021.413187.
- M. Faizan, et al., Electronic and optical properties of vacancy ordered double perovskites A2BX6 (A = Rb, Cs; B = Sn, Pd, Pt; and X = Cl, Br, I): a first principles study, Sci. Rep., 2021, 11(1), 6965, DOI:10.1038/s41598-021-86145-x.
- J. Zhou, et al., Lead-Free Perovskite Derivative Cs2SnCl6−xBrx Single Crystals for Narrowband Photodetectors, Adv. Opt. Mater., 2019, 7(10) DOI:10.1002/adom.201900139.
- G. Yuan, et al., Compressibility of Cs2SnBr6 by X-ray diffraction and Raman spectroscopy, Solid State Commun., 2018, 275, 68–72, DOI:10.1016/j.ssc.2018.03.014.
- D. Shao, W. Zhu, G. Xin, J. Lian and S. Sawyer, Inorganic vacancy-ordered perovskite Cs2SnCl6:Bi/GaN heterojunction photodiode for narrowband, visible-blind UV detection, Appl. Phys. Lett., 2019, 115(12) DOI:10.1063/1.5123226.
- B. Ehrler, E. Alarcón-Lladó, S. W. Tabernig, T. Veeken, E. C. Garnett and A. Polman, Photovoltaics Reaching for the Shockley–Queisser Limit, ACS Energy Lett., 2020, 5(9), 3029–3033, DOI:10.1021/acsenergylett.0c01790.
- P. Subudhi and D. Punetha, Pivotal avenue for hybrid electron transport layer-based perovskite solar cells with improved efficiency, Sci. Rep., 2023, 13(1), 19485, DOI:10.1038/s41598-023-33419-1.
- I. Alam and M. A. Ashraf, Effect of different device parameters on tin-based perovskite solar cell coupled with In2S3 electron transport layer and CuSCN and Spiro-OMeTAD alternative hole transport layers for high-efficiency performance, Energy Sources, Part A, 2024, 46(1), 17080–17096, DOI:10.1080/15567036.2020.1820628.
- N. Khoshsirat and N. A. Md Yunus, Numerical Analysis of In2S3 Layer Thickness, Band Gap and Doping Density for Effective Performance of a CIGS Solar Cell Using SCAPS, J. Electron. Mater., 2016, 45(11), 5721–5727, DOI:10.1007/s11664-016-4744-6.
- K. D. Jayan and V. Sebastian, Comparative performance analysis of mixed halide perovskite solar cells with different transport layers and back metal contacts, Semicond. Sci. Technol., 2021, 36(6), 065010, DOI:10.1088/1361-6641/abf46c.
- M. H. Ali, M. A. Al Mamun, M. D. Haque, M. F. Rahman, M. K. Hossain and A. Z. Md Touhidul Islam, Performance Enhancement of an MoS2-Based Heterojunction Solar Cell with an In2Te3 Back Surface Field: A Numerical Simulation Approach, ACS Omega, 2023, 8(7), 7017–7029, DOI:10.1021/acsomega.2c07846.
- F. Behrouznejad, S. Shahbazi, N. Taghavinia, H.-P. Wu and E. Wei-Guang Diau, A study on utilizing different metals as the back contact of CH3NH3PbI3 perovskite solar cells, J. Mater. Chem. A, 2016, 4(35), 13488–13498, 10.1039/C6TA05938D.
- Ferdiansjah, Faridah and K. Tirtakusuma Mularso, Analysis of Back Surface Field (BSF) Performance in P-Type And N-Type Monocrystalline Silicon Wafer, E3S Web Conf., 2018, 43, 01006, DOI:10.1051/e3sconf/20184301006.
- M. H. K. Rubel, et al., First-principles calculations to investigate physical properties of single-cubic (Ba0.82K0.18)(Bi0.53Pb0.47)O3 novel perovskite superconductor, Mater. Today Commun., 2022, 33 DOI:10.1016/j.mtcomm.2022.104302.
- M. I. Khan, et al., Impact of molybdenum doping on the optoelectronic and structural properties of CsPbIBr2 perovskite solar cell, Phys. B, 2024, 678, 415758, DOI:10.1016/j.physb.2024.415758.
- M. I. Khan, et al., Impact of Cr doping on the structural and optoelectronic properties of a CsPbIBr2 perovskite solar cell, New J. Chem., 2024, 48(16), 7205–7212, 10.1039/D4NJ00681J.
- H. Mouhib, et al., Numerical investigation of eco-friendly MASnI3 perovskite-based solar cell: effect of defect density and hole transport layer, Model. Simul. Mater. Sci. Eng., 2022, 30(3), 035011, DOI:10.1088/1361-651X/ac55b0.
- Ihtisham-ul-haq, et al., Bandgap reduction and efficiency enhancement in Cs2AgBiBr6 double perovskite solar cells through gallium substitution, RSC Adv., 2024, 14(8), 5440–5448, 10.1039/D3RA08965G.
- B. S. Almutairi, et al., Impact of La doping on the optoelectronic and structural properties of CsPbIBr2 perovskite solar cell, Opt. Mater., 2024, 152, 115415, DOI:10.1016/j.optmat.2024.115415.
- M. K. Hossain, et al., An extensive study on multiple ETL and HTL layers to design and simulation of high-performance lead-free CsSnCl3-based perovskite solar cells, Sci. Rep., 2023, 13(1), 2521, DOI:10.1038/s41598-023-28506-2.
- A. Mujtaba, M. I. Khan, M. Fatima, M. Atif, M. S. Al-Sharif and D. I. Saleh, Enhanced the efficiency of TMs (Co and Ag) doped lead based mixed halides perovskite solar cells through the conduction band gap engineering, J. Indian Chem. Soc., 2025, 102(4), 101618, DOI:10.1016/j.jics.2025.101618.
- A. Mujtaba, M. I. Khan, M. Mushtaq, B. S. Almutairi and S. Ezzine, Impact of CsPbI3 incorporation on the structural, optical, and electrical properties of mixed-halide perovskite solar cells, J. Sol-Gel Sci. Technol., 2025, 115(1), 73–83, DOI:10.1007/s10971-025-06782-w.
- Mamta, K. K. Maurya and V. N. Singh, Influence of buffer layers on antimony selenide based solar cell, Opt. Mater., 2022, 126, 112240, DOI:10.1016/j.optmat.2022.112240.
- X. Li, et al., Low-Temperature Solution-Processed ZnSe Electron Transport Layer for Efficient Planar Perovskite Solar Cells with Negligible Hysteresis and Improved Photostability, ACS Nano, 2018, 12(6), 5605–5614, DOI:10.1021/acsnano.8b01351.
- I. Alam and M. A. Ashraf, Effect of different device parameters on tin-based perovskite solar cell coupled with In2S3 electron transport layer and CuSCN and Spiro-OMeTAD alternative hole transport layers for high-efficiency performance, Energy Sources, Part A, 2020, 1–17, DOI:10.1080/15567036.2020.1820628.
- Y. Gan, et al., Numerical Investigation Energy Conversion Performance of Tin-Based Perovskite Solar Cells Using Cell Capacitance Simulator, Energies, 2020, 13(22), 5907, DOI:10.3390/en13225907.
- M. F. Rahman, M. M. Tasdid, M. M. Fadhali, M. Sharma and M. Akermi, Unlocking Cesium based new double absorber perovskite solar cells with efficiency above 28% for next generation solar cell, Phot. Nano. Fund. Appl., 2025, 64, 101371, DOI:10.1016/j.photonics.2025.101371.
- W. R. Mateker and M. D. McGehee, Progress in Understanding Degradation Mechanisms and Improving Stability in Organic Photovoltaics, Adv. Mater., 2017, 29(10) DOI:10.1002/adma.201603940.
- S. Gohri, et al., Achieving 24.6% efficiency in 2D perovskite solar cells: Bandgap tuning and MXene contact optimization in (BDA)(MA)n−1PbnI3n+1 structures, Chem. Phys. Lett., 2024, 845, 141291, DOI:10.1016/j.cplett.2024.141291.
- M. A. Monnaf, A. K. M. M. Haque, M. H. Ali, S. Bhattarai, M. D. Haque and M. F. Rahman, Design and simulation of Cu2SnSe3-based solar cells using various hole transport layer (HTL) for performance efficiency above 32%, Phys. Scr., 2023, 98(12), 125903, DOI:10.1088/1402-4896/ad0529.
- S. Kumar, L. Allam, S. Bharadwaj and B. Barman, Enhancing SrZrS3 perovskite solar cells: A comprehensive SCAPS-1D analysis of inorganic transport layers, J. Phys. Chem. Solids, 2025, 196, 112378, DOI:10.1016/j.jpcs.2024.112378.
- H. Karmaker, A. Siddique, B. K. Das and M. N. Islam, Modeling and performance investigation of novel inorganic Cs4CuSb2Cl12 nanocrystal perovskite solar cell using SCAPS-1D, Results Eng, 2024, 22, 102106, DOI:10.1016/j.rineng.2024.102106.
- S. Banik, A. Das, B. K. Das and N. Islam, Numerical simulation and performance optimization of a lead-free inorganic perovskite solar cell using SCAPS-1D, Heliyon, 2024, 10(1), e23985, DOI:10.1016/j.heliyon.2024.e23985.
- M. Atowar Rahman, Performance analysis of WSe2-based bifacial solar cells with different electron transport and hole transport materials by SCAPS-1D, Heliyon, 2022, 8(6), e09800, DOI:10.1016/j.heliyon.2022.e09800.
- Mamta, K. K. Maurya and V. N. Singh, Sb2Se3/CZTS dual absorber layer based solar cell with 36.32% efficiency: A numerical simulation, J. Sci. Adv. Mater. Devices, 2022, 7(2), 100445, DOI:10.1016/j.jsamd.2022.100445.
- S. Ullah, et al., Optimizing the lead-free CsSnBr3/Cs2SnI6 perovskite solar cells: a theoretical study using SCAPS-1D, Opt. Quantum Electron., 2025, 57(2), 126, DOI:10.1007/s11082-024-08028-5.
- A. Najim, L. Moulaoui, A. Laassouli, O. Bajjou and K. Rahmani, Design and simulation of an organic–inorganic GO/P3HT/MASnI3 solar cell using the SCAPS-1D program, Electr. Eng., 2025 DOI:10.1007/s00202-024-02941-4.
- A. D. Adewoyin, M. A. Olopade, O. O. Oyebola and M. A. Chendo, Development of CZTGS/CZTS tandem thin film solar cell using SCAPS-1D, Optik, 2019, 176, 132–142, DOI:10.1016/j.ijleo.2018.09.033.
- P. Roy, N. Kumar Sinha and A. Khare, An investigation on the impact of temperature variation over the performance of tin-based perovskite solar cell: A numerical simulation approach, Mater. Today Proc., 2021, 39, 2022–2026, DOI:10.1016/j.matpr.2020.09.281.
- P. Sinsermsuksakul, et al., Enhancing the efficiency of SnS solar cells via band-offset engineering with a zinc oxysulfide buffer layer, Appl. Phys. Lett., 2013, 102, 5, DOI:10.1063/1.4789855.
- H. Heriche, Z. Rouabah and N. Bouarissa, New ultra thin CIGS structure solar cells using SCAPS simulation program, Int. J. Hydrogen Energy, 2017, 42(15), 9524–9532, DOI:10.1016/j.ijhydene.2017.02.099.
- E. Karimi and S. M. B. Ghorashi, Simulation of perovskite solar cell with P 3 HT hole-transporting materials, J. Nanophotonics, 2017, 11(3), 032510, DOI:10.1117/1.JNP.11.032510.
- M. K. Hossain, M. H. K. Rubel, G. F. I. Toki, I. Alam, M. F. Rahman and H. Bencherif, Effect of Various Electron and Hole Transport Layers on the Performance of CsPbI3-Based Perovskite Solar Cells: A Numerical Investigation in DFT, SCAPS-1D, and wxAMPS Frameworks, ACS Omega, 2022, 7(47), 43210–43230, DOI:10.1021/acsomega.2c05912.
- W. Ahmad, M. Noman, S. Tariq Jan and A. D. Khan, Performance analysis and optimization of inverted inorganic CsGeI3 perovskite cells with carbon/copper charge transport materials using SCAPS-1D, R. Soc. Open Sci., 2023, 10(3) DOI:10.1098/rsos.221127.
- H.-J. Park, H. Son and B.-S. Jeong, SCAPS-1D Simulation for Device Optimization to Improve Efficiency in Lead-Free CsSnI3 Perovskite Solar Cells, Inorganics, 2024, 12(4), 123, DOI:10.3390/inorganics12040123.
- A. Tara, V. Bharti, S. Sharma and R. Gupta, Device simulation of FASnI3 based perovskite solar cell with Zn(O0.3, S0.7) as electron transport layer using SCAPS-1D, Opt. Mater., 2021, 119, 111362, DOI:10.1016/j.optmat.2021.111362.
- F. B. Sumona, et al., Optimization of Perovskite-KSnI3 Solar Cell by Using Different Hole and Electron Transport Layers: A Numerical SCAPS-1D Simulation, Energy Fuels, 2023, 37(23), 19207–19219, DOI:10.1021/acs.energyfuels.3c02397.
- K. Afridi, M. Noman and S. T. Jan, Evaluating the influence of novel charge transport materials on the photovoltaic properties of MASnI 3 solar cells through SCAPS-1D modelling, R. Soc. Open Sci., 2024, 11(1) DOI:10.1098/rsos.231202.
- M. Harun-Or-Rashid, M. F. Rahman, M. Amami, L. Ben Farhat, M. M. Islam and A. Benami, Exploring new lead-free halide perovskites RbSnM3 (M = I, Br, Cl) and achieving power conversion efficiency >32%, J. Phys. Chem. Solids, 2025, 197, 112437, DOI:10.1016/j.jpcs.2024.112437.
- Y. Liu, X. Tan, J. Liang, H. Han, P. Xiang and W. Yan, Machine Learning for Perovskite Solar Cells and Component Materials: Key Technologies and Prospects, Adv. Funct. Mater., 2023, 33(17) DOI:10.1002/adfm.202214271.
- J. Li, B. Pradhan, S. Gaur and J. Thomas, Predictions and Strategies Learned from Machine Learning to Develop High-Performing Perovskite Solar Cells, Adv. Energy Mater., 2019, 9, 46, DOI:10.1002/aenm.201901891.
- Z. Guo and B. Lin, Machine learning stability and band gap of lead-free halide double perovskite materials for perovskite solar cells, Sol. Energy, 2021, 228, 689–699, DOI:10.1016/j.solener.2021.09.030.
- E. C. Gok, et al., Predicting Perovskite Bandgap and Solar Cell Performance with Machine Learning, Sol. RRL, 2022, 6(2) DOI:10.1002/solr.202100927.
- M. Harth, et al., Comparative convolutional neural networks for perovskite solar cell PCE predictions, npj Comput. Mater., 2025, 11(1), 251, DOI:10.1038/s41524-025-01744-w.
- W. Li, et al., Performance prediction and optimization of perovskite solar cells based on the Bayesian approach, Sol. Energy, 2023, 262, 111853, DOI:10.1016/j.solener.2023.111853.
- A. I. Shimul, M. M. Hossain and S. A. Dipa, Investigating the effectiveness of Ca3AsCl3-based Perovskite Solar Cells with optimal hole transport layer selection through numerical optimization and machine learning, Opt. Commun., 2025, 586, 131916, DOI:10.1016/j.optcom.2025.131916.
- O. Saidani, A. Yousfi, Y. Belhadad, R. Zouache, A. Brahimi and G. S. Sahoo, Predictive Modeling of Rb2ScCuCl6-Based Perovskite Solar Cells Performance Using Neural Networks-Guided Optimization and SHAP-based Interpretability, J. Phys. Chem. Solids, 2025, 113084, DOI:10.1016/j.jpcs.2025.113084.
- S. Aftab, F. Ahmad, S. Naeem, S. R. M. Sayed and M. A. A. Ibrahim, Examining the Relationship between Synthetic Accessibility and Efficiency in Organic Solar Cells: A Statistical Analysis, ACS Appl. Energy Mater., 2025, 8(7), 4484–4493, DOI:10.1021/acsaem.5c00031.
- M. M. Salah, Z. Ismail and S. Abdellatif, Selecting an appropriate machine-learning model for perovskite solar cell datasets, Mater. Renew. Sustain. Energy, 2023, 12(3), 187–198, DOI:10.1007/s40243-023-00239-2.
| This journal is © The Royal Society of Chemistry 2025 |







