DOI:
10.1039/D5MA00332F
(Paper)
Mater. Adv., 2025,
6, 4418-4437
Utilization of a cadmium sulfide/nickel–ferric layered double hydroxide nanocomposite decorated with silver nanoparticles for efficient adsorption and photocatalytic degradation of 2,4-dichlorophenoxyacetic acid†
Received
5th April 2025
, Accepted 16th May 2025
First published on 4th June 2025
Abstract
This study examined the efficacy of the hydrotalcite-like materials of Zn–Fe, Mg–Fe, and Ni–Fe layered double hydroxides as adsorbents of 2,4-dichlorophenoxyacetic acid (2,4-D) by synthesizing them using a coprecipitation process at an M2+/M3+ molar ratio of 3. This study presents a novel cadmium sulfide/Ni–Fe LDH and its decorated form with silver nanoparticles as a plasmonic element, Ag@CdS/Ni–Fe LDH, to overcome conventional photocatalyst limitations such as weak photoresponsivity and unstable structure. The physicochemical characteristics of Ag@CNFL were analyzed, revealing a hierarchical pore structure, a large specific surface area (113.10 m2 g−1), a particle size of 68 nm, a total pore volume of 0.1658 cm3 g−1, an average pore size of 5.8638 nm, a pHPZC of 8.34, and a band gap of 1.96 eV. Our findings showed a notable maximum adsorption capacity of 203.75 mg g−1 at 23 °C for NFL and fast adsorption kinetics within 8 h. The exothermic and spontaneous adsorption process was well described by Avrami and pseudo-second-order kinetics, Redlich–Peterson, and Langmuir isotherms. Under visible irradiation, the Ag@CNFL heterojunction demonstrated remarkable photocatalytic activity in the 2,4-D degradation, reaching a 100% degradation percentage at 15 mg L−1 and 110 min. Additionally, following eight cycles of 2,4-D photodegradation, the efficiency of NFL, C, CNFL, and Ag@CNFL was only decreased by 8.4, 3.4, 3.2, and 7.0%, respectively. It was shown that the produced materials were very effective at removing 2,4-D from water.
1. Introduction
In recent years, it has been difficult to meet the high demand for food due to the growing population. Therefore, pesticides, which mostly consist of insecticides, herbicides, rodenticides, and fungicides, are used in current agricultural practices to increase productivity. Worldwide, 2 million tons of pesticides are used with herbicides, making up 47.5% of the total amount.1 Overuse of pesticides has been harmful to the ecosystem overall, and in particular, residues of organophosphates and organochlorines have been discovered in several food products and drinking water.2 Among the phenoxy family of herbicides, 2,4-dichlorophenoxyacetic acid (2,4-D) stands out for being widely used in agriculture to promote fruit development and stop pre-harvest fruit dropping. This is because of its cost-efficiency, water solubility, and selective effect on broadleaf weeds. The acidic carboxylic acid groups are responsible for the solubility of this polar molecule. However, under natural pH conditions, there is greater mobility due to the prevalence of its anionic form, which is controlled by a low pKa value of 2.8.3 As a result, this mobility causes groundwater resource contamination. Furthermore, polychlorinated di-benzo-p-dioxins, which are known for their extreme toxicity and tenacious nature, are formed from the precursors of 2,4-D.4 When 2,4-D is misused, it can harm animals and accumulate in the organism, which can have teratogenic effects at high levels and may also be carcinogenic and mutagenic. According to certain research, 2,4-D is regarded as an endocrine disruptor as well, having negative effects on the reproductive and immunological systems, enzyme activity, and gene expression.5 Additionally, exposure to 2,4-D causes nausea, weakness, fatigue, and irritation in the eyes and skin, which can have neurotoxic effects, such as nerve ending inflammation.6 The World Health Organisation (WHO) suggests that the maximum permissible concentration of 2,4-D that can be found in drinking water should not be greater than 70 μg L−1.5 2,4-D was included in group 2B (possible) of the International Agency for Research on Cancer (IARC) classification in 2018.7 Considering these important concerns and because 2,4-D has high durability and fluidity in water, the development of effective, cheap, safe, and simple methods to eliminate 2,4-D from waterbodies has attracted wide attention from researchers.
Nowadays, to eliminate 2,4-D from polluting sources, several environmental remediation techniques are adopted like advanced oxidation processes,8 aerobic degradation, photo-catalytic degradation,9 combined photo-Fenton, coagulation, ozonation,10 flocculation, electrochemical degradation,11 catalytic hydrochlorination, biological treatment, and adsorption.1 Compared with these techniques, the adsorption method is regarded as being among the most efficient methods to remove 2,4-D due to its operation simplicity, mild conditions, moderate price, fewer by-products, and low energy consumption.5 Adsorption is a useful technology for transforming a contaminant from an aqueous solution into a solid phase. To date, activated carbon, graphene, carbon nanotubes, layered double hydroxide, nanofibers, and biochar are among the potential adsorbents that can be utilized to remove 2,4-D from water.7 Photodegradation is also an innovative method that mineralizes the contaminants into water and carbon dioxide by using photocatalysts to create free radicals in the aqueous medium, which then change extremely hazardous pollutants into smaller and non-toxic molecules through redox processes.12 In recent years, photocatalysts such as TiO2, WO3, Fe2O3, ZnO, etc. have been applied for the photodegradation of pollutants as safe, renewable, economical, and clean semiconductors.13
Layered double hydroxides (LDHs) are inorganic matrices with extremely tunable structures created by cationic layers of bivalent and trivalent cations hexa-coordinated to hydroxyl groups in an octahedral configuration. The general formula for the chemical composition of these hydrotalcite compounds is [M1−x2+ Mx3+(OH)2]x+ [Ax/nn–]·qH2O, where M2+ is a divalent metal cation (e.g. Mg2+, Zn2+, Ni2+, Cd2+, and Co2+), M3+ is a trivalent metal cation (e.g. Fe3+, Al3+, and Cr3+), and An– is an interlayer anionic species.14 There are numerous methods for synthesizing LDH, including urea hydrolysis, coprecipitation, sol–gel, and reconstruction.15 Thus, this material has various applications such as catalysis, water splitting reactions, electrochemical applications such as electrodes, antimicrobial materials, drug delivery, and adsorption.16 Layered double hydroxide is considered as a suitable candidate for the adsorption of several conventional contaminants such as heavy metals,17 dyes,18 phosphate,19 pesticides, and other pollutants. This is due to its large surface area, high ion exchange capacity, abundant interstitial spaces, large number of active sites, versatile chemical composition, high chemical and thermal stability, and ability to restore the original layered structure upon rehydrating the calcined LDH through the “memory effect”.14 Adsorption of 2,4-D was reported using Co–Al–Cl LDH16 and CMS@ZnAl–LDH,20 which achieved adsorption capacities of 27.17 and 223.02 mg g−1 as adsorbent materials, respectively.
Moreover, LDHs exhibit unique optical properties and strong photocatalytic performance due to their strong sensitivity to both visible and ultraviolet light, indicating their prospective benefits in the photocatalytic field. Band gaps less than 3.1 eV in LDHs show excellent visible light sensitivity.21 In previous research, Mantilla et al. used ZnAlFe LDH as a photocatalyst for the degradation of 2,4-D.9 FeCo-LDH derived from a MOF was utilized to completely remove 2,4-D within a very short period.22 However, due to their low carrier separation efficiency, LDHs were connected to other photo-active semiconductors like BiOCl,23 Cu2O,24 and g-C3N425 to create heterojunctions with smaller band gaps, thus accelerating the photogenerated electron–hole pairs’ separation and increasing the intensity of visible-light absorption.
Among the nanostructures utilized for photocatalysis, cadmium sulfide (CdS) has been very attractive because of its strong light absorption, large surface area, and higher conduction band.26 CdS has a narrow band gap (2.4 eV), which allows it to respond to sunlight up to 520 nm.27 However, since photogenerated holes during the photocatalytic activity can easily oxidize S2− ions, CdS would photocorrode and become extremely unstable. Moreover, the photocatalytic efficiency is reduced due to the quick recombination of the photo-induced electron–hole pairs.28 Fortunately, it was discovered that the valence and conduction bands of LDH and CdS are highly appropriate for heterostructure construction because of their well-matched overlapping band energies. The heterostructure can quickly separate photogenerated electron–hole pairs, which increases the activity of the photocatalytic reaction. Moreover, the quick migration of photogenerated holes in the CdS's valence band can effectively prevent photocorrosion, enhancing stability. For instance, CdS was coupled with LDH in previous reports, forming excellent heterostructures such as CdS@NiCo-LDH.29,30 Consequently, coupling LDH and CdS is a workable way to address the drawbacks of both LDH and CdS at the same time.
Another method for increasing photocatalytic efficiency is constructing a three-component heterojunction system loaded with a noble metal. The noble metals' surface plasmon resonance effect has been shown to increase the visible light absorption capacity of semiconductors. Noble metallic nanoparticles may play the electron traps’ role, speeding up the charge transfer process between photocatalysts and improving photocatalytic efficiency.31 To date, no study has been reported to remove 2,4-D from water using CdS/Ni–Fe LDH loaded with metallic Ag as an effective plasmonic element.
In current research, Zn–Fe, Mg–Fe, and Ni–Fe LDH nanoparticles (ZFL, MFL, and NFL) were primarily fabricated to study their adsorption efficiency in the removal of 2,4-D. Ni–Fe LDH was selected as an adsorbent for the photocatalytic degradation mechanism, and modified with the prepared cadmium sulfide (C), constructing a heterojunction photocatalyst (CdS/Ni–Fe LDH (CNFL) nanocomposite). Then, metallic Ag was utilized to modify CdS/Ni–Fe LDH further, forming the Ag@CdS/Ni–Fe LDH (Ag@CNFL) nanocomposite, to investigate its adsorption and photocatalytic activity in the elimination of 2,4-D. Secondly, the structure, chemical composition, and morphological characteristics of the samples were examined through systematic characterization. Thirdly, the effect of water chemistry parameters on the adsorption and photocatalytic behavior of 2,4-D was carefully studied. Some abbreviations are shown in Table S1 (ESI†).
2. Materials and methods
2.1. Materials
Ni(NO3)2·6H2O (≥98.5%), Zn(NO3)2·6H2O (≥98.5%), Mg(NO3)2·6H2O (99%), Fe(NO3)2·9H2O (≥98.0%), HCl (37%), NaOH (≥98.0%), 2,4-dichlorophenoxyacetic acid (M wt. 221.04 g mol−1), CdCl2 (anhydrous, ≥99%), Na2S·9H2O (≥98%), and AgNO3 (≥99.0%) were purchased from Sigma Aldrich. Each chemical was of pure analytical grade.
2.2. Synthesis of samples
2.2.1. Synthesis of Zn–Fe, Mg–Fe, and Ni–Fe LDH nanoparticles (ZFL, MFL, and NFL).
The co-precipitation route was used to synthesize layered double hydroxides based on Zn–Fe, Mg–Fe, and Ni–Fe. This involved slowly adding a solution (B, NaOH) into a second solution (A, M2+/M3) that contains divalent and trivalent metal cation solution (M2+/M3+ molar ratio = 3) and also the target anion to be intercalated. A further step was used to precipitate LDHs using an inorganic base, which led to an increase in pH and the creation of LDH structures.
Aqueous separated solutions of different divalent metal salts of Zn(NO3)2·6H2O, Mg(NO3)2·6H2O, and Ni(NO3)2·6H2O with a concentration of 0.4 mol L−1 were prepared. Each solution was mixed with a solution of Fe(NO3)2·9H2O (0.133 mol L−1) with stirring for 0.5 h (solution A). Then, a NaOH solution (1.0 mol L−1) was prepared (solution B). Subsequently, solution B was dropped slowly into solution A under strong magnetic stirring while regulating this addition to keep the mixture pH at 9.0–9.5, 8.7–12.5, and 10.0–10.5 to precipitate Zn–Fe, Mg–Fe, and Ni–Fe LDH, respectively. This is according to the solubility product constant (Ksp) of the metal hydroxides (Zn(OH)2, Mg(OH)2, and Ni(OH)2) and the avoidance of precipitation of other phases. Each mixture was stirred for 3 h at 60 °C and aged overnight. Finally, each sample was filtered, washed with distilled water, and dried at 80 °C. The dried samples were calcined at 400 °C for 3 h to remove the interlayer anions partially.32
2.2.2. Synthesis of cadmium sulfide (C).
Typically, 0.05 mol of Na2S·9H2O and 0.05 mol of CdCl2 were dissolved separately in 50 and 300 mL of distilled water under continuous stirring for complete dissolution, respectively. Afterward, Na2S·9H2O was added gradually into CdCl2 solution under magnetic stirring for 1 h at 50 °C. The light color of the precursor solution gradually changed to dark yellow or orange. The chemical reaction was as follows:33| | | CdCl2 + Na2S·9H2O → CdS + 2NaCl + 9H2O | (1) |
The final product was centrifuged and washed several times to get highly pure CdS nanoparticles, which were gathered and dried at 85 °C.
2.2.3. Synthesis of the CdS/Ni–Fe LDH (CNFL) nanocomposite.
0.665 g of Na2S·9H2O and 0.508 g of CdCl2 were dissolved in 50 and 150 mL of distilled water separately under magnetic stirring. 2.0 g of the as-prepared Ni–Fe LDH was ultrasonicated and then dispersed into CdCl2 solution under stirring for 15 min. Next, Na2S·9H2O was added gradually into the previous solution while being stirred magnetically for 1 h at 50 °C. Eventually, the CdS/Ni–Fe LDH nanocomposite with a loading of 20% CdS was gathered by washing with distilled water and drying at 80 °C.
2.2.4. Synthesis of the Ag@CdS/Ni–Fe LDH (Ag@CNFL) nanocomposite.
In brief, 2 g of the CdS/Ni–Fe LDH nanocomposite was dispersed in 70 mL of distilled water and treated ultrasonically for 10 min. 50 mL of aqueous solution of AgNO3 (4.6353 × 10−4 mol) was added to the previous solution with magnetic stirring for 15 min. After that, the mixture was irradiated by a 400 W xenon lamp for 30 min under stirring. The resulting solution was treated by similar processes to that of the above composite.31
2.3. Characterization of the solid samples
The thermogravimetric study was carried out using TGA apparatus (Setaram-Labsys-Evo S60) to assess the thermal stability behavior of the materials up to 820 °C at a nitrogen flow rate of 15 mL min−1. The crystalline nature of samples was assessed by X-ray diffraction (XRD, Bruker D2 Phaser 2nd Gen) under the following conditions: operating at a current of 10 mA, a voltage of 30 kV, and a spinner operating at 15 rpm at a step of 132 s in the range of 20–80°. A gas sorption analyzer (BELSORP MAX X, MicrotracBEL Corp., Japan) was used to determine specific surface area SBET (m2 g−1), average pore size ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (nm) and total pore volume VT (cm3 g−1) through the analysis of nitrogen gas adsorption–desorption isotherms at 77 K. An ATR-FTIR (Nicolet Impact-400 D with a ZnSe crystal) spectrometer was used to investigate the different functional groups for all the prepared samples and any surface changes before and after adsorption for Ag@CNFL as a selected sample. It was operated in the 4000–400 cm−1 region with a resolution of 4.0 cm−1 and 16 accumulations. Zeta potential changes were measured using a Zetasizer (Nano S, Malvern Instrument, UK) to determine the point of zero charge (pHPZC) of adsorbents. Diffuse reflectance spectroscopy (UV-vis DRS, Shimadzu, Japan) was utilized to measure the band gap of the studied catalysts (NFL, C, CNFL, and Ag@CNFL). Tauc's equation was used to estimate the band gap values of these photocatalysts to assess the optical properties:34where the type of transition determines the absorption coefficient (α), constant (A), light frequency (v), band gap value (Eg), Planck constant (h), and exponent n. Plotting (αhv)2 as the y-axis against hν as the x-axis and then extrapolating the straight part of the curve on the hν axis at α = 0 yields the samples' direct band gap.
(nm) and total pore volume VT (cm3 g−1) through the analysis of nitrogen gas adsorption–desorption isotherms at 77 K. An ATR-FTIR (Nicolet Impact-400 D with a ZnSe crystal) spectrometer was used to investigate the different functional groups for all the prepared samples and any surface changes before and after adsorption for Ag@CNFL as a selected sample. It was operated in the 4000–400 cm−1 region with a resolution of 4.0 cm−1 and 16 accumulations. Zeta potential changes were measured using a Zetasizer (Nano S, Malvern Instrument, UK) to determine the point of zero charge (pHPZC) of adsorbents. Diffuse reflectance spectroscopy (UV-vis DRS, Shimadzu, Japan) was utilized to measure the band gap of the studied catalysts (NFL, C, CNFL, and Ag@CNFL). Tauc's equation was used to estimate the band gap values of these photocatalysts to assess the optical properties:34where the type of transition determines the absorption coefficient (α), constant (A), light frequency (v), band gap value (Eg), Planck constant (h), and exponent n. Plotting (αhv)2 as the y-axis against hν as the x-axis and then extrapolating the straight part of the curve on the hν axis at α = 0 yields the samples' direct band gap.
Scanning electron microscopy (SEM) and transmission electron microscopy (TEM) investigations were employed to evaluate the surface morphology using the JEOL JSM-6510LV model and the JEOL-JEM-2100 model, Japan apparatus, respectively.
2.4. Batch adsorption studies of 2,4-D
The adsorption tests were performed in a batch system using four prepared materials (ZFL, MFL, NFL, and Ag@CNFL) by the controlled agitation of 25 mL of known 2,4-D concentration with 0.06 g of the adsorbent at 23 °C and pH 2 for 14 h. Subsequently, the unadsorbed 2,4-D concentration was centrifuged to be determined by a PerkinElmer UV-vis spectrophotometer at a wavelength of 283 nm. A calibration curve at 2,4-D concentration up to 300 mg L−1 was created using the necessary dilution within Lambert–Beer law's linearity range. Each run was performed three times, the average was stated for calculations, and the error bars were shown in the related figures. The effect of adsorption variables, namely adsorbent dosage (0.4–4.0 g L−1), pH (2–10), initial 2,4-D concentration (40–800 mg L−1), shaking time (0.25–20.00 h), and temperature (23–42 °C) was studied. The equilibrium adsorption capacity (qe, mg g−1, eqn (3)) and removal efficiency (R%, eqn (4)) were expressed by the following equations:| | 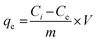 | (3) |
| |  | (4) |
wherein Ci and Ce mark the 2,4-D concentration (mg L−1) at the start and the adsorption end, respectively. V denotes solution volume (L) and m is the adsorbent mass (g).
2.4.1. Adsorption kinetic models.
The adsorption mechanism of 2,4-D was analyzed using the nonlinear form of some kinetic models: pseudo-first-order (PFO, eqn (6)), pseudo-second-order (PSO, eqn (7)), Avrami (eqn (8)), Elovich (eqn (9)), Bangham's pore diffusion (eqn (10)), and intra-particle diffusion (eqn (11)) and linear Boyd (eqn (12)).35,36| |  | (5) |
| | 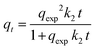 | (7) |
| | | qt = [1 − e−(KAVt)nAV] × qAV | (8) |
| |  | (9) |
| |  | (10) |
| |  | (12) |
where qt (mg g−1), qexp (mg g−1), and Ct (mg L−1) are the adsorbed amounts of 2,4-D at time t (h) and equilibrium, and the residual 2,4-D concentration at time t, respectively. k1 (h−1) and k2 (g mg−1 h−1) are the rate constants of PFO and PSO models, respectively. qAV (mg g−1), KAV (h−1), and nAV are related to the adsorption capacity, rate constant, and order model of Avrami, respectively. β (g mg−1) refers to the surface coverage amount and α (mg g−1 h−1) is the initial adsorption rate. B (<1) and KB (mL L g−1) are Bangham's constants. The boundary layer thickness and intra-particle diffusion rate constant are represented by C and ko (mg g−1 h−1/2), respectively, while Bt is related to the Boyd constant.
2.4.2. Adsorption isotherm models.
The 2,4-D adsorption behavior and experimental results were explained by various nonlinear adsorption isotherms: Langmuir (eqn (13)), Freundlich (eqn (15)), Temkin (eqn (16)), Dubinin–Radushkevich (DR) (eqn (17)), Redlich–Peterson (eqn (19)), Sips (eqn (20)), and Toth (eqn (21)) models.36,37| | 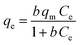 | (13) |
| | 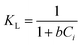 | (14) |
| |  | (15) |
| |  | (16) |
| |  | (18) |
| |  | (19) |
| |  | (20) |
| |  | (21) |
Herein, qm (mg g−1) is the Langmuir maximum adsorption capacity and b (L mg−1) is the Langmuir constant. To determine whether the adsorption process is unfavorable (KL > 1), favorable (0 < KL < 1), or irreversible (KL = 0), the separation factor (KL) was calculated using eqn (14). n and KF (L1/n mg1−1/n g−1) denote the heterogeneity factor and Freundlich constant, respectively. KT (L g−1) and bT (J mol−1) are Temkin constants. The absolute temperature and gas adsorption constant are represented by T (K) and R (8.314 J mol−1 K−1), respectively. KDR (mol2 kJ−2), EDR (kJ mol−1), and ε refer to the DR constant, mean adsorption-free energy, and Polanyi potential, respectively. qDR, qs, and qth are DR, Sips, and Toth adsorption capacity (mg g−1), respectively. (KRP (L g−1) and αRP (mg L−1)−g), Ks (L g−1), and Kth (L mg−1) are Redlich–Peterson, Sips, and Toth isotherm constants, respectively. g, ns, and nth are Redlich–Peterson, Sips, and Toth isotherm exponents, respectively.
2.4.3. Adsorption thermodynamic parameters.
The energy transfer during adsorption and adsorption feasibility of 2,4-D on the prepared adsorbents were defined using thermodynamic factors like standard enthalpy change (ΔH°, kJ mol−1), standard entropy change (ΔS°, kJ mol−1 K−1), and standard free energy change (ΔG°, kJ mol−1) using eqn (22)–(24).38,39| |  | (22) |
| | 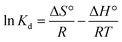 | (24) |
where Kd refers to the adsorption distribution coefficient and Cs is the equilibrium 2,4-D concentration (mg L−1) on the solid adsorbent.
2.5. Photocatalytic degradation experiments of 2,4-D
The photocatalytic performance of NFL, C, CNFL, and Ag@CNFL was studied for 2,4-D degradation using a 300 W xenon visible lamp placed 15 cm apart from the glass batch reactor equipped with an external water jacket to regulate the solution temperature. Furthermore, the reactor was shielded from external foreign light by covering it with aluminum foil, and a magnetic stirrer was used to mix the solution to ensure the catalyst suspension and homogeneity. The process was carried out using a 0.15 g catalyst and 150 mL of 15 mg L−1 2,4-D solution at pH = 3.2 and 20 °C for 110 min of irradiation time. Besides, the photocatalytic tests were performed at initial 2,4-D concentrations of 10, 15, 20, and 30 mg L−1, catalyst amounts of 0.5, 0.75, 1.0, 1.5, and 2.0 g L−1, and temperatures of 20, 30, 35, and 40 °C. By centrifuging 2 mL of solution at selected time intervals up to 110 min, the degradation was investigated by detecting the concentration of undegraded 2,4-D that was measured using the specified spectrophotometer at 283 nm as shown in the adsorption method. The degradation percent (D%) of 2,4-D was determined based on eqn (25).| |  | (25) |
where Ct (mg L−1) is the undegraded 2,4-D concentration at irradiation time t (min) and Ci (mg L−1) is the initial concentration.
2.5.1. Photocatalytic degradation kinetics of 2,4-D.
The photodegradation kinetics onto CNFL and Ag@CNFL were explained by the Langmuir–Hinshelwood (L–H) model (eqn (26)). This model can be simplified to the pseudo-first-order kinetic model with an apparent rate constant kapp (min−1). The half-life time (t1/2) for the 2,4-D photodegradation was calculated using eqn (27).2| |  | (26) |
| |  | (27) |
2.5.2. Photocatalytic degradation thermodynamics of 2,4-D onto CNFL and Ag@CNFL.
Thermodynamic factors of photocatalytic degradation such as activation entropy change (Δ‡S°, kJ mol−1 K−1), activation enthalpy change (Δ‡H°, kJ mol−1), and activation energy (Ea, kJ mol−1) were assessed using Arrhenius (eqn (28)) and Eyring–Polanyi (eqn (29)) models. Eqn (30) was used to determine activation Gibb's free energy change (Δ‡G°, kJ mol−1).40| |  | (28) |
| |  | (29) |
Herein A (s−1), kb (1.381 × 10−23 J K−1), and h (6.626 × 10−34 J s−1) refer to Arrhenius, Boltzmann, and Planck constants, respectively.
2.6. Reusability of the prepared photocatalysts
The reusability was investigated after eight cycles of 2,4-D photodegradation, utilizing 150 mL of 15 mg L−1 2,4-D concentration at 20 °C, pH = 3.2, 1.0 g L−1 catalyst amount and 110 min of irradiation time. After each run, the catalyst was separated by centrifugation, gently washed with hot distilled water, and dried at 85 °C to reuse the photocatalyst.
3. Results and discussion
3.1. Characterization of the synthesized materials
The thermal stability of the fabricated samples was assessed using TGA analysis as plotted in Fig. 1a. The samples (ZFL, MFL, NFL, C, CNFL, and Ag@CNFL) lost weight with 22.5, 13.2, 4.3, 12.4, 5.7, and 9.0%, respectively, over temperatures from 27 to 820 °C. Generally, the temperature at which LDHs decomposed varied according to their chemical composition. For three-layered structures, TGA data can be used to describe three main mass loss events. The first event was attributed to the release of physically adsorbed water with temperatures ranging from 27 to 240 °C and mass losses of 1.2% for ZFL and 3.0% for each of MFL and NFL.41 In the second event, other 7.6, 5.8, and 0.5% weight losses of ZFL, MFL, and NFL, respectively, appeared between 240 and 415 °C, where the dehydroxylation of brucite structure, which released interlayer water molecules, and the intercalated nitrate anion decomposition significantly impacted the composition of the layered structure.42 Lastly, complete destruction of interlayer anions and dehydroxylation were observed between 415 and 500 °C with a loss of 3.5 and 0.8% for MFL and NFL, respectively, and the weight loss of MFL (only 0.9%) and NFL stabilized above 500 °C. The TGA curve of ZFL shows a 1.5% decrease in mass from 415 to 567 °C, then a sharp mass decline from 567 to 820 °C with 12.2%, indicating the total structure collapse. Generally, after LDH dehydroxylation was finished, an amorphous M2+ oxide phase was formed, followed by the crystalline oxide phase production. At a temperature of nearly 500 °C, spinel phases were formed.43 Therefore, it can be concluded that the NFL structure was more thermally stable than the equivalent phase of magnesium and zinc. TGA curves of C, CNFL, and Ag@CNFL demonstrated a mass loss of 12.1, 1.2, and 3.5%, respectively up to 175 °C, assigned to volatile impurities or moisture loss. Notably, CdS did not nearly lose weight after 175 °C, showing that it is stable and did not undergo sublimation or breakdown, revealing the successful synthesis of highly thermal stable cadmium sulfide nanoparticles. CNFL and Ag@CNFL depicted low loss in their weight (1.6 and 3.0%, respectively) with increasing temperature from 175 to 733 °C, verifying that the incorporation of Ni–Fe LDH with CdS enhanced the thermal stability of the formed nanocomposites. Also, the dispersion of metallic Ag onto the CNFL structure decreased the thermal stability by 3.4%.
 |
| | Fig. 1 TGA (a), XRD (b), N2 adsorption (c), and ATR-FTIR (d) of all the samples, zeta potential (e) of adsorbents, UV-vis DRS (inset: band gap energy values) (f) curves of the catalysts, and, the ATR-FTIR curve of Ag@CNFL after 2,4-D adsorption. | |
XRD patterns of the prepared materials (ZFL, MFL, NFL, C, CNFL, and Ag@CNFL) are presented in Fig. 1b. The examination of XRD patterns of LDHs revealed the partial destruction of the lamellar structure of LDHs with incomplete dehydroxylation and the elimination of some interlayer anions and water during the calcination of LDHs for 3 h at 400 °C, forming the cubic metal oxides.44 The major diffraction lines of ZFL indexed as ZnO reflections with (100), (002), (101), (102), (110), (103), (200), (112), and (201) planes corresponded to the angles at 2θ of 32.0, 34.1, 36.7, 47.5, 56.6, 62.8, 66.5, 68.0, and 69.3°, respectively.45 The wider diffraction peaks of MFL and NFL implied that either nanocrystalline particles in the resulting LDH are smaller or the structure is amorphous. The diffractograms of MFL demonstrated peaks at 2θ = 35.5, 42.8, and 62.1° attributed to (111), (200), and (220) reflections of the periclase MgO phase, respectively.44 The characteristic NFL peaks assigned to the major reflections of NiO appeared at 2θ = 37.1, 43.3, 62.7, 75.3, and 79.3° of (111), (200), (220), (311), and (222) planes, respectively. The absence of segregated phases indicated that the transition metal oxides were evenly distributed across M2+ and M3+ oxide matrices.46 The XRD chart of CdS (C) shows four main peaks with well-defined lattice planes (111), (220), (311), and (331) at 2θ of 26.5, 43.9, 51.8, and 71.0°, respectively, unveiling the cubic crystalline nanostructure of CdS (ICDD PDF 89-0440).47 Furthermore, the absence of any other notable peaks reflected the great purity of CdS nanoparticles. The creation of nanoscale ranged particles was confirmed by the broad peak at 71.0°. Notably, the diffraction peaks of CNFL, compared to NFL, became stronger with the CdS loading. The lack of the peak of metallic Ag in the XRD pattern suggested low loading quantity and considerable Ag dispersion in the Ag@CNFL composite. XRD patterns of CNFL and Ag@CNFL are similar to pure Ni–Fe LDH and CdS, indicating that the combination with CdS and metallic Ag restructured LDH, verifying the successful preparation of nanocomposites.31
The isotherms of nitrogen adsorption–desorption of all the samples (ZFL, MFL, NFL, C, CNFL, and Ag@CNFL) are shown in Fig. 1c. The isotherm adsorption branches were below the branches of desorption, and each isotherm had a visible hysteresis loop since the constrictions of pores slowed down the nitrogen desorption. The synthesized materials generally showed type IV isotherms, forming multilayers.22 The hysteresis loop at comparatively high relative pressures (P/P0) for all samples ranging from 0.65–0.99 to 0.46–0.99, 0.38–0.99, 0.33–0.99, 0.43–0.95, and 0.43–0.96, respectively, was classified as type H3. This suggested that the aggregated nanosheets’ secondary particles had slit-like pores. According to the textural parameters listed in Table 1, the specific surface area (SBET) of NFL > MFL > ZFL by 5.0 and 70.8%, compared to NFL, and this sequence was confirmed by the total pore volume (VT) and average pore size (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ). The prepared LDHs demonstrated a high surface area with a porous structure and holes produced by the partial collapse of layers and interlayer loss after calcination at 400 °C for 3 h. Thus, Ni–Fe LDH can provide significant active adsorption sites for 2,4-D. Furthermore, cadmium sulfide (C) depicted a good surface area (95.70 m2 g−1). However, the modification of Ni–Fe LDH with cadmium sulfide reduced the surface area by 37.6%. After the dispersion of metallic Ag onto the CNFL surface, the surface area decreased to 113.10 m2 g−1 as proved by the total pore volume values.48 This could be explained by the incorporation effect of Ag metallic and cadmium sulfide, which blocked some pores on the LDH surface. Nevertheless, the average pore size increased after the modification of NFL. The mesopores (ranging in size from 2 to 50 nm) that developed between the laminar crystal sheets were linked to
). The prepared LDHs demonstrated a high surface area with a porous structure and holes produced by the partial collapse of layers and interlayer loss after calcination at 400 °C for 3 h. Thus, Ni–Fe LDH can provide significant active adsorption sites for 2,4-D. Furthermore, cadmium sulfide (C) depicted a good surface area (95.70 m2 g−1). However, the modification of Ni–Fe LDH with cadmium sulfide reduced the surface area by 37.6%. After the dispersion of metallic Ag onto the CNFL surface, the surface area decreased to 113.10 m2 g−1 as proved by the total pore volume values.48 This could be explained by the incorporation effect of Ag metallic and cadmium sulfide, which blocked some pores on the LDH surface. Nevertheless, the average pore size increased after the modification of NFL. The mesopores (ranging in size from 2 to 50 nm) that developed between the laminar crystal sheets were linked to ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) values between 2.0378 and 6.0144 nm.48
values between 2.0378 and 6.0144 nm.48
Table 1 Characterization parameters for the synthesized solid samples
| Sample |
pHPZC |
S
BET (m2 g−1) |
V
T (cm3 g−1) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (nm) (nm) |
| ZFL |
8.41 |
57.12 |
0.0291 |
2.0378 |
| MFL |
6.86 |
185.96 |
0.1554 |
3.3427 |
| NFL |
8.43 |
195.75 |
0.2697 |
5.5111 |
| C |
— |
95.70 |
0.1031 |
4.3093 |
| CNFL |
— |
122.24 |
0.1838 |
6.0144 |
| Ag@CNFL |
8.34 |
113.10 |
0.1658 |
5.8638 |
ATR-FTIR curves of the prepared samples and Ag@CNFL following 2,4-D adsorption are shown in Fig. 1d. The spectra of LDHs (ZFL, MFL, and NFL) demonstrated four main groups of bands; many absorption peaks noted between 408 and 760 cm−1 were associated with the skeleton vibration modes of metal oxides (M–O or M–O–M). The intense bands around 1382 cm−1 were related to the intercalated nitrate ion stretching vibration. Small bands around 1627 cm−1 and strong broad peaks around 3429 cm−1 were attributed to the bending and stretching vibrations of the hydrogen-bonded (H–O–H) hydroxyl groups from the interlayer and/or surface, successively.20,49 The spectrum of CdS was reported at wavenumbers 429–660, 810–999, 1129, 1377, 1628, and 3426 cm−1, signifying Cd–S bond stretching vibration, C–C vibration, C–O stretching, asymmetrical stretching vibration of O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, O–H bending, and O–H stretching modes resulting from the interaction of water with CdS, respectively.47 FTIR spectra of CNFL and Ag@CNFL showed all of the characteristic bands of Ni–Fe LDH and CdS with a small positive shift in wavenumbers, which verified the strong contact during heterojunction formation.50 Also, the distinctive band of nitrate ions disappeared. The band intensity of metal oxides in the Ag@CNFL spectrum, compared to that of CNFL, weakened after loading the metallic Ag. The FTIR curve of Ag@CNFL after 2,4-D adsorption depicted the same one before the adsorption with a slight shift in bands and an increase in the band intensity, and the faint absorption peak at 1921 cm−1 may be related to the hydrogen bonding between hydroxyl groups of 2,4-D molecules and Ag@CNFL.29 Related bands to 2,4-D are present alongside Ag@CNFL bands. The new bands near 1340 and 1460 cm−1 may be linked to C–O–C and C
O, O–H bending, and O–H stretching modes resulting from the interaction of water with CdS, respectively.47 FTIR spectra of CNFL and Ag@CNFL showed all of the characteristic bands of Ni–Fe LDH and CdS with a small positive shift in wavenumbers, which verified the strong contact during heterojunction formation.50 Also, the distinctive band of nitrate ions disappeared. The band intensity of metal oxides in the Ag@CNFL spectrum, compared to that of CNFL, weakened after loading the metallic Ag. The FTIR curve of Ag@CNFL after 2,4-D adsorption depicted the same one before the adsorption with a slight shift in bands and an increase in the band intensity, and the faint absorption peak at 1921 cm−1 may be related to the hydrogen bonding between hydroxyl groups of 2,4-D molecules and Ag@CNFL.29 Related bands to 2,4-D are present alongside Ag@CNFL bands. The new bands near 1340 and 1460 cm−1 may be linked to C–O–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations in the aromatic ring, respectively. Consequently, the identification and attribution of these bands confirmed that 2,4-D was effectively adsorbed on the Ag@CNFL nanocomposite.
C stretching vibrations in the aromatic ring, respectively. Consequently, the identification and attribution of these bands confirmed that 2,4-D was effectively adsorbed on the Ag@CNFL nanocomposite.
Fig. 1e shows the plot of zeta potential vs. pH for the adsorbents. ZFL, MFL, NFL, and Ag@CNFL had pHPZC values of 8.41, 6.86, 8.43, and 8.34, respectively (Table 1). Ag@CNFL had a smaller positive deviation below pHPZC and a smaller negative deviation above pHPZC for NFL. This suggested that H+ ions interacted with the basic adsorbent sites below pHPZC, raising the suspension pH. The pH of the suspension dropped above pHPZC due to H+ being lost from the more acidic sites. Thus, pHPZC is the pH below and above which the adsorbent has a positive and negative charge, respectively.51
As shown by UV-vis DRS spectra in Fig. 1f, the samples showed broad reflectance in the 200–800 nm range, indicating that they can absorb UV and visible light. DRS analysis was used to examine the optical absorption properties and photocatalyst bandgap using the Tauc equation (Fig. 1f inset).34 The bandgap energies of NFL and C were about 2.35 and 2.30 eV, while those of CNFL and Ag@CNFL were reported as 2.25 and 1.96 eV, respectively. Consequently, the addition of C to the NFL structure reduced the bandgap energy and enhanced the conductive electrical structure and charge transfer kinetics, boosting the photocatalytic activity. The structural and morphological variations of photocatalysts may be related to this shift in optical absorption. Furthermore, changes in the band gap could be caused by varying levels of electron–hole pair absorption and transfer, which could be influenced by the photocatalytic mechanism.30 The narrower band gap of Ag@CNFL can be related to the fact that visible light radiation used to photoexcite the sample produced greatly electron–hole pairs on the catalytic surface, verifying its stronger photo-absorption that stimulated the chemical redox reactions and increased photocatalytic activity.29
SEM and TEM analyses were used to describe the morphological characteristics of the samples. Fig. 2a–f displays the high-magnification SEM images of ZFL, MFL, NFL, C, CNFL, and Ag@CNFL. SEM micrographs (Fig. 2a–c) reveal that the prepared LDHs were shown to be agglomerated and to have a platelike morphology, laying on top of one another, with heterogeneous and irregular porous surfaces.52 These characteristics were common to hydrotalcite synthesized using the co-precipitation technique. Fig. 2d shows the SEM image of cadmium sulfide, indicating its very small spherical homogenous particles with high porosity. SEM micrographs (Fig. 2e–f) of CNFL and Ag@CNFL show the uniform dispersion of cadmium sulfide and metallic Ag onto the NFL surface, proving the effective incorporation. Possibly, there was some deformation to the surface structure of composites, most likely caused by Ag and CdS loading, causing the nanosheets to thicken and agglomerate. TEM images are presented in Fig. 2g–l and depict the ultrathin properties of nanosheets. High-resolution TEM micrographs of ZFL, MFL, NFL, C, CNFL, and Ag@CNFL display particle sizes of nearly 30, 50, 25, 20, 65, and 68 nm, respectively. The particle size of the stacked-disc-shaped in Mg–Fe LDH was higher than that in Zn–Fe LDH, which was larger than that in Ni–Fe LDH. Fig. 2g–i indicate that the morphology of LDHs was hexagonal rough platelets. Also, it reveals that the structure had many pores because of the interparticle spaces.49 The TEM image (Fig. 2j) of CdS reveals that the particles were uniformly dispersed and of the same size when they were in an assemblage. In TEM images of CNFL and Ag@CNFL, all elements were homogenously distributed, verifying the successful synthesis of heterojunctions. Ag element was distributed in a very small size and a low quantity. Finally, these findings show that the samples were successfully prepared.
 |
| | Fig. 2 SEM (a)–(f) and TEM (g)–(l) images of ZFL, MFL, NFL, C, CNFL, and Ag@CNFL, respectively. | |
3.2. Static adsorption studies of 2,4-D
3.2.1. Impact of adsorbent dose.
The effect of varying adsorbent doses (0.4–4.0 g L−1) on the adsorption capacity (qe, mg g−1, eqn (3)) and removal efficiency (R%, eqn (4)) was examined through tests at pH 2, 23 °C, and 25 mL of 300 mg L−1 2,4-D concentration for 20 h of shaking time as displayed in Fig. 3a. It was noted from these data that upon elevating the adsorbent dose from 0.4 to 2.4 g L−1, the 2,4-D removal efficiency increased rapidly from 25, 26, 31, and 28% to 58, 68, 76, and 71% for ZFL, MFL, NFL, and Ag@CNFL, respectively. This relationship can be explained by creating more accessible active sites to bind with 2,4-D molecules, improving their removal at higher dosages. The saturation and equilibrium were nearly achieved at more than 2.4 g L−1 dose. However, the dose effect on the adsorption capacity showed a consistent decline from 187.5, 195.0, 232.5, and 210.0 mg g−1 to 45.0, 54.0, 60.0, and 56.2 mg g−1 for ZFL, MFL, NFL, and Ag@CNFL, respectively as the dose enhanced from 0.4 to 4.0 g L−1. This decrease was mainly caused by the restricted accessibility of the inner active adsorbent spots for 2,4-D molecules, which may be due to the aggregation of the binding sites onto the adsorbent surface.3 Additionally, the adsorption capacity decreased when the adsorbent dose was increased as a result of more adsorption sites being vacant during the adsorption process with a fixed volume and concentration of 2,4-D solution.53 A dose of 2.4 g L−1 was chosen as the ideal dose for subsequent experiments.
 |
| | Fig. 3 Adsorbent dosage (a) and pH (b) effects for 2,4-D adsorption onto ZFL, MFL, NFL, and Ag@CNFL at 300 mg L−1 2,4-D concentration for 20 h of shaking time at 23 °C. | |
3.2.2. Impact of adsorbate pH.
The solution pH levels were manipulated in the range of 2–10 to investigate the correlation between the adsorption efficiency and solution pH in eliminating 2,4-D. Experiments were executed by changing the pH using 2.4 g L−1 adsorbent dose mixed with 25 mL of 300 mg L−1 2,4-D concentration for 20 h of shaking time at 23 °C (Fig. 3b). Fig. 3b reveals that at pH 2, the highest removal efficiency was achieved where R% of ZFL, MFL, NFL, and Ag@CNFL was 60, 72, 80, and 74%, respectively. The results showed a noteworthy decrement in the 2,4-D adsorption as the pH elevated from 2 to 10 by 75.0, 61.1, 62.5, and 60.8% for ZFL, MFL, NFL, and Ag@CNFL, successively. This observation highlighted that at the ideal pH of 2, the lower solution pH value compared to the pKa value (2.8) of 2,4-D caused the 2,4-D molecules to undergo a transition towards a more neutrally charged state and a minor protonation.54 Consequently, a potential π–π stacking conjugation between the aromatic ring of 2,4-D and adsorbents could have happened; additionally, the lower pH of 2 enhanced electrostatic attraction between highly positively charged LDH or its composite and 2,4-D molecules, further augmenting the contact.54 It was concerned with the obtained pHPZC of ZFL (8.41), MFL (6.86), NFL (8.43), and Ag@CNFL (8.34). At pH > pHPZC, the adsorption was impeded more because of the repulsion between anionic 2,4-D and the negatively charged surface of adsorbents. The hydrogen bonding between the electronegative oxygen atom of the carboxylic group of 2,4-D and the hydrogen atom of the adsorbent, and furthermore, donor–acceptor interactions between the Cl atom of 2,4-D species and the hydroxyl group of the adsorbents may be established.55 When pH > pKa, there were anionic species of 2,4-D in the solution, and the positivity of the adsorbent surface decreased with increasing pH value, reducing the previous interactions and removal efficiency.
3.2.3. Adsorption kinetic modeling.
To assess the time needed to attain equilibrium, time-based experiments were conducted by plotting adsorption capacity (qt) versus shaking time (t) for the adsorption of 2,4-D onto ZFL, MFL, NFL, and Ag@CNFL. This effect was carried out over a duration extending from 0.25 to 20.00 h, using 2.4 g L−1 adsorbent dose added to 25 mL of 800 mg L−1 2,4-D concentration at 23 °C and pH 2. In the spots of Fig. 4a–e, it was evident that all the adsorbents demonstrated fast adsorption kinetics, attaining 90.0, 112.0, and 125.0 mg g−1 for ZFL, MFL, and Ag@CNFL, respectively, within the first 6 h, and 166.1 mg g−1 for NFL within the initial 8 h. This result demonstrated that the adsorption rate was more directly correlated with the effective number of available adsorption sites instead of the concentration of 2,4-D.6 Next, 2,4-D molecules gradually filled the active adsorption sites, resulting in progressive deceleration in the adsorption rate until equilibrium was achieved at 10 h for all the samples except for NFL at 14 h. The adsorbent surface then started to get close to saturation.
 |
| | Fig. 4 The nonlinear plots of PFO and PSO (a), Avrami (b), Elovich (c), Bangham's pore diffusion (d), intra-particle diffusion (e), and linear Boyd (f) models for 2,4-D adsorption onto ZFL, MFL, NFL, and Ag@CNFL at 800 mg L−1 2,4-D concentration, 2.4 g L−1 adsorbent dose, 23 °C, and pH 2. | |
Adsorption kinetic evaluations are essential for predicting the 2,4-D removal mechanism and rate-limiting steps. In this study, the nonlinear forms of some kinetic models (PFO (eqn (6)), PSO (eqn (7))), Avrami (eqn (8)), Elovich (eqn (9)), Bangham's pore diffusion (eqn (10)), and intra-particle diffusion (eqn (11)) and linear Boyd (eqn (12)) were used to describe the experimental data as shown in Fig. 4a–f, respectively. The estimated parameters from these models are shown in Table 2. The outcomes showed that the regression correlation coefficients (R2) of PFO, PSO, and Avrami kinetics spanned from 0.8507 to 0.9935, 0.9483 to 0.9917, and 0.9829 to 0.9943. The average reduced chi-square (χ2) values are 5.04 (high), 1.83 (low), and 0.80 (low). Furthermore, the difference between the adsorption capacities (qexp and qAV) calculated from these kinetic models and Langmuir adsorption amounts (qm) is 13.9–18.6% (large), 0.2–3.2% (negligible), and 0.0–11.7% (small), respectively, based on the previous trend of models. The prior observations suggested the high accuracy degree of performance of PSO and Avrami models for the description of 2,4-D removal by ZFL, MFL, NFL, and Ag@CNFL. Conversely, the PFO model had the least capability to predict 2,4-D adsorption. The successful application of the PSO model corroborated that the rate-limiting phase was mostly influenced by multiple interactions of physisorption, particularly hydrogen bonding and π–π interactions.54 The rate constant values (k2) of PSO kinetics follow the sequence NFL > Ag@CNFL > MFL > ZFL by 1.1, 1.3, and 2.3 times, compared to NFL, respectively, implying the higher adsorption rate, small particle size, high surface area, and larger pore apertures of NFL.13 The fractional Avrami order (nAV) values (0.4459–0.9438) of ZFL > MFL > Ag@CNFL > NFL, which were attributed to the possible change in the adsorption mechanism, showed that the adsorption was multi-pathway or complex.56 The high R2 ≥ 0.9615 and low χ2 (0.6168–2.5811) improved the effectiveness of the Elovich model in explaining significantly the adsorption process. The α value of NFL > Ag@CNFL > MFL > ZFL affirmed the higher initial adsorption rate on NFL, as agreed with k2 of PSO, and the β value of ZFL > MFL > Ag@CNFL > NFL revealed the faster surface coverage of ZFL with 2,4-D molecules. The success of Bangham's pore diffusion model in illustrating the 2,4-D adsorption onto the prepared adsorbents was clearly shown by B (<1) values (0.3551–0.4796) and the higher values of R2 (≥ 0.9134) coupled with the low χ2, validating the involvement of pore diffusion in the 2,4-D uptake.57 Additionally, the experimental data were highly consistent with the intra-particle diffusion model based on the higher R2 (0.9013–0.9698) and low χ2 values (1.9216–6.9784). The sequence of ko and KB values was in agreement with k2 of PSO, confirming the highest adsorption rate and capacity of NFL. The results showed that the fitting line did not cross the origin based on the C values (2.3822–41.7342), suggesting that diffusion within the particles was not the sole main speed control step.53 This confirmed that other diffusion processes influenced the adsorption process and multi-adsorption stages occurred as proved by the Bangham model. It can be observed that the linear plot of the Boyd model (R2 ≥ 0.9584) didn’t pass through the origin. Therefore, it can be inferred that the rate-controlling phase for the 2,4-D adsorption onto the produced adsorbents included film diffusion (extra particular transport).58 As shown in Table 2, the fitting kinetic degree followed the sequence: Avrami > Elovich > PSO > Bangham's pore diffusion > intra-particle diffusion > PFO based on the average reduced chi-square (χ2) values.
Table 2 PFO, PSO, Avrami, Elovich, Bangham's pore diffusion, intra-particle diffusion, and Boyd parameters for the adsorption of 2,4-D onto ZFL, MFL, NFL, and Ag@CNFL at 23 °C
| Models |
Parameters |
ZFL |
MFL |
NFL |
Ag@CNFL |
|
|
q
m (mg g−1) |
130.32 |
151.25 |
203.75 |
167.20 |
| PFO |
q
exp (mg g−1) |
112.25 |
123.04 |
167.90 |
138.24 |
|
k
1 (h−1) |
0.2880 |
0.4991 |
0.6785 |
0.5059 |
|
R
2
|
0.9935 |
0.9766 |
0.8507 |
0.9207 |
|
χ
2
|
0.4616 |
1.5461 |
13.3115 |
4.8555 |
| PSO |
q
exp (mg g−1) |
133.71 |
146.40 |
203.41 |
165.82 |
|
k
2 (g mg−1 h−1) |
0.0023 |
0.0042 |
0.0054 |
0.0049 |
|
R
2
|
0.9917 |
0.9915 |
0.9483 |
0.9752 |
|
χ
2
|
0.5278 |
0.6498 |
4.6511 |
1.5024 |
| Avrami |
q
AV (mg g−1) |
117.94 |
133.50 |
207.78 |
167.18 |
|
K
AV (h−1) |
0.2842 |
0.3973 |
0.3159 |
0.2857 |
|
n
AV
|
0.9438 |
0.8102 |
0.4459 |
0.5943 |
|
R
2
|
0.9930 |
0.9829 |
0.9884 |
0.9943 |
|
χ
2
|
0.4720 |
1.1734 |
1.1461 |
0.4208 |
| Elovich |
α (mg g−1.h) |
61.624 |
158.713 |
428.801 |
246.774 |
|
β (g mg−1) |
0.0322 |
0.0310 |
0.0275 |
0.0303 |
|
R
2
|
0.9712 |
0.9615 |
0.9949 |
0.9880 |
|
χ
2
|
1.7593 |
2.5811 |
0.6168 |
0.8389 |
| Bangham's pore diffusion |
K
B (mL L g−1) |
1.2017 |
1.9014 |
3.3672 |
2.3400 |
|
B
|
0.4796 |
0.3793 |
0.3551 |
0.3667 |
|
R
2
|
0.9336 |
0.9134 |
0.9852 |
0.9699 |
|
χ
2
|
4.4925 |
5.9501 |
1.4671 |
2.2257 |
| Intra-particle diffusion |
k
o (mg g−1 h−1/2) |
35.5186 |
40.5150 |
44.6910 |
43.3619 |
|
C
|
2.3822 |
8.4598 |
41.7342 |
22.1649 |
|
R
2
|
0.9424 |
0.9013 |
0.9457 |
0.9698 |
|
χ
2
|
3.4604 |
6.9784 |
5.1570 |
1.9216 |
| Boyd |
R
2
|
0.9584 |
0.9892 |
0.9882 |
0.9877 |
3.2.4. Adsorption isotherm modeling.
The equilibrium adsorption experiments were an essential foundation for assessing the adsorption capacity of the prepared materials and developing the adsorption theoretical models. The purpose of the adsorption isotherm investigations was to determine the relationship between the 2,4-D equilibrium concentration (Ce, mg L−1) and the amount of 2,4-D adsorbed (qe) onto the produced adsorbents. The experimental data were obtained after conducting the tests across a broad range of 25 mL of initial 2,4-D concentration (40–800 mg L−1) under the following conditions: T = 23 °C, t = 14 h, adsorbent dosage = 2.4 g L−1, and pH = 2 as illustrated in the spots of Fig. 5a–d. The spots of Fig. 5a–d depict that the adsorption capacity increased noticeably at low equilibrium concentrations because of the strong affinity of 2,4-D molecules for the adsorbent surface. After Ce was approximately 113 mg L−1, the qe values gradually enhanced. However, the adsorption capacity of ZFL, MFL, NFL, and Ag@CNFL remained relatively stable and tended to saturate when Ce was up to around 300 mg L−1.53
 |
| | Fig. 5 The nonlinear plots of Langmuir and Freundlich (a), Temkin (b), DR (c), and Redlich–Peterson, Sips, and Toth (d) models at 14 h of shaking time, 2.4 g L−1 adsorbent dose, 23 °C, and pH 2, and Van’t Hoff plot (e) of 2,4-D adsorption onto ZFL, MFL, NFL, and Ag@CNFL. | |
To scrutinize the major adsorption mechanism, the adsorption process was interpreted using various nonlinear adsorption models: Langmuir (eqn (13) and Fig. 5a), Freundlich (eqn (15) and Fig. 5a), Temkin (eqn (16) and Fig. 5b), Dubinin–Radushkevich (DR) (eqn (17) andFig. 5c), Redlich–Peterson (eqn (19) and Fig. 5d), Sips (eqn (20) and Fig. 5d), and Toth (eqn (21) and Fig. 5d) isotherms. The respective adsorption parameters can be seen in Table 3. The correlation coefficients and reduced chi-square (χ2) values stood at 0.9811–0.9929 and 0.5395–1.9884 corresponding to the Langmuir isotherm and at 0.8592–0.9380 and 3.8220–15.0994 for the Freundlich model. It was clear that the Langmuir isotherm best fitted the isotherm data because of its high R2 and low χ2 values. This portrayed that the 2,4-D adsorption was mostly homogeneous and monolayer in nature.59 Notably, the Langmuir adsorption capacity of NFL (203.75 mg g−1) > Ag@CNFL (167.20 mg g−1) > MFL (151.25 mg g−1) > ZFL (130.32 mg g−1) by 17.9, 25.8, and 36.0%, respectively, compared with NFL was related to the better hydrophobicity, great surface area, structural characteristics, and high functional groups on the NFL surface. This trend agreed with that of KF of the Freundlich model. The parameters b and KF, which represent the interaction strength between the adsorbent surface and 2,4-D in Langmuir and Freundlich models, are 1.1–3.0 times bigger for NFL than those of other investigated adsorbents, further evidencing that 2,4-D can be tightly adsorbed onto NFL.13 The separation parameter (KL) values ranged from 0.0486 to 0.1832, suggesting that the studied materials easily adsorbed 2,4-D molecules.59 The adsorption intensity (1/n) values ranging from 0.2873 to 0.4065 corroborated the feasibility of the adsorption process.6 Temkin and Dubinin–Radushkevich isotherms showed remarkable concurrence with the 2,4-D adsorption results, exhibiting a notable R2 of ≥0.9470 and 0.9624, respectively, in addition to their low χ2 values. NFL required the least quantity of heat to adsorb 2,4-D molecules as indicated by Temkin parameter values (bT) in the following order: ZFL > MFL > Ag@CNFL > NFL, which demonstrated that 2,4-D adsorption took place physically onto the studied adsorbents (bT < 8000 J mol−1). The results verified that the adsorption by all the adsorbents was accompanied by a physical interaction based on EDR values, which varied from 0.0215 to 0.0412 kJ mol−1 (<8 kJ mol−1). R2 values ranged from 0.9874 to 0.9971 for Redlich–Peterson, 0.9914 to 0.9940 for Sips, and 0.9900 to 0.9956 for Toth; moreover, the χ2 values ranged from 0.2663 to 1.4002, 0.4634 to 1.6865, and 0.3288 to 1.5382, respectively, for the previous models. Hence, the great R2 and χ2 values of these isotherms underscored their success in explaining the 2,4-D adsorption. The best fitting of the Redlich–Peterson model presumed that the surface texture of the adsorbents was regarded as homogeneous with uniform interaction energy as proved by the Langmuir model.60 It was observed that KT (L g−1), KRP (L g−1), αRP (mg L−1)−g, Ks (L g−1), and Kth (L mg−1) constants followed the same sequence of the Langmuir constant (b) (NFL > Ag@CNFL > MFL > ZFL), corroborating the high adsorption strength of 2,4-D molecules with NFL. The adsorption capacity (qDR, qs, and qth) values were close to those of the Langmuir isotherm (qm) with small variances spanning from 6.4 to 11.6% for DR, 0.1 to 4.9% for Sips, and 0.1 to 8.4% for Toth isotherms between each two amounts of them. The empirical exponent values of g (0.9623–1.1164), ns (0.7835–1.0339), and nth (0.8953–1.3703) were near and surpassed unity, signifying a homogenous monolayer adsorption mechanism, in addition to the possible heterogeneous multilayer adsorption system.60 Therefore, the previous findings substantiated the accurate performance of DR, Redlich–Peterson, Sips, and Toth models in illustrating the experimental data of 2,4-D adsorption onto ZFL, MFL, NFL, and Ag@CNFL surfaces. Overall, the order of the best-fit isotherm was ranked as DR > Redlich–Peterson > Toth > Sips > Langmuir > Temkin > Freundlich according to χ2 values and Redlich–Peterson > Toth > Sips > Langmuir > DR ≥ Temkin > Freundlich based on R2 values.
Table 3 Langmuir, Freundlich, Temkin, Dubinin–Radushkevich, Redlich–Peterson, Sips, and Toth parameters for the adsorption of 2,4-D onto ZFL, MFL, NFL, and Ag@CNFL at 23 °C, in addition to the thermodynamic parameters
| Models |
Parameters |
Temp. |
ZFL |
MFL |
NFL |
Ag@CNFL |
| Langmuir |
q
m (mg g−1) |
|
130.32 |
151.25 |
203.75 |
167.20 |
|
b (L mg−1) |
|
0.0115 |
0.0163 |
0.0342 |
0.0290 |
|
K
L
|
|
0.1832 |
0.1203 |
0.0486 |
0.0633 |
|
R
2
|
|
0.9912 |
0.9929 |
0.9903 |
0.9811 |
|
χ
2
|
|
0.5395 |
0.6371 |
1.8158 |
1.9884 |
| Freundlich |
1/n |
|
0.4065 |
0.3469 |
0.2873 |
0.3038 |
|
K
F (L1/n mg1−1/n g−1) |
|
10.195 |
17.548 |
31.190 |
28.398 |
|
R
2
|
|
0.9347 |
0.9162 |
0.9380 |
0.8592 |
|
χ
2
|
|
3.8220 |
7.3890 |
11.3580 |
15.0994 |
| Temkin |
b
T (J mol−1) |
|
89.156 |
79.295 |
64.629 |
69.490 |
|
K
T (L g−1) |
|
0.1376 |
0.2003 |
0.4226 |
0.3026 |
|
R
2
|
|
0.9710 |
0.9722 |
0.9937 |
0.9470 |
|
χ
2
|
|
1.8350 |
2.5007 |
1.1292 |
5.5059 |
| Dubinin–Radushkevich |
q
DR (mg g−1) |
|
115.13 |
134.01 |
190.67 |
154.09 |
|
E
DR (kJ mol−1) |
|
0.0215 |
0.0308 |
0.0341 |
0.0412 |
|
R
2
|
|
0.9624 |
0.9867 |
0.9635 |
0.9799 |
|
χ
2
|
|
0.0808 |
0.4880 |
1.6283 |
0.1933 |
| Redlich–Peterson |
K
RP (L g−1) |
|
1.2189 |
1.9966 |
8.3133 |
4.0397 |
|
α
RP (mg L−1)−g |
|
0.0027 |
0.0054 |
0.0636 |
0.0122 |
|
g
|
|
1.1164 |
1.1056 |
0.9623 |
1.0633 |
|
R
2
|
|
0.9949 |
0.9971 |
0.9929 |
0.9874 |
|
χ
2
|
|
0.3289 |
0.2663 |
1.4002 |
1.2930 |
| Sips |
q
s (mg g−1) |
|
128.85 |
151.14 |
201.17 |
159.01 |
|
K
s (L g−1) |
|
0.0136 |
0.0181 |
0.0336 |
0.0333 |
|
n
s
|
|
0.9229 |
0.9467 |
1.0339 |
0.7835 |
|
R
2
|
|
0.9928 |
0.9940 |
0.9914 |
0.9929 |
|
χ
2
|
|
0.4634 |
0.5557 |
1.6865 |
0.7398 |
| Toth |
q
th (mg g−1) |
|
119.34 |
144.76 |
203.93 |
159.11 |
|
K
th (L mg−1) |
|
0.0096 |
0.0135 |
0.0420 |
0.0228 |
|
n
th
|
|
1.3703 |
1.2289 |
0.8953 |
1.3324 |
|
R
2
|
|
0.9949 |
0.9956 |
0.9922 |
0.9900 |
|
χ
2
|
|
0.3288 |
0.4109 |
1.5382 |
1.0301 |
| Thermodynamic parameters |
R
2
|
|
0.9172 |
0.9324 |
0.9806 |
0.9867 |
| −ΔH° (kJ mol−1) |
|
22.646 |
30.496 |
40.453 |
38.198 |
| −ΔS° (kJ mol−1 K−1) |
|
0.0713 |
0.0957 |
0.1191 |
0.1155 |
| −ΔG° (kJ mol−1) |
23 °C |
1.5412 |
2.1688 |
5.1994 |
4.0100 |
| 30 °C |
1.0421 |
1.4989 |
4.3657 |
3.2015 |
| 35 °C |
0.6856 |
1.0204 |
3.7702 |
2.6240 |
| 42 °C |
0.1865 |
0.3505 |
2.9365 |
1.8155 |
3.2.5. Adsorption thermodynamic modeling.
The viability of 2,4-D adsorption onto ZFL, MFL, NFL, and Ag@CNFL was rigorously assessed through thermodynamic studies carried out at 23–42 °C, using 2.4 g L−1 adsorbent dose mixed with 25 mL of 300 mg L−1 2,4-D concentration for 14 h of shaking time at pH 2. Table 3 lists the thermodynamic parameter values. The outcomes showed that the negative values of ΔG° (−0.1865 to −5.1994 kJ mol−1) evidenced the spontaneity and favorability of 2,4-D adsorption onto the prepared materials, possibly because of their high surface area.61 Furthermore, the increment in ΔG° values as the temperature rose revealed that adsorption became less favorable at elevated temperatures. Furthermore, ΔG° values fell between 0 and −20 kJ mol−1, indicating that the physisorption mechanism dominated the adsorption process. It can be noted that ΔH° values were negative, attesting to the exothermicity of 2,4-D adsorption and meaning the release of heat during the process.39 This observation aligned with the physical adsorption mechanism, specifically electrostatic interactions and hydrogen bonding since ΔH° values (−22.646 to −40.453 kJ mol−1) fell below 80 kJ mol−13. Likewise, the negative values of ΔS° signified a decline in randomness at the interface between the adsorbate solution and the adsorbents during the adsorption process. The high R2 values (0.9172–0.9867) of the Van’t Hoff plot (Fig. 5e) displayed reasonable fitting goodness for the 2,4-D adsorption. The more negative thermodynamic values were observed in NFL, revealing that the adsorption was more exothermic, favorable, and spontaneous onto its surface. This thermodynamic analysis provided important details on the energetics and potential for 2,4-D adsorptive removal onto the studied adsorbents.
Based on the previously described findings, the possible 2,4-D adsorption mechanism onto Ag@CNFL was projected using characterization and adsorption data as shown graphically in Fig. S1 (see ESI†).
3.3. Photocatalytic degradation of 2,4-D
3.3.1. Impact of photocatalyst dose.
It is worth noting that catalyst loading plays a critical role in 2,4-D disintegration efficiency. Thus, the effect of changing the photocatalyst dose from 0.5 to 2.0 g L−1 on the degradation percent (D%, eqn (25)) has been investigated at a fixed initial 2,4-D concentration (150 mL of 15 mg L−1), pH 3.2, 20 °C, and an irradiation time of 110 min as illustrated in Fig. 6a. The results described that improving the catalyst dosage from 0.5 to 1.0 g L−1 led to significantly increased 2,4-D photodegradation by 12.2, 17.3, 25.7, and 33.3% for NFL, C, CNFL, and Ag@CNFL, respectively. This can be attributed to an increased number of reactive catalytic surface sites, which accelerated the absorption of photons and the excitation of the catalyst electrons from the valence to the conduction band, generating holes and more active hydroxyl and superoxide radicals to degrade 2,4-D molecules and resulting in a high rise in the degradation rate.62 Conversely, when the catalyst dose increased to 2.0 g L−1, D% of NFL, C, CNFL, and Ag@CNFL dropped by 6.0, 2.3, 3.2, and 4.0%, respectively. A high dosage favored the catalyst particle aggregation, the light scattering effect, and the increase in the turbidity of the solution with a following decline in the light penetration in the suspension, thereby minimizing the surface area for the light absorption and eventually reducing the degradation efficiency.63 Therefore, an ideal dosage of 1.0 g L−1 was applied to the subsequent tests. Ag@CNFL had the greatest degradation efficiency (100%) among other catalysts due to its lowest band gap and decorated two photocatalysts with a highly active plasmonic element (silver).
 |
| | Fig. 6 The effect of photocatalyst dosage (a), initial 2,4-D concentration (b)–(e) for NFL, C, CNFL, and Ag@CNFL, respectively, on the photolysis and photocatalytic degradation of 2,4-D (f), and temperature (g) and (h) for CNFL and Ag@CNFL, respectively at pH 3.2. | |
3.3.2. Impact of initial 2,4-D concentration.
The influence of the initial 2,4-D concentration of 10–30 mg L−1 on the photodegradation by NFL, C, CNFL, and Ag@CNFL was discovered, maintaining the catalyst dose (1.0 g L−1), pH 3.2, and 20 °C constant for 110 min of irradiation time as depicted in Fig. 6b–e. There is an upward sequence of D% from 50.0, 46.9, 61.2, and 65.6% to 75.0, 80.6, 85.0, and 92.5% for NFL, C, CNFL, and Ag@CNFL, respectively by increasing the 2,4-D concentration from 10 to 15 mg L−1 through 80 min, attaining equilibrium. This is because there are more readily available 2,4-D molecules, more visible light can enter the solution, and more catalyst molecules can be excited at less initial concentrations and the start of the reaction. A slight rise in D% occurred to 84.0, 88.0, 94.4, and 100.0% for NFL, C, CNFL, and Ag@CNFL, respectively, at 15 mg L−1 and 110 min. A decrease in the degradation rate was noted until 110 min, which may be caused by photodegradation holes not being present on the catalyst surface. The outcomes disclosed that rising 2,4-D concentration from 15 to 30 mg L−1 caused a gradual decline in the degradation efficiency by 20.2, 18.3, 13.8, and 16.2% for NFL, C, CNFL, and Ag@CNFL, successively. The downward trend was primarily justified by the active site occupation of the photocatalyst surface by 2,4-D molecules at greater initial concentrations, increasing the light absorption, which generated the screening surface effect.64 The 2,4-D molecules can compete with each other to react with the reactive oxygen species produced and may be adsorbed on the catalyst's active sites. Additionally, related studies verified that a specific quantity of catalyst can produce a finite quantity of light-induced electron–hole pairs.62 Moreover, the reduction in reaching light to the photocatalyst led to a decrease in reactive oxygen species creation, decreasing the photodegradation efficiency. Hence, 15 mg L−1 was selected as an optimum initial concentration for further tests.
3.3.3. Photolysis and photocatalytic degradation of 2,4-D.
These experiments were assessed in the presence and absence of NFL, C, CNFL, and Ag@CNFL, using the catalyst dose of 1.0 g L−1 and 150 mL of 15 mg L−1 initial pollutant concentration at pH 3.2 and 20 °C for 110 min of irradiation time as shown in Fig. 6f. Fig. 6f depicts that 30% of 2,4-D concentration was degraded under visible light alone through 80 min. It was found that NFL, C, CNFL, and Ag@CNFL achieved higher 2,4-D degradation of 76.2, 81.2, 87.5, and 93.8%, respectively after 80 min of irradiation. After that, the degradation rate began to decelerate. The previous photocatalysts attained a greater degradation efficiency percent than that under visible irradiation by 2.8, 3.0, 3.2, and 3.3 folds, respectively after 110 min. This meant that every synthetic material could efficiently absorb the visible light energy needed for the photocatalytic reaction. Notably, Ag@CNFL had the greatest photodegradation efficiency, which was 17.6, 12.7, and 5.3% higher than NFL, C, and CNFL, successively. Finally, because Ag was incorporated into the CNFL surface, the Ag@CNFL nanocomposite exhibited a superior photocatalytic performance than the other catalysts due to the SPR effect of Ag nanoparticles, which served as electron intermediaries in the creation of a Z-scheme heterojunction, to raise the activity of the photocatalyst.31 Moreover, Ag@CNFL possessed a high surface area, the lowest band gap, and a high amount of surface functional groups.
3.3.4. Impact of temperature.
Fig. 6g and h displays the photodegradation profiles of 2,4-D at various temperatures (20, 30, 35, and 40 °C) vs. reaction time (5–100 min) utilizing CNFL and Ag@CNFL, respectively, at a dose of 1.0 g L−1, 150 mL of 15 mg L−1 initial 2,4-D concentration, pH 3.2, and 20 °C. The findings manifested that the increment in temperature from 20 to 40 °C can improve the degradation efficiency from 81.2 to 100% by 23.2% for CNFL through 70 min and 83.1 to 100% by 20.3% for the Ag@CNFL photocatalyst after 60 min only. After that, the reaction started to decelerate. This was explained by the strong 2,4-D molecule diffusivity on the catalyst surface at higher temperatures.
3.3.5. Photodegradation kinetics.
The kinetics of photocatalytic degradation of 2,4-D by CNFL and Ag@CNFL were investigated by fitting the linear form of the pseudo-first-order model (L–H model) (eqn (26)) to experimental results. The fitted model for CNFL and Ag@CNFL is shown in Fig. 7a and b, respectively, at various temperatures (20, 30, 35, and 40 °C). Table 4 enlists the corresponding kinetic parameters. The experimental data of 2,4-D photodegradation were well described by the good linear relationship of the pseudo-first-order model based on its high correlation coefficients (0.9816–0.9989).2 The results revealed that the apparent degradation rate constants (kapp) are inversely proportional to half-life times and directly proportional to the temperatures, where kapp values increased by 1.6 folds from 0.0246 to 0.0388 min−1 for CNFL and 0.0303 to 0.0395 min−1 by 1.3 folds for Ag@CNFL upon rising the temperature from 20 to 40 °C. This demonstrated that the increment in temperature caused the enhancement of the photocatalytic rate, resulting from the high 2,4-D oxidation with the produced hydroxyl radicals and its higher diffusion in the solution at a higher temperature, making the process endothermic.40 Moreover, 2,4-D half-life time (t1/2) was reduced from 28.171 to 17.861 min by 36.6% for CNFL and 22.871 to 17.544 min by 23.3% for Ag@CNFL when enhancing the temperature from 20 to 40 °C. Notably, Ag@CNFL attained greater values of kapp and shorter t1/2 than those of CNFL, particularly at 40 °C due to its lowest band gap requiring fewer energy for the excitation, indicating its greater efficiency in degrading 2,4-D in a short time. The improved photocatalytic activity can be related to the heterogeneous development, producing an intimate contact interface between the three components. This makes it possible for photogenerated carriers to migrate quickly and for electron–hole pair separation efficiency to significantly increase.
 |
| | Fig. 7 The linear plots of the L–H kinetic model (a) and (b) for CNFL and Ag@CNFL, respectively, and Arrhenius (c) and Eyring–Polanyi (d) models for CNFL and Ag@CNFL. | |
Table 4 Pseudo-first-order kinetic model, half-life time, and thermodynamic parameters for photocatalytic degradation of 2,4-D onto CNFL and Ag@CNFL at 20, 30, 35, and 40 °C
| Models |
Parameters |
Temp. |
CNFL |
Ag@CNFL |
| Pseudo-first-order kinetics |
k
app (min−1) |
20 °C |
0.0246 |
0.0303 |
| 30 °C |
0.0319 |
0.0374 |
| 35 °C |
0.0356 |
0.0379 |
| 40 °C |
0.0388 |
0.0395 |
|
R
2
|
20 °C |
0.9989 |
0.9884 |
| 30 °C |
0.9913 |
0.9816 |
| 35 °C |
0.9918 |
0.9906 |
| 40 °C |
0.9930 |
0.9983 |
| Half-life time |
t
1/2 (min) |
20 °C |
28.171 |
22.871 |
| 30 °C |
21.724 |
18.529 |
| 35 °C |
19.466 |
18.285 |
| 40 °C |
17.861 |
17.544 |
| Thermodynamic parameters |
E
a (kJ mol−1) |
|
17.648 |
10.316 |
|
A (s−1) |
|
34.540 |
2.122 |
|
R
2
|
|
0.9960 |
0.9441 |
| Δ‡H° (kJ mol−1) |
|
15.122 |
7.883 |
| Δ‡S° (kJ mol−1 K−1) |
|
−0.2240 |
−0.2468 |
| Δ‡G° (kJ mol−1) |
20 °C |
80.754 |
80.195 |
| 30 °C |
82.994 |
82.663 |
| 35 °C |
84.114 |
83.897 |
| 40 °C |
85.234 |
85.131 |
|
R
2
|
|
0.9906 |
0.9156 |
3.3.6. Photodegradation thermodynamics.
Thermodynamic parameters were evaluated using Arrhenius (eqn (28)) and Eyring–Polanyi (eqn (29)) models as displayed in Fig. 7c and d, respectively. According to the outcomes in Table 4, through the photocatalytic reaction of 2,4-D, CNFL showed an activation energy value of 17.648 kJ mol−1, which was 71.1% higher than the value (10.316 kJ mol−1) of Ag@CNFL, indicating that Ag@CNFL required less minimum energy to execute the reaction than CNFL. The fact that the value of Ea is less than 40 kJ mol−1 attested to the photocatalytic physical reaction.40 CNFL was found to have an Arrhenius factor (A) 16.3 times greater than Ag@CNFL. The excellent R2 values (0.9156–0.9960) supported the best fit of Arrhenius and Eyring–Polanyi models. The positive Δ‡H° values (7.883 and 15.122 kJ mol−1 for Ag@CNFL and CNFL, respectively) indicated the endothermic character of 2,4-D photocatalytic degradation and the least heat needed for the process by Ag@CNFL. The Δ‡S° values (<0) revealed the decrease in the randomness of 2,4-D onto the catalyst surface. The Δ‡G° values (>0) indicated that photocatalytic degradation was nonspontaneous.
3.4. Photocatalyst reusability
After eight cycles of 2,4-D photodegradation, Fig. S2 (ESI†) highlights that the efficiency of NFL, C, CNFL, and Ag@CNFL was reduced by only 8.4, 3.4, 3.2, and 7.0%, respectively, which may be caused by the coagulation of catalyst nanoparticles, indicating the greatest reusability of the prepared photocatalysts.
An accurate explanation for the increased 2,4-D photodegradation mechanism upon photocatalysis by the ternary heterogeneous Ag@CNFL is schematically depicted in Fig. S3 (see ESI†).
3.5. Efficiency comparison
Table S2 (ESI†) shows the comparison of 2,4-D removal efficacy by NFL and Ag@CNFL with other materials, indicating the highest adsorption capacity of NFL and the efficient photocatalytic degradation by Ag@CNFL.2,3,5–7,12,54,55,58,59,64–66 In conclusion, NFL is thought to be a very good adsorbent with high efficacy, adaptability, and reusability for the removal of 2,4-D by adsorption. The NFL composite is a good option for eliminating hazardous herbicides from wastewater because of its exceptional qualities, which include a quick adsorption profile, ease of separation, strong selectivity, and renewability. Also, the unique characteristics of NFL and Ag@CNFL, such as their mechanical strength, large surface area, high adsorption or catalytic efficiencies, and repeatability, justify their use as innovative materials in the current water treatment methods. Ag@CNFL showed higher photocatalytic effectiveness towards 2,4-D than other materials. The Ag@CNFL composite was an excellent material that combined the advantages of being environmentally safe and very pH insensitive with exceptional catalytic performance and appropriate recyclability. Therefore, it has a lot of potential for removing 2,4-D from industrial wastewater. The produced composite may find applications in catalysis, adsorption, and drug delivery.
4. Conclusion
The synthesis and rational design of highly efficient adsorbents and photocatalysts for the removal of herbicides are essential for environmental applications. Here, Zn–Fe, Mg–Fe, and Ni–Fe LDH nanoparticles (ZFL, MFL, and NFL), as well as the Ag@CdS/Ni–Fe LDH nanocomposite (Ag@CNFL) were prepared as adsorbents. Also, Ni–Fe LDH and cadmium sulfide (C), in addition to CdS/Ni–Fe LDH (CNFL) and Ag@CdS/Ni–Fe LDH (Ag@CNFL) nanocomposites, were fabricated as efficient heterojunction photocatalysts. In photocatalysis, the creation of a heterojunction composite has shown to be a viable method for preventing the recombination of photogenerated charge carriers. In this study, the heterostructure of the Ag@CdS/Ni–Fe LDH nanocomposite (Ag@CNFL) has been produced using a self-assembly approach for the first time. The properties and morphology of all samples were studied by XRD, TEM, SEM, ATR-FTIR, nitrogen adsorption–desorption analysis, TGA, zeta potential, and DRS. Furthermore, the Ag@CNFL nanocomposite was characterized by its high thermal stability and crystalline nanostructure, successful loading of CdS and highly efficient plasmonic element Ag onto the LDH surface, high specific surface area, narrow band gap, and stronger photo-absorption. The adsorption kinetics, equilibrium, and thermodynamics of 2,4-D removal by the Ag@CNFL nanocomposite were studied concerning adsorbent dosage, pH, time, initial 2,4-D concentration, and temperature. The equilibrium and kinetic adsorption data were fitted well by Redlich–Peterson and Langmuir isotherms and Avrami and pseudo-second-order models, attaining higher adsorption capacity for NFL. According to thermodynamic data, the adsorption process was also exothermic, spontaneous, favorable, and physisorption. The possible 2,4-D adsorption mechanism onto Ag@CNFL was controlled by the electrostatic interaction, pore filling, π–π stacking, hydrogen bonding, chlorine bonding, and van der Waals force. Through the photocatalysis process, 100% 2,4-D was degraded by Ag@CNFL over 110 min at a catalyst dose of 1.0 g L−1, pH 3.2, 15 mg L−1, and 20 °C, achieving the endothermic and nonspontaneous process. Based on the photodegradation mechanism, upon the SPR effect, the Ag doping made the bandgap narrow in the band catalyst and enhanced the optical absorption capacity, and the produced superoxide and hydroxyl radicals oxidized 2,4-D into CO2 and H2O. In summary, this work showed the great efficacy of Ag@CNFL as an adsorbent and visible-light active photocatalyst.
Author contributions
Asaad F. Hassan: conceptualization and methodology; Walaa A. Shaltout: formal analysis, investigation, and data analysis; and H. Hafez and Maha S. Elsayed: writing – original draft preparation and data handling.
Data availability
Data will be made available upon request.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this work.
References
- A. Samanth, R. Vinayagam, G. Murugesan, T. Varadavenkatesan, R. Selvaraj and A. Pugazhendhi, Chemosphere, 2023, 336, 139143 CrossRef CAS PubMed.
- P. G. Moradeeya, M. A. Kumar, A. Sharma and S. Basha, Chemosphere, 2022, 298, 134360 CrossRef CAS PubMed.
- A. Samanth, R. Selvaraj, G. Murugesan, T. Varadavenkatesan and R. Vinayagam, Chemosphere, 2024, 361, 142513 CrossRef CAS PubMed.
- R. Gurav, S. Mandal, L. M. Smith, S. Q. Shi and S. Hwang, Chemosphere, 2023, 339, 139715 CrossRef CAS PubMed.
- S. Li, F. Feng, S. Chen, X. Zhang, Y. Liang and S. Shan, Ecotoxicol. Environ. Saf., 2020, 194, 110440 CrossRef CAS PubMed.
- S. Mustafa, H. N. Bhatti, M. Maqbool, A. Khan, A. M. Alraih and M. Iqbal, Sustainable Chem. Pharm., 2024, 39, 101577 CrossRef CAS.
- B. Liu, N. Guo, Z. Wang, Y. Wang, X. Hao, Z. Yang and Q. Yang, J. Environ. Chem. Eng., 2022, 10, 107472 CrossRef CAS.
- H. Luo, X. Zhou, Q. Chen and J. Zhou, Sep. Purif. Technol., 2021, 259, 118196 CrossRef CAS.
- A. Mantilla, F. Tzompantzi, J. L. Fernández, J. A. I. Díaz Góngora, G. Mendoza and R. Gómez, Catal. Today, 2010, 148, 119–123 CrossRef.
- X. Zhu, B. Wang, J. Kang, J. Shen, P. Yan, X. Li, L. Yuan, S. Zhao, Y. Cheng, Y. Li, J. Zuo and Z. Chen, Sep. Purif. Technol., 2022, 299, 121777 CrossRef CAS.
- H. R. Barzoki, A. Dargahi, A. Shabanloo, A. Ansari and S. Bairami, J. Water Process Eng., 2023, 56, 104429 CrossRef.
- M. J. Paz, T. Vieira, H. Enzweiler and A. T. Paulino, J. Environ. Chem. Eng., 2022, 10, 106967 CrossRef CAS.
- Y. Zhang, Y. Lei, T. Yan, Y. Liao and G. Han, Sep. Purif. Technol., 2024, 334, 126120 CrossRef CAS.
- M. E. Mahmoud, N. K. Kamel, M. F. Amira and N. A. Fekry, Sep. Purif. Technol., 2024, 344, 127067 CrossRef CAS.
- A.-L. Johnston, E. Lester, O. Williams and R. L. Gomes, Environ. Technol. Innov., 2024, 33, 103490 CrossRef CAS.
- J. S. Calisto, I. S. Pacheco, L. L. Freitas, L. K. Santana, W. S. Fagundes, F. A. Amaral and S. C. Canobre, Heliyon, 2019, 5, 0–8 CrossRef PubMed.
- M. Zhao, Y. Wang, H. Zhao, Z. Zhang, J. Su, X. Ma, F. Kong, Y. Xie, Z. Ma, Q. Zhang and Z. Meng, Sep. Purif. Technol., 2023, 327, 124886 CrossRef CAS.
- E. E. Abdel-Hady, H. F. M. Mohamed, S. H. M. Hafez, A. M. M. Fahmy, A. Magdy, A. S. Mohamed, E. O. Ali, H. R. Abdelhamed and O. M. Mahmoud, Sci. Rep., 2023, 13, 1–19 CrossRef PubMed.
- R. Benhiti, A. Ait Ichou, A. Zaghloul, R. Aziam, G. Carja, M. Zerbet, F. Sinan and M. Chiban, Environ. Sci. Pollut. Res., 2020, 27, 45767–45774 CrossRef CAS PubMed.
- B. Zhang, S. Yuan, D. Sun, Y. Li and T. Wu, RSC Adv., 2018, 8, 856–866 RSC.
- J. Bai, X. Zhang, C. Wang, X. Li, Z. Xu, C. Jing, T. Zhang and Y. Jiang, J. Cleaner Prod., 2024, 436, 140705 CrossRef CAS.
- B. Liu, Y. Wang, X. Hao, J. Wang, Z. Yang and Q. Yang, J. Water Process Eng., 2022, 46, 102602 CrossRef.
- J. Ma, J. Ding, L. Yu, L. Li, Y. Kong and S. Komarneni, Appl. Clay Sci., 2015, 109–110, 76–82 CrossRef CAS.
- T. Zhu, B. Wu, J. Xie, H. Yang, W. Zhang and Y. Sun, ACS Sustainable Chem. Eng., 2023, 11, 17482–17491 CrossRef CAS.
- K. Kumar Mandari and M. Kang, Appl. Surf. Sci., 2024, 655, 159550 CrossRef CAS.
- S. Munyai, Z. N. Tetana, M. M. Mathipa, B. Ntsendwana and N. C. Hintsho-Mbita, Optik, 2021, 247, 167851 CrossRef CAS.
- H. Zhou, Y. Song, Y. Liu, H. Li, W. Li and Z. Chang, Int. J. Hydrogen Energy, 2018, 43, 14328–14336 CrossRef CAS.
- G. Li, B. Wang, J. Zhang, R. Wang and H. Liu, Appl. Surf. Sci., 2019, 478, 1056–1064 CrossRef CAS.
- A. Pirkarami, S. Rasouli and E. Ghasemi, J. Alloys Compd., 2022, 911, 164736 CrossRef CAS.
- A. Pirkarami, S. Rasouli and E. Ghasemi, Appl. Catal., B, 2019, 241, 28–40 CrossRef CAS.
- P. R. Lestari, T. Takei and N. Kumada, J. Solid State Chem., 2021, 294, 121858 CrossRef CAS.
- L. A. Cano, D. Barrera, J. Villarroel-Rocha and K. Sapag, Catal. Today, 2023, 422, 114222 CrossRef CAS.
- R. Arunadevi, M. Latha, S. Velumani, G. Oza, P. Reyes-Figueroa, M. Rohini, I. G. Becerril-Juarez, J. H. Lee and J. Yi, J. Nanosci. Nanotechnol., 2015, 15, 8434–8439 CrossRef PubMed.
- R. Fazaeli, H. Aliyan, D. Richeson and Y. Li, J. Environ. Sci., 2025, 148, 437–450 CrossRef CAS PubMed.
- M. A. Khoj, A. F. Hassan, N. S. Awwad, H. A. Ibrahium and W. A. Shaltout, Int. J. Biol. Macromol., 2024, 255, 128234 CrossRef CAS PubMed.
- M. Benjelloun, Y. Miyah, G. Akdemir Evrendilek, F. Zerrouq and S. Lairini, Arab. J. Chem., 2021, 14, 103031 CrossRef CAS.
- A. F. Hassan, A. Elhassanein, M. A. Khoj and W. A. Shaltout, Int. J. Biol. Macromol., 2024, 276, 133999 CrossRef CAS PubMed.
- A. F. Hassan, G. A. El-Naggar, G. Esmail and W. A. Shaltout, Appl. Surf. Sci. Adv., 2023, 13, 100388 CrossRef.
- K. L. T. Nguena, C. G. Fotsop, A. Bopda, D. R. Tchuifon Tchuifon, F. H. Kamgang Djioko, A. M. Soukoua Ngueabouo, C. Ada Madu, F. I. Ezema and E. E. Oguzie, Mater. Adv., 2024, 579–597 Search PubMed.
- L. M. Alshandoudi, A. Y. Al Subhi, S. A. Al-Isaee, W. A. Shaltout and A. F. Hassan, Environ. Sci. Pollut. Res., 2023, 30, 88704–88723 CrossRef CAS PubMed.
- W. Xu, M. Mertens, T. Kenis, E. Derveaux, P. Adriaensens and V. Meynen, Mater. Chem. Phys., 2023, 295, 127113 CrossRef CAS.
- J. S. Valente, J. Hernandez-Cortez, M. S. Cantu, G. Ferrat and E. López-Salinas, Catal. Today, 2010, 150, 340–345 CrossRef CAS.
- V. R. Magri, A. Duarte, G. F. Perotti and V. R. L. Constantino, ChemEngineering, 2019, 3, 1–17 CrossRef.
- L. A. Ramirez-Llamas, R. Leyva-Ramos, A. Jacobo-Azuara, J. M. Martinez-Rosales and E. D. Isaacs-Paez, Adsorpt. Sci. Technol., 2015, 33, 393–410 CrossRef CAS.
- H. Djezar, K. Rida and M. Salhi, Inorg. Nano-Met. Chem., 2022, 52, 161–172 CrossRef CAS.
- A. Dalma, B. Nancy, E. Griselda and C. Mónica, Front. Chem. Eng., 2022, 4, 1–10 Search PubMed.
- A. Regmi, Y. Basnet, S. Bhattarai and S. K. Gautam, J. Nanomater., 2023 DOI:10.1155/2023/8187000.
- L. Tabana, D. R. Booysens and S. Tichapondwa, J. Photochem. Photobiol., A, 2023, 444, 114997 CrossRef CAS.
- R. Elmoubarki, F. Z. Mahjoubi, A. Elhalil, H. Tounsadi, M. Abdennouri, M. Sadiq, S. Qourzal, A. Zouhri and N. Barka, J. Mater. Res. Technol., 2017, 6, 271–283 CrossRef CAS.
- R. Sharma, S. Sambyal, P. Mandyal, N. Islam, A. Priye, I. Kainthla, M. Kumar, V. Chauhan and P. Shandilya, J. Environ. Chem. Eng., 2024, 12, 112203 CrossRef CAS.
- I. Maseeh, F. Anwar, S. Aroob, T. Javed, I. Bibi, A. Almasoudi, A. Raheel, M. A. Javid, S. A. C. Carabineiro and M. B. Taj, Mater. Adv., 2024, 5, 5080–5095 RSC.
- K. M. Parida and L. Mohapatra, Chem. Eng. J., 2012, 179, 131–139 CrossRef CAS.
- X. Zha, W. Sun, J. Liu, G. Sun, S. Lu and Y. Wang, Mater. Today Chem., 2024, 35, 101883 CrossRef CAS.
- R. Vinayagam, V. Nagendran, L. C. Goveas, M. K. Narasimhan, T. Varadavenkatesan, A. Samanth and R. Selvaraj, Chemosphere, 2024, 350, 141130 CrossRef CAS PubMed.
- M. E. Fernandez, M. R. Morel, A. C. Clebot, C. S. Zalazar and M. M. Ballari, J. Environ. Chem. Eng., 2022, 10, 106877 CrossRef CAS.
- I.-H. T. Kuete, D. R. T. Tchuifon, G. N. Ndifor-Angwafor, A. T. Kamdem and S. G. Anagho, J. Encapsulation Adsorpt. Sci., 2020, 10, 1–27 CrossRef CAS.
- A. A. Inyinbor, F. A. Adekola and G. A. Olatunji, Water Resour. Ind., 2016, 15, 14–27 CrossRef.
- S. Nethaji and A. Sivasamy, Ecotoxicol. Environ. Saf., 2017, 138, 292–297 CrossRef CAS PubMed.
- R. Vinayagam, S. Ganga, G. Murugesan, G. Rangasamy, R. Bhole, L. C. Goveas, T. Varadavenkatesan, N. Dave, A. Samanth, V. Radhika Devi and R. Selvaraj, Chemosphere, 2023, 310, 136883 CrossRef CAS PubMed.
- J. O. Ighalo, V. E. Ojukwu, C. T. Umeh, C. O. Aniagor, C. E. Chinyelu, O. J. Ajala, K. Dulta, A. O. Adeola and S. Rangabhashiyam, J. Water Process Eng., 2023, 56, 104514 CrossRef.
- J. N. Naat, S. Suyanta and N. Nuryono, Mater. Adv., 2025, 6(10), 3220–3236 RSC.
- T. Sadeghi Rad, E. S. Yazici, A. Khataee, E. Gengec and M. Kobya, Surf. Interfaces, 2023, 36, 102628 CrossRef CAS.
- K. A. Azalok, A. A. Oladipo and M. Gazi, Chemosphere, 2021, 268, 128844 CrossRef CAS PubMed.
- N. Alikhani, M. Farhadian, A. Goshadrou, S. Tangestaninejad and P. Eskandari, Environ. Nanotechnol., Monit. Manage., 2021, 15, 100415 CAS.
- A. F. Hassan, Desalin. Water Treat., 2019, 141, 187–196 CrossRef CAS.
- J. S. Valente, F. Tzompantzi, J. Prince, J. G. H. Cortez and R. Gomez, Appl. Catal., B, 2009, 90, 330–338 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Asaad F.
Hassan
*a,
Asaad F.
Hassan
 b,
Maha S.
Elsayed
c and
H.
Hafez
d
b,
Maha S.
Elsayed
c and
H.
Hafez
d
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (nm) and total pore volume VT (cm3 g−1) through the analysis of nitrogen gas adsorption–desorption isotherms at 77 K. An ATR-FTIR (Nicolet Impact-400 D with a ZnSe crystal) spectrometer was used to investigate the different functional groups for all the prepared samples and any surface changes before and after adsorption for Ag@CNFL as a selected sample. It was operated in the 4000–400 cm−1 region with a resolution of 4.0 cm−1 and 16 accumulations. Zeta potential changes were measured using a Zetasizer (Nano S, Malvern Instrument, UK) to determine the point of zero charge (pHPZC) of adsorbents. Diffuse reflectance spectroscopy (UV-vis DRS, Shimadzu, Japan) was utilized to measure the band gap of the studied catalysts (NFL, C, CNFL, and Ag@CNFL). Tauc's equation was used to estimate the band gap values of these photocatalysts to assess the optical properties:34
(nm) and total pore volume VT (cm3 g−1) through the analysis of nitrogen gas adsorption–desorption isotherms at 77 K. An ATR-FTIR (Nicolet Impact-400 D with a ZnSe crystal) spectrometer was used to investigate the different functional groups for all the prepared samples and any surface changes before and after adsorption for Ag@CNFL as a selected sample. It was operated in the 4000–400 cm−1 region with a resolution of 4.0 cm−1 and 16 accumulations. Zeta potential changes were measured using a Zetasizer (Nano S, Malvern Instrument, UK) to determine the point of zero charge (pHPZC) of adsorbents. Diffuse reflectance spectroscopy (UV-vis DRS, Shimadzu, Japan) was utilized to measure the band gap of the studied catalysts (NFL, C, CNFL, and Ag@CNFL). Tauc's equation was used to estimate the band gap values of these photocatalysts to assess the optical properties:34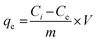


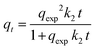



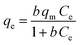
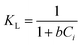







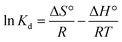





![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ). The prepared LDHs demonstrated a high surface area with a porous structure and holes produced by the partial collapse of layers and interlayer loss after calcination at 400 °C for 3 h. Thus, Ni–Fe LDH can provide significant active adsorption sites for 2,4-D. Furthermore, cadmium sulfide (C) depicted a good surface area (95.70 m2 g−1). However, the modification of Ni–Fe LDH with cadmium sulfide reduced the surface area by 37.6%. After the dispersion of metallic Ag onto the CNFL surface, the surface area decreased to 113.10 m2 g−1 as proved by the total pore volume values.48 This could be explained by the incorporation effect of Ag metallic and cadmium sulfide, which blocked some pores on the LDH surface. Nevertheless, the average pore size increased after the modification of NFL. The mesopores (ranging in size from 2 to 50 nm) that developed between the laminar crystal sheets were linked to
). The prepared LDHs demonstrated a high surface area with a porous structure and holes produced by the partial collapse of layers and interlayer loss after calcination at 400 °C for 3 h. Thus, Ni–Fe LDH can provide significant active adsorption sites for 2,4-D. Furthermore, cadmium sulfide (C) depicted a good surface area (95.70 m2 g−1). However, the modification of Ni–Fe LDH with cadmium sulfide reduced the surface area by 37.6%. After the dispersion of metallic Ag onto the CNFL surface, the surface area decreased to 113.10 m2 g−1 as proved by the total pore volume values.48 This could be explained by the incorporation effect of Ag metallic and cadmium sulfide, which blocked some pores on the LDH surface. Nevertheless, the average pore size increased after the modification of NFL. The mesopores (ranging in size from 2 to 50 nm) that developed between the laminar crystal sheets were linked to ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) values between 2.0378 and 6.0144 nm.48
values between 2.0378 and 6.0144 nm.48![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) (nm)
(nm)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, O–H bending, and O–H stretching modes resulting from the interaction of water with CdS, respectively.47 FTIR spectra of CNFL and Ag@CNFL showed all of the characteristic bands of Ni–Fe LDH and CdS with a small positive shift in wavenumbers, which verified the strong contact during heterojunction formation.50 Also, the distinctive band of nitrate ions disappeared. The band intensity of metal oxides in the Ag@CNFL spectrum, compared to that of CNFL, weakened after loading the metallic Ag. The FTIR curve of Ag@CNFL after 2,4-D adsorption depicted the same one before the adsorption with a slight shift in bands and an increase in the band intensity, and the faint absorption peak at 1921 cm−1 may be related to the hydrogen bonding between hydroxyl groups of 2,4-D molecules and Ag@CNFL.29 Related bands to 2,4-D are present alongside Ag@CNFL bands. The new bands near 1340 and 1460 cm−1 may be linked to C–O–C and C
O, O–H bending, and O–H stretching modes resulting from the interaction of water with CdS, respectively.47 FTIR spectra of CNFL and Ag@CNFL showed all of the characteristic bands of Ni–Fe LDH and CdS with a small positive shift in wavenumbers, which verified the strong contact during heterojunction formation.50 Also, the distinctive band of nitrate ions disappeared. The band intensity of metal oxides in the Ag@CNFL spectrum, compared to that of CNFL, weakened after loading the metallic Ag. The FTIR curve of Ag@CNFL after 2,4-D adsorption depicted the same one before the adsorption with a slight shift in bands and an increase in the band intensity, and the faint absorption peak at 1921 cm−1 may be related to the hydrogen bonding between hydroxyl groups of 2,4-D molecules and Ag@CNFL.29 Related bands to 2,4-D are present alongside Ag@CNFL bands. The new bands near 1340 and 1460 cm−1 may be linked to C–O–C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibrations in the aromatic ring, respectively. Consequently, the identification and attribution of these bands confirmed that 2,4-D was effectively adsorbed on the Ag@CNFL nanocomposite.
C stretching vibrations in the aromatic ring, respectively. Consequently, the identification and attribution of these bands confirmed that 2,4-D was effectively adsorbed on the Ag@CNFL nanocomposite.






