Open Access Article
Open Access ArticleUnveiling the electrical and energy storage performance of SrBi4Ti4O15 for device applications
Rojalin
Panda
 *,
Sudhansu Sekhar
Hota
*,
Sudhansu Sekhar
Hota
 ,
Debasish
Panda
,
Debasish
Panda
 and
Ram Naresh Prasad
Choudhary
and
Ram Naresh Prasad
Choudhary
Multifunctional Res. Lab., ITER, S‘O’A University, BBSR, 751030, India. E-mail: pandarojalin72@gmail.com
First published on 2nd July 2025
Abstract
This research focuses on utilizing ceramic technology and traditional methods to create electronic components with high energy storage density in compact sizes. The bismuth layer-structured ferroelectric material SrBi4Ti4O15 (SBT) is synthesized through a solid-state reaction process. The crystal structure of the material was analyzed using X-ray powder diffraction, indicating orthorhombic symmetry. Rietveld refinement yielded lattice parameters of a = 5.4280 Å, b = 5.4280 Å, and c = 40.9400 Å. The SEM micrograph shows a homogeneous arrangement of the grains in the sample, with the grain size calculated to be 120 μm. This study delves into the intriguing properties of our synthesized material by examining its dielectric behaviour, modulus, impedance, and conductivity. Our comprehensive studies cover a captivating temperature range from 25 °C to 500 °C and frequencies from 1 kHz to 1 MHz. The conductivity plot follows Jonscher's power law, indicating the presence of the NSPT and CBH conduction mechanisms in the material. The role of grains and grain boundaries in the electrical properties of the material is confirmed through the Nyquist plot, demonstrating the NTCR behaviour of the sample. The reduction in activation energy with increasing frequency in the AC conductivity plot, along with the indication of a non-Debye relaxation mechanism in the KWW fitting of the modulus plot, supports the hopping process in the material. The hysteresis loop was used to calculate the efficiency and maximum power density (Pdmax), which came out to be 62% and 12.9662 MW cm−3, respectively. These findings imply that the material is appropriate for applications requiring high-performance energy storage capacitors.
1. Introduction
Ferroelectric materials are those that exhibit spontaneous polarization when subjected to an external electric field. Researchers are highly interested in these materials due to their multifunctional capabilities, including piezoelectric, pyroelectric, and dielectric properties.1 Various devices, including actuators, printing devices, supercapacitors, dynamic non-volatile memory (RAM), ultrasonic transducers, and electro-optic detectors, are constructed using these materials in device engineering and equipment.2 Ferroelectric oxides can be classified into four types of structures: bismuth layer-structured compounds (BLSF, also known as Aurivillius), tungsten bronzes, perovskites, and pyrochlores.3 The qualities of ceramics, including size, shape, purity, chemical composition, and preparation technique, significantly influence their physical properties. As a result, many researchers have attempted to produce these oxides using various methods. However, techniques such as sol–gel, hydrothermal, colloid emulsions, and wet chemical processes often require challenging reaction conditions, are time-consuming, and involve highly unstable alkoxides. Among these methods, the solid-state reaction approach has gained recognition as a promising technique for developing ferroelectric materials.(Am−1BmO3m+1)2−(Bi2O2)2+ is the general formula for the BLSF system, where A is a mono, di, or trivalent element that permits dodecahedral coordination, such as Ca2+, Ba2+, Sr2+, Bi3+, etc.; the B-site is a transition element that has octahedral coordination, such as Fe3+, Ti4+, Nb5+, Ta5+, and W6+; and m is the number of octahedral layers in the perovskite slab, which ranges from 1 to 6.4–6 SrBi4Ti4O15 (SBT) is one of the compositions that we examine in this study. SrBi4Ti4O15 (SBT), CaBi4Ti4O15 (CBT), and BaBi4Ti4O15 (BBT) are four-layer BLSF compounds that have garnered significant attention due to their low operating voltage, quick switching speed, and minimal fatigue up to 1012 switching cycles,7 low leakage current density, and outstanding retention properties, high Curie temperature, low coercive field, and large residual polarization. Because of these characteristics, ferroelectric random access memory (FRAM) and high-temperature sensor applications can employ these systems.8
According to Mamatha et al., SBT made with a modified sol–gel method has electrical and piezoelectric qualities.9 Kennedy et al. studied the room temperature ABi4Ti4O15 (A = Ca, Sr, Ba, Pb) orthorhombic structure with space group A21am. They found that heating causes the structure to change to a tetragonal paraelectric structure for A = Sr, Pb, and Ba.10
The electrical and optical properties of ABi4Ti4O15 (where A = Sr, Ba, and Ca) were reported by Nayak et al. They observed that SBT and CBT were normal ferroelectrics in the dielectric study, while BBT was a relaxor type. The direct band gap is also computed. They did not investigate the electrical modulus and the impedance of the sample.11 The temperature dependences of the Raman scattering spectra of ABi4Ti4O15 (where A = Sr, Ba, Ca, and Pb) were measured by Kojima et al. and clearly visible under-damped soft modes were found in CaBi4Ti4O15 and SrBi4Ti4O15.12 According to Badapanda et al., the conductivity, modulus, and impedance of BaBi4Ti4O15 Aurivillius ceramic exhibit frequency and temperature dependent behaviour. Impedance spectroscopy reveals a dielectric relaxation in the material that is consistent with Maxwell–Wagner relaxations.13 Jabeen et al. analyzed zinc-intercalated SrBi4Ti4O15-based ceramics. Their study focused on the dielectric, piezoelectric, ferroelectric, energy storage efficiency and magnetic properties of the material. However, they did not cover the modulus, Nyquist plot, or conductivity analysis of the ceramics.14
The effects of (Ho, Yb)3+ modification on the electrical properties and luminescent performance of SBT ceramics were studied by Zhang et al., but their results did not explain the modulus and Nyquist study and also did not explain the Johnscher's power law and KWW fitting to determine the nature of conduction and types of relaxation in the sample.15
The synthesis and characterization of SBT in terms of its structural, dielectric, and ferroelectric properties has been the subject of numerous papers in recent years. Few studies have been reported about the electrical and optical properties of SBT at a limited temperature and frequency range. In this paper, we briefly provide the high temperature and frequency study of dielectric and electrical properties related to the conduction mechanism, as well as the impedance properties of the sample. This paper briefly explains the type of conduction mechanism using Jonscher's power law, and the type of relaxation that occurs in the sample is studied using the Kohlrausch–Williams–Watts (KWW) function in a complex modulus plot. Additionally, we study the efficiency and energy storage density of this material for device applications.
2. Experimental idea
2.1 Synthesis process
The conventional solid-state methods used to manufacture the SBT ferroelectric ceramic samples are shown below (Fig. 1). The sample is prepared using a stoichiometric ratio of SrCO3, Bi2O3, and TiO2 according to the following equation (eqn (1)).| SrCO3 + 2Bi2O3 + 4TiO2 → SrBi4Ti4O15 + CO2↑ | (1) |
After three hours of dry grinding in a mortar and pestle, the powder was wet ground for two hours alongside methanol. The entire mixture was calcined at 1100 °C for 14 hours. The calcined powder was combined with polyvinyl alcohol (PVA) as a binding agent, and the mixture was compressed using a hydraulic press (4 MPa) to create pellets that were 1.148 cm in diameter and 0.172 cm in thickness. The pellets underwent two hours of sintering at 1130 °C. Lastly, extremely pure silver paint is applied to both sides of the pellet to electroplate it.
2.2. Material characterization
The structural characteristics of the SBT pellets were examined using an X-ray diffractogram and X'pert High Score Plus. In XRD, the Bragg's angle ranges from 20° ≤ 2θ ≤ 80°. SEM was used to study the morphological properties. LCR meters (LCR PSM N4L, Model: 3750, UK) were used for the electrical study. For electrical investigation using an LCR meter, the frequency ranges from 1 kHz to 1 MHz, where the temperature ranges from room temperature to 500 °C. The PE loop is traced for the prepared sample using a PE loop tracer.3. Results and discussion
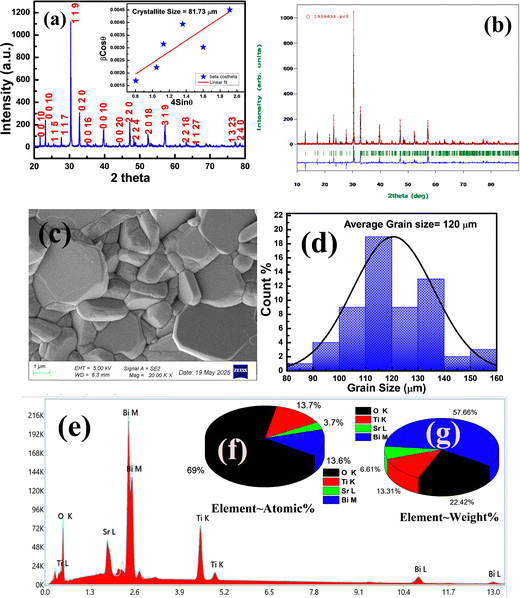
3.1. Structural and morphological study
The X-ray diffraction pattern of SBT is shown in Fig. 2(a). No impurity phase is visible in the specimens, indicating that the correct compositions occurred as expected. An orthorhombic structure with space group A21am and space group number 36 is associated with all the diffraction peaks.16–18The crystallite size was calculated using the Williamson–Hall (W–H) method, where 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and β
θ and β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ are shown along the x and y axes. With strain 0.0022, the average crystallite size is 81.73 μm, as shown by the following expression of the W–H relation.
θ are shown along the x and y axes. With strain 0.0022, the average crystallite size is 81.73 μm, as shown by the following expression of the W–H relation.
 | (2) |
We have estimated the equation provided above, and the crystallite size is calculated using the equation below.19
 | (3) |
In Fig. 2(b) is shown the Rietveld refinement of the XRD data of the SBT ceramic. With the pseudo-Voigt peak shape function, the Rp = 39.3, Rwp = 52.5, Re = 38.54 and also the calculated cell parameters a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.4543
5.4543![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, b
Å, b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.4394
5.4394![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Å, c
Å, c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40.9830 Å, cell volume (V) = 1215.8885 (Å), α = β = γ
40.9830 Å, cell volume (V) = 1215.8885 (Å), α = β = γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90° and space group A21am are obtained (Table 1).
90° and space group A21am are obtained (Table 1).
Fig. 2(c) shows the SEM micrograph of SBT, which shows the densely packed grains. The grains have a needle-like and plate-like structure, indicating the anisotropic growth of the grains.20–22
This suggests that high-quality grains with minimal porosity are formed. Additionally, the sample shows well-developed crystal particles and distinct grain boundaries. The grain size is calculated using ImageJ software, as shown in Fig. 2(d), and it is approximately 120 μm. Fig. 2(e) demonstrates EDX information, which supports the weight and atomic percentage of all constituent elements on the surface. Fig. 2(f) and (g) show the atomic percentage and weight percentage of the sample to detect the elements present in the material. The bulk density of the sample, which is mass per volume, is calculated as 6.02 g cm−3, and the theoretical density is 6.46 g cm−3. The porosity of the sample is 6.87%, indicating low porosity. This suggests that your sample is quite dense, a characteristic typical of well-sintered ceramics.
The agglomeration ratio (AR) is a quantitative parameter used to estimate the extent of particle clustering in ceramic materials. It is the ratio of grain size to crystallite size. Utilizing the average particle size from SEM (120 nm) and the crystallite size from XRD (81.73 nm), the agglomeration ratio was computed. The result was roughly 1.47, suggesting mild agglomeration because of partial crystallite clustering during the synthesis process.
3.3. Dielectric and polarization analysis
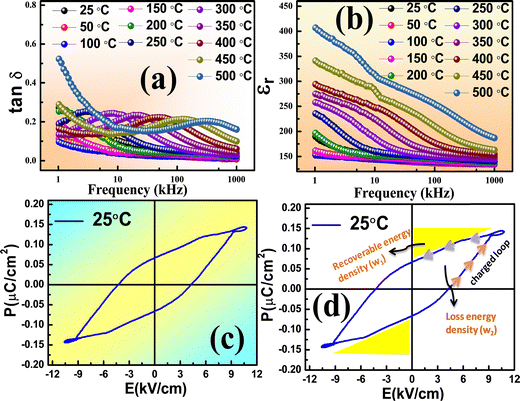
Fig. 3(a) and (b) shows the variation of dielectric loss (tan δ) and electric permittivity with respect to frequency. Here, the dielectric loss is tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = ε′′/ε′. It is evident that the peak intensity moved toward a higher frequency zone and rose with temperature. The change showed an increase in peak intensity and a decrease in relaxation time.23,24 At low frequencies, the high value of tan
δ = ε′′/ε′. It is evident that the peak intensity moved toward a higher frequency zone and rose with temperature. The change showed an increase in peak intensity and a decrease in relaxation time.23,24 At low frequencies, the high value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is due to the high resistivity of the grain boundaries, which are more effective than grains. This occurs because of charge accumulation at the sample-electrode contacts.25 In this instance, it is found that the permittivity value steadily rises as the temperature and frequency decrease and remains almost constant at higher frequencies. This kind of behaviour is consistent with Koop's macroscopic theory and the Maxwell–Wagner26 pattern of interfacial polarization. Space charge polarization and the larger value of εr at lower frequencies are the reasons for the high value of εr near the minimum-frequency zone.27
δ is due to the high resistivity of the grain boundaries, which are more effective than grains. This occurs because of charge accumulation at the sample-electrode contacts.25 In this instance, it is found that the permittivity value steadily rises as the temperature and frequency decrease and remains almost constant at higher frequencies. This kind of behaviour is consistent with Koop's macroscopic theory and the Maxwell–Wagner26 pattern of interfacial polarization. Space charge polarization and the larger value of εr at lower frequencies are the reasons for the high value of εr near the minimum-frequency zone.27
Table 2 shows the reported value and the observed value of the dielectric constant and loss at nearly 500 °C and 100 kHz.
Fig. 3(c) and (d) illustrate the polarisation–electrical field (P–E) plot or hysteresis loop of the SBT at 25 °C. The hysteresis loop of the sample reveals the ferroelectric nature and dynamic polarizability. Its maximum field is 10.747 kV cm−1; its coercivity is 6.743 kV cm−1, its maximum polarisation is 0.144 μC cm−2, and its remanent polarization is 0.066 μC cm−2 at 25 °C. The material under investigation may have a stable ferroelectric phase with a slight departure from our analysis, according to the proper P–E loop analysis.28
High energy storage density, outstanding electrical breakdown performance, relatively low dielectric loss, and rapid charge and discharge rates are some of the remarkable properties of ferroelectric materials that make them ideal for energy storage in electronics and electric power systems. An important component of technical applications is assessing the energy storage density and efficiency of ferroelectric compounds. The crucial factor in evaluating the effectiveness of energy storage systems is power density and energy-storage efficiency (η). Using the energy storage density, the energy storage efficiency is computed as follows:
 | (4) |
In this case, the recovered (or dischargeable) energy density is denoted by w1 (calculated as 1.126413), the dissipated energy density by w2 (calculated as 0.684926) and the efficiency is 62%. The discharged energy density w1 can be computed using the discharge loop, symbolized by the symbol PL (PL stands for the left loop). The right loop is represented by the charged loop, or PR, which can compute the dissipated energy density. A greater recovered energy density is achieved in energy storage dielectrics with a higher Pmax to Pr ratio. Ragone theory states that the power density (Pd) can be computed as:
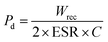 | (5) |
 | (6) |
Here, ESR stands for equivalent series resistance, which is calculated using capacitive reactance (Xc) and dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ). Eqn (5) and (6) can be used to determine the maximum value of Pd as follows;
δ). Eqn (5) and (6) can be used to determine the maximum value of Pd as follows;
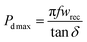 | (7) |
The maximum power density of the material at room temperature is 12.966 MW cm−3 at 1 kHz, according to calculations, which illustrate the greater power density. Hence, as a lead-free substance, it can be used for energy-storage capacitors.29
Table 3 compares the remnant polarisation (Pr) and coercive field (Ec) of SBT from our results with those of others.
3.4. Complex impedance analysis
Fig. 4(a) and (b) depict the variation of real and imaginary parts of the impedance with respect to temperature. The Z′ drops with increasing frequency, which may be due to defects and charges that are not responsive in the chosen frequency range. In the low-frequency domain, Z′ declines with increasing temperature, merges with itself at high frequencies, and eventually stabilizes at a value that indicates the sample contains a space charge. The real part of the impedance decreases, and is nearly zero at higher frequencies indicating a rise in conductivity. The imaginary part of the impedance also decreases with frequency, and is nearly zero at higher frequency regions indicating a rise in conductivity. | ||
| Fig. 4 (a) Frequency dependence of real impedance (Z′), (b) frequency dependence of imaginary impedance (Z′′), and (c) temperature dependence of the Nyquist plot. | ||
The Nyquist plot is displayed in Fig. 4(c). An equivalent circuit comprising an RC network (ZSIMP WIN version 2.0) and a constant phase element (Q), where n is the frequency power, can be used to examine these. From this plot, it can be found that from room temperature to 150 °C, the plot was fitted with an equivalent electrical circuit (CQR), implying the existence of the effect of grains, and then from 200 °C to 500 °C the plot was fitted with an equivalent electrical circuit {(CQR)(CQR)}, which suggests that at higher temperatures, the compound exhibits two semicircular arcs, suggesting that the electrical response is caused by grain and grain boundary effects, which are represented by the first large and second small semicircular arcs. The fitted parameters are tabulated below (Table 4).30
Here,
| Q = A(jω)n−1 | (8) |
| C = A(jω)m−1 | (9) |
The strongly semiconducting character is shown by the observed decrease in bulk (grain) resistance from 3.653 × 107 at 25 °C to 1.570 × 106 at 500 °C and in grain boundary resistance from 1.414 × 108 at 200 °C to 1.004 × 10−2 at 500 °C. The NTCR feature and thermally triggered relaxation phenomenon are supported by the decreasing radius seen in the depressed semi-circles as the temperature rises.30
| T (°C) | Model | C b (F cm−2) | Q | N | R b (Ω-cm2) | C gb (F cm−2) | Q | n | R gb (Ω-cm2) |
|---|---|---|---|---|---|---|---|---|---|
| 25° (expt.) | (CQR) | 1.004 × 10−10 | 2.977 × 10−9 | 8.000 × 10−1 | 3.653 × 10+7 | ||||
| (fitting) | 1.005 × 10−10 | 3.040 × 10−9 | 5.391 × 10−1 | 4.057 × 10+7 | |||||
| 50° (expt.) | (CQR) | 9.929 × 10−11 | 3.39 × 10−10 | 8.000 × 10−1 | 4.928 × 10+7 | ||||
| (fitting) | 9.928 × 10−11 | 3.455 × 10−10 | 6.853 × 10−1 | 5.240 × 10+7 | |||||
| 100° (expt.) | (CQR) | 9.817 × 10−11 | 1.046 × 10−10 | 8.000 × 10−1 | 2.766 × 10+7 | ||||
| (fitting) | 9.816 × 10−11 | 1.043 × 10−10 | 8.023 × 10−1 | 2.764 × 10+7 | |||||
| 150° (expt.) | (CQR) | 9.204 × 10−11 | 8.401 × 10−11 | 8.000 × 10−1 | 8.741 × 10+6 | ||||
| (fitting) | 9.409 × 10−11 | 9.226 × 10−11 | 8.543 × 10+1 | 8.976 × 10+6 | |||||
| 200° (expt.) | (CQR) (CQR) | 3.470 × 10−10 | 3.605 × 10−13 | 2.939 × 10−13 | 3.009 × 10+6 | 1.167 × 10−11 | 2.293 × 10−10 | 9.679 × 10−1 | 1.414 × 10+8 |
| (fitting) | 3.468 × 10−10 | 2.939 × 10−13 | 1.140 × 10−8 | 3.012 × 10+5 | 1.163 × 10−11 | 2.295 × 10−10 | 9.679 × 10−1 | 1.459 × 10+8 | |
| 250° (expt.) | (CQR) (CQR) | 1.104 × 10−10 | 2.180 × 10−10 | 8.858 × 10−1 | 2.487 × 10+7 | 3.886 × 10−10 | 1.680 × 10−17 | 4.988 × 10−3 | 1.000 × 10+5 |
| (fitting) | 1.104 × 10−10 | 2.180 × 10−10 | 8.858 × 10−1 | 2.487 × 10+8 | 3.886 × 10−10 | 1.607 × 10−17 | 1.564 × 10−3 | 1.000 × 10+5 | |
| 300° (expt.) | (CQR) (CQR) | 1.362 × 10−10 | 2.012 × 10−10 | 8.707 × 10−1 | 4.236 × 10+7 | 3.364 × 10−10 | 1.224 × 10−5 | 6.412 × 10−2 | 1.726 × 10+12 |
| (fitting) | 1.335 × 10−10 | 1.827 × 10−10 | 8.859 × 10−1 | 3.466 × 10+7 | 3.304 × 10−10 | 1.141 × 10−5 | 6.860 × 10−2 | 1.454 × 10+12 | |
| 350° (expt.) | (CQR) (CQR) | 3.783 × 10−10 | 3.005 × 10−5 | 6.502 × 10−2 | 1.491 × 10+5 | 1.326 × 10−10 | 2.927 × 10−10 | 8.507 × 10−1 | 2.909 × 10+7 |
| (fitting) | 3.783 × 10−10 | 3.005 × 10−5 | 6.501 × 10−2 | 1.491 × 10+5 | 1.326 × 10−10 | 2.927 × 10−10 | 8.507 × 10−1 | 2.909 × 10+7 | |
| 400° (expt.) | (CQR) (CQR) | 1.038 × 10−10 | 3.820 × 10−10 | 8.691 × 10−1 | 1.424 × 10+7 | 4.988 × 10−10 | 2.226 × 10−5 | 9.758 × 10−25 | 5.667 × 10+14 |
| (fitting) | 1.038 × 10−10 | 3.821 × 10−10 | 8.691 × 10−1 | 1.425 × 10+7 | 4.988 × 10−10 | 2.226 × 10−4 | 2.752 × 10−22 | 9.283 × 10+13 | |
| 450° (expt.) | (CQR) (CQR) | 8.842 × 10−12 | 5.772 × 10−10 | 8.626 × 10−1 | 5.113 × 10+6 | 6.309 × 10−10 | 1.523 × 10−9 | 9.870 × 10−28 | 1.519 × 10+3 |
| (fitting) | 8.829 × 10−11 | 5.770 × 10−10 | 8.627 × 10−1 | 5.111 × 10+6 | 6.314 × 10−10 | 5.879 × 10−10 | 2.922 × 10−28 | 1.518 × 10+3 | |
| 500° (expt.) | (CQR) (CQR) | 1.000 × 10−16 | 8.223 × 10−10 | 8.907 × 10−1 | 1.570 × 10+6 | 1.197 × 10+2 | 2.407 × 10+15 | 1.712 × 10−2 | 1.00 × 10−2 |
| (fitting) | 9.98 × 10−017 | 8.224 × 10−10 | 8.907 × 10−1 | 1.570 × 10+6 | 1.197 × 10+2 | 2.408 × 10+15 | 1.715 × 10−2 | 1.004 × 10−2 |
3.5. Modulus study
The electrical response can be studied using the formalism of the complex electric modulus M*(ω). The electrical modulus is used to study the dielectric relaxation mechanisms of the compounds. The complex electric modulus was calculated from the dielectric permittivity using the following relation (eqn (10)).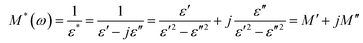 | (10) |
 and
and  . Here, M′ and M′′ are the real and imaginary parts of the modulus, and ε′ and ε′′ are the real and imaginary parts of the electrical permittivity.32–35
. Here, M′ and M′′ are the real and imaginary parts of the modulus, and ε′ and ε′′ are the real and imaginary parts of the electrical permittivity.32–35
The graph in Fig. 5(a) depicts the relationship between M′ and frequency (from 1 kHz to 1 MHz) at various temperatures throughout the operational frequency range. The measured characteristics make it clear that the value of M′ tends toward zero at higher temperatures, suggesting a monotone dispersion as the frequency drops. On the other hand, M′ shows an increasing trend as the frequency rises. This behaviour indicates that the effect of the electric field on the sample loses its effectiveness at higher frequencies. The existence of short-range mobile charge carriers and conduction phenomena explains this. It demonstrates how carriers moving under the influence of a continuous electric field lack a restoring force.36
The imaginary part of the modulus, i.e., M′′ variation with frequency at different temperatures, is seen in Fig. 5(b). In this plot, it is clearly visible that the relaxation occurs from 200 °C to 500 °C. The position of the  shifted towards the higher frequency region. The movement of
shifted towards the higher frequency region. The movement of  (the peak of the imaginary component of the electric modulus) to higher frequencies signifies a reduction in relaxation time, indicating quicker dipolar or ionic relaxation processes within the material. This phenomenon is often linked to improved conductivity or lower energy barriers for charge carrier movement, as the material responds more efficiently to alternating electric fields.
(the peak of the imaginary component of the electric modulus) to higher frequencies signifies a reduction in relaxation time, indicating quicker dipolar or ionic relaxation processes within the material. This phenomenon is often linked to improved conductivity or lower energy barriers for charge carrier movement, as the material responds more efficiently to alternating electric fields.
Fig. 5(c) illustrates electric modulus (M′ vs. M′′) changes with temperature. The M′′ peak moves toward higher M′ values as the temperature rises from 25 °C to 500 °C, signifying a shorter relaxation time and quicker ionic or dipolar motion. As the temperature rises, the peak height decreases. A distribution of relaxation times is suggested by peak broadening at higher temperatures. The shift in the peak position with increasing temperature suggests that the relaxation time decreases, implying faster dipolar or ionic motion at elevated temperatures.
Bergman-proposed Kohlrausch, Williams, and Watts (KWW) function was used to fit the imaginary part of the modulus with a frequency plot. This relationship is provided by:
 | (11) |
In this context,  represents the maximum peak value, while β is the stretching factor that determines the characteristics of the sample. In Fig. 5(d), using the Bergman-proposed Kohlrausch, Williams, and Watts (KWW) function, the
represents the maximum peak value, while β is the stretching factor that determines the characteristics of the sample. In Fig. 5(d), using the Bergman-proposed Kohlrausch, Williams, and Watts (KWW) function, the  curves were employed to accurately fit the symmetric, non-linear peaks of the imaginary component of the electric modulus. We found that the
curves were employed to accurately fit the symmetric, non-linear peaks of the imaginary component of the electric modulus. We found that the  is 0.0012, β is 0.67675, and ω is 9810.34562 for 300 °C. The results indicate that the β is less than one, which signifies a non-Debye nature of the sample.37,38
is 0.0012, β is 0.67675, and ω is 9810.34562 for 300 °C. The results indicate that the β is less than one, which signifies a non-Debye nature of the sample.37,38
3.6. Conductivity study
As shown in Fig. 6(a), it is clear from our observations that the conductivity progressively rises as the frequency increases. The temperature causes the conductivity levels to rise, indicating strong frequency dependence.39 In Fig. 6(b), using Jonscher's power law equation, the ac conductivity (σac) was fitted with increasing frequency at various temperatures:40| σac = σdc + Aωn | (12) |
| T (°C) | σ dc (S m−1) | A | n |
|---|---|---|---|
| 25 | 3.73932 × 10−7 | 7.7965 × 10−8 | 0.50927 |
| 50 | 1.16833 × 10−7 | 1.10937 × 10−8 | 0.631 |
| 100 | 2.4984 × 10−7 | 3.95235 × 10−9 | 0.71362 |
| 150 | 1.39996 × 10−6 | 2.05246 × 10−9 | 0.76208 |
| 200 | 2.97432 × 10−6 | 4.45516 × 10−9 | 0.74326 |
| 250 | 1.01666 × 10−6 | 1.67139 × 10−8 | 0.74288 |
| 300 | 1.0196 × 10−8 | 2.65017 × 10−9 | 1 |
| 350 | 1.09 × 10−8 | 2.30698 × 10−9 | 1 |
| 400 | 4.50721 × 10−7 | 1.98722 × 10−9 | 1 |
| 450 | 3.22999 × 10−6 | 4.87555 × 10−9 | 0.8893 |
| 500 | 5.11466 × 10−6 | 1.3679 × 10−7 | 0.56566 |
Fig. 6(d) presents the Arrhenius plot of AC conductivity as a function of temperature. The plot reveals that conductivity increases with rising temperature. At higher temperatures, the conductivity exhibits a linear response, indicating thermally activated conduction behaviour, which follows the Arrhenius-type relationship written in eqn (13):46,47
 | (13) |
| S. no. | Frequency (Hz) | Activation energy (eV) |
|---|---|---|
| 1 | 5 kHz | 0.3337 |
| 2 | 1 MHz | 0.2136 |
The activation energy of the material was calculated and tabulated in Table 6. As the frequency of occurrences increases, the value of activation energy decreases, indicating enhanced hopping of charge carriers between localized sites. The comparision of reported and observed ac conductivity is tabulated below (Table 7).50
| Compounds | σ ac | Ref. |
|---|---|---|
| BaBi4Ti4O15 | 3.6 × 10−6 | 49 |
| SrBi4Ti4O15 | 2.75 × 10−6 | |
| PbBi4Ti4O15 | 7.4 × 10−6 | |
| SrBi4Ti4O15 | 3.58 × 10−5 | This work |
4. Conclusion
The SBT ceramic was successfully produced using the high-temperature solid-state reaction technique. XRD examination demonstrates an orthorhombic unit cell of crystallite size 81.73 μm, confirming the single-phase growth of the sample. The FESEM microstructure shows the uniform formation of the sample, with a calculated grain size of approximately 120 μm. The dielectric analysis demonstrates that the behaviour is in line with the Maxwell–Wagner pattern of interfacial polarization and Koop's macroscopic theory. The shrinking radius seen in the depressed semi-circles as the temperature rises is proof of the NTCR characteristic and the thermally induced relaxation effect. The Nyquist plot shows up to 150 °C, the grain effect was seen, and later, both the grain and grain boundary effect were seen. In the modulus investigation, the shift in peak position with rising temperature indicates a decrease in relaxation time. This suggests that dipolar or ionic movement occurs more rapidly at higher temperatures, highlighting the potential of the sample as a promising material for electronic devices. The KWW fitting suggested that the sample has a non-Debye type of relaxation. Jonscher's power law analysis shows that, between room temperature and 300 °C, the conductivity of the sample is attributed to non-overlapping small polaron tunnelling (NSPT), followed by correlated barrier hopping (CBH). The behaviour of the hysteresis loop demonstrates the ferroelectric properties and dynamic polarizability of the sample. The efficiency and maximum power density (Pdmax) calculated from the polarisation–electric field (PE) loop are 62% and 12.9662 MW cm−3, respectively. These results indicate that the material is suitable for high-performance energy storage capacitor applications.Conflicts of interest
The authors confirm that they have no financial conflicts of interest or significant personal relationships that could have impacted the research presented in this paper to disclose.Data availability
The author is open to providing the data from the paper upon receiving a reasonable request.Acknowledgements
This research did not receive any financial assistance or support. The authors would like to thank the host university for SEM and KIIT University for XRD and EDX.References
- S. S. Hota, D. Panda and R. N. P. Choudhary, Structural, topological, dielectric, and electrical properties of a novel calcium bismuth tungstate ceramic for some device applications, J. Mater. Sci.:Mater. Electron., 2023, 34(10), 900, DOI:10.1007/s10854-023-10240-0.
- A. Mayeen and N. Kalarikkal, Development of ceramic-controlled piezoelectric devices for biomedical applications, Fundam. Biomater.:Ceram., 2018, 47–62, DOI:10.1016/B978-0-08-102203-0.00002-0.
- M. M. V. Petrovic and J. D. Bobic, Perovskite and aurivillius: Types of ferroelectric metal oxides, In Magnetic, ferroelectric, and multiferroic metal oxides, Elsevier, 2018, pp. 35–49 DOI:10.1016/B978-0-12-811180-2.00002-5.
- Y. Zhao, H. Fan, X. Ren, C. Long, G. Liu and Z. Liu, Lead-free Bi5−xLaxTi3FeO15 (x = 0, 1) nanofibers toward wool keratin-based biocompatible piezoelectric nanogenerators, J. Mater. Chem. C, 2016, 4(30), 7324–7331, 10.1039/C6TC01828A.
- Q. Chang, H. Fan and C. Long, Effect of isovalent lanthanide cations compensation for volatilized A-site bismuth in Aurivillius ferroelectric bismuth titanate, J. Mater. Sci.:Mater. Electron., 2017, 28, 4637–4646, DOI:10.1007/s10854-016-6102-0.
- K. Mitra. Synthesis and Characterization of ABi4Ti4O15 (A = Sr, Ba, Ca) Ceramic. PhD diss., 2015. https://ethesis.nitrkl.ac.in/7314/.
- A. Z. Simoes, M. A. Zaghete, B. D. Stojanovic, A. H. Gonzalez, C. S. Riccardi, M. Cantoni and J. Arana Varela., Influence of oxygen atmosphere on crystallization and properties of LiNbO3 thin films, J. Eur. Ceram. Soc., 2004, 24(6), 1607–1613, DOI:10.1016/S0955-2219(03)00453-9.
- T. Watanabe, H. Funakubo and K. Saito,, J. Mater. Res., 2001, 16, 303 CrossRef CAS.
- B. Mamatha, M. B. Suresh, A. R. James, M. Vithal and P. Sarah., Synthesis and electrical properties of SrBi4Ti4O15 piezoelectric ceramics., Phys. Scr., 2011, 84(5), 055704 CrossRef.
- B. J. Kennedy, Q. Zhou, Y. Kubota and K. Kato., Cation disorder and phase transitions in the four-layer ferroelectric Aurivillius phases ABi4Ti4O15 (A = Ca, Sr, Ba, Pb), J. Solid State Chem., 2008, 181(6), 1377–1386 CrossRef CAS.
- P. Nayak, K. Mitra and S. Panigrahi, Electrical and optical properties of four-layered perovskite ferroelectric ABi4Ti4O15 (with A = Sr, Ba, Ca), Mater. Lett., 2018, 216, 54–57 CrossRef CAS.
- S. Kojima, R. Imaizumi, S. Hamazaki and M. Takashige, Raman study of ferroelectric bismuth layer-oxides ABi4Ti4O15J, Mol. Struct., 1995, 348, 37–40 CrossRef CAS.
- T. Badapanda, R. K. Harichandan, S. S. Nayak, A. Mishra and S. Anwar., Frequency and temperature dependence behaviour of impedance, modulus, and conductivity of BaBi4Ti4O15 Aurivillius ceramic, Process. Appl. Ceram., 2014, 8(3), 145–153 CrossRef.
- N. Jabeen, A. U. Rehman, N. U. Hassan, M. A. Qaiser, A. Zaidi, M. U. Khan, I. A. Khan and M. Nouman., Boosting of magnetic, ferroelectric, energy storage efficiency, and piezoelectric properties of Zn intercalated SrBi4Ti4O15-based ceramics, Materials, 2022, 15(14), 5057 CrossRef CAS PubMed.
- Y. Zhang, L. Duan, A. Zhang, D. Wang, R. Chu, Z. Xu, G. Li and C. Zhang, Photoluminescence, electrical properties and electron band structure of (Ho, Yb) 3+ co-doped SrBi4Ti4O15 multifunctional ceramics, Ceram. Int., 2022, 48(7), 9248–9257 CrossRef CAS.
- R. Jose and K. V. Saravanan, Dielectric and AC conductivity studies on SrBi4Ti4O15, In AIP Conference Proceedings, AIP Publishing, 2018, vol. 1953, no. 1 Search PubMed.
- L. Yu., J. Hao, Z. Xu, W. Li and R. Chu., Bright green emission and enhanced electrical properties in SrBi4-xHoxTi4O15 multifunctional ceramics, Mater. Chem. Phys., 2018, 203, 82–88 CrossRef CAS.
- P. Nayak, T. Badapanda and S. Panigrahi., Investigation of site selectivity of lanthanum in SrBi 4 Ti 4 O 15 ceramic by structural, dielectric, ferroelectric and conduction behavior, J. Mater. Sci.:Mater. Electron., 2017, 28, 625–632 CrossRef CAS.
- S. S. Rout, S. S. Hota, D. Panda, L. Biswal, S. Joshi, A. Shukla and P. Mohanty, Choudhary. Investigation of structural, dielectric, impedance, and conductivity properties of layered perovskite-type compound: LiNdSnO4, J. Mater. Sci.:Mater. Electron., 2024, 35(29), 1898 CrossRef CAS.
- B. Mamatha, M. B. Suresh, A. R. James, M. Vithal and P. Sarah., Synthesis and electrical properties of SrBi4Ti4O15 piezoelectric ceramics, Phys. Scr., 2011, 84(5), 055704 CrossRef.
- M. V. Gelfuso, D. Thomazini and J. A. Eiras, Synthesis and structural, ferroelectric, and piezoelectric properties of SrBi4Ti4O15 ceramics, J. Am. Ceram. Soc., 1999, 82(9), 2368–2372 CrossRef CAS.
- A. Rambabu and K. C. J. Raju., Impact of Sm-substitution and microwave sintering on dielectric and mechanical properties of SrBi 4 Ti 4 O 15 ceramics, J. Mater. Sci.:Mater. Electron., 2020, 31, 19698–19712 CrossRef.
- R. P. Parida, B. Parida, R. K. Bhuyan and S. K. Parida., Structural, mechanical and electric properties of La-doped BNT-BFO perovskite ceramics, Ferroelectrics, 2021, 571(1), 162–174 CrossRef CAS.
- S. Ramesh, Transport properties of Sm doped CeO2 ceramics, Process. Appl. Ceram., 2021, 15(4), 366–373 CrossRef CAS.
- C. Rayssi, S. E. Kossi, J. Dhahri and K. Khirouni., Frequency and temperature-dependence of dielectric permittivity and electric modulus studies of the solid solution Ca 0.85 Er 0.1 Ti 1− x Co 4x/3 O 3 (0≤ x≤ 0.1), Rsc Adv., 2018, 8(31), 17139–17150 RSC.
- D.-W. Fu, H.-L. Cai, Y. Liu, Q. Ye, W. Zhang, Y. Zhang and X.-Y. Chen, et al., Diisopropylammonium bromide is a high-temperature molecular ferroelectric crystal, Science, 2013, 339(6118), 425–428 CrossRef CAS PubMed.
- M. Padhy, R. N. P. Choudhary and P. G. R. Achary., Electrical and Dielectric Characteristics of BiSmO3, Phys. Solid State, 2021, 63(10), 1501–1507 CrossRef CAS.
- A. Kumar, K. J. Raju, J. Ryu and A. R. James, Composition dependent Ferro-piezo hysteresis loops and energy density properties of mechanically activated (Pb 1− x La x)(Zr 0.60 Ti 0.40) O 3 ceramics, Appl. Phys. A:Mater. Sci. Process., 2020, 126, 1–10 CrossRef.
- S. S. Hota, D. Panda and R. N. P. Choudhary, Development of ultra-high energy storage density and ultra-wide operating temperature behavior of a lead-free capacitor sensor;(Bi1/2 K1/2)(Fe1/3Mn1/3W1/3) O3, J. Power Sources, 2024, 599, 234223 CrossRef CAS.
- S. S. Hota, D. Panda and R. N. P. Choudhary, Sensitivity and accuracy of dielectric measurements of significantly improved coupled capacitive-dependent scheelite crystal, In 2023 International Conference in Advances in Power, Signal, and Information Technology (APSIT), IEEE, 2023, pp. 1–6 Search PubMed.
- M. A. Ahmed, S. F. Mansour and M. A. Abdo., Electrical properties of Cu substituted Co nano ferrite., Phys. Scr., 2012, 86(2), 025705 CrossRef.
- P. B. Macedo, C. T. Moynihan and R. Bose, The role of ionic diffusion in polarisation in vitreous ionic conductors. (1972).
- M. Ganguli, M. H. Bhat and K. J. Raol, Lithium-ion transport in Li2SO4–Li2O–B2O3 glasses, Phys. Chem. Glasses, 1999, 40(6), 297–304 CAS.
- S. Ghosh and A. Ghosh, Electrical conductivity and conductivity relaxation in mixed alkali fluoride glasses, Solid State Ionics, 2002, 149(1–2), 67–72 CrossRef CAS.
- S. Lanfredi, P. S. Saia, R. Lebullenger and A. C. Hernandes, Electric conductivity and relaxation in fluoride, fluorophosphate and phosphate glasses: analysis by impedance spectroscopy, Solid State Ionics, 2002, 146, 329–339 CrossRef CAS.
- N. Kumar, S. S. Hota, D. Panda, S. K. Samal, R. N. P. Choudhary and U. Prasad., Investigation of structural, dielectric and electrical properties of lead-free bismuth-based layered multifunctional material: CaBiGdNbVO9 for device fabrication, Journal of the Korean Physical Society, 2024, 85(6), 510–519 CrossRef CAS.
- R. Bergman, J. Appl. Phys., 2000, 88, 1356 CrossRef CAS.
- R. Charguia, S. Hcini, M. Boudard and A. Dhahri, Microstructural properties, conduction mechanism, dielectric behavior, impedance and electrical modulus of La 0.6 Sr 0.2 Na 0.2 MnO 3 manganite, J. Mater. Sci.:Mater. Electron., 2019, 30, 2975–2984 CrossRef CAS.
- S. S. Hota, D. Panda and R. N. Choudhary., Studies of structural, dielectric, electrical, and optical properties of a multi-doped novel complex perovskite (Bi1/2Na1/2)(Fe1/3Mn1/3W1/3) O3 ceramic for Opto-electronic application, Chin. J. Phys., 2024, 87, 430–451 CrossRef CAS.
- A. K. Jonscher, Nature (London)., J. Phys. D: Appl. Phys., 1999, 32, R5710 CrossRef.
- A. Ghosh, Frequency-dependent conductivity in bismuth-vanadate glassy semiconductors., Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 41(3), 1479 CrossRef CAS PubMed.
- K. P. Maity, A. Patra and V. Prasad., Influence of the chemical functionalization of carbon nanotubes on low temperature ac conductivity with polyaniline composites., J. Phys. D:Appl. Phys., 2020, 53(12), 125303 CrossRef CAS.
- A. Ghosh, Transport properties of vanadium germanate glassy semiconductors., Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 42(9), 5665 CrossRef CAS PubMed.
- Y. B. Taher, A. Oueslati, K. Khirouni and M. Gargouri, Impedance spectroscopy and conduction mechanism of LiAlP2O7 material., Mater. Res. Bull., 2016, 78, 148–157 CrossRef.
- S. Mollah, K. K. Som, K. Bose and B. K. Chaudhuri, ac conductivity in Bi4Sr3Ca3Cu y O x (y = 0–5) and Bi4Sr3Ca3− z Li z Cu4O x (z = 0.1–1.0) semiconducting oxide glasses, J. Appl. Phys., 1993, 74(2), 931–937 CrossRef CAS.
- Y. Ben Taher, A. Oueslati, N. K. Maaloul, K. Khirouni and M. Gargouri., Conductivity study and correlated barrier hopping (CBH) conduction mechanism in diphosphate compound, Appl. Phys. A:Mater. Sci. Process., 2015, 120, 1537–1543 CrossRef CAS.
- S. Chatterjee, P. K. Mahapatra, R. N. P. Choudhary and A. K. Thakur., Complex impedance studies of sodium pyrotungstate–Na2W2O7, Phys. Status Solidi A, 2004, 201(3), 588–595 CrossRef CAS.
- T. Rana and J. P. Sharma, Dielectric and ferroelectric properties of dysprosium doped BaBi4Ti4O15 layered ceramics, Next Mater., 2025, 6, 100293 CrossRef.
- T. G. Reddy, B. R. Kumar and T. S. Rao. Studies on Structural and Dielectric Properties of ABi 4 Ti 4 O 15 (A = Ba, Sr & Pb) Ceramics, In AIP Conference Proceedings, American Institute of Physics, 2010, vol. 1313, 1, pp. 134–136 Search PubMed.
- S. Mishra and S. K. Parida., Lead-free complex double perovskite SrLiFeWO6: Structural, microstructure, electrical and optical study., Phys. B, 2023, 668, 415246 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |