Open Access Article
Open Access ArticleOptimizing the processing parameters of producing Al–Si alloys using sodium fluosilicate via artificial neural network
Gamal M. A.
Mahran
 *a,
Abdel-Nasser M.
Omran
bc,
Hassan E. M.
Gomaa
d and
Mahamed Abd-El-Hakeem
Mahamed
e
*a,
Abdel-Nasser M.
Omran
bc,
Hassan E. M.
Gomaa
d and
Mahamed Abd-El-Hakeem
Mahamed
e
aMining Engineering Department, Faculty of Engineering, King Abdulaziz University, Jeddah 21589, Saudi Arabia. E-mail: gmahran@kau.edu.sa
bHigh Institute of Engineering and Technology Tod – Luxor, Luxor, Egypt
cMining and Metallurgical Dept., Faculty of Engineering, Al-Azhar University, Qena 83513, Egypt
dDepartment of Nuclear Safety Engineering, Atomic Energy Authority, Cairo 11765, Egypt
eEelectrical Engineering Dept., Faculty of Engineering, Al-Azhar University, Qena 83513, Egypt
First published on 11th June 2025
Abstract
This study investigates the optimal conditions for producing Al–Si cast alloys by reacting sodium fluorosilicate (Na2SiF6) with molten aluminium, employing artificial neural network via the Levenberg–Marquardt algorithm (LMA-ANN). The goal is to identify the lowest reaction times that yield the highest silicon recovery percentages at minimal stirring speeds and reaction temperatures, optimizing processing parameters and economic outcomes. Characterization techniques such as XRD and LOM confirmed the presence of α Al, and a uniform fine fibrous eutectic silicon. Differential thermal analysis (DTA) showed an exothermic peak at approximately 871 °C, indicating a multi-step reaction involving Al and Na2SiF6. The efficiency of silicon recovery was directly proportional to the stirring speed and temperature within the reaction time range of 15 to 30 minutes. The cascade-forward back-propagation ANN was trained to optimize silicon recovery, considering reaction time, temperature, and stirring speed. Analysis revealed that higher temperatures led to increased silicon recoveries, with significant gains at higher temperatures for all stirring speeds. The maximum silicon recovery efficiency of 92.14% was obtained with a reaction time of 25.86 minutes, a temperature of 950 °C, and a stirring speed of 600 rpm. This study highlights the effectiveness of the ANN-LMA approach in deriving optimal processing conditions for high-efficiency silicon recovery in Al–Si alloys.
1. Introduction
Aluminium–silicon (Al–Si) alloys are a significant category of casting alloys, representing over 80% of all cast aluminium alloys. These alloys are highly valued for their excellent physical, mechanical, and tribological properties, including good casting characteristics, corrosion resistance, fluidity, low specific gravity, minimal shrinkage, and superior weldability. The corrosion and erosion resistance of Al–Si alloys further enhance their desirability across various industrial applications.1–5 Despite their widespread use, the needle-shaped silicon present in these alloys can negatively impact their mechanical and tribological properties. Therefore, modifying the shape and size of silicon is crucial to enhance these properties. Strontium (Sr) and sodium (Na) are commonly employed to alter the silicon morphology in Al–Si alloys. Traditional methods of producing Al–Si alloys are expensive and require additional modifiers. Consequently, researchers are exploring more cost-effective alternatives, such as reducing the silicon from sodium fluosilicate (Na2SiF6). This study investigates sodium fluorosilicate, a by-product of superphosphate fertilizer plants, as a silicon source for Al–Si alloy production. Na2SiF6 offers economic advantages and contains sodium, providing self-modification properties to the alloy. Various factors, including temperature, reaction time, stirring speed, and the amount and size of additive particles, influence the production of Al–Si alloys.6–8 Optimizing these variables is essential to achieve maximum silicon recovery efficiency, minimize additive material usage, and reducing operational costs. Artificial intelligence (AI) neural network algorithms are increasingly utilized to optimize complex processes by identifying primary relationships in data sets and adapting to changing inputs. These algorithms can predict the properties of materials, analyze the impact of varying factors, and determine optimal parameters for chemical and metallurgical reactions.9,10 Recent advancements in neural network methodologies, including multi-layer perceptrons, recurrent neural networks, radial basis functions, and trainable cascade-forward back-propagation networks, have proven effective in numerous applications.11–14 The Levenberg–Marquardt algorithm (LMA) is particularly noted for its robustness and speed in optimization tasks.15–18 The back-propagation network is significant and widespread nowadays concerning the available neural networks due to weaknesses in other available networks. The network is structured as a layered model, consisting of input and output layers with at least one hidden layer. The back-propagation network used in this study was chosen due to its suitability for handling the complexity of the problem, including the number of inputs, outputs, hidden layers, and their respective neurons.9,19 The back-propagation model operates in two main steps. In the first step, each neuron receives input data and generates corresponding output results. Neurons are organized within a layer and connected across different layers. The strength of the connections, or the weight structure, is initially assigned arbitrary values and later adjusted during the training process. In the second step, after defining the system constraints, the model produces output by providing input data to the network, a process referred to as system testing. The training process relies on the gradient descent algorithm, which adjusts the weights iteratively to minimize the overall system error.9,19–22 This study aims to optimize the processing parameters for the production of Al–Si alloys using Na2SiF6 as a reducing agent with molten aluminium. Specifically, the research seeks to maximize the silicon recovery efficiency by systematically studying the effects of reaction time, temperature, and stirring speed. This optimization is accomplished using an artificial neural network model with the Levenberg–Marquardt algorithm (ANN-LMA), providing a comprehensive understanding of the optimal conditions required for high-efficiency silicon recovery in Al–Si alloy production. The choice of this model is particularly significant due to its strong capability in handling complex, nonlinear relationships between multiple processing parameters. ANN-LMA is known for its fast convergence and high accuracy in optimization tasks, making it well-suited for modeling the intricate dependencies among reaction time, temperature, and stirring speed. This, in turn, contributes to enhancing efficiency, reducing material waste, and improving the overall economic feasibility of the process.2. Materials and methods
2.1. Materials
Na2SiF6 used in this study has a purity of 99%; it was supplied from Al-Gomhoria Company, Egypt for chemicals and is of 99% purity, comprising approximately 24.8% Na, 60.3% F, and 14.6% Si by weight. The chemical analysis of the as received Na2SiF6 was performed by X-ray fluorescence spectroscopy(XRF). The aluminium employed had a purity of approximately 99.7%. The elemental analysis of aluminium was performed with an inductively coupled plasma (ICP) model (OES).2.2. Procedure
The experiments were conducted using a vertical tube muffle furnace, Russian model equipped with a multi-speed mechanical stirrer and a thermocouple to monitor the temperature of the molten aluminium. Each experiment involved melting 250 grams of aluminium in a silicon carbide crucible within the furnace. Upon reaching the preset temperature, 250 grams of Na2SiF6 powder was gradually added to the molten aluminium with continuous stirring using the mechanical stirrer, Fig. 1. After the designated reaction period, the crucible was removed from the furnace, the upper slag layer was skimmed off, and the molten ingots were poured into cast iron moulds measuring 30 mm in diameter and 25 mm in depth. Reaction times ranged from 5 to 30 minutes, and temperatures from 800 °C to 1000 °C in 50 °C increments, with stirring speeds of 200, 400, and 600 rpm.2.3. Chemical, microstructure, and spectroscopic analysis
The ingots were chemically analyzed to determine the silicon percentage and recovery efficiency. The theoretical silicon content in the produced alloy was calculated based on the ratio of Na2SiF6 to total aluminium. Silicon recovery efficiency was calculated using the following equations: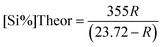 | (1) |
 | (2) |
The microstructure was inspected using scanning electron microscope (SEM), INSPECT S50, USA model, equipped with energy dispersive spectroscopy (EDS). Crystallinity and phases were analyzed using X-ray diffraction (XRD, D5000, Bruker, Germany) with Ni-filtered, Cu-Kβ radiation (λ = 1.5408 Å). The thermal stability and decomposition of Al and Na2SiF6 mixtures were examined using differential temperature analysis (DTA).
2.4. Optimization process using artificial neural network (ANN)
During the construction of the proposed model, a meeting was conducted with the person responsible for creating the model. A detailed explanation was provided of the boundary conditions used to improve the efficiency of silicon extraction in the preparation of Al–Si alloys, ensuring that the experimental and computational models are consistent with realistic conditions. These include for example:– Temperature boundary conditions: operating range: 800 to 1000 °C (increasing by 50 °C).
– Temperatures exceeding 1000 °C may cause excessive evaporation of aluminum and undesirable side reactions.
– Temperatures below 800 °C may slow down significantly below this temperature, leading to inefficient silicon extraction.
– The presence of molten aluminum in a silicon carbide (SiC) crucible also ensures the reaction remains at a near-uniform temperature due to its high thermal conductivity.
– A thermocouple ensures real-time temperature monitoring to maintain stability within ±5 °C of the setpoint.
– Stirring speeds: 200, 400, and 600 rpm. Stirring ensures a well-mixed system after a short transition period (approximately 30 seconds).
– Na2SiF6 powder is added gradually to the molten aluminum to prevent sudden thermal shock and excess gas emission.
– Reaction: Na2SiF6 + Al → Si (melt) + AlF3 (slag)
– The rest of the effective boundary conditions were explained to the person who coded the model.
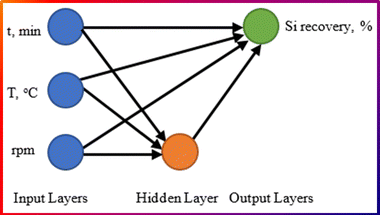
Fig. 2 is a diagram representing a trainable cascade (forward back-propagation) ANN model designed to predict silicon (Si) recovery efficiency (%) in an Al–Si alloy production process. The model consists of input, hidden, and output layers, each playing a crucial role in data processing and prediction. The input layer includes three key process parameters affecting silicon recovery; reaction time, min; temperature of the molten aluminum, (°C); and stirring speed (rpm). These independent variables are used by the model to predict silicon recovery efficiency. The hidden layer contains neurons that process the inputs using weighted connections and activation functions. It identifies complex relationships between reaction time, temperature, and stirring speed to predict silicon recovery. The network is trained using an optimization algorithm to adjust the weights and improve prediction accuracy as indicated in eqn (3) and (4). The single output node represents the predicted silicon recovery efficiency (%), which is the dependent variable. The ANN model uses trained weights to compute this output based on the given inputs.
 | (3) |
| f(netj) = netj | (4) |
Optimizing the processing parameters using the Levenberg–Marquardt algorithm: the optimized reaction conditions to maximize the Si recovery efficiency were probed employing the objective function formulated in eqn (5). Eqn (5) depends on the function produced by modeling the % Si recovery efficiency using the trainable cascade-forward back-propagation network. The Levenberg–Marquardt algorithm (LMA) provides a solution to this problem employing the nonlinear least squares minimization calculation scheme, which implies that it aims to provide an intuitive explanation for this algorithm.9
| J = min[1 − f(T.N.t)] | (5) |
Fig. 3 represents the cascade-forward back-propagation used to predict the optimum reaction time and silicon recovery efficiency in an Al–Si alloy production process. The network consists of input, hidden, and output layers, each playing a key role in processing data. The input layer consists of two key process parameters: temperature of the molten aluminum and stirring speed (rpm). These inputs are the independent variables that influence the outcome of the process. The hidden layer consists of neurons that process the inputs using weighted connections and activation functions. The model is trained using an algorithm (e.g., Levenberg–Marquardt algorithm, LMA) to adjust these weights for accurate predictions. The network generates two outputs: optimum reaction time (min), the best duration for maximizing silicon recovery and optimum silicon recovery efficiency (%), the predicted recovery percentage under the given conditions. These outputs help optimize the alloy production process by identifying the best temperature and stirring speed for maximum efficiency. The importance of this model is that it predicts optimal process parameters without excessive experiments, reduces cost and time in silicon recovery studies and improves efficiency in Al–Si alloy production by finding the best conditions.
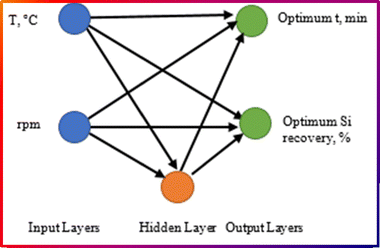 | ||
| Fig. 3 The proposed ANN via the Levenberg–Marquardt algorithm to estimate the optimum reaction time corresponding to the maximum Si recovery efficiency. | ||
3. Results and discussion
3.1. Characterization of the produced alloys
The XRD pattern of the Al–Si alloys fabricated by reducing Na2SiF6 using molten aluminium was as in Fig. 4. It shows that two phases of α Al and an Al3.21Si0.47 intermetallic compound are identified. Calculating the elemental ratios of aluminium and silicon in the Al3.21Si0.47 compound shows that it contains about 87.3% Al and 12.7% Si, which is too close to the eutectic composition.Fig. 5 represents a SEM with an EDS mapping technique for the produced Al–Si alloys containing 7.6% Si. Image (a) shows the microstructure of the alloy sample indicating an α Al-kidney shape (white areas) surrounded by uniform fine fibrous eutectic Si (dark gray portions). It shows the contrast between the two main phases in the alloy: aluminum and silicon. Image (b) – lower left in red color, SEM mapping shows the distribution of the aluminum atoms (Al-K) in the image. Aluminum is concentrated in the areas that form the main matrix of the alloy. The red color indicates the locations with a high percentage of aluminum.
Image (c) (green). A map of the distribution of the silicon element (Si-KA) in the sample. Note that silicon is concentrated in the dark regions in image (a), which are the silicon-rich regions. This structure is typical of Al–Si alloys, where silicon appears as neddle like clusters within the matrix. The image highlights the eutectic structure, which consists of an aluminum matrix with silicon particles distributed within it. The distribution of aluminum and silicon in the images shows the interaction between them during the solidification process, where silicon crystallizes in the areas between the primary aluminum phase. The modification in the silicon phase is due to Na2SiF6 found in the reaction bath. Sodium (Na) from Na2SiF6 acts as a modifier, altering the morphology of the eutectic Si from acicular (needle-like) to fine fibrous.23–25
3.2. The parameters affecting the production of Al–Si using Na2SiF6
The effect of the different factors on silicon recovery efficiency of the produced Al–Si alloys from reduction of sodium fluosilicate (Na2SiF6), like time, temperature and stirring speeds.Table 1 reflects the experimental work for finding the relationship between silicon recovery efficiency and reaction time (5 to 30 min) at temperatures ranging from 800 °C to 1000 °C, with different stirring speeds (200, 400, and 600 rpm).
| Time, min | Stirring speed, rpm | Silicon recovery efficiency | ||||
|---|---|---|---|---|---|---|
| 800 °C | 850 °C | 900 °C | 950 °C | 1000 °C | ||
| 5 | 48.27 | 51.79 | 56.09 | 63.14 | 64.74 | |
| 10 | 51.35 | 58.01 | 61.86 | 65.38 | 67.95 | |
| 15 | 200 | 53.40 | 61.73 | 64.87 | 67.63 | 71.79 |
| 20 | 57.12 | 66.99 | 72.82 | 73.14 | 76.28 | |
| 25 | 60.58 | 71.47 | 76.41 | 78.01 | 80.77 | |
| 30 | 58.33 | 67.31 | 73.08 | 73.72 | 77.56 | |
| 5 | 57.82 | 61.41 | 65.38 | 67.31 | 67.63 | |
| 10 | 60.90 | 66.99 | 70.51 | 72.44 | 73.85 | |
| 15 | 400 | 63.46 | 71.47 | 75.32 | 76.73 | 77.37 |
| 20 | 67.31 | 75.96 | 81.79 | 82.56 | 84.10 | |
| 25 | 70.19 | 80.45 | 86.22 | 87.50 | 88.46 | |
| 30 | 67.95 | 76.28 | 82.69 | 89.23 | 85.26 | |
| 5 | 67.95 | 70.96 | 76.28 | 78.53 | 80.77 | |
| 10 | 70.26 | 75.96 | 79.49 | 80.13 | 81.22 | |
| 15 | 600 | 71.35 | 80.06 | 82.12 | 82.76 | 83.40 |
| 20 | 76.03 | 84.10 | 86.54 | 87.69 | 88.40 | |
| 25 | 79.74 | 87.50 | 89.17 | 89.36 | 89.62 | |
| 30 | 76.28 | 84.29 | 87.18 | 87.82 | 89.10 | |
3.3. Prediction of the Si recovery efficiency using an artificial neural network model
The silicon (Si) recovery efficiency is modeled as a response-dependent function of the processing parameters for Al–Si alloys produced via Na2SiF6 reduction, utilizing a trainable cascade-forward back-propagation network, as illustrated in Fig. 2. The model was trained to minimize errors by incorporating reaction time, temperature, and stirring speed as key inputs. The training phase is critical to the model's success. Among the commonly used training techniques, back-propagation and quick propagation methods are the most prominent. The input matrix of processing parameters, the actual Si recovery efficiency, and the predicted values derived from the constructed ANN model are presented in Table 2.| Time (min.) | Stirring (rpm) | Si recov. eff.% | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 800 °C | 850 °C | 900 °C | 950 °C | 1000 °C | |||||||
| Actual | Predict | Actual | Predict | Actual | Predict | Actual | Predict | Actual | Predict | ||
| 5 | 67.95 | 66.56 | 70.96 | 71.02 | 76.28 | 74.85 | 78.53 | 77.72 | 80.77 | 79.32 | |
| 10 | 70.26 | 70.86 | 75.96 | 75.68 | 79.49 | 79.08 | 80.13 | 80.86 | 81.22 | 80.91 | |
| 15 | 600 | 71.35 | 73.13 | 80.06 | 78.82 | 82.12 | 82.40 | 82.76 | 83.87 | 83.40 | 83.26 |
| 20 | 76.03 | 77.24 | 84.10 | 83.64 | 86.54 | 87.41 | 87.69 | 88.69 | 88.40 | 87.69 | |
| 25 | 79.74 | 80.27 | 87.50 | 86.95 | 89.17 | 90.78 | 89.36 | 91.99 | 89.62 | 90.85 | |
| 30 | 76.28 | 76.83 | 84.29 | 83.80 | 87.18 | 88.02 | 87.82 | 89.70 | 89.10 | 89.06 | |
| MSE (%) | 1.258 | 0.395 | 1.056 | 2.311 | 0.702 | ||||||
Fig. 6 presents the relationship between temperature (°C) and silicon (Si) recovery efficiency (%) for different stirring speeds (200, 400, and 600 rpm). The curves display both predicted and actual values, allowing the evaluation of the model's accuracy. From this figure, the Si recovery efficiency increases as temperature increase across all stirring speeds, and this trend is expected since higher temperatures enhance the reaction kinetics between Na2SiF6 and molten aluminum, leading to better silicon recovery. Also, higher rpm values (600, 400) result in higher Si recovery efficiency compared to lower rpm (200). Faster stirring improves mass transfer, ensuring better mixing of Na2SiF6 in the molten aluminum, leading to more effective silicon extraction. The predicted values closely follow the actual data, validating the accuracy of the artificial neural network (ANN) model. It can be concluded that higher temperatures (closer to 1000 °C) and faster stirring (600 rpm) result in the best silicon recovery efficiency. The ANN model effectively predicts the experimental results with minimal errors. The statistic mean square error (MSE) is used to evaluate and validate the performance of the ANN as it computes the difference between the measured data and the expected data from the ANN model.19,22 The MSEs for 600 rpm stirring speed are 1.258, 0.395, 1.056, 2.311, and 0.702 for 800, 850, 900, 950, and 1000 °C, respectively, signifying the excellent performance of the developed ANN model, Fig. 2. The use of the ANN-LMA model provided a predictive framework that was closely aligned with the actual experimental outcomes, demonstrating its reliability and effectiveness.
3.4. Deriving the optimum reaction time yielding the maximum Si recovery efficiency
The developed ANN-LMA algorithm, discussed above and shown in Fig. 3, is used to mine the optimum compromised processing parameters, yielding the maximum recovery efficiency of Si for the Al–Si alloys produced by Na2SiF6. The cascade-forward back-propagation ANN is trained to maximize the Si recovery and the corresponding processing parameters are generated using the Levenberg–Marquardt algorithm.Fig. 7a–c clarifies the effects of processing parameters (i.e., reaction time, temperature, and stirrer speeds) on Si recovery efficiency estimated from ANN-LMA. Fig. 7a shows the effect of temperature on the Si recovery efficiency with reaction time and at a stirring speed of 200 rpm. It clarifies that the higher the temperature, higher silicon recoveries are achieved at lower periods. Any slight change in reaction time corresponds to a significant increase in the percentage of silicon recovery in the alloy at higher temperatures. With the temperature going up from 800 to 1000 °C, the silicon recovery efficiency increased from 61.23 to 81.04, from 71.04 to 86.41, and from 80.31 to 91.49% for stirring speeds 200, 400, and 600 rpm, respectively. Meanwhile, the optimum reaction time changes from 25.83 to 26.22, from 25.64 to 26.03, and 25.68 to 25.84 minutes for stirring speeds of 200, 400, and 600 rpm, respectively, with the temperature increase from 800 to 1000 °C considered insignificant. Increasing the stirring speed decreases the reaction time required to achieve maximum Si recovery efficiency as at 200, 400, and 600 rpm and a temperature of 950 °C, the silicon recovery efficiencies were 80.05, 86.28, and 92.14%, at times of 26.15, 26, and 25.86, respectively. So, the processing parameter combination that yields maximum efficiency of Si recovery (92.14%) was a reaction time of 25.86 minutes, a temperature of 950 °C, and a stirring speed of 600 rpm.
 | ||
| Fig. 7 Prediction of the minimum reaction time and the corresponding optimal value of Si recovery efficiency % at different temperatures at stirring speed: (a) 200 rpm, (b) 400 rpm and (c) 600 rpm. | ||
It can be concluded that the data analysis using an artificial neural network (ANN-LMA) model shows that achieving the highest silicon recovery efficiency depends mainly on temperature, reaction time, and stirring speed. The results indicate that when the temperature increases from 800 to 1000 °C, the silicon recovery rate increases significantly across all stirring speeds. However, the greatest effect is achieved at higher stirring speeds, as this helps reduce the reaction time required to reach the maximum efficiency.
Based on these results, it can be said that improving the efficiency of silicon recovery requires a balance between temperature, stirring speed, and reaction time, where the optimum conditions (950 °C, 25.86 min, 600 rpm) provide the maximum recovery rate of silicon while minimizing losses and undesirable reactions.29 The findings support the ANN-LMA model as a reliable tool for optimizing Al–Si alloy production. Overall, the study effectively addresses its research objectives while identifying areas for refinement, offering a strong foundation for further advancements in silicon recovery optimization.
4. Conclusions
The current study successfully applied the cascade-forward back-propagation ANN integrated with the Levenberg–Marquardt algorithm (LMA) to analyze the results of the experiments conducted on producing Al–Si alloys using Na2SiF6 at different process variables. The process variables selected are reaction time, temperature, and stirring speeds, with silicone recovery as the response optimization parameter. Numerous concluding remarks are drawn and summarized in the following bullets.(1) The efficiency of Si recovery increases with reaction time across all temperatures, showing a clear peak stage between 23 and 28 minutes.
(2) High temperatures (950 °C to 1000 °C) consistently result in better silicon recovery. 1000 °C yields the highest recovery, but 950 °C provides a balance between cost and performance, making it a potentially more cost-effective option.
(3) At a high stirring speed, at 600 rpm, the maximum recovery efficiency is achieved, indicating that optimal mixing improves the diffusion and reaction rates between silicon and aluminum. However, excessive stirring speeds may lead to turbulence, resulting in material losses and oxidation.
(4) The ANN model with the Levenberg–Marquardt algorithm (LMA) effectively predicts the silicon recovery efficiency, with low mean squared error (MSE) values, indicating good accuracy.
(5) The optimum processing parameters to yield maximum efficiency of Si recovery (92.14%) employing the artificial neural network (ANN) utilizing the Levenberg–Marquardt algorithm (LMA-ANN) approach are a reaction time of 25.86 minutes, temperature of 950 °C, and a stirring speed of 600 rpm.
(6) This study demonstrates the potential of using Na2SiF6 in producing high-efficiency Al–Si alloys and highlights the effectiveness of ANN in optimizing metallurgical processes.
(7) Future work could focus on further refining the process parameters and exploring the scalability of this method for industrial applications.
Data availability
Data will be made available on request.Conflicts of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.Acknowledgements
This project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant no. (GPIP: 1640-135-2024). The authors, therefore, acknowledge with thanks DSR for technical and financial support.References
- J. Zhang, H. Chen, H. Yu and Y. Jin, Study on Dual Modification of Al-17%Si Alloys by Structural Heredity, Metals, 2015, 5, 1112–1126 CrossRef.
- P. M. Kalhapure and M. G. Dighe, Impact of Silicon Content on Mechanical Properties of Aluminium Alloys, Int. J. Sci. Res., 2015, 4, 38–40 Search PubMed.
- E. Fracchia, F. S. Gobber and M. Rosso, Effect of Alloying Elements on the Sr Modification of Al-–Si Cast Alloys, Metals, 2021, 11, 342, DOI:10.3390/met11020342.
- I. H. Aly, E. E. Ebrahiem, A. A. Noval and A. M. Omran, Dissolution kinetics of silicon-containing sodium fluosilicate in stirred bath of molten aluminium, Light Met. Proc. Sess. TMS Annu. Meet., Warrendale, Pennsylvania, 2002, pp. 45–49.
- G. M. A. Mahran, A. N. M. Omran and E. S. S. Abu Seif, The formation mechanism and characterization of Al-–Si master alloys from sodium fluosilicate, Medziagotyra, 2020, 26, 185–191, DOI:10.5755/j01.ms.26.2.21896.
- A. K. Jassim and A. S. Hammood, Prediction of Hardness, Yield Strength and Tensile Strength for Single Roll Melt Spinning of 5083 Al-alloy Ribbons, J. Mater. Sci. Eng., 2016, 06, 1–4 Search PubMed.
- K. Li, Q. Pan, R. Li, S. Liu, Z. Huang and X. He, Constitutive Modeling of the Hot Deformation Behavior in 6082 Aluminium Alloy, J. Mater. Eng. Perform., 2019, 28, 981–994, DOI:10.1007/s11665-019-3873-5.
- A. P. Sekhar, S. Nandy, K. Kumar Ray and D. Das, Hardness - Yield Strength Relation of Al-Mg-Si Alloys, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 338, 012011, DOI:10.1088/1757-899X/338/1/012011.
- M. Mahmoud Ali, A. N. M. Omran and M. Abd-El-Hakeem Mohamed, Prediction the correlations between hardness and tensile properties of aluminium-silicon alloys produced by various modifiers and grain refineries using regression analysis and an artificial neural network model, Eng. Sci. Technol. Int. J., 2021, 24, 105–111, DOI:10.1016/j.jestch.2020.12.010.
- P. C. Verpoort, P. MacDonald and G. J. Conduit, Materials data validation and imputation with an artificial neural network, Comput. Mater. Sci., 2018, 147, 176–185, DOI:10.1016/j.commatsci.2018.02.002.
- M. Hu, Q. Tan, R. Knibbe, S. Wang, X. Li, T. Wu, S. Jarin and M. X. Zhang, Prediction of Mechanical Properties of Wrought Aluminium Alloys Using Feature Engineering Assisted Machine Learning Approach, Metall. Mater. Trans. A, 2021, 52, 2873–2884, DOI:10.1007/s11661-021-06279-5.
- G. M. A. Mahran and A. N. M. Omran, Using a neural network model and regression analysis to predict the wear and impact energy of Al-–Si alloys modified with various modifiers and grain refiners using its hardness, Mater. Today Commun., 2023, 37, 107138, DOI:10.1016/j.mtcomm.2023.107138.
- G. M. A. Mahran and A.-N. M. Omran, Using a neural network model to evaluate the mechanical and tribological properties of vermicular cast iron based on hardness, Heliyon, 2023, 9, e21119 Search PubMed.
- L. C. Jain and L. R. Medsker, Recurrent Neural Networks Design and Applications, CRC Press, Boca Raton, 1st edn, 1999 DOI:10.1201/9781003040620.
- M. D. Buhmann, Radial Basis Functions: Theory and Implementations, Cambridge University Press, Cambridge, 2003 DOI:10.1017/CBO9780511543241.
- U. B. Basaran and M. Kurban, A New Approach for the Short-Term Load Forecasting with Autoregressive and Artificial Neural Network Models, Int. J. Comput. Intell. Res., 2007, 3, 66–71, DOI:10.5019/j.ijcir.2007.88.
- M. McBride, N. Persson, E. Reichmanis and M. A. Grover, Solving materials’ small data problem with dynamic experimental databases, Processes, 2018, 6, 79 CrossRef.
- A. M. A. Shohda, M. A. M. Ali, G. Ren, J. G. Kim and M. A. E. H. Mohamed, Application of Cascade Forward Backpropagation Neural Networks for Selecting Mining Methods, Sustainability, 2022, 14, 635 CrossRef.
- A. Dokht Shakibjoo, M. Moradzadeh, S. Z. Moussavi, A. Mohammadzadeh and L. Vandevelde, Load frequency control for multi-area power systems: A new type-2 fuzzy approach based on Levenberg–Marquardt algorithm, ISA Trans., 2022, 121, 40–52, DOI:10.1016/j.isatra.2021.03.044.
- F. A. Shah, T. Zamir, N. S. Akbar and A. Mikhaylov, Levenberg-Marquardt Design For Analysis Of Maxwell Fluid Flow Onternary Hybrid Nanoparticles Passing Over a Riga Plate Under Convective Boundary Conditions, Results Eng., 2024, 24, 103502 Search PubMed.
- N. S. Akbar, T. Zamir, J. Akram, T. Noor and T. Muhammad, Simulation of hybrid boiling nano fluid flow with convective boundary conditions through a porous stretching sheet through Levenberg Marquardt artificial neural networks approach, Int. J. Heat Mass Transfer, 2024, 228, 125615 CrossRef CAS.
- M. Khalefa, Use of artificial neural network for prediction of mechanical properties of Al-–Si alloys synthesized by stir casting, J. Pet. Min. Eng., 2019, 21, 97–103, DOI:10.21608/jpme.2019.13857.1004.
- J. Campbell, Castings, Butterworth-Heinemann, 2003 Search PubMed.
- T. Wang, et al., High-Temperature Kinetics of Silicon Incorporation in Al-–Si Alloys, J. Mater. Sci. Technol., 2021, 78, 99–106 Search PubMed.
- Y. Liu and L. Zhang, Diffusion-Controlled Growth of Silicon Phases in Al-–Si Alloys, Mater. Lett., 2020, 263, 127381 Search PubMed.
- J. Zhang, et al., Effect of Stirring on Homogenization of Aluminum Alloys, Materialia, 2019, 8, 100636 Search PubMed.
- Y. Liu, et al., Influence of Stirring Speed on Alloy Homogeneity, Mater. Lett., 2020, 275, 127625 Search PubMed.
- M. Makhlouf and J. Li, Mass Transfer in Al-–Si Melts, J. Mater. Sci. Technol., 2022, 78, 99–106 Search PubMed.
- H. Sun, et al., ANN-Based Optimization of Metallurgical Processes, J. Mater. Sci. Technol., 2021, 78, 10–19 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |