GSAG:Ce scintillator: material optimization and intrinsic bottlenecks

Abstract

Several Sc-admixed garnet single crystals of the general composition (Gd,Sc)₃(Sc,Al)₅O₁₂:Ce and the well-established Gd₃Ga_2.7Al_2.3O₁₂:Ce (GGAG:Ce) one were grown using the micropulling down method. Their optical, luminescence and scintillation characteristics were measured and mutually compared to further optimize the former compositions and reveal the reason for their lower scintillation performance with respect to GGAG:Ce. Correlated experiments of time-resolved luminescence and scintillation spectroscopies further completed by thermoluminescence glow curve measurement and electron paramagnetic resonance (performed on Gd-free Sc-admixed garnets) indicate that Sc³⁺ is situated at the dodecahedral site of the garnet lattice as a dominant electron trap, creating a bottleneck in the scintillation mechanism of Sc-admixed garnets. This is mainly responsible for the degradation of scintillation efficiency in comparison with GGAG:Ce despite nearly the same effects of Sc and Ga in lowering the conduction band edge in these multicomponent garnets. Calculations of the electronic band structure confirm that the 3d energy levels of Sc³⁺ at the dodecahedral site are situated in the forbidden gap in Sc-admixed garnets.

---

1. Introduction

Single-crystal multicomponent garnet scintillators of the general formula (Gd,Y,Lu)₃(Al,Ga)₅O₁₂:Ce were introduced in 2011,^1,2 and Czochralski-grown crystals with the composition Gd₃Ga_xAl_5−xO₁₂:Ce (x = 2.0–3.0), abbreviated as GGAG:Ce, reached the highest light yield of 58 000 ph MeV⁻¹ (x = 2.7) or best energy resolution of 4.2%@662 keV (x = 2.4).³ Luminescence and scintillation mechanisms, charge traps and different technological preparations have been studied in many laboratories worldwide.^4–16 In analogy to simple YAG:Ce and LuAG:Ce garnets, in GGAG:Ce, Mg²⁺ and Ca²⁺ codoping was used to accelerate the scintillation response owing to the stabilization of Ce⁴⁺ at the expense of reduction of light yield.^17–20 Despite such extended experimental efforts, electronic band structure calculations were absent for a long time and the first report appeared very recently,²¹ confirming that the down energy shift of the conduction band (CB) edge is mainly due to the Ga energy levels.

Despite its excellent scintillation performance, a GGAG-based single-crystal scintillator poses a problem from the viewpoint of production economy. Large crystals can be grown only using the Czochralski technique with a very expensive iridium crucible. This is because the presence of gallium excludes the use of a reduction atmosphere and cheaper molybdenum or tungsten crucibles.^22,23 Thus, an alternative chemical composition was searched that provides a similar down energy shift of the CB bottom edge while enabling the use of cheaper crucibles. One such alternative could be Sc-admixed garnet, for which electronic band structure calculations have shown a substantial down energy shift of the CB bottom;²⁴ moreover, it has been shown that the addition of an admixture of Sc into GGAG:Ce slightly decreases the ionization barrier for Ce³⁺ 5d₁ state quenching.²⁵ Kaurova et al.²⁶ determined that the crystal growth via the Czochralski technique from the initial melt composition of Gd₃Sc₂Al₃O₁₂ results in a crystal composition of {Gd_2.69Sc_0.31}{Sc_1.93Gd_0.07}Al₃O₁₂, i.e., with pronounced occupation of the dodecahedral site by Sc and a minor occupation of the octahedral site by the Gd cation. The congruent composition for melt growth was determined to be Gd_2.88Sc_1.89Al_3.23O₁₂. Recently, the micropulling down (μ-PD) method was employed to prepare crystals of the Ce-doped congruent melting composition of Gd_2.88Sc_1.89Al_3.23O₁₂,²⁷ and the Bridgman method was used to prepare crystals of the congruent and stoichiometric melt compositions,²⁸ both from a molybdenum crucible under a reduction atmosphere. Their scintillation characteristics were reported to reach a maximum light yield of about 10 000 ph MeV⁻¹, which is about four times lower than that of μ-PD down grown crystals of GGAG:Ce in ref. 1. Very recently, a substantial light yield increase of up to 15 000 ph MeV⁻¹ was achieved in Gd₃Sc₂Al₃O₁₂:Ce (GSAG:Ce) crystals grown from a stoichiometric melt composition using the μ-PD method.²⁹

This paper aims to search for further optimization of the scintillation characteristics of Gd-rich near-stoichiometric melt compositions of GSAG:Ce using the μ-PD crystal preparation method. By combining several optical and electron paramagnetic resonance (EPR) spectroscopies, we search for an explanation for its lower performance compared to that of the GGAG:Ce crystal prepared by applying the same technology. Furthermore, we perform quantum computation of the electronic band structure of various compositions of GSAG with different Sc concentrations to support the hypothesis of trapping migrating electrons in the transport stage of the scintillation mechanism derived from the experiment.

2. Experimental and calculation methods

2.1. Experimental methods

Crystals were grown by applying the μ-PD method; see the details in ref. 27 and 29 with radiofrequency inductive heating. The growth was performed using an Ir crucible with a die of 3 mm in diameter and a nozzle diameter of 0.5 mm under N₂(4N) + 1% O₂ atmosphere for the Gd₃Ga_2.7Al_2.3O₁₂:Ce crystal. The crucible was placed on an Ir afterheater with windows and an alumina pedestal. The hot zone around the crucible consisted of 3 layers of alumina shielding for thermal insulation. Other crystals were grown with a Mo crucible under an Ar + 5% H₂ reducing atmosphere to further verify a more economical method of crystal growth from the melt.^27–29 The gas flow was always kept at 0.5 L min⁻¹. The pulling speed was 0.3 mm min⁻¹. From crystal rods (see Fig. 1), plates of about 1 mm thick were cut and polished. Their chemical analysis was performed using the electron microanalyzer Jeol JX-8230 with energy-dispersive spectrometer Bruker QUANTAX 200 and using Esprit 2.2 software.

Fig. 1 Photographs of some of the grown crystals: (a) Gd₃Sc₂ as grown; (b) Gd₃Sc₂ air-annealed (1200 °C/12 h); (c) Gd₃Ga_2.7 as grown; and (d) Y₃Sc₂Al₃O₁₂ as grown.

Measurement of absorption spectra within 200–800 nm was performed by applying the UV/VIS/NIR spectrometer, Shimadzu 3101PC. The photoluminescence (PL) excitation (PLE) and emission spectra and PL decay curves were measured using custom-made spectrofluorometer 5000 M (Horiba Jobin Yvon) with excitation sources: (i) steady-state laser-driven xenon lamp (PL and PLE spectra, Energetiq EQ-99X LDLS–A Hamamatsu company) and (ii) nanosecond nanoLED pulsed light sources (IBH Scotland, fast PL decays). The detection part of 5000 M consists of a single-grating monochromator and photon counting detector TBX04 (IBH Scotland). The measured spectra were corrected for the spectral dependence of excitation energy (PLE) and the spectral dependence of detection sensitivity (PL). A convolution procedure was applied to the decay curves to determine true decay times using the SpectraSolve software package (Ames Photonics).

Radioluminescence (RL) spectra and afterglow were measured on 5000 M using an X-ray tube with a Mo anode (40 kV, 15 mA, Seifert GmbH) as an excitation source. Thermoluminescence (TSL) glow curves were measured at 5000 M in the range of 77–500 K using a Janis cryostat with a heating rate of 0. 1 K s⁻¹ after excitation by applying the X-ray tube at 77 K. The scintillation light yield measurements were performed on the sample wrapped in reflective PTFE tape and optically coupled with silicon grease to a hybrid photomultiplier (HPMT) Photonis PP0475B with a built-in preamplifier. The excitation gamma source, radioisotope ¹³⁷Cs (662 keV) and the amplifier shaping time of 1 μs were used in the measurement of pulse-height spectra. Scintillation decay curves were measured using the same ¹³⁷Cs (662 keV) excitation and the Hamamatsu PMT U7600 and digital oscilloscope TDS3052 in the detection part. The convolution procedure was used similarly to that used for the PL decay evaluation.

The EPR spectra were measured using a commercial Bruker EMX plus spectrometer operating at the X-band (microwave frequency 9.25–9.5 GHz) within the temperature range of 10–290 K.

2.2. Electronic band structure calculations

They were performed using MedeA software³⁰ with the implemented program VASP for electronic structure calculations. All calculations were based on the density functional theory (DFT) using the generalized gradient approximation (GGA)³¹ and the projector augmented wave (PAW)³² method. Specific pseudopotentials were set, Gd for Gd³⁺ and Sc_sv for Sc³⁺, as recommended by MedeA. In the self-consistent field method, the tetrahedron method with Blöchl corrections was used as the integration scheme over the first Brillouin zone. A typical k-mesh density of 0.25 Å⁻³ was applied. Owing to the strong correlation, we used LSDA + U with U = 7 eV for Gd-4f.³³ The calculation was spin-polarized magnetic with a default planewave cutoff energy of 400 eV. As the initial atomic structure of Gd₃Al₅O₁₂, we used a file from the ICSD database with a collection code of 23849.³⁴ All other initial Sc-doped garnet structures were created by lowering symmetry from Ia-3d to Pcca and changing the relevant atomic sites to Sc so that the dopant was evenly distributed. In some cases, multiple configurations with the same Sc concentration were calculated, and only the structure with the lowest energy was used afterwards. Structural optimization was performed with the conjugate gradient update algorithm with a convergence of 0.03 eV Å⁻¹. We optimized all atomic sites and lattice parameters so that the Pcca symmetry and lattice parameters were retained. All optimizations converged after circa 15 iterations because the initial system was very close to the optimized state. For the optimized structures, we calculated the density of states, where only the tetrahedron method was applied.

3. Results and discussion

3.1. Crystal growth

Using micropulling down technology, the crystals with initial melt composition of Gd₃Sc₂Al₃O₁₂:Ce0.3 at% (further denoted as Gd₃Sc₂), Gd_3.03Sc₂Al3O₁₂:Ce0.3 at% (further denoted as Gd_3.03Sc₂) and Gd_3.09Sc₂Al₃O₁₂:Ce0.3 at% (further denoted as Gd_3.09Sc₂) were grown using a molybdenum crucible and Ar + H₂ reduction atmosphere. For comparison purposes, we grew Gd₃Ga_2.7Al_2.3O₁₂:Ce0.3 at% crystal (further denoted as Gd₃Ga_2.7) using the same technology but with an Ir crucible and N₂ + 1% O₂ atmosphere. Photographs of selected crystals are illustrated in Fig. 1, and the composition measured at the sample plates is in Table 1. Crystals grown from molybdenum crucible were annealed at 1200 °C/12 h in the air to remove their dark color due to unspecified color centres (see Fig. 1). To enable EPR measurements requiring Gd-free compositions, we grew isostructural Gd-free crystals with melt compositions of Y₃Sc₂Al₃O₁₂ and Y_2.89Sc_1.16Al_3.95O₁₂, see also Fig. 1. The Gd-free crystals showed cracks in the initial part owing to a non-optimized temperature profile beneath the crucible in the crystal growth process.

Table 1 Composition of each oxide component is provided in formula units. Samples were annealed at 1200 °C/12 h in air

Sample	Gd2O3	Sc2O3	Al2O3	Ce2O3
Gd3Sc2	3.001	1.987	3.002	0.010
Gd3.03Sc2	3.032	2.007	2.953	0.008
Gd3.09Sc2	3.073	2.076	2.843	0.008
Gd3Ga2.7	3.050	2.700 (Ga2O3)	2.200	0.008

---

3.2. Absorption spectra

As depicted in Fig. 2, the absorption spectra of Gd₃Sc₂ and Gd₃Ga_2.7 samples are shown. Different relative amplitudes of 4f–5d₁ (440–450 nm), 4f–5d₂ (340 nm) and 4f–5d_3,4,5 (220–240 nm) are noticed when both samples are compared, while their positions are almost the same. Long wavelength shift of 4f–5d₁ absorption band by about 8 nm in Gd₃Sc₂ indicates a slightly enhanced crystal field at the dodecahedral site when the Ga cation is changed to the Sc one. As expected, the positions and amplitudes of the Gd³⁺ 4f–4f transitions at 275 nm and 305–312 nm are the same in both samples. Most importantly, the position of the host band edge onset around 210–215 nm is almost the same in both samples, which evidences very similar positioning of the conduction band bottom edge.

Fig. 2 Absorption spectra of Gd₃Sc₂ and Gd₃Ga_2.7 samples annealed at 1200 °C for 12 hours in air.

The absorption spectra of the Gd_3.03Sc₂ and Gd_3.09Sc₂ samples in Fig. S1 (ESI†) are closely similar to that of Gd₃Sc₂ in Fig. 2.

3.3. Radioluminescence spectra

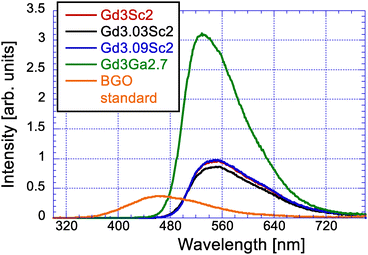
The RL spectra maxima of the Gd₃Sc₂, Gd_3.03Sc₂ and Gd_3.09Sc₂ samples (cca 550 nm) have long wavelength shifted with respect to the Gd₃Ga_2.7 one (530 nm), as illustrated in Fig. 3, which is consistent with the 4f–5d₁ band shift in the absorption spectra depicted in Fig. 2. The RL amplitudes of the Gd₃Sc₂, Gd_3.03Sc₂ and Gd_3.09Sc₂ samples are similar, about 2.5 times that of BGO, while that of Gd₃Ga_2.7 is much higher, about 8.3 times that of BGO, which indicates a much higher scintillation efficiency of the Gd₃Ga_2.7 sample.

Fig. 3 RL spectra of the sample set in absolute comparison with the BGO standard scintillator.

3.4. Scintillation decays and afterglow

The scintillation decay of the Gd₃Sc₂ sample in Fig. 4 shows an even faster dominant decay component with a decay time of 90.1 ns 90.1 ns compared to the 111 ns of the Gd₃Ga_2.7, but its timing performance measured by the 1/e decay time (DT) is degraded by the presence of an intense rise component with a rise time of 70.6 ns. Even longer 1/e DT's is obtained for Gd_3.03Sc₂ (274 ns) and Gd_3.09Sc₂ (266 ns) samples (see Fig. S2a and b (ESI†) and Table 2). Such intensely rising components were also evidenced in GSAG:Ce crystals prepared by applying the Bridgman method.²⁸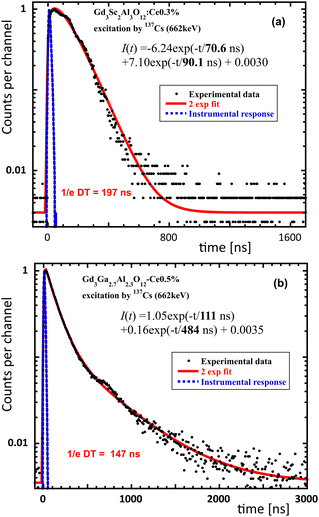

Fig. 4 Scintillation decays of (a) Gd₃Sc₂ and (b) Gd₃Ga_2.7, spectrally unresolved. The red line is the convolution of the instrumental response and function I(t) in the figure.

Table 2 Summary of LY values and 1/e decay times for the sample set and the BGO standard sample. Excitation by ¹³⁷Cs (662 keV) and a shaping time of 1 μs. The errors of the LY and 1/e decay time values are within 5% and 1%, respectively

Sample	LY (ph MeV^−1) annealed 1200 °C	LY (ph MeV^−1) annealed 1200 & 1500 °C	1/e decay time (ns)
Gd3Sc2	15 080	16 810	197
Gd3.03Sc2	15 060	17 320	274
Gd3.09Sc2	14 030	15 360	266
Gd3Ga2.7	42 760	n/a	147
BGO standard	7850 (no annealing)	n/a	n/a

---

The afterglow of all the samples in Fig. 5 is very competitive, within 0.02–0.03% at 10 ms after the X-ray cut-off, and that of the BGO standard is about 0.01%.

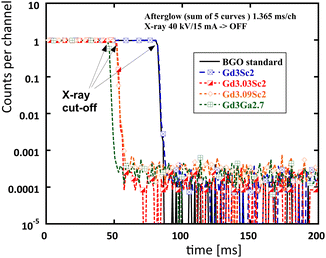Fig. 5 Afterglow of all samples and the BGO standard. Curves are horizontally shifted for clarity, and the X-ray cut-off is indicated.

3.5. Photoluminescence decays

To determine the influence of the deteriorating processes of any kind acting at the excited state of the Ce³⁺ luminescence center at room temperature, PL decays are the best probe. As illustrated in Fig. 6, the PL decays of Gd₃Sc₂ and Gd₃Ga_2.7 are shown for direct comparison. The PL decays of Gd_3.03Sc₂ and Gd_3.09Sc₂ are very similar to that of Gd₃Sc₂, as shown in Fig. S3a and b (ESI†).

Fig. 6 PL decays at RT of (a) Gd₃Sc₂ and (b) Gd₃Ga_2.7 samples. Exc = 452 nm, Em = 550 nm (a) and 530 nm (b). The red solid line is the convolution of the instrumental response and the function I(t) in the figure.

Considering the low temperature lifetimes of the 530 nm band in GGAG:Ce¹ and the 550 nm band in GSAG:Ce²⁷ around 55–60 ns and 65 ns, respectively, and the significantly faster decay of the Gd₃Sc₂ sample depicted in Fig. 6b, it can be concluded that the Ce³⁺ center in Gd₃Sc₂ is significantly quenched compared to the Gd₃Ga_2.7 host. The PLQY at RT, estimated from the mentioned decay times in the Gd₃Sc₂ sample, is about 49/65 = 0.75. The quenching process is due to the 5d₁ excited state ionization.^1,27 However, the difference in the range of a few tens of percent cannot explain the huge difference in scintillation efficiency derived from the RL spectra depicted in Fig. 3. It is also worth noting that the PL decays are faster compared to the scintillation ones in Fig. 4 and Fig. S2a and b (ESI†), indicating additional delay/slowdown in the transfer stage of the scintillation mechanism.

3.6. Scintillation light yield

Scintillation light yield (LY) was measured with a 1 μs shaping time so that only fast enough scintillation light generated within this time window is registered here. As illustrated in Table 2, the values are summarized in ph MeV⁻¹ units. Furthermore, the 2nd annealing in the air at 1500 °C/12 h was applied, which has shown a clear positive effect on all the Gd₃Sc₂, Gd_3.03Sc₂ and Gd_3.09Sc₂ samples. We applied yet another 3rd annealing at 1550 °C/12 h, which did not show any effect.

From all the data presented in Section 3.2–3.6, it can be observed that despite the similar decrease in CB bottom edge due to the Ga or Sc admixture in the garnet composition, which should deactivate some parts of the electron traps, the scintillation efficiency and the light yield are considerably lower in all the Sc-containing garnets compared to Gd₃Ga_2.7 prepared by applying the same μ-PD method. Somewhat more severe quenching observed in PL decays of Sc-containing garnets cannot explain such a huge difference, so the reason must involve a different mechanism of charge capture and nonradiative recombination processes in materials with Sc or Ga cations. This is discussed in Section 3.7.

3.7. Electron traps in Sc-containing garnets

In the Ce³⁺-doped scintillators, most holes generated in the conversion stage of the scintillation mechanism are immediately and effectively captured by the Ce³⁺ ions owing to their high concentration and high ability for hole capture, becoming temporarily Ce⁴⁺. The electrons, however, can be captured during the transfer stage of the scintillation mechanism at various electron traps, which delays their transport towards temporary Ce⁴⁺ to radiatively recombine here and yield scintillation photons. Thus, the study of electron traps in Ce-doped scintillation materials is of the utmost importance in revealing eventual bottlenecks and the limits of their performance.³⁵

For the study of charge carrier capture in the lattice, the TSL and EPR experiments can be effectively correlated to reveal the acting traps and understand their nature. In Gd-based compounds, however, EPR cannot be used as a superstrong EPR signal from paramagnetic Gd³⁺ obscures signals from any other centers. Moreover, spins from any defect are exchange-coupled to Gd³⁺ spins, creating a very non-informative broad EPR signal. Thus, we prepared structurally equivalent Y₃Sc₂Al₃O₁₂ and Y_2.89Sc_1.16Al_3.95O₁₂ single crystals for the EPR study of electron traps.

3.7.1. Thermally stimulated luminescence measurement. The TSL glow curves depicted in Fig. 7 were corrected for quantum efficiency of the Ce³⁺ emission center using the temperature dependence of the integral of PL spectra; see Fig. S3 and S4 (ESI†) for the Gd₃Sc₂ and Gd₃Ga_2.7 samples, respectively. The TSL pattern of the Gd₃Sc₂ and Gd_3.03Sc₂ samples in Fig. 7 is very similar to that of the peak positions and shows a rich structure with intense glow peaks towards the highest temperatures, indicating the presence of deep electron traps in the material. The Gd₃Ga_2.7 sample shows the dominant peak at a lower temperature compared with the other two samples, and above room temperature, there is a nearly negligible TSL signal, which is consistent with the difference in LY values, as the deepest traps are usually responsible for LY loss in scintillation materials.³⁶ The lowest TSL signal in the range of 250–350 K illustrated in Fig. 7 in the Gd₃Sc₂ and Gd_3.03Sc₂ samples correlates with a lower intensity of afterglow in Fig. 5 within tens of ms after the X-ray cut-off compared with the Gd₃Ga_2.7 sample, which shows higher TSL intensity in this region and a somewhat higher level of afterglow as well.

Fig. 7 TSL glow curves of selected samples corrected for the temperature dependence of PL spectra.

3.7.2. Optical and EPR spectroscopy of Y₃Sc₂Al₃O₁₂ and Y_2.89Sc_1.16Al_3.95O₁₂ crystals. In the absorption spectrum of the as-grown sample shown in Fig. 8, there is a broad absorption band in the range of 600–900 nm, which is identical with the band observed in the undoped GSAG crystal ascribed to Sc²⁺ (or complex defect containing Sc²⁺). It is destroyed after annealing at 1200 °C/3 h in the air accompanied by an increase in absorption below 400 nm, which could be due to unidentified hole centers.³⁷

Fig. 8 Absorption spectra of Y₃Sc₂Al₃O₁₂ as grown and annealed in air at 1200 °C/12 h.

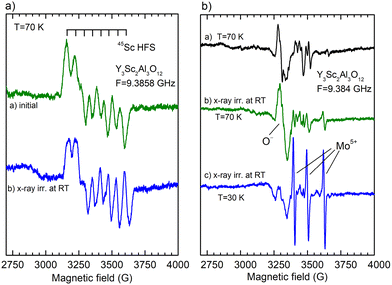
The EPR experiment confirmed the presence of defects containing Sc²⁺ ions in the as-grown crystal (Fig. 9, panel a). The spectrum in the as-grown sample is nearly isotropic (it is almost the same in the crystal and in the ground crystal) and is described by a g-factor of 1.980. It also shows a well-resolved hyperfine (HF) structure with eight equidistant lines that clearly originate from the ⁴⁵Sc isotope (nuclear spin I = 7/2, natural abundance = 100%, and hyperfine splitting A = 54 × 10⁻⁴ cm⁻¹). Annealing the crystal in the air leads to the disappearance of the Sc²⁺ spectrum (Fig. 9, panel b). These facts indicate that the center is of an F⁺-type (an electron trapped at an oxygen vacancy), as observed previously in YAG³⁸ and LuAG crystals.³⁹ In contrast to the F⁺ center in YAG or LuAG, an electron in the Y₂Sc₂Al₃O₁₂ is trapped at an oxygen vacancy in the vicinity of the Sc ion, as the electron density is markedly localized at the Sc ion (it follows from the observed hyperfine interaction with the ⁴⁵Sc nuclear spin). The center can thus be designed for the Sc²⁺-V_O center. All these experimental facts suggest that the coloration of the as-grown Y₃Sc₂Al₃O₁₂ crystal is surely related to the presence of Sc²⁺-V_O centers, which is consistent with the conclusion made in ref. 37 for the undoped GSAG crystal.

Fig. 9 Panel (a): EPR spectra in the Y₃Sc₂Al₃O₁₂ as-grown crystal; panel (b): EPR spectra in the Y₃Sc₂Al₃O₁₂ crystal annealed in air. Panel (a) presents EPR spectra measured in the crystal before X-ray irradiation (a) and in the crystal after X-ray irradiation at room temperature (b). The as-grown crystal shows an HF structure from the ⁴⁵Sc isotope (eight equidistant lines). Panel (b) presents EPR spectra measured in the crystal annealed in the air before X-ray irradiation (a) and after X-ray irradiation (b and c). In the annealed crystal, the spectrum with the ⁴⁵Sc HF structure is absent. Instead, the spectra of the O⁻ center and Mo⁵⁺ ions appear.

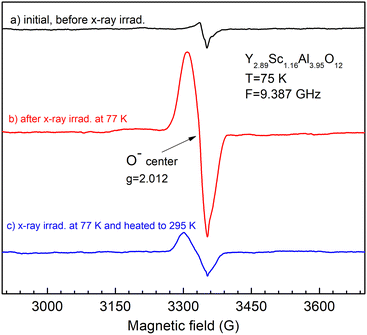
X-ray irradiation of the as-grown crystal does not create any additional EPR-active defects (Fig. 9, panel a, spectrum b). In contrast, the X-ray irradiation of air-annealed crystal creates O⁻ paramagnetic centers (Fig. 9, panel b, spectrum b). This is the most common defect created by X-ray or γ-ray irradiation in garnet crystals.³⁸ The O⁻ EPR spectrum is unusually strong in intensity in the Y_2.89Sc_1.16Al_3.95O₁₂ melt composition (Fig. 10), suggesting that O⁻ centers can be created in the vicinity of Sc ions at antisite position by trapping a hole by an oxygen lattice ion (such Sc ion makes strong perturbation for host oxygen ion, thus increasing the thermal stability of the O⁻ center). Besides, the EPR spectrum of Mo⁵⁺ ions appears as well (Fig. 9, panel b, spectrum c). The Mo ions come from the Mo crucible and, under irradiation, recharge to the Mo⁵⁺ valence state to compensate for (together with O⁻ ions) the excess negative charge in the lattice introduced by annealing in the air. Their concentration is estimated in the range of 0.1–1 at. ppm.

Fig. 10 O⁻ EPR spectrum measured in the X-ray irradiated (at 77 K) grinded Y_2.89Sc_1.16Al_3.95O₁₂ crystal. All spectra are measured at 75 K.

4. Electronic band structure calculations

Following,²⁶ we worked with the assumption that Sc can occupy only the octahedral and dodecahedral sites. We proposed and optimized superstructures with six different concentrations of evenly distributed Sc atoms on the octahedral and dodecahedral sites in Gd₃Al₅O₁₂ (GAG). With the optimized structures, we calculated the density of states and compared the energies of the bands, revealing primarily the character of the Sc valence states.

As depicted in Fig. 11 and 12, the density of states plots are presented, focusing on the valence and conduction bands. Partial DOS (PDOS) projected on the respective valence states of elements was multiplied by the number of equivalent Wyckoff positions to obtain the total PDOS per formula unit, i.e. for all equivalent atoms.

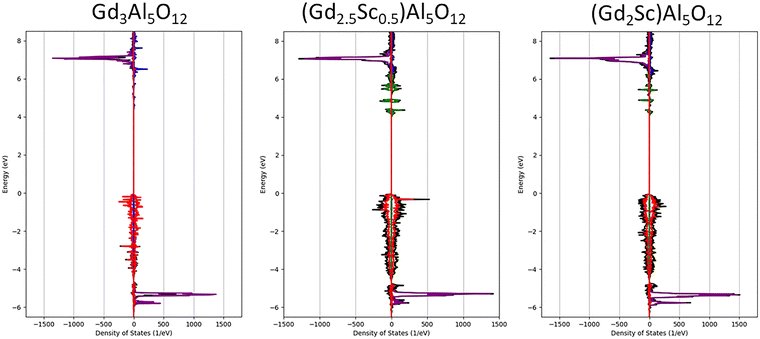Fig. 11 Density of states of structures without Sc in the octahedral site. Total DOS is black, Gd-4f is purple, Gd-5d is blue, Sc-3d on the dodecahedral site is green and O-2p is red.

Fig. 12 Density of states of structures with Sc in both the octahedral and dodecahedral sites. Total DOS is black, Gd-4f is purple, Gd-5d is blue, Sc-3d on the dodecahedral site is green, Sc-3d on the octahedral site is yellow and O-2p is red. The Gd-5d band is hidden under the Sc-3d line.

By calculating the DOS of the optimized structures of these Sc-admixed garnets, our results support the hypothesis drawn from the experiments, which demonstrates that the energies of the Sc³⁺-3d states in dodecahedral sites are located in the bandgap under the conduction band minimum, creating electron traps. The shift of the Sc-3d levels deeper into the gap is imposed by weaker covalent bonding, making the Sc-3d orbitals less antibonding due to weaker metal–ligand orbital overlap, despite a slightly stronger crystal field of the dodecahedral position with a higher coordination number.

5. Conclusions

Using micropulling down technology, single crystals of the starting melt composition Gd₃Sc₂Al₃O₁₂:Ce0.3 at%, Gd_3.03Sc₂Al₃O₁₂:Ce0.3 at%, and Gd_3.09Sc₂Al₃O₁₂:Ce0.3 at% were grown from a molybdenum crucible under a reduction atmosphere and Gd₃Ga_2.7Al_2.3O₁₂:Ce0.3 at% crystal from an Ir crucible under N₂ + 1%O₂ atmosphere. Crystal compositions were determined by applying an electron microprobe method. Annealing in the air at 1200 °C/12 h and 1500 ⁰C/12 h was applied to the former group in two steps. The optical, luminescence and scintillation characteristics were measured for all of them to compare characteristics between the Sc-admixed and Ga-admixed crystals. The highest light yield was obtained in the doubly air annealed Gd_3.03Sc₂Al₃O₁₂:Ce0.3 at% crystals, providing a value of 17 320 ph MeV⁻¹, while that of Gd₃Ga_2.7Al_2.3O₁₂:Ce0.3% was 42 760 ph MeV⁻¹. Similarly, the amplitudes of their RL spectra compared to BGO were about 2.5 and 8.3, respectively. Furthermore, the Y₃Sc₂Al₃O₁₂ and Y_2.89Sc_1.16Al_3.95O₁₂ crystals were grown similarly to the Sc-admixed Gd-based ones and used for the EPR experiment to determine the nature of the electron traps. Electronic band structure calculations were performed for several compositions of the Sc-admixed garnet structure.

The significantly lower scintillation performance of the Sc-admixed garnets compared with the well-established Gd₃Ga_2.7Al_2.3O₁₂:Ce0.3 at% multicomponent garnets is explained by the antisite Sc³⁺ ion at the dodecahedral position of Gd³⁺(Sc_Gd) in the garnet structure, which forms a deep electron trap. Electron capture at Sc³⁺ was proved by EPR, creating the Sc²⁺-V_O center in the as-grown Y₃Sc₂Al₃O₁₂ crystal, which is also responsible for absorption bands in the range of 600–900 nm. This center and its related absorption disappear after annealing in air at 1200 °C/12 h. An anomalously high concentration of O⁻ centers is revealed in Y_2.89Sc_1.16Al_3.95O₁₂ annealed in air at 1200 °C/12 h by EPR compared to Y₃Al₅O₁₂ or Lu₃Al₅O₁₂ crystals. Such centers require charge compensation in the lattice, and the Sc²⁺ is the most probable option. Intense TSL glow curves above room temperature evidence the existence of deep electron traps in the Ce-doped Sc-admixed crystals, and the electronic band structure calculations show that the Sc³⁺ at the dodecahedral position forms the energy levels within the forbidden gap below the bottom of the conduction band, which provides further support for such an explanation.

Thus, despite a similar downshift of conduction band bottom edge in the Gd₃Sc₂Al₃O₁₂ and Gd₃Ga_2.7Al_2.3O₁₂ structures, which should deactivate shallow electron traps, such a new deep electron trap in the Sc-admixed garnets, the formation of which is an intrinsic feature in the crystal grown from the melt, significantly deteriorates its scintillation performance for the overall scintillation efficiency and light yield characteristics.

Author contributions

Martin Nikl: conceptualization, data curation, investigation, validation, visualization, writing – original draft, writing – review & editing, funding acquisition, supervision. Jan Pejchal: crystal growth, writing – review & editing. Jakub Ježek and David Sedmidubský: theoretical calculations, writing – original draft, writing – review & editing. Kučerková Romana: data curation, formal analysis, investigation, visualization. Valentin Laguta: EPR experiment, data curation, formal analysis, investigation, visualization, writing – original draft writing – review & editing. Vladimir Babin: TSL experiment, data curation, formal analysis, investigation, visualization, writing – review & editing. Alena Beitlerová, Romana Kučerková: data curation, formal analysis, investigation.

Data availability

The data related to figures are available upon request from the corresponding author.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This research was supported by Czech Science Foundation project no. 21-17731S and by OP JAC financed by ESIF and MEYS (project LASCIMAT–CZ.02.01.01/00/23_020/0008525). Computational resources were provided by the e-INFRA CZ project (project ID no.: 90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic. We acknowledge the help of K. Jurek and M. Jarošová, who performed chemical analysis of the samples.

References

1. K. Kamada, T. Yanagida, T. Endo, K. Tsutumi, Y. Fujimoto, A. Fukabori, A. Yoshikawa, J. Pejchal and M. Nikl, Cryst. Growth Des., 2011, 11, 4484–4490.
2. K. Kamada, T. Yanagida, J. Pejchal, M. Nikl, T. Endo, K. Tsutumi, Y. Fujimoto, A. Fukabori and A. Yoshikawa, J. Phys. D: Appl. Phys., 2011, 44, 505104.
3. K. Kamada, S. Kurosawa, P. Prusa, M. Nikl, V. V. Kochurikhin, T. Endo, K. Tsutumi, H. Sato, Y. Yokota, K. Sugiyama and A. Yoshikawa, Opt. Mater., 2014, 36, 1942–1945.
4. O. Sidletskiy, V. Kononets, K. Lebbou, S. Neicheva, O. Voloshina, V. Bondar, V. Baumer, K. Belikov, A. Gektin and B. Grinyov, Mater. Res. Bull., 2012, 47, 3249–3252.
5. P. Dorenbos, J. Lumin., 2013, 134, 310–318.
6. J. M. Ogiegło, A. Katelnikovas, A. Zych, T. Justel, A. Meijerink and C. R. Ronda, J. Phys. Chem. A, 2013, 117, 2479–2484.
7. K. Brylew, W. Drozdowski, A. J. Wojtowicz, K. Kamada and A. Yoshikawa, J. Lumin., 2014, 154, 452–457.
8. V. Laguta, Y. Zorenko, V. Gorbenko, A. Iskaliyeva, Y. Zagorodniy, O. Sidletskiy, P. Bilski, A. Twardak and M. Nikl, J. Phys. Chem. C, 2016, 120, 24400–24408.
9. I. I. Vrubel, R. G. Polozkov, I. A. Shelykh, V. M. Khanin, P. A. Rodnyi and C. R. Ronda, Cryst. Growth Des., 2017, 17, 1863–1869.
10. C. Wang, D. Ding, Y. Wu, H. Li, X. Chen, J. Shi, Q. Wang, L. Ye and G. Ren, Appl. Phys. A, 2017, 123, 1–6.
11. M. Kitaura, H. Zen, K. Kamada, S. Kurosawa, S. Watanabe, A. Ohnishi and K. Hara, Appl. Phys. Lett., 2018, 112, 031112.
12. V. Kochurikhin, K. Kamada, K. J. Kim, M. Ivanov, L. Gushchina, Y. Shoji, M. Yoshino and A. Yoshikawa, J. Cryst. Grow., 2020, 531, 125384.
13. M. Li, M. Meng, J. Chen, Y. Sun, G. Cheng, L. Chen, S. Zhao, B. Wan, H. Feng, G. Ren and D. Ding, Phys. Status Solidi B, 2021, 258, 2000603.
14. S. Nargelas, Y. Talochka, A. Vaitkevičius, G. Dosovitskiy, O. Buzanov, A. Vasil'ev, T. Malinauskas, M. Korzhik and G. Tamulaitis, J. Lumin., 2022, 242, 118590.
15. T. Wu, et al. , Cryst. Growth Des., 2022, 22, 180–190.
16. A. Yoshikawa, V. V. Kochurikhin, M. Yoshino, R. Murakami, T. Tomida, I. Takahashi, K. Kamada, Y. Shoji, H. Sato, R. Kucerkova, A. Beitlerova and M. Nikl, Cryst. Growth Des., 2023, 23, 2048–2054.
17. Y. Wu, F. Meng, Q. Li, M. Koschan and C. L. Melcher, Phys. Rev. Appl., 2014, 2, 044009.
18. K. Kamada, M. Nikl, S. Kurosawa, A. Beitlerova, A. Nagura, Y. Shoji, J. Pejchal, Y. Ohashi, Y. Yokota and A. Yoshikawa, Opt. Mater., 2015, 41, 63–66.
19. G. Tamulatis, G. Dosovitskiy, A. Gola, M. Korjik, A. Mazzi, S. Nargelas, P. Sokolov and A. Vaitkevičius, J. Appl. Phys., 2018, 124, 215907.
20. M. Korzhik, V. Alenkov, O. Buzanov, G. Dosovitskiy, A. Fedorov, D. Kozlov, V. Mechinsky, S. Nargelas, G. Tamulaitis and A. Vaitkevičius, CrystEngComm, 2020, 22, 2502–2506.
21. F. Zajíc, V. Jarý, J. Pospíšil, P. Boháček, Z. Umar, M. Piasecki, M. G. Brik, R. Kučerková, A. Beitlerová and M. Nikl, Mater. Adv., 2024, 6, 777–787.
22. O. Sidletskiy, P. Arhipov, S. Tkachenko, Ia Gerasymov, D. Kurtsev, V. Jarý, R. Kučerková, M. Nikl, K. Lebbou and E. Auffray, Engineering of Scintillation Materials and Radiation Technologies, ISMART, in Springer Proceedings in Physics, ed. M. Korzhik, A. Gektin, 2018, vol. 227, Springer, Cham.
23. K. Kamada, et al. , J. Cryst. Grow., 2020, 535, 125510.
24. Y.-N. Xu, W. Y. Ching and B. K. Brickeen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 1817–1824.
25. D. Spassky, et al. , CrystEngComm, 2020, 22, 2621–2631.
26. I. A. Kaurova, E. N. Domoroshchina, G. M. Kuz’micheva and V. B. Rybakov, J. Cryst. Grow., 2017, 468, 452–456.
27. O. Zapadlík, J. Pejchal, R. Kučerková, A. Beitlerová and M. Nikl, Cryst. Growth Des., 2021, 21, 7139–7149.
28. K. L. Hovhannesyan, M. V. Derdzyan, G. Badalyan, G. Kharatyan, J. Pejchal, M. Nikl, C. Dujardin and A. G. Petrosyan, CrystEngComm, 2024, 26, 4812–4819.
29. O. Zapadlík, J. Pejchal, V. Babin, V. Jarý, V. Vaněček, R. Kučerková, K. Jurek, A. Beitlerová and M. Nikl, RSC Adv., 2025, 15, 2140–2151.
30. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
32. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
33. L. Dudarev, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
34. F. Euler and J. A. Bruce, Acta Crystallogr., 1965, 19, 971–978.
35. M. Nikl, V. V. Laguta and A. Vedda, Phys. Status Solidi B, 2008, 245, 1701–1722.
36. F. Moretti, G. Patton, A. Belsky, M. Fasoli, A. Vedda, M. Trevisani, M. Bettinelli and C. Dujardin, J. Phys. Chem. C, 2014, 118, 9670–9676.
37. K. L. Hovhannesyan, M. V. Derdzyan, I. A. Ghambaryan, T. I. Butaeva, C. Dujardin and A. G. Petrosyan, Phys. Status Solidi A, 2023, 220, 2300386.
38. V. Laguta, M. Buryi, P. Arhipov, O. Sidletskiy, O. Laguta, M. G. Brik and M. Nikl, Phys. Rev. B, 2020, 101, 024106.
39. V. Laguta, M. Buryi, J. Pejchal, V. Babin and M. Nikl, Phys. Rev. Appl., 2018, 10, 034058.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ma00095e

---