Open Access Article
Open Access ArticleHigh-concentration Mn4+ doping in boron-modified Ca14Zn6Al10O35 – based phosphors: decoding superior luminescence performances†
Jiquan
Huang
 *ab,
Ting
Lv
a,
Yuqing
Lin
a,
Zhonghua
Deng
a,
Zhuguang
Liu
a and
Wang
Guo
*ab,
Ting
Lv
a,
Yuqing
Lin
a,
Zhonghua
Deng
a,
Zhuguang
Liu
a and
Wang
Guo
 *ab
*ab
aKey Laboratory of Optoelectronic Materials Chemistry and Physics, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Fuzhou 350002, P. R. China. E-mail: hjq@fjirsm.ac.cn; guowang@fjirsm.ac.cn
bFujian Science & Technology Innovation Laboratory for Optoelectronic Information of China, Fuzhou 350108, P. R. China
First published on 4th March 2025
Abstract
The application prospects of Mn4+-activated oxide phosphors are hindered by their relatively weak absorption of blue light, which stems mainly from severe concentration quenching. Ca14Zn6Al10O35:Mn4+, noted for its high quantum efficiency and minimal thermal quenching, experiences concentration quenching arising from the direct energy transfer from Mn4+ ions to the adjacent crystal defects. In this study, a synergistic strategy involving B2O3 flux and B3+ doping was introduced to mitigate the crystal defects. This strategy elevates the optimal Mn4+ doping concentration effectively from 1% to 6%, thereby ensuring efficient light absorption in the UV-to-blue band and facilitating intense deep-red emission within the 650–780 nm range. Notably, the quantum efficiency remains above 90% with Mn4+ doping levels ranging from 1% to 5%. The emission intensity remains stable between 300 and 460 K, with a marked decline only above 500 K. Additionally, the decay lifetime exhibits a linear variation with temperature. These characteristics suggest that the optimal phosphors hold great promise for applications in areas such as indoor agriculture, luminescent thermometers, and solar cells.
1. Introduction
With the widespread application of solid-state lighting based on phosphor-converted light-emitting diodes (LEDs) for general lighting, indoor agriculture, and liquid crystal display backlighting, there is a high demand for efficient red-emitting phosphors excited by InGaN-based LED chips (λ = 360–470 nm).1–3 The most popular commercial white LED lamps are fabricated by merging broadband-emitting yellow and red phosphors on a blue LED chip, or alternatively, by coating red, green and blue phosphors on a near-ultraviolet (NUV) LED chip.4–6 In the context of agriculture lighting, an LED lamp capable of promoting plant growth should emit blue (420–500 nm) and red (640–750 nm) light, as photons with these wavelengths are indispensable for the four main plant pigments (chlorophyll a and b, phytochrome PR and PFR).7,8 When LEDs are used as backlight, narrowband-emitting red phosphors are essential.9,10 In addition, red-emitting phosphors can serve as spectral converters in photovoltaic devices to enhance conversion efficiency, since they can convert incident high-energy phonons (typically, with λ < 520 nm) that cannot be utilized efficiently by the photovoltaic materials into long wavelength photons (with λ = 630–750 nm) to which the solar cells have a better response.11–13The current commercial red-emitting phosphors fall mainly into two categories: Eu2+-activated nitrides and Mn4+-activated fluorides. The former, such as Sr2Si5N8:Eu2+ and CaAlSiN3:Eu2+, excel in blue LED absorption, quantum efficiency (QE), and chemical stability.14–16 However, they exhibit serious reabsorption of green/yellow light emitted by other phosphors, which leads to color offset and diminished luminous efficacy of LED devices.16,17 In comparison, Mn4+-doped fluorides (and oxyfluorides), represented by K2SiF6:Mn4+, offer narrow-band red emission between 610 and 650 nm, and efficient blue light excitation at approximately 460 nm with absorption cut-off around 510 nm.18 Nevertheless, they suffer from poor chemical/thermal stability and environmental hazards.19,20 The inherent drawbacks of nitrides and fluorides have thus spurred the search for alternative materials. Mn4+-activated oxides, with their innate advantages such as environmental friendliness, cost-efficiency, narrow-band deep-red emission, and especially outstanding thermal and chemical stability, have drawn escalating attention.19–21
The excitation spectrum of Mn4+-activated phosphors typically features broad absorption bands in the NUV-to-visible wavelength range, arising mainly from the spin-allowed 4A2g → 4T2g, 4A2g → 4T1g,a(4F), and 4A2g → 4T1g,b(4P) transitions within the 3d orbitals of the Mn4+ ions.3,21 However, these transitions are parity-forbidden since they occur between levels of the d shell.22,23 As a result, the molar absorption coefficient for Mn4+ is indeed low compared to that for Ce3+ or Eu2+. This challenge is more pronounced in oxide materials, since the optimal Mn4+ doping concentration is approximately 5% for fluorides but falls below 1% for most oxides. Therefore, a high Mn4+ doping concentration (e.g., 5%) in oxides is crucial for ensuring sufficient absorption of blue light, as it holds great significance for their prospective commercial viability.24 Notably, as the doping concentration of Mn4+ increases, the emission intensity and QE will decline once effective concentration quenching takes place. This is an issue that warrants particular attention.
According to Dexter's theory,25,26 concentration quenching in inorganic phosphors occurs as a result of the migration of excitation energy from one activator center to another until it reaches an imperfection that serves as an energy sink. His research reveals that, for activators with electric dipole or electric quadrupole transitions, quenching phenomena are likely to emerge when the activator concentration is on the order of 10−3 to 10−2. As previously indicated, such a concentration level is considerably insufficient for Mn4+ ions to achieve optimal performance. However, this is exactly the circumstance observed in the majority of Mn4+-activated oxides. The concentration quenching in Mn4+-activated oxides is principally attributed to the multi-polar interaction.24,27–29 Recently, we performed a study on the fundamental luminescence properties of Mn4+-activated Ca14Zn6Al10O35 (CZAO:Mn4+).30 It was found that the concentration quenching in this compound arises mainly from the direct energy transfer from Mn4+ ions to neighboring defects, which is consistent with the observations in fluorides possessing high Mn4+ doping concentrations such as K2SiF6:Mn4+ and RbSbF6:Mn4+.31,32 This finding implies that high-concentration doping and high QE can be achieved by reducing crystal defects in CZAO:Mn4+ phosphors. The primary crystal defects in CZAO:Mn4+ phosphors are oxygen vacancies and zinc vacancies, as well as Mn5+ or Mn2+ ions, which are generated during the high-temperature sintering process.30,33
In this study, we propose to introduce B2O3 as a flux to lower the sintering temperature, improve the crystallinity, and inhibit the volatilization of Zn, thereby reducing the crystal defects and mitigating the concentration quenching. The experiment results show that, in the high-temperature solid-state reaction, B2O3 not only functions as a flux, but also enables some B3+ ions to occupy the lattice sites of CZAO host. This synergistic effect improves the optimal Mn4+ doping concentration in CZAO from 1% to 6%, ensuring sufficient light absorption in the NUV-to-blue band. The optimized Ca14Zn6Al9.85−2xB0.15MnxMgxO35 − 0.42% B2O3 phosphors exhibit high QE exceeding 90% when the doping concentrations of Mn4+ are between 1% and 5%, which is much higher than the 76.8% for Ca14Zn6Al9.8Mn0.1Mg0.1O35 without B-modification. Based on the experimental results, we conducted a thorough analysis of the photoluminescence performances of B-modified CZAO:Mn4+ phosphors, and evaluated their potential applications in indoor agricultural lighting, optical thermometers, and solar cells.
2. Experimental section
2.1. Sample preparation
Three groups of phosphors, namely Ca14Zn6Al9.8Mn0.1Mg0.1O35 − z wt% B2O3, Ca14Zn6Al9.8−yByMn0.1Mg0.1O35, and Ca14Zn6Al9.85−2xB0.15MnxMgxO35 − 0.42% B2O3, were synthesized by the traditional solid-state reaction method. CaCO3 (99.9%), ZnO (99.9%), Al2O3 (99.9%), MnCO3 (99.95%), MgO (99.9%), and H3BO3 (99.5%) were employed as the starting materials (note: H3BO3 will dehydrate during calcination, and we assume that the solid product is exclusively B2O3. Hence, the chemical composition of the sample is labeled as B2O3 instead of H3BO3. Correspondingly, the dosage of H3BO3 is weighed according to the stoichiometric ratio of B2O3). These reagents were mixed in stoichiometric proportions and ball-milled in ethanol for 24 h. The resulting slurry was dried, ground, and sieved. The obtained fine powders were calcined in a muffle furnace at 1220–1280 °C under an oxygen-rich atmosphere to obtain the final products.2.2. Characterizations
The crystal structure of the obtained phosphors was analyzed by powder X-ray diffraction (XRD, Mini Flex600, Rigaku, Japan) with Cu Kα radiation. The reflection was measured by an UV-Vis-NIR spectrophotometer (Lambda-900, PerkinElmer, USA). The photoluminescence excitation (PLE) and emission (PL) spectra, and PL decays of the samples were measured with an FLS1000 luminescence spectrometer (British Edinburgh Instrument Company) equipped with red photomultiplier tube (R928P; spectral range: 200–870 nm) as detector. For temperature-dependent measurement from 80 to 660 K, the samples were placed on a thermal stage (HFS 600, Linkam Scientific Instruments). For QE measurement, the sample was put inside an optical integrating sphere coupled to the spectrometer. For evaluating the electroluminescence (EL) performance, LEDs were fabricated by integrating the phosphors on a blue InGaN LED chip (λ = 450 nm) mounting on a metal-backed printed circuit board, and their optical properties were tested by using the integrated optical and electrical measuring system (Everfine, Hangzhou).3. Results and discussion
3.1. Effect of B2O3 flux on crystallinity and photoluminescence
Fig. 1a shows the XRD patterns of Ca14Zn6Al9.8Mn0.1Mg0.1O35 phosphors sintered at different temperatures for 5 h, which indicates that the optimal sintering temperature is approximately 1250 °C. Variation in sintering temperature, both higher and lower, can be detrimental to phase purity. For instance, when sintered at 1220 °C, the sample contained unreacted CaO, ZnO, and the intermediate product Ca12Al14O33. Even when the temperature was increased to 1240 °C, a trace of Ca12Al14O33 was still detected. In principle, raising the sintering temperature promotes the solid-state reactions and enhances the crystallinity of the final product, but it also intensifies the volatilization of zinc.33 When the sintering temperature was raised to 1280 °C, the significant volatilization of zinc led to partial decomposition of CZAO, subsequently regenerating impurities including Ca12Al14O33 and CaO. Fig. 1b shows the XRD patterns of the Ca14Zn6Al9.8Mn0.1Mg0.1O35 phosphors with different amounts of B2O3 flux, which were sintered at 1240 °C for 4 h, and no diffraction peak of impurity phase was observed. This indicates that the introduction of B2O3 flux can reduce the sintering temperature and time, which is of great significance in preventing crystal defects caused by zinc volatilization.The B2O3 flux not only promotes the crystallization of CZAO but also enhances its photoluminescence properties. Fig. 2a shows the PLE spectra of Ca14Zn6Al9.8Mn0.1Mg0.1O35 − z wt% B2O3 phosphors, which indicate strong absorption from UV (∼250 nm) to visible light region (∼530 nm). The PLE spectrum can be decomposed into five Gaussian peaks located at approximately 464, 397, 332, 289, and 258 nm. These peaks correspond to the transitions from the ground state (4A2g) to the 4T2g, 2T2g, 4T1g,a, 2A1g, and 4T1g,b (or charge transfer (CT) band) excitation states, respectively.30Fig. 2c shows the PL spectra of the samples, featuring five sharp peaks at about 677, 686, 695, 705, and 713 nm. These peaks can be attributed to the anti-Stokes ν4 and ν6 vibrations, the zero-phonon line (ZPL), and the Stokes ν6 and ν4 vibrations, respectively.33,34 With the increase in B2O3 content, the PLE and PL intensities initially increased and then decreased. As shown in panels (b) and (d) of Fig. 2, when the B2O3 content reached 0.42 wt% (z = 0.42), both the PLE and PL intensities reached their maximum, increasing by 87% and 112%, respectively, compared to the sample without B2O3 (z = 0). The QE also showed an improvement, increasing from 76.8% at z = 0 to 84.6% at z = 0.42, and remaining above 83% when 0.28 ≤ z ≤ 0.56. The improvement in light absorption/emission, as well as the QE, can be attributed primarily to the improved crystallinity and the reduced crystal defects facilitated by the B2O3 flux. Besides, the introduction of B2O3 was found to alter the profile of the PLE spectrum. As shown in Fig. 2b, the percentage of the 4A2g → 4T2g transition in the PLE spectrum increased rapidly from 25% at z = 0 to 35% at z = 0.28, and then leveled off at around 36% with further increases in B2O3 content. This observation suggests that some B atoms may occupy the lattice site of CZAO. To verify this hypothesis, we prepared B-doped CZAO samples and studied their spectral properties, as detailed below.
3.2. Effect of B3+-doping on crystallinity and photoluminescence
Fig. 3 shows the XRD patterns of the Ca14Zn6Al9.8−yByMn0.1Mg0.1O35 phosphors. As the B3+ doping concentration increased, the diffraction peaks shifted slightly towards higher angles when y ≤ 0.2, and remained almost unchanged for y > 0.2. This shift is attributed to the substitution of Al3+ ions by the smaller B3+ ions, which reduces the lattice parameters. These results indicate that B3+ ions were successfully incorporated into the CZAO lattice, with a solid solubility limit of about 2% (y = 0.2). Beyond this threshold, excessive B3+ ions cannot enter the crystal lattice, which will lead to the formation of Al vacancies. Meanwhile, the volatilization of Zn will result in Zn vacancies.33 The scarcity of cations in the Al and Zn sites creates crystal defects and potentially gives rise to impurity phases. Notably, at y = 0.7, CaO minor phase was detected in the sample, which can be attributed to the relative excess of Ca compared to the deficiency of Al and Zn. | ||
| Fig. 3 (a) XRD patterns of the Ca14Zn6Al9.8−yByMn0.1Mg0.1O35 phosphors sintered at 1250 °C for 5 h, (b) enlarged patterns around 2θ = 34.1°. | ||
Fig. 4 shows the reflectance spectra of the Ca14Zn6Al9.8−yByMn0.1Mg0.1O35 (0 ≤ y ≤ 0.70) phosphors. There were four remarkable absorption peaks located at about 460, 350, 260, and 225 nm, corresponding to the 4A2g → 4T2g, 4A2g → 4T1g,a, 4A2g → 4T1g,b (and/or CT band) transitions, and host lattice absorption, respectively.21,33 Noticeably, the absorption of blue light around 460 nm (as well as UV light around 360 nm) was enhanced continuously with increasing B3+ doping concentration, reaching the maximum at y = 0.20, and then began to decrease with further increases in B content. This occurrence is highly associated with the doping behavior of B3+ in the CZAO lattice. As shown in Fig. 3, the doping limit of B3+ in CZAO is about 2%, and the corresponding sample exhibits the most powerful blue light absorption ability. However, further increase in boron content promotes the generation of crystal defects and may even induce the formation of impurities (such as CaO), which in turn leads to a decrease in the light absorption capacity.
Fig. 5a presents the PL spectra of the Ca14Zn6Al9.8−yByMn0.1Mg0.1O35 phosphors, revealing a strong dependence of luminescence intensity on the B3+ doping level, with a similar pattern to that of light absorption. Fig. 5b illustrates that the emission intensity surged with increasing boron content, peaking at y = 0.15, where it was 1.9 times that of the undoped case (y = 0). Subsequently, the emission intensity began to decline, dropping to 83% of the undoped level at y = 0.7. Concurrently, the QE increased from 76.8% at y = 0 to 84.7% at y = 0.15, then decreases progressively to 83.2% at y = 0.7.
 | ||
| Fig. 5 (a) Room-temperature PL spectra of the Ca14Zn6Al9.8−yByMn0.1Mg0.1O35 phosphors. (b) Dependence of the PL intensity and QE on the B-doping concentration. | ||
3.3. Photoluminescence properties of Ca14Zn6Al9.85−2xB0.15MnxMgxO35 − 0.42% B2O3 phosphors
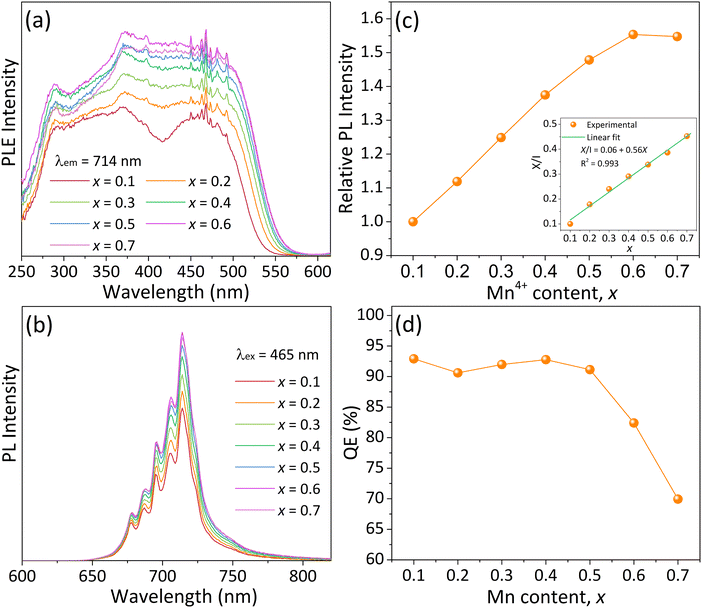
It is found from the above experimental results that the ideal amount of B2O3 flux is about 0.42%, and the optimal doping concentration of B3+ ions in the CZAO lattice is approximately 1.5% (y = 0.15). Therefore, we synthesized a series of Ca14Zn6Al9.85−2xB0.15MnxMgxO35 phosphors with the addition of 0.42% B2O3 flux to investigate their photoluminescence performance. Particularly focusing on the concentration quenching and thermal quenching.Fig. 6a presents the PLE spectra of the Ca14Zn6Al9.85−2xB0.15MnxMgxO35 − 0.42% B2O3 samples. With the increase in Mn4+ content (x), the excitation peak broadened and its intensity increased. This led to the gradual disappearance of the valley positioned at around 415 nm, which was discernible in the sample with x = 0.1 and those without B-modification (see Fig. 2a). Concomitantly, the full width at half maximum (FWHM) expanded progressively from 240 nm when x = 0.1 to 280 nm when x = 0.6. The pronounced light absorption within the 360–500 nm range for samples with x > 0.2 endows them highly compatible with the current mainstream NUV and blue LED chips. The PLE intensity reached a maximum at x = 0.6 and declined subsequently, indicating that concentration quenching becomes significant. The PL spectra of the samples are presented in Fig. 6b, and the dependence of PL intensity on Mn4+ doping concentration is illustrated in Fig. 6c. Similar to the PLE spectra, the emission intensity reached its maximum at x = 0.6. Therefore, it can be considered that the critical concentration of Mn4+ in Ca14Zn6Al9.85−2xB0.15MnxMgxO35 − 0.42% B2O3 is 6% (x = 0.6). Correspondingly, the critical distance (Rc) was calculated to be approximately 19 Å, which means that energy migration through short-range exchange interactions among Mn4+ ions is infeasible.24,30,32 In fact, for the reported Mn4+-activated oxides that we know of, Mn4+ ions cannot form neighbors within 5 Å due to their low doping concentration. Alternatively, concentration quenching of Mn4+ ions in oxide hosts is usually attributed to the multi-polar interactions, which can be described by the following equation based on Dexter theory:24,29,35
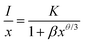 | (1) |
 | (2) |
Fig. 7a and b show the temperature-dependent PLE and PL spectra of a representative sample, Ca14Zn6Al9.65B0.15Mn0.1Mg0.1O35 − 0.42% B2O3. Several phenomena are observed. The first is the variation in the positions of the excited states with temperature. As depicted in Fig. 7c, upon increasing the temperature from 80 K to 660 K, the ZPL emission energy, E(2Eg)ZPL, decreased slightly from 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409 cm−1 to 14
409 cm−1 to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 332 cm−1, a reduction of only 77 cm−1. In contrast, the zero-phonon energy of the 4T2g level (E(4T2g)ZPL, determined by the Franck–Condon analysis of the PLE spectra) decreased significantly by 3376 cm−1, from 19
332 cm−1, a reduction of only 77 cm−1. In contrast, the zero-phonon energy of the 4T2g level (E(4T2g)ZPL, determined by the Franck–Condon analysis of the PLE spectra) decreased significantly by 3376 cm−1, from 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531 cm−1 to 16
531 cm−1 to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155 cm−1. The strong temperature dependence of the E(4T2g)ZPL can be attributed to two primary factors: (1) temperature-induced band broadening. As shown in Fig. 7d, for the 4A2g → 4T2g transition, the FWHM increased from ∼2680 cm−1 at 80 K to ∼4760 cm−1 at 660 K. The broadening was slow at cryogenic temperatures but became rapid as the temperature exceeded 270 K. This is because the optical absorption transition initiates from the lowest vibrational level of the ground state at cryogenic temperatures close to 0 K, and higher vibrational levels become involved as temperature increases, resulting in band broadening.22 However, it should be noted that thermal broadening does not cause a shift in the ZPL energy due to temperature changes. Therefore, when fitting the PLE spectra at elevated temperatures, the obtained values of E(4T2g)ZPL will be lower than the actual values due to the involvement of higher vibrational levels of the ground state (as well as E(4T1g,a)ZPL). (2) Downshift of the 4T2g energy level due to thermal expansion of the host material. According to the point charge crystal field model, the ZPL energy of the 4T2g level, i.e., the crystal-field splitting energy 10Dq, is inversely proportional to a5 (where a is the lattice constant).36–38 Therefore, even a slight thermal expansion of the host lattice may lead to a significant change in E(4T2g)ZPL.38 The effect of lattice dilation on the 4T2g energy position can be expressed as E(T) = E(0) − 5E(0)Δl/l0 when Δl is far smaller than l0 (where Δl/l0 is the thermal lattice dilation, E(T) and E(0) are the energies of the 4T2g level at an elevated temperature T and the initial low temperature, respectively).36 As shown in Fig. 7d, when the temperature was raised from 80 K to 660 K, the value of E(4T2g)ZPL obtained from spectral analysis decreased by 3376 cm−1, while the corresponding peak energy, E(4T2g)P, decreased by about 964 cm−1. Assuming that the reduction in peak energy is primarily attributed to lattice expansion, the thermal expansion coefficient was calculated to be 1.7 × 10−5 K−1, which is close to the experimentally determined value of 1.2 × 10−5 K−1 for CZAO.39 Therefore, considering that the redshift of the ZPL energy is due to lattice thermal expansion rather than spectral thermal broadening, we can roughly estimate the change in E(4T2g)ZPL based on the redshift of the peak position of the 4T2g transition band, instead of its low-energy tail. This method allows us to correct the E(4T2g)ZPL values at different temperatures, as illustrated in Fig. S1 (ESI†).
155 cm−1. The strong temperature dependence of the E(4T2g)ZPL can be attributed to two primary factors: (1) temperature-induced band broadening. As shown in Fig. 7d, for the 4A2g → 4T2g transition, the FWHM increased from ∼2680 cm−1 at 80 K to ∼4760 cm−1 at 660 K. The broadening was slow at cryogenic temperatures but became rapid as the temperature exceeded 270 K. This is because the optical absorption transition initiates from the lowest vibrational level of the ground state at cryogenic temperatures close to 0 K, and higher vibrational levels become involved as temperature increases, resulting in band broadening.22 However, it should be noted that thermal broadening does not cause a shift in the ZPL energy due to temperature changes. Therefore, when fitting the PLE spectra at elevated temperatures, the obtained values of E(4T2g)ZPL will be lower than the actual values due to the involvement of higher vibrational levels of the ground state (as well as E(4T1g,a)ZPL). (2) Downshift of the 4T2g energy level due to thermal expansion of the host material. According to the point charge crystal field model, the ZPL energy of the 4T2g level, i.e., the crystal-field splitting energy 10Dq, is inversely proportional to a5 (where a is the lattice constant).36–38 Therefore, even a slight thermal expansion of the host lattice may lead to a significant change in E(4T2g)ZPL.38 The effect of lattice dilation on the 4T2g energy position can be expressed as E(T) = E(0) − 5E(0)Δl/l0 when Δl is far smaller than l0 (where Δl/l0 is the thermal lattice dilation, E(T) and E(0) are the energies of the 4T2g level at an elevated temperature T and the initial low temperature, respectively).36 As shown in Fig. 7d, when the temperature was raised from 80 K to 660 K, the value of E(4T2g)ZPL obtained from spectral analysis decreased by 3376 cm−1, while the corresponding peak energy, E(4T2g)P, decreased by about 964 cm−1. Assuming that the reduction in peak energy is primarily attributed to lattice expansion, the thermal expansion coefficient was calculated to be 1.7 × 10−5 K−1, which is close to the experimentally determined value of 1.2 × 10−5 K−1 for CZAO.39 Therefore, considering that the redshift of the ZPL energy is due to lattice thermal expansion rather than spectral thermal broadening, we can roughly estimate the change in E(4T2g)ZPL based on the redshift of the peak position of the 4T2g transition band, instead of its low-energy tail. This method allows us to correct the E(4T2g)ZPL values at different temperatures, as illustrated in Fig. S1 (ESI†).
 | ||
| Fig. 7 Temperature-dependent photoluminescence properties of Ca14Zn6Al9.65B0.15Mn0.1Mg0.1O35 − 0.42% B2O3. (a) PLE spectra, (b) PL spectra, (c) ZPL energies of the 2Eg, 4T2g, and 4T1g,a levels; (d) variation of the FWHM, the ZPL and peak energies (ΔE(4T2g)ZPL and ΔE(4T2g)P, with respect to that at 80 K) of the 4A2g → 4T2g transition; (e) crystal-field and Racah parameters; (f) Dq/B and C/B; (g) excitation/emission energies (divided by B) vs. Dq/B on the Tanabe–Sugano energy diagram; (h) integrated PL intensity; (i) integrated PL intensities for the Stokes (IS), anti-Stokes (IaS), ZPL (IZPL) emission components, and the ratio of IaS to IS (IaS/IS). In (h), the inset is a configuration coordinate diagram schematically showing the thermal quenching of Mn4+-activated phosphors; the blue solid line represents the fitted results using eqn (11), while the violet and green solid lines represent the fitted results using eqn (12) with hν = 0.0653 and 0.0472 eV, respectively. The solid line in (i) represents the fitted result using eqn (10) with EZPL = 1.783 eV and hν = 0.0472 eV. | ||
By utilizing the values of E(4T2g)ZPL, E(4T1g,a)ZPL, and E(2Eg)ZPL determined from the PLE and PL spectra, the crystal-field and Racah parameters Dq, B, and C can be calculated using the following equations:30,40
| Dq = E(4T2g)ZPL/10 | (3) |
 | (4) |
 | (5) |
| ΔET = E(4T1g,a)ZPL − E(4T2g)ZPL | (6) |
It should be noted that eqn (5) is an approximate relationship obtained by diagonalizing the matrix elements of the crystal field and Coulomb interaction for the 2E excited states of Cr3+ ions, and it is valid within the range of values where 1.5 < Dq/B < 3.5 and 3 < C/B < 5, as proposed by Henderson and Imbusch.40 Recently, Brik et al. introduced an alternative equation:41
 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 to 16
800 to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1.
200 cm−1.
Fig. 7g presents the Tanabe–Sugano energy-level diagram for the experimentally determined ZPL energies of 4T1g,a, 4T2g, and 2Eg levels at various temperatures. It was found that the ratios Dq/B, E(4T1g,a)ZPL/B, E(4T2g)ZPL/B, and E(2Eg)ZPL/B decreased consistently with increasing temperatures. The values of E(4T1g,a)ZPL/B changed almost linearly with Dq/B, which was in good accordance with the Tanabe–Sugano diagram. In contrast, the trend of E(2Eg)ZPL/B with respect to Dq/B departed from the theoretical prediction, possibly due to the deviation of C/B ratio from the set value of 4.5. As is known, the Tanabe–Sugano diagram for d3 configuration is constructed based on the assumptions that B = 918 cm−1 and C/B = 4.5.42 Upon juxtaposing Fig. 7g and f, it became evident that at 660 K, with the C/B ratio at 4.58, the experimentally determined value of E(2Eg)ZPL/B was in close alignment with the theoretical expectation. However, as the temperature decreased, the C/B ratio increased, diverging from the set value of 4.5. Concomitantly, the experimental values of E(2Eg)ZPL/B deviated progressively from the predicted curve. Similarly, for the corrected E(4T2g)ZPL and E(4T1g,a)ZPL values based on the peak position of the corresponding transition bands, the obtained C/B ratio was around 8.25, and consequently, the E(2Eg)ZPL/B values deviated significantly from the predicted curve, as shown in Fig. S1 (ESI†). However, it is important to note that the accurate determination of E(4T1g,a)ZPL from the PLE spectra of Mn4+-activated oxides (such as Fig. 6a) is nearly impossible. Moreover, even minor variations in the E(4T1g,a)ZPL value can lead to considerable changes in the Racah parameters. Consequently, the calculated Racah parameters and their ratio C/B may deviate substantially from their actual values. To address this issue, Adachi proposed a new analytical model that sets the C/B ratio at a constant value of 4.7.34 This approach allows for the calculation of E(4T1g,a)ZPL and Racah parameters based on the easily and accurately determined values of E(2Eg)ZPL and E(4T2g)ZPL.34 Based on the correction of the E(4T1g,a)ZPL value according to the change in the peak positon of the 4T2g transition band, we adopted this new model to fit the values of E(4T1g,a)ZPL and Racah parameters. The results were shown in Fig. S1(e)–(h) (ESI†). As the temperature increased, E(4T2g)ZPL, E(4T1g,a)ZPL, and Dq/B only exhibited a slight decrease, while B and C remained virtually unchanged. Since the C/B ratio was set at 4.7—very close to 4.5—the calculated E(2Eg)ZPL/B value aligned well with the predicted curve in the Tanabe–Sugano diagram.
Another concern is the thermal quenching of the Mn4+ emission, particularly its anomalous behavior below room temperature. Fig. 7h shows the integrated emission intensity (IPL) as a function of temperature. When the sample was heated steadily from an initial cryogenic temperature of 80 K, the IPL increased gradually and reached a maximum at 420 K. Within the temperature range of 300–460 K, the IPL remained relatively constant, varying between 110% and 113% of the initial intensity at 80 K. Above 500 K, however, the IPL underwent a sharp decline due to the rapid increase of non-radiative transitions with temperature. The quenching temperature, T0.5, defined as the temperature at which the IPL drops to half of its initial value at a low temperature (80 K in this study), was determined to be approximately 600 K. Such a high quenching temperature is rarely achieved in Mn4+-activated phosphors, and is fully compliant with the thermal stability requirements for luminescence in LEDs and laser diodes (LDs).
The anomalous increase in emission intensity as the sample temperature rises from cryogenic to elevated levels, has also been observed in other Mn4+-activated phosphors, such as the classic A2XF6:Mn4+ (where A represents alkali metal ions such as K+ and Na+; X represents tetravalent cations such as Ti4+ and Si4+).43 This phenomenon is commonly referred to as “negative thermal quenching”.44 The account for its origination is customarily predicated on the recognition that the 2Eg → 4A2g transition is spin- and parity-forbidden and gain intensity mainly through coupling with local lattice vibrations.44,45 As shown in Fig. 7i, the ZPL emission intensity (IZPL) constituted less than 20% of the total emission and continued to decrease with increasing temperature. In contrast, the anti-Stokes emission intensity (IaS), which was very weak at 80 K, increased significantly with temperature up to 500 K. Therefore, the negative thermal quenching behavior of the phosphor between 80–420 K can be attributed mainly to the enhancement of anti-Stokes vibrations.18,33 The Stokes and anti-Stokes radiative transition probabilities of vibronic emissions are determined by the thermal population of phonon modes, and their intensity can be described by3,46
 | (8) |
 | (9) |
 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 386 cm−1 (1.783 eV), hν3 = 559 cm−1, hν4 = 379 cm−1, hν6 = 206 cm−1. The average lattice vibration energy was calculated as hν = 381 cm−1 (0.0472 eV), and the value of ((EZPL + hν)/(EZPL − hν))4 was 1.235. Consequently, eqn (10) can be written as IaS(T)/IS(T) = 1.235
386 cm−1 (1.783 eV), hν3 = 559 cm−1, hν4 = 379 cm−1, hν6 = 206 cm−1. The average lattice vibration energy was calculated as hν = 381 cm−1 (0.0472 eV), and the value of ((EZPL + hν)/(EZPL − hν))4 was 1.235. Consequently, eqn (10) can be written as IaS(T)/IS(T) = 1.235![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.0472/(kBT)), with the calculated results shown as the green solid line in Fig. 7i. Obviously, the experimental data for IaS(T)/IS(T) agreed well with the fitted curve within the range of 80–400 K. Beyond 400 K, the experimental data deviated from the fitted curve, which was due to the aggravation of non-radiative transition at high temperature. In general, the thermal quenching can be described by the Arrhenius equation:30
exp(−0.0472/(kBT)), with the calculated results shown as the green solid line in Fig. 7i. Obviously, the experimental data for IaS(T)/IS(T) agreed well with the fitted curve within the range of 80–400 K. Beyond 400 K, the experimental data deviated from the fitted curve, which was due to the aggravation of non-radiative transition at high temperature. In general, the thermal quenching can be described by the Arrhenius equation:30 | (11) |
 | (12) |
In general, eqn (11) works well for most phosphors, but it often fails with those activated by Mn4+ ions. As shown in Fig. 7h, eqn (11) can describe the thermal quenching behavior of Ca14Zn6Al9.65B0.15Mn0.1Mg0.1O35 − 0.42% B2O3 at temperatures above 340 K appropriately, but it is ineffective at explain the temperature dependence of emission intensity below room temperature. On the contrary, eqn (12) can describe the temperature dependence of luminescence intensity in Mn4+-activated phosphors adequately with parameters hν = 0.0653 eV, D1 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, ΔE1 = 0.685 eV, D2 = 2.850, and ΔE2 = 0.095 eV, as indicated by the violet solid line in Fig. 7h. It should be noted that the fitting value of hν deviates from the average lattice vibration energy (0.0472 eV). On the other hand, when setting hν to 0.0472 eV, the fitting curve of eqn (12) aligned well with the experimental data at temperatures below 340 K and above 540 K, with fitted values of ΔE1 and ΔE2 being 0.685 eV and 0.0443 eV, respectively. However, there was a palpable deviation in the 340–540 K range. Based on the above observation, we propose that the origin of this discrepancy lies in the fact that eqn (12) captures the relationship between vibronic emissions and temperature but neglects the effect of ZPL emission, which decreases with increasing temperature as described by eqn (11). Therefore, eqn (12) is suitable for Mn4+-activated phosphors with weak ZPL emission, such as K2SiF6:Mn4+, BaSiF6:Mn4+, Cs2NbOF5:Mn4+, and Ba2LaTaO6:Mn4+. Yet, it falls short for phosphors with strong ZPL emission, like Rb2GeF6:Mn4+, Na5Zr2F13:Mn4+ and Ca14Zn6Al10O35:Mn4+. Adachi integrated the temperature characteristics of ZPL, Stokes, and anti-Stokes emissions, and took the contribution of acoustic phonon modes into consideration, constructing a complex thermal quenching model (for details, see review articles44,48). However, it should be kept in mind that, the emission spectrum of Mn4+ ions is greatly influenced by the crystal structure, composition, and crystalline quality of the host, and the contributions of optical and acoustic phonons vary significantly across different materials. Furthermore, the impact of lattice thermal expansion on metal–ligand distance and the resulting changes in crystal-field strength should not be overlooked. Therefore, developing a thermal quenching model that is physically meaningful and universally applicable for Mn4+-activated phosphors remains a significant challenge.
000, ΔE1 = 0.685 eV, D2 = 2.850, and ΔE2 = 0.095 eV, as indicated by the violet solid line in Fig. 7h. It should be noted that the fitting value of hν deviates from the average lattice vibration energy (0.0472 eV). On the other hand, when setting hν to 0.0472 eV, the fitting curve of eqn (12) aligned well with the experimental data at temperatures below 340 K and above 540 K, with fitted values of ΔE1 and ΔE2 being 0.685 eV and 0.0443 eV, respectively. However, there was a palpable deviation in the 340–540 K range. Based on the above observation, we propose that the origin of this discrepancy lies in the fact that eqn (12) captures the relationship between vibronic emissions and temperature but neglects the effect of ZPL emission, which decreases with increasing temperature as described by eqn (11). Therefore, eqn (12) is suitable for Mn4+-activated phosphors with weak ZPL emission, such as K2SiF6:Mn4+, BaSiF6:Mn4+, Cs2NbOF5:Mn4+, and Ba2LaTaO6:Mn4+. Yet, it falls short for phosphors with strong ZPL emission, like Rb2GeF6:Mn4+, Na5Zr2F13:Mn4+ and Ca14Zn6Al10O35:Mn4+. Adachi integrated the temperature characteristics of ZPL, Stokes, and anti-Stokes emissions, and took the contribution of acoustic phonon modes into consideration, constructing a complex thermal quenching model (for details, see review articles44,48). However, it should be kept in mind that, the emission spectrum of Mn4+ ions is greatly influenced by the crystal structure, composition, and crystalline quality of the host, and the contributions of optical and acoustic phonons vary significantly across different materials. Furthermore, the impact of lattice thermal expansion on metal–ligand distance and the resulting changes in crystal-field strength should not be overlooked. Therefore, developing a thermal quenching model that is physically meaningful and universally applicable for Mn4+-activated phosphors remains a significant challenge.
Fig. 8a presents the PL decay curves of Ca14Zn6Al9.65B0.15Mn0.1Mg0.1O35 − 0.42% B2O3 measured between 80 and 630 K. At temperature below 530 K, the decay curves exhibited mono-exponential behavior, which suggests that radiative transition is predominant and thus highlights the excellent thermal stability of the phosphor. At higher temperatures of 580 K and 630 K, the bi-exponential fitting was more in line with the experimental data, indicating that the non-radiative transition becomes significant. Fig. 8b shows the temperature dependence of decay lifetime (τ), which decreased from 6.002 ms at 80 K to 0.969 ms at 630 K. In most phosphors, the decrease in decay lifetime τ and emission intensity IPL with temperature is mainly due to the enhancement of non-radiative transitions. Consequently, the lifetime typically exhibits a temperature dependence that mirrors the emission intensity, which can be described by the Arrhenius equation:38,45
 | (13) |
 | (14) |
 | ||
| Fig. 8 (a) PL decay curves at 80–630 K for Ca14Zn6Al9.65B0.15Mn0.1Mg0.1O35 − 0.42% B2O3. (b) and (c) Temperature dependence of the decay lifetime. The solid lines in (b) represent fits to eqn (15) with hν = 0.0472 eV (curve (i)) or hν = 0.0402 eV (curve (ii)), eqn (13) with ΔE = 0.685 eV (curve (iii)), and eqn (16) with hν = 0.0402 eV and ΔE = 0.685 eV (curve (iv)), respectively. The solid line in (c) gives the linear fit. | ||
However, for Mn4+-activated phosphors, the decay lifetime often displays a temperature dependence that diverges significantly from the behavior of luminescence intensity. Particularly at low temperatures, the IPL tends to increase to some extent with temperature, while the lifetime τ decreases consistently. This phenomenon was also observed in the CZAO:Mn4+ phosphors in this study. As the temperature increased from 80 K to 300 K, the IPL increased by about 10% (Fig. 7i), while τ decreased by approximately one-third (Fig. 8b). Obviously, this significant decrease in τ is not due to thermal quenching, as the QE at room temperature is higher than 90% (Fig. 6d). Consequently, the variation of τ with temperature does not follow eqn (13), as indicated by the curve (iii) in Fig. 8b.
To explain the diminishing lifetime of Mn4+ luminescence with temperature, it is essential to understand the luminescence mechanism of Mn4+ in solid hosts. As we know, the 2Eg → 4A2g transition is originally forbidden due to spin and parity selection rules. However, the spin–orbit coupling mixes the 2Eg and 4T2g states, relaxing the spin selection rules and allowing the observation of the ZPL emission.44 Additionally, the asymmetric distortion of the [MnO6] octahedral, caused by the interaction between electrons and lattice vibrations, makes this transition partially parity-allowed.45 This relaxation is achieved through coupling with the odd-symmetry vibrations of the [MnO6] octahedron (ν3, ν4, and ν6 modes), which results in the emission spectrum typically containing strong Stokes and anti-Stokes peaks (hν3, hν4, and hν6).44 The weakening of selection rules leads to an increase in transition probability and a decrease in lifetime τ. At low temperatures where thermal quenching has not yet begun, the Stokes and anti-Stokes radiative transition probabilities of vibronic emissions increase with rising temperature. According to eqn (8) and (9), the intensity of vibronic emissions can be expressed as I(T) = IS(T) + IaS(T) = I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coth(hν/(2kBT)), which is essentially the numerator term of the luminescence thermal quenching eqn (12). Correspondingly, the variation of τ with temperature can be expressed as:24
coth(hν/(2kBT)), which is essentially the numerator term of the luminescence thermal quenching eqn (12). Correspondingly, the variation of τ with temperature can be expressed as:24
 | (15) |
At temperature higher than 430 K, the fitting curve of eqn (15) deviated from the experimental data, indicating the onset of thermal quenching. Substituting eqn (15) into eqn (14), we can get:
 | (16) |
As indicated by curve (iv) in Fig. 8b, eqn (16) with ΔE = 0.685 eV and hν = 0.0402 eV can well describe the variation of decay lifetime with temperature.
3.4. Potential application of Ca14Zn6Al9.85−2xB0.15MnxMgxO35 − B2O3 phosphors
The principal application of red-emitting phosphors is in white LEDs to improve their color rendering performance. However, in the case of Mn4+-activated oxides, including CZAO:Mn4+, their emission spectra fall predominantly within the deep-red spectral region with wavelengths exceeding 650 nm, which is less perceptible to the human eye. As a result, they are not commonly used in white LEDs for general lighting, except in full-spectrum products that require an extremely high level of color rendering and gamut. Despite this, they have found significant applications in indoor agricultural LEDs. As illustrated in Fig. 9a, the EL spectrum of the LED device, which was composed of a blue LED chip and a representative CZAO:Mn4+ phosphor (Ca14Zn6Al9.25B0.15Mn0.3Mg0.3O35 − 0.42% B2O3), showed strong deep-red emission between 680–730 nm. This emission aligned well with the absorption spectrum of PFR, and overlapped with the absorption spectra of PR and chlorophyll a and b to some extent, which indicates that B-modified CZAO:Mn4+ phosphor is highly beneficial for the growth of indoor plants.Another potential application of B-modified CZAO:Mn4+ lies in ratio optical thermometers. As mentioned above, the dependence of its decay lifetime on temperature can be described by a complex exponential function, namely eqn (16) (see Fig. 8b). In fact, as shown in Fig. 8c, this relationship can be simplified to a linear function: τ(T) = 6.76 − 0.00902T, with a high R-square of 0.997. This characteristic renders CZAO:Mn4+ suitable for use in luminescent thermometers, as it allows for a constant absolute sensitivity of 0.00902 ms K−1, a value that is large enough to be measured with high precision. As reported in the vast literature, most phosphor-based luminescent thermometers exhibit sensitivity that varies with temperature, which complicates practical operations and may result in significant errors within certain temperature ranges. In contrast, for B-modified CZAO:Mn4+ phosphors, their linear variation of decay lifetime with temperature provides convenience for practical applications.
The B-modified CZAO:Mn4+ phosphor also holds significant potential in the spectral conversion of solar cells. The conversion of sunlight into electricity through photovoltaic devices is an appealing approach for generating green and renewable energy. However, typical semiconductor-based solar cells that have reached a certain level of maturity, such as crystalline silicon (c-Si), CdS-CdTe, and Cu(In,Ga)Se2 (CIGS), fail to fully utilize the entire solar spectrum.12,49–51 As shown in Fig. 9b, the QE of these solar cells drops sharply in the short-wavelength region below 520 nm. Meanwhile, the absorption in the long-wavelength region is also cut off due to their inherent material limitations. As a result, these solar cells can efficiently convert only 40% to 60% of the total solar radiation, with theoretical conversion efficiency limits around 30%.52–54 This constraint impedes the cost competitiveness of solar energy relative to traditional fossil fuels.55
Considering that sunlight with wavelengths shorter than 520 nm accounts for about 20% of the total solar radiation, it is essential to absorb these high-energy photons using phosphors and converting them into low-energy photons within the high spectral response range of photovoltaic materials to improve the overall efficiency of solar cells. Historically, research on spectral converters has focused mainly on phosphors activated by rare earth ions such as Yb3+, Nd3+, and Dy3+.56 However, these phosphors exhibit only weak and narrow f–f excitation lines in the near-ultraviolet to visible light region due to the selection rules, which restricts their practical application.56 In contrast, Ca14Zn6Al9.25B0.15Mn0.3Mg0.3O35 − B2O3 phosphors can strongly absorb sunlight in the range of 250–520 nm and emit intense deep-red light within the 650–780 nm range (see Fig. 6 and 9b), where the absorption and conversion efficiencies of c-Si, CIGS and CdS-CdTe solar cells are at a high level. The QE of this down-conversion exceeds 90% (Fig. 6d), indicating that the spectral conversion strategy based on the CZAO:Mn4+ phosphors can improve the overall energy conversion efficiency of solar cells markedly. Besides, the temperature stability of the CZAO:Mn4+ phosphors is a notable advantage. Photovoltaic devices operate at temperature higher than ambient temperature, potentially exceeding 360 K in extreme cases. Therefore, phosphors used for solar spectrum modification must possess excellent thermal stability to avoid photoluminescence thermal quenching.56 As mentioned previously, the quenching temperature T0.5 of the B-modified CZAO:Mn4+ phosphors is as high as 600 K. More specifically, as the temperature rises from 270 K to 380 K, the light absorption capability decreases by only about 12%, while the emission intensity increases by 6%, which ensures effective modification of solar spectrum.
4. Conclusions
In summary, we synthesized B-modified Ca14Al10Zn6O35:Mn4+ phosphors through the conventional solid-state reaction method and investigated the effects of B2O3 flux and lattice B doping on their photoluminescence properties. It is found that B2O3 not only serves as a flux to reduce the sintering temperature, minimize Zn volatilization, and enhance the crystallinity of the phosphors, but also incorporates B3+ ions into the lattice sites of Ca14Al10Zn6O35, further refining the luminescence performance. Within the Ca14Zn6Al9.8Mn0.1Mg0.1O35 − z% B2O3 system, optimizing the B2O3 content to 0.42 wt% results in a remarkable enhancement, by 87% and 112% respectively, in light absorption and emission, with QE improving from 76.8% to 84.6%. For the Ca14Zn6Al9.8−yByMn0.1Mg0.1O35 samples, it is demonstrated that the solid solubility of B is approximately 2%, and the optimal doping concentration is 1.5% (y = 0.15), at which the phosphors exhibit the strongest light absorption and emission, along with the highest QE. These findings lead to the fabrication of Ca14Zn6Al9.85−2xB0.15MnxMgxO35 − 0.42% B2O3 phosphors. By virtue of the synergistic effects of B2O3 flux and lattice B doping, the optimal Mn4+ doping concentration is increased significantly from 1% to 6%, which greatly strengthens the absorption of NUV/blue light and enhances their potential for commercial applications. Notably, samples with Mn4+ doping concentrations between 1% and 5% show high QE exceeding 90%. Moreover, the phosphors exhibit a negative thermal quenching phenomenon between 80–420 K, with an extremely high thermal quenching temperature T0.5 of about 600 K, outperforming most reported Mn4+-activated phosphors. Such oxide phosphors, characterized by high Mn4+ doping concentration, high QE, and superior thermal stability, are rarely documented. The outstanding performance of these phosphors also suggests their broad application prospects in areas such as indoor agricultural lighting, optical thermometers, and solar cells. We hope that this study provides valuable insights for the development of Mn4+-activated red phosphors.Data availability
The data that support the findings of this study are available on request from the corresponding author.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Science and Technology Project of Fujian Province (2023H0044) and Fujian Science & Technology Innovation Laboratory for Optoelectronic Information of China (No. 2021ZZ113).References
- M. Abraham, K. K. Thejas, A. K. Kunti, N. Amador-Mendez, R. Hernandez, J. Duras, K. G. Nishanth, S. K. Sahoo, M. Tchernycheva and S. Das, Adv. Opt. Mater., 2024, 12, 2401356 CrossRef CAS.
- Y. B. Hua, J. S. Yu and L. Li, J. Adv. Ceram., 2023, 12, 954–971 CrossRef CAS.
- S. Adachi, ECS J. Solid State Sci. Technol., 2020, 9, 016001 CrossRef CAS.
- A. G. Bispo-Jr, L. F. Saraiva, S. A. M. Lima, A. M. Pires and M. R. Davolos, J. Lumin., 2021, 237, 118167 CrossRef CAS.
- G. Li, Y. Tian, Y. Zhao and J. Lin, Chem. Soc. Rev., 2015, 44, 8688–8713 RSC.
- Y. Liu, Z. Li, W. Zhang, X. Yan, P. Guo and J. Yan, Dalton Trans., 2024, 53, 11800–11808 RSC.
- R. Cao, X. Hu, J. Nie, B. Lan, J. Wang, T. Chen, Y. Chen and J. Wang, J. Mol. Struct., 2024, 1318, 139405 CrossRef CAS.
- Z. Wang, Y. Li, X. Yang, B. Wang, R. Mi and Y. Liu, J. Mater. Chem. C, 2024, 12, 18840–18848 RSC.
- M. Zhao, H. X. Liao, L. X. Ning, Q. Y. Zhang, Q. L. Liu and Z. G. Xia, Adv. Mater., 2018, 30, 1802489 CrossRef PubMed.
- J. Gao, H. Zhu, R. Li, D. Huang, B. Luo, W. You, J. Ke, X. Yi, X. Shang, J. Xu, Z. Deng, L. Xu, W. Guo and X. Chen, J. Mater. Chem. C, 2019, 7, 7906–7914 RSC.
- P. K. Tawalare, AIP Adv., 2021, 11, 100701 CrossRef CAS.
- P. K. Tawalare, P. D. Belsare and S. V. Moharil, J. Alloys Compd., 2020, 825, 154007 CrossRef CAS.
- E. Klampaftis, D. Ross, K. R. McIntosh and B. S. Richards, Sol. Energy Mater. Sol. Cells, 2009, 93, 1182–1194 CrossRef CAS.
- R. J. Xie, N. Hirosaki, T. Suehiro, F. F. Xu and M. Mitomo, Chem. Mater., 2006, 18, 5578–5583 CrossRef CAS.
- X. Q. Piao, K. Machida, T. Horikawa, H. Hanzawa, Y. Shimomura and N. Kijima, Chem. Mater., 2007, 19, 4592–4599 CrossRef CAS.
- L. Wang, R. J. Xie, T. Suehiro, T. Takeda and N. Hirosaki, Chem. Rev., 2018, 118, 1951–2009 CrossRef CAS PubMed.
- Z. Yang, G. Lu, T. Yang, X. Zhou, L. Li, Y. Zhou and Z. Wang, J. Phys. Chem. C, 2024, 128, 13612–13619 CrossRef CAS.
- H. Zhu, C. C. Lin, W. Luo, S. Shu, Z. Liu, Y. Liu, J. Kong, E. Ma, Y. Cao, R. S. Liu and X. Chen, Nat. Commun., 2014, 5, 4312 CrossRef CAS PubMed.
- T. K. Kuttiat, M. Abraham, A. K. Kunti, N. Amador-Mendez, M. Tchernycheva and S. Das, ACS Appl. Mater. Interfaces, 2023, 15, 7083–7101 CrossRef PubMed.
- J. Huang, P. Jiang, Z. Cheng, R. Wang, R. Cong and T. Yang, Inorg. Chem. Front., 2023, 10, 2776–2787 RSC.
- S. Adachi, J. Lumin., 2018, 202, 263–281 CrossRef CAS.
- G. Blasse, Luminescent Materials, Springer-Verlag, Berlin, 1994 Search PubMed.
- S. Wang, T. Seto, B. Liu, Y. Wang, C. Li, Z. Liu and H. Dong, Adv. Sci., 2023, 10, 2204418 CrossRef CAS PubMed.
- T. Senden, R. J. A. van Dijk-Moes and A. Meijerink, Light:Sci. Appl., 2018, 7, 8 CrossRef PubMed.
- D. L. Dexter and J. H. Schulman, J. Chem. Phys., 1954, 22, 1063–1070 CrossRef CAS.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850 CrossRef CAS.
- K. Shan, B. Jing, J. Han, H. Fei, Y. Zhou, X. Xu and X. Zhang, J. Lumin., 2024, 269, 120528 CrossRef CAS.
- Z. Lu, A. Fu, F. Gao, X. Zhang and L. Zhou, J. Lumin., 2018, 203, 420–426 CrossRef CAS.
- J. Liang, B. Devakumar, L. Sun, S. Wang, Q. Sun, H. Guo and X. Huang, J. Alloys Compd., 2019, 804, 521–526 CrossRef CAS.
- T. Lv, J. Q. Huang, C. L. Yang, Y. Wang, Q. F. Huang, J. Chen and W. Guo, J. Mater. Chem. C, 2022, 10, 9773–9785 RSC.
- F. Garcia-Santamaria, J. E. Murphy, A. A. Setlur and S. P. Sista, ECS J. Solid State Sci. Technol., 2017, 7, R3030–R3033 CrossRef.
- T. Deng, S. Zhang, R. Zhou, T. Yu, M. Wu, X. Zhang, K. Chen and Y. Zhou, Dalton Trans., 2022, 51, 608–617 RSC.
- T. Lv, J. Q. Huang, Z. H. Deng, C. L. Yang and W. Guo, J. Alloys Compd., 2021, 874, 159863 CrossRef CAS.
- S. Adachi, ECS J. Solid State Sci. Technol., 2020, 9, 046004 CrossRef CAS.
- J. Liang, L. Sun, B. Devakumar, S. Wang, Q. Sun, H. Guo, B. Li and X. Huang, RSC Adv., 2018, 8, 27144–27151 RSC.
- C. J. Donnelly, S. E. Healy, T. J. Glynn, G. F. Imbusch and G. P. Morgan, J. Lumin., 1988, 42, 119–125 CrossRef CAS.
- S. Sugano, Y. Tanabe and H. Kaminura, Multiplets of transition-metal ions in crystals, Academic Press, New York, 1970 Search PubMed.
- S. Yan, ECS J. Solid State Sci. Technol., 2021, 10, 086005 CrossRef.
- V. Kahlenberg and H. Kruger, Z. Kristallogr. – Cryst. Mater., 2022, 237, 219–232 CrossRef CAS.
- B. Henderson and G. F. Imbusch, Optical spectroscopy of inorganic solids, Clarendon Press, Oxford, 1989 Search PubMed.
- C. G. Ma, Y. Wang, D. X. Liu, Z. Li, X. K. Hu, Y. Tian, M. G. Brik and A. M. Srivastava, J. Lumin., 2018, 197, 142–146 CrossRef CAS.
- Y. Tanabe and S. Sugano, J. Phys. Soc. Jpn., 1954, 9, 766–779 CrossRef CAS.
- S. Yan, ECS J. Solid State Sci. Technol., 2020, 9, 106004 CrossRef CAS.
- S. Adachi, ECS J. Solid State Sci. Technol., 2022, 11, 036001 CrossRef CAS.
- S. Adachi, ECS J. Solid State Sci. Technol., 2021, 10, 026002 CrossRef CAS.
- T. Takahashi and S. Adachi, J. Electrochem. Soc., 2008, 155, E183–E188 CrossRef CAS.
- M. S. Kurboniyon, A. M. Srivastava, B. Lou, D. D. Nematov, A. Burhonzoda, T. Yamamoto, C. G. Ma and M. G. Brik, Inorg. Chem., 2024, 63, 21212–21221 CrossRef CAS PubMed.
- S. Adachi, ECS J. Solid State Sci. Technol., 2022, 11, 066001 CrossRef CAS.
- S. Ito, H. Matsui, K. Okada, S. Kusano, T. Kitamura, Y. Wada and S. Yanagida, Sol. Energy Mater. Sol. Cells, 2004, 82, 421–429 CrossRef CAS.
- A. Virtuani, E. Lotter and M. Powalla, Sol. Energy Mater. Sol. Cells, 2006, 90, 2141–2149 CrossRef CAS.
- J. Liu, K. Wang, W. Zheng, W. Huang, C. H. Li and X. Z. You, Prog. Photovoltaics Res. Appl., 2013, 21, 668–675 CrossRef CAS.
- M. A. Green and S. P. Bremner, Nat. Mater., 2016, 16, 23–34 CrossRef PubMed.
- D. Yu, T. Yu, H. Lin, S. Zhuang and D. Zhang, Adv. Opt. Mater., 2022, 10, 2200014 CrossRef CAS.
- J. Yang, J. Wang, K. Zhao, T. Izuishi, Y. Li, Q. Shen and X. Zhong, J. Phys. Chem. C, 2015, 119, 28800–28808 CrossRef CAS.
- W. Li, T. Chen, W. Xia, X. Yang and S. Xiao, J. Lumin., 2018, 194, 547–550 CrossRef CAS.
- P. K. Tawalare, V. B. Bhatkar, S. K. Omanwar and S. V. Moharil, J. Alloys Compd., 2019, 771, 534–540 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ma00059a |
| This journal is © The Royal Society of Chemistry 2025 |