Highly efficient rewritable thin polarization holograms through paraxial recording in azo-carbazole copolymer-based composite films

Abstract

Polarization holography has emerged as a promising technique for high-density data storage, security, and optical communication applications. In this study, thin-polarization gratings have gained significant attention because of their superior optical properties, such as high diffraction efficiency, polarization selectivity, and a high signal-to-noise ratio. This paper investigates thin circular polarization holograms within an azo-carbazole copolymer-based composite film. Our findings show an outstanding diffraction efficiency of over 90% in circular polarization holograms, even with a low-intensity writing beam and a few seconds writing time. The recorded hologram shows a high retention time of more than 50 days with a retention ratio of more than 50% when stored at a low temperature in the dark. We conducted a thorough analysis of the polarization characteristics of the diffracted beam in both circular and linear polarization holograms, which we applied to polarization multiplexing applications. We evaluated the rewritable property of the material and successfully recorded and erased more than 60 holograms in less than 10 min. This study comprehensively analyzes thin polarization holograms within an azo-carbazole copolymer-based composite film and highlights their potential for use in various applications.

---

1. Introduction

Holography is a technique that enables the (i) recording and (ii) reconstruction of 3D images.¹ It is also a versatile technology with applications in various fields such as data storage, displays, medical imaging, data security, virtual reality, and augmented reality.^2–7 In the process of recording a hologram, two light beams (object beam and reference beam) superpose on the recording materials, and in the process of reconstruction, a reading beam (sometimes the same as the reference beam) passes through the recorded area of the medium to retrieve the object information.⁸ Based on the polarization of the object and reference beams, the holograms are divided into two categories: (i) intensity holograms and (ii) polarization holograms. In intensity holograms, the object and reference beams have the same polarization state, and in polarization holograms, the object and reference beams have an orthogonal polarization state.^9,10

Polarization holograms can be further classified as thick or thin polarization holograms depending upon the grating spacing, wavelength, and thickness of the sample.¹¹ The polarization holograms are recorded as a periodic change in the refractive index modulation. Hence, only a few materials that have birefringence (e.g., azopolymers) or are especially nano-fabricated (e.g., metamaterials) can record/generate polarization holograms.^12–16 Earlier, different types of polymers have been explored to record polarization holograms. Some materials like photopolymers, liquid crystals, azo-derivatives polymers, etc. have been explored for volume (or thick) polarization holograms.^17–24 Among these polymers, azo-derivative polymers generally have a high absorption coefficient, and hence, most of the holograms recorded in polymers remain thin.^25–28 Thick polarization holograms can be recorded in the azopolymers with a thickness of a few tens of μm at a large recording angle (angle between object and reference beams) or by increasing the penetration depth (by diluting the concentration of azopolymer) in the sample.^22,29

The generation of polarization holograms in azopolymers is indeed attributed to the formation of surface relief, birefringence, or both. This has been studied extensively in the field of holography and has led to significant advancements in the development of new materials for holographic applications.^{14,25,28,30–35} Most of the previously reported azopolymer films in pure form or with some dopant generally have long recording times and not-so-high diffraction efficiencies.^26,28,36

Earlier, we investigated azo-carbazole copolymer-based composite films to solve most of the existing problems. We have investigated thin-intensity holograms, thick-intensity, polarization, and vector holograms with high diffraction efficiency in this polymer film.^22,37–43 However, in our previous studies, we did not examine the relationship between recording time and the intensity of the writing beam needed to record holograms of various types. In this paper, we have investigated the thin polarization hologram property in the azo-carbazole copolymer-based composite film for the first time. We record the circular polarization hologram at a paraxial angle in order to increase the fringe width to make the hologram thin. We investigate in detail the recording light intensity and recording time of a thin polarization hologram in the film. We subsequently measured the diffraction efficiency and investigated the polarization properties of the diffracted beam in different cases of writing and reading of the polarization hologram. Utilizing the result from the investigation of polarization properties, we find the optimal condition to record the double-shot multiplexed circular polarization hologram in the polymer film. We provide a detailed analysis of the rewritable property of the azo-carbazole copolymer-based composite film when thin circular polarization holograms are recorded and erased with different intensities of writing and erasing beams. Finally, we investigate the diffractive properties of the thin linear polarization hologram in the azo-carbazole copolymer-based composite film.

2. Experimental

The azo-carbazole copolymer-based composite film was prepared by mixing three components, CACzE (3-[(4-cyanophenyl)azo]-9H-carbazole-9-ethanol), poly(CACzE–MMA) (MMA: methyl methacrylate) and DPP (diphenyl phthalate). The chemical structure of all three components is shown in Fig. 1. Each component serves a distinct purpose, with CACzE facilitating the photoisomerization process, poly(CACzE–MMA) enhancing the retention time of the recorded polarization hologram, and DPP, functioning as a plasticizer, elevating transparency, flexibility, and durability.

Fig. 1 Structural formulas of the materials used in this study.

The film preparation involves a four-step process. In the initial step, the three components, poly(CACzE–MMA), CACzE, and DPP, were mixed in a ratio of 45/15/5 wt%. The mixed sample was then stirred for 48 h, and in the subsequent step, it was dried at 70 °C for 48 h. In the final step, the dried sample was sandwiched between two glass plates with two 35 μm-thick imide spaces, melted at 140–180 °C, and melt-pressed to fabricate the sample film. The sample film sandwiched between two glass plates was designed so that only birefringence, without surface relief, contributes to the grating generation process. Details of the synthesis and sample preparation can be found in our previous publications.^37,40 The absorption spectrum of the sample film prepared was examined and presented in Fig. S1 (ESI†). The spectrum revealed that the maximum absorption wavelength was 421 nm, corresponding to cis–trans photoisomerization phenomena. However, the isosbestic wavelength, where trans–cis–trans photoisomerization is expected to occur, was found to be around 520 nm.⁴¹ Based on this, a 532 nm wavelength laser was selected for writing the polarization hologram. It is worth noting that the absorption coefficient decreases significantly at higher wavelength regions (λ > 600 nm). Therefore, a 635 nm wavelength laser was chosen to read the polarization hologram.

The optical setup used to record the thin circular polarization hologram is shown in Fig. S2 (ESI†). The experimental setup involved the use of a laser beam with a 532 nm wavelength and a 5 mm beam diameter. The beam passed through a polarizer and a half-waveplate (HWP) to become a linearly polarized light beam split into two orthogonal polarization states using a polarization beam splitter (PBS). Quarter-waveplates (QWP) were used in both arms to produce a circularly polarized light beam. However, in the case of a linear polarization hologram, the QWP was substituted with an HWP. Both beams were superposed on the sample film at an angle of 4.5°. The recorded hologram in the polymer film was then illuminated by a red laser beam with a wavelength of 633 nm and a diameter of 2 mm. The arbitrary polarization of the red laser beam was achieved by using HWP and QWP, as shown in Fig. S3 (ESI†). In order to achieve the perfect recording time for maximum diffraction efficiency, both green and red laser beams were turned on simultaneously, and the intensity of the diffracted beam was subsequently analyzed. After finding the optimal conditions, the writing beam is only turned on for a few seconds, while the reading beam is turned on after turning off the writing beam. The intensity of the writing beam was changed directly from the laser. After recording different holograms under optimal conditions, the diffraction efficiency of the first-order (−1st order) diffracted beam was calculated using eqn (1),

where I₊₁ and I₋₁ are the intensity of the transmitted diffracted beams, and I₀ is the intensity of the non-diffracted zeroth order beam.

External diffraction efficiency is given by eqn (2),

where α is the absorption coefficient, d is the film thickness, and θ is the internal reading angle of 2.25°. The recorded grating pattern was observed using a polarization phase-contrast microscope (OLYMPUS BX53M). The response time (build-up time) of the first-order diffracted beam estimated the time needed to form the grating. To evaluate the response time τ, optical diffraction with time was fitted by the Kohlrausch–Williams–Watts (KWW) stretched exponential function of eqn (3), as follows:where t is the time, η₁ is the steady-state first-order diffraction efficiency, and β (0 < β ≤ 1) is the parameter related to a dispersion.

3. Results and discussion

3.1 Thin circular polarization holographic grating

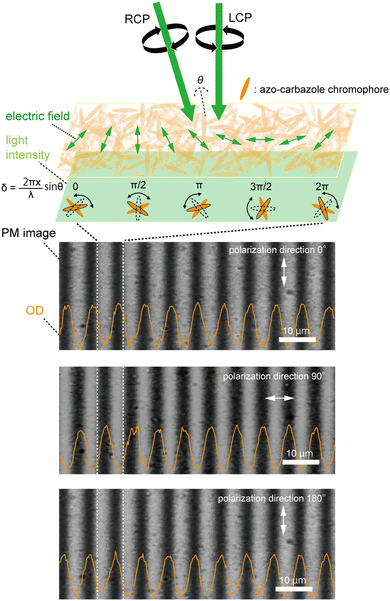
The grating pattern recorded by a right circular polarized (RCP) and a left circular polarized (LCP) writing configuration was observed using a polarization phase-contrast microscope; the findings, the distribution of the interference field in the orthogonal polarization state, and the corresponding molecular distribution as well as orientation are shown in Fig. 2. The grating pattern in Fig. 2 reveals a fringe width (Λ) of approximately 6.7 μm. The light penetration depth (d_p) within the sample is estimated to be 20–25 μm.^37,44 By applying the relationship Λ² > λd_p (a criterion for a thin (Raman-Nath) hologram), it is affirmed that the recorded hologram indeed qualifies as a thin hologram. Subsequently, the intensity patterns were investigated by adjusting the orientation of the polarizer in the microscope, and the change in the intensity profile is shown in Fig. 2. Notably, upon a 90° rotation of the polarizer, the bright region (indicative of maximum intensity) transitions to a dark region (zero intensity), as evident in Fig. 2. Furthermore, with a continued rotation to 180°, the intensity pattern remains consistent with the 0° orientation, as shown in Fig. 2. These findings provide conclusive evidence for successfully generating thin and polarization holograms.

Fig. 2 The distributions of the interference fields in polarization holography using the RCP+LCP configuration and the corresponding molecular distributions and orientations. Grating pattern (contrast-enhanced) and variation of optical density for the thin polarization hologram (RCP+LCP) observed through the phase-contrast microscope at polarization angles of 0°, 90°, and 180°.

3.2 Polarization property of the diffracted beam from thin circular polarization holograms

We conducted a detailed investigation into the dependence of the diffraction order of the diffracted beam, polarization of the diffracted beam, and the handedness of the polarization of the diffracted beam. The diffracted and non-diffracted order beam of a hologram recorded with RCP+LCP configuration and read with a differently polarized beam are shown in Fig. 3. From Fig. 3(c1), it is evident that when an LCP-polarized reading beam traverses the recorded area of a hologram, only a single diffracted order is observed, and other orders are negligible. The intensity of the diffracted order (+1st order) significantly surpasses that of the 0th order, resulting in a diffraction efficiency exceeding 90%. Upon altering the polarization of the reading beam to linear polarization (LP) through a 45° rotation of the quarter-wave plate, two strong diffracted beams (±1st order) appear, while the non-diffracted beam remains minimal. The average diffraction efficiency under this condition ranges between 43 and 47%, as shown in Fig. 3(c3 and c4). Subsequently, when the polarization of the reading beam shifts to RCP, a single and highly efficient diffracted beam in −1st order is obtained, surpassing 94% efficiency, as shown in Fig. 3(c6). These findings underscore that when a hologram is recorded with an RCP+LCP configuration in an azo-carbazole copolymer-based composite film, only one highly intense diffracted order (+1st order) is observed with an LCP reading beam. Upon changing the polarization state to RCP via LP, the intensity of the +1st order almost completely shifts to −1st order. Polar plots are employed to exhibit the polarization state of the diffracted beam (±1st order) under different reading beam polarization. The polar plots are generated by introducing a polarizer into the path of each beam (writing, reading, and diffracting) and rotating it a full 360°. Within the polar plot, if the intensity ranges from 0 to 1, the beam exhibits linear polarization, and if the intensity remains constant at 1, the beam demonstrates circular polarization. In all other cases, the beam retains elliptical polarization. The ellipticity in the circular beam sometimes appears due to the misalignment of waveplates or polarizers. In our experiments, the level of ellipticity is minimal, and therefore, we consider it negligible. The polar plot of the writing beam (RCP+LCP) is shown in Fig. 3(a1 and a2). When the reading beam is LCP, a circularly polarized diffracted beam is obtained in +1st order only, while the −1st order yields null reconstruction, as shown in Fig. 3(c1 and c2). However, the optical setup (Fig. S3, ESI†) does not definitively determine the handedness of circular polarization; the results are discussed later.

Fig. 3 Polar plot of (a) RCP+LCP writing beam, (b) reading beams of different polarization, (c) diffracted beams corresponding to each reading beam, and (d) intensity patterns of the diffracted and non-diffracted beam for circular polarization holograms.

It is important to note that for non-paraxial angle holograms or the Bragg hologram, the polarization of the diffracted beam is highly dependent on the exposure ratio. However, this parameter is not crucial for paraxial recorded polarization holograms. The reading beam polarization is changed to LP, and in this case, both diffracted beams (±1st order) exhibit circular polarization (Fig. 3(c3 and c4)). Similarly, when the reading beam polarization is RCP, the +1st order diffracted beams yield null reconstruction, and the −1st order is circularly polarized, as shown in Fig. 3(c5 and c6).

To evaluate the handedness of circular polarization in the diffracted beam, an additional quarter-wave plate (QWP2) and a polarizer were introduced into its path, as shown in the optical setup (Fig. S4, ESI†). When two QWPs (one positioned before the sample as QWP1 and the other after the sample as QWP2) induce circular polarization, the resultant state becomes linearly polarized, with its direction depending on the handedness of the circular polarization induced by QWP1 and QWP2. The direction of the resultant linear polarization can be examined by placing a polarizer after QWP2. If QWP1 generates a linearly polarized light beam, then QWP2 generates a circularly polarized light beam. In Table 1, when the reading beam is right circularly polarized (RCP) (used as QWP1), the 0th order beam also becomes RCP. As this beam passes through QWP2, which is set to RCP, and the polarizer, the intensity remains high since the polarizer transmits the entire beam. However, for the diffracted beam (−1st order), the intensity becomes negligible because the polarizer blocks the entire beam, indicating that the diffracted beam is orthogonal to the reading beam (or the 0th order beam). This result is further confirmed when the polarization is switched to left circular polarization (LCP) using QWP2, leading to negligible intensity for the 0th order beam and maximum intensity for the −1st order beam. Therefore, the −1st order beam is identified as LCP. Similarly, when the reading beam is LCP, the diffracted beam (+1st order) becomes RCP, which is verified by setting QWP2 to both RCP and LCP orientations. Consequently, in the case of circularly polarized writing and reading, the diffracted beam remains orthogonal to the reading beam. Finally, in the case of a linearly polarized reading beam, the +1st order and −1st order beams are confirmed to be orthogonal to each other, specifically in RCP and LCP states, respectively, while the 0th order beam remains linearly polarized. In summary, the investigation into the order and polarization of the diffracted beam for the RCP+LCP (object beam + reference beam) writing beam reveals distinct reconstruction effects. A faithful reconstruction effect, where the polarization of the diffracted beam matches that of the object beam, is achievable solely in the +1st order when the reading beam is either LCP or LP. An orthogonal reconstruction effect, characterized by obtaining orthogonal polarization in the diffracted beam compared to the object beam, is exclusively possible in the −1st order when the reading beam is either RCP or LP. A null reconstruction effect, signifying no diffracted beam, is attainable in both +1st order and −1st order diffracted beams when the reading beam has RCP and LCP polarization, respectively.

Table 1 The power of the diffracted beam after polarization filtering (for a hologram recorded with RCP+LCP configuration) to find the handedness of the circularly polarized diffracted beam

Pol (QWP1)	Pol (QWP2)	I +1 (μW)	I 0 (μW)	I −1 (μW)
RCP	RCP	—	41.3	0.3
RCP	LCP	—	1.0	42.0
LCP	RCP	42.3	0.8	—
LCP	LCP	0.1	43.5	—
LP	RCP	20.3	27.4	0.1
LP	LCP	0.1	19.4	23.0

---

These distinct reconstruction effects play a crucial role in holographic data storage through hologram multiplexing techniques. This approach allows the recording of two different holograms in the same area of the azo-carbazole copolymer-based composite film, enabling their simultaneous reconstruction without information overlap.

3.3 Dependence of writing beam intensity on diffraction efficiency for the thin polarization hologram

After confirming the relationship between the writing and reading for the thin circular polarization holograms, an in-depth examination was conducted on the recording time of polarization holograms at various intensity levels (W cm⁻²) of the writing beam. In order to determine the optimal recording time for thin circular polarization holograms, an (RCP+LCP)/RCP configuration was used to write/read the hologram. The optical setup to read the recorded hologram is shown in Fig. S3 (ESI†). Fig. 4 shows the change in normalized intensity (I/I_max) of the diffracted beam while the recording beam remains turned on. The results, shown in Fig. 4, reveal that even at a low beam intensity of 0.02 W cm⁻² (Fig. 4(a)), hologram writing is possible within a duration of less than one minute. These findings underscore the material's capability to handle holographic writing and reading with minimal beam intensity requirements. Furthermore, as the intensity of the writing beam was increased, a notable decrease in recording time was observed, as shown in Fig. 4(b–g). At higher beam intensity levels, such as 0.64 W cm⁻², the recording time is notably reduced to approximately 1.7 s. This result provides evidence that the material exhibits a significantly faster response time at high recording beam intensity. Simultaneously, it is noteworthy that successful hologram recording can be achieved even at low beam intensity levels. Based on the relationship between recording beam intensity, recording time, and absorption coefficient, the optical energy required to build thin circularly polarized holograms was estimated to be in the range of 4.7–5.4 mJ, with an average value of 5.0 mJ. Using these results, we record the thin circular polarization holograms (RCP+LCP) at different beam intensities and recording times. After recording the hologram, the green laser at 532 nm was turned off, and the red laser at 635 nm was turned on. Using the intensity of the diffracted and zero-order beam, we evaluated the diffraction efficiency for the RCP+LCP/RCP (writing/reading) configuration, and the result thus obtained is shown in Table 2. This result indicates that the maximum diffraction efficiency (diffraction efficiency immediately after recording) thus obtained is more than 90%, which shows that the material is very suitable for recording thin circular polarization holograms. These results indicate that the birefringent properties of the free CACzE chromophores and the side-chain CACzE moieties dispersed in the azo-carbazole copolymer-based composite film, synergistically contribute to the diffraction efficiency. Furthermore, the decrease observed after reaching the maximum diffraction efficiencies are attributed to over-modulation caused by excessive refractive index modulation.³⁷ The free CACzE chromophores play a dominant role in determining the formation time of the refractive index grating, and some side-chain CACzE moieties are thought to align with the orientation of the free CACzE chromophores. Additionally, the thermal stability of the refractive index gratings, which is also an important factor in the discussion of retention described below, is suggested to result from the interaction between the free CACzE chromophores and the side-chain CACzE moieties, as well as the stabilization of their orientation.⁴⁰ In addition, the results of the external diffraction efficiencies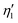 , considering the absorption path, were estimated using eqn 2. Here, the absorption coefficient α of 11.4 cm⁻¹ was used as the azo-carbazole copolymer-based composite film at 635 nm, and the film thickness d was 35 μm. As a result, ranged from 83.7% to 89.0% (Table 2), meaning there is almost no loss due to absorption by the azo-carbazole copolymer-based composite film itself, making it beneficial when reading out diffracted light for optical communication.

Fig. 4 Time variation of normalized −1st order diffraction efficiency for thin circular polarization hologram relative to the writing beam intensity at (a) 0.02 W cm⁻², (b) 0.13 W cm⁻², (c) 0.22 W cm⁻², (d) 0.33 W cm⁻², (e) 0.45 W cm⁻², (f) 0.54 W cm⁻² and (g) 0.64 W cm⁻².

Table 2 Dependence of maximum first-order diffraction efficiency and its response time (build-up time) of thin circular polarization holograms on the writing beam intensity

	Circular polarization			Linear polarization
I (W cm^−2)	η 1 (%)	(%)	τ (s)	η 1 (%)	(%)	τ (s)
Film thickness d = 35 μm, absorption coefficient α = 11.4 cm^−1.
0.02	92.6	89.0	52.6	16.5	15.9	52.9
0.13	94.3	90.6	8.4	16.5	15.9	11.3
0.22	90.5	87.0	3.9	16.8	16.1	7.6
0.33	92.6	89.0	3.2	15.7	15.1	5.0
0.45	91.4	87.8	2.1	16.8	16.1	3.8
0.54	92.3	88.7	2.0	17.7	17.0	3.2
0.64	87.1	83.7	1.7	16.7	16.1	1.9

---

Additionally, we recorded a thin linear polarization hologram and evaluated the diffractive properties at various intensity levels (W cm⁻²) of the writing beam. The optical setup used for recording and reading the linear polarization hologram is shown in Fig. S2 and S3 (ESI†). In this optical setup, all quarter-wave plates were replaced with half-wave plates to evaluate the optimal recording beam intensity and the corresponding response time for achieving maximum recording efficiency of the linear polarization hologram. Table 2 presents the variation in diffracted beam intensity (+1st order) over time for different writing beam intensities.

Based on the results shown in Fig. S5 (ESI†), the recording times for the thin linear polarization hologram are approximately 52.9 s at a recording beam intensity of 0.02 W cm⁻², 11.3 s at 0.13 W cm⁻², 7.6 s at 0.22 W cm⁻², 5.0 s at 0.33 W cm⁻², 3.8 s at 0.45 W cm⁻², 3.2 s at 0.54 W cm⁻², and 1.9 s at 0.64 W cm⁻², respectively. Compared to the thin circular polarization holograms, the grating of the linear polarization hologram in the azo-carbazole copolymer-based composite film exhibits a longer response time during recording. Based on the relationship between the recording beam intensity, recording time, and absorption coefficient, the optical energy required to build thin linearly polarized holograms was estimated to be in the range of 5.2–8.5 mJ, with an average energy of 7.4 mJ. Next, when the recorded hologram is read with a P-polarized reading beam, multiple diffracted orders are observed, as shown in Fig. S6 (ESI†). These multiple diffracted orders indicate the successful formation of a thin linear polarization hologram in this film. Furthermore, the diffraction efficiency of the +1st order diffracted beams ranges between 16% and 18% under different recording beam intensities (Table 2), which is relatively low compared to circular polarization holograms and the theoretical limit of 33.9%.⁹ Subsequently, an analysis of the polarization properties of the diffracted beams was conducted, and the results are shown in Fig. S7 (ESI†). The thin linear polarization hologram was recorded with a P+S polarization configuration, and the polarization of the reading beam (identical to the 0th order beam) was used. When a P-polarized reading beam passes through the recorded area, the ±1st order diffracted beams exhibit polarization orthogonal to the reading beam (i.e., S-polarization), while the ±2nd order diffracted beams maintain the same polarization state as the reading beam (i.e., P-polarization). Similarly, when an S-polarized reading beam passes through the recorded area, the ±1st order diffracted beams exhibit P-polarization, and the ±2nd order diffracted beams exhibit S-polarization. In summary, regardless of the polarization of the reading beam (P/S), odd-order diffracted beams consistently exhibit polarization orthogonal to the reading beam (or 0th order beam), while even-order diffracted beams consistently exhibit the same polarization as the reading beam.

3.4 Retention and multiplexing for circular polarization holograms

Retention (R_t%, a measure of diffraction efficiency over time relative to diffraction efficiency immediately after recording) was measured under various storage temperatures of the recorded holograms, as shown in Fig. 5(a). The R_300s% value for the RCP+LCP/RCP (writing/reading) configuration indicates that the red laser remains inactive (off) throughout the entire reading process and for 300 s. If the laser is switched on after 300 seconds of recording, the value indicates an approximate range of 94–96%. However, the R_300s% range is 91–93% when the red laser is active (on) throughout the entire reading process. This result indicates that the wavelength of the red laser does not erase the recorded holograms. As long-term storage of the holograms is important, storage conditions were assessed at 25 °C, 6 °C, under light and dark environments respectively: the retention of the diffraction efficiency R_50day% after 50 days was 1.5% for light and 25 °C storage conditions. The diffraction efficiency at R_50day% for dark and 25 °C storage conditions was 27.5%. This improvement in retention is apparently due to the disappearance of the diffraction grating as a result of visible light-inducing isomerization. When the samples were stored in the dark and at a lower temperature of 6 °C to increase the retention time, the diffraction efficiency of R_50day% was 55.8%. The diffraction efficiencies of R_210day% after 210 days under the respective conditions were 0.6%, 18.6%, and 42.9%. These results suggest that temperature has a significant effect on the preservation of recorded holograms. Additionally, the R_300s% of the recorded thin linear polarization hologram was approximately 90–92%.

Fig. 5 (a) Retention ratio of −1st order diffraction efficiency for thin circular polarization hologram at various storage conditions. (b) Variation of ±1st order diffraction efficiency with different recording times of the second hologram for polarization hologram multiplexing.

The generation of multiplexed holograms was carried out in two steps. In the first step, a hologram was recorded using the RCP+LCP configuration for 5 s, followed by reading with an RCP light beam. In this process, only the −1st order diffracted beam with LCP polarization appeared, achieving a diffraction efficiency of >90%. This state is represented as 0 s in Fig. 5(b). In the second step, another hologram was recorded for 1 to 5 s using the LCP+RCP configuration with inverted circular polarization, while keeping the reading beam fixed in the RCP configuration. In this case, ±1st order diffraction beams appeared, each with different diffraction efficiencies. The efficiency of the second hologram depended on its recording time, and as the second hologram was recorded, the first thin circular polarization hologram was erased, leading to a reduction in the diffraction efficiency of the first thin circular polarization hologram. Therefore, estimating the recording times that result in equal efficiencies for both holograms is important for effective multiplexing. Fig. 5(b) shows the variation in ±1st order diffraction efficiencies when the first thin circular polarization hologram is recorded for a fixed duration of 5 s, followed by varying the recording time of the second hologram from 1 to 5 s. As shown in Fig. 5(b), when the recording times are equal (5 s each: RCP+LCP and LCP+RCP), the −1st order diffraction efficiency from the first thin circular polarization hologram significantly decreases to 16%, while the +1st order diffraction efficiency from the second hologram increases to 59%. On the other hand, with unequal recording times—5 s for the first thin circular polarization hologram and approximately 2.7 s for the second hologram—the ±1st order diffraction efficiencies are both balanced at around 30%, achieving a more even distribution of RCP and LCP simultaneously. Based on these results, it is demonstrated that the azo-carbazole copolymer-based composite film exhibits high effectiveness for data storage through double recording of polarization holograms with unequal exposure times, successfully achieving circular polarization multiplexing.

3.5 Rewritable property for circular polarization holograms

The rewritable property of the azo-carbazole copolymer-based composite film was evaluated in detail by writing and erasing circular polarization holograms multiple times. The recorded hologram in the azo-carbazole copolymer-based composite film can be erased by using two methods: (a) heating and (b) single-beam illumination. In the first method, the recorded hologram can be erased by keeping the polymer film at high temperatures (around 80–150 °C). In the previous study, a holographic stereogram was heated to 80 °C using a transparent heater immediately after recording, and the interference fringes were erased within 50 s.⁴⁰ In this paper, the second method was employed, namely erasing the hologram by a single-beam illumination.

Fig. 6 demonstrates the multiple cycles of writing and erasing of the thin circular polarization holograms. In this evaluation of rewritability, the writing beam utilized the RCP+LCP configuration, while the reading beam was the RCP. To erase the recorded thin circular polarization holograms, one of the writing beams (RCP) was blocked, and the LCP beam was used as the erasing beam and illuminated the recording area. In the case of recording a thin circular polarization hologram, the intensity of the writing beam (object beam + reference beam) was set to beam intensity, I, and the intensity of the erasing beam (reference beam only) was approximately 0.5I. Fig. 6 shows multiple cycles of recording and erasing a thin circular polarization hologram when the writing beam intensity is 0.22 W cm⁻¹ and the erasing beam intensity is 0.11 W cm⁻¹. In this case, the average recording time is 7 s, and the average erasing time is 24 s. Therefore, one complete recording and erasing cycle requires approximately 31 s. Similarly, as shown in Fig. 6, increasing the intensities of the writing and erasing beams reduces both the recording and erasing times. For instance, when the writing beam intensity is 0.33 W cm⁻¹, the average recording time is 5 s, and the average erasing time is 14 s, requiring approximately 19 s for one complete cycle. Subsequently, increasing the writing beam intensity to 0.45 W cm⁻¹ results in an average recording time of 4 s and an average erasing time of 12 s, requiring approximately 16 s for a complete cycle. By increasing the beam intensity and using the most efficient recording and erasing times with the highest writing beam intensity in this study (0.64 W cm⁻¹), it is found that approximately 12 cycles of thin circular polarization holograms recording and erasing could be achieved in 2 min. Therefore, it can be concluded that the azo-carbazole copolymer-based composite film is demonstrated to be a reliable medium for rewritable polarization holograms.

Fig. 6 Multiple cycles of writing and erasing of the thin circular polarization holograms relative to the writing beam intensity at (a) 0.02 W cm⁻², (b) 0.13 W cm⁻², (c) 0.22 W cm⁻², (d) 0.33 W cm⁻², (e) 0.45 W cm⁻², (f) 0.54 W cm⁻² and (g) 0.64 W cm⁻².

Remarkably, even after multiple cycles of recording and erasing, there are no changes in the maximum diffraction efficiency, recording time, or erasing time, confirming the high stability and fatigue resistance of the azo-carbazole copolymer-based composite film. Considering the potential to increase the number of recording and erasing cycles to several hundred, the azo-carbazole copolymer-based composite film is an excellent material for rewritable polarization holograms. Furthermore, the results of this study suggest the potential to contribute to fundamental technologies in photonics and quantum optics, where improving polarization conversion efficiency remains a challenge, as also pointed out in the research by Y. Yuan et al.⁴⁵ Additionally, similar to this prior study, we have successfully demonstrated experimentally that utilizing the superposition of eigenstates of a non-orthogonal Jones matrix enables more efficient polarization conversion compared to conventional orthogonal polarization optical systems. Therefore, the azo-carbazole copolymer-based composite film and optical system proposed in this study are expected to become an important optical technology that enables highly efficient and precise simultaneous control of the polarization state of light.

4. Conclusions

In conclusion, this research paper presents a thorough investigation of thin polarization holograms in azo-carbazole copolymer-based composite films. The results show that these films are capable of recording thin polarization holograms with a high diffraction efficiency of over 90% even at low recording beam intensity. Additionally, the recorded holograms have a good retention ratio of more than 50% even after 30 days of storage in the dark, low humidity, and low temperature. The polarization characteristics of the diffracted beam have been analyzed and utilized in the polarization multiplexing application. Moreover, the material's rewritable property has been successfully tested, recording and erasing more than 60 holograms in less than 10 minutes. Finally, a thin linear polarization hologram has been recorded in the polymer film, resulting in a maximum diffraction efficiency of 16–18% under different conditions. These findings demonstrate that azo-carbazole copolymer-based composite films have great potential for recording thin polarization holograms, as well as other applications.

Data availability

The data supporting this article have been included as part of the ESI† and in the main manuscript.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by JSPS KAKENHI Grant Number JP22H00535 (Grant-in-Aid for Scientific Research (A)).

Notes and references

1. D. Gabor, Nature, 1948, 161, 777–778.
2. Y. Lim, B. Kang, S. J. Hong, H. Son, E. Im, J. Bang and S. Lee, Adv. Funct. Mater., 2021, 31, 2104105.
3. P. Forcén, L. Oriol, C. Sánchez, F. J. Rodríguez, R. Alcalá, S. Hvilsted and K. Jankova, Eur. Polym. J., 2007, 43, 3292–3300.
4. L. Kang, H. Liu, S. Fu, X. Li, N. Li, J. Wu, X. Wang, X. Zhang and J. Li, J. Appl. Polym. Sci., 2020, 137, 48537.
5. E. Zarins, K. Balodis, A. Ruduss, V. Kokars, A. Ozols, P. Augustovs and D. Saharovs, Opt. Mater., 2018, 79, 45–52.
6. O. Sakhno, Y. Gritsai, H. Sahm, J. Stumpe and M. Wegener, Digital Optics for Immersive Displays, 2018, pp. 91–107.
7. C. Rianna, A. Calabuig, M. Ventre, S. Cavalli, V. Pagliarulo, S. Grilli, P. Ferraro and P. A. Netti, ACS Appl. Mater. Interfaces, 2015, 7, 16984–16991.
8. P. Hariharan, Basics of holography, Cambridge University Press, 2002.
9. L. Nikolova and P. S. Ramanujam, Polarization holography, Cambridge University Press, 2009.
10. K. Kuroda, Y. Matsuhashi, R. Fujimura and T. Shimura, Opt. Rev., 2011, 18, 374–382.
11. M. Moharam and L. Young, Appl. Opt., 1978, 17, 1757–1759.
12. Q. Xu, X. Zhang, Y. Xu, C. Ouyang, Z. Tian, J. Gu, J. Li, S. Zhang, J. Han and W. Zhang, Laser Photonics Rev., 2017, 11, 1600212.
13. Q. Song, A. Baroni, R. Sawant, P. Ni, V. Brandli, S. Chenot, S. Vézian, B. Damilano, P. de Mierry and S. Khadir, et al. , Nat. Commun., 2020, 11, 2651.
14. D. Nazarova, G. Mateev, L. Nedelchev, E. Stoykova, B. Blagoeva, N. Berberova, K. Hong and J. Park, Optik, 2021, 226, 165882.
15. T. Yan, Q. Ma, S. Sun, Q. Xiao, I. Shahid, X. Gao and T. J. Cui, Adv. Theory Simul., 2021, 4, 2100046.
16. A. Meshalkin, C. Losmanschii, A. Prisacar, E. Achimova, V. Abashkin, S. Pogrebnoi and F. Macaev, Adv. Phys. Res., 2019, 1, 86–98.
17. S. Cho, H. Yoshida and M. Ozaki, Opt. Express, 2022, 30, 1607–1614.
18. S. H. Lin, S.-L. Cho, S.-F. Chou, J. H. Lin, C. M. Lin, S. Chi and K. Y. Hsu, Opt. Express, 2014, 22, 14944–14957.
19. Y. Chen, P. Hu, Z. Huang, J. Wang, H. Song, X. Chen, X. Lin, T. Wu and X. Tan, ACS Appl. Mater. Interfaces, 2021, 13, 27500–27512.
20. M. Häckel, L. Kador, D. Kropp and H.-W. Schmidt, Adv. Mater., 2007, 19, 227–231.
21. A. Kozanecka-Szmigiel, K. A. Rutkowska, M. Nieborek, M. Kwasny, M. A. Karpierz, E. Schab-Balcerzak, J. Konieczkowska and D. Szmigiel, J. Mater. Chem. C, 2020, 8, 968–976.
22. S. K. Singh, K. Kinashi, N. Tsutsumi, W. Sakai and B. J. Jackin, Opt. Mater. Express, 2024, 14, 277–292.
23. Y. Zhai, L. Cao, Y. Liu and X. Tan, Materials, 2020, 13, 5562.
24. A. Shishido, Polym. J., 2010, 42, 525–533.
25. N. Berberova-Buhova, L. Nedelchev, G. Mateev, E. Stoykova, V. Strijkova and D. Nazarova, Opt. Mater., 2021, 121, 111560.
26. L. Nedelchev, D. Ivanov, N. Berberova, V. Strijkova and D. Nazarova, Opt. Quantum Electron., 2018, 50, 1–9.
27. L. Nedelchev, G. Mateev, L. Nikolova, D. Nazarova, B. Ivanov, V. Strijkova, E. Stoykova, K. Choi and J. Park, Appl. Opt., 2023, 62, D1–D7.
28. N. Berberova, D. Daskalova, V. Strijkova, D. Kostadinova, D. Nazarova, L. Nedelchev, E. Stoykova, V. Marinova, C. Chi and S.-H. Lin, Opt. Mater., 2017, 64, 212–216.
29. S. Hvilsted, C. Sánchez and R. Alcalá, J. Mater. Chem., 2009, 19, 6641–6648.
30. J. Zhou, J. Yang, Y. Ke, J. Shen, Q. Zhang and K. Wang, Opt. Mater., 2008, 30, 1787–1795.
31. G. Cipparrone, P. Pagliusi, C. Provenzano and V. P. Shibaev, J. Phys. Chem. B, 2010, 114, 8900–8904.
32. L. Nedelchev, G. Mateev, V. Strijkova, V. Salgueiriño, D. S. Schmool, N. Berberova-Buhova, E. Stoykova and D. Nazarova, Photonics, 2021, 306.
33. P. Pagliusi, B. Audia, C. Provenzano, M. Pinol, L. Oriol and G. Cipparrone, ACS Appl. Mater. Interfaces, 2019, 11, 34471–34477.
34. N. Tverdokhleb, S. Loebner, B. Yadav, S. Santer and M. Saphiannikova, Polymers, 2023, 15, 463.
35. L. Nedelchev, E. Stoykova, G. Mateev, B. Blagoeva, A. Otsetova, D. Nazarova, K. Hong and J. Park, Opt. Commun., 2020, 461, 125269.
36. D. Nazarova, L. Nedelchev, N. Berberova-Buhova and G. Mateev, Nanomaterials, 2023, 13, 2946.
37. K. Kinashi, I. Nakanishi, W. Sakai and N. Tsutsumi, Macromol. Chem. Phys., 2019, 220, 1800456.
38. B. Jackin, M. Shirai, H. Haginaka, K. Kinashi, N. Tsutsumi and W. Sakai, Nanoscale Res. Lett., 2022, 17, 44.
39. S. K. Singh, H. Haginaka, B. J. Jackin, K. Kinashi, N. Tsutsumi and W. Sakai, J. Imaging, 2022, 8, 144:1–144:15.
40. K. Kinashi, I. Nakanishi, W. Sakai, N. Tsutsumi and B. J. Jackin, New J. Chem., 2023, 47, 5751–5758.
41. K. Kinashi, T. Fukami, Y. Yabuhara, S. Motoishi, W. Sakai, M. Kawamoto, T. Sassa and N. Tsutsumi, NPG Asia Mater., 2016, 8, e311–e311.
42. S. K. Singh, S. Notte, R. Yamaguchi, K. Kinashi, N. Tsutsumi, W. Sakai, Y. Awatsuji and B. J. Jackin, Opt. Lett., 2024, 49, 1053.
43. S. K. Singh, K. Kinashi, N. Tsutsumi, W. Sakai and B. J. Jackin, Opt. Express, 2024, 32, 31162.
44. S. K. Singh, K. Kinashi, N. Tsutsumi, W. Sakai and B. J. Jackin, Opt. Express, 2024, 32, 22602.
45. Y. Yuan, K. Zhang, Q. Wu, S. N. Burokur and P. Genevet, Nat. Commun., 2024, 15, 6682.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma01286k

---