Open Access Article
Open Access ArticleObservation of Griffiths-like phase and magnetocaloric effect in disordered Y2CoCrO6 double perovskite†
M. A.
Islam‡
ab,
Mohasin
Tarek‡
 a,
Rimi
Rashid
c,
M. A. A.
Bally
d,
Ferdous
Ara
a,
Rimi
Rashid
c,
M. A. A.
Bally
d,
Ferdous
Ara
 e and
M. A.
Basith
e and
M. A.
Basith
 *a
*a
aNanotechnology Research Laboratory, Department of Physics, Bangladesh University of Engineering and Technology, Dhaka-1000, Bangladesh. E-mail: mabasith@phy.buet.ac.bd
bDepartment of Physics, University of Chittagong, Chittagong-4331, Bangladesh
cMaterials Science Division, Atomic Energy Center, Dhaka 1000, Bangladesh
dGovernment Shaheed Suhrawardy College, Dhaka, Bangladesh
eInstitute of Multidisciplinary Research of Advanced Materials, Tohoku University, 2-1-1, Katahira, Aoba-ku, Sendai 980-0877, Japan
First published on 16th January 2025
Abstract
The increasing demand for advanced materials with multifunctional magnetic properties has sparked growing interest in rare-earth and transition metal-based double perovskites. In this study, we comprehensively investigate disordered Y2CoCrO6 (YCCO), synthesized via the sol–gel method. Structural analysis confirms a single-phase orthorhombic crystal structure with B-site disorder, as revealed by X-ray photoelectron spectroscopy, which also identifies mixed valence states of Co and Cr due to antisite disorder and oxygen vacancies. This structural disorder profoundly impacts YCCO′s magnetic properties, leading to the emergence of a Griffiths-like phase, detected through inverse susceptibility measurements. Additionally, the material exhibits both antiferromagnetic and weak ferromagnetic behaviors, evidenced by a negative Curie–Weiss temperature and unsaturated magnetic hysteresis loops. Arrott plot analysis indicates a second-order phase transition and magnetocaloric measurements reveal a maximum entropy change (Smax) of 0.217 J kg−1 K−1, a relative cooling power (RCP) of 17.36 J kg−1, and a temperature averaged entropy change (TEC) of 0.17 J kg−1 K−1 over a temperature span (Tlift) of 30 K under a 5 T field, showcasing its potential for low-temperature and multistage cooling applications. Although its modest magnetocaloric effect (MCE) performance is attributed to its antiferromagnetic nature with weak ferromagnetic contributions and a low Curie temperature, this work represents a significant step in unveiling the potential of YCCO for multifunctional applications. Future optimization through chemical doping, nanostructuring, and compositional modifications is proposed to enhance its magnetocaloric and functional properties, positioning YCCO as a strong candidate for advanced magnetic and cooling technologies.
1. Introduction
The global push towards sustainable energy and advanced technology has created an urgent demand for materials that can meet the rigorous performance requirements of modern applications.1–3 As the world transitions to cleaner energy sources and more efficient electronic devices, there is an increasing need for materials that can perform reliably under extreme conditions, while also offering multifunctionality. For instance, in the realms of energy storage, spintronics, and environmental remediation, materials are required that not only exhibit robust electrical and magnetic properties but also maintain these properties over long periods and across a range of temperatures and environments.3,4 Traditional materials often fall short of these demands, prompting the exploration of new classes of compounds with enhanced capabilities. The rare-earth and transition metal-based double perovskite (DP) materials, with the formula R2BB′O6 (where R stands for rare-earth elements and B, B′ are transition metals), have gained attention for their multifunctional properties, such as magnetocaloric, magnetoresistance, magnetocapacitance, magnetodielectric, and multiferroic characteristics.1,5–7 Ongoing research focuses on harnessing the potential of these materials for applications in spintronics, memory storage devices, energy storage devices, optoelectronics, catalysis, and other diverse fields.5,8–10 When B and B′ are different transition metals with distinct sizes and charges, they often form ordered structures.11 These different cations within a DP can occupy specific crystallographic locations in an organized manner, reducing repulsive forces and leading to a well-defined crystal structure. Conversely, if B and B′ are similar in size and charge, they are more likely to be distributed over the octahedral sites in a disordered manner.11–13 The similar characteristics of these ions make them interchangeable within the crystal lattice, leading to an absence of long-range order.12,14 Additionally, transition metals that commonly exhibit multiple oxidation states play a crucial role in creating a disordered structure in DP compounds.1,15Oxygen vacancies in crystal lattices are known to induce mixed valency in compounds, particularly in transition metal oxides.16,17 This structural feature, along with the specific steps involved in the synthesis process and the occurrence of octahedral distortion, significantly contributes to the disordered structure of double perovskite (DP) materials.18,19 In ordered DP materials, interactions among B-site cations are facilitated through the long-range B–O–B′ network. However, when B-site disorder, or antisite disorder (ASD), is present, it introduces two additional interaction pairs: B–O–B and B′–O–B′.11,19 The resulting disorder in the arrangement of B-site cations, coupled with oxygen vacancies, can substantially affect the electronic and magnetic properties of DP materials, leading to complex phenomena such as the Griffiths-like phase, exchange bias effect, magnetocaloric effect, and sign reversal of magnetization, among others.2,8,14,20,21
The Griffiths phase (GP), initially proposed by Robert B. Griffiths in the study of randomly diluted Ising ferromagnets, exemplifies one such phenomenon, characterized by the coexistence of ferromagnetic (FM) clusters within a paramagnetic (PM) matrix.7,22 This phase reflects a unique coexistence of disordered and ordered regions within the system, which notably disappears upon the application of a critical magnetic field.2,7 The disappearance of the GP under a critical applied magnetic field (AMF) highlights the pronounced sensitivity of disordered systems to external parameters, illustrating the dynamic nature of magnetic phase transitions. Consequently, exploring the GP as a function of AMF and temperature becomes a particularly complex and intriguing aspect of magnetic systems.7,8 Previous studies have identified the GP within the temperature range (TC < T < TG), where TC represents the ferromagnetic-like transition temperature and TG denotes the Griffiths temperature.7,8 In this intermediate temperature range, the system lacks both long-range FM ordering and true PM behavior, thus revealing the highly intricate underlying physics that governs these disordered magnetic systems.
Furthermore, rare-earth based DP materials often exhibit multiple magnetic phases, contributing to their complex magnetic behavior.2,23,24 This complexity, in turn, facilitates the emergence of the exchange bias (EB) phenomenon. The EB effect manifests at the interfaces between different magnetic phases within the perovskite materials, introducing a unidirectional FM exchange anisotropy.25 This effect is characterized by shifts in the magnetic hysteresis (M–H) loop along either the horizontal or vertical axis, deviating from its normal symmetric position as the system is cooled in the presence of an external magnetic field through its transition temperature. When the shift in the M–H loop occurs without the influence of an external magnetic field during the cooling process, it is indeed referred to as the spontaneous EB effect or zero-field-cooled EB effect. This effect offers substantial potential for developing a wide range of technological applications, including sensing technologies, magnetic data storage, and the development of novel spintronic devices.2,19,26 The coexistence of GP and EB in rare-earth and transition metal-based DPs is noteworthy from both fundamental physics and potential technological applications standpoints.14,21,26,27
In recent years, the magnetocaloric effect (MCE) has gained considerable attention as a promising phenomenon for developing efficient and eco-friendly cooling technologies.28,29 The MCE describes the temperature change of a material in response to an applied magnetic field and has emerged as a viable alternative to conventional refrigeration methods. Among the various materials investigated for their MCE properties, double perovskite compounds have attracted significant interest due to their complex magnetic interactions and potential for high-performance cooling applications.8,30 Moreover, structural disorder, such as oxygen vacancies, can further influence the magnetic interactions and enhance the MCE in these materials.15 Double perovskites with oxygen vacancies create unique opportunities to modulate the magnetic properties and the MCE. These vacancies can disrupt the local magnetic environment, causing changes in the exchange interactions between magnetic ions. Such disturbances have the potential to enhance the magnetic entropy change (ΔS) and adiabatic temperature change (ΔT) associated with the MCE. In double perovskites, magnetic behavior can be significantly altered by oxygen vacancies, leading to an increased MCE, as demonstrated by previous investigation.15 However, in systems dominated by antiferromagnetic (AFM) interactions with minor contributions from weak ferromagnetic (FM) ordering, the magnetocaloric effect (MCE) performance is inherently limited due to reduced magnetic moment alignment and lower magnetic entropy changes, particularly under moderate external magnetic fields.31 These limitations hinder their efficiency in practical magnetic refrigeration applications. To overcome these challenges, strategies such as chemical doping to introduce magnetic impurities or modify exchange interactions, nanocomposite formation to exploit interfacial effects and enhance local magnetic coupling, and compositional modifications to tune the magnetic phase transitions and improve entropy change can be employed.31,32
The observation of the Griffiths-like phase in rare-earth and transition metal-based double perovskites, such as YCCO, is significant from both fundamental and applied perspectives. These phenomena enhance our understanding of magnetic interactions in disordered systems while also offering potential for further advancements in technology. Furthermore, the magnetocaloric effect observed in YCCO contributes to the broader exploration of magnetic materials with distinct thermal and magnetic properties. By exploring these multifunctional properties, our research connects fundamental physics with practical innovations, paving the way for the development of next-generation magnetic systems.
2. Experimental details
The YCCO double perovskite was synthesized using a facile sol-gel method.33 At first, stoichiometric volume of Y(NO3)3·6H2O, Co(NO3)3·6H2O, and Cr(NO3)3·9H2O were dissolved individually in 40 mL of deionized water and stirred for approximately 15 minutes with a magnetic stirrer. Afterwards, the separate solutions were combined, and citric acid (C6H8O7) was incorporated into the mixture. After adding ammonium hydroxide, the pH of the mixture was balanced within a range of between 6 and 7. Following this, ethylene glycol has been added to form a polymeric metal cationic network, resulting in the formation of a gel precursor. After four hours, the temperature increased to 200 °C, causing the gel to burn entirely and yield a powder form material. The resultant material was ground by an agate mortar and then calcined with air at approximately 800 °C for 6 hours to achieve the desired crystallization.The crystal system as well as lattice parameters of YCCO DP have been investigated through the analysis of powder X-ray diffraction (XRD) data collected at room temperature. This XRD data was collected using a Rigaku SmartLab X-ray diffractometer equipped with Cu-Kα radiation. Subsequently, the acquired XRD patterns were subjected to Rietveld analysis using FULLPROF software34 to ascertain the crystal structure with space group, lattice parameters, atomic positions, bond lengths, and bond angles. To identify the functional groups in the YCCO, Fourier transform infrared (FTIR) spectroscopy was utilized with 400 cm−1 to 4000 cm−1 wavenumber. Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) were conducted in a nitrogen environment employing the instrument (NETZSCH STA 449 F3 Jupiter), with the heating rate programmed at 10 °C min−1. The morphology and particle-size distribution of the synthesized YCCO compound were scrutinized using a field emission scanning electron microscope (FE-SEM) coupled with energy dispersive X-ray (EDX). Furthermore, transmission electron microscopy (TEM) imaging was performed to assess the size, crystallographic orientation, and crystal planes. To identify the oxidation states of various components present in YCCO, X-ray photoelectron spectroscopy (XPS) was employed. Magnetic measurements were conducted using a SQUID magnetometer. The temperature-dependent magnetization M(T) was conducted at various applied magnetic fields under zero-field-cooled (ZFC) and field-cooled (FC) approaches. Moreover, field-dependent magnetization measurements were carried out at various temperatures. Furthermore, the magnetocaloric effect (MCE) was determined from magnetization measurements as a function of the applied magnetic field at different temperatures, with a temperature interval of ΔT = 5 K.
3. Results and discussion
3.1. Crystal structure analysis
The crystallographic parameters of YCCO DP have been determined using Rietveld refinement of the powder XRD pattern,35,36 as shown in Fig. 1(a). From this analysis, it is evident that the YCCO displays a single-phase orthorhombic crystal structure with Pbnm space group. Notably, most DP based on 3d transitional metals and rare-earth elements have orthorhombic or monoclinic crystalline structures.37 Our observed outcome is consistent with the theoretically predicted result, as determined through the calculation of the tolerance factor, which yielded a value of 0.865.38 The reliability factors Rp = 2.20%, Rw = 2.82%, and χ2 = 2.84 confirm good consistent between the refined and experimental XRD patterns of YCCO double perovskite. The Rietveld refinement of YCCO provided the following value of lattice constants: a = 5.20, b = 5.48, c = 7.46, α = β = γ = 90°, with a unit cell volume of 212.75 Å3. The extensive local crystalline structures, as generated by the VESTA software,39 are visually presented in Fig. 1(b)–(f). Fig. 1(b) illustrates the orthorhombic unit cell, while Fig. 1(c) through Fig. 1(f) provide a comprehensive view of the interatomic bond distance and interbond angle, offering insights into the different orientations of octahedral coordination involving Co/Cr atoms, each surrounded by six oxygen atoms. The Fig. 1(c)–(f) reveal that the bond distance and interbond angles in the different octahedra are not exactly same (Co/Cr–O1 ≠ Co/Cr–O2, and Co/Cr–O1–Co/Cr ≠ Co/Cr–O2–Co/Cr ≠ 180°), and (Co/Cr–O1–Co/Cr ≠ Co/Cr–O2–Co/Cr ≠ 180°), as presented in Table 1. The observed value of the interbond angle indicates the existence of a distorted unit cell within the YCCO system. The average bond distance (Co/Cr–O) and interbond angle (Co/Cr–O–Co/Cr) were found to be 1.929 and 150.12 respectively. To quantify the distortion of YCCO system, we calculated the tilt angle (ϕ) by considering the interbond angle (θ) of Co/Cr–O–Co/Cr, following the expression: ϕ = (180 − θ)/2. The calculated value of ϕ is 14.94°, suggests that the octahedra exhibit a deviation from their equilibrium positions, in consistent with the previously reported double perovskite materials.24,40 The structural parameters from the Rietveld refined analysis are presented in Table 1.| Atom | Wyckof site | x | y | z | Bond distance(Å) | Interbond angle(°) |
|---|---|---|---|---|---|---|
| Y | 4c | −0.016 | 0.066 | 0.250 | Co/Cr−O1 = 1.926 | 〈Co/Cr−O1 −Cr/Co〉 = 149.89 |
| CO | 4b | 0.5 | 0 | 0 | Co/Cr−O2 = 1.932 | 〈Co/Cr−O2−Cr/Co〉 = 150.33 |
| Cr | 4b | 0.5 | 0 | 0 | ||
| O1 | 4c | 0.290 | 0.293 | 0.052 | ||
| O2 | 8d | 0.294 | 0.665 | 0.963 | ||
3.2. FTIR and Thermal stability analyses
To obtain insight into the chemical bonds, functional groups, and bond lengths within the YCCO material, we performed room-temperature FTIR analysis. The stretching and bending vibrations of the metal–oxygen (Co/Cr–O) bonds within the CoO6/CrO6 octahedra were observed, and no undesired functional groups were detected in YCCO. Detailed discussions are provided in the ESI† (Note S1).Moreover, TGA-DSC measurements were performed to study thermal stability. The TGA curve presented in ESI,† Fig. S1(b) demonstrates the thermal stability of YCCO powder, with a slight weight loss of about 3% recorded from the temperature 30 °C to 1000 °C, consistent with other DP materials.24,41 The weight loss at lower temperatures in YCCO is due to the combined effects of water evaporation and the adsorption of various gases onto or within this material.42 At higher temperatures, YCCO oxides may break down, possibly through a process that entails the thermal decomposition of metal oxide or the release of oxygen from the crystal lattice.42,43 The DSC analysis of YCCO conducted from 30 °C and 1000 °C reveals that the material exhibits thermal stability and does not experience crystallographic phase changes within this temperature. This information is valuable in understanding the thermal behavior and stability of YCCO, which can be important in various scientific and industrial applications such as solid oxide fuel cells, thermoelectric power generator, etc.44,45
3.3. Surface morphology
The morphology of the synthesized YCCO material was investigated using electron microscopy techniques, with the FESEM and low-magnification TEM images presented in Fig. 2(a) and (b), respectively. The analysis of these images revealed that the nanoparticles have an average size of 80 nm, ranging from 30 to 150 nm, and a detailed particle size distribution histogram is available in Fig. S2 of the ESI.† To confirm the elemental composition, EDX analysis was performed, verifying the presence of Y, Co, and Cr elements in the YCCO DP, as documented in Table S1 of the ESI.† Notably, the EDX results were consistent with theoretical predictions, reinforcing the synthesis accuracy. Further structural insights were obtained through high-resolution transmission electron microscopy (HRTEM), as shown in Fig. 2(c), which identified interplanar spacings of 2.7 Å, 3.2 Å, and 4.3 Å corresponding to the (0 2 0), (1 1 1), and (1 0 1) crystal planes, respectively. Complementing this, the selected area electron diffraction (SAED) pattern in Fig. 2(d) displayed a regular periodic diffraction pattern with bright spots, confirming the nanocrystalline structure of the material. Using CrysTbox software,46 the crystallographic zone axis was determined to be (0 0 −1), with associated vector notations (0 0 −2), (0 1 −2), (0 1 −1), and (0 1 0), providing a comprehensive understanding of the material's crystallographic orientation.3.4. XPS analysis
The XPS spectrum of YCCO, represented in Fig. S3 (ESI†), confirms the absence of undesirable elements in the synthesized YCCO material. Analysis of the XPS spectrum of yttrium (Fig. 3(a)) exhibits two well-defined peaks at binding energies of 156.2 eV and 158.2 eV, which are attributed to the 3d5/2 and 3d3/2 orbitals, respectively, and are indicative of the Y3+ in YCCO. In Fig. 3(b), the cobalt (2p3/2 and 2p3/2) peaks exhibit doublet patterns due to spin-orbit splitting, with lower energy peaks at 780.3 and 795.3 eV indicating the Co3+, while higher energy peaks at 782.2 and 797.1 eV correspond to the Co2+.47 Furthermore, two additional peaks at 790 and 805 eV are recognized as satellite peaks in the spectrum of the Co region. These observed Co peaks align with those observed in previous studies of Co-based compounds.15,26,41,48 The molar ratio of Co2+ to Co3+ ions, determined through peak fitting of the Co-2p3/2 and Co-2p3/2 spectrum, was found to be 24% to 76%. Moreover, the deconvolution analysis of the chromium (2p3/2 and 2p1/2) peaks, as depicted in Fig. 3(c), displayed 4 different peaks, indicating the multiple oxidation states of Cr. More precisely, the peaks identified at 575.9 and 585.5 eV are attributed to Cr2+, while the peaks at 579.3 and 588.5 eV are indicative of Cr3+.24,49–51 The molar ratio of Cr2+ to Cr3+ was determined to be 43%:57%. Analysis of the oxygen 1s spectra (Fig. 3(d)) displays multiple peaks after deconvolution, located at binding energies of 529.1 eV, 530.5 eV, and 531.8 eV. These peaks correspond to Co/Cr–O bonds (Olat), oxygen vacancies (Ovac), and surface hydroxyls (Oads), with respective molar proportions of 41%, 34%, and 25%.52–55 This oxygen vacancy is consistent with the similar Dy-based DP.52 The coexistence of mixed valence states in both Co and Cr ions within the YCCO material is indicative of disorder at the B-site and the absence of long-range ordering, potentially imparting an impact on the magnetic properties elucidated in the following section.3.5. Magnetic characterization
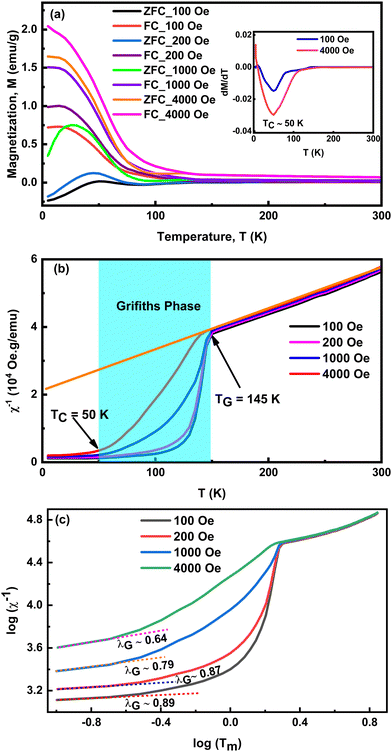
Fig. 4(a) presents temperature-dependent magnetization (M–T) curves for YCCO over the temperature range of 5 K to 300 K, measured under various applied magnetic fields (AMF) (100 Oe, 200 Oe, 1000 Oe, 4000 Oe), with data collected using the ZFC and FC measurement techniques. It appears that all the M–T curves are identical and exhibit a linear behavior from 145 K to 300 K. A notable bifurcation was observed in the ZFC–FC curves, persisting even under high AMF up to 4000 Oe, and this divergence can be due to the magnetic frustration present within the YCCO DP.20,56,57 This magnetic frustration arises may be due to the mixed valence states of Co and Cr cations, as confirmed by the results of XPS, leading to a complicated and distinct magnetic behavior.20 The observed bifurcation in magnetic behavior decreases with increasing AMF, as a result of the spin reorientation process. Notably, the MZFC exhibits an unusual negative magnetization in the low-temperature range under lower magnetic fields of 100 Oe and 200 Oe. The negative magnetization observed at low magnetic fields, a phenomenon also noted in similar DP compounds, has been previously documented.5,14,56,58 However, when a higher magnetic field above 1000 Oe is applied, MZFC shifts to positive values. Notably, the disordered LaSrCoRuO6 compound revealed negative MZFC value at the lower AMF, while the ordered LaSrCoRuO6 showed consistently positive MZFC values all over the temperature range.59 In the YCCO compound, this negative MZFC may be due to the disordering of Co and Cr cations.26,56The magnetic phase transition (TC) is determined by locating the minimum point on the differential curve of FC magnetization, as depicted in inset Fig. 4(a). The value of (TC) was observed to be approximately 50 K for AMF of both 100 Oe and 4000 Oe.
Fig. 4(b) demonstrated the temperature dependant inverse susceptibilities (χ−1) curves in FC conditions for different AMF. This figure demonstrates that χ−1 follows a linear trend between 145 and 300 K, suggesting a PM nature. Furthermore, within this temperature region, χ−1 conforms the Curie–Weiss (C–W) law, χ−1(T) = (T − ΘCW)/2. Here, C and ΘCW are the Curie constant, and C–W temperature, respectively. The linear fit analysis yielded a ΘCW value of −165 K. This large negative ΘCW value points to the existence of AFM components within the YCCO compound. The observed AFM behavior may be attributed to the distortion of octahedra in the DP materials. According to the Goodenough–Kanamori rule, the ideal condition for a FM superexchange interaction occures when the angle involving B–O–B′ is 180°.60,61 However, in this investigation, the Rietveld refinement analysis revealed that the superexchange angle between Co and Cr ions, mediated by the oxygen ion, was found to be 150.12°. The existence of this distortion results in the appearance of an AFM interaction with the FM phase in the YCCO material.8,62
Moreover, the effective magnetic moment (μeff) of 5.042μB f.u.−1 in the paramagnetic state was determined by applying the given equation and the C–W parameter  .33,41,58 Further, we have conducted a comparison between the experimentally determined effective magnetic moment (μeff) and the theoretical magnetic moment (μcal) which was determined using the provided expression41
.33,41,58 Further, we have conducted a comparison between the experimentally determined effective magnetic moment (μeff) and the theoretical magnetic moment (μcal) which was determined using the provided expression41
 | (1) |
The electronic configurations and corresponding high spin magnetic moment of Co and Cr cations employed in eqn (1) are as follows: Co2+ [μCo2+ = 3.88μB], Cr2+ [μCr2+ = 4.90μB], Co3+ [μCo3+ = 4.99μB], and Cr3+ [μCr3+ = 3.88μB].8,15,27 The calculated value of μcal is 6.385μB f.u.−1, surpassing μeff, possibly due to the presence of B-site disorder (ASD) component in the YCCO compound. The ASD in the YCCO system is linked to the presence of mixed valence states for both Co (Co2+/Co3+) and Cr (Cr2+/Cr3+) ions, as revealed by XPS analysis. The initiation of the disordered state introduces interactions of the Co2+/Cr2+–O2−–Co2+/Cr2+, Co3+/Cr3+–O2−–Co3+/Cr3+ configurations.8 On the other hand, the ordered state is attributed to the only two interactions Co2+–O2−–Cr2+ and Co3+–O2−–Cr3+.8
Notably, the value of χ−1 deviates significantly below 145 K, as shown in Fig. 4(b). This deviation (below 145 K) from the Curie–Wiess law gradually decreases as AMF increases. This phenomenon is generally considered as Griffiths-like phase (GP), which is observed in other B-site disordered DP materials.8,56,63 Within the GP region, the relationship between the inverse magnetic susceptibility (χ−1) and temperature (T) obeys the following power law expression:8,56
| χ−1(T) ∝ (T − TRC)(1−λ) | (2) |
Furthermore, field-dependent magnetization (M–H) measurements of the YCCO material were performed at temperatures of 5 K, 100 K, and 300 K, as depicted in Fig. 5(a). It is observed that at 300 K, the M–H curve of the YCCO nanoparticles demonstrates an entirely straight line, indicating a PM behavior. Similarly, at 100 K, the M–H curve of the YCCO material exhibits a linear behavior with a narrow loop, indicating a PM nature of the material at this temperature. In addition, it is noteworthy that this temperature is situated in the GP region, which is a PM dominant region. The observation of a wide hysteresis loop at 5 K that remains unsaturated up to 70 kOe indicates the existence of weak FM and AFM behavior in YCCO material.
Therefore, we have determined the saturation magnetization (MS) from the M–H curve (5 K), applying the following relationship:65
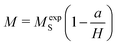 | (3) |
For theoretical MS calculation of YCCO, we considered the magnetic moments of Ni and Cr cations, incorporating their molar percentage ratios [(Co2+)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Co3+) = 24%
(Co3+) = 24%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76% and (Cr2+)
76% and (Cr2+)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (Cr3+) = 43%
(Cr3+) = 43%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57%]. Hence, the magnetic moment of Co and Cr could be calculated using the following expressions:
57%]. Hence, the magnetic moment of Co and Cr could be calculated using the following expressions:
| 〈mCo〉 = μCo2+ × 24% + μCo3+ × 76% | (4) |
| 〈mCr〉; = μCr2+ × 43% + μCr3+ × 57% | (5) |
The magnetic moments were 4.655μB f.u.−1 for Ni and 4.318μB f.u.−1 for Cr. Moreover, it has been considered that the YCCO sample consists of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios of Co and Cr, along with an AFM interaction between the Co and Cr ions. Subsequently, we calculated the theoretical value of MS using the following equation:
1 molar ratios of Co and Cr, along with an AFM interaction between the Co and Cr ions. Subsequently, we calculated the theoretical value of MS using the following equation:
| MtheoS = 〈mCo〉 − 〈mCr〉 | (6) |
The theoretically calculated value of MS was 0.337μB f.u.−1, exceeding the experimentally obtained value of 0.223μB f.u.−1 The discrepancy between theoretical and experimental observations may be due to the substantial ASD and the presence of oxygen vacancies in the YCCO perovskite.16
Moreover, the presence of mixed magnetic state indicates the existence of the EB effect in YCCO. The magnetic hysteresis (M–H) loop analysis performed at 5 K temperature reveals that the loop shifts towards the positive x-axis direction (Inset Fig. 1(a)). The positive coercive field (Hc1) and negative coercive field (Hc2) for the hysteresis loop were found to be 3120 Oe and 2818 Oe, respectively. Therefore, we have calculated the EB field strength using the following equation:19
 | (7) |
The HEB in YCCO was found to be 151 Oe. The observed EB in our YCCO system is likely attributed to the exchange interactions between the FM region comprising ordered Co/Cr cations and the AFM region consisting of disordered Co/Cr cations.
To investigate the magnetocaloric effect (MCE) in YCCO double perovskite, isothermal magnetization measurements were performed as a function of the magnetic field at various constant temperatures, ranging from 10 to 100 K in 5 K intervals near the transition temperature. Fig. 6(a) presents the isothermal magnetization curves of the YCCO compound, revealing changes in its magnetic behavior as the sample transitions from the AFM to PM phase with increasing temperature. Below the Curie temperature (TC), all curves show a rapid increase in magnetization at low fields, though magnetic saturation was not observed up to an applied field of 5 T. This behavior suggests the coexistence of FM and AFM phases in the compound.66 Notably, a significant change in magnetic behavior occurs around TC, where the curves exhibit linear behavior above TC, indicating the PM phase.
 | ||
| Fig. 6 (a) Isothermal magnetization curves near the transition temperature. (b) Arrott plots confirming the second-order phase transition. | ||
Critical exponents were used to analyze the behavior near the phase transition, providing insights into the magnetocaloric properties of the material. The critical exponent δ, in particular, describes the field dependence of the critical isothermal magnetization at TC.67 This exponent follows the power-law relation given below:67
| M = DH1/δ, at T = TC | (8) |
The critical exponent δ was determined from the critical isotherm analysis at TC using eqn (8). ESI,† Fig. S4(a) shows the M vs. H curves for the YCCO compound at TC, while ESI,† Fig. S4(b) presents the corresponding log–log plot of the M–H data, which is non-linear, indicating unusual behavior. According to eqn (8), the slope of the straight line in the log–log plot corresponds to (1/δ), yielding a δ value of 1.54. Several models, including the mean field model, 3D Heisenberg model, 3D Ising model, and tri-critical mean field model, describe magnetic interactions near the phase transition temperature. Table 2 compares the theoretical δ values for these models with the experimental δ value obtained for YCCO.68 The comparison reveals that the experimental δ does not match any of the four models typically associated with the FM to PM phase transition. This discrepancy suggests the coexistence of both FM and AFM phases in the YCCO compound.
The M–H data for YCCO were analyzed by plotting M2vs. H/M, known as Arrott plots, to determine the nature of the magnetic phase transition, as shown in Fig. 6(b). The positive slope of the Arrott plots confirms a second-order phase transition in the YCCO compound. According to the Banerjee criterion,70 the positive slope indicates a second-order FM–PM phase transition. This is a favorable characteristic in magnetic materials, as second-order transitions ensure a continuous change in magnetic entropy, whereas first-order transitions cause a discontinuous shift.70 The second-order phase transition also allows the construction of a universal master curve near the transition temperature, which will be discussed later. The observed mixed valence states and phase transition behavior in YCCO are consistent with those reported for other perovskite materials.7,8,66
To evaluate the MCE in our YCCO compound, we calculated the magnetic entropy change (ΔSm) and the relative cooling power (RCP). As the MCE typically peaks near the magnetic phase transition temperature, our investigations focus on this critical region. The ΔSm value of any magnetic material is usually calculated using the Maxwells thermodynamic relation:71
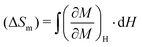 | (9) |
The magnetic entropy change (ΔSm) of YCCO as a function of temperature under various applied magnetic fields has been calculated from the isothermal M–H data using eqn 9, as presented in Fig. 7(a). The calculated values of ΔSm are negative, which is characteristic of a FM system. For clarity, the plot of −ΔSmvs. temperature reveals that the maximum magnetic entropy change, denoted as (−ΔSm)max, occurs around TC, where the change in magnetization is at its peak. This is due to the proportional relationship between entropy change and the derivative of magnetization with respect to temperature (dM/dT). It is also observed that the −ΔSmvs. T curves broaden, and (−ΔSm)max increases with higher applied fields. This behavior is attributed to changes in the spin ordering process influenced by the applied magnetic field.72 For the investigated sample, the (−ΔSm)max values are 0.035, 0.099, 0.125, 0.165, and 0.217 J (kg−1 K−1) for applied magnetic field changes (ΔH) of 1, 2, 3, 4, and 5 T, respectively. Fig. 7(b) illustrates how the maximum entropy of the YCCO compound varies with changes in the applied magnetic field at the Curie temperature (TC). The results indicate that as the applied field increases, the change in maximum entropy gradually slows, a trend that is consistent with observations in other ferromagnetic perovskite materials.73,74 The temperature-averaged entropy change (TEC), a critical parameter for assessing the performance of magnetocaloric materials, is calculated by the following equation75–77 and plotted as a function of temperature lift (Tlift) in the inset of Fig. 7(a). is plotted as a function of temperature lift (Tlift) in the inset of Fig. 7(a).
 | (10) |
The TEC exhibits a steady increase with Tlift across all applied magnetic fields (1 T to 5 T), reflecting the ability of the material to sustain entropy changes over a broad temperature range. This behavior is vital for practical cooling technologies, where the refrigerant's performance depends on its capacity to operate efficiently over extended temperature spans. At a field of 1 T, the TEC is modest (0.04 J kg−1 K at Tlift = 30 K), but it significantly improves at higher fields, reaching 0.17 J kg−1 K−1 at Tlift = 30 K under 5 T. This trend highlights the dependence of TEC on magnetic field strength, as higher fields facilitate greater magnetic moment alignment by overcoming AFM interactions and intrinsic magnetic inhomogeneities. The linear dependence of TEC on Tlift also indicates a consistent and predictable performance, which is advantageous for engineering magnetic refrigeration devices. From an application perspective, the moderate TEC values of YCCO compared to other high-performance magnetocaloric materials suggest that its cooling efficiency may not be optimal for single-cycle applications. However, its ability to maintain entropy changes over a wide temperature range is advantageous for multistage or cascade cooling systems, where uniform cooling over a broad thermal span is required. Furthermore, the materials performance under higher magnetic fields suggests its suitability for low-temperature applications, such as cryogenic cooling, where stronger fields are typically available.
The scaling law quantifies the degree of magnetic field dependence of the maximum entropy change in materials exhibiting second-order phase transitions. This scaling law is expressed as follows:78
| (ΔSm)max ∝ μ0Hn | (11) |
At high magnetic fields, the coexistence of AFM and PM phases can occur in two ways:79
(i) AFM may manifest as secondary phases within the PM region, which hinders the construction of a universal master curve for the MCE.
(ii) A canted magnetic state may emerge due to the competition between AFM and FM interactions, resulting in the merging of all normalized MCE curves into a single master curve.
To address this, we rescaled the magnetic entropy change across various applied magnetic fields into normalized entropy and plotted it against the rescaled temperature (Θ). Each entropy change curve was normalized by its respective maximum entropy change, while the temperature axis was rescaled using the relation provided below:
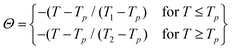 | (12) |
 | (13) |
Fig. 7(c) presents the normalized entropy change plotted against the rescaled temperature for the YCCO compound. The data indicate that the YCCO double perovskite does not converge into a universal curve for temperatures both below and above the TC. The divergence of the curves below TC suggests that the transition does not correspond to a pure second-order magnetic transition. Similarly, the divergence of the curves above TC does not reflect a purely PM state. The presence of a secondary phase may impede the universal behavior of the curves in the PM region, confirming the existence of AFM as a secondary phase within the PM region.79 This analysis aligns with the results observed in Fig. 5(a), 6(a) and 7(c).
Another important property of magnetocaloric materials is RCP. RCP is defined as the amount of heat transferred from a hot reservoir to a cold reservoir during an ideal refrigeration cycle. It is typically calculated using the following formula:73
| RCP= (ΔSm)max·δTFWHM | (14) |
In this context, δTFWHM = the full width at half maximum of the (−ΔSm) versus temperature curve.73 This parameter represents the temperature range over which a material can be effectively utilized for refrigeration applications. The values of RCP and δTFWHM are summarized in Table 3. As illustrated in Fig. 3(d), both δTFWHM and RCP for the YCCO compound increase with the applied magnetic field. The observed broadening of the phase transition with increasing field is associated with a wider temperature range, represented by the full width at half maximum (FWHM) of the ΔSmversus temperature curve. This wider temperature range of δTFWHM results from the enhanced broadening of the phase transition with increasing applied field, as evidenced by the FC and ZFC curves (Fig. 4(a)). This behavior is attributed to the presence of ferromagnetic clusters exhibiting short-range interactions in the paramagnetic region near the phase transition temperature.
| H(T) | (−ΔSm)max (J (Kg−1 K−1)) | FWHM (K) | RCP (J kg−1) |
|---|---|---|---|
| 1 | 0.035 | 57 | 1.995 |
| 2 | 0.099 | 50 | 4.950 |
| 3 | 0.125 | 65 | 8.125 |
| 4 | 0.165 | 75 | 12.375 |
| 5 | 0.217 | 80 | 17.36 |
4. Conclusions
In this study, we successfully synthesized Y2CoCrO6 (YCCO) double perovskite using the sol–gel method and thoroughly investigated its structural and magnetic properties. The YCCO compound displayed a single-phase orthorhombic crystal structure with significant octahedral distortion, as confirmed by Rietveld refinement analysis. This structural distortion, along with antisite disorder at the B-site, greatly influenced the material's magnetic behavior. Magnetic characterization revealed the presence of a Griffiths-like phase, where ferromagnetic (FM) clusters coexist within a paramagnetic (PM) matrix, highlighting the complex magnetic interactions stemming from the disordered arrangement of Co and Cr cations. The observed exchange bias (EB) effect at low temperatures, coupled with unusual negative magnetization under low magnetic fields, indicated the coexistence of FM and antiferromagnetic (AFM) phases, further illustrating YCCO's intricate magnetic behavior. Furthermore, we observed the magnetocaloric effect (MCE) in YCCO, particularly around the magnetic transition temperature, with the broad temperature range attributed to the presence of ferromagnetic clusters embedded within the paramagnetic matrix. The observed magnetocaloric effect (MCE) values, including entropy change and relative cooling power, are modest, primarily due to dominant antiferromagnetic interactions and structural imperfections that constrain the magnetic entropy change. This moderate performance is attributed to the intrinsic antiferromagnetic interactions and B-site disorder inherent in YCCO. Nonetheless, significant enhancement of its magnetocaloric performance could be achieved through strategies such as chemical doping, nanocomposite formation, and compositional modifications. These approaches, which have been successfully employed in similar double perovskites, offer the potential to mitigate structural limitations and optimize magnetic properties. Tailoring YCCOs material characteristics through such methods could unlock its full potential for magnetic refrigeration, particularly in applications requiring moderate cooling efficiency or operation across a broad temperature range.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We express our sincere gratitude to the Committee for Advanced Studies and Research (CASR), Bangladesh University of Engineering and Technology (BUET), Bangladesh for their financial support.References
- M. G. Basavarajappa and S. Chakraborty, ACS Mater. Au, 2022, 2, 655–664 CrossRef CAS PubMed.
- M. Alam, L. Ghosh, S. Majumder, P. Singh, S. V. Kumar, S. Dixit, D. Kumar, K. Anand, S. Kumari, A. K. Ghosh, R. J. Choudhary and S. Chatterjee, J. Phys. D: Appl. Phys., 2022, 55, 255003 CrossRef CAS.
- S.-W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13–20 CrossRef CAS PubMed.
- M. Fiebig, T. Lottermoser, D. Fröhlich, A. V. Goltsev and R. V. Pisarev, Nature, 2002, 419, 818–820 CrossRef CAS PubMed.
- M. Nasir, S. Kumar, N. Patra, D. Bhattacharya, S. N. Jha, D. R. Basaula, S. Bhatt, M. Khan, S.-W. Liu, S. Biring and S. Sen, ACS Appl. Electron. Mater., 2019, 1, 141–153 CrossRef CAS.
- S. Kundu, A. Pal, A. Chauhan, K. Patro, K. Anand, S. Rana, V. G. Sathe, A. G. Joshi, P. Pal, K. Sethupathi, B. R. K. Nanda and P. Khuntia, Phys. Rev. Mater., 2022, 6, 104401 CrossRef CAS.
- S. Saha, A. Dutta, S. Gupta, S. Bandyopadhyay and I. Das, Phys. Rev. B, 2022, 105, 214407 CrossRef CAS.
- R. SilvaJr, C. Santos, M. Escote, B. Costa, N. Moreno, S. Paz, R. Angélica and N. Ferreira, Phys. Rev. B, 2022, 106, 134439 CrossRef CAS.
- A. Biswal, J. Ray, P. Babu, V. Siruguri and P. Vishwakarma, J. Appl. Phys., 2014, 115, 194106 CrossRef.
- M. Devi, I. Rogge, J. Singh, A. L. Sharma, A. Kumar and A. Kumar, ECS Adv., 2023, 034001 CrossRef CAS.
- S. Chakraverty, A. Ohtomo, D. Okuyama, M. Saito, M. Okude, R. Kumai, T. Arima, Y. Tokura, S. Tsukimoto, Y. Ikuhara and M. Kawasaki, Phys. Rev. B, 2011, 84, 064436 CrossRef.
- X. Wang, Z. Liu, H. Deng, S. Agrestini, K. Chen, J.-F. Lee, H.-J. Lin, C.-T. Chen, F. Choueikani, P. Ohresser, F. Wilhelm, A. Rogalev, L. H. Tjeng, Z. Hu and Y. Long, Inorg. Chem., 2022, 61, 16929–16935 CrossRef CAS PubMed.
- H. S. Nair, R. Pradheesh, Y. Xiao, D. Cherian, S. Elizabeth, T. Hansen, T. Chatterji and T. Brückel, J. Appl. Phys., 2014, 116, 123907 CrossRef.
- W. Liu, L. Shi, S. Zhou, J. Zhao, Y. Li and Y. Guo, J. Appl. Phys., 2014, 116, 193901 CrossRef.
- R. S. J. Silva, J. Gainza, C. dos Santos, J. E. F. S. Rodrigues, C. Dejoie, Y. Huttel, N. Biskup, N. M. Nemes, J. L. Martínez, N. S. Ferreira and J. A. Alonso, Chem. Mater., 2023, 35, 2439–2455 CrossRef.
- M. Hoffmann, V. N. Antonov, L. V. Bekenov, K. Kokko, W. Hergert and A. Ernst, J. Condens. Matter Phys., 2018, 30, 305801 CrossRef PubMed.
- M. V. Ganduglia-Pirovano, A. Hofmann and J. Sauer, Surf. Sci. Rep., 2007, 62, 219–270 CrossRef CAS.
- S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1–36 CrossRef CAS.
- R. Sahoo, Y. Takeuchi, A. Ohtomo and Z. Hossain, Phys. Rev. B, 2019, 100, 214436 CrossRef CAS.
- K. Aswathi, J. P. Palakkal and M. R. Varma, J. Magn. Magn. Mater., 2020, 514, 167276 CrossRef CAS.
- K. Aswathi, J. P. Palakkal and M. RaamaVarma, J. Magn. Magn. Mater., 2019, 476, 45–53 CrossRef CAS.
- R. B. Griffiths, Phys. Rev. Lett., 1969, 23, 17 CrossRef.
- R. Sahoo, S. Giri, P. Dasgupta, A. Poddar and T. Nath, J. Alloys Compd., 2016, 658, 1003–1009 CrossRef CAS.
- M. A. Islam, T. Sato, F. Ara and M. A. Basith, J. Alloys Compd., 2023, 944, 169066 CrossRef CAS.
- L. T. Coutrim, E. M. Bittar, F. Stavale, F. Garcia, E. Baggio-Saitovitch, M. Abbate, R. J. O. Mossanek, H. P. Martins, D. Tobia, P. G. Pagliuso and L. Bufai, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 174406 CrossRef.
- A. Pal, P. Singh, V. K. Gangwar, A. G. Joshi, P. Khuntia, G. D. Dwivedi, P. K. Gupta, M. Alam, K. Anand, K. Sethupathi, A. K. Ghosh and S. Chatterjee, J. Phys.: Condens. Matter, 2020, 32, 215801 CrossRef CAS PubMed.
- H. Zhang, L. Xie, X. Liu, M. Xiong, L. Cao and Y. Li, Phys. Chem. Chem. Phys., 2017, 19, 25186–25196 RSC.
- J. Y. Moon, M. K. Kim, Y. J. Choi and N. Lee, Sci. Rep., 2017, 7, 16099 CrossRef CAS PubMed.
- R. C. Sahoo, S. Das and T. K. Nath, J. Appl. Phys., 2018, 124, 103901 CrossRef.
- Z. Zhang, P. Xu, Y. Jia and L. Li, J. Phys. Energy, 2023, 5, 014017 CrossRef CAS.
- W. Zhong, C.-T. Au and Y.-W. Du, Chin. Phys. B, 2013, 22, 057501 CrossRef.
- S. M. Borchani, W. C.-R. Koubaa and M. Megdiche, R. Soc. Open Sci., 2017, 4, 170920 CrossRef.
- M. A. Islam, M. Tarek, M. A. Adib and M. A. Basith, J. Phys. D: Appl. Phys., 2024, 57, 215302 CrossRef CAS.
- J. Rodrguez-Carvajal, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 192, 55–69 CrossRef.
- M. Yadav, A. Agarwal, S. Sanghi, R. Kotnala, J. Shah, T. Bhasin, M. Tuteja and J. Singh, J. Alloys Compd., 2018, 750, 848–856 CrossRef CAS.
- F. Yasmeen, M. Tarek and M. A. Basith, ACS Appl. Mater. Interfaces, 2024, 16, 47535–47550 CrossRef CAS.
- M. Das, P. Sarkar and P. Mandal, Phys. Rev. B, 2020, 101, 144433 CrossRef CAS.
- M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeier, Prog. Solid State Chem., 1993, 22, 197–233 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- D. Mazumdar and I. Das, Phys. Chem. Chem. Phys., 2021, 23, 5596–5606 RSC.
- M. J. Hosen, M. A. Basith and I. M. Syed, RSC Adv., 2023, 13, 17545–17555 RSC.
- M. D. I. Bhuyan, S. Das and M. A. Basith, J. Alloys Compd., 2021, 878, 160389 CrossRef CAS.
- H. Ding, Z. Tao, S. Liu and Y. Yang, J. Power Sources, 2016, 327, 573–579 CrossRef CAS.
- M. Saxena, P. Roy, M. Acharya, I. Bose, K. Tanwar and T. Maiti, Appl. Phys. Lett., 2016, 109, 263903 CrossRef.
- L. Zhang, S. Li, T. Xia, L. Sun, L. Huo and H. Zhao, Int. J. Hydrogen Energy, 2018, 43, 3761–3775 CrossRef CAS.
- M. Klinger, J. Appl. Crystallogr., 2017, 50, 1226–1234 CrossRef CAS.
- M. Tarek and M. A. Basith, J. Mater. Chem. C, 2023, 11, 16605–16622 RSC.
- B. Cui, H. Lin, Y.-Z. Liu, J.-B. Li, P. Sun, X.-C. Zhao and C.-J. Liu, J. Phys. Chem. C, 2009, 113, 14083–14087 CrossRef CAS.
- F. Sharmin and M. A. Basith, ACS Omega, 2022, 7, 34901–34911 CrossRef CAS PubMed.
- J. P. Palakkal, C. Raj Sankar and M. R. Varma, J. Appl. Phys., 2017, 122, 073907 CrossRef.
- B. Sarkar, B. Dalal and S. De, J. Magn. Magn. Mater., 2016, 417, 160–164 CrossRef CAS.
- R. Hossain, A. Billah, M. Ishizaki, S. Kubota, F. Hirose and B. Ahmmad, Dalt. Trans., 2021, 50, 9519–9528 RSC.
- M. Tarek, F. Yasmeen and M. A. Basith, J. Mater. Chem. A, 2024, 12, 25475–25490 RSC.
- M. Tarek, F. Yasmeen and M. A. Basith, J. Mater. Chem. A, 2025, 13, 499–516 RSC.
- M. M. Rahman, F. Yasmeen, M. Tarek and M. A. Basith, J. Alloys Compd., 2025, 1010, 177295 CrossRef CAS.
- M. Nasir, M. Khan, S. A. Agbo, S. Bhatt, S. Kumar and S. Sen, J. Phys. D: Appl. Phys., 2020, 53, 375003 CrossRef CAS.
- K. Shinde, C. Hwang, M. Manawan, Y.-S. Choi, S.-Y. Park, Y. Jo, S. Lee, D.-H. Kim and J. Park, RSC Adv., 2023, 13, 9099–9108 RSC.
- P. Mandal and T. Nath, Mater. Res. Express, 2015, 2, 066101 CrossRef.
- P. Murthy, K. Priolkar, P. Bhobe, A. Das, P. Sarode and A. Nigam, J. Magn. Magn. Mater., 2010, 322, 3704–3709 CrossRef CAS.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- K. Ueda, H. Tabata and T. Kawai, Science, 1998, 280, 1064–1066 CrossRef CAS PubMed.
- A. Pal, P. Singh, V. Gangwar, S. Ghosh, P. Prakash, S. Saha, A. Das, M. Kumar, A. Ghosh and S. Chatterjee, Appl. Phys. Lett., 2019, 114, 252403 CrossRef.
- S. Zhou, Y. Guo, J. Zhao, L. He and L. Shi, J. Phys. Chem. C, 2011, 115, 1535–1540 CrossRef CAS.
- K. Yi, Q. Tang, Z. Wu, J. Gu and X. Zhu, J. Alloys Compd., 2023, 933, 167742 CrossRef CAS.
- T. D. Thanh, D. C. Linh, N. T. U. Tuyen, T.-L. Phan and S.-C. Yu, J. Alloys Compd., 2015, 649, 981–987 CrossRef CAS.
- M. E. Fisher, Rep. Prog. Phys., 1967, 30, 615 CrossRef CAS.
- D. Kim, B. Revaz, B. Zink, F. Hellman, J. Rhyne and J. Mitchell, Phys. Rev. Lett., 2002, 89, 227202 CrossRef CAS PubMed.
- G. Jagadish Kumar, A. Jose, E. P. Jinu, T. T. Saravanan, E. S. Kumar, M. Navaneethan, H. Sreemoolanadhan and K. K. Bharathi, J. Phys. D: Appl. Phys., 2022, 55, 215001 CrossRef.
- B. K. Banerjee, Phys. Lett., 1964, 12, 16–17 CrossRef.
- A. Varvescu and I. G. Deac, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 470, 96–101 CrossRef.
- C. Zener, Phys. Rev., 1951, 83, 299 CrossRef CAS.
- M. A. A. Bally, M. A. Islam, M. Z. Ahasan and F. A. Khan, J. Magn. Magn. Mater., 2022, 557, 169462 CrossRef CAS.
- M. A. A. Bally, M. A. Islam, S. M. Hoque, R. Rashid, M. F. Islam and F. A. Khan, Results Phys., 2021, 28, 104546 CrossRef.
- D. Mazumdar, K. Das and I. Das, J. Appl. Phys., 2020, 127, 093902 CrossRef CAS.
- C. L. Wang, J. Liu, Y. Mudryk, Y. Zhu, B. Fu, Y. Long and V. Pecharsky, J. Alloys Compd., 2019, 777, 152–156 CrossRef CAS.
- L. Coutrim, E. Bittar, F. Stavale, F. Garcia, E. Baggio-Saitovitch, M. Abbate, R. Mossanek, H. Martins, D. Tobia and P. Pagliuso, et al. , Phys. Rev. B, 2016, 93, 174406 CrossRef.
- H. E. Stanley, Phase transitions and critical phenomena, Clarendon Press, Oxford, 1971, vol. 7 Search PubMed.
- S. Chatterjee, A. Dutta and I. Das, J. Appl. Phys., 2024, 136, 044101 CrossRef CAS.
- A. Selmi, R. Mnassri, W. Cheikhrouhou-Koubaa, N. C. Boudjada and A. Cheikhrouhou, Ceram. Int., 2015, 41, 10177–10184 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: FTIR spectra analysis of Y2CoCrO6; TGA and DSC curve; Particle size distribution histogram of FESEM and TEM imaging; table for the mass and atom percentage of different elements in YCCO material as obtained by EDX analysis; XPS full survey spectrum of YCCO nanoparticles; critical isotherm and the log–log plot of the critical isotherm of the YCOO compound. See DOI: https://doi.org/10.1039/d4ma01092b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |