Microwave-assisted intercalation: exploring electronic and structural features of metastable MMo₆S₈ (M = Ag, Sn)

Abstract

Presented in this work is a synthetic approach for metastable Type I Chevrel phase sulfides, MMo₆S₈ (M = Ag, Sn), utilizing rapid microwave-assisted medium temperature intercalation. Using X-ray absorption spectroscopy the electronic structure and local coordination of sulfur and molybdenum bonding environments are probed as a function of a Type I metal intercalant. Intercalant promoter-induced electron donation effects were observed through analysis of the sulfur K-edge pre-edge feature and Mo L₃-edge in the X-ray absorption near edge regions. Calculated electron density maps reveal more covalent interactions between Ag and S atoms versus more ionic interactions between Sn and S. Changes in the Chevrel phase structure upon intercalation are investigated through Mo K-edge extended X-ray absorption fine structure analysis. Evaluation of Mo–Mo intracluster distances allows the cluster anisotropy of Type I CPs to be calculated as low as 1.84%. These findings help elucidate how electronic and local structures can be modulated through intercalation and the importance of cation identity to fine tune structures.

---

1. Introduction

Chevrel phases represented by the formula M_yMo₆X₈, where M includes alkali, alkaline earth, transition, post-transition, and lanthanide metals, and X = S, Se, or Te, serve as a versatile platform for exploring structure–function correlations,^1,2 thus allowing for an examination of how changes in elemental composition influence local coordination environments and electronic properties. Initially recognized for their potential as high-temperature superconductors,^3–6 Chevrel phases (CPs) have demonstrated valuable properties for applications such as multivalent cathode materials,^7–9 photovoltaic systems,¹⁰ hydrodesulfurization,^11–13 and electrocatalysts for diverse small-molecule transformations.^1,14–16 Recent advancements in machine learning techniques have enabled the evaluation of CP synthesizability via enthalpy descriptors, unveiling a plethora of thermodynamically stable and metastable CPs.¹⁷

Structurally, CPs are composed of a Mo₆ octahedron centrally positioned within a chalcogenide pseudo-cubic arrangement (X₈), defining the Mo₆X₈ cluster motif (Fig. 1a). Bridging via sulfur atoms results in three-dimensional solids with interstitial cavities suitable for metal intercalation. The incorporation of metals stabilizes the electron-deficient Mo₆X₈ framework, permitting tunability in both electronic and structural domains.^18,19 Multinary Chevrel phases are categorized into two primary classes based on the nature of the metallic intercalant. These distinctions are primarily governed by the intercalated cation's localization within the CP framework and its ionic diffusivity.^20–23 Type I CPs are characterized by large, stationary cations with ionic radii greater than 1 Å, such as Ag, Sn, and Pb. These cations are centrally positioned within the cavities of the Chevrel structure, with a stoichiometric ratio (y) fixed at 1 (Fig. 1a). Conversely, Type II CPs incorporate smaller, more mobile cations with ionic radii less than 1 Å, including Cu, Ni, Fe, Li, and Na. These cations are delocalized within the structure's cavities, exhibiting a variable stoichiometry in the range of y = 1–4 shown in the different position probability for the outer ring of the cavity in Fig. 1b.²⁴

Fig. 1 Structure of (a) the Chevrel phase with Type I cations located in the cavity and (b) the CP structure viewed down the 3-fold inversion axis to show the central location of Type I cations and delocalized location of cations in the position probability location of the outer ring for type II cations.

The thermodynamic stability of CPs is influenced by both the identity of the cation and the stoichiometric ratio. Type I CPs are susceptible to destabilization due to steric hindrance between the bulky cation and electronegative chalcogen elements.²⁵ This effect becomes stronger when moving from sulfides to tellurides, which causes a decrease in the stability of Type I telluride CPs. In contrast, Type II CPs are unstable when the stoichiometric intercalation of small cations exceeds y = 4, resulting in a higher electron concentration in the Mo antibonding orbitals.¹⁹

X-ray absorption near edge spectroscopy (XANES) was employed to elucidate the electronic structure modifications occurring after cation intercalation. This provided valuable insights into electron density donation and the occupancy of electronic states post-intercalation. Complementary to XANES, extended X-ray absorption fine structure (EXAFS) analysis offers detailed information regarding the local structural configuration of the CP clusters, including insights into structural distortions and variations in bond distances.

Historically, the synthesis of Type I CPs has been conducted via conventional high-temperature methods, a process that typically extends over several days.^4,5,26–30 Such methods often result in the formation of impurities, with MoS₂ and elemental Mo being common by-products.^{4,27,28,31,32} Achieving phase purity, especially for the SnMo₆S₈ CP, is notably challenging due to issues with reproducibility.²⁸ Tarascon et al. demonstrated that phase-pure materials could be obtained through medium temperature (temperatures below ∼ 500 °C to avoid decomposition of binary CP) intercalation. In previous studies, pre-synthesized Mo₆S₈ is combined with the target stoichiometric ratios of Sn or Pb and subjected to solid-state synthesis at 500 °C in a tube furnace for a prolonged period.²⁵ However, the extended reaction times associated with this method are suboptimal. Conversely, microwave mediated solid state synthesis has demonstrated a significant reduction in synthesis time for Chevrel phases to mere minutes, providing a more efficient approach for both synthesis and cation intercalation.^{15–17,19,33–36}

Therefore, this study aims to develop a facile synthesis technique for Type I, MMo₆S₈ (M = Ag, Sn) Chevrel phases that conserves both time and energy. Additionally, it seeks to provide a comprehensive analysis of the electronic and local structural changes accompanying cation intercalation into the Mo₆S₈ framework.

2. Materials and methods

2.1. Synthesis

The CPs studied were synthesized via high temperature microwave-assisted solid-state methods as described in our previous work, and medium temperature intercalation (MTI).^15,17 Starting materials were MoS₂ powder (>98%, ∼325 mesh) purchased from Thermo Scientific, Mo powder (99.99%, ∼250 mesh), Cu₂S powder (99.5%, ∼200 mesh), Sn powder (99.995%, ∼100 mesh) and graphite powder (<20 μm) purchased from Sigma-Aldrich, and Ag powder (99.9%, 5–8 μm) purchased Alfa Aesar. To access binary Mo₆S₈, Cu₂Mo₆S₈ must be synthesized and followed with subsequent leaching of Cu using 6 M HCl.

Briefly, the proper stoichiometric amounts of precursor powders were weighed out under an inert N₂ atmosphere and ball-milled for 12 h and pressed into pellets. The pellet is transferred into a quartz tube purchased from AdValue Technology and made into closed bottom tubes using an in house oxy-hydrogen torch and packed with layers of Al₂O₃ microfiber purchased from Thermo Fisher Scientific and graphite. Prepared tubes were then placed in a graphite bath in an alumina crucible and irradiated in a conventional microwave oven for several minutes at a power of 1000 W. Phase pure binary Mo₆S₈ was then used as a precursor for the synthesis of AgMo₆S₈ and SnMo₆S₈ along with elemental Sn and Ag powder.

M + Mo₆S₈ → MMo₆S₈ (M = Ag, Sn) (2)

For samples accessed through MTI, samples were irradiated with a power up to 375 W and temperatures <500 °C for 3–5 minutes, which was sufficient time to intercalate Ag and Sn into the existing binary CP framework.

2.2. Structural and electronic characterization

CP crystal structures were evaluated through powder X-ray diffraction (PXRD) using a Bruker D8 Advance diffractometer with Cu K alpha radiation source (1.54 Å). Through Rietveld refinement experimental lattice parameters were obtained. Scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDX) were utilized to evaluate morphology and bulk composition using an FEI Scios Dual Beam FIB/SEM system with an Oxford EDX detector.

Surface composition was probed via X-ray photoelectron microscopy (XPS) using a Kratos Supra Axis spectrometer with an Al anode (1486.6 eV).

Local structural and electronic information were analyzed through ex situ X-ray absorption spectroscopy (XAS) at SSRL and NSLS-II to observe X-ray absorption near edge spectroscopy (XANES) and extended X-ray absorption fine structure (EXAFS) for Mo K- and L₃-edges and S K-edges. CPs Mo K-edges were screened at NSLS-II beamline SST-2, Mo L₃-edges and S K-edges were screened at SSRL beamline 4–3. For Mo K-edge scans, a reference foil corresponding to the Mo edge was placed in the beam path behind the sample of interest in transmission data acquisition mode and the fluorescence signal was taken simultaneously allowing for calibration of beam energy.³⁷ For S K-edge scans, Na₂S₂O₃ powder was used as a reference standard with a white line peak set to 2472 eV.^38–40 Scans with energy less than 5000 eV were gathered under He to reduce beam interactions with air which can lead to a diminishment of the fluorescence signal. All data shown is the average of multiple spectra to decrease noise. Simulated S K-edge spectra were calculated using the many-body X-ray absorption spectroscopy method (MBXAS, details in ESI† under computational details from collaborator). Cation oxidation state was calculated through Bader charge analysis of AgMo₆S₈, SnMo₆S₈, CuMo₆S₈, and Cu₂Mo₆S₈ structures.

3. Results and discussion

3.1. Synthesis of MMo₆S₈ (M = Ag, Sn)

The stability of Chevrel phases (CPs) can be classified into three distinct ranges of decomposition enthalpies (ΔH_d). CPs exhibit thermodynamic stability when their decomposition enthalpies are below 0 meV per atom, metastability within the range of 0 to 65 meV per atom and instability when the enthalpies exceed 65 meV per atom.¹⁷ In the metastable range, materials are typically synthesized via high-temperature methods; however, those approaching the unstable boundary (45 meV per atom > ΔH_d > 65 meV per atom) are frequently accessible only through medium temperature intercalation (MTI). This approach is particularly suitable for Chevrel phases at the upper end of the metastable range, as it mitigates the destabilization of the octahedral unit (Fig. 1a.) by employing pre-synthesized binary CPs that remain stable at temperatures below 500 °C.

Synthesis was originally attempted through microwave-assisted solid-state high temperature synthesis (900–1100 °C), as the computational decomposition enthalpy published in our previous work has both the Ag and Sn sulfide CPs in the metastable regime.¹⁷ High temperature microwave synthesis efforts for SnMo₆S₈ proved unsuccessful, resulting in Mo₂S₃ and MoS₂ side phase impurities (Fig. S1, ESI†). In turn, MTI resulted in phase pure SnMo₆S₈, as indicated in the PXRD pattern (Fig. 2b). Owing to its success in synthesizing the Sn sulfide CP, MTI was also used to successfully access phase pure AgMo₆S₈ (Fig. 2a). Lattice parameters obtained through Rietveld refinement are in close agreement to previously reported literature values for CP chalcogenides (Type I/II) in the R3̄H space group and are shown in Table S1 (ESI†). EDX spectra (Fig. S2 and S3, ESI†) in tandem with Rietveld refinement reveal the bulk composition of Ag and Sn in Chevrel phases to be slightly less than y = 1. Experiments were performed to access y = 1 stoichiometry by weighing out slightly excess Ag and this proved successful (Fig. S4, ESI†). To the best of our knowledge, the synthesis method presented in this study is the first instance of microwave-assisted solid-state synthesis utilized for the preparation of Type I Chevrel phase sulfides.

Fig. 2 Powder X-ray diffraction patterns for (a) AgMo₆S₈ and (b) SnMo₆S₈ with (c) corresponding micrographs.

Samples subjected to temperatures exceeding 500 °C displayed the emergence of a minor MoS₂ peak at 14.4°, indicative of the onset of the Mo₆S₈ decomposition. To prevent decomposition and facilitate cation intercalation, we utilized a reaction temperature of 450 °C for three and five minutes for AgMo₆S₈ and SnMo₆S₈, respectively. The longer intercalation time for Sn compared to Ag is anticipated, as oxidized Sn experiences a higher energy barrier for cation diffusion into the Chevrel phase cavity than Ag.⁴¹ This phenomenon is attributed to electrostatic repulsive interactions with the electronegative pseudo-sulfur cube illustrated in Fig. 1a.

The micrographs shown in Fig. 2c reveal the faceted morphology of the bulk polycrystalline material. The subsequent ball-milling after acid leaching of the Cu intercalant to achieve the Mo₆S₈ binary Chevrel phase, along with the metal intercalant, results in the sporadic formation of smaller agglomerated particles. To evaluate the applicability of medium temperature intercalation (MTI) via microwave irradiation for other Chevrel phases, attempts were made with the Ag and Sn selenide and telluride analogues. Successful syntheses of AgMo₆Se₈ and SnMo₆Se₈ were achieved (Fig. S5, ESI†); however, AgMo₆Te₈ and SnMo₆Te₈ proved inaccessible via MTI, with attempts yielding only unintercalated Mo₆Te₈ along with residual Sn and Ag. Further investigations will be conducted to better elucidate the limitations of MTI within Chevrel phases.

3.2. Electronic structure

Both AgMo₆S₈ and SnMo₆S₈, along with binary Mo₆S₈, were evaluated at the Mo L₃-edge and S K-edge to probe promoter induced charge transfer and electronic structure of both Mo and S. In Fig. S6 (ESI†) you can see the first derivative of the peak maxima at approximately 2525 eV for all phases indicating that there is no large change in the oxidation state of Mo upon intercalation in good agreement with previous studies.⁸ While the oxidation state of Mo remains largely unchanged during intercalation, a noticeable change in the electronic environment of sulfur within the cluster becomes evident when analyzing the S K-edge. The Mo₆S₈ S K-edge spectra are recognized for featuring a pre-edge peak, the intensity of which decreases when different cations intercalate into cavities. This phenomenon provides valuable insights into charge transfer processes as well as changes to sulfur coordination. This charge-transfer and coordination trend has been well studied by Prendergast et al.^8,9,36 The pre-edge peak at approximately 2471 eV arises from electronic transitions originating from the S 1s orbital into the S 3p and Mo 4d hybridized orbital. When these hybridized orbitals remain unfilled, the pre-edge feature is more pronounced; however, upon filling of these frontier orbitals the pre-edge peak diminishes. The intercalated cations serve as electron donors to the Mo₆S₈ cluster unit, occupying its orbitals and resulting in a reduction of the pre-edge feature.

Similar to observations on the intercalation of various stoichiometries of Mg into Mo₆S₈ cathodes for multivalent batteries, both experimentally and theoretically,⁸ a more significant reduction of the pre-edge feature is observed upon Sn intercalation compared to Ag. The S K-edge of Mo₆S₈, AgMo₆S₈, and SnMo₆S₈ were calculated using first-principles many-body X-ray absorption spectroscopy (MBXAS). This methodology calculated the absorption cross-section between the initial (ground) state and various final (core-excited) states approximated as Slater determinants of DFT orbitals (see computational details in the ESI†). The calculated S K-edge spectra (Fig. 3a) are in good agreement with the experimental data, with a larger depression in the pre-edge feature observed when Sn is intercalated compared to Ag (Fig. 3b). In addition to insights on charge transfer, information on sulfur coordination changes upon intercalation can also be obtained. Within the binary CP you have two types of sulfur ions, S1 which is tetra-coordinated to molybdenum and S2 which is tri-coordinated (undercoordinated) to molybdenum and lies along the 3-fold inversion axis (Fig. 1a). Using the MBXAS method, the spectra for these different sulfur environments in AgMo₆S₈ and SnMo₆S₈ are calculated (Fig. S7, ESI†). Prior to intercalation the S1 and S2 spectra have distinct differences arising from their unique coordination environment (Fig. S8, ESI†). Upon intercalation with Ag and Sn the pre-edge features of S2 and S1 become more similar, as was also observed with Mg and Cu.^8,36 With the intercalant occupying the cavity, S2 acquires a tetra-coordinated environment, alike S1.

Fig. 3 Sulfur K-edge XANES spectra for binary and ternary sulfide Chevrel phases. (a) Experimental spectra in solid lines compared to calculated spectra in dashed lines, and (b) overlapped experimental spectra to highlight differences in pre-edge features. Visual representation of electron density for specific isosurface values around (c) Ag in AgMo₆S₈ and (d) Sn in SnMo₆S₈.

This difference in pre-edge is attributed to the preferred +2 oxidation state of Sn, providing more electron density available for donation to the CP framework compared to Ag's +1 preferred oxidation state. Nevertheless, this contrasts with the findings of Yu et al., who observed that Li⁺ has a more pronounced dampening effect on the pre-edge peak than Mg²⁺. They attributed this difference to Li exhibiting a greater degree of cation electron density delocalization compared to Mg.⁴² In the case of Ag and Sn cations being centrally located in the cavity, the oxidation state determines charge transfer rather than delocalization of electron density of the intercalants. This suggests that the amount of electron density available for donation serves as an additional means to modulate charge transfer within CPs alongside variations in the equivalence of intercalants.

Bader charge analysis of AgMo₆S₈ and SnMo₆S₈ give Bader charge values of +0.49 and +0.93 for the metal intercalant, respectively, to which we assign nominal oxidation states of +1 and +2 (Table S2, ESI†). These charge differences reflect differences in bonding interactions between the intercalated metal and surrounding sulfur atoms. Fig. 3c and d visually represent these interactions using an isosurface of the electron density. Ag atoms exhibit linear bonding with neighboring S atoms, sharing electron density with neighboring S atoms, which we interpret as a more covalent interaction (Fig. 3c). For Sn atoms, there is a clear separation between the electron density of the metal intercalant and nearby S atoms, which we interpret as a more ionic interaction (Fig. 3d). Fig. S9 (ESI†) offers additional images of the difference in bonding environment and electron density distribution with Ag vs Sn intercalated. This difference in ionicity is not seen when comparing CuMo₆S₈ and Cu₂Mo₆S₈ with an estimated oxidation state of +1 for Cu in both CPs (Fig. S10, ESI†), further elucidating the importance of cation identity in controlling the local bonding environment in CPs.

Surface composition was analyzed through XPS measurements, where spectra showed corresponding expected elements and a native oxide layer. XPS was also used to approximate the oxidation state for intercalated metal cations. Binding energy peaks for Ag 3d are in good agreement with literature values for a +1 oxidation state (Fig. S11, ESI†).^43,44 Due to the overlap of binding energies for the Sn +2 and +4 oxidation state XPS cannot distinguish between the two (Fig. S12, ESI†).⁴⁵ However, analysis of the S K-edge for SnMo₆S₈ allows for an approximation of the oxidation state as if Sn was in the +4 oxidation state no pre-edge feature would be visible. Mo 3d and S 2p spectra are in good agreement with past published data for the binding energies of CPs (Fig. S11 and S12, ESI†).⁴⁶

3.3. Local structure examination upon intercalation

The incorporation of metal cations to Mo₆S₈ through intercalation induces alterations in both the intercluster Mo–Mo and Mo–S distances, as well as intracluster Mo–Mo and Mo–S distances. A visual depiction of these changes is presented in Fig. 5. To comprehend the effects of Type I cation intercalation, the Mo K-edge EXAFS region was analyzed for AgMo₆S₈ and SnMo₆S₈ and the results were juxtaposed with previously published Mo₆S₈ data by our group.^33,36 The Fourier-transformed EXAFS data, featuring both magnitudes (top) and real (bottom) components is presented in Fig. 4. The EXAFS data were analyzed with the R range of 1.25 to 3.5 Å to confine the fit to near neighbour contributions. Fig. 5 displays scattering paths, and extracted distances are detailed in Table 1. Comprehensive fitting parameters and extracted data can be found in Tables S3 and S4 (ESI†). Notably, both AgMo₆S₈ and SnMo₆S₈ demonstrate an expansion in intercluster Mo–S distances compared to previously reported binary Mo₆S₈. The Type I CPs Mo–S_inter distances are approximately 0.1 Å further apart than the binary CP, resembling the observed trend when two equivalents of Cu are intercalated into Mo₆S₈.³⁶ Additional Mo K-edge first derivative plots and fits in k-space can be found in Fig. S13 and S14 (ESI†), respectively.

Fig. 4 Mo K-edge FT-EXAFS data (circle) and fits (lines) with components of the FT k³χ(k) in non-phase corrected magnitude on the top and in real on the bottom for (a) AgMo₆S₈ and (b) SnMo₆S₈.

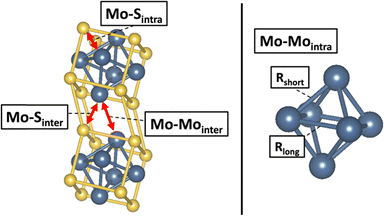Fig. 5 Visual representation of intercluster and intracluster scattering paths listed in Table 1 from 1s Mo scattering photoelectrons to neighboring Mo and S atoms.

Following intercalation, structural modifications in the Mo₆ cluster unit can be monitored through the Mo–Mo_intra distances. Percent anisotropy, a metric used to quantify these structural changes, was calculated from the obtained intracluster Mo–Mo distances. The percent anisotropy equation was defined previously by Levi and Aurbach.²¹ The resulting values and associated errors from these calculations are listed in Table 2. In the unintercalated, state the undercoordinated S sites are less electronegative compared to their intercalated counterparts leading to reduced electron donation to the Mo₆ octahedra (electronic factor). This reduction in electron donations results in the octahedra adopting a trigonal antiprismatic geometry. Upon intercalation, the geometry becomes more octahedral with a smaller difference between R_short and R_long for Mo–Mo_intra distances. Both Ag and Sn CPs show a decreased % anisotropy in comparison to Mo₆S₈ and Cu₂Mo₆S₈. The more pronounced reduction in % anisotropy with the incorporation of Type I cations compared to Type II may be ascribed to increased Mo–Mo intercluster distances. This increase is likely due to greater contributions from chalcogen repulsion, which directly influences the intracluster Mo–Mo bonding environment (geometric factor). The intercalation of Sn appears to have a more significant impact on % anisotropy than Ag, as Sn can donate more electron density resulting in larger chalcogen repulsion between neighbouring clusters.

Table 1 Extracted bond lengths from EXAFS fittings

Chevrel phase	Scattering path	Fitted R (Å)
AgMo6S8	Mo–Mointra	2.70, 2.79
	Mo–Mointer	3.15
	Mo–Sintra	2.42
	Mo–Sinter	2.48
SnMo6S8	Mo–Mointra	2.66, 2.72
	Mo–Mointer	3.17
	Mo–Sintra	2.39
	Mo–Sinter	2.45

---

Table 2 Cluster anisotropy for Type I CPs compared to binary CP and Type II CP. Anisotropy was calculated following ref. 20, using equation ((R_long − R_short)/R_long) × 100, where R_long and R_short are intra-atomic distances between Mo–Mo_intra atoms. Distances can be visualized in Fig. 5

Chevrel phase	Cluster e-count	Cluster anisotropy (%)
a % anisotropy results from previously published studies by our group^36
Mo6S8	20	8.85 ± 1.63^a
AgMo6S8	21	3.33 ± 0.45
SnMo6S8	22	1.74 ± 0.31
Cu2Mo6S8	22	4.44 ± 1.64^a

---

4. Conclusions

This study highlights the significant advantages of microwave-assisted solid-state synthesis for Type I Chevrel phase sulfides. Notably, to the best of our knowledge, we report the first instance of employing microwave-assisted solid-state techniques for synthesizing Type I Chevrel phases. Using medium temperature intercalation through microwave irradiation offers a robust method for incorporating Ag and Sn Type I cations into Chevrel phases and could be adapted to explore other multinary metastable composition spaces of interest.

Extensive experimental X-ray absorption spectroscopy (XAS) studies, alongside theoretical many-body X-ray absorption spectroscopy (MBXAS) and electron density mapping, have provided valuable insights into the local electronic structure of Type I Chevrel phases. This work enhances our understanding of how the choice of intercalant can influence the Chevrel phase framework and bonding environment. This is seen through a more covalent interaction observed between the intercalant and neighbor sulfurs with Ag intercalated vs. a more ionic interaction observed when Sn is intercalated. Analysis of the sulfur K-edge underscores the tunability of electron density donation and its effects on sulfur coordination, which can be achieved through stoichiometric adjustments and selectively choosing the oxidation state of the intercalant species.

Furthermore, the Mo K-edge extended X-ray absorption fine structure (EXAFS) analysis indicates a more pronounced reduction in Mo₆ cluster anisotropy in Type I Chevrel phases compared to Type II intercalants, which we attribute to a greater contribution from the geometric factor when Type I cations are intercalated. Continuing to deepen our foundational understanding of how composition affects chemical coordination and electronic structure is essential for advancing design principles in solid-state materials, especially those critical for energy conversion and storage applications.

Author contributions

R. Smiley: conceptualization, validation, investigation, formal analysis, experimental, manuscript writing. K. Mason: formal analysis (XPS, PXRD refinement). R. Lam and D. Ingargiola: experimental setup, experimental. B. Wuille Bille: formal analysis support (XAS), manuscript writing. A. Giem: data acquisition (EXAFS). D. Prendergast: software, theoretical calculation, manuscript writing. J. Velázquez: supervision, conceptualization, and manuscript writing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JMV thanks the University of California, Davis for start-up funding. JMV also acknowledges support from the Camille Dreyfus Teacher-Scholar Awards Program (TC-22-096) and the Alfred P. Sloan Foundation Award (FG-2023-203903), as well as support from the National Science Foundation through the Faculty Early Career Development Program (DMR-2044403). DI was funded for summer research through the National Science Foundation ChemEnergy Research Undergrad Experience program (CHE1950933). Part of this study was carried out at the UC Davis Center for Nano and Micro Manufacturing (CNM2). Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. This research used resources of the National Synchrotron Light Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract No. DESC0012704. JMV would also like to thank Professor Sarbajit Banerjee at Texas A&M for the use of beam time at Brookhaven National Lab. Density functional theory based X-ray spectral analysis was facilitated through a user project at the Molecular Foundry which is supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Open Access funding provided by the Max Planck Society.

Notes and references

1. J. C. Ortiz-Rodríguez and J. M. Velázquez, Curr. Opin. Electrochem., 2022, 34, 101002.
2. J. T. Perryman and J. M. Velázquez, Chem. Mater., 2021, 33, 7133–7147.
3. D. Guenzburger, D. E. Ellis, P. A. Montano, G. K. Shenoy, S. K. Malik, D. G. Hinks, P. Vaishnava and C. W. Kimball, Phys. Rev. B:Condens. Matter Mater. Phys., 1985, 32, 4398–4409.
4. F. S. Delk and M. J. Sienko, Inorg. Chem., 1980, 19, 788–789.
5. A. P. Petrović, R. Lortz, G. Santi, C. Berthod, C. Dubois, M. Decroux, A. Demuer, A. B. Antunes, A. Paré, D. Salloum, P. Gougeon, M. Potel and Ø. Fischer, Phys. Rev. Lett., 2011, 106, 017003.
6. C. W. Kimball, L. Weber, G. Van Landuyt, F. Y. Fradin, B. D. Dunlap and G. K. Shenoy, Phys. Rev. Lett., 1976, 36, 412–415.
7. J. M. Tarascon, T. P. Orlando and M. J. Neal, J. Electrochem. Soc., 1988, 135, 804–808.
8. L. F. Wan, J. Wright, B. R. Perdue, T. T. Fister, S. Kim, C. A. Apblett and D. Prendergast, Phys. Chem. Chem. Phys., 2016, 18, 17326–17329.
9. F. Thöle, L. F. Wan and D. Prendergast, Phys. Chem. Chem. Phys., 2015, 17, 22548–22551.
10. M. L. Agiorgousis, Y.-Y. Sun, D. West and S. Zhang, ACS Appl. Energy Mater., 2018, 1, 440–446.
11. K. F. McCarty and G. L. Schrader, Ind. Eng. Chem. Prod. Res. Dev., 1984, 23, 519–524.
12. K. F. McCARTY, J. W. Anderegg and G. L. Schrader, J. Catal., 1985, 93, 375–387.
13. M. Ekman, J. Catal., 1989, 117, 246–257.
14. N. R. Singstock and C. B. Musgrave, J. Am. Chem. Soc., 2022, 144, 12800–12806.
15. J. T. Perryman, J. C. Ortiz-Rodríguez, J. W. Jude, F. P. Hyler, R. C. Davis, A. Mehta, A. R. Kulkarni, C. J. Patridge and J. M. Velázquez, Mater. Horiz., 2020, 7, 193–202.
16. J. C. Ortiz-Rodríguez, N. R. Singstock, J. T. Perryman, F. P. Hyler, S. J. Jones, A. M. Holder, C. B. Musgrave and J. M. Velázquez, ACS Appl. Mater. Interfaces, 2020, 12, 35995–36003.
17. N. R. Singstock, J. C. Ortiz-Rodríguez, J. T. Perryman, C. Sutton, J. M. Velázquez and C. B. Musgrave, J. Am. Chem. Soc., 2021, 143, 9113–9122.
18. T. Hughbanks and R. Hoffmann, J. Am. Chem. Soc., 1983, 105, 1150–1162.
19. K. Lilova, J. T. Perryman, N. R. Singstock, M. Abramchuk, T. Subramani, A. Lam, R. Yoo, J. C. Ortiz-Rodríguez, C. B. Musgrave, A. Navrotsky and J. M. Velázquez, Chem. Mater., 2020, 32, 7044–7051.
20. E. Levi, M. D. Levi, O. Chasid and D. Aurbach, J. Electroceram., 2009, 22, 13–19.
21. E. Levi and D. Aurbach, Chem. Mater., 2010, 22, 3678–3692.
22. E. Levi, G. Gershinsky, D. Aurbach, O. Isnard and G. Ceder, Chem. Mater., 2009, 21, 1390–1399.
23. E. Levi, G. Gershinsky, D. Aurbach and O. Isnard, Inorg. Chem., 2009, 48, 8751–8758.
24. K. A. Ritter, K. G. Mason, S. Yew, J. T. Perryman, J. C. Ortiz-Rodríguez, N. R. Singstock, B. A. Wuille Bille, C. B. Musgrave and J. M. Velázquez, J. Mater. Chem. A, 2024, 12, 7199–7206.
25. J. M. Tarascon, F. J. Disalvo, D. W. Murphy, G. W. Hull, E. A. Rietman and J. V. Waszczak, J. Solid State Chem., 1984, 54, 204–212.
26. F. Y. Fradin and J. W. Downey, Mater. Res. Bull., 1979, 14, 1525–1528.
27. W. H. Wright and D. M. Ginsberg, J. Low Temp. Phys., 1986, 64, 73–86.
28. W. H. Wright and D. M. Ginsberg, J. Low Temp. Phys., 1987, 69, 203–208.
29. R. Chevrel, C. Rossel and M. Sergent, J. Less-Common Met., 1980, 72, 31–43.
30. G. B. Hertel, T. P. Orlando and J. M. Tarascon, Physica, 1985, 135B, 168–171.
31. T. Tsubota, M. Ohtaki and K. Eguchi, J. Ceram. Soc. Jpn., 1999, 107, 697–701.
32. X. Shi, L. Wang, L. Chen and X. Chen, Trans. Nonferrous Met. Soc. China, 2009, 19, 642–645.
33. J. T. Perryman, F. P. Hyler, J. C. Ortiz-Rodríguez, A. Mehta, A. R. Kulkarni and J. M. Velázquez, J. Coord. Chem., 2019, 72, 1322–1335.
34. J. C. Ortiz-Rodríguez, J. T. Perryman and J. M. Velázquez, Ind. Eng. Chem. Res., 2021, 60, 16153–16161.
35. J. T. Perryman, A. R. Kulkarni and J. M. Velázquez, J. Mater. Chem. C, 2020, 8, 10742–10748.
36. F. P. Hyler, B. A. Wuille Bille, J. C. Ortíz-Rodríguez, A. Sanz-Matias, S. Roychoudhury, J. T. Perryman, C. J. Patridge, N. R. Singstock, C. B. Musgrave, D. Prendergast and J. M. Velázquez, Phys. Chem. Chem. Phys., 2022, 24, 17289–17294.
37. S. J. George, O. B. Drury, J. Fu, S. Friedrich, C. J. Doonan, G. N. George, J. M. White, C. G. Young and S. P. Cramer, J. Inorg. Biochem., 2009, 103, 157–167.
38. M. J. Morra, S. E. Fendorf and P. D. Brown, Geochim. Cosmochim. Acta, 1997, 61, 683–688.
39. J. Prietzel, A. Botzaki, N. Tyufekchieva, M. Brettholle, J. Thieme and W. Klysubun, Environ. Sci. Technol., 2011, 45, 2878–2886.
40. A. A. Gambardella, C. M. Schmidt Patterson, S. M. Webb and M. S. Walton, Microchem. J., 2016, 125, 299–307.
41. Z. W. B. Iton and K. A. See, Chem. Mater., 2022, 34, 881–898.
42. P. Yu, X. Long, N. Zhang, X. Feng, J. Fu, S. Zheng, G. Ren, Z. Liu, C. Wang and X. Liu, J. Phys. Chem. Lett., 2019, 10, 1159–1166.
43. T. C. Kaspar, T. Droubay, S. A. Chambers and P. S. Bagus, J. Phys. Chem. C, 2010, 114, 21562–21571.
44. E. Tomaszewicz and M. Kurzawa, J. Mater. Sci., 2004, 39, 2183–2185.
45. A. Wieczorek, H. Lai, J. Pious, F. Fu and S. Siol, Adv. Mater. Interfaces, 2023, 10, 2201828.
46. J. Richard, A. Benayad, J.-F. Colin and S. Martinet, J. Phys. Chem. C, 2017, 121, 17096–17103.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma01090f

---