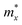DOI:
10.1039/D4MA00924J
(Paper)
Mater. Adv., 2025,
6, 849-859
Thermoelectric performance of Bi-based novel Janus monolayer structures†
Received
12th September 2024
, Accepted 12th December 2024
First published on 24th December 2024
Abstract
This work systematically investigates the stability and electronic and thermoelectric characteristics of newly discovered 2D Janus monolayers BiYZ (Y ≠ Z = Te, Se and S) according to the first-principles theory. Janus BiYZ monolayers are stable based on the AIMD simulations, positive phonon spectra plots and the evaluation of elastic strain tensor. These monolayers show a high carrier mobility (∼103 cm2 V−1 s−1) and an indirect bandgap nature. The Janus monolayers BiTeSe, BiTeS and BiSeS show an ultralow lattice thermal conductivity of 0.04 W m−1 K−1, 0.20 W m−1 K−1 and 0.02 W m−1 K−1, respectively, at room temperature. Low lattice thermal conductivity is obtained due to a small phonon group velocity, high Grüneisen parameter, small phonon relaxation time and significantly reduced phonon transport. The maximum ZT values at 500 K reach up to 0.97, 0.60 and 1.78 for BiTeSe, BiSeS, and BiTeS monolayers, respectively. Our results suggest Janus BiYZ monolayers to be promising thermoelectric candidates due to their superior thermal and electrical transport characteristics and subsequent strong thermoelectric performance.
1. Introduction
Currently, there is a severe energy shortage issue in our society.1 Resources like coal and gas are running low, and they might be completely used up by 2050. Thus, there is a demand for alternate, sustainable and green energy sources.2 In response to the higher demand for energy, researchers are attempting to explore new energy resources for sustainable and green energy to alleviate energy-related issues and avoid environmental contamination.3,4 Renewable energy sources such as sun, wind, heat, etc. are good for the environment and alternatives to fossil fuels.5
Thermoelectric (TE) materials can change the heat/thermal energy of the sun or waste heat directly into electricity. These materials are suitable for making efficient thermoelectric devices for developing sustainable and green energy from waste heat.6 Thermoelectric devices offer several benefits such as noiselessness, zero-emission, long service life,7–9 no moving parts, accurate temperature control and the ability to function under challenging circumstances.2 Now the efficiency of TE materials is figured out using a special formula: ZT = S2σT/(κl + κe), where ZT is the figure of merit, T is the temperature, S depicts the Seebeck coefficient, σ represents the electrical conductivity, S2σ denotes the power factor (PF), κl is the lattice thermal conductivity, and κe is the electron thermal conductivity. The κl should be low and σ and S should be high for good thermoelectric materials.10 In the ideal situation, reducing the κl would result in outstanding TE performance without decreasing the PF values of TE materials.
After the synthesis of Janus MoSSe11 and Janus WSSe12 monolayers, other Janus 2D compounds have been the subject of considerable investigation and attention toward thermal transport characteristics.13 In crystal formations, their mirror asymmetry can reduce κl by increasing phonon anharmonicity.14–16 For example, gallium chalcogenide-based Janus monolayers have been demonstrated with κl ≈ 11.95–26.16 W m−1 K−1,14 significantly lower than those of conventional monolayers such as GaS (κl ≈ 100 W m−1 K−1) and GaSe (κl ≈ 74 W m−1 K−1) at 300 K.15 The ZT value at 300 K of the Janus Al2STe monolayer is reported to be 1.38 (n-type), comparatively greater than those for conventional Al-chalcogenide monolayers (ZT ≈ 0.52–0.59).17 Furthermore, the Janus WSTe monolayer has a smaller κl than 2D WS2, leading to a higher ZT at 1200 K of 2.56.16
Furthermore, several novel Janus monolayers like AsTeX (X = Cl, Br and I),18 AsSBr,19 NiSX (X = O, Se and Te),20 In2XO (X = S, Se and Te),21 HfX2 (X = S, Se),22 PdSX (X = Se and Te),23 BiOCl24 and SbYZ (Y = S, Se; Z = Cl, Br and I)25 with excellent thermoelectric properties (ZT ≈ 0.06–2.54 at ∼300–900 K) have been reported. Hence, the Janus materials with excellent thermal and electron transport properties are suitable for advanced thermoelectric applications.
Advancing past their binary counterparts, 2D ternary metal chalcogenides26 are becoming the next generation of 2D semiconductors.27,28 In particular, ternary compounds based on bismuth, like bismuth oxychalcogenides (Bi2O2X where X = S, Se, and Te), have been recently realized, and their extraordinary qualities such as high carrier mobility and stability under ambient conditions have drawn a lot of attention.29,30 Additionally, recent experimental research shows that bismuth oxyhalides (BiOX, where X = Cl, Br, and I) exhibit superior performance in energy harvesting applications because of their distinct electronic characteristics.31 Also, in theoretical studies, BiOX (X = Cl, Br) has shown good thermochemical stability.32 Another significant class of ternary frameworks composed of bismuth is Janus bismuth chalcogenides Bi2X2Y (X = Te, Se; Y = Te, Se, S), which have been shown to possess good energy harvesting potential.33
This work is inspired by the previous explorations of pnictogen-based dichalcogenide monolayers in a novel structure34 for optoelectronic applications. We extensively studied the novel Janus monolayers BiYZ (Y ≠ Z = Te, Se and S) employing density functional theory (DFT). The dynamical stability and thermal stability of Janus BiYZ are confirmed by performing phonon dispersion and ab initio molecular dynamics (AIMD) simulations. We investigated the mechanical response for material stability. We examined that 2D BiYZ exhibits high thermoelectric performance having very low lattice thermal conductivity including electron–phonon interaction mechanisms. In accordance with the deformation potential theory, these monolayers exhibit high carrier mobility.
2. Computational details
The current study uses the quantum espresso (QE) software35 to perform first-principles computations on Janus BiYZ monolayers using density functional theory (DFT). To compute the exchange–correlation energy, the GGA-PBE functional36 was utilized. The valence electrons were described using potentials created by the projected-augmented-wave (PAW) approach.37 The structures were optimized with gamma (Γ) centered 12 × 12 × 1 k-meshes. The electron convergence for energy and force was set at 10−8 eV and 10−7 eV Å−1 respectively, for structure relaxation within a plane-wave kinetic energy cutoff of 80 Ry. The z-direction was maintained at 20 Å vacuum to avoid interactions between neighboring images of supercell. Density functional perturbation theory (DFPT) computations were performed using dynamical matrices on 16 × 16 × 1 k-point mesh and 6 × 6 × 1 Γ-centered q-point grid to simulate the phonon dispersion spectra.38 AIMD calculations using a Nosé–Hoover thermostat39,40 were performed with a time step of 1 fs for 5000 fs. The thermoelectric transport coefficients such as electron thermal conductivity (κe) and electrical RTA (relaxation time approximation)29 were determined using the BoltzTrap code41via semi-classical Boltzmann transport equations (BTE). According to RTA, electronic thermal conductivity (κe/τ) and (σ/τ) are estimated using BoltzTraP within the BTE framework. The EPW software,42,43 which makes use of maximally localized Wannier functions (MLWFs) for effective interpolation of electron–phonon interaction (EPI) matrix components onto a fine k- and q-mesh32,44–48 of 80 × 80 × 1, was used to calculate the relaxation time. Phono3py49 which is interfaced with the QE package was adopted to calculate the lattice thermal conductivity (κl). A 3 × 3 × 1 supercell was used to obtain interatomic force constants of 2nd and 3rd order, with 4 × 4 × 1 k-point sampling.
3. Results and discussion
3.1 Geometrical structure and stability analysis
The optimized structures of Janus BiYZ monolayers with a cm11 space group (no. 13) are shown in Fig. 1. There are six atoms in the unit cell with a rhombus structure and 12 atoms in a rectangular unit cell. Table 1 lists the structural parameters of Janus monolayers. In this work, we adopted a rhombus unit cell for all the material properties except for the mechanical response where a rectangular unit cell is used. With an increase in the radius of constituent atoms, the lattice constant (a = b) of Janus BiYZ monolayers increases (Table 1). Moreover, the reduced attractive forces among the atoms with bigger radii lead to a rise in total thickness (h) and bond lengths (dBi–Y, and dBi–Z), while bond angles decreased with larger atoms of Janus BiYZ monolayers, as shown in Table 1. The Janus BiYZ monolayers’ estimated structural properties fall between those of their parent monolayers. Our calculated values of parent monolayers BiY2 (Y = S, Se, Te) are consistent with the prior literature.34
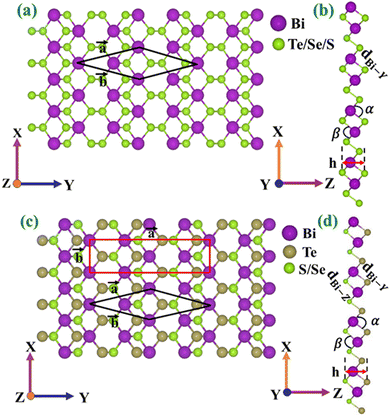 |
| | Fig. 1 The top (a) and side (b) views of BiY2 (Y = Te, Se and S) monolayers and top (c) and side (d) views of Janus BiYZ (Y ≠ Z = Te, Se and S) monolayers. The rhombus (with black color) and rectangular (with red color) unit cells utilized in the computations are displayed. The related lattice vectors (a and b), bond angles (α and β), bond lengths (dBi–Y, and dBi–Z) and thickness (h) of the Janus BiYZ (Y ≠ Z = S, Se, Te) monolayers are also shown. | |
Table 1 The optimized lattice parameters (a and b), atomic bond lengths (dBi–Y, and dBi–Z), bond angles between Y–Bi–Y and Z–Bi–Z (α and β), thickness (h), work functions (ΦY, ΦZ,) for different surfaces Y and Z, and their differences ΔΦ and cohesive energy (Ecoh) for Janus BiYZ (Y ≠ Z = S, Se, Te) and BiY2 (Y = Te, Se, S) monolayers
| 2D monolayers |
(a,b) (Å) |
d
Bi–Y, d (Å) |
d
Bi–Z
d (Å) |
α (°) |
β (°) |
h (Å) |
Φ
W (eV) |
Φ
X (eV) |
ΔΦ (eV) |
E
coh (eV per atom) |
| BiTe2 |
8.53 |
2.89 |
— |
87.76 |
92.23 |
4.39 |
4.33 |
4.33 |
0 |
4.68 |
| BiSe2 |
7.86 |
2.70 |
— |
89.85 |
90.14 |
4.01 |
4.85 |
4.85 |
0 |
4.55 |
| BiS2 |
7.59 |
2.57 |
— |
92.25 |
87.74 |
3.75 |
5.06 |
5.06 |
0 |
4.34 |
| BiTeSe |
8.22 |
2.89 |
2.70 |
87.63 |
90.38 |
4.21 |
3.20 |
3.26 |
0.06 |
3.57 |
| BiTeS |
8.13 |
2.88 |
2.56 |
85.58 |
90.94 |
4.09 |
2.98 |
2.93 |
0.05 |
3.74 |
| BiSeS |
7.74 |
2.96 |
2.57 |
87.27 |
89.98 |
3.88 |
3.20 |
3.18 |
0.02 |
3.95 |
We computed the cohesive energies to determine the energetic stability of monolayers as:
| |  | (1) |
where
EBiYZ is the total energy of BiYZ, and
EBi,
EY,
EY and
EZ are single atom energies of Bi, Y and Z elements, respectively.
m,
n and
o represent the atom counts in the respective unit cells.
The cohesive energies of Janus BiTeSe, BiTeS, and BiSeS monolayers are in between the cohesive energies of their constituent parent monolayer counterparts (Table 1). The computed Ecoh of Janus BiYZ monolayers is comparable to those of Janus SbXY (3.21–3.84 eV per atom),25 BiXY (2.46–3.58 eV per atom)44 and Ge2XX′ (3.14–3.68 eV per atom)45 monolayers, indicating the energetic stability of Janus BiYZ monolayers and their possibility of experimental synthesis.
In addition, we compute the work function Φ, which is an important electron property. Fig. S1(a)–(e), ESI† demonstrates the average electrostatic potential energy curves of BiY2 and Janus BiYZ along the thickness of the monolayers where the dipole correction is included. Table 1 shows the work function of two different surfaces ΦX and ΦY along with their difference ΔΦ. As effective electron emission is desired in electronic and optoelectronic devices, the observed alterations in the work function may have important significance for future applications.46
3.1.1 Dynamical and thermal stability.
We then investigate Janus BiYZ monolayers’ dynamical and thermal stability. By computing phonon dispersion spectra, Janus BiYZ monolayers’ dynamical stability is verified. The absence of imaginary frequencies in the phonon dispersion spectra of Janus BiYZ monolayers suggests that these monolayers are dynamically stable, as seen in Fig. 2(a)–(c). The dispersion spectra of BiYZ monolayers show eighteen vibrational modes, i.e., three acoustic phonon (AP) modes (flexural acoustic (ZA) branch, the transverse acoustic (TA) branch, and the longitudinal acoustic (LA)) and 15 optical phonon (OP) modes. Similar to other 2D monolayers predicted by the continuum elasticity theory, the ZA branch displays quadratic dispersion while the TA and LA branches exhibit linear dispersion around the Γ-point. As the atomic mass of constituent atoms became larger, the phonon modes of BiYZ monolayers changed to lower frequencies as shown in Fig. 2(a)–(c). Because of the weak bond between the atoms in BiSeS, a gap appears between the AP and OP modes. Next, AIMD simulations are used to assess the thermal stability of the Janus BiTeSe, BiTeS, and BiSeS monolayers at room temperature (300 K) using a comparatively bigger 4 × 4 × 1 supercell. Fig. 2(d)–(f) depicts the small thermal fluctuation in temperature and energy as a function of the simulated time steps at room temperature. The significantly less distortion of monolayer structures without bond-breaking suggests that the Janus BiTeSe, BiTeS, and BiSeS monolayers are thermally stable.
 |
| | Fig. 2 (a)–(c) Phonon dispersion spectrum with flexural acoustical (ZA), transverse acoustical (TA) and longitudinal acoustical (LA) phonon modes and (d)–(f) the AIMD energy and temperature fluctuations at 300 K of Janus BiYZ (Y ≠ Z = S, Se, Te) monolayers. The snapshots of Janus monolayers after 5000 fs AIMD simulations are also shown. | |
3.1.2 Mechanical stability.
Following the unveiling of the structural stability, the mechanical stability of the suggested structures as determined by the Born and Huang criteria47 is examined by computing the elastic strain tensor. The non-zero elastic constants Cij such as C11, C12, and C66 are obtained as shown in Table 2. 2D Janus BiYZ monolayers' mechanical stability satisfies C11 > |C12| and C66 (C11 − C12)/2 > 0 indicating their mechanical stability.
Table 2 Elastic coefficients (C11, C12), Young's modulus (Y2D) and Poisson's ratio (ν) of Janus BiYZ (Y ≠ Z = S, Se, Te) monolayers
| 2D monolayers |
C
11 (N m−1) |
C
12 (N m−1) |
Y
2D (N m−1) |
Poisson's ratio (ν) |
| BiTeSe |
160.46 |
52.50 |
143.28 |
0.32 |
| BiTeS |
180.76 |
86.20 |
148.63 |
0.42 |
| BiSeS |
260.42 |
94.08 |
226.43 |
0.32 |
The elastic characteristics of BiYZ monolayers are analyzed using two constants: the Young's modulus (Y2D) and the Poisson ratio (ν):
| |  | (2) |
| |  | (3) |
The computed values of Poisson's ratio (ν) for Janus BiTeSe, BiTeS and BiSeS monolayers are listed in Table 2. The value of Poisson's ratio for monolayers BiTeSe and BiSeS is the same as 0.32 which is less than one-third, implying that these monolayers are fragile according to the Frantsevich rule48 whereas Janus BiTeS monolayers show a ductile nature. The Y2D values of Janus BiYZ monolayers are listed in Table 2, which are higher than those of the Janus SbYZ (Y = S and Se and Z = Cl, Br, and I)25 (0.28–0.38 N m−1) and Ga2SX2 (X = O, S, Se, Te)50 (20.8–116.08 N m−1) monolayers and XBi2Se4 (X = Sn Pb)51 (79.32 N m−1) and comparable to that of the MoS2 (130 N m−1)52 monolayer.
3.2 Electronic structure
The band structures of Janus BiYZ monolayers are obtained using the PBE and PBE + SOC level of theory along high-symmetry paths of the Brillouin zone (Fig. 3(a)–(c)). The calculated band gaps with PBE (PBE + SOC) of Janus BiTeSe, BiTeS and BiSeS monolayers are 1.02 eV (0.50 eV), 1.07 eV (0.57 eV) and 1.44 eV (0.96 eV), respectively, which underscore the importance of including SOC effects in the studied monolayers. As an indirect bandgap semiconductor, the Janus monolayers are found to have the valence-band maximum (VBM) and conduction-band minimum (CBM) on the Γ point along the Γ–K direction. Considering SOC effects, the bandgap decreases in these monolayers due to heavy Bi and Te atoms. The band gaps of the corresponding parent BiTe2, BiSe2, and BiS2 monolayers using PBE (PBE + SOC) are calculated to be 0.92 eV (0.32 eV), 1.29 eV (0.80 eV) and 1.59 eV (0.93 eV) as depicted in Fig. S2(a)–(c), ESI.† These values are consistent with previously reported bandgaps of these monolayers.34 We also calculated the partial density of states (PDOS) to further analyze the electronic structure. The PDOS analysis (Fig. S3(a)–(c), ESI†) reveals that the p-orbitals are involved in the states near the Fermi energy of BiYZ monolayers.
 |
| | Fig. 3 The calculated band structure of Janus (a) BiTeSe, (b) BiTeS and (c) BiSeS monolayers with PBE (violet color) and PBE + SOC (red color) level of theory. | |
Furthermore, we investigated the Janus BiYZ monolayer's optical characteristics in a broad range of 0–10 eV of photon energy ħω, with the incoming photon being parallel polarized. The optical absorbance that has been used to analyze is given as:
| |  | (4) |
where
L denotes the cell's length in the
Z-direction. Fig. S4, ESI
† clearly shows in-plane light absorption maxima in the notably visible range (1.75–8 eV), suggesting potential uses of these materials in optoelectronic devices.
3.2.1 Carrier mobility.
The materials' suitability for use in electronic devices is largely determined by their electronic transport characteristics, particularly carrier mobility (μ2D). Deformation potential approximation (DPA) is a widely used technique for determining the carrier mobility,53μ2D of 2D materials, which was first proposed by Bardeen and Shockley and can be written as:53–55| |  | (5) |
where ħ is the Planck constant, e is the electron charge, T is the temperature, which is fixed at 300 K, kB is the Boltzmann constant, C2D indicates elastic constants, m* represents effective masses of electron and holes,  is the average effective mass and Ed is the deformation potential (DP) constant. The DP constant is obtained by calculating the band edges and concerning the uniaxial strain (Fig. S5, ESI†). The effective mass and deformation potential of Janus BiYZ monolayers are comparable with those of TlAgX (X = S, Se) monolayers56 and HG monolayers.57 It is determined that the carrier mobility of Janus BiYZ monolayers is highly anisotropic, indicating directional dependence of the effective masses and deformation potentials of holes and electrons. The values of μ2D of Janus BiYZ monolayers for both electrons and holes are listed in Table 3. Note that the electron (hole) mobility of the Janus SMoSiN2 monolayer is 298.7 (1377.9) cm2 V−1 s−1.58 Also the electronic mobility of layered PbBi2Se4 is estimated to be 153 cm2 V−1 s−1.59 The Janus BiYZ monolayers also possess mobilities higher than those of other Janus monolayers such as MoSSe (250 cm2 V−1 s−1 (ref. 60)), HG (14.18 × 103 cm2 V−1 s−1) and Mo8S6Se6 (104 cm2 V−1 s−1),61 suggesting that these Janus monolayers would be promising materials for electronic and thermoelectric applications.
is the average effective mass and Ed is the deformation potential (DP) constant. The DP constant is obtained by calculating the band edges and concerning the uniaxial strain (Fig. S5, ESI†). The effective mass and deformation potential of Janus BiYZ monolayers are comparable with those of TlAgX (X = S, Se) monolayers56 and HG monolayers.57 It is determined that the carrier mobility of Janus BiYZ monolayers is highly anisotropic, indicating directional dependence of the effective masses and deformation potentials of holes and electrons. The values of μ2D of Janus BiYZ monolayers for both electrons and holes are listed in Table 3. Note that the electron (hole) mobility of the Janus SMoSiN2 monolayer is 298.7 (1377.9) cm2 V−1 s−1.58 Also the electronic mobility of layered PbBi2Se4 is estimated to be 153 cm2 V−1 s−1.59 The Janus BiYZ monolayers also possess mobilities higher than those of other Janus monolayers such as MoSSe (250 cm2 V−1 s−1 (ref. 60)), HG (14.18 × 103 cm2 V−1 s−1) and Mo8S6Se6 (104 cm2 V−1 s−1),61 suggesting that these Janus monolayers would be promising materials for electronic and thermoelectric applications.
Table 3 The effective mass (m*), average effective mass (md), deformation potential Ed (eV), elastic modulus C2D (J m−2) and charge carrier mobilities μ2D (cm2 V−1 s−1) along the x- and y-directions of the Janus BiYZ (Y/Z = Te, Se, S) monolayers
3.3 Thermoelectric properties
3.3.1 Lattice thermal transport properties.
The lattice thermal conductivity (κl) calculation relies heavily on the phonon transport parameters. Gruneisen parameter (γ) and phonon group velocity (vk) are phonon transport characteristics that characterise the κl of Janus BiYZ monolayers. By aggregating the contributions of all phonon modes represented by the wave vector q and the dispersion branch λ, one may evaluate the κl, as the following equation:62| |  | (6) |
where Cλq is the mode-specific heat capacity, τλq is the phonon relaxation time of phonon mode with λ and q and Vλq is the group velocity of phonon mode.
Phonon–phonon anharmonic interactions affect the κl expected for 2D materials because of the Umklapp process and it decreases with temperature as κlα 1/T (ref. 63) as shown in Fig. 4. The calculated values of κl at room temperature are 0.02 W m−1 K−1, 0.20 W m−1 K−1 and 0.04 W m−1 K−1 for Janus BiTeSe, BiTeS and BiSeS monolayers, respectively, indicating good thermoelectric performance of these materials. The Janus BiYZ monolayers show ultralow values of κl similar to those of the well-known 2D Janus WSTe (κl ≈ 0.08 W m−1 K−1)16 and TlPo monolayers (κl ∼ 0.17 W m−1 K−1).64
 |
| | Fig. 4 Lattice thermal conductivity as a function of temperature for Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers. | |
Next, we obtain Debye temperature (ΘD) which can be computed as:65
| |  | (7) |
where
Θi is defined as
Θ =
ħvm/
kB for each mode,
i = ZA, TA, and LA.
kB,
ħ and
vm represent the Boltzmann constant, the Planck constant and the maximum frequency of normal mode vibration (Fig. S6(a)–(c), ESI
†).
The Debye temperatures (ΘD) of Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers are comparable to those of other monolayers as listed in Table 4. Low ΘD signifies that phonon modes are activated at low temperatures, which makes phonon scattering channels available at low temperatures. Consequently, the lattice thermal conductivity shows a decrease in the values.66
Table 4 The Debye temperature (ΘD) for Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers
| Materials |
(ΘD) (K) |
|
| BiTeSe |
74.22 |
This work |
| BiTeS |
77.39 |
This work |
| BiSeS |
79.95 |
This work |
| PdSeTe |
60 |
67
|
| SbTeI |
86.4 |
68
|
| BiTeI |
82.1 |
| PbI2 |
69 |
69
|
| PdSe2 |
63 |
70
|
| PdTe2 |
45 |
| SnSe |
52 |
71
|
Also, the specific heat capacity (CV) of Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers is obtained in Fig. 5. The CV of the Janus BiSeS monolayer (10.98 J mol−1 K−1) is higher than that of the other two Janus BiTeSe (9.53 J mol−1 K−1) and BiTeS (and 8.27 10.98 J mol−1 K−1) monolayers. The CV exhibits the anticipated T3 law behaviour in the low-temperature limit.72 After saturation, the CV curve of these Janus monolayers remains constant with temperature. This type of behavior of the CV curve is similar to that of other monolayers such as WXY (X, Y = S, Se, and Te),73 PdXY (Y = Se, Te)74 and M2XY (M = Ga; X, Y = S, Se, Te).14
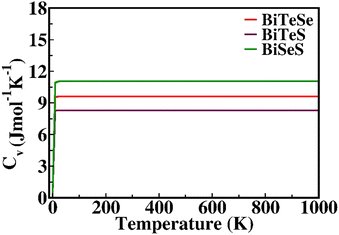 |
| | Fig. 5 Temperature dependence of specific heat capacity (CV) of Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers. | |
The most significant parameter for evaluating thermal transportation is the phonon group velocities which are expressed as:
| |  | (8) |
where
k,
ω and
q represent the frequency of wave vector, phonon modes and vibrational mode index, respectively. In monolayer systems, the acoustic modes typically dominate the
κl.
75 The high-frequency modes show relatively small group velocities, while the low-frequency zone displays larger values of group velocities. The calculated low group velocities 6.2, 4.9, and 3.6 km s
−1 of BiTeSe, BiTeS and BiSeS from ZA mode (Fig. S6(a)–(c), ESI
†) is the reason for the ultralow lattice thermal conductivity. Also, as seen in Fig. S7 (ESI
†), Janus BiYZ monolayer's phonon lifetime mostly lies between 0.1 and 2.9 ps. The
κl is also decreased by the small phonon relaxation time.
To further get deeper insight into the low lattice thermal conductivity, for every phonon mode, the Grüneisen parameter is computed to measure the anharmonicity of monolayers. The Grüneisen parameter (γ) is evaluated as:76
| |  | (9) |
where
a0 is the equilibrium lattice constant. From
eqn (8), we notice that a larger Grüneisen parameter is observable in the low-frequency domain as shown in Fig. S6(d)–(f), ESI.
† Usually, a larger Grüneisen parameter indicates strong anharmonicity, which is also responsible for the ultralow value of
κl.
3.3.2 Electronic transport properties.
The carriers’ semi-classical Boltzmann transport equations (BTE) are solved to derive the thermoelectric transport properties under relaxation time approximation (RTA) theories. Proper handling of the carrier relaxation time through intricate scattering processes is crucial in this case. Previous works have employed the deformation potential theory, in which the computed value is typically exaggerated and the relaxation time is represented as a constant.77 In the current study, we use complete electron–phonon interactions to obtain the relaxation time from the imaginary component of the electron self-energy. The k-resolved relaxation time can be estimated as:| |  | (10) |
where ωq is the BZ weight associated with wave vector q of phonons,  is the electron–phonon coupling strength, and Ψnk represents the electronic wave function for eigenvalue εnk, wave-vector k and band index m. ωqv is derivative of the self-consistent potential ∂qvV with branch index v and wave vector q· fmk+q represent the electronic state occupation. The relaxation time as a function of carrier's energy is shown in Fig. 6(a)–(c). The estimated value of relaxation time is of the order of ∼10−15 s at different temperatures for Janus BiYZ monolayers.
is the electron–phonon coupling strength, and Ψnk represents the electronic wave function for eigenvalue εnk, wave-vector k and band index m. ωqv is derivative of the self-consistent potential ∂qvV with branch index v and wave vector q· fmk+q represent the electronic state occupation. The relaxation time as a function of carrier's energy is shown in Fig. 6(a)–(c). The estimated value of relaxation time is of the order of ∼10−15 s at different temperatures for Janus BiYZ monolayers.
 |
| | Fig. 6 The relaxation time as a function of carrier's energy of Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers. Zero represents the Fermi energy. | |
The Wiedemann–Franz law78 states that the electronic thermal conductivity κe can be calculated as follows:
where
L represents the Lorenz constant; based on the Seebeck coefficient (
S), we can calculate the Lorenz numbers using the formula

;
78T is the temperature and
σ is the electrical conductivity. The
κe with variation of chemical potential ranges from ∼0.4 to ∼1.5 W m
−1 K
−1 at 500 K of Janus BiYZ monolayers (
Fig. 7(a)). The variations of
κe with chemical potential at temperatures 300 K and 700 K are also shown in Fig. S8(a), ESI.
†
 |
| | Fig. 7 The calculated (a) electronic thermal conductivity (κe), (b) electrical conductivity (σ), (c) Seebeck coefficient (S) and (d) power factor (S2σ) of Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers at 500 K. | |
Moreover, the electrical conductivity and Seebeck coefficient of BiYZ monolayers are computed within the context of Boltzmann transport theory utilizing the equations:
| |  | (12) |
| |  | (13) |
where
T is the electronic temperature,
V is the cell volume,
fnk is the Fermi–Dirac distribution function,
EF is the Fermi energy,
Vnk is an aspect of group velocity in a specific direction at each
k point and
N depicts the
k point number.
In addition, the electrical conductivity, Seebeck coefficient, and power factor (P = S2σ) concerning chemical potential at 500 K are presented in Fig. 7(b)–(d) and also in Fig. S8(b)–(d) (ESI†) at 300 K and 700 K. The increase in temperature decreases the value of S. The highest values of power factor obtained at 500 K temperature for p(n)-type carriers are 0.14 × 10−3 W m−1 K−2 (0.05 × 10−3 W m−1 K−2), 0.02 × 10−3 W m−1 K−2 (0.03 × 10−3 W m−1 K−2), and 0.08 × 10−3 W m−1 K−2 (0.05 × 10−3 W m−1 K−2) of Janus BiTeSe, BiTeS and BiSeS monolayers, respectively. The maximum value of power factor indicates that BiTeSe and BiSSe are p-type while BiTeS is an n-type semiconductor due to the high Seebeck coefficient as displayed in Fig. 7(c) at 500 K and Fig. S8(c), ESI† at 300–700 K. The power factor of these monolayers is comparable to that of the Janus 2D B2P6 monolayer.79
3.3.3 Thermoelectric figure of merit.
A high thermoelectric figure-of-merit (ZT) value requires large values of σ and S and considerably small values of κe and κl as shown by the expression:The assumption of constant relaxation time does not consider electron–phonon interactions. We computed accurate relaxation time by considering electron–phonon interactions using the EPI method. Fig. 8(a)–(c) demonstrates the figure-of-merit (ZT) for a p-(n)-type of Janus BiYZ monolayers with respect to chemical potential. The maximum ZT values of Janus BiTeSe, BiTeS, and BiSeS monolayers obtained at 500 K are 0.97 (0.76), 0.46 (0.60), and 1.78 (1.35) for p-(n)-type carriers. Table S1, ESI† shows that ZT values for monolayers BiTeSe, BiTeS, and BiSeS are high enough at 700 K. Table 5 displays the thermoelectric performance of previously reported thermoelectric materials comparable with BiYZ monolayers. A weighted average of the thermoelectric figure-of-merit (z![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ) is used to obtain the thermoelectric efficiency ηmax (%) as:80,81
) is used to obtain the thermoelectric efficiency ηmax (%) as:80,81| |  | (15) |
where Tc and TH represent the cold and hot temperatures. Our calculations revealed that the thermoelectric unit's output power and efficiency could be increased up to 63.14% (57.90%), 53.76% (78.67%) and 64.14% (63.53%) of Janus BiTeSe, BiTeS and BiSeS monolayers for p-(n) type charge carriers, respectively. The reported TE efficiency of other 2D monolayers such as Bi2Te382 and X2YH2 (X = Si, Ge; Y = P, As, Sb, Bi)83 is 5–18%. Also the TE efficiencies of Janus BiSbTeSeS, BiSbTeSeTe, and BiSbTeSTe monolayers are 34%, 30%, and 33%,84 respectively. On comparison of the TE efficiency with other Janus monolayers, the reported efficiency is comparatively higher; hence, the Janus BiTeSe, BiTeS, and BiSeS monolayers are candidate materials for thermoelectric devices to convert waste heat directly into electricity.
 |
| | Fig. 8 The calculated figure-of-merit (ZT) concerning the chemical potential (μ) of Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers at 300–700 K. | |
Table 5 The comparison of ZT of 2D Janus BiYZ monolayers with other similar monolayers at temperature 300–700 K
| 2D monolayers |
Figure-of-merit (ZT) |
Temperature (K) |
Ref. |
| BiTeSe |
0.18–2.11 |
300–700 |
This work |
| BiTeS |
0.10–2.85 |
300–700 |
This work |
| BiSeS |
0.58–2.38 |
300–700 |
This work |
| Janus BiSbTeSeS, BiSbTeSeTe, and BiSbTeSTe |
035, 0.55, 0.70 |
300 |
84
|
| Bi2TeSe2 |
0.87–3.45 |
300–900 |
13
|
| Bi2Te2Se |
1.4–2.0 (p) |
300–500 |
85
|
| Bi2SSe2 |
0.50–0.28 (p) |
300–700 |
86
|
| Bi2S2Se |
1.39–0.93 (p) |
| WSTe |
0.742 |
300 |
16
|
| TlPo |
1.88 |
300 |
64
|
| NiSO and NiSSe |
∼1 |
300 |
20
|
| ScYCBr2 |
∼0.28–0.70 |
300–700 |
87
|
| BaAgBi |
0.42 |
300–600 |
88
|
| γ-GeSe |
0.84–2.04 |
300–600 |
89
|
Conclusions
In summary, the work reports a combined density functional theory and semi-classical Boltzmann transport calculations of Janus BiYZ (Y ≠ Z = Te, Se, S) monolayers. The dynamical stability for Janus BiYZ monolayers was verified from the phonon dispersion relations, which are free from imaginary frequencies. The elastic tensors and AIMD simulation represented that these Janus monolayers are thermally and mechanically stable. Poisson ratio (ν) and Young's modulus (Y2D) are computed to investigate the mechanical response of suggested monolayers. The obtained band gaps of monolayers are indirect in nature with superior carrier mobility. The thermoelectric efficiency of these monolayers is calculated in the range of ∼53–78%. The ultralow lattice thermal conductivity and high thermoelectric figure-of-merit make Janus BiYZ monolayers a promising candidate for thermoelectric devices.
Data availability
The data supporting this article have been included in this article and in the ESI.†
Conflicts of interest
The authors declared no conflicts of interest.
Acknowledgements
KM Sujata is thankful to the M.P. Council of Science and Technology MPCST (FTYS) for financial assistance in the form of a Young Scientist Fellowship. NV acknowledges the senior research fellowship from CSIR. The findings reported in this work were obtained using the computational facility at the Central University of Punjab, Bathinda.
References
- G. Zhang and Y.-W. Zhang, Strain effects on thermoelectric properties of two-dimensional materials, Mech. Mater., 2015, 91, 382–398 CrossRef.
- M. Hong and Z.-G. Chen, Chemistry in advancing thermoelectric GeTe materials, Acc. Chem. Res., 2022, 55(21), 3178–3190 CrossRef CAS PubMed.
- Z.-G. Chen,
et al., Nanostructured thermoelectric materials: Current research and future challenge, Prog. Nat. Sci.:Mater. Int., 2012, 22(6), 535–549 CrossRef.
- T. Zhu,
et al., Compromise and synergy in high-efficiency thermoelectric materials, Adv. Mater., 2017, 29(14), 1605884 CrossRef.
- A. R. Natarajan,
et al., Bulk and monolayer thermoelectric and optical properties of anisotropic NbS2Cl2, Mater. Today Commun., 2023, 34, 105309 CrossRef CAS.
- B. Ali,
et al., Optical and thermoelectric properties of new Janus ZnMN2 (M = Ge, Sn, Si and N = S, Se, Te) monolayers: a first-principles study, Nanoscale Adv., 2024, 6(2), 680–689 RSC.
- S. Ortega,
et al., Bottom-up engineering of thermoelectric nanomaterials and devices from solution-processed nanoparticle building blocks, Chem. Soc. Rev., 2017, 46(12), 3510–3528 RSC.
- R. Kroon,
et al., Thermoelectric plastics: from design to synthesis, processing and structure–property relationships, Chem. Soc. Rev., 2016, 45(22), 6147–6164 RSC.
- Z.-H. Ge,
et al., Low-cost, abundant binary sulfides as promising thermoelectric materials, Mater. Today, 2016, 19(4), 227–239 CrossRef CAS.
- X.-L. Zhu,
et al., KAgX (X = S, Se): high-performance layered thermoelectric materials for medium-temperature applications, ACS Appl. Mater. Interfaces, 2020, 12(32), 36102–36109 CrossRef CAS PubMed.
- J. Zhang,
et al., Janus monolayer transition-metal dichalcogenides, ACS Nano, 2017, 11(8), 8192–8198 CrossRef CAS.
- B. Zheng,
et al., Band alignment engineering in two-dimensional lateral heterostructures, J. Am. Chem. Soc., 2018, 140(36), 11193–11197 CrossRef CAS PubMed.
- N. Wang,
et al., High-temperature thermoelectric monolayer Bi2TeSe2 with high power factor and ultralow thermal conductivity, ACS Appl. Energy Mater., 2022, 5(2), 2564–2572 CrossRef CAS.
- Q. Zhong,
et al., Phonon thermal transport in Janus single layer M2XY (M = Ga; X, Y = S, Se, Te): A study based on first-principles, Phys. E, 2020, 115, 113683 CrossRef CAS.
- T. Pandey, D. S. Parker and L. Lindsay,
Ab initio phonon thermal transport in monolayer InSe, GaSe, GaS, and alloys, Nanotechnology, 2017, 28(45), 455706 CrossRef PubMed.
- A. Patel,
et al., High thermoelectric performance in two-dimensional Janus monolayer material WS-X (X = Se and Te), ACS Appl. Mater. Interfaces, 2020, 12(41), 46212–46219 CrossRef CAS.
- G. S. Khosa,
et al., Janus Al2STe monolayer: a prospective thermoelectric material, Solid State Commun., 2022, 341, 114579 CrossRef CAS.
- P. Chauhan, J. Singh and A. Kumar, As-based ternary Janus monolayers for efficient thermoelectric and photocatalytic applications, J. Mater. Chem. A, 2023, 11(19), 10413–10424 RSC.
- M. Liu,
et al., Thermoelectric properties of Janus AsSBr monolayer from first-principles study, Solid State Commun., 2022, 342, 114612 CrossRef CAS.
- S. Ahmadi,
et al., A theoretical prediction of novel Janus NiSX (X = O, Se, Te) Monolayers: Electronic, optical, and thermoelectric properties, Appl. Surf. Sci., 2023, 616, 156560 CrossRef CAS.
- T. V. Vu,
et al., Theoretical prediction of electronic, transport, optical, and thermoelectric properties of Janus monolayers In2XO (X = S, Se, Te), Phys. Rev. B, 2021, 103(8), 085422 CrossRef CAS.
- J. Bera, A. Betal and S. Sahu, Spin orbit coupling induced enhancement of thermoelectric performance of HfX2 (X = S, Se) and its Janus monolayer, J. Alloys Compd., 2021, 872, 159704 CrossRef CAS.
- W.-L. Tao,
et al., Thermoelectric properties of Janus MXY (M = Pd, Pt; X, Y = S, Se, Te) transition-metal dichalcogenide monolayers from first principles, J. Appl. Phys., 2020, 127(3), 035101 CrossRef CAS.
- C.-W. Wu,
et al., Enhanced high-temperature thermoelectric performance by strain engineering in BiOCl, Phys. Rev. Appl., 2022, 18(1), 014053 CrossRef CAS.
- P. Chauhan, J. Singh and A. Kumar, Two-dimensional Janus antimony chalcohalides for efficient energy conversion applications, J. Mater. Chem. A, 2024, 12, 16129–16142 RSC.
- L. Dong, J. Lou and V. B. Shenoy, Large in-plane and vertical piezoelectricity in Janus transition metal dichalchogenides, ACS Nano, 2017, 11(8), 8242–8248 CrossRef CAS PubMed.
- A. Ramasubramaniam, Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(11), 115409 CrossRef.
- Q. Ji,
et al., Chemical vapour deposition of group-VIB metal dichalcogenide monolayers: engineered substrates from amorphous to single crystalline, Chem. Soc. Rev., 2015, 44(9), 2587–2602 RSC.
- M. J. Varjovi and E. Durgun, First-principles study on structural, vibrational, elastic, piezoelectric, and electronic properties of the Janus Bi XY (X = S, Se, Te and Y = F, Cl, Br, I) monolayers, Phys. Rev. Mater., 2021, 5(10), 104001 CrossRef CAS.
- J. Wu,
et al., Controlled synthesis of high-mobility atomically thin bismuth oxyselenide crystals, Nano Lett., 2017, 17(5), 3021–3026 CrossRef CAS.
- J. Di,
et al., Bismuth oxyhalide layered materials for energy and environmental applications, Nano Energy, 2017, 41, 172–192 CrossRef CAS.
- T. Das and S. Datta, Thermochemical stability, and electronic and dielectric properties of Janus bismuth oxyhalide BiOX (X = Cl, Br, I) monolayers, Nanoscale Adv., 2020, 2(3), 1090–1104 RSC.
- S.-H. Cao,
et al., The coexistence of high piezoelectricity and superior optical absorption in Janus Bi2X2Y (X = Te, Se; Y = Te, Se, S) monolayers, Phys. Chem. Chem. Phys., 2024, 26(5), 4629–4642 RSC.
- J. D. Mella,
et al., Prediction of BiS2-type pnictogen dichalcogenide monolayers for optoelectronics, npj 2D Mater. Appl., 2024, 8(1), 4 CrossRef CAS.
- P. Giannozzi,
et al., Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29(46), 465901 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758 CrossRef CAS.
- P. Giannozzi,
et al., Ab initio calculation of phonon dispersions in semiconductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(9), 7231 CrossRef CAS.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A:At., Mol., Opt. Phys., 1985, 31(3), 1695 CrossRef PubMed.
- S. Nosé, An extension of the canonical ensemble molecular dynamics method, Mol. Phys., 1986, 57(1), 187–191 CrossRef.
- W. X. Zhou,
et al., Thermal conductivity of amorphous materials, Adv. Funct. Mater., 2020, 30(8), 1903829 CrossRef CAS.
- J. Noffsinger,
et al., EPW: A program for calculating the electron–phonon coupling using maximally localized Wannier functions, Comput. Phys. Commun., 2010, 181(12), 2140–2148 CrossRef CAS.
- H. Lee,
et al., Electron–phonon physics from first principles using the EPW code, npj Comput. Mater., 2023, 9(1), 156 CrossRef CAS.
- M. J. Varjovi and E. Durgun, First-principles study on structural, vibrational, elastic, piezoelectric, and electronic properties of the Janus BiXY (X = S, Se, Te and Y = F, Cl, Br, I) monolayers, Phys. Rev. Mater., 2021, 5(10), 104001 CrossRef CAS.
- M. J. Varjovi, S. Ershadrad and B. Sanyal, Structural, vibrational, elastic, electronic, and piezoelectric properties of binary γ-GeX and ternary γ-Ge2XX′ monolayers (X, X′ = S, Se, and Te), Phys. Rev. B, 2023, 107(19), 195421 CrossRef CAS.
- N. Al Bouzieh, M. Benkraouda and N. Amrane, Exploring Hafnium-induced transformations in SnSe allotropes: Insights into structural, electronic, optical, and mechanical modifications for enhanced optoelectronic utilization, Mater. Today Commun., 2024, 38, 107574 CrossRef.
- F. Mouhat and F.-X. Coudert, Necessary and sufficient elastic stability conditions in various crystal systems, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(22), 224104 CrossRef.
-
I. N. Frantsevich, Elastic constants and elastic moduli of metals and insulators, Reference book, 1982 Search PubMed.
- A. Togo, L. Chaput and I. Tanaka, Distributions of phonon lifetimes in Brillouin zones, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(9), 094306 CrossRef.
- N. N. Hieu,
et al., Structural, electronic, and transport properties of quintuple atomic Janus monolayers Ga2SX2 (X = O, S, Se, Te): First-principles predictions, Phys. Rev. B, 2022, 105(7), 075402 CrossRef CAS.
- C. Yao,
et al., Single-layer XBi2Se4 (X = Sn Pb) with multi-valley band structures and excellent thermoelectric performance, Ceram. Int., 2023, 49(15), 25455–25462 CrossRef CAS.
- R. C. Cooper,
et al., Nonlinear elastic behavior of two-dimensional molybdenum disulfide, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(3), 035423 CrossRef.
- J. Bardeen and W. Shockley, Deformation potentials and mobilities in non-polar crystals, Phys. Rev., 1950, 80(1), 72 CrossRef CAS.
- P. L. Tran,
et al., First-principles examination of two-dimensional Janus quintuple-layer atomic structures XCrSiN2 (X = S, Se, and Te), Nanoscale Adv., 2023, 5(11), 3104–3113 RSC.
- Y. Liu,
et al., Monolayer Bi2Se3−xTex: novel two-dimensional semiconductors with excellent stability and high electron mobility, Phys. Chem. Chem. Phys., 2020, 22(17), 9685–9692 RSC.
- Q. Zhang,
et al., Tl-based TlAgX (X = S, Se) monolayers with ultra-low lattice thermal conductivity and high ZT: a first-principles study, J. Mater. Sci., 2022, 57(47), 21607–21619 CrossRef CAS.
- D. Singh, V. Shukla and R. Ahuja, Optical excitations and thermoelectric properties of two-dimensional holey graphene, Phys. Rev. B, 2020, 102(7), 075444 CrossRef CAS.
- S. G. Rudi,
et al., Enhanced performance of Janus XMSiY2 (X = S, Se; M = Mo, W; and Y = N, P) monolayers for photocatalytic water splitting via strain engineering, J. Phys. Chem. Solids, 2023, 181, 111561 CrossRef CAS.
- A. Chatterjee, S. N. Guin and K. Biswas, Ultrathin septuple layered PbBi2Se4 nanosheets, Phys. Chem. Chem. Phys., 2014, 16(28), 14635–14639 RSC.
- W.-J. Yin,
et al., The unique carrier mobility of monolayer Janus MoSSe nanoribbons: a first-principles study, Dalton Trans., 2021, 50(29), 10252–10260 RSC.
- Y. Peng,
et al., Prediction of high carrier mobility for novel Janus Mo8S6Se6 monolayers with different phases: first principles calculations, J. Mater. Chem. C, 2024, 12, 15024–15031 RSC.
- N. de Koker, Thermal conductivity of MgO periclase from equilibrium first principles molecular dynamics, Phys. Rev. Lett., 2009, 103(12), 125902 CrossRef.
- X.-L. Zhu,
et al., High thermoelectric performance of new two-dimensional IV–VI compounds: A first-principles study, J. Phys. Chem. C, 2019, 124(3), 1812–1819 CrossRef.
- M. N. Çınar,
et al., Ballistic thermoelectric transport properties of two-dimensional group III–VI monolayers, Phys. Rev. B, 2021, 103(16), 165422 CrossRef.
- M. K. Mohanta,
et al., Ultra-low thermal conductivity and super-slow hot-carrier thermalization induced by a huge phononic gap in multifunctional nanoscale boron pnictides, Phys. E, 2020, 124, 114222 CrossRef CAS.
- M. K. Mohanta, F. Is and A. De Sarkar, Valley Hall effect in graphene-like Sn X (X = Si, Ge) buckled monolayers with high charge carrier mobility and low lattice thermal conductivity, Phys. Rev. B, 2023, 107(3), 035429 CrossRef CAS.
- H. Huang,
et al., Janus penta-PdSeTe: A two-dimensional candidate with high thermoelectric performance, J. Alloys Compd., 2022, 924, 166581 CrossRef CAS.
- S.-D. Guo, A.-X. Zhang and H.-C. Li, Potential 2D thermoelectric material ATeI (A = Sb and Bi) monolayers from a first-principles study, Nanotechnology, 2017, 28(44), 445702 CrossRef PubMed.
- E. Bolen, E. Deligoz and H. Ozisik, Origin of low thermal conductivity in monolayer PbI2, Solid State Commun., 2021, 327, 114223 CrossRef CAS.
- L. Li,
et al., Theoretical analysis of the thermoelectric properties of penta-PdX2 (X = Se, Te) monolayer, Front. Chem., 2022, 10, 1061703 CrossRef CAS PubMed.
- D. Wan,
et al., Anharmonicity and weak bonding-driven extraordinary thermoelectric performance in wrinkled SnSe monolayer with low lattice thermal conductivity, Ceram. Int., 2024, 50(6), 9591–9603 CrossRef CAS.
- G. Liu,
et al., First-principles study of lattice thermal conductivity of Td–WTe2, New J. Phys., 2016, 18(3), 033017 CrossRef.
- N. K. Sharma,
et al., Ultralow thermal conductivity of W-Janus bilayers (WXY: X, Y = S, Se, and Te) for thermoelectric devices, Nanoscale, 2024, 16(6), 3091–3100 RSC.
- E. A. Moujaes and W. Diery, Thermoelectric properties of 1 T monolayer pristine and Janus Pd dichalcogenides, J. Phys.: Condens. Matter, 2019, 31(45), 455502 CrossRef CAS PubMed.
- G. Xie, D. Ding and G. Zhang, Phonon coherence and its effect on thermal conductivity of nanostructures, Adv. Phys.:X, 2018, 3(1), 1480417 Search PubMed.
- N. Mounet and N. Marzari, First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(20), 205214 CrossRef.
- Z. Zhou,
et al., High thermoelectric performance originating from the grooved bands in the ZrSe3 monolayer, ACS Appl. Mater. Interfaces, 2018, 10(43), 37031–37037 CrossRef CAS PubMed.
- N. Stojanovic,
et al., Thermal conductivity in metallic nanostructures at high temperature: Electrons, phonons, and the Wiedemann-Franz law, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(7), 075418 CrossRef.
- V. Van Thanh and N. T. Hung, Janus 2D B2P6: A promising anisotropic thermoelectric material with high power factor, Surf. Interfaces, 2024, 44, 103829 CrossRef.
- W. Hussain,
et al., Advances in nanoparticle-enhanced thermoelectric materials from synthesis to energy harvesting: A review, ACS Omega, 2024, 9(10), 11081–11109 CrossRef CAS.
- G. J. Snyder and T. S. Ursell, Thermoelectric efficiency and compatibility, Phys. Rev. Lett., 2003, 91(14), 148301 CrossRef.
- D. Luo,
et al., Realizing ultrahigh ZT value and efficiency of the Bi2Te3 thermoelectric module by periodic heating, Energy Convers. Manage., 2023, 296, 117669 CrossRef CAS.
- M. A. Mohebpour,
et al., Thermoelectric characteristics of X2YH2 monolayers (X = Si, Ge; Y = P, As, Sb, Bi): a first-principles study, Sci. Rep., 2021, 11(1), 23840 CrossRef CAS PubMed.
- K. Sujata,
et al., Two-dimensional BiSbTeX2 (X = S, Se, Te) and their Janus monolayers as efficient thermoelectric materials, Phys. Chem. Chem. Phys., 2024, 26(42), 27163–27175 RSC.
- N. T. Hung, A. R. Nugraha and R. Saito, Designing high-performance thermoelectrics in two-dimensional tetradymites, Nano Energy, 2019, 58, 743–749 CrossRef CAS.
- S.-H. Cao,
et al., Electronic and thermoelectric properties of semiconducting Bi2SSe2 and Bi2S2Se monolayers with high optical absorption, Phys. Chem. Chem. Phys., 2022, 24(43), 26753–26763 RSC.
- M. Ould-Mohamed,
et al., Janus ScYCBr2 MXene as a Promising Thermoelectric Material, ACS Appl. Energy Mater., 2024, 7(15), 6598–6611 CrossRef CAS PubMed.
- Z. Zhou,
et al., Anomalous Thermoelectric Performance in Asymmetric Dirac Semimetal BaAgBi, J. Phys. Chem. Lett., 2022, 13(10), 2291–2298 CrossRef PubMed.
- Z. Shu,
et al., High-performance thermoelectric monolayer γ-GeSe and its group-IV monochalcogenide isostructural family, Chem. Eng. J., 2023, 454, 140242 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a






 is the average effective mass and Ed is the deformation potential (DP) constant. The DP constant is obtained by calculating the band edges and concerning the uniaxial strain (Fig. S5, ESI†). The effective mass and deformation potential of Janus BiYZ monolayers are comparable with those of TlAgX (X = S, Se) monolayers56 and HG monolayers.57 It is determined that the carrier mobility of Janus BiYZ monolayers is highly anisotropic, indicating directional dependence of the effective masses and deformation potentials of holes and electrons. The values of μ2D of Janus BiYZ monolayers for both electrons and holes are listed in Table 3. Note that the electron (hole) mobility of the Janus SMoSiN2 monolayer is 298.7 (1377.9) cm2 V−1 s−1.58 Also the electronic mobility of layered PbBi2Se4 is estimated to be 153 cm2 V−1 s−1.59 The Janus BiYZ monolayers also possess mobilities higher than those of other Janus monolayers such as MoSSe (250 cm2 V−1 s−1 (ref. 60)), HG (14.18 × 103 cm2 V−1 s−1) and Mo8S6Se6 (104 cm2 V−1 s−1),61 suggesting that these Janus monolayers would be promising materials for electronic and thermoelectric applications.
is the average effective mass and Ed is the deformation potential (DP) constant. The DP constant is obtained by calculating the band edges and concerning the uniaxial strain (Fig. S5, ESI†). The effective mass and deformation potential of Janus BiYZ monolayers are comparable with those of TlAgX (X = S, Se) monolayers56 and HG monolayers.57 It is determined that the carrier mobility of Janus BiYZ monolayers is highly anisotropic, indicating directional dependence of the effective masses and deformation potentials of holes and electrons. The values of μ2D of Janus BiYZ monolayers for both electrons and holes are listed in Table 3. Note that the electron (hole) mobility of the Janus SMoSiN2 monolayer is 298.7 (1377.9) cm2 V−1 s−1.58 Also the electronic mobility of layered PbBi2Se4 is estimated to be 153 cm2 V−1 s−1.59 The Janus BiYZ monolayers also possess mobilities higher than those of other Janus monolayers such as MoSSe (250 cm2 V−1 s−1 (ref. 60)), HG (14.18 × 103 cm2 V−1 s−1) and Mo8S6Se6 (104 cm2 V−1 s−1),61 suggesting that these Janus monolayers would be promising materials for electronic and thermoelectric applications.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 573
573![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 099
099![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 367
367![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126
126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 920
920






 is the electron–phonon coupling strength, and Ψnk represents the electronic wave function for eigenvalue εnk, wave-vector k and band index m. ωqv is derivative of the self-consistent potential ∂qvV with branch index v and wave vector q· fmk+q represent the electronic state occupation. The relaxation time as a function of carrier's energy is shown in Fig. 6(a)–(c). The estimated value of relaxation time is of the order of ∼10−15 s at different temperatures for Janus BiYZ monolayers.
is the electron–phonon coupling strength, and Ψnk represents the electronic wave function for eigenvalue εnk, wave-vector k and band index m. ωqv is derivative of the self-consistent potential ∂qvV with branch index v and wave vector q· fmk+q represent the electronic state occupation. The relaxation time as a function of carrier's energy is shown in Fig. 6(a)–(c). The estimated value of relaxation time is of the order of ∼10−15 s at different temperatures for Janus BiYZ monolayers.

 ;78T is the temperature and σ is the electrical conductivity. The κe with variation of chemical potential ranges from ∼0.4 to ∼1.5 W m−1 K−1 at 500 K of Janus BiYZ monolayers (Fig. 7(a)). The variations of κe with chemical potential at temperatures 300 K and 700 K are also shown in Fig. S8(a), ESI.†
;78T is the temperature and σ is the electrical conductivity. The κe with variation of chemical potential ranges from ∼0.4 to ∼1.5 W m−1 K−1 at 500 K of Janus BiYZ monolayers (Fig. 7(a)). The variations of κe with chemical potential at temperatures 300 K and 700 K are also shown in Fig. S8(a), ESI.†


![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ) is used to obtain the thermoelectric efficiency ηmax (%) as:80,81
) is used to obtain the thermoelectric efficiency ηmax (%) as:80,81