Open Access Article
Open Access Article2D monolayer molybdenum(IV) telluride TMD: an efficient electrocatalyst for the hydrogen evolution reaction†
Vikash
Kumar
 a and
Srimanta
Pakhira
a and
Srimanta
Pakhira
 *ab
*ab
aTheoretical Condensed Matter Physics and Advanced Computational Materials Science Laboratory, Department of Physics, Indian Institute of Technology Indore, Khandwa Road, Simrol, Indore, Madhya Pradesh, 453552, India. E-mail: spakhira@iiti.ac.in; spakhirafsu@gmail.com
bTheoretical Condensed Matter Physics and Advanced Computational Materials Science Laboratory, Centre for Advanced Electronics (CAE), Indian Institute of Technology Indore, Khandwa Road, Simrol, Indore, Madhya Pradesh 453552, India
First published on 7th March 2025
Abstract
An electrocatalyst is needed to efficiently lower the reaction barriers to produce hydrogen through the H2 evolution reaction (HER). Recently, two-dimensional transition metal dichalcogenides (2D TMDs), such as the pure 2D monolayer MoTe2, MoS2, WS2, etc. TMDs, have become attractive materials for the HER. Using the first principles-based hybrid density functional theory (DFT) method, we have computationally designed a pure 2D monolayer MoTe2 TMD and examined its structural and electronic properties with electrocatalytic efficacy towards the HER. A non-periodic finite molecular cluster model Mo10Te21 system has been employed to explore the feasibility of both the Volmer–Heyrovsky (V–H) and Volmer–Tafel (V–T) reaction mechanisms for the HER. The solvent-phase calculations demonstrate that this material can effectively undergo either V–H or V–T reaction pathways. This conclusion is supported by our determination of low reaction barriers for the H*-migration, Heyrovsky, and Tafel transition states (TSs), which were found to be approximately 9.80, 12.55, and 5.29 kcal mol−1, respectively. These results highlight the potential utility of 2D monolayer MoTe2 TMD as a promising electrocatalyst for the HER. The unusual electrocatalytic activity of the pristine 2D monolayer MoTe2 TMD is evidenced by its ability to significantly reduce reaction barriers, achieving impressive turnover frequency (TOF) values of 3.91 × 103 and 8.22 × 108 s−1 during the Heyrovsky and Tafel reaction steps, respectively. Additionally, it demonstrates a remarkably low Tafel slope of 29.58 mV dec−1. These outstanding performance metrics indicate that the pure 2D monolayer MoTe2 TMD is a highly efficient electrocatalyst for the HER, surpassing the capabilities of traditional platinum group metal-based alternatives. Further exploration of its potential applications in electrocatalysis is warranted. The present work provides valuable insights into the atomic modulation of active sites for enhanced electrocatalytic performance towards the HER, paving the way for designing advanced non-noble metal-free electrocatalysts.
1. Introduction
For centuries, fossil fuels, which include coal, petroleum, natural gas, oil shale, bitumen, tar sands, and heavy oils, have been widely used as a primary source of energy to fulfill the world's energy needs and demands. Due to the widespread use of traditional energy sources like coal, petroleum, natural gas, and oil, there is a growing global energy crisis and environmental pollution, which are both serious issues in today's society and human life.1 Nonetheless, the extraction and consumption of these conventional energy sources contribute to their depletion and emit harmful pollutants including greenhouse gases to the environment. These emissions are major drivers of climate change, causing severe consequences such as rising global temperatures and detrimental impacts on human health. The pressing concerns surrounding energy depletion and environmental pollution have spurred a growing interest among researchers to explore and develop sustainable and green energy storage and conversion technologies. Among the promising solutions, fuel cells, electrochemical water splitting, and metal–air batteries stand out for their high energy density and eco-friendly features.2 Hydrogen boasts a substantial energy content and a remarkable energy density when stored in its molecular form, H2. It also occurs abundantly in various organic and inorganic compounds, including water, making it an attractive and efficient candidate for clean energy resources. Most commercially available H2 fuels are produced through a steam reforming process in today's world. During this process, H2 is produced along with the emission of toxic gases such as carbon monoxide (CO) and carbon dioxide (CO2). Water splitting is widely regarded as the most environmentally friendly approach to producing hydrogen, yielding hydrogen and oxygen as its primary outputs. Among various water-splitting methods, electrocatalytic hydrogen evolution holds a special position in energy storage due to its independence from geographic constraints, weather patterns, and solar intensity fluctuations, making it an exceptionally reliable and efficient technology.3In general, platinum (Pt) and other noble metals are considered to be well-known HER electrocatalysts due to their low overpotentials and small Tafel slopes. Despite its many advantages, the high expense and scarcity of this resource severely curtail its potential applications.4 Realizing large-scale hydrogen production hinges upon the development of economical and high-performance electrocatalysts that can enhance the energy efficiency of electrochemical water splitting. Developing stable and efficient electrocatalyst materials are essential to achieve hydrogen production on an industrial scale.5 These materials should be earth-abundant and possess superior properties to facilitate water electrolysis into hydrogen. Extensive research has been conducted to seek alternative materials to replace Pt in hydrogen production. There is a strong emphasis on exploring non-precious metal catalysts that are cost-effective and highly active. These earth-abundant materials are expected to possess exceptional durability and efficiency, making them a viable substitute for precious metal catalysts that are prohibitively expensive.6,7
Recently, two-dimensional (2D) materials have offered numerous advantages, such as a large specific surface area, exceptional mechanical characteristics, and high carrier mobility. Therefore, in recent years, 2D materials have become one of the most promising candidate materials for electrocatalysts. Especially, the 2D layer structure of transition metal dichalcogenides (TMDs) has various special characteristics, including excellent stability, electrical tunability, high-density active edges, tunable electronic band gap, high electrical conductivity, and the potential for defect engineering.4,8 These exceptional features have garnered significant attention from the scientific community, particularly in the context of studying H2 evolution and its numerous practical applications. In recent times, considerable research has been focused on exploring the potential of 2D transition metal dichalcogenide monolayers (such as MoSe2, WSe2, and MoS2) as substitutes for Pt catalysts. This is mainly due to their remarkable electronic, magnetic, and chemical properties that make them attractive alternatives to traditional catalysts.6,9 The chemical formula of Earth-abundant TMDs is MX2, where M is a transition metal (TM) atom such as Mo, W, etc., and X is a chalcogen atom such as S, Se, and Te. While the layers of TMDs are weakly held together by out-of-plane van der Waals (vdW) interactions, the in-plane atoms are held together by strong chemical bonds.1,4,10
Based on research analysis, it has been discovered that the MoTe2 semiconductor possesses exceptional catalytic activity, particularly in the vicinity of the Fermi energy level (EF) and exhibits high carrier mobility. These properties make MoTe2 a promising candidate for use as an electrocatalyst beyond the HER, with potential uses in the ORR and OER in fuel cell technology.11,12 Here, we introduce a 2D monolayer MoTe2 TMD material as a unique and efficient non-noble metal catalyst for the HER. The present research work highlights the various phases of monolayers of molybdenum telluride (MoTe2) as very efficient HER electrocatalysts.13,14 A finite molecular cluster model system, Mo10Te21, has been computationally designed to investigate the reaction process and identify the most effective 2D monolayer MoTe2 phase and HER active sites using quantum mechanical density functional theory (DFT) calculations.5,15–17 This DFT approach offers a comprehensive means of exploring the catalytic activity of the 2D single-layer MoTe2, as well as the potential to enhance its performance in comparison to traditional electrocatalytic materials. The Mo10Te21 cluster model system has been chosen specifically to represent the edge-specific properties of 2H-MoTe2, as it captures localized surface interactions that are relevant to the HER. The primary goal of the cluster model is to provide a computationally efficient framework for studying localized reaction pathways and energy barriers with transition states (TSs), which is especially important for understanding the HER mechanism in small, edge-specific regions. In this study, we have computationally designed a 2D monolayer MoTe2 TMD material and investigated its electronic properties, including the electronic band structure, total density of states (DOS), Fermi energy level (EF), and electronic band gap (Eg), to gain insight into its potential for HER applications by employing the periodic DFT method. The density of exposed active edge sites is critical in determining the HER catalytic activity of the 2D monolayer TMDs. The hydrogen adsorption-free energy (ΔGH) reflects the strength of the interaction between the catalyst and the reactant and is a key indicator of the catalyst's activity. The turnover frequency (TOF) is the rate of hydrogen evolution per active site and is a measure of the efficiency of an electrocatalyst. We have utilized M06-L, a local meta-generalized gradient approximation (meta-GGA) method to investigate the HER catalytic activity of the pristine 2D monolayer of MoTe2 by considering the finite molecular model system of the subject material. Our focus is on determining the reaction pathway of the subject reaction (i.e., HER) at the Mo edge (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) of the 2D single-layer MoTe2 TMD material through theoretical and computational analysis. The exposed Te-edge (
0) of the 2D single-layer MoTe2 TMD material through theoretical and computational analysis. The exposed Te-edge (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010) and Mo-edge (10
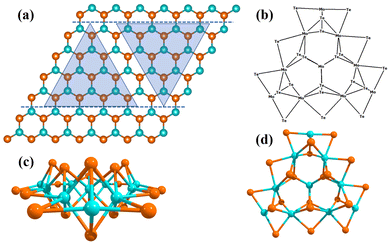
010) and Mo-edge (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) of the 2D monolayer TMD MoTe2 have been found to be catalytically active for the HER, while the Te–Mo–Te tri-layer of the MoTe2 TMD is the exposed surface. To describe the Mo edge of the 2D monolayer MoTe2, we have used a finite non-periodic molecular cluster model of Mo10Te21 (as shown in Fig. 1). The polarization continuum model (PCM) was used to account for the solvation effects of water as a solvent, allowing for the exact integration of the M06-L method to compute reaction barriers.18–20 The first-principles-based M06-L meta-GGA method has been used to investigate the reaction pathways, kinetics, and barrier energies for the HER on the surfaces of the 2D monolayer MoTe2 TMD by considering the finite cluster model system of the MoTe2 (Mo10Te21) TMD, as shown in Fig. 1. It should be noted here that surprisingly, M06-L stands out for its striking accuracy, outperforming any other investigated functionals and it is very fast, good for transition metals, and inorganic and organometallic chemical reactions.
0) of the 2D monolayer TMD MoTe2 have been found to be catalytically active for the HER, while the Te–Mo–Te tri-layer of the MoTe2 TMD is the exposed surface. To describe the Mo edge of the 2D monolayer MoTe2, we have used a finite non-periodic molecular cluster model of Mo10Te21 (as shown in Fig. 1). The polarization continuum model (PCM) was used to account for the solvation effects of water as a solvent, allowing for the exact integration of the M06-L method to compute reaction barriers.18–20 The first-principles-based M06-L meta-GGA method has been used to investigate the reaction pathways, kinetics, and barrier energies for the HER on the surfaces of the 2D monolayer MoTe2 TMD by considering the finite cluster model system of the MoTe2 (Mo10Te21) TMD, as shown in Fig. 1. It should be noted here that surprisingly, M06-L stands out for its striking accuracy, outperforming any other investigated functionals and it is very fast, good for transition metals, and inorganic and organometallic chemical reactions.
2. Computational details
Computational methods are used during the present theoretical studies, and the other parameters play a significant role in determining the electrocatalytic activity of an efficient HER. Here, a periodic 2D monolayer structure of the MoTe2 TMD is computationally designed to examine its structural and electronic properties by using the first principles-based hybrid DFT method.6,21 The HER mechanism at the active edge was further investigated by DFT computations using a non-periodic finite molecular cluster model system Mo10Te21 corresponding to the pristine 2D monolayer MoTe2. A further discussion of both the periodic and non-periodic systems is explained below.2.1. Periodic structure DFT calculations
For the periodic 2D structure calculations, the monolayer of 2D MoTe2 TMD is bound by Mo-edge (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) and Te-edge (
0) and Te-edge (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010), as shown in Fig. 1, and the two horizontal blue color dashed lines indicate terminations along the (10
010), as shown in Fig. 1, and the two horizontal blue color dashed lines indicate terminations along the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) Mo-edge and (
0) Mo-edge and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010) Te-edge. First, we performed a computational study of 2D monolayer MoTe2 to obtain the equilibrium structure and geometry of the TMD. To determine the equilibrium geometry and electronic properties of the 2D monolayer MoTe2 material, we utilized the quantum mechanical first-principles-based B3LYP-D3 (in short DFT-D) method implemented in CRYSTAL17 suite code.22–26 It is expected that the material chemistry of the edges of the bulk structure of the MoTe2 may be similar to that of a single MoTe2 layer. It has been shown that additional layers decrease the current density due to electron hopping across the layers, such that the top layers are not as active as the bottom layers. Spin-polarized calculations were also incorporated into the computation by defining the electron occupancy (i.e., α for up spin and β for down spin). The spin-polarized solution was obtained by the keywords “ATOMSPIN” and “SPINLOCK” when the DFT-D method was executed in the CRYSTAL17 program.16,20 Compared to the Hartree–Fock (HF) method, the DFT method (here, B3LYP-D3) suffers from less or no spin contamination, which helps provide excellent geometry, energy, and electron density calculations. To account for non-bonded weak van der Waals (vdW) interactions between atoms and different layers, we incorporate the semi-empirical Grimme's third-order dispersion correction (Grimme's-D3) in our calculations to obtain accurate equilibrium geometries.27,28 In order to accurately capture the electronic and structural properties of the system under investigation, we employed the density functional theory with dispersion correction (DFT-D) method, specifically the B3LYP-D3 variant, to account for exchange–correlation effects.1,29
010) Te-edge. First, we performed a computational study of 2D monolayer MoTe2 to obtain the equilibrium structure and geometry of the TMD. To determine the equilibrium geometry and electronic properties of the 2D monolayer MoTe2 material, we utilized the quantum mechanical first-principles-based B3LYP-D3 (in short DFT-D) method implemented in CRYSTAL17 suite code.22–26 It is expected that the material chemistry of the edges of the bulk structure of the MoTe2 may be similar to that of a single MoTe2 layer. It has been shown that additional layers decrease the current density due to electron hopping across the layers, such that the top layers are not as active as the bottom layers. Spin-polarized calculations were also incorporated into the computation by defining the electron occupancy (i.e., α for up spin and β for down spin). The spin-polarized solution was obtained by the keywords “ATOMSPIN” and “SPINLOCK” when the DFT-D method was executed in the CRYSTAL17 program.16,20 Compared to the Hartree–Fock (HF) method, the DFT method (here, B3LYP-D3) suffers from less or no spin contamination, which helps provide excellent geometry, energy, and electron density calculations. To account for non-bonded weak van der Waals (vdW) interactions between atoms and different layers, we incorporate the semi-empirical Grimme's third-order dispersion correction (Grimme's-D3) in our calculations to obtain accurate equilibrium geometries.27,28 In order to accurately capture the electronic and structural properties of the system under investigation, we employed the density functional theory with dispersion correction (DFT-D) method, specifically the B3LYP-D3 variant, to account for exchange–correlation effects.1,29
During calculations in the CRYSTAL17 program, a Gaussian-type of atomic basis set (GTO) has been used for all atoms as this code uses only the Gaussian-types of atomic basis sets for quantum mechanical calculations. This basis set offers a more efficient alternative to the plane-wave basis set for hybrid DFT calculations. Gaussian-type basis sets are widely used in quantum chemistry calculations due to their flexibility in accurately describing the electron density around atomic nuclei.1,2,23 They are especially useful for hybrid DFT calculations, which incorporate local and non-local exchange–correlation effects, as they compromise computational cost and accuracy. In comparison, plane-wave basis sets require larger cut-off energies and k-point sampling to achieve similar accuracy in hybrid DFT calculations, which can result in higher computational expenses. In the context of hybrid density functionals, localized Gaussian type of basis set-based codes are better suited for solving the Hartree–Fock (HF) component of the calculation. Gaussian basis sets can handle a wide range of system sizes and molecular geometries, making them a versatile choice for various computational chemistry studies. In this study, we have employed triple ζ valence polarized (TZVP) Gaussian-type basis sets for both the Mo and Te atoms.30 We set the value of convergence threshold for evaluating forces, electron density, and energy to 10−7 atomic units (a.u.), ensuring accurate and precise results. Gaussian-type basis sets are particularly well-suited for describing the electron density around atomic nuclei, making them a popular choice for quantum solid state chemistry calculations. To prevent any interactions between the slabs and their periodic images, we have implemented a vacuum space of approximately 500 Å in the z-direction of the simulated cells. The standard convention adopted in CRYSTAL17 suite code with a specific keyword “SLAB” considers the reference 500 Å vacuum space for the 2D layer structure calculations. This approach differs from the plane-wave codes (e.g., VASP, Quantum Espresso, etc.); however, both reach similar results. 20 Å or 30 Å vacuum space is generally allowed in the VASP software package, which is completely different from the CRYSTAL17 code. Moreover, taking the vacuum region of 500 Å provides more accuracy in computations because there is no possibility of any kind of interaction of other layers in the z-direction during the calculations.1,3,5,9,10
Using the same level of theory, we conducted electronic property calculations at the optimized structure of the 2D monolayer MoTe2 TMD material. To accurately capture the electronic properties of the system, we employed Monkhorst k-mesh grids with a size of 20 × 20 × 1 to compute the 2D electronic layer structure, geometry, band structure, and total density of states.31 The use of k-mesh grids allows for a thorough sampling of the Brillouin zone, ensuring accurate results. We calculated eight electronic bands around the Fermi energy level in the high-symmetry Γ–M–K–Γ direction within the first Brillouin zone. To accurately capture the electronic states of the 2D monolayer MoTe2 TMD material, we considered all the atomic orbitals of both Mo and Te atoms in calculating the total density of states (DOSs). The electronic band structures and DOS were both estimated with respect to the vacuum to account for the effects of the electrostatic potential. The equilibrium 2D monolayer structure of MoTe2 TMD was shown using VESTA, a visualization program.32
2.2. Finite non-periodic molecular cluster modelling
We have computationally designed a Mo10Te21, non-periodic finite molecular cluster model system of the 2D single layer MoTe2 TMD, as shown in Fig. 1, to find out the HER mechanisms with equilibrium structures, geometries, molecular properties and reaction barriers. This Mo10Te21 cluster model system consists of 10 Mo atoms and 21 Te atoms representing the parent MoTe2 periodic slab structure, as shown in Fig. 1. The right triangle represents non-periodic finite cluster models terminating along the Te-edge (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010), and the inverted triangle corresponds to non-periodic cluster models terminating along the Mo-edge (
010), and the inverted triangle corresponds to non-periodic cluster models terminating along the Mo-edge (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 010). In the finite molecular cluster model system, which has been considered in the present investigation, each Mo atom in the basal plane (001) has a “+4” oxidation state and each Mo atom forms six bonds with six adjacent Te atoms. Due to this configuration, a stabilized structure results in each Mo–Te bonding having 4/6 = 2/3 electron contributions in the inert basal plane. The stabilization of the molecular cluster model also can be understood from the oxidation state of Te atoms in the basal plane. Each Te atom has a “−2” oxidation state and creates bonding with 3 Mo atoms, contributing 2/3 electrons towards each Mo–Te bonding in the basal plane. Again, the edges of the molecular cluster model are stabilized with the 2 local electron Mo–Te bonds with a single electron contribution towards four Mo–Te bonds in the basal plane, as shown in Fig. 1. This 14/3 {i.e., (2 × 1) + [4 × (2/3)]} contribution of electrons towards the Mo–Te bonds of the edge Mo atom is satisfied with the d2 configuration of one Mo atom and the d1 configuration of two Mo atoms at the edges. With this configuration, a stabilized molecular cluster model with periodicity 3 is achieved that derives the molecular cluster model having three edges without any unsatisfied valency. Thus, we have considered a molecular cluster Mo10Te21 model system (noted by [MoTe2]) to represent the Te-terminated Mo-edges on the surfaces of 2D monolayer MoTe2 TMD, as shown in Fig. 1, and this Mo10Te21 molecular cluster model system is good enough to explain the HER process.9
010). In the finite molecular cluster model system, which has been considered in the present investigation, each Mo atom in the basal plane (001) has a “+4” oxidation state and each Mo atom forms six bonds with six adjacent Te atoms. Due to this configuration, a stabilized structure results in each Mo–Te bonding having 4/6 = 2/3 electron contributions in the inert basal plane. The stabilization of the molecular cluster model also can be understood from the oxidation state of Te atoms in the basal plane. Each Te atom has a “−2” oxidation state and creates bonding with 3 Mo atoms, contributing 2/3 electrons towards each Mo–Te bonding in the basal plane. Again, the edges of the molecular cluster model are stabilized with the 2 local electron Mo–Te bonds with a single electron contribution towards four Mo–Te bonds in the basal plane, as shown in Fig. 1. This 14/3 {i.e., (2 × 1) + [4 × (2/3)]} contribution of electrons towards the Mo–Te bonds of the edge Mo atom is satisfied with the d2 configuration of one Mo atom and the d1 configuration of two Mo atoms at the edges. With this configuration, a stabilized molecular cluster model with periodicity 3 is achieved that derives the molecular cluster model having three edges without any unsatisfied valency. Thus, we have considered a molecular cluster Mo10Te21 model system (noted by [MoTe2]) to represent the Te-terminated Mo-edges on the surfaces of 2D monolayer MoTe2 TMD, as shown in Fig. 1, and this Mo10Te21 molecular cluster model system is good enough to explain the HER process.9
This molecular cluster model system allows us to investigate the unique properties and potential applications of the 2D monolayer MoTe2 TMD. The development of the finite molecular cluster model has computationally been built in such a way that it has the same chemical properties as the periodic 2D slab of MoTe2 TMD. We have used the M06-L DFT method to determine the reaction barriers, kinetics, and bond energies. This method provides more flexibility and accuracy while using molecular clusters and gives very precise results for the HER calculations. It is computationally easy to use a cluster model with net charges, which is not possible to consider in the case of a periodic system using the CRYSTAL17 suite code. Several studies have investigated the performance of the HER of the MoTe2 TMD using periodic GGA calculations implemented in VASP, typically employing slab models to analyze adsorption energies, reaction barriers, and electronic structure modifications.4,33 While these studies provide valuable insights into HER catalysis, they do not explicitly capture the stepwise electron transfer (ET) and proton transfer (PT) processes or their dependence on electrochemical potential and pH. Such mechanistic details are critical for a comprehensive understanding of the reaction pathways. It should be mentioned here that explicitly solvent phase calculations with the reaction barriers and solvation effects have not been studied yet. To address these limitations, we have employed a finite molecular cluster model system in this study, which offers significant advantages over periodic slab models. One key distinction is that the periodic DFT-D calculations implemented in CRYSTAL or VASP do not support stepwise ET and PT analysis, which is essential for accurately describing the HER mechanism. Instead, we have utilized Gaussian 16, which allows for detailed proton-coupled electron transfer (PCET) calculations, enabling us to track separate ET and PT steps. This approach provides deeper mechanistic insights, as it accurately models reaction intermediates, captures charge redistribution, and allows for the computation of free energy changes as a function of electrochemical potential and pH. Additionally, the cluster model allows explicit treatment of net charges, which is computationally challenging in periodic systems. This capability enables the incorporation of electrons (e−) and protons (H+) at various reaction steps, facilitating a more accurate representation of electrochemical conditions. Incorporation of simultaneous electrons (e−) and protons (H+) while performing the chemical reaction studies of various steps in the HER becomes very easy when the molecular cluster model is used.
We have used a periodic 2D slab model of the 2D monolayer MoTe2 to study the electronic properties, i.e., band structure, electronic band gap (Eg), position of the Fermi energy level (EF) in the electronic band structure and total density of states (DOS), and we have designed a molecular cluster model (Mo10Te21) of the 2D monolayer MoTe2 to explore the HER mechanism. This molecular cluster model system allows us to investigate the unique properties and potential applications of the MoTe2 TMD. The development of the finite molecular cluster model was done in such a way that it has the same chemical properties as the periodic 2D slab of MoTe2 TMD. We have used the M06-L DFT method to determine the reaction barriers, kinetics, and bond energies. This method provides more flexibility and accuracy while using molecular clusters and gives very precise results for the HER calculations. It is easy to use a cluster model with net charges, which is not possible to consider in the case of a periodic system using the CRYSTAL17 suite code. Incorporation of simultaneous electrons (e−) and protons (H+) while performing the chemical reaction studies of various steps in the HER becomes very easy when the molecular cluster model is used. The molecular cluster model system has computationally been designed in such a way so that it consists of properties similar to those of the periodic 2D monolayer MoTe2 TMD. For the validation of the molecular cluster model system Mo10Te21, which has the same chemical properties as the 2D monolayer periodic slab Mo-edges of the MoTe2 TMD, we have calculated the hydrogen adsorption energies for the molecular cluster model system and periodic 2D monolayer slab both under vacuum conditions. The calculated values of hydrogen adsorption energies for both systems are almost equal. Fig. S1 (ESI†) shows that the hydrogen binding energies were calculated by using both the finite molecular cluster model system and periodic 2D slab structure of the subject material. Thus, it can be mentioned here that the molecular cluster model system has the same chemical properties as the periodic 2D MoTe2 TMD. A similar cluster model system for other TMDs or Janus TMDs, such as MoS2, WS2, MoSSe, WSSe, WxMo1−xS2, etc., has been considered in previous theoretical and experimental studies.3,6,9,10,21 The DFT-M06-L method was used to study the HER mechanism on the active surface of MoTe2 through the Mo10Te21 finite molecular model. A previously reported report says that the DFT-M06-L method gives authentic energy barriers for reaction mechanisms of transition metal-based catalysts.18,34–36 For all the calculations, we have used 6-31+G** (double-ζ Pople-type) basis sets for O37 and H38 atoms and LANL2DZ basis sets for Mo39 and Te40 atoms with effective core potentials (ECPs) and include the solvent effect of water by utilizing the polarizable continuum model (PCM).41 For the PCM calculations, water was taken as a solvent with the dielectric constant of 80.13.42 PCM is one of the best models to consider the solvation effects, and it is a commonly used method in computational quantum chemistry to model solvation effects.
All periodic density functional theory (DFT) calculations, including geometry optimizations and electronic structure calculations, were performed at 0 K within the framework of DFT-D methods. However, the thermodynamic analysis, based on the non-periodic finite molecular cluster model, was conducted at room temperature (298.15 K) to incorporate thermal energy contributions into the reaction energetics. To account for temperature effects, we have performed a harmonic vibrational analysis at 298.15 K using the Gaussian 16 software package. This approach allows us to include zero-point vibrational energy (ZPE), enthalpic, and entropic contributions in our free energy calculations, which are crucial for understanding reaction thermodynamics under experimental conditions. By incorporating these thermal effects, we ensure that key parameters such as adsorption energies, reaction barriers, and transition states (TSs) accurately represent the material's behavior at room temperature rather than at absolute zero. Thus, while our periodic DFT simulations provide fundamental electronic and structural insights at 0 K, our thermodynamic calculations at 298.15 K bridge the gap between theoretical predictions and practical experimental conditions. This approach enhances the reliability of our findings for real-world applications.
The ZPE and frequencies were calculated using the same methods and basis sets at the optimized geometry of all the intermediates. Transitions states (TSs) were observed and confirmed by obtaining only one imaginary frequency (negative value) in the modes of vibrations. All the computations were performed with the general-purpose electronic structure quantum chemistry program Gaussian16 to obtain the optimized geometries and TSs to explain the HER mechanism.43 All the transition state (TS) structures were computed at the optimized geometries and ChemCraft software was used to visualize them.44 In this study, all the transition states were verified by analyzing the vibrational frequencies and the intrinsic reaction coordinates (IRCs).45
3. Results
3.1. Structural and electronic properties
The main objective of this work is to find the equilibrium 2D monolayer structure of MoTe2 TMD belonging to the 2H phase and find the electrocatalytic activity of the same TMD. The equilibrium 2D monolayer structure of 2H-MoTe2 TMD is shown in Fig. 2, obtained by the DFT-D method. By using VESTA software, a 2D monolayer MoTe2 primitive cell was developed, and its structure was optimized by using the first principles-based periodic dispersion-correction hybrid DFT (DFT-D3) method, as displayed in Fig. 2. The layer slab structure of the 2D monolayer MoTe2 TMD material belongs to the trigonal symmetry with a P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 layer group number in the symmetry table. The unit cell of the material is defined by the lattice parameters a = b = 3.40 Å, which is in excellent agreement with previously reported values.46 Each unit cell consists of one Mo and one Te atom, as shown in Fig. 2. The equilibrium bond length between Mo and Te atoms was found to be 2.66 Å. The electronic characteristics have been examined by calculating and examining the electronic band structure and density of states (DOS) of the 2D single-layer MoTe2 TMD. Analysis of the electronic properties can be useful to obtain information about electron distribution on the catalytic surface, which is useful for fully understanding the electrocatalytic performance of the TMD.
m2 layer group number in the symmetry table. The unit cell of the material is defined by the lattice parameters a = b = 3.40 Å, which is in excellent agreement with previously reported values.46 Each unit cell consists of one Mo and one Te atom, as shown in Fig. 2. The equilibrium bond length between Mo and Te atoms was found to be 2.66 Å. The electronic characteristics have been examined by calculating and examining the electronic band structure and density of states (DOS) of the 2D single-layer MoTe2 TMD. Analysis of the electronic properties can be useful to obtain information about electron distribution on the catalytic surface, which is useful for fully understanding the electrocatalytic performance of the TMD.
We used the DFT-D technique to calculate the equilibrium electronic properties of the 2D single-layer MoTe2 TMDs at equilibrium geometries. The electronic band structure, energy gap (Eg), Fermi level (EF), and density of states (DOS) were all computed using the same level of DFT method and were one of the main subjects of our investigation in the present work. This made it possible for us to explore and comprehend the electronic characteristics of the 2D monolayer pristine MoTe2 TMD consistently. We have computed the electronic band structures of 2D monolayer MoTe2 along the Γ–M–K–Γ band pathway (which is the high symmetric k-path direction consisting of the original symmetry of the 2D slab MoTe2 TMD) with respect to the vacuum, taking into account the initial symmetry of the subject material. The corresponding results are presented in Fig. 2b. This approach enabled us to gain valuable insights into the electronic properties of the 2D single-layer MoTe2 TMD systematically and accurately. In our electronic band structure calculations around the Fermi level (EF) of the 2D monolayer MoTe2, we took into account the number of four valence bands (VBs) and four conduction bands (CBs), as depicted in Fig. 2b. Our computations revealed that the EF of MoTe2 was located at −4.50 eV, and the material exhibits a direct band gap of approximately 1.65 eV at the K point, which is much lower than the pristine monolayer MoS2 2D TMD. Notably, this finding is consistent with earlier reported data, confirming the accuracy and reliability of our calculations.47 We estimated the density of states (DOS) of the monolayer MoTe2 using the same theoretical framework in order to further study its electrical characteristics. The resultant DOS, which corresponds to the electronic band structures of the pure 2D monolayer MoTe2, has been displayed in Fig. 2c. The electronic bandgap Eg of the 2D monolayer MoTe2 TMD was determined by our DOS calculations to be around 1.65 eV, which is consistent with the direct band gap found at the K point in the band structure calculations. Thus, it is abundantly clear from our calculations of the electronic properties that the pure 2D monolayer MoTe2 is a semiconductor with a recognizable bandgap, which may be useful for electrocatalytic activities toward H2 evolution. The same DFT-D method obtained the intrinsic electronic and structural properties at the equilibrium geometries. After obtaining the equilibrium structure (see Table 1), we computed the electronic properties of the 2D slab structure of the monolayer MoTe2 TMD by employing the B3LYP-D3 method. These findings are crucial for understanding the catalytic performance of the catalyst and finding a suitable electrocatalyst for the hydrogen evolution reaction. The stability of the material has been confirmed by computing the thermodynamic potentials, and the computations are consistent with the previously reported values. The results provide valuable insights into the electronic properties of 2D MoTe2 and its potential applications in electrocatalysis.
| Materials | Lattice parameter (in Å) | Bond angles (in °) | Bond distance Mo–Se (in Å) | Thickness (in Å) | Band gap (in eV) | Ref. |
|---|---|---|---|---|---|---|
| MoTe2 (previously reported) | a = b = 3.51 | α = β = 90 | 2.71 | 3.60 | 1.15 | 43 and 44 |
| γ = 120 | ||||||
| MoTe2 | a = b = 3.40 | α = β = 90 | 2.66 | 3.59 | 1.65 | This work |
| γ = 120 |
3.2. HER pathway
The hydrogen evolution reaction (HER), which takes place at the cathode of an electrolyzer, is a half-reaction in which protons (in an acidic environment) are reduced, followed by the generation of gaseous hydrogen via the water-splitting process. The overall HER pathway can be described by eqn (1)48 | (1) |
(i) The Volmer reaction occurs when a proton and an electron combine on the electrode surface to form a hydrogen atom (proton discharge):
| * + H+ + e− → *Had | (2) |
| *Had + H+ + e− → H2 + * | (3) |
| 2*Had → H2 + * | (4) |
The aforementioned fundamental processes result in the Volmer–Heyrovsky (V–H) and Volmer–Tafel (V–T) mechanisms. Volmer, Heyrovsky, and Tafel are three rate-determining steps (RDS) that can be used with the aforementioned two reaction mechanisms or methods. Eqn (1) can be used to explain the overall HER route during standard conditions. It includes the beginning state, H+ + e−, the intermediate, absorbed H*, and the ultimate result, 1/2H2 (g). The sum of the energies of 1/2H2 (g) and H+ + e− is the same. As a result, the change of Gibbs free energy of the intermediate hydrogen adsorption on a catalyst (ΔGH*), which can be calculated using eqn (5), is a crucial indicator of the HER activity of the catalyst.
| ΔGH = ΔEH + ΔEZPE − TΔSH | (5) |
| ΔGH = ΔEH + 0.30 eV | (6) |
We use a cluster model Mo10Te21 for the present work for the HER. In this cluster, we calculated the adsorption energy of hydrogen on the surface of the catalyst. The site which is more active for hydrogen adsorption will favor the adsorption of hydrogen easily. We have calculated hydrogen adsorption at both the sites, Te and Mo. First, we calculated hydrogen adsorption free energy at the Te site, which resulted in the formation of [MoTe2]HTe as an intermediate (where the subscript Te indicates that the hydrogen is bound to the Te atom) with free energy change (ΔG) of −1.92 eV. The equilibrium bond length of the Te–H in the equilibrium structure of the intermediate [MoTe2]HTe is 1.67 Å. Here, we found a negative change in free energy, meaning hydrogen strongly bonds with the Te atom. Now, we also calculated hydrogen adsorption at the Mo site and found that the change in free energy (ΔG) is −1.78 eV. The equilibrium bond length of the Mo–H in the intermediate [MoTe2]HMo is 1.72 Å. At both sites Te and Mo changes in free energy are negative. But at the Te site, the change in free energy is slightly more negative compared to the Mo site. So, the first H energetically prefers to form a bond with the Te atom, as the direct hydrogen adsorption at the Mo-edge site is not thermodynamically favorable in the early stage of the HER.
Inspired by previous works on 2D TMDs towards the HER, 2D single-layer MoTe2 is highly expected to enhance the electrochemical HER performance and stability of the system by the overlapping of d-orbitals of the Mo and p-orbitals from Te and provide an alternate way to tune and control the electronic and material properties of the subject material. The purpose of this paper is to suggest the synthesis and predict the properties of 2D single-layer MoTe2 as this 2D material studied here has not been synthesized experimentally and has not been experimented with for the HER and electrochemical performances. However, the calculated vibrational frequencies and binding energies predict that the subject material is thermodynamically stable. The harmonic frequency analysis and binding energy have been shown to be enough to demonstrate material stability and a posteriori synthesis in previous works on 2D TMDs followed by our published research works.3,6,10,21 Thus, we expect this 2D single layer MoTe2 to be readily fabricated experimentally and it can be used as an efficient electrocatalyst towards the HER.
In our study, we calculated the hydrogen adsorption energy on MoTe2 to be −1.92 eV, which contrasts with the previously reported value of 2.15 eV.4 The discrepancies between our results and previously reported values can be attributed to several factors. First, our study has utilized a finite cluster model (Mo10Te21) to represent edge-specific properties, which differ inherently from the periodic models used in other studies. This difference in model choice affects the adsorption characteristics due to the localized nature of edge-specific interactions in the cluster model.
The optimal performance of a catalyst toward the HER is governed by its ability to adhere to the Sabatier principle. A good catalyst should not bind too strongly to reagents and intermediates, as this would inhibit desorption and impede the catalytic cycle. Simultaneously, it should bind moderately enough to facilitate effective adsorption and subsequent reaction of the reagents on its surface. According to the Sabatier principle, the ideal catalyst achieves a delicate balance between adsorption and desorption energies.49 Our theoretical study supports this principle by demonstrating a moderate binding energy that ensures efficient adsorption of hydrogen while allowing easy desorption of the products. To study the HER performance of 2D monolayer MoTe2 materials, we created a finite non-periodic cluster model system of Mo10Te21. The HER process is being studied from several angles, including reaction pathways, thermodynamics, chemical kinetics, transition state structures, and reaction barriers. Fig. 3 and 6 show the Volmer–Heyrovsky and Volmer–Tafel mechanisms that we looked at in order to assess the HER pathways. We can determine the rate-limiting steps by calculating the intermediates and transition states during the production of H2 and by looking at the energy barriers of particular reaction steps. The electrocatalytic properties of the 2D monolayer MoTe2 material have been underexplored, which motivated our study to predict the most dominant HER mechanisms for these kinds of TMD materials by analyzing the proposed reaction pathway for both the Volmer–Heyrovsky and Volmer–Tafel mechanisms.
 | ||
| Fig. 3 Volmer–Heyrovsky HER mechanism of the detailed two electron transfer reaction pathways on the surface of the 2D MoTe2 material. | ||
(1) The [MoTe2] material can be found in its most stable state with a neutral Mo-edge under typical circumstances of the standard hydrogen electrode (SHE) at pH = 0, which serves as the starting point for our estimates of the thermodynamic potential. [MoTe2] represents the abbreviation for the finite molecular cluster Mo10Te21. Fig. 4a shows the equilibrium structure of the [MoTe2] material.
(2) The [MoTe2] material absorbs an electron onto its surface to start the HER process, which produces a negatively charged cluster of [MoTe2]−1 that is solvated in water and has a delocalized electron on its surface. The DFT technique yielded a value of roughly −424.97 mV for the first reduction potential of the suggested chemical pathway, which entails generating [MoTe2]−1 from the pure [MoTe2] by introducing a single electron. Fig. 4b shows the equilibrium geometry of [MoTe2]−1.
(3) According to a study,9 the first hydrogen atom has a strong preference for binding to the Te-edge rather than the Mo atom. As a result, an intermediate molecule called [MoTe2]HTe is created when a proton (H+) is added to the Te-edge, which has an additional electron. The subscript Te denotes the hydrogen atom's bond to the Te atom. The formation of this intermediate incurs an energy cost of approximately 1.93 kcal mol−1. The Te–H equilibrium bond length in the [MoTe2]HTe intermediate's equilibrium structure is 1.67 Å. The equilibrium geometry of the complex is depicted in Fig. 4c.
(4) A second reduction happens after adding one more electron to the [MoTe2]HTe intermediate, producing [MoTe2]HTe−1 (as shown in Fig. 4d). The second reduction potential is roughly equal to −766.68 mV.
(5) The hydride ion (H*) moves from the Se-site to the neighboring Mo-site in the following process, creating a transition state (TS) of [MoTe2]HTe−1. It is the first transition state to arise during the hydrogen evolution reaction (HER) process and is known as the H*-migration reaction or Volmer transition state (TS1). In order to locate the TS, a harmonic vibrational frequency analysis was carried out, and intrinsic reaction coordinate (IRC) calculations were done in order to confirm the existence of TS1.50,51 During the transfer of H* from the Te-site to the Mo-site, it was discovered that this TS1 had a single hypothetical vibrational frequency, i.e., one imaginary frequency. The equilibrium geometry of TS1 is shown in Fig. 4e. It is interesting to note that the current DFT work found that, when computed in the gas phase, the activation energy barrier for the H*-migration reaction to create TS1 in the pure 2D monolayer MoTe2 is about G = 8.47 kcal mol−1.
(6) Using the DFT approach, it was found that the energy needed to create the [MoTe2]HMo−1 complex from TS1 was around G = −18.69 kcal mol−1. The equilibrium geometry of the system is shown in Fig. 4f. The Mo–H equilibrium bond length in the [MoTe2]HMo−1 intermediate equilibrium structure is about 1.73 Å. The M06-L DFT method was used to calculate the changes in electronic energy (ΔE), relative enthalpy (ΔH), and Gibbs free energy (ΔG) that occurred during the HER process in each of the several reaction stages and are shown in Table 2.
| HER reaction intermediates | ΔE (kcal mol−1) | ΔH (kcal mol−1) | ΔG (kcal mol−1) | |
|---|---|---|---|---|
| Gas phase | Gas phase | Gas phase | ||
| 1 | [MoTe2] → [MoTe2]−1 | 10.63 | 10.57 | 9.80 |
| 2 | [MoTe2]−1 → [MoTe2]HTe | −2.04 | 2.51 | 1.93 |
| 3 | [MoTe2]HTe → [MoTe2]HTe−1 | 17.18 | 17.05 | 17.68 |
| 4 | [MoTe2]HTe−1 → H*-migration TS1 | 9.50 | 8.18 | 8.47 |
| 5 | Volmer TS → [MoTe2]HMo−1 | −20.89 | −19.14 | −18.69 |
| 6 | [MoTe2]HMo−1 → [MoTe2]HMoHTe | −6.01 | −1.25 | −1.97 |
| 7 | [MoTe2]HMoHTe → [MoTe2]HMoHTe + 3H2O + H3O+ | −21.60 | −20.82 | −6.08 |
| 8 | [MoTe2]HMoHTe + 3H2O + H3O+ → Heyrovsky TS2 | 11.13 | 9.32 | 8.85 |
| 9 | Heyrovsky TS → [MoTe2]HTe+1 | −0.95 | 0.63 | −15.34 |
(7) To form the [MoTe2]HMoHTe complex, an additional H+ from the solvent medium was added to the Te-site of the [MoTe2]HMo−1 complex, resulting in a complex where one hydrogen is bound to the Mo atom, and the other hydrogen is bound to the Te atom, as shown in Fig. 4g. According to Table 2, the DFT calculation showed that this step cost energy around −1.97 kcal mol−1. Using the same DFT technique, the equilibrium structure of the [MoTe2]HMoHTe complex was found to have equilibrium bond lengths of Mo–H around 1.72 Å and Te–H approximately 1.67 Å, respectively. The optimized equilibrium structures of all the intermediates and transition states involved in the HER process are displayed in Fig. 4.
(8) For H2 evolution, the [MoTe2]HMoHTe complex can proceed through the Heyrovsky or Tafel reactions. We added a hydronium water cluster (3H2O + H3O+) close to the active site of the Mo10Te21 non-periodic molecular cluster to aid the Heyrovsky reaction process. The cluster forms the [MoTe2]HMoHTe + 3H2O + H3O+ complex as an intermediate with an energy cost of ΔG = −6.08 kcal mol−1 because it has one H at the transition metal Mo site and another H at the Te site. Fig. 4h depicts the equilibrium structure of the [MoTe2]HMoHTe + 3H2O + H3O+ complex as a reaction intermediate formed during the Heyrovsky reaction step.
(9) In order to continue with the HER, we formed the second transition state (TS) known as Heyrovsky's transition state (TS2), as depicted in Fig. 4i. The [MoTe2]HMoHTe + 3H2O + H3O+ intermediate, where the H* from the Mo-site and the H+ from the hydronium water cluster combine to produce H2, which separates from the system, is where the Heyrovsky TS2 is obtained. A red circle with a dot in it appears in Fig. 4i to represent the generation of H2 during the reaction in TS2. According to the present calculations accomplished in the gas phase, the activation energy barrier of the Heyrovsky TS2 is approximately 8.85 kcal mol−1.
(10) After the formation of the Heyrovsky TS2, the system changes into [MoTe2]HTe+1, and one H2 molecule and four H2O molecules are released with an energy cost of −15.34 kcal mol−1. As depicted in Fig. 3, this is where the H2 molecule emerges through the catalyst's surface, and the reaction process resumes from the beginning by either absorbing one electron or releasing a proton.
As already mentioned, a very promising route for efficient HER of the catalysts containing transition metals is the Volmer–Heyrovsky mechanism.9 As a result, we concentrated primarily on determining the activation energy barriers for two important saddle points, the H*-migration TS (noted by TS1) and Heyrovsky TS (noted by TS2). According to gas phase calculations, Table 2 lists the variations in relative electronic energy (ΔE), enthalpy (ΔH), and free energy (ΔG) that occur during the numerous reaction intermediates and TSs involved in the HER via the Volmer–Heyrovsky reaction route.
A reaction barrier of approximately ΔG = 8.47 kcal mol−1 was found in the current investigation for the H*-migration process or TS1 formation, which was obtained in the gas phase. Corresponding to this, a reaction barrier of 8.85 kcal mol−1 was obtained (in gas phase calculation) during the TS2 formation in the Heyrovsky reaction process at the Mo-edges of the pure 2D monolayer MoTe2 material. In the case of the pure 2D monolayer MoTe2 TMD, the Heyrovsky reaction step is likely to be the rate-determining step in the Volmer–Heyrovsky reaction mechanism of the HER process given that the Heyrovsky TS2 has a slightly higher value of reaction barrier than the H*-migration transition state TS1. The HER pathway followed by the Volmer–Heyrovsky reaction mechanism is shown in Fig. 5, which shows the fluctuations of relative Gibbs free energies (ΔG) with regard to the reaction coordinates involved in the Volmer–Heyrovsky reaction. The activation energy barriers must also be calculated in the solvent phase because the reactions in commercial fields are typically conducted in solutions. In order to account for the solvent effect of water, the solvent phase calculation was performed using the polarizable continuum model (PCM) analysis, and the corresponding reaction barriers were noted down, as described in the Volmer–Heyrovsky mechanism steps above.
 | ||
| Fig. 5 The HER pathway followed by the Volmer–Heyrovsky reaction mechanism is shown here as it occurs during the HER process at the surface of the 2D monolayer MoTe2 material. | ||
We used the PCM analysis in our study to take into account the solvation impact during the HER process. Our DFT-D calculations showed that the energy barrier for the H*-migration during the formation of TS1 in a water environment was about 9.80 kcal mol−1. In comparison to other pristine TMDs, this 2D MoTe2 TMD exhibits better hydrogen migration/adsorption capabilities due to its low energy barrier value in both the solvent and gas phases. We estimated the energy barrier of the TS2 to be about 12.55 kcal mol−1 in the solvent phase during the Heyrovsky reaction step for H2 production and evolution. It is significant to note that this number exceeds the relevant energy barrier determined by calculations in the gas phase. We first investigated the reaction in the gas phase and then carried out solvent phase calculations utilizing the equilibrium geometries of all the reaction intermediates/TSs estimated in the gas phase because, in reality, the HER happens in a solvent phase. The equilibrium geometries of the systems involved in the reaction, which were estimated in the gas phase, were used for the PCM calculations. Usually, the solvent phase has higher reaction barriers than the gas phase. Significant energy changes result from the explicit consideration of the solvent–reactant interaction by the addition of solvent characteristics. Both the gas and solvent phases are two separate phases with totally different characteristics. Several other kinds of chemical bonds and interactions, including hydrogen bonds, ion–dipole interactions, and weak van der Waals (vdW) forces, are created during the solvation process.
 | ||
| Fig. 6 Volmer–Tafel HER mechanism with the detailed two-electron transfer reaction pathway on the surface of the 2D MoTe2 material. | ||
(1) The [MoTe2]HMo− intermediate turns into an [MoTe2]HMoHTe intermediate by taking an additional proton (H+), and here is the place of H2 evolution where the Volmer–Tafel process diverges from the Volmer–Heyrovsky mechanism. This phase has a −1.97 kcal mol−1 energy cost, which is consistent with the Volmer–Heyrovsky mechanism pathway. This intermediate, which acts as the starting point for the creation of molecular hydrogen, is essential to the overall reaction mechanism.
(2) The interaction of two adsorbed hydrogen atoms, one at the Mo-site and the other at the Te-site, during the HER, leads to the formation of H2, which is a result of the Tafel reaction. A transition state (TS3) is created as a result of this reaction, and it has a single imaginary frequency, an equilibrium Mo–H bond length of 1.73 Å, an equilibrium Te–H bond length of 1.68 Å, and a final H–H bond length of roughly 1.74 Å. Using the M06-L DFT approach, it was discovered that the energy barrier of TS3 in the gas phase is 6.07 kcal mol−1. Fig. 7 illustrates the TS3's equilibrium geometry and schematic representation. Additionally, using the same level of theory, it was determined that the energy barrier of TS3 for H2 evolution during the Tafel reaction step is approximately 5.29 kcal mol−1 obtained in the solvent phase calculations (water). These findings suggest that the energetics and kinetics of the Tafel reaction are strongly influenced by the solvent environment.
 | ||
| Fig. 7 The Volmer–Tafel reaction mechanism equilibrium geometries of [MoTe2]HMoHTe and TS3 are shown here. | ||
(3) The last stage of the Volmer–Tafel mechanism, [MoTe2], is reached once Tafel TS3 is generated. As indicated in Table 3, one H2 molecule is produced from the catalyst's surface in this step, requiring −23.34 kcal mol−1 of free energy. The HER process is finished with the development of H2, giving it an ideal avenue for the creation of clean and sustainable energy.
| HER reaction intermediates | ΔE (kcal mol−1) | ΔH (kcal mol−1) | ΔG (kcal mol−1) | |
|---|---|---|---|---|
| Gas phase | Gas phase | Gas phase | ||
| 1 | [MoTe2] → [MoTe2]−1 | 10.63 | 10.57 | 9.80 |
| 2 | [MoTe2]−1 → [MoTe2]HTe | −2.04 | 2.51 | 1.93 |
| 3 | [MoTe2]HTe → [MoTe2]HTe−1 | 17.18 | 17.05 | 17.68 |
| 4 | [MoTe2]HTe−1 → H*-migration TS1 | 9.50 | 8.18 | 8.47 |
| 5 | Volmer TS → [MoTe2]HMo−1 | −20.89 | −19.14 | −18.69 |
| 6 | [MoTe2]HMo−1 → [MoTe2]HMoHTe | −6.01 | −1.25 | −1.97 |
| 7 | [MoTe2]HMoHTe → Tafel TS3 | 6.93 | 5.84 | 6.07 |
| 8 | Tafel TS3 → [MoTe2] | −14.45 | −14.54 | −23.34 |
In the present calculations for both the gas and the solvent phases, the energy barrier for the Tafel reaction step (TS3) is lower than the energy barrier for the Heyrovsky reaction step (TS2) for H2 evolution. According to gas phase calculations, the H*-migration step in the TS1 of the Volmer–Tafel reaction pathway of the HER has a reaction barrier of around ΔG = 8.47 kcal mol−1, while the Tafel reaction step in the TS3 has a substantially lower reaction barrier of roughly 6.07 kcal mol−1. Fig. 8 shows how the Gibbs free energies, also known as the HER pathway, diverge relatively with respect to the various reaction steps in the Volmer–Tafel reaction mechanism. The values of relative changes in various energies during the Volmer–Tafel reaction pathway of the HER are reported in Table 3.
 | ||
| Fig. 8 The PES of the Volmer–Tafel reaction mechanism is shown here as it occurs during the HER process at the surface of the MoTe2 material. | ||
The Mo10Te21 non-periodic finite molecular cluster model system of the pure 2D monolayer MoTe2 was the subject of this DFT investigation, which looked into the HER on its surfaces. According to the calculations in both the gas and the solvent phases, the activation reaction barrier of the TS3 in the Tafel reaction step ranges from 6.07 to 5.29 kcal mol−1 computed by the DFT method. It is important to note that the reaction energy barrier (ΔG) of the Heyrovsky transition state, TS2, in the Volmer–Heyrovsky reaction mechanism, computed in both the gas and solvent phases, is about 8.85–12.55 kcal mol−1 higher than the barrier of TS3, which is the Tafel reaction step. These numbers are within the DFT accuracy range, indicating that both the HER pathways have comparable low energy barriers and can enhance the HER catalytic performance of the 2D monolayer MoTe2 TMD material. With comparable reaction barriers to the noble metal-based catalysts, these decreased reaction barriers suggest that the H2 evolution can occur through either pathway.
The current DFT calculations demonstrate that, in comparison to the other materials listed in Table 4, the 2D monolayer MoTe2 material has a lower reaction energy barrier for both the H*-migration TS in the Volmer reaction step and H2 formation in the Heyrovsky and Tafel reaction steps for the HER mechanism. The turnover frequency (TOF) was calculated, and it was discovered that it had a high TOF and a low Tafel slope, as mentioned in the ESI.† This implies that the 2D monolayer MoTe2 can act as a powerful HER catalyst with high efficiency. We carried out NBO (natural bond orbital), HOMO, and LUMO calculations to determine the TS1, TS2, and TS3 for the H*-migration, Heyrovsky, and Tafel transition states in order to better understand the electrocatalytic activity and stability of this material. According to the calculations, the Tafel TS3, which takes into account the charge cloud and molecule orbital overlap during H2 formation, offers a better justification for the effective HER process. We can find more details about the HOMO–LUMO study in the ESI.†
| Catalysts | H* migration TS1 barrier | Heyrovsky TS2 barrier | Tafel TS3 barrier | Ref. | |||
|---|---|---|---|---|---|---|---|
| Gas phase (kcal mol−1) | Solvent phase (kcal mol−1) | Gas phase (kcal mol−1) | Solvent phase (kcal mol−1) | Gas phase (kcal mol−1) | Solvent phase (kcal mol−1) | ||
| Mn-MoS2 | 7.23 | 10.34 | 10.59 | 10.79 | 90.13 | 93.72 | 5 |
| MoSSe | 3.93 | 7.10 | 5.61 | 4.72 | 8.52 | — | 3 |
| MoTe2 | 8.47 | 9.80 | 8.85 | 12.55 | 6.07 | 5.29 | This work |
An electrocatalyst lowers the activation energy of an electrochemical reaction, often lowering the electric potential at which the reaction occurs. In our present work, we used a non-periodic cluster model MoTe2 for the HER mechanism. For the stability of the molecular cluster model and all the reaction steps of the HER, we have performed geometry optimization followed by thermodynamic calculations, including electronic energy, enthalpy, and Gibbs free energy. We have also performed frequency calculations for all the structures. Our present calculations found that all the structures have real frequency (positive) except the three TSs. All three TSs (H*-migration, Tafel, and Heyrovsky TS) have one imaginary frequency, which confirms it to be transition state structures. This information, i.e., electronic energy, enthalpy, Gibbs free energy, frequency, and charges of the various structures, are listed in Tables S2 and S3 (ESI†), respectively. All the energy values are negative, which corresponds to the stability of all the reaction step structures.
4. Conclusions
We used first principles-based DFT-D3 computations (more particularly, the B3LYP-D3 method) to analyze the electronic and structural features of a 2D monolayer slab of the MoTe2 TMD. The present study has found that the 2D MoTe2 monolayer TMD has a direct band gap of about 1.65 eV. Furthermore, we have studied that the 2D monolayer MoTe2 is a good candidate as an efficient electrocatalyst towards the HER because of its lower bandgap and lower activation energy barrier during the HER. We looked at the variation in the adsorption energy of the HER intermediates taking place on the MoTe2 (Mo10Te21) surface to examine the catalytic performance of the TMD. Using the M06-L DFT approach, we have carried out each reaction step of both the Volmer–Heyrovsky and Volmer–Tafel reaction pathways to comprehend the HER mechanism route. According to our findings, the Volmer reaction during H*-migration across the 2D MoTe2 TMD material surface, when H* transfers from the Te-site to the Mo-site was around 8.47 kcal mol−1 in the gas phase and 9.80 kcal mol−1 in the solvent phase calculations. In the Heyrovsky reaction step, the activation energy barriers for the production of H2 were about 8.85 kcal mol−1 obtained in the gas phase and 12.55 kcal mol−1 computed in the solvent phase analysis. Also, the activation energy barriers of the Volmer–Tafel HER mechanism were about 6.07 kcal mol−1 in the gas phase and 5.29 kcal mol−1 in the solvent phase during the production of H2 in the Tafel reaction step. Due to the lower energy barrier of the Tafel TS3 compared to the Heyrovsky TS2, we understood that the Volmer–Heyrovsky mechanism is less advantageous or favorable than the Volmer–Tafel mechanism for the HER.The HOMO and LUMO calculations show that the H*-migration happens during the Volmer steps, whereas H2 evolution happens during Heyrovsky or Tafel stages. The extraordinary HER catalytic activity of the 2D monolayer MoTe2 material is explained by this computation. In the solvent phase, the predicted TOF of the Volmer–Heyrovsky reaction mechanism is about 3.91 × 103 s−1, whereas that of the Volmer–Tafel reaction mechanism is 8.22 × 108 s−1. The catalyst's efficient hydrogen evolution per active site per unit time is confirmed by these increased TOF values. Also, the theoretical Tafel slope is around 29.58 mV dec−1. This exceptional electrocatalytic activity of the 2D monolayer MoTe2 for the HER is demonstrated by the extremely low reaction barrier values, low Tafel slope, and extremely high TOF values. These results imply the need for additional experimental and theoretical research into the potential of 2D monolayer TMD-based materials as HER catalysts.
Data availability
The ESI† is available free of charge on the RSC Publications website. We have used CRYSTAL17 and Gaussian16 suite code and we developed our own GNUPLOT and python scripts to generate both the band structure and density of states (DOS). The equilibrium structures with the coordination of the 2D MoTe2 TMD and intermediates have been provided in the ESI† to reproduce our computed data.Conflicts of interest
The authors announce that there are no competing financial interests, and conflicts of interest.Acknowledgements
The authors are grateful to the Science and Engineering Research Board Department of Science and Technology (SERB-DST), Government of India, under Grant No. ECR/2018/000255 and CRG/2021/000572 for providing financial support for this research work. Dr Srimanta Pakhira acknowledges the SERB-DST for his Early Career Research Award (ECRA) under project number ECR/2018/000255 and his highly prestigious Ramanujan Faculty Fellowship under scheme number SB/S2/RJN-067/2017. Mr Vikash Kumar thanks the Indian Institute of Technology Indore (IIT Indore) and UGC, Govt. of India, for his doctoral fellowship UGC Ref. No: 1403/(CSIR-UGC NET JUNE 2019). The authors would like to acknowledge the SERB-DST for providing computing cluster/server and programs and IIT Indore for providing the basic infrastructure to conduct this research work. We acknowledge the National Supercomputing Mission (NSM) for providing computing resources of ‘PARAM Brahma’ at IISER Pune, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and Department of Science and Technology (DST), Government of India. We thank the CSIR, Govt of India for providing the research funds under scheme no. 22/0883/23/EMR-II and this work is financially supported by the CSIR. We extend our thanks to the Centre for Rural Development and Technology (CRDT), IIT Indore, for providing the research funds under the scheme no. IITI/CRDT/2024-25/26. We thank Dr Shrish Nath Upadhyay, Department of Physics, IIT Indore and Department of Chemical Engineering, IIT Kanpur for helpful discussions during the revisions of the manuscript.References
- S. Pakhira, V. Kumar and S. Ghosh, Adv. Mater. Interfaces, 2023, 10, 2202075 CrossRef CAS.
- S. N. Upadhyay and S. Pakhira, Phys. Chem. Chem. Phys., 2022, 24, 22823–22844 RSC.
- S. Pakhira and S. N. Upadhyay, Sustainable Energy Fuels, 2022, 6, 1733–1752 RSC.
- J. Wang, J. Liu, B. Zhang, X. Ji, K. Xu, C. Chen, L. Miao and J. Jiang, Phys. Chem. Chem. Phys., 2017, 19, 10125–10132 CAS.
- J. Ekka, S. N. Upadhyay, F. J. Keil and S. Pakhira, Phys. Chem. Chem. Phys., 2022, 24, 265–280 CAS.
- Y. Lei, S. Pakhira, K. Fujisawa, X. Wang, O. O. Iyiola, N. Perea López, A. Laura Elías, L. Pulickal Rajukumar, C. Zhou and B. Kabius, et al. , ACS Nano, 2017, 11, 5103–5112 CAS.
- L. Ju, M. Bie, X. Tang, J. Shang and L. Kou, ACS Appl. Mater. Interfaces, 2020, 12, 29335–29343 CAS.
- N. N. Som and P. K. Jha, Int. J. Hydrogen Energy, 2020, 45, 23920–23927 CAS.
- Y. Huang, R. J. Nielsen, W. A. Goddard and M. P. Soriaga, J. Am. Chem. Soc., 2015, 137, 6692–6698 CrossRef CAS PubMed.
- V. Kumar and S. Pakhira, Mol. Syst. Des. Eng., 2023, 8, 1060–1074 RSC.
- H. H. Huang, X. Fan, D. J. Singh, H. Chen, Q. Jiang and W. T. Zheng, Phys. Chem. Chem. Phys., 2016, 18, 4086–4094 RSC.
- Y. Xiao and C. Shen, Energy Fuels, 2021, 35, 8275–8285 CrossRef CAS.
- J. C. McGlynn, T. Dankwort, L. Kienle, N. A. G. Bandeira, J. P. Fraser, E. K. Gibson, I. Cascallana-Matias, K. Kamarás, M. D. Symes and H. N. Miras, et al. , Nat. Commun., 2019, 10, 4916 CrossRef PubMed.
- K. S. Bhat and H. S. Nagaraja, Int. J. Hydrogen Energy, 2019, 44, 17878–17886 CrossRef CAS.
- A. D. Beck, J. Chem. Phys., 1993, 98, 5646–5648 CrossRef.
- J. Baker, A. Scheiner and J. Andzelm, Chem. Phys. Lett., 1993, 216, 380–388 CrossRef CAS.
- S. Pakhira, K. Sen, C. Sahu and A. K. Das, J. Chem. Phys., 2013, 138, 164319 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 120, 215–224 Search PubMed.
- S. Pakhira, K. P. Lucht and J. L. Mendoza-Cortes, J. Phys. Chem. C, 2017, 121, 21160–21170 CrossRef CAS.
- K. Liang, S. Pakhira, Z. Yang, A. Nijamudheen, L. Ju, M. Wang, C. I. Aguirre-Velez, G. E. Sterbinsky, Y. Du and Z. Feng, et al. , ACS Catal., 2018, 9, 651–659 CrossRef.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima and S. Salustro, et al. , Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- Y. Lei, S. Pakhira, K. Fujisawa, H. Liu, C. Guerrero-Bermea, T. Zhang, A. Dasgupta, L. M. Martinez, S. Rao Singamaneni, K. Wang, J. Shallenberger, A. L. Elías, R. Cruz-Silva, M. Endo, J. L. Mendoza-Cortes and M. Terrones, Mater. Today, 2021, 51, 108–116 CAS.
- C. Patel, R. Singh, M. Dubey, S. K. Pandey, S. N. Upadhyay, V. Kumar, S. Sriram, M. Than Htay, S. Pakhira, V. V. Atuchin and S. Mukherjee, ACS Appl. Nano Mater., 2022, 5, 9415–9426 CAS.
- S. N. Upadhyay, V. B. Sardar, A. Singh, V. Kumar and S. Pakhira, Phys. Chem. Chem. Phys., 2022, 24, 28283–28294 RSC.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, et al., CRYSTAL17, 2017 Search PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 34112 Search PubMed.
- S. Ehrlich, J. Moellmann, W. Reckien, T. Bredow and S. Grimme, ChemPhysChem, 2011, 12, 3414–3420 CAS.
- S. N. Upadhyay and S. Pakhira, J. Mater. Chem. C, 2021, 9, 11331–11342 CAS.
- J. Laun and T. Bredow, J. Comput. Chem., 2022, 43, 839–846 CAS.
- R. A. Evarestov and V. P. Smirnov, Phys. Rev. B:Condens. Matter Mater. Phys., 2004, 70, 1–4 Search PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CAS.
- Y. Huang, Y. Chen, Y. Zhang, H. Zhang, K. Xiong, X. Ye, Q. Liu and J. Zhu, Appl. Surf. Sci., 2025, 680, 161335 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef.
- W. Niu, S. Pakhira, K. Marcus, Z. Li, J. L. Mendoza-Cortes and Y. Yang, Adv. Energy Mater., 2018, 8, 1800480 CrossRef.
- A. J. Garza, S. Pakhira, A. T. Bell, J. L. Mendoza-Cortes and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 24058–24064 RSC.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- F. Lipparini and B. Mennucci, J. Chem. Phys., 1985, 82, 284–298 Search PubMed.
- M. Uematsu and E. U. Frank, J. Phys. Chem. Ref. Data, 1980, 9, 1291–1306 CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Inc., Wallingford, CT, 2016, vol. 3.
- G. A. Andrienko, Chemcraft-Graphical Software for Visualization of Quantum Chemistry Computations, 2010, https://www.chemcraftprog.com Search PubMed.
- S. Pakhira, R. I. Singh, O. Olatunji-Ojo, M. Frenklach and W. A. Lester, J. Phys. Chem. A, 2016, 120, 3602–3612 CAS.
- W. G. Dawson and D. W. Bullett, J. Phys. C-Solid State Phys., 1987, 20, 6159 CAS.
- M. B. Kanoun, Nano-Sized Multifunctional Materials, Elsevier, 2019, pp. 207–218 Search PubMed.
- G. Gao, A. P. O’Mullane and A. Du, ACS Catal., 2017, 7, 494–500 CAS.
- A. B. Laursen, A. S. Varela, F. Dionigi, H. Fanchiu, C. Miller, O. L. Trinhammer, J. Rossmeisl and S. Dahl, J. Chem. Educ., 2012, 89, 1595–1599 CAS.
- S. Pakhira, B. S. Lengeling, O. Olatunji-Ojo, M. Caffarel, M. Frenklach and W. A. Lester, J. Phys. Chem. A, 2015, 119, 4214–4223 CrossRef CAS.
- C. Sahu, S. Pakhira, K. Sen and A. K. Das, J. Phys. Chem. A, 2013, 117, 3496–3506 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00892h |
| This journal is © The Royal Society of Chemistry 2025 |