Photothermal patterning of polydimethylsiloxane

Abstract

The surface patterning of polymers is an important approach to enhancing material properties for a large variety of applications. Due to the formation of irreversible crosslinks however, thermoset polymers tend to be challenging to pattern. In this paper we present a novel method of patterning a commonly used thermoset polymer, polydimethylsiloxane (PDMS), through controlled photothermal curing. We show that by incorporating 0.05% carbon black by weight into PDMS and moving a continuous wave-based laser engraver over the surface in a snake pattern, we can photothermally generate micron-scale surface features, and that these patterns can be controlled through laser parameters. Finally, we show that the photothermally patterned PDMS surfaces undergo changes in the optical properties as a result of patterning.

---

Introduction

Micron-scale patterning of polymer surfaces is a widely used method used to improve material functionality.¹ These modifications can be used to tune material properties such as wettability,² biocompatibility,³ and optical properties.⁴ Several applications including biomedical devices,³ electronics,⁵ optics,⁴ and coatings,⁶ utilize surface patterning to better tailor a material for a specific application.

The process of patterning is relatively simple for thermoplastics, which can be reheated and reshaped multiple times.⁷ In contrast, thermosets form irreversible crosslinks and cannot be reshaped once cured.⁸ Consequently, surface patterning of thermosets is typically performed in one of two ways. In one, the thermoset is generated without patterns, and then patterns are milled or ablated into the material.^9–11 Successive iterations of this ablation can lead to the formation of complex patterns.¹¹ A disadvantage of this approach is that the polymer surface can be damaged during the removal.¹² A second approach is to use soft lithography, generating micro/nano scale features on a polymer surface by curing the material in a mold.¹³ Soft lithography offers an accurate method of generating sub-micron features for various applications.¹⁴ However, the technique has several drawbacks. For instance, creating a master mold necessitates a clean room and involves several intricate steps to generate. This makes the process expensive, impedes its scalability, limits its accessibility, and prohibits rapid changes in pattern design.^9,13,15 Furthermore, attaining high fidelity matching between the mold and the surface can prove challenging. Therefore, there is a need for an inexpensive, accessible method of patterning thermoset polymers that allows easy reconfigurability of the patterns.

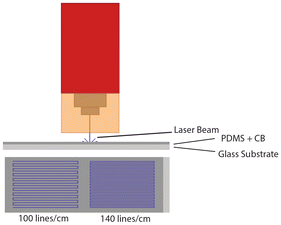
Herein, we demonstrate that photothermal curing is one avenue for directly writing patterns into thermosetting polymers. This approach leverages photothermal heating by small light absorbing particles, which produce tightly localized heat upon illumination.¹⁶ Though the heat is local, it has been shown effective in driving bulk-scale transformations of polymers.^17–21 At the same time, the heat produced is local, and so too must be the chemical changes it drives—a fact that could be harnessed to write patterns into a polymer during its curing. For instance, cured thermosetting polymers are expected to have a different surface potential than uncured pre-polymers, thereby yielding differences in surface tension and driving a Maragoni flow.²² Thus, if photothermal heating could be applied in a manner sufficient to realize a different in local surface tensions, we would expect this could be harnessed to draw physical features into a thermosetting polymer. We demonstrate such patterning via photothermal curing of a PDMS/carbon black composite. Specifically, we use a laser engraver to expose the PDMS composite to light following a ‘snake’ pattern with two different line spacings (Fig. 1). Prior work by ourselves and others have shown photothermal heating is effective for driving the curing of PDMS.^23–25 We find that this approach generates controllable micron scale features in cured PDMS. We note that prior efforts have demonstrated that photothermal heating can be used to generate patterns in PDMS by pyrolysis of the existing polymer,¹¹ while our work demonstrates such patterning through curing of the polymer. Though we briefly consider the ramifications of these patterns for the polymer properties, the focus of the manuscript is on the generation of these patterns, as well as their regularity and fidelity.

Fig. 1 Schematic of photothermal patterning using a laser etcher. Control over the patterns can be done by changing the spacing between lines in a ‘snake’ pattern.

Experimental

Formation of PDMS and carbon black composite

A mixture of 1.1 w/w% powdered carbon black (CB), Vulcan XC 72, and PDMS prepolymer (from Sylgard 184, Dow Inc. USA) was mixed in a centrifugal mixer (ARV-310P, Thinky USA Inc., USA) for 2 min at 2000 rpm under 30 kPa vacuum to produce the initial polymer mix prior to curing.

The stock solution was diluted 20-fold using the PDMS pre-polymer to yield a carbon black loading of 0.055 w/w%. For every 10 parts of this mixture, 1 part of curing agent is added, resulting in the final formulation of 0.05 w/w% CB in PDMS.

The final composite was mixed by hand until the CB was thoroughly dispersed in the PDMS, followed by degassing at 80 kPa for 20 minutes. A casting knife was used to coat 1 × 3 inch clear glass microscope slides to a thickness of 5 mils. Immediately following slide coating, the PDMS film is patterned.

Light source

A commercial laser engraver (xTOOl D1 Pro 10W, xTool, China) with a wavelength of 455 nm and spot size of 0.023 mm² was the light source used to drive photothermal patterning. The stepper motor provides a lateral (xy) resolution of 10 microns.

Photothermal generation of patterns

To produce photothermally patterned PDMS surfaces, a laser engraver was used to generate a line pattern according to Fig. 1. The thickness of the coating, prior to patterning, was measured out with a casting knife set to 5 mils (120 μm). Two rectangles with varying line densities (100 lines per cm and 140 lines per cm) were generated. In both cases, the laser power and xy scanning speed were set the same. The laser was set to deliver 35 W mm⁻² and the scanning speed was 20 mm s⁻¹. Following laser exposure, the sample was heated to 100 °C in an oven for thirty minutes to ensure the coating was cured completely. While PDMS is able to cure in ambient conditions over a 48 hours period, the patterns generated, deform without curing immediately after laser treatment (Fig. S1†).

UV-Vis characterization

A UV-Vis-NIR spectrometer (Cary 5000 UV-Vis-NIR spectrometer, Agilent, USA) with an integrating sphere attachment was used to measure the reflectivity and transmission of the samples. Wavelength ranged from 400 nm–1000 nm with a 0.1 s acquisition.

Contact angle measurements

A contact angle goniometer (Ramé-Hart 295, Ramé-Hart instrument co., USA) was used to dispense deionized water droplets and measure the contact angle between the surface and the droplet. Five droplets (7 μL) were dispensed onto separate portions of each surface. The angle between the droplet and surface on the right and left of the droplet were measured for a total of ten different angles. The ten angles were then averaged and represent the contact angle of that surface.

Surface analysis

An optical microscope (Zeiss Smartzoom 5, Zeiss, Germany) with a 1.6× objective and 336× zoom was used to image the sample surfaces. A 50/50 ring and coaxial light setting was used, and images were taken at locations representative of the sample. Scanning electron microscopy imaging was also performed (Thermoscientific Q250 SEM, ThermoFisher Scientific, USA). The microscope slide was mounted onto a pin mount with double sided carbon tape. Copper tape was then attached to the coating and mount to establish a ground contact. Images were taken of areas of the surface representative of the material.

To characterize the surface roughness and features generated by photothermal patterning, an optical profilometer (NexviewTM NX2 3D Optical Profilometer, Zygo Corportation, USA) with a 2.75× objective and 1× zoom was used. A total of five scans from different areas of the surface were taken for each sample type.

Results and discussion

Photothermal pattern generation

Photothermal generation of micron-scale features requires control over light distribution on the micron scale. The laser engraver used generates spot sizes on the order of a 16 microns, and has lateral stepper motor resolution of 10 microns, making it appropriate for generation of such features. Though several commercial engravers exist that meet these requirements, we also felt that the 455 nm light source was advantageous, as shorter wavelengths imply smaller laser spot sizes, all else being equal and 455 nm light is absorbed by the carbon black, but not the PDMS. For this initial study, we focused on a pattern that is simple to generate: lines written into the surface via passing the laser over the sample in a ‘snake’ pattern, as shown in Fig. 1. For all samples bearing patterns, we used PDMS bearing 0.05 w/w% CB. For all patterns generated, the power of the laser was set to 8% of its maximum (calculated power density of 210 W mm⁻²) and we used a scanning speed of 20 mm s⁻¹. This power and speed combination was chosen following preliminary experiments that revealed this power/speed was significant enough to generate visible surface features, but resulted in minimal burning of the sample. When burning is present, the sample bears noticeably blackened regions.

We can also consider a rough estimate of the lower limit of resolution we expect for lines drawn using the xTOOl. As noted above, the spot size is 16 μm. However, during irradiation, the thermal energy can diffuse away from the plot, increasing the size of the feature being written. Given the translation speed of the laser, the spot size, and thermal diffusivity of PMDS, as well as the fact that significantly elevated temperatures are needed to cure PDMS, we estimate that the lower limit of our resolution will be around 100 microns. The rationale for this estimate is given in the ESI.†

Outside of where the laser passed, the composite material remained liquid; however, the surface features generated by the laser were solid and could be manipulated physically. We assume that the solid features are cured polymer, as the power density used is well known to produce cured PDMS.²⁴ While PDMS is able to cure over a 48 hours period, the patterns are left distorted and delaminated. This is shown in Fig. S1.† In order to ensure that the patterns generated were affixed in place for further evaluation, the slide was heated in an oven for 30 min at 100 °C. This treatment ensured the material was fully cured, thereby securing the patterns. Though this two-step process of laser curing followed by oven curing does not offer a significant speed advantage over conventional heating, we note that the patterns are generated in a manner that is new for thermosetting polymers and offers a simple means to change the pattern dynamically—a capability that is not attainable using conventional lithographic techniques. Additionally, we are working with pre-polymers, rather than cured systems, as would be done for milling or ablating.

In order to demonstrate that it was the scanning of the laser that produced the features in the PDMS and to demonstrate that we have control over the patterns via parameters of the laser, we generated samples in which the targeted line density was either 100 lines per cm (left side) and 140 lines per cm (right side). Fig. 2A shows an image of these samples, produced side by side on a single slide. This was done by depositing a single polymer film, and then curing the samples, changing the line density half way across the slide. Visual examination of this slide shows that there is a clear transition in the appearance of the films, when the line density changes. In particular, the higher line density produces a larger blurring effect on the image behind the slide. To demonstrate that this blurring is not the result of the glass slide or the polymer film, Fig. 2B and C shows the results of viewing the same background through slide that was coated with unpatterned PDMS with 0.05 w/w% CB and a slide coated with pure PDMS (i.e., no CB), respectively. From these photographs, it is clear that patterning is associated with increased blurring.

Fig. 2 Microscope slides with different treatments, demonstrating the resulting clarity. (A) Photothermally patterned coating bearing (left) 100 and (right) 140 lines per cm. These patterns were generated using PDMS with 0.05 w/w% CB. (B) Unpatterned PDMS with 0.05 w/w% CB. (C) A glass slide with an unpatterned PDMS coating (no CB).

Surface characterization

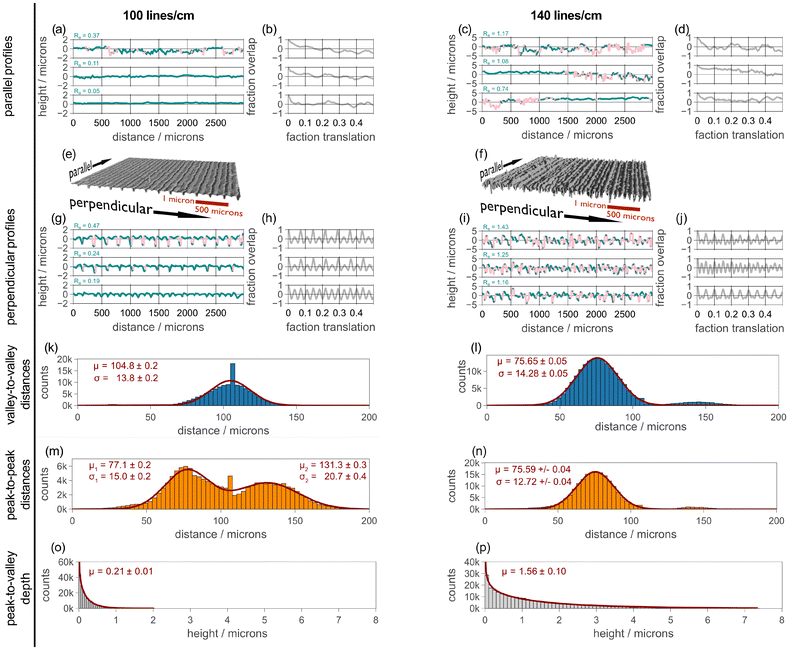
To gain better insight into the nature of the photothermally-generated surface features, optical microscopy images of the patterned samples were taken. The images, shown in Fig. 3, reveal the line pattern generated through laser irradiation have some structure. Perhaps most evident, the lines are not completely straight, but have some deviations along their length. Additionally, the lines appear to be constructed from multiple, smaller features, strung together. From the optical images, the origin and nature of these features are unclear. The 100 lines per cm sample also has two additional aspects of note. First, the lines do not appear to be continuous, but have breaks in them. Second, the contrast in the features display an every-other-line pattern, suggesting that some property of the lines must also alternate, such as the depth. However, the optical microscopy images do not resolve such aspects of the patterns. Thus, we turned to optical profilometry to characterize the 3D nature of the patterns.

Fig. 3 Optical microscopy images of samples patterned with line densities of (A) 100 lines per cm, and (B) 140 lines per cm.

Using a Zygo NexView 3D, with a 2.75× objective and operating at 1× zoom, we sampled five different regions for both of our line spacings. Fig. 4 presents a summary of the optical profilometry data. The data presented is after any large scale features (a.k.a., form) have been removed. Details of the data processing are found in the ESI.† Exemplars of regions for both 100 lines per cm and 140 lines per cm are shown in Fig. 4e and f, respectively. In these images the height is magnified by 10×, relative to this scale. From examining these images, one can see that the 100 lines per cm sample does indeed appear to have lines of alternating depth. In comparing the regions from the 100 lines per cm and 140 lines per cm, we can also easily see that the lines spacing is closer for the 140 lines per cm sample.

Fig. 4 Summary of profilometry data and analysis. (a, c, g and i) Profiles running parallel (a and c) and perpendicular (g and i) to the lines for the 100 lines per cm (a and g) and 140 lines per cm (c and i) samples. From top to bottom, the profiles are those associated with the largest roughness, the median roughness, and the smallest roughness. (b, d, h and j) Autocorrelation for the above profiles. (e and f) 3D rendering of a region for the 100 lines per cm and 140 lines per cm sample, respectively. The height is rendered at a scale 10× for that of the x and y. For each the width of the sample is 2982 microns wide. (k and l) Histograms for the valley-to-valley separations in profiles running perpendicular to the line patterns for 100 lines per cm and 140 lines per cm samples, respectively. Also shown are fits of a single Gaussian distribution to the histograms, as well as the means and standard deviations (as associated uncertainties) extracted from these fits. (m and n) Histograms for the peak-to-peak separations in profiles running perpendicular to the line patterns for 100 lines per cm and 140 lines per cm samples, respectively. Also shown are fits to two Gaussian distributions (100 lines per cm) and a single Gaussian distribution (140 lines per cm), as well as the means and standard deviations (as associated uncertainties) extracted from these fits. (o and p) Histograms for the peak-to-valley depths for the 100 lines per cm and 140 lines per cm samples, respectively. Also shown are fits of gamma distributions to these histograms, as well as the mean depth (and uncertainty) extracted from the fit.

When considering the profilometry data, it is critical to note that data is acquired using illumination of the samples from above. Because of this, sharp features in a sample can obscure some of the data. For our 100 lines per cm samples an average of 2% of the sample was obscured. However, the 140 lines per cm sample contains sharper features and roughly 27% of the sample is obscured. In processing the data, missing data is replaced by local averages, as described in the ESI.† However, this is done simply to aid in the processing of the data, as the analysis presented below is performed using only the acquired data points, which are unaffected by the local averaging. We also note that the missing data points are almost exclusively located on the walls of the ridges and furrows of the lines, and that data for the top and bottom of the features is retained. This can be see in Fig. S2,† where we present the same profile regions, color-coded by presence or absence of data.

The presence of the line pattern introduces a directionality to the samples and it makes sense to consider profiles that are taken parallel and perpendicular to the line pattern. In Fig. 4, these profiles are shown above and below the 3D rendering of the region, respectively. These profiles are color coded such that real data is dark cyan and missing data is pink. Looking over the profiles, one can see that the missing data (pink) is largely localized to the walls of the features.

For both the parallel and perpendicular profiles, we show three profiles: the profile with the largest roughness for the areal region, the median roughness for the areal region, and the lowest roughness for the areal region, as calculated using eqn (1):²⁶

R_a = ∑abs(z_i − z_mean)/n (1)

where z_i is the height of the i^th point of the profile, z_mean is the mean height of the profile, and n is the number of points in the profile. The roughness values are displayed above each profile. As a reminder, only acquired data (dark cyan points in the profiles) is used for this analysis. Inspecting these roughness values, we can see that the profiles running perpendicular to the lines are, in general, more rough. Additionally, it is clear that the profiles that run perpendicular to the lines show a more regular pattern.

To better visualize the presence or absence of a pattern, we also calculate the auto correlation for all profiles, and the corresponding auto correlation is shown to the right of the profiles. The auto correlation profiles are found by calculating the Pearson correlation coefficient between the profile and itself, but translated by a given distance. Details for this process are given in the ESI.† The autocorrelation coefficient can run between values of 1 and −1, with a value of 0 indicating no correlation. In inspecting these auto correlations, it is immediately clear that there is an underlying pattern contained within the profiles perpendicular to the line pattern, but that there is essentially no pattern within those profiles running parallel to the lines.

To further characterize the profiles running perpendicular to the drawn lines, we can consider the distance between features. For this, one might consider the distance between the minima (i.e., “valleys”). Given the reasoning presented in the introduction, we believe these are the locations where the laser directly passed. The heating results in pushing material out of the way yielding a valley, and forming maxima (i.e., “peaks”) to either side. This suggests that one might also be interested in the distance between peaks, as well as the height difference between adjacent peaks and valleys. Thus, we processed each of the 5320 perpendicular profile, across all 5 regions for each pattern and found the peaks and valleys. Details on this processing are given in the ESI,† and examples of the results are shown in Fig. S3.† Fig. 4k–p presents histograms for all three metrics, as well as fits of appropriate distributions to these histograms. Each of these reveal some information about the nature of the patterns, and how they are formed.

We first consider the valley-to-valley separations, shown in the blue histograms. These histograms reveal a single major feature for both the 100 lines per cm and 140 lines per cm samples, with an approximately Gaussian shape. Both histograms also show minor features with peaks at roughly twice those of the major feature. We ascribe these to a small number of separations where an intervening valley is missed, and so the separation between two valleys becomes twice that of the average. The 100 lines per cm also has a feature that is at shorter distances, and we believe this is due to rougher valleys (see discussion of SEM results, below), which can result in multiple locations found within a single valley. However, both of these additional features are relatively minor and do not significantly influence the analysis.

We fit each valley-to-valley histogram to a single Gaussian profile and the results are shown as the bold dark red line. The mean and standard deviation extracted from this fit, as well as the uncertainties in these values, are also given next to the histograms. When considering the mean values, we can see that the separation between features is smaller for the 140 lines per cm samples than the 100 lines per cm sample. Using the mean separations found, we find that the sample for which we tried to write 100 lines per cm produced a mean spacing associated with 95 lines per cm, while the sample for which we tried to write 140 lines per cm produced a mean spacing associated with 132 lines per cm. Thus, both samples produced lines that were roughly 95% of the desired density. We believe that this is likely due to calibration issues with the laser engraver, rather than a fundamental limitation of photothermal patterning.

Considering the standard deviations of the distributions, we find them to be quite similar. Thus, the standard deviations are not tied to the parameters of the pattern, but either to the behavior of the laser-engraver's stepper motors or the behavior of the PDMS upon exposure. At this time, we are unable to make a clear distinction between these two possibilities. However, a discussion of the standard deviation also speaks to reproducibility, and it is natural to ask how well-preserved the patterns are across the entire sample. As noted above, we sampled our patterns at 5 different regions each, and so we can also perform the valley-to-valley distance analysis separately for each measured region of the patterns. The values that are extracted from this analysis are reported in Table S1.† What we find is that the variation in valley-to-valley measurements are largely within a few microns of one another, except for an outlier for the 100 line per cm sample. Thus, we conclude that our approach can write patterns with close to micron-scale fidelity, though again we are uncertain if the fluctuations in the pattern spacing is due to the behavior of the PDMS or of the engraver.

Turning to the peak-to-peak separations, presented in the orange histograms in Fig. 4, the most obvious difference is that the 100 lines per mm sample is bimodal, while the 140 lines per mm samples is monomodal. The monomodal distribution was fit to a single Gaussian lineshape, and the extracted mean and standard deviations are not meaningfully different from those associated with the valley-to-valley separations for the 140 lines per cm patterns. Thus, for the 140 lines per cm pattern the peaks and valleys appear to be fully determined by the lines being written.

The bimodal distribution found for the 100 lines per cm pattern was fit to two Gaussian profiles, and the resulting fit is shown in dark red. From this we find that the intensity of the two features is nearly identical; the intensity of the Gaussian with the larger mean value is 93% that of the Gaussian with the smaller value. Furthermore, we find that the weighted average of the means for the two Gaussians is 100 microns—close to that that found for the valley-to-valley separation. Thus, we conclude that the process generating the valleys also responsible for generating the peaks. Specifically, we hypothesize that, while the sample is pushed away through heating by the laser (at a spacing of 104 microns), the degree to which the sample is pushed varies every other line. In testing our laser, we found that the intensity of the laser could vary every other pass, which explains these results. This result, while leading to irregular features in this particular sample, highlights that changes in the light intensity can be used to modulate the final patterns within the film.

Finally, we can turn to the peak-to-valley height differences, shown in Fig. 4 using grey histograms. The shape of these histograms, together with the fact that there cannot be negative differences suggests that the data should follow a gamma distribution, and the dark red lines in the histograms are fits of the data to this distribution. From these fits, we can extract a mean value and an uncertainty in this value, which is also shown on the histograms. We find that the mean depth for the 140 lines per mm patterns are 7.4 times deeper than for the 100 lines per mm sample.

Something else that is of interest in the peak-to-valley data is that the 100 lines per cm sample is fit to a single gamma distribution, despite the fact that the image of the region shown in Fig. 4e seems to indicate that there are two distinct heights. Indeed, if we perform the same analysis on a single region, we find that two gamma distributions are needed, as shown in Fig. S4.† Thus, it seems that there is enough variance across the sample that, when different regions are combined, the distinction between heights is blurred and the distribution can be fit to a single gamma distribution. Close inspection of the profile exemplars shown in Fig. 4g reveals that the every-other height variation is not as great for the smoothest profile as for the roughest profile. Thus, even within the areal region shown in Fig. 4g, there is not a clear retention of the two peak-to-valley heights. This is some indication that improvements in pattern uniformity across the cm scale is needed.

While optical profilometry allows us to construct a 3D image of the surface, the loss of data for the steepest features means that we do not have a good indication of morphology of the lines at the smallest scale. To address this limitation, SEM imaging was performed to investigate the morphology within these features. SEM images of each patterned surface are shown in Fig. 5.

Fig. 5 SEM images of (A) 100 lines per cm and (B) 140 lines per cm surfaces as well as plots of roughness and average height for profiles running parallel to the lines for (C) 100 lines per cm and (D) 140 lines per cm samples.

In this figure, we can again see that the 100 lines per cm sample contains clear alteration between adjacent lines, with one of the lines being very difficult to see. Within the easier to see line, we can observe some smaller scale structures, which appear to be circular in shape. The 140 lines per cm sample share similar appearance of these circular features within the sample and, while all lines were fairly easy to see for the 140 lines per cm samples, the SEM does show some variability between adjacent lines. In particular, the circular features present within these lines are more pronounced every other line. Given the intense nature of the heating, we hypothesize that these circular features could be the remnants of an explosive volatilization reaction within the curing PDMS, leaving behind these features in the cured sample. This volitization could arise from trace amounts of solvent, or even lighter weight components of the pre-polymer.

If our hypothesis as to the nature of the circular features is correct, then we might expect that the roughness of the surface is greatest where they occur, and they should be occurring where the laser intensity was greatest (i.e., the valleys). We can confirm this is the case by returning to the profilometry data and computing the roughness for each profile parallel to the lines, and then plotting this for each position in the profile. This shown as the blue traces in Fig. 5C (100 lines per cm) and D (140 lines per cm). In this data, one can see clear spikes in the roughness, which is especially clear for the 100 lines per cm sample. To aid in understanding of these features, we also show the average height for each profile, as the orange traces in Fig. 5C and D. From this plot, it does seem that areas of high roughness correspond to the valleys drawn in the sample, consistent with our hypothesis. However, we do note that this these are much more clearly correlated for the 100 lines per cm pattern than the 140 lines per cm pattern.

The conclusion of this surface analysis that we are clearly generating patterns within the PDMS using laser scanning, and that the nature of these patterns is dependent on the scan parameters. To understand if these lead to control of other properties, we next examine the optical properties and hydrophobic properties of the films.

Characterization of optical properties

The blurring of background images seen in Fig. 2 makes it clear that the optical properties of the sample are influenced by the patterns. In an attempt to quantify the optical effects, UV-visible spectroscopy was used to measure the transmission and reflectivity of both patterned and non-patterned samples (Fig. 6). In addition to the two patterned surfaces, we also measured the optical properties of the glass slide, unpatterened pure PDMS, and unpatterned PDMS with the same loading of carbon black. Taken together, this will help us understand which optical properties are due to the PDMS, carbon black, and patterning.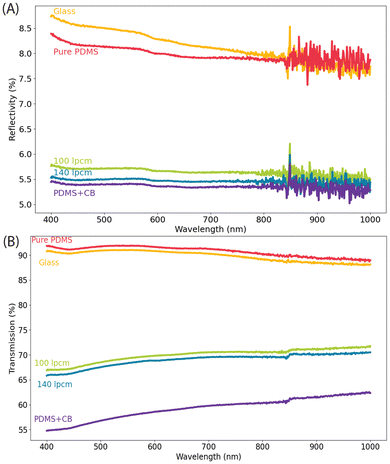

Fig. 6 (A) Reflectivity, and (B) transmission spectra of various surfaces compared to photothermally patterned PDMS.

As shown in Fig. 6A, the reflectivity of pure PDMS is similar to that of uncoated glass, but the reflectivity decreased significantly with the addition of CB. This outcome is expected owing to the absorptive properties of CB. Introduction of patterns did not change the reflectivity as significantly as addition of CB. Nevertheless, there is a small increase in reflectivity, the origins of which we do not fully understand. It is possible that the small scale features that are seen in the SEM image (Fig. 5) are on a scale appropriate to increase the scattering of light, relative to the unpatterned sample. However, we have not directly tested this hypothesis.

Turning to transmission (Fig. 6B), we again see that the properties of glass and pure PMDS are similar, while addition of CB to the PDMS results in a dramatic decrease in transmission. This is again expected, given the absorptive properties of CB. However, introduction of patterns to the PDMS now introduces a substantial increase in transmission. The creation of feature via pushing of material makes some pathlengths longer and some shorter, without removing material. The non-linear dependence of transmission on the pathlength, as explained via Beer's law, means that such patterns must result in an overall increase in the transmission.

Hydrophobicity

Many studies have shown that hydrophobic surfaces become more hydrophobic with added surface roughness or patterning.^7,10,27 This is a result of either increased surface area due to the patterns, or to trapped air within high-aspect ratio patterns.^28,29 To investigate if the patterns we manufactured were capable of such an effect, we measured the contact angle on both flat and our patterned PDMS surfaces. Flat PDMS has a contact angle >100°. Fig. 7 presents the results of these measurements. In this figure, the bars are the mean values and the error bars the standard deviation of 5 measurements at different places for each surface. From this measurement, we do not observe any statistically meaningful change in the hydrophobicity, due to patterning. We hypothesize that the features we are writing are not deep enough to create such effects, and future work will function on changing the parameters of photothermal curing in order to induce deeper patterns. For now, we simply note that this result demonstrates the ability to separately tune optical and hydrophobicity properties.

Fig. 7 Average contact angle measurements of water droplets on various nonpatterned and photothermally patterned surfaces.

Conclusions

Overall photothermal patterning offers an accessible, inexpensive method of patterning thermoset polymers. By combining carbon black and PDMS, and moving a laser engraver over the surface in a snake pattern, micronscale features were generated through controlled photothermal curing. Our findings conclude that during photothermal patterning, material is displaced by heat, leading to the production of peaks and valleys on the surface. Moreover, the pattern depth and separation are laser parameter dependent. Finally, we conclude that photothermally patterned PDMS undergoes changes in optical properties as a result of patterning. Specifically, the transmission of light through the patterned coating increases. This is explained by the features altering the path length of light. Changes in the hydrophobicity of photothermally patterned PDMS was not observed. However, future work will focus on increasing the hydrophobicity of these patterns through generating deeper, high aspect ratio features. Combining our curing approach with existing photothermal degradation approaches to patterning¹¹ could also allow for more complex and functional patterns. Though this work considered only two simple patterns differing only in line spacing, the results are built upon the idea of promoting thermal reactivity pathways, implying a general solution for direct patterning of thermosetting polymers, though this hypothesis will need to be tested in the future.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data for this article are available at the Penn State Data Commons at https://doi.org/10.26208/384e-pc40. All data reported, Python codes used, and Blender files are available at that URL.

Acknowledgements

The authors thank the Office of Naval Research NURP program (N00014-23-1-2675) for financial support of this work.

References

1. J. N. Cabrera, M. M. Ruiz, M. Fascio, N. D’Accorso, R. Mincheva, P. Dubois, L. Lizarraga and R. M. Negri, Increased Surface Roughness in Polydimethylsiloxane Films by Physical and Chemical Methods, Polymers, 2017, 9, 331.
2. Y. Fu, M. Soldera, W. Wang, S. Milles, K. Deng, B. Voisiat, K. Nielsch and A. F. Lasagni, Wettability control of polymeric microstructures replicated from laser-patterned stamps, Sci. Rep., 2020, 10, 22428.
3. D. S. Kohane and R. Langer, Polymeric Biomaterials in Tissue Engineering, Pediatr. Res., 2008, 63, 487–491.
4. A. Zahid, B. Dai, R. Hong and D. Zhang, Optical properties study of silicone polymer PDMS substrate surfaces modified by plasma treatment, Mater. Res. Express, 2017, 4, 105301.
5. J. M. R. Tan, Y. Farraj, A. Kamyshny and S. Magdassi, Fabrication Approaches of Soft Electronics, ACS Appl. Electron. Mater., 2023, 5, 1376–1393.
6. O. Al-Khayat, J. K. Hong, D. M. Beck, A. I. Minett and C. Neto, Patterned Polymer Coatings Increase the Efficiency of Dew Harvesting, ACS Appl. Mater. Interfaces, 2017, 9, 13676–13684.
7. K. Maghsoudi, E. Vazirinasab, G. Momen and R. Jafari, Advances in the Fabrication of Superhydrophobic Polymeric Surfaces by Polymer Molding Processes, Ind. Eng. Chem. Res., 2020, 59, 9343–9363.
8. B. Zhang, K. Kowsari, A. Serjouei, M. L. Dunn and Q. Ge, Reprocessable thermosets for sustainable three-dimensional printing, Nat. Commun., 2018, 9, 1831.
9. D. L. Pugmire, E. A. Waddell, R. Haasch, M. J. Tarlov and L. E. Locascio, Surface Characterization of Laser-Ablated Polymers Used for Microfluidics, Anal. Chem., 2002, 74, 871–878.
10. J. Yong, F. Chen, Q. Yang, D. Zhang, G. Du, J. Si, F. Yun and X. Hou, Femtosecond Laser Weaving Superhydrophobic Patterned PDMS Surfaces with Tunable Adhesion, J. Phys. Chem. C, 2013, 117, 24907–24912.
11. J. Shin, J. Ko, S. Jeong, P. Won, Y. Lee, J. Kim, S. Hong, N. L. Jeon and S. H. Ko, Monolithic digital patterning of polydimethylsiloxane with successive laser pyrolysis, Nat. Mater., 2021, 20, 100–107.
12. S. Ravi-Kumar, B. Lies, X. Zhang, H. Lyu and H. Qin, Laser ablation of polymers: a review, Polym. Int., 2019, 68, 1391–1401.
13. U. M. Sonmez, S. Coyle, R. E. Taylor and P. R. LeDuc, Polycarbonate Heat Molding for Soft Lithography, Small, 2020, 16, 2000241.
14. S. H. Lee, S.-H. Shin, M. Madsen, K. Takei, J. Nah and M. H. Lee, A soft lithographic approach to fabricate InAs nanowire field-effect transistors, Sci. Rep., 2018, 8, 3204.
15. X.-M. Zhao, Y. Xia and G. M. Whitesides, Soft lithographic methods for nano-fabrication, J. Mater. Chem., 1997, 7, 1069–1074.
16. A. O. Govorov and H. H. Richardson, Generating heat with metal nanoparticles, Nano Today, 2013, 2, 30–38.
17. R. C. Steinhardt, T. M. Steeves, B. M. Wallace, B. Moser, D. A. Fishman and A. P. Esser-Kahn, Photothermal Nanoparticle Initiation Enables Radical Polymerization and Yields Unique, Uniform Microfibers with Broad Spectrum Light, ACS Appl. Mater. Interfaces, 2017, 9, 39034–39039.
18. M. E. Matter, L. Čamdžić and E. E. Stache, Photothermal conversion by carbon black facilitates aryl migration by photon-promoted temperature gradients, Angew. Chem., Int. Ed. Engl., 2023, 62, e202308648.
19. C.-U. Lee, K. C. H. Chin and A. J. Boydston, Additive manufacturing by heating at a patterned photothermal interface, ACS Appl. Mater. Interfaces, 2023, 15, 16072–16078.
20. J. Dong, G. E. Firestone, J. R. Bochinski, L. I. Clarke and R. E. Gorga, In situ curing of liquid epoxy via gold-nanoparticle mediated photothermal heating, Nanotechnology, 2017, 28, 065601.
21. G. Firestone, H. Huang, J. R. Bochinski and L. I. Clarke, Photothermally-driven thermo-oxidative degradation of low density polyethylene: heterogeneous heating plus a complex reaction leads to homogeneous chemistry, Nanotechnology, 2019, 30, 475706.
22. J. M. Katzenstein, D. W. Janes, J. D. Cushen, N. B. Hira, D. L. McGuffin, N. A. Prisco and C. J. Ellison, Patterning by photochemically directing the Marangoni Effect, ACS Macro Lett., 2012, 1, 1150–1154.
23. M. Fedoruk, M. Meixner, S. Carretero-Palacios, T. Lohmüller and J. Feldmann, Nanolithography by plasmonic heating and optical manipulation of gold nanoparticles, ACS Nano, 2013, 7, 7648–7653.
24. R. Joseph Fortenbaugh and B. J. Lear, On-demand curing of polydimethylsiloxane (PDMS) using the photothermal effect of gold nanoparticles, Nanoscale, 2017, 9, 8555–8559.
25. A. Katona and B. J. Lear, Effective photothermal curing of PDMS using ultralow loadings of carbon black, Macromolecules, 2024, 57, 7508–7515.
26. D. J. Whitehouse, Handbook of Surface Metrology, CRC Press, 1994.
27. Z. Burton and B. Bhushan, Hydrophobicity, Adhesion, and Friction Properties of Nanopatterned Polymers and Scale Dependence for Micro- and Nanoelectromechanical Systems, Nano Lett., 2005, 5, 1607–1613.
28. S. Kim, D. H. Kim, S. H. Choi, W. Y. Kim, S. Kwon and Y. T. Cho, Effect of surface pattern morphology on inducing superhydrophobicity, Appl. Surf. Sci., 2020, 513, 145847.
29. M. S. Ambrosia, M. Y. Ha and S. Balachandar, The effect of pillar surface fraction and pillar height on contact angles using molecular dynamics, Appl. Surf. Sci., 2013, 282, 211–216.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lp00093a

---