Sustainable high-yield h-BN nanosheet production by liquid exfoliation for thermal interface materials

Abstract

Thermally conductive and electrically insulating hexagonal boron nitride (h-BN) is essential for thermal interface materials (TIMs) to effectively transfer heat from the source to sink in laptops and optoelectronic devices. Currently, thermal compounds rely on energy-intensive techniques and require nanofillers in very high loading percentages. Additionally, using mixtures of several fillers is an unreliable approach for heat management. In this work, we demonstrate the high-yield synthesis of atomically thin h-BN nanosheets in a natural surfactant/aqueous medium using liquid phase exfoliation (LPE). The exfoliated nanosheets are characterized by electron microscopy, absorbance spectroscopy, and XPS techniques. Extinction and gravimetry measurements confirm an overall yield of ∼89% after four cycles of exfoliation, successfully converting thick and bulk h-BN into h-BN nanosheets (h-BNNS) in water. Approximately 90% of the exfoliated nanosheets in ink form are recovered from the dispersion through low-speed centrifugation, indicating that the surfactant molecules are loosely bonded to the surface of the nanosheets. The quality of the exfoliated h-BNNS, including the lateral length (∼269 nm) and the number of layers (∼6), remains consistent during recycling. A 20 wt% h-BNNS in PVA thermal film reduces the surface temperature of a 10 W light-emitting diode (LED) bulb by ∼11 °C, while a 20 wt% h-BNNS in silicone oil (SO) thermal grease performs comparably to commercial thermal paste with 50 wt% particle loading for heat management. The thermal conductivity of the h-BNNS-based thermal film and thermal grease was measured using a modified transient plane source (MTPS) method and modelled using finite element analysis (FEA) to calculate thermal resistance. This study explores the utilization of a high-yield LPE process for h-BN nanosheets with natural stabilizers, enabling scalable exfoliation for heat management applications.

---

Introduction

Unwanted heat is detrimental to the operation of electronic devices and light emitting diodes, affecting their efficiency and longevity.¹ Rapid advancements in miniaturization, component density, and clock speed generate large amounts of heat in a short period.² The rate of heat generation must match the rate of heat spreading or dissipation. Conventionally, this is achieved by integrating a heat sink with a heat source, with a thermal compound used as an interface material placed between them to eliminate the air gaps and facilitate heat transfer. To address this issue, an efficient thermal interface material is required to operate continuously between the heat source and the heat sink. In recent years, polymer composite materials have been used as thermal interface materials for electronics cooling.³ However, polymers with nanofillers as additives are insufficient due to the low thermal conductivity of polymers and the unsustainable methods used for synthesizing reinforcing nanomaterials.^4–7 To enhance the thermal conductivity of polymer-based composite materials, highly thermally conductive fillers such as graphene,⁵ carbon nanotubes,⁸ alumina nanoparticles,⁹ silver nanoparticles,¹⁰ boron arsenide, and boron nitride^11,12 are commonly used. Metal-based fillers and metal oxides have been reported; however issues such as oxidation, corrosion and aggregation are unavoidable. Hexagonal boron nitride (h-BN) is considered as an ideal filler for composite materials due to its exceptional thermal properties, chemical stability, excellent electrical insulating properties and low dielectric loss.^13–17 h-BN is also known as white graphite due to its structural similarity to graphite.¹⁸ Bulk h-BN is a layered material consisting of atomically thin h-BN nanosheets (h-BNNS), with individual layers held together by van der Waals forces.¹⁸ Compared to bulk h-BN, atomically thin h-BNNS exhibit higher thermal conductivity and can easily form heat transfer networks between nanosheets within the polymer matrix.¹⁹ Although h-BNNS is a promising material with significant demand in thermal management, there is a lack of sustainable exfoliation methods that achieve high yield of h-BNNS using environmentally friendly stabilizers and solvents such as water, from bulk h-BN. Moreover, the aqueous-phase synthesis of layered nanomaterials using sustainable chemicals is gaining popularity due to its minimum environmental impact.²⁰

Over the past few years, the primary methods for preparing h-BNNS from h-BN include ball milling,²¹ chemical exfoliation,²² chemical vapor deposition,²³ hydrothermal methods,²⁴ and liquid phase exfoliation.^25,26 Among all these methods, liquid phase exfoliation is a simple, versatile, economical and scalable approach for preparing h-BNNS. These layered materials are delaminated and fragmented in a liquid medium using ultrasonic agitation,²⁷ shear forces,²⁸ electro-chemical exfoliation,²⁹ and microfluidic flows.¹⁵ However, the solvents used for exfoliation are not environmentally friendly.³⁰ Water is an economical and environmentally friendly solvent, but surfactants are often needed to stabilize nanosheets. Chemically synthesized surfactants such as sodium cholate, urea, sucrose are used to stabilize nanosheets in water (see Table S1 in the ESI†). Commercially available thermal interface materials have thermal conductivity in the range of 0.5–5 W m⁻¹ K⁻¹, but they often contain either high filler loadings or unsustainable fillers.³¹ Detailed literature analysis was conducted by Lin et al.³² where different strategies for heat management in graphene and h-BN based thermal interface materials are discussed. Next generation electronic devices for gaming and high end computing require thermal interface materials with high thermal conductivity at low filler weight percentages.³³ Although high thermal conductivity is required for efficient thermal interface materials (TIM), the efficiency of the heat transfer depends on the thermal contact resistance. The composite thermal conductivity is influenced by the intrinsic thermal conductivity of the filler, dispersibility and alignment of the filler within the matrix, and filler–matrix interface. TIMs are essential to be in the viscous solid state for ease of application on the surfaces of light emitting diodes and electronic devices.³⁴

The natural surfactant used here to stabilize the h-BN nanosheets in water is Sapindus mukorossi (SM). In our previous report, this surfactant was tested for graphene exfoliation and demonstrated that high quality graphene could be produced in water.³⁵ The prepared h-BNNS has the maximum concentration of ∼7.2 mg ml⁻¹ and the maximum yield is 33% in one cycle of experiment. When the unexfoliated h-BN is recycled, a maximum yield of ∼89% is achieved after 4 cycles. h-BNNS/PVA thermal films are prepared by the solution casting method for curing TIMs in the solid state, and h-BNNS/silicone oil-based composite thermal grease is prepared by solution mixing of non-curing TIMs. The h-BNNS for this composite is prepared by ultrasonication-assisted liquid-phase exfoliation using water/surfactant as a medium. The h-BNNS fillers are dispersed in the polymer matrix and are tested by infrared imaging to dissipate the heat from the electronic device.

Experimental section

Materials

Boron nitride (∼1 μm size) was purchased from Sigma Aldrich (255475-50G), silicone oil (viscosity 350 cSt) and acetone were purchased from SRL Chemicals, polyvinyl alcohol was purchased from Alfa Aesar, and Sapindus mukorossi (Reetha) powder was purchased from the Amazon online store. All the chemicals were used without any purification.

Exfoliation and recycling of h-BN nanosheets

The schematic representation for the exfoliation and stabilization of h-BNNS using a natural surfactant is shown in Fig. 1. Reetha surfactant was dissolved in distilled (DI) water. Bulk h-BN powder, at a concentration of 20 mg ml⁻¹ in water, was then added to the SM surfactant/DI water solution. The reaction volume is 100 ml. The mixture was then subjected to probe sonication (Sonics & materials VCX750) with an ice bath to prevent excess heating during sonication. The sample was sonicated for 1 h with 40% amplitude, 3 s/3 s with ON/OFF pulse. The sonicated h-BN sample was allowed to stand overnight. The top 90% of the top supernatant was then taken and centrifuged (Thermo Scientific Sorvall™ ST8R) for 90 min at 1500 rpm with a fixed angle rotor, after balancing the samples with ±50 mg to remove the unexfoliated h-BN from the dispersion. The top 50% of the centrifuged sample was carefully pipetted out from the center of the centrifuge tube using a 1 ml pipette. The pipetted sample was dried at 60 °C for 12 h. The dried powder sample was used for further experiments. To maximize the yield of h-BN nanosheets in water, the sediment of h-BN after each cycle was subjected to further exfoliation under similar conditions, using it as a starting solid precursor. The top 95% of the supernatant from the idle sample was taken and centrifuged at 500 RPM for 270 min with a fixed angle rotor to remove unexfoliated h-BN from the dispersion. Subsequently, 99% of the sample was collected using a 1 mL micropipette from the center, carefully avoiding disturbing the sides of the centrifuge tube. The sediment samples from both the idle state and after centrifugation were taken and dried in an oven at 80 °C for 12 hours. The dried sediment samples were then added to 60 mg ml⁻¹ SM surfactant/DI water. They were then sonicated for 1 hour using the same parameters as in the first cycle. This procedure was repeated for a total of 4 cycles. The exfoliated dispersions from all 4 cycles were used for further analysis.

Fig. 1 Scheme for liquid-phase exfoliation and processing of bulk h-BN into few-layered h-BN nanosheets using a natural SM surfactant.

Preparation of h-BNNS based thermal film and thermal grease

The schematic representation for the preparation of h-BN/PVA thermal film is shown in Fig. S1(A).† 100 mg of PVA powder was added to 5 mL of DI water, and the mixture was kept on a hotplate at 90 °C and stirred at 500 rpm for 1 hour. The PVA-dissolved water solution was then poured into a 60 mm glass Petri dish and kept in an oven at 60 °C for 12 hours. To prepare composites with different weight percentages of h-BNNS, the PVA-dissolved solution was taken, and the corresponding weight of h-BNNS dispersion was added. The mixture was then stirred at 90 °C and 500 rpm for 1 hour. The sample was then poured into a glass Petri dish and kept in an oven at 60 °C for 12 hours to prepare the composite film.

The schematic representation of the h-BNNS/S.O thermal paste preparation is shown in Fig. S1(B).† The dried h-BNNS was dispersed in 5 mL of IPA using a bath sonicator (Branson, M series, 90 W) for 1 hour at a temperature below 20 °C. Similarly, the dispersed h-BNNS was added to pre-weighed silicone oil. This sample was bath sonicated for 1 h at temperature below 20 °C. After sonication, the sample was kept on a hot plate for 3 h at 90 °C to remove the IPA solvent from the prepared paste.

Characterization

The absorbance spectrum of the exfoliated h-BNNS dispersion was recorded using a UV-vis-NIR spectrophotometer (Agilent Cary 5000/60 Model). Double-sided transparent quartz cuvettes (Hellma Inc., 10 mm path length) were used for absorption spectrum measurements. For measuring the absorbance, samples were diluted at 30-fold to maintain the maximum absorption value below 2. The exfoliated h-BNNS concentration was measured using Beer–Lambert's law (A = εCl). Raman spectra were measured using a Horiba Jobin Yvon Lab RAM-HR evolution (532 nm and 633 nm lasers). The exfoliated h-BNNS dispersion was bath sonicated for ∼20 min. Then, 50 μl of the h-BNNS dispersion was drop-cast on the pre-heated silicon substrate. The silicon substrate was preheated at 150 °C for 5 min. Subsequently, the substrate was kept on a hot plate for 10 min for drying. Finally, the substrate was kept in a vacuum oven for ∼22 hours at 60 °C to dry the sample. The samples were then stored in a vacuum desiccator. Scanning electron microscopy images were acquired using a Thermo Scientific Apreo S FE-SEM in low vacuum mode at an operating voltage range of 5–10 kV. To avoid charging effects of the h-BNNS, a 5 nm chromium thin film was deposited for 25 seconds using a sputter coater (Quorum Q150T S plus). Transmission electron microscopy (TEM) images were obtained using a JEM-2100 Plus (JEOL, Japan) operated at an accelerating voltage of 200 kV. For the recycled samples, the samples were bath sonicated for ∼30 min, and then 10 μL of 30-times diluted dispersion was further diluted into 1 ml. Then, 20 μL of diluted sample was drop-cast onto a lacey carbon-coated copper grid (400 mesh). The grid was kept in a vacuum oven at 60 °C for 12 hours. The X-ray photoelectron spectroscopy (XPS) spectrum was recorded using a PHI VersaProbe III (Physical Electronics). An Al monochromatic X-ray beam (hν = 1486.6 eV) with a micrometer-sized spot (∼100 μm) was used for data acquisition, and the measurements were performed under the base pressure (∼10⁻⁷ mbar). 15 ml of the 500 rpm centrifuged sample was filtered using vacuum filtration on a cellulose acetate membrane and washed with 600 ml of DI water to remove the surfactant. The film was dried at 80 °C for overnight. A Fluke TiS45 model thermal camera was used to record the thermal images of the LED bulb from the top view. The power of the LED bulb used for recording the thermal images was 10 W. The thermal grease and thermal film were placed between the LED bulb and the heat sink. Thermal images were captured from the top surface of the LED. Thermal conductivity measurements were performed using a C-Therm trident system with the modified transient plane source method (MTPS, ASTM D7984 standard). The error bars are reported out of 5 measurements conducted at room temperature. In this instrument, nickel spiral coil is used as a heating and sensing element with a diameter of 18 mm. The measurement accuracy for this method is ∼5%. The thermal paste and thermal film samples were directly used for these measurements.

Results and discussion

The h-BNNS were exfoliated using a sonication-assisted liquid-phase exfoliation method (see the Experimental section).³⁶ In this work, a natural surfactant, i.e., Sapindus mukorossi (SM) powder dissolved in water, was used to stabilize the exfoliated h-BNNS. The photograph of bulk h-BN is shown in Fig. 2(A) and the appearance of h-BN is cloud white. The scanning electron microscopy (SEM) image of the bulk h-BN confirms the platelet morphology, as shown in Fig. 2(B). The bulk sample exhibits a disk-shaped morphology with diameters ranging from 0.3–1 μm and thickness ranging from 20–110 nm (max 320 layers). The unit cell structure of bulk h-BN is shown in Fig. 2(C). The bonding between B and N atoms is covalent and strong, while the layers of atoms are held together by weak van der Waals forces. SM surfactant powder is shown in Fig. 2(D); its colour is brown, although it contains 20% of undissolved solids in water and saponin as a surfactant chemical constituent by 10% weight. Fig. 2(E) represents the structure of the surfactant, highlighting its hydrophobic and hydrophilic parts. This bulk h-BN is considered as an initial precursor for liquid exfoliation. The exfoliated h-BN nanosheet (h-BNNS) dispersion in water–SM surfactant solution is shown in Fig. 2(F) after exfoliation under the following conditions: 40% amplitude, 1 hour of exfoliation time, 100 ml sample volume, and subjected to 1500 rpm centrifugation to separate the unexfoliated h-BN from thin layers. Typical UV-vis absorption spectra of the h-BNNS dispersion, diluted 10 to 30 times with DI water, were recorded and are shown in Fig. S2.† These spectra confirm that h-BNNS has a band gap above 4 eV, consistent with the literature. The concentration of the h-BNNS in the dispersion was measured using Beer–Lambert's law (A = εCl), where A is the absorption value at 300 nm, ε – extinction coefficient (ml mg⁻¹ m⁻¹), C – concentration (mg ml⁻¹), and l – path length of the quartz cuvette (10 mm). The extinction coefficient of the SM surfactant-stabilized h-BNNS was measured using the vacuum filtration method (for more details, refer to Fig. S2†).³⁷ The value of the extinction coefficient for the exfoliated h-BNNS was determined to be 1787 ml mg⁻¹ m⁻¹ from the slope of concentration vs. A/L plot using linear fitting (Fig. S2†). The extinction coefficient value was the used to calculate the concentration of the exfoliated h-BNNS in the dispersion. The processing parameters were optimized to maximize the concentration of the SM surfactant-stabilized h-BNNS in water. These parameters included the initial h-BN concentration (C_i BN), SM surfactant concentration (C_i SM), sonication time (T), amplitude (A), and centrifugation rate (RPM). While one processing parameter was varied, the other parameters were kept constant. A detailed explanation of the optimization process is provided in ESI† Fig. S3. The maximum concentration of h-BNNS achieved is 7.2 mg ml⁻¹ at 500 RPM for 270 min, which is equal to ∼33% yield from the initial h-BN concentration (20 mg ml⁻¹). The space parameter study as a function of surfactant mass, h-BN mass, sonication time, sonication amplitude and centrifugation speed is presented in Fig. S2 and S3.† These figures indicate that there is no significant change in the quality of h-BNNS produced in water.

Fig. 2 Precursors and characterization of few layered h-BNNS using natural SM surfactant. Photograph of bulk h-BN (A), scanning electron microscopy image of bulk h-BN and its size distribution (B), crystal structure of h-BN (C), photograph of Reetha (Sapindus mukorossi) surfactant powder (D), crystal structure of the SM surfactant used (E), photograph of the exfoliated h-BNNS dispersion (1 L capacity) stabilized in SM–water medium, exhibiting transparent milky white characteristics after high-speed centrifugation at 1500 rpm (F), transmission electron microscopy image of overlapping exfoliated h-BN layers (inset: SAED pattern of hexagonal BN nanosheets) (G), histogram for lateral length distribution from a set of TEM images (H), zeta potential distribution of the h-BNNS dispersion after 30-fold dilution (I), Raman spectra of drop-cast h-BNNS on the Si/SiO₂ substrate with an optical excitation energy of 532 nm (inset: Scheme of in-plane vibrations of B and N atoms) (J), high-resolution X-ray photoelectron spectroscopic plot for the core level 1s spectrum for boron (K) and high-resolution X-ray photoelectron spectroscopic plot for the core level 1s spectrum for nitrogen (L).

The TEM image of exfoliated h-BNNS is shown in Fig. 2(G). It reveals a thin, flat, disk-shaped morphology with a transparent in nature. Using ImageJ software, 100 individual h-BNNS samples were analysed and measured and the corresponding histogram is shown in Fig. 2(H). The mean value of the lateral dimensions of these h-BNNS is ∼269 nm. The zeta potential of SM surfactant-stabilized h-BNNS in water was measured, and the corresponding zeta potential distribution is shown in Fig. 2(I). Despite the non-ionic nature of SM surfactant, we observed a negative value of zeta potential which is −40.9 mV. This is attributed to the potential lip–lip interactions and orientation effects of SM surfactant.³⁸ In our earlier report on graphene stabilization by SM surfactant,³⁵ the zeta potential was ∼−23 mV when the particle size was ∼1 micron reflecting the effects of surfactant density on h-BN. The exfoliated h-BNNS were further analyzed using Raman spectroscopy, and the resultant spectrum is shown in Fig. 2(J). A single dominant peak was observed at 1366 cm⁻¹ which is due to E_2g B–N in-plane vibration mode.³⁹ This vibration mode is analogous to the graphitic G-band, as shown in the inset of Fig. 2(J). The full width half maximum (FWHM) for this peak is ∼9.32 cm⁻¹ which indicates the reduction in the thickness of the nanosheets and production of atomically thin nanosheets. This FWHM value is comparable to that reported for thin h-BNNS.⁴⁰ These results obtained from TEM and Raman spectroscopy studies collectively confirm the few-layered nature of exfoliated h-BNNS. The proposed mechanism is that SM surfactant is a molecular non-ionic surfactant where the hydrophobic tail group attaches to the surface of the h-BNNS, while its hydrophilic head group interacts water molecules. The coverage of surfactant molecules on both surfaces of nanosheets results in the creation of steric repulsive forces between h-BN nanosheets, counteracting the attractive van der Waals forces and leading to their stabilization in water.³⁵ When the two nanosheets approach each other in liquid medium the hydrophobic tails of the surfactant molecules begin to bend, generating osmotic repulsion between the two nanosheets.⁴¹ The exfoliation conditions were optimized for achieving high yield by varying different parameters as shown in Fig. S3.† X-ray photoelectron spectroscopy (XPS) was used to determine the chemical state of B and N in the exfoliated h-BNNS. The XPS survey spectrum, shown in Fig. S3(F),† reveals boron (B) and nitrogen (N) elements as the main elements while carbon (C) and oxygen (O) represent the impurities originating from the surfactant. We measured the core level spectra of B 1s and N 1s which are shown in Fig. 2(K and L). The B 1s peak can be deconvoluted into a component corresponding to the B–N bond in h-BNNS (190.5 eV).^42,43 The N 1s peak can be deconvoluted into three components, the N–B bond in h-BNNS (398.1 eV), N–H bond (398.6 eV) and N–O bond (397.8 eV).⁴⁴ The presence of peaks corresponding to bonds other than B–N in both the B 1s and N 1s spectra can be attributed to the physical adsorption of small amounts of surfactant residues.

To estimate the mass of stabilized h-BNNS in water–SM surfactant medium as a function of their dimensions (lateral length and thickness), liquid cascading centrifugation was performed.⁴⁵ In this study, 2 g of bulk h-BN was exfoliated with 0.6 mg ml⁻¹ of SM-surfactant in water at a sonication amplitude 40% for 1 h, followed by centrifugation at 500 rpm for 270 min. The top 50% of the dispersion was collected after centrifugation and designated as the stock solution. The stock solution was then subjected to centrifugation at 1000 RPM for 90 min. After centrifugation, the top 99% of the dispersion was collected, while the sediment was used for further analysis, and labelled as 1000 rpm sediment. The 1000 rpm supernatant (top 99% dispersion) was subsequently centrifuged at 2000 rpm for 90 min. After centrifugation, the top 99% was collected and used for the subsequent centrifugation step. This centrifugal procedure was repeated till 6000 rpm, with samples labelled accordingly. The color of the dispersion changes from creamy white to almost water like color after centrifugation at 6000 rpm, indicating that most of the nanosheets have sedimented from the dispersion as shown in Fig. 3(A). The sediment samples were re-dispersed in a water–surfactant solution and their absorption spectra were recorded (as shown in Fig. 3(B)) for each centrifugal speed. The spectra exhibit characteristic features of h-BN without any impurity peaks from the surfactant. The concentration of the dispersion decreases as the centrifugal speed increases. The recovery yield is calculated by using this formula yield (%) = ((mass of exfoliated h-BN)/(initial mass of bulk h-BN)) × 100. A significant amount of h-BNNS is sedimented within 2000 rpm, with the total sediment mass reaching ∼80%. The sediment mass remains minimal beyond this point as shown in Fig. 3(C). Interestingly, centrifugation is not only a process for recovering nanomaterials from the dispersion but also a method for separating exfoliated nanosheets based on size, thereby narrowing the polydispersity index in liquid-phase exfoliation. To investigate the effect of the particle size, zeta potential, and recovery yield of exfoliated h-BNNS, centrifugation at different speeds from 500 rpm to 6000 rpm was performed. This was based on the fractional mass study to separate the sediment of the h-BNNS dispersion at a constant time of 90 min. The zeta potential of the h-BNNS sediments obtained at each centrifugation speed was measured using a Malvern/Nano ZS-90 zeta sizer. All sediment samples exhibited a monomodal zeta potential distribution. The mean of the average zeta potential (1000 rpm to 6000 rpm) was −24.22 mV. The zeta potential of the h-BNNS sediment was reduced from −30.53 ± 6.88 mV to −18.85 ± 5.9 mV when the centrifugation speed increased from 1000 RPM to 6000 rpm as shown in Fig. 3(D) and S4.† Using a Malvern zeta sizer (SZ-90), the particle size distribution of each h-BNNS sediment was measured and the average particle size values with respect to different centrifugation speeds are shown in Fig. 3(E). The particle size of h-BNNS sediment was also measured. The particle size of the dispersant was calculated based on dynamic light scattering (DLS), which measures the hydrodynamic size. The average particle size obtained from DLS measurements decreased from 309.7 nm to 115.35 nm, while the average particle size determined from TEM analysis decreased from 240 ± 77.8 nm to 38.4 ± 11.8 nm as the centrifugation speed increased from 1000 rpm to 6000 rpm, as shown in Fig. 3(E) and S4.† These results confirm that a maximum number of exfoliated nanosheets with lateral dimensions exceeding 100 nm are sedimented before the centrifugation at 3000 rpm. The Raman spectra for the sediment h-BNNS samples are shown in Fig. 3F. The average peak position of h-BNNS sediment increases from 1366.1 cm⁻¹ to 1366.6 cm⁻¹ when the centrifugation speed is increased from 1000 rpm to 5000 rpm, as shown in Fig. 3(F). This confirms that the number of layers also decreases from the few layers to bilayers or monolayers after 5000 RPM.⁴⁶ However, the change is marginal, and further investigations are required to address the polydispersity influence. Importantly after the centrifugation, the top 50% of the dispersion was taken for further analysis for uniform comparison.⁴⁷ A minimum of 40 to a maximum 170 nanosheets were measured and histograms are shown in Fig. 3(G, H) and S4.† Using log-normal distribution, the average value of the nanosheet size at different centrifugation rates was obtained and is shown in Fig. 3(G and H). Note that the diameter of the disc is considered as the size of the nanosheet. To gain a more comprehensive understanding of the vibrational properties of size-selected h-BNNS sediments, Raman spectroscopy characterization was performed.

Fig. 3 Sample recovery and characteristics of recovered h-BNNS. Photograph of the supernatant and sediment obtained from each centrifugation speed (A), UV-visible absorbance spectra of h-BNNS dispersions separated at different centrifugation speeds as a function of wavelength (B), recovered mass from the sediment and yield with respect to the initial mass (C), average zeta potential of the h-BNNS sediments (D), average particle size from dynamic light scattering (DLS) and average lateral size from TEM image analysis (E), Raman spectra of h-BNNS sediments obtained at different centrifugation speeds (F), histogram of lateral size from TEM analysis of 1k rpm sediment and its corresponding TEM image (G), and histogram of lateral size from TEM analysis of 6k rpm sediment and its corresponding TEM image inset (H).

To test the applicability of the SM surfactant for stabilizing the h-BNNS in water, we recycled the exfoliated h-BN sediment samples by adding them to fresh surfactant-dissolved DI water. The photograph of the resulting exfoliated and re-cycled h-BNNS dispersion is shown in the inset of Fig. 4(A), and the corresponding absorption spectrum of the recycled h-BNNS is shown in Fig. 4(A). The h-BNNS concentration decreased with each successive cycle due to the decrease in sediment concentration after each cycle. The results of the cycle number and h-BNNS total concentration are plotted on the first y-axis, while the concentration of h-BNNS in each cycle is plotted on the second y-axis in Fig. 4(B). The total concentration was calculated by summing the concentrations from all previous cycles. For example, the concentration of the fourth cycle includes the concentration of the first to fourth cycle. We achieved a yield of ∼89% of the exfoliated h-BNNS in water–SM surfactant medium within four cycles of the sediment recycling process. The achieved maximum yield of the exfoliated h-BNNS was compared with the literature values, as shown in Fig. S3(E) and Table S1.† Literature reports suggest that the yield of h-BNNS obtained through liquid exfoliation methods is typically less than 5%. Moreover, many of these methods rely on the use of organic solvents, which can have a detrimental impact on the environment. In contrast, we have introduced an ecofriendly natural surfactant for high-yield exfoliation in an aqueous medium.

Fig. 4 Recycle of h-BNNS. Absorbance spectra as a function of wavelength for different cycle numbers (inset: photograph of h-BN nanosheets dispersion at each recycle stage) (A), concentration and yield as a function the number of cycles (B), average particle size from dynamic light scattering (DLS) and average lateral length from TEM image analysis as a function of the number of cycles (C), TEM image of h-BNNS after the 1st cycle (D), TEM image of h-BNNS after the 2nd cycle (E), TEM image of h-BNNS after 3rd cycle (F), TEM image of h-BNNS after 4th cycle (G), histogram of lateral size from TEM of the 1st cycle (H), histogram of lateral size from TEM of the 3rd cycle (I), particle size distribution spectra from dynamic light scattering (DLS) (J), Raman spectra of h-BNNS of each recycled sample (K), and average zeta potential as a function of the number of cycles (L).

To further understand the quality of the re-cycled h-BNNS dispersions, we performed transmission electron microscopy (TEM), particle size analysis, zeta potential measurements, and Raman analysis. The size of the nanosheets was analyzed using both particle size analysis and TEM image statistics, as shown in Fig. 4(C) and S5.† The average size of the nanosheets determined by DLS ranged from 258 ± 109 nm for the first cycle to 295 ± 148 nm for the fourth cycle, as shown in Fig. 4(C and J). TEM images for the all the recycled samples are shown in Fig. 4(D to G). From the TEM images, the lateral size of the nanosheets was measured using ImageJ software. The average lateral size of the nanosheets ranged from 233 ± 96 nm to 266 ± 105 nm from the 1st cycle to 4th cycle, respectively, and the corresponding histograms are shown in Fig. 4(H, I) and S5.† When the recycle time increases, the average particle size of the nanosheets remains relatively constant. This observation suggests that during the initial sonication cycles, most of the h-BN are effectively scissored into small flakes and the exfoliated nanosheets are stabilized in the water–surfactant medium. The sediment obtained after each cycle contains a higher amount of few-layered h-BN.

The Raman spectra were acquired for the recycled samples, as shown in Fig. 4(K). For h-BN, the G peak is observed at around 1366 cm⁻¹ for all the recycled samples. The full width half maximum (FWHM) for all the recycled samples falls within a range of 11–12 cm⁻¹. These findings confirm that the quality of h-BNNS remains relatively consistent across all recycled samples. When the number of cycles increases, few layered h-BN is continuously exfoliated and stabilised in water. To understand the stabilization of the recycled samples, zeta potential measurements were performed. The zeta potential of the exfoliated h-BNNS remained relatively constant across all cycles, with an average value of ∼−29.03 ± 6.75 mV shown in Fig. 4(L). This indicates that surfactant coverage density remains relatively consistent throughout all cycles. Consequently, the stability of the exfoliated h-BNNS remains consistent across all cases.

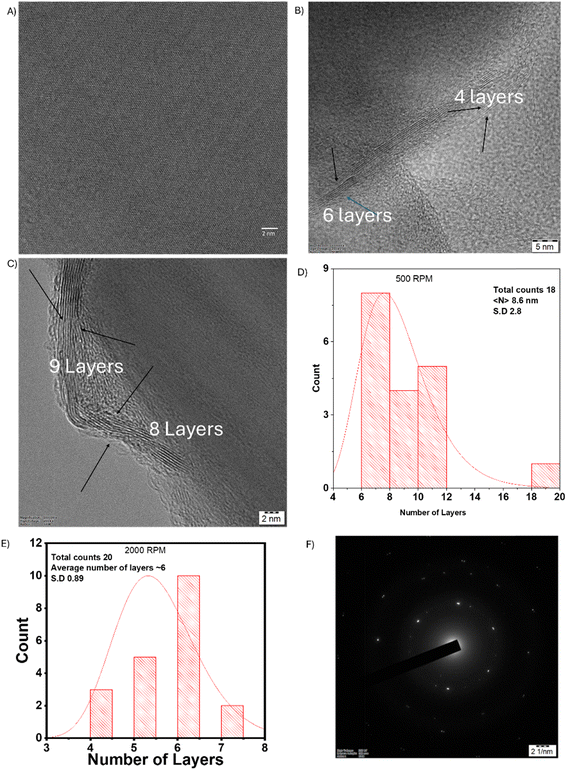
The number of layers for the exfoliated nanosheets was calculated from the TEM images of the 500 rpm sample and 2000 rpm sediment using edge image analysis. Fig. 5(A) demonstrates the absence of defects in the exfoliated h-BNNS as confirmed by high-resolution TEM imaging. The number of layers, as determined from TEM images, is shown in Fig. 5(B) and (C) for 2000 rpm and 500 rpm respectively. Fig. 5(D) and (E) represent the histograms of the number of layers measured from the TEM images. The average number of layers for the 500 rpm sample is ∼9 layers while for the 2000 rpm sample, it is ∼6 layers. These values were calculated based on measurements from a minimum of 18 to a maximum of 20 exfoliated h-BNNS sheets. The selected area electron diffraction (SAED) pattern shown in Fig. 5(F) exhibits six-fold symmetry, confirming crystalline characteristics of h-BNNS.

Fig. 5 High-resolution transmission electron microscopy (HR-TEM) imaging of h-BNNS at the edges. HR-TEM image of exfoliated h-BNNS displaying a defect-free nanosheet (A), HR-TEM image of nanosheet edges from the 500 rpm sample (B), TEM image of nanosheet edges from the 2000 rpm sample (C), histogram of the number of layers of exfoliated h-BNNS from TEM images of the 500 rpm sample (D), histogram of the number of layers of exfoliated h-BNNS from TEM images of the 2000 rpm sample (E) and SAED pattern of h-BNNS (F).

The SAED pattern confirms that the exfoliated nanosheets exhibit six-fold symmetry as shown in Fig. 5(F). To further confirm the number of layers, AFM studies were conducted on the 500 RPM sample and 2000 rpm, shown in Fig. S6.† Although the disc shaped nature of the sample is observed from AFM images, the number of layers determined from AFM analysis is erroneous due to unavoidable experimental conditions and errors due to measurement techniques. However, the number of layers from TEM image analysis is more realistic.

h-BNNS composite films and pastes were prepared using dispersion techniques and solvent casting methods, as explained in the Experimental section, by systematically varying the weight percentage of the filler. The physical appearance confirms the absence of aggregated h-BNNS clumps in the polymer matrix and shows uniform color. This is attributed to the effective dispersion of h-BNNS in the polymer, ensuring smooth flow characteristics of the thermal grease. To investigate the interaction between the nanofiller and the matrix, FTIR and Raman spectroscopy were performed on thermal grease and thermal films at different weight percentages of h-BNNS. Fig. 6(A) shows the FTIR spectra of pure silicone oil, h-BNNS, and composites with varying weight percentages of exfoliated h-BNNS. The bare silicone oil exhibits transmittance peaks at ∼2960 cm⁻¹ referred to the stretching vibrations of the methyl groups (CH_x), the small peak observed in ∼1408 cm⁻¹ is due to the asymmetric deformation of CH₃, and the symmetric deformation of Si–CH₃ resulted in a sharp peak at ∼1257 cm⁻¹. The peaks present at 1018 cm⁻¹ and 1080 cm⁻¹ are due to the Si–O–Si stretching and Si–C symmetric deformation.^48,49 The transmittance peaks for pure exfoliated h-BNNS are observed at 1360 cm⁻¹ and 776 cm⁻¹ corresponding to the B–N stretching vibration and B–N bending vibrations, respectively.^50–52 At 10 and 20 wt% of h-BNNS, the FTIR spectra remain largely unchanged, indicating the presence of both filler and matrix vibrations without shifts in wavenumbers. It signifies that the filler is merely distributed within the medium uniformly without significantly affecting the chemical environment of the matrix and filler. Fig. 6(B) shows the Raman spectra of h-BNNS modified thermal grease as a function of the weight percent of exfoliated h-BNNS, compared to the control matrix. The bare matrix exhibits a Raman shift at 2900 cm⁻¹, attributed to the vibrations of CH₄ aliphatic groups within the silicone oil matrix. The appearance of Raman shift at 1363 cm⁻¹, which is characteristic of the in-plane vibrations of B–N atoms,⁵³ confirms the presence of h-BNNS in the modified grease. It is observed that there is no significant change in the position of the Raman shift for the h-BNNS/silicone oil at different loadings, suggesting that the interaction between the filler and matrix is weak likely due to weak van der Waals forces.

Fig. 6 Investigation of interaction between the h-BNNS filler and matrix. A and B) Fourier-transform infrared spectra and Raman spectra of silicon oil-based thermal grease with different percentages of exfoliated h-BNNS and C and D) FTIR and Raman spectra of polyvinyl alcohol-based thermal film with different percentages of exfoliated h-BNNS.

Similarly, Raman and FTIR studies were performed on h-BNNS modified thermal films to investigate the interactions between the h-BNNS and the PVA matrix. Fig. 6C shows the FTIR spectra of the thermal film as a function of the filler weight percentage. The bare PVA matrix exhibits a broad and strong transmittance peak in the range of 3000–3600 cm⁻¹ attributed to OH stretching vibrations of the hydroxyl group. The low intensity peak observed at ∼2900 cm⁻¹ is due to the CH₂ symmetric stretching vibrations. The CH₂ bending vibrations of the PVA backbone result in a sharp peak at ∼1408 cm⁻¹, while the peak observed at ∼1323 cm⁻¹ is attributed to C–H deformation. The peak at ∼1083 cm⁻¹ is due to C–O stretching vibrations and the intensity of this peak is reduced with the addition of 20 wt% h-BNNS. The peak at ∼916 cm⁻¹ is attributed to the C–C stretching vibrations.⁵⁴ The C–H rocking peak for bare PVA observed at ∼831 cm⁻¹ undergoes a blue shift to ∼848 cm⁻¹ in the 20 wt% h-BNNS composite film. This shift is likely due to the hydrogen bonding interactions between the h-BNNS and PVA matrix.⁵⁵ In the h-BNNS-modified thermal films, the B–N stretching and bending vibrations, which typically appear at ∼1360 cm⁻¹ in pure h-BNNS, overlap with matrix vibrations, resulting in a broad peak in the FTIR spectra. However, the intensities of B–N bending and stretching vibrations from the h-BNNS increase sharply, and these peaks exhibit a slight red shift, which may be attributed to hydrogen bonding interactions between the filler and matrix.⁵⁶Fig. 6(D) presents the Raman spectra of PVA-based thermal films with different weight fractions of h-BNNS. Low intensity peaks observed at ∼1440 cm⁻¹ are attributed to the C–H and O–H bond bending vibrations, while the peak observed at ∼2900 cm⁻¹ is due to the C–H stretching vibrations.^57,58 Although the spectra looks somewhat noisy, the presence of in-plane vibrations of h-BNNS is confirmed by the increasing intensity of the peak at 1363 cm⁻¹ (ref. 53) with increasing filler loading. Meanwhile the peak positions of the matrix and filler remain relatively unchanged, indicating weak interactions. However, the FTIR spectra of h-BNNS modified thermal films suggest the occurrence of moderate reactions during the film formation process, possibly due to the thermal energy applied during composite preparation. Overall, FTIR and Raman spectroscopy confirm the presence and homogeneous distribution of the exfoliated h-BNNS within the base matrices, such as silicone oil and PVA polymer.

The silicone oil-based paste composite was prepared using a solvent-mixing process. Fig. 7(A) shows images of the silicone oil and as-prepared thermal grease. The cooling efficiency of the thermal pastes (pure silicone oil and the composite paste) was evaluated under real-time operating conditions to understand heat dissipation properties. To conduct this evaluation, the thermal paste was applied between an LED bulb (10 W) and a heat sink. A schematic diagram of the experimental setup is shown in Fig. 7(A). The surface temperature of the LED bulb as a function of time was recorded using an infrared thermal camera for samples with different weight percentages used as a heat spreader. The resulting temperature profiles as a function of time and the corresponding thermal images are presented in Fig. 7(B) and (C), respectively.

Fig. 7 h-BNNS modified thermal grease for thermal management. A) Bare silicone oil, h-BNNS modified thermal grease and a schematic of the experimental set-up from heat generation to heat sink to measure the surface temperature, B) surface temperature of the LED chip (10 W) as a function of glowing time using different types of heat-spreading composites (inset: photograph of heat source-sink configuration with TIM placed for IR imaging) and C) thermal infrared images of the samples at specific intervals.

The LED bulb was turned on for 10 min and the thermal images were recorded with 1 min intervals. After 10 minutes, the temperature for the pure silicone oil reached 46.85 °C, while the temperature for the 20 wt% h-BNNS composite paste was 42.75 °C, representing a decrease of ∼3 °C compared to the pure silicone oil. Notably, the temperature of the 20 wt% h-BNNS grease was nearly identical to that observed with commercial thermal grease (HY 510, Halzinye). However, a temperature reduction of ∼2 °C for the 20 wt% h-BNNS composite compared to pure silicone oil was observed starting from 20 s. The rise in temperature of the LED bulb is dependent on the heat-spreading capability of the h-BNNS/silicone oil thermal paste. It depends on the thermal transport properties of h-BNNS within the composite. Within the matrix, the h-BNNS are randomly oriented. Due to the unique structure of h-BNNS and its efficient phonon transfer in the in-plane direction of the nanosheets, the thermal conductivity (k) of the composite is significantly enhanced, facilitating more effective heat transfer. In contrast, the commercial paste, which contains 50 wt% of fillers, utilizes a hybrid filler system to achieve heat transfer.⁵⁹

The real-time demonstration was performed using a Dell laptop equipped with Intel i2 processor. The thermal paste was applied on top of the processor, as shown in Fig. S7(B).† The core temperature of the system was monitored using a built-in temperature sensor with the aid of Speccy software. During the measurement, a YouTube video was played continuously in all cases for better comparison, while no other software applications were opened. Once the video began playing, the core temperature transitioned from 70 °C and 69 °C to 75 °C and 72 °C, respectively with the surrounding atmospheric temperature at 30 °C. In the absence of any paste, the temperature quickly rises to 80 °C. This sequence is depicted within the boundaries illustrated in Fig. S7A.† It is evident that the h-BNNS based thermal compounds exhibit better cooling performance compared to commercially available thermal compounds.

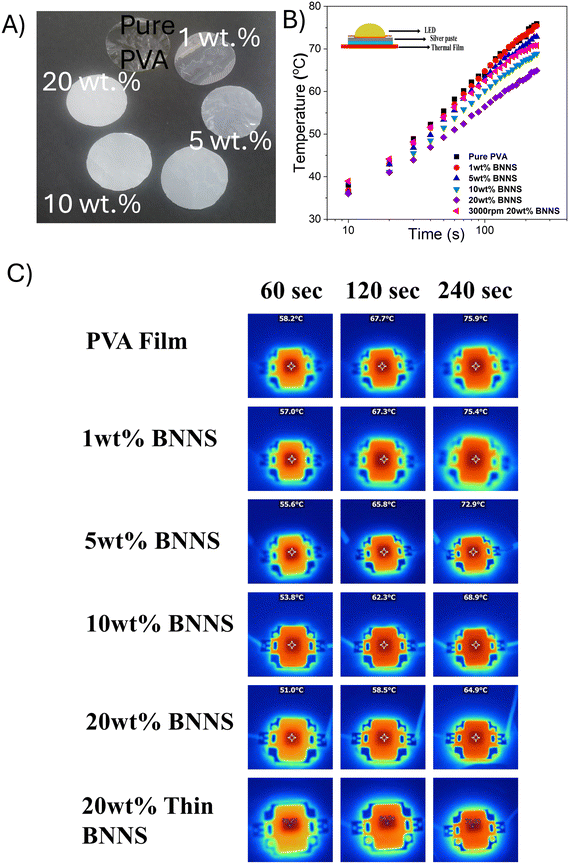
The prepared thermal films with different weight percentages are shown in Fig. 8(A). The cooling efficiency of the thermal films was evaluated under real-time operating conditions by comparing the performance of pure PVA film and the composite films. This was done to understand the heat dissipation properties of the films using a bulb (10 W). A schematic representation for this experimental setup is shown in Fig. 8(B inset). The rise in surface temperature of the LED bulb as a function of time was recorded using different wt% of the thermal films as a heat spreader, employing an infrared thermal camera. The resulting temperature profiles as a function of time and the corresponding thermal images are shown in Fig. 8(B and C) respectively. The LED bulb was turned on for 250 s. The surface temperature of the pure PVA film reached 75.9 °C while that of the 20 wt% h-BNNS film reached 64.9 °C, representing 11 °C reduction compared to the pure PVA film.¹⁵ Heat dissipation occurs primarily through downward spreading from the LED bulb to the top surface of the film. The rate of temperature rise on the LED bulb depends on the heat-spreading capability of the film, which in turn relies on the thermal transport properties of h-BNNS within the composite. At lower filler loadings, the thermal transfer within the composite is limited due to higher phonon scattering at the interfaces between the filler. However, as the h-BNNS loading increases, stronger interfacial contacts are established between the filler particles. At 20 wt% h-BNNS filler loading, efficient thermal transport between the nanosheets is facilitated by the increased interfacial contact area leading to the formation of long mean free paths and subsequent reduction in phonon scattering.⁶⁰

Fig. 8 h-BNNS modified polymer film for thermal management. A) Photograph of bare PVA film and h-BNNS embedded thermal films with different weight percentages of the filler, B) progression of the surface temperature of the LED bulb (10 W) as a function of glowing time using different types of heat-spreading composite films (inset: architecture of the device for testing) and C) thermal infrared images of the LED bulb at specific intervals.

Hexagonal boron nitride nanosheets, with their distinctive layered structure, exhibit electrically insulating and thermally conductive properties, making them a material of particular interest in thermal management. These nanosheets are promising fillers for enhancing the thermal conductivity of polymer composites. Fig. 9(A) shows the thermal conductivity of the thermal grease as a function of the weight of h-BNNS. The thermal conductivity of the thermal grease increases with increase in h-BNNS, reaching a maximum value of 0.26 W m⁻¹ K⁻¹ for 20 wt% of h-BNNS. The inset of Fig. 9(B) shows sample loading on the MTPS cell and a schematic illustration of conduction pathways through the composite at low and high filler concentrations. Despite the observed increase in thermal conductivity with higher filler loading percentages, the desired threshold is not met in the silicone oil-based thermal grease. This clustering phenomenon can elevate the volume fraction of h-BNNS, thereby counteracting the intended reduction in thermal resistance and bond line thickness.^34,59 The thermal films were prepared by incorporating h-BNNS dispersion into a PVA solution using the solvent casting method. Fig. 9B shows the thermal conductivity of the thermal film as a function of the weight percentage of h-BNNS. The thermal conductivity of the thermal film increases with increasing h-BNNS, reaching a maximum value of 0.54 W m⁻¹ K⁻¹ at 20 wt% of h-BNNS.

Fig. 9 Thermal conductivity of thermal grease and thermal film. A) Thermal conductivity of the h-BNNS embedded silicone oil-based thermal compound as a function of weight percentage of the h-BNNS filler and B) thermal conductivity of the PVA based thermal compound as a function of weight percentage of the h-BNNS filler (inset A: weight placed on thermal grease for thermal conductivity (k) measurement and inset B: scaffold of the thermal film at low and high weight percentages of the nanofiller, thermal film placed on the heating sensor in the MTPS technique).

The interfacial thermal resistance between the adjacent h-BNNS interfaces was calculated using the nonlinear model proposed by Foygel et al.⁶¹ The thermal conductivity of the composite is defined by the given equation^62,63

k = k₀(V_f − V_c)^τ

where k is the thermal conductivity of the composite, V_f is the volume fraction of the h-BNNS, k₀ is the pre-exponential factor related to the h-BNNS contribution, τ is the conductivity exponent that depends on the aspect ratio of h-BNNS and V_c is the critical volume fraction of the h-BNNS. By fitting the experimental data for the film and the paste composites shown in Fig. S7,† the value of V_c was determined to be 0.029 for the thermal film and the value of V_c is 0.017 for the thermal paste. To obtain the value of k₀ and τ, the linear form of the aforementioned equation is needed which is given below¹⁵

log k = log k₀ + τ log(V_f − V_c)

where log k is the linear independent variable of h-BNNS content in the composites, log k₀ and τ are constants. By using the linear fit in the experimental data, the values of k₀ and τ are calculated as shown in Fig. S7.† For the thermal film, the values of k₀ and τ are 79.78 and 2.11. For the thermal paste, the values of k₀ and τ are 0.387 and 0.176. Based on these values the interfacial thermal resistance between the adjacent h-BNNS was calculated using the following equation^15,62–64

where L is the length of the h-BNNS with an average length of the h-BNNS of ∼250 nm in this study. The calculated interfacial thermal resistance value for the film is 1.1 × 10⁸ K W⁻¹ and 2.1 × 10⁷ K W⁻¹ for the paste indicating more efficient phonon transport between the nanosheets within the matrix. The h-BNNS are uniformly dispersed in the PVA matrix, forming thermal conductive pathways with a nearly horizontal arrangement of h-BNNS. h-BN possesses a unique hexagonal structure, which facilitates high-speed phonon transport along the in-plane direction of h-BNNS at high speeds. This characteristic enables faster and more efficient heat transfer within the composite, thereby minimizing scattering at the interfaces.¹⁶

Conclusions

The h-BNNS are exfoliated and stabilized in an aqueous medium using natural and sustainable non-ionic SM surfactant. An ink-like concentration of 7.2 mg ml⁻¹ of exfoliated h-BN nanosheets was achieved within 1 hour of ultrasonication. The yield of exfoliated h-BNNS after four cycles of recycling reached 89%. These exfoliated nanosheets were used as fillers in the preparation of thermal compounds and films using solution mixing and solvent casting methods. The nanosheets were well-dispersed within the prepared thermal films and thermal paste composites. The dispersed nanosheets exhibited weak interactions with the polymers, as confirmed by Raman and IR spectroscopy. The maximum thermal conductivity enhancement achieved for the thermal film was ∼20% at 20 wt% h-BNNS in PVA, with the calculated thermal resistance being 1.1 × 10⁸ K W⁻¹ using Foygel's model. For thermal grease, the maximum thermal conductivity enhancement is 73% at 20 wt% of h-BNNS in a silicone oil matrix, with the calculated thermal resistance being 2.1 × 10⁷ K W⁻¹. The thermal management application for the thermal film was demonstrated using an LED bulb. Additionally, thermal paste and thermal films were applied to demonstrate real-world heat management applications. This method demonstrates a sustainable and economical approach for utilizing high-yield and natural material-stabilized h-BN nanosheets in the development of effective thermal interface materials.

Data availability

The authors declare that the data supporting the findings of this study are available in ESI† files. In addition, data sets generated during the current study are available from the corresponding author on reasonable request.

Author contributions

Vanmathi Ravichandran: data curation, methodology, writing – original draft, writing – review & editing. Eswaraiah Varrla: conceptualization, supervision, visualization, writing – review & editing, validation, funding acquisition, and investigation.

Conflicts of interest

The authors declare that there are no conflicts of interest to disclose.

Acknowledgements

The authors acknowledge the SRM IST start up grant and the Department of Science and Technology (DST), Government of India, sanction order INT/RUS/RFBR/386 for supporting this work. We are thankful to SRM IST for HR-TEM, HR-SEM, TGA, FT-IR, micro-Raman, UV-vis-NIR spectrophotometer, XRD and zeta potential facilities. We acknowledge Dr. Senthil Kumar, Mechanical Engineering, SRMIST for providing the fluke thermal camera for recording thermal images. We are thankful to i-STEM portal and Sophisticated instrumentation facility in NIT Trichy for thermal conductivity measurements (Trident). Microcube laptop service centre in Potheri is acknowledged for providing the test laptop with i2 processor for temperature measurements using inbuilt programmes using commercial thermal paste and SNT lab developed thermal grease. Research scholar Ms Vanmathi Ravichandran would like to express gratitude to SRM IST for providing PhD fellowship.

References

1. C. Yegin, N. Nagabandi, X. Feng, C. King, M. Catalano, J. K. Oh, A. J. Talib, E. A. Scholar, S. V. Verkhoturov, T. Cagin, A. V. Sokolov, M. J. Kim, K. Matin, S. Narumanchi and M. Akbulut, ACS Appl. Mater. Interfaces, 2017, 9, 10120–10127.
2. W. Dai, T. Ma, Q. Yan, J. Gao, X. Tan, L. Lv, H. Hou, Q. Wei, J. Yu, J. Wu, Y. Yao, S. Du, R. Sun, N. Jiang, Y. Wang, J. Kong, C. Wong, S. Maruyama and C.-T. Lin, ACS Nano, 2019, 13, 11561–11571.
3. Z. Barani, A. Mohammadzadeh, A. Geremew, C.-Y. Huang, D. Coleman, L. Mangolini, F. Kargar and A. A. Balandin, Adv. Funct. Mater., 2020, 30, 1904008.
4. D. Hu, H. Liu, Y. Guo, M. Yang and W. Ma, Composites, Part A, 2022, 158, 106970.
5. Y. Ruan, N. Li, C. Liu, L. Chen, S. Zhang and Z. Wang, New J. Chem., 2020, 44, 18823–18830.
6. X. Xu, J. Chen, J. Zhou and B. Li, Adv. Mater., 2018, 30, 1705544.
7. J. Ying, X. Tan, L. Lv, X. Wang, J. Gao, Q. Yan, H. Ma, K. Nishimura, H. Li, J. Yu, T.-H. Liu, R. Xiang, R. Sun, N. Jiang, C. Wong, S. Maruyama, C.-T. Lin and W. Dai, ACS Nano, 2021, 15, 12922–12934.
8. R. Zou, F. Liu, N. Hu, H. Ning, Y. Gong, S. Wang, K. Huang, X. Jiang, C. Xu, S. Fu, Y. Li and C. Yan, ACS Appl. Mater. Interfaces, 2020, 12, 57391–57400.
9. D. Liu, C. Ma, H. Chi, S. Li, P. Zhang and P. Dai, RSC Adv., 2020, 10, 42584–42595.
10. F. Wang, X. Zeng, Y. Yao, R. Sun, J. Xu and C.-P. Wong, Sci. Rep., 2016, 6, 19394.
11. C. Dai, Y. Tanaka, M. Awais, X. Chen and A. Paramane, ACS Appl. Electron. Mater., 2021, 3, 5345–5354.
12. Y. Lin, Y. Jia, G. Alva and G. Fang, Renewable Sustainable Energy Rev., 2018, 82, 2730–2742.
13. Q. Cai, D. Scullion, W. Gan, A. Falin, P. Cizek, S. Liu, J. H. Edgar, R. Liu, B. C. C. Cowie, E. J. G. Santos and L. H. Li, Phys. Rev. Lett., 2020, 125, 085902.
14. X. Kong, Y. Chen, R. Yang, Y. Wang, Z. Zhang, M. Li, H. Chen, L. Li, P. Gong, J. Zhang, K. Xu, Y. Cao, T. Cai, Q. Yan, W. Dai, X. Wu, C.-T. Lin, K. Nishimura, Z. Pan, N. Jiang and J. Yu, Composites, Part B, 2024, 271, 111164.
15. Q. Yan, W. Dai, J. Gao, X. Tan, L. Lv, J. Ying, X. Lu, J. Lu, Y. Yao, Q. Wei, R. Sun, J. Yu, N. Jiang, D. Chen, C.-P. Wong, R. Xiang, S. Maruyama and C.-T. Lin, ACS Nano, 2021, 15, 6489–6498.
16. K. K. Kim, A. Hsu, X. Jia, S. M. Kim, Y. Shi, M. Dresselhaus, T. Palacios and J. Kong, ACS Nano, 2012, 6, 8583–8590.
17. J. Taha-Tijerina, T. N. Narayanan, G. Gao, M. Rohde, D. A. Tsentalovich, M. Pasquali and P. M. Ajayan, ACS Nano, 2012, 6, 1214–1220.
18. Y. Lin and J. W. Connell, Nanoscale, 2012, 4, 6908–6939.
19. C. Wang, J. Guo, L. Dong, A. Aiyiti, X. Xu and B. Li, Sci. Rep., 2016, 6, 25334.
20. E. Subbotina, F. Ram, S. V. Dvinskikh, L. A. Berglund and P. Olsén, Nat. Commun., 2022, 13, 6924.
21. Y. Zhou, L. Xu, M. Liu, Z. Qi, W. Wang, J. Zhu, S. Chen, K. Yu, Y. Su, B. Ding, L. Qiu and H.-M. Cheng, ACS Nano, 2022, 16, 10179–10187.
22. B. Shen, T.-W. Zhang, Y.-C. Yin, Z.-X. Zhu, L.-L. Lu, C. Ma, F. Zhou and H.-B. Yao, Chem. Commun., 2019, 55, 7703–7706.
23. L. Li, Y. Zhang, R. Zhang, Z. Han, H. Dong, G. Yu, D. Geng and H. Y. Yang, Nanoscale, 2021, 13, 17310–17317.
24. K. Sharma and N. K. Puri, J. Electrochem. Soc., 2021, 168, 056512.
25. W. Zhou, Y. Zhang, J. Wang, H. Li, W. Xu, B. Li, L. Chen and Q. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 46767–46778.
26. Q. Shan, X. Shi, X. Wang and W. Wu, Chem. Eng. Process., 2021, 169, 108602.
27. N. Mittal, G. Kedawat, Kanika, S. Gupta and B. Kumar Gupta, ChemistrySelect, 2020, 5, 12564–12569.
28. K. R. Paton, E. Varrla, C. Backes, R. J. Smith, U. Khan, A. O'Neill, C. Boland, M. Lotya, O. M. Istrate, P. King, T. Higgins, S. Barwich, P. May, P. Puczkarski, I. Ahmed, M. Moebius, H. Pettersson, E. Long, J. Coelho, S. E. O'Brien, E. K. McGuire, B. M. Sanchez, G. S. Duesberg, N. McEvoy, T. J. Pennycook, C. Downing, A. Crossley, V. Nicolosi and J. N. Coleman, Nat. Mater., 2014, 13, 624–630.
29. Y. Wang, C. C. Mayorga-Martinez, X. Chia, Z. Sofer and M. Pumera, Nanoscale, 2018, 10, 7298–7303.
30. H. Wang, X. Su, T. Song, Z. Li, Y. Zhao, H. Lou and J. Wang, Appl. Surf. Sci., 2019, 488, 656–661.
31. J. P. Gwinn and R. L. Webb, Microelectron. J., 2003, 34, 215–222.
32. W. Dai, Y. Wang, M. Li, L. Chen, Q. Yan, J. Yu, N. Jiang and C.-T. Lin, Adv. Mater., 2024, 36(37), 2311335.
33. A. Bar-Cohen, K. Matin and S. Narumanchi, J. Electron. Packag., 2015, 137, 040803.
34. S. Naghibi, F. Kargar, D. Wright, C. Y. T. Huang, A. Mohammadzadeh, Z. Barani, R. Salgado and A. A. Balandin, Adv. Electron. Mater., 2020, 6, 1901303.
35. A. Sethurajaperumal and E. Varrla, ACS Sustainable Chem. Eng., 2022, 10, 14746–14760.
36. H. Ye, T. Lu, C. Xu, B. Han, N. Meng and L. Xu, Macromol. Chem. Phys., 2018, 219, 1700482.
37. J. N. Coleman, M. Lotya, A. O'Neill, S. D. Bergin, P. J. King, U. Khan, K. Young, A. Gaucher, S. De, R. J. Smith, I. V. Shvets, S. K. Arora, G. Stanton, H.-Y. Kim, K. Lee, G. T. Kim, G. S. Duesberg, T. Hallam, J. J. Boland, J. J. Wang, J. F. Donegan, J. C. Grunlan, G. Moriarty, A. Shmeliov, R. J. Nicholls, J. M. Perkins, E. M. Grieveson, K. Theuwissen, D. W. McComb, P. D. Nellist and V. Nicolosi, Science, 2011, 331, 568–571.
38. B. Gupta and H. S. S. R. Matte, ACS Appl. Electron. Mater., 2019, 1, 2130–2139.
39. R. V. Gorbachev, I. Riaz, R. R. Nair, R. Jalil, L. Britnell, B. D. Belle, E. W. Hill, K. S. Novoselov, K. Watanabe, T. Taniguchi, A. K. Geim and P. Blake, Small, 2011, 7, 465–468.
40. L. Song, L. Ci, H. Lu, P. B. Sorokin, C. Jin, J. Ni, A. G. Kvashnin, D. G. Kvashnin, J. Lou, B. I. Yakobson and P. M. Ajayan, Nano Lett., 2010, 10, 3209–3215.
41. N. Pal, A. Verma, K. Ojha and A. Mandal, J. Mol. Liq., 2020, 310, 113193.
42. Z. Wang, Y. Zhu, H. Yu and Z. Li, Mater. Charact., 2020, 168, 110508.
43. M. W. Akhtar, J. S. Kim, M. A. Memon and M. M. Baloch, Compos. Sci. Technol., 2020, 195, 108183.
44. Y. Chen, X. Wang, C. Yu, J. Ding, C. Deng and H. Zhu, Sci. Rep., 2019, 9, 16338.
45. A. Griffin, A. Harvey, B. Cunningham, D. Scullion, T. Tian, C.-J. Shih, M. Gruening, J. F. Donegan, E. J. G. Santos, C. Backes and J. N. Coleman, Chem. Mater., 2018, 30, 1998–2005.
46. M. Krečmarová, D. Andres-Penares, L. Fekete, P. Ashcheulov, A. Molina-Sánchez, R. Canet-Albiach, I. Gregora, V. Mortet, J. P. Martínez-Pastor and J. F. Sánchez-Royo, Nanomaterials, 2019, 9, 1047.
47. F. Goni, A. Chemelli and F. Uhlig, Nanomaterials, 2021, 11(12), 3253.
48. L. Mandrile, A. M. Giovannozzi, F. Pennecchi, A. Saverino, C. Lobascio and A. M. Rossi, Anal. Methods, 2015, 7, 2813–2821.
49. C. H. Kim, C.-K. Joo, H. J. Chun, B. R. Yoo, D. I. Noh and Y. B. Shim, Appl. Surf. Sci., 2012, 262, 146–152.
50. Z. Wang, G. Meng, L. Wang, L. Tian, S. Chen, G. Wu, B. Kong and Y. Cheng, Sci. Rep., 2021, 11, 1–11.
51. D. Lee, B. Lee, K. H. Park, H. J. Ryu, S. Jeon and S. H. Hong, Nano Lett., 2015, 15, 1238–1244.
52. J. Wie and J. Kim, Polymers, 2021, 13(3), 456.
53. Y. Yao, Z. Lin, Z. Li, X. Song, K.-S. Moon and C.-p. Wong, J. Mater. Chem., 2012, 22, 13494–13499.
54. E. F. d. Reis, F. S. Campos, A. P. Lage, R. C. Leite, L. G. Heneine, W. L. Vasconcelos, Z. I. P. Lobato and H. S. Mansur, Mater. Res., 2006, 9, 185–191.
55. N. Ahad, E. Saion and E. Gharibshahi, J. Nanomater., 2012, 2012, 94.
56. P. Sahoo, A. Chaturvedi, U. Ramamurty and H. S. S. R. Matte, Nanotechnology, 2023, 34, 095703.
57. C.-C. Yang, S.-J. Chiu, K.-T. Lee, W.-C. Chien, C.-T. Lin and C.-A. Huang, J. Power Sources, 2008, 184, 44–51.
58. T. Morishita and N. Takahashi, RSC Adv., 2017, 7, 36450–36459.
59. W. Yu, H. Xie, L. Yin, J. Zhao, L. Xia and L. Chen, Int. J. Therm. Sci., 2015, 91, 76–82.
60. F. Jiang, N. Song, R. Ouyang and P. Ding, ACS Appl. Mater. Interfaces, 2021, 13, 7556–7566.
61. M. Foygel, et al. , Phys. Rev. B, 2005, 71(10), 104201.
62. J. Hu, Y. Huang, Y. Yao, G. Pan, J. Sun, X. Zeng, R. Sun, J.-B. Xu, B. Song and C.-P. Wong, ACS Appl. Mater. Interfaces, 2017, 9, 13544–13553.
63. X. Zeng, Y. Yao, Z. Gong, F. Wang, R. Sun, J. Xu and C.-P. Wong, Small, 2015, 11, 6205–6213.
64. Y. Huang, J. Hu, Y. Yao, X. Zeng, J. Sun, G. Pan, R. Sun, J.-B. Xu and C.-P. Wong, Adv. Mater. Interfaces, 2017, 4, 1700446.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lf00338a

---