3D-printed micro-pore evaporator for increasing concentration of analytes in aqueous solutions

Abstract

To address the detection limit challenges of analytical instruments at low concentrations, this study explores the development of a concentrator, fabricated via micro-3D printing technology, relying on solvent evaporation through micro-pores. The operating temperature can be as low as room temperature, allowing for compatibility with biomolecules that are sensitive to high temperatures. Moreover, the device is suitable for processing small sample volumes ranging from hundreds to tens of microliters. There are three designs of the hydrophilic biocompatible polymer tube, each featuring micro-pores with diameters of 30, 50 and 70 μm, spaced at distances of 150, 250 and 350 μm, respectively. All designs have the same total length of 16 mm and identical contact surface area. The tube is surrounded by an outer tube for a sweeping gas at a flow between 20 and 100 mL min⁻¹ for evaporation rate control. Theoretical calculations and experimental data were used to quantify device's performance and capabilities. Experiments conducted with deionized water and with aqueous glucose solutions demonstrate the device's capability to achieve up to a 10-fold concentration increase. The study also addresses potential issues such as analyte loss and the influence of various parameters like sweeping gas flow rates and liquid feeding rates on the concentration process. This work demonstrates the potential of the micro-3D printed device as a reliable and efficient method for sample concentration, critical for enhancing detection sensitivities for various applications such as bioassays and biosensors.

---

1. Introduction

In analytical chemistry and biochemical processing, concentrating analytes can improve detection or measurement sensitivity and make sample preparation easier. Preconcentration is essential under certain circumstances to enhance the detectability and accuracy of analytical measurements, especially when dealing with samples that contain very low concentrations of the target analyte.¹ Recent advances in microfluidic technologies have facilitated the development of miniaturized devices that enable efficient sample concentration. Various methods have been employed to increase analyte concentration via evaporation, usually by increasing the surface-to-volume ratio to enhance the evaporation rate. Complete evaporation is one way to concentrate analytes. Some researchers achieve this by evaporating the liquid entirely and analyzing the dried residue left behind. Su et al. evaporated a droplet containing bacillus bacteria and polystyrene beads,² achieving particle enrichment through complete evaporation based on the coffee ring effect.³ Shao et al. evaporated droplets of fluorescent material on various surfaces and demonstrated that superhydrophobic surfaces retain less fluorescent material after the droplets have fully evaporated, highlighting how evaporation influences analyte deposition.⁴ Similarly, recent studies have shown that as droplets evaporate or dissolve, the shrinking volume concentrates solutes, accelerates reaction rates, and amplifies electrochemical signals – revealing the critical role of droplet dynamics in enhancing analytical sensitivity and reaction kinetics.^5–7 Similar to droplet evaporation, Kachel et al. conducted open-channel evaporation and studied the relationship between the evaporation rate and the channel dimensions.⁸ Additionally, paper-based analyte concentration systems utilize complete evaporation to achieve enrichment, and their low cost, ease of use, and portability contribute to their popularity.^9,10 Since complete evaporation removes the solvent entirely, it prevents the use of analytical instruments to measure analyte concentration in solutions. Additionally, for continuous measurements – where the goal is to track real-time changes in solution concentration rather than just measuring initial and final states – complete evaporation is not a viable option, as it disrupts ongoing analysis and alters the analyte's physical and chemical properties.¹¹ Therefore, alternative methods to complete evaporation are desirable.

Centrifugation is also an efficient and widely used method for analyte concentration, but instead of removing the solvent completely, it concentrates analytes by leveraging density differences.¹² Centrifugation offers the ability to handle large sample volumes. However, its efficiency depends on the sample type, as highly diluted solutions may require prolonged centrifugation or additional steps for effective concentration. Moreover, centrifugation is a batch process, making it unsuitable for applications that require continuous monitoring of analyte concentration.

Various technological solutions have been proposed to achieve continuous, efficient evaporation-based concentration, notably the introduction of evaporator–concentrator.¹ An evaporator–concentrator is a device designed to enhance the concentration of analytes in a liquid via solvent evaporation process, which involves removing the solvent, typically water, thereby increasing the concentration of the less volatile analytes. Such ability proves particularly valuable in applications that require high sensitivity in chemical analysis, as concentrating the analyte can significantly improve detection limits. Output from the evaporator–concentrator can be effectively integrated with sophisticated detection methods like spectrophotometric detection to enhance analytical performance.¹³ This integration proves particularly beneficial in the field where rapid and sensitive detection of low-concentration analytes is needed such as biomedical diagnostics and environmental monitoring.

The typical structure of an evaporator is a ‘sandwich’ configuration where a porous membrane is positioned between a liquid channel and a gas channel. The membrane functions as a separator that blocks liquid solution due to surface tension but allows vapor molecules to pass through. The properties of this separator, such as pore size, hole structure, and material, directly influence the efficiency of the evaporation process. For example, devices employing micro-pillar arrays^14–18 or porous polymer membranes^19–21 have proven effective in controlling the evaporation process, thereby enabling precise management of concentration. Some researchers model it as a series of micro-pores,²² which block liquid due to surface tension and capillary action, but permit vapor to diffuse. Practically, many membranes have a complex structure with multiple micro- or nano-sized holes, rather than being simple straight channels connecting one side to the other. This complexity makes membranes difficult to model mathematically. Moreover, membranes can become clogged due to the accumulation of particles or biofilms over time, particularly when processing biological samples or impure solutions.²³ Additionally, membranes can degrade chemically or physically over time and potentially due to exposure to strong solvents, high temperatures, or UV light.²⁴

To overcome the abovementioned problems associated with membranes, researchers have designed and fabricated well defined micro-pore structures. Zhang et al. fabricated a series of micro-holes, each 2 μm in diameter and 250 nm in thickness using silicon nitride as the separator.²⁵ However, these tiny holes still exhibit some of the inherent shortcomings of membranes, such as the accumulation of unwanted material within the pores, which reduces the efficiency and lifespan of the structure.

Micro 3D printing allows for precise and customized fabrication of tiny microfluidic chips. High-resolution printing techniques, including liquid-crystal display (LCD) 3D printing, have achieved resolutions as low as 18–50 μm, making it possible to create detailed microfluidic channels and structures needed for applications like organ-on-a-chip devices and biological tests.²⁶ Micro 3D printing facilitates rapid design iteration and prototyping, enabling researchers to swiftly test and refine their designs, which is beneficial for developing complex microfluidic systems for diverse applications.²⁷ While such high-resolution techniques are powerful, leveraging more accessible and cost-effective hardware remains a significant and active area of research. Recent studies have demonstrated the feasibility of using low-cost fused deposition modeling (FDM) 3D printers for fabricating microscale features, expanding the accessibility of microfabrication. For example, researchers have achieved functional microchannels and micropores using standard FDM systems, despite the inherent limitations in resolution.^28,29 These efforts highlight the potential of using low-cost methods to produce functional micro-pore evaporator–concentrators and related microfluidic chips.

In this study, we introduce a micro-pore evaporator–concentrator fabricated via micro-3D printing using a hydrophilic and biocompatible material. The evaporator operates at low temperatures, which are favorable for biomolecules, and handles micro-volume samples as small as tens to hundreds of microliters. The design consists of an inner tube (inner diameter 400 μm, outer diameter: 1000 μm) with micro-holes through which the solution is injected, and an outer tube (inner diameter 1.9 mm, outer diameter 2.9 mm) through which drying gas is flown. Three types of evaporators are designed and fabricated, each with micro-pores of either 30, 50, or 70 μm diameter positioned on the inner tube. The theoretical evaporation rate from the meniscus shape of a single micro-pore is calculated, and a method employing a relative humidity sensor for estimating total evaporation over time is demonstrated. Evaporation and concentration experiments were conducted with deionized water and with aqueous glucose solutions which were analyzed using infrared spectroscopy. We achieved controlled evaporation, attaining a concentration factor of up to 10-fold with an accuracy of ±5%, under conditions of 40 °C, a liquid flow rate of 1 μL min⁻¹, and a nitrogen gas flow rate of 50 mL min⁻¹. Additionally, the effect of pressure on liquid leakage through pores of each evaporator was studied and tested. The micro-pore evaporator–concentrator has been shown to enrich a water-soluble small molecule; however, its applicability can be extended to proteins, microparticles, bacteria and more.

2. Microfluidic concentrator design

The concept of our design is based on maximizing the evaporation by using micro-pores all around the outer surface of the inner tube. This is unique compared to the previous designs where evaporation is only in one direction (i.e. in 2D) as with membranes^19–21 or on two sides, as with microfabricated microfluidic chips.^14–16 Fig. 1a shows the overall device with inlets for liquid sample and for gas, an outlet for the concentrated sample and an outlet for the humidified gas. Fig. 1b displays a cross-section of the 3D computer-aided design (CAD) model, showing arrows indicating evaporation in all dimensions. To realize this multidirectional evaporation concept, the geometry shown in Fig. 1 was optimized within the resolution constraints of micro 3D printing to achieve a balance between capillary liquid retention, vapor permeability, and integration with standard fluidic components.

Fig. 1 (a) 3D computer-aided design of the micro-pore evaporator (50 μm pore evaporator as example). Diameter of the micro-pores (Φ) = 50 μm. Distance between adjacent micro-pores (d) = 250 μm. Effective length of the porous portion (s) = 10 mm. Total length (L) = 16 mm. (b) Cross section of the design showing arrows of evaporation through the micro-pores in all directions from the inner tube into the outer tube where a gas is flown. Thickness of the inner liquid tube (m) = 300 μm.

It is well understood that the extent of the liquid–gas interface area significantly influences the efficiency of the evaporation process.²⁵ The total interface surface area (where liquid is exposed to the gas) is calculated by summing up the areas of all the micro-pores. In our unique 3D design, the sweeping gas entirely surrounds the liquid channel, maximizing the contact area for evaporation via forced convection. Three different pore diameters – 30, 50, and 70 μm – were fabricated, and tested while the total length and interface area for evaporation were kept constant.

It is crucial to ensure that the micro-pores are neither too large nor too small, as their size directly impacts both liquid retention and evaporation efficiency. If the pores are too large, liquid leakage may occur due to insufficient capillary pressure. Conversely, if the pores are too small, the liquid–gas interface area may be reduced, limiting the evaporation rate. The inner liquid tube containing the micro-pores serves as a barrier to liquid flow as long as the liquid pressure remains below the capillary penetration pressure. If the liquid pressure exceeds this threshold, the liquid will undesirably penetrate through the pores. Smaller pores create a higher capillary pressure barrier, preventing liquid from passing through unless sufficient external pressure is applied. However, higher liquid feeding rates, increased tube length, and additional system components (e.g., analytical instruments) all contribute to greater flow pressure, necessitating smaller pores to prevent unintended leakage. Larger pores allow liquid to pass through more easily, limiting the choices of liquid flow rate and flow pressure. However, they also provide a larger liquid–gas interface, promoting evaporation. This creates a tradeoff: while larger pores enhance evaporation efficiency, they also increase the risk of liquid leakage. Therefore, optimizing pore size is essential to balance evaporation performance with liquid flow stability, ensuring efficient and controlled operation of the system.

Table 1 summarizes the design parameters of the micro-pore evaporator, including pore diameter (Φ), pore spacing (d), effective length (s), total length (L), and interface area (A). Three designs feature increasing pore diameters of 30, 50, and 70 μm, respectively, with corresponding increases in pore spacing from 150 to 350 μm. The effective length (10 mm) and total length (16 mm) remain constant across all designs. As the pore diameter increases, the interface area slightly increases from 1.238 mm² to 1.262 mm². The internal volume of the liquid paths is the same for all devices, measuring 1.34 μL.

Table 1 Summary of the micro-pore evaporator design parameters

	Pore diameter Φ (μm)	Distance between pores d (μm)	Effective length s (mm)	Total length L (mm)	Interface area A (mm^2)	Internal volume (μL)
I	30	150	10	16	1.238	1.34
II	50	250	10	16	1.241	1.34
III	70	350	10	16	1.262	1.34

---

The length of the segment housing the micro-pores is termed here as ‘effective length’, represented by the letter s in the image. The pore diameter, the distance between adjacent pores, and the effective length collectively determine the total interface area. These dimensions are influenced and constrained by the limitations of the manufacturing process. The pore diameter and the distance between adjacent pores are dictated by the resolution of the micro 3D printer, which sets a limit on the minimum achievable pore size. If the effective length s, the total length L, or the thickness of the liquid tube m are too large relative to the mechanical stability of the printed material, shrinkage and bending may occur due to uneven stress distribution and material deformation during the printing and curing processes.

The design is a single part that does not require assembly and can function directly after 3D printing. Being a concentric-shaped cylinder with intricate structures on the inner tube, micro-3D printing surpasses traditional mechanical manufacturing methods. Additionally, the integration of fine microstructures enhances the precision and efficiency of the evaporation process. While the concentrator device inherits the typical limitations of additive manufacturing – such as material constraints, size limitations, and potential deformation – the design has been carefully designed to mitigate these challenges. The result is a compact, high-precision device that enables controlled evaporation with high reproducibility, demonstrating the advantages of 3D printing in microfluidic applications.

3. Materials and methods

3.1. Evaporator–concentrator system

The device was fabricated using a 3D printer (S230, Boston Micro Fabrication) with a BMF MED resin,³⁰ which is a rigid, amber-colored, hydrophilic, and biocompatible material. Fig. 2a shows a photograph of the device next to a ruler. Fig. 2b shows the image of the inner tube, and the individual micro-pores. It can be seen that the pore shapes slightly deviate from a perfect circle.

Fig. 2 (a) Photograph of the fabricated device next to a one cent coin. (b) Photograph of the inner tube showing the micro-pores under a microscope. (c) CT images displaying both the front (left) and cross-section (right) views of the 50 μm micro-pore evaporator, highlighting the micro-pores and the channel within. The scale bar at the top right of the front view applies to both images. (d) Schematic of the experimental system for evaporator–concentrator testing.

To study the morphology of the device, a micro computed-tomography (CT) scanner, Zeiss Xradia 620, was used. Image of a 50 μm pore evaporator is shown in Fig. 2c. The morphology study is mainly concentrated on the pore diameter, pore circularity, distance between pores, and the shape of the pore channel. Table 2 summarizes the pore geometry distribution as measured from CT images, for all three different pore-size evaporators. Statistical analysis was performed using ImageJ on the CT image data. Detailed information on the CT image analysis, including the formula for circularity calculation, is provided in Section S1 of the ESI,† with Fig. S1 illustrating the processing steps used to obtain the statistical measurements.

Table 2 Comparison of design and actual measurements for three evaporators, detailing the diameter and circularity of each micro-pore, as well as the distance between adjacent micro-pores

	Design diameter (μm)	Actual diameter (μm)	Design distance (μm)	Actual distance (μm)	Circularity
I	30	25.4 ± 11.7	150	143.7 ± 4.3	0.65 ± 0.27
II	50	49.0 ± 4.4	250	242.3 ± 7.3	0.79 ± 0.16
III	70	72.6 ± 5.1	350	344.2 ± 5.5	0.71 ± 0.17

---

As shown in Table 2, the measured pore diameters are close to the design values but exhibit a relatively large variation within the 95% confidence interval. The actual center-to-center distance between adjacent pores are slightly smaller than the design distance but remains within an acceptable tolerance for the application. The printed pores exhibit a circularity of ranging from 0.65 to 0.79. Compared to larger pores, the 30 μm pores show greater variability in both measured diameter and circularity. This increased variation in smaller pores may be attributed to limitations in the fabrication process, such as resolution constraints during printing. Additionally, the cross-section view (image on the right) in Fig. 2c shows that the micro-pore channels are straight, with no obstacles in the middle. This morphological information of the micro-pores is crucial for mathematical modeling and simulations of evaporation through the pores.

Fig. 2d shows the schematic of the experimental setup used for device testing. The setup includes a syringe pump (Pump 11 Elite, Harvard Apparatus) connected to the evaporator, and an outlet of the evaporator leads to a sealed collection well positioned in ice to minimize evaporation during collection. The device's heating system comprises a polyimide heater plate attached to the underside of the box containing the device, along with an on–off temperature controller (W1209). During the evaporation experiments, the temperature inside the heating box is maintained within 0.2 degrees Celsius of the target temperature. Pure nitrogen gas (Airgas, ultra-high purity: >99.999%) is used as the sweeping gas, which removes vapor during evaporation. A humidity sensor (SHT41, Sensirion) is positioned at the outlet to continuously monitor the relative humidity of the outlet gas, serving as a measure of the evaporation process.

3.2. Evaporator functionality: water evaporation and glucose concentration

To obtain a preliminary understanding of the evaporation rate of this device, deionized water was used in evaporation experiments. By continuously injecting 1000 μL of water at a constant rate and measuring the weight of the remaining liquid after evaporation, the evaporated volume can be determined. The water evaporation experiment is also used to calculate the evaporation ratio and concentration factor under specific system parameters. In this section, the dry nitrogen flow rate ranges from 20 to 100 mL min⁻¹, liquid flow rate ranges from 1 to 10 μL min⁻¹, and temperature ranges from 20 to 40 °C.

Following initial tests with water, the next phase focuses on analyzing glucose concentration increase after evaporation. Various concentrations of glucose solutions are produced through serial dilution. Glucose is first weighed and dissolved in deionized water to prepare a 100 mmol L⁻¹ solution. This glucose solution is then diluted to concentrations of 10, 20, and 40 mmol L⁻¹ by mixing with deionized water, which are subsequently used for calibration. 10 mmol L⁻¹ glucose solution was used at the inlet of the concentrator.

The evaporation process of aqueous glucose solution follows the same protocol as that of deionized water. Glucose concentration was measured using a Fourier transform infrared (FTIR) spectrometer (iS50, ThermoFisher) in transmittance mode using a liquid flow cell with a fixed path length of 50 μm. Each recorded spectrum, ranging from 650 to 4000 cm⁻¹, is an average of 256 individual scans, obtained at a resolution of 0.482 cm⁻¹. The flow cell is rinsed with deionized water for 1 minute after each use to prevent cross contamination between measurements. Spectra are collected in a single-beam mode. Calculations of absorbance values are subsequently performed. The concentration of glucose samples can be calculated from absorbance at specific peaks compared to a calibration curve, given that the peak height is a linear function of concentration.³¹

3.3. Leakage pressure measurement

The pressure at which liquid begins to leak through the pores was measured using a pressure sensor (uPS0800-T116, LabSmith, USA). The pressure was generated by continuously injecting liquid at a constant flow rate into a fused silica capillary tubing with a 75.5 μm inner diameter (1068160775, Polymicro Technologies, USA). The experimental setup involved connecting the syringe pump, pressure sensor, evaporator, and capillary tubing in sequence, with the liquid flow rate set to a constant 1 μL min⁻¹.

4. Theoretical analysis of the evaporator–concentrator

The control of the evaporation rate is important to the operation of the evaporator–concentrator to achieve a desired concentration of solutes in aqueous solutions. The evaporation rate is influenced by factors such as the diffusion coefficient of water vapor, liquid–gas interface area, and the vapor pressure gradient between the liquid surface and the surrounding gas. This gradient is typically driven by the humidity of the sweeping gas. In this study, dry nitrogen is used as the sweeping gas therefore humidity gradient is present. Instead, the gradient is influenced by the flow rate of the gas, which affects the transport of water vapor away from the liquid surface. The aim of the theoretical calculations is to provide insights into the relationship between the evaporation rate and key system parameters, enabling control of the evaporation.

Fig. 3 presents a schematic of the micro-pore evaporator, illustrating both liquid retention in a single hydrophilic pore and the overall evaporation process, where water escapes through micro-pores while the non-volatile analytes are concentrated.

Fig. 3 (a) Schematic of capillary-driven liquid retention in a single hydrophilic micro-pore. Φ represents the diameter of the micro-pore, and θ represents the contact angle. (b) General schematic of a micro-pore evaporator.

The inner channel with micro-pores prevents liquid passage while permitting vapor diffusion through the pores. The water mass rate balance of the evaporator is represented by eqn (1):

ṁ_in = ṁ_out + ṁ_evp (1)

where ṁ_in and ṁ_out denote the rates of liquid water in and out, respectively, and ṁ_evp represents the evaporated water vapor.

Fig. 3a shows a schematic of a cross-section of a hydrophilic single micro-pore. The surface area increases due to the meniscus, compared to a flat liquid–gas interface, and the meniscus evaporation is governed by the Kelvin equation:^32,33

where P_M is the equilibrium vapor pressure over the meniscus curved surface, P_F is the equilibrium vapor pressure over a flat surface of the same liquid, γ is the surface tension of the liquid (in this case, 72.8 × 10⁻³ N m⁻¹), V_m is the molar volume of the liquid (pure water V_m = 18 cm³ mol⁻¹), θ is the contact angle, approximately 50 degrees between water and the material, Φ is the diameter of the pore, R is the ideal gas constant, and T is the temperature in Kelvin. To estimate the contact angle, a small drop of water was placed on the surface of the material, and a photograph was taken. The contact angle was then measured from the image. This data was also verified by the manufacturer's datasheet.³⁰ Using these values, it has been calculated that P_M = 1.00003P_F.

A simplified version of the meniscus evaporation rate ṁ_M equation can be related to the diffusion coefficient J, the total area of the micro-pores A, and the water vapor pressure difference from the meniscus surface to the sweeping gas, as defined in eqn (3),³⁴ which is derived from Fick's first law.

ṁ_M = JA(P_M − P_amb) (3)

When dry gas (such as dry nitrogen) is used as the sweeping gas, there is no water vapor in the gas, so the ambient pressure of water vapor, P_amb, is approximately 0. Therefore, the meniscus evaporation rate ṁ_M can be related to the flat surface evaporation ṁ_F.²⁵ For the detailed derivation process, please refer to Section S2 in the ESI.†

The vapor pressure difference between the meniscus and flat surface calculated using the Kelvin equation is minimal in this case. However, based on eqn (2), the difference becomes more noticeable as the pore size decreases. For nano sized pores, the vapor pressure over the curved meniscus surface can be several percent higher than that over a flat surface. For example, when the pore diameter is 50 nm, the meniscus vapor pressure is 3% higher than that of a flat surface. Additionally, decreasing the contact angle, using a liquid with higher surface tension and molar volume, or operating at a lower temperature will further amplify the vapor pressure difference.

A higher vapor pressure difference enhances the evaporation rate by increasing the driving force for mass transfer, which is beneficial for rapid preconcentration. However, excessively high vapor pressure differences may lead to instability at the meniscus, potential pore drying, or inconsistent evaporation rates. Conversely, a lower vapor pressure difference results in more stable and controlled evaporation but may limit the overall efficiency of the process. The optimal balance depends on the desired evaporation rate, system stability, and the ability to maintain a continuous liquid supply to the meniscus.

A relative humidity sensor can be used to estimate evaporation over time. By monitoring the relative humidity level at the outlet of the evaporator, we can estimate the total evaporation. The mass of water evaporated from the micro-pores is equal to the mass of water vapor carried away by the sweeping gas at the outlet, based on the water vapor mass balance. Therefore, we first calibrate the water vapor mass flow rate using different sweeping gas flow rates, then calculate the evaporation ratio (ER). The evaporation ratio is defined as the amount of liquid evaporated relative to the total amount of liquid injected, i.e. .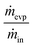

The theoretical evaporation ratio can be calculated from relative humidity calibration curve using eqn (4):³⁵

where C is a constant empirical correction factor, RH is the relative humidity increase from inlet to outlet of the sweeping gas, M_W and M_G are the molar masses of water vapor and sweeping gas, respectively, P_W,SAT and P_G are the saturation pressures of water vapor at a specific temperature and pressure of the sweeping gas, ṁ_G and ṁ_S are the mass flow rates of sweeping gas and liquid solution, calculated from volumetric flow rates and their respective densities.

The correction factor C is set to 0.75 and is determined experimentally by calibrating the system at a controlled flow rate of 10 μL min⁻¹. At this high flow rate, the total experimental duration is shorter under a fixed total volume condition. This reduces the exposure time to environmental fluctuations, making the system less susceptible to external influences such as ambient humidity changes or temperature variations. This makes it easier to isolate the inherent discrepancies between theoretical predictions and experimental results, which stem from factors like sensor inaccuracies, non-ideal airflow, and experimental setup limitations. The humidity sensor may introduce response delays, leading to overestimated relative humidity and consequently a higher calculated evaporation coefficient. Additionally, the theoretical model assumes uniform airflow and complete mixing, whereas experimental conditions may involve localized variations in vapor concentration and flow distribution. Furthermore, deviations in micro-pore geometry, partial clogging, or contamination could reduce the effective evaporation rate, contributing to the discrepancy between theoretical and experimental values.

The concentration factor (CF) represents the ratio of the analyte's concentration after evaporation to its original concentration. The concentration factor can be calculated from the evaporation ratio using eqn (5), assuming the solution's density does not vary significantly before and after the evaporation process.

5. Results and discussion

5.1. Evaporation calculation based on measured relative humidity

Fig. 4 illustrates the relative humidity and minimum liquid feeding rate at different dry nitrogen gas flow rates of 20 to 100 mL min⁻¹ at 30 °C using the 50 μm micro-pore evaporator. The liquid flow rate is 2 μL min⁻¹. The evaporation process can be modeled as a mixture process: dry nitrogen gas and evaporated water vapor are mixed in the micro-3D printed channel, and the mixture is expelled by the continuous gas flow. The error bars for relative humidity calibration in Fig. 4a are based on three measurements and fall within a consistent range, primarily due to the humidity in the surrounding environment. This indicates that the method is highly repeatable and reliable for theoretical evaporation calculations.

Fig. 4 Experimentally determined (a) relative humidity and (b) liquid flow rate for various dry nitrogen gas flow rates range from 20 to 100 mL min⁻¹ at 30 °C. The liquid flow rate is 2 μL min⁻¹.

As observed in Fig. 4a, the relative humidity increases as the dry nitrogen gas flow rate decreases. This can be explained by the fact that with a slower gas flow rate, more water evaporates within a fixed amount of time and volume, resulting in the sweeping gas carrying more water vapor. As a result, the relative humidity is higher. Conversely, with a faster gas flow rate, less water has time to evaporate, so the gas carries less water vapor, and the mixture exhibits characteristics closer to dry nitrogen, leading to lower relative humidity.

The minimum liquid flow rate represents the lowest volumetric flow rate of the liquid solution at a specific temperature and sweeping gas flow rate. Since the evaporation rate is influenced by the sweeping gas flow rate, each gas flow rate has a corresponding minimum liquid flow rate. Intuitively, a higher gas flow rate results in a higher evaporation ratio, which also sets the minimum liquid flow rate. Fig. 4b illustrates the minimum liquid flow rate for each dry nitrogen gas flow rate at 30 °C. The usable range is above the curve, while the area below indicating complete evaporation. For instance, at 30 °C with a dry nitrogen gas flow rate set to 60 mL min⁻¹, the minimum liquid flow rate is 0.99 μL min⁻¹. If the liquid flow rate is set less than 0.99 μL min⁻¹, the injected liquid will completely evaporate before reaching the outlet. To prevent the analyte from drying out completely during the concentration process, the infusion flow rate must be higher than the minimum liquid flow rate.

5.2. Impact of experimental variables on evaporation: liquid flow, gas flow, and temperature

In a fixed-dimension evaporator, three critical independent variables are the liquid sample flow rate, sweeping gas flow rate, and temperature, while the relative humidity is consistently recorded. Fig. 5 illustrates how liquid flow rates, temperature and sweeping gas flow rate influence the evaporation process. Increasing the liquid flow rate decreases the residence time of liquid in the evaporation area, thus reducing evaporation. Moreover, an increase in temperature raises the saturation pressure of water vapor, thereby enhancing the pressure gradient between the sweeping gas and the liquid–gas interface, ultimately resulting in faster evaporation. Furthermore, a higher sweeping gas flow rate enhances vapor removal, thereby increasing the vapor pressure difference between the gas channel and the liquid surface, which in turn accelerates evaporation. The highest evaporation ratio in Fig. 5a is 0.899, occurring at a 1.0 μL min⁻¹ liquid flow rate, 40 °C, and at a gas flow rate of 50 mL min⁻¹, where the corresponding concentration factor is 9.9 calculated using eqn (5). Under these conditions, the residence time of the solution within the evaporation section is approximately 7 minutes.

Fig. 5 (a) Evaporation ratio and concentration factor as a function of temperature for various liquid flow rates, with a constant sweeping gas flow rate of 50 mL min⁻¹. (b) Evaporation ratio and concentration factor for different sweeping gas flow rates, with a constant temperature of 30 °C and liquid flow rate of 1.0 μL min⁻¹.

In this work, the evaporation variables are varied between specific ranges. Temperatures up to 40 °C because the evaporation process accelerates at higher temperatures, and this temperature will not damage certain analytes, such as most proteins, from denaturation.³⁶ The liquid flow rate ranges from 1 to 10 μL min⁻¹ to balance efficient evaporation without risking excessive pressure that could cause leaks. Higher flow rates can lead to increased pressure within the system, potentially causing unintended leakage. The gas flow rate ranges from 20 to 100 mL min⁻¹, which is well-suited for achieving a concentration factor between 1 and 10-fold or higher. This range allows for adjustments based on specific requirements, given the limited liquid flow rates and experimental temperatures.

The results can be used to optimize the operating conditions for maximum efficiency allowing one to determine the optimal combination of temperature and flow rates that yields the desired evaporation ratio. For instance, to concentrate a sample that can tolerate a maximum temperature of 40 °C, requiring an evaporation ratio of at least 0.2, Fig. 5a suggests using conditions of 30 °C, a 2.5 μL min⁻¹ liquid flow rate, and a 50 mL min⁻¹ gas flow rate.

5.3. Theoretical and experimental evaporation results comparison

Fig. 6 presents both theoretical and experimental values of the evaporation ratio and concentration factor from the deionized water evaporation experiment. The theoretical evaporation ratio and concentration factor are calculated using eqn (4) and (5), respectively.

Fig. 6 Deionized water evaporation and corresponding concentration factors under experimental conditions of 30 °C temperature and a 50 mL min⁻¹ dry nitrogen gas flow rate. (a) Evaporation ratio versus liquid flow rate from 1 to 10 μL min⁻¹. (b) Concentration factor versus liquid flow rate from 1 to 10 μL min⁻¹.

The experimental evaporation ratios and concentration factors closely match theoretical calculations, particularly at higher liquid flow rates. This confirms the theory's close approximation of the actual evaporation process. The theoretical calculations were based on eqn (4), which considers factors such as the saturation pressure of water vapor and mass flow rates. Key assumptions made include constant liquid and gas flow rates and uniform temperature distribution throughout the microfluidic chip during the evaporation process.

The shapes of Fig. 6a and b are similar, except at lower liquid flow rates, where the concentration factor changes more rapidly than the evaporation ratio. This difference is evident through the derivative of eqn (5), which shows that as the evaporation ratio increases, the concentration factor experiences a faster rate of change. At lower flow rates, larger error bars in the experimental data, as well as a greater discrepancy between the experimental results and theoretical predictions, are observed. This is primarily because at lower flow rates, a longer time is required to pass the same total volume of liquid, potentially increasing uncertainties during evaporation. Additionally, approximations in experimental values may accumulate, leading to greater errors over time.

5.4. Effect of micro-pore diameter on evaporation performance

In order to determine the effect of the pore size, the evaporation ratio was measured for the three micro-pore diameters of 30, 50 and 70 μm. Fig. 7 shows evaporation ratio as a function of liquid flow rate for the three diameters. It can be seen that the micro-pore diameters have little to no influence on evaporation performance in the evaporators, for which the total effective evaporation length and total interface area are kept constant. As shown in eqn (3), the mass flow rate of the evaporation process is a function of the diffusion coefficient and total area. Since these parameters are kept constant for all three evaporators, it is reasonable that they exhibit similar evaporation performance. This suggests that the variation in micro-pore diameter has little impact on the evaporation ratio under the tested conditions. Detailed calculations for the diffusion coefficient can be found in Section S3 in the ESI.†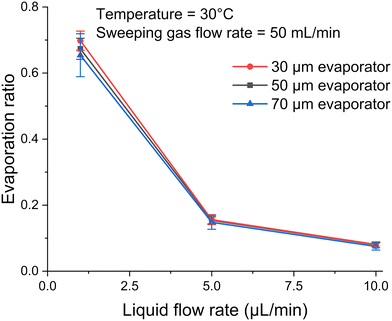

Fig. 7 Deionized water evaporation versus liquid flow rate from 1 to 10 μL min⁻¹ for three different pore diameters under the condition of 30 °C and 50 mL min⁻¹ of sweeping gas flow rate.

5.5. Example: increasing the concentration of an aqueous glucose solution

Fig. 8 presents the FTIR results for four known aqueous glucose calibration solutions at different concentrations and three unknown aqueous glucose samples. Fig. 8a shows distinct peaks at specific wavenumbers (1036, 1080, 1108, and 1152 cm⁻¹). These peaks, characteristic of glucose, are used to quantify its concentration. Peak height is calculated by subtracting a baseline from the maximum near the specific wavenumber. Baseline is selected to be the average absorbance around 1190 cm⁻¹, where most spectra are flat and overlap. As shown in Fig. 8b, the absorbance peak height at 1036 cm⁻¹ was used to demonstrate the relationship between concentration and absorbance. The peak corresponds to a characteristic vibrational mode of glucose molecules, specifically related to the C–OH stretching or C–O stretching vibrations. The linear fit equation with a high coefficient of determination (R² > 0.99) in Fig. 8b indicate a strong linear relationship between peak height and glucose concentration, as expected from the Beer–Lambert law.³¹

Fig. 8 (a) FTIR absorbance spectra of glucose at concentrations of 10, 20, 40, and 100 mmol L⁻¹, together with those of three unknown samples (sample 1, sample 2, and sample 3). (b) Calibration curve derived from peak heights at 1036 cm⁻¹ for known glucose concentrations (10, 20, 40, and 100 mmol L⁻¹), including peak height comparisons for three unknown samples.

An aqueous glucose concentration of 10 mmol L⁻¹ was prepared. After passing though the concentrator, the concentration of glucose in the outlet was measured using FTIR. Sample 1 was obtained for conditions of 2.5 μL min⁻¹ sample flow rate, 30 °C, and a 50 mL min⁻¹ dry nitrogen flow rate. Sample 2 was obtained for conditions of 1 μL min⁻¹ sample flow rate, 30 °C, and a 50 mL min⁻¹ dry nitrogen flow rate. Sample 3 was obtained for conditions of 1 μL min⁻¹ sample flow rate, 40 °C, and a 50 mL min⁻¹ dry nitrogen flow rate. These three samples are also plotted on the calibration curve in Fig. 8b, allowing estimation of their concentrations. From the linear fit of the known concentrations of aqueous glucose solutions, the glucose concentration of unknown samples in the outlet can be estimated, as 13.0 mmol L⁻¹, 25.1 mmol L⁻¹, and 88.0 mmol L⁻¹, respectively. Using these results, the concentration factors were calculated by dividing the outlet concentrations by the initial concentrations; the concentration factors for sample 1, sample 2, and sample 3 were 1.30, 2.51, and 8.80, respectively.

Table 3 summarizes concentration factors for the three samples derived using different methods: theoretical analysis, the reduction in weight of deionized water and the increase in concentration of a glucose solution. There are slight differences in the concentration factors between the three methods. The theoretical value is the highest because, under ideal conditions, evaporation can reach its maximum theoretical limit. The concentration measured by FTIR is the lowest and is considered to be the most accurate representation of the actual concentration. This is because FTIR directly measures the concentration, rather than relying on calculations, making it more reliable. The concentration factor from the deionized water experiment falls between the theoretical and FTIR values, suggesting that the underlying assumptions are somewhat reflective of reality. Nonetheless, assuming a constant density during the evaporation process could introduce significant bias, especially at higher concentration factors. This is because a higher concentration factor results from greater evaporation, which leads to more substantial changes in density.

Table 3 Summary of concentration factors (CFs) for the three samples derived using different methods: theoretical calculation, predictions from deionized water experiment and FTIR measurements

Sample details				Concentration factor (CF)
Glucose concentration [mmol L^−1]	Concentrator temperature [°C]	Dry nitrogen flow rate [mL min^−1]	Liquid flow rate [μL min^−1]	Theoretical CF	CF from deionized water experiment	CF from FTIR
10	30	50	2.5	1.39	1.35 ± 0.01	1.30 ± 0.02
10	30	50	1	3.40	2.68 ± 0.14	2.51 ± 0.05
10	40	50	1	12.1	9.90 ± 0.21	8.80 ± 0.07

---

The deionized water experiment and FTIR measurements are generally consistent with each other and closely align with theoretical predictions, particularly for lower concentration factors. The small error bars suggest high precision in both the deionized water experiment and FTIR measurements. The concentration factor differences between FTIR and deionized water experiments are 4%, 6%, and 11% for samples 1, 2, and 3, respectively. This trend suggests that the concentration factor measurements are more consistent at lower values.

5.6. Effect of pressure on liquid leakage through pores

When the pressure inside the channel becomes too high, liquid will leak through the micro-pores. The leakage pressure is the sum of the pressure required to pass through the pore entrance and the pressure drop as the liquid flows through the pore channel.

P_t = P_p + P_c (6)

where P_t represents the total leakage pressure required for liquid to leak through a pore, P_p represents the capillary pressure caused by surface tension, and P_c accounts for the pressure buildup along the same pore channel.

The pressure difference across a curved liquid interface can be calculated using the Young–Laplace equation:³⁷

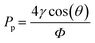where γ is the surface tension of the liquid, θ is the contact angle, and Φ is the pore diameter. For a pore with a diameter of 50 μm, the pressure is calculated to be 3.7 × 10³ Pa.

The pressure drop as the liquid flows through the pore channel can be calculated using the Hagen–Poiseuille equation:³⁸

where μ represents the dynamic viscosity of water (in this case, 7.98 × 10⁻⁴ kg m⁻¹ s⁻¹), L is the channel length (300 μm for the pore channel length, as indicated by letter m in Fig. 1b), and Q is the liquid flow rate. When the liquid flow rate Q is set to 1 μL min⁻¹, the pressure drop along the channel is calculated to be 26 Pa, significantly lower than the capillary pressure. Therefore, for the 50 μm evaporator, the theoretical leakage pressure P_t is calculated to be 3.73 × 10³ Pa.

This theoretical value is then compared with the experimental value. Theoretically, the pressure will first accumulate due to flow into the narrow tube, then decrease when leakage occurs. The highest pressure observed is considered the leakage pressure. These results are summarized in Table 4 with the theoretically calculated pressure.

Table 4 Summary of theoretical and experimental leakage pressures for evaporators with three different pore diameters

Pore diameter (μm)	Theoretical leakage pressure (Pa)	Experimental leakage pressure (Pa)
30	6.37 × 10^3	(6.80 ± 0.25) × 10^3
50	3.73 × 10^3	(3.97 ± 0.11) × 10^3
70	2.65 × 10^3	(2.95 ± 0.15) × 10^3

---

Although pore diameter does not significantly influence evaporation performance, a smaller pore diameter will definitely increase the required leakage pressure. As shown in Table 4, the leakage pressure significantly increases as the pore diameter decreases from 50 to 30 μm. As indicated by eqn (6) and (7), as the pore diameter decreases, the pressure increases more rapidly.

The experimental pressure is slightly higher than the theoretical leakage pressure, mainly because real-world conditions do not meet all theoretical assumptions. For example, in theory, the surfaces of the tubes and channels are assumed to be smooth. In reality, however, microscopic roughness can significantly alter curvature and pressure predictions. Additionally, the pressure sensor is placed far from the evaporator end, resulting in a slightly higher pressure due to tubing and connections.

A higher leakage pressure will enhance the stability of the evaporation concentration system and expand its potential application scenarios. During the evaporation process, any fluctuation will increase the pressure in the channel, and thus, higher pressure limit will better protect the experiment from failure. Additionally, significant pressure will be added to the system if researchers wish to place an analytical instrument downstream of the evaporator. For example, if a liquid flow cell with a pressure restriction of 4 kPa is added to the evaporation system, only the 30 μm evaporator would be suitable, as this pressure would cause leakage in evaporators with larger pore diameters. Therefore, a higher leakage pressure limit will enable the evaporator to function in more scenarios.

Flow rate Q is the parameter most commonly altered in microfluidics experiments. As indicated by eqn (8), a larger flow rate will result in a higher pressure. Although in previous calculations for the 50 μm evaporator, the pressure drop in the micro-pore channel (26 Pa) is negligible compared to the capillary pressure (3700 Pa), as the flow rate increases, the channel pressure will also increase linearly. If the flow rate is set to 10 μL min⁻¹, the pressure will be 10 times higher, and this pressure must also be taken into consideration.

In the evaporation experiments, the 3D-printed tube with micro-pores effectively separated liquid and gas across all three pore diameters (30, 50, and 70 μm).

6. Design considerations

Our results indicate that, within the tested range of pore diameters of 30–70 μm, the size of individual pores has little effect on evaporation performance when the total surface area is kept constant (as discussed in section 5.4). However, pore diameter significantly affects leakage pressure (as discussed in section 5.6). For example, the 30 μm pore evaporator can withstand more than twice the pressure of the 70 μm version. This suggests that, when prioritizing evaporation efficiency and device stability, smaller pore sizes are preferable – assuming the overall geometry and surface area remain the same. On the other hand, systems operating under high internal pressures (e.g., those integrated with analytical instruments) may face leakage risks with larger pores. It is also important to note that smaller pores are more challenging to fabricate, especially using methods like 3D printing. Therefore, selecting the optimal pore size requires balancing evaporation performance, pressure tolerance, and manufacturability.

There are several advantages of this additive manufactured micro-pore evaporator–concentrator. First, the setup is easy to design and fabricate. Traditional microfluidics fabrication methods typically require complex multilayer CAD designs and diverse manufacturing processes. Using micro-3D printing technology, researchers can easily design and print 3D microfluidic channels like standard 3D printed parts. Second, the fabrication's repeatability allows for easy adjustment of the evaporator's dimensions, particularly the sizes and shapes of the micro-pores. The additive manufacturing process ensures that the printed micro-pore diameters fall within an acceptable range. Additionally, with known micro-pore dimensions and channel materials, researchers can more easily and accurately model and simulate the evaporation process mathematically. Second, the evaporator–concentrator is designed to operate at low temperatures (<40 °C) to prevent the degradation of sensitive analytes, especially biomolecules. This low-temperature operation ensures that the structural integrity and functionality of proteins, nucleic acids, and other delicate biomolecules are preserved during the concentration process. This feature makes the device particularly suitable for concentrating biological samples where maintaining the activity and stability of the analytes is essential.

Although 3D printing enables rapid and customizable fabrication of microfluidic devices, it still presents several limitations. First, the intrinsic resolution of conventional 3D printers limits the minimum attainable feature size; in this study, the smallest achievable pore diameter was approximately 10 μm. Second, a trade-off exists between the minimum feature size and the overall device dimensions – fabricating finer structures typically limits the maximum printable length or volume. For example, fabricating evaporator pores as small as 30 μm limited the total device length to approximately 25 mm. Third, the selection of printable materials imposes functional constraints. Certain polymers may absorb analytes or undergo chemical interactions with solvents, potentially compromising analyte recovery and device integrity. Although such effects were not observed in this study, they remain important considerations for the broader application of 3D printing in microfluidic device development.

Another limitation of this concept is that it only functions effectively when the solvent is less volatile than the analyte. As previously mentioned in the glucose concentration experiment with an aqueous solution, the solvent, deionized water, evaporates more easily than glucose, resulting in glucose enrichment. However, the evaporator cannot be used to concentrate analytes such as ethanol or acetone in aqueous solutions, as these analytes evaporate more easily under normal conditions than water.

The loss of analyte is a critical issue in the concentration process, as we aim to retain as much analyte as possible while increasing its concentration. Analyte loss can occur in several ways: for an aqueous-soluble analyte like glucose, crystallization can occur in the evaporator channel or in the collection well when the evaporation rate exceeds the liquid solution feeding rate. For aqueous-insoluble analytes like polystyrene beads, they may become lodged in the micro-pores or in connection tubes with minimal inner diameters. This issue can be effectively addressed by carefully controlling the evaporation ratio for aqueous-soluble analytes and matching the micro-pore size to the desired particle dimensions for aqueous-insoluble analytes.

In addition to crystallization and physical entrapment, potential chemical and physical interactions between analytes or solvents and the 3D-printed structures must be carefully considered. Adsorption of analytes onto the surfaces of the printed device can lead to analyte loss, which is particularly problematic at trace concentrations. The surface chemistry, hydrophilicity, and roughness of the printed material all influence adsorption behavior. Moreover, although the current device is designed for aqueous systems, its broader applicability requires consideration of the effects of non-aqueous solvents. Certain organic solvents may swell, degrade, or chemically react with the 3D-printed polymer, potentially causing material leakage, structural failure, or contamination. These limitations constrain the device's compatibility with solvent systems such as alcohols, ketones, or aromatic hydrocarbons, highlighting the importance of using solvent-resistant and biocompatible materials.

To evaluate the potential adsorption of the analyte (glucose) on the walls of 3D-printed material, the concentration factors obtained from deionized water tests and glucose tests, under identical conditions, are compared. As shown in Table 3, FTIR-derived concentration factors for glucose closely align with those from deionized water, particularly under the first two conditions, where the values fall within experimental uncertainty (1.30 vs. 1.35; 2.51 vs. 2.68). Under the third condition (40 °C), a slightly larger discrepancy (8.80 vs. 9.90) was observed. This discrepancy might be attributed to the higher glucose concentration, which reduces the number of free water molecules available for evaporation, leading to a lower concentration factor measured by FTIR. The consistent increase in this deviation with rising glucose concentration suggests a systematic trend that may warrant further investigation into the molecular-level interactions affecting evaporation efficiency. Nevertheless, our findings suggest minimal glucose loss after analyte concentration and indicate that adsorption effects are negligible for this specific analyte. However, device's compatibility with other analytes, particularly electrically charged, needs to be further explored, thus future studies will investigate the behavior of both positively and negatively charged analytes to assess potential surface interactions and further validate the device's broader applicability.

A fundamental assumption for calculating the concentration factor shown in Fig. 6b is that the solution's density remains relatively constant before and after the evaporation process. This assumption holds in most cases where the evaporation ratio or concentration factor is not excessively high, as under these conditions, the solvent predominates, maintaining the solution's characteristics with a reasonable and controllable increase in concentration. However, when the evaporation ratio is very high (>0.95), and sufficient solvent remains to prevent the precipitation of the analyte's crystals (if aqueous-soluble), the solution's density will change significantly, leading to substantial bias in calculating the concentration factor.

The concentration factor can be increased by stimulating evaporation using the parameters mentioned previously. Effective methods include increasing the gas flow rate, raising the temperature, and decreasing the liquid flow rate. However, the parameters required to achieve a specific concentration factor need to be carefully tested against the theoretical values. Additionally, it is important to control the temperature to prevent the analyte from being destroyed and to ensure that the solvent evaporates faster than the analyte. It is reasonable to estimate that the concentration factor can be improved to over fifty-fold.

Another limitation of the theoretical framework is that the calibration is only valid for a limited range of sweeping gas flow rates, specifically 20 to 100 mL min⁻¹, as noted in previous sections. However, at times the liquid solution feeding rate is limited, and even the lowest gas flow rate specified in the calibration curve can completely evaporate the solution, resulting in unwanted analyte loss. For example, researchers studying traumatic brain injury (TBI) typically utilize a consistently low flow rate of 0.3 μL min⁻¹.³⁹ In such cases, the sweeping gas flow rate should be reduced to about 5 mL min⁻¹, at which point the calibration curve ceases to be linear. This occurs because at very low gas flow rates, the gas's capacity to carry water vapor is weakened, allowing other factors, such as temperature, to dominate the evaporation process. Consequently, the relative humidity at the channel's outlet can be too high—approximately 100%—for humidity sensors to accurately detect and report. Therefore, this can lead to significantly inflated and unrealistic concentration factors from theoretical humidity calculations.

Compared to other evaporators, the micro-3D printed evaporator–concentrator operates at low temperatures and is suitable for micro-volume biomolecular samples. Fornells et al. used membrane-assisted evaporation with a liquid flow rate greater than 10 μL min⁻¹, achieving a concentration factor up to 27-fold at a temperature above 50 °C.¹⁹ Tseng et al. achieved around a 5-fold concentration using a total sample volume of 10 mL at a temperature of 100 °C.²⁰ Although some of these evaporators achieved higher concentration factors, their approach cannot be applied to temperature-sensitive biomolecules or extremely small sample volumes due to their substantial total length. Additionally, commercial tubular membranes typically feature larger inner diameters, which result in a lower surface area-to-volume ratio – an unfavorable condition that can reduce evaporation efficiency. Our design addresses this by using a smaller diameter and maximizing surface area between liquid and air, thus improving evaporation performance. This compact geometry is especially critical for biomedical applications such as monitoring TBI patients, where the sampling rate from brain microdialysis probes can be as low as 0.3 μL min⁻¹. In such cases, minimizing the size of the device is essential. The micro-3D printed evaporator strikes a good balance among the concentration factor, the operating temperature and micro-volume-biomolecular compatibility. Nonetheless, the micro-3D printed evaporator maintains reasonable repeatability, underscoring its reliability as a precise and robust concentrator.

7. Conclusions

The research presented in this paper focuses on the development, validation, and application of a novel micro-pore evaporator–concentrator fabricated through micro-3D printing technology. Utilizing a hydrophilic, biocompatible material, the device is engineered to optimize the evaporation process, thereby enhancing the concentration of analytes within an aqueous solution by manipulating factors such as temperature and sweeping gas flow rates. Key experiments with deionized water and glucose validate the theoretical models and highlight the device's capacity to achieve significant concentration increases, crucial for sensitive analytical detections in biomedical diagnostics and environmental monitoring. The evaporator has been validated to function effectively at temperatures below 40 degrees Celsius, concentrating micro-volume biomolecules as low as hundreds of microliters. The study addresses the challenges of analyte loss during the concentration process and evaluates the effects of various operational parameters. The findings confirm the device's efficacy and repeatability, positioning it as a robust tool for future applications in biochemical analysis. Future work will focus on studying evaporation across various evaporator dimensions and experimental variables. Precision and repeatability can be further enhanced by carefully adjusting the variables. Furthermore, the application of the evaporator–concentrator will be expanded to include studies involving both aqueous-soluble and aqueous-insoluble analytes.

Data availability

Data for this article are available at Texas Data Repository at [https://doi.org/10.18738/T8/UMO2GA].

Conflicts of interest

The authors declare that Tanya Hutter and Yufeng Su are inventors on a patent application related to the work described in the manuscript. This intellectual property is owned by The University of Texas at Austin.

Acknowledgements

The work was partially funded by the Texas Innovation Center at The University of Texas at Austin. The authors gratefully acknowledge Boston Micro Fabrication (BMF) for assistance with sample fabrication.

References

1. E. Fornells, E. F. Hilder and M. C. Breadmore, Preconcentration by Solvent Removal: Techniques and Applications, Anal. Bioanal. Chem., 2019, 411(9), 1715–1727,  DOI:10.1007/s00216-018-1530-8.
2. Y. Su and T. Hutter, Imaging of Microparticles Separated by the Coffee Ring Effect via Infrared Photothermal Spectroscopy, in Optica Imaging Congress (3D, COSI, DH, FLatOptics, IS, pcAOP), Optica Publishing Group, Boston, Massachusetts, 2023, p. ITh3E.2,  DOI:10.1364/ISA.2023.ITh3E.2.
3. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Capillary Flow as the Cause of Ring Stains from Dried Liquid Drops, Nature, 1997, 389(6653), 827–829,  DOI:10.1038/39827.
4. F. Shao, T. W. Ng, O. W. Liew, J. Fu and T. Sridhar, Evaporative Preconcentration and Cryopreservation of Fluorescent Analytes Using Superhydrophobic Surfaces, Soft Matter, 2012, 8(13), 3563,  10.1039/c2sm07127d.
5. A. Rana, C. Renault and J. E. Dick, Understanding Dynamic Voltammetry in a Dissolving Microdroplet, Analyst, 2024, 149(15), 3939–3950,  10.1039/D4AN00299G.
6. S. Neugebauer, S. R. Evans, Z. P. Aguilar, M. Mosbach, I. Fritsch and W. Schuhmann, Analysis in Ultrasmall Volumes: Microdispensing of Picoliter Droplets and Analysis without Protection from Evaporation, Anal. Chem., 2004, 76(2), 458–463,  DOI:10.1021/ac0346860.
7. C. J. Chen and E. R. Williams, The Role of Analyte Concentration in Accelerated Reaction Rates in Evaporating Droplets, Chem. Sci., 2023, 14(18), 4704–4713,  10.1039/D3SC00259D.
8. S. Kachel, Y. Zhou, P. Scharfer, C. Vrančić, W. Petrich and W. Schabel, Evaporation from Open Microchannel Grooves, Lab Chip, 2014, 14(4), 771–778,  10.1039/C3LC50892G.
9. S. Y. Wong, M. Cabodi, J. Rolland and C. M. Klapperich, Evaporative Concentration on a Paper-Based Device to Concentrate Analytes in a Biological Fluid, Anal. Chem., 2014, 86(24), 11981–11985,  DOI:10.1021/ac503751a.
10. J. Cortez and C. Pasquini, Ring-Oven Based Preconcentration Technique for Microanalysis: Simultaneous Determination of Na, Fe, and Cu in Fuel Ethanol by Laser Induced Breakdown Spectroscopy, Anal. Chem., 2013, 85(3), 1547–1554,  DOI:10.1021/ac302755h.
11. A. Kimble, C. Ratanski and T. A. Kremer, Chemical Changes Over Time Associated with Protein Drying, Biomed. Instrum. Technol., 2023, 57(2), 52–57,  DOI:10.2345/0899-8205-57.2.52.
12. C. Suwanvecho, L. K. Krčmová and F. Švec, Centrifugal-Assisted Sample Preparation Techniques: Innovations and Applications in Bioanalysis, TrAC, Trends Anal. Chem., 2024, 180, 117909,  DOI:10.1016/j.trac.2024.117909.
13. J. Paluch, J. Kozak, M. Wieczorek, M. Woźniakiewicz, M. Gołąb, E. Półtorak, S. Kalinowski and P. Kościelniak, Novel Approach to Sample Preconcentration by Solvent Evaporation in Flow Analysis, Molecules, 2020, 25(8), 1886,  DOI:10.3390/molecules25081886.
14. J.-W. Choi, S. M. Hosseini Hashemi, D. Erickson and D. Psaltis, A Micropillar Array for Sample Concentration via In-Plane Evaporation, Biomicrofluidics, 2014, 8(4), 044108,  DOI:10.1063/1.4890943.
15. J. Cheng, J. Shao, Y. Ye, Y. Zhao, C. Huang, L. Wang and M. Li, Microfluidic Preconcentration Chip with Self-Assembled Chemical Modified Surface for Trace Carbonyl Compounds Detection, Sensors, 2018, 18(12), 4402,  DOI:10.3390/s18124402.
16. Z. Zhao, X. Ma, K. Zhao, X. Chen, S. Li and S. Yang, Experimental Investigation of the Characteristics of Thermosyphon with Flat Evaporator and Micro-Pillar Arrays, Int. J. Therm. Sci., 2020, 158, 106541,  DOI:10.1016/j.ijthermalsci.2020.106541.
17. G. Yuncu, Y. Akkus and Z. Dursunkaya, Elliptical Pillars for the Thermal Performance Enhancement of Micro-Structured Evaporators, Int. Commun. Heat Mass Transfer, 2023, 148, 107036,  DOI:10.1016/j.icheatmasstransfer.2023.107036.
18. A. Constantinou, F. Ghiotto, K. F. Lam and A. Gavriilidis, Stripping of Acetone from Water with Microfabricated and Membrane Gas–Liquid Contactors, Analyst, 2014, 139(1), 266–272,  10.1039/C3AN00963G.
19. E. Fornells, B. Barnett, M. Bailey, R. A. Shellie, E. F. Hilder and M. C. Breadmore, Membrane Assisted and Temperature Controlled On-Line Evaporative Concentration for Microfluidics, J. Chromatogr. A, 2017, 1486, 110–116,  DOI:10.1016/j.chroma.2016.12.003.
20. W.-Y. Tseng and R. M. Van Dam, Compact Microfluidic Device for Rapid Concentration of PET Tracers, Lab Chip, 2014, 14(13), 2293–2302,  10.1039/C4LC00286E.
21. J. Y. Zhang, J. Do, W. R. Premasiri, L. D. Ziegler and C. M. Klapperich, Rapid Point-of-Care Concentration of Bacteria in a Disposable Microfluidic Device Using Meniscus Dragging Effect, Lab Chip, 2010, 10(23), 3265,  10.1039/c0lc00051e.
22. J. Zhang, M. Mahalanabis, L. Liu, J. Chang, N. Pollock and C. Klapperich, A Disposable Microfluidic Virus Concentration Device Based on Evaporation and Interfacial Tension, Diagnostics, 2013, 3(1), 155–169,  DOI:10.3390/diagnostics3010155.
23. Z. He, D. J. Miller, S. Kasemset, L. Wang, D. R. Paul and B. D. Freeman, Fouling Propensity of a Poly(Vinylidene Fluoride) Microfiltration Membrane to Several Model Oil/Water Emulsions, J. Membr. Sci., 2016, 514, 659–670,  DOI:10.1016/j.memsci.2016.04.018.
24. C. Chen, G. Levitin, D. W. Hess and T. F. Fuller, XPS Investigation of Nafion® Membrane Degradation, J. Power Sources, 2007, 169(2), 288–295,  DOI:10.1016/j.jpowsour.2007.03.037.
25. H. Zhang, R. M. Tiggelaar, S. Schlautmann, J. Bart and H. Gardeniers, In-line Sample Concentration by Evaporation through Porous Hollow Fibers and Micromachined Membranes Embedded in Microfluidic Devices, Electrophoresis, 2016, 37(3), 463–471,  DOI:10.1002/elps.201500285.
26. H. Shafique, V. Karamzadeh, G. Kim, M. L. Shen, Y. Morocz, A. Sohrabi-Kashani and D. Juncker, High-Resolution Low-Cost LCD 3D Printing for Microfluidics and Organ-on-a-Chip Devices, Lab Chip, 2024, 24(10), 2774–2790,  10.1039/D3LC01125A.
27. R. Su, F. Wang and M. C. McAlpine, 3D Printed Microfluidics: Advances in Strategies, Integration, and Applications, Lab Chip, 2023, 23(5), 1279–1299,  10.1039/D2LC01177H.
28. T. Sebechlebská, E. Vaněčková, M. K. Choińska-Młynarczyk, T. Navrátil, L. Poltorak, A. Bonini, F. Vivaldi and V. Kolivoška, 3D Printed Platform for Impedimetric Sensing of Liquids and Microfluidic Channels, Anal. Chem., 2022, 94(41), 14426–14433,  DOI:10.1021/acs.analchem.2c03191.
29. R. F. Quero, G. D. da Silveira, J. A. F. da Silva and D. P. de Jesus, Understanding and Improving FDM 3D Printing to Fabricate High-Resolution and Optically Transparent Microfluidic Devices, Lab Chip, 2021, 21(19), 3715–3729,  10.1039/D1LC00518A.
30. BMF MED resin, https://bmf3d.com/wp-content/uploads/2024/05/DATA-SHEET-BMF-MEDRESIN-051024.pdf.
31. A. Beer, Bestimmung Der Absorption Des Rothen Lichts in Farbigen Flüssigkeiten, Ann. Phys., 1852, 62, 78–88,  DOI:10.1002/andp.18521620505.
32. S. J. Gregg and K. S. W. Sing, Adsorption, Surface Area and Porosity, Academic Press, New York, 2nd edn, 1982, p. 121.
33. A. W. Adamson and A. P. Gast, Physical Chemistry of Surfaces, Wiley-Blackwell, 6th edn, 1997, p. 54.
34. A. Fick, Ueber Diffusion, Ann. Phys., 1855, 170(1), 59–86,  DOI:10.1002/andp.18551700105.
35. ASHRAE Handbook—Fundamentals, American Society of Heating, Refrigerating and Air-Conditioning Engineers, Atlanta, GA, 2017, ch. 1, Psychrometrics.
36. R. Nikam, A. Kulandaisamy, K. Harini, D. Sharma and M. M. Gromiha, ProThermDB: thermodynamic database for proteins and mutants revisited after 15 years, Nucleic Acids Res., 2021, 49, D420–D424,  DOI:10.1093/nar/gkaa1035.
37. R. Finn, Capillary Surface Interfaces, Notices of the American Mathematical Society, 1999, 46, 770–781.
38. S. P. Sutera and R. Skalak, The History of Poiseuille's Law, Annu. Rev. Fluid Mech., 1993, 25, 1–19,  DOI:10.1146/annurev.fl.25.010193.000245.
39. F. C. Alimagham, D. Hutter, N. Marco-García, E. Gould, V. H. Highland, A. Huefner, S. Giorgi-Coll, M. J. Killen, A. P. Zakrzewska, S. R. Elliott, K. L. H. Carpenter, P. J. Hutchinson and T. Hutter, Cerebral Microdialysate Metabolite Monitoring Using Mid-Infrared Spectroscopy, Anal. Chem., 2021, 93(35), 11929–11936,  DOI:10.1021/acs.analchem.1c01149.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lc00329f

---