Open Access Article
Open Access ArticleMagSity platform: a hybrid magnetic levitation-based lensless holographic microscope platform for liquid density and viscosity measurements†
Oyku
Doyran Ince
 a and
H. Cumhur
Tekin
a and
H. Cumhur
Tekin
 *ab
*ab
aDepartment of Bioengineering, Izmir Institute of Technology, Izmir 35430, Türkiye. E-mail: cumhurtekin@iyte.edu.tr
bMETU MEMS Center, Ankara 06520, Türkiye
First published on 13th March 2025
Abstract
The viscosity and density of liquids are the most extensively studied material properties, as their accurate measurement is critical in various industries. Although developments in micro-viscometers have overcome the limitations of traditional bulky methods, more accessible technologies are required. Here, we introduce a novel magnetic levitation-based method to measure the viscosity and density of solutions in a microcapillary channel. This principle exploits microparticles as microsensors to correlate levitation time and height with solutions' viscosity and density, using buoyancy and drag forces. The platform has an integrated lensless holographic microscope, providing a hybrid system for in situ and precise measurements. By utilizing this hybrid technology, portable, rapid and cost-effective measurements can be conducted. This platform enables viscosity and density measurements within 7 minutes, achieving high accuracies of at least 97.7% and 99.9%, respectively, across an operation range of 0.84–5.09 cP and 1.00–1.09 g cm−3. The platform is utilized to clearly distinguish differences in the spent cell culture medium across various cell lines. This method, as presented, can be readily applied to measure a diverse array of liquids in multiple domains, encompassing biotechnology, medicine, and engineering.
1. Introduction
Monitoring the rheological properties (i.e., viscosity) and density of fluids is crucial across industries,1–4 playing a critical role in diagnosing various health conditions based on bodily fluid analysis.5,6 Changes in blood plasma rheology (1.1–3 cP)7,8 and density (∼1.00 g cm−3)9 are linked to increased morbidity and mortality risks under severe conditions like cardio and cerebrovascular diseases,10–12 while cerebrospinal fluid (CSF) that has water-like density (∼1.00 g cm−3) and viscosity (∼1.00 cP)13 can be used to monitor physiologic function and the homeostasis of the central nervous system, emphasizing the need for accurate, simultaneous measurements of these properties, particularly in the biomedical field.14 However, existing technologies often require large sample volumes and expensive, complex instruments, which limits their use for rapid analysis and point-of-care (POC) testing. Similarly, analyzing fresh and spent cell culture media offers valuable insights into cell health, metabolic activity, and growth, as well as their viscosity and density range, which closely mimic those of bodily fluids.15 The ability to detect subtle changes in these properties is vital not only in biomedical research but also in clinical applications ranging from stem cell therapy,16 regenerative medicine,17 and biopharmaceutical production18 to optimize therapeutic formulations,19,20 emphasizing the need for accessible, precise, and sensitive measurement techniques.Typically, liquid viscosity and density are measured independently using a viscometer and densitometer, with density calculated by dividing the solution's mass by its volume and viscosity determined conventionally through falling-ball,21 rotational,22 and oscillatory viscometers,23 based on drag force.24,25 Although multifunctional devices can measure both properties, they face limitations including regular maintenance and calibration necessities, requiring skilled operators, large sample sizes, high energy consumption, high costs, and lack of portability.26
Microfluidic devices have been developed to measure bulk rheometric properties of small sample volumes with miniaturized flow conditions.27,28 Micro-viscometers using microfluidic channels integrated with sensors quantify pressure or flow rates to measure shear viscosity,29 and the integration of optical techniques allows non-contact fluid characterization.30–32 Methods include deflection of polydimethylsiloxane (PDMS) microstructures,33–35 droplet characterization,36,37 fluid interface evaluation,27 meniscus inspection,38 tracer displacement,39 scattered intensity analysis,40 and digital holography microscopy (DHM), monitoring three-dimensional spatial velocity fields of tracer microparticles for viscoelastic characterization.6,41
Microelectromechanical system (MEMS)-based viscometers, as alternatives to traditional viscometers42,43 and densitometers,44 stand out in clinical applications due to their portability, robustness, and reduced sample requirements for POC applications.40,45–48 They utilize mechanical,49 electrical,50 magnetic,51 or piezoelectric52–54 actuation for measurements and enable simultaneous viscosity and density measurements through various configurations like cantilevers,55 vibrating membranes,56 and atomic force microscopy (AFM)-integrated piezoresistive sensors.6,57,58 However, while miniaturised systems overcome the disadvantages of conventional methods, such as high energy consumption, lack of portability, and large sample volume requirements, they still rely on complex modeling and precise microfabrication, leading to increased costs and reduced accessibility.4,59,60
In contrast, magnetic levitation (MagLev) technology has proven to be a cost-effective, highly sensitive, and straightforward approach in many research disciplines.61 Primarily, measuring particle density with MagLev technology has led to breakthroughs, paving the way for various applications.62,63 Currently, it is a method that has been successfully applied not just in macro systems but also in different micro-scale domains, including protein detection,64 cell separation,63,65–68 cell sorting,69 cell manipulation,70 tissue engineering,71–73 drug testing,74,75 and fluid control.76 To date, conventional miniaturized MagLev-based systems have been limited to measuring only the density of solutions, typically within a droplet-scale environment, and cannot assess both density and viscosity.77–79 Simultaneous measurement of liquid density and viscosity has been demonstrated using the principle of unidirectional levitation of the measuring body (i.e., an object80 or a magnet81,82). This method uses an actively controlled magnetic field to correlate the oscillation or rotation frequency of the measuring body immersed in the liquid with its properties. However, this approach has some drawbacks, including high sample volume requirements and challenges associated with measurement verification. Moreover, these platforms' complex circuitry, control mechanisms, and measurement systems also increase their overall cost. Additionally, the repetitive utilization of the measuring body increases the risk of contamination, which is particularly pronounced in biological sample analysis. To overcome these limitations, there is a growing demand for a compact, cost-effective, and easily fabricated platform that can accurately measure viscosity and density within the same system using minute sample volumes.
Moreover, MagLev applications typically rely on sophisticated optical imaging systems, especially traditional microscopes, to inspect samples. Since the bulky lens-based nature of these systems is incompatible with miniaturized technologies, easy-to-integrate and compact imaging systems have emerged.83 Hence, integrating a lensless holographic microscope, where pinholes replace lenses, into the magnetic levitation platform offers numerous advantages, including real-time and automated imaging, enhanced portability, and significant weight, cost, and complexity reductions.65,75
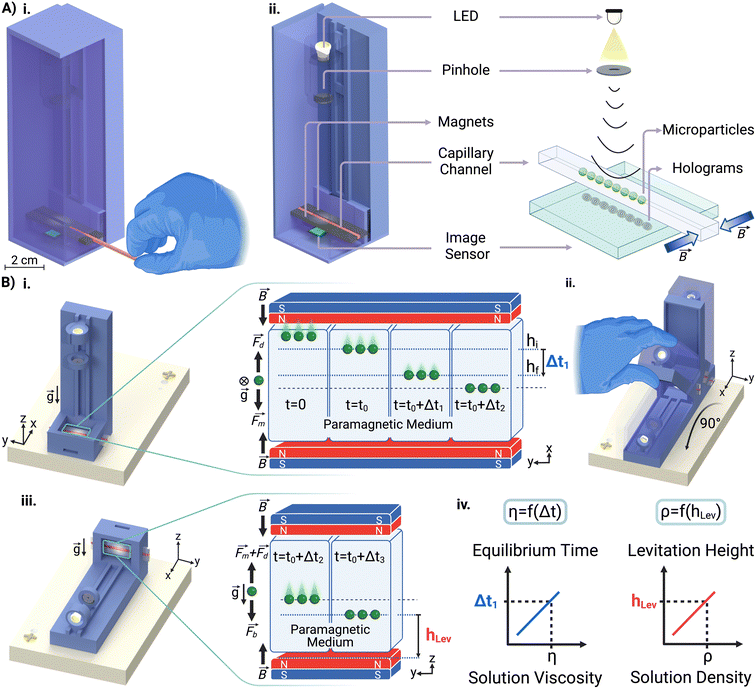
In this study, we present a novel MagLev-based approach for simultaneously measuring the density and viscosity of solutions within a miniaturized platform called the MagSity platform (Fig. 1A and S1†). This platform employs an integrated lensless holographic microscope, which offers a hybrid system for sensitive, rapid, portable, and cost-effective measurements of solution properties in a disposable microcapillary channel by monitoring microparticles spiked into the solutions as microsensors while eliminating the risk of contamination. The hybrid platform operates in dual configurations to measure the viscosity and density (Fig. 1B) of the solutions. In this setup, the equilibrium times and levitation heights of the microparticles are correlated with the viscosity and density of the solution, respectively. MagSity offers a powerful tool for detecting subtle changes in liquids across a wide range of viscosities and densities, working with minute sample volumes. This makes it a promising candidate for applications in disease diagnostics, regenerative medicine, and biopharmaceutical monitoring.
2. Materials and methods
2.1. Measurements in the MagSity platform
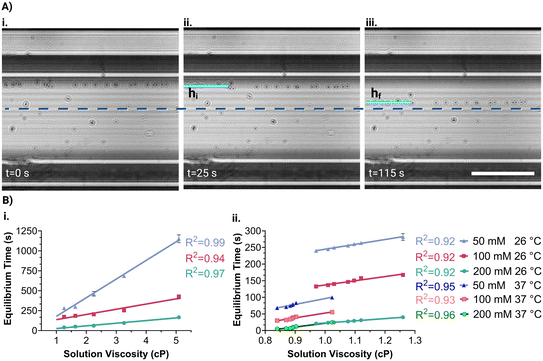
A liquid sample is prepared with microparticles in the presence of a nonionic paramagnetic solution (Gadavist, Gd3+) and subsequently introduced in a microcapillary (ESI†). First, the microcapillary containing the sample is placed beside a single magnet for 5 minutes. This causes the dispersed diamagnetic microparticles to be repelled by the magnetic field and gather on the opposite capillary wall. Afterward, the microcapillary was placed between opposing magnets in the platform. Thus, microparticles move from the same position under magnetic induction, ensuring the consistency of the analysis results. The microcapillary is then imaged to reveal microparticle velocities for viscosity measurement. Later, the platform is rotated 90° to measure levitation heights of microparticles for density measurement and imaging is continued. The entire analysis process is demonstrated in Video S1.†The holographic images captured during the experiment were reconstructed to obtain real object images. To determine the equilibrium time of the particles, the time taken to move from their initial (hi) to their final (hf) position concerning the centerline is measured (Fig. 1B). It was considered that the visual quality deteriorates as the particles are near the capillary wall and the movement of the microparticles is the slowest when approaching the centerline. Thus, the reference initial and final positions were 260 μm (hi) and 60 μm (hf) away from the centerline. Hence, the equilibrium time of the particle is measured at a 200 μm fixed distance, where the acting magnetic forces on the microparticles remain constant for all analyses.
2.2. Principles of viscosity measurement
Initially, the platform is placed in an upright configuration, which arranges the opposing magnets perpendicular to gravity for viscosity measurement (Fig. 1B). In this configuration, particles tend to move toward the midpoint between the two magnets, where the magnetic induction is at its minimum (Fig. S2†). The particles move through the solution until the acting magnetic force (Fm) becomes zero. During this movement, the drag force (Fd) acts in the opposite direction of the movement.63 Since the inertia forces on the microparticles can be neglected, the force balance equation of the particles is expressed as Fm = Fd. Hence, this equation is used to calculate the viscosity of the solution (η) for spherical microparticles with a radius of R as follows: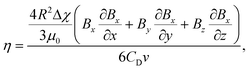 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63), μ0 is the vacuum permeability (1.2566 × 10−6 kg m A−2 s−2), B is the magnetic induction value, CD is the drag coefficient (CD = 1 for the microparticle far from the channel wall as in the measurements), and v is the velocity of the microparticle. The equation reveals that the velocity of microparticles is inversely proportional to the viscosity of the solution. Hence, the viscosity of a solution can be determined by measuring the particle's velocity and, consequently, its equilibrium time in the channel.
63), μ0 is the vacuum permeability (1.2566 × 10−6 kg m A−2 s−2), B is the magnetic induction value, CD is the drag coefficient (CD = 1 for the microparticle far from the channel wall as in the measurements), and v is the velocity of the microparticle. The equation reveals that the velocity of microparticles is inversely proportional to the viscosity of the solution. Hence, the viscosity of a solution can be determined by measuring the particle's velocity and, consequently, its equilibrium time in the channel.
2.3. Principles of density measurement
The platform is rotated 90° to orient the opposing magnets horizontally to the gravity to perform MagLev-based density measurements of the solution (Fig. 1B). In this configuration, the microparticles tend to move from high to low magnetic induction due to their magnetic susceptibility difference with the surrounding medium. The microparticles then become stable at a certain levitation height when the magnetic and buoyant (Fb) forces balance each other.63 The equation of the balanced forces (Fm = Fb) acting on the microparticles is rearranged to calculate the density of the solution as follows: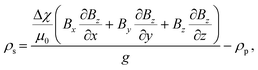 | (2) |
2.4. Numerical analysis
This study used a finite element method (FEM) to solve the magnetic induction value across the microcapillary generated by opposing magnets. A 3D model comprising two magnets with a magnetization of 400 kA m−1 was generated and computed under stationary conditions (Fig. S2†). A custom-built Python code was used to model the MagSity platform principle, and microparticle movements were examined in the microcapillary by calculating the velocity due to magnetic and drag forces acting at each position (ESI†). The equilibrium time between hi and hf was calculated for 1–5 cP solution viscosity using 50, 100, and 200 mM Gd3+. Additionally, the equations of the magnetic and buoyant forces acting on the microparticle in the 90° rotated platform were solved, and the equilibrium heights for solution densities of 0.95–1.10 g cm−3 were calculated for 50, 100, and 200 mM Gd3+.2.5. Image acquisition and analysis
The microparticles are imaged in the microcapillary via an integrated lensless holographic microscopy system. In this system, the LED emits light waves that pass through a pinhole and illuminate microparticles. The reference wave and the wave created by the object interaction combine on the image sensor, where they are recorded. A custom-built Python program was used to control the imaging duration and frequency (ESI†). The recorded hologram image is then reconstructed through the angular spectrum algorithm as follows:84ΨP(x, y; z) = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) −1{ −1{![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) {ΨPo(x, y)}H(kx, ky; z)}, {ΨPo(x, y)}H(kx, ky; z)}, | (3) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/i_char_e141.gif) is the Fourier transform and H(kx, ky; z) is the phase factor. Here, the phase factor was utilized to back-propagate the image with increasing z-steps along the z-axis as follows:
is the Fourier transform and H(kx, ky; z) is the phase factor. Here, the phase factor was utilized to back-propagate the image with increasing z-steps along the z-axis as follows: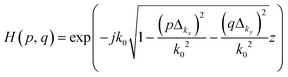 | (4) |
2.6. Statistical analysis
Data are shown as the mean ± standard deviation (SD) of 6 replicates of experiments. The coefficient of determination (R2) was assessed through linear regression with a 95% confidence interval. Multiple group comparisons were analyzed employing analysis of variance (ANOVA) with a statistical significance set to p < 0.05 and Tukey's honestly significant difference (HSD) post hoc test. All analyses were performed using GraphPad software (Prism 9 version, GraphPad, USA).3. Results and discussion
3.1. Modeling of viscosity and density measurements
A solution containing microparticles suspended in a paramagnetic medium is injected into a microcapillary and positioned on the platform. The initial configuration of the platform (Fig. 1B) enables the microparticles to reach the midpoint between magnets. The velocity of particles depends mainly on the concentration of the paramagnetic medium and the viscosity of the solution. Finite element modeling results of magnetic induction values (Fig. S2†) within the capillary were used to simulate the velocity of particles with a diameter of 15 μm at a 0.1 s period in liquids having different viscosities (1–5 cP) and Gd3+ concentrations (50–200 mM). Simulation results indicate that the particle reaches the final position more rapidly in a medium with lower viscosity (Fig. 2A). Additionally, as the difference between the microparticle and medium magnetic susceptibility decreases (i.e., with lower Gd3+ concentration), the particle reaches the final position more slowly. Hence, by monitoring the equilibrium time of microparticles, the viscosity of the solutions can be depicted at a fixed Gd3+ concentration. The sensitivity of viscosity measurement can be enhanced by decreasing the concentration of Gd3+, as it results in a steeper slope between viscosity and equilibrium time (Fig. 2A).The 90° rotated platform enables the microparticles to reach an equilibrium levitation height where buoyant force equals magnetic force (Fig. 1B). This stable levitation height is unique to the solution density and depends on the magnetic susceptibility difference between the particle and the paramagnetic medium. Levitation heights of a microparticle with a 1.05 g cm−3 density were simulated in solutions having different densities (0.95–1.10 g cm−3) and Gd3+ concentrations (50–200 mM). The results suggest that the microparticle levitates closer to the lower magnet in solutions with a density lower than that of the particle itself (Fig. 2B). When the solution's density increased, the particle's levitation height increased also. Hence, the density of the solution can be assessed by monitoring the levitation heights of microparticles. As the Gd3+ concentration increases, the magnetic levitation height difference between solutions with different densities decreases, resulting in a reduced measurement sensitivity. However, the range of density measurements is improved.
3.2. Viscosity and density measurements in glycerol solutions
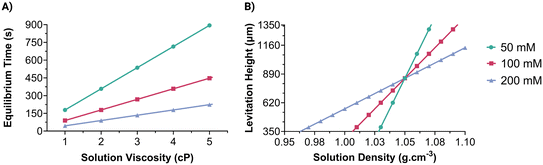
Calibration curves for viscosity measurement were obtained by calculating the equilibrium time of microparticles in the MagSity platform (Fig. 3A). These particles were prepared in solutions with known viscosities and densities (Fig. S3 and S4†) containing Gd3+ at a constant temperature. Therefore, calibration is done to account for the measured viscosity and density, considering those of the Gadavist solution itself. Linear relations between the microparticle equilibrium time (teq in s) and the solution viscosity (η in cP) were obtained as follows: teq = 234η − 56.61, teq = 65.27η − 71.87, and teq = 33.20η − 6.925 for 50, 100, and 200 mM Gd3+, respectively (Fig. 3B). The results showed a gradual increase in microparticle equilibrium time as the solution viscosity increased. Additionally, as Gd3+ concentration decreases, the rate of change in microparticle equilibrium time increases with the viscosity grade. Hence, the sensitivity of the viscosity measurement can be improved while reducing the Gd3+ concentration as expected. The analysis time depends on the Gd3+ concentration and solution viscosity range. For instance, the microparticles achieved their final positions in 4.3 ± 0.2, 2.5 ± 0.2, and 0.47 ± 0.1 minutes for the solutions with 0.9–1.3 cP viscosity using 50, 100, and 200 mM Gd3+, respectively. Conversely, longer analysis times were necessary for higher viscosities (1.3–5 cP), namely 10.8 ± 5.4, 4.4 ± 1.6, and 1.6 ± 0.8 minutes for 50, 100, and 200 mM Gd3+, respectively. The experimental results also showed a good correlation with simulated microparticle equilibrium times (Fig. 2A and S5A†).For low viscosities (<1.3 cP) covering the range of biological samples (1.0–1.3 cP85), the equilibrium time showed a good linear relationship with the viscosities, as follows: teq = 145.5η + 99.26, teq = 126.3η − 10.82, and teq = 66.57η + 43.94 for 50, 100, and 200 mM Gd3+, respectively (Fig. 3B). Although viscosity characteristics can be changed with temperature, a linear relationship was still obtained for elevated temperature (i.e., 37 ± 1 °C) as follows: teq = 175η − 78.91, teq = 143.7η − 91.19, and teq = 112.6η − 90.67 for 50, 100, and 200 mM Gd3+, respectively.
After the viscosity measurements, the MagSity platform was rotated 90° for the density measurement of the same solution. A calibration curve for the density measurement was obtained by determining the levitation height of microparticles (hlev), defined as the distance between their final position and the bottom magnet (Fig. 4A). A linear correlation was observed between levitation height (hlev in μm) and solution density (ρs in g cm−3) as follows: hlev = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353ρs − 13
353ρs − 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192, hlev = 9896ρs − 9533, and hlev = 4511ρs − 3864 for 50, 100, and 200 mM Gd3+, respectively (Fig. 4B). As the concentration of Gd3+ increased, the slope of the fitting line decreased, leading to an expansion of the density measurement range within the microcapillary. For instance, the predicted measurable density range was 1.014–1.089 g cm−3 for 50 mM Gd3+, while the density measurement ranges widened to 0.999–1.100 g cm−3 and 0.934–1.156 g cm−3 for 100, and 200 mM Gd3+, respectively. On the other hand, the density measurement resolution is decreased from 7.49 × 10−5 to 2.22 × 10−4 g cm−3 μm−1 with an increase in Gd3+ concentration from 50 mM to 200 mM. Fitting lines of different concentrations intersected at the levitation of ∼850 μm, which is nearly the midpoint between the magnets, and the density of ∼1.05 g cm−3, which is the density of the microparticles. The results also correlate well with the simulated levitation heights in the MagSity platform for different solution densities (Fig. 2B and S5B†).
192, hlev = 9896ρs − 9533, and hlev = 4511ρs − 3864 for 50, 100, and 200 mM Gd3+, respectively (Fig. 4B). As the concentration of Gd3+ increased, the slope of the fitting line decreased, leading to an expansion of the density measurement range within the microcapillary. For instance, the predicted measurable density range was 1.014–1.089 g cm−3 for 50 mM Gd3+, while the density measurement ranges widened to 0.999–1.100 g cm−3 and 0.934–1.156 g cm−3 for 100, and 200 mM Gd3+, respectively. On the other hand, the density measurement resolution is decreased from 7.49 × 10−5 to 2.22 × 10−4 g cm−3 μm−1 with an increase in Gd3+ concentration from 50 mM to 200 mM. Fitting lines of different concentrations intersected at the levitation of ∼850 μm, which is nearly the midpoint between the magnets, and the density of ∼1.05 g cm−3, which is the density of the microparticles. The results also correlate well with the simulated levitation heights in the MagSity platform for different solution densities (Fig. 2B and S5B†).
The time required for density analysis depended on the time elapsed for microparticles to reach the final levitation heights. Hence, this time was influenced by factors such as the concentration of Gd3+, viscosity, and the density of the solution. As the Gd3+ concentration increased, the time of reaching the final levitation height decreased, resulting in a shorter analysis time (Fig. S6†). While using 100 mM Gd3+, the total analysis time for the viscosity and density measurement can be less than 10 minutes for a wide range of liquids (Table S1†). Since 100 mM Gd3+ shows better sensitivity than 200 mM Gd3+ and offers both fast analysis and a broader density measurement range than 50 mM Gd3+ (Table S1†), we chose to use 100 mM Gd3+ concentration for viscosity and density measurements in the platform.
3.3. Viscosity and density measurements in various solutions
Fetal bovine serum (FBS), bovine serum albumin (BSA), and cell culture media solutions (ESI†) with 100 mM Gd3+ were analyzed using the MagSity platform, whose calibration curves of viscosity and density measurements are shown in Fig. 3B and 4B. A commercial viscometer (Brookfield DV-II+ Pro), with an accuracy of 99%, was employed alongside an analytical balance (AND GH-252) to establish gold standard measurements for validating the solution measurements. The results are presented in Table 1. The increase in FBS volume percentage in Dulbecco's modified Eagle's high glucose (DMEM) and BSA concentration in FBS led to a noticeable increase in both viscosity and density values. Furthermore, the viscosity and density values of the spent cell media were significantly higher (P < 0.0001) compared to a standard cell culture medium, i.e., DMEM with 5% (v/v) FBS. In the measurements, each spent cell line medium exhibits significantly distinct properties from each other (Fig. S7†), showing that despite metabolism occurring in all cell types, the intricacies of metabolic activity can vary depending on the specific cellular context.17,86 The densities of the Roswell Park Memorial Institute (RPMI) medium, DMEM, and FBS with 2 mM BSA solutions could not be measured since their density values did not fall within the 100 mM Gd3+ measurement range. However, the measurement range can be adjusted within the MagSity platform; for instance, the range can be increased when higher paramagnetic concentrations (i.e., 200 mM Gd3+) are used. The MagSity's measurable viscosity and density ranges effectively assess the properties of biological samples within the platform's sensitivity limits. However, whole blood poses significant challenges for our platform due to its high cellular content, which interferes with image clarity in lensless holographic microscopy.75,87 Nonetheless, representative cell-free fluids, such as serum and cell-culture media, have demonstrated the relevance and applicability of the MagSity for measuring the density and viscosity of biological fluids.| Solution | MagSity measurements | Gold standard measurements | Difference between measured values | |||
|---|---|---|---|---|---|---|
| η (cP) | ρ (g cm−3) | η (cP) | ρ (g cm−3) | Δη (%) | Δρ (%) | |
| a Not detected. | ||||||
| RPMI | 0.8773 ± 0.0061 | NDa | 0.8700 ± 0.0001 | 0.999 ± 0.0001 | 0.8411 ± 0.7045 | ND |
| DMEM | 0. 9294 ± 0.0034 | ND | 0.9267 ± 0.0047 | 1.000 ± 0.0001 | 0.5805 ± 0.2127 | ND |
| FBS | 1.4790 ± 0.0180 | 1.0095 ± 0.0001 | 1.5150 ± 0.0050 | 1.0089 ± 0.0006 | 2.2366 ± 0.7352 | 0.0593 ± 0.0492 |
| DMEM with 5% (v/v) FBS | 0.9697 ± 0.0058 | 1.0006 ± 0.0002 | 0.9533 ± 0.0047 | 1.0006 ± 0.0002 | 1.7237 ± 0.9676 | 0.0030 ± 0.0018 |
| DMEM with 10% (v/v) FBS | 1.0179 ± 0.0023 | 1.0010 ± 0.0002 | 1.0200 ± 0.0082 | 1.0010 ± 0.0001 | 0.6736 ± 0.1816 | 0.0135 ± 0.0033 |
| DMEM with 20% (v/v) FBS | 1.1105 ± 0.0012 | 1.0020 ± 0.0002 | 1.0867 ± 0.0047 | 1.0020 ± 0.0002 | 2.1922 ± 0.3536 | 0.0345 ± 0.0207 |
| DMEM with 30% (v/v) FBS | 1.3897 ± 0.0070 | 1.0059 ± 0.0002 | 1.4000 ± 0.0001 | 1.0062 ± 0.0002 | 0.7352 ± 0.4974 | 0.0237 ± 0.0081 |
| Phosphate-buffered saline (PBS) with 0.5 mM BSA | 2.0460 ± 0.0051 | 1.0206 ± 0.0002 | 2.0433 ± 0.0047 | 1.0199 ± 0.0008 | 0.1614 ± 0.1591 | 0.0701 ± 0.0559 |
| FBS with 0.5 mM BSA | 2.3495 ± 0.0340 | 1.0225 ± 0.0004 | 2.3333 ± 0.0471 | 1.0225 ± 0.0004 | 1.0847 ± 0.0153 | 0.0045 ± 0.0029 |
| FBS with 1 mM BSA | 2.4542 ± 0.0397 | 1.0393 ± 0.0002 | 2.4667 ± 0.0471 | 1.0398 ± 0.0002 | 1.3279 ± 1.0024 | 0.0440 ± 0.0047 |
| FBS with 2 mM BSA | 2.9232 ± 0.0090 | ND | 2.9000 ± 0.0001 | 1.0920 ± 0.0001 | 0.8008 ± 0.3116 | ND |
| HUVEC spent medium | 1.3458 ± 0.0070 | 1.0040 ± 0.0002 | 1.3533 ± 0.0047 | 1.0036 ± 0.0002 | 0.5578 ± 0.4043 | 0.0440 ± 0.0002 |
| MCF-7 spent medium | 1.0932 ± 0.0053 | 1.00309 ± 0.0184 | 1.0967 ± 0.0047 | 1.0022 ± 0.0001 | 0.3150 ± 0.2749 | 0.0309 ± 0.0184 |
| MDA-MB 231 spent medium | 1.1049 ± 0.0071 | 1.0029 ± 0.0001 | 1.0867 ± 0.0047 | 1.0032 ± 0.0000 | 1.6789 ± 0.2215 | 0.0235 ± 0.0095 |
Standard viscosity measurement techniques have error margins ranging from 1% to 5%, while density measurement techniques range from 0.01% to 0.1%, depending on the instrument.88,89 In contrast, the MagSity method is comparable to standard measurement methods, with a difference of 0.161–2.236% and 0.003–0.070% for viscosity and density measurements, respectively (Table 1). Hence, the MagSity measurements demonstrate at least 97.76% accuracy for viscosity and 99.93% for density. While the current proof-of-concept involves manual measurement of microparticle displacement and equilibrium height, the platform's image-based nature makes it highly amenable to automation for further accuracy improvement. Integrating machine learning algorithms for automated image analysis would not only reduce human error but also enhance the system's robustness and precision and improve the platform's scalability, particularly in clinical and industrial settings where consistency and throughput are critical.90,91 To further enhance user convenience, Gadavist and microparticles can be pre-coated within the capillary channel, simplifying the preparation process and ensuring consistent solution mixing for accurate measurements and increasing the platform's portability by reducing the need for on-site reagent handling.
Analysis of the obtained data consistently showed low standard deviation values, indicating a high level of reproducibility and precision in the measurements. These findings highlight the efficacy of the MagSity method in accurately monitoring liquid viscosity and density for diverse industrial and scientific applications.
3.4. Comparison of the MagSity platform with the state-of-the-art miniaturized devices for viscosity and density measurements
The advent of miniaturized technologies has revolutionized conventional measurement methodologies, driven by the growing demand for POC devices, especially in biological applications. Numerous studies have been carried out for sensitive and accurate measurements of fluid viscosity and density (Table S2†) since even minor changes are critical for early disease diagnosis and treatment monitoring.92 While fundamental research on microviscometers has enabled efficient handling of minute sample volumes, these techniques highly rely on embedded sensors and bulky and costly microscopy inspection systems, which are incompatible with the nature of miniaturized systems.4 Additionally, simultaneous analysis of fluid properties remains a significant challenge in POC diagnostics, particularly in economically and infrastructurally challenged, resource-limited environments.93 Alternatively, MEMS-based microsystems have demonstrated the integration of multiple functions on a compact platform, enabling rapid and simultaneous measurements.48,68 Despite recent advancements, these techniques still face inherent limitations, such as the necessity for sophisticated equipment and costly, precise microfabrication.In response to these challenges, we introduced a novel hybrid MagSity platform that seamlessly integrates the magnetic levitation principle and image-based sensing via a lensless holographic microscope to measure the density and viscosity of solutions. This integration overcomes the limitations of relying on expensive, bulky optical systems in magnetic levitation platforms and enables simultaneous measurement of fluid properties. While MagLev-based platforms traditionally allow measuring microparticle and droplet-based solution densities, our study is the first to simultaneously measure solution viscosity alongside density in a single platform (Table S3†). The measurement principle based on the magnetic field gradient generated by opposing permanent magnets offers simpler modeling and plain fabrication of the platform. The lensless digital image-based nature of the platform enhanced portability, compactness, and non-invasive analysis of the density and viscosity of solutions with a production cost of ∼$120 and a single test cost of $2.40 (Table S4†). The platform achieves biological range measurement accuracies of at least 97.7% for viscosity and 99.3% for density with 1.01 × 10−4 μm g−1 cm−3 and 1.53 × 10−2 s cP−1 sensitivity. It should be noted that the sensitivity and range of the measurements can be adjusted by changing the paramagnetic medium concentration. Drawing upon these attributes, the presented technique surpasses existing miniaturized fluid property measurement methods by offering a combination of low cost, high sensitivity, and accuracy. Notably, it achieves this by simultaneously measuring viscosity and density, thereby enhancing its utility and performance (Table S2†). The measurements conducted on the presented platform pave the way for potential future applications, such as assessing blood coagulation and detecting imbalances in biofluid properties that serve as indicators for various disorders.
4. Conclusion
A hybrid lensless holographic microscope integrated MagLev-based solution viscosity and density measurement platform, called the MagSity platform, was introduced. This platform utilizes the microparticles as a kind of microsensor spiked in a sample to determine levitation height and time, enabling measurements of liquid density and viscosity, respectively. By eliminating the need for traditional lenses for inspections, the system offers a cost-effective alternative to conventional approaches for monitoring levitation profiles. The platform enables measurements of liquids with viscosities ranging from 0.84 to 5.09 cP and densities from 1.00 to 1.09 g cm−3 in under 7 minutes, utilizing a minute amount of sample (30 μL). It achieves over 97.7% accuracy for viscosity and over 99.9% accuracy for density. The advantages of the hybrid method will significantly contribute to portable and rapid tests that will reduce the time and financial burden of institutions where regular monitoring of fluid properties is essential.Data availability
The data are available from the corresponding author upon reasonable request.Author contributions
Oyku Doyran Ince: conceptualization, data curation, formal analysis, methodology, validation, data analysis, writing – original draft, and visualization; H. Cumhur Tekin: conceptualization, data curation, formal analysis, methodology, validation, resources, writing – review & editing, supervision, project administration, and funding acquisition.Conflicts of interest
The authors have submitted a patent application (2024/018026) associated with the innovation described in this manuscript. H. C. T. is a founder of Saniber Inc., a company dedicated to the development of telemedicine solutions, as well as integrated microfluidic and biomedical devices for point-of-care diagnosis and monitoring. The authors' interests were diligently reviewed and overseen in strict adherence to the conflict-of-interest policies by Izmir Institute of Technology (IZTECH).Acknowledgements
This study was supported by the Scientific and Technological Research Council of Türkiye (TUBITAK) under Grant Number 22AG032. The authors would like to acknowledge the support from TUBITAK through the 2210/C National MSc Scholarship Program in the Priority Fields in Science and Technology. The authors thank Assoc. Prof. Nur Basak Surmeli Eraltug and Prof. Erdal Bedir from the Bioengineering Department of IZTECH, and Prof. Sevcan Unluturk from the Food Engineering Department of IZTECH for generously providing the incubator, analytical balance, and viscometer, respectively. The authors would like to thank Berkay Berk from the Food Engineering Department of IZTECH for conducting viscosity measurements of reference solutions.References
- O. Skurtys and J. M. Aguilera, Food Biophys., 2008, 3, 1 CrossRef
.
- M. J. Iqbal and M. A. Chaudhry, J. Chem. Thermodyn., 2009, 41, 221 CrossRef CAS
.
- M. Gonzalez, H. R. Seren, G. Ham, E. Buzi, G. Bernero and M. Deffenbaugh, IEEE Trans. Instrum. Meas., 2018, 67, 804 CAS
.
- S. B. Puneeth, M. B. Kulkarni and S. Goel, Eng. Res. Express, 2021, 3, 022003 CrossRef
.
- M. K. Dehghan Manshadi, D. Khojasteh, M. Mohammadi and R. Kamali, Int. J. Numer. Model.: Electron. Netw. Devices Fields, 2016, 29, 845 Search PubMed
.
- N. McLoughlin, S. L. Lee and G. Hähner, Appl. Phys. Lett., 2006, 89, 184106 CrossRef
.
- M. Ranucci, T. Laddomada, M. Ranucci and E. Baryshnikova, Physiol. Rep., 2014, 2, e12065 CrossRef PubMed
.
- O. Cakmak, C. Elbuken, E. Ermek, A. Mostafazadeh, I. Baris, B. Erdem Alaca, I. H. Kavakli and H. Urey, Methods, 2013, 63, 225 CrossRef CAS PubMed
.
- D. J. Vitello, R. M. Ripper, M. R. Fettiplace, G. L. Weinberg and J. M. Vitello, J. Vet. Med., 2015, 2015, 152730 Search PubMed
.
- G. Chen, L. Zhao, Y. Liu, F. Liao, D. Han and H. Zhou, Chin. Sci. Bull., 2012, 57, 1946 CrossRef
.
- T. Kenner, Basic Res. Cardiol., 1989, 84, 111 Search PubMed
.
- G. D. O. Lowe, Thromb. Haemostasis, 1992, 67, 494 CrossRef CAS
.
- H. Balasundaram, S. Sathyamoorthi, U. Fernandez-Gamiz, S. Noeiaghdam and S. S. Santra, Theor. Appl. Mech. Lett., 2023, 13, 100418 Search PubMed
.
- J. C. P. Hollister, A. C. Wang, W. Kim, C. C. Giza, M. L. Prins and H. P. Kavehpour, Front. Phys., 2023, 11, 1308136 CrossRef
.
- J. Lee, Y. Leng, K. Chow, F. Ren, X. Ge, K. Wang and X. Lu, Acta Biomater., 2011, 7, 2615–2622 CrossRef CAS PubMed
.
- M. J. de los Santos, P. Gámiz, J. M. de los Santos, J. L. Romero, N. Prados, C. Alonso, J. Remohí and F. Dominguez, PLoS One, 2015, 10, e0142724 Search PubMed
.
- C. Poon, J. Mech. Behav. Biomed. Mater., 2022, 126, 105024 Search PubMed
.
- S. Nikita, S. Mishra, K. Gupta, V. Runkana, J. Gomes and A. S. Rathore, Biotechnol. Bioeng., 2023, 120, 1189 CAS
.
- E. Ko, Y. J. Song, K. Choe, Y. Park, S. Yang and C. H. Lim, J. Korean Med. Sci., 2022, 37, e71 Search PubMed
.
- M. Attebäck, B. Hedin and S. Mattsson, Sci. Pharm., 2022, 90, 15 Search PubMed
.
- M. Brizard, M. Megharfi, E. Mahé and C. Verdier, Rev. Sci. Instrum., 2005, 76, 025109 Search PubMed
.
- R. N. Weltmann and P. W. Kuhns, J. Colloid Sci., 1952, 7, 218 CAS
.
- K. Häusler, W. H. Reinhart, P. Schaller, J. Dual, J. Goodbread and M. Sayir, Biorheology, 1996, 33, 397 Search PubMed
.
- S. Kim, Y. I. Cho, A. H. Jeon, B. Hogenauer and K. R. Kensey, J. Non-Newtonian Fluid Mech., 2000, 94, 47 CAS
.
- I. B. Lee, B. H. Cho, H. H. Son and C. M. Um, Dent. Mater., 2007, 23, 425 CAS
.
-
A. Pinto and C. Trejo Soto, Front Microrheometry of Newtonian Fluids, 2021 Search PubMed
.
- S. Gupta, W. S. Wang and S. A. Vanapalli, Biomicrofluidics, 2016, 10, 043402 CrossRef PubMed
.
- S. J. Haward, Biomicrofluidics, 2016, 10, 043401 CrossRef CAS PubMed
.
- P. Guillot, P. Panizza, J.-B. Salmon, M. Joanicot, A. Colin, C.-H. Bruneau and T. Colin, Langmuir, 2006, 22, 6438 CrossRef CAS PubMed
.
- D. Solomon, A. Abdel-Raziq and S. Vanapalli, Rheol. Acta, 2016, 55, 727–738 CrossRef CAS
.
- D. E. Solomon and S. A. Vanapalli, Microfluid. Nanofluid., 2014, 16, 677 CrossRef CAS
.
- N. M. M. Pires, T. Dong, U. Hanke and N. Hoivik, Sensors, 2014, 14, 15458 CrossRef PubMed
.
- A. Mustafa, D. Haider, A. Barua, M. Tanyeri, A. Erten and O. Yalcin, Sens. Diagn., 2023, 2, 1509 CAS
.
- A. Mustafa, A. Eser, A. C. Aksu, A. Kiraz, M. Tanyeri, A. Erten and O. Yalcin, Anal. Chim. Acta, 2020, 1135, 107 CrossRef CAS PubMed
.
- R. M. Judith, B. Lanham, M. R. Falvo and R. Superfine, PLoS One, 2018, 13, e0200345 CrossRef PubMed
.
- E. André, N. Pannacci, C. Dalmazzone and A. Colin, Soft Matter, 2019, 15, 504 RSC
.
- S. E. Mena, Y. Li, J. McCormick, B. McCracken, C. Colmenero, K. Ward and M. A. Burns, Biomicrofluidics, 2020, 14, 014109 CrossRef CAS PubMed
.
- N. Srivastava and M. A. Burns, Anal. Chem., 2006, 78, 1690 CrossRef CAS PubMed
.
- G. Degré, P. Joseph, P. Tabeling, S. Lerouge, M. Cloitre and A. Ajdari, Appl. Phys. Lett., 2006, 89, 024104 CrossRef
.
- J. Lee and A. Tripathi, Anal. Chem., 2005, 77, 7137 CAS
.
- S. Gupta and S. A. Vanapalli, Phys. Fluids, 2020, 32, 012006 CrossRef CAS
.
- P. Arosio, K. Hu, F. A. Aprile, T. Müller and T. P. J. Knowles, Anal. Chem., 2016, 88, 3488 CrossRef CAS PubMed
.
- R.-H. Ma, D.-A. Wang, T.-H. Hsueh and C.-Y. Lee, Sensors, 2009, 9, 5460 CrossRef CAS PubMed
.
- D. Sparks, R. Smith, M. Straayer, J. Cripe, R. Schneider, A. Chimbayo, S. Anasari and N. Najafi, Lab Chip, 2003, 3, 19 RSC
.
- M. A. Nour and M. M. Hussain, Sensors, 2020, 20, 3907 CrossRef CAS
.
-
M. C. Bourne, in Food Texture and Viscosity, ed. M. C. Bourne, Academic Press, London, 2nd edn, 2002, pp. 1–32 Search PubMed
.
- J. W. Judy, Smart Mater. Struct., 2001, 10, 1115 CrossRef
.
- P. Singh, K. Sharma, I. Puchades and P. B. Agarwal, Sens.
Actuators, A, 2022, 338, 113456 CrossRef CAS
.
- M. Heinisch, T. Voglhuber-Brunnmaier, E. Reichel, I. Dufour and B. Jakoby, Sens. Actuators, A, 2015, 226, 163–174 CrossRef CAS
.
- P. Brunetto, L. Fortuna, P. Giannone, S. Graziani and F. Pagano, 2010 IEEE Instrumentation & Measurement Technology Conference Proceedings, 2010, DOI DOI:10.1109/IMTC.2010.5488156.
- B. A. Bircher, R. Krenger and T. Braun, Sens. Actuators, B, 2016, 223, 784 CAS
.
- G. Wang, C. Tan and F. Li, Sens. Actuators, A, 2017, 267, 401 CAS
.
- C. Riesch, E. Reichel, F. Keplinger and B. Jakoby, J. Sens., 2008, 2008, 697062 Search PubMed
.
- T. Voglhuber-Brunnmaier and B. Jakoby, Meas. Sci. Technol., 2021, 33, 012001 Search PubMed
.
- O. Cakmak, E. Ermek, N. Kilinc, G. G. Yaralioglu and H. Urey, Sens. Actuators, A, 2015, 232, 141–147 CAS
.
-
E. K. Reichel, B. Jakoby and C. Riesch, in 2007 IEEE Sensors, IEEE, Atlanta, GA, USA, 2007, pp. 908–911 Search PubMed
.
- R. Motamedi and P. M. Wood-Adams, J. Rheol., 2010, 54, 959 CAS
.
- T. Naik, E. K. Longmire and S. C. Mantell, Sens. Actuators, A, 2003, 102, 240 CrossRef CAS
.
- I. Etchart, H. Chen, P. Dryden, J. Jundt, C. Harrison, K. Hsu, F. Marty and B. Mercier, Sens. Actuators, A, 2008, 141, 266 CAS
.
- G. F. Christopher, J. Myung Yoo, N. Dagalakis, S. D. Hudson and K. B. Migler, Lab Chip, 2010, 10, 2749 CAS
.
- E. Turker and A. Arslan-Yildiz, ACS Biomater. Sci. Eng., 2018, 4, 787 CrossRef CAS PubMed
.
- S. Yaman, M. Anil-Inevi, E. Ozcivici and H. C. Tekin, Front. Bioeng. Biotechnol., 2018, 6, 192 CrossRef PubMed
.
- N. G. Durmus, H. C. Tekin, S. Guven, K. Sridhar, A. Arslan Yildiz, G. Calibasi, I. Ghiran, R. W. Davis, L. M. Steinmetz and U. Demirci, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E3661 CrossRef CAS
.
- S. Yaman and H. C. Tekin, Anal. Chem., 2020, 92, 12556 CrossRef CAS PubMed
.
-
K. Delikoyun, S. Yaman, M. Anil-Inevi, E. Ozcivici and H. C. Tekin, in 2019 Medical Technologies Congress (TIPTEKNO), IEEE, Izmir, Turkey, 2019, pp. 1–4 Search PubMed
.
- O. Sarigil, M. Anil-Inevi, E. Yilmaz, G. Mese, H. C. Tekin and E. Ozcivici, Analyst, 2019, 144, 2942 RSC
.
- S. Tasoglu, J. A. Khoory, H. C. Tekin, C. Thomas, A. E. Karnoub, I. C. Ghiran and U. Demirci, Adv. Mater., 2015, 27, 3901 CrossRef CAS PubMed
.
- L. Zhao, Y. Hu, T. Wang, J. Ding, X. Liu, Y. Zhao and Z. Jiang, Sensors, 2016, 16, 830 CrossRef PubMed
.
- S. Kecili, E. Yilmaz, O. S. Ozcelik, M. Anil-Inevi, Z. E. Gunyuz, O. Yalcin-Ozuysal, E. Ozcivici and H. C. Tekin, Biosens. Bioelectron.: X, 2023, 15, 100392 CAS
.
- M. A. M. Gijs, F. Lacharme and U. Lehmann, Chem. Rev., 2010, 110, 1518 CrossRef CAS PubMed
.
- M. Anil-Inevi, K. Delikoyun, G. Mese, H. C. Tekin and E. Ozcivici, Biotechnol. Bioeng., 2021, 118, 4771 CrossRef CAS PubMed
.
- M. Anil-Inevi, S. Yaman, A. A. Yildiz, G. Mese, O. Yalcin-Ozuysal, H. C. Tekin and E. Ozcivici, Sci. Rep., 2018, 8, 7239 CrossRef PubMed
.
- O. Sarigil, M. Anil-Inevi, B. Firatligil-Yildirir, Y. C. Unal, O. Yalcin-Ozuysal, G. Mese, H. C. Tekin and E. Ozcivici, Biotechnol. Bioeng., 2021, 118, 1127 CrossRef CAS PubMed
.
- S. Kecili, S. V. Kaymaz, B. Ozogul, H. C. Tekin and M. Elitas, Analyst, 2023, 148, 5588 RSC
.
- K. Delikoyun, S. Yaman, E. Yilmaz, O. Sarigil, M. Anil-Inevi, K. Telli, O. Yalcin-Ozuysal, E. Ozcivici and H. C. Tekin, ACS Sens., 2021, 6, 2191 CrossRef CAS
.
- P. Dunne, T. Adachi, A. A. Dev, A. Sorrenti, L. Giacchetti, A. Bonnin, C. Bourdon, P. H. Mangin, J. M. D. Coey, B. Doudin and T. M. Hermans, Nature, 2020, 581, 58 CrossRef CAS PubMed
.
- S. Ge, Y. Wang, N. J. Deshler, D. J. Preston and G. M. Whitesides, J. Am. Chem. Soc., 2018, 140, 7510 CrossRef CAS PubMed
.
- K. A. Mirica, S. S. Shevkoplyas, S. T. Phillips, M. Gupta and G. M. Whitesides, J. Am. Chem. Soc., 2009, 131, 10049 CrossRef CAS PubMed
.
- B. Karakuzu, M. Anil İnevi, E. A. Tarim, O. Sarigil, M. Guzelgulgen, S. Kecili, S. Cesmeli, S. Koc, M. S. Baslar, C. Oksel Karakus, E. Ozcivici and H. C. Tekin, Emergent Mater., 2024, 7, 2323 CrossRef CAS
.
- R. Dudek and V. Kolář, Levitation-Vibrating Device for Measuring Viscosity, Density and Interfacial Tension, 2014, CZ304430B6.
- S. Clara, H. Antlinger, A. Abdallah, E. Reichel, W. Hilber and B. Jakoby, Sens. Actuators, A, 2016, 248, 46 CrossRef CAS
.
- D. Breuer, S. Clara, F. Feichtinger and B. Jakoby, IEEE Sens. J., 2018, 18, 7786 Search PubMed
.
- M. J. Pioz, R. L. Espinosa, M. F. Laguna, B. Santamaria, A. M. M. Murillo, Á. L. Hueros, S. Quintero, L. Tramarin, L. G. Valle, P. Herreros, A. Bellido, R. Casquel and M. Holgado, Biosensors, 2022, 12, 1091 CrossRef PubMed
.
- K. Delikoyun, S. Yaman, E. Yilmaz, O. Sarigil, M. Anil-Inevi, K. Telli, O. Yalcin-Ozuysal, E. Ozcivici and H. C. Tekin, ACS Sens., 2021, 6, 2191 CrossRef CAS PubMed
.
- I. Jang, K. E. Berg and C. S. Henry, Sens. Actuators, B, 2020, 319, 128240 CrossRef CAS
.
- S. Y. Lunt and M. G. Vander Heiden, Annu. Rev. Cell Dev. Biol., 2011, 27, 441 CrossRef CAS PubMed
.
- S. Seo, S. O. Isikman, I. Sencan, O. Mudanyali, T.-W. Su, W. Bishara, A. Erlinger and A. Ozcan, Anal. Chem., 2010, 82, 4621 CrossRef CAS PubMed
.
-
D. W. Green and R. H. Perry, Perry's Chemical Engineers' Handbook, McGraw-Hill Education, New York, 8th edn, 2008 Search PubMed
.
- ASTM International, ASTM D4052-18a: Standard Test Method for Density, Relative Density, and API Gravity of Liquids by Digital Density Meter, ASTM International, West Conshohocken, PA, 2018 Search PubMed.
- J. Alghazo and G. Latif, Diagnostics, 2023, 13, 3671 CrossRef PubMed
.
- J. Valente, J. António, C. Mora and S. Jardim, J. Imaging, 2023, 9, 207 CrossRef PubMed
.
- P. Soltani Zarrin, F. Ibne Jamal, N. Roeckendorf and C. Wenger, Healthcare, 2019, 7, 11 CrossRef PubMed
.
- B. Heidt, W. F. Siqueira, K. Eersels, H. Diliën, B. van Grinsven, R. T. Fujiwara and T. J. Cleij, Biosensors, 2020, 10, 133 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5lc00144g |
| This journal is © The Royal Society of Chemistry 2025 |