Orientation-independent bubble trap with internal partition for robust operation of microfluidic systems

Abstract

A new monolithic bubble trap has been developed with a unique, orientation-independent design. The bubble trap has a spherical cavity and a central partition with internal passages that eliminate air bubbles effectively for extended periods of time. Flow testing was performed in a closed-loop microfluidic system to demonstrate effectiveness and robustness of the bubble trap. Flow rate was continually monitored on a stationary benchtop and also in simulated microgravity conditions on a 3-D random positioning machine. Data collected from flow sensors placed fore and aft of the bubble trap confirmed that randomly occurring bubbles were effectively eliminated by the trap throughout 24 hour closed-loop perfusion tests. To highlight the orientation-independent benefit of the bubble trap in a specific application of interest, continuous-flow experiments were conducted using human umbilical vein endothelial cells in a closed-loop microfluidic system. The bubble trap successfully protected the integrity of confluent layers that otherwise suffered from cell detachment without the trap. Image analysis showed that random orientation reduced directional alignment of cell nuclei, relative to baseline experiments performed under normal gravity.

---

Introduction

Bubbles represent a persistent challenge for the functionality and reliability of fluidic systems. Especially in small dimensions where surface tension at liquid–gas phase boundaries have a proportionally larger effect than inertial forces or pressure-driven flow, bubbles can pose many problems including channel blockage, fatal damage to cells, and inaccurate measurements.^1–3 The problem of bubbles is further exacerbated for perfusion systems on mobile platforms that might be subject to rotation, as changes in orientation can release bubbles trapped in crevices or adhered to surfaces.⁴ Robust mitigation strategies are necessary especially for long-duration studies, such as organ-on-a-chip systems⁵ and in situ microfluidic sample analysis in space.⁶ In a microgravity environment, bubble mitigation strategies are especially challenging because nucleation and growth have been reported to be ∼30× higher than on Earth.⁷

Many microfluidic systems rely on the use of a bubble trap to maintain functional viability,⁸ with successes demonstrated using both passive,^9–11 and active^12,13 design concepts. Many approaches take advantage of semipermeable membranes to separate gas from liquid.^14–16 In addition to the delicate balance between transmembrane pressure and surface tension, a fundamental concern for membrane-based approaches is ensuring sufficient dwell time for gas transport across the membrane, which limits the operating flow rate of such devices. A bubble trap with a semipermeable membrane requires that the gas be in contact with the membrane for a duration that exceeds the transit time through the device. For example, for a mean flow rate of Q = 6 mL min⁻¹ through a cross-sectional area of A = 1 mm², the average fluid velocity is 100 mm s⁻¹. For a channel that is L = 25 mm long, the corresponding transit time is 0.25 s. Such a brief transit time is typically insufficient for gas permeation to occur reliably in a membrane-based trap, thereby limiting effectiveness at high flow rate. Other concerns include the possibility of pore blockage by small particles or solutes in the fluid and changes in wetting characteristics of the membrane (e.g., hydrophobic recovery). Based on the working principle of a liquid meniscus at the entrance of a pore,¹⁷ equilibrium is subject to the critical Laplace pressure, given by Δp = 4σ cos(θ)/d, where σ is the surface tension of the liquid, θ is the contact angle on the membrane, and d is the characteristic pore diameter. A suboptimal pressure balance can lead to liquid infusion that can block pores or liquid breach across the membrane. This paper presents a monolithic, orientation-independent bubble trap design that does not rely on a gas-permeable membrane. Two distinct advantages over membrane-based approaches are that (1) this design does not rely on an optimal pressure difference for effective gas transport across a membrane and (2) it does not depend on sufficient residence time for the gas-membrane interface.

Bubble trap design and principle of operation

Our bubble trap design has a spherical internal cavity and uses internal passages within a solid partition to ensure that only gas-free liquid is able to escape through its egress port (Fig. 1).

Fig. 1 Bubble trap features shown in wireframe (A) and cross-section (B) views, featuring a midplane partition with embedded channels in a spherical cavity. The bubble trap is designed to work in any orientation, as shown in upright (C), vertical (D), and random (E) cases. When the ingress port is pointed downward (E), bubbles must travel around the periphery of the partition in order to rise to the free surface, far from the egress port.

The bubble trap design leverages buoyancy to separate gas bubbles from liquid, while taking advantage of a partially filled spherical cavity to ensure that a gas accumulation region is confined near the outer radius of the cavity, regardless of orientation (Fig. 1C–E). The ingress and egress ports are located near the centroid of the suspended partition, and fluid is routed in and out of the overall device by channels embedded within the partition (Fig. 1B). The outer diameter of the disk-shaped partition is smaller than the inner diameter of the spherical cavity, leaving a “crossover gap”. This gap at the periphery ensures that fluid (whether gas or liquid) can pass freely from one hemisphere to the other hemisphere only near the outer wall of the cavity. This novel geometric design ensures that any air bubbles must arrive (and coalesce) in the gas accumulation region at the top of the cavity before having any opportunity to reach the egress port. The video clips included as ESI† (Movies S1–S4) demonstrate how our bubble trap is also not limited by transit time.

Regardless of 3-D orientation, the egress port at the center of the spherical cavity is always fully submerged in liquid, such that only bubble-free liquid exits through the outlet port. The unique design of the bubble trap enables it to be used for a wide range of bubble sizes and flow rates, where its ability to handle a wide range of air volume and flow rates are showcased in short video demonstrations included as ESI.† Although buoyancy is the dominant driving force in ordinary usage, the same design would be capable of performing bubble trapping with other means of maintaining phase separation.¹⁸ For example, there is supporting evidence to suggest that bubble coalescence and surface forces are highly influential in microgravity.^19–21 Accordingly, even in the absence of gravity and buoyant forces, hydrophilic material selection or surface treatment for the inner walls of the spherical cavity could potentially localize the gas accumulation region at the periphery of the partition.

For any given flow rate, as the gas volume inside the trap increases, the air–liquid surface approaches the centroid. The trap will continue to function as intended as long as the egress port remains submerged in liquid, and failure would occur only if the air–liquid surface reaches it. The limiting capacity of the trap (i.e., the maximum allowable air volume accumulated) can readily be scaled by selection of cavity dimensions, and the derivation for a spherical cavity is shown as ESI.† Volume accumulation with large air slugs was confirmed by experimental trials to proceed as expected according to flow rate (ESI,† Fig. S1). Assuming a constant rate of gas accumulation, the time to failure t can be calculated analytically:

where Q is the constant volume flow rate of incoming fluid, and (ϕ_gas)_in is the assumed volume fraction of gas in the fluid that is separated when passing through the bubble trap. (V_gas)_max is the limiting capacity of air in the bubble trap, and (V_gas)_init is the initial gas volume in the chamber. Assuming 60 nL bubbles (roughly 0.5 mm in diameter), a bubble trap with 3 mL limiting capacity could accommodate 50 000 such bubbles. Even if a new bubble were to appear as frequently as once per minute on average, the bubble trap could operate for over 800 hours before needing intervention.

Experimental

Bubble trap fabrication

Bubble traps with internal spherical radius of 15 mm were fabricated monolithically using stereolithography on a commercial 3D printer (Form 3, Formlabs, Boston, Massachusetts, USA) using standard Formlabs resins (e.g., Clear, High Temp). While both resins are geometrically viable, the High Temp resin has an additional advantage of better dimensional stability at elevated temperatures. Both resins are translucent, such that liquid level can be readily viewed for inspection. Embedded channels were manually flushed with 70% isopropanol during washing. Low-friction fugitive inserts (e.g., perfluoroalkoxy alkanes (PFA) tubing) were inserted into the channel cavities during the curing stage to prevent blockage from partially cured resin. Before use, the bubble traps are boiled in deionized water for 5 minutes to minimize resin residue, following precedent whereby boiling was demonstrated as a method of improving cell viability in resin-printed fluidic devices.²² Plasma cleaning was then performed for 30 seconds at 10 W and 200 mTorr to further eliminate resin residue.²³

Perfusion system components and assembly

For testing purposes, the bubble trap was assembled with a commercial microfluidic chip (μ-Slide VI 0.4, ibidi GmbH, Gräfelfing, Germany) in a closed-loop configuration (Fig. 2A). Flow was driven by a piezoelectric micropump (mp6-liq, Bartels Mikrotechnik GmbH, Dortmund, Germany) operating at 100 Hz. Volume flow rate was measured by thermal flow sensors fore and aft of the bubble trap, with output logged by data acquisition software. This particular sensor is engineered to recognize air-in-line (i.e., bubble) events by acute spikes in flow rate, as described in the product datasheet (SLF3S-1300F, Sensirion, Stäfa, Switzerland). Components were connected by medical-grade tubing (Tygon ND-100-65, Saint-Gobain Performance Plastics, Charny, France) with 1.6 mm inner diameter. The system was primed by submerging the microfluidic chip in a container filled with the working fluid (deionized water) and using the micropump to draw liquid into the system. Once stable fluid flow was established in the loop, the fluidic connections at the chip were sealed and the bubble trap was filled to ensure that the ingress and egress ports at the center were fully immersed in liquid.

Fig. 2 Perfusion system components and assembly, showing closed-loop circuit configuration (A), two replicate assemblies with open electronics enclosure shown in foreground (B), and a fully assembled system mounted on a random positioning machine (C).

An integrated and self-contained perfusion system was also custom-engineered with an electronics enclosure (Fig. 2B) and fluidic components integrated onto reconfigurable mounting decks. The electronics enclosure protects the controller board (mp-Multiboard, Bartels Mikrotechnik GmbH, Dortmund, Germany) from humidity and potential liquid spills. The fully assembled system fits within a compact volume (140 mm × 140 mm × 140 mm), such that it can be mounted onto the payload platform of a random positioning machine (Fig. 2C). Reconfigurable decks provide versatility in component placement (e.g., having the microfluidic chip at the center of rotation and having fill ports accessible from the top of the assembly, as shown). The representative assembly in Fig. 2C is shown with two independent channels. At maximum capacity, up to four channels can be operated simultaneously.

Bubble trap performance testing

For demonstrating efficacy of bubble elimination over long duration, closed-loop tests were run continuously using deionized water at 37 °C for 24 h. Mean flow rate was maintained at ∼5 mL min⁻¹, and flow rate was recorded with a sampling period of 5 ms. The micropump was operated at 100 Hz driving frequency with deionized water and a nominal mean flow rate of 5.3 mL min⁻¹. For verifying the ability of the bubble trap to remove bubbles effectively regardless of orientation, continuous perfusion was tested on a random positioning machine (RPM 2.0, Airbus Defence and Space Netherlands, Leiden, Netherlands), as used for simulated microgravity.^24,25 The perfusion system was mounted onto the RPM and rotated under the default “0 g” program (provided by the manufacturer) for 24 h at room temperature. As in the stationary experiments, deionized water was used as the working fluid, and a mean flow rate of ∼5 mL min⁻¹ was logged with a 5 ms sampling period. The flow readings are plotted as a moving average of ten consecutive data points to account for the high-frequency driving oscillation of the micropump.

Endothelial cell culture under flow

In order to demonstrate the utility and benefit of the perfusion system and bubble trap for cell culture under flow, experiments were performed to determine if random orientation (i.e., simulated microgravity) alters cell morphology. The orientation and morphology of endothelial cells (cells that line the blood vessels) are sensitive to the wall shear stress.^26–28 For comparison between normal and simulated microgravity, cell culture experiments with endothelial cells were performed in six-channel microfluidic chips: two channels under flow with bubble traps, two under flow without bubble traps, and two static control lines. For simulated microgravity experiments, the closed-loop system consisting of cell culture chambers was mounted on the RPM. For sterilization, all system components were first cleaned using ethanol wipes. Ethanol (7 mL volume, 70% concentration) was then circulated through the assembled system, followed by rinsing with 20 mL of sterile water. The system was then primed with DMEM (Dulbecco's modified Eagle medium, Thermo Fisher Scientific) supplemented with 10% fetal bovine serum (FBS, SH30071.03, Cytiva, South Logan, Utah), 1% antibiotic/antimycotic solution (Cytiva, SV30079.01, South Logan, Utah), and ATCC endothelial cell growth kit (VEGF, PCS-100-041, American Type Culture Collection).

Primary human umbilical vein endothelial cells (HUVEC, PCS-100-013, American Type Culture Collection, Manassas, Virginia), were seeded in microchannels (μ-Slide VI 0.4, ibidi GmbH, Gräfelfing, Germany), having dimensions 17 mm long × 3.8 mm wide × 0.4 mm tall. The channels were coated with 250 μg mL⁻¹ rat tail collagen I (R&D Systems, 3440-100-01) per manufacturer instructions, at a density of 500 000 cells per mL. Before the start of perfusion, baseline cell confluence in the channels was established at ∼75%. The experiment was conducted in an incubator set at 37 °C with 5% CO₂. Perfusion was run continuously for 24 hours for the four circulating channels. Throughout this period, the system maintained a flow rate (6.1 mL min⁻¹) corresponding to a shear stress of 7.5 dyn cm⁻², and the flow rate was logged at a 5 ms sampling rate. After 24 h, the cells were fixed with 4% formaldehyde, and the nuclei were stained with Hoechst 33342 (Thermo Fisher Scientific, Inc., Waltham, MA), with a 1 : 2000 dilution in 1% bovine serum albumin (BSA) in 1× phosphate-buffered saline (PBS) solution. Actin was stained with CF594 phalloidin (Biotium, Inc., Fremont, CA), with a 1 : 300 dilution in 1% BSA in 1× PBS solution. The cells were imaged using a laser scanning confocal microscope (Zeiss LSM 700). The experiments were performed in three replicates on different days.

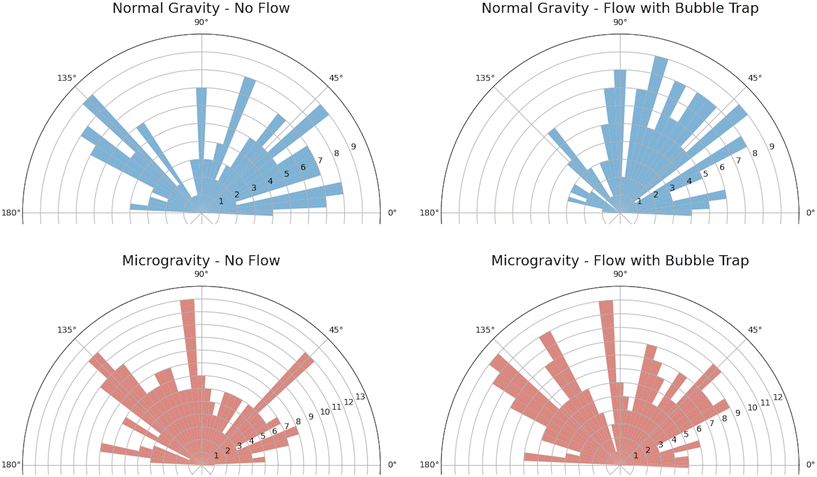
Morphometric analysis was conducted using the OrientationJ²⁹ plugin for ImageJ to quantify the orientation of cell nuclei. Channels were split to isolate the blue-stained nuclei and then binarized. A circular region of interest (ROI) was used to select individual nuclei manually, from which encircled ellipses were detected automatically using the “OrientationJ Measure” function with the Laplacian of Gaussian pre-filter set to zero (similar to a method used for retinal ganglion cells³⁰). A representative set of ellipses is shown in the ESI.† For each condition (normal gravity with/without flow and microgravity with/without flow), wind rose plots were generated to visualize the distribution of orientations. The code accounted for orientations across the vertical and horizontal axes by mirroring to show all angles between 0 and 180 degrees.

Results and discussion

Bubble elimination

In normal gravity conditions, flow rate measurements fore and aft of the bubble trap demonstrated successful bubble elimination over 24 h (Fig. 3A), where air bubbles appear as acute spikes. There is no evidence of a change in hydraulic resistance in the circuit, as evidenced by a constant flow rate throughout the 24 h time frame. Even though early-stage bubbles were not present in the first hour, random spikes were observed after ∼1 h and at other moments throughout the 24 hour period. Each bubble occurrence was successfully mitigated by the bubble trap. Causes of the random bubble occurrences may include multiple factors. Air may be introduced into the system via gas permeable tubing or imperfect seals at fittings. Gas bubbles may also occur autogenously within the bulk by aggregation or upon desorption from crevices or other surface irregularities (e.g., corners and crevices),^31,32 Two additional runs to confirm repeatability are included as ESI† (Fig. S3).

Fig. 3 Representative flow rate measurements fore and aft of a bubble trap in normal gravity (A), and an example of ability to eliminate bubbles under extreme conditions without and with a bubble trap on a rotating microgravity platform (B).

To demonstrate orientation-independent functionality, bubble traps were operated on a random position machine, as shown in Fig. 2C. Without a bubble trap, the occurrence of spikes is typically far more frequent on the moving platform compared to stationary tests in normal gravity. Flow spikes typically not only persist throughout the run (Fig. 3B, top), but the severity also tends to increase after the first few hours. A plausible cause for the frequent occurrence of spikes is the detachment of bubbles from interior surfaces due to orientation-dependent disruptions in surface tension.³³ In contrast, no bubbles are detected in a system that was assembled and tested under identical conditions with the addition of an inline bubble trap (Fig. 3B, bottom).

Perfusion culture of endothelial cells in normal gravity and microgravity

To evaluate the effectiveness of bubble traps in maintaining cell attachment and preventing bubble formation in perfusion systems, channels were operated continuously with cell culture medium at 37 °C for 24 hours. The setup included two channels with bubble traps, two without, and two static control lines, as detailed in section 2.4. Representative images of cell layers are shown in Fig. 4.

Fig. 4 Representative images of endothelial cells in microchannels in normal gravity (top row) and simulated microgravity (bottom row): (A and D) static control with confluent cell layer; (B and E) flow without bubble trap, whereby nearly all cells are detached; (C and F) flow with bubble trap, preserving cell adhesion. Actin is shown in red and nuclei in blue. Scale bars = 200 μm.

The imaging results demonstrate that in channels without flow, the endothelial cells grew to confluence with cobblestone morphology (Fig. 4A), as has been reported in previous studies.³⁴ In the channel with continuous flow and without bubble traps, hardly any cells were seen (Fig. 4B). Inspection of the flow through these systems showed the presence of numerous bubbles, which may likely have sheared and detached the cell monolayers. In contrast, in flow channels equipped with bubble traps, confluent cell growth was seen with few to no bubbles observed throughout the 24 hour period (ESI†). Actin staining showed increased concentrations around the nuclei and cell body periphery, indicating healthy cytoskeletal organization and cell adherence to the channel substrate (Fig. 4C). The endothelial cells were cultured under flow conditions in simulated microgravity. Here again, while the cells did not survive perfusion culture without bubble trap but in the presence of bubble trap, the monolayer remained intact (Fig. 4D–F).

The impact of fluid shear stress and microgravity (i.e., diminished gravitational force) was quantified from the orientation of the cells, based on the angle of the major axis of the elliptically shaped nuclei. Fig. 5 shows wind rose plots for cells with and without flow, under normal gravity and microgravity. For each of the four subfigures, approximately 160 nuclei were randomly sampled from images that were captured from two separate channels (between 61 and 88 nuclei per image).

Fig. 5 Rose plots of cell nuclei under normal gravity and microgravity, with and without flow. Each plot shows the frequency of orientations in 5 degree sectors. Normal gravity with flow exhibits directional alignment, whereas nuclei are randomly oriented otherwise.

In normal gravity, the distribution of angles for the long axis of nuclei (Fig. 5) exhibits a lack of directional bias in static conditions but a more tightly aligned orientation under perfusion, consistent with expected results in normal gravity.²⁶ In contrast, cell culture in microgravity maintains a lack of orientational bias under both static and perfusion conditions, suggesting that random orientation diminishes the influence of flow on alignment of cell nuclei.

Conclusions

A robust, orientation-independent bubble trap has been designed and demonstrated for effective elimination of air bubbles in closed-loop perfusion systems. The bubble trap was fabricated using stereolithography with a partitioned spherical cavity and embedded channels. The trap was tested in a fluid circuit with a piezoelectric micropump, a microfluidic chip, and inline flow sensors. Orientation independence was demonstrated by successful operation on a random positioning machine to simulate microgravity. The bubble trap enabled the continuous, long-term perfusion culture of endothelial cells under both normal gravity and simulated microgravity conditions. This innovation distinguishes itself from membrane-based bubble traps by providing a robust, scalable solution for future advancements in bubble-free microfluidic systems.

Data availability

Data for this article, including flow rate log files and microscope images are available at the San José State University ScholarWorks institutional digital repository at https://doi.org/10.31979/mybn-rkdh.

Author contributions

BV contributed to conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing of the original draft, and review and editing of writing. CL contributed to conceptualization, formal analysis, investigation, methodology, validation, visualization, and writing of the original draft. MK and JT contributed to conceptualization, investigation, and methodology. MP contributed to investigation, methodology, validation, and visualization. AKR contributed to conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, and review and editing of writing. SJL contributed to conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, visualization, writing of the original draft, and review and editing of writing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Funding was made available by NASA Space Biology grant # 80NSSC21K0272. The authors thank Wei-Ching Wang for help with flow rate data logging and file processing, William He for assistance with ImageJ macro writing, and Josie Landeck and Riya Pravin for assistance in recording some of the supplementary demonstration videos.

References

1. S. L. Anna, Annu. Rev. Fluid Mech., 2016, 48, 285–309.
2. T. Fu and Y. Ma, Chem. Eng. Sci., 2015, 135, 343–372.
3. X. He, B. Wang, J. Meng, S. Zhang and S. Wang, Langmuir, 2021, 37, 2187–2194.
4. M. S. Kim, M.S. thesis, Chemical and Materials Engineering, San Jose State University, 2023.
5. C. G. Alver, S. Álvarez-Cubela, I. Altilio, E. Hutchison, E. Warrner, M. E. Viso, G. Vitale, D. Oliver, R. L. Pastori, J. Dominguez-Bendala and A. Agarwal, Lab Chip, 2024, 24, 1557–1572.
6. M. R. Padgen, L. C. Liddell, S. R. Bhardwaj, D. Gentry, D. Marina, M. Parra, T. Boone, M. Tan, L. Ellingson, A. Rademacher, J. Benton, A. Schooley, A. Mousavi, C. Friedericks, R. P. Hanel, A. J. Ricco, S. Bhattacharya and S. R. Santa Maria, Astrobiology, 2023, 23, 637–647.
7. Q. Zhang, D. Mo, S. Moon, J. Janowitz, D. Ringle, D. Mays, A. Diddle, J. Rexroat, E. Lee and T. Luo, npj Microgravity, 2024, 10, 13.
8. M. Yang, N. Sun, Y. Luo, X. Lai, P. Li and Z. Zhang, Biomicrofluidics, 2022, 16, 031503.
9. C. Liu, J. A. Thompson and H. H. Bau, Lab Chip, 2011, 11, 1688–1693.
10. W. Zheng, Z. Wang, W. Zhang and X. Jiang, Lab Chip, 2010, 10, 2906–2910.
11. J. H. Sung and M. L. Shuler, Biomed. Microdevices, 2009, 11, 731–738.
12. A. M. Skelley and J. Voldman, Lab Chip, 2008, 8, 1733–1737.
13. J. M. Karlsson, M. Gazin, S. Laakso, T. Haraldsson, S. Malhotra-Kumar, M. Mäki, H. Goossens and W. van der Wijngaart, Lab Chip, 2013, 13, 4366–4373.
14. H. G. Derami, R. Vundavilli and J. Darabi, Microsyst. Technol., 2017, 23, 2685–2698.
15. T. Christoforidis, C. Ng and D. T. Eddington, Biomed. Microdevices, 2017, 19, 58.
16. M. J. Williams, N. K. Lee, J. A. Mylott, N. Mazzola, A. Ahmed and V. V. Abhyankar, Micromachines, 2019, 10(6), 360–371.
17. J. Xu, R. Vaillant and D. Attinger, Microfluid. Nanofluid., 2010, 9, 765–772.
18. R. M. Jenson, A. P. Wollman, M. M. Weislogel, L. Sharp, R. Green, P. J. Canfield, J. Klatte and M. E. Dreyer, Int. J. Multiphase Flow, 2014, 65, 68–81.
19. Q. Kang, H. L. Cui, L. Hu, L. Duan and W. R. Hu, J. Colloid Interface Sci., 2007, 310, 546–549.
20. M. Q. Raza, M. von Köckritz, J. Sebilleau, C. Colin, M. Zupancic, M. Bucci, T. Troha and I. Golobic, Phys. Fluids, 2023, 35, 023333.
21. A. I. Nowak, L. Pietrasanta, C. Czajkowski, M. Marengo and S. Pietrowicz, Int. J. Heat Mass Transfer, 2022, 192, 122905.
22. N.-E. Nam, N.-K. Hwangbo, G. Jin, J.-S. Shim and J.-E. Kim, J. Prosthodont. Res., 2023, 67, 121–131.
23. A. Urrios, C. Parra-Cabrera, N. Bhattacharjee, A. M. Gonzalez-Suarez, L. G. Rigat-Brugarolas, U. Nallapatti, J. Samitier, C. A. DeForest, F. Posas, J. L. Garcia-Cordero and A. Folch, Lab Chip, 2016, 16, 2287–2294.
24. J. J. W. A. van Loon, Adv. Space Res., 2007, 39, 1161–1165.
25. S. L. Wuest, S. Richard, S. Kopp, D. Grimm and M. Egli, Biomed Res. Int., 2015, 1, 971474.
26. U. M. Sonmez, Y.-W. Cheng, S. C. Watkins, B. L. Roman and L. A. Davidson, Lab Chip, 2020, 20, 4373–4390.
27. A.-C. Vion, T. Perovic, C. Petit, I. Hollfinger, E. Bartels-Klein, E. Frampton, E. Gordon, L. Claesson-Welsh and H. Gerhardt, Front. Physiol., 2020, 11, 623769.
28. L. Jin, Y. Qin, Y. Zhao, X. Zhou and Y. Zeng, J. Biomech., 2025, 182, 112579.
29. Z. Püspöki, M. Storath, D. Sage and M. Unser, Adv. Anat., Embryol. Cell Biol., 2016, 219, 69–93.
30. J. Hertz, R. Robinson, D. A. Valenzuela, E. B. Lavik and J. L. Goldberg, Acta Biomater., 2013, 9, 7622–7629.
31. S. F. Jones, G. M. Evans and K. P. Galvin, Adv. Colloid Interface Sci., 1999, 80, 27–50.
32. I. Pereiro, A. Fomitcheva Khartchenko, L. Petrini and G. V. Kaigala, Lab Chip, 2019, 19, 2296–2314.
33. Y. Gao, M. Wu, Y. Lin and J. Xu, Lab Chip, 2020, 20, 4512–4527.
34. R. Steward Jr, D. Tambe, C. C. Hardin, R. Krishnan and J. J. Fredberg, Am. J. Physiol., 2015, 308, C657–C664.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc01060d

---