A hybrid dielectrophoretic trap–optical tweezers platform for manipulating microparticles in aqueous suspension

Abstract

We demonstrate that a set of microfabricated electrodes can be coupled to a commercial optical tweezers device, implementing a hybrid electro-optical platform with multiple functionalities for the manipulation of micro-/nanoparticles in suspension. We show that the hybrid scheme allows enhanced manipulation capabilities, including hybrid dynamics, controlled accumulation in the dielectrophoretic trap from the optical tweezers, selectivity, and video tracking of the individual trajectories of trapped particles. This creates opportunities for novel studies in statistical physics and stochastic thermodynamics with multi-particle systems, previously limited to investigations with individual particles.

---

1 Introduction

The capabilities to store, accumulate, separate, or filter micro-/nanoparticles dispersed in a liquid are highly demanded for basic science and industry applications. Novel approaches that provide enhanced performance are continuously sought and developed, taking advantage of different physical principles and the distinguishing properties of the involved particles.¹ Many of these functionalities are implemented in lab-on-a-chip devices for biomedical and chemical applications such as cancer diagnosis,² detection of molecules,³ or detection of cells,⁴ to name but a few.

During the past few decades, mature techniques such as optical tweezers have demonstrated their excellence in many applications,^5,6 including single-molecule and single-cell mechanics,⁷ microrheology,⁸ and sorting⁹ as well as spectroscopic^10,11 and non-equilibrium dynamic studies.¹² The versatility of optical tweezers has favoured the development of commercial devices with different capabilities. Nonetheless, optical tweezers have some drawbacks. Heating occurs even in the case of dielectric particles,^13,14 leading to increased Brownian motion and instability,^15–17 and even damage when working with absorbing particles.⁶ Moreover, there are limitations regarding the optical properties of the used particles since their refractive index must be larger than that of the surrounding medium.¹⁸ Another characteristic of optical trapping that can be a drawback for some applications lies in one of its strengths, i.e., they are intended to handle individual particles, not groups. One can typically trap a few particles in a single trap, but studying the dynamics of the individual particles in the trapping region would not be possible.¹⁹ In addition, optical tweezers are limited by diffraction phenomena, which prevents particles with sizes below a certain limit, typically of the order of 10 nm, from being trapped using standard techniques.²⁰

Trapping can also be achieved using electric fields. A dielectrophoretic trap is a device that uses dielectrophoresis (DEP) to confine the particles. This phenomenon appears when particles move in the presence of an electric field gradient.^21–23 Depending on the dielectric properties of the particles and the electric field itself, DEP can be either positive (pDEP) or negative (nDEP), i.e. a particle can be attracted or repelled by the electrodes. DEP was comprehensively studied in the 50s by Herbert Pohl,^24,25 and applications have been developed during the past few decades thanks to its versatility regarding manipulation, sorting, accumulation, exclusion, and trapping of particles with various sizes and properties.^26–31

When particles are charged, Coulomb force can also lead to stable trapping in a device known as a Paul or quadrupole trap.³² In this case, stable trapping of charged particles can be obtained at a saddle point in an inhomogeneous AC electric field thanks to the appearance of a ponderomotive force. Interestingly, Paul traps can work in either liquid,³³ air,³⁴ or vacuum³⁵ and also need to be considered in the analysis of DEP, leading to rich dynamics.^36,37

Enhanced manipulation abilities can be achieved by combining two trapping mechanisms. For example, Paul traps were used along with optical tweezers in a vacuum to reduce the laser power required to stably trap nanoparticles and hence mitigate photodamage.^38–41 Inspired by these developments and previous designs in which circular electrodes were used to create both DEP^42,43 and quadrupole traps,⁴⁴ we here propose a hybrid trapping platform that couples a set of microelectrodes to a commercial optical tweezers device (see Fig. 1). The video tracking capability of the microscope available in the optical tweezers device allows us to measure the dynamics of multiple particles together in the same potential well, which we illustrate by changing the number of trapped particles and modulating the trapping potential. Furthermore, we demonstrate selectivity in terms of the dielectric properties of the particles, as expected in DEP traps. Finally, we show that optical tweezers allow one to selectively load the DEP trap from the optical tweezers by switching off the optical trap next to the DEP trap and analyze the dynamics of a particle that simultaneously feels the two trapping mechanisms. Previous approaches discussed experiments in which optical tweezers were used to measure the frequency-dependent DEP force of individual particles under different conditions.^45,46 Alternatively, our work focuses on the implementation and analysis of DEP trapping of groups of microparticles in the same potential well.

Fig. 1 Experimental setup of the hybrid DEP–optical trap. (a) Schematic representation of the experimental platform. A fluidic chamber about 100 μm thick made by sandwiching two glass slides separated with high viscosity KORASILON® paste contains an aqueous suspension of microparticles. Two concentric ring-shaped microelectrodes (depicted in golden colour) lie on the top of the chamber, creating a dielectrophoretic trap that confines several microparticles to a small volume. The DEP trap also generates an exclusion volume in which no particles are allowed. The infrared beam (represented by the red-shaded area) of the optical tweezers device can trap particles at its focus and can be used to bring new particles to the DEP trapping region, thanks to the capability of the device to steer the beam through the whole field of view of the microscope. The setup can therefore be configured as a DEP trap, optical trap, or hybrid DEP–optical trap by switching on/off the electric field or the laser beam. (b) The chip is introduced in a commercial optical tweezers platform (Bruker JPK Nanotracker II), which consists of an inverted microscope with a tightly focused infrared laser beam (λ = 1064 nm, 63× objective, NA = 1.2). (c) Microscopy images of the central part of the microelectrodes illustrating the trapping of groups of 1 μm (left) and 500 nm (right) diameter polystyrene particles trapped in the centre of the inner electrode. We estimate a particle concentration of about 0.6 particles per μm² for the left image and about 1.2 particles per μm² for the right image, assuming in both cases that they are arranged in a single plane. (d) The microelectrodes are fed with a sinusoidal voltage signal with amplitudes of several tens of volts at frequencies in the MHz range.

The article is organized as follows. First, we provide a theoretical background for the trapped particles and their trapping mechanisms. Further, we present simulations of the electric field created by our microelectrode arrangement that show the existence of a position that can stably trap particles with nDEP. We then present experimental evidence of the stability of the hybrid trap, in particular demonstrating the transfer of particles from the optical tweezers to the DEP trap, which will allow us to perform experiments with a controlled number of particles in the DEP potential. Afterwards, we present the DEP trap, characterizing its performance for individual particles, and then demonstrating some key capabilities, including selective trapping and control of the local density of trapped particles. Finally, we conclude with a summary of the results and a discussion of the potentialities of the presented device for further studies.

2 Theoretical background

2.1 Dynamics of trapped particles

Micro- and nanoparticles dispersed in a fluid with viscosity η at temperature T are subjected to Brownian motion and diffusion, characterized by the diffusion coefficient D. The Einstein formula for the diffusion coefficient is D = k_BT/γ, where k_B is the Boltzmann constant and γ is the friction coefficient of the particle, which, in the case of a sphere of radius R far away from any walls, can be written as γ = 6πηR. Particle trapping techniques confine particles to a small region by applying a restoring force that pushes the particles to an equilibrium position. The restoring force can be of different origins, as we discuss below. The trapping mechanism prevents particles from diffusing away from an equilibrium position, which is given by the trap centre, but does not completely cancel Brownian fluctuations. Regardless of the trapping mechanism, the overdamped Langevin equation describes the dynamics of Brownian particles dispersed in a liquid:where x is the instantaneous position of the particle, κ is the trap stiffness, which can be due to diverse mechanisms, and ξ(t) is a Gaussian white noise term that accounts for Brownian motion, with 〈ξ(t)〉 = 0, 〈ξ(t)ξ(t′)〉 = δ(t − t′). The solution of this equation is well known, and its description of the dynamics of a trapped particle can be done considering the mean squared displacement (MSD) of the particle in the trap, which for the case of motion in a plane can be shown to be:⁵This expression shows that the particle's motion has two regimes separated by a time scale τ = γ/κ. The particle diffuses freely at short times (MSD(t ≪ τ) ∼ 4Dt), while it features a plateau at long times (MSD(t ≫ τ) = 4k_BT/κ), indicating that the trap limits the maximum excursions that it can execute away from the trap's centre.

2.2 Trapping mechanisms

This section briefly describes the two trapping mechanisms used in this paper, namely optical tweezers and dielectrophoresis (see Fig. 1). Interestingly, these two mechanisms are closely related and can be treated on similar grounds,⁴⁷ although we will discuss them separately.

First, a non-uniform electric field exerts a dielectrophoretic force on a polarisable particle. The time-averaged expression of this force in the dipole approximation is:²⁷

where ε_m is the electric permittivity of the medium where the particle is suspended, ω is the angular frequency of the applied electric field E̲ and is the Clausius–Mossotti (CM) factor. For a bead, which can be considered a lossy dielectric uniform sphere, the expression of this factor is given bywhere and are the complex electric permittivities of the medium and the particle, respectively.

Regarding the CM factor, a particle can be attracted or repelled by the electric field gradient, i.e., the particle is pushed to or away from it, respectively. This behaviour depends on the value of the CM factor. In many cases, each bead has one cut-off frequency, where the factor changes its sign from positive to negative. In the case of the polystyrene particles used in our experiments, the cut-off frequency is in the low MHz range.

Second, an optical tweezers device is based on a single tightly focused light beam, which mainly exerts two optical forces, namely the gradient and the scattering force. Let us briefly introduce the optical force experienced by an electric dipole in the presence of a time-varying electric field:⁴⁸

where E is the electric field amplitude, S is the time-averaged Poynting vector of the incoming wave, σ_ext is the extinction cross section, α^′_p = Re {α_p} is the real part of the polarisability, and c is the speed of light. The polarisability can be expressed as:⁴⁸where ε_r is the relative electric permittivity and k₀ = 2π/λ. In addition, , where ε₀ is the electric permittivity of the vacuum and V_s = 4/3πR³ is the volume of the sphere.

The first term of eqn (5) corresponds to the gradient force, which is responsible for confinement in optical tweezers. This is due to the potential energy of a dipole in the electric field and, thus, it is a conservative force. On the other hand, the second term is related to the scattering force. This one is non-conservative and is produced by the transfer of momentum from the field to the particle. This is due to the scattering and absorption processes as revealed by the fact that it is proportional to the extinction cross section σ_ext.⁴⁸

In all situations discussed in this work, the forces given by eqn (3) and (5) can be assumed to follow Hooke's law in all three directions of space, and for every axis and force one finds a relation:

F_j,q = − κ_j,q(q − q_0,j) (7)

where j ∈ {DEP,OT} indicates the considered trap, q ∈ {x, y, z} are the coordinates of the particle, and q_0,j are the corresponding locations of the equilibrium position of each trap.

3 Results and discussion

3.1 COMSOL Multiphysics simulations

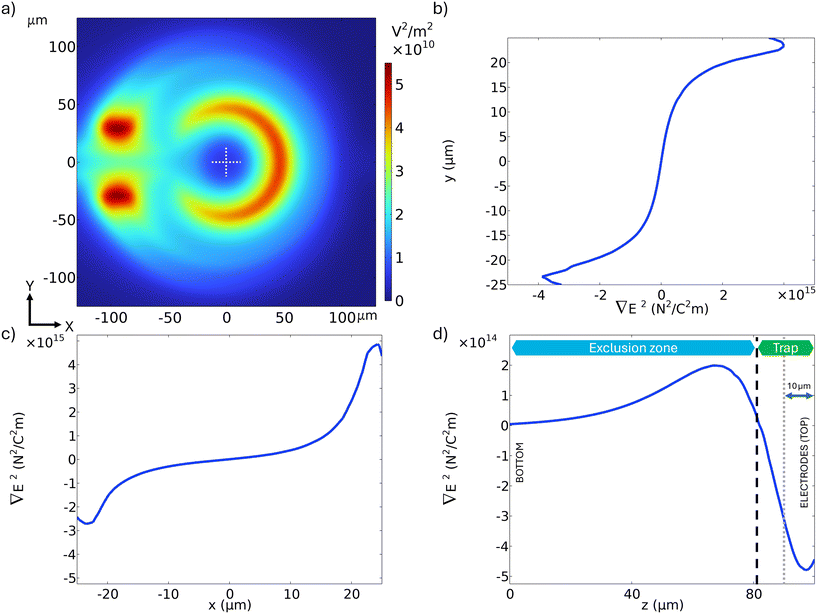
We performed electrostatics simulations with the COMSOL Multiphysics finite-elements platform to estimate the electric field created by our microelectrode configuration and to help interpret the experimental results. The simulation workflow is detailed in the ESI.†

Fig. 2a shows the squared electric-field distribution in the XY plane at a distance of 10 μm, i.e. z = 90 μm, from the glass where the planar microelectrodes lie as obtained from simulations (see dotted line in Fig. 2d). There, an electric field minimum can be observed in the centre of the electrodes at (x, y) = (0, 0), which leads to a stable dielectrophoretic trap if the CM factor is negative, which is in agreement with the experimental results. Fig. 2b–d depict the gradient of the squared electric field for the Y-axis, X-axis, and Z-axis, respectively. Fig. 2d shows that particles with a negative CM factor are pushed toward the top wall above z ≃ 80 μm (20 μm from the plane where the electrodes lie, see dashed line in Fig. 2d and S1†). Experimentally, we observed that this force is sufficient to overcome the gravity of the tested particles. Moreover, the positive value of the gradient below zero crossing leads to an exclusion region in which no particles are allowed, as shown in Fig. 2d and in Video S1.† This exclusion region is useful for conducting clean experiments in the trap; thus, no undesired particles are allowed to accidentally enter the trapping region as they freely diffuse and/or are brought by convection that might be present in the chamber.

Fig. 2 COMSOL Multiphysics simulation results. (a) Simulated squared electric field norm at 10 μm from the electrodes (dotted line in (d)). The white-dotted cross indicates the minimum at the centre of the electrodes. Linear profiles of the gradient of the squared electric field norm are also shown in (b) x = 0 and z = 98 μm, (c) y = 0 and z = 98 μm and (d) x = 0 and y = 0. The dashed line depicts the approximate position of the frontier, which separates the trapping region and the exclusion zone. The z values correspond to a distance of 2 μm from the electrodes.

3.2 Experimental results

3.2.1 Hybrid trap. One of the most interesting features of our design is the possibility it offers to be combined with optical tweezers, leading to a hybrid trap with enhanced manipulation capabilities, which allows the controlled load of particles in the DEP trap.^40,41,49 We here demonstrate that optical tweezers are compatible with the DEP trap and illustrate how these two approaches can be used to, e.g., load the DEP trap with particles previously trapped in optical tweezers. In the first experiment, we trapped one 1 μm polystyrene particle with the optical trap (see Fig. 1 and Materials and methods) at a power of 1 mW and then brought it to the vicinity of the electrodes when the electric signal was switched off. After recording one passive trajectory, we obtained the position histograms depicted with green diamonds in Fig. 3. As can be seen, the histogram thus obtained is Gaussian, and from its variance and equipartition theorem, we obtain estimations of the stiffness along the X–Y axes in different configurations. The stiffness of the optical trap (OT) in the X-axis is κ_OT,x ≃ 1.4 × 10⁻⁷ N m⁻¹ and κ_OT,y ≃ 1.1 × 10⁻⁷ N m⁻¹ in the Y-axis. As the laser power was very small, the optical trap alone was not stable enough to hold the particle for a long time. The hybrid trap was stable at such low power under stable DEP trapping conditions. In this case, the particle did not escape from the optical trap but remained trapped for some minutes. The trajectory analysis in this experiment returns the histogram shown in orange squares in Fig. 3. In this case, one can observe non-Gaussian tails due to the presence of the electric field, but this did not destabilize the trap. The stiffness of the hybrid trap (HT) is slightly reduced, obtaining κ_HT,x ≃ 7 × 10⁻⁸ N m⁻¹ and κ_HT,y ≃ 5 × 10⁻⁸ N m⁻¹, but similar to that obtained only with the OT. Finally, the DEP trap captured the particle when the optical trap was switched off. In this case, the histogram of the position is significantly broader (blue triangles in the figure), returning smaller values of the stiffness (κ_DEP,x ≃ 6 × 10⁻⁹ N m⁻¹ and κ_DEP,y ≃ 4 × 10⁻⁹ N m⁻¹). Under typical working conditions, the stiffness obtained with optical tweezers is higher than that achieved with DEP traps, although the potential depth of the latter is larger.

Fig. 3 Hybrid DEP–optical trap. 1D histograms of the (a) x and (b) y positions of a 1 μm polystyrene particle. The blue triangles correspond to the DEP trap, the green diamonds to the optical trap, and the orange squares to the combined trap. The solid lines represent fits to Gaussian functions. The power of the laser beam was the same (1 mW) in both the experiments performed with the optical and hybrid traps.

In addition to demonstrating the hybrid trap, we present an example of the manipulation capabilities of the hybrid trap. In this case, as shown in Fig. 4 (see also Video S5†), we optically trapped a few 1 μm SiO₂ particles arranged in a circumference thanks to an acousto-optic deflector that allows the optical tweezers to work in time-sharing mode,^5,50 thus effectively generating multiple traps (a). The acousto-optic deflector is controlled by software included in the commercial optical tweezers device. In the same image, the presence of particles stored in the DEP trap can be seen in a different plane (see the electrodes are out of focus). Moments later, we switched off the optical traps, so the particles moved toward the DEP trap (b). Finally, in the last frame (c), all the particles were inside the trapping region of the DEP trap. Hybrid trapping with the exclusion region allows experiments under clean conditions because no particles can accidentally enter the DEP trapping region.

Fig. 4 Controlled loading of the DEP trap from optical tweezers. (a) 1 μm SiO₂ particles optically trapped within the DEP trap. (b and c) After we switched off the optical traps, the particles quickly moved to the centre of the DEP trap. The white arrows indicate the net particle displacement throughout the video.

3.2.2 Dielectrophoretic trap characterization. The DEP trap presented here features a large influence volume, where particles that would otherwise freely diffuse are either pushed to the centre of the trap or away from its influence region, generating an exclusion region. This can be expected from the field distribution shown in Fig. 2d, which is in agreement with the experimental results (see Video S1†). The exclusion region is even more apparent in the case of dense particles, since in our design the DEP trap is located on the top of the fluidic chamber, and sedimentation also contributes to the exclusion effect. This could be overcome with the aforementioned hybrid trap configuration that allows a controlled load of particles.

We are interested in trapping at the centre of the ring (see Fig. 1), away from electrodes, where video tracking of particles is possible. As electrodes were made of gold (see Materials and methods), we avoided shining them directly. Thus, we maintained a distance of approximately 5 μm from the electrode border to avoid heating. Although not included in this paper, we also built electrodes with a smaller diameter and it worked adequately. According to simulations, there is a zero electric field with a positive slope in the XY plane at this position, so we need to work under conditions where the CM factor is negative. This is typically achieved above a characteristic frequency ω_c ≃ (K_p + 2K_m)/(ε_p + 2ε_m), where K_p and K_m are the conductivities of the particles and the medium, respectively.⁵¹

Dielectrophoretic traps are well known for their selective stability based on the cut-off frequency of the CM factor. To demonstrate this capability in our device, we introduced a mixture of 0.9 μm and 3.1 μm ProMag® particles. We used particles with a clear difference in radius to clearly demonstrate their different behaviors. As shown in Fig. 5a (see also Video S2†), we observe that at an electric voltage signal of 40 V_pp and a frequency of 20 MHz (Fig. 5b), both large and small particles are trapped. The smaller particles were expelled from the trap when the frequency was reduced to 4 MHz (Fig. 5b). Further, pushing out the large particles is possible by reducing the frequency to 600 kHz (Fig. 5c). The final ejection can also be achieved by turning off the electric field. However, in this case, the particles leave the trap mainly by diffusion and sedimentation, whereas in the previous case, the particles are expelled by the positive DEP force.

Fig. 5 Selective trapping. (a) The experiment starts with four 0.9 μm ProMag® 1 particles and three 3.1 μm ProMag® 3 particles trapped with an electric field of 40 V_pp and 20 MHz. (b) At a given time, we changed the frequency to 4 MHz, kicking out the small particles. (c) Larger particles can also be expelled from the trap by reducing the frequency down to 600 kHz.

We evaluated the DEP trapping device's characteristic frequency for different spherical particles. To do so, we selected particles from different sizes and materials, including polystyrene, ProMag® (a type of composite particles made of a mixture of polymeric matrix with embedded magnetite), and SiO₂ particles (see Materials and methods). We will leave for future experiments the use of particles with a non-spherical shape, where high-order DEP effects come into play⁵² but can be optically trapped,⁵³ and with more exotic materials, such as carbons⁵⁴ or other type of light-absorbing materials. Our results are shown in Table 1, demonstrating that this parameter can be used as a way to selectively push particles out of the trap. In particular, the cut-off frequency decreases with particle size, in agreement with previous observations.⁵¹ A detailed analysis of how the cut-off frequency depends on particle properties is out of the scope of the present work.

Table 1 Cut-off frequency for different particles. Frequency below which trapping is not possible at the electric field minimum due to a change to positive CM factor, i.e., the frequency at which there is a transition from nDEP to pDEP

	Polystyrene (PS)			ProMag®		Silica (Si)
Size (μm)	0.2	0.5	1	1	3	0.5	1
f c (MHz)	10	7	3	9	2	5	2

---

We characterized the trapping performance for a single absorbing microparticle (ProMag® 1, mean diameter 0.906 μm) in the DEP device, obtaining the results shown in Fig. 6. Due to their strong absorption, these particles are hard to trap in an optical tweezers device.^16,55,56 To that aim, we recorded videos of the Brownian motion of a single particle in the trap and computed the MSD of the trajectories obtained with Trackpy, which is a particle tracking package for Python (see Materials and methods).^57,58 The motion corresponds to quasi-2D diffusion in a parabolic potential, as shown in Fig. 6a. The MSD is proportional to time for short times, while it features a plateau above a characteristic time, in agreement with eqn (2). We observe that the confinement increases as the voltage is raised, and for a fixed T ≃ 300 K, this means an increase in the stiffness of the trap. Even if our device does not have precise temperature control, the fact that the slope of the MSD at short times does not change significantly (∼12% between 16 and 40 V_pp) with voltage indicates that the temperature was moderately stable throughout the experiment, and the observed variation in the plateau level cannot be explained by temperature changes. From fits of experimental data to eqn (2), we obtain values for the stiffness of the trap κ and the friction coefficient γ. As shown in Fig. 6b, the stiffness increases linearly with the applied voltage. In contrast, the friction coefficient did not show any clear dependence with voltage, so we compute the average of the values obtained from the fits, obtaining γ = 1.02 ± 0.25 × 10⁻⁸ Ns m⁻¹, where the uncertainty refers to the standard error of the mean. This value is larger than the expected value from the Stokes friction coefficient γ ≃ 0.73 × 10⁻⁸ Ns m⁻¹ at T = 300 K. This disagreement can be solved by considering that the trapping occurs very close to the top of the chamber and that the friction coefficient should be corrected for the hydrodynamic interactions.⁵⁹ Using Faxen's law, the dependence of γ with the distance to the wall can be evaluated, obtaining that trapping occurs at a distance of about 0.4 μm to the wall, in agreement with the fact that we observe that trapping occurs slightly displaced from the plane where the electrodes are seen in focus.

Fig. 6 Evaluation of the trapping performance of individual particles. (a) Mean squared displacement for different voltages for ProMag® 1 particles with the electric field frequency fixed at 10 MHz. Notice that the particles behave as freely diffusing for short times with the slope 4k_BT/γ, while featuring a plateau at 4k_BT/κ above the characteristic time defined by γ/κ. (b) Trap stiffness κ for different voltage values. The dashed line corresponds to a linear fit with slope 0.15 ± 0.01 fN Vμm⁻¹ and intercept −1.60 ± 0.28 fN μm⁻¹.

3.2.3 Tracking the Brownian dynamics of groups of particles in the DEP trap. A key capability of the DEP trap, as opposed to conventional optical tweezers, consists of trapping several particles while tracking their trajectories individually. The information obtained this way can be used, e.g., to analyse how interactions between particles affect their Brownian dynamics inside a parabolic potential. To illustrate this capability, we recorded videos with increasing numbers of ProMag® 1 particles in the trap at 40 V_pp and f = 10 MHz, conditions that we had previously found to lead to a stable trapping situation. After that, the trajectories were extracted for every particle in each video using a modified Trackpy code.⁵⁷ Further, we calculated for every experiment the individual mean square displacement (IMSD) and the ensemble mean square displacement (EMSD), i.e., the average of all of the individuals in each group. We analysed experiments with up to 10 particles simultaneously stored in the trap since our tracking code did not provide reliable results for larger groups of particles. The results of these experiments are summarized in Fig. 7, where we used the EMSD data to calculate the fitting parameters κ and γ. Increasing the number of particles in the trap leads to a decrease in stiffness and an increase in the friction coefficient. However, these results should be considered with caution. Even if an increase in the friction coefficient is expected because of particle–particle interactions, the observed decreasing trend in trap stiffness is not justified and is likewise due to interactions unaccounted in our description based on eqn (1) and (2), which consider a single particle in a parabolic potential.

Fig. 7 Characterization of the effect of multiple ProMag® 1 particles in the DEP trap. Trap stiffness (left axis) and viscous friction coefficient (right axis) for different groups of ProMag® 1 particles. Error bars stand for the uncertainty of the fit.

3.2.4 DEP trap modulation. The trap stiffness can be controlled through the voltage applied to the electrodes. When several particles are trapped together, modulating the voltage also modulates the trap stiffness, effectively changing the local density of particles, as shown in Fig. 8. In Fig. 8a, we illustrate the effect of voltage modulation with some tens of 1 μm polystyrene particles (see also Videos S3 and S4†). When the voltage is low (below 4 V, see Fig. 8a, left), the particles explore a large volume due to Brownian fluctuations. The stiffness increases as the voltage is raised (above 4 V) and the particles are strongly pushed towards the trap's centre, as seen in the right image in Fig. 8a.

Fig. 8 Trap modulation. (a) Cycles of expansion (left) and compression (right) of 1 μm polystyrene particles. Average distance between the 1 μm polystyrene particles for 2 (b) and 5 s (c) period cycles, respectively. The green dashed line is the modulated amplitude of the feed voltage, while the blue dots are the averaged distance between every two particles, vs. cycle time. The error bars represent the standard deviation from the repeated cycles.

Quantitative density modulation experiments can be performed using a small number of particles. We conducted two experiments in which the amplitude of the electric field was modulated according to the protocols shown in Fig. 8b and c, corresponding to modulation cycles of period 2 s and 5 s, respectively. We arbitrarily selected two values of the periods that were sufficiently different to allow us to understand how the frequency affects the system's behavior. We analyzed this type of experiment by recording videos at 5 fps of the trajectories of 16 (600 cycles of modulation at 500 mHz, i.e., cycles of period 2 s) and 14 particles (240 cycles of modulation at 200 mHz, i.e., cycles of period 5 s). These trajectories were analyzed using Trackpy, and the distance between each pair of particles was measured and averaged over each time frame. Finally, further averaging over cycles yields the results shown in Fig. 8b and c. The average distance between particles decreases when the amplitude of the 10 MHz signal is maximum, while it increases in the parts of the cycle when the trap is relaxed and even switched off. Notice that the particles do not move only in the focal plane (XY) but are also displaced along the optical axis (Z), being defocused when the electric field is low and getting back into focus when the electric field is high. Unfortunately, our tracking software could not account for displacements along this axis, and the data provided correspond to the projection on the XY plane. Although during some parts of the period the voltage was zero, the particles did not escape the trap because the diffusion time of the particles is greater than the time-lapse with 0 V, and the particles are recaptured periodically. The average distance allows us to quantify the increase or decrease of the volume explored by the particles during the expansion or compression parts of the cycle. That distance could be used as a way to evaluate the interactions between particles, because these will strongly affect the explored volume.⁶⁰

4 Conclusions and outlook

We designed and characterized a novel hybrid optical–DEP platform that can store microparticles in aqueous suspension. The microelectrode arrangement used for DEP trapping has broad optical access, so it can be combined with an optical tweezers platform, allowing for a hybrid trapping scheme, which favours the controlled loading of the DEP trap. We have shown that a single particle in the DEP trap behaves like an overdamped Brownian particle confined in a parabolic potential, similar to a particle in optical tweezers. Interestingly, the DEP trap is not limited to dielectric particles but sets the stage for experiments with different materials (e.g., carbon, metallic, or other types of light-absorbing particles).⁵⁴

We also demonstrated that the DEP trap allows one to store several Brownian particles in the same potential well and simultaneously track their dynamics either in equilibrium or under the modulation of the trapping potential. This opens the door to the implementation of paradigmatic experiments in statistical physics that have so far only been performed with individual particles in optical tweezers, including fundamental questions in stochastic thermodynamic^61–63 implementation of stochastic heat engines^12,64,65 or counter-intuitive relaxation phenomena,^66–69 to the case of multiple interacting particles.

Regarding the device limitations, care must be taken when using the laser close to the electrodes. Strong absorption can generate local heating, leading to unwanted effects such as electrothermal flow,^70–72 or bubble formation⁷³ followed by Marangoni flows, which can destabilize the trap. However, these mechanisms could also be used to rapidly bring new particles to the trapping region, as has been recently demonstrated,^74–76 and their control in our platform is therefore worth exploring in the future. Another issue can arise when trapping absorbing particles, since the absorption of radiation will increase the internal temperature of the particles themselves and the surrounding liquid, thus changing their dielectric properties. Moreover, a radial temperature gradient is expected to appear around illuminated particles, with concomitant gradients in viscosity. This generates a non-equilibrium steady-state known as hot Brownian motion, which could further increase the complexity of the problem.^16,17,77

Finally, the demonstrated capabilities of selective trapping and hybrid operation permit the realization of applications where sorting, filtering, or selective loading can be needed during the implementation of biochemical assays because the interaction of different species can be forced or modulated for sensing applications.

5 Materials and methods

Our dielectrophoretic trap is constructed by two concentric gold ring microelectrodes deposited on borosilicate glass (see experimental setup in Fig. 1) and implemented together with an optical tweezers setup that allows us to create a hybrid trap for enhanced manipulation capabilities. In our case, the radius of the inner ring electrode was set to a = 36 μm, while the outer one to b = 100 μm.

The electrodes were fabricated using optical lithography and a wet etching process. A 100 nm layer of gold was deposited using e-beam evaporation on a 4 inch diameter and 500 μm thick borosilicate wafer. A 5 nm thick chromium layer was used as an adhesion layer. Then, the wafer was coated with HMDS vapor phase and later spin-coated with 1.2 μm of AZ1512 photoresist. After exposure, the sample was developed and shortly exposed to oxygen plasma (200 W for 30 s) before the wet etching process. Gold and chromium solutions were prepared at 1 : 1 (TFA) and 1 : 4 (TechniEtch Cr n : 1) parts with deionized water and the sample was etched at room temperature for 50 s and 15 s, respectively. Next, the resist was stripped with acetone in an ultrasonic bath for 10 minutes. Lastly, the sample was prepared with a protective resist coating for dicing.

We used one microfluidic cell for each sample. Before experiments, a certain preparation of the extracted chip (the electrode pair deposited over a borosilicate substrate) from the wafer was required. They were first cleaned with acetone and then welded to two wolfram gold-coated wires using a conducting epoxy resin (Chemtronics CW2400). Next, the chip with the two welded wires was glued with high-viscosity KORASILON® paste, at two opposite edges, to a #1 high-precision coverslip (thickness 170 ± 5 μm), leaving some free vertical space of 100 μm where the suspension will subsequently be introduced. It was left for 24 hours for the epoxy to be fully cured. Then the particle suspension was introduced into the chamber and sealed with more KORASILON® paste.

A JPK Bruker NanoTracker II optical tweezers platform and a signal generator from RSPro, RSDG 1032X, were utilized. The commercial optical tweezers platform consists of an inverted microscope (63×, NA = 1.2) with a near-infrared laser with a wavelength of 1064 nm, as schematically depicted in Fig. 1. A microfluidic chip with embedded microelectrodes was placed in the stage of the optical tweezers device, and the electrodes were connected to a signal generator via BNC cables (see Fig. 1 and S2†). In our experiments, the electrodes were located on the top of the fluidic microchamber, so trapping occurs even against gravity. We measured the thickness of every chamber, obtaining a value of around 100 μm in all cases.

The microparticles used were 0.2 ± 0.1 μm, 0.5 ± 0.1 μm and 1.0 ± 0.2 μm diameter commercially available polystyrene particles supplied by IKERLAT, 0.5 ± 0.1 μm and 1.0 ± 0.3 μm commercially available silica particles supplied by Sigma-Aldrich Co., and 0.9 ± 0.2 μm and 3.1 ± 0.3 μm mean diameter commercially available ProMag® particles supplied by Bangs Laboratories, Inc. The latter ones strongly polarize in the presence of an AC electric field and tend to form chains. We adjusted the required particle concentrations for each experiment by diluting the initial samples with Milli-Q water.

Table 2 provides more data on the particles used in the experiments. Due to their rapid sedimentation, we could not measure the electrophoretic mobility of ProMag® 3. The data for the magnetite content of ProMag® 1 and ProMag® 3 was supplied by Bangs Laboratories, Inc. Polystyrene samples were purchased from IKERLAT, and SiO₂ ones from Sigma-Aldrich Co. LLC. The electrophoretic mobility and hydrodynamic radius were measured using a Malvern PANalytical Zetasizer Nano S.

Table 2 Properties of the different microparticles used in experiments

Catalog code	PMC1N/14514	PMC3HP/11653	Polystyrene			Silica
Product name	ProMag® 1 COOH	ProMag® 3 COOH	PS200	PS500	PS1000	Si500	Si1000
Mean diameter (μm)	0.9 ± 0.2	3.1 ± 0.3	0.2 ± 0.1	0.5 ± 0.1	1.0 ± 0.2	0.5 ± 0.1	1.0 ± 0.3
Density (g cm^−3)	1.8	1.4	1.05	1.05	1.05	2.6	2.6
Magnetite content (wt%)	26.5	16.0	—	—	—	—	—
Electrophoretic mobility (μmcm Vs^−1)	−2.7 ± 0.1	—	−2.7 ± 0.2	−1.7 ± 0.1	−2.3 ± 0.1	−3.4 ± 0.1	−3.8 ± 0.1
Hydrodynamic radius (nm)	864 ± 38	—	197.9 ± 2.5	424 ± 29	644 ± 10	428.8 ± 2.7	832 ± 80

---

The tracking experiments were recorded with the CMOS camera available from the optical tweezers setup, and the tracking analysis was carried out with modified Trackpy codes^57,58 tailored for each experiment. Once the particle trajectories were obtained, we performed the different analyses corresponding to each experiment.

Data availability

Data for this article, including datasets for the figures, are available at Zenodo at https://doi.org/10.5281/zenodo.14184936. The data supporting the COMSOL Multiphysics simulation have been included in the ESI† and in the Zenodo repository. The code for Trackpy can be found at https://zenodo.org/records/4682814 with DOI https://doi.org/10.5281/zenodo.4682814. The version of the code used in this study is version v0.5.0.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

Financial support from Grant PID2021-127427NB-I00 funded by MICIU/AEI/10.13039/501100011033, ERDF/EU European Union, and FEDER/Junta de Andalucía-Consejería de Economía y Conocimiento/Project P18-FR-3583 is acknowledged. Funding for open access charge: Universidad de Granada.

Notes and references

1. K. Lee, R. Mishra and T. Kim, Review of Micro/Nanofluidic Particle Separation Mechanisms: Toward Combined Multiple Physical Fields for Nanoparticles, Sens. Actuators, A, 2023, 363, 114688,  DOI:10.1016/j.sna.2023.114688.
2. E. Lambert, E. Barthout, T. Provent, R. Manczak, S. Saada and B. Bessette, et al. Lab-On-Chip UHF-Dielectrophoretic Cytometer for Colorectal Cancer Stem Cells Sorting, IEEE J. Electromagn. RF Microw. Med. Biol., 2023, 1–8,  DOI:10.1109/JERM.2023.3234463.
3. J. Xie, H. Pang, R. Sun, T. Wang, X. Meng and Z. Zhou, Development of Rapid and High-Precision Colorimetric Device for Organophosphorus Pesticide Detection Based on Microfluidic Mixer Chip, Micromachines, 2021, 12(3), 290,  DOI:10.3390/mi12030290.
4. M. Z. H. Khan, M. R. Hasan, S. I. Hossain, M. S. Ahommed and M. Daizy, Ultrasensitive detection of pathogenic viruses with electrochemical biosensor: State of the art, Biosens. Bioelectron., 2020, 166, 112431,  DOI:10.1016/j.bios.2020.112431.
5. J. Gieseler, J. R. Gomez-Solano, A. Magazzù, I. P. Castillo, L. P. García and M. Gironella-Torrent, et al. Optical tweezers—from calibration to applications: a tutorial, Adv. Opt. Photonics, 2021, 13, 74–241,  DOI:10.1364/AOP.394888.
6. G. Volpe, O. M. Maragò, H. Rubinsztein-Dunlop, G. Pesce, A. B. Stilgoe and G. Volpe, et al. Roadmap for optical tweezers, JPhys Photonics, 2023, 5, 022501,  DOI:10.1088/2515-7647/acb57b.
7. C. J. Bustamante, Y. R. Chemla, S. Liu and M. D. Wang, Optical tweezers in single-molecule biophysics, Nat. Rev. Methods Primers, 2021, 1, 25,  DOI:10.1038/s43586-021-00021-6.
8. R. M. Robertson-Anderson, Optical Tweezers Microrheology: From the Basics to Advanced Techniques and Applications, ACS Macro Lett., 2018, 7, 968–975,  DOI:10.1021/acsmacrolett.8b00498.
9. S. C. Chapin, V. Germain and E. R. Dufresne, Automated trapping, assembly, and sorting with holographic optical tweezers, Opt. Express, 2006, 14, 13095–13100,  DOI:10.1364/OE.14.013095.
10. J. Penders, I. J. Pence, C. C. Horgan, M. S. Bergholt, C. S. Wood and A. Najer, et al. Single particle automated raman trapping analysis, Nat. Commun., 2018, 9, 1–11,  DOI:10.1038/s41467-018-06397-6.
11. X. Dai, W. Fu, H. Chi, V. S. D. Mesias, H. Zhu and C. W. Leung, et al. Optical tweezers-controlled hotspot for sensitive and reproducible surface-enhanced Raman spectroscopy characterization of native protein structures, Nat. Commun., 2021, 12, 1292,  DOI:10.1038/s41467-021-21543-3.
12. I. A. Martínez, E. Roldán, L. Dinis and R. A. Rica, Colloidal heat engines: a review, Soft Matter, 2017, 13, 22–36,  10.1039/C6SM00923A.
13. E. J. Peterman, F. Gittes and C. F. Schmidt, Laser-induced heating in optical traps, Biophys. J., 2003, 84, 1308–1316,  DOI:10.1016/S0006-3495(03)74946-7.
14. F. Català, F. Marsà, M. Montes-Usategui, A. Farré and E. Martín-Badosa, Influence of experimental parameters on the laser heating of an optical trap, Sci. Rep., 2017, 7, 16052,  DOI:10.1038/s41598-017-15904-6.
15. D. Lu, F. Gámez and P. Haro-González, Temperature effects on optical trapping stability, Micromachines, 2021, 12, 954,  DOI:10.3390/mi12080954.
16. M. A. Fernandez-Rodriguez, S. Orozco-Barrera, W. Sun, F. Gámez, C. Caro and M. L. García-Martín, et al., Hot Brownian Motion of thermoresponsive microgels in optical tweezers shows discontinuous volume phase transition and bistability, Small, 2023, 19, 2301653,  DOI:10.1002/smll.202301653.
17. E. Ortiz-Rivero, S. Orozco-Barrera, H. Chatterjee, C. D. González-Gómez, C. Caro and M. L. García-Martín, et al. Light-to-heat conversion of optically trapped hot Brownian particles, ACS Nano, 2023, 17, 24961–24971,  DOI:10.1021/acsnano.3c07086.
18. S. E. S. Spesyvtseva and K. Dholakia, Trapping in a material world, ACS Photonics, 2016, 3, 719–736,  DOI:10.1021/acsphotonics.6b00023.
19. C. Min, Z. Shen, J. Shen, Y. Zhang, H. Fang and G. Yuan, et al. Focused Plasmonic Trapping of Metallic Particles, Nat. Commun., 2013, 4, 2891,  DOI:10.1038/ncomms3891.
20. M. L. Juan, M. Righini and R. Quidant, Plasmon nanooptical tweezers, Nat. Photonics, 2011, 5, 349–356,  DOI:10.1038/nphoton.2011.56.
21. C. Zhang, K. Khoshmanesh, A. Mitchell and K. Kalantar-zadeh, Dielectrophoresis for manipulation of micro/nano particles in microfluidic systems, Anal. Bioanal. Chem., 2010, 396, 401–420,  DOI:10.1007/s00216-009-2922-6.
22. R. Pethig, Dielectrophoresis: Status of the theory, technology, and applications, Biomicrofluidics, 2010, 4(2), 022811,  DOI:10.1063/1.3456626.
23. L. D'Amico, N. Ajami, J. Adachi, P. Gascoyne and J. Petrosino, Isolation and concentration of bacteria from blood using microfluidic membraneless dialysis and dielectrophoresis, Lab Chip, 2017, 17, 1340–1348,  10.1039/C6LC01277A.
24. H. A. Pohl, The Motion and Precipitation of Suspensoids in Divergent Electric Fields, J. Appl. Phys., 1951, 22, 869–871,  DOI:10.1063/1.1700065.
25. H. A. Pohl, Some Effects of Nonuniform Fields on Dielectrics, J. Appl. Phys., 1958, 29, 1182–1188,  DOI:10.1063/1.1723398.
26. H. Morgan and N. G. Green, AC Electrokinetics: Colloids and Nanoparticles, Microtechnologies and Microsystems Series, Research Studies Press, 2003.
27. A. Rosenthal and J. Voldman, Dielectrophoretic Traps for Single-Particle Patterning, Biophys. J., 2005, 88, 2193–2205,  DOI:10.1529/biophysj.104.049684.
28. M. Lorenz, D. Malangré, F. Du, M. Baune, J. Thöming and G. R. Pesch, High-throughput dielectrophoretic filtration of submicron and micro particles in macroscopic porous materials, Anal. Bioanal. Chem., 2020, 412, 3903–3914,  DOI:10.1007/s00216-020-02557-0.
29. L. A. N. Julius, H. Scheidt, G. Krishnan, M. Becker, O. Nassar and S. M. Torres-Delgado, et al. Dynamic dielectrophoretic cell manipulation is enabled by an innovative electronics plat-form, Biosens. Bioelectron.:X, 2023, 14, 100333,  DOI:10.1016/j.biosx.2023.100333.
30. I. Turcan and M. A. Olariu, Dielectrophoretic Manipulation of Cancer Cells and Their Electrical Characterization, ACS Comb. Sci., 2020, 22, 554–578,  DOI:10.1021/acscombsci.0c00109.
31. G. I. Russo, N. Musso, A. Romano, G. Caruso, S. Petralia, L. Lanzanò, G. Broggi and M. Camarda, The Role of Dielectrophoresis for Cancer Diagnosis and Prognosis, Cancers, 2022, 14(1), 198,  DOI:10.3390/cancers14010198.
32. W. Paul, Electromagnetic traps for charged and neutral particles, Rev. Mod. Phys., 1990, 62, 531–540,  DOI:10.1103/RevModPhys.62.531.
33. W. Guan, S. Joseph, J. H. Park and P. S. Krstić, Reed MA. Paul trapping of charged particles in aqueous solution, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9326–9330,  DOI:10.1073/pnas.1100977108.
34. U. K. Krieger, C. Marcolli and J. P. Reid, Exploring the complexity of aerosol particle properties and processes using single particle techniques, Chem. Soc. Rev., 2012, 41, 6631–6662,  10.1039/C2CS35082C.
35. R. F. Wuerker, H. Shelton and R. Langmuir, Electrodynamic containment of charged particles, J. Appl. Phys., 1959, 30, 342–349,  DOI:10.1063/1.1735165.
36. W. Guan, J. H. Park, P. S. Krstić and M. A. Reed, Non-vanishing ponderomotive AC electrophoretic effect for particle trapping, Nanotechnology, 2011, 22, 245103,  DOI:10.1088/0957-4484/22/24/245103.
37. J. H. Park and P. S. Krstić, Stability of an aqueous quadrupole microtrap, J. Phys.: Condens. Matter, 2012, 24, 164208,  DOI:10.1088/0953-8984/24/16/164208.
38. J. Millen, P. Fonseca, T. Mavrogordatos, T. Monteiro and P. Barker, Cavity cooling a single charged levitated nanosphere, Phys. Rev. Lett., 2015, 114, 123602,  DOI:10.1103/PhysRevLett.114.123602.
39. G. P. Conangla, A. W. Schell, R. A. Rica and R. Quidant, Motion Control and Optical Interrogation of a Levitating Single Nitrogen Vacancy in Vacuum, Nano Lett., 2018, 18, 3956–3961,  DOI:10.1021/acs.nanolett.8b01414.
40. G. P. Conangla, R. A. Rica and R. Quidant, Extending Vacuum Trapping to Absorbing Objects with Hybrid Paul-Optical Traps, Nano Lett., 2020, 20, 6018–6023,  DOI:10.1021/acs.nanolett.0c02025.
41. D. S. Bykov, M. Meusburger, L. Dania and T. E. Northup, Hybrid electro-optical trap for experiments with levitated particles in vacuum, Rev. Sci. Instrum., 2022, 93, 073201,  DOI:10.1063/5.0096391.
42. C. A. Carlson, X. S. Udad, Q. Owen, A. P. Amin-Patel, W. J. Chang and J. C. Woehl, DC corral trapping of single nanoparticles and macromolecules in solution, J. Chem. Phys., 2022, 156, 164201,  DOI:10.1063/5.0087039.
43. T. J. Kwak, H. Lee, S. W. Lee, J. C. Woehl and W. J. Chang, Size-Selective Particle Trapping in Dielectrophoretic Corral Traps, J. Phys. Chem. C, 2021, 125, 6278–6286,  DOI:10.1021/acs.jpcc.0c10592.
44. I. Alda, J. Berthelot, R. A. Rica and R. Quidant, Trapping and manipulation of individual nanoparticles in a planar Paul trap, Appl. Phys. Lett., 2016, 109, 163105,  DOI:10.1063/1.4965859.
45. M. T. Wei, J. Junio and H. D. Ou-Yang, Direct measurements of the frequency-dependent dielectrophoresis force, Biomicrofluidics, 2009, 3, 012003,  DOI:10.1063/1.3058569.
46. J. Wang, M. T. Wei and H. D. Ou-Yang, Low-frequency dielectrophoretic response of a single particle in aqueous suspensions, Biomicrofluidics, 2016, 10, 014108,  DOI:10.1063/1.4940037.
47. M. Riccardi and O. J. Martin, Electromagnetic forces and torques: From dielectrophoresis to optical tweezers, Chem. Rev., 2023, 123, 1680–1711,  DOI:10.1021/acs.chemrev.2c00576.
48. P. H. Jones, O. M. Maragò and G. Volpe, Optical Tweezers: Principles and Applications, Cambridge University Press, 2015,  DOI:10.1017/CBO9781107279711.
49. E. Bonvin, L. Devaud, M. Rossi, A. Militaru, L. Dania and D. S. Bykov, et al. Hybrid Paul-optical trap with large optical access for levitated optomechanics, Phys. Rev. Res., 2024, 6, 043129,  DOI:10.1103/PhysRevResearch.6.043129.
50. G. Pesce, P. H. Jones, O. M. Maragò and G. Volpe, Optical tweezers: theory and practice, Eur. Phys. J. Plus, 2020, 135, 1–38,  DOI:10.1140/epjp/s13360-020-00843-5.
51. N. G. Green and H. Morgan, Dielectrophoresis of submicrometer latex spheres. 1. Experimental results, J. Phys. Chem. B, 1999, 103, 41–50,  DOI:10.1021/jp9829849.
52. H. Nili and N. G. Green, Higher-order dielectrophoresis of nonspherical particles, Phys. Rev. E, 2014, 89, 063302,  DOI:10.1103/PhysRevE.89.063302.
53. O. Brzobohatý, M. Šiler, J. Trojek, L. Chvátal, V. Karásek and P. Zemánek, Non-spherical gold nanoparticles trapped in optical tweezers: shape matters, Opt. Express, 2015, 23, 8179–8189,  DOI:10.1364/OE.23.008179.
54. C. Zhang, K. Khoshmanesh, F. J. Tovar-Lopez, A. Mitchell, W. Wlodarski and K. Klantar-zadeh, Dielectrophoretic separation of carbon nanotubes and polystyrene microparticles, Microfluid. Nanofluid., 2009, 7, 633–645,  DOI:10.1007/s10404-009-0419-4.
55. M. Siler, P. Jákl, O. Brzobohatý, J. Jezek and P. Zemánek, Anomalous behavior of a three-dimensional, optically trapped, superparamagnetic particle, in Optical Trapping and Optical Micromanipulation XI, SPIE, 2014, vol. 9164, pp. 475–482,  DOI:10.1117/12.2062148.
56. P. A. Quinto-Su, A microscopic steam engine implemented in an optical tweezer, Nat. Commun., 2014, 5, 5889,  DOI:10.1038/ncomms6889.
57. D. B. Allan, T. Caswell, N. C. Keim, C. M. van der Wel and R. W. Verweij, Trackpy v0.5.0. Zenodo, 2021, p. 1,  DOI:10.5281/zenodo.4682814.
58. G. D. Vanrossum and J. M. DeBoer, Interactively Testing Remote Servers Using The Python Programming Language, CWI Quarterly, 1991, 4, 283–304.
59. E. Schäffer, S. F. Nørrelykke and J. Howard, Surface Forces and Drag Coefficients of Microspheres near a Plane Surface Measured with Optical Tweezers, Langmuir, 2007, 23, 3654–3665,  DOI:10.1021/la0622368.
60. P. Hurtado and P. Krapivsky, Compact waves in microscopic nonlinear diffusion, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2012, 85, 060103,  DOI:10.1103/PhysRevE.85.060103.
61. S. Toyabe, T. Sagawa, M. Ueda, E. Muneyuki and M. Sano, Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality, Nat. Phys., 2010, 6, 988–992,  DOI:10.1038/nphys1821.
62. A. Bérut, A. Arakelyan, A. Petrosyan, S. Ciliberto, R. Dillenschneider and E. Lutz, Experimental verification of Landauer's principle linking information and thermodynamics, Nature, 2012, 483, 187–189,  DOI:10.1038/nature10872.
63. S. Ciliberto, Experiments in stochastic thermodynamics: Short history and perspectives, Phys. Rev. X, 2017, 7, 021051,  DOI:10.1103/PhysRevX.7.021051.
64. V. Blickle and C. Bechinger, Realization of a micrometresized stochastic heat engine, Nat. Phys., 2012, 8, 143–146,  DOI:10.1038/nphys2163.
65. I. A. Martínez, É. Roldán, L. Dinis, D. Petrov, J. M. R. Parrondo and R. A. Rica, Brownian Carnot engine, Nat. Phys., 2016, 12, 67–70,  DOI:10.1038/nphys3518.
66. I. A. Martínez, A. Petrosyan, D. Guéry-Odelin, E. Trizac and S. Ciliberto, Engineered swift equilibration of a Brownian particle, Nat. Phys., 2016, 12, 843–846,  DOI:10.1038/nphys3758.
67. A. Kumar and J. Bechhoefer, Exponentially faster cooling in a colloidal system, Nature, 2020, 584, 64–68,  DOI:10.1038/s41586-020-2560-x.
68. L. B. Pires, R. Goerlich, A. L. da Fonseca, M. Debiossac, P. A. Hervieux and G. Manfredi, et al. Optimal time-entropy bounds and speed limits for Brownian thermal shortcuts, Phys. Rev. Lett., 2023, 131, 097101,  DOI:10.1103/PhysRevLett.131.097101.
69. M. Ibánez, C. Dieball, A. Lasanta, A. Godec and R. A. Rica, Heating and cooling are fundamentally asymmetric and evolve along distinct pathways, Nat. Phys., 2024, 20, 135–141,  DOI:10.1038/s41567-023-02269-z.
70. N. G. Green, A. Ramos, A. González, A. Castellanos and H. Morgan, Electric field induced fluid flow on microelectrodes: the effect of illumination, J. Phys. D: Appl. Phys., 2000, 33, L13,  DOI:10.1088/0022-3727/33/2/102.
71. N. G. Green, A. Ramos, A. Gonzalez, A. Castellanos and H. Morgan, Electrothermally induced fluid flow on microelectrodes, J. Electrost., 2001, 53, 71–87,  DOI:10.1016/S0304-3886(01)00132-2.
72. J. S. Kwon and S. T. Wereley, Light-actuated electrothermal microfluidic motion: experimental investigation and physical interpretation, Microfluid. Nanofluid., 2015, 19, 609–619,  DOI:10.1007/s10404-015-1587-z.
73. Y. Wang, M. E. Zaytsev, H. L. The, J. C. Eijkel, H. J. Zandvliet and X. Zhang, et al. Vapor and gas-bubble growth dynamics around laser-irradiated, water-immersed plasmonic nanoparticles, ACS Nano, 2017, 11, 2045–2051,  DOI:10.1021/acsnano.6b08229.
74. J. C. Ndukaife, A. V. Kildishev, A. G. A. Nnanna, V. M. Shalaev, S. T. Wereley and A. Boltasseva, Long-range and rapid transport of individual nano-objects by a hybrid electrothermoplasmonic nanotweezer, Nat. Nanotechnol., 2016, 11, 53–59,  DOI:10.1038/nnano.2015.248.
75. J. Garcia-Guirado, R. A. Rica, J. Ortega, J. Medina, V. Sanz and E. Ruiz-Reina, et al. Overcoming diffusion-limited biosensing by electrothermoplasmonics, ACS Photonics, 2018, 5, 3673–3679,  DOI:10.1021/acsphotonics.8b00681.
76. A. Kotnala, P. S. Kollipara, J. Li and Y. Zheng, Overcoming diffusion-limited trapping in nanoaperture tweezers using opto-thermal-induced flow, Nano Lett., 2019, 20, 768–779,  DOI:10.1038/nmat1528.
77. D. Rings, R. Schachoff, M. Selmke, F. Cichos and K. Kroy, Hot Brownian Motion, Phys. Rev. Lett., 2010, 105, 090604,  DOI:10.1103/PhysRevLett.105.090604.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00982g

---