Microfluidic system for efficient molecular delivery to artificial cell membranes

Abstract

The cell membrane is a crucial biological interface to consider in biomedical research, as a significant proportion of drugs interacts with this barrier. While understanding membrane–drug interactions is important, existing in vitro platforms for drug screening predominantly focus on interactions with whole cells or tissues. This preference is partly due to the instability of membrane-based systems and the technical challenges associated with buffer replacement around lipid membranes formed on microfluidic chips. Here, we introduce a novel microfluidic design capable of forming stable freestanding lipid bilayers with efficient replacement of the media in their local environment for molecular delivery to the membrane. With the use of bubble traps and resistance channels, we achieved sufficient hydrodynamic control to maintain membrane stability during the membrane formation and the molecular delivery phases. As a proof of concept, we successfully formed 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC) bilayers on the chip and delivered the antibiotic azithromycin at low (5 μM) and high (250 μM) doses. Using optical tweezers, we characterized how azithromycin influenced the membrane elastic properties, including tension and bending rigidity. This microfluidic device is a versatile tool that can deliver various buffers, molecules or nano-/microparticles to freestanding membranes, and study the resulting impact on the membranes' properties.

---

1. Introduction

Drug discovery is a time-consuming, complex and expensive process. The drug industry is heavily researching on developing in vitro platforms for evaluating the absorption, distribution, metabolism, excretion, and toxicity (ADMET) of therapeutic agents at early stages of drug development.^1,2 A large group of therapeutic agents targets the cell membrane or has to infiltrate it to reach the cell content.^3,4 In either case, the cell membrane is at the frontline, hence the importance of considering the physicochemical and mechanical properties of membranes when evaluating drug–membrane interactions.^5,6 The interaction between drugs and cell membranes can also be viewed from another angle: drug molecules can alter membrane properties (e.g. elasticity,⁷ which is linked to vital processes like cell growth and division⁸). Therefore, an in vitro platform for controlled molecular delivery to cell membranes is highly demanded, preferably with high throughput.⁹ This would provide insights into how the physicochemical properties of molecules delivered to the membrane (e.g., drug candidates) affect the cell membrane properties.^10–12

While drug–membrane interactions are an important aspect to consider in pharmaceutical research, most microfluidic drug-screening systems are cell-based with on-chip drug delivery to bacteria,¹³ cellular tissues,¹⁴ cell monolayers,¹⁵ or biofilms.¹⁶ Cellular models are limited in their ability to facilitate controlled biophysical studies or provide detailed molecular-level information, both of which are crucial for accurate ADMET profiling and molecular optimization.^9,17 The use of on-chip artificial membranes would enable such biophysical studies of pharmaceutical relevance. Artificial membranes are in vitro models of biological cell membranes that can be formed in microfluidic chips,^18,19 and that are frequently used to study the physical properties of cell membranes.²⁰ However, due to the challenges of artificial membrane stability and throughput,²¹ there is a need for better microfluidic platforms for molecular screening.⁹

The reversible replacement of the media around on-chip artificial membranes is a known experimental challenge,^22–24 which is specifically due to the low stability of such in vitro membranes.^18,22,25 Hence, in such assays, the artificial membranes are typically established initially with the treating agent already present in the buffer to circumvent the need for media exchange.¹⁹ However, this strategy is not ideal as the molecules initially present in the buffer might influence the bilayer formation process, and online monitoring of changes caused by the treating agent is not feasible. Reversible media replacement is not limited to the drug delivery field, but it also applies to studying how buffer changes (e.g. shift in pH)²³ or molecule/particle delivery (like microplastics²⁶) affect artificial membranes.

Various methods have been proposed to treat membranes post their formation via replacing their surrounding media, such as using microinjection for giant vesicles to alter the milieu or to deliver specific molecules to the membrane.²³ However, this approach lacks high-throughput capabilities and falls short in providing precise control over concentration and reversibility of the treatment.²² An alternative method involves the use of microfluidics, such as incorporating a diffusion chamber into vesicle-on-chip systems. This approach allows molecules to diffuse and reach the bilayer without the conventional damage that flow causes to membranes, making it a promising tool.^22,24 Nonetheless, this approach necessitates the production of vesicles off-chip and is also low-throughput. Previous microfluidic approaches for solution exchange around freestanding lipid bilayers have been reported,^27,28 but these systems show low throughput or require complex multi-layer chip fabrication. A microfluidic platform acceptable for membrane screening should provide a stable array of such bilayers.²² Moreover, for numerous measurements including those requiring the accessibility of both sides of the membrane, vesicles may not be suitable, and the use of a planar freestanding configuration becomes essential.^29,30

In this study, we introduce an easy-to-operate microfluidic chip capable of forming an array of stable freestanding planar lipid bilayers and reversibly replacing the aqueous buffer around them for the goal of molecular delivery on artificial membranes. The chip enables rapid delivery of molecular agents to a whole array of several membranes with media being exchanged on both sides of the planar vertical membranes without imposing significant fluidic tension on them. The chip functions with two separate conventional syringe pumps without the need for any off-chip preparations or any mid-experiment connecting/disconnecting of the tubes. Delivery of the new media to replace the old one is done through convection, making the whole process faster than diffusion-based delivery methods. Thanks to the chip's favourable hydrodynamic design and the fluidic dampers incorporated into it, the membranes remain stable during the molecular delivery process. The chip benefits also from two passive bubble traps enhancing the membrane formation and facilitating the delivery of the substitute media to the bilayers. As a proof of concept, we formed arrays of freestanding planar POPC bilayers on the chip and used optical tweezers to investigate the effect of azithromycin on the elastic properties of the membranes.

2. Microfluidic system description

The microfluidic device is made of Norland Optical Adhesive 81 (NOA81)³¹ with an architecture as shown in Fig. 1. It comprises dual inlets supplying two parallel channels, each driven by separate syringe pumps. One inlet is for the “membrane channel”, and the other one is for the “replacement channel”. These two parallel channels are connected together via two resistance channels. There are two additional resistance channels on the other side of the membrane channel to keep flow symmetry, which is necessary for the formation of planar bilayers.^30,32 With this design, the flow in the membrane channel experiences the same pressure condition on both sides via symmetric resistance channels both connected to atmospheric pressure. From one side, the resistance channels are connected to exit 1 and exit 2 which are at atmospheric pressure. From the other side, the resistance channels are connected to the yet empty replacement channel, itself connected to atmospheric pressure via its outlet. The chip contains four total outlet ports. Outlets 1 and 2 serve as the egress points for the membrane channel and replacement channel respectively. Exits 1 and 2 allow for balancing the flow during the membrane formation process and for better flow control during the replacement process. More details on the channels and their dimensions can be found in the ESI† (Fig. S1 and Table S1).

Fig. 1 Graphical description of the microfluidic design and its main components: the bubble trap, the membrane channel, the replacement channel, and the resistance channels.

The working principle of the chip is illustrated schematically in Fig. 2. The formation of artificial cell membranes around micropillars was already described,³⁰ and is based on flowing lipids dissolved in chloroform into the chip from inlet 1 followed by an aqueous medium, called here aqueous phase I (Fig. 2A). From inlet 2, the replacement medium (aqueous phase II) is flowed into the chip until the flow front reaches the first resistance channel (Fig. 2B). The bubble traps ensure that a bubble-free liquid flows toward the pillars. Then, by pushing the flow further in the membrane channel, the flow is partitioned into three separate streams when reaching the two rows of micropillars, and these three streams repetitively join again at the gaps. Lipid monolayers, which are present at the water–chloroform interfaces, join at the gaps and zip with one another to form lipid bilayers, i.e. artificial membranes (Fig. 2C). This partitioning–zipping process goes on continually until all the gaps are filled with bilayers (Fig. 2D). At this stage, a part of aqueous phase I flows through the resistance channels toward exit 1 and the replacement channel. The amount of aqueous phase I in the resistance channels is limited since the resistance channels are engineered with a narrow size and an extended zig-zag length to induce a substantial pressure drop.

Fig. 2 Schematic representation of the different stages of chip function. A) Lipids dissolved in chloroform (yellow) are introduced from inlet 1 followed by aqueous phase I (blue). Aqueous phase II (green) is introduced from inlet 2. B) Bubbles get trapped at the bubble traps. C and D) Replacement flow is stopped before the first resistance channel while the flow in the membrane channel is pushed further until membranes are formed at the gaps. E) After membrane formation, outlet 2 is blocked and the replacement flow is pumped into the system. F) Pumping is continued until all medium around bilayers is replaced by aqueous phase II. G) Aqueous phase I can fill again the membrane channel by flowing aqueous phase I into the chip again, while outlet 2 and both exit 1 and 2 are blocked. H) As a solution to the occasional clogging of the resistance channel (connected to exit 1), the second resistance channel can be implemented as a substitute.

Once the lipid bilayers are formed, the pump feeding the membrane channel is stopped and the pump for the replacement medium (aqueous phase II, which could contain e.g. drugs) is started. The replacement flow initially washes away all of aqueous phase I that had reached the replacement channel out to outlet 2, after which outlet 2 is blocked. Then, aqueous phase II is pushed through the resistance channels (Fig. 2E) and fills the membrane channel. At this stage, the medium around the lipid bilayers is fully replaced and the content of aqueous phase II (e.g. the drug) is delivered to the artificial membranes (Fig. 2F).

Finally, the membrane channel can be filled again with aqueous phase I by simply running again the pump connected to the membrane channel while both exits are sealed (Fig. 2G). This reversible replacement can be useful for example when delivering fluorescent molecules to the artificial membranes and then washing those molecules from the channel after a specific time for fluorescence imaging with less background.

A second resistance channel and its corresponding exit port (exit 2), located downstream the micropillar section, are incorporated in the design in case the first resistance channel fails (Fig. 2H). This can happen if the first resistance channel is clogged by droplets formed via the unwanted mixing happening between chloroform and aqueous buffer at the connecting points of the resistance channels to the membrane channel or even in the resistance channel itself. In this case, both outlets and exit 2 are blocked, and the replacement medium is pumped to go through the resistance channels and treat the membrane and finally leave the system from exit 1 port.

3. Experimental section

3.1 Microfluidic chip fabrication

The master mold was fabricated following conventional cleanroom techniques. Briefly, positive resist S1813 (MICROPOSIT®) was spin-coated on a 4 inch silicon wafer to reach a thickness of ∼3 μm. The design of the chip was drawn in Autocad and converted into a dxf file using Klayout. Utilizing a laser writer (μMLA, Heidelberg Instruments) the design was patterned on the resist and later developed for 80 seconds in MF322 solution (MICROPOSIT®), followed by rinsing with deionised water. The mask was spun to dry. The developed mask was descumed with low power plasma (100 watts for 5 minutes) and then etched using PlasmaPro 100 Estrelas DRIE (Oxford Instruments) to reach a channel depth of approximately 75 μm. For the etching process the conventional Bosch process of silicon etching was implemented. To remove any remaining resists, the final mold was immersed in the remover (Ar600-71) and sonicated for 5 minutes and rinsed with isopropanol. The mold is then dried using nitrogen gas. Then, plasma cleaning (PVA Tepla 300) was performed on the mold (600 watts for 5 minutes). Finally, vapor deposition of trichloro(1H,1H,2H,2H-perfluorooctyl)silane (PFTOS, Sigma-Aldrich) on the mold was done overnight in a vacuum chamber. For the silanization, 50 mL of PFOTS silane was placed in a glass tube and connected to the evacuated chamber via a tightly sealed connector. The chamber was maintained under vacuum for at least 2 hours to allow the silane to vaporize and treat the mold surface.

The PDMS mold was fabricated by first thoroughly mixing PDMS with its curing agent (SYLGARD®) in a 10 : 1 ratio. The mixture was then degassed in a standard desiccator. Casting of PDMS onto the master mold was followed by another round of degassing. Subsequent curing was accomplished in an oven at 85 °C for 8 h. After curing, PDMS was carefully diced out from the master mold, and surface silanization with PFTOS was performed as described above.

Finally, NOA81 (Norland Products) was cast onto the PDMS mold. A microscope glass slide was placed on top of liquid NOA, allowing it to flatten and form a uniform layer beneath it. Subsequently, the assembly was exposed to UV light (Promed UVL-36 with four UV-9W-L bulbs) for 5 min. Following UV exposure, the PDMS was peeled off from the NOA channels. All ports were drilled with 1 mm tips. NOA81 was spin-coated onto a glass coverslip (Deckglaser, thickness: 170 ± 5 μm, previously thoroughly washed with Hellmanex and rinsed), and partially cured for 1 minute. The NOA-coated coverslip was then bonded to the NOA channels. The bonded chip was exposed to the same UV light for 10 minutes and subsequently baked for 8 h at 85 °C on a hot plate.

3.2 Chemicals, buffers, lipids, and flows

POPC (1-palmitoyl-2-oleoyl-glycero-3-phosphocholine) was purchased from Avanti in chloroform with 25 mg ml⁻¹ concentration, stored at −20 °C, and directly used for experiments. To create the aqueous phase that we refer to as the HEPES solution, 10 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) was adjusted to pH 7.4 using concentrated KOH, KCl (150 mM) and bovine serum albumin (0.5 mg ml⁻¹) were added, and the solution was filtered with a 0.2 μm sterile filter. For the bead-containing experiments, after filtration, 2 μm polystyrene beads (real diameter = 1.93 μm, Polysciences Inc.) were dissolved in the buffer. Two identical ProSense NE-30 syringe pumps were used to infuse the flow into the chip via inlet 1 and inlet 2. For membrane formation, flow rates in the range of 5–9 μl min⁻¹ usually gave several stable bilayers. However, for the (reversible) replacement of the media we advise to use a flow rate of 2.5 μl min⁻¹. To minimize the residual flow after stopping the pumps, tubing with short length was used (no longer than 5 cm). For the laser-induced fluorescence tests, Rhodamine B was dissolved in the HEPES solution. For the drug experiment, azithromycin (Sigma-Aldrich) was dissolved in 0.1 M HCl and then added to the HEPES solution to reach a final azithromycin concentration of 5 μM or 250 μM. For blocking outlet ports during the drug delivery phases, UV curing glass repair adhesive (Bison) was used.

3.3 Numerical simulations

All simulations were conducted using COMSOL Multiphysics 5.6. To model the fluid flow, two COMSOL modules were used: one to model the laminar flow and another to model the transport of dilute species. The fluid flow was solved in steady-state, and a time-dependent study was implemented for the mass transport model. Free triangular mesh was used in the two-dimensional domain of the chip with an average skewness quality of 93%.

3.4 Video and image analysis

To track the beads for the observation of flow streamlines, the TrackMate module of ImageJ was used. To pre-process the images, each image was subtracted by the average image of all the stacks to remove the chip structures and the background noises. Then, the intensity was reversed to have high intensity for the beads and a dark background. Laser-induced fluorescence tests were analysed in ImageJ without any pre/post-processing.

3.5 Optical tweezers experiments

The optical tweezers (OT) methods for both the shearing and pushing experiments were previously described.^19,29,30 All experiments were conducted at a height of 30 μm above the surface of the flow cell. A 1.2 NA water immersion objective (FI Plan Apo VC 60×, Nikon) was used to optically trap a bead inside microchannels mounted on a piezo stage (NANO-LPS100, Mad City Labs) with a 1064 nm trapping laser (YLR-10-LP-Y12, IPG Laser) and an 830 nm detection laser (LDT830-30GC, TOPAG). Anti-aliasing filtering and pre-amplification (10 dB) was done (KROHN-HITE 3364) on the voltage signals coming from a position-sensitive detector (PSD, DL100-7-PCBA3, First Sensor).

In the pushing experiments, fine positioning of the bead relative to the membrane was controlled using the piezo stage. The stage was moved sequentially in steps from 120–240 nm, and at each position, data collection was performed by recording the PSD signal for 0.5 seconds at a sampling rate of 1 kHz with a cut-off frequency of 500 Hz. For setup calibration and trap stiffness calculation, signals were sampled at 50 kHz with a cut-off frequency of 24.5 kHz. All signals from the PSD were processed and converted to nm and pN using a custom-made Python code. The trap stiffness used for pushing membranes was in the range of 0.10–0.13 pN nm⁻¹. Prior to pushing each membrane, calibration of the trap was performed with the bead center at a distance of 3 μm from the membrane.

To calculate membrane tension (σ), the formula was used, using the force values (F) from the first part (linear region) of the force-displacement curves, with δ being the distance between the bead center and the point where the angle θ of the membrane is measured. To calculate θ, a previously published method was used.³⁰ Bending rigidity (κ) was calculated via formula , where F_t is the force required to extend the tube, also obtained from the same force–displacement curves as for tension measurements.

3.6 Statistical analysis

A Kruskal–Wallis one-way statistical analysis was conducted using a significance threshold of p = 0.05 to determine significance. P-Values on the graphs are indicated as follows: * for p < 0.05, ** for p < 0.01, and *** for p < 0.001. Error bars in all figures denote the standard deviation. In all box plots, the box represents the quartiles, the horizontal line indicates the median, and the whiskers extend to the most extreme data points. The number of independent optical tweezers experiments performed is as follows: 38 experiments for tests done before the replacement, 15 experiments for the HEPES solution control, 7 experiments of the low-dose, and 12 experiments for the high-dose drug exposure. Each experiment was performed on a different membrane using a different bead on at least four different microfluidic chips.

4. Results and discussion

4.1 Flow simulation

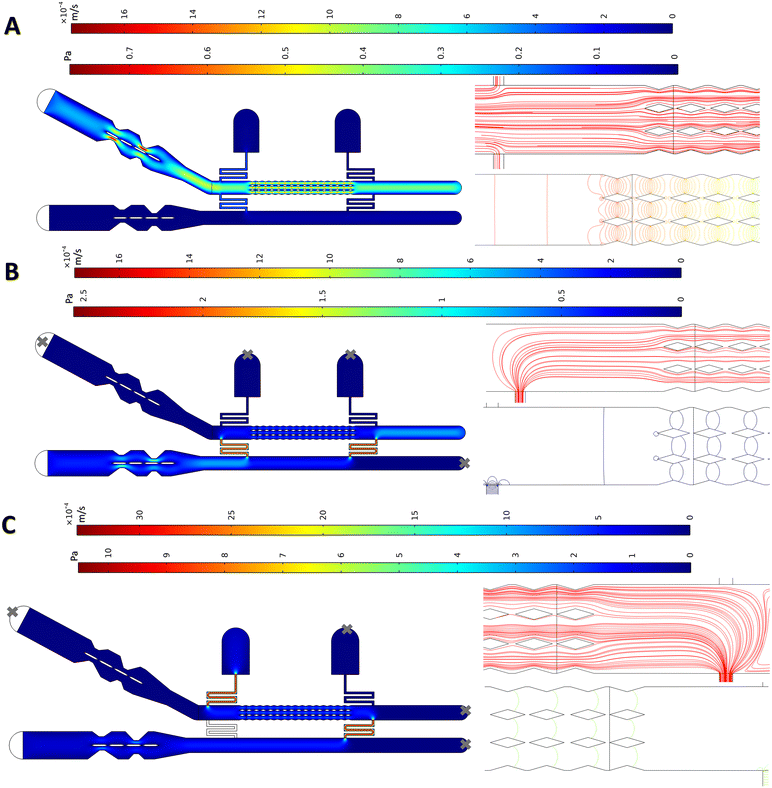
To optimize and test the microchip, we used a finite element method (FEM) in COMSOL Multiphysics 5.6. The chip was designed taking three key criteria into account: ensuring a symmetric flow on both sides of membranes at all time; keeping the drug concentration at the desired level with even distribution over all membranes; and minimizing shear stress applied on the membranes to avoid rupturing them or altering their properties.^22,33 For these purposes, the resistance channels should be long and narrow enough such that the flow would not easily go through them and leave the system during the membrane formation phase. On the other hand, if they impose too much resistance, a very high fluidic pressure would be needed to push the replacement buffer into the main membrane channel. The dimensions were optimized to satisfy both aspects. Furthermore, the resistance channels should have their junction with the membrane channel far enough from the pillars to ensure symmetric flow streamlines around the pillars.

The laminar flow in the channels was modelled using the laminar flow module in COMSOL.^15,16,34,35 In the first simulations, the pump connected to inlet 1 was run as done when membranes are formed (Fig. 2C) with an inlet flow rate of 5 μl min⁻¹.³⁰ It is crucial that the flow remains symmetric at the gaps to ensure that flat membranes form without any significant warping that may lead to membrane rupture. To help with flow symmetry across the gaps, a streamline-shaped design was used for the outer walls of the membrane channels (in the micropillar sections), making the geometry through which the liquid flows identical and symmetrical. The COMSOL simulations show that aqueous phase I reaches the pillars such that the flow and pressure on either side of the gap remain similar during this phase (Fig. 3A). As a result, the three fingers of the flow partitioned by the two rows of pillars behave similarly, with less than a 5% deviation between each finger for the average flow rate passing by the pillars. Additionally, the corresponding resistance channels on either side of the membrane channel exhibit very similar behaviour, with less than 5% deviation in the average flow rate through each resistance. These two factors cause parallel streamlines and balanced pressure distribution (Fig. 3A) at the gaps throughout the micropillar section, which is favourable for the stable formation of flat membranes.

Fig. 3 Flow simulation results for different stages of operation of the chip. Pressure distribution, velocity field, and flow pattern for the A) membrane formation, B) replacement, and C) fallback delivery stages. Grey crosses (x) in each figure indicate that in these simulations, the crossed-out inlet/outlet port was considered blocked. The left side of each panel represents the flow velocity field within the chip. The color bar indicates the color code for velocities. The right side of each panel shows (at the top) the flow streamlines when the flow is entering the pillar region, and (at the bottom) the pressure contours. The gradient of the color bar varies from blue to red (zero value to maximum value).

After membrane formation, the replacement flow is pumped into the system (as shown in Fig. 2E and F). This simulation was conducted with a flow rate of 2.5 μl min⁻¹ infusing into the chip via inlet 2 (Fig. 3B). The streamline patterns at the gaps are parallel and a balanced pressure at all the gaps is observed. The crucial point in the replacement phase is that it is carried out in such a way to minimize shearing the membranes, thanks to the gap design and the profile of the pillars, which create an almost zero-velocity stationary region between the gaps (see Fig. S2† for a closer look at the velocity field around the gaps during the delivery phase).

A simulation was also performed to evaluate the “fallback delivery” scenario (shown in Fig. 2H), which occurs if the first resistance channel becomes clogged and the second one is used for media replacement. The results for pressure distribution and flow patterns show that the flow remains symmetric and balanced at all the gaps (Fig. 3C), which is favourable for membrane stability.

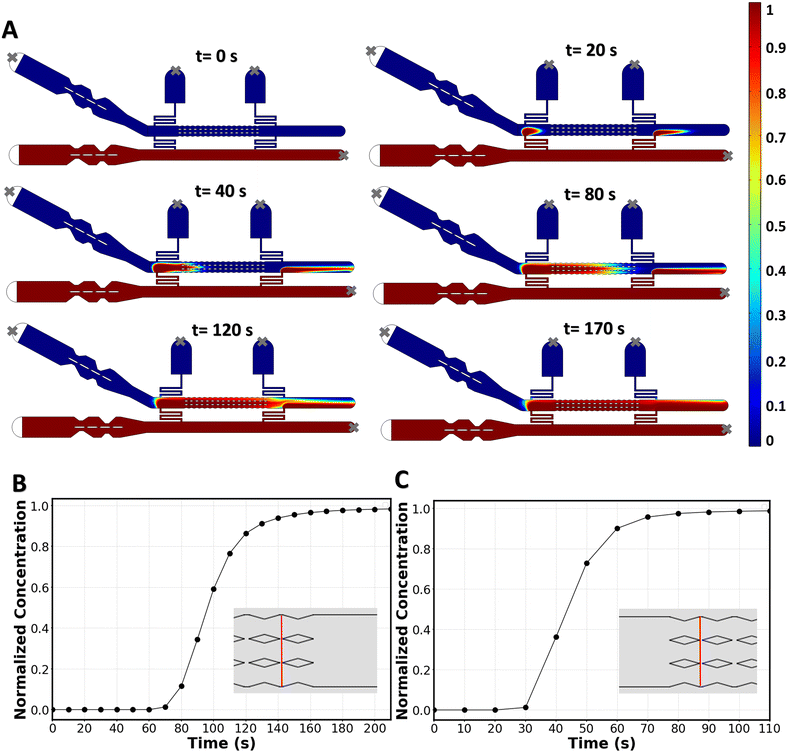
COMSOL simulations were also used to investigate whether the molecule of interest at inlet 2 reaches all the membranes with a uniform concentration, and to determine the time required for aqueous phase II to fully replace aqueous phase I. To achieve this, we coupled the laminar flow equations with the dilute mass transport equation, and solved them in 2D for molecular species with a diffusion coefficient of D = 10⁻⁹ m² s⁻¹.³⁶ This simulation technique is well described in drug-delivery screening microchips.^15,16,34Fig. 4A shows the time-dependent delivery of the new solution to the bilayer. The average local concentration at the last two gaps (Fig. 4B) shows that, in 170 s, the two membranes furthest downstream receive the same concentration of delivered molecules (with less than 3% deviation) as the membranes upstream. In the case of using the second resistance channel when the first one is out of circuit (fallback delivery), it takes 70 s for the membranes downstream to experience a complete media replacement (Fig. 4C). The homogenous delivery and short delivery times that are achieved with this chip highlight the effectiveness of a convection-based replacement method.

Fig. 4 Results of the mass transport simulation. A) Timeline of media replacement simulated in COMSOL. The color bar represents the drug concentration normalized by the concentration at the inlet. Grey crosses (x) indicate which inlet/outlet ports were considered blocked. B) Average drug concentration at the last two membranes, normalized by the concentration at the inlet. The averaging is performed over the width of the membrane channel passing through the last two gaps (i.e. over the red line in the inset). C) Average drug concentration at the first two membranes during the “fallback delivery”, normalized by the concentration at the inlet. The averaging is done over the width of the membrane channel going through the first two gaps (i.e. over the red line in the inset).

If the microchip is to be used for long term incubation times, it is important to consider the diffusion of the drug toward inlet 1 which is connected to the drug-free source. Our COMSOL simulations show that after the delivery phase is completed and the pump is turned off, the drug concentration around the first row of membranes drops by 2.5% in 1 hour and 7% in 2 hours, while the concentration drop is minimal for the rest of the membranes (Fig. S3†). To prevent such concentration drop around the first membranes in long-term incubations, one can simply keep exit 1 open (while blocking all other ports) and keep the replacement flow pumping to the system during the long incubation time.

4.2 Experimental characterization of media replacement around membranes

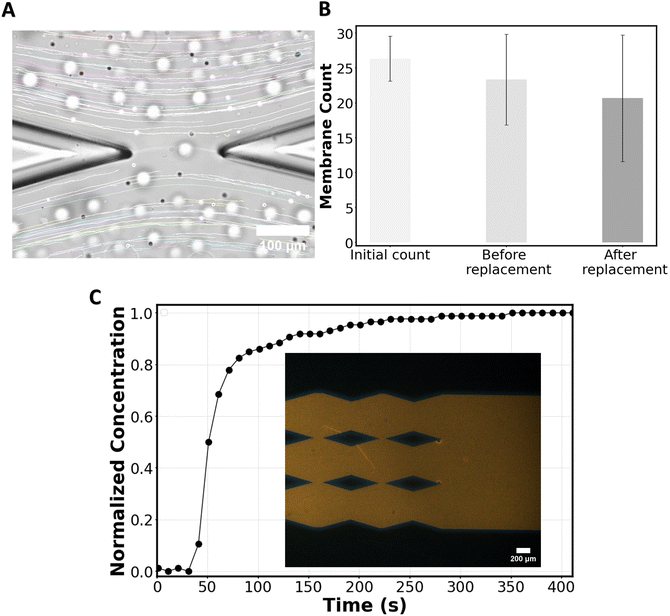
To experimentally observe the applicability of the chip in forming bilayers and delivering molecules of interest without disrupting the bilayers, a particle tracking experiment was performed. Chloroform containing POPC lipids was flowed from inlet 1, followed by the HEPES solution. Consequently, membranes were formed at the gaps of the micropillars, and after formation, the chloroform was absorbed into NOA81 until the annuli reduce in size.¹⁹ During this process, some membranes may pop, but the remaining membranes maintain their stability at the gaps.

During the replacement phase, 2 μm polystyrene beads diluted 3000 times in the HEPES solution were introduced into the system from inlet 2 at a flow rate of 2.5 μl min⁻¹. Although the chip can handle higher flow rates, we experimentally found that at 2.5 μl min⁻¹, while the membranes start to warp (Fig. 5A), they remain stable, and after the flow is stopped the membranes flatten. Above 2.5 μl min⁻¹, the warping risks to disrupt the membranes. For particle tracking, the maximum flowrate (2.5 μl min⁻¹) is chosen to minimize beads sinking in the channel while traveling in the channels, which would affect particle tracking.

Fig. 5 Experimental validation of the chip. A) Flow streamlines around the first membrane illustrated by tracking 2 μm beads. B) Membrane count just after they are formed (initial count), 1 hour after formation (before replacement), and after the medium surrounding the membranes is replaced via the replacement channel; from 3 independent experiments. C) Rhodamine-B concentration at the location of the two last membranes normalized over Rhodamine-B concentration at the inlet of the drug channel. Data points are averaged over 3 independent experiments. The inset of panel C shows an image of the distribution of Rhodamine-B around the last gaps 170 s after the start of the media replacement procedure.

To verify flow symmetry during the replacement process, particle flow around the first membrane (the one at the highest risk of flow asymmetry) was tracked using ImageJ. The streamlines of the flow were found to be parallel to the channel's direction (Fig. 5A), as predicted in simulations (Fig. 3B). Additionally, we conducted a count of membranes that were initially formed and that survived after the flow replacement with beads (Fig. 5B), showing that while some membranes did not survive the process, a significant number of membranes remained intact following the flow replacement on the chip, allowing for subsequent measurements. By observing the flow of beads in the vicinity of the membranes (Video S1†) one can appreciate the capability of the chip regarding online monitoring of the membranes during the delivery phase of the molecule of interest (here, beads as a proxy of such molecules).

To experimentally assess the concentration of molecules delivered to the membranes and the minimum time required to achieve a homogenous concentration throughout the chip, a laser-induced fluorescence test was conducted. For this purpose, chloroform (no lipids) followed by the HEPES solution (no beads) was flowed into the system from inlet 1 and when the membrane channel was filled, Rhodamine B in the HEPES solution was pushed from inlet 2 at the rate of 2.5 μl min⁻¹. The relative change in Rhodamine-B concentration at the most downstream gaps was recorded over time. Within ∼200 seconds the dye concentration around the last gaps reaches the input concentration (Fig. 5C) as predicted from the mass transport simulations (Fig. 4B).

The high number of stable freestanding membranes (Fig. 5B) formed within a few seconds (∼30 seconds) and available to receive the molecule of interest in a short period of time (Fig. 5C) demonstrates that our device enables a higher throughput than existing methods.^19,31,32

4.3 On-chip delivery of azithromycin to POPC lipid bilayers

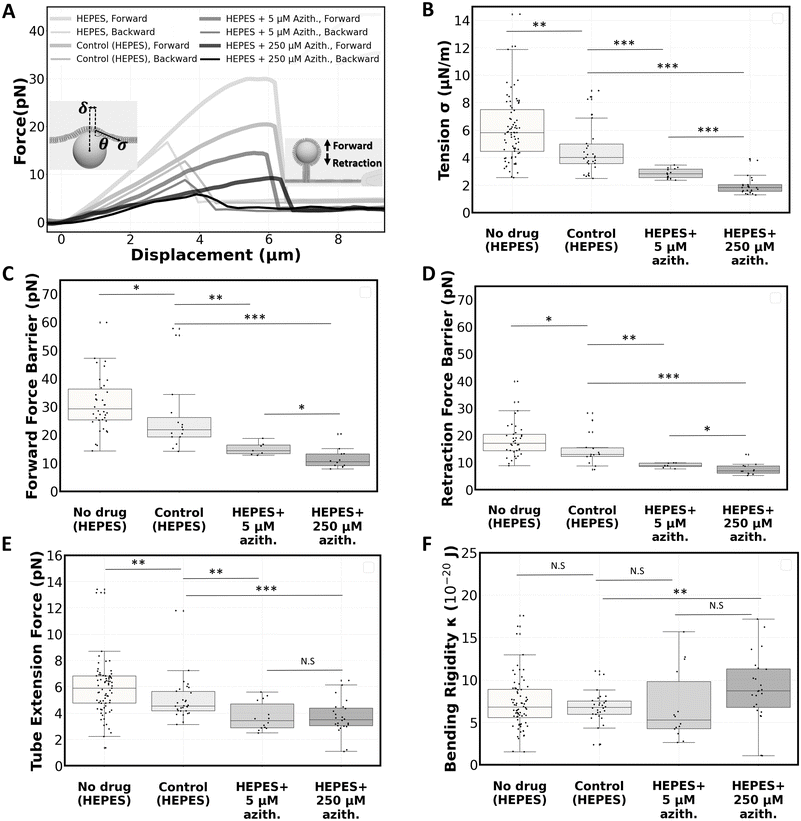
We proceeded with a proof-of-concept study to deliver an antibiotic drug, azithromycin, to POPC bilayers on the chip. In this study, we investigated the drug's effects on the membranes through mechanical characterization before and after drug delivery. The mechanical characterization of the bilayers focused on particle entry/release force barriers, membrane tension, and bending rigidity, and was performed using optical tweezers interfaced with the membranes on the chip as previously described.^19,30

POPC lipid dissolved in chloroform was flowed into the chip via the membrane channel inlet followed by a solution of 2 μm polystyrene beads diluted 25 000 times in HEPES solution. After membranes were formed at the gaps, they were left for 2 hours to rest, and mechanical characterizations were performed using optical tweezers. Representative force–displacement curves for both forward and backward pushing with the optical tweezers are depicted in Fig. 6A. The behaviour follows the classic force–displacement curves observed in pushing³⁷ or pulling³⁸ vesicles using optically trapped microbeads. In short, upon bead–membrane contact, the membrane deformed and began to wrap around the bead. As the pushing continued, this deformation progressed linearly until reaching a maximum force (force barrier for particle entry), after which a nanotube was formed. Extending the nanotube required a constant force. Upon reaching a few microns of extension, the direction of movement was reversed towards retraction, leading to the disappearance of the tube. Subsequently, the bead transitioned from a partially wrapped state back to its original unwrapped state in a linear force manner, mirroring the forward pushing process until returning to the zero-force state when the bead is fully released from the membrane.

Fig. 6 Effect of azithromycin on the mechanical properties of POPC membranes at low and high dosages of the drug. A) Force displacement representative curves. The inset displays the procedure for calculating the tension and rigidity. B) Membrane tension, C) forward force barrier, D) retraction force barrier, E) tube extension force and F) bending rigidity obtained before delivery, and after medium exchange with either the HEPES solution (control), the low-dose, or the high-dose azithromycin solution.

Using the force values extracted from these force–displacement curves, we calculated membrane tension and bending rigidity values. Fig. 6B–F present the results of these experiments on the POPC bilayer (prior to any flow replacement), illustrating tension (σ = 6.1 ± 2.5 μN m⁻¹), forward (32.1 ± 12.2 pN) and retraction (18.3 ± 6.5 pN) force barriers, tube extension force (5.9 ± 2.1 pN), and bending rigidity (κ = 7.7 ± 4.4 × 10⁻²⁰ J). These measurements are comparable to those obtained using a similar method on POPC bilayers.³⁰

Afterwards, we investigated how azithromycin affects the elastic properties of the lipid bilayers. For this purpose, azithromycin (at a concentration of either 0 μM, 5 μM, or 250 μM) and 2 μm polystyrene beads were added to the HEPES solution and introduced from the replacement channel to replace the initial HEPES solution surrounding the membranes (Fig. 2E and F). The membranes were then incubated in the new media for one hour, after which the optical experiments were repeated. The control with 0 μM azithromycin aimed to assess any potential effects of the flow replacement procedure on the bilayers.

Representative force–displacement curves for the drug-free, low-dose, and high-dose drug tests are all shown in Fig. 6A. After replacing the medium with the drug-free solution, we find that the membrane tension showed a slight decrease (Fig. 6B), leading to a decrease in the force barriers (Fig. 6C and D) and tube extension force (Fig. 6E). However, bending rigidity remained unchanged (Fig. 6F). The sole process of replacing the media affects the membrane tension. The buffer replacement possibly affects the annulus size/composition and/or washes away some lipid molecules out of the system, which can affect the membrane tension, showing the importance of performing this control at 0 μM azithromycin. Replacing the medium once more with the initial drug-free solution (as shown in Fig. 2G) does not significantly affect the membrane tension and bending rigidity (Fig. S4†). In this specific experiment, beads were added to both the initial and the control buffers to enable optical trapping after reversible media replacement. This experiment demonstrates an example of application of reversible flow replacement.

When the lipid bilayers were exposed to azithromycin, a significant decrease in membrane tension was observed, particularly at the higher dose. We report an average membrane tension of σ = 2.9 ± 0.4 μN m⁻¹ for the low-dose and σ = 2.0 ± 0.7 μN m⁻¹ for the high-dose treatment (Fig. 6B). A comparison of the force barrier for particle entry before and after drug treatment indicates that azithromycin facilitates particle entry into POPC membranes (15.1 ± 2.2 pN for low-dose and 11.5 ± 3.6 pN for high-dose, Fig. 6C). Similarly, Fig. 6D shows a decrease in the force barrier for particle release from membranes treated with azithromycin (9.0 ± 0.9 pN for low-dose and 7.5 ± 2.1 pN for high-dose). Fig. 6E demonstrates that the tube extension force from POPC bilayers is also significantly reduced after drug treatment. It drops to 3.7 ± 1.1 pN and 3.7 ± 1.3 pN to for low-dose and high-dose experiments respectively. Bending rigidity is unaffected by the drug at low doses, but shows a slight increase to κ = 9.0 ± 3.9 × 10⁻²⁰ J at the 250 μM concentration (Fig. 6F).

Our findings on the effect of azithromycin on bending rigidity of POPC freestanding bilayers differ from the ones reported for DOPC vesicles having their outer leaflet treated with azithromycin.⁷ This can be due to differences in lipid composition, in drug/lipid ratio, and/or in drug distribution across the bilayer since membrane asymmetry is known to affect bending rigidity.^39–41 Azithromycin was previously shown to have different effects on membrane fluidity depending on the lipid composition.⁴² Also noteworthily, the mentioned drug dosage corresponds to the input concentration into the system. It is possible that not all drug molecules end up in the membrane, because some molecules might adhere to the channels. However, the use of NOA81 channels is likely an advantage here since the absorption of some small molecules (e.g., ATP analog 3-MBPP1) was found to be reduced on NOA81 in comparison to PDMS.⁴³

In summary, membranes exposed to azithromycin exhibited lower membrane tension, requiring significantly lower forces for deformation, particle entry/release, and nanotube formation/extension, particularly at higher drug concentrations. Azithromycin is expected to interact electrostatically with the negative charged group in the polar head of PCs, as demonstrated by ³¹P NMR spectroscopy.⁴⁴ Also, given its amphipathic nature,⁴⁵ azithromycin can insert into membranes. Specifically, it was found that azithromycin insertion within the polar heads of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) induces an expansion in the area occupied by each lipid molecule, increasing it from 68.6 Ų in its pure form to 75.9 Ų. This interaction decreases the lipid–lipid interaction energy, making the membranes more easily deformable.⁷ A similar effect might be at the origin of the decrease in membrane tension and in force barrier values after drug treatment.

5. Conclusion

We have engineered a robust and efficient microfluidic design serving as a reliable instrument for the delivery of drugs or other molecules/particles to freestanding planar membranes, and the subsequent screening of their impact on the membranes. Unlike conventional chips that focus on drug–cell interactions, our system enables direct drug delivery to artificial cell membranes, facilitating detailed studies of membrane–drug interactions. Our microfluidic design successfully addresses the longstanding challenge of rapidly and reversibly changing buffer solutions around lipid bilayers.²²

Moreover, our platform allows targeted delivery of molecules to freestanding planar membranes post-formation, achieved through integrated features such as membrane modules, drug delivery channels, bubble traps, and specialized resistance channels. The chip underwent testing via numerical simulation and experimental validation using particle tracking and laser-induced fluorescence techniques. As a proof of concept, we investigated the impact of azithromycin on the mechanical properties of POPC bilayers formed on the chip. Our findings revealed a reduction in membrane tension, in force barriers for particle entry and release, and in nanotube extension forces in drug-affected membranes, particularly at higher drug concentrations.

Although the current design does not have the ability to apply the drug to a single leaflet with buffer control on a specific side of the membrane, which would better mimic cell membrane–drug interactions, it provides a solid foundation for more advanced systems in the future. We expect this microchip to become a valuable tool in the field of artificial cell membranes, facilitating a wide range of applications including drug delivery studies, pH variation experiments, protein or fluorescent molecule delivery to membranes, and assays that depend on buffer replacement after membrane formation.

Data availability

The data underlying this study is openly available at the 4TU.ResearchData repository: https://doi.org/10.4121/6D8A0DCE-4E1D-4BD2-8AFD-8574A5A83650 [to be released when paper is published].

Author contributions

Conceptualization: Arash Yahyazadeh Shourabi, Marie-Eve Aubin-Tam. Data curation: Arash Yahyazadeh Shourabi, Martina Iacona. Formal analysis: Arash Yahyazadeh Shourabi, Martina Iacona. Investigation: Arash Yahyazadeh Shourabi, Martina Iacona. Methodology: Arash Yahyazadeh Shourabi, Martina Iacona, Marie-Eve Aubin-Tam. Project administration: Marie-Eve Aubin-Tam. Resources: Marie-Eve Aubin-Tam. Supervision: Marie-Eve Aubin-Tam. Writing – original draft: Arash Yahyazadeh Shourabi. Writing – review & editing: Arash Yahyazadeh Shourabi, Martina Iacona, Marie-Eve Aubin-Tam.

Conflicts of interest

Two patents have been submitted related to the contents of the present article.

Acknowledgements

The authors thank Nemo Andrea for his technical help and input in cleanroom fabrication of the microfluidic master mold.

References

1. F. N. Kök, A. A. Yildiz and F. Inci, Biomimetic lipid membranes: fundamentals, applications, and commercialization, Springer, 2019.
2. D. B. Catacutan, J. Alexander, A. Arnold and J. M. Stokes, Nat. Chem. Biol., 2024, 20, 960–973.
3. R. M. Epand, C. Walker, R. F. Epand and N. A. Magarvey, Biochim. Biophys. Acta - Biomembr., 2016, 1858, 980–987.
4. N. P. Buijs, E. J. Matheson, S. A. Cochrane and N. I. Martin, Chem. Commun., 2023, 59, 7685–7703.
5. A. H. Delcour, Biochim. Biophys. Acta - Proteins Proteom., 2009, 1794, 808–816.
6. N. Marín-Medina, D. A. Ramírez, S. Trier and C. Leidy, Appl. Microbiol. Biotechnol., 2016, 100, 10251–10263.
7. N. Fa, L. Lins, P. J. Courtoy, Y. Dufrêne, P. Van Der Smissen, R. Brasseur, D. Tyteca and M.-P. Mingeot-Leclercq, Biochim. Biophys. Acta - Biomembr., 2007, 1768, 1830–1838.
8. S. Salinas-Almaguer, M. Mell, V. G. Almendro-Vedia, M. Calero, K. C. M. Robledo-Sánchez, C. Ruiz-Suarez, T. Alarcón, R. A. Barrio, A. Hernández-Machado and F. Monroy, Sci. Rep., 2022, 12, 933.
9. E. Fernandes, V. F. Cardoso, S. Lanceros-Méndez and M. Lúcio, Adv. Funct. Mater., 2024, 2315166.
10. D. Barata, C. van Blitterswijk and P. Habibovic, Acta Biomater., 2016, 34, 1–20.
11. S. Kresák, T. Hianik and R. L. Naumann, Soft Matter, 2009, 5, 4021–4032.
12. R. Ronen, Y. Kaufman and V. Freger, J. Membr. Sci., 2017, 523, 247–254.
13. M. Azizi, A. V. Nguyen, B. Dogan, S. Zhang, K. W. Simpson and A. Abbaspourrad, ACS Appl. Mater. Interfaces, 2021, 13, 19581–19592.
14. F. N. Ju, C.-H. Kim, K.-H. Lee, C.-D. Kim, J. Lim, T. Lee, C. G. Park and T.-H. Kim, Biosens. Bioelectron., 2023, 222, 115003.
15. A. Y. Shourabi, N. Kashaninejad and M. S. Saidi, J. Sci.: Adv. Mater. Devices, 2021, 6, 280–290.
16. A. V. Nguyen, A. Y. Shourabi, M. Yaghoobi, S. Zhang, K. W. Simpson and A. Abbaspourrad, PLoS One, 2022, 17, e0272294.
17. S. Ramadurai, N. K. Sarangi, S. Maher, N. MacConnell, A. M. Bond, D. McDaid, D. Flynn and T. E. Keyes, Langmuir, 2019, 35, 8095–8109.
18. P. Heo, S. Ramakrishnan, J. Coleman, J. E. Rothman, J. B. Fleury and F. Pincet, Small, 2019, 15, 1900725.
19. A. Dols-Perez, V. Marin, G. J. Amador, R. Kieffer, D. Tam and M.-E. Aubin-Tam, ACS Appl. Mater. Interfaces, 2019, 11, 33620–33627.
20. C. Sebaaly, H. Greige-Gerges and C. Charcosset, Current trends and future developments on (bio-) membranes, Elsevier, 2019, pp. 311–340.
21. X. T. Zheng, L. Yu, P. Li, H. Dong, Y. Wang, Y. Liu and C. M. Li, Adv. Drug Delivery Rev., 2013, 65, 1556–1574.
22. S. Vrhovec, M. Mally, B. Kavčič and J. Derganc, Lab Chip, 2011, 11, 4200–4206.
23. N. Khalifat, N. Puff, S. Bonneau, J.-B. Fournier and M. I. Angelova, Biophys. J., 2008, 95, 4924–4933.
24. M. Mally, B. Božič, S. V. Hartman, U. Klančnik, M. Mur, S. Svetina and J. Derganc, RSC Adv., 2017, 7, 36506–36515.
25. A. Blicher, K. Wodzinska, M. Fidorra, M. Winterhalter and T. Heimburg, Biophys. J., 2009, 96, 4581–4591.
26. J.-B. Fleury and V. A. Baulin, J. Chem. Phys., 2024, 161, 144902.
27. M. Zagnoni, M. E. Sandison, P. Marius, A. G. Lee and H. Morgan, Lab Chip, 2007, 7, 1176–1183.
28. R. Kawano, T. Osaki, H. Sasaki and S. Takeuchi, Small, 2010, 6, 2100–2104.
29. G. J. Amador, D. Van Dijk, R. Kieffer, M.-E. Aubin-Tam and D. Tam, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2100156118.
30. A. Y. Shourabi, R. Kieffer, D. de Jong, D. Tam and M.-E. Aubin-Tam, Soft Matter, 2024, 20, 8524–8537.
31. V. Marin, R. Kieffer, R. Padmos and M.-E. Aubin-Tam, Anal. Chem., 2016, 88, 7466–7470.
32. N. Khangholi, R. Seemann and J.-B. Fleury, Biomicrofluidics, 2020, 14, 024117.
33. N. Färber, J. Reitler, A. Kamenac and C. Westerhausen, Biochim. Biophys. Acta - Gen. Subj., 2022, 1866, 130199.
34. A. Yahyazadeh Shourabi, R. Salajeghe, M. Barisam and N. Kashaninejad, Sensors, 2021, 21, 5529.
35. E. Westein, A. D. van der Meer, M. J. Kuijpers, J.-P. Frimat, A. van den Berg and J. W. Heemskerk, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1357–1362.
36. M. Ebadi, K. Moshksayan, N. Kashaninejad, M. S. Saidi and N.-T. Nguyen, Chem. Eng. Sci., 2020, 212, 115339.
37. Y. Shitamichi, M. Ichikawa and Y. Kimura, Chem. Phys. Lett., 2009, 479, 274–278.
38. G. Koster, A. Cacciuto, I. Derényi, D. Frenkel and M. Dogterom, Phys. Rev. Lett., 2005, 94, 068101.
39. L. Lu, W. J. Doak, J. W. Schertzer and P. R. Chiarot, Soft Matter, 2016, 12, 7521–7528.
40. Y. Elani, S. Purushothaman, P. J. Booth, J. M. Seddon, N. J. Brooks, R. V. Law and O. Ces, Chem. Commun., 2015, 51, 6976–6979.
41. K. Karamdad, R. Law, J. Seddon, N. Brooks and O. Ces, Chem. Commun., 2016, 52, 5277–5280.
42. A. Berquand, N. Fa, Y. Dufrene and M.-P. Mingeot-Leclercq, Pharm. Res., 2005, 22, 465–475.
43. T. Chen, B. Gomez-Escoda, J. Munoz-Garcia, J. Babic, L. Griscom, P.-Y. J. Wu and D. Coudreuse, Open Biol., 2016, 6, 160156.
44. D. Tyteca, A. Schanck, Y. Dufrene, M. Deleu, P. J. Courtoy, P. M. Tulkens and M.-P. Mingeot-Leclercq, J. Membr. Biol., 2003, 192, 203–215.
45. J.-P. Montenez, F. Van Bambeke, J. Piret, R. Brasseur, P. M. Tulkens and M.-P. Mingeot-Leclercq, Toxicol. Appl. Pharmacol., 1999, 156, 129–140.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00930d

---