Insect wing circulation: transient perfusion through a microfluidic dragonfly forewing model

Abstract

Insect wings are made of an acellular composite material that forms a thin membrane and a complex network of veins. Veins are tubes that not only serve to stabilize the wing membrane, but they are also filled with hemolymph (insect blood). Thus, veins supply the sensory organs located on the wing veins with water and nutrients and enable the removal of waste products. In addition, the composite material of the wing is permanently hydrated by the hemolymph and thus retains the necessary flexibility. Hemolymph flow through the microfluidic vein network is therefore crucial for the functionality of insect wings. However, how perfusion occurs throughout the vein network in relation to hemolymph circulation is poorly understood. To investigate the dynamics of transient perfusion in complex wing venation, we developed a microfluidic wing vein model of the forewing of the common green darner dragonfly, Anax junius, using polydimethylsiloxane. Transient perfusion was simulated by injecting dye into the model filled with clear water; inversely, clear water was injected into dye in a separate trial. Visualized perfusion patterns suggest that the perfused portion of the vein network logarithmically increased with respect to time, which could be explained by a theoretical model of a simplified wing vein network, and that time differences occurred between the arrival of a new substance and the complete removal of an old substance in veins. Our biomimetic wing vein device enables further investigation into the unique circulatory system and transport phenomena of the insect wing. Also, our microfluidics-based approach proves a potential use of microfluidics in entomology and related fields.

---

1. Introduction

Flying insects need functioning and healthy wings for complex behaviors including foraging, pollination, mating, and evading predators. Insect wings are made of cuticle, the acellular composite material of the exoskeleton of these animals which consists largely of the polysaccharide chitin and various proteins. In the wings, the cuticle forms a thin membrane and a vein network in which longitudinal veins run along the length of the wing, interconnected by shorter cross-veins.¹ Longitudinal veins primarily bear load on the wings while cross-veins hold and support the entire vein structure.²

Insect wings have a venation hierarchy of varying diameters and lengths.³ Veins toward to the base and leading edge of a wing are thicker and more rigid, whereas veins towards the trailing edge are thinner and more deformable.^2,3 Although the numbers of longitudinal veins often change by branching, fusion, or loss, their basic pattern is consistent within major taxonomic groups such as insect families and orders. By contrast, cross-veins exhibit more variable patterns than longitudinal veins.⁴ Longitudinal veins can be matched between the left and right wings of an individual insect whereas cross-veins cannot.⁵ As such, cross-veins form a unique pattern on every wing. Regarding vein-bounded domains of insect wings, the following general pattern of vein morphology is observed: sparsely venated wings tend to have more rectangular domains with larger fractional areas, whereas dense venation indicates smaller, more circular domains.³

The veins are tubes that not only stabilize the wing blade but also serve as conduits for the transport of hemolymph (insect blood, which includes cells called hemocytes) as well as neurons (which serve hundreds of sensilla) and air-filled tracheal tubes (which are used for gas exchange).^6–9 The supply of hemolymph to the wings is necessary for several reasons. First, insect wings are not only flight organs, but also important sensory appendages. They carry hundreds of small bristles and other types of sensory organs along their veins that are important for insect flight control and spatial orientation.¹ The associated sensory neurons require supply in several ways. While their gas exchange takes place via air-filled tracheae, which run through the lumen of the veins and reach these cells directly, the supply of nutrients and other substances, as well as the removal of waste products, occurs via the hemolymph. Second, hemolymph supply is necessary for expanding insect wings and maintaining the mechanical integrity of the wing through its continuous hydration.^10–12 In the wing cuticle, the structural material is organized into multiple layers, with its basal layer, the endocuticle, containing a significant amount of water. This layer is particularly well developed in the wing veins¹³ and determines their degree of elasticity.¹¹ In multiple locations in the wing, especially in flexible regions of the veins, the cuticle also contains the highly elastic protein resilin, which, as a hydrogel, is particularly water-dependent.¹⁴ Therefore, if the supply of hemolymph to the wings is disrupted, for example due to injury, the wings lose their elasticity relatively quickly, becoming dry and brittle.^15–17

The patterns of hemolymph flow through their wing vein network have been found to be well-defined.^15,18 In insects with transparent wing veins, the flow routes of hemolymph can be followed by the movement of hemocytes,^15,19,20 or can be made visible by injecting fluorescent dyes²¹ or microspheres.^9,22 Such approaches made it possible to establish that the exchange of hemolymph in the wings occurs in almost all insects, often through a kind of loop flow through the vein network: the hemolymph enters the wing at the base of the anterior veins, then flows to the tip (efferent flow) and returns to the thorax from the posterior veins (afferent flow). From an evolutionary perspective, this flow pattern is ancestral¹ and also occurs in some dragonflies.^15,23 By contrast, in an oscillating (tidal) flow, another observed flow pattern, hemolymph flows into and out of the wing in sequence, switching between afferent and efferent flows, which occurs simultaneously in all wing veins. Such oscillating flow has so far only been observed in Lepidoptera and some Coleoptera.^7,21,24,25

The driving force for hemolymph flow in the wing veins is not generated in the wing itself and depends on several factors. Because the body cavity is filled with hemolymph (reflecting the open circulatory system of insects), wing circulation is influenced by the pressure conditions at the base of the wing veins. The flow through the wing vein network is driven by specific wing circulatory organs located in the thorax. These so-called “wing hearts” are connected via tubular structures to the posterior wing veins from which they continuously suck hemolymph. As a result, hemolymph is drawn from the thoracic cavity into the anterior wing veins, which in turn leads to loop flow through the wing vein network. Hemolymph flow may also be influenced by the flapping of the wings during flight.^11,23,26 Despite this knowledge, quantitative information about the exact values of flows within the wing is scarce, with the most detailed data from a mosquito²² and a grasshopper.⁹

Although previous studies have successfully used live insects to investigate hemolymph flow through insect wing veins, the use of living insects limits the examination of flow. For instance, restraining an insect can cause irregular hemolymph flow or even reversed flow (via the dorsal vessel), and it is difficult to modify hemolymph flow paths or to test non-physiological flow conditions with live insects. One way to circumvent such limitations is by using an engineering model, which can be used to simulate hemolymph flow in the wing vein network in vitro. Furthermore, detailed flow patterns can be investigated by manipulations that are difficult or impossible in living animals.

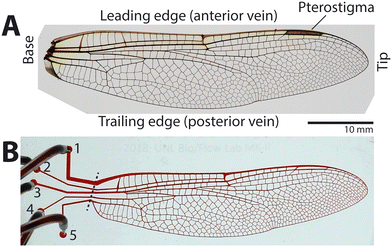
Toward this aim, we used microfluidics technology to create artificial insect wing veins on a silicone-based microfluidic chip, modelled after a high-performance insect flier and predator, the common green darner dragonfly, Anax junius. The forewing of this dragonfly (Fig. 1A) was chosen for the following reasons. First, the wing has a well-defined loop-flow route.¹⁵ Second, the wing size is appropriate for microfluidic device fabrication at scale (about 30 mm long and 10 mm wide). Lastly, dragonflies have been actively studied for insect flight and biomimetic wings,^23,27–30 providing a base of knowledge of this system. Using the microfluidic model, we simulated steady hemolymph flow through the vein network of the dragonfly by injection of water and studied transient perfusion through the vein network caused by steady circulation.

Fig. 1 Microfluidic wing vein model. (A) Forewing of common green darner, Anax junius showing common wing features: base, leading edge (anterior wing edge, often thicker veins), trailing edge (posterior wing edge), and pterostigma (a large wing tip hemolymph sinus). (B) Image of a fabricated device with five flow ports numbered from 1 to 5. The blue dashed line was used to determine the time point of 0 s for the dye to enter the vein network.

2. Methods and materials

2.1 Fabrication of a microfluidic wing vein device

A microfluidic master mold of the wing's vein network was fabricated with a scale ratio of 1 : 1 using photolithography (Fig. S1†). A high-resolution image of the forewing of A. junius (Fig. 1A) was taken with a digital camera (EOS Rebel T3, Canon with a Tamron 28–75 mm f/2.8 lens), and the image was processed into a binary image using image processing software (Adobe Photoshop). Flow ports (diameter: 1 mm) were added at the base-side end of each longitudinal vein, numbered 1 to 5 from leading to trailing edge (Fig. 1B). The channel design was printed as a high-resolution photomask (25 400 dpi; CAD/Art Services). SU-8 100 (MicroChem) was spin-coated on a 3 inch-diameter silicon wafer to form a uniform photoresist layer of 100 μm thickness. The wing vein channel pattern was printed on the SU-8 layer using photolithography and the photomask.

A microfluidic wing vein device was fabricated using the master mold, polydimethylsiloxane (PDMS), and soft lithography (Fig. S1†). 25 g of PDMS (Sylgard 184, Dow Corning) was mixed with the standard weight ratio of 10 : 1 between the base and agent, poured onto the master mold, which was previously coated with (tridecafluoro-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane (T2492, United Chem), degassed, and then cured at 60 °C overnight in an oven. After the cured PDMS channel body was peeled off from the mold, 0.5 mm diameter holes were punched using a biopsy punch (Rapid Core Punch, World Precision Instruments) to serve as the flow ports of the device (labeled 1–5 in Fig. 1B).

As the base substrate of the device, a ∼60 μm-thick PDMS layer was formed on a clean slide glass (75 × 50 mm²) by spin-coating and curing. Then, the prepared PDMS body and the substrate were plasma-treated using a plasma cleaner (PDC-32G, Harrick Plasma) and then bonded together. The bonded device was post-cured at 80 °C overnight for enhanced bonding. Then, the device was connected to tubing (inner diameter: 0.020 in, outer diameter: 0.060 in; ND-100-80, Tygon) via needles (inner diameter: 0.017 in, outer diameter: 0.025 in, length: 0.5 in; NE-1300-01, New England Small Tube Corporation) inserted into the ports.

2.2 Single port injection

The fabricated device had five ports, and it needed to be determined which ports would serve as the inlet to produce simulated hemolymph flow of the dragonfly wing. For this purpose, flow visualization experiments were conducted by injecting red food dye (Red Food Color, Tone's) through each different port in successive trials. In other words, one port served as the inlet while the rest served as outlets; the port for dye injection was then changed sequentially from port 1 to port 5 in separate trials. For example, when port 2 was the inlet, ports 1, 3, 4, and 5 served as outlets, and in the next trial, port 3 served as the inlet.

The device was prefilled with clear deionized water, and hydrostatic pressure was maintained overnight to remove air bubbles trapped in the channel. Then, dye was injected into the device at a volume flow rate (Q) of 5 mL min⁻¹ using a syringe pump (Fusion 200, Chemyx Fusion). We tested different volume flow rates and chose 5 mL min⁻¹ because it best facilitated data collection: the device could be perfused with the dye quickly without bursting the device. Perfusion of the dye was imaged at 30 frames per seconds (fps) using the digital camera.

2.3 Image processing

To analyze recorded perfusion patterns quantitatively, image processing was conducted using MATLAB (MathWorks) as follows (Fig. 2). The reference time of t = 0 s was set for the image in which the dye began to enter the vein network. Specifically, the video frame where the dye reached the blue dashed line shown in Fig. 1B was found, and the time stamp for the image was set to 0 s. Then, the video was downsampled to 1 fps and exported as a series of images.

Fig. 2 Image processing procedure used to determine the boundary of the perfused area.

The color images were converted to grayscale using the function “rgb2gray”, and then the images were converted to binary using “imbinarize” with options of “adaptive” and “sensitivity” of 0.61. In the binary images, the channel area filled with the dye appeared white and the remaining area appeared black. Speckles and disconnected parts were removed using “bwareafilt”, and then the boundary of the dye-filled area was determined by using “bwtraceboundary”. As shown in Fig. 2, the boundary determined by image processing matched well with the perfused area.

The area of the perfused veins was measured by counting the number of white pixels. This value was divided by the area of the entire channel to calculate the ratio between the perfused area to the entire vein area (A). When clear water was injected into the device pre-filled with red dye (see section 2.4), the area of the perfused veins was measured by subtracting the area of the dye-filled veins from the entire vein area.

2.4 Multiple port injection

The dye perfusion patterns of the single port injection trials were compared after image processing, and overall perfusion patterns were found to be different between trials when ports 1, 2, and 3 were the inlet vs. when ports 4 and 5 were the inlet (see section 3.1). In other words, the dye perfused similarly when it was injected into port 1, 2, or 3, and thereby these ports were defined as the ‘inlet’ group. Similarly, ports 4 and 5 were defined as the ‘outlet’ group.

First, the dye was injected into the inlet group to simulate perfusion occurring through the vein network of the dragonfly forewing when hemolymph enters the wing through the inlet ports. For this purpose, a custom PDMS-based adaptor was used to connect the inlet ports to one tube. The device was prefilled with water, and air bubbles were removed. Then, the dye was injected into the device using the syringe pump, and perfusion of the dye was imaged. In separate trials, the three different injection rates (Q = 0.5, 1 and 5 mL min⁻¹) were tested to examine any differences in perfusion depending on the rates. The device was washed completely after each run.

Second, a trial was conducted by injecting the dye into the outlet group. This trial simulated a case in which hemolymph flows in a reversed fashion in the wing.

Lastly, injection was conducted in an inverse fashion, injecting clear water instead of dye. The device was prefilled with the dye, and air bubbles were removed. Then, clear water was injected into the device into the inlet group at Q = 1 mL min⁻¹, and perfusion of clear water was imaged.

3. Results and discussion

3.1 Perfusion of the red dye into water with single port injection

The fabricated microfluidic wing vein device had five ports, modeled after the dragonfly's five major longitudinal veins that connect the forewing with the wing hinge and the thoracic cavity (Fig. 1B). To determine which ports serve as inflow (i.e., inlet ports), the device was pre-filled with clear water, and then the red dye solution was injected at 5 mL min⁻¹ through each port while the perfusion pattern of the dye was imaged. Fig. 3A shows how the dye propagated through or perfused into the vein network.

Fig. 3 Results of dye perfusion via single-port injection (Q = 5 mL min⁻¹). (A) Visualized perfusion of the injected dye. (B) Moving front of the dye through time. Colored numbers around each wing figure represent time in seconds, and the black number shown at the wing tip is the time to completely perfuse the device (t_max). Arrows indicate the port used for injection. (C) Temporal change of the perfused area ratio. Inset: log-linear plot.

When the dye was injected through either port 1, 2, or 3, it flowed out through the remaining ports, partly filling the device near the wing base (see the top three rows in Fig. 3A and Video S1–S3†). Then the perfused area grew toward the wing tip, which made the front of the perfused area (the blue dashed line in Fig. 3A) move toward the wing tip. As a result, the dye appeared to move toward the tip through the anterior and posterior veins. This result, the dye moving along the posterior vein toward the tip, apparently stands in contrast to real biological flows, as hemolymph is known to flow along the posterior vein from the tip toward the base;^15,26 however, see section 3.4. Because the anterior vein was perfused earlier than the posterior vein was, the moving front of the perfusing dye formed an acute angle with respect to the horizontal axis. As the dye front approached the tip, the dye perfusing through the anterior vein moved over the tip, and water was trapped near the tip-side end of the posterior vein (the arrow in top row in Fig. 3A). As the trapped water disappeared, the vein network was completely perfused with the dye.

When the dye was injected through port 4 or 5, the dye flowed along the posterior vein first and then flowed out through the remaining ports, partly filling the device near the wing base (see the bottom two rows in Fig. 3A and Video S4 and S5†). Afterwards, the perfused area grew toward the wing tip, and the front of the perfused area moved toward the wing tip. Because the posterior vein was perfused earlier than the anterior vein was, the moving dye front formed an obtuse angle with respect to the horizontal axis, which was the key difference from the single port injection trials through ports 1, 2, or 3. As the dye front approached the tip, water was trapped near the tip-side end of the anterior vein. As the trapped water disappeared, the vein network was completely perfused with dye.

Recorded images of the dye perfusing the microfluidic wing vein device were processed to determine the moving front of the dye (Fig. 3B) and to measure the area ratio between the perfused area to the entire vein area (A). Fig. 3B shows how the moving front advanced toward the wing tip, comparing times that were chosen for their approximately similar increase in A (i.e., ΔA ≈ 0.1). Because overall perfusion patterns were similar among single port injection trials of ports 1–3 and between ports 4 and 5 as shown in Fig. 3B, ports 1–3 were grouped as the inlet ports for the forward or natural flow direction, and ports 4–5 as the outlet ports. This finding agrees with what has been described in dragonflies previously, that the three anterior longitudinal veins (the costa, subcosta, and radius) of the dragonfly's wings exhibit afferent flow, while the two posterior longitudinal veins (the cubitus and anal veins) exhibit efferent flow.¹⁵ The first three longitudinal veins corresponded to ports 1–3, and the last two longitudinal veins corresponded to ports 4–5.

Fig. 3C shows how A increased with time for each single-port injection case. Overall, perfusion first proceeded quickly, and then it became slower. The time to completely perfuse the vein network (t_max) was defined as the time when 99% of the vein network had been perfused [i.e., A(t = t_max) ≈ 0.99]. t_max differed depending on the injection port, and the values were 17 s via port 1, 43 s via port 2, 49 s via port 3, 16 s via port 4, and 11 s via port 5. As expected from Fig. 3B, port 2 and 3 trials show very similar trends in A(t). Noticeably, port 1 and port 4 trials showed similar trends in A with similar t_max despite different perfusion patterns. The inset of Fig. 3C shows the same A data in the log scale of t. The roughly constant slopes of the data points in this log-linear plot show that the perfused area increased roughly with log(t) [i.e., A ∼ log(t)] regardless of the injection port.

3.2 Perfusion of the red dye into water through grouped ports

After the inlet ports were determined, the next perfusion experiment was conducted by injecting the dye through the collected inlet group (ports 1–3 connected to single tubing; Fig. 4A and Video S6–S8†), which corresponds to the forward or natural hemolymph circulation in the dragonfly wing as previously observed,¹⁵ and then through the outlet group (ports 4 and 5 connected to single tubing; Fig. 4B and Video S9–S11†), which corresponds to the reversed flow, at three different flow rates (Q = 0.5, 1, and 5 mL min⁻¹). The injection through the inlet group was repeated twice for Q = 0.5 mL min⁻¹, and perfusion patterns were found to be similar (top two figures in Fig. 4A), which shows that the perfusion achieved with the microfluidic wing vein device was repeatable. As expected, overall perfusion patterns were similar to those seen in individual port injection trials shown in Fig. 3B: perfusion patterns shown in Fig. 4A resemble the top three figures in Fig. 3B (single port injection through port 1, 2, or 3), and those of Fig. 4B the bottom two figures of Fig. 3B (single port injection through port 4 or 5).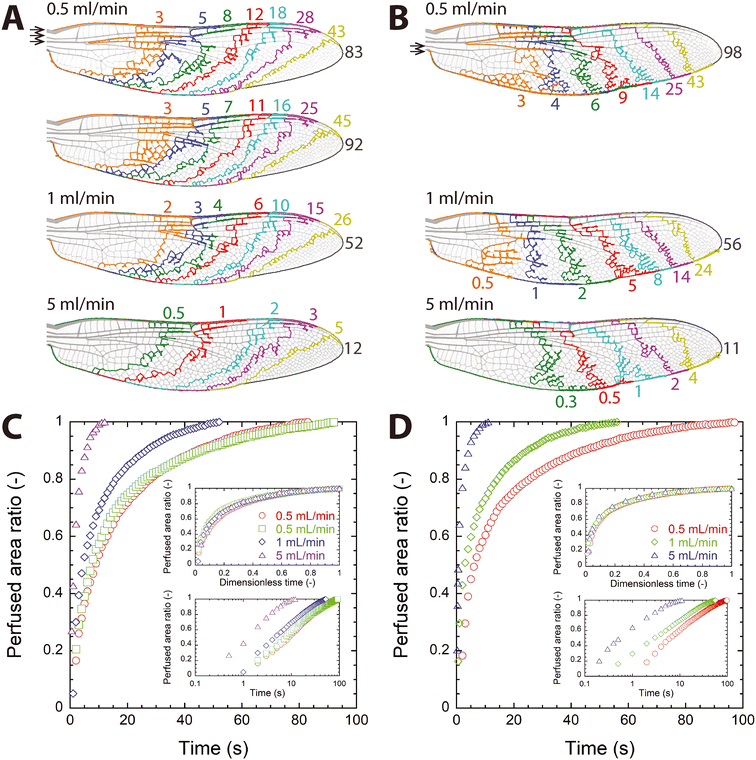

Fig. 4 Perfusion of dye into water through grouped ports (Video S6–S11†). (A and B) Moving front of the dye through time for injection through the inlet port group (ports 1–3) and the outlet port group (ports 4–5), respectively. Numbers shown in each figure are time in seconds, and the time shown near the wing tip is the time to completely perfuse the vein network (t_max). Arrows indicate ports for injection. (C and D) Temporal change of the perfused area ratio in the vein network for injection through the inlet port group and the outlet port group, respectively. Inset: (top) dimensionless plot, (bottom) log-linear plot.

It is also noticeable that perfusion pattern did not change significantly despite an order-of-magnitude increase in the flow rate. This observation can be explained by considering Reynolds number (Re), the ratio of inertial to viscous forces in flow. The Reynolds number is defined as Re = VD_h/ν, where V is the average flow speed through a channel, D_h the hydraulic diameter of the channel, and ν the kinematic viscosity of the fluid. The largest possible Re value for water flowing through the wing vein device (Re_max) can be estimated by using the highest injection flow rate (Q = 5 mL min⁻¹), the channel height (100 μm), and the thinnest channel width for an injection port (≈200 μm for port 4). With these channel dimensions and flow rate, V was found to be approximately 4.2 m s⁻¹. Using the hydraulic diameter (D_h ≈ 133 μm) of the channel and the kinematic viscosity of water (ν ≈ 10⁻⁶ m² s⁻¹), Re_max is evaluated to be about 560, which is far lower than the critical Re value for laminar-to-turbulent flow transition (≈2300) for pipe flows. Because the above estimation of Re_max assumes a single port injection through port 4, injection through the inlet port group should result in a lower Re value, and local Re values are expected to be much smaller than Re_max. Previously, we measured the local Re value in the microfluidic wing vein device to be approximately 10 at Q = 10 mL min⁻¹.³¹ As Q decreased by one order of magnitude, Re also decreased by one order of magnitude. Therefore, the water flow through the microfluidic wing vein model was laminar regardless of Q, and resultant perfusion patterns were similar regardless of Q. This finding suggests that similarity exists in flow in the vein network, and that the results of the current study can be applied to even lower injection rates if they are analyzed in terms of dimensionless parameters.

Fig. 4C and D show how A increased with time when the dye was injected through the inlet and outlet port groups, respectively. As expected from the single-port injection trials (Fig. 3C), perfusion took place quickly in the early phase of injection and then became slower. Regardless of the port group, t_max decreased with inverse proportionality to the injection flow rate (i.e., t_max ∼ 1/Q).

When t was normalized by t_max (t* = t/t_max), the data collapsed on a single curve in each group regardless of Q, as shown by the top insets of Fig. 4C and D. This agreement upon nondimensionalization was expected as discussed previously based on Re. The perfusion of the dye through the wing vein model was governed by the detailed flow path through the vein network, and the flow path was thought to be same regardless of Q because the flow through the vein network was laminar for all tested Q values. Although local flow speeds increased as Q increased, which resulted in decreased t_max, the flow path remained the same. Therefore, the temporal increase in A, which is dimensionless, was similar regardless of Q when expressed in t*.

Similar to the individual port inject cases, the relationship of A ∼ log(t) was observed as shown in the bottom insets of Fig. 4C and D, regardless of the injection port group. To compare the dependence of A increase on time, a linear function was fitted between the whole data of A and log(t*) for each port group using the method of least squares. The line of best fit was A = 0.502 log(t*) + 1.033 (R² = 0.983, p = 1.91 × 10⁻²⁰⁹) for the inlet port group (i.e., forward flow) and A = 0.425 log(t*) + 1.035 (R² = 0.983, p = 3.97 × 10⁻¹⁵⁰) for the outlet port group (i.e., reversed flow) (Fig. S2†). The similarity of these lines suggests that the temporal increase of A with respect to t* was similar regardless of the direction of the resultant circuitous flow, despite different perfusion patterns. The found logarithmic increase of A with respect to time seems to result from the geometry of the vein network and the flow path through the network (see section 3.4).

It is possible that diffusion occurring at the dye-water front could introduce bias into our measurement of A. To qualitatively address this question, the diffusion of the dye at the front was tested by stopping the injection of the dyed water at a certain point and then imaging the front over a time period of 180 s. As Fig. S3† shows, the dye did not exhibit substantial diffusion into the water at the front over this time period. Considering that the perfusion of the dye was completed in less than 90 seconds at the lowest volume flow rate of this study (= 0.5 mL min⁻¹), this test showed that the error introduced by diffusion was negligible.

Separately, the significance of diffusion was evaluated using the Péclet number, which quantifies the relative importance of advection to diffusion. Here, Péclet number is defined as Pe = VD_h/D, where D is the diffusion coefficient between the dye and water. Because the order of magnitude of D typically ranges from 10⁻¹¹ to 10⁻⁹ m² s⁻¹,^32,33 the D value for the dye was conservatively assumed to be 10⁻⁹ m² s⁻¹. Previously, we measured the local flow speed to be about 2 m s⁻¹ at a location where the channel width was about 50 μm (D_h ≈ 67 μm), injected at Q = 10 mL min⁻¹.³¹ Because the local flow speed is expected to be proportional to the injection flow rate, the flow speed at the same location would be V = 0.1 m s⁻¹ at Q = 0.5 mL min⁻¹. With these values, Pe of the dyed water in the device was estimated to be about 6700. This Pe value indicates that advection was dominant, supporting the previous test that showed that the diffusion of the dye was negligible.

3.3 Perfusion of water into the red dye

Similar to the single-port injection cases (for example, the arrow in Fig. 3A), we observed a puzzling situation in the grouped port injection trials in which as the red dye perfused the vein network, clear water was trapped near the wing tip, and the trapped water eventually disappeared. Sometimes a small volume of water was trapped between the red dye plugs in certain channel segments of the device, and the trapped water decreased in volume gradually and disappeared during perfusion (Fig. S4†). Based on these observations, we hypothesized that the dye and clear water flowed together through veins, and that water could not be seen in such co-occupied veins because of the dye.

To test this hypothesis, we conducted a perfusion experiment with the colors switched: the wing vein device was prefilled with the red dye, and clear water was injected through the inlet port group at Q = 1 mL min⁻¹ (see Video S12†). Fig. 5A shows the perfusion pattern of water into the dye-filled device. In comparison to the third figure in Fig. 4A showing the dye perfusion case with the same Q, the perfusion pattern of water was substantially different. First, as water began to flow into the device, the spot indicated by the dashed circle in Fig. 5A cleared up first, and then the water-perfused area began to grow from that location. This pattern was quite different from that of the dye injection trials because the dye perfused the area near the wing base first, and then propagated toward the wing tip. Also, the shape of the moving front was very different between the two cases. Second, perfusion took a longer time with water injection than with dye injection, seen in Fig. 5B comparing the temporal increase of A of the two cases. Lastly, the slope of A with respect to log(t) changed around at 10 s and 30 s (inset of Fig. 5B), indicating that the increase in A with water injection consisted of three phases. By contrast, A increased smoothly or continuously with dye injection, which could be represented by one single logarithmic function of time (Fig. S2†).

Fig. 5 Perfusion of clear water into the red dye solution (Video S12†). (A) Moving front of the water in time for water injection through the inlet port group. Numbers are time in seconds. Arrows indicate ports for injection, and the blue dashed circle shows the first area cleared by water perfusion. (B) Temporal change of the perfused area ratio for injection of water into dye. Δt: Time difference in achieving the same A value between the two cases. Inset: log-linear plot.

The observed differences in perfusion pattern and A(t) between water injection and dye injection support our hypothesis that water and dye co-existed in the veins during perfusion. If the water and dye could not flow in parallel in veins and instead flowed as two separate plugs in the vein, the perfusion pattern would be similar between the two perfusion experiments. However, Fig. 5 shows that the perfusion patterns were very different, which supports the hypothesis.

The results shown in Fig. 5 can be interpreted in terms of the arrival of a new substance and the complete removal of an old substance. In this interpretation, the moving front of the dye in dye perfusion represents when a new substance (the dye) reaches local veins filled with an old substance (water). The reason is because once a certain vein segment began to be perfused with dye (the new substance), it appeared red even though water (the old substance) was still present in the segment. By contrast, the moving front of water (a new substance) in water perfusion represents when an old substance (the dye) is completely removed in local veins. The reason is because a certain vein segment could appear clear only when the dye (the old substance) was completely replaced by water (the new substance). Fig. 5B shows that the time difference between water injection and dye injection for certain A (Δt in Fig. 5B) increased as A increased. Because Δt can be seen the time difference between the arrival of a new substance and the complete removal of an old substance, increasing Δt suggests that the time difference between the arrival of a new substance and the complete removal of an old substance varies across the vein network.

3.4 Theoretical model

The dye perfusion experiments had a few similar features regardless of ports for dye injection. First, the injected dye flowed out through other ports before it reached the wing tip. In other words, the dye flowed out of the device before filling the entire device, and the perfusion of the dye occurred while the dye kept flowing out of the device. Second, the perfusion rate of the dye (dA/dt) decreased with time. In other words, the perfused area of the device appeared to increase quickly at the beginning and then slowly toward the end of perfusion.

Moreover, the perfusion direction through the posterior vein was opposite to the hemolymph flow direction through this particular vein. As observed in previous physiological studies,^9,15 hemolymph in some insect species flows from the wing tip toward the wing base along the posterior vein. By contrast, the injected red dye perfused toward the wing tip through this vein (Fig. 3B and 4A). To examine this puzzling observation, we flowed 20 μm-diameter polystyrene beads (polystyrene microspheres, Phosphorex) with clear water through the microfluidic wing vein device³¹ and examined their motion flowing through the posterior part of the device. This manipulation showed that in actuality, the beads moved toward the wing base, congruent with the biological observations.

In addition, the flow through the microfluidic model was steady (given the steady injection³¹), but the resulting perfusion behaviour was transient, as shown by the time-dependence of A. This puzzling observation was reflected in the moving front of the perfusing dye in Fig. 3B and 4A. Although the flow pattern through the vein network was steady and circuitous, the injected dye appeared to unsteadily propagate toward the tip because of the spatial variation of flow velocity.

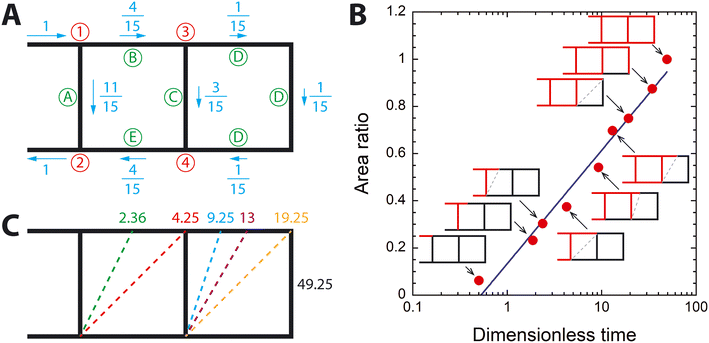
To further probe this finding, we developed a simple theoretical model for the wing vein network (Fig. 6A) and conducted a virtual experiment of dye injection using an analytical model. The model consists of two horizontal veins, which represent the anterior and posterior veins, and three cross-veins. The length of these vein segments is L while the length of the inlet and outlet veins is L/2. The cross-sectional area of the vein is the same, and water flows into the vein network through the inlet vein at a speed of V. Steady, laminar flow (i.e., Hagen–Poiseuille flow) is assumed based on the discussion of Re in Section 3.2. Using the conservation of mass and the relation between pressure difference across a vein segment and flow rate of Hagen–Poiseuille flow, flow speed in each segment is reported as a ratio of V, shown in Fig. 6A (see ESI†).

Fig. 6 Theoretical vein network model for dragonfly wings. (A) Local flow speeds are shown for each vein in terms of a fraction of the injection speed, and blue arrows show the direction of the flow. The green circled letters (A, B, C, and D) indicate veins, and the red circled numbers (1, 2, 3, and 4) indicate nodes in the model. (B) Result of the theoretical experiment to inject red dye into the vein network model. Temporal change of the perfused area ratio. The blue line shows A ∼ log(t). (C) The moving front of the dye. The numbers above the anterior vein show time points for each moving front, and the number at the wing tip is t_max.

The virtual experiment of dye perfusion is illustrated in Fig. 6B. As red dye is introduced at the inlet, the dye gradually perfuses the inlet vein, and the front of the dye moves with speed V. When the dye reaches node 1, it branches into vein A and vein B. The dye perfuses faster in vein A than in vein B because of different flow velocities. When the dye reaches node 2 via vein A, it begins to flow through the outlet vein while the dye front in vein B still moves forward. When the dye moving in vein B reaches node 3, it branches into vein C and vein D. The dye flows faster in vein C than in vein D. While the dye moves through the loop of vein D, the dye in vein C reaches node 4 and then enters vein E. As a result, water is trapped between the dye in the outlet vein and the dye entering vein E, which was also observed in our microfluidic experiment as shown in Fig. S4† and discussed in section 3.3, and the trapped water flows through the outlet vein with the dye. As the dye moves through vein D, water in vein D is also trapped by the dye. Once the loop of vein D has been completely perfused with the dye, the theoretical vein network is completely perfused with the dye.

It is possible to calculate the total length of the vein perfused with the dye as a function of time, as shown in Table S2.† The A of the theoretical model can be calculated by dividing this length with the total length of the vein network. Fig. 6B shows how A increases with dimensionless time, which is t divided by L/V (t* = tV/L). When plotted with the logarithmic scale of t*, the A of the theoretical model surprisingly shows the same scaling relationship of A ∼ log(t) as seen in the microfluidic experiments. This log(t)-dependence cannot be observed with a theoretical model with only two cross-veins (see Fig. S5†), and adding one more cross-vein makes A increase following log(t). As more cross-veins are added to the theoretical model, the dye will flow much slower through the added cross-veins because the flow speed decreases further due to branching out as shown in Fig. 6A. Consequently, the time rate of A (dA/dt) decreases as the dye approaches the wing tip, which may explain the observed A ∼ log(t) scaling relationship.

The theoretical model also helps to explain why the moving front of the dye-perfused area moved through the posterior vein of the microfluidic wing model in the opposite direction to the known flow direction of hemolymph in the real animal. The moving front of the perfused area in the theoretical model was found by connecting two frontmost points of the perfused area, as shown by the gray dashed lines in Fig. 6B. For example, at t = 2.36, the red dye reached about one-third point in vein B in the anterior vein while it reached node 2 in the posterior vein. The gray dashed line connecting these two points represents the moving front of the perfused area. When these dashed lines are plotted together with their respective time point as shown in Fig. 6C, the moving front of the dye appears to move from the base toward the tip in the posterior vein, although water flows through the posterior vein from the tip toward the base.

This difference is a consequence of the advection acceleration of the flow velocity field. Because the method of tracking the moving dye front is Lagrangian, the material or substantial acceleration of the flow fields needs to be considered in understanding the motion of the dye front. Clearly by design, the flow through the theoretical model is steady, which means that the local acceleration of the flow is zero (i.e., ∂V⃑/∂t = 0). By contrast, the flow velocity is not uniform across the model as shown in Fig. 6A, which results in non-zero advection acceleration (i.e., V⃑·∇V⃑ ≠ 0). As a result, the material acceleration of the flow field is not zero, and although the flow field is steady, the dye front moves transiently.

3.5 Advantages and limitations of the microfluidic insect wing vein model

The newly developed microfluidic wing vein model provides new opportunities for future studies. First, flow through the vein network could be modulated to test other non-physiological conditions, enabling the exploration of the physical parameters of the network. For instance, fluid could be injected through ports 1 and 5 so that it flows out through ports 2, 3, and 4. It is also possible to modify the model vein network to simulate physiological pathologies, such as damage of the wings and blockage of local veins. Second, it should be possible to characterize the pressure drop across the wing by measuring the pressure difference between the inlet and outlet port groups as a function of injection flow rate. Such information can be used to estimate the pumping capacity of an insect's multiple accessory pumping organs (e.g., thoracic wing hearts). Third, the transparency of the model lends itself micro particle image velocimetry (μPIV), which would enable the measurement of local velocity fields and a mapping of the entire flow field in the wing vein network.³¹ Such work would lend insight into the fluid dynamics that underly the perfusion patterns revealed by this study.

The microfluidic insect wing vein device used in this study has several limitations. First, anatomical structures within the real vein, such as nerves and tracheae, were not considered in the microfluidic model. These structures vary in size and complexity within the wing, and they are flexible as well. Tracheae in particular can be compressible depending on the fluidic pressure.³⁴ Second, the cross-sectional shape and dimension of channels were different from those of corresponding veins of the dragonfly forewing. For ease of fabrication and due to the limitation of the conventional photolithography method used for mold fabrication, rectangular channels with a common channel height (100 μm) were used for the microfluidic wing vein model; these channel widths were equal to the outer diameter of veins measured from the wing image (Fig. 1A). By contrast, cross-sections of real dragonfly wing veins are more circular and range in shape^13,26,30 where the wall thickness of the vein also changes across the wing span and chord.³⁵ For instance, in a forewing of dragonfly Pantala flavescens, the wall thickness of veins ranged from 5 μm to 15 μm, while the outer diameter of veins varied from 600 μm near the pterostigma to 30 μm near the trailing edge.²⁶ The inner and outer radius of wing veins of dragonfly Crocothemis servilia was measured to be 0.1 mm and 0.16 mm in the leading edge area and 0.031 mm and 0.045 mm in the trailing-edge area.³⁶ These differences in the cross-sectional shape and dimension may cause differences in local flow velocities, which may have affected overall perfusion patterns. More realistic microfluidic wing vein network models can be fabricated by using high resolution 3D imaging of the inner surface of wing veins³⁷ and advanced mold-fabrication methods.³⁸ Lastly, specialized regions like the pterostigma were not considered. A dragonfly's pterostigma is a relatively large hemolymph reservoir on the leading edge near the wing tip (Fig. 1A), and including it in the microfluidic model might result in changes in flow pattern and perfusion.^9,39

The injection flow rates employed for the perfusion experiment were not based on the actual hemolymph speeds in a dragonfly wing, because they have not been experimentally determined. Few studies have quantified flows within an insect wing. The average speed of hemolymph flowing through mosquito wings was measured to be 99 μm s⁻¹ and 458 μm s⁻¹ at the inlet and outlet of the wing, respectively.²² Within the entire wing network of a grasshopper, local flows were found to be highly variable with an inlet flow speed of 0.12 m s⁻¹.⁹ Because of the lack of in vivo flow speed measurements of a dragonfly wing, a previous computational simulation of the hemolymph flow within the forewing of wandering glider (Pantala flavescens) assumed an inlet pressure of 20 Pa, and the flow speed at inlets and outlets approximately ranged 0.2–0.4 mm s⁻¹.²⁶ This simulation result was validated by comparing the travel time of hemolymph from the wing base to pterostigma between the simulation (150 s) and the fluorescent dye perfusion experiment using living specimens (142 s). Thus, the hemolymph flow speed at the wing base of dragonflies seems to be in the order of 0.1 mm s⁻¹, which is similar to that in the mosquito wing.²² In the current study, the injected red dye reached the pterostigma in 18 s at Q = 0.5 mL min⁻¹ as shown in Fig. 4A, which is one order of magnitude shorter than the simulation result.²⁶ Although a direct comparison between the two different dragonfly species may not be appropriate, this comparison suggests that a physiological injection rate is in the order of 0.01 mL min⁻¹. However, the observed similarity in perfusion patterns and agreement in dimensionless curves of perfusion area ratio (top insets in Fig. 4C and D) between three different injection rates suggests that the current study's finding is reasonable for perfusion within the dragonfly forewing with even lower injection rates.

The consideration of injection rates in this study is also justified by the Reynolds number of the flow. As discussed previously in section 3.2, water flow through the device was laminar, and local Re values are expected to be much lower than the largest possible Re value (Re_max ≈ 560) of the current study. We previously measured a local Re value to be about 10 when water was injected at Q = 10 mL min⁻¹.³¹ Along with our discussion in section 3.2, this result suggests that the local Re value would become 0.01 for Q = 0.01 mL min⁻¹. Although Re decreases over three orders of magnitude as Q does, the viscous behavior of steady water flow through the channel network of the device would not change because Re values are still significantly lower than the critical Re value. Therefore, it appears valid to consider the results of this study as lending insight into the steady hemolymph circulation through a real-life green darner wing.

Water was used in this study as a working fluid instead of real hemolymph for several reasons. First, it would be difficult to collect a large amount of hemolymph from dragonflies for the microfluidic experiment. More importantly, extracted hemolymph clots extremely quickly, which changes its physical properties⁴⁰ and thereby made it impractical to use for our experiments. The difference in viscosity between water and insect hemolymph might also be a concern. The hemolymph viscosity of some insects (both larvae or adults) was measured previously enabling quantitative comparisons. The hemolymph of the larvae of hornworm Manduca sexta was measured to be shear thinning with a viscosity of ∼3 mPa s.⁴⁰ By contrast, the hemolymph of adult butterflies and moths was shown to be Newtonian with a viscosity range of 1.3–2.2 mPa s.^41,42 Similarly, the hemolymph of fruit fly Drosophila melanogaster larvae was measured to be Newtonian with an average viscosity of 1.34 mPa s.⁴³ These studies suggest that adult insect hemolymph can be considered as a Newtonian fluid roughly two to three times more viscous than water. However, this difference in viscosity does not influence the significance of the current study for the following reasons. First, because the viscosity of water and insect hemolymph are in the same order of magnitude, the Reynolds numbers of their flow through the insect wing model are expected to be in the same order of magnitude. Therefore, flow characteristics would be similar between hemolymph and water flow through the device. Second, because flow through the model device was created by injection with a fixed volume flow rate, local velocity distribution would be very similar between hemolymph and water. If the flow is driven by constant pressure, hemolymph will flow slower than water because of its higher viscosity. Lastly, similarity in transient perfusion dynamics confirmed in the dimensionless plots (the top insets of Fig. 4C and D) suggests that perfusion of hemolymph would be similar to that of water when analyzed in terms of dimensionless perfusion area and time.

4. Conclusions

In this study, we characterized the transient perfusion through the forewing of the common green darner dragonfly (Anax junius) using a microfluidic model fabricated using a high-resolution picture of the wing, photolithography, soft lithography, and PDMS. The hemolymph circulation through the wing vein network is crucial for maintaining healthy wings, and the functionality of the wing depends essentially on its unique microfluidic vein network. However, experimentally manipulating circulation in the wings of living specimens is difficult. To overcome this limitation, we created a microfluidic model of the dragonfly forewing. The major findings of this study are 1) the perfusion of a new introduced substance could be represented by a dimensionless relationship between the perfused area ratio (the ratio of the area perfused with the new substance to the entire vein network area) and dimensionless time (the ratio of time to the time for complete perfusion), 2) the perfusion area ratio increased with a logarithmic function of time, and 3) there existed a time difference between the arrival of a new substance and the complete removal of an old substance in the veins. We also created a theoretical model to explain how perfusion is determined by the flow paths through the vein network and why the perfusion area ratio scaled with the logarithmic function of time. The simplified geometry and dimension of veins of the models enabled a detailed investigation of the microfluidic principles underlying insect wing circulation and provides a new basis for the development of applied bioinspired devices.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Conceptualization: SR, HZ. Formal analysis: SR, HZ, MKS, GP, JJS. Funding acquisition: SR. Investigation: SR, HZ, TP. Methodology: SR, HZ, TP. Project administration: SR. Resources: SR. Software: SR. Supervision: SR. Validation: SR, HZ. Visualization: SR. Writing – Original draft: SR, HZ, MKS, GP, JJS. Writing – Review & editing: SR, HZ, MKS, GP, JJS.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by the Collaboration Initiative Grant of the Nebraska University and NASA Nebraska EPSCoR Research Infrastructure Development (RID) FY22-26 (Federal Award #80NSSC22M0048). TP was supported by the Undergraduate Creative Activities & Research Experiences (UCARE) Program of the University of Nebraska-Lincoln. SR and HZ appreciate Ana Maria Vélez for her assistance in initial conceptualization. We appreciate Stephen Morin and his lab for their assistance in photolithography, and Don Paseka and Janis Paseka (Nebraska dragonflies and damselflies. https://unsm-ento.unl.edu/Odonata/index.html) for identifying the species of the dragonfly.

References

1. R. F. Chapman, The Insects: Structure and Function, Cambridge University Press, 5th edn, 2013.
2. S. Lin, N. Chou, G. Li, D. Bao, Y. Cai, Y. M. Xie and G. Wang, Adv. Eng. Softw., 2024, 190, 103600.
3. M. K. Salcedo, J. Hoffmann, S. Donoughe and L. Mahadevan, Biol. Open, 2019, 8, bio040774.
4. O. Shimmi, S. Matsuda and M. Hatakeyama, Proc. R. Soc. B, 2014, 281, 20140264.
5. J. Hoffmann, S. Donoughe, K. Li, M. K. Salcedo and C. H. Rycroft, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9905–9910.
6. G. Pass, M. Tögel, H. Krenn and A. Paululat, Zool. Anz., 2015, 256, 82–95.
7. C.-C. Tsai, R. A. Childers, N. N. Shi, C. Ren, J. N. Pelaez, G. D. Bernard, N. E. Pierce and N. Yu, Nat. Commun., 2020, 11, 1–14.
8. J. Fabian, I. Siwanowicz, M. Uhrhan, M. Maeda, R. J. Bomphrey and H.-T. Lin, iScience, 2022, 25, 104150.
9. M. K. Salcedo, B. H. Jun, J. J. Socha, N. E. Pierce, P. P. Vlachos and S. A. Combes, Commun. Biol., 2023, 6, 313.
10. G. Pass, Arthropod Struct. Dev., 2018, 47, 391–407.
11. C. Lietz, C. F. Schaber, S. N. Gorb and H. Rajabi, Commun. Biol., 2021, 4, 737.
12. M. K. Salcedo, T. E. Ellis, Á. S. Sáenz, J. Lu, T. Worrell, M. L. Madigan and J. J. Socha, Sci. Rep., 2023, 13, 6298.
13. E. Appel, L. Heepe, C.-P. Lin and S. N. Gorb, J. Anat., 2015, 227, 561–582.
14. E. Appel, J. Michels and S. N. Gorb, Adv. Funct. Mater., 2023, 2215162.
15. J. W. Arnold, Mem. Entomol. Soc. Can., 1964, 96, 5–60.
16. H. Rajabi, J. H. Dirks and S. N. Gorb, J. Exp. Biol., 2020, 223, jeb215194.
17. J. H. Dirks and D. Taylor, J. Exp. Biol., 2012, 215, 1502–1508.
18. M. K. Salcedo and J. J. Socha, Integr. Comp. Biol., 2020, 60, 1208–1220.
19. J. F. Yeager and G. O. Hendrickson, Proc. Soc. Exp. Biol. Med., 1933, 30, 858–860.
20. J. F. Yeager and G. O. Hendrickson, Ann. Entomol. Soc. Am., 1934, 27, 257–272.
21. L. T. Wasserthal, Zoomorpholgy, 1983, 103, 177–192.
22. R. T. V. Chintapalli and J. F. Hillyer, J. Exp. Biol., 2016, 219, 3945–3951.
23. L. Wang and Z. Zhong, Acta Mech., 2014, 225, 1471–1485.
24. L. T. Wasserthal, J. Comp. Physiol., 1982, 147, 27–40.
25. J. Sun, M. Ling, W. Wu, B. Bhushan and J. Tong, Int. J. Mol. Sci., 2014, 15, 6009–6018.
26. Y. Wang, Y. Yin, G. Zheng and H. Yao, Anim. Biol., 2021, 71, 85–101.
27. X.-S. Wang, Y. Li and Y.-F. Shi, Compos. Sci. Technol., 2008, 68, 186–192.
28. S. R. Jongerius and D. Lentink, Exp. Mech., 2010, 50, 1323–1334.
29. E. Appel and S. N. Gorb, Bioinspiration Biomimetics, 2011, 6, 046006.
30. D. Hou, Y. Yin, H. Zhao and Z. Zhong, Comput. Biol. Med., 2015, 58, 14–19.
31. H. Zhang and S. Ryu, presented at the American Society of Mechanical Engineers Fluids Engineering Division Summer Meeting, Anaheim, CA, USA, 2024, FEDSM2024-130930.
32. A. Konda, D. Lee, T. You, X. Wang, S. Ryu and S. A. Morin, Adv. Intell. Syst., 2019, 1, 1900027.
33. D.-H. Noh, A. H. Zadeh, H. Zhang, F. Wang, S. Ryu, C. Zhang and S. Kim, Ann. Biomed. Eng., 2024, 52, 1693–1705.
34. J. F. Harrison, K. Adjerid, A. Kassi, C. J. Klok, J. M. VandenBrooks, M. E. Duell, J. B. Campbell, S. Talal, C. D. Abdo, K. Fezzaa and J. J. Socha, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 2180–2186.
35. S. Sudo, K. Tsuyuki, T. Ikohagi, F. Ohta, S. Shida and J. Tani, JSME Int. J., 1999, 42, 721–729.
36. D. Hou, Y. Yin, Z. Zhong and H. Zhao, Bioinspiration Biomimetics, 2015, 10, 016020.
37. T. Schubnel, A. Mazurier, A. Nel, P. Grandcolas, L. Desutter-Grandcolas, F. Legendre and R. Garrouste, Methods Ecol. Evol., 2023, 14, 2036–2048.
38. M. Fenech, V. Girod, V. Claveria, S. Meance, M. Abkarian and B. Charlot, Lab Chip, 2019, 19, 2096–2106.
39. J. W. Arnold, Can. Entomol., 1963, 95, 13–16.
40. M. C. Kenny, M. N. Giarra, E. Granata and J. J. Socha, J. Exp. Biol., 2018, 221, jeb186338.
41. A. Brasovs, A. V. Palaoro, P. Aprelev, C. E. Beard, P. H. Adler and K. G. Kornev, Proc. R. Soc. B., 2023, 290, 20222185.
42. P. Aprelev, A. Brasovs, T. F. Bruce, C. E. Beard, P. H. Adler and K. G. Kornev, Front. Soft Matter, 2024, 4, 1341129.
43. A. Zabihihesari, S. Parand and P. Rezai, Microfluid. Nanofluid., 2023, 27, 8.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lc00714j

---