Open Access Article
Open Access ArticleCoarse-grained models for ionic liquids and applications to biological and electrochemical systems
Yang
Ge
 a,
Qiang
Zhu
ab,
Xueping
Wang
a and
Jing
Ma
a,
Qiang
Zhu
ab,
Xueping
Wang
a and
Jing
Ma
 *a
*a
aKey Laboratory of Mesoscopic Chemistry of Ministry of Education, Institute of Theoretical and Computational Chemistry, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing, 210023, China. E-mail: majing@nju.edu.cn
bMolecular Horizons and School of Chemistry and Molecular Bioscience, University of Wollongong, NSW 2522, Australia
First published on 9th June 2025
Abstract
Ionic liquids (ILs) are a class of molten salts with a collection of exciting properties and have been employed for wide-ranging applications across chemistry, biology, and materials science. However, the high viscosity of ionic liquids challenges atomistic molecular dynamics (MD) simulations in studying their structure–property relationships on large spatiotemporal scales. Coarse-grained (CG) models provide insight into the microscopic structure and intermolecular interactions underlying various properties by eliminating unnecessary atomic details. The general protocol for proposing a new CG model is reviewed, including determination of CG representation and force field (FF) parameterization. Recent advances in polarizable CG models were discussed with the emphasis on Drude oscillators and QM-based polarizable models. An overview was given on some recent applications of machine learning (ML) techniques on development of CG potentials, including the utilization of an ML surrogate model for FF parameterization and the development of ML potentials. Applications and challenges of IL CG models in treating complex systems, including pure solvents, mixtures, biological systems, and electrochemically confined environments, were presented. Finally, prospects for the development of transferable IL CG models are highlighted to extend the applicability to more mesoscopic systems.
Keywords: Ionic liquids; Coarse-grained models; Polarization effect; Machine learning; Molecular dynamics simulation.
1 Introduction
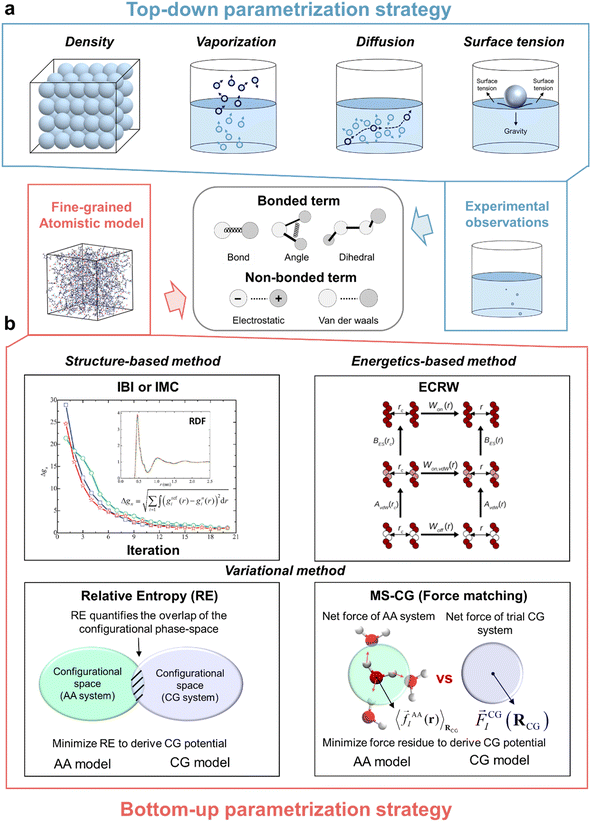
Ionic liquids (ILs) are a class of molten salts composed entirely of organic cations and organic/inorganic anions, which retain the liquid state at room temperature.1 Broad attention has been drawn due to their unique physicochemical properties, such as nonvolatility, nonflammability, high (thermal, chemical, and electrochemical) stability, and high ionic conductivity.2,3 These properties make them promising ingredients involved in diverse industrial applications, such as energy storage,4–10 electrotunable lubrication,11–14 separation processes,15–19 gas capture,20,21 and protein stability.22,23 These applications require an understanding of the microscopic origin underlying various thermophysical and transport properties. The molecular dynamics (MD) simulation method based on the classical force field (FF) is a powerful tool to obtain insights into the microscopic nanostructure and interactions and also an essential property prediction tool.24 The accuracy of the prediction mainly relies on the quality of the FF. Many IL atomistic FFs have been developed over the years, including the APPLE&P,25 AMOEBA-based,26 CL&P,27–29 GAFF-based,30 SAPT-based,31 and OPLS-based32–34 IL FFs.The application of atomistic models to biological and electrochemical systems (systems with hundreds of thousands to millions of atoms for a long time of micro- to milliseconds) is often limited by the immense computational demands, especially for the viscous IL media. Coarse-grained (CG) models are attractive to extend the spatiotemporal scale with sufficient computational efficiency and chemical specificity.35 A CG model simplifies a fine-grained atomistic representation by grouping related atoms into a single quasi-particle according to a predefined CG mapping scheme. This reduction smooths out high-frequency atomic vibrations and flattens the corresponding free-energy landscape, and such operation reduces the molecular friction, leading to a faster exploration of the underlying free-energy landscape.36 CG models generally allow for a larger time step relative to AA models (1–2 fs). For example, a time step of 10–20 fs is often adopted for the MARTINI CG model.37–39Fig. 1a illustrates a coarse-graining process that simplifies an all-atom (AA) model of a typical 1-n-butyl-3-methylimidazolium cation ([C4mim]) into different CG resolutions. The CG mapping should capture the essential features of a given system, while eliminating “unimportant” atomic details. Besides using chemical intuition, many studies have been conducted for designing CG mapping schemes with systematic methods, such as relative entropy theory,40 autoencoder techniques,41 and graph neural networks.42
In the context of classical MD simulations, molecular interactions are primarily described by empirical potential energy functions, which determine the energies of configurations and the forces acting on each interaction site.43 The FF can be divided into two distinct parts, including bonded and nonbonded terms. The analytical functional form of both terms is typically predefined, with their parameters determined by fitting target properties across different scales, including quantum mechanism (QM) calculations, atomistic MD simulations, and experimental data (Fig. 1b). Once the CG representation is determined, different parameterization protocols are available for CG potentials. These protocols include a top-down strategy, where CG models are directly fitted to a set of macroscopic experimental properties, and bottom-up CG methods, where CG models utilize statistical mechanics principles to preserve the microscopic properties of the atomistic models. Examples of bottom-up CG methods include inverse Boltzmann inversion (IBI),44,45 inverse Monte-Carlo (IMC),46 multiscale CG methodology (MS-CG),47–49 relative entropy (RE),40,50,51 and extended conditional reversible work (ECRW).52–54 Most IL CG models commonly adopt a hybrid strategy, where a bottom-up CG method is utilized for bonded terms, while nonbonded parameterization varies with each model.55 Taking [C4mim][BF4] as an example, Table 1 compares the performance of CG models developed by different methods with that of AA models and experimental data.
| Resolutions | Models | Density (ρ, kg m−3) | Diffusion (D+/D−, 10−11 m2 s−1) | Conductivity (σ, S m−1) | Heat of vaporization (ΔHvap, kJ mol−1) | Ref. |
|---|---|---|---|---|---|---|
| a The temperature is noted in parentheses with the unit of K ignored. b The atomistic FF of 0.8*OPLS is a refined version of the original one,34 which introduces a charge scaling factor of 0.8. c CL&Pol is the polarizable version of CL&P.27 | ||||||
| CG | MARTINI-based | 1181 (300) | 120/145 (293) | — | — | 84 |
| Top-down | 1209 (298) | 1.12/0.59 (298) | — | — | 85 | |
| ECRW | 1173 (300) | 1.55/1.74 (313) | — | — | 54 | |
| Drude-based | — | 5.8/7.3 (350) | 17 (350) | 114 (350) | 86 | |
| Electrostatic-variable CG model (VaCG) | 1168 (303) | 1.20/0.53 (303) | 0.45 (303) | 123.51 (303) | 74 | |
| ML potential | — | 48.58/35.49 (300) | — | — | 87 | |
| AA | OPLS | 1178 (298) | 7.3/6.6 (425) | — | 125.52 (298) | 34 |
| 0.8*OPLSb | 1150 (298) | 43.1/42.9 (425) | — | 140.5 (298) | 33 | |
| SAPT-based | 1180 (298) | 1.1/0.8 (298) | 0.29 (298) | 126 (298) | 31 | |
| CL&P | 1154 (343) | 1.19/0.88 (343) | — | — | 29 | |
| CL&Polc | 1134 (343) | 9.3/13.5 (343) | — | — | 29 | |
| GAFF-Drude | 1194 (300) | 6.8/6.7(343) | — | — | 30 | |
| AMOEBA-IL | 1229 (313) | 2.9/0.67 (313) | — | 135 (350) | 26 | |
| APPLE&P | 1193 (298) | 1.01/1.05 (298) | 0.28 (298) | 140.8 (298) | 25 | |
| Exp. | 1170 (343)29 | 40.0/47.6 (425)56 | 2.17 (350)56 | 128.03 (303)57 | ||
| 1198 (303)58 | 8.0/8.2 (343)29 | 0.295 (303)59 | ||||
| 1.44/2.89 (313)56 | ||||||
| 10.5/11(350)56 | ||||||
| 1.83/1.78 (303)60 | ||||||
The nature of ILs lies in their composition of ions, which generate local electric fields that polarize the surrounding molecular environment. The quality of description of the electrostatic polarization effect in the FF is crucial for the prediction of properties, especially for dynamic ones.61 One route to consider this effect is to introduce higher-order multipole effects in the FF, such as a fluctuating charge model,62,63 an induced point dipole model,64–68 and a classical Drude oscillator model.43,69 However, their self-consistency nature is computationally expensive and the additional degrees of freedom incurred by polarization make their parametrization more complex. By taking advantage of the fragment-based QM methods,70 such as the generalized energy-based fragmentation (GEBF) approach,71–73 polarization effects can be described at the QM level by using a large molecular cluster to mimic the bulk polarization environment.74 In addition, the utilization of variable electrostatic parameters can further implicitly consider different polarization environments for a mixture of ILs with other polar molecules, enhancing the FF transferability.74
FF parametrization is often a tedious and time-consuming process, particularly when bridging the relationship between desired physical properties and FF parameters. For example, optimization of nonbonded parameters against experimental data often requires running at least hundreds of MD trajectories. With more molecules included, the number of trial MD trajectories for optimization will sharply increase. Recently, increasing attention has been gained over data-driven ML techniques, which serve as efficient surrogate models to approximate the mapping between desired physical properties and FF parameters.75–77 Various ML models have been utilized in the field of FF parametrization, such as the random forest model (RF),75,78 Gaussian process regressor model (GPR),79,80 deep neural network model (DNN),81 and automatic differentiation technique.82 In addition, various ML potentials (MLPs) are emerging as alternatives to traditional FFs. These MLPs eliminate traditional empirical function forms and directly predict the potential energy and forces with atomic coordinates.83
In this review, we will summarize recent advances in CG modeling of ILs, including basic concepts of CG models, determination of CG representation, FF parametrization, polarizable IL CG models, integration of ML techniques into IL CG models, and various applications of IL CG models. We also discuss the capabilities and limitations of IL CG models in each context and provide an outlook on the development of transferable IL CG models for more complex systems.
2 Procedure for proposing a new CG model
When constructing a particle-based FF model for a specific system, one must first define the particles that represent the system and define the inter-/intra-molecular interactions between atoms (or collections of atoms). Compared to AA models, CG models require an additional AA-to-CG structural transformation, commonly referred to as CG mapping. This transformation treats a group of atoms into a certain CG particle based on predefined rules. The following FF parametrization is often informed by higher-resolution AA simulations and QM calculations. The detailed procedure for proposing a new CG model is depicted in Fig. 2. This section will detail these two steps, supplemented by literature examples, and highlight key considerations essential for IL CG models to accurately predict various properties.2.1 Definition of the CG mapping
Most IL CG mappings rely on chemical intuition. The positions of CG particles are generally determined by the center of mass (COM) of a group of atoms. Some representative CG mappings can be seen in Fig. 3, including various cations (e.g., imidazolium,54,84–105 pyrrolidinium,106 ammonium107) and anions (e.g., halides,92,101 hexafluorophosphate ([PF6]),86,93,94,97–99,101,104,108 tetrafluoroborate ([BF4]),84,85,88,90,108 nitrate ([NO3]),54,102,105 bistriflimide ([TFSI]),89,106 dicyanamide ([DCA])95). For cations, polar and nonpolar groups are coarse-grained into separate CG particles, though the partitioning scheme for specific groups may vary. For anions of small size and symmetric structure (e.g., [BF4], [PF6], and halides), they are often coarse-grained into a single CG particle. However, for [TFSI] and [DCA], multiple CG particles are introduced to better capture their structural features.The widely used MARTINI model,37–39 originally developed for biomolecules, has been extended to ILs, such as [Cnmim][BF4] (n = 2, 4, 8, 12).84 In this case, the anion [BF4] with the Td symmetry is represented by a single CG particle and the imidazolium ring with the attached methyl group is represented by three CG particles. This CG representation is essential for capturing the stacking interactions between the imidazolium cation and other aromatic compounds, which play a key role in simulating liquid–liquid extraction processes. The aforementioned is a special case. To achieve better transferability and balance between needed accuracy and computational efficiency, the MARTINI model categorizes different chemical fragments into a model library for CG mapping. While a four-to-one CG mapping is commonly employed, i.e., four heavy atoms are represented by a single CG particle, a three-to-one mapping is often adopted for the ring structure.37 For molecules with more complex structures, some automatic topology builders have been developed in the context of the MARTINI model, such as autoMARTINI109 and graph-based cg_param110 algorithms.
The CG representation can also be determined by systematic methods, such as the hierarchical graph-based framework,111 relative entropy theory,112 and variational autoencoder (VAE) technique.41 For example, the VAE technique, an unsupervised ML technique, simultaneously determines an encoder that maps complex data into a low-dimensional space, i.e., a CG mapping process, and a decoder that probabilistically infers the real data distribution via a generating process, i.e., a reconstruction from a CG representation to an atomistic representation. The VAE technique has been applied to the determination of CG representation for [C4mim][BF4], where an optimal CG representation is determined by training a VAE that is able to best reconstruct a given atomistic representation.87 A limitation of this method is that the number of CG particles must be specified in advance rather than being automatically determined.
2.2 FF parametrization
In the context of classical MD simulation, molecular interactions are mainly described by additive empirical potential energy functions.43 The total potential energy (Utotal) is categorized into the intramolecular bonded term (Ubonded) and the intramolecular/intermolecular nonbonded term (Unon-bonded):| Utotal = Ubonded + Unon-bonded | (1) |
 | ||
| Fig. 4 (a) Representative experimental properties commonly utilized by the top-down strategy for parametrization of typical bonded and nonbonded terms in the CG model; (b) schematic illustration of the key thoughts behind some bottom-up CG strategy on the basis of structure-based (e.g. IBI45,96 and IMC46), energetics-based (e.g., ECRW54), and variational methods (e.g., relative entropy40,50,51 and MS-CG47–49). The upper-left plot of (b) is reprinted with permission from ref. 96. Copyright 2013 The Royal Society of Chemistry. The upper-right plot of (b) is reprinted with permission from ref. 54. Copyright 2019 American Chemical Society. | ||
 | (2) |
Besides manual adjustment, the Boltzmann inversion (BI) method is one of the commonly used systematic methods for bonded parametrization.44 The BI method holds the assumption that the CG potential of a specific bonded type can be approximated by Boltzmann-inverting the corresponding probability distribution obtained from a fine-grained atomistic model under a canonical ensemble, as follows:
 | (3) |
 | (4) |
| Udihedral(φ) = − kBTln P(φ) + cd | (5) |
 | (6) |
In the context of the top-down strategy, the initial guess for nonbonded parameters is often derived by summing the parameters from atomistic models within individual mapped atomic groups. Subsequently, the vdW and electrostatic parameters are adjusted to match experimental properties. For example, a 4-site CG model of [C4mim][PF6] was developed with its nonbonded parameters directly summed from a CHARMM-based AA model, which qualitatively reproduced the experimental results, though the dynamics are unrealistically slow.98 With introduction of a new anion, [BF4], the original 4-site CG model98 was further refined by manually adjusting the vdW parameters of [BF4] to match the experimental density and diffusion coefficient.85 The parameter σ was found to play a more important role in the density and ε is more critical for the diffusion.85 This CG model has been used to assess the impact of different MD simulation parameters on the performance of viscosity prediction.119 The vdW parameters of a CG model of [C4mim][DCA]were also tuned to fit ionic conductivity.95 Besides density and surface tension, a microstructural property, the radius distribution function (RDF), is also encompassed as a target property to optimize vdW parameters for a CG model of [C7mim][Br], though no prior statistics mechanisms are known to guide this process.104
As for the bottom-up strategy, it can be divided into three groups: structural-based, energetics-based, and variational-based methods.120 The theoretical background of each method will be introduced, as well as their applications on IL CG models. Some more insightful reviews about this topic are recommended.35,120–123 In addition, some automated programs have been developed to assist researchers in implementing the bottom-up CG strategy on their own systems, such as VOTCA,116,124,125 OpenMSCG,126 MagiC,127 and BOCS.128
Structural-based methods, e.g., iterative Boltzmann inversion (IBI)45 and inverse Monte-Carlo (IMC),46 determine nonbonded CG potentials from the microstructural distribution function, P(r), e.g., RDF. IBI adopts an iterative strategy to refine the BI-derived potentials, as follows:
 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) U2,
U2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) …Un}, and the potential update of the IMC method is calculated by solving a set of nonlinear multidimensional equations through the Newton–Raphson method:
…Un}, and the potential update of the IMC method is calculated by solving a set of nonlinear multidimensional equations through the Newton–Raphson method:| Uk+1 = Uk + J−1(〈SCG〉 − SAA) | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈S2〉,
〈S2〉,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) …〈Sn〉} is the number of particle pairs in terms of interparticle distance r = {r1,
…〈Sn〉} is the number of particle pairs in terms of interparticle distance r = {r1,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r2,
r2,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) …rn}, for example, 〈Sa〉 is shown as follows:
…rn}, for example, 〈Sa〉 is shown as follows: | (9) |
 | (10) |
For the inverse iterative procedure, the root-mean-square deviation (RMSD) of the target RDFs (Δgn) is often selected as a metric to evaluate the convergence (eqn (11)), as follows:
 | (11) |
The energetics-based method like extended conditional reversible work (ECRW) determines an optimal CG potential directly based on the AA potential between mapped molecular fragments.52–54 The ECRW method defines this potential as the reversible work needed upon introducing nonbonded interactions between mapped molecular fragments. The ECRW method separates the effective pair potential into the effective vdW potential (AvdW(r)) and electrostatic potential (BES(r)). They can be calculated through a thermodynamic cycle using the reversible work W of relocating mapped molecular fragments from a quasi-infinite cutoff distance, rc, to a finite distance r:
| AvdW(r) = Won,vdW(r) − Woff(r) + AvdW(rc) | (12) |
| BES(r) = Won(r) − Won,vdW(r) + BES(rc) | (13) |
Variational-based methods minimize an objective function to determine an optimal CG potential, such as the relative entropy (RE) method and multiscale coarse-graining (MS-CG) method. Relative entropy, originating from information theory, is a convenient metric to quantify the extent of information lost upon coarse-graining.40,50,51 The RE method determines an optimal CG potential by minimizing the RE metric, SRE, which measures the difference between the trial CG model and the target AA model.
 | (14) |
| λk+1 = λk − αH−1·∇λSRE | (15) |
The MS-CG method,47–49 originating from the force-matching (FM) method,130 maps mean forces at the AA level onto the simpler CG level by minimizing a force residue between trial CG and AA models using a linear least-squares technique:
 | (16) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) CGI(RCG) is the net force acting on CG particle I using the trial parameters, 〈
CGI(RCG) is the net force acting on CG particle I using the trial parameters, 〈![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif) IAA(r)〉RCG is the projected net force on CG particle I from the target AA model subject to the constraint that the CG particle positions are fixed at RCG, and the outer big bracket represents an average over all CG configurations of the system sampled in an AA simulation. The use of splines to describe the functional form of the forces is needed to guarantee a linear parametrization.131 The MS-CG method determines the CG potential directly from mapped AA simulation without requiring additional trial CG simulations. The MS-CG method has been used to determine the vdW parameters of a CG model of [Cnmim][NO3] (n = 1–12).102,105 It was demonstrated that the MS-CG-based CG model exhibited very good transferability over different systems at various temperatures and reproduced an experimentally observed mesoscopic heterogeneous structure for long-chain ILs.
IAA(r)〉RCG is the projected net force on CG particle I from the target AA model subject to the constraint that the CG particle positions are fixed at RCG, and the outer big bracket represents an average over all CG configurations of the system sampled in an AA simulation. The use of splines to describe the functional form of the forces is needed to guarantee a linear parametrization.131 The MS-CG method determines the CG potential directly from mapped AA simulation without requiring additional trial CG simulations. The MS-CG method has been used to determine the vdW parameters of a CG model of [Cnmim][NO3] (n = 1–12).102,105 It was demonstrated that the MS-CG-based CG model exhibited very good transferability over different systems at various temperatures and reproduced an experimentally observed mesoscopic heterogeneous structure for long-chain ILs.
3 Polarizable CG models
The presence of ions in pure ILs or their mixtures with polar solvents generates a strong local electric field, which polarizes neighboring ions or molecules. However, due to their limited ability to adapt to external environmental changes, non-polarizable fixed-charge force fields cannot accurately predict the dynamic properties of ILs, such as viscosity and the diffusion coefficient.61 Their electrostatic parameters are mostly based on a single ion, ignoring the polarization effects intrinsic to the densely packed liquid state. It often requires either explicit or implicit inclusion of polarization effects for the molecular FF to be more accurate and predictive. There mainly exist two categories of polarizable models, including physics-inspired and mean-field polarization models. This section will explore the applications of these two types of polarizable models in IL CG modeling. More comprehensive reviews on the polarizable FF are highly recommended.43,61,132–134In the context of atomistic models, physics-inspired polarization models explicitly incorporate contributions from induced dipole interactions, such as the fluctuating charge (FQ) model,62,63 induced dipole (ID) model,64–68 and Drude oscillator model.43,69 Currently, only the Drude model has been applied to the IL CG modeling. After brief introduction of the FQ and ID models, we will discuss the Drude model in detail, with specific emphasis on the target data used for optimizing the nonbonded parameters. Atomic charges in the FQ model can be dynamically changed in response to the local electric field, generating a larger or smaller dipole moment of the target molecule. The ID model assigns explicit polarizability (α) at the center of atoms or virtual sites to describe anisotropy and spatial distribution response to the polarization. The Drude model introduces additional mass-charged particles, i.e., Drude particles (the yellow particles shown in Fig. 5a), attached to the nuclei of their core atomic particles via a harmonic spring, which mimics the induced dipole on each atom site. The polarizability αi of a Drude oscillator is given by:
 | (17) |
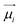 under an external electric field
under an external electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) can be calculated as:
can be calculated as: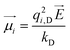 | (18) |
 | ||
| Fig. 5 (a) Schematic illustration of the physics-inspired Drude-based polarizable CG model of [C4mim][BF4]; yellow particles represent the Drude particles attached to the nuclei of their core CG particles via a harmonic spring; the displacement of the spring under the influence of an electric field mimics the induced polarization effect; (b) schematic illustration of the QM-based polarizable VaCG model of [C4mim][BF4]; CG charges are derived from QM calculations on IL clusters containing up to 30 anion–cation pairs, using the GEBF method; these CG charges are further fused into the electrostatic terms of the VaCG model. The plot (a) is reprinted with permission from ref. 94. Copyright 2017 IOP Publishing. The plot (b) is reprinted with permission from ref. 74. Copyright 2022 Elsevier. | ||
The Drude oscillator model has been implemented into polarizable CG models of [Cnmim][BF4]86 and [Cnmim][PF6] (n = 2, 4, 6),94 where Drude particles are attached to each CG particle, as shown in Fig. 5a. It has been demonstrated that there exists a semiquantitative relationship between isotropic molecular polarizability and molecular volume calculated by Bader's atoms-in-molecules (AIM) theory.135,136 An isotropic polarizability is assumed in these polarizable CG models and the polarizability of CG particle i is determined according to the ratio of the volume of the corresponding molecular fragment Vi to the total molecule volume Vtot. To avoid the polarization catastrophe, i.e., the inducible dipoles diverge if they are spatially too close to each other, a screening function is adopted to calculate dipole–dipole interactions, as follows:
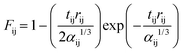 | (19) |
The mean-field method is a more cost-effective approach that implicitly accounts for the polarization effect by directly reducing the value of electrostatic parameters. Many ab initio calculations of ion pairs or large-sized IL clusters suggest that the net ionic charge is reduced because of the polarization-induced charge transfer.137–139 For example, the net partial charges of ions for a pair of [C4mim][BF4] calculated by density functional theory (DFT) at the level of M06-2X/6-31G** are ±0.92 e instead of ±1 e of an isolated ion.74 An empirical charge scaling factor of around 0.8 was introduced by many IL CG models to compensate for the absence of electrostatic polarization.54,89,90,92,97,99,101,114,117,140 For example, the original 4-site CG model of [BMIM][PF6]98 was refined by reducing the CG charge to ± 0.78 e, achieving a better temperature dependence of diffusion coefficients.99 Further validation also demonstrated the good ability of the refined model to predict the surface tension (39.4 mN m−1 predicted at 400 K vs. experimental 40.8 mN m−1 at 393 K).97 For the aqueous IL solution, a smaller charge scalar is often used to compensate for the polarization effect. For instance, a charge scalar of 0.25 is adopted to simulate the phase behavior of an aqueous long-chain IL.101,141,142
Alternatively, introduction of electrostatic parameters from QM calculations of large-sized IL clusters more explicitly treats the polarization effect of bulk ILs. It avoids the process of artificially specifying parameters. However, the computational cost of traditional QM methods increases nonlinearly with the size of the system, which limits their applicability. A linear-scale electronic structure method, generalized energy-based fragmentation (GEBF),71–73 offers a practical solution to this challenge. The GEBF method calculates the ground-state energy (or properties) of a target system as a linear combination of the ground-state energies (or properties) of a series of small electrostatically embedded subsystems. It has been demonstrated that the GEBF method with an ion-pair-based fragmentation scheme provides satisfactory descriptions on ground-state energies, optimized structures, and vibrational spectra of various IL clusters.139 The GEBF calculations of IL clusters, including ([EtNH3][Cl])n, ([EtNH3][NO]3)n, and ([C1mim][NO]3)n, at the M06-2X/6-31G** level, indicated that the average ionic charge exhibits transferability when n = 10.139 Inspired by this, the electrostatic-variable coarse-grained (VaCG) model, a 3-site polarizable CG model for [C4mim][BF4], was developed. The VaCG model sets the molecular fragment charge derived from the GEBF calculation of IL clusters with 30 cation–anion pairs (Fig. 5b).74
The polarization effect is highly susceptible to the surrounding environments and could be reflected by the dielectric permittivity (ε) in an average mean-field manner. The VaCG model introduces a concentration-dependent dielectric constant to consider the variable polarization environment under different water concentrations.74 The electrostatic term of the VaCG model is shown in the following equation:
 | (20) |
4 ML techniques for the IL CG models
Thanks to advancements in computing power and the abundance of data, ML techniques have been widely used in IL modeling, such as the use of ML algorithms as property prediction tools and as integral components in the development of high-quality FFs for MD simulation. Extensive studies in IL research have focused on evaluating the predictive ability of different ML algorithms with respect to physicochemical properties. For example, a series of transformer-CNN models144 have been trained to predict IL antibacterial activity, phase transition and decomposition temperature, melting temperature, electrical conductivity, viscosity, and density.145–148 These well-trained ML models can be used to perform virtual screening of new ILs with desired properties. Some insightful reviews about this area are highly recommended.149–152 Another important application is the development of interatomic potentials in MD simulations.83,153,154 Their utilization primarily involves two aspects: the construction of ML potentials (MLPs) of small molecules and materials or functioning as an optimization tool in the context of classic FFs.154 Unlike classic FFs, which treat the potential energy surface (PES) through separated interaction terms, ML potentials discard the empirical function forms by representing interatomic potentials as functions of descriptors that characterize the atoms within the system of interest. As shown in Fig. 6, the widely used Behler–Parrinello neural network (BPNN) potential155 has been taken as an example to briefly explain their working principle. | ||
| Fig. 6 Architecture illustration of the Behler–Parrinello neural network potential;155 the red region represents the chemical environments of the centered atoms within the cutoff sphere of radius Rc; the Cartesian coordinates of atom i is denoted as Ri, and they are transformed into a set of symmetry functions Gi to ensure translational, rotational, and permutational invariances of the PES; they are further used as input for the individual atomic neural networks (NNs) to predict each contribution (Ei) to the total energy; finally, these individual energy contributions are summed to obtain the total energy (E). | ||
The potential energy (E) is divided into contributions from individual atoms (Ei) (eqn 21),
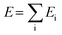 | (21) |
The graph-based SchNet model158 has been used to develop CG potentials for ILs.87 Separated graph convolutional neural networks were employed to treat intramolecular and intermolecular interactions of a 5-site or 3-site CG model for the IL ([C4mim][BF4]]). Temperature was incorporated as an input to the neural network to parameterize a temperature-transferable CG potential. Moreover, a classical bond prior with fixed bond lengths between CG particles of the cation and an excluded volume prior were added to better describe intramolecular and intermolecular interactions. The neural network architecture for fitting the CG potential is shown in Fig. 7a. The ML model was trained with the MS-CG force metric as the loss function. There are some advantages for this metric: atomic forces can be calculated instantaneously from a given AA configuration; MS-CG is a non-iteration scheme which determines an optimal potential without additional trial simulation, while adequate sampling requires a large database of AA configurations.120 The microstructural properties calculated using the CG model with the ML potential show good agreement with those from the AA model, and the Arrhenius relation for self-diffusivity was successfully reproduced. Although the temperature-dependent trend of the self-diffusion coefficient is captured, it exhibits faster dynamics. For instance, the computed self-diffusion coefficients (D+/D−) at room temperature are 48.58/35.49 × 10−11 m2 s−1, approximately one order of magnitude higher than the experimental values (1.83/1.78 × 10−11 m2 s−1), as shown in Table 1.
 | ||
| Fig. 7 (a) Overview of the neural network architecture to predict the CG potential,87 where the local environment of CG particles was incorporated as input and two separate neural networks were employed to learn the intra- and inter-molecular potential; additionally, the temperature influence was considered as another input, alongside classical priors such as excluded volume and bond length; (b) the left side shows a general diagram of the mixed-resolution model that combines a united-atom model of diphenylalanine and a CG model of an aqueous IL solution ([C4mim][BF4]);75 the right side illustrates the ML-guided parametrization protocol,75 designed to optimize the coupling terms of the mixed-resolution model; this workflow includes prior MD simulations, parameter learning, and parameter selection. The plot (a) is reprinted with permission from ref. 87. Copyright 2020 American Institute of Physics. The plot (b) is reprinted with permission from ref. 75. Copyright 2023 American Chemical Society. | ||
Some challenges remain for the application of the ML CG potential to ILs. For viscous ILs, large spatiotemporal MD simulations are often needed to ensure sufficient sampling. The main advantage of CG modeling lies in its high efficiency, but the ML potential suffers from poor efficiency relative to classic FFs.120 Given the rare benchmark studies comparing efficiency between graph neural network (GNN)-based ML and classic CG FFs, we use an atomistic model to illustrate this point. As shown in Table 2, relative to other GNN-based ML FFs like MACE,159 Allegro,160 ViSNet,161 and BAMBOO,162 the classic atomistic FF, OpenFF2.0.0,163 achieves a higher inference speed. Development of a more efficient ML CG potential would significantly enhance its practical applicability. Moreover, properly accounting for long-range electrostatic interactions in the ML potential for ILs remains a challenge.164 One solution is to increase the cutoff radius to capture such an effect; however, this would substantially increase the cost of model training and prediction.164 Another solution is to additionally embed physically interpretable quantities into the ML potential. For example, in the charge equilibration (Qeq) scheme,165 the charge that incorporates a polarization effect can be determined by atomic electronegativities, which can be expressed as environment-dependent atomic properties learned by atomic neural networks.166 Recently, such a method has been generalized into a GNN-based atomic ML potential and tested on the OE62 dataset.167 However, such techniques haven't been extended to the ML potential of IL CG models.
| Index | FF | N atom | N GPU | Speed (million steps per day) |
|---|---|---|---|---|
| a The data of indices 1–4 were summarized from ref. 162. The model compound is 3-(benzyloxy)pyridin-2-amine. There are no direct speed data available for gas-phase MD simulations using the GNN-based ML FFs mentioned above. Only the inference speed for a single molecular structure has been reported. Therefore, the total number of simulation steps was estimated based on the total time of one day. b As for the data of index 5, condensed-phase MD simulation was performed. All the tests (indices 1–5) were run on an NVIDIA A100 GPU. c The data of index 6 were summarized from ref. 168. The model compound is an inhibitor bound to cyclin-dependent kinase (CDK8). Gas-phase MD simulation with a 1 fs time step was performed using OpenMM 8 (ref. 168) on an NVIDIA RTX 4080 GPU. | ||||
| 1a | MACE159 | 27 | 1 | 4.9 |
| 2a | Allegro160 | 6.6 | ||
| 3a | VisNet161 | 7.1 | ||
| 4a | BAMBOO162 | 12.5 | ||
| 5b | BAMBOO162 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2 | |
| 6c | OpenFF2.0.0 (ref. 163) | 53 | 1 | 140.5 |
Here, we focus on the applications of ML techniques to the optimization of classic FFs, with special emphasis on vdW optimization. In the context of the classic atomic FF, the atom types are first assigned based on the specific FF rules, and then the bonded and electrostatic parameters are calibrated against QM data followed by vdW parameter optimization targeting condensed-phase experimental data. A full description of classic FF parametrization is beyond the scope of this review. Some insightful reviews are highly recommended.43,61 Optimization of vdW parameters has been a long standing challenge for the classic FF. Different from the atom-specific electrostatic parameters, different atoms share the same vdW parameters if they are in a similar chemical environment. To ensure parameter robustness, vdW optimization often requires simultaneously targeting multiple experimental properties. With the increase of parameter size, the computational cost of MD simulations will be more expensive. For such a muti-variable and multi-objective optimization task, it's expensive to evaluate the loss function and difficult to define the gradients with respect to parameters using a traditional optimization algorithm.153,169 Development of optimization methods to explore high-dimensional parameter spaces with high efficiency remains a challenge.
ML techniques offer a solution by serving as computationally inexpensive surrogate model to assist vdW optimization. ML models approximate the mapping between the desired physical properties and vdW parameters, facilitating quick screening of potential parameters. Typically, ML-guided vdW optimization follows an iterative workflow, including three key steps: 1. prior MD simulations, 2. parameter learning, and 3. parameter selection. Throughout this process, the ML surrogate can be continuously updated, refining the search and enhancing predictive accuracy. In step 1, prior dispersed parameter sets are generated within reasonable parameter space. MD simulations are performed using these parameter sets, and then, the properties of interest are collected. In step 2, an ML model is trained to learn prior parameter sets to fit the target properties, which is then evaluated to predict the desired properties, for a large number of trial parameter sets. The bounds of trial parameter sets are determined by the parameter sets used to build the ML surrogate. In step 3, a subset of promising parameters is selected using some user-defined metrics, thus initializing the next cycle. Such an iteration continues until the MD simulations with the parameter set identified in this step yield a satisfactory performance.
Recently, such an ML-assisted FF parametrization strategy has been used to optimize coupling interaction terms in a mixed resolution model.75Fig. 7b shows this mixed model, which combines a GROMOS-based united-atom (UA) model of diphenylalanine (P) with a CG model of the aqueous IL ([C4mim][BF4]]) solution, i.e., the VaCG model.74 Four coupling nonbonded parameters were selected for optimization, including three parameters (λP-A, λP-B, and λP-C) that impact vdW interaction strength between the P molecule and different molecular fragments of the IL (anion: A; methylimidazolium, and butyl unit of the cation: B and C) and a dielectric constant (εP) that regulates the electrostatic interaction strength between the P molecule and surrounding solvent molecules. As for target properties, similarity scores170,171 that quantify the resemblance between the microstructural properties calculated by AA simulations and the mixed model were adopted. The random forest regressor model is utilized to carry out multi-output regression tasks. At the stage of parameter selection, the mean absolute error of similarity scores for each target is used to evaluate the performance of each potential parameter set. The whole ML-guided FF parametrization process requires 11 iterations to reach convergence, where a total of 327 UA/CG MD trajectories were performed. The optimized mixed model was used to study diphenylalanine self-assembly in an aqueous IL solution with various IL concentrations. The trend observed in MD simulations is consistent with that of experiments.
Here, some challenges of ML-assisted vdW optimization are highlighted. The ML-assisted vdW optimization protocol is built on the foundation of domain expertise. Its performance is strongly influenced by some key prior parameters, such as the initial guess for vdW parameters and the boundary of parameter space. These parameters necessitate prior careful evaluation. A good initial guess can improve efficiency by directing the optimization towards the region of interest without consuming too much computational cost. The general principle for selection of the initial guess is to assess the reliability of assigning existing parameters from similar chemical environments. If the existing parameters are very limited, it begins with assessing the initial guess based on analogy using some classic atomic FF sources, such as CGenFF,172 GAFF,173 and OPLS.174 The atomic vdW parameters are summed up based on CG mapping rules to derive the corresponding CG values. The initial guess can also be derived using QM methods.86 The C6 dispersion coefficient relates σ and ε through C6 = 4εσ6, which can be determined by various QM methods.175 The radius of the vdW parameter (σ) can be estimated from QM volume according to the assumption of the sphere volume of the interaction site.86 Another key consideration is to ensure that the initial guesses well balance the conflicting objectives. With the concept of Pareto fronts in multi-objective optimization, the optimal solutions are those where improving one objective necessarily leads to the degradation of another. Spending more effort on determination of the optimal initial guess is often crucial and necessary.
While ML surrogate-level evaluation is much faster than simulation-level evaluation, it often requires a large number of real MD simulations to build accurate ML surrogates. The setup for the parameter sampling space should balance the trade-off between accuracy and efficiency. The space with too wide boundaries would cover some unphysical results, and the space with a too narrow region would miss some high-quality parameters. Currently, parameter bounds are primarily manually chosen.176 It is necessary to develop a more automated method to achieve this goal with minor human intervention. In addition, with the increase of parameter dimensionality, the size of parameter space would exhibit exponential growth. For example, if there are two vdW parameters to be optimized, with 200 points sampled on each dimension, the total number of possible parameter sets will be 4 × 104. However, if the number increases to 6, there will be 6.4 × 1013 points to be sampled using the brute force method. Construction of such ML surrogates heavily negates their speedup on prediction. One solution is to use advanced sampling techniques to reduce computational expenses. For example, Latin hypercube sampling (LHS)177 has been in conjunction with ML surrogates to optimize vdW parameter sets of the Drude general FF (DGenFF),81 where 200 near-random distributed points were generated to represent 6.66 × 1017 possible parameter sets. Leveraging the power of Bayesian optimization, a comprehensive automated machine learning (AutoML) framework was proposed for simultaneously tuning vdW and electrostatic parameters of a three-center water model under the framework of the polarizable Gaussian model (pGM).178 Although the parameter space extends to nine dimensions, great efficiency was achieved, and transferability was demonstrated among different thermodynamic properties across different temperatures. However, there are no studies systematically evaluating the impact of different sampling methods on the performance of ML-assisted FF optimization.
Another challenge lies in parameter correlation, where multiple distinct vdW parameter sets yield equally accurate thermodynamic properties. For example, when using an ML surrogate to optimize LJ parameters of alkenes in the context of Drude FFs, there are 105 trial parameter sets with their objective function lower than the pre-defined threshold.81 Validation of the whole parameter sets at the simulation level becomes highly nontrivial. Even though some clustering algorithms like K-means can be used to reduce this number,75 how to design an effective protocol to determine the final optimal parameter set remains a challenge. One solution is to introduce additional objective properties to assess the robustness of the potential parameter sets. For example, in the context of CHARMM-based atomic FFs, QM data have been used to screen reasonable vdW parameters after validation through condensed-phase simulations, such as ab initio interaction energies and distances with rare-gas elements.179 Another solution is to evaluate the performance of the potential parameter using experimental properties not included in the optimization process. Such properties are often computationally expensive, so they are rarely selected as target properties for the ML surrogate, such as hydration free energies, the dielectric constant, and a series of dynamic properties.
5 Applications
5.1 Microscopic structure
Dissecting the microscopic structure of bulk ILs is essential for unraveling the mechanisms that underpin their unique physicochemical properties. It plays a pivotal role in the systematic design of ILs tailored to specific requirements.180 ILs typically consist of small anions and bulky cations with polar headgroups and nonpolar alkyl side chains. Both experimental and computational studies have revealed that ILs with an intermediate side-chain length exhibit microstructural heterogeneity.2,3 As shown in Fig. 8a, the chain length-dependent nanostructures of bulk ILs were first explored using a CG model of [Cnmim][NO3] (n = 1–12).180–183 The findings indicate that cations with a short side-chain length (n < 4) exhibit higher anisotropy. As the side-chain length increases, the tail groups aggregate to form non-polar domains, while the headgroups of both cations and anions retain their local structures. The non-polar domains, i.e., tail groups represented by white particles, are separated by the continuous polar network, i.e., headgroups of cations and anions represented by yellow and red particles. A Gaussian-like heterogeneity order parameter (HOP) revealed that the degree of heterogeneity becomes more pronounced with increasing alkyl side-chain length.181 The homogeneous distribution of polar moieties has been attributed to the strong electrostatic interactions, while the formation of heterogeneous domains is driven by the hydrophobic interaction between alkyl chains.181 This observation was later verified by X-ray diffraction experiments on pure [Cnmim][Cl] (n = 4–10) and [Cnmim][BF4] (n = 4–8).184 Other CG simulations of ILs with an intermediate side-chain length also captured the microphase segregation, such as [Cnmim][PF6] (n = 4–10),100,104 [Cnmim][BF4] (n = 4–10),90,91 and [C10mim][TFSI].89 | ||
| Fig. 8 (a) The left side shows the IL CG model for the study of bulk heterogeneity; the right side shows a snapshot that illustrates the nanoscale segregation liquid, where red and yellow particles represent anions and cationic polar head groups; the regions circled by blue lines indicate the nonpolar tail domains composed of cationic nonpolar terminal groups (white particles); (b) the left side shows the IL CG model with a long side chain for the study of phase transition; the right side shows the snapshot of the structural transition from the isotropic to the SmA phase at 505 K and the SmA to the crystal phase at 480 K. The plot (a) is reprinted with permission from ref. 180. Copyright 2007 American Chemical Society. The plot (b) is reprinted with permission from ref. 183. Copyright 2015 American Chemical Society. | ||
Experimental evidence reveals that when the alkyl side-chain length of the cation is sufficiently long, e.g., at least n > 11 for [Cnmim][BF4],185 ILs tend to form peculiar ionic liquid crystals (ILCs).186 ILCs exhibit unique features that go beyond those of conventional liquid crystals (LCs), particularly in their high anisotropic ion conductivity.186–188 These features make them widely employed as electrolytes for batteries188,189 and dye-sensitized solar cells (DSSCs).190–192 Through heating a solid or cooling an isotropic liquid (or another mesophase), a thermotropic mesophase (LC phase) can be induced.193 CG simulations of [C16mim][NO3] were employed to study such behavior.183,194,195 CG simulations successfully capture three distinct experimentally-observed phases, i.e., the crystal (Cr) phase, the smectic A (SmA) phase, and the isotropic liquid (Iso) phase.194Fig. 8b shows the isotropic-to-SmA transition and SmA-to-crystal phase structural transition. It has been demonstrated that a liquid crystalline-like structure emerges only when the side-chain length of cations is sufficiently long, typically n > 14 for [Cnmim][NO3]. This finding qualitatively coincides well with experimental observations.185,196 This structural transition has been attributed to the fact that the stronger hydrophobic interactions between nonpolar tails prevail over the continuous polar network and form a more ordered lamellar structure rather than separated tail domains.183,195 Notably, the phase transition temperatures are still poorly reproduced with current IL CG models.88,194 For example, the crystal-to-smectic transition temperature estimated by the CG model (550 K) exceeds the experimental results by approximately 225 K. For IL CG models, enhancing temperature transferability near the phase transition region is essential for better description of phase behaviors.197
5.2 Biological system
Compared to simple electrolytes, ILs exhibit more sophisticated molecular interactions with biomolecules, including hydrogen bonding, pi–pi stacking, hydrophobic interactions, and ionic interactions (Fig. 9a). These interactions further underscore the diverse range of behaviors and properties exhibited by ILs. Research into the IL biological activity has garnered considerable interest, particularly for potential applications in pharmaceutics,198 medicine,199 and food science.200 An urgent need is required to gain a deeper understanding of their molecular interactions with diverse biomolecular species, including phospholipids, proteins and peptides, DNA and RNA, and carbohydrates.201 | ||
| Fig. 9 (a) Typical interactions between biomolecules and ILs in the first solvation layer; (b) IL ([C4mim][Cl]) facilitates cellulose deconstruction; (c) IL induces membrane disruption; (d) aqueous solution with a high IL concentration suppresses diphenylalanine self-assembly into ordered nanostructures. The plot (b) is reprinted with permission from ref. 202. Copyright 2011 American Chemical Society. The plot (c) is reprinted with permission from ref. 206. Copyright 2016 American Chemical Society. The plot (d) is reprinted with permission from ref. 75. Copyright 2023 American Chemical Society. | ||
Cellulose, a natural polysaccharide, consists of linear chains ranging from several hundreds to tens of thousands of β(1 → 4)-glycosidic units. It is widely found in lignocellulosic biomass, an abundant renewable energy source in nature. Its biological functions, such as catalytic or enzymatic breakdown, rely on the exposure of buried glycosidic bonds. Cellulose is difficult to dissolve in water and most organic solvents, but it can be dissolved in certain classes of ILs. A pretreatment solvent is required to disrupt the strong interactions that arise from the coupling between the equatorial and axial moieties of glucose residues. Simulations of cellulose deconstruction have been conducted at the all-atom level by peeling off an 11-residue glucan chain from a cellulose microfibril (Fig. 9b). To dissect the force interactions, the AA trajectories were mapped into CG configurations, and a bottom-up force-matching strategy was utilized to derive radial mean forces between the solvent and glucan CG particles. The results indicate that ILs exhibit stronger interaction with glucan compared to water molecules, with anions interacting strongly with the hydroxyl groups and cations favorably interacting with side chains and linker oxygens.202
Some ILs exhibit stronger toxicity than traditional organic solvents. For example, a class of imidazolium-based ILs have been found to be chronically toxic to a variety of aquatic species203,204 and can be used as antimicrobial agents.205 CG MD simulations were carried out to investigate the effects of imidazolium-based ILs ([Cnmim], n = 4–10) on the morphology of the 1-palmitoyl-2-oleoylphosphatidylcholin (POPC) lipid bilayer, a model system of the cell membrane.206,207 The cross-interaction parameters between lipids and ILs were optimized by matching the potential of mean force (PMF) during the process of inserting a single cation into a lipid bilayer at the AA level. To quantitatively characterize the structural transitions, a parameter called the leaflet strain parameter (εc) is used. This parameter is defined as the difference in surface area between the upper and lower leaflets. This indicated that cations prefer to insert into the lipid bilayer, with their alkyl tails embedded within the bilayer. When a critical value (εc ≈ 0.2) is reached, this insertion triggers a morphological disruption in the bilayer (Fig. 9c).
Diphenylalanine (P) can self-assemble into well-ordered nanostructures, such as nanotubes,208,209 nanofibrils,210 and nanospheres,211 with potential applications in functional nanomaterials.212,213 Experimental studies have shown that the introduction of water into [C4mim][BF4] induces diphenylalanine self-assembly into nanotubes, whereas no ordered structure is observed in the pure IL.214 A mixed resolution model was proposed to study the impact of the aqueous IL solution on self-assembly of P molecules.75 The mixed resolution model incorporates the united-atom (UA) model for diphenylalanine (P) and the polarizable VaCG model for the aqueous ionic liquid ([C4mim][BF4]) solution. The parameters of coupling IL–P interaction terms were parametrized by an adaptive ML-guided scheme, as detailed in section 4. It is found that at high IL concentrations, ILs suppress the self-assembly of P into ordered nanostructures through competitive P–An HB and Ca–π stacking interactions. The P–An HB and Ca–Ph π-stacking interactions gradually replace the P–P HB and Ph–Ph π-stacking interactions as the IL content increases. It is found that the ordered fibril structure appears in the pure water system, whereas it disappears in the pure IL system (Fig. 9d), in agreement with experimental observation.75
5.3 Electrochemical system
 | ||
| Fig. 10 (a) Schematic illustration of an electrical double layer capacitor (EDLC); three types of electrode models are employed to study the energy storage mechanism in the EDLC with the IL CG solvent model, including the ideal-geometry electrode model, realistic porous electrode model, and amorphous porous electrode model; the model system includes the (b) planar electrode surface, (c) slit-like pore model, and (d) cylindrical model; the ordered porous electrode model includes (e) zeolite-templated porous carbons (ZTCs), (f) metal–organic frameworks (MOFs), (g) hydrogen substituted graphdiynes (HsGDYs), and (h) MoS2; (i) carbide-derived carbon is a typical amorphous porous electrode model. The plots (b–i) are reprinted with permission from ref. 228 (Copyright 2014 American Chemical Society), ref. 231 (Copyright 2020 American Chemical Society), ref. 234 (Copyright 2016 The Royal Society of Chemistry), ref. 237 (Copyright 2021 American Chemical Society), ref. 238 (Copyright 2020 Elsevier), ref. 239 (Copyright 2023 Wiley), ref. 241(Copyright 2022 American Chemical Society), and ref. 244 (Copyright 2014 American Chemical Society). | ||
To simulate charged electrodes, two methods can be used in MD simulation, including the constant-charge model (CCM) and constant-potential model (CPM).219 The CCM method assigns equal charge on equivalent sites of the electrode, which induces a uniform electric field between two electrodes, corresponding to a charged isolated capacitor. The CPM method assigns variable charges whose magnitudes are changed on-the-fly to maintain a constant potential difference between two electrodes. The computationally efficient CCM method can reasonably approximate planar electrodes but may be unsuitable for a complex realistic-morphology electrode, where the electrode polarization considerably impacts the dynamics of confined ions and capacitive properties.220 Some insightful reviews are recommended for detailed introduction of methodologies in MD simulations for electrochemical interfaces.6,218,220–224
IL CG models have been incorporated with charged electrode models of varying different chemical complexity, such as the ideal-geometry electrode model (e.g., planar slab, slit-like pore, and cylindrical electrode model) and the realistic-morphology electrode model (e.g., ordered and amorphous porous electrode models). In the case of the planar electrode model (Fig. 10b), a generic 2-site IL CG model, not specified to any particular IL, was used to study the effects of ion size and valency on the differential capacitance. Their results qualitatively agreed with the trend predicted by the analytical model using mean-field theory.225 Asymmetry in the ion shape was further considered by replacing the spherical cation model with a triangular model that approximates the aromatic ring of the imidazole-based cation. It was found that the different preferred orientations of the cations adsorbed on the electrode induce a distinct feature in the differential capacitance.226 A 4-site IL CG model85,97 of [C4mim][PF6] and an atomic three-layered graphite electrode model227 were used to study the influence of the electrode potential on the EDL structure.228 A potential-driven structural transition between the ordered (small electrode potential) and disordered phases (negative electrode potential) of the first adsorbed ion layer was observed. The anomalous dependence of differential capacitance on the applied electrical potential can be attributed to this structural transition.229 The solvent effect on the structural and capacitive properties of the EDL was also tested under the same system setup.230 Distinct interfacial characteristics between [C4mim][PF6] and [C4mim][BF4] were observed, but very similar characteristics emerged upon mixing with acetonitrile (1.5 M).
Electrode materials mainly employ porous materials that process good electronic conductivity and large surface area. The slit-like pore model (Fig. 10c) and cylindrical nanopore model (Fig. 10d) are simplistic models to approximate the pore effect. A 4-site model of [C2mim][BF4]85,97 and a pair of slit pores were adopted to explore the pore size on charging dynamics.231 A non-monotonic relationship between charging time and pore size is found, where some small pores (∼0.45 nm) are able to accelerate the charging process, contrary to the conventional view that only large pores facilitate charging. It is further demonstrated that the charging enhancement is related to the structural transition of the confined in-pore ions. The nanoconfinement effects on disjoining pressure was investigated by a four-site CG model of [C2mim][BF4] and a slit-like pore model.232 The disjoining pressure exhibits damped oscillations at pore widths below 5 nm and this phenomenon diminishes with increasing pore size. A following AA MD simulation shows that the disjoining pressure at large pore widths can be approximated by an exponential function, which enables the estimation of the decay length that correlates with the electrostatic screening length.233 A fused CG model of [Cnmim][BF4] (n = 2, 4, 6) and a three-layer carbon nanotube (CNT) model were used to study the effect of pore size on the structural and capacitive properties.234 It is found that the relationship between electric potential and surface charge densities is non-monotonic when the pore is narrow.
These slit-like and cylindrical nanopore models capture the pore size and curvature effects, but they fail to capture the complex microscopic structures of the porous electrode, where factors, such as the intricate pore size, elementary composition, and topological structure, impact ion transport.222 The realistic porous electrode model is a good choice to mimic real conditions.5 There are two types of realistic porous electrodes: ordered porous electrodes, such as zeolite-templated carbons (ZTCs) (Fig. 10e),235–237 metal–organic frameworks (MOFs) (Fig. 10f),238 hydrogen substituted graphdiynes (HsGDYs) (Fig. 10g),239 and MoS2 (Fig. 10h),240,241 and amorphous microporous carbons such as carbide-derived carbons (CDCs) (Fig. 10i).242–244 For example, a series of CDC electrode models with different pore sizes were generated using the quenched MD procedure.242,245 These electrode models have been used together with a 4-site CG model of [C4mim][PF6]85,97 to study the capacitance enhancement mechanics induced by sub-nanometer pores.246 The enhanced capacity has been reproduced, which has been attributed to the separation of oppositely charged ions inside the disordered pores. In addition, two CDC materials with similar pore size distributions (CDS-950 and CDC-1200) exhibit distinctive capacities, indicating that the local structure has a profound effect on the capacitance values. More examples of MD simulations of supercapacitors with ILs and porous electrodes are overviewed in Mo′s review.5,224
 | ||
| Fig. 11 (a) Typical MD simulation setups for electrotunable friction with IL lubricants. Different factors that influence electrotunable friction with IL lubricants, including (b) cation chain length, (c) mixtures with other polar solvent molecules, and (d) surface roughness. The plots (a and b) are reprinted from ref. 254 (Copyright 2020 American Chemical Society); the plots (c and d) are reprinted from ref. 255 (Copyright 2020 American Chemical Society) and ref. 260 (Copyright 2017 The Royal Society of Chemistry). | ||
The electric field can impact the structural characteristics of the confined IL film, such as ionic arrangement, layering, and orientation, which are responsible for the variation of friction force. A generic 2-site IL CG model was used to study the structural response of a nanoscale IL film to the surface charge.252 A volcano-shaped nonmonotonic dependency between friction force and surface charge has been found. This phenomenon can be ascribed to the shift of the slippage plane, in which the maximum friction corresponds to the transition point from the solid–cation interface to the interior of the anion–cation interface. Further simulations using a 4-site CG model99,253 revealed that the increase of surface charge induces anions to detach from the surface and cations to reorient from a tilted configuration to a flat one, facilitating the shift of the slippage plane.
The molecular structure is an important factor that affects friction. The effect of the alkyl chain length of the cation ([Cnmim][BF4], n = 2, 4, 6) on the electrotunable friction in ILs (Fig. 11b) was investigated.90,254 It reveals that cations with a short hydrocarbon chain length (n = 2) yield a lower friction force (∼40%) than cations with longer chains (n = 4). Structural analysis revealed that smaller cations are more compact and ordered, while cations with longer alkyl chains promote the segregation of charged polar and apolar regions. In this case, the hydrophobic domains tend to insert into the interior of the IL film, occupying the space available for anions.
The microscopic mechanisms of electrotunable lubrication in dilute IL solutions with other polar solvents have been studied using the IL CG model.255–257 A 4-site CG model of [C4mim][PF6]99 has been combined with the SPC/E water model258 to represent diluted IL–water mixtures with the coupling parameters parameterized against density and RDFs from AA simulations.257 It indicated that water adsorption screens the repulsive interactions between like-charged ions on the charged surface and makes the IL film softer. In the case of dilute IL solutions with acetonitrile (ACN), the nanoscale films formed in diluted mixtures of IL provide lower friction forces than the pure IL films, preserving a profound electrotunable response (Fig. 11c).255,259
The inhomogeneity and asperity characteristics of real surfaces also influence the electrotunable friction. Periodic ridges were used to approximate the roughness on the surface and combined with a 4-site CG model of [C4mim][PF6] to inspect the role of surface roughness in electrotunable friction in ILs (Fig. 11d).260 It has been found that the variation of the friction coefficient strongly depends on the substrate structure and shear direction, such as smooth, transversal and longitudinal cases.261 A similar volcano-shaped dependency between friction force and surface charge is also observed.
6 Challenges and future opportunities
In this section, we attempt to summarize key challenges for IL CG models and highlight some potential solutions, as complemented by recent studies. We refer readers to several insightful reviews on this topic.35,36,120,122,123,262The first challenge lies in how to improve the transferability of CG models. The transferability refers to the ability of a CG model to maintain similar predictive accuracy across a wider range of thermodynamic state points (e.g., temperature, pressure, and composition) beyond the ones for parameterization. One straightforward solution is to develop environment-dependent CG potentials. For top-down CG models, a concentration-dependent dielectric constant was introduced into the electrostatic term to improve the composition transferability for an aqueous IL solution.74 The variable dielectric constants were optimized at some representative concentrations to match experimental properties. They are then fitted to an equation as a function of concentration. As for bottom-up CG models, a temperature scalar  is added into an IBI-derived CG potential of ethylbenzene to reproduce the correct thermal expansion behaviors.263 Different functional forms for the temperature scaling factor were also evaluated using a CG model of hexane.264 The ML CG potential can also benefit from such a strategy. Environmental variables can be treated as input features to enable the CG potential to learn its effect.87
is added into an IBI-derived CG potential of ethylbenzene to reproduce the correct thermal expansion behaviors.263 Different functional forms for the temperature scaling factor were also evaluated using a CG model of hexane.264 The ML CG potential can also benefit from such a strategy. Environmental variables can be treated as input features to enable the CG potential to learn its effect.87
Improving transferability can also be achieved by optimizing general CG potentials targeting properties across multiple thermodynamic state points. For example, the multi-state IBI (ms-IBI) method improves the original single point IBI method by additionally introducing a constraint to simultaneously match a series of target RDFs at different thermodynamic states.265 The ms-IBI method has been applied to octane–benzene mixtures, achieving high structural fidelity across the entire concentration range.266 The extended ensemble method uses a variational principle to identify the optimal CG potential that can best capture the structural correlations of an atomistic extended ensemble.267 The CG simulation of alkane–alcohol mixtures indicates that the extended ensemble potentials have improved transferability of structural properties compared to potentials parametrized in a single system. However, such a bottom-up CG method often focuses on reproduction of microstructural properties, with limited reliability in thermodynamic properties.120 Some statistical mechanics theories that link microscopic molecular properties to macroscopic properties can inform the FF parametrization to address this problem. For mixture systems, the Kirkwood–Buff (KB) theory relates volume integrals over the radial distribution function, the so-called Kirkwood–Buff integrals (KBIs), to various macroscopic thermodynamic properties.268 This theory have been applied to parametrization of a CG model for aqueous urea, where a correction term is added into the IBI-derived CG potential to best reproduce the exact KBIs.269 Another important theory for the mixture system is the statistical associating fluid theory (SAFT).270 In particular, the SAFT-γ group contribution method has been used to develop a series of CG models,271–274 where FF parameters are calibrated against a molecular-based equation of state derived from experimental data.
Parameterization of polarizable CG models using high-quality QM data often suffers from expensive computational cost. Larger molecular or condensed-phase systems are often desired for FF parametrization to better capture the polarization effect. For example, in the development of the Drude FF for monatomic ions, targeting the QM PES of larger ion–polar compound complexes yields parameters that better reproduce experimental properties. However, DFT scales as O(N3–4) with the increasing number of electrons, N, so it is still expensive to construct a high-quality QM database for molecular systems involving large biomolecules or interfaces with different solids. Fragment-based QM methods provide a practical solution.70 Their basic idea is to partition a large system into small subsystems according to some prior rules and then evaluate the total energy as the linear combination of energies of small subsystems, thus dramatically reducing computational cost and making calculations more feasible. Fragment-based QM methods can directly predict FF parameters based on predefined fragments. For example, the energy-based GEBF method71–73 has been used to derive fragment charge74 and dipoles275,276 for polarizable IL and protein CG models. Besides, the energy information calculated by fragment-based QM methods can also guide optimization of the polarizable CG model, such as utilization of QM interaction energies between small molecules and large biomolecules to validate their nonbonded parameters.72,139 Notably, the performance of fragment-based QM methods is highly dependent on fragmentation schemes. These fragmentation schemes are often user-defined and involve significant human intervention. Development of more automatic fragmentation schemes would enhance the applicability of such QM fragment-based methods for FF parametrization.
ILs feature flexible tunability due to the vast combination space between different ions and their diverse chemical modifications. However, general IL CG models that cover a wide range of ILs remain scarce, which limits the high-throughput screening of ILs for material design. Parametrization of a general CG model often requires the involvement of a broad range of model compounds, making the process increasingly time-consuming. Herein, the development of a fully automated protocol that integrates CG mapping and FF parametrization together with minor human intervention holds great promise. Given the fact that most toolkits116,124–128 primarily focus on parameter optimization, autoMARTINI109 and AMOFMS277 further integrates automated CG mapping functionality. However, these toolkits currently lack the capability to parameterize polarizable models. Such toolkits have been reported for polarizable atomic FF models, like FFparam278–280 for the Drude FF,43 though fully end-to-end parametrization remains unattained. FFparam provides a graphical user interface to help users prepare and analyze necessary MM and QM files to streamline the optimization process. Besides manual adjustment, electrostatic parameters can also be optimized in an automated fashion using the Monte Carlo simulated annealing (MCSA) algorithm. Enhancing automated CG toolkits with polarizable model optimization will be a key direction for the development of high-precision general IL CG models.
7 Conclusions
By averaging over atomic details, CG models offer a significant computational advantage to study complex systems involving ILs across a larger spatiotemporal scale. Here, we have presented representative IL CG models developed by different top-down and bottom-up methods and summarized key challenges related to their accuracy, efficiency, and transferability. The integration of ML techniques into CG model development has been reviewed, including utilization of an ML surrogate to facilitate FF optimization and development of the ML potential. We expect that future studies will not only leverage these advances to develop more general and transferable IL CG models without the need for case-by-case parameterization but also make them more accessible and user-friendly for the computational community. Such efforts will broaden the applicability of IL CG models to more complicated systems, potentially leading to new discoveries.Data availability
No primary research results, software or code have been included, and no new data were generated or analyzed as part of this reviewConflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 22033004, 22373049) and the Natural Science Foundation of Jiangsu Province (BK20232012).References
- H. Weingärtner, Understanding ionic liquids at the molecular level: Facts, problems, and controversies, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef
.
- Y. L. Wang, B. Li, S. Sarman, F. Mocci, Z. Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Microstructural and dynamical heterogeneities in ionic liquids, Chem. Rev., 2020, 120, 5798–5877 CrossRef CAS
.
- R. Hayes, G. G. Warr and R. Atkin, Structure and nanostructure in ionic liquids, Chem. Rev., 2015, 115, 6357–6426 CrossRef CAS
.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Ionic-liquid materials for the electrochemical challenges of the future, Nat. Mater., 2009, 8, 621–629 CrossRef CAS
.
- T. Mo, H. He, J. Zhou, L. Zeng, Y. Long and G. Feng, Molecular understanding of charging dynamics in supercapacitors with porous electrodes and ionic liquids, J. Phys. Chem. Lett., 2023, 14, 11258–11267 CrossRef CAS PubMed
.
- M. V. Fedorov and A. A. Kornyshev, Ionic liquids at electrified interfaces, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed
.
- D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy applications of ionic liquids, Energy Environ. Mater., 2014, 7, 232–250 CAS
.
- M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Application of ionic liquids to energy storage and conversion materials and devices, Chem. Rev., 2017, 117, 7190–7239 CrossRef CAS
.
- V. Ganesan, Ion transport in polymeric ionic liquids: Recent developments and open questions, Mol. Syst. Des. Eng., 2019, 4, 280–293 RSC
.
- T. Zhou, C. Gui, L. Sun, Y. Hu, H. Lyu, Z. Wang, Z. Song and G. Yu, Energy applications of ionic liquids: Recent developments and future prospects, Chem. Rev., 2023, 123, 12170–12253 CrossRef CAS
.
- M. Palacio and B. Bhushan, A review of ionic liquids for green molecular lubrication in nanotechnology, Tribol. Lett., 2010, 40, 247–268 CrossRef CAS
.
- F. Bresme, A. A. Kornyshev, S. Perkin and M. Urbakh, Electrotunable friction with ionic liquid lubricants, Nat. Mater., 2022, 21, 848–858 CrossRef CAS PubMed
.
- A. E. Somers, P. C. Howlett, D. R. MacFarlane and M. Forsyth, A review of ionic liquid lubricants, Lubricants, 2013, 1, 3–21 CrossRef
.
- M. Cai, Q. Yu, W. Liu and F. Zhou, Ionic liquid lubricants: When chemistry meets tribology, Chem. Soc. Rev., 2020, 49, 7753–7818 RSC
.
- K. R. Baca, K. Al-Barghouti, N. Wang, M. G. Bennett, L. Matamoros Valenciano, T. L. May, I. V. Xu, M. Cordry, D. M. Haggard and A. G. Haas, Ionic liquids for the separation of fluorocarbon refrigerant mixtures, Chem. Rev., 2024, 124, 5167–5226 CrossRef CAS
.
- L. C. Branco, J. G. Crespo and C. A. Afonso, Highly selective transport of organic compounds by using supported liquid membranes based on ionic liquids, Angew. Chem., Int. Ed., 2002, 41, 2771–2773 CrossRef CAS
.
- M. A. Martins, U. Domanska, B. Schröder, J. A. Coutinho and S. P. Pinho, Selection of ionic liquids to be used as separation agents for terpenes and terpenoids, ACS Sustainable Chem. Eng., 2016, 4, 548–556 CrossRef CAS
.
- X. Han and D. W. Armstrong, Ionic liquids in separations, Acc. Chem. Res., 2007, 40, 1079–1086 CrossRef CAS PubMed
.
- S. P. Ventura, F. A. e Silva, M. V. Quental, D. Mondal, M. G. Freire and J. A. Coutinho, Ionic-liquid-mediated extraction and separation processes for bioactive compounds: Past, present, and future trends, Chem. Rev., 2017, 117, 6984–7052 CrossRef CAS
.
- G. Li, K. Chen, Z. Lei and Z. Wei, Condensable gases capture with ionic liquids, Chem. Rev., 2023, 123, 10258–10301 CrossRef CAS
.
- S. Zeng, X. Zhang, L. Bai, X. Zhang, H. Wang, J. Wang, D. Bao, M. Li, X. Liu and S. Zhang, Ionic-liquid-based CO(2) capture systems: Structure, interaction and process, Chem. Rev., 2017, 117, 9625–9673 CrossRef CAS PubMed
.
- R. Patel, M. Kumari and A. B. Khan, Recent advances in the applications of ionic liquids in protein stability and activity: A review, Appl. Biochem. Biotechnol., 2014, 172, 3701–3720 CrossRef CAS PubMed
.
-
C. Schröder, Proteins in ionic liquids: current status of experiments and simulations, Ionic liquids II, 2018, pp. 127–152 Search PubMed
.
- E. J. Maginn, Atomistic simulation of the thermodynamic and transport properties of ionic liquids, Acc. Chem. Res., 2007, 40, 1200–1207 CrossRef CAS PubMed
.
- O. Borodin, Polarizable force field development and molecular dynamics simulations of ionic liquids, J. Phys. Chem. B, 2009, 113, 11463–11478 CrossRef CAS PubMed
.
- J. E. Vazquez-Cervantes and G. A. Cisneros, Development of imidazolium-based parameters for AMOEBA-IL, J. Phys. Chem. B, 2023, 127, 5481–5493 CrossRef CAS
.
- J. N. Canongia Lopes, J. Deschamps and A. A. Pádua, Modeling ionic liquids using a systematic all-atom force field, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef
.
- K. Goloviznina, Z. Gong and A. A. H. Padua, The CL&Pol polarizable force field for the simulation of ionic liquids and eutectic solvents, WIREs Comput. Mol. Sci., 2021, 12, 1572 CrossRef
.
- K. Goloviznina, J. N. Canongia Lopes, M. Costa Gomes and A. A. H. Padua, Transferable, polarizable force field for ionic liquids, J. Chem. Theory Comput., 2019, 15, 5858–5871 CrossRef CAS PubMed
.
- N. Wang and E. J. Maginn, GAFF-based polarizable force field development and validation for ionic liquids, J. Phys. Chem. B, 2024, 128, 871–881 CrossRef CAS PubMed
.
- J. G. McDaniel, E. Choi, C. Y. Son, J. R. Schmidt and A. Yethiraj, Ab initio force fields for imidazolium-based ionic liquids, J. Phys. Chem. B, 2016, 120, 7024–7036 CrossRef CAS PubMed
.
- B. Doherty, X. Zhong and O. Acevedo, Virtual site OPLS force field for imidazolium-based ionic liquids, J. Phys. Chem. B, 2018, 122, 2962–2974 CrossRef CAS
.
- B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, Revisiting OPLS force field parameters for ionic liquid simulations, J. Chem. Theory Comput., 2017, 13, 6131–6145 CrossRef CAS PubMed
.
- S. V. Sambasivarao and O. Acevedo, Development of OPLS-AA force field parameters for 68 unique ionic liquids, J. Chem. Theory Comput., 2009, 5, 1038–1050 CrossRef CAS
.
- W. G. Noid, Perspective: Coarse-grained models for biomolecular systems, J. Chem. Phys., 2013, 139, 090901 CrossRef CAS PubMed
.
- M. G. Guenza, Everything you want to know about coarse-graining and never dared to ask: Macromolecules as a key example, WIREs Comput. Mol. Sci., 2025, 15, e70022 CrossRef
.
- S. J. Marrink, L. Monticelli, M. N. Melo, R. Alessandri, D. P. Tieleman and P. C. T. Souza, Two decades of Martini: Better beads, broader scope, WIREs Comput. Mol. Sci., 2022, 13, e1620 CrossRef
.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, The MARTINI force field: Coarse grained model for biomolecular simulations, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed
.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grunewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domanski, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Martini 3: A general purpose force field for coarse-grained molecular dynamics, Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed
.
- M. S. Shell, The relative entropy is fundamental to multiscale and inverse thermodynamic problems, J. Chem. Phys., 2008, 129, 144108 CrossRef PubMed
.
- W. Wang and R. Gómez-Bombarelli, Coarse-graining auto-encoders for molecular dynamics, npj Comput. Mater., 2019, 5, 125 CrossRef
.
- Z. Li, G. P. Wellawatte, M. Chakraborty, H. A. Gandhi, C. Xu and A. D. White, Graph neural network based coarse-grained mapping prediction, Chem. Sci., 2020, 11, 9524–9531 RSC
.
- J. A. Lemkul, J. Huang, B. Roux and A. D. MacKerell Jr, An empirical polarizable force field based on the classical drude oscillator model: Development history and recent applications, Chem. Rev., 2016, 116, 4983–5013 CrossRef CAS
.
- W. Tschöp, K. Kremer, J. Batoulis, T. Bürger and O. Hahn, Simulation of polymer melts. I. Coarse-graining procedure for polycarbonates, Acta Polym., 1998, 49, 61–74 CrossRef
.
- D. Reith, M. Pütz and F. Müller-Plathe, Deriving effective mesoscale potentials from atomistic simulations, J. Comput. Chem., 2003, 24, 1624–1636 CrossRef CAS
.
- A. P. Lyubartsev and A. Laaksonen, Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 3730–3737 CrossRef CAS PubMed
.
- S. Izvekov and G. A. Voth, A multiscale coarse-graining method for biomolecular systems, J. Phys. Chem. B, 2005, 109, 2469–2473 CrossRef CAS PubMed
.
- W. G. Noid, J.-W. Chu, G. S. Ayton, V. Krishna, S. Izvekov, G. A. Voth, A. Das and H. C. Andersen, The multiscale coarse-graining method. I. A rigorous bridge between atomistic and coarse-grained models, J. Chem. Phys., 2008, 128, 244114 CrossRef CAS
.
- W. Noid, P. Liu, Y. Wang, J.-W. Chu, G. S. Ayton, S. Izvekov, H. C. Andersen and G. A. Voth, The multiscale coarse-graining method. II. Numerical implementation for coarse-grained molecular models, J. Chem. Phys., 2008, 128, 244115 CrossRef CAS
.
- A. Chaimovich and M. S. Shell, Relative entropy as a universal metric for multiscale errors, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2010, 81, 060104 CrossRef PubMed
.
- A. Chaimovich and M. S. Shell, Coarse-graining errors and numerical optimization using a relative entropy framework, J. Chem. Phys., 2011, 134, 094112 CrossRef PubMed
.
- E. Brini, V. Marcon and N. F. A. van der Vegt, Conditional reversible work method for molecular coarse graining applications, Phys. Chem. Chem. Phys., 2011, 13, 10468–10474 RSC
.
- G. Deichmann and N. F. A. van der Vegt, Conditional reversible work coarse-grained models of molecular liquids with coulomb electrostatics – A proof of concept study on weakly polar organic molecules, J. Chem. Theory Comput., 2017, 13, 6158–6166 CrossRef CAS PubMed
.
- G. Deichmann and N. F. A. van der Vegt, Conditional reversible work coarse-grained models with explicit electrostatics-An application to butylmethylimidazolium ionic liquids, J. Chem. Theory Comput., 2019, 15, 1187–1198 CrossRef CAS PubMed
.
- S. Y. Joshi and S. A. Deshmukh, A review of advancements in coarse-grained molecular dynamics simulations, Mol. Simul., 2020, 47, 786–803 CrossRef
.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, Physicochemical properties and structures of room temperature ionic liquids. 1. Variation of anionic species, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef CAS
.
- A. Deyko, S. G. Hessey, P. Licence, E. A. Chernikova, V. G. Krasovskiy, L. M. Kustov and R. G. Jones, The enthalpies of vaporisation of ionic liquids: New measurements and predictions, Phys. Chem. Chem. Phys., 2012, 14, 3181–3193 RSC
.
- Q. Zhou, L.-S. Wang and H.-P. Chen, Densities and viscosities of 1-butyl-3-methylimidazolium tetrafluoroborate+ H2O binary mixtures from (303.15 to 353.15) K, J. Chem. Eng. Data, 2006, 51, 905–908 CrossRef CAS
.
- Y.-H. Yu, A. N. Soriano and M.-H. Li, Heat capacity and electrical conductivity of aqueous mixtures of [Bmim][BF4] and [Bmim][PF6], J. Taiwan Inst. Chem. Eng., 2009, 40, 205–212 Search PubMed
.
- J. Cascao, W. Silva, A. S. Ferreira and E. J. Cabrita, Ion pair and solvation dynamics of [Bmim][BF4]+ water system, Magn. Reson. Chem., 2018, 56, 127–139 CrossRef CAS PubMed
.
- D. Bedrov, J. P. Piquemal, O. Borodin, A. D. MacKerell, Jr., B. Roux and C. Schroder, Molecular dynamics simulations of ionic liquids and electrolytes using polarizable force fields, Chem. Rev., 2019, 119, 7940–7995 CrossRef CAS PubMed
.
- S. Patel and C. L. Brooks III, Fluctuating charge force fields: Recent developments and applications from small molecules to macromolecular biological systems, Mol. Simul., 2006, 32, 231–249 CrossRef CAS
.
- L. R. Olano and S. W. Rick, Fluctuating charge normal modes: An algorithm for implementing molecular dynamics simulations with polarizable potentials, J. Comput. Chem., 2005, 26, 699–707 CrossRef CAS PubMed
.
- Y.-P. Liu, K. Kim, B. Berne, R. A. Friesner and S. W. Rick, Constructing ab initio force fields for molecular dynamics simulations, J. Chem. Phys., 1998, 108, 4739–4755 CrossRef CAS
.
- G. A. Kaminski, H. A. Stern, B. J. Berne, R. A. Friesner, Y. X. Cao, R. B. Murphy, R. Zhou and T. A. Halgren, Development of a polarizable force field for proteins via ab initio quantum chemistry: First generation model and gas phase tests, J. Comput. Chem., 2002, 23, 1515–1531 CrossRef CAS
.
- Y. Shi, Z. Xia, J. Zhang, R. Best, C. Wu, J. W. Ponder and P. Ren, Polarizable atomic multipole-based AMOEBA force field for proteins, J. Chem. Theory Comput., 2013, 9, 4046–4063 CrossRef CAS PubMed
.
- W. L. Jorgensen, K. P. Jensen and A. N. Alexandrova, Polarization effects for hydrogen-bonded complexes of substituted phenols with water and chloride ion, J. Chem. Theory Comput., 2007, 3, 1987–1992 CrossRef CAS PubMed
.
- A. Warshel and M. Levitt, Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS
.
- G. Lamoureux and B. Roux, Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm, J. Chem. Phys., 2003, 119, 3025–3039 CrossRef CAS
.
- K. Raghavachari and A. Saha, Accurate composite and fragment-based quantum chemical models for large molecules, Chem. Rev., 2015, 115, 5643–5677 CrossRef CAS PubMed
.
- W. Li, H. Dong, J. Ma and S. Li, Structures and spectroscopic properties of large molecules and condensed-phase systems predicted by generalized energy-based fragmentation approach, Acc. Chem. Res., 2020, 54, 169–181 CrossRef PubMed
.
- S. Li, W. Li and J. Ma, Generalized energy-based fragmentation approach and its applications to macromolecules and molecular aggregates, Acc. Chem. Res., 2014, 47, 2712–2720 CrossRef CAS PubMed
.
- W. Li, S. Li and Y. Jiang, Generalized energy-based fragmentation approach for computing the ground-state energies and properties of large molecules, J. Phys. Chem. A, 2007, 111, 2193–2199 CrossRef CAS
.
- Y. Ge, Q. Zhu, Y. Li, H. Dong and J. Ma, An electrostatic-variable coarse-grained model for predicting enthalpy of vaporization, surface tension, diffusivity, conductivity, and dielectric constant of aqueous ionic liquid, J. Mol. Liq., 2022, 346, 118230 CrossRef CAS
.
- Y. Ge, X. Wang, Q. Zhu, Y. Yang, H. Dong and J. Ma, Machine learning-guided adaptive parametrization for coupling terms in a mixed united-atom/coarse-grained model for diphenylalanine self-assembly in aqueous ionic liquids, J. Chem. Theory Comput., 2023, 19, 6718–6732 CrossRef CAS PubMed
.
- S. Bag, M. K. Meinel and F. Müller-Plathe, Toward a mobility-preserving coarse-grained model: A data-driven approach, J. Chem. Theory Comput., 2022, 18, 7108–7120 CrossRef CAS PubMed
.
- J. M. Sestito, M. L. Thatcher, L. Shu, T. A. Harris and Y. Wang, Coarse-grained force field calibration based on multiobjective bayesian optimization to simulate water diffusion in poly-ε-caprolactone, J. Phys. Chem. A, 2020, 124, 5042–5052 CrossRef CAS
.
- H. Nakata and S. Bai, Development of a new parameter optimization scheme for a reactive force field based on a machine learning approach, J. Comput. Chem., 2019, 40, 2000–2012 CrossRef CAS
.
- B. J. Befort, R. S. DeFever, E. J. Maginn and A. W. Dowling, Machine learning-enabled optimization of force fields for hydrofluorocarbons, Comput.-Aided Chem. Eng., 2022, 49, 1249–1254 CAS
.
- B. J. Befort, R. S. DeFever, G. M. Tow, A. W. Dowling and E. J. Maginn, Machine learning directed optimization of classical molecular modeling force fields, J. Chem. Inf. Model., 2021, 61, 4400–4414 CrossRef CAS
.
- P. Chatterjee, M. Y. Sengul, A. Kumar and A. D. MacKerell Jr, Harnessing deep learning for optimization of lennard-jones parameters for the polarizable classical drude oscillator force field, J. Chem. Theory Comput., 2022, 18, 2388–2407 CrossRef CAS
.
- X. Wang, J. Li, L. Yang, F. Chen, Y. Wang, J. Chang, J. Chen, W. Feng, L. Zhang and K. Yu, Dmff: An open-source automatic differentiable platform for molecular force field development and molecular dynamics simulation, J. Chem. Theory Comput., 2023, 19, 5897–5909 CrossRef CAS PubMed
.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müller, Machine learning force fields, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed
.
- L. I. Vazquez-Salazar, M. Selle, A. H. de Vries, S. J. Marrink and P. C. T. Souza, Martini coarse-grained models of imidazolium-based ionic liquids: From nanostructural organization to liquid–liquid extraction, Green Chem., 2020, 22, 7376–7386 RSC
.
- C. Merlet, M. Salanne and B. Rotenberg, New coarse-grained models of imidazolium ionic liquids for bulk and interfacial molecular simulations, J. Phys. Chem. C, 2012, 116, 7687–7693 CrossRef CAS
.
- F. Uhlig, J. Zeman, J. Smiatek and C. Holm, First-principles parametrization of polarizable coarse-grained force fields for ionic liquids, J. Chem. Theory Comput., 2018, 14, 1471–1486 CrossRef CAS
.
- J. Ruza, W. Wang, D. Schwalbe-Koda, S. Axelrod, W. H. Harris and R. Gomez-Bombarelli, Temperature-transferable coarse-graining of ionic liquids with dual graph convolutional neural networks, J. Chem. Phys., 2020, 153, 164501 CrossRef CAS
.
- Y. L. Wang, B. Li and A. Laaksonen, Coarse-grained simulations of ionic liquid materials: From monomeric ionic liquids to ionic liquid crystals and polymeric ionic liquids, Phys. Chem. Chem. Phys., 2021, 23, 19435–19456 RSC
.
- S. Kloth, M. P. Bernhardt, N. F. van der Vegt and M. Vogel, Coarse-grained model of a nanoscale-segregated ionic liquid for simulations of low-temperature structure and dynamics, J. Condens. Matter Phys., 2021, 33, 204002 CrossRef CAS
.
- O. Y. Fajardo, S. Di Lecce and F. Bresme, Molecular dynamics simulation of imidazolium CnMIM-BF4 ionic liquids using a coarse grained force-field, Phys. Chem. Chem. Phys., 2020, 22, 1682–1692 RSC
.
- Y. L. Wang, Y. L. Zhu, Z. Y. Lu and A. Laaksonen, Electrostatic interactions in soft particle systems: Mesoscale simulations of ionic liquids, Soft Matter, 2018, 14, 4252–4267 RSC
.
- J. Tong, Y. Guo, F. Huo, X. Xie, H. He, N. von Solms, X. Liang and S. Zhang, Developing a coarse-grained model for 1-alkyl-3-methyl-imidazolium chloride ionic liquids, Ind. Eng. Chem. Res., 2018, 57, 15206–15215 CrossRef CAS
.
- A. Moradzadeh, M. H. Motevaselian, S. Y. Mashayak and N. R. Aluru, Coarse-grained force field for imidazolium-based ionic liquids, J. Chem. Theory Comput., 2018, 14, 3252–3261 CrossRef CAS
.
- J. Zeman, F. Uhlig, J. Smiatek and C. Holm, A coarse-grained polarizable force field for the ionic liquid 1-butyl-3-methylimidazolium hexafluorophosphate, J. Phys.: Condens. Matter, 2017, 29, 504004 CrossRef PubMed
.
- C. Schroder and O. Steinhauser, Charged, dipolar soft matter systems from a combined microscopic-mesoscopic viewpoint, J. Phys.: Condens. Matter, 2016, 28, 344008 CrossRef PubMed
.
- Y. L. Wang, A. Lyubartsev, Z. Y. Lu and A. Laaksonen, Multiscale coarse-grained simulations of ionic liquids: Comparison of three approaches to derive effective potentials, Phys. Chem. Chem. Phys., 2013, 15, 7701–7712 RSC
.
- C. Merlet, M. Salanne, B. Rotenberg and P. A. Madden, Imidazolium ionic liquid interfaces with vapor and graphite: Interfacial tension and capacitance from coarse-grained molecular simulations, J. Phys. Chem. C, 2011, 115, 16613–16618 CrossRef
.
- D. Roy, N. Patel, S. Conte and M. Maroncelli, Dynamics in an idealized ionic liquid model, J. Phys. Chem. B, 2010, 114, 8410–8424 CrossRef
.
- D. Roy and M. Maroncelli, An improved four-site ionic liquid model, J. Phys. Chem. B, 2010, 114, 12629–12631 CrossRef PubMed
.
- H. A. Karimi-Varzaneh, F. Muller-Plathe, S. Balasubramanian and P. Carbone, Studying long-time dynamics of imidazolium-based ionic liquids with a systematically coarse-grained model, Phys. Chem. Chem. Phys., 2010, 12, 4714–4724 RSC
.
- B. L. Bhargava and M. L. Klein, Formation of micelles in aqueous solutions of a room temperature ionic liquid: A study using coarse grained molecular dynamics, Mol. Phys., 2010, 107, 393–401 CrossRef
.
- Y. Wang, S. Feng and G. A. Voth, Transferable coarse-grained models for ionic liquids, J. Chem. Theory Comput., 2009, 5, 1091–1098 CrossRef
.
- W. Jiang, Y. Wang, T. Yan and G. A. Voth, A multiscale coarse-graining study of the liquid/vacuum interface of room-temperature ionic liquids with alkyl substituents of different lengths, J. Phys. Chem. C, 2008, 112, 1132–1139 CrossRef
.
- B. L. Bhargava, R. Devane, M. L. Klein and S. Balasubramanian, Nanoscale organization in room temperature ionic liquids: A coarse grained molecular dynamics simulation study, Soft Matter, 2007, 3, 1395–1400 RSC
.
- Y. Wang, S. Izvekov, T. Yan and G. A. Voth, Multiscale coarse-graining of ionic liquids, J. Phys. Chem. B, 2006, 110, 3564–3575 CrossRef PubMed
.
- T. D. Stoffel, J. B. Haskins, J. W. Lawson and S. Markutsya, Coarse-grained dynamically accurate simulations of ionic liquids: [pyr14][TFSI] and [EMIM][BF4], J. Phys. Chem. B, 2022, 126, 1819–1829 CrossRef CAS PubMed
.
- N. Mehta and D. Levin, Molecular dynamics electrospray simulations of coarse-grained ethylammonium nitrate (EAN) and 1-ethyl-3-methylimidazolium tetrafluoroborate (EMIM-BF4), Aerospace, 2017, 5, 1 CrossRef
.
- D. Sun and J. Zhou, Ionic liquid confined in Nafion: Toward molecular-level understanding, AIChE J., 2013, 59, 2630–2639 CrossRef CAS
.
- T. Bereau and K. Kremer, Automated parametrization of the coarse-grained Martini force field for small organic molecules, J. Chem. Theory Comput., 2015, 11, 2783–2791 CrossRef CAS
.
- T. D. Potter, E. L. Barrett and M. A. Miller, Automated coarse-grained mapping algorithm for the martini force field and benchmarks for membrane-water partitioning, J. Chem. Theory Comput., 2021, 17, 5777–5791 CrossRef CAS PubMed
.
- M. Chakraborty, C. Xu and A. D. White, Encoding and selecting coarse-grain mapping operators with hierarchical graphs, J. Chem. Phys., 2018, 149, 134106 CrossRef PubMed
.
- M. Giulini, R. Menichetti, M. S. Shell and R. Potestio, An information-theory-based approach for optimal model reduction of biomolecules, J. Chem. Theory Comput., 2020, 16, 6795–6813 CrossRef CAS
.
- S. Kmiecik, D. Gront, M. Kolinski, L. Wieteska, A. E. Dawid and A. Kolinski, Coarse-grained protein models and their applications, Chem. Rev., 2016, 116, 7898–7936 CrossRef CAS PubMed
.
- T. Pal and M. Vogel, Role of dynamic heterogeneities in ionic liquids: Insights from all-atom and coarse-grained molecular dynamics simulation studies, ChemPhysChem, 2017, 18, 2233–2242 CrossRef
.
- G. P. Pereira, R. Alessandri, M. Dominguez, R. Araya-Osorio, L. Grunewald, L. Borges-Araujo, S. Wu, S. J. Marrink, P. C. T. Souza and R. Mera-Adasme, Bartender: Martini 3 bonded terms via quantum mechanics-based molecular dynamics, J. Chem. Theory Comput., 2024, 20, 5763–5773 CrossRef
.
- V. Ruhle, C. Junghans, A. Lukyanov, K. Kremer and D. Andrienko, Versatile object-oriented toolkit for coarse-graining applications, J. Chem. Theory Comput., 2009, 5, 3211–3223 CrossRef PubMed
.
- Q. Li, Y. Guo, J. Tong, H. He, X. Zhang and F. Huo, Development of a coarse-grained force field model of polymeric 1-vinyl-3-ethylimidazolium tetrafluoroborate ionic liquids, Chem. Phys. Lett., 2020, 754, 137656 CrossRef CAS
.
- Y. Wang, H. He, C. Wang, Y. Lu, K. Dong, F. Huo and S. Zhang, Insights into ionic liquids: From Z-bonds to quasi-liquids, JACS Au, 2022, 2, 543–561 CrossRef CAS PubMed
.
- E. G. Odintsova, D. L. Gurina, S. E. Kruchinin, M. G. Kiselev and Y. A. Budkov, Shear viscosity of short-chain imidazolium ionic liquids from equilibrium and nonequilibrium molecular dynamics: Atomistic and coarse-grained levels, Ind. Eng. Chem. Res., 2025, 64, 3531–3543 CrossRef CAS
.
- W. G. Noid, Perspective: Advances, challenges, and insight for predictive coarse-grained models, J. Phys. Chem. B, 2023, 127, 4174–4207 CrossRef CAS PubMed
.
- E. Brini, E. A. Algaer, P. Ganguly, C. Li, F. Rodríguez-Ropero and N. F. A. van der Vegt, Systematic coarse-graining methods for soft matter simulations – A review, Soft Matter, 2013, 9, 2108–2119 RSC
.
- J. Jin, A. J. Pak, A. E. P. Durumeric, T. D. Loose and G. A. Voth, Bottom-up coarse-graining: Principles and perspectives, J. Chem. Theory Comput., 2022, 18, 5759–5791 CrossRef CAS
.
- W. G. Noid, R. J. Szukalo, K. M. Kidder and M. C. Lesniewski, Rigorous progress in coarse-graining, Annu. Rev. Phys. Chem., 2024, 75, 21–45 CrossRef CAS PubMed
.
- S. Y. Mashayak, M. N. Jochum, K. Koschke, N. R. Aluru, V. Ruhle and C. Junghans, Relative entropy and optimization-driven coarse-graining methods in VOTCA, PLoS One, 2015, 10, e0131754 Search PubMed
.
- V. Rühle and C. Junghans, Hybrid approaches to coarse-graining using the VOTCA package: Liquid hexane, Macromol. Theory Simul., 2011, 20, 472–477 Search PubMed
.
- Y. Peng, A. J. Pak, A. E. P. Durumeric, P. G. Sahrmann, S. Mani, J. Jin, T. D. Loose, J. Beiter and G. A. Voth, OpenMSCG: A software tool for bottom-up coarse-graining, J. Phys. Chem. B, 2023, 127, 8537–8550 CrossRef PubMed
.
- A. Mirzoev, L. Nordenskiöld and A. Lyubartsev, Magic v.3: An integrated software package for systematic structure-based coarse-graining, Comput. Phys. Commun., 2019, 237, 263–273 Search PubMed
.
- N. J. Dunn, K. M. Lebold, M. R. DeLyser, J. F. Rudzinski and W. Noid, BOCS: Bottom-up open-source coarse-graining software, J. Phys. Chem. B, 2017, 122, 3363–3377 CrossRef
.
- A. Chaimovich and M. S. Shell, Coarse-graining errors and numerical optimization using a relative entropy framework, J. Chem. Phys., 2011, 134, 094112 Search PubMed
.
- F. Ercolessi and J. B. Adams, Interatomic potentials from first-principles calculations: The force-matching method, Europhys. Lett., 1994, 26, 583 Search PubMed
.
- S. Izvekov and G. A. Voth, Multiscale coarse graining of liquid-state systems, J. Chem. Phys., 2005, 123, 134105 CrossRef PubMed
.
- H. Yu and W. F. van Gunsteren, Accounting for polarization in molecular simulation, Comput. Phys. Commun., 2005, 172, 69–85 CrossRef
.
- F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, Force fields for studying the structure and dynamics of ionic liquids: A critical review of recent developments, ChemPhysChem, 2012, 13, 1625–1637 Search PubMed
.
- Q. Zhu, Y. Ge, W. Li and J. Ma, Treating polarization effects in charged and polar bio-molecules through variable electrostatic parameters, J. Chem. Theory Comput., 2023, 19, 396–411 CrossRef PubMed
.
- S. A. Blair and A. J. Thakkar, Relating polarizability to volume, ionization energy, electronegativity, hardness, moments of momentum, and other molecular properties, J. Chem. Phys., 2014, 141, 074306 CrossRef PubMed
.
- K. E. Laidig and R. F. Bader, Properties of atoms in molecules: Atomic polarizabilities, J. Chem. Phys., 1990, 93, 7213–7224 CrossRef
.
- J. Schmidt, C. Krekeler, F. Dommert, Y. Zhao, R. Berger, L. D. Site and C. Holm, Ionic charge reduction and atomic partial charges from first-principles calculations of 1, 3-dimethylimidazolium chloride, J. Phys. Chem. B, 2010, 114, 6150–6155 Search PubMed
.
- K. Wendler, S. Zahn, F. Dommert, R. Berger, C. Holm, B. Kirchner and L. D. Site, Locality and fluctuations: Trends in imidazolium-based ionic liquids and beyond, J. Chem. Theory Comput., 2011, 7, 3040–3044 CrossRef PubMed
.
- Y. Li, D. Yuan, Q. Wang, W. Li and S. Li, Accurate prediction of the structure and vibrational spectra of ionic liquid clusters with the generalized energy-based fragmentation approach: Critical role of ion-pair-based fragmentation, Phys. Chem. Chem. Phys., 2018, 20, 13547–13557 RSC
.
- G. Reyes, H. Segura and A. Mejía, Coarse-grained molecular dynamic simulations of selected thermophysical properties for 1-Butyl-3-methylimidazolium hexafluorophosphate, J. Mol. Liq., 2013, 186, 106–115 CrossRef
.
- E. A. Crespo, N. Schaeffer, J. A. P. Coutinho and G. Perez-Sanchez, Improved coarse-grain model to unravel the phase behavior of 1-alkyl-3-methylimidazolium-based ionic liquids through molecular dynamics simulations, J. Colloid Interface Sci., 2020, 574, 324–336 CrossRef PubMed
.
- N. Schaeffer, G. Perez-Sanchez, H. Passos, J. R. B. Gomes, N. Papaiconomou and J. A. P. Coutinho, Mechanisms of phase separation in temperature-responsive acidic aqueous biphasic systems, Phys. Chem. Chem. Phys., 2019, 21, 7462–7473 RSC
.
- S. O. Yesylevskyy, L. V. Schafer, D. Sengupta and S. J. Marrink, Polarizable water model for the coarse-grained MARTINI force field, PLoS Comput. Biol., 2010, 6, e1000810 CrossRef PubMed
.
- P. Karpov, G. Godin and I. V. Tetko, Transformer-CNN: Swiss knife for QSAR modeling and interpretation, Aust. J. Chem., 2020, 12, 1–12 Search PubMed
.
- D. Makarov, Y. A. Fadeeva, E. Safonova and L. Shmukler, Predictive modeling of antibacterial activity of ionic liquids by machine learning methods, Comput. Biol. Chem., 2022, 101, 107775 CrossRef PubMed
.
- D. M. Makarov, Y. A. Fadeeva, L. E. Shmukler and I. V. Tetko, Beware of proper validation of models for ionic Liquids!, J. Mol. Liq., 2021, 344, 117722 CrossRef
.
- D. M. Makarov, Y. A. Fadeeva and L. E. Shmukler, Predictive modeling of physicochemical properties and ionicity of ionic liquids for virtual screening of novel electrolytes, J. Mol. Liq., 2023, 391, 123323 CrossRef
.
- D. M. Makarov, Y. A. Fadeeva, L. E. Shmukler and I. V. Tetko, Machine learning models for phase transition and decomposition temperature of ionic liquids, J. Mol. Liq., 2022, 366, 120247 CrossRef
.
- A. Racki and K. Paduszynski, Recent advances in the modeling of ionic liquids using artificial neural networks, J. Chem. Inf. Model., 2025, 65, 3161–3175 Search PubMed
.
- S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, A review on machine learning algorithms for the ionic liquid chemical space, Chem. Sci., 2021, 12, 6820–6843 RSC
.
- Z. Song, J. Chen, J. Cheng, G. Chen and Z. Qi, Computer-Aided molecular design of ionic liquids as advanced process media: A review from fundamentals to applications, Chem. Rev., 2024, 124, 248–317 CrossRef CAS PubMed
.
- G. R. Pastel, T. P. Pollard, O. Borodin and M. A. Schroeder, From Ab initio to instrumentation: A field guide to characterizing multivalent liquid electrolytes, Chem. Rev., 2025, 125, 3059–3164 Search PubMed
.
- J. Chen, Q. Gao, M. Huang and K. Yu, Application of modern artificial intelligence techniques in the development of organic molecular force fields, Phys. Chem. Chem. Phys., 2025, 27, 2294–2319 Search PubMed
.
- Y. Ding, K. Yu and J. Huang, Data science techniques in biomolecular force field development, Curr. Opin. Struct. Biol., 2023, 78, 102502 CrossRef CAS
.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401 Search PubMed
.
- J. Behler, Atom-centered symmetry functions for constructing high-dimensional neural network potentials, J. Chem. Phys., 2011, 134, 074106 CrossRef PubMed
.
- M. Niepert, M. Ahmed and K. Kutzkov, Learning convolutional neural networks for graphs, in International Conference on Machine Learning, 2016, pp. 2014–2023 Search PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, Schnet–A deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148, 241722 CrossRef
.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csányi, MACE: Higher order equivariant message passing neural networks for fast and accurate force fields, Adv. Neural Inf. Process. Syst., 2022, vol. 35, pp. 11423–11436, DOI:10.48550/arXiv.2206.07697.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning local equivariant representations for large-scale atomistic dynamics, Nat. Commun., 2023, 14, 579 CrossRef CAS
.
- Y. Wang, T. Wang, S. Li, X. He, M. Li, Z. Wang, N. Zheng, B. Shao and T.-Y. Liu, Enhancing geometric representations for molecules with equivariant vector-scalar interactive message passing, Nat. Commun., 2024, 15, 313 CrossRef CAS PubMed
.
- S. Gong, Y. Zhang, Z. Mu, Z. Pu, H. Wang, X. Han, Z. Yu, M. Chen, T. Zheng, Z. Wang, L. Chen, Z. Yang, X. Wu, S. Shi, W. Gao, W. Yan and L. Xiang, A predictive machine learning force-field framework for liquid electrolyte development, Nat. Mach. Intell., 2025, 7, 543–552 Search PubMed
.
- S. Boothroyd, P. K. Behara, O. C. Madin, D. F. Hahn, H. Jang, V. Gapsys, J. R. Wagner, J. T. Horton, D. L. Dotson and M. W. Thompson, Development and benchmarking of open force field 2.0. 0: The sage small molecule force field, J. Chem. Theory Comput., 2023, 19, 3251–3275 Search PubMed
.
- D. M. Anstine and O. Isayev, Machine learning interatomic potentials and long-range physics, J. Phys. Chem. A, 2023, 127, 2417–2431 Search PubMed
.
- A. K. Rappe and W. A. Goddard III, Charge equilibration for molecular dynamics simulations, J. Phys. Chem., 1991, 95, 3358–3363 Search PubMed
.
- M. Gubler, J. A. Finkler, M. R. Schafer, J. Behler and S. Goedecker, Accelerating fourth-generation machine learning potentials using quasi-linear scaling particle mesh charge equilibration, J. Chem. Theory Comput., 2024, 20, 7264–7271 Search PubMed
.
- P. Fuchs, M. Sanocki and J. Zavadlav, Learning non-local molecular interactions via equivariant local representations and charge equilibration, arXiv, 2025, preprint, arXiv:2501.19179, DOI:10.48550/arXiv.2501.19179.
- P. Eastman, R. Galvelis, R. P. Pelaez, C. R. A. Abreu, S. E. Farr, E. Gallicchio, A. Gorenko, M. M. Henry, F. Hu, J. Huang, A. Kramer, J. Michel, J. A. Mitchell, V. S. Pande, J. P. Rodrigues, J. Rodriguez-Guerra, A. C. Simmonett, S. Singh, J. Swails, P. Turner, Y. Wang, I. Zhang, J. D. Chodera, G. De Fabritiis and T. E. Markland, OpenMM 8: Molecular dynamics simulation with machine learning potentials, J. Phys. Chem. B, 2024, 128, 109–116 Search PubMed
.
- C. R. Rupakheti, A. D. MacKerell Jr and B. Roux, Global optimization of the lennard-jones parameters for the drude polarizable force field, J. Chem. Theory Comput., 2021, 17, 7085–7095 Search PubMed
.
- Q. Xiong, Y. Jiang, X. Cai, F. Yang, Z. Li and W. Han, Conformation dependence of diphenylalanine self-assembly structures and dynamics: Insights from hybrid-resolution simulations, ACS Nano, 2019, 13, 4455–4468 CrossRef CAS PubMed
.
- X. Cai and W. Han, Development of a hybrid-resolution force field for peptide self-assembly simulations: optimizing peptide–peptide and peptide–solvent interactions, J. Chem. Inf. Model., 2022, 62, 2744–2760 CrossRef CAS
.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes and I. Vorobyov, CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS
.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef PubMed
.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef
.
- A. Tkatchenko and M. Scheffler, Accurate molecular van der waals interactions from ground-state electron density and free-atom reference data, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed
.
- Y. Kokane Yati and A. Mondal, Active-learning assisted general framework for efficient parameterization of force-fields, J. Chem. Theory Comput., 2025, 21, 2638–2654 CrossRef PubMed
.
- V. R. Joseph and Y. Hung, Orthogonal-maximin Latin hypercube designs, Stat. Sin., 2008, 18, 171–186 Search PubMed
.
- Y. Wu, Q. Zhu, Z. Huang, P. Cieplak, Y. Duan and R. Luo, Automated refinement of property-specific polarizable Gaussian multipole water models using bayesian black-box optimization, J. Chem. Theory Comput., 2025, 21, 3563–3575 CrossRef PubMed
.
- D. Yin and A. D. MacKerell Jr, Combined ab initio/empirical approach for optimization of Lennard–Jones parameters, J. Comput. Chem., 1998, 19, 334–348 CrossRef
.
- Y. Wang, W. Jiang, T. Yan and G. A. Voth, Understanding ionic liquids through atomistic and coarse-grained molecular dynamics simulations, Acc. Chem. Res., 2007, 40, 1193–1199 CrossRef PubMed
.
- Y. Wang and G. A. Voth, Tail aggregation and domain diffusion in ionic liquids, J. Phys. Chem. B, 2006, 110, 18601–18608 CrossRef PubMed
.
- Y. Wang and G. A. Voth, Unique spatial heterogeneity in ionic liquids, J. Am. Chem. Soc., 2005, 127, 12192–12193 Search PubMed
.
- G. Saielli, A. Bagno and Y. Wang, Insights on the isotropic-to-smectic a transition in ionic liquid crystals from coarse-grained molecular dynamics simulations: The role of microphase segregation, J. Phys. Chem. B, 2015, 119, 3829–3836 CrossRef PubMed
.
- A. Triolo, O. Russina, H.-J. Bleif and E. Di Cola, Nanoscale segregation in room temperature ionic liquids, J. Phys. Chem. B, 2007, 111, 4641–4644 CrossRef PubMed
.
- J. D. Holbrey and K. R. Seddon, The phase behaviour of 1-alkyl-3-methylimidazolium tetrafluoroborates; ionic liquids and ionic liquid crystals, J. Chem. Soc., Dalton Trans., 1999, 2133–2140 RSC
.
- K. Goossens, K. Lava, C. W. Bielawski and K. Binnemans, Ionic liquid crystals: Versatile materials, Chem. Rev., 2016, 116, 4643–4807 CrossRef PubMed
.
- K. Binnemans, Ionic liquid crystals, Chem. Rev., 2005, 105, 4148–4204 CrossRef PubMed
.
- Q. Ruan, M. Yao, D. Yuan, H. Dong, J. Liu, X. Yuan, W. Fang, G. Zhao and H. Zhang, Ionic liquid crystal electrolytes: Fundamental, applications and prospects, Nano Energy, 2023, 106, 108087 CrossRef
.
- J. Sakuda, E. Hosono, M. Yoshio, T. Ichikawa, T. Matsumoto, H. Ohno, H. Zhou and T. Kato, Liquid-crystalline electrolytes for lithium-ion batteries: Ordered assemblies of a mesogen-containing carbonate and a lithium salt, Adv. Funct. Mater., 2015, 25, 1206–1212 CrossRef
.
- N. Yamanaka, R. Kawano, W. Kubo, T. Kitamura, Y. Wada, M. Watanabe and S. Yanagida, Ionic liquid crystal as a hole transport layer of dye-sensitized solar cells, Chem. Commun., 2005, 740–742 RSC
.
- D. Högberg, B. Soberats, R. Yatagai, S. Uchida, M. Yoshio, L. Kloo, H. Segawa and T. Kato, Liquid-crystalline dye-sensitized solar cells: Design of two-dimensional molecular assemblies for efficient ion transport and thermal stability, Chem. Mater., 2016, 28, 6493–6500 CrossRef
.
- G. Bousrez, O. Renier, B. Adranno, V. Smetana and A.-V. Mudring, Ionic liquid-based dye-sensitized solar cells—insights into electrolyte and redox mediator design, ACS Sustainable Chem. Eng., 2021, 9, 8107–8114 CrossRef
.
- K. V. Axenov and S. Laschat, Thermotropic ionic liquid crystals, Materials, 2011, 4, 206–259 CrossRef
.
- G. Saielli, MD simulation of the mesomorphic behaviour of 1-hexadecyl-3-methylimidazolium nitrate: assessment of the performance of a coarse-grained force field, Soft Matter, 2012, 8, 10279–10287 RSC
.
- Y. Ji, R. Shi, Y. Wang and G. Saielli, Effect of the chain length on the structure of ionic liquids: From spatial heterogeneity to ionic liquid crystals, J. Phys. Chem. B, 2013, 117, 1104–1109 CrossRef
.
- Y. Nozaki, K. Yamaguchi, K. Tomida, N. Taniguchi, H. Hara, Y. Takikawa, K. Sadakane, K. Nakamura, T. Konishi and K. Fukao, Phase transition and dynamics in imidazolium-based ionic liquid crystals through a metastable highly ordered smectic phase, J. Phys. Chem. B, 2016, 120, 5291–5300 CrossRef PubMed
.
- B. Mukherjee, L. Delle Site, K. Kremer and C. Peter, Derivation of coarse grained models for multiscale simulation of liquid crystalline phase transitions, J. Phys. Chem. B, 2012, 116, 8474–8484 CrossRef
.
- K. S. Egorova, E. G. Gordeev and V. P. Ananikov, Biological activity of ionic liquids and their application in pharmaceutics and medicine, Chem. Rev., 2017, 117, 7132–7189 CrossRef
.
- N. Adawiyah, M. Moniruzzaman, S. Hawatulaila and M. Goto, Ionic liquids as a potential tool for drug delivery systems, MedChemComm, 2016, 7, 1881–1897 RSC
.
- A. A. Toledo Hijo, G. J. Maximo, M. C. Costa, E. A. Batista and A. J. Meirelles, Applications of ionic liquids in the food and bioproducts industries, ACS Sustainable Chem. Eng., 2016, 4, 5347–5369 CrossRef
.
- A. Benedetto and P. Ballone, Room temperature ionic liquids meet biomolecules: A microscopic view of structure and dynamics, ACS Sustainable Chem. Eng., 2015, 4, 392–412 CrossRef
.
- H. M. Cho, A. S. Gross and J. W. Chu, Dissecting force interactions in cellulose deconstruction reveals the required solvent versatility for overcoming biomass recalcitrance, J. Am. Chem. Soc., 2011, 133, 14033–14041 CrossRef
.
- A. Romero, A. Santos, J. Tojo and A. Rodríguez, Toxicity and biodegradability of imidazolium ionic liquids, J. Hazard. Mater., 2008, 151, 268–273 CrossRef
.
- K. M. Docherty and C. F. Kulpa Jr, Toxicity and antimicrobial activity of imidazolium and pyridinium ionic liquids, Green Chem., 2005, 7, 185–189 RSC
.
- P. Madaan and V. K. Tyagi, Quaternary pyridinium salts: A review, J. Oleo Sci., 2008, 57, 197–215 CrossRef
.
- B. Yoo, Y. Zhu and E. J. Maginn, Molecular mechanism of ionic-liquid-induced membrane disruption: Morphological changes to bilayers, multilayers, and vesicles, Langmuir, 2016, 32, 5403–5411 CrossRef
.
- B. Yoo, B. Jing, S. E. Jones, G. A. Lamberti, Y. Zhu, J. K. Shah and E. J. Maginn, Molecular mechanisms of ionic liquid cytotoxicity probed by an integrated experimental and computational approach, Sci. Rep., 2016, 6, 19889 CrossRef PubMed
.
- M. Reches and E. Gazit, Casting metal nanowires within discrete self-assembled peptide nanotubes, Science, 2003, 300, 625–627 CrossRef PubMed
.
- C. H. Görbitz, Nanotube formation by hydrophobic dipeptides, Chem. – Eur. J., 2001, 7, 5153–5159 CrossRef
.
- X. Yan, Y. Cui, Q. He, K. Wang and J. Li, Organogels based on self-assembly of diphenylalanine peptide and their application to immobilize quantum dots, Chem. Mater., 2008, 20, 1522–1526 CrossRef CAS
.
- L. Adler-Abramovich and E. Gazit, Controlled patterning of peptide nanotubes and nanospheres using inkjet printing technology, J. Pept. Sci., 2008, 14, 217–223 CrossRef CAS
.
- A. Kholkin, N. Amdursky, I. Bdikin, E. Gazit and G. Rosenman, Strong piezoelectricity in bioinspired peptide nanotubes, ACS Nano, 2010, 4, 610–614 CrossRef CAS PubMed
.
- K. Tao, P. Makam, R. Aizen and E. Gazit, Self-assembling peptide semiconductors, Science, 2017, 358, eaam9756 CrossRef PubMed
.
- J. Wang, C. Yuan, Y. Han, Y. Wang, X. Liu, S. Zhang and X. Yan, Trace water as prominent factor to induce peptide self-assembly: Dynamic evolution and governing interactions in ionic liquids, Small, 2017, 13, 1702175 CrossRef PubMed
.
- M. Hayyan, F. S. Mjalli, M. A. Hashim, I. M. AlNashef and T. X. Mei, Investigating the electrochemical windows of ionic liquids, J. Ind. Eng. Chem., 2013, 19, 106–112 CrossRef CAS
.
- S. Kazemiabnavi, Z. Zhang, K. Thornton and S. Banerjee, Electrochemical stability window of imidazolium-based ionic liquids as electrolytes for lithium batteries, J. Phys. Chem. B, 2016, 120, 5691–5702 CrossRef CAS PubMed
.
- C. Lian, H. Liu, C. Li and J. Wu, Hunting ionic liquids with large electrochemical potential windows, AIChE J., 2019, 65, 804–810 CrossRef CAS
.
- G. Jeanmairet, B. Rotenberg and M. Salanne, Microscopic simulations of electrochemical double-layer capacitors, Chem. Rev., 2022, 122, 10860–10898 CrossRef
.
- C. Merlet, C. Pean, B. Rotenberg, P. A. Madden, P. Simon and M. Salanne, Simulating supercapacitors: Can we model electrodes as constant charge surfaces?, J. Phys. Chem. Lett., 2013, 4, 264–268 CrossRef PubMed
.
- S. Kondrat, G. Feng, F. Bresme, M. Urbakh and A. A. Kornyshev, Theory and simulations of ionic liquids in nanoconfinement, Chem. Rev., 2023, 123, 6668–6715 CrossRef PubMed
.
- L. Zeng, J. Peng, J. Zhang, X. Tan, X. Ji, S. Li and G. Feng, Molecular dynamics simulations of electrochemical interfaces, J. Chem. Phys., 2023, 159, 091001 CrossRef CAS PubMed
.
- J. Wu, Understanding the electric double-layer structure, capacitance, and charging dynamics, Chem. Rev., 2022, 122, 10821–10859 CrossRef PubMed
.
- L. Scalfi, M. Salanne and B. Rotenberg, Molecular simulation of electrode-solution interfaces, Annu. Rev. Phys. Chem., 2021, 72, 189–212 CrossRef
.
- L. Zeng, X. Ji, J. Zhang, N. Huang, Z. Wang, D. Yu, J. Peng and G. Feng, Enhancing molecular dynamics simulations of electrical double layers: From simplified to realistic models, WIREs Comput. Mol. Sci., 2025, 15, e70009 CrossRef
.
- K. Breitsprecher, P. Kosovan and C. Holm, Coarse-grained simulations of an ionic liquid-based capacitor: I. Density, ion size, and valency effects, J. Phys.: Condens. Matter, 2014, 26, 284108 CrossRef PubMed
.
- K. Breitsprecher, P. Kosovan and C. Holm, Coarse-grained simulations of an ionic liquid-based capacitor: II. Asymmetry in ion shape and charge localization, J. Phys.: Condens. Matter, 2014, 26, 284114 CrossRef PubMed
.
- M. W. Cole and J. R. Klein, The interaction between noble gases and the basal plane surface of graphite, Surf. Sci., 1983, 124, 547–554 CrossRef CAS
.
- C. Merlet, D. T. Limmer, M. Salanne, R. van Roij, P. A. Madden, D. Chandler and B. Rotenberg, The electric double layer has a life of its own, J. Phys. Chem. C, 2014, 118, 18291–18298 CrossRef
.
- B. Rotenberg and M. Salanne, Structural transitions at ionic liquid interfaces, J. Phys. Chem. Lett., 2015, 6, 4978–4985 CrossRef PubMed
.
- C. Merlet, M. Salanne, B. Rotenberg and P. A. Madden, Influence of solvation on the structural and capacitive properties of electrical double layer capacitors, Electrochim. Acta, 2013, 101, 262–271 CrossRef
.
- T. Mo, S. Bi, Y. Zhang, V. Presser, X. Wang, Y. Gogotsi and G. Feng, Ion structure transition enhances charging dynamics in subnanometer pores, ACS Nano, 2020, 14, 2395–2403 CrossRef CAS PubMed
.
- D. Gurina, E. Odintsova, A. Kolesnikov, M. Kiselev and Y. Budkov, Disjoining pressure of room temperature ionic liquid in charged slit carbon nanopore: Molecular dynamics study, J. Mol. Liq., 2022, 366, 120307 CrossRef CAS
.
- D. L. Gurina, E. G. Odintsova and Y. A. Budkov, Disjoining pressure decay length in room-temperature ionic liquids: A molecular simulation study, J. Phys. Chem. B, 2024, 128, 2215–2218 CrossRef CAS
.
- B. Li, K. Ma, Y. L. Wang, M. Turesson, C. E. Woodward and J. Forsman, Fused coarse-grained model of aromatic ionic liquids and
their behaviour at electrodes, Phys. Chem. Chem. Phys., 2016, 18, 8165–8173 RSC
.
- Y. M. Liu, C. Merlet and B. Smit, Carbons with regular pore geometry yield fundamental insights into supercapacitor charge storage, ACS Cent. Sci., 2019, 5, 1813–1823 CrossRef CAS
.
- E. H. Lahrar, A. Belhboub, P. Simon and C. Merlet, Ionic liquids under confinement: From systematic variations of the ion and pore sizes toward an understanding of the structure and dynamics in complex porous carbons, ACS Appl. Mater. Interfaces, 2020, 12, 1789–1798 CrossRef CAS
.
- E. H. Lahrar, I. Deroche, C. Matei Ghimbeu, P. Simon and C. Merlet, Simulations of ionic liquids confined in surface-functionalized nanoporous carbons: Implications for energy storage, ACS Appl. Nano Mater., 2021, 4, 4007–4015 CrossRef CAS
.
- S. Bi, H. Banda, M. Chen, L. Niu, M. Chen, T. Wu, J. Wang, R. Wang, J. Feng, T. Chen, M. Dinca, A. A. Kornyshev and G. Feng, Molecular understanding of charge storage and charging dynamics in supercapacitors with MOF electrodes and ionic liquid electrolytes, Carbon, 2020, 19, 552–558 CAS
.
- T. Mo, Z. Wang, L. Zeng, M. Chen, A. A. Kornyshev, M. Zhang, Y. Zhao and G. Feng, Energy storage mechanism in supercapacitors with porous graphdiynes: Effects of pore topology and electrode metallicity, Adv. Mater., 2023, 35, e2301118 CrossRef
.
- Z. Liang, C. Zhao, W. Zhao, Y. Zhang, P. Srimuk, V. Presser and G. Feng, Molecular understanding of charge storage in MoS2 supercapacitors with ionic liquids, Energy Environ. Mater., 2021, 4, 631–637 CrossRef CAS
.
- S. Bi and M. Salanne, Co-ion desorption as the main charging mechanism in metallic 1T-MoS2 supercapacitors, ACS Nano, 2022, 16, 18658–18666 CrossRef CAS PubMed
.
- C. Merlet, B. Rotenberg, P. A. Madden, P. L. Taberna, P. Simon, Y. Gogotsi and M. Salanne, On the molecular origin of supercapacitance in nanoporous carbon electrodes, Nat. Mater., 2012, 11, 306–310 CrossRef
.
- C. Merlet, C. Pean, B. Rotenberg, P. A. Madden, B. Daffos, P. L. Taberna, P. Simon and M. Salanne, Highly confined ions store charge more efficiently in supercapacitors, Nat. Commun., 2013, 4, 2701 CrossRef
.
- C. Péan, C. Merlet, B. Rotenberg, P. A. Madden, P.-L. Taberna, B. Daffos, M. Salanne and P. Simon, On the dynamics of charging in nanoporous carbon-based supercapacitors, ACS Nano, 2014, 8, 1576–1583 CrossRef
.
- J. Palmer, A. Llobet, S.-H. Yeon, J. Fischer, Y. Shi, Y. Gogotsi and K. Gubbins, Modeling the structural evolution of carbide-derived carbons using quenched molecular dynamics, Carbon, 2010, 48, 1116–1123 CrossRef CAS
.
- J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P.-L. Taberna, Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer, Science, 2006, 313, 1760–1763 CrossRef CAS PubMed
.
- A. Pensado, M. Comunas and J. Fernández, The pressure–viscosity coefficient of several ionic liquids, Tribol. Lett., 2008, 31, 107–118 CrossRef CAS
.
- Y. Lu, Y. Wang, F. Huo, W. Chen, M. Ma, W.-L. Ding, H. He and S. Zhang, Ultralow friction and high robustness of monolayer ionic liquids, ACS Nano, 2022, 16, 16471–16480 CrossRef CAS
.
- X. Gong and L. Li, Nanometer-thick ionic liquids as boundary lubricants, Adv. Eng. Mater., 2017, 20, 1700617 CrossRef
.
- I. Minami, Ionic liquids in tribology, Molecules, 2009, 14, 2286–2305 CrossRef CAS PubMed
.
- Y. He, H. Li, C. Qu, W. Cao and M. Ma, Recent understanding of solid-liquid friction in ionic liquids, Green Chem. Eng., 2021, 2, 145–157 CrossRef
.
- O. Y. Fajardo, F. Bresme, A. A. Kornyshev and M. Urbakh, Electrotunable lubricity with ionic liquid nanoscale films, Sci. Rep., 2015, 5, 7698 CrossRef CAS
.
- O. Y. Fajardo, F. Bresme, A. A. Kornyshev and M. Urbakh, Electrotunable friction with ionic liquid lubricants: How important is the molecular structure of the ions?, J. Phys. Chem. Lett., 2015, 6, 3998–4004 CrossRef CAS PubMed
.
- S. Di Lecce, A. A. Kornyshev, M. Urbakh and F. Bresme, Electrotunable lubrication with ionic liquids: the effects of cation chain length and substrate polarity, ACS Appl. Mater. Interfaces, 2020, 12, 4105–4113 CrossRef CAS
.
- K. Pivnic, F. Bresme, A. A. Kornyshev and M. Urbakh, Electrotunable friction in diluted room temperature ionic liquids: Implications for nanotribology, ACS Appl. Nano Mater., 2020, 3, 10708–10719 CrossRef CAS
.
- K. Pivnic, F. Bresme, A. A. Kornyshev and M. Urbakh, Structural forces in mixtures of ionic liquids with organic solvents, Langmuir, 2019, 35, 15410–15420 CrossRef CAS PubMed
.
- O. Y. Fajardo, F. Bresme, A. A. Kornyshev and M. Urbakh, Water in ionic liquid lubricants: Friend and foe, ACS Nano, 2017, 11, 6825–6831 CrossRef CAS
.
- H. J. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS
.
- D. M. Edwards, P. A. Madden and I. R. McDonald, A computer simulation study of the dielectric properties of a model of methyl cyanide: I. The rigid dipole case, Mol. Phys., 1984, 51, 1141–1161 CrossRef CAS
.
- A. David, O. Y. Fajardo, A. A. Kornyshev, M. Urbakh and F. Bresme, Electrotunable lubricity with ionic liquids: the influence of nanoscale roughness, Faraday Discuss., 2017, 199, 279–297 Search PubMed
.
- A. C. Mendonca, A. A. Padua and P. Malfreyt, Nonequilibrium molecular simulations of new ionic lubricants at metallic surfaces: Prediction of the friction, J. Chem. Theory Comput., 2013, 9, 1600–1610 CrossRef CAS
.
- N. J. H. Dunn, T. T. Foley and W. G. Noid, Van der waals perspective on coarse-graining: Progress toward solving representability and transferability problems, Acc. Chem. Res., 2016, 49, 2832–2840 CrossRef CAS PubMed
.
- H.-J. Qian, P. Carbone, X. Chen, H. A. Karimi-Varzaneh, C. C. Liew and F. Müller-Plathe, Temperature-transferable coarse-grained potentials for ethylbenzene, polystyrene, and their mixtures, Macromolecules, 2008, 41, 9919–9929 CrossRef CAS
.
- K. Farah, A. C. Fogarty, M. C. Bohm and F. Muller-Plathe, Temperature dependence of coarse-grained potentials for liquid hexane, Phys. Chem. Chem. Phys., 2011, 13, 2894–2902 RSC
.
- T. C. Moore, C. R. Iacovella and C. McCabe, Derivation of coarse-grained potentials via multistate iterative Boltzmann inversion, J. Chem. Phys., 2014, 140, 224104 CrossRef
.
- T. D. Potter, J. Tasche and M. R. Wilson, Assessing the transferability of common top-down and bottom-up coarse-grained molecular models for molecular mixtures, Phys. Chem. Chem. Phys., 2019, 21, 1912–1927 RSC
.
- J. Mullinax and W. Noid, Extended ensemble approach for deriving transferable coarse-grained potentials, J. Chem. Phys., 2009, 131, 104110 CrossRef
.
- J.-M. Simon, P. Krüger, S. K. Schnell, T. J. Vlugt, S. Kjelstrup and D. Bedeaux, Kirkwood–Buff integrals: From fluctuations in finite volumes to the thermodynamic limit, J. Chem. Phys., 2022, 157, 130901 CrossRef CAS PubMed
.
- P. Ganguly, D. Mukherji, C. Junghans and N. F. van der Vegt, Kirkwood-Buff coarse-grained force fields for aqueous solutions, J. Chem. Theory Comput., 2012, 8, 1802–1807 CrossRef CAS PubMed
.
- W. G. Chapman, K. E. Gubbins, G. Jackson and M. Radosz, SAFT: Equation-of-state solution model for associating fluids, Fluid Phase Equilib., 1989, 52, 31–38 CrossRef CAS
.
- E. A. Muller and G. Jackson, Force-field parameters from the SAFT-gamma equation of state for use in coarse-grained molecular simulations, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 405–427 CrossRef CAS
.
- C. Avendano, T. Lafitte, A. Galindo, C. S. Adjiman, G. Jackson and E. A. Müller, SAFT-γ force field for the simulation of molecular fluids. 1. A single-site coarse grained model of carbon dioxide, J. Phys. Chem. B, 2011, 115, 11154–11169 CrossRef CAS PubMed
.
- C. Avendano, T. Lafitte, C. S. Adjiman, A. Galindo, E. A. Müller and G. Jackson, SAFT-γ force field for the simulation of molecular fluids: 2. Coarse-grained models of greenhouse gases, refrigerants, and long alkanes, J. Phys. Chem. B, 2013, 117, 2717–2733 CrossRef CAS
.
- M. Fayaz-Torshizi and E. A. Müller, Coarse-grained molecular simulation of polymers supported by the use of the SAFT-γ Mie equation of state, Macromol. Theory Simul., 2022, 31, 2100031 CrossRef CAS
.
- N. Jiang and J. Ma, Conformational simulations of aqueous solvated α-conotoxin GI and its single disulfide analogues using a polarizable force field model, J. Phys. Chem. A, 2008, 112, 9854–9867 CrossRef CAS
.
- N. Jiang and J. Ma, Multi-layer coarse-graining polarization model for treating electrostatic interactions of solvated α-conotoxin peptides, J. Chem. Phys., 2012, 136, 134105 CrossRef
.
- Z. Zhong, L. Xu and J. Jiang, A neural-network-based mapping and optimization framework for high-precision coarse-grained simulation, J. Chem. Theory Comput., 2025, 21, 859–870 CrossRef CAS PubMed
.
- A. Kumar, O. Yoluk and A. D. MacKerell Jr, FFParam: Standalone package for CHARMM additive and Drude polarizable force field parametrization of small molecules, J. Comput. Chem., 2020, 41, 958–970 CrossRef CAS
.
- A. Kumar and A. D. MacKerell Jr, FFParam-v2. 0: A comprehensive tool for CHARMM additive and drude polarizable force-field parameter optimization and validation, J. Phys. Chem. B, 2024, 128, 4385–4395 CrossRef CAS PubMed
.
- A. Kumar, P. Pandey, P. Chatterjee and A. D. MacKerell Jr, Deep neural network model to predict the electrostatic parameters in the polarizable classical drude oscillator force field, J. Chem. Theory Comput., 2022, 18, 1711–1725 CrossRef CAS PubMed
.
| This journal is © Institute of Process Engineering of CAS 2025 |