The importance of indirect hotspots when prioritizing research in green chemical synthesis

Abstract

A default assumption in green chemistry research and development is that every step of every process should be made as green as possible. That assumption is flawed. In some cases, a modification to an individual step that makes it more harmful is environmentally beneficial if the change decreases the harm or scale of another step. In this Perspective paper, we explain how the concept of an indirect hotspot can be used to understand the effects of any one step on the harm of another. A direct hotspot is a step that causes more harm than other steps. An indirect hotspot may cause very little harm on its own but has an outsized influence on the harm of the direct hotspot, and therefore the total harm of the process. These concepts can be used to prioritize green chemistry research, so that the environmental benefit of such research can be maximized.

---

Green foundation

1. Not all modifications to a chemical process are equally effective at reducing the total harm. Research is expensive, time-consuming, and environmentally harmful, so green chemists should prioritize those projects or potential process modifications that are most likely to reduce the total harm. The likelihood of a significant reduction in harm occurring from a change to a single process step can be predicted by identifying which process steps are direct hotspots, indirect hotspots, or neither.

2. A direct hotspot is a step that causes a large proportion of the harm of the overall process. The best way to modify a direct hotspot is to reduce the harm of the step. An indirect hotspot doesn't necessarily cause much harm itself but it has a flaw that indirectly makes a direct hotspot more harmful. Making an indirect hotspot greener is much less likely to be fruitful – instead we should fix its flaw, even if that causes the indirect hotspot to become more harmful. Some steps are neither direct nor indirect hotspots; such steps should not be prioritized in green chemistry research. Categorizing steps as direct hotspots, indirect hotspots, or neither can help green chemists prioritize which steps to work on and what kind of improvements should be sought.

3. This perspective is written using artificial examples to illustrate the concepts. Future work could include LCA studies of actual multistep chemical processes, in which direct and indirect hotspots are identified and the benefits of modifications are quantitatively evaluated.

Introduction

When a green chemist wishes to make a synthesis less harmful, there are many options, but not all of them are equally effective. Any of the steps in a synthesis could, in theory, be made greener (i.e. be modified to cause less harm), could be changed to give a higher yield, or could be modified so as to facilitate post-reaction purification, thereby making that purification less harmful. In practise, however, some steps are easier for chemists to modify than others. Some steps, like mining or agricultural production of feedstocks, may be outside of the scope of a chemist's research expertise. Other steps might be recalcitrant in the sense that no potential improvements appear to be feasible. Green chemists are most likely to embark upon research to improve only those steps that are both within their expertise and reasonably likely to be modifiable. However for these steps, what modification should be made? It's tempting to believe that the best thing to do, in order to make the entire process greener, is to make all modifiable steps as green as they can be. That's not correct. As we will see in this perspective, in some cases, it would be better to make modifications that cause a step to be more harmful!

For example, let us suppose that the third step in a synthetic sequence is the easiest to modify. Perhaps there are many different solvents that would work reasonably well, or perhaps there are several different reagents that would achieve the same transformation. If we assume that the goal of the research is to minimize the harm of the entire process, in terms of harm per kg of product, then what is the best approach? Should we make the third step greener or is it more important to do something else like increase the yield, make the product mixture easier to separate, or increase selectivity?

This paper compares the effectiveness of “greening” a step (decreasing the harm caused by the step) versus other modifications that are less obviously related to harm, like improving the yield, in order to determine which is the best approach for the reduction of the total harm of the process per g of final product. We will mostly describe the application of this kind of analysis to multi-step chemical processes but the analysis can be equally well applied to life cycles or processes outside of the field of chemistry.

Of course, in any situation, optimizing everything, including yield, selectivity, purity, rate, and green-ness for every step would be ideal, but in practice that is not possible. Research time and research funds limit the amount of work that can be done. Some steps are more easily modified than others. Higher yields may come at the price of greater step harm. Because green chemists can't possibly do everything, we need to prioritize what we choose to work on. This discussion is a part of the concept of hotspot-driven research, wherein identification of the most harmful steps in a process guides the selection and prioritization of green chemistry projects.¹

Here we report environmental impact as “harm”. This could be global warming, ecotoxicity, or any of the other harms that can be quantified. Harms that cannot be quantified are still important and the concepts described herein still apply, but such harms don't readily lend themselves to the mathematical approach we take in this article. We will also discuss the effect of considering multiple impacts.

Before we begin, it is necessary to define several terms. Step yield is the % yield of an individual step. Step harm is the environmental harm of an individual step per g of that step's starting material. Total harm is the harm of the entire process per g of final product.

Direct and indirect hotspots

Lifecycle assessment (LCA) is a process in which the inputs and outputs of every stage in a product's life cycle are recorded in an inventory, and environmental harm is assigned based on the harmfulness and quantity of each input/output. Environmental harm is calculated for various impact categories such as global warming, toxicity, and eutrophication. LCA studies are conceptualized with a fixed boundary, or portion of a product's lifetime, and a set functional unit, which is the output or product of the process being studied. LCA is a powerful tool for quantifying harm, but isn't particularly easy to do. Fortunately, the quantity and quality of LCA studies related to chemical processes have increased over the past decade.

Published LCAs often include a contribution analysis, with harm displayed for each process step. This allows one to identify the steps responsible for the greatest portion of the process's harm. These most damaging steps are the hotspots of the process and, therefore, high priority steps to fix if the goal is to reduce the overall harm of the process. This is the basis of hotspot-driven research and the subject of our previous publication on the topic.¹

A process step may be a hotspot for one harm index but not another. For example, a step that uses a harmful organic solvent may be the hotspot for global warming potential and inhalation toxicity but contribute little to resource depletion. The opposite may be true for a step that uses a precious metal catalyst in the same hypothetical process, with that step being the hotspot for resource depletion.

For the rest of this paper, we will use the expression “direct hotspot” rather than simply “hotspot” to refer to this traditional meaning of a step that is more harmful than the others.

An indirect hotspot is a process step which, despite not being responsible for a great deal of harm, contains a flaw that requires a direct hotspot to be more harmful to compensate. This flaw could be poor yield, thus requiring that a previous direct hotspot step be conducted on a larger scale. Alternatively, the flaw of an indirect hotspot could be that it generates a product with poor purity, therefore requiring a subsequent purification or separation step. In either case, there are two highly effective options for reducing the harm of the overall process: (a) reduce the harm of the direct hotspot step by making it greener or (b) fix the flaw in the indirect hotspot. Deliberate consideration of which of these two solutions would produce a greater reduction in total process harm would help green chemistry researchers maximize the impact of limited research time and funding. On the other hand, some modifications to a synthesis are unlikely to significantly reduce the total harm. For example, making an indirect hotspot greener is unlikely to lead to significant benefit. Similarly, modifying steps that are neither direct nor indirect hotspots is also unlikely to result in significant reductions in environmental harm.

If we look only at the harm of a single step at a time, and never at the harm of the entire life cycle, then it seems obvious that every step must be made as green as possible. That shortsightedness or myopia leads to erroneous decision-making. A famous example of this is the popular concept of “Food Miles”, a metric that focuses entirely on the harm of a single step, the transportation of food products from the production location to the consumer, and not on the whole life cycle. That focus is misguided because transportation is rarely a hotspot for food products.² For example, consider the case of fresh tomatoes sold in the UK. Domestic tomatoes travel a very short distance from producer to consumer, while imported tomatoes must travel much further, roughly doubling the harm of the packaging and transportation step (Fig. 1).³ Focusing on only that step, one would conclude that the domestic tomatoes are greener. However, this is wrong. The packaging and transportation step makes only a tiny contribution to the overall harm. The direct hotspot is the cultivation step, which is worse for domestic tomatoes due to the use of heated greenhouses. Thus imported tomatoes are the greener choice, despite having a significantly worse packaging & transportation step.

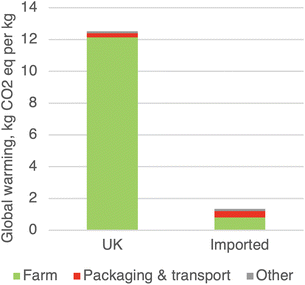Fig. 1 The contribution of life cycle steps to the total global warming contribution of fresh tomatoes consumed in the UK. The tomatoes are either grown in the UK (left column) or imported from the Netherlands and Spain (right column). Data from ref. 3.

Researchers who regularly perform LCA comparisons such as that shown in Fig. 1 would never express any concern about a single step becoming more harmful because the focus of any comparative LCA study is to reduce total harm, not step harm. However, green chemists rarely have the same perspective. We tend to see the harms or flaws of individual steps rather than totals. Thus in keeping with the concept of System Thinking,⁴ the analysis of direct and indirect hotspots can help us escape from the myopia of traditional approaches to greening chemical syntheses.

Prioritization of green chemistry research using hotspot analysis (direct or indirect) hasn't been practical until recently due to the scarcity of relevant LCAs. However, now that they are becoming much more common (Fig. 2), chemists have the opportunity to take advantage of this data to maximize the environmental benefit of our research.

Fig. 2 The number of publications listed in SciFinder that contain the terms “life cycle assessment” or “life cycle analysis” as of March 2025. Those in white also contained the terms “chemistry” or “synthesis”.

Discussion

Let us assume, for the purposes of this discussion, that we can only modify one step in a process, not all of them. We wish to know what kind of modification to that step would be best at reducing the total harm. For the improvement of one process step, let us consider two strategies. The first, which we will call the greening strategy (G strategy), is to make the step greener – to reduce the step's harm by a certain percentage. For argument's sake, we will assume that a 50% reduction in harm is possible and that the change has no effect on any other step. The second strategy, which we will call the better yield strategy (BY strategy), is to improve the step's yield. Again, for argument's sake, we will arbitrarily assume that the step's yield is changing from 60% to 90%, which is a 50% increase in product yield. What we wish to determine is whether the G or the BY strategy is the most effective at reducing the overall harm of the process per kg of product.

We will make the following simplifying assumptions for the initial discussion.

• All chemicals have the same MW so we don't have to correct for differing MWs.

• All reactions have 1 : 1 stoichiometry.

• The harm of any step includes the harm of making, using, and/or disposing of the reagents (except the starting material), byproducts, side products, solvents, and energy.

• The harm of generating the first starting material “A” is not included in the analysis. “A” could be a chemical feedstock, a farmer's field, or even a mineral deposit.

• The steps in the tables and figures are shown as if they are chemical synthesis steps, but they could instead be agricultural, mining, purification, or almost any other kind of process or life cycle steps. The same principles would apply.

These simplifying assumptions will allow us to illustrate the basic trends. Later in the paper we will describe a more complex model that does not require as many assumptions.

Sequences with one direct hotspot

In a linear sequence having a direct hotspot, the best strategy, if possible, is to modify that hotspot to reduce its step harm (the G strategy). For the hypothetical example shown in Table 1, the direct hotspot is step 2. A 50% reduction in the harm of that step reduces the total harm by 40%. In some cases, increasing the hotspot step yield (the BY strategy) may also be very effective.^5,6

Table 1 A linear sequence of steps with one direct hotspot

	Step 1	Step 2	Step 3	Step 4	Step 5
The rows entitled G and BY indicate the % reduction in total harm that would be achieved by applying the G or BY strategies to the indicated step and making no modifications to any of the other steps.
Hotspot	—	Direct	Indirect	Indirect	Indirect
% harm	5	80	5	5	5
G	2.5	40	2.5	2.5	2.5
BY	2	28	30	32	33

---

However, if researchers are considering making modifications to a step that causes little harm, then attempting to make that step greener would be of little benefit to the environment. For example, reducing the step harm of any one of the other steps in Table 1 only decreases the total harm by 2.5% (see the G row in Table 1).

Instead, if a step that causes little harm is going to be changed, then the priority should be on modifications that can indirectly reduce the step harm of the direct hotspot, and therefore the total harm of the entire process. Consider step 5. It is an indirect hotspot because, while it doesn't cause much harm by itself, modifications to the step can have an outsized influence on the total harm of the overall process. Improving the yield of this step from 60 to 90% causes the total harm of the entire process to drop by 33%. The low yield of this step is a flaw that, if rectified, would greatly reduce the overall harm of the process. Thus, the type of modification we need to make to this indirect hotspot is an improvement in its step yield, not its step harm. Thus one could say that step 5 is an indirect hotspot in terms of yield. Improving the yield of such a step is highly effective because it lowers the scale at which the direct hotspot must operate. That causes a significant reduction in overall harm.

All the steps after the direct hotspot in Table 1 are indirect hotspots because they have yields low enough that significant improvements are possible. Making any of them greener isn't particularly effective because they already don't cause much harm. Instead, improving the step yield is the best modification to make. In such a sequence of indirect hotspots, improving the yield of the lowest-yielding indirect hotspot should be the priority. If they all have equal yields (as in the example in Table 3), then indirect hotspots that occur later in the sequence should be prioritized.

The first step, in contrast, is not an indirect hotspot even though its yield is low. Improving its yield has little effect on the overall harm of the process because such an improvement does not modify the scale at which the direct hotspot must operate. In general, indirect hotspots in terms of yield occur after, not before, the direct hotspot.

Improving the yield of an indirect hotspot can be so effective that it's worthwhile even if the step ends up causing more harm. For example, if step 4 in Table 1 were to be modified so that the yield was improved to 90% at the cost of three times more step harm, the total harm still decreases by 25%. Thus, for an indirect hotspot, a modification that increases the step harm can be environmentally beneficial if that modification lowers the harm of the direct hotspot.

Indirect hotspots in terms of yield can be found in biomass conversion processes where the cultivation, transportation and initial processing of the biomass cause much more harm than the conversion of the processed biomass into organic products. The conversion steps, unless they're particularly harmful, are likely to be indirect hotspots. For example, consider the synthesis of 1,6-hexanediamine from starch (Scheme 1). Most of the global warming from this process is caused by the cultivation of the starch crop and the fermentation and drying to make high fructose corn syrup (steps 1 and 2). In comparison, the acid-catalyzed dehydration of the fructose to hydroxymethylfurfural (step 3) causes very little global warming. However, the yield of that dehydration step is crucial. It is an indirect hotspot. Increasing its step yield from 49 to 88% reduces the total harm by 33%.⁷

Scheme 1 The synthesis of 1,6-hexanediamine from starch.⁷

In a convergent synthesis (Table 2), one observes the same trends. Making individual steps greener is only effective for direct hotspots. All steps with low yield that occur after the direct hotspot are indirect hotspots. Any steps that occur before the direct hotspot, in a side branch causing little harm, or having high yields are not indirect hotspots.

Table 2 A convergent synthesis with one direct hotspot

	Step 1	Step 2	Step 3	Step 4	Step 5	Step 6
Hotspot	Direct	Indir.	—	—	Indir.	Indir.
% harm	70	6	6	6	6	6
G	35	3	3	3	3	3
BY	23	25	2	4	31	33

---

Low chemical yield isn't the only type of flaw that could cause an indirect hotspot to appear after a direct hotspot. Other flaws could include, for example, low physical yields, such as in subtractive manufacturing, meaning the use of techniques such as machining or blanking to remove excess material and create the desired part. Blanking is the use of a punch (like a cookie-cutter) to cut out a part from a larger sheet of metal or plastic. Because the manufacture of the raw sheet material is likely to be more harmful than the blanking process, the sheet material manufacture would be a direct hotspot and the blanking step would be an indirect hotspot. Any modification to the blanking step that would allow more product to be obtained from the same amount of metal or plastic would be better for the environment than any attempt to make the blanking step greener.

Sequences with very similar steps

In a linear sequence of identical steps (Table 3), the first step causes the most harm because it operates on the largest scale. It is therefore the direct hotspot. As shown in the table, reducing the harm of this individual step by 50% (the G strategy) would reduce the total harm by 22%. Greening any of the other individual steps would result in a smaller overall reduction in harm. Thus the G strategy is most effective for the first step and has decreasing effectiveness for later steps.

Table 3 A linear sequence of identical steps

	Step 1	Step 2	Step 3	Step 4	Step 5
Hotspot	Direct	Indirect	Indirect	Indirect	Indirect
% harm	43	26	16	9	6
G	22	13	8	5	3
BY	15	23	28	32	33

---

The BY strategy is the opposite. Improving the yield of the last step is the most effective because that reduces the scale at which all previous steps must be performed. The last step in this reaction sequence is an indirect hotspot because, while it doesn't cause much harm by itself, modifications to the step cause an outsized influence on the total harm of the overall process.

If we plan to embark upon research to decrease the harm of this multistep synthesis, the most effective thing to do would be to increase the yield of step 5. In contrast, the G strategy (making a particular step less harmful) would be less effective at reducing overall harm, even if it were applied to the direct hotspot.

A similar situation is observed in a sequence of steps having equal harm (Table 4). Here there are no direct hotspots because the steps cause exactly the same amount of harm. Once again, for any step other than the first, increasing the yield is more effective than making the step greener because a better yield means all prior steps can be performed at a smaller scale.

Table 4 A linear sequence of steps of equal harm

	Step 1	Step 2	Step 3	Step 4	Step 5
Hotspot	—	—	—	—	—
% harm	20	20	20	20	20
G	10	10	10	10	10
BY	7	13	20	27	33

---

Sequences with two direct hotspots

In a linear sequence having two equal direct hotspots (Table 5), greening either of them is equally effective. However, increasing the yield of the second direct hotspot is more effective than making it greener. That counterintuitive result happens because the second direct hotspot is an indirect hotspot relative to the first. The 5^th step in this sequence is an indirect hotspot relative to both of the direct hotspots. In a linear sequence with two direct hotspots, any low-yield step after both is a doubly indirect hotspot. Therefore improving its yield is very effective at lowering the overall harm.

Table 5 A linear sequence of steps with two direct hotspots

	Step 1	Step 2	Step 3	Step 4	Step 5
Hotspot	—	Direct	Indirect	Direct & indirect	Indirect
% harm	4	44	4	44	4
G	2	22	2	22	2
BY	1	16	17	32	33

---

If we consider two types of harm, such as global warming and ecotoxicity, then a synthetic sequence might have two direct hotspots that differ in the type of harm being caused. For example, in the sequence in Table 6, step 2 is a direct hotspot for global warming and step 4 is a direct hotspot for ecotoxicity. There is no step for which the G strategy is effective at reducing both global warming and ecotoxicity. Only the BY strategy is capable of doing that. Improving the yield of either step 4 or step 5 simultaneously lowers both the global warming and the ecotoxicity by a third.

Table 6 A linear sequence of steps with one direct hotspot for global warming (GW) and another for ecotoxicity (ET)

	Step 1	Step 2	Step 3	Step 4	Step 5
The first 4 rows in the table consider only global warming. The last 4 rows consider only ecotoxicity.
GW	—	Direct	Indirect	Indirect	Indirect
% harm	5	80	5	5	5
G	2.5	40	2.5	2.5	2.5
BY	2	28	30	32	33
ET	—	—	—	Direct	Indirect
% harm	5	5	5	80	5
G	2.5	2.5	2.5	40	2.5
BY	2	3	5	32	33

---

A general mathematical model helps prioritization

The above examples were calculated with quite restrictive assumptions. We can eliminate those assumptions by developing a generic mathematical model. Here we take a generic two-step reaction sequence (Scheme 2) and define the following variables:

 starting mass of A = a (in grams)

 stoichiometric coefficient of step 1 = b

 stoichiometric coefficient of step 2 = c

 molar masses of A, B, and C are M_A, M_B, and M_C

 yield of step 1 (before modification) = y_i

 yield of step 1 (after BY1 modification) = y_f

 yield of step 2 (before modification) = z_i

 yield of step 2 (after BY2 modification) = z_f

 harm of step 1 per g A (before modification) = m (g CO₂ eq. per g A)

 harm of step 1 per g A (after G1 modification) = xm (g CO₂ eq. per g A)

 harm of step 2 per g B (before modification) = n (g CO₂ eq. per g B)

 harm of step 2 per g B (after G2 modification) = xn (g CO₂ eq. per g B).

Scheme 2 A two-step reaction with variable amounts of harm and variable reaction stoichiometry.

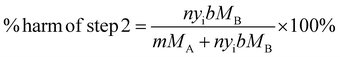Before any modifications are made, the % harm caused by steps 1 and 2 can be calculated from eqn (1) and (2).

Then we can calculate whether the G strategy or the BY strategy is more effective. For every possible modification, we calculate the % reduction in the total harm of the process per g of final product. The derivations of the equations are given in the ESI.†

There are four possible options here: we could green either step or improve the yield of either step.

G1 strategy. The harm of the 1^st step is reduced by a factor of x. For example, if x = 0.8 then the step harm changes from m to 0.8 m (i.e. it is reduced by 20%). The % reduction in the total harm of the process per g of final product is calculated using eqn (3).

BY1 strategy. The yield of the 1^st step is increased from y_i to y_f. The total harm reduction is calculated using eqn (4).

G2 strategy. The harm of the 2^nd step is reduced by a factor of x. The total harm reduction is calculated using eqn (5).

BY2 strategy. The yield of the 2^nd step is increased from z_i to z_f. The total harm reduction is calculated using eqn (6).

total harm reduction = 1 − z_i/z_f (6)

Which of these four strategies is the most effective depends strongly on how much of the harm comes from steps 1 or 2 before modification. If we plot the total harm reductions as a function of the % of harm from each step, then we can see which strategy is the most effective (Fig. 3). This graph, and the conclusions we draw from it, are independent of the values of M_A, M_B, M_C, a, b, and c. Here we assume that the yields of both steps are 60% but can, in the BY1 and BY2 strategies, be improved to 90%. We also assume that the step harms of steps 1 and 2 can be reduced by 50% in the G1 and G2 strategies, respectively.

Fig. 3 The % reduction in total harm for the synthesis in Scheme 2 that can be obtained by different strategies, as a function of the % harm that comes from step 2 before any modification is made. Here we assume that the G1 and G2 strategies reduce the harm of the corresponding step by 50%, while the BY1 and BY2 strategies increase the yield of either step 1 or step 2 by 50% (e.g. an initial yield of 60% changes to a yield of 90%). Thus y_f/y_i and z_f/z_i are 1.5 for BY1 and BY2, respectively. If changes to only step 1 are being contemplated, ignore the dashed lines. If changes to only step 2 are being contemplated, ignore the solid lines.

In the left side of the diagram (unshaded area), step 1 is the direct hotspot. It's clear from the diagram that greening the direct hotspot is the most effective strategy, followed by increasing the yield of the indirect hotspot (step 2). In the right side of the diagram, step 2 causes most of the harm and is therefore the direct hotspot. There, the best strategy is to green that step, and increasing its yield is the second best. Trying to improve step 1 in any way (G1 or BY1) would have little benefit if step 2 is the direct hotspot. In the middle of the diagram (shaded area), both steps cause roughly equal amounts of harm and therefore neither is a direct hotspot. Increasing the yield of step 2 is the best approach, while the other three strategies are nearly as good.

However, there may be situations in which a larger improvement in yield is possible. Instead of a change from 60% to 90%, what if it were a change from 40% to 90%? Increasing y_f/y_i above our default value of 1.5 causes the BY1 line to have a steeper slope (Fig. 4). Increasing z_f/z_i to a value of 2 or more moves the horizontal BY2 line upwards, so that BY2 becomes the most effective strategy regardless of which step causes the most harm.

Fig. 4 The % reduction in total harm per gram of product C that can be obtained for the reaction sequence in Scheme 2, where a large improvement in yield is possible. The assumptions are the same as those in Fig. 3 except that the BY1 and BY2 strategies increase the yield of either step 1 or step 2 by 125% (e.g. an initial yield of 40% changes to a yield of 90%). Thus y_f/y_i and z_f/z_i are 2.25 for BY1 and BY2, respectively.

In other situations, a modification of a process step may be able to achieve better than a 50% reduction in the harm of that step. For example, if we assume that a 75% reduction in step harm is possible (x = 0.25), but that only modest step yield improvements are possible in the BY1 and BY2 strategies (y_f/y_i and z_f/z_i are both 1.5) then the most effective strategy is to green whichever step causes the most harm (Fig. 5).

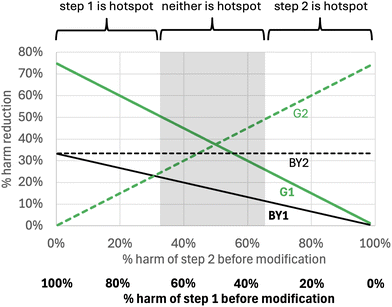Fig. 5 The % reduction in total harm that can be obtained for the reaction sequence in Scheme 2, where a large reduction in the harm of individual steps is possible. The assumptions are the same as those in Fig. 3 except that we assume the G strategy reduces the harm of an individual step by 75%.

The above discussion assumes that the BY1, BY2, G1, and G2 options are equally feasible. In practice, however, that is rarely the case. We may have good ideas about how to improve one step but not the other. In such a situation, is it better to modify the step by making it greener or by improving its yield? The answer depends on which is the hotspot.

If step 1 is the hotspot then step 2 is an indirect hotspot. This situation is represented in the left (unshaded) portions of Fig. 3–5. We can make two conclusions that seem to apply in most or all cases. First, if we are going to embark on research to improve step 1 (the solid lines in the diagrams) then we should prioritize making it greener. Improving the yield should be a secondary consideration unless very large increases in yield are possible (Fig. 4). Second, if we are to embark upon research to improve step 2 (the indirect hotspot, dashed lines in the figures), then we should prioritize improving its yield. Making it greener is not a priority.

If steps 1 and 2 cause roughly equal amounts of harm then neither step is a hotspot. This situation is represented by the centre (shaded) portion of Fig. 3–5. If we are going to embark on research to improve step 1 (the solid lines in the diagrams) then we should prioritize making it greener. Improving the yield should be a secondary consideration unless very large increases in yield are possible (Fig. 4). Second, if we are to embark on research to improve step 2 (the dashed lines), then we should prioritize improving its yield unless very large reductions in its environmental harm are feasible (Fig. 5).

If step 2 is the hotspot then step 1 is neither a direct nor an indirect hotspot. This situation is represented in the right (unshaded) portions of Fig. 3–5. If we are going to embark on research to improve step 1 (the solid lines) then little environmental benefit should be expected from our work. On the other hand, if we are to embark on research to improve step 2 (the dashed lines), then we should prioritize making it greener, unless large improvements in yield are possible (Fig. 4).

Indirect hotspots that appear before the direct hotspot

Not all indirect hotspots occur after direct hotspots; they may occur before if, for example, a flawed reaction step necessitates a very harmful purification or separation step. That purification would often but not always be the subsequent step. In such a sequence (e.g. Table 7), the flawed reaction step is the indirect hotspot and the purification step is the direct hotspot.

Table 7 A synthetic sequence in which the purification step (“purif”) is a direct hotspot

	Step 1	Step 2
Hotspot	Indirect	Direct
% harm	20	80
G	10	40
BY	7	33
Change 1 so purif is less harmful	40	—
Change 1 so purif is higher yielding	33	—
Change 1 so purif is unnecessary	88	—

---

It is well known that in chemical plants most of the financial cost comes from the separation and purification steps, not the reaction steps.⁸ The same is likely true for energy consumption and environmental harm. While technically purification and separation are somewhat different activities, we will consider them together as “purification” steps for the purposes of this discussion. LCA studies may lump each reaction step together with the subsequent purification step(s), but having them listed as separate steps gives greater clarity for identifying the best strategies for process optimization.

The example in Table 7 contains an indirect hotspot that appears before the direct hotspot. The direct hotspot is the purification step, because it causes the majority of the harm. The reaction step is an indirect hotspot; it causes little harm but modifications to it can greatly reduce the total harm. Modifications to the reaction step should be designed to facilitate the purification step or, if possible, make it unnecessary. Example modifications could include an increase in selectivity, a replacement of a stoichiometric reagent with a catalyst, or the use of a different solvent. Thus an indirect hotspot can appear before a direct hotspot when changes to the indirect hotspot decrease the need for a harmful subsequent purification step. This reaction step could be considered an indirect hotspot in terms of purity.

What would be the effect of modifying the reaction step in such a sequence? Decreasing its harm or raising its yield would make little difference to the total harm. It would be much better to change the reaction step so that the subsequent purification would become less harmful, higher yielding, or completely unnecessary. If changes to the reaction step make the purification step 50% less harmful or 50% higher yielding, then the overall harm is reduced by 33% or 40%, respectively. If the reaction step can be modified to make the purification step unnecessary, then the overall harm is reduced by 88%.

In general, if a flaw in an earlier step makes a later direct hotspot more harmful, or makes it necessary, then the earlier step is an indirect hotspot. Such a flaw could include poor selectivity, an unfortunate choice of solvent, or any other situation that necessitates a purification step. The flaw could be unrelated to chemistry, such as manufacturing very bulky products at a location far from the customers, so that transportation over long distances are required. Fixing the earlier step so that the later direct hotspot becomes less harmful or is rendered unnecessary is a very effective strategy.

In Table 8 we see an example sequence where a purification step (step 3) is not a direct hotspot but is an indirect hotspot in terms of yield. In fact, steps 2 and 3 are both indirect hotspots relative to step 1 (the direct hotspot) because improvements to the yield of either steps 2 or 3 would reduce the scale at which step 1 must operate, and thereby greatly lower the total harm. If we were to embark upon research to improve step 2, what would be the best strategy? Greening it by lowering its step harm by 50% would be ineffective because it isn't causing much harm. Raising the yield of step 2 would be much more effective because it's an indirect hotspot relative to step 1. However, a peculiar feature of this sequence is that step 2 has an indirect influence on the direct hotspot via step 3. For example, if we modify step 2 to facilitate the step 3 purification, and as a result step 3 becomes higher yielding, then the direct hotspot (step 1) can operate at a lower scale. Such an extended indirect influence may be less obvious but is likely commonplace.

Table 8 A synthetic sequence in which the purification step (“purif”) is an indirect hotspot in terms of yield

	Step 1	Step 2	Step 3
Hotspot	Direct	Indirect	Indirect
% harm	80	10	10
G	40	5	5
BY	27	30	33
Change 2 so purif is less harmful	—	5	—
Change 2 so purif is higher yielding	—	33	—
Change 2 so purif is unnecessary	—	46	—

---

Our last example (Table 9) is a sequence in which a purification step (step #2) is neither a direct nor an indirect hotspot. The preceding reaction step, step #1, could in theory be modified to make the purification step either less harmful or higher yielding, or even to make the purification step unnecessary, but the resulting reductions in environmental harm are small. Neither the reaction step #1 nor the purification step (#2) are direct or indirect hotspots.

Table 9 A synthetic sequence in which the purification step (“purif”) is neither an indirect nor a direct hotspot

	Step 1	Step 2	Step 3
Hotspot	—	—	Direct
% harm	10	10	80
G	5	5	40
BY	3	7	33
Change 1 so purif is less harmful	5	—	—
Change 1 so purif is higher yielding	7	—	—
Change 1 so purif is unnecessary	14	—	—

---

Alternatives to LCA-based hotspot identification

Even though LCAs are rapidly becoming more common (Fig. 2), there will still be many cases in which LCA data is unavailable and therefore hotspots (direct or indirect) can not be readily identified. In such cases, there are three alternative strategies that do not require an LCA-based identification of hotspots.

Alternative strategy #1. Improve steps that seem the easiest to improve. This strategy is essentially what many chemists have been doing up to now. Because most steps are not direct hotspots, the risk of this strategy is that most research time will be spent on improvements that have little benefit to the environment.

Alternative strategy #2. Use intuition or life cycle thinking⁹ to identify likely direct or indirect hotspots. This is better because the probability of identifying and fixing a hotspot is greater than with random selection, but it's difficult to say how much better.

Alternative strategy #3. Use the mass of waste to identify the waste-based direct and indirect hotspots. For example, one could calculate the amount of waste produced by each step in a synthesis. The step that makes the most waste is the mass-based direct hotspot. Note that E-factor and process mass intensity should not be used because they may mis-identify the mass-based direct hotspot. For example, step 5 in the process shown in Table 10 has the highest step PMI and step E-factor, but step 1 is the mass-based direct hotspot. In the absence of impact data, one could assume that the mass-based direct hotspot may also be the impact-based direct hotspot. This is risky because mass of waste is an inaccurate predictor of environmental impact; for example, a highly energy-consuming step might be an impact-based hotspot and yet produce very little waste. However, it's reasonable to assume that a mass-based direct hotspot has a better-than-random probability of being an impact-based hotspot. Therefore, this approach improves the likelihood of significant environmental benefit from research compared to alternative strategy #1 but would not be as accurate as an LCA-based approach.

Table 10 A five-step sequence with a waste-based direct hotspot and subsequent indirect hotspots

	Step 1	Step 2	Step 3	Step 4	Step 5
Note that the step with the largest E-factor or process mass intensity (PMI) is not necessarily the mass-based direct hotspot.
Hotspot	Direct	Indirect	Indirect	Indirect	Indirect
%waste	45	14	14	14	14
E factor	17	8	14	23	39
PMI	18	9	15	24	40

---

Conclusions

Careful identification of hotspots, both direct and indirect, can help green chemists prioritize R&D efforts to reduce the harm of a chemical process. One's first instinct may be make any modifiable step greener, but such efforts are unlikely to result in significant environmental benefits unless the researcher accidentally chooses to work on the direct hotspot. Deliberately identifying the probable direct hotspot, and modifying it to reduce its step harm is much more likely to significantly reduce total harm. However, there are many cases where fixing a flaw in an indirect hotspot may be just as beneficial, or even more beneficial, at reducing the harm of a process. Fixing the flaw in each indirect hotspot has an outsized effect on harm reduction. For example, indirect hotspots that are flawed in terms of yield always appear after the direct hotspot – improving the step yield is highly effective because the more harmful preceding direct hotspots may now be run on a smaller scale to deliver the same amount of product. On the other hand, an indirect hotspot in terms of purity always appears before the direct hotspot. Fixing the flaw in such an indirect hotspot means making modifications that would facilitate the direct hotspot purification/separation step, allowing that step to cause less harm, have a higher yield, or become entirely unnecessary.

Any reduction in the harm of a process is worthwhile, but consideration of hotspots helps maximize the effect of research efforts. The LCA data and mathematical models discussed illustrate that although making an indirect hotspot or non-hotspot greener does decrease the overall process harm, the benefit is relatively minor compared to making a direct hotspot greener or fixing a flaw in an indirect step. These solutions should, therefore, be prioritized.

Though LCA data may not be available for every synthesis, and most chemists lack the ability to make an LCA themselves, data quality and availability are improving, increasing the feasibility of designing research projects guided by hotspots. In cases where LCA data is unavailable, researchers can still use these concepts by mapping out the entire cradle-to-gate life cycle, from mining or agriculture to the final product. A synthesis tree is a suitable format for such a map.^9,10 Then steps that are likely to be direct hotspot can be tentatively identified for various impacts. For example, agricultural cultivation steps are often hotspots for land use, water consumption, and eutrophication. Steps requiring very high temperatures, distillations, or water removal are likely to be hotspots for global warming.

If the goal of any research is the reduction of environmental impact resulting from chemical processes, careful consideration of the direct and indirect hotspots within a process, as well as a holistic view of the potential solutions, should help to maximize the potential environmental benefits from the research efforts.

Author contributions

PJ: conceptualization, methodology, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition; AM: investigation, writing – original draft, writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge valuable advice from Prof. Dr Niklas von der Aßen (RWTH Aachen) and funding from the Natural Sciences and Engineering Research Council of Canada (NSERC, grant RGPIN-2023-05700) and the Canada Research Chairs Program.

References

1. P. G. Jessop and A. R. MacDonald, Green Chem., 2023, 25, 9457–9462.
2. C. L. Weber and H. S. Matthews, Environ. Sci. Technol., 2008, 42, 3508–3513.
3. A. Frankowska, H. K. Jeswani and A. Azapagic, Sci. Total Environ., 2019, 682, 80–105.
4. J. E. Hutchinson, J. Chem. Educ., 2019, 96, 2777–2783.
5. S. Kressirer, D. Kralisch, A. Stark, U. Krtschil and V. Hessel, Environ. Sci. Technol., 2013, 47, 5362–5371.
6. V. Larnaudie, M. Bule, K.-Y. San, P. V. Vadlani, J. Mosby, S. Elangovan, M. Karanjikar and S. Spatari, Fuel, 2020, 279, 118429.
7. A. B. Dros, O. Larue, A. Reimond, F. D. Campo and M. Pera-Titus, Green Chem., 2015, 17, 4760–4772.
8. J.-G. Concepcion and D. J. C. Constable, Green Chemistry and Engineering: A Practical Design Approach, Wiley, Hoboken, NJ, USA, 2011.
9. P. Jessop, Green Chem., 2020, 22, 13–15.
10. P. G. Jessop, Green Chem., 2011, 13, 1391–1398.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5gc01085c

---