Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Automated descriptors for high-throughput screening of peptide self-assembly†
Raj Kumar
Rajaram Baskaran
 ,
Alexander
van Teijlingen
,
Alexander
van Teijlingen
 and
Tell
Tuttle
and
Tell
Tuttle
 *
*
Pure and Applied Chemistry, University of Strathclyde, 295 Cathedral Street, Glasgow, G1 1XL, UK. E-mail: tell.tuttle@strath.ac.uk
First published on 28th January 2025
Abstract
We present five automated descriptors: Aggregate Detection Index (ADI); Sheet Formation Index (SFI); Vesicle Formation Index (VFI); Tube Formation Index (TFI); and Fibre Formation Index (FFI), that have been designed for analysing peptide self-assembly in molecular dynamics simulations. These descriptors, implemented as Python modules, enhance analytical precision and enable the development of screening methods tailored to specific structural targets rather than general aggregation. Initially tested on the FF dipeptide, the descriptors were validated using a comprehensive dipeptide dataset. This approach facilitates the identification of promising self-assembling moieties with nanoscale properties directly linked to macroscale functions, such as hydrogel formation.
1 Introduction
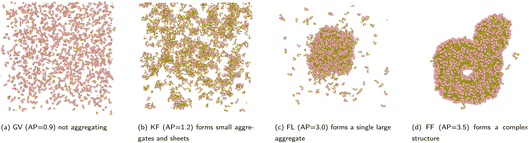
Peptide self-assembly refers to the spontaneous organisation of short amino acid sequences1 into ordered nanostructures2 through non-covalent interactions such as hydrogen bonding, π–π stacking, and hydrophobic effects.3 This behaviour underlies the design and development of innovative biomaterials for drug delivery, tissue engineering, and nanotechnology.The resulting architectures vary in size and dimensionality. At the nanoscale, the formation of three-dimensional micelles and vesicles (Fig. 1b) enables targeted encapsulation and transport of therapeutic molecules.4 These assemblies provide essential platforms for building more complex structures, laying the groundwork for advanced biomaterials with tunable functionalities.
As the size scale increases, one-dimensional fibres (Fig. 1c) and tubes (Fig. 1d) emerge, offering robust scaffolds suitable for cell growth and tissue engineering. Planar two-dimensional aggregates such as sheets (Fig. 1a) and bilayers provide large surface areas that support cell attachment and proliferation. A thorough understanding and classification of these structures facilitates rational design strategies that link molecular properties to specific architectural outcomes.
Expanding into applied settings, peptide nanostructures have been incorporated into nanowires, nanotubes, and other constructs of interest in sensor technology and biocompatible electronics.5,6 In biomedical contexts, peptide hydrogels serve as controlled drug release platforms, where adjustable mechanical and degradation properties enhance therapeutic efficacy. Continued research in this direction contributes to refining predictive models and experimental designs that meet clinical and technological demands.7
Increased emphasis on automation and computational methods offers a pathway to more efficient materials discovery. By integrating structural descriptors with high-throughput screening, large sets of peptide candidates can be rapidly evaluated, accelerating the identification of promising sequences for diverse applications. The development of automated descriptors of structure within simulations further enhances this process by enabling these descriptors to serve as target properties in machine learning or screening methods. This approach not only strengthens the connection between molecular design and biomaterial performance but also expands the sequence space available for exploration, unlocking new possibilities in the discovery and design of functional peptides. Ultimately, access to automated classification models shortens development cycles and drives innovation in biomaterials research.
Current descriptors often underestimate the inherent complexity of peptide self-assembly. Static metrics overlook the dynamic interplay of non-covalent interactions and fail to represent mesoscale phenomena, aggregation kinetics, and environmental factors such as solvents, pH, and temperature.8,9 Addressing these limitations requires a more comprehensive framework that links molecular-level events to emerging architectures.
The Aggregation Propensity (AP) score,10 based on shifts in Solvent Accessible Surface Area (SASA),11 serves as a useful starting point. However, AP focuses predominantly on early events and solvent interactions while neglecting the morphological intricacies of the aggregates (Fig. 2). The resulting shapes and configurations that directly impact the final properties of the material remain unspecified. This gap underscores the need for refined descriptors that highlight structural features critical to guiding subsequent design strategies.
Although complete exploration of the dipeptide and tripeptide space has been achieved, the challenge grows as the sequences lengthen and functionalities diversify.10,12 Traditional brute-force scanning is no longer feasible, prompting the integration of machine learning methods that efficiently pinpoint promising sequences from vast combinatorial landscapes.13,14 The ability to train algorithms using meaningful structural descriptors expands the search horizon and streamlines the discovery of peptides tailored for advanced hydrogel formation and beyond.
This work introduces five computational descriptors that capture essential features of peptide self-assembly, guiding the analysis beyond initial aggregation trends and toward the full landscape of resulting morphologies.15 Each metric is designed for efficiency and consistency, enabling comparisons across diverse peptide systems and simulation conditions without relying on manual inspection.
The descriptors offer standardised, quantitative measurements that unify data evaluation procedures, improving reproducibility and interpretability across research efforts. Moreover, we envision that these descriptors will be critical features in downstream machine learning approaches aimed at sequence discovery, structural optimisation, and the targeted synthesis of next-generation peptide-based biomaterials.
2 Results and discussion
2.1 Simulation setup
This study used coarse-grained molecular dynamics (CGMD) simulations employing the MARTINI 2.1 force field16,17 to investigate the self-assembly behaviour of dipeptides. The MARTINI force field's simplified representation of biomolecules, grouping atoms into larger beads, enables efficient simulations of larger systems over extended timescales, making it particularly suitable for studying the self-assembly of large numbers of peptide in order to investigate their higher-order structure formation.All simulations were conducted using the GROMACS 2020.7 simulation package18 on a high-performance computing cluster. Each simulation was initialised within a cubic box measuring 21.5 nm × 21.5 nm × 21.5 nm, containing 1200 randomly distributed dipeptide molecules explicitly solvated with MARTINI coarse-grained water. The systems underwent energy minimisation using the steepest descent algorithm, followed by a 1 ns equilibration under constant volume and temperature (NVT) conditions and an additional 1 ns equilibration under constant pressure and temperature (NPT) conditions. All CGMD simulations were carried out with a time step of 25 fs, employing periodic boundary conditions in all directions.
Temperature was maintained at 303 K using the velocity-rescale thermostat19 with a coupling constant of 1.0 ps. The pressure was coupled isotropically at 1 bar using the Berendsen barostat20 with a coupling constant of 12 ps. Checkpointing was performed every 5000 steps to ensure computational efficiency and data integrity. All simulation parameters adhered to standard MARTINI protocol guidelines.16,17
Initially, we conducted simulations of all 400 dipeptide systems for 6 million steps with a time step of 25 fs, resulting in a total simulation time of 150 ns. The MARTINI coarse-grained model accelerates dynamics by a factor of 4 compared to atomistic simulations. Therefore, our formal simulation time of 150 ns corresponds to an effective time of 600 ns. All times reported in this paper refer to this effective timescale. Among the 400 dipeptides in the sequence space, 29 fell within the mid AP range (1.1–1.9, Table 1) and 30 within the high AP range (2–3.7, Table 2). We then selected these 59 dipeptides for further analysis, running simulations for 60 million steps (1.5 μs), corresponding to an equivalent duration of 6.5 μs.
| AP score | Dipeptides |
|---|---|
| 1.1 | FC, FD, FH, HF, HS, HT, HW, KD, RD, RF, SY, WH, WK, WR, YC |
| 1.2 | KF, RW, SH, YS |
| 1.3 | KW |
| 1.6 | MW, WM, WY |
| 1.7 | YW |
| 1.9 | FM, MF, PW, WL, YF |
| AP score | Dipeptides |
|---|---|
| 2.0 | WP |
| 2.1 | FP, LW, PF |
| 2.2 | CW, FT, FY, TF |
| 2.3 | VW |
| 2.4 | CF, SF, TW, VF, WC, WV |
| 2.5 | FS, FV, WT |
| 2.6 | IW, WI |
| 2.7 | LF |
| 2.9 | FI, WS |
| 3.0 | FL |
| 3.1 | IF, SW |
| 3.2 | WW |
| 3.3 | WF |
| 3.5 | FF |
| 3.7 | FW |
2.2 Implementation of shape descriptors
The FF dipeptide system was selected for validating the descriptors due to its extensively documented capacity to self-assemble into a variety of nanostructures, as illustrated in Fig. 1.21 The five descriptors are implemented as Python modules within a Conda environment. Scientific libraries such as MDAnalysis22 were utilised for loading trajectories, while libraries such as scikit-learn,23 SciPy,24 NumPy,25 and Pandas26 were used for mathematical calculations. Visualisation modules such as Matplotlib27 and Seaborn28 were used for generating plots. Through rigorous geometric, topological, and density-based analyses, these descriptors were designed to capture a broad range of molecular assemblies, including aggregates, sheets, vesicles, tubes, and fibres.Each descriptor provides distinct insights into the self-assembly process of FF dipeptides. The initial stages are characterised by significant reorganization, with various shapes forming and dissociating dynamically. To highlight this behaviour, the plots include a marked transient region. Together, these descriptors comprehensively classify and quantify the diverse morphologies observed in FF dipeptide self-assembly.
The RDF g(r) is calculated as:
 | (1) |
The adaptive cutoff distance dcutoff is determined by finding the first minimum in the RDF g(r) after the first peak:
| dcutoff = min{r∣g(r) = min(g(r)) for r > rpeak} | (2) |
The ADI workflow begins with preprocessing the simulation trajectory to account for periodic boundary conditions and ensure accurate spatial relationships. This involves unwrapping and centring the peptide beads within the simulation box to enable precise and reliable shape calculations. The RDF between peptide beads is computed over a specified distance range, providing a detailed profile of inter-peptide distances. The adaptive cutoff distance obtained from the RDF is then utilised to construct an adjacency matrix, indicating contacts between peptides when their separation is below the cutoff.
The adjacency matrix A is constructed as follows:
 | (3) |
Graph theory is applied to identify and characterize aggregates within the peptide system. Peptides are represented as nodes and their interactions as edges in a graph. Connected components are efficiently detected using algorithms from the NetworkX library.30 This graph-based approach allows for the flexible identification of clusters of varying sizes and complexities, accommodating dynamic changes in the system's topology over time. Consequently, ADI enables the detection of both small oligomers and larger aggregates, providing a comprehensive overview of the aggregation landscape.
The size of each aggregate is determined by the number of nodes in each connected component. To analyse the persistence of aggregates, we define a contact persistence criterion. A contact between two peptides is considered persistent if it exists for at least 5 frames (Pmin = 5). The persistence of an aggregate is then calculated as the fraction of frames in which the aggregate exists.
Fig. 3 provides a comprehensive visualization of ADI results, highlighting the dynamic evolution of self-assembly patterns in the FF dipeptide system. Over the time course of the simulation, smaller aggregates consolidate into larger aggregates as evidenced by the increase in the average number of dipeptides per aggregate and concomitant decrease in the number of aggregates identified.
For planar sheets, the SFI leverages the Radial Distribution Function (RDF) to analyze the spatial distribution of peptide beads. By examining the RDF, the SFI determines characteristic peaks corresponding to the regular spacing of peptides in a flat sheet conformation. This method allows for the accurate detection of planar sheets by identifying regions where the RDF indicates a consistent and repeating pattern of inter-peptide distances, which are indicative of stable, flat sheet structures.
To identify curved sheets, the SFI employs quadratic fitting techniques. This approach involves fitting a quadratic surface to the spatial coordinates of peptide beads, thereby capturing the inherent curvature of non-planar aggregates. The quadratic fit quantifies the degree of curvature, enabling the differentiation between flat and curved sheets. By assessing the root mean square deviation (RMSD) of peptide positions from the fitted quadratic surface, the SFI can effectively classify aggregates as either planar or curved, providing a nuanced understanding of the sheet morphologies present in the system.
The quadratic surface is fitted using the equation:
| z = ax2 + by2 + cxy + dx + ey + f | (4) |
The RMSD from the quadratic surface is calculated as:
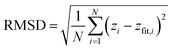 | (5) |
SFI also utilizes computational topology, specifically through the calculation of the Euler characteristic. The Euler characteristic serves as a topological invariant that quantifies the connectivity of a structure, allowing the SFI to distinguish between single-layer and multilayered sheet formations. By computing the Euler characteristic for each detected sheet structure, the SFI can assess the complexity of the aggregate, identifying whether a sheet is composed of a single layer of peptides or multiple interacting layers. This topological analysis complements the geometric assessments provided by the RDF and quadratic fitting, enhancing the robustness and accuracy of sheet detection.
The Euler characteristic χ is calculated as:
| χ = V − E + F | (6) |
The potential development, variation, and evolution of sheets on the nanoscale is a key feature in the FF dipeptide self-assembly pathway. A detailed visualization of the SFI results is provided in Fig. 4, illustrating the progression of planar and curved sheet structures in the FF dipeptide system. Initially, there is a high occurrence of smaller sheet structures, which are rapidly reorganized. This transient phase is highlighted in the plot.
VFI employs radial density profiling (RDP) to distinguish hollow vesicles from solid aggregates by analyzing the distribution of peptide beads relative to the aggregate's center of mass. A significant density gap detected by the RDP indicates the presence of a hollow core, characteristic of vesicles.
The radial density ρ(r) is calculated as:
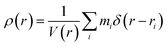 | (7) |
To further characterize vesicle morphology, VFI utilizes surface mesh generation to calculate surface area and volume, enabling the assessment of sphericity and the detection of structural deviations from ideal vesicle shapes.
The sphericity Ψ is calculated using the formula:
 | (8) |
Internal void analysis is performed using voxelization and flood-fill algorithms,31 which quantify the size and presence of internal cavities, thereby providing precise measures of vesicle integrity.
The hollowness ratio H is calculated as:
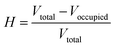 | (9) |
Additionally, asphericity and acylindricity derived from the gyration tensor of the aggregates are used to capture the geometric complexity of vesicles. These descriptors offer insights into the overall shape and symmetry, facilitating the differentiation between perfectly spherical vesicles and those exhibiting irregular or partially collapsed structures.
Asphericity Δ is defined as:
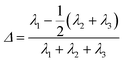 | (10) |
Acylindricity Ac is defined as:
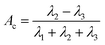 | (11) |
Following the development of sheet-like structures, FF continues to evolve and the sheets wrap up to form vesicle structures. This is highlighted in Fig. 5, which shows the VFI results. The initial transient region is shorter compared to sheets; however, vesicles dominate the later stages of the simulation, indicating their metastable state.
By utilizing moments of inertia,32 the FFI classifies the three-dimensional geometry of aggregates, determining properties such as elongation and linearity that are characteristic of fibre structures. This geometric classification enables the differentiation of elongated, linear assemblies from more compact or irregular aggregate forms.
The moments of inertia I are calculated using the inertia tensor I:
 | (12) |
The shape ratios are then calculated from the eigenvalues λ1, λ2, λ3 of the inertia tensor:
 | (13) |
 | (14) |
Orientation distribution analysis within the FFI framework provides insights into the alignment of peptides along the principal axis of the fibre. This analysis assesses the degree of internal ordering, which is essential for understanding the mechanical properties and stability of the fibres.
The orientation of each peptide is represented by a vector vi. The alignment of these vectors with the principal axis p is quantified using the cosine of the angle θi between vi and p:
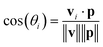 | (15) |
The mean and standard deviation of the angles θi are then calculated to assess the alignment.
Additionally, cross-sectional profiling examines the uniformity and consistency of the fibre's structure along its length, identifying variations that may indicate deviations from ideal fibre morphologies. By incorporating shape anisotropy metrics derived from the gyration tensor, the FFI also captures the geometric complexity and symmetry of fibre assemblies.
The cross-sectional area A at a position z along the fibre is calculated using the convex hull of the projected positions onto the plane perpendicular to the principal axis:
| A(z) = ConvexHull({ri·p = z}) | (16) |
Fig. 6 displays the FFI results, detailing the formation of elongated, linear assemblies and characterizing their structural progression in the FF dipeptide system. As expected, their occurrence is limited in the case of FF, which is well-known to form nanotubes.
TFI employs cylindrical harmonic analysis to transform peptide positions into cylindrical coordinates, facilitating the detection of both straight and curved tubular structures. This transformation allows for the accurate identification of the principal axis of the tube and the assessment of its geometric properties.
The cylindrical coordinates (r,θ,z) are calculated as:
 | (17) |
| θi = arctan2(yi,xi) | (18) |
| zi = zi | (19) |
To effectively capture variations in tube structure, TFI implements segment-based analysis. The segment-based analysis involves dividing the tube into segments of length L and performing cylindrical harmonic analysis on each segment. By dividing the tube into smaller segments, TFI can accommodate local irregularities and curvature, ensuring the detection of long, curved tubes and identifying deviations from ideal cylindrical shapes. This localized approach enhances the ability to recognize complex tube morphologies that may arise during peptide self-assembly.
TFI utilizes Radial Density Profiling (RDP) to verify the hollowness of detected tube structures. By calculating the distribution of peptide beads relative to the central axis of the tube, TFI identifies density gaps indicative of hollow cores, distinguishing vesicular tubes from solid cylindrical aggregates. This analysis provides critical insights into the internal geometry of the tubes, enabling the differentiation between various aggregate types.
TFI also incorporates shape anisotropy analysis using the gyration tensor to compute asphericity and acylindricity. These descriptors offer insights into the overall shape and symmetry, facilitating the differentiation between perfectly cylindrical tubes and those exhibiting irregular or partially collapsed structures.
Fig. 7 illustrates TFI results, showcasing the emergence of cylindrical structures in the FF dipeptide system. Initially, there is low confidence in the detection due to rapid reorganization and false positives caused by elongated vesicles; however, during the later stages, only one tube is observed, alternating with fibres and vesicles. While it is well known that FF forms tubes, the interplay between fibres, vesicles, and tubes observed in the latter stages of the simulation highlights the truly dynamic nature of the nanostructure. Compression of a tube at some stage can result in its reclassification as a fibre, while an expansion of a tube may lead to its reclassification as a vesicle. Similarly, in the final snapshots of the simulation (Fig. 2d) the wrapping of the tube-like structure into a doughnut shape can again result in the classification of the structure as a vesicle. These observations underscore the inherent relationship between these structures and the degree of subjectivity involved in their classification. However, while thresholds can be defined to ensure the average structure aligns with visual classifications or to report only a dominant structure, we have allowed structures to be classified under multiple shapes if they meet the criteria. This approach ensures we capture transient structures that may occur simultaneously along the assembly pathway, providing a more comprehensive understanding of the system's dynamics.
2.3 Assembly pathway
In addition to analysing the individual structural descriptors, it is possible to plot the individual shapes that occur along the self-assembly pathway. Fig. 8 illustrates the evolution of FF self-assembly over the simulation time, highlighting the dynamic reorganization of different structures before achieving stabilisation. This progression underscores the intricate self-assembly mechanisms that can lead to a variety of morphologies, such as aggregates, sheets, vesicles, and tubes.Following the successful validation using the FF dipeptide, we extended our analysis to include all 59 dipeptide candidates to evaluate their self-assembly behaviours. Among these candidates, several exhibited significant reordering dynamics. Fig. 9 displays the WI dipeptide, which achieved an AP score of 2.6. WI has an initial period of rapid reorganization, however, after 750 ns there is a clear stabilization of the system, with a dominant vesicle structure being formed.
Conversely, other candidates demonstrated early stabilization with minimal reorganization. Fig. 10 shows RF dipeptide with a lower AP score, reflecting its tendency to quickly reach a stable configuration without extensive structural changes. These contrasting behaviours highlight the diversity in self-assembly mechanisms among the candidates, providing valuable insights for selecting optimal dipeptides for specific nanostructure applications.
2.4 High-throughput screening
The descriptors developed are capable of tracking the evolution of nanostructures throughout the self-assembly pathway, providing invaluable insights into peptide self-assembly. The ultimate objective is to utilize these descriptors to predict the final self-assembled structure from a simulation, enabling the targeting of specific architectures as a design property. To this end, we have applied these descriptors to the mid- and high-AP score dipeptides identified during the initial screen. The final frames of each simulation were categorized into one of four shapes: sheet, vesicle, fibre, and tube, with a fifth classification of ‘undetermined’ if no clear shape could be evaluated.Table 3 presents the distribution output, illustrating the normalized occurrence of different shapes among the 59 candidates. This provides valuable insights into the prevalence of various structural formations and can aid in feature selection, enabling the identification of specific shapes as desirable targets for diverse applications.
| Shape distribution | Dipeptides |
|---|---|
| V(99%), S(1%) | IF, FI, FL, FY, FT, FW, SF, CW, PF, WT, WW, LW, FF, FS, VW, FV, WC, WF, WS, WI, WV, LF, TW, IW, FP, SW, WP, TF, YW, SH, MW, WL, WY, YS, SY |
| V(98%), S(2%) | VF, CF, HS, YF, PW |
| V(98%), T(2%), S(1%) | KF |
| V(97%), S(3%) | FM |
| S(100%) | MF |
| V(97%), T(3%), S(1%) | RF, FH |
| V(96%), T(3%), S(1%) | FD, RD |
| V(4%), T(3%), S(96%) | WM |
| V(95%), T(4%), S(1%) | HF, FC, KD, RW |
| V(94%), T(5%), S(1%) | HT, HW |
| V(93%), T(6%), S(1%) | KW, WH, WK |
| V(92%), T(8%) | WR |
| V(84%), T(16%), S(1%) | YC |
2.5 Limitations
The descriptor hyperparameters (such as the minimum tube size and RDF range) used in this study have been selected to reflect the force field, type of molecule and methods of simulations we are performing and may need to be changed in future studies where different, possibly all-atom, force fields are used. Parameters such as the minimum fibre length and asphericity threshold require careful calibration when applied to higher sequence spaces and larger systems. While the current framework is adaptable to larger peptides, empirical validation for these extended sequences remains to be conducted in future studies.Currently, the Python modules developed are utilising only a single CPU core, which hampers the processing of thousands of frames. Implementing parallel processing would substantially reduce analysis time. The calculation of RDF across all frames is time-consuming, with average RDF cutoff distances ranging from 6.2 Å to 6.6 Å. In smaller systems, a static cutoff of 4.5 Å is effective, reducing computational load without compromising accuracy.
3 Conclusions
This study successfully introduced and validated five automated descriptors for analyzing peptide self-assembly in molecular dynamics simulations. These descriptors demonstrated robust performance in characterizing diverse morphologies, including aggregates, sheets, vesicles, tubes, and fibers, and facilitated high-throughput screening of dipeptide systems. By addressing existing limitations in computational analysis, this approach advances the discovery of peptide-based biomaterials, offering a scalable and efficient framework for future applications in drug delivery, tissue engineering, and beyond.In addition, we have demonstrated the ability to apply these descriptors to follow the assembly pathway of nanostructures during extended MD simulations. This capability was showcased in the case of FF, where a variety of structures are formed throughout the assembly mechanism, as well as in rapidly forming structures like RF, which adhere to a single shape class. Furthermore, we have shown that these descriptors can not only track the entire assembly evolution but also quantify the amount of sheet, vesicle, fiber, and tube characteristics in the final snapshot of the simulation.
Our ultimate goal is to leverage these descriptors in machine learning methods to target specific molecular nanostructures, enabling the design of macroscale functional materials such as soft materials, gels, and emulsions. By characterizing and measuring the development of nanostructures, this work represents a significant step toward the development of an efficient machine learning search algorithm to discover novel peptide-based supramolecular gels.
Data availability
The code supporting this study is openly available on the Tuttlelab GitHub repository (https://github.com/Tuttlelab/Descriptors). The simulation datasets for the five selected dipeptide systems (FF, WI, RF, KF, and FL) are available via the PURE Portal (https://doi.org/10.15129/e4a8a70c-9e37-44ed-896e-55e7dd923b56).Author contributions
R. B. R. K. designed the descriptors and conducted the computational data analyses. A. V. T. provided assistance with the coding aspects and contributed conceptual ideas. T. T. conceptualized the research and oversaw the project. R. B. R. K., A. V. T., and T. T. collaboratively wrote the manuscript, with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Horizon Europe Marie Skłodowska-Curie Action (MSCA) MultiSMART (grant no. 101072585), with local funding of this international network being provided by EPSRC (grant no. EP/X029980/1). Results were obtained using the EPSRC-funded ARCHIE-WeSt High-Performance Computer (https://www.archie-west.ac.uk; EPSRC grant no. EP/K000586/1).References
- A. Aggeli, M. Bell, N. Boden, J. Keen, P. Knowles, T. McLeish, M. Pitkeathly and S. Radford, Nature, 1997, 386, 259–262 CrossRef CAS PubMed.
- S. Zhang, T. Holmes, C. Lockshin and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 3334–3338 CrossRef CAS PubMed.
- E. Gazit, FASEB J., 2002, 16, 77–83 CrossRef CAS PubMed.
- C. J. Edwards-Gayle and I. W. Hamley, Org. Biomol. Chem., 2017, 15, 5867–5876 RSC.
- S. Zhang, F. Gelain and X. Zhao, Semin. Cancer Biol., 2005, 15, 413–420 CrossRef PubMed.
- J. B. Matson and S. I. Stupp, Chem. Commun., 2012, 48, 26–33 RSC.
- M. Rivas, L. J. Del Valle, C. Alemán and J. Puiggalí, Gels, 2019, 5, 14 CrossRef CAS PubMed.
- C. A. Hauser, R. Deng, A. Mishra, Y. Loo, U. Khoe, F. Zhuang, D. W. Cheong, A. Accardo, M. B. Sullivan and C. Riekel, et al. , Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1361–1366 CrossRef CAS PubMed.
- A. M. Smith, R. J. Williams, C. Tang, P. Coppo, R. F. Collins, M. L. Turner, A. Saiani and R. V. Ulijn, Adv. Mater., 2008, 20, 37–41 CrossRef CAS.
- P. W. Frederix, R. V. Ulijn, N. T. Hunt and T. Tuttle, J. Phys. Chem. Lett., 2011, 2, 2380–2384 CrossRef CAS PubMed.
- B. Koshti, H. W. Swanson, B. Wilson, V. Kshtriya, S. Naskar, H. Narode, K. H. A. Lau, T. Tuttle and N. Gour, Phys. Chem. Chem. Phys., 2023, 25, 11522–11529 RSC.
- P. W. Frederix, G. G. Scott, Y. M. Abul-Haija, D. Kalafatovic, C. G. Pappas, N. Javid, N. T. Hunt, R. V. Ulijn and T. Tuttle, Nat. Chem., 2015, 7, 30–37 CrossRef CAS PubMed.
- A. van Teijlingen, M. C. Smith and T. Tuttle, Acc. Chem. Res., 2023, 56, 644–654 CrossRef CAS PubMed.
- A. van Teijlingen and T. Tuttle, J. Chem. Theory Comput., 2021, 17, 3221–3232 CrossRef CAS PubMed.
- T. Tuttle, Isr. J. Chem., 2015, 55, 724–734 CrossRef CAS.
- L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S.-J. Marrink, J. Chem. Theory Comput., 2008, 4, 819–834 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126(1), 014101 CrossRef PubMed.
- H. J. Berendsen, J. v. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- L. Adler-Abramovich and E. Gazit, Chem. Soc. Rev., 2014, 43, 6881–6893 RSC.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- F. Pedregosa, J. Mach. Learn. Res., 2011, 12, 2825 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser and J. Bright, et al. , Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- C. R. Harris, K. J. Millman, S. J. Van Der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg and N. J. Smith, et al. , Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- W. McKinney, Proc. 9th Python in Science Conf., 2010, pp. 56–61 Search PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- M. L. Waskom, J. Open Source Softw., 2021, 6, 3021 CrossRef.
- B. G. Levine, J. E. Stone and A. Kohlmeyer, J. Comput. Phys., 2011, 230, 3556–3569 CrossRef CAS PubMed.
- S. Anuyah, V. Bolade and O. Agbaakin, arXiv, 2024, preprint, arXiv:2411.09999, DOI:10.48550/arXiv.2411.09999.
- J. van der Zwet, A. Delissen and M. Langelaar, Adv. Eng. Softw., 2023, 186, 103530 CrossRef.
- V. A. Lubarda and Y. Liu, Arch. Appl. Mech., 2011, 81, 111–122 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Molecular dynamics simulations parameters and distribution of measured shapes across the self-assembling dipeptides. See DOI: https://doi.org/10.1039/d4fd00201f |
| This journal is © The Royal Society of Chemistry 2025 |