 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vibrationally excited molecule–metal surface reactions in heterogeneous and plasma catalysis: going beyond the Fridman–Macheret α model
Nick
Gerrits
 *a and
Annemie
Bogaerts
*a and
Annemie
Bogaerts
 bc
bc
aLeiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University, P.O. Box 9502, 2300 RA Leiden, The Netherlands. E-mail: n.gerrits@lic.leidenuniv.nl
bResearch Group PLASMANT, Department of Chemistry, University of Antwerp, Universiteitsplein 1, BE-2610, Wilrijk, Antwerp, Belgium
cElectrification Institute, University of Antwerp, Olieweg 97, 2020 Antwerp, Belgium
First published on 22nd April 2025
Abstract
Vibrational excitation of reactants plays an important role in heterogeneous and plasma catalysis by increasing the reactivity of various rate-controlling steps. Therefore, state-of-the-art microkinetic models attempt to include this effect by modelling the change in reaction rate with the Fridman–Macheret α approach. Although this approach is ubiquitous in simulations of plasma catalysis, it is not well established how accurate it is. In this work, we evaluate the Fridman–Macheret α approach by comparing it to vibrational efficacies obtained with molecular dynamics simulations. Unfortunately, the agreement is extremely poor (R2 = −0.35), raising questions about the suitability of using this method in describing vibrationally excited dissociative chemisorption on metal surfaces, as is currently the norm in plasma catalysis. Furthermore, the approach lacks vibrational mode specificity. Instead, we propose an alternative model at comparable computational cost, which is fitted to theoretical vibrational efficacies obtained with molecular dynamics. Our model uses (1) the barrier height to dissociative chemisorption, (2) an indication of how “late” the barrier is, and (3) the overlap of vibrational modes and the reaction coordinate at the barrier. These three features lead to a considerable qualitative and quantitative (R2 = 0.52) improvement over the Fridman–Macheret α approach. Therefore, we advise to make use of our new model, since it can be readily plugged into existing microkinetic models for heterogeneous and plasma catalysis.
Broader contextPlasma catalysis has the potential to convert (green) electricity into valuable chemical products with high efficiency. Unfortunately, for this technology to become mature, a considerable amount of research is still required. For example, the ionized plasma can induce many different changes in both the reactants and the catalyst. One such effect is the vibrational excitation of reactants, which boosts reactivity in heterogeneous and plasma catalysis by mainly affecting key rate-determining steps. To account for this, current microkinetic models often use the Fridman–Macheret α approach. While common in plasma catalysis simulations, its accuracy is unclear. In this study, we compare the Fridman–Macheret α method with vibrational efficacies from literature molecular dynamics simulations. The results show poor agreement, casting doubt on the method's suitability for describing vibrationally excited reactions on metal surfaces. We propose an alternative model that, at a similar computational cost but with considerable improvements, uses three physical fingerprints of the reaction: (1) the dissociative chemisorption barrier height, (2) the barrier's “lateness”, and (3) the overlap of vibrational modes with the reaction coordinate at the barrier. We recommend adopting this new model, as it can be easily used in existing microkinetic models for heterogeneous and plasma catalysis. |
1 Introduction: role of vibrational excitation in heterogeneous and plasma catalysis
Dissociative chemisorption (DC) is a chemical process where a reactant (typically a molecule) adsorbs on a surface (often metallic) and simultaneously breaks a bond in the reactant. This is an extremely important reaction in heterogeneous and plasma catalysis, since it is often the rate-controlling step. Therefore, fundamental understanding and predictions of the DC of molecules on metal surfaces is important in order to improve catalysis. For example, how energy is partitioned can affect how chemical reactions proceed. One such important aspect of energy partitioning in catalysis is the vibrational excitation of gaseous reactants, which has been shown to promote the DC of many different molecules on metal surfaces.1–8 This effect can especially be important in plasma catalysis, where vibrational excitation is ubiquitous.9–17 Likewise, if the rate-controlling step is highly activated and the chemical process is operated under high temperatures, it is likely that vibrational excitation is important in conventional thermal heterogeneous catalysis as well.Generally, when translational kinetic energy is not so effective in promoting reactivity, vibrational energy is considerably more effective at increasing reactivity than translational energy. This is especially the case for reactions classified as a late barrier system combined with a large barrier height, often referred to as Polanyi's rules.18 The reason is that, in such a case, the molecule requires a large amount of energy to overcome the barrier to DC. The minimum energy path (MEP) will then also typically exhibit a large amount of curvature, prior to reaching the transition state (TS). Thus, if the energy in the reactant originates primarily from the translational degrees of freedom (DOFs), it is difficult for the molecule to stick to the MEP and it will “go off the rails”. This deviation from the MEP results in even larger barrier heights that need to be overcome, which is typically referred to as the bobsled effect.19,20 An example of this is shown in Fig. 1 (blue line, right panel) for an atom reacting with a diatomic molecule, i.e., A + BC → AB + C. If instead a large portion of the energy comes from the vibration, it is easier to round the corner and the molecule will manage to remain closer to the MEP, resulting in lower accessible barrier heights (Fig. 1, orange line, right panel). Of course, for an early barrier system, the reverse holds true (Fig. 1, left panel): vibrational energy is not effective in promoting reactivity, because its motion is perpendicular to the reaction coordinate at the TS and parallel with the dividing surface that defines the barrier. In other words, the vibrational energy cannot be used to overcome the barrier. Translational energy, on the other hand, is now perpendicular to the barrier and thus more effective at promoting reactivity. Additionally, there is no “corner” in the MEP prior to the TS, ensuring that the bobsled effect does not affect the reactivity. For the DC of a diatomic molecule, Fig. 1 remains similar, but atom A and the bond length RAB are typically replaced by the surface and the distance between surface and molecule BC, respectively. Similar potential energy surface (PES) cuts can be made for polyatomic molecules in reduced dimensionality, by only varying the distance between the molecule and the surface as well as the dissociating bond length, while all other DOFs are either relaxed or fixed at their TS value.
2 Microkinetic models in plasma catalysis and the effect of vibrational excitation
Microkinetic models (MKMs) have been invaluable in understanding the reactivity of metal catalysts under realistic catalytic conditions. An MKM simulates a chemical process as a network of elementary reaction steps using rate equations. This way, the effect of catalytic conditions like concentration, temperature, and pressure on the entire chemical process can be investigated, but also the effect of changing the catalyst itself. Moreover, it can provide insights on the reaction pathways. Often, the Arrhenius equation is employed to obtain the rate coefficient k for an elementary reaction step: | (1) |
3 Evaluation of the Fridman–Macheret α model
As discussed above, it can be important to capture the effect of vibrational excitation in MKMs, which is typically approximated with the Fridman–Macheret (FM) α approach.27,28 This approach was originally designed for the gas phase reaction A + BC → AB + C depicted in Fig. 1 and tries to enforce Polanyi's rules, by assuming that the “lateness” of the barrier determines the effectiveness of vibrational energy relative to translational energy. Furthermore, it is assumed that the lateness of the barrier and the ratio between the forward and backward barrier heights are proportional. By computing this ratio, the so-called vibrational yield α is obtained:27 | (2) |
Subsequently, eqn (1) is modified to reduce the effective barrier height by the vibrational energy Eν as follows:28
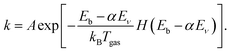 | (3) |
Mehta et al. were the first to apply the FM α approach to molecule–metal surface reactions, instead of gas phase reactions.28 By doing so, they predicted that plasma catalysis can break away from the traditional scaling relations present in thermal heterogeneous catalysis, which was also supported by experiments.14,28 This work fueled many subsequent theoretical studies that employed the FM α approach, providing valuable new insights into plasma catalysis.17 For example, Ma et al. were able to rationalize their experiments on the plasma-catalytic oxidation of N2 with such simulations.29 For the plasma-catalytic synthesis of ammonia, Engelmann et al. modelled both vibrational excitation and radical-induced Langmuir–Rideal reactions, where a gas phase reactant reacts directly with an adsorbate, i.e., without thermalization or adsorption prior to the reaction.30 (We note in passing that the Langmuir–Rideal reaction mechanism, also an important reaction process in plasma catalysis, is often erroneously referred to as the Eley–Rideal mechanism.31,32 However, Eley worked on a different mechanism, namely the reaction between a physisorbed and a chemisorbed adsorbate that are in thermal equilibrium with the surface.32,33) Their conclusion was that radical reactions were generally much more important than vibrational excitation. Similarly, for CO2 hydrogenation, Michiels et al. concluded that plasma-generated radicals and reaction intermediates were orders of magnitude more effective at increasing the turnover frequency than vibrational excitation.34 In contrast, for the non-oxidative coupling of methane, vibrational excitation was found to be considerably more competitive with other reaction channels, depending on the binding strength of the catalyst surface.35 Furthermore, the FM α approach allowed Engelmann et al. to make predictions for the optimal plasma conditions.35 Although the overall effect was again limited, Loenders et al. predicted that vibrational excitation could improve the selectivity of certain products in the partial oxidation of methane on Pt(111).36 In short, the FM α approach has enabled theoretical studies of vibrational excitation in plasma catalysis. It should also be noted that this approach has only been applied to vibrational excitation of gaseous reactants, and not to adsorbates. Vibrational excitation and subsequent reaction of adsorbates would involve very different reaction dynamics and likely require different models than those discussed in this work.37–39
It is clear that the Fm α approach is a computationally attractive model for plasma catalysis. Unfortunately, the model has several fundamental shortcomings, which we will discuss now. The determination of the vibrational yield α relies only on the ratio between the ground state forward and backward barrier heights. It is assumed that the position of the TS along the reaction coordinate is related to this ratio, but unfortunately there is no guarantee that this assumption is correct. Furthermore, there is no dependence on the actual vibrational mode other than the excitation energy Eν. Unfortunately, depending on the specific vibrational mode(s) being excited, vibrational excitation of polyatomic molecules often leads to very different reactivity. For example, for the DC of methane on several metal surfaces, excitation of the stretch modes is considerably more effective than the bend modes.1,40–44 Conversely, for CO2 + W(110), the bending mode has been found to be more effective.45 Moreover, the reaction of vibrationally excited methane can become more sterically hindered, since the excitation can be comparatively local, i.e., the four CH bonds are not necessarily energized in the same way.46 Similarly, overtone excitation leads to complex vibrational distributions, where the localization can occur in a more localized or delocalized manner, again affecting reactivity of the CH bonds differently.44 The effect of vibrational excitation is also dependent on the specific vibrational level, because overtones do not necessarily yield, at least quantitatively, the same effect.4 Additionally, since α ∈ [0,1], vibrational energy can never be more effective than translational energy. Yet, many instances have been discovered where vibrational energy is actually more effective.7 Again for methane, it is often observed that excitation of the stretch mode is more effective than increasing the translational energy.3–5,47,48 Likewise, for the excitation and dissociation of the CO bond in methanol on Cu(111), vibrational energy was found to be remarkably 3.4–5.3 times as effective as translational energy at promoting the reaction.49
Another issue with the Fm α approach is that it assumes that the effect of vibrational energy is independent of other DOFs. However, for HCl + Au(111), a large synergistic effect between vibrational and rotational excitation is observed (see Fig. 2).6 From the initial rovibrational state-selected reaction probability Rν,J(Ei), the so-called vibrational efficacy η (which measures how effective increasing the vibrational energy is at promoting the reaction relative to increasing Ei for the reactant in the state ν,J to obtain the reaction probability R) is determined as follows:
 | (4) |
 | ||
| Fig. 2 (a) Reaction probabilities for normally incident HCl on Au(111) and (b) the corresponding vibrational efficacies (η). Results for ν = 0, 1, and 2 are shown in grey, blue, and orange, respectively. The vibrational efficacy is computed relative to ν = 0 with the same rotational state Boltzmann distribution. The solid (dashed) lines indicate results for Trot = 0 K (506 K). This figure has been adapted from ref. 6 | ||
As discussed above, vibrational efficacies (η) can be extracted from molecular dynamics (MD) simulations with eqn (4). In Fig. 3(a) and Table 1, we compare the FM α model with the extracted efficacies η, as found in literature. If η is missing from literature, we compute it from published vibrational state-resolved reaction probabilities, by computing the range of energy shifts between the published continuous curves or discrete data points. The R2 value between the two is only −0.35 (see the black dashed line compared to the rectangles in Fig. 3(a)), signaling an extremely poor agreement. Overall, the FM α approach underestimates vibrational efficacies considerably. Even if α is reweighted through a linear regression, an R2 of only 0.39 is obtained (see red solid line). We expect that approaches that attempt a similar reweighting (as suggested by, e.g., Kunova et al.50) would achieve similar limited success. Furthermore, the FM α approach does not consider vibrational mode specificity. It is clear that the need for a way to include the effect of vibrational excitation on reaction rates is large, but that the workhorse FM α approach is unsuitable for, at least, DC. Therefore, we now turn to potential alternatives.
 | ||
| Fig. 3 Vibrational efficacies (η, rectangles) obtained from MD studies of the DC of various molecules on metal surfaces (see Table 1 for the data and their references). The black dashed lines are the efficacies as predicted by the FM α model (panel a) and our alternative approach (panel b), whereas the red solid lines are linear regression fits to the vibrational efficacies. The (color coded) R2 values are indicated in the figure. Panels c–e show the correlation between η and the three individual parts of our alternative approach (forward barrier height, ratio between dissociating bond lengths in the gas phase and TS, and SVP of the vibrational mode, respectively). In other words, the linear regression fits in panels c–e employ different weights compared to the fit to the full model in panel b. | ||
| Molecule (excitation) + metal surface | FM α | η | η fit | E forwardb | R ‡/Req | SVP |
|---|---|---|---|---|---|---|
| CHD3 (s. stretch) + Pt(111) | 0.523 | 0.3–0.857 | 0.91 | 78.73 | 1.433 | 0.4442 |
| CHD3 (s. stretch) + Ni(111) | 0.6158 | 0.9–1.357 | 1.19 | 97.948 | 1.4748 | 0.8454 |
| CH4 (s. stretch) + Ni(211) | 0.6059 | 0.8–1.059 | 0.96 | 80.659 | 1.5059 | 0.4052 |
| CHD3 (s. stretch) + Cu(111) | 0.7353 | 0.8–1.74 | 2.26 | 166.653 | 1.6453 | 0.9053,54 |
| H2 + Al(110) | 0.7060 | 1.060 | 1.58 | 105.960 | 1.8060 | 0.9051 |
| H2 + Cu(111) | 0.4661 | 0.762 | 0.70 | 60.663 | 1.3963 | 0.9051 |
| H2 + Pt(111) | 0.0064 | 0.0–0.265 | 0.00 | 0.064 | 1.0464 | 0.9051 |
| HCl + Au(111) | 0.6066 | 1.7–3.36 | 1.42 | 100.656 | 1.7156 | 0.94 |
| N2 + Ru(0001) | 0.3867 | 1.668 | 2.32 | 177.563 | 1.5863 | 0.94 |
| CH3OH (CO stretch) + Cu(111) | 0.7749 | 3.4–5.349 | 2.22 | 167.949 | 1.6049 | 0.7549 |
| CH3OH (OH stretch) + Cu(111) | 0.5449 | 1.6–2.749 | 2.17 | 148.649 | 1.7949 | 0.5149 |
| CH3OH (CH stretch) + Cu(111) | 0.5349 | 0.8–1.149 | 1.48 | 116.749 | 1.5449 | 0.8749 |
| CO2 (bend) + Ni(100) | 0.1669 | 0.2–0.469 | 0.27 | 23.269 | 1.5670 | 0.2870 |
| CO2 (as. stretch) + W(110) | 0.0845 | 0.1–0.345 | 0.06 | 12.545 | 1.0345 | 0.0245 |
| CO2 (s. stretch) + W(110) | 0.0845 | 0.1–0.445 | 0.06 | 12.545 | 1.0345 | 0.0345 |
| CO2 (bend) + W(110) | 0.0845 | 0.6–0.945 | 0.10 | 12.545 | 1.0345 | 0.3545 |
| H2O (stretch) + Cu(111) | 0.6071 | 1.3–1.972 | 1.57 | 117.672 | 1.6271 | 0.7071 |
| H2O (bend) + Cu(111) | 0.6071 | 1.0–1.372 | 1.11 | 117.672 | 1.6271 | 0.1071 |
| D2O (stretch) + Cu(111) | 0.6071 | 1.2–1.773 | 1.57 | 117.672 | 1.6271 | 0.7071 |
| D2O (bend) + Cu(111) | 0.6071 | 0.8–1.373 | 1.11 | 117.672 | 1.6271 | 0.1071 |
4 Our alternative approach
In principle, the most obvious way to compute accurate reaction rates is to perform vibrational state-specific MD simulations.7 These dynamical calculations do not require approximations to the reaction rate equation, because the obtained reaction probabilities can be directly converted into reaction rates.74 However, such simulations are not trivial to perform, nor are they typically computationally tractable (even with machine learning), especially for a complete reaction network. As such, for now, more approximate methods are required to improve the predictions made by MKMs.In this work, we propose to use a combination of (1) the forward barrier height (Eforwardb), (2) the ratio of the dissociating bond length between the TS and the reactant (R‡/Rgas), and (3) the sudden vector projection (SVP) approach, to obtain vibrational state-specific efficacies for use in MKMs. These three “features” can be determined with comparatively standard density functional theory (DFT) calculations (similar as used in determining the FM α), which we will discuss in detail further below. This combination has been fitted to the average vibrational efficacies η reported in Table 1 as follows:
| ηfit = a1Eforwardb(R‡/Req)erf(a2(SVP + a3)), | (5) |
4.1 Explanation of the individual features of our new model
We examine the three individual features of eqn (5) in Fig. 3(c)–(e), by fitting a linear regression to the individual features Eforwardb, (R‡/Req), and a2erf(SVP + a3), i.e., the linear regression fits deviate from the fit in Fig. 3(b) (red line). The fitted slope a and intercept b of the linear regression fits are a = 0.012335 mol kJ−1 and b = 0.0647 (panel c), a = 2.109 and b = −1.929 (panel d), and a = 2.423 and b = −1.023 (panel e), compared to a = 0.914716 mol kJ−1 and b = 0.140 in panel b. The first feature of our model is the forward barrier height Eforwardb. It should be noted that this barrier height is also employed in the FM α approach, but only to approximate the “lateness” of the TS. However, in Fig. 3(c), we can observe that the vibrational efficacy correlates considerably more with the absolute forward barrier height (R2 = 0.50) than the ratio between the forward and backward barrier heights as employed in the FM α model (R2 = −0.35). In general, the larger Eforwardb is, the larger η is. Moreover, the second feature employs geometric details of the reactant and the TS, by computing the ratio of the dissociating bond length between the reactant and the TS (i.e., R‡/Req) to estimate the lateness of the barrier. This seems much more effective (R2 = 0.30, Fig. 3(d)) than employing the ratio between the forward and backward barrier heights.The final feature we include in our model is aimed at incorporating vibrational mode specificity. The SVP model75 might be a good starting point for obtaining reasonable predictions on vibrational mode specific excitation at a limited computational cost. In this model, the overlap between the gas phase reactant's vibrational modes and the direction of the reaction coordinate at the TS (i.e., the imaginary mode) are computed, with the requirement that the reaction occurs rapidly and without equilibration. For DC, this requirement is often fulfilled, although exceptions are known. For example, the DC of ammonia on Ru(0001) is rapid and direct (i.e., not trapping mediated), but it proceeds through a precursor state before it reaches the TS. It is suspected that this precursor state scrambles the vibrational energy, which leads to vibrational efficacies always being unity.76,77 Thus, we have excluded such reactions from the data our model is fitted to, focusing on direct, rapid DC without precursor states. In the SVP approach, vibrational modes that yield a small overlap with the reaction coordinate are expected to contribute little to the reactivity, as has indeed been observed in MD simulations (see, e.g., Table 1). Opposite to the FM α model, this allows for vibrational mode-specific predictions. Moreover, the SVP model has an explicit dependence on the shape of the PES at the TS, which is also lacking in the FM α model. Even though the correlation between the vibrational efficacies and erf(a2(SVP + a3)) is still very poor (R2 = 0.14, see Fig. 3(e)), it does seem to provide improvement over the FM α approach (R2 = −0.35) when combined with Eforwardb and R‡/Req (R2 = 0.52). Without reweighting or refitting, the SVP approach yields values in the interval [0,1], because it is a dot product between the unit vectors of two vibrational modes. However, as can be seen in Fig. 3(e) and Table 1, an SVP value close to zero should not necessarily yield a low vibrational efficacy. For example, even though the SVP value for the bending modes of water on Cu(111) is low (0.10), the vibrational efficacy is large (0.8–1.3). Overall, we find that a shifted sigmoidal function (like the error function erf(a2(SVP + a3)) employed here), combined with the other two features, yields a qualitative improvement compared to a linear relationship, without worsening the overall quantitative agreement. Another benefit is that in many cases the computational cost of the SVP approach is negligible, because the necessary vibrational eigenvectors are often already computed to obtain thermodynamic corrections for the reaction network, or at least to confirm whether the TS is a first-order saddle point. Also, since there is a reliance on the computed vibrational eigenvectors, isotopologues can be distinguished as well.
4.2 Limitations of our model and outlook
Currently, our model still considerably underestimates the reactivity of HCl + Au(111) and CH3OH (CO) + Cu(111) (see Fig. 3 and Table 1). For the former reaction, it is well understood that dynamical effects along the reaction coordinate, prior to the TS, are the cause of the comparatively large vibrational efficacy.6 Specifically, the molecule needs to undergo rapid angular reorientation, or it will hit a repulsive wall and scatter back into the gas phase. Both vibrational and rotational motion aid in this reorientation, but in a complex manner that is not captured by the TS and concomitantly our model. For CH3OH + Cu(111), we suspect that the stereodynamics prior to the TS of breaking the CO bond are also heavily constrained.5,49 Therefore, future models might be improved by somehow including the curvature along and perpendicular to the MEP. If the curvature is decomposed into the relevant energetic DOFs and projected onto the corresponding reactant's inertia, it is likely that this model would retain its vibrational mode specificity and describe dynamical effects better. Subsequently, the model might be able to better distinguish between high and extremely high vibrational efficacies. For example, ηfit for CHD3 + Cu(111) and N2 + Ru(0001) (i.e., examples of high vibrational efficacy, see Table 1) is likely to decrease and improve the agreement with MD, because for these systems such dynamical curvature effects are considerably less severe. Possibly, this approach would enable prediction of rotational efficacies as well, allowing for rovibrational state distribution dependent MKMs. We note that similar approaches have been successfully employed in reaction path Hamiltonian simulations of molecule–metal surface reactions, where a harmonic approximation to the expansion of the DOFs along the 1D reaction coordinate is employed.78,79Furthermore, MD studies are often still limited in their accuracy, therefore also limiting the accuracy of our model compared to experiments.7 For example, if the charge transfer at the TS is large, the self-interaction error in DFT is also large.80 Unfortunately, the workhorse generalized gradient approximation density functionals employed in plasma catalysis are expected to underestimate the barrier height if the charge transfer is large.81 Similarly, the employed dynamical approach can sometimes cause issues with zero-point energy conservation and artificial intramolecular vibrational energy redistribution, again affecting the computed reaction probabilities.82 Still, the MD simulations tend to yield qualitatively and semi-quantitatively correct results, in reasonable agreement with experiments. As such, future methodological developments in simulations of DC and concomitant improvement of the data should lead to an improvement of our model as well.
Finally, gas phase reactions occurring in, e.g., plasma, atmospheric and astrochemistry often exhibit similar dynamical behaviour as DC in heterogeneous and plasma catalysis.83 Therefore, we suspect that if our model is refitted for gas phase reactions, it might be also suitable for MKMs that describe gas phase reactivity.
5 Conclusions: modelling of vibrational excitation in heterogeneous and plasma catalysis
In short, simulations and understanding of DC of (ro)vibrationally excited reactants in heterogeneous and plasma catalysis are of fundamental and practical importance. The FM α approach is the current workhorse method for simulating the effect of vibrational excitation in MKMs. In this work, we have compared literature values of vibrational efficacies η, which describe the change in reactivity due to vibrational excitation, obtained by MD simulations, with the FM α approach. Since the agreement is extremely poor (R2 = −0.35), we conclude that this approach is unsuitable for DC. Fortunately, we are able to provide an alternative model that is based on a few physical fingerprints of the reaction: (1) the forward barrier height, (2) the “lateness” of the TS (akin to Polanyi's rules18), and (3) the overlap of the excited vibrational mode with the reaction coordinate at the TS using the SVP approach.84 This model yields considerably improved agreement with MD (R2 = 0.52). Furthermore, opposite to the FM α approach, our model is suitable for polyatomic molecules, because it is vibrational mode specific. Considering the similar computational costs of the two approaches, in addition to the qualitative and quantitative improvements, we advice to use our proposed model (ηfit) in MKMs instead of the FM α approach.Unfortunately, the required data to further improve our model for ηfit is not publicly available and requires considerable work, perhaps in addition to performing more MD studies and improvement of the underlying simulation techniques. The lack of data also precludes application of other (machine learning) data sciences. Nevertheless, our simple model is physically motivated and can be used with comparative ease. Moreover, our proposed future improvements might lead to accurate, computationally cheap reaction rates for a diverse set of reaction steps, which are dependent on both the rotational and vibrational state. This should lead to next-generation MKMs in (plasma) catalysis, which are not only quantitatively more accurate, but can hopefully also lead to new insights. Fitting our model to gas phase data might make it suitable for, e.g., plasma, atmospheric and astrochemistry as well.
Data availability
All data and their source (see, e.g., Table 1) is present in the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Ivan Tsonev for the useful discussion. AB is financially supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 810182 – SCOPE ERC Synergy project).References
- R. Bisson, M. Sacchi and R. D. Beck, Mode-Specific Reactivity of CH4 on Pt(110)-(1 × 2): The Concerted Role of Stretch and Bend Excitation, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 121404 CrossRef.
- P. M. Hundt, B. Jiang, M. E. van Reijzen, H. Guo and R. D. Beck, Vibrationally Promoted Dissociation of Water on Ni(111), Science, 2014, 344, 504–507 CrossRef CAS PubMed.
- D. Migliorini, H. Chadwick, F. Nattino, A. Gutiérrez-González, E. Dombrowski, E. A. High, H. Guo, A. L. Utz, B. Jackson and R. D. Beck, et al., Surface Reaction Barriometry: Methane Dissociation on Flat and Stepped Transition-Metal Surfaces, J. Phys. Chem. Lett., 2017, 8, 4177–4182 CrossRef CAS PubMed.
- N. Gerrits, K. Shakouri, J. Behler and G.-J. Kroes, Accurate Probabilities for Highly Activated Reaction of Polyatomic Molecules on Surfaces Using a High-Dimensional Neural Network Potential: CHD3 + Cu(111), J. Phys. Chem. Lett., 2019, 10, 1763–1768 CrossRef CAS PubMed.
- N. Gerrits and G.-J. Kroes, An AIMD Study of Dissociative Chemisorption of Methanol on Cu(111) with Implications for Formaldehyde Formation, J. Chem. Phys., 2019, 150, 024706 CrossRef PubMed.
- N. Gerrits, J. Geweke, D. J. Auerbach, R. D. Beck and G.-J. Kroes, Highly Efficient Activation of HCl Dissociation on Au(111) via Rotational Preexcitation, J. Phys. Chem. Lett., 2021, 12, 7252–7260 CrossRef CAS PubMed.
- G.-J. Kroes, Computational Approaches to Dissociative Chemisorption on Metals: Towards Chemical Accuracy, Phys. Chem. Chem. Phys., 2021, 23, 8962–9048 RSC.
- T. Liu, B. Fu and D. H. Zhang, Mode Specificity of Water Dissociating on Ni(100): An Approximate Full-Dimensional Quantum Dynamics Study, J. Chem. Phys., 2023, 158, 214305 CrossRef CAS PubMed.
- H. L. Chen, H. M. Lee, S. H. Chen, Y. Chao and M. B. Chang, Review of Plasma Catalysis on Hydrocarbon Reforming for Hydrogen Production--Interaction, Integration, and Prospects, Appl. Catal., B, 2008, 85, 1–9 CrossRef CAS.
- B. S. Patil, Q. Wang, V. Hessel and J. Lang, Plasma N2-Fixation: 1900–2014, Catal. Today, 2015, 256, 49–66 CrossRef CAS.
- E. C. Neyts, K. K. Ostrikov, M. K. Sunkara and A. Bogaerts, Plasma Catalysis: Synergistic Effects at the Nanoscale, Chem. Rev., 2015, 115, 13408–13446 CrossRef CAS PubMed.
- E. C. Neyts, Plasma-Surface Interactions in Plasma Catalysis, Plasma Chem. Plasma Process., 2016, 36, 185–212 CrossRef CAS.
- P. Mehta, P. Barboun, D. B. Go, J. C. Hicks and W. F. Schneider, Catalysis Enabled by Plasma Activation of Strong Chemical Bonds: A Review, ACS Energy Lett., 2019, 4, 1115–1133 CrossRef CAS.
- K. H. R. Rouwenhorst, H.-H. Kim and L. Lefferts, Vibrationally Excited Activation of N2 in Plasma-Enhanced Catalytic Ammonia Synthesis: A Kinetic Analysis, ACS Sustainable Chem. Eng., 2019, 7, 17515–17522 CrossRef CAS.
- A. Bogaerts, X. Tu, J. C. Whitehead, G. Centi, L. Lefferts, O. Guaitella, F. Azzolina-Jury, H.-H. Kim, A. B. Murphy and W. F. Schneider, et al., The 2020 Plasma Catalysis Roadmap, J. Phys. D: Appl. Phys., 2020, 53, 443001 CrossRef CAS.
- A. Bogaerts, E. C. Neyts, O. Guaitella and A. B. Murphy, Foundations of Plasma Catalysis for Environmental Applications, Plasma Sources Sci. Technol., 2022, 31, 053002 CrossRef.
- B. Loenders, R. Michiels and A. Bogaerts, Is a Catalyst Always Beneficial in Plasma Catalysis? Insights from the Many Physical and Chemical Interactions, J. Energy Chem., 2023, 85, 501–533 CrossRef CAS.
- J. C. Polanyi, Concepts in Reaction Dynamics, Acc. Chem. Res., 1972, 5, 161–168 CrossRef CAS.
- R. A. Marcus, On the Analytical Mechanics of Chemical Reactions. Quantum Mechanics of Linear Collisions, J. Chem. Phys., 1966, 45, 4493–4499 CrossRef CAS.
- E. A. McCullough and R. E. Wyatt, Quantum Dynamics of the Collinear (H, H2) Reaction, J. Chem. Phys., 1969, 51, 1253–1254 CrossRef CAS.
- D. A. King and M. G. Wells, Reaction Mechanism in Chemisorption Kinetics: Nitrogen on the {100} Plane of Tungsten, Proc. R. Soc. A, 1974, 339, 245–269 CAS.
- V. P. Zhdanov, Impact of Surface Science on the Understanding of Kinetics of Heterogeneous Catalytic Reactions, Surf. Sci., 2002, 500, 966–985 CrossRef CAS.
- C.-Y. Lu, D. E. Makarov and G. Henkelman, Communication: κ-Dynamics–An Exact Method for Accelerating Rare Event Classical Molecular Dynamics, J. Chem. Phys., 2010, 133, 201101 CrossRef PubMed.
- C. T. Rettner, H. E. Pfnür and D. J. Auerbach, Dissociative Chemisorption of CH4 on W(110): Dramatic Activation by Initial Kinetic Energy, Phys. Rev. Lett., 1985, 54, 2716–2719 CrossRef CAS PubMed.
- G. Kyriakou, E. R. M. Davidson, G. Peng, L. T. Roling, S. Singh, M. B. Boucher, M. D. Marcinkowski, M. Mavrikakis, A. Michaelides and E. C. H. Sykes, Significant Quantum Effects in Hydrogen Activation, ACS Nano, 2014, 8, 4827–4835 CrossRef CAS PubMed.
- J. Zuo, C. Xie, H. Guo and D. Xie, Accurate Determination of Tunneling-Affected Rate Coefficients: Theory Assessing Experiment, J. Phys. Chem. Lett., 2017, 8, 3392–3397 CrossRef CAS PubMed.
- A. Fridman, Plasma Chemistry, Cambridge University Press, 2008 Search PubMed.
- P. Mehta, P. Barboun, F. A. Herrera, J. Kim, P. Rumbach, D. B. Go, J. C. Hicks and W. F. Schneider, Overcoming Ammonia Synthesis Scaling Relations with Plasma-Enabled Catalysis, Nat. Catal., 2018, 1, 269–275 CrossRef.
- H. Ma, R. K. Sharma, S. Welzel, M. C. M. van de Sanden, M. N. Tsampas and W. F. Schneider, Observation and Rationalization of Nitrogen Oxidation Enabled Only by Coupled Plasma and Catalyst, Nat. Commun., 2022, 13, 402 CrossRef CAS PubMed.
- Y. Engelmann, K. van’t Veer, Y. Gorbanev, E. C. Neyts, W. F. Schneider and A. Bogaerts, Plasma Catalysis for Ammonia Synthesis: A Microkinetic Modeling Study on the Contributions of Eley–Rideal Reactions, ACS Sustainable Chem. Eng., 2021, 9, 13151–13163 CrossRef CAS.
- I. Langmuir, Part II.—“Heterogeneous Reactions”. Chemical Reactions on Surfaces, Trans. Faraday Soc., 1922, 17, 607–620 RSC.
- R. Prins, Eley-Rideal, the Other Mechanism, Top. Catal., 2018, 61, 714–721 CrossRef CAS.
- E. K. Rideal, A Note on a Simple Molecular Mechanism for Heterogeneous Catalytic Reactions, Math. Proc. Cambridge Philos. Soc., 1939, 35, 130–132 CrossRef CAS.
- R. Michiels, Y. Engelmann and A. Bogaerts, Plasma Catalysis for CO2 Hydrogenation: Unlocking New Pathways toward CH3OH, J. Phys. Chem. C, 2020, 124, 25859–25872 CrossRef CAS.
- Y. Engelmann, P. Mehta, E. C. Neyts, W. F. Schneider and A. Bogaerts, Predicted Influence of Plasma Activation on Non-Oxidative Coupling of Methane on Transition Metal Catalysts. ACS Sustainable, Chem. Eng., 2020, 8, 6043–6054 CAS.
- B. Loenders, Y. Engelmann and A. Bogaerts, Plasma-Catalytic Partial Oxidation of Methane on Pt(111): A Microkinetic Study on the Role of Different Plasma Species, J. Phys. Chem. C, 2021, 125, 2966–2983 CrossRef CAS.
- H. Arnolds, Vibrational Dynamics of Adsorbates – Quo Vadis?, Prog. Surf. Sci., 2011, 86, 1–40 CrossRef CAS.
- P. R. Shirhatti, I. Rahinov, K. Golibrzuch, J. Werdecker, J. Geweke, J. Altschäffel, S. Kumar, D. J. Auerbach, C. Bartels and A. M. Wodtke, Observation of the Adsorption and Desorption of Vibrationally Excited Molecules on a Metal Surface, Nat. Chem., 2018, 10, 592–598 CrossRef CAS PubMed.
- R. Moiraghi, A. Lozano, E. Peterson, A. Utz, W. Dong and H. F. Busnengo, Nonthermalized Precursor-Mediated Dissociative Chemisorption at High Catalysis Temperatures, J. Phys. Chem. Lett., 2020, 11, 2211–2218 CrossRef CAS PubMed.
- L. B. F. Juurlink, D. R. Killelea and A. L. Utz, State-Resolved Probes of Methane Dissociation Dynamics, Prog. Surf. Sci., 2009, 84, 69–134 CrossRef CAS.
- S. Nave, A. K. Tiwari and B. Jackson, Dissociative Chemisorption of Methane on Ni and Pt Surfaces: Mode-Specific Chemistry and the Effects of Lattice Motion, J. Phys. Chem. A, 2014, 118, 9615–9631 CrossRef CAS PubMed.
- P. M. Hundt, H. Ueta, M. E. van Reijzen, B. Jiang, H. Guo and R. D. Beck, Bond-Selective and Mode-Specific Dissociation of CH3D and CH2D2 on Pt(111), J. Phys. Chem. A, 2015, 119, 12442–12448 CrossRef CAS PubMed.
- H. Guo and B. Jackson, Methane Dissociation on Stepped Ni Surfaces Resolved by Impact Site, Collision Energy, Vibrational State, and Lattice Distortion, J. Chem. Phys., 2019, 150, 204703 CrossRef PubMed.
- P. M. Hundt, M. E. van Reijzen, R. D. Beck, H. Guo and B. Jackson, Quantum-State-Resolved Reactivity of Overtone Excited CH4 on Ni(111): Comparing Experiment and Theory, J. Chem. Phys., 2017, 146, 054701 CrossRef PubMed.
- R. Yin and H. Guo, Dynamics of CO2 Dissociative Chemisorption on W(110), J. Phys. Chem. C, 2022, 126, 17935–17941 CrossRef CAS.
- B. L. Yoder, R. Bisson and R. D. Beck, Steric Effects in the Chemisorption of Vibrationally Excited Methane on Ni(100), Science, 2010, 329, 553–556 CrossRef CAS PubMed.
- R. R. Smith, D. R. Killelea, D. F. DelSesto and A. L. Utz, Preference for Vibrational over Translational Energy in a Gas-Surface Reaction, Science, 2004, 304, 992–995 CrossRef CAS PubMed.
- F. Nattino, D. Migliorini, G.-J. Kroes, E. Dombrowski, E. A. High, D. R. Killelea and A. L. Utz, Chemically Accurate Simulation of a Polyatomic Molecule-Metal Surface Reaction, J. Phys. Chem. Lett., 2016, 7, 2402–2406 CrossRef CAS PubMed.
- J. Chen, X. Zhou, Y. Zhang and B. Jiang, Vibrational Control of Selective Bond Cleavage in Dissociative Chemisorption of Methanol on Cu(111), Nat. Commun., 2018, 9, 4039 CrossRef PubMed.
- O. Kunova, E. Kustova and A. Savelev, Generalized Treanor-Marrone Model for State-Specific Dissociation Rate Coefficients, Chem. Phys. Lett., 2016, 659, 80–87 CrossRef CAS.
- B. Jiang and H. Guo, Six-Dimensional Quantum Dynamics for Dissociative Chemisorption of H2 and D2 on Ag(111) on a Permutation Invariant Potential Energy Surface, Phys. Chem. Chem. Phys., 2014, 16, 24704–24715 RSC.
- H. Guo and B. Jackson, Mode-Selective Chemistry on Metal Surfaces: The Dissociative Chemisorption of CH4 on Pt(111), J. Chem. Phys., 2016, 144, 184709 CrossRef PubMed.
- N. Gerrits, D. Migliorini and G.-J. Kroes, Dissociation of CHD3 on Cu(111), Cu(211), and Single Atom Alloys of Cu(111), J. Chem. Phys., 2018, 149, 224701 CrossRef PubMed.
- X. Zhou and B. Jiang, Mode-Specific and Bond-Selective Dissociative Chemisorption of CHD3 and CH2D2 on Ni(111) Revisited Using a New Potential Energy Surface, Sci. China: Chem., 2018, 61, 1134–1142 CrossRef CAS.
- K. Shakouri, J. Behler, J. Meyer and G.-J. Kroes, Accurate Neural Network Description of Surface Phonons in Reactive Gas-Surface Dynamics: N2 + Ru(0001), J. Phys. Chem. Lett., 2017, 8, 2131–2136 CrossRef CAS PubMed.
- N. Gerrits, J. Geweke, E. W. F. Smeets, J. Voss, A. M. Wodtke and G.-J. Kroes, Closing the Gap Between Experiment and Theory: Reactive Scattering of HCl from Au(111), J. Phys. Chem. C, 2020, 124, 15944–15960 CrossRef CAS.
- N. Gerrits, H. Chadwick and G.-J. Kroes, Dynamical Study of the Dissociative Chemisorption of CHD3 on Pd(111), J. Phys. Chem. C, 2019, 123, 24013–24023 CrossRef CAS PubMed.
- K. G. Prasanna, R. A. Olsen, Á. Valdésa and G.-J. Kroes, Towards an Understanding of the Vibrational Mode Specificity for Dissociative Chemisorption of CH4 on Ni(111): A 15 Dimensional Study, Phys. Chem. Chem. Phys., 2010, 12, 7654–7661 RSC.
- H. Guo, J. P. Menzel and B. Jackson, Quantum Dynamics Studies of the Dissociative Chemisorption of CH4 on the Steps and Terraces of Ni(211), J. Chem. Phys., 2018, 149, 244704 CrossRef PubMed.
- T. Tchakoua, A. D. Powell, N. Gerrits, M. F. Somers, K. Doblhoff-Dier, H. F. Busnengo and G.-J. Kroes, Simulating Highly Activated Sticking of H2 on Al(110): Quantum versus Quasi-Classical Dynamics, J. Phys. Chem. C, 2023, 127, 5395–5407 CrossRef CAS PubMed.
- O. Galparsoro, S. Kaufmann, J. Auerbach, D. Kandratsenka and A. M. Wodtke, A. First Principles Rates for Surface Chemistry Employing Exact Transition State Theory: Application to Recombinative Desorption of Hydrogen from Cu(111), Phys. Chem. Chem. Phys., 2020, 22, 17532–17539 RSC.
- C. Díaz, R. A. Olsen, D. J. Auerbach and G. J. Kroes, Six-Dimensional Dynamics Study of Reactive and Non Reactive Scattering of H2 from Cu(111) Using a Chemically Accurate Potential Energy Surface, Phys. Chem. Chem. Phys., 2010, 12, 6499–6519 RSC.
- T. Tchakoua, N. Gerrits, E. W. F. Smeets and G.-J. Kroes, SBH17: Benchmark Database of Barrier Heights for Dissociative Chemisorption on Transition Metal Surfaces, J. Chem. Theory Comput., 2023, 19, 245–270 CrossRef CAS PubMed.
- E. N. Ghassemi, M. Wijzenbroek, M. F. Somers and G.-J. Kroes, Chemically Accurate Simulation of Dissociative Chemisorption of D2 on Pt(111), Chem. Phys. Lett., 2017, 683, 329–335 CrossRef.
- G. Laurent, C. Díaz, H. F. Busnengo and F. Martín, Nonmonotonic Dissociative Adsorption of Vibrationally Excited H2 on Metal Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 161404 CrossRef.
- G. Füchsel, M. del Cueto, C. Díaz and G.-J. Kroes, Enigmatic HCl + Au(111) Reaction: A Puzzle for Theory and Experiment, J. Phys. Chem. C, 2016, 120, 25760–25779 CrossRef.
- E. Tayyebi, Y. Abghoui and E. Skúlason, Elucidating the Mechanism of Electrochemical N2 Reduction at the Ru(0001) Electrode, ACS Catal., 2019, 9, 11137–11145 CrossRef CAS.
- K. Shakouri, J. Behler, J. Meyer and G.-J. Kroes, Analysis of Energy Dissipation Channels in a Benchmark System of Activated Dissociation: N2 on Ru(0001), J. Phys. Chem. C, 2018, 122, 23470–23480 CrossRef CAS PubMed.
- A. Farjamnia and B. Jackson, The Dissociative Chemisorption of CO2 on Ni(100): A Quantum Dynamics Study, J. Chem. Phys., 2017, 146, 074704 CrossRef PubMed.
- B. Jiang and H. Guo, Communication: Enhanced Dissociative Chemisorption of CO2via Vibrational Excitation, J. Chem. Phys., 2016, 144, 091101 CrossRef PubMed.
- B. Jiang and H. Guo, Prediction of Mode Specificity, Bond Selectivity, Normal Scaling, and Surface Lattice Effects in Water Dissociative Chemisorption on Several Metal Surfaces Using the Sudden Vector Projection Model, J. Phys. Chem. C, 2014, 118, 26851–26858 CrossRef CAS.
- Z. Zhang, T. Liu, B. Fu, X. Yang and D. H. Zhang, First-Principles Quantum Dynamical Theory for the Dissociative Chemisorption of H2O on Rigid Cu(111), Nat. Commun., 2016, 7, 11953 CrossRef CAS PubMed.
- T. Liu, B. Fu, H. Zhang and D. An, Approximate Full-Dimensional Quantum Dynamics Study of the Mode Specificity in the Dissociative Chemisorption of D2O on Rigid Cu(111), Phys. Chem. Chem. Phys., 2017, 19, 11960–11967 RSC.
- K. Reuter and M. Scheffler, First-Principles Kinetic Monte Carlo Simulations for Heterogeneous Catalysis: Application to the CO Oxidation at RuO2(110), Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045433 CrossRef.
- B. Jiang and H. Guo, Relative Efficacy of Vibrational vs. Translational Excitation in Promoting Atom-Diatom Reactivity: Rigorous Examination of Polanyi's Rules and Proposition of Sudden Vector Projection (SVP) Model, J. Chem. Phys., 2013, 138, 234104 CrossRef PubMed.
- N. Gerrits and G.-J. Kroes, Curious Mechanism of the Dissociative Chemisorption of Ammonia on Ru(0001), J. Phys. Chem. C, 2019, 123, 28291–28300 CrossRef CAS.
- X. Hu, M. Yang, D. Xie and H. Guo, Vibrational Enhancement in the Dynamics of Ammonia Dissociative Chemisorption on Ru(0001), J. Chem. Phys., 2018, 149, 044703 CrossRef PubMed.
- B. Jackson, F. Nattino and G.-J. Kroes, Dissociative Chemisorption of Methane on Metal Surfaces: Tests of Dynamical Assumptions Using Quantum Models and Ab Initio Molecular Dynamics, J. Chem. Phys., 2014, 141, 054102 CrossRef PubMed.
- H. Guo, A. Farjamnia and B. Jackson, Effects of Lattice Motion on Dissociative Chemisorption: Toward a Rigorous Comparison of Theory with Molecular Beam Experiments, J. Phys. Chem. Lett., 2016, 7, 4576–4584 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Insights into Current Limitations of Density Functional Theory, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- N. Gerrits, E. W. F. Smeets, S. Vuckovic, A. D. Powell, K. Doblhoff-Dier and G.-J. Kroes, Density Functional Theory for Molecule-Metal Surface Reactions: When Does the Generalized Gradient Approximation Get It Right, and What to Do If It Does Not, J. Phys. Chem. Lett., 2020, 11, 10552–10560 CrossRef CAS.
- N. Gerrits, B. Jackson and A. Bogaerts, Accurate Reaction Probabilities for Translational Energies on Both Sides of the Barrier of Dissociative Chemisorption on Metal Surfaces, J. Phys. Chem. Lett., 2024, 15, 2566–2572 CrossRef CAS PubMed.
- D. J. Auerbach, J. C. Tully and A. M. Wodtke, Chemical Dynamics from the Gas-Phase to Surfaces, Nat. Sci., 2021, 1, e10005 CrossRef CAS.
- B. Jiang, R. Liu, J. Li, D. Xie, M. Yang and H. Guo, Mode Selectivity in Methane Dissociative Chemisorption on Ni(111), Chem. Sci., 2013, 4, 3249–3254 RSC.
| This journal is © The Royal Society of Chemistry 2025 |

