Interpretable attention-based transfer learning in plasma catalysis: a study on the role of surface charge

Abstract

Low-temperature plasma catalysis holds promise for electrification of energy-intensive chemical processes such as methane reforming and ammonia synthesis. However, fundamental understanding of plasma–catalyst interactions, essential for catalyst design and screening for plasma catalysts, remains largely limited. Recent work has demonstrated the importance of first-principles studies, including density functional theory (DFT), for elucidating the role of electro- and photo-effects such as electric field and charge in plasma catalysis. The availability of increasing amounts of DFT data in thermal catalysis presents a unique opportunity for plasma catalysis research to efficiently leverage this existing first-principles knowledge of thermal catalysis towards investigating plasma–catalyst interactions. To this end, this paper investigates interpretable transfer learning from thermal to plasma catalysis, with a focus on the role of surface charge. Pre-trained attention-based graph neural networks (GNNs) from the Open Catalysis Project, trained using millions of thermal catalysis DFT data points, are structurally adapted to account for surface charge effects and fine-tuned using plasma catalysis DFT data of single metal atoms on an Al₂O₃ support and adsorbates involved in plasma-catalytic ammonia synthesis. Not only does the fine-tuned attention-based GNN model provide high test accuracy for predicting adsorption energies and atomic forces in plasma catalysis, but it also exhibits adequate extrapolation for unseen single metal atoms in the plasma catalysis data used for model fine-tuning. To distinguish the effects of surface charge from other dissimilarities in DFT data of thermal and plasma catalysis, a dual-model framework is presented that relies on two pre-trained GNNs, one of which is specifically tasked to capture surface charge effects using an attention mechanism that provides interpretable insights into their role. Lastly, it is demonstrated how the attention-based GNNs developed for single metal atoms can be efficiently adapted for predicting adsorption energies and atomic forces for metal clusters in plasma catalysis. This work highlights the vast potential of interpretable transfer learning from thermal catalysis to plasma catalysis to mitigate excessive computational requirements of first-principles studies in plasma catalysis, towards accelerating fundamental research in this domain.

---

Broader context

Low-temperature plasmas (LTPs) have received increasing attention for renewably electrified synthesis of chemicals, such as methane reforming, NO_x generation, and ammonia synthesis, amongst others. This is due to the unique ability of LTPs to facilitate chemical reactions under atmospheric pressure and low temperatures. Additionally, LTPs are characterized by an abundance of high-energy electrons that can induce vibrationally-excited species, potentially resulting in new reaction pathways and reduced energy consumption. As such, LTP processes have the potential to enable decentralized and on-demand chemical production, as an alternative to large-scale and energy-intensive centralized chemical processes. The performance of LTP processes in terms of energy efficiency and productivity can be further enhanced via integration with catalysts. The availability of increasing amounts of DFT data in thermal catalysis presents a unique opportunity for plasma catalysis research to efficiently leverage this existing first-principles knowledge of thermal catalysis towards investigating plasma–catalyst interactions. This work highlights the vast potential of interpretable transfer learning from thermal catalysis to plasma catalysis to mitigate excessive computational requirements of first-principles studies in plasma catalysis, towards accelerating fundamental research in this domain.

1 Introduction

In recent years, low-temperature plasmas (LTPs) have received increasing attention for (renewably) electrified synthesis of chemicals, such as methane reforming,¹ NO_x generation,² and ammonia synthesis,³ amongst others. This is due to the unique ability of LTPs to facilitate chemical reactions under atmospheric pressure and low temperatures.^4,5 Additionally, LTPs are characterized by an abundance of high-energy electrons that can induce vibrationally-excited species,⁶ potentially resulting in new reaction pathways and reduced energy consumption. As such, LTP processes have the potential to enable decentralized and on-demand chemical production, as an alternative to large-scale and energy-intensive centralized chemical processes.⁷

The performance of LTP processes in terms of energy efficiency and productivity can be further enhanced via integration with catalysts.^8–12 These improvements are postulated to arise from the intricate, but poorly-understood, synergies between the plasma and catalyst.^13,14 Despite extensive experimental efforts on investigating the role of factors such as electric field,¹⁵ surface charges,^16–18 surface reactions involving excited species,⁸ atoms, and photons,^19,20 amongst others, there remain significant gaps in the fundamental understanding of plasma–catalyst interactions, let alone designing effective catalysts tailored for plasma catalysis.²¹ On the other hand, first-principles studies, particularly density functional theory (DFT), have proven useful for the investigation of plasma–catalyst interactions. Liu et al.²² used DFT to investigate the role of Eley–Rideal (E–R), Langmuir–Hinshelwood (L–H), and radical adsorption and dissolution processes in plasma catalysis across nine different metals, identifying a viable pathway for ammonia synthesis through the formation of NNH via radical reactions. Mehta et al.⁸ studied vibrational excitation of N₂ and the resulting surface reactions with excited species via DFT, uncovering distinct routes for plasma-catalytic ammonia synthesis. Bal et al.²³ introduced DFT methods for probing charged surfaces, which revealed an altered CO₂ binding energy on γ-Al₂O₃ surfaces under the influence of surface charge. Lele et al.²⁴ investigated the effects of surface charge on plasma-catalytic NH₃ synthesis, showing that charged catalytic surfaces can enhance NH₃ production. Shao and Mesbah²⁵ used an integrated microkinetic-DFT model to investigate how the electric field, along with other LTP process parameters such as gas temperature, can influence plasma-catalytic ammonia synthesis, providing new insights into trade-offs between the NH₃ production rate and energy consumption.

Despite these advances, the use of DFT for catalyst design and screening remains an open problem in plasma catalysis. The challenge is two-fold. First, there is a need for new theory, and possibly computational methods, to effectively account for the myriad of plasma-induced effects on surfaces via DFT. Second, the inclusion of these effects in DFT calculations can significantly increase their complexity, cost, and computational requirements. On the other hand, DFT is increasingly used to guide catalyst design and screening in thermal catalysis,²⁶ which has led to an abundance of data generated from DFT calculations. These efforts are further facilitated by the advances in machine learning to learn computationally efficient surrogates for DFT, towards accelerating the discovery of thermal catalysts.²⁷ Notably, DFT surrogates are trained on millions of data points that encompass various metal surfaces and adsorbates.²⁸ These surrogates can then perform tasks such as rapid prediction of system energy and atomic forces, as well as fast geometry relaxation. By predicting atomic forces and thus the relaxed system energy, DFT surrogates can significantly speed up catalyst screening, enabling resource-efficient evaluation of potential catalysts without the need for costly full DFT calculations.

Yet, there are barely any similar efforts in the area of plasma catalysis. One notable work is by Wan et al.²⁹ in which graph neural networks (GNNs) were used to study electric field-dipole effects in ammonia synthesis using a Ru catalyst, a topic closely related to plasma-catalytic ammonia synthesis. It was demonstrated that a pre-trained GNN model for Ru catalyst could be fine-tuned using a limited amount of DFT data for Fe catalysts to efficiently transfer acquired knowledge from Ru to Fe, while maintaining high accuracy in predicting adsorption energy. Another significant effort in this direction is by Zhang et al.,³⁰ wherein an attention-based GNN was developed to explore the compositional space of Ni–Co–Fe–Pd–Pt for high-entropy electrocatalysis. The proposed GNN model successfully predicted adsorption Gibbs energies and atomic forces for OOH, O, and OH at surface sites across various compositions. These predictions in turn enabled identification of optimal compositions, including non-equal atomic compositions (e.g., Ni_0.13Co_0.13Fe_0.13Pd_0.10Pt_0.50 and Ni_0.10Co_0.10Fe_0.10Pd_0.30Pt_0.40), using volcano plots, which were subsequently validated through experiments. This study effectively showcased the utility of DFT surrogate models in accelerating catalyst design by avoiding the costly exploration of vast catalyst composition spaces.

Nonetheless, these works generally rely on training DFT surrogates from scratch, disregarding existing knowledge and data from thermal catalysis. Despite the intricacies of electro- and photo-effects such as electric field and charge in plasma catalysis, fundamental insights into atomic interactions and bonding can be akin to those in thermal catalysis. Leveraging existing DFT data for thermal catalysis can present a unique opportunity for enabling fundamental plasma–surface studies and accelerating catalyst design and screening in the plasma catalysis domain. Central to this is transfer learning,³¹ where knowledge from one task is systematically utilized to solve problems in related tasks with a limited amount of data. A recent study by Kolluru et al.³² illustrates the potential of transfer learning in thermal catalysis using an attention-based adaptor and pre-trained models derived from the Open Catalyst 2020 (OC20) dataset,²⁸ which was generated based on extensive DFT calculations performed using the Vienna ab initio simulation package (VASP).^33,34 The findings of this work revealed that not only does the transferred model excel in learning in-domain tasks similar to the OC20 dataset, but it also exhibits a remarkable performance for out-of-domain tasks. Meanwhile, transfer learning significantly mitigates the intensive computational requirements when compared to training the DFT surrogate model entirely from scratch. Furthermore, recent work by Wang et al.³⁵ demonstrates that transfer learning can substantially reduce the number of required DFT calculations in out-of-domain transfer learning from inorganic to organic adsorbates in heterogeneous catalysis. Another useful concept is the attention mechanism, which has shown significant promise, in particular in natural language processing,³⁶ since it can provide interpretability by automatically assigning weights to the importance of relationships between a central word/node and its neighbors.³⁷ Zhang et al.³⁰ demonstrated that the attention mechanism can reveal how variations in energy and atomic forces are confined to the third nearest atom of O in high-entropy electrocatalysis. This can be explained by the destabilization of the second-nearest-neighbor atoms of oxygen, as the binding strength of the first-nearest-neighbor atoms is shared by the adsorbed oxygen atoms. However, the utility of the attention mechanism in thermal catalysis thus far generally lacks the incorporation of rich physical information, such as the angles formed by three atoms or the geometric configuration formed by multiple atoms, as demonstrated, e.g., in SchNet³⁸ and GemNet.³⁹ Most recently, Liao et al.⁴⁰ introduced an attention-based GNN EquiformerV2 tailored specifically for catalysis, a promising development in this direction. This model currently shows the best prediction accuracy for system/adsorption energy, atomic forces and geometry relaxation, as can be seen in the Open Catalyst Project Leaderboard.²⁸

Despite the rich body of knowledge on thermal heterogeneous catalysis, this knowledge remains underutilized in plasma catalysis due to a lack of effective tools for systematic and interpretable knowledge transfer in this domain. This paper addresses this gap by demonstrating the promise of attention-based transfer learning for leveraging the extensive DFT knowledge in thermal catalysis for first-principles plasma catalysis studies. To this end, we consider plasma-catalytic ammonia synthesis as the model system. We show how small amounts of plasma catalysis DFT data can be used to efficiently fine-tune existing pre-trained models of thermal catalysis to obtain accurate predictions of adsorption energy and atomic forces for single metal atoms and metal clusters. Moreover, transfer learning allows the model to have a strong extrapolation ability for unseen atoms in the plasma catalysis dataset. Thus, the fine-tuned model has the potential to enable rapid geometry relaxation, since it can be used to replace or reduce DFT calculations, as also shown in thermal catalysis.³⁵ The ability to develop models for predicting adsorption energies and atomic forces in a resource-efficient way can in turn open new avenues for catalyst design and screening for plasma-catalytic systems, which remain grand open challenges in this field.^21,41 Furthermore, integrating predictions of these quantities with microkinetic models serves as a critical step towards establishing a foundational understanding of plasma–catalyst interactions,^21,41 which is a prerequisite for advancing theoretical and practical insights into plasma-catalytic processes.

We use two pre-trained GNNs, namely the EquiformerV2 model with the attention mechanism and the GemNet-dT model, both of which are trained using the OC20 dataset from the Open Catalyst Project.²⁸ For model refinement, DFT calculations for N_xH_y species adsorbed onto single metal atoms supported on Al₂O₃ are performed using CP2K⁴² to account for plasma-induced charge effects, arguably one of the key contributors to plasma–catalyst synergy, on adsorption energies and atomic forces of the atoms. Although we are not aware of any experimental study combining single metal atom catalysts and plasma, single metal atom catalysts have been experimentally and theoretically studied for almost two decades,⁴³ including on Al₂O₃ as a support. Nonetheless, the focus of this work is to isolate and systematically study the effect of surface charging across several common catalysts. Hence, we have adopted the single metal atom model for transfer learning. We demonstrate that by structurally adapting the pre-trained EquiformerV2 model and freezing a subset of its learnable parameters during transfer learning, the fine-tuned model can provide accurate predictions of adsorption energies and atomic forces for unseen single metal atoms. This indicates the ability of the fine-tuned model to effectively retain knowledge from thermal catalysis since the unseen single metal atoms were only a part of the OC20 dataset and not the plasma catalysis DFT data used for fine-tuning the EquiformerV2 model. Moreover, we show that the pre-trained EquiformerV2 model can be efficiently fine-tuned with only a limited amount of plasma catalysis DFT data for Pt metal clusters, along with the single-metal-atom data, to predict adsorption energies and atomic forces for unseen Ru metal clusters.

A standard practice in transfer learning is to use data acquired for a new task to fine-tune pre-trained models by adapting all their learnable parameters, typically without delineating various discrepancies that may exist between the old and new tasks.⁴⁴ In this work, to enhance the interpretability of the fine-tuned attention-based EquiformerV2 model with respect to plasma-induced surface charge effects, we look to delineate these effects from other dissimilarities between the OC20 dataset and the DFT data generated for plasma catalysis, namely the dissimilarities in atomic interactions and discrepancies between DFT calculations performed by VASP and CP2K. To this end, we propose a dual-model framework for interpretable transfer learning that combines the pre-trained GemNet-DT model³⁹ for thermal catalysis and the above-described structurally-adapted pre-trained EquiformerV2 model, which is tasked to account for surface charge effects. The surface charge effects are encoded into the fine-tuned EquiformerV2 model via a loss function designed for this purpose. The attention scores extracted from the fine-tuned EquiformerV2 model in this dual-model framework exhibit strong correlations to surface charge distribution, providing useful insights into the important role of charge distribution on adsorption processes in plasma catalysis.

2 Methods

2.1 Density functional theory

To model the effect of plasma-induced surface charge on catalytic surfaces, we used single-metal-atom and metal-cluster models, as reported in ref. 23 and 24. The DFT calculations that describe surface charge effects on adsorption energies for single metal atoms and the corresponding free atom atomic forces are performed using CP2K.^24,42 Briefly, these calculations make use of the Quickstep module of the CP2K code. Fig. 1 shows a schematic of the DFT calculations, which are performed for a γ-Al₂O₃(110) surface (6 aluminum layers with 2 × 2 anhydrous super cell), as derived from ref. 45. The hydrous 110 surface is the most stable surface termination for γ-Al₂O₃. However, it has been shown that the surface charge effect can be effectively modelled using an anhydrous surface.²³ Hence, to reduce computational complexity, we employ an anhydrous γ-Al₂O₃(110) supercell in the DFT calculations performed in this work. The Quickstep module uses the combined Gaussian and plane wave method to calculate system energies. The exchange and correlation is calculated using the Perdew–Burke–Ernzerhof (PBE)⁴⁶ functional supplemented by D3 dispersion correction.⁴⁷ The DFT calculations use GTH pseudopotentials with a polarized double-ζ (m-DZVP) basis set. Considering the size of the system geometry, the calculations are performed at Γ-point only. To account for the effects of surface charge, a proton is introduced in the simulation cell by defining an H atom type without a basis set, preventing electron assignment. The proton is fixed at a Z-height of 40 Å, while forcing the entire system to be charge neutral. Hence, this proton introduces a negative charge on the surface. This counter-ion or proton position is chosen to minimize the effects of electric field generated by the charge-countercharge system. The charge-countercharge interactions become negligible if the countercharge is placed at a Z-height of more than 30 Å. However, to be on the conservative side and to further isolate the effect of surface charge, we decided to place the counter-ion 40 Å away from the surface. This countercharge introduces a negative charge on the surface. The simulation cell is treated non-periodically in the z-direction using Martyna–Tuckerman Poisson solver.^48,49 The convergence and accuracy of the calculations are examined in relation to parameters such as the location of counter-ion, choice of functional, and energy cut-off; see ref. 24 for further details. We use a single positive counter-ion in our calculations, resulting in a surface charge density of 0.06 C m⁻². This is considered to be within the range of plasma-induced surface charge, as measured experimentally⁵⁰ and reported in modeling studies.⁵¹ We note that this method can be easily adopted to account for different surface charge densities in a plasma catalytic process.

Fig. 1 Schematic of a typical DFT calculation with surface charge. A counter-ion (shown by the + symbol) is placed away from and in the surface normal direction of the γ-Al₂O₃ surface to introduce a negative charge on the surface (shown by the – symbol). “M” represents a single metal atom, or a metal cluster, and “Ads” represents different adsorbed N_xH_y species.

To account for the surface charge effects on the adsorption of different N_xH_y species on different catalysts, a set of single metal atoms and metal clusters are first adsorbed on the γ-Al₂O₃ surface. Then, the adsorption energies of the different adsorbates are calculated by:

E_ads = E_{slab+adsorbate} − E_slab − E_adsorbate

in the presence and absence of the surface charge. γ-Al₂O₃ offers 7 unique adsorption sites, including 2 or 3 coordinated O atom sites and 3 or 4 coordinated Al atom sites. All these adsorption sites are explored for the single metal atoms. For metal clusters, they are first energy minimized without the support and then adsorbed on the γ-Al₂O₃ support. Although more realistic, direct surface adsorption calculations on metal-cluster models (metal clusters adsorbed on the γ-Al₂O₃(110) surface) are configuration dependent. That is, the size and shape of the metal clusters can impact the extent of the surface charge effect. Single-metal-atom models, on the other hand, provide a more consistent way to compare the effect of surface charge on different catalysts due to their relative configurational independence.

We consider 11 single metal atoms, namely Ag, Au, Cu, Re, Ru, Co, Ni, Pd, Fe, Pt and Rh, using the single metal atom model, where the last three metals are only used for testing the generalization performance of the fine-tuned model for the single metal atoms. We consider the adsorption of seven different adsorbates, namely N, N₂, H, H₂, NH, NH₂, and NH₃, which are involved in NH₃ synthesis. DFT calculations are also performed for metal clusters of Ru and Pt on the γ-Al₂O₃ surface. To ensure that the sensitivity of the adsorbates to surface structures is considered, we calculated the adsorption energies for all adsorbates on the seven unique adsorption sites offered by the γ-Al₂O₃(110) support, as well as their co-adsorption on the support and metal atom combined. Our analysis showed that adsorption on the metal atom/cluster was always favored for the adsorbates investigated in this work. Additional details about the DFT calculations performed in this work can be found in ref. 23 and 24.

2.2 Data structure

For each pairing of the eleven single metal atoms with the seven distinct adsorbates, the complete geometry relaxations are treated as individual data points. That is, for example, given the combination of H + Au + γ-Al₂O₃, if achieving the final relaxed structure involved creating 100 profiles during the geometry relaxation, these 100 profiles would be counted as 100 separate data points. Since only CP2K is used in this work to generate data, to account for the discrepancies stemming from using VASP software to generate the OC20 dataset for thermal catalysis²⁸ and CP2K software, the above-described DFT calculations are performed both in the presence and absence of the surface charge. Consequently, a dataset of 5164 data points is compiled for Ag, Au, Cu, Re, Ru, Co, Ni, and Pd, whereas the independent datasets for Fe, Rh, and Pt include 472, 435, and 587 data points, respectively. The former dataset is then divided into training, validation, and test sets in the ratio of 70/20/10%. The data labels consist of the adsorption energy and atomic forces for each individual atom.

A similar data structure is also used for Pt and Ru metal clusters on γ-Al₂O₃, yielding datasets of 3965 and 3627 data points for Pt and Ru clusters, respectively. The Pt cluster dataset is further divided into training, validation, and test sets using the same ratio as above to aid in model fine-tuning. The Ru cluster dataset is only utilized for testing the generalization performance of the fine-tuned model for the metal clusters.

2.3 Pre-trained models from thermal catalysis

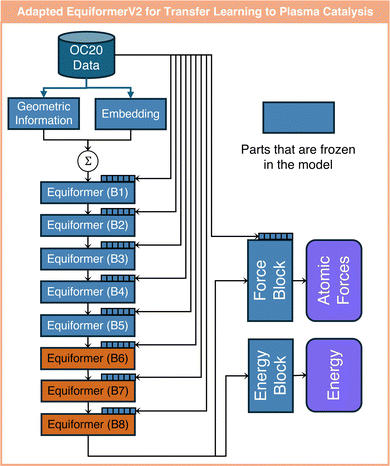
In this work, we utilize two GNNs from the Open Catalyst Project, i.e., pre-trained using the OC20 dataset,²⁸ to enable transfer learning from thermal to plasma catalysis. The two models are an EquiformerV2 model using the attention mechanism and a GemNet-dT model popular in thermal catalysis. These architectures are depicted in Fig. 2. The EquiformerV2 model first converts atoms to their corresponding embeddings according to their atomic number. The geometric information among atoms, such as atom–atom distance, is encoded into the embeddings that are vectors with the same dimensions as the atom embeddings. These two embeddings are then summed up and fed into an arbitrary number of Equiformer blocks. Within each Equiformer block, new learnable atom embeddings are defined to further learn the atom–atom edge geometric information. Along with this geometric information, the fed embedding of each atom is updated according to the embeddings of its N closest neighbors within each Equiformer block. Here, attention scores are learned that weigh the contribution of the N surrounding atoms. Therefore, the attention scores provide a degree of interpretability as they reveal the interactions between atoms. EquiformerV2 also uses a multi-head attention mechanism, where each head has its own attention score to capture different aspects of relationships between atoms; see ref. 40 for further details on the attention scores of EquiformerV2, which are different from classical attention scores as in ref. 36. The outputs of the final Equiformer block are fed into a force and an energy block to predict the atomic force for each atom in xyz directions and the structure adsorption energy. The force block is a graph attention layer, which is also a structure used in the Equiformer blocks. The energy block is a feedforward layer. Here, we choose the lightest pre-trained EquiformerV2 model with eight Equiformer blocks based on OC20,^28,40 since it demonstrated a sufficiently good performance for the transfer learning task at hand. This model considers N = 20 closest neighbors for each atom in each attention head, and uses eight-head attention in each Equiformer and force block. This EquiformerV2 model is used in all three transfer learning tasks of this work, as detailed in the next section.

Fig. 2 Architectures of the two graph neural network models, pre-trained using the OC20 dataset for thermal catalysis.²⁸ The left is the EquiformerV2 architecture with eight Equiformer blocks.⁴⁰ The right is the GemNet-dT architecture³⁹ with a multi-head attention adaptor for improved transfer learning.³² The number of additional interaction blocks is set to one.

The construction of the initial part of the GemNet-dT model is similar to that of EquiformerV2, with the geometric information extracted and atoms converted into embeddings. Then, graph interaction blocks update these embeddings according to the geometric information. In the original GemNet-dT model without an adaptor, each interaction block, as well as the initial embedding are followed by a feedforward block. The outputs of these feedforward blocks are added to predict the adsorption energy and atomic forces. In this work, however, we use a modified GemNet-dT model that utilizes a multi-head attention adaptor to balance information from the intermediate graph-based blocks for improved transfer learning.³² In the modified GemNet-dT model, the feedforward layers in the interaction blocks are removed and, instead, a weighted summation is performed in the adaptor to make predictions. To further enhance transfer learning ability, additional interaction blocks with feedforward layers are introduced.³² The outputs of these interaction blocks are directly added to the output from the multi-head attention adaptor, yielding the adsorption energy and atomic force predictions. In the modified GemNet-dT model, the parameters of the adaptor, the additional interaction blocks and their feedforward layers must be trained, whereas other parts of the model are based on the pre-trained GemNet-dt model of OC20 with three interaction blocks. We note that the modified GemNet-dT model is only used in the dual-model framework of the task “interpretation of surface charge effects” to capture discrepancies between the thermal catalysis and plasma catalysis datasets other than the surface charge effects.§

2.4 Attention-based transfer learning tasks

In this work, we investigate three different tasks to demonstrate the usefulness of transfer learning from thermal catalysis to plasma catalysis. In the first task, we focus on assessing the prediction accuracy and generalizability of fine-tuned models for the case of single metal atoms. In the second task, we use attention-based transfer learning to provide interpretable insights into the effects of surface charge in plasma catalysis. In the third task, we investigate transfer learning from single atoms to metal clusters.

2.4.1 Task 1: transfer learning from thermal catalysis to plasma catalysis for single metal atoms. In this transfer learning task, we use the pre-trained EquiformerV2 model introduced in the Pre-trained models from thermal catalysis section, due to its superior performance on the OC20 dataset. Several adaptations to the original EquiformerV2 model architecture are made for the transfer learning task at hand. An example of the structurally adapted EquiformerV2 model is shown in Fig. 3, where only the middle three Equiformer blocks B6–8 and all the proton embeddings are unfrozen during transfer learning. In the geometric information, B1 to B8 and force blocks of the adapted model, each atom is impacted by its 20 closest neighbors and the proton.

Fig. 3 An example of the adapted EquiformerV2 model for transfer learning to plasma catalysis. The layers up to and including the fifth Equiformer block (B5) and the force and energy blocks are frozen. The atom embeddings are frozen, including in the Equiformer blocks B6–B8. However, the proton embeddings of all layers are unfrozen and are updated during transfer learning, initialized from hydrogen embeddings of the pre-trained model.

These adaptations are made out of several considerations. First, proton is placed far away from all atoms, whereas the impact of proton may be appreciable on all atoms. Therefore, since the EquiformerV2 model only considers the nearest 20 atoms for each atom, the model is adapted to also account for the effects of the proton. Furthermore, atom embeddings remain constant during transfer learning. This is because the updated embeddings may affect the attention blocks of the EquiformerV2 model adversely, potentially hindering the extrapolation capability on unseen atoms. Earlier layers of the pre-trained model tend to capture structural knowledge, such as edge between atoms and rotational equivalence of the catalyst structure.^32,40 Therefore, freezing these layers can also be beneficial to the extrapolation capability of the fine-tuned model. However, the number of initial layers to be frozen can have a significant influence on the model performance. Thus, we investigate the impact of freezing different numbers of initial layers of the pre-trained model on the extrapolation capability of the fine-tuned model. Additionally, freezing of the output energy and force blocks is also tested since these blocks are responsible for projecting the outputs from the eight Equiformer block (B8) to the energy and force predictions. As for learning the proton embeddings, they are initialized using the hydrogen embeddings from the pre-trained EquiformerV2 model and their parameters are updated during transfer learning. In theory, hydrogen embeddings represent the closest approximation to that of protons. Table 1 summarizes all the adaptations of the pre-trained EquiformerV2 model used for transfer learning from thermal to plasma catalysis. An ablation study is performed to test the performance of these models.

Table 1 Adaptations of the pre-trained EquiformerV2 model from the Open Catalyst Project^28,40 used for transfer learning from thermal to plasma catalysis. F means the weights do not start from those of the pre-trained model. T means the weights start from those of the pre-trained model. H means the proton embeddings are unfrozen and start from the hydrogen embeddings of the pre-trained model. — means this part is unfrozen. × means this part is frozen

Model abbreviation	Pretrained	Proton embedding	Atom embedding	Geometric Info.	Equiformer and output blocks
					B1	B2	B3	B4	B5	B6	B7	B8	Energy & force
S	F	—	—	—	—	—	—	—	—	—	—	—	—
H	T	H	—	—	—	—	—	—	—	—	—	—	—
A	T	—	×	—	—	—	—	—	—	—	—	—	—
HA	T	H	×	—	—	—	—	—	—	—	—	—	—
L1	T	H	×	×	×	—	—	—	—	—	—	—	—
L3	T	H	×	×	×	×	×	—	—	—	—	—	—
L5	T	H	×	×	×	×	×	×	×	—	—	—	—
L7	T	H	×	×	×	×	×	×	×	×	×	—	—
L8	T	H	×	×	×	×	×	×	×	×	×	×	—
EF	T	H	×	—	—	—	—	—	—	—	—	—	×
L1EF	T	H	×	×	×	—	—	—	—	—	—	—	×
L3EF	T	H	×	×	×	×	×	—	—	—	—	—	×
L5EF	T	H	×	×	×	×	×	×	×	—	—	—	×
L7EF	T	H	×	×	×	×	×	×	×	×	×	—	×

---

2.4.2 Task 2: interpretable transfer learning to elucidate the role of surface charge. There are several discrepancies between the OC20 data used for learning the pre-trained EquiformerV2 model and the plasma catalysis DFT data used for fine-tuning the model. These include differences in DFT calculations made by VASP and CP2K for generating thermal and plasma catalysis data, respectively, the catalyst–adsorbate configurations shifting from metal clusters plus adsorbates in the OC20 dataset to single metal atoms plus adsorbate with support in the plasma catalysis dataset, the overall atom count, and the introduction of surface charge by protons. While using the above-described fine-tuned EquiformerV2 models can enable satisfactory transfer learning outcomes, including good test and extrapolation scores, extracting meaningful insights from the attention mechanism of the Equiformer blocks, such as B6–B8 in Fig. 3, can be infeasible since they cannot delineate the above discrepancies. This is because the attention scores, which capture the impact of the 20 closest atoms and proton on any atom, are updated based on the plasma catalysis DFT data, making discerning the surface charge effects from other differences impossible.

To elucidate the role of surface charge, we propose a dual-model architecture that isolates the effects of proton-induced surface charges in the EquiformerV2 model. Meanwhile, to ensure that all other discrepancies are effectively captured, we employ the GemNet-dT + A architecture, as proposed in ref. 32, which has demonstrated strong transfer learning capabilities for out-of-domain tasks. As shown in Fig. 4, the proposed architecture consists of two pre-trained models operating concurrently: the GemNet-dT + A model that is fine-tuned using single metal atom data of CP2K when proton is removed, and the EquiformerV2 model fine-tuned with CP2K data with the proton effects accounted for. For fine-tuning of the GemNet-dT + A model using single metal atom data of CP2K, proton is removed before a single metal atom structure is fed to the model. This allows the fine-tuned GemNet-dT + A model to learn the discrepancies between the pre-trained model using the OC20 thermal catalysis data and the CP2K data generated in this work. This is while a single metal atom structure with proton is fed to the EquiformerV2 model, serving as a corrector to predictions of the fine-tuned GemNet-dT + A model by accounting for surface charge effects. This way the dual-model architecture can delineate the role of surface charge from other discrepancies between the thermal and plasma catalysis data. The combined outputs of the two models yield the predictions for adsorption energy and atomic forces. To train the models, the following loss functions are devised. For single metal atom structures with proton, the loss function J_plasma is defined as in eqn (1), whereas for structures without proton, the loss function J_thermal takes the form of eqn (2), i.e.,

Here, E denotes the actual adsorption energy, while Ê_a and Ê_b represent the energy predictions from the GemNet-dT + A and EquiformerV2 models, respectively. A stands for the total number of free atoms in the structure, and F̂_j,x,a, F̂_j,x,b (similarly for y and z directions) are the atomic force predictions from the GemNet-dT + A and EquiformerV2 models, respectively. The coefficients α and β trade off the loss contributions from the energy and atomic force predictions, with values of α = 4 and β = 100 used in this work, as in ref. 28.

Fig. 4 The dual-model architecture that isolates the surface charge effects from other differences in thermal and plasma catalysis data. The EquiformerV2 model is used for capturing the surface charge effects, where only the eight Equiformer block (B8) and proton embeddings are relaxed. The GemNet-dT + A model is used to retain the thermal catalysis knowledge, wherein the additional interaction block, the multi-head attention adaptor, and the energy and force feedforward block are unfrozen. The outputs of the two models are added to give the energy and force predictions. A single metal atom structure for plasma catalysis is directly fed to the EquiformerV2 model, whereas proton is removed when the structure is fed to the GemNet-dT + A model. Accordingly, EquiformerV2 is tasked to “correct” the predictions of GemNet-dT + A by capturing the surface charge effects. If a structure does not have proton, it is fed to both models, while the EquiformerV2 model predicts an output correction of 0.

To fine-tune the GemNet-dT + A model, the initial atom embeddings and the existing interaction blocks in the pre-trained model are frozen. One additional interaction block is added and the number of heads in the multi-head attention adaptor is set as five, as in ref. 32. Since these newly added layers are not pre-trained, they are initialized randomly. For the EquiformerV2 model, we utilize the model architecture outlined in Fig. 3. However, we only allow fine-tuning of proton embeddings and the 8th Equiformer block (B8),^36,40 in the pre-trained EquiformerV2 model. Additionally, the output layers responsible for predicting energy and atomic forces remain unchanged during model fine-tuning. This is based on the consideration that each Equiformer block within the pre-trained EquiformerV2 model has its own atom embeddings. Allowing all Equiformer blocks to adapt during model fine-tuning could disperse the surface charge effects across various blocks, rendering the predictions uninterpretable.

2.4.3 Task 3: transfer learning from single atoms to metal clusters. In this task, we look to investigate if the pre-trained models for single metal atoms can be effectively fine-tuned for metal clusters. To this end, we use the single metal atom data for all the above-mentioned metals and the metal cluster data of Pt, leaving the Ru cluster data for testing the generalization performance of the model. Note that we avoid any potential bias caused due to excluding the single metal atom data for Pt in model refinement; for example, as a result of missing the connections between Pt and other metals, and the link between single Pt and Pt cluster systems. In this task, we use the same pre-trained EquiformerV2 model as in task 1. The choice of which blocks of the pre-trained model to freeze is made based on the best performing models of task 1 in terms of both test accuracy and generalization performance. We investigated three strategies for transfer learning, as summarized in Table 2. The first strategy involves using the metal cluster data for fine-tuning of the pre-trained model. The second strategy further fine-tunes the transfer learning model of task 1 using metal cluster data, whereas the third strategy uses the mixture of single metal atom and metal cluster data to fine-tune the pre-trained model. For all three strategies, we maintain a training-validation-test ratio of 70/20/10%.

Table 2 Transfer learning from single atoms to metal clusters

Strategy	Description
S1 (baseline)	Use the pre-trained EquiformerV2 model and metal cluster data to directly perform transfer learning.
S2	Use the pre-trained EquiformerV2 model and single metal atom data to perform transfer learning. Then, the updated model is further fine-tuned using the metal cluster data.
S3	Use the pre-trained EquiformerV2 model and the mixture of the single metal atom and metal cluster data to fine-tune the model in one step.

---

3 Results and discussion

3.1 Task1: transfer learning from thermal catalysis to plasma catalysis for single metal atoms

To enable effective transfer learning towards extrapolation to unseen single metal atoms, we first discuss how relevant knowledge, such as atom–atom interactions, from thermal catalysis is retained within the fine-tuned models. In transfer learning, the initial layers of a model generally encapsulate geometric information. For example, the initial layers in a pre-trained GNN learn more basic representations of a catalyst structure, such as edges between atoms.³² This is while the final layers of a pre-trained GNN contain more abstract, high-level information amenable to fine-tuning. Here, we investigate which components of a pre-trained EquiformerV2 model should remain unchanged to enable accurate predictions for previously unseen metal atoms during transfer learning. Fig. 5 demonstrates the performance of several fine-tuned models, as detailed in Table 1, in terms of their test accuracy and extrapolation capability on unseen single metal atoms of Fe, Rh and Pt. The analysis reveals that the majority of the fine-tuned models in Table 1 exhibit comparable performance in the adsorption energy and atomic forces on the test data, as evidenced by their R² scores close to 1. Model S, which is an EquiformerV2 model architecture trained from scratch using the same training dataset, and model L8, wherein only the output blocks for energy and force are fine-tuned, show a notably worse test accuracy than other models. The poor performance of model S corroborates the successful transfer of thermal catalysis knowledge from the pre-trained model to the plasma catalysis domain. Moreover, the excessive rigidity of a fine-tuned model by freezing too many layers as in L8 can severely constrain transfer learning.

Fig. 5 Transfer learning from thermal to plasma catalysis for single metal atoms. Accuracy of the different fine-tuned models, detailed in Table 1, in predicting the adsorption energy and atomic force is quantified by the R² score. (a) The test accuracy of the fine-tuned models for all atoms in the test dataset. (b) The predictive accuracy of the fine-tuned models for the unseen Fe atom. (c) The predictive accuracy of the fine-tuned models for the unseen Rh atom. (d) The predictive accuracy of the fine-tuned models for the unseen Pt atom.

A comparison of models H and HA, which differ solely in whether the atom embeddings are fixed, demonstrates that relaxing the pre-trained atom embeddings significantly diminishes the model's extrapolation capability. This is evident in predicting atomic forces for the unseen metals Fe, Rh and Pt as shown in Fig. 5(c) and (d). Yet, both models exhibit relatively poor extrapolation for Fe as in Fig. 5(b), likely due to its minuscule atomic forces near the optimal structure. This difficulty stems from the transfer learning process of the model H, which also updates the embeddings for metals present in the transfer learning data. This means the differences between thermal catalysis and plasma catalysis impact the embeddings of the seen metals in the model H, while leaving the embeddings for unseen metals unchanged. Using these embeddings of unseen metals for extrapolation thus will lead to missing information on these differences. On the other hand, comparing the performance of models A and HA suggest that initializing the proton embedding using the pre-trained hydrogen embedding may not have a notable impact on the model's generalization performance. Model A outperforms model HA in terms of predicting the adsorption energy for Rh, while showing an inferior performance in predicting the atomic force, as can be seen in Fig. 5(c). This is reversed for the case of Pt, where model A performs better in predicting the atomic force and worse in predicting the adsorption energy (Fig. 5(d)). The reason that initializing the proton embedding from the hydrogen embedding does not yield superior predictions can be attributed to the inherent flexibility of the pre-trained EquiformerV2 model with fixed atom embeddings. As the large number of weights of other layers are unfrozen, it makes the starting point of the proton embedding unimportant. Given the chemical similarity between proton and hydrogen, we opted to initiate the proton embedding based on the hydrogen embedding in the rest of the fine-tuned models in Table 1.

We now examine the impact of the number of frozen layers in the pre-trained EquiformerV2. Fig. 5(b) shows that the fine-tuned models with a greater degree of flexibility (i.e., a fewer number of frozen layers) underperform in extrapolation in the case of Fe. This underscores the important role of the initial layers of the EquiformerV2 model shown in Fig. 5. In particular, in the case of atomic force predictions for the unseen atoms, freezing layers up to and including the seventh Equiformer block (B7) yields the best performing models, as seen in Fig. 5(b)–(d). This is while the extrapolation performance of models L7 and L7EF is comparable, suggesting that freezing the output energy and force blocks may not be critical. Note that these output blocks are responsible for converting the abstract output from the eighth Equiformer block (B8) to the adsorption energy and atomic force predictions. Hence, with the eighth Equiformer layer unfrozen, allowing the energy and force blocks to be fine-tuned as in model L7, can enable a more effective transfer learning to plasma catalysis.

We now compare the performance of the fine-tuned model L7 to that of model S, i.e., an EquiformerV2 model architecture fully trained using the same training dataset. Fig. 6 shows parity plots of the predicted adsorption energy and atomic force for the unseen metals Fe, Rh and Pt against their corresponding true values. Model L7 significantly outperforms model S trained from scratch, in particular for atomic force predictions, as depicted in Fig. 6(b), (d) and (f). Notice that model S tends to either over predict the atomic forces, as in Fig. 6(b) and (d), or yield numerous zero predictions as in Fig. 6(f). These parity plots imply that via careful fine-tuning of the EquiformerV2 model pre-trained on thermal catalysis data adequate generalization performance can be achieved for single metal atoms in the case of plasma catalysis. Additionally, for a metal seen with a large amount of thermal catalysis data during the EquiformerV2 pre-training, the fine-tuned model provides satisfactory generalization performance for these metals even if not seen during transfer learning. We note that only 3614 plasma catalysis datapoints were used for the fine-tuning model, as compared to the millions of datapoints used to establish the pre-trained EquiformerV2 model. Therefore, transfer learning using a pre-trained model based on a large dataset and a large array of atom types can provide valuable extrapolative predictions for unseen catalysts in plasma catalysis with a much smaller amount of new DFT data, thus accelerating the catalyst discovery process.

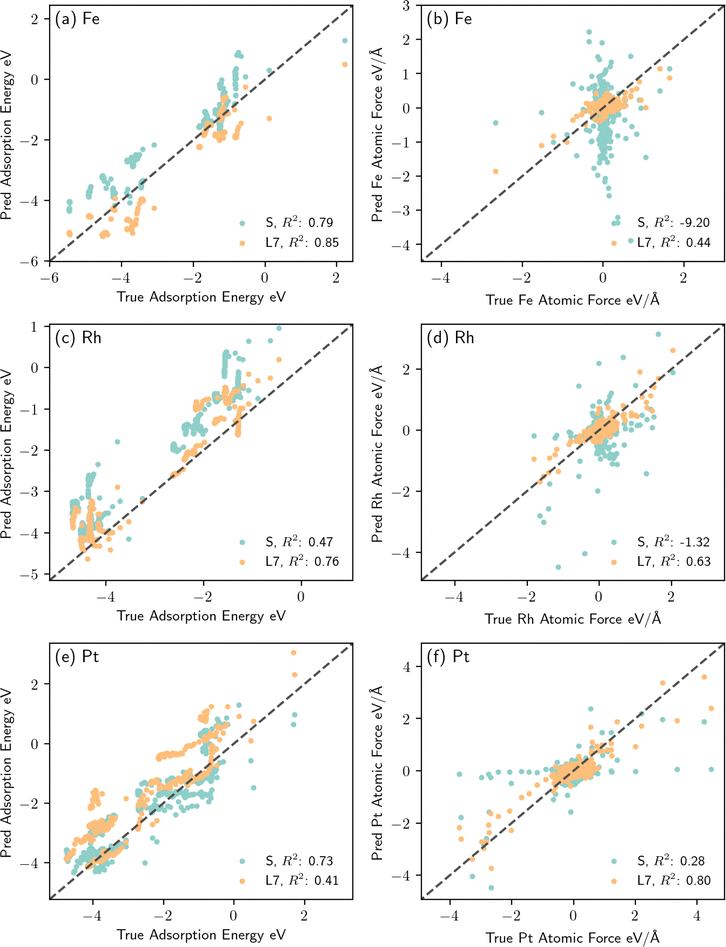Fig. 6 Parity plots of the adsorption energy and atomic force predictions of models S and L7, as detailed in Table 1, for the unseen metal atoms of Fe, Rh and Pt. (a) and (b) Adsorption energy against its corresponding predicted values for structures containing Fe, as well as the atomic forces experienced by Fe versus predicted atomic forces. (c) and (d) Adsorption energy against its corresponding predicted values for structures containing Rh, as well as the atomic forces experienced by Rh versus predicted atomic forces. (e) and (f) Adsorption energy against its corresponding predicted values for structures containing Pt, as well as the atomic forces experienced by Pt versus predicted atomic forces.

3.2 Task 2: elucidating the role of surface charge

As detailed in the methods section, we use an attention-based, dual-model framework that is designed to distinguish surface charge effects on model predictions from other discrepancies between the OC20 data used for pre-training the models and the plasma catalysis DFT data used for model fine-tuning. By unfreezing the eighth Equiformer block (B8) and the proton embedding, the pre-trained EquiformerV2 model in Fig. 4 captures the surface charge effects via B8. Specifically, we focus on the nitrogen adsorbate, which plays an important role in plasma-catalytic synthesis of ammonia.^14,52 The attention scores for nitrogen reflect the influence of its 20 neighboring atoms and proton, a row vector of dimension 1 × 21. The pre-trained EquiformerV2 model leverages an eight-head attention in each of its Equiformer blocks to capture different aspects of atom–atom relationships,³⁶ such as atom–atom interactions induced by charges. Therefore, the attention scores of the eight heads from B8 are concatenated, forming a row vector of 1 × 168. We then apply principal component analysis (PCA) to this high-dimensional vector to project it onto a 3-dimensional space. We do not apply methods like SHAP,⁵³ since attention scores inherently represent the importance of neighboring atoms and are intermediate values that can vary across training instances. The PCA results shown in Fig. 7 reveal interpretable patterns for the single metal atoms. Notably, Au and Ag, which have a valence electron count of 1, can be clustered as one group in the 3D principal component space. Similarly, Cu and Ni form another cluster, likely due to their sequential placement in the periodic table and their ability to create 1⁺ and 2⁺ ions, unlike Ag and Au. The remaining metals—Re, Ru, Co, and Pd—establish distinct groups, possibly due to their different valence electron counts of 7, 8, 9, and 10, respectively.

Fig. 7 Principal component analysis is applied to project the 168th-dimensional attention scores of the eight blocks of the Equiformer model of Fig. 4 onto a 3-dimemsional space. This figure shows the projected attention scores onto the 3-dimensional space. The 2-dimensional contours of the 3-dimensional space can be found in figures SP1, SP2 and SP3.

We now investigate the relationship between the attention scores and the surface charge distribution for the Al₂O₃–Ni–N system. It is observed that some of the eight attention heads give large weights to the attention scores of the single metal atom and proton. This is expected as the single metal atom bonds with the N adsorbate, and proton imposes the additional negative charge on the surface. Conceivably, both of these atoms would play an important role on the adsorption energy and forces of the system. However, a notable correlation is also observed between some of the attention heads and the partial charge of atoms. Fig. 8(a) demonstrates the importance of the closest 19 atoms in the Al₂O₃ support to the N adsorbate, as captured by the third attention head of the Equiformer block B8 for the Al₂O₃–Ni–N system. An atom with a color closer to purple has a larger attention score, demonstrating a more significant contribution to the N adsorbate. The contributions of Ni atoms and protons are not considered, as they both hold a large amount of charge. Fig. 8(b) illustrates the Mulliken charge distribution on the 19 atoms. Here, a deeper red color indicates a stronger positive charge on aluminum, while a deeper blue color indicates a stronger negative charge on oxygen. The correlation between the attention scores and the absolute Mulliken charges tends to be inverse. That is, an oxygen atom with deeper blue color (i.e., more negatively charged) in Fig. 8(b) shows a smaller attention score, as indicated by lighter purple in Fig. 8(a). Alternatively, an aluminum atom with a more positive charge (deeper red) in Fig. 8(b) has a lower attention score, as shown in orange in Fig. 8(a). This can be attributed to the excess negative charge on the surface that modifies the reactivity of the surface atoms. The adsorption energy of an adsorbate would be affected by the distribution of the excess negative charge on the surface. Hence, the distribution of the excess surface charge introduced on the catalyst surface, calculated in terms of Mulliken charges, is a strong indicator of the effect of surface charge on adsorption energies. Less absolute charge on Al and O atoms receiving higher attention scores could mean that these atoms affect the distribution of additional charge on the surface more significantly than other Al and O atoms, as their Mulliken charges differ from other Al and O atoms highlighted in Fig. 8. The inverse correlation between the attention score and the absolute surface charge distribution is also validated through Spearman correlation analysis,⁵⁴ which measures the strength of association based on the ranking of values. This analysis results in a correlation coefficient of −0.68 and a p-value of 0.0021, indicating a strong correlation between the attention score and the absolute surface charge distribution. Notably, the inputs to the dual-model framework shown in Fig. 4 are solely structural (atom types, edges and distances between atoms), without any explicit charge information. This highlights the ability of the attention mechanism to infer underlying physical concepts. Similar analyses for the other single metal atoms and adsorbates consistently show strong correlations between the attention scores and the Mulliken charges, with absolute values of Spearman correlation coefficients ranging between 0.6 to 0.8 and p values always less than 0.01, further demonstrating the model's interpretability. Such interpretable attention-based models can highlight the key atoms in a catalyst structure that have significant interactions with the adsorbate, beyond the Mulliken net charge effects considered in this study. These insights can in turn inform further targeted DFT studies on these surface atoms for catalyst design and discovery. Furthermore, Mulliken net charge effects could be isolated by treating them as additional learning targets, similar to atomic forces. This could enhance the interpretability of attention-based models, enabling a deeper understanding of how surface charge would impact the catalyst.

Fig. 8 (a) Visual representation of scores of the third attention head of the Equiformer block B8 of the dual-model framework in Fig. 4 for the Al₂O₃–Ni–N system. These scores weigh the influence of the closest 19 atoms in the Al₂O₃ support to the nitrogen adsorbate, while the attention scores for Ni and proton are omitted. (b) Visualization of the Mulliken net charge calculated by CP2K for the same 19 atoms. Darker red signifies a larger positive charge on Al, whereas a deeper blue denotes a larger negative charge on O. The color bar in (b) is a merged scale for both negative and positive charges, meaning no atom holds exactly zero charge.

3.3 Task 3: transfer learning from single atoms to metal clusters

The first transfer learning task focused on a system composed of Al₂O₃, a single metal atom, and an adsorbate. In practice, however, catalytic systems typically involve metal clusters on a support. Due to the resource-intensive nature of DFT calculations for such systems, we look to investigate whether knowledge of simpler single metal atom systems under the impact of surface charge can be effectively transferred to complex metal cluster systems. To this end, we consider two distinct strategies S2 and S3, both of which use the single-metal-atom data, as detailed in Table 2. This is while the baseline strategy S1 fine-tunes the pre-trained model using the metal cluster data directly. The transfer learning strategies S1, S2 and S3 are applied to the model fine-tuning schemes L5, L5EF, L7 and L7EF, as summarized in Table 1. Fig. 9 shows the performance of the different fine-tuned models. In comparison with direct transfer learning using the Pt cluster data (strategy S1), the models fine-tuned using strategies S2 and S3 have a higher generalization performance despite their slightly lower test accuracy. The better generalization performance may be attributed to the initial model parameter updates for the single metal atom systems, which necessitates subsequent adjustments towards metal clusters during further fine-tuning, potentially causing information loss. Conversely, strategy S3 fine-tunes model parameters in a manner that benefits both the single metal atom and metal cluster systems. For example, not only does model L5-S3 almost match the test accuracy of model L5-S1, but it also yields more accurate predictions for the unseen Ru compared to model L5-S2. Similar trends are also observed for the other models fine-tuned using the S3 strategy. Additionally, it is seen that unfreezing more blocks of the pre-trained EquiformerV2 model would result in higher test accuracies, but at the expense of reduced extrapolation performance; for example, compare models L5-S3 and L7-S3, or L5EF-S3 and L7EF-S3. Among the 12 fine-tuned models in Fig. 9, model L7-S3 is considered to have the overall best performance, demonstrating both high test accuracy and extrapolation performance. This suggests that fine-tuning the pre-trained model using the mixture of single metal and metal cluster data in one shot (S3) can be a more effective transfer learning strategy than first performing the transfer learning from thermal to plasma catalysis using single metal atom and then fine-tuning the resulting model using the metal cluster data (S2).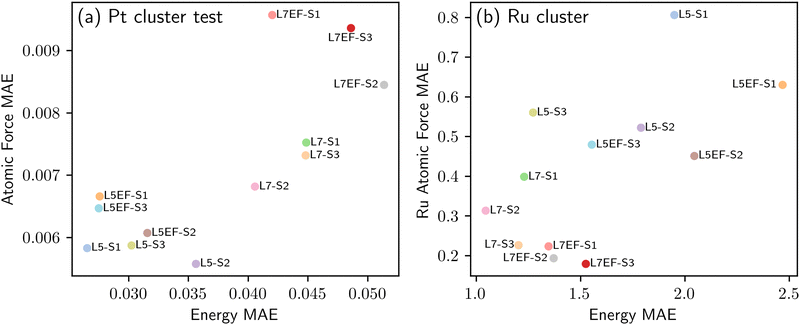

Fig. 9 Transfer learning from single atoms to metal clusters. Accuracy of the fine-tuned models of Table 2 in predicting the adsorption energy and atomic forces, as quantified in terms of mean absolute error (MAE). (a) Test accuracy of the fine-tuned models for the Pt cluster test data. (b) Predictive accuracy of the fine-tuned models for the unseen Ru cluster.

Fig. 9(b) suggests that model L7 has a superior extrapolation performance for predicting adsorption energy, whereas model L7EF is superior for predicting atomic forces. Fig. 10 shows the parity plots for predictions made by these two models when fine-tuned via the three transfer learning strategies of Table 2 for metal clusters. The results indicate that strategies S2 and S3, which include single-atom data, outperform strategy S1 in extrapolating energy and force predictions, as seen with model L7 in Fig. 10(a) and (b). While strategy S3 excels in predicting atomic forces (Fig. 10(d)) under model L7EF with even lower MAE for force predictions, it does not consistently provide the best energy predictions (Fig. 10(c)), highlighting the trade-off between predicting system energy and atomic forces in extrapolation tasks. While incorporating single-atom data clearly enhances transfer learning for metal clusters, the optimal strategy may depend on whether the focus is on energy or force predictions. We note that the particularly large deviation for strongly negative adsorption energies in the case of Ru clusters (Fig. 10(a) and (c)) can be attributed to the limited amount of training data with adsorption energies below −10 eV for Pt clusters, as shown in Fig. SP4 (ESI†). As such, the extrapolation to Ru clusters becomes more challenging, leading to underfitting in this energy range due to insufficient data.

Fig. 10 Parity plots of adsorption energy and atomic force predictions for unseen Ru metal clusters. (a) Predicted vs. actual adsorption energy for model L7 fine-tuned with transfer learning strategies S1, S2, and S3. (b) Predicted vs. actual atomic force for model L7 fine-tuned with S1, S2, and S3. (c) Predicted vs. actual adsorption energy for model L7EF fine-tuned with S1, S2, and S3. (d) Predicted vs. actual atomic force for model L7EF fine-tuned with S1, S2, and S3.

4 Conclusions and future work

This paper investigated how the extensive knowledge from thermal catalysis could be transferred to plasma catalysis in a systematic and interpretable manner, specifically addressing plasma–catalyst interactions involving surface charges. We employed a model pre-trained on the OC20 dataset, consisting of millions of DFT calculations for thermal catalysis. After fine-tuning the pre-trained model using limited plasma catalysis DFT data, the fine-tuned model exhibited accurate predictions of adsorption energies and atomic forces, as well as extrapolation capacity for unseen metals in the plasma catalysis data. This observation suggests that essential chemical kinetic information from thermal catalysis is preserved during transfer learning to plasma catalysis. Moreover, by leveraging the attention mechanism within the pre-trained model, we examined how attention scores could reveal the underlying physical phenomena in the data, namely the surface charge effects. We observed a strong correlation between the attention scores and surface charge distributions calculated using DFT, despite the model never encountering charge distribution data during the transfer learning task. This underscores the high interpretability of the attention mechanism. Additionally, we observed that metals with similar chemical properties clustered closely in the reduced-dimensional space. The attention scores highlighted the main surface atoms crucial for the adsorbate, suggesting that the attention mechanism could inform catalyst design for plasma catalysis by grouping metals and pinpointing pivotal surface atoms for manipulation. Lastly, we examined how pre-trained models for simpler single-metal-atom systems could be transferred to more complex metal cluster systems.

Our future work will focus on studying a broader range of plasma–catalyst interactions to further evaluate the effectiveness of transfer learning approaches for developing more comprehensive plasma–catalyst interaction models. Larger and more diverse plasma catalysis datasets will likely improve the quality of transfer learning. Additionally, we will incorporate Mulliken net charge as an extra prediction target to explore whether it enhances the GNN's learned representations. Furthermore, we will integrate predictions of atomic forces and adsorption energies with microkinetic models to enable holistic investigations of plasma–catalyst synergies and reaction mechanisms in plasma–catalytic systems, towards experimental validation of the presented approach.

Author contributions

Conceptualization: KS, ADL, and AM. Data curation: KS and ADL. Formal analysis: KS and ADL. Funding acquisition: AM and YY. Methodology: KS, ADL, and AM. Software: KS, ADL, and ZS. Supervision: AM and YY. Visualization: KS, ADL, and VVM. Writing – original draft: KS, ADL, and AM. Writing – review & editing: all authors.

Data availability

Source data are provided with this paper. The data from DFT calculations can be found at https://www.github.com/wwwccttoo/ocp. These data are available in the form of both CP2K output files and processed Python-readable databanks. The data used for producing figures can also be found in the same repository. Code availability: the scripts for DFT calculations and transfer learning can be found at https://www.github.com/wwwccttoo/ocp.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. Shao and A. Mesbah acknowledge support from the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences, under award DE-SC0020232. Y. Ju was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under award DE-SC0023357 (multiscale modeling), Fusion Energy Sciences, under award DE-SC0025371 and the Energy Earthshot Initiative as part of Plasma-Enhanced H2 Production (PEHPr) Energy Earthshot Research Center (EERC) at Princeton Plasma Physics Laboratory under contract DE-AC0209CH11466 (nonequilibrium catalysis). This work used SDSC Expanse CPU and SDSC Expanse Projects Storage at San Diego Supercomputer Center (SDSC) through allocation CHM230049 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by the National Science Foundation grants 2138259, 2138286, 2138307, 2137603, and 2138296.

Notes and references

1. A. H. Khoja, M. Tahir and N. A. S. Amin, Fuel Process. Technol., 2018, 178, 166–179.
2. K. H. Rouwenhorst, F. Jardali, A. Bogaerts and L. Lefferts, Energy Environ. Sci., 2021, 14, 2520–2534.
3. K. H. Rouwenhorst, Y. Engelmann, K. van’t Veer, R. S. Postma, A. Bogaerts and L. Lefferts, Green Chem., 2020, 22, 6258–6287.
4. B. Patil, Q. Wang, V. Hessel and J. Lang, Catal. Today, 2015, 256, 49–66.
5. H. Chen, D. Yuan, A. Wu, X. Lin and X. Li, Waste Disposal Sustainable Energy, 2021, 3, 201–217.
6. W. Wang, B. Patil, S. Heijkers, V. Hessel and A. Bogaerts, ChemSusChem, 2017, 10, 2145–2157.
7. Z. Huang, A. Xiao, D. Liu, X. Lu and K. Ostrikov, Plasma Processes Polym., 2022, 19, 2100198.
8. P. Mehta, P. Barboun, F. A. Herrera, J. Kim, P. Rumbach, D. B. Go, J. C. Hicks and W. F. Schneider, Nat. Catal., 2018, 1, 269–275.
9. K. H. Rouwenhorst, H. G. Burbach, D. W. Vogel, J. N. Paul, B. Geerdink and L. Lefferts, Catal. Sci. Technol., 2021, 11, 2834–2843.
10. P. M. Barboun, L. L. Daemen, C. Waitt, Z. Wu, W. F. Schneider and J. C. Hicks, ACS Energy Lett., 2021, 6, 2048–2053.
11. J. Xu, P. Xia, Q. Zhang, F. Guo, Y. Xia and H. Tian, Int. J. Hydrogen Energy, 2021, 46, 23174–23189.
12. X. Pei, D. Gidon, Y.-J. Yang, Z. Xiong and D. B. Graves, Chem. Eng. J., 2019, 362, 217–228.
13. M. L. Carreon, J. Phys. D: Appl. Phys., 2019, 52, 483001.
14. Y. Wang, M. Craven, X. Yu, J. Ding, P. Bryant, J. Huang and X. Tu, ACS Catal., 2019, 9, 10780–10793.
15. F. Che, J. T. Gray, S. Ha and J.-S. McEwen, ACS Catal., 2017, 7, 551–562.
16. K. H. Rouwenhorst and L. Lefferts, J. Phys. D: Appl. Phys., 2021, 54, 393002.
17. P. Ambrico, M. Ambrico, A. Colaianni, L. Schiavulli, G. Dilecce and S. De Benedictis, J. Phys. D: Appl. Phys., 2010, 43, 325201.
18. Y. Xu, N. Liu, Y. Lin, X. Mao, H. Zhong, Z. Chang, M. N. Shneider and Y. Ju, Nat. Commun., 2024, 15, 3092.
19. M. Bonn, S. Funk, C. Hess, D. N. Denzler, C. Stampfl, M. Scheffler, M. Wolf and G. Ertl, Science, 1999, 285, 1042–1045.
20. T. Hertel, M. Wolf and G. Ertl, J. Chem. Phys., 1995, 102, 3414–3430.
21. I. Adamovich, S. Agarwal, E. Ahedo, L. L. Alves, S. Baalrud, N. Babaeva, A. Bogaerts, A. Bourdon, P. Bruggeman and C. Canal, et al. , J. Phys. D: Appl. Phys., 2022, 55, 373001.
22. T.-W. Liu, F. Gorky, M. L. Carreon and D. A. Gómez-Gualdrón, ACS Sustainable Chem. Eng., 2022, 10, 2034–2051.
23. K. M. Bal, S. Huygh, A. Bogaerts and E. C. Neyts, Plasma Sources Sci. Technol., 2018, 27, 024001.
24. A. D. Lele, Y. Xu and Y. Ju, Phys. Chem. Chem. Phys., 2024, 26, 9453–9461.
25. K. Shao and A. Mesbah, JACS Au, 2024, 4(2), 525–544.
26. M. P. Andersson, T. Bligaard, A. Kustov, K. E. Larsen, J. Greeley, T. Johannessen, C. H. Christensen and J. K. Nørskov, J. Catal., 2006, 239, 501–506.
27. M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C.-T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli and P. Brodersen, et al. , Nature, 2020, 581, 178–183.
28. L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho and W. Hu, et al. , ACS Catal., 2021, 11, 6059–6072.
29. M. Wan, H. Yue, J. Notarangelo, H. Liu and F. Che, JACS Au, 2022, 2, 1338–1349.
30. J. Zhang, C. Wang, S. Huang, X. Xiang, Y. Xiong, B. Xu, S. Ma, H. Fu, J. Kai and X. Kang, et al. , Joule, 2023, 7, 1832–1851.
31. K. Weiss, T. M. Khoshgoftaar and D. Wang, J. Big Data, 2016, 3, 1–40.
32. A. Kolluru, N. Shoghi, M. Shuaibi, S. Goyal, A. Das, C. L. Zitnick and Z. Ulissi, J. Chem. Phys., 2022, 156, 184702.
33. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54(16), 11169–11186.
34. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59(3), 1758–1775.
35. X. Wang, J. Musielewicz, R. Tran, S. K. Ethirajan, X. Fu, H. Mera, J. R. Kitchin, R. C. Kurchin and Z. W. Ulissi, Mach. Learn.: Sci. Technol., 2024, 5, 025018.
36. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser and I. Polosukhin, Adv. Neural Inf. Process. Syst., 2017, 30, 1–11.
37. S. Serrano and N. A. Smith, arXiv, 2019, preprint, arXiv:1906.03731 DOI:10.48550/arXiv.1906.03731.
38. K. Schütt, P.-J. Kindermans, H. E. Sauceda Felix, S. Chmiela, A. Tkatchenko and K.-R. Müller, Adv. Neural Inf. Process. Syst., 2017, 30, 1–11.
39. J. Gasteiger, F. Becker and S. Günnemann, Adv. Neural Inf. Process. Syst., 2021, 34, 6790–6802.
40. Y.-L. Liao, B. Wood, A. Das and T. Smidt, arXiv, 2023, preprint, arXiv:2306.12059 DOI:10.48550/arXiv.2306.12059.
41. A. Bogaerts, X. Tu, J. C. Whitehead, G. Centi, L. Lefferts, O. Guaitella, F. Azzolina-Jury, H.-H. Kim, A. B. Murphy and W. F. Schneider, et al. , J. Phys. D: Appl. Phys., 2020, 53, 443001.
42. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al. , J. Chem. Phys., 2020, 152, 194103.
43. A. Wang, J. Li and T. Zhang, Nat. Rev. Chem., 2018, 2, 65–81.
44. F. Zhuang, Z. Qi, K. Duan, D. Xi, Y. Zhu, H. Zhu, H. Xiong and Q. He, Proc. IEEE, 2020, 109, 43–76.
45. M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, J. Catal., 2004, 226, 54–68.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
47. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
48. G. J. Martyna and M. E. Tuckerman, J. Chem. Phys., 1999, 110, 2810–2821.
49. D. A. Yarne, M. E. Tuckerman and G. J. Martyna, J. Chem. Phys., 2001, 115, 3531–3539.
50. F. Peeters, R. Rumphorst and M. Van De Sanden, Plasma Sources Sci. Technol., 2016, 25, 03LT03.
51. Q.-Z. Zhang, W.-Z. Wang and A. Bogaerts, Plasma Sources Sci. Technol., 2018, 27, 065009.
52. L. R. Winter, B. Ashford, J. Hong, A. B. Murphy and J. G. Chen, ACS Catal., 2020, 10, 14763–14774.
53. S. Lundberg, arXiv, 2017, preprint, arXiv:1705.07874 DOI:10.48550/arXiv.1705.07874.
54. L. Myers and M. J. Sirois, Spearman Correlation Coefficients, Differences Between, in Encyclopedia of Statistical Sciences, ed. S. Kotz, N. Balakrishnan, C. B. Read and B. Vidakovic, 2nd edn, John Willey and Sons, Hoboken, pp. 7901–7903.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ey00256c

‡ A. D. Lele is currently with the Department of Mechanical Engineering, Rowan University, Glassboro, USA.

§ Fine-tuning of all the pre-trained models is based on the same setting as in OC20, but a different batch size of 4 and number of epochs 100 were used. We used a batch size of 4, since for GNNs the batch size refers to the number of graphs used during training. In this study, each graph consists of around 240 atoms and approximately 240 × 21 = 5040 edges, creating a substantial load on the GPUs. We utilized four GPUs with 12 GB of memory, each capable of processing only one graph at a time. We observed that increasing the batch size would yield minimal improvement in the transfer learning results. Therefore, we opted to use a batch size of 4 for computational efficiency.

---