 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Heating dictates the scalability of CO2 electrolyzer types†
Jan-Willem
Hurkmans
a,
Henri M.
Pelzer
a,
Tom
Burdyny
 a,
Jurriaan
Peeters
b and
David A.
Vermaas
a,
Jurriaan
Peeters
b and
David A.
Vermaas
 *a
*a
aDepartment of Chemical Engineering, Delft University of Technology, 2629 HZ Delft, The Netherlands. E-mail: D.A.Vermaas@tudelft.nl
bProcess & Energy Department, Delft University of Technology, 2628 CB Delft, The Netherlands
First published on 27th December 2024
Abstract
Electrochemical CO2 reduction offers a promising method of converting renewable electrical energy into valuable hydrocarbon compounds vital to hard-to-abate sectors. Significant progress has been made on the lab scale, but scale-up demonstrations remain limited. Because of the low energy efficiency of CO2 reduction, we suspect that significant thermal gradients may develop in industrially relevant dimensions. We describe here a model prediction for non-isothermal behavior beyond the typical 1D models to illustrate the severity of heating at larger scales. We develop a 2D model for two membrane electrode assembly (MEA) CO2 electrolyzers; a liquid anolyte fed MEA (exchange MEA) and a fully gas fed configuration (full MEA). Our results indicate that full MEA configurations exhibit very poor electrochemical performance at moderately larger scales due to non-isothermal effects. Heating results in severe membrane dehydration, which induces large Ohmic losses in the membrane, resulting in a sharp decline in the current density along the flow direction. In contrast, the anolyte employed in the exchange MEA configuration is effective in preventing large thermal gradients. Membrane dehydration is not a problem for the exchange MEA configuration, leading to a nearly constant current density over the entire length of the modeled domain, and indicating that exchange MEA configurations are well suited for scale-up. Our results additionally indicate that a balance between faster kinetics, higher ionic conductivity, smaller pH gradients and lower CO2 solubility causes an optimum operating temperature between 60 and 70 °C.
Broader contextIn order to meet the goals set by the European Union to become climate-neutral by 2050, the industrial- and transport sectors will have to be de-fossilized. Electrification and implementation of hydrogen shows great potential in replacing fossil fuels, however certain hard-to-abate sectors such as airline travel and chemical manufacturing are very challenging to decarbonize and projected to still require hydrocarbon sources in 2050. These necessary hydrocarbon chemicals and fuels, responsible for 10–20% of the global greenhouse gas emission, can be produced sustainably by the electrolysis of captured CO2 using renewable electricity. While the figures for renewable hydrocarbon fuels (e-liquids) and carbon-based chemicals (methanol, ethylene, etc.) are astronomical and urgent, the knowledge about CO2 electrolysis upscaling is very limited. Heat management will be a crucial factor for successfully upscaling CO2 electrolysis, as the high overpotentials for CO2 reduction render approximately 50% of the electrolyzer's energy input to heat, and the reaction kinetics and CO2 solubility are sensitive to temperature. Therefore, understanding heat sources and temperature distributions are a necessity for developing the urgently demanded electrochemical CO2 conversion. |
Introduction
Hydrocarbon chemicals and fuels can be produced sustainably by the electrolysis of captured CO2 using renewable electricity.1,2 CO2 electrolyzers, to synthesize a variety of products including CO, formate or C2+ hydrocarbons, have seen significant developments over the last two decades and reports of industrially relevant current densities become more and more frequent on the lab scale.3–6 As the geometric size of CO2 electrolyzers increases, however, additional factors must be considered to enable lab-scale performance demonstrations to be replicated for larger systems. Many previous works have already identified and addressed operational issues such as mass transport limitations at high current density,7–9 flooding and pressure control for taller electrolyzers,10,11 salt precipitation and CO2 crossover.12–16 One aspect not well-considered so far is how the substantial amount of heat generated in a CO2 electrolyzer will impact operation at larger scales. To determine these effects the heat- and temperature distributions inside a CO2 electrolyzer are required, which are currently largely unknown.We expect that the generation of heat in large-scale CO2 electrolyzers can cause more substantial constraints compared to e.g. fuel cells and PEM electrolyzers, as CO2 electroreduction suffers from high overpotentials and homogeneous reactions in the anolyte- and ionomer-phase add an additional source of heat. Moreover, large interfacial- and Ohmic losses can be expected within these electrochemical cells since components such as membranes have not been tailored for CO2 reduction.17 Combined with the inherent poor heat transfer characteristics of gas diffusion electrode (GDE) configurations, it is important to understand where large thermal gradients exist and if these limit system performance or scalability. Accordingly, it is important to understand and predict heating phenomena in order to realize CO2 electrolysis on an industrial scale.
It is understood that many aspects of the electroreduction of CO2 are influenced by temperature as shown by experimental studies using different initial operating conditions. Löwe et al. varied the operating temperature for a GDE based system between 20 and 70 °C finding an optimum performance at 50 °C.18 The authors attribute this optimum to the fact that while mass transport and the kinetics are enhanced at higher temperatures, the solubility of CO2 in water significantly decreases with temperature. Similar optima were observed for the electroreduction of CO2 using membrane electrode assembly (MEA) configurations employing poly(aryl piperidinium)-based anion exchange membranes (AEM) and alkaline polymer electrolyte membranes with pure water as electrolyte.3,19 The magnitude of heating at industrially relevant conditions has only been reported in two modeling studies by Weng et al.20,21 However, these models are implemented in a one-dimensional domain which cannot fully capture the extent of the non-isothermal effects due to the exclusion of down-the-channel effects which have been shown to vary significantly.22,23 Thus the temperature development along a flow channel which can impact hydration, current density distribution and CO2 solubility have yet to be understood.
In this study, we develop a two-dimensional model displaying large-scale heating effects of an electrolyzer, with an emphasis on the temperature profile from inlet to outlet. We aim to compare temperature distributions for two AEM-based MEA configurations (full MEA and exchange MEA), producing CO from CO2, utilizing an IrO2 anode and an Ag cathode, respectively, to investigate their thermal scalability. In our model, CO is considered the only product for CO2R competing with the hydrogen evolution reaction (HER). However, the thermoneutral potential of CO2R to CO is in the same order of magnitude as the thermoneutral potential of other gaseous CO2R products like ethylene (C2H4) implying similar heating rates for MEA configurations aiming to produce other gaseous products than CO.24
The model underlines the significance of heating and thus the analysis of non-isothermal effects, necessary to further understand the multi-scale phenomena at play in CO2 electrolyzers. Our results demonstrate that the temperature within the cell can differ more than 10 °C in a 20 cm tall cell, depending on the MEA configuration and current density.
Model development
The Multiphysics model developed in this work is an expansion based on the seminal one dimensional model developed by Weng et al. for CO2 MEA electrolyzers.20,21 We consider two 2D electrolyzer configurations schematically shown below; an exchange MEA which is supplied with saturated 0.5 M KHCO3 electrolyte to the anode and a full MEA which is supplied with fully humidified gas (Fig. 1a and b). This choice of electrolyte and electrode configuration is to illustrate the cases with minimal resistance, which can be considered as conservative heating scenarios. | ||
| Fig. 1 Schematic representations of the computational domains used in this work. The feed flows in the y-direction whereby the serpentine motion is neglected for simplicity. (a) Full MEA configuration is fed with a gaseous feed at both anode and cathode. (b) Exchange MEA configuration is fed liquid electrolyte at the anode side. The cathode compartment is fed humidified CO2. Details regarding dimensions are provided in the ESI,† Table S8. | ||
In order to simulate an MEA configuration in a scaled-up setting, the computational domain includes bipolar plates that separate MEA cells. Periodic boundary conditions for the temperature field are implemented for the outer boundaries along the y-direction. This resembles a stack that is sufficiently large to neglect heat dissipation via the walls. The flow path of the model is 20 cm, whereby the serpentine geometry is neglected which means that the depth of the flow channel is infinite. We recognize that not taking into account the three-dimensional geometry will result in discrepancies with heat transfer in reality, our goal however is to give an idea of the heat development in an idealized electrolyzer. Non-steady-state phenomena of importance like flooding and salt formation are out of the scope of this work and thus not covered. Further, the model neglects contact resistances as the used configuration most closely resembles a catalyst-coated membrane (CCM). The model validation as well as an in depth comparison between the model and experimental work can be seen in Section 1 of the ESI.†
The gaseous compartments contain GDEs constructed of a fibrous diffusion media through which the gaseous species diffuse to- and from the catalytic layers. The catalytic layers are a very thin multiphase domain which consists of a mixture of anion exchange ionomer, catalytic particles and void whereby it is assumed that the catalytic particles are homogeneously coated with a thin film of the ionomer which acts as the electrolyte as it contains a significant amount of water. At the surface of the catalytic particles, heterogeneous electrochemical reactions take place (Fig. 1a).
The porous domains are modeled as a volume averaged medium, thereby ignoring local heterogeneities. While exchange MEA configurations historically use a mesh as the anode, the anode in this work resembles a catalyst coated membrane which has shown to greatly improve electrochemical performance.3,4 The two catalytic layers sandwich an AEM which allows for an ionic current due to the simultaneous diffusion and migration of dissolved charged species. We apply a volumetric flow rate of CO2 of 50 SCCM per cell, which is sufficient to reach high faradaic efficiencies considering the dimensions of our models and the maximum investigated current density.25 For a serpentine flow channel, this translates to an average gas velocity of approximately 3 m s−1 for a cross-sectional area of 0.25 mm2. The liquid flowrate is taken as 5 SCCM. The following sections will present the key assumptions and governing equations (variables and governing equations that are not essential with respect to the results are provided in Section 7 of the ESI†). General parameters regarding operating conditions are provided in Table 1. Details regarding dimensions, parameters and variables are provided in Table S8 (ESI†). A comparison to the model by Weng et al. and to experimental work is given in Section 1 of the ESI.† Details regarding the meshes used in the simulations are provided in ESI,† Section 5.
| Parameter | Description | Value | Unit | Ref. |
|---|---|---|---|---|
| P op | Operating pressure | 1 | atm | — |
| T op | Operating (inlet) temperature | 20 | °C | — |
| ū l | Average liquid velocity | 0.3 | m s−1 | — |
| ū g | Average gas velocity | 3 | m s−1 | — |

|
Porosity CL | 0.675 | — | 26 |

|
Ionomer fraction CL | 0.225 | — | [ESI, Section 7.5] |

|
Solid fraction CL | 0.1 | — | [ESI, Section 7.5] |
| a v,CL | Active specific surface area CL | 6 × 106 | m−1 | 26 |

|
Porosity diffusion medium | 0.8 | — | 27 |
| c KHCO3 | Concentration anolyte | 0.5 | M | — |
In order to simulate large scale electrolyzer behavior, an expansion method is employed which essentially decomposes the computational domain in small sub cells which are solved sequentially.22 The applied potential is kept constant over the entire geometry, which allows the current density to change along the channel length, capturing local variations across the electrode. The domains are electrically homogeneous, and we assume no contact resistance between them. A detailed description and validation of this approach is given in ESI,† Section 2.
In the anode catalytic domain we consider the oxygen evolution reaction (OER) on an IrO2 catalyst through both the acidic pathway and the alkaline pathway, respectively:
| 2H2O → O2 + 4H+ + 4e− | (1) |
| 4OH− → O2 + 2H2O + 4e− | (2) |
| CO2 + H2O + 2e− → CO + 2OH− | (3) |
| 2H2O + 2e− → H2 + 2OH− | (4) |
 | (5) |
| ηk = (ϕs − ϕl) − Ueq,k | (6) |
 | (7) |
 | (8) |
The electric potential and the electrolyte potential required to solve for the current densities are determined by solving the following charge conservation equations for the electrolyte phase and the solid phase:
| il = −σl,eff∇ϕl is = −σs,eff∇ϕs | (9) |
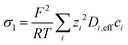 | (10) |
Water transport in ionomer domains
The membrane is one of the key components within a MEA-based electrolyzer as it transports water, ions and thermal energy and its associated transport properties can vary greatly depending on operating conditions. As such, it can have major implications on the modeling results. We will follow the mathematical transport model for proton exchange membrane (PEM) transport by Weber et al.38,39 While CO2 electrolyzers typically employ AEMs, similar transport behavior has been observed experimentally.40–42 The transport model builds on the notion that two types of transport modes co-exist depending on whether the membrane is equilibrated with liquid water or with water vapor. The balance of these transport modes are dependent on the dimensionless water content of the ionomer, commonly denoted with λ. λ depends on the water activity, aw [−], and the state of the membrane, which is expressed through the fraction of expanded channels, S [−]. The method used to compute S, and subsequently λ, is given in the ESI† (Section 7.3). The water activity aw, required for λ, is derived from the gradient in chemical potential of water in the ionomer phase, ∇μw, defined as: | (11) |
 is the molar volume of liquid water and pl [Pa] is the liquid pressure relative to a reference pressure. The ∇μw is solved from the conservation equation for the water content:
is the molar volume of liquid water and pl [Pa] is the liquid pressure relative to a reference pressure. The ∇μw is solved from the conservation equation for the water content: | (12) |
Transport and interactions of dissolved species
In the electrolyte and ionomer phase domains the concentrations of the species OH−, H+, HCO3−, CO32−, K+ and CO2 [M] are simulated. The gaseous products found in eqn (1)–(4) have a very low solubility in water and are therefore neglected. The conservation of species i is computed with the steady state Nernst–Planck equation: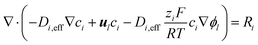 | (13) |
 is used to compute the concentration distribution of the inert ion K+ from the remaining species. For the full MEA model, this approach is problematic since the amount of K+ in a vapor-equilibrated AEM is finite and relatively small, resulting in negative K+ concentrations. In order to prevent charge separation and ensure physical concentrations everywhere, the Nernst–Planck equation is adjusted with an artificial charge separation limiting term to ensure a homogeneous charge distribution. Details and argumentation for this adjustment can be found in the ESI,† Section 3.
is used to compute the concentration distribution of the inert ion K+ from the remaining species. For the full MEA model, this approach is problematic since the amount of K+ in a vapor-equilibrated AEM is finite and relatively small, resulting in negative K+ concentrations. In order to prevent charge separation and ensure physical concentrations everywhere, the Nernst–Planck equation is adjusted with an artificial charge separation limiting term to ensure a homogeneous charge distribution. Details and argumentation for this adjustment can be found in the ESI,† Section 3.
At the interface of electrolyte and the ionomer phase, a Donnan potential (Δϕl,Donnan [V]) arises which creates an energy barrier for oppositely charged species (relative to the membrane background charge) to enter, resulting in the partial exclusion of co-ions. The relationship used to relate the potential jump to the concentration difference of species i between electrolyte and ionomer phase is:
 | (14) |
The temperature dependent diffusion coefficients, Di,w [m2 s−1], in the liquid domain are given in Table S6 (ESI†). Inside the ionomer phase, the coefficients are corrected for the membrane water content, λ, following Grew et al.:43,44
 | (15) |
In the ionomer- and liquid domains, the following homogeneous reactions take place:
 | (16) |
 | (17) |
 | (18) |
 | (19) |
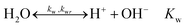 | (20) |
Momentum and gaseous species transport
A Poiseuille flow profile is assumed for the velocity fields in the gas and liquid compartment (uy = −6ū[(x/Wchannel)2 − x/Wchannel]), where ū [m s−1] is the average velocity. It is important to note that the evolution of gas bubbles in the liquid compartment will likely distort the parabolic velocity profile. Additionally, the presence of bubbles in this domain will affect the effective liquid properties. Nevertheless, the thermal properties in the exchange MEA cell configuration are mainly governed by the flow rate of the liquid electrolyte phase, which remains constant along the channel. Thus, bubble formation is expected to not strongly affect the average temperature profile and is therefore neglected, as the accurate simulation of bubble formation would extend the computational complexity of this work.In the gaseous porous domains, the flow is computed with Darcy's law. The transport of gaseous species are solved with the Maxwell–Stefan model whereby the temperature dependence of the gaseous diffusion coefficients is incorporated using the framework of Fuller et al.48 For details regarding the governing equations concerning mass and momentum transport in the gas phase, the reader is pointed towards the ESI,† Section 7.1.
Heat transfer
The steady state thermal energy balance summed over all domains can be written as: | (21) |
1. Irreversible reaction heating – The heat associated with the irreversible losses due to the activation potential of the charge transfer reaction k is:
 | (22) |
2. Reaction entropy heating – The heat related to the reversible entropy change of the charge transfer reaction k is:
 | (23) |
 . The Peltier coefficients used in this modeling study are based on the values used by Weng et al., who averaged the values of several experimental studies.20,49
. The Peltier coefficients used in this modeling study are based on the values used by Weng et al., who averaged the values of several experimental studies.20,49
3. Ohmic heating – The heat associated with resistive losses of the conducting medium are expressed as:
 | (24) |
4. Enthalpy change of homogeneous reactions – The heat associated with the homogeneous reactions (such as carbonate buffering) in the electrolyte domains are determined by the enthalpy change of said reaction determined by the Van't Hoff Equation for a homogeneous reaction j:
 | (25) |
5. Heat of vaporization – The enthalpy change related to the phase changes of water is accounted for with:
| QPT = ΔHw,vapRw,PT | (26) |
Results and discussion
Significant thermal gradients develop in MEA configurations
Using the expansion method (ESI,† Section 2) it is possible to simulate the two dimensional electrolyzer in the flow-direction. Fig. 2 shows the results for an exchange MEA configuration, where we applied constant potentials along the length, to iteratively calculate the temperature and current density profiles, and arrive at average current densities of 250, 500 and 750 mA cm−2 for a down-the-channel length of 20 cm.Unsurprisingly, higher applied potentials result in higher current densities and larger thermal gradients (Fig. 2d). Considering the chosen channel thickness (0.5 mm), the gradient perpendicular to the electrode is an order of magnitude higher than the gradient along the fluid flow, with a peak temperature in the cathodic catalytic domain (Fig. 2a–c). This peak at the cathode is caused by the higher overpotentials of the COER compared to the OER and the high enthalpy change of carbonate buffering in the cathode (eqn (18) and (19)) compared to the anode. Both contributions completely overshadow the cooling due to the heat of vaporization and the reaction entropy changes within this domain.
In the electrolyte compartment, the thermal boundary layer has not yet penetrated the full width of the channel after 20 cm. Conversely, the thermal boundary layer in the gas compartment already fully develops in the first 4 cm, indicated by the linear temperature profiles within this domain. The faster boundary layer development in the gas phase can be attributed to the lower Prandtl in the gas phase compared to the liquid phase, which is approximately 10× as low at ambient conditions. Over the entire simulated length, the current density is relatively constant, indicated by the local current density of 98–102% of the average current density (Fig. 2e). The current density gradually increases with the increasing temperature, due to faster kinetics at higher temperature, until the temperature becomes sufficiently high to cause mass transfer limitations as the solubility of CO2 decreases with temperature (Fig. 2f). As the average current density increases, the peak in local current density shifts to an earlier position in the flow cell, because the temperature increases faster. In our study, CO2 does not deplete in the bulk gas phase, since a sufficiently high enough gas flow rate has been chosen.
We note that the overall temperature differences across the geometry are relatively mild for the exchange MEA configuration; even at a high current density of 750 mA cm−2 the temperature increase is no more than 10 degrees after 20 cm. The anolyte is highly effective in transporting heat from the catalytic domains to the outflow, owing to its superior thermophysical properties of water relative to the gas phase. In practice, the heat transfer to the anolyte is likely affected by bubble-induced convection and local changes in thermophysical properties.50,51 The bubble-induced convection could theoretically increase the present heat transfer which would decrease the temperature increase in the exchange MEA electrolyzer. As mentioned above, however, the thermal properties are mainly influenced by the liquid electrolyte, hinting at a lesser importance of bubble formation for the thermal evaluation of an exchange MEA electrolyzer. Therefore, accurately predicting this multiphase phenomena is considered as beyond the scope of this work. In particular, the temperature rise at the walls  is relatively mild, due to the high thermal conductivity of the bipolar plates, reflecting a cooling mechanism in the bipolar plates. We also simulated the case without heat exchange to the bipolar plates, i.e. a single isolated exchange MEA (ESI,† Section 4). In this case, the bipolar plates and the periodic boundary conditions are omitted. This results in a larger temperature difference between the electrolyte- and gas compartment, peaking to 36 °C at the cathode and gas channel after 20 cm at 3.058 V. In comparison, this is 6 degrees higher than for the case with bipolar plates cooling, which is 60% more temperature rise. Consequently, the isolated exchange MEA reaches a lower average current density of 695 mA cm−2, at even slightly higher cell voltage, compared to the periodic case with an average of 750 mA cm−2.
is relatively mild, due to the high thermal conductivity of the bipolar plates, reflecting a cooling mechanism in the bipolar plates. We also simulated the case without heat exchange to the bipolar plates, i.e. a single isolated exchange MEA (ESI,† Section 4). In this case, the bipolar plates and the periodic boundary conditions are omitted. This results in a larger temperature difference between the electrolyte- and gas compartment, peaking to 36 °C at the cathode and gas channel after 20 cm at 3.058 V. In comparison, this is 6 degrees higher than for the case with bipolar plates cooling, which is 60% more temperature rise. Consequently, the isolated exchange MEA reaches a lower average current density of 695 mA cm−2, at even slightly higher cell voltage, compared to the periodic case with an average of 750 mA cm−2.
In an isothermal large-scale modeling study of a flowing-catholyte configuration performed by Blake et al., a significant decrease in current density was observed along the flow direction.22 It was attributed to pH gradients in the catholyte boundary layer, adjacent to the cathodic CL. Our results, using a configuration without catholyte layer, shows a relatively homogeneous current density, which minimizes the energy losses. In addition to the well-known breakthrough problem of flow catholyte configurations,52 this nearly constant current density over the entire length suggests that a MEA configuration is more suited for scaling up CO2 electrolysis.
For the full MEA, the profiles for temperature and current densities completely change (Fig. 3). The temperature profiles show significant thermal gradients, even at relatively low current densities. The temperature sharply increases over the first few centimeters (Fig. 3a–d), accompanied by a sharp reduction in current density (Fig. 3e). This drastic decrease in current density is directly correlated to the dehydration of the membrane, shown in Fig. 3f, which has also been observed in experimental work.53 The elevated temperatures in the catalytic domains locally lowers the saturated water vapor pressure thereby allowing water to evaporate from the ionomer phase. The decreased water content lowers the conductivity significantly resulting in high Ohmic losses. While the dehydration phenomena can be observed in 1D models,20 its severity is largely underestimated since along-the-channel effects are neglected. Due to the severity of the dehydration, it becomes clear why full MEA configurations for CO2 reduction are so difficult to realize.
The membrane dehydration becomes a serious concern in particular for high current densities. At higher current density, the temperature increases faster, which creates a positive feedback loop of faster dehydration (Fig. 3f), which in turn leads to more Ohmic heating and so on. At the highest applied potential (3.45 V cell voltage), the initial current density is over 400 mA cm−2, but decreases rapidly below 150 mA cm−2 within 3 cm flow height. Further pushing the cell voltage leads to relatively small increase in average current density; a substantial increase in cell voltage from 3.05 V (which is already higher than the highest voltage in the exchange MEA configuration) to 3.45 V, yields only ∼20% higher current density at y = 20 cm. The severity of the temperature-induced dehydration in the full MEA configuration is emphasized when realizing that the current density is 3.5× lower than for the exchange MEA, at a substantially higher cell voltage, while already assuming an optimistic case with bipolar plate cooling and relatively small channel length of 20 cm.
The significance of the Ohmic losses with respect to the total energy requirements for the full MEA can easily be observed when the energy losses of the two configurations are directly compared. Fig. 4 compares the polarization plots and breaks down the different losses according to the method described by Gerhardt et al.54 The difference in Ohmic losses becomes increasingly pronounced at higher current densities, while the other contributions only show minor differences. The results shown in Fig. 4 do not consider an expanded domain (i.e. y = 0). Therefore, even greater Ohmic losses are expected for along-the-channel results due to the significant decrease in water content as shown in Fig. 3f.
Higher feed temperatures boost performance of full MEA configuration
One way of countering membrane dehydration is simply supplying the system with more water. This can be achieved by increasing the temperature of the inlet gases while keeping the gas feed fully humidified, thereby increasing the partial pressure of water in the gas feed. We performed 1D simulations with fully humidified gas inlets at different inlet temperature conditions. The resulting cell voltage and water content (λ) for the full MEA configuration are in Fig. 5. The polarization curves in Fig. 5a indicate a significant reduction in power losses, especially at higher current densities where dehydration is particularly prevalent at near ambient conditions. Fig. 5b shows the corresponding average membrane water content which confirms the notion that the membrane is able to retain more water at higher feed temperatures. However, it is likely that dehydration will still be a problem for y > 0, which is not considered in the simulations for these results. We expect that significant gradients in the flow direction will still occur based on the results given in Fig. 3 which may lead to even higher temperatures and a higher probability of degradation. An alternative solution would be to periodically inject liquid electrolyte to improve hydration of membranes in full MEA systems.Dehydration is not an issue for exchange MEA configurations since the ionomer phase is in direct contact with liquid electrolyte at all times. Deviating from ambient temperatures may however still pose advantages. The polarization curves in Fig. 6a show that, dependent on the total current density, different optimum conditions exist. At current densities past 600 mA cm−2, the polarization curves of 60 and 70 °C essentially overlap and surpass 80 °C in terms of electrochemical performance. This agrees with the experimental observations by Löwe et al. who showed that the optimum performance is not obtained at the highest operating temperature.18
To elucidate the phenomena causing an optimum at 60–70 °C, we break down the energy losses again to differentiate between the kinetic, Nernstian, mass transfer and Ohmic losses for operating temperatures of 20, 50 and 80 °C, up to 1000 mA cm−2 (Fig. 6b).54 Unsurprisingly, for voltage losses due to reaction kinetics and Ohmic contributions decrease at higher operating temperatures. The higher losses due to CO2 mass transfer limitations reflect the reduced solubility of CO2 at higher temperatures. The Nernstian- and Kinetic losses are more complex and have intersecting curves. That is because both terms are temperature dependent, but also highly dependent on the local OH− concentration within the catalytic domains. The OH− concentration varies with temperature due to the temperature-dependence of the diffusion, but particularly because of slower water dissociation rates at higher temperatures. Overall, this results in milder pH gradients which reduce the Nernstian losses. The breakdown analysis also reveals the origin of the bend in the polarization curves for the exchange MEA around 100 mA cm−2. It can be attributed to the kinetic- and Nernstian losses, both of which are functions of the local pH, which undergoes a large shift in the catalytic domains as carbonate buffering becomes less effective at higher current densities.
Parasitic hydrogen evolution reaction in the full MEA configuration enhances dehydration
The faradaic efficiency (FE) of CO2 conversion is an important metric for determining its feasibility. Low FECOER can be a consequence of the contamination of the catalytic domain with metallic impurities. For example, work by Won et al. found that iron impurities decreased the FECOER from 80% to 20% in a matter of 30 minutes for the electrochemical reduction of CO2.55 As opposed to when COER and OER are prevalent (eqn (2) and (3)), occurrence of HER and OER (eqn (2) and (4)) will result in net water consumption. Combined with our observation that dehydration is already a significant problem for the full MEA configuration (Fig. 3), it is to be expected that a poor FE towards the COER will result in amplified dehydration.In order to illustrate this likely problem, the kinetic parameters of the HER were manually altered by multiplying the exchange current density of the HER with a factor Γ [−], reflecting the case of metallic impurities with a high affinity towards HER. Γ is varied between 1 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 which results in a FECOER varying between 0 and 1 as can be seen in Fig. 7a. In case of the unmodified kinetic parameters (Γ = 1), FECOER is 1 for almost the entire applied potential range. Fig. 7b shows the applied potential plotted against the partial current density towards the COER. With decreased FECOER, the required energy to synthesize CO increases significantly. The energy per produced CO increases rapidly both because the supplied energy is now channeled towards the HER, and partly because the Ohmic resistance increases due to the rapid membrane dehydration as shown in Fig. 7c.
000 which results in a FECOER varying between 0 and 1 as can be seen in Fig. 7a. In case of the unmodified kinetic parameters (Γ = 1), FECOER is 1 for almost the entire applied potential range. Fig. 7b shows the applied potential plotted against the partial current density towards the COER. With decreased FECOER, the required energy to synthesize CO increases significantly. The energy per produced CO increases rapidly both because the supplied energy is now channeled towards the HER, and partly because the Ohmic resistance increases due to the rapid membrane dehydration as shown in Fig. 7c.
Evaluating the heat generation mechanisms
In order to gain further insights into the heating phenomena and guide future simulation work, it is worthwile to breakdown the various heating generation terms. For this analysis, we focus on the heat generation in the catalytic layers and the membrane, since the majority of the heat is generated here. Absolute heating profiles for the exchange MEA given in Fig. 8a reveal that most thermal energy is generated in the catalyst layers, especially at the interface between the catalyst layer and the membrane (see inset). Although it is not surprising to observe a peak in heating rate at the interface where the electrochemical activity is concentrated, and in agreement with previous modeling work,21 the volumetric heating rate is an impressive 10–1000× larger at this interface compared to the rest of the catalytic domain. The heating profiles also suggest that the heating rate within the anodic catalyst layer is more significant, at most 150× higher at 750 mA cm−2. While the overpotential for the COER compared to that of the OER is higher, substantial cooling occurs within the cathodic catalytic domain as the reaction entropy term is negative resulting in a lower overall heating rate compared to the anodic catalytic domain.The heating rates in the considered domains are integrated and normalized with the total heating rate to yield the normalized heating contributions which are plotted for three current densities (Fig. 8b). For the full MEA, the increased resistance due to a reduced water content is represented by a significant increase of the Ohmic heating contribution. At a current density of 250 mA cm−2 at y = 0, the contribution is only 6% which increases to 25% at 750 mA cm−2. We can expect, based on the 2D results in Fig. 3, that the Ohmic losses are increasingly important for the full MEA when progressing further down the channel.
Besides the Ohmic heating, most heat is released in the form of irreversible reaction losses (i.e., reaction overpotentials), followed by heat associated to the enthalpy changes of the homogeneous reactions (such as carbonate buffering) and reaction entropy changes. Homogeneous reactions are sometimes omitted in models for simplicity, however as our models suggests, their high reaction rates in the catalytic domains play an integral role in the generation of heat. Additionally, their effect on the composition of the local micro-environment has a significant effect on the physical phenomena within the catalytic domains and they should therefore be included. The heating contribution due to the evaporation of water is insignificant for the full MEA configuration as the membrane water content is in equilibrium with the gaseous water content at steady state.
The normalized contribution for the exchange MEA shows a similar heating distribution whereby the most prevalent heating is because of irreversible reaction losses, examplifying the poor kinetics associated with electrochemical CO2 reduction. The ranking is followed by heating due to homogeneous reactions and entropy changes. Ohmic heating also shows an increasing contribution due to the quadratic nature of resistance, but is of a much lesser importance compared to the full MEA configuration as dehydration is insignificant. The continuous evaporation of water from the ionomer phase to the gas channel at the cathode side results in a cooling contribution which increases with current density. This can be attributed to the larger temperature gradients at higher current densities, leading to an increase in the local saturation vapor pressure which increases the driving forces for evaporation.
Conclusions
In this work, we developed a non-isothermal model capable of predicting large-scale 2D effects for the electrolysis of CO2 into CO using a MEA configuration. We observed that the majority of heat is produced within the catalytic domains because of the high overpotentials associated with the kinetics- and entropy changes of the charge transfer reactions as well as the homogeneous reactions such as carbonate buffering. Ohmic heating plays a major role in full MEA configurations since dehydration of the membrane greatly increases the resistance of the ionomer phase. This adverse effect becomes increasingly pronounced at higher current densities or when the faradaic efficiency for CO2 conversion decreases. Our two-dimensional model demonstrates significant thermal gradients, from 20 °C to 55 °C in 20 cm flow length, at an average current density of 210 mA cm−2. The dehydration and thermal gradients induce poor electrochemical performance. By operating at elevated temperatures, membrane dehydration can theoretically be mitigated as this allows for more water to be delivered to the system. Unfortunately, this only delays inevitable dehydration-related problems which suggests that full MEA configurations are not suitable for scale-up.In contrast, our simulations of the exchange MEA configurations indicate minor thermal gradients which have little to no effect on the electrochemical performance along the channel, indicating promising results for scale-up. The high performance is attributed to the high heat transfer rates of the anolyte as well as the superior mass transport of liquid-equilibrated membranes. The performance of an exchange MEA configuration can be further improved by tuning the feed temperature. In that case, a trade-off establishes between faster kinetics, higher ionic conductivity and smaller pH gradients at one hand, and lower CO2 solubility at the other hand, which predicts an optimum feed temperature between 60–70 °C.
Data availability
The complete models (as.mph COMSOL files), for both the exchange MEA and full MEA, including the model result and readme file, are available at Zenodo, with DOI https://doi.org/10.5281/zenodo.13379477. Additional results are available in the ESI.† This contains details about model expansions and validations, computational details and boundary conditions, parameters and additional equations, and temperature distributions for isolated MEAs.Conflicts of interest
There are no conflicts to declare.References
- W. J. Zhang, et al., Progress and Perspective of Electrocatalytic CO Reduction for Renewable Carbonaceous Fuels and Chemicals, Adv. Sci., 2018, 5(1), 1700275 CrossRef PubMed.
- J. Resasco and A. T. Bell, Electrocatalytic CO Reduction to Fuels: Progress and Opportunities, Trends Chem., 2020, 2(9), 825–836 CrossRef CAS.
- B. Endrődi, et al., High carbonate ion conductance of a robust PiperION membrane allows industrial current density and conversion in a zero-gap carbon dioxide electrolyzer cell, Energy Environ. Sci., 2020, 13(11), 4098–4105 RSC.
- K. U. Hansen, L. H. Cherniack and F. Jiao, Voltage Loss Diagnosis in CO2 Electrolyzers Using Five-Electrode Technique, ACS Energy Lett., 2022, 7, 4504–4511 CrossRef CAS.
- K. Fernández-Caso, et al., Electroreduction of CO2: Advances in the Continuous Production of Formic Acid and Formate, ACS Energy Lett., 2023, 1992–2024 CrossRef.
- Q. Chen, et al., Electrocatalytic CO2 Reduction to C2+ Products in Flow Cells, Adv. Mater., 2024, 36(5), 2303902 CrossRef CAS PubMed.
- F. P. G. de Arquer, et al., CO2 electrolysis to multicarbon products at activities greater than 1 A cm−2, Science, 2020, 367(6478), 661–666 CrossRef PubMed.
- B. Endrödi, et al., Operando cathode activation with alkali metal cations for high current density operation of water-fed zero-gap carbon dioxide electrolysers, Nat. Energy, 2021, 6(4), 439–448 CrossRef PubMed.
- Z. Abdin, C. J. Webb and E. M. Gray, Modelling and simulation of an alkaline electrolyser cell, Energy, 2017, 138, 316–331 CrossRef CAS.
- L. M. Baumgartner, et al., When Flooding Is Not Catastrophic-Woven Gas Diffusion Electrodes Enable Stable CO2 Electrolysis, ACS Appl. Energy Mater., 2022, 5(12), 15125–15135 CrossRef CAS PubMed.
- M. Grosseheide, et al., A falling film design for electrochemical CO2 reduction, Electrochem. Commun., 2023, 150, 107487 CrossRef CAS.
- D. G. Wheeler, et al., Quantification of water transport in a CO2 electrolyzer, Energy Environ. Sci., 2020, 13(12), 5126–5134 RSC.
- M. Sassenburg, et al., Zero-Gap Electrochemical CO Reduction Cells: Challenges and Operational Strateges for Prevention of Salt Precipitation, ACS Energy Lett., 2023, 8(1), 321–331 CrossRef CAS PubMed.
- B. Endrodi, et al., Multilayer Electrolyzer Stack Converts Carbon Dioxide to Gas Products at High Pressure with High Efficiency, ACS Energy Lett., 2019, 4(7), 1770–1777 CrossRef CAS PubMed.
- Y. Xu, et al., Self-Cleaning CO Reduction Systems: Unsteady Electrochemical Forcing Enables Stability, ACS Energy Lett., 2021, 6(2), 809–815 CrossRef CAS.
- G. O. Larrazábal, et al., Analysis of Mass Flows and Membrane Cross-over in CO2 Reduction at High Current Densities in an MEA-Type Electrolyzer, ACS Appl. Mater. Interfaces, 2019, 11(44), 41281–41288 CrossRef PubMed.
- D. A. Salvatore, et al., Designing anion exchange membranes for CO electrolysers, Nat. Energy, 2021, 6(4), 339–348 CrossRef CAS.
- A. Lowe, et al., Influence of Temperature on the Performance of Gas Diffusion Electrodes in the CO2 Reduction Reaction, ChemElectroChem, 2019, 6(17), 4497–4506 CrossRef.
- Z. Yin, et al., An alkaline polymer electrolyte CO2 electrolyzer operated with pure water, Energy Environ. Sci., 2019, 12(8), 2455–2462 RSC.
- L.-C. Weng, A. T. Bell and A. Z. Weber, Towards membrane-electrode assembly systems for CO2 reduction: a modeling study, Energy Environ. Sci., 2019, 12(6), 1950–1968 RSC.
- L. C. Weng, A. T. Bell and A. Z. Weber, A systematic analysis of Cu-based membrane-electrode assemblies for CO(2) reduction through multiphysics simulation, Energy Environ. Sci., 2020, 13(10), 3592–3606 RSC.
- J. W. Blake, et al., Inhomogeneities in the Catholyte Channel Limit the Upscaling of CO2 Flow Electrolysers, ACS Sustainable Chem. Eng., 2023, 11(7), 2840–2852 CrossRef CAS PubMed.
- R. Kas, et al., Along the Channel Gradients Impact on the Spatioactivity of Gas Diffusion Electrodes at High Conversions during CO2 Electroreduction, ACS Sustainable Chem. Eng., 2021, 9(3), 1286–1296 CrossRef CAS.
- Y. Zheng, et al., Energy related CO conversion and utilization: advanced materials/nanomaterials, reaction mechanisms and technologies, Nano Energy, 2017, 40, 512–539 CrossRef CAS.
- T. Haas, et al., Technical photosynthesis involving CO electrolysis and fermentation, Nat. Catal., 2018, 1(1), 32–39 CrossRef CAS.
- D. McLaughlin, et al., Tomographic Reconstruction and Analysis of a Silver CO2 Reduction Cathode, Adv. Energy Mater., 2020, 10(19), 2000488 CrossRef CAS.
- J. T. Gostick, et al., In-plane and through-plane gas permeability of carbon fiber electrode backing layers, J. Power Sources, 2006, 162(1), 228–238 CrossRef CAS.
- Y. Hori, Electrochemical CO2 Reduction on Metal Electrodes, Modern Aspects of Electrochemistry, Springer, New York, 2008, pp. 89–189 Search PubMed.
- X. Liu, M. C. O. Monteiro and M. T. M. Koper, Interfacial pH measurements during CO reduction on gold using a rotating ring-disk electrode, Phys. Chem. Chem. Phys., 2023, 25(4), 2897–2906 RSC.
- N. T. Nesbitt and W. A. Smith, Water and Solute Activities Regulate CO2 Reduction in Gas-Diffusion Electrodes, J. Phys. Chem. C, 2021, 125(24), 13085–13095 CrossRef CAS.
- E. Nurlaela, et al., Temperature Dependence of Electrocatalytic and Photocatalytic Oxygen Evolution Reaction Rates Using NiFe Oxide, ACS Catal., 2016, 6(3), 1713–1722 CrossRef CAS.
- J. Durst, et al., Hydrogen Oxidation and Evolution Reaction Kinetics on Carbon Supported Pt, Ir, Rh, and Pd Electrocatalysts in Acidic Media, J. Electrochem. Soc., 2015, 162(1), F190–F203 CrossRef CAS.
- W. C. Sheng, H. A. Gasteiger and Y. Shao-Horn, Hydrogen Oxidation and Evolution Reaction Kinetics on Platinum: Acid vs. Alkaline Electrolytes, J. Electrochem. Soc., 2010, 157(11), B1529–B1536 CrossRef CAS.
- D. Y. Kuo, et al., Influence of Surface Adsorption on the Oxygen Evolution Reaction on IrO2(110), J. Am. Chem. Soc., 2017, 139(9), 3473–3479 CrossRef CAS PubMed.
- W. C. Sheng, et al., Correlating hydrogen oxidation and evolution activity on platinum at different pH with measured hydrogen binding energy, Nat. Commun., 2015, 6, 5848 CrossRef CAS PubMed.
- J. Durst, et al., New insights into the electrochemical hydrogen oxidation and evolution reaction mechanism, Energy Environ. Sci., 2014, 7(7), 2255–2260 RSC.
- J. Zheng, et al., Universal dependence of hydrogen oxidation and evolution reaction activity of platinum-group metals on pH and hydrogen binding energy, Sci. Adv., 2016, 2(3), e1501602 CrossRef PubMed.
- A. Z. Weber and J. Newman, Transport in polymer–electrolyte membranes – II. Mathematical model, J. Electrochem. Soc., 2004, 151(2), A311–A325 CrossRef CAS.
- A. Z. Weber and J. Newman, Modeling transport in polymer–electrolyte fuel cells, Chem. Rev., 2004, 104(10), 4679–4726 CrossRef CAS PubMed.
- Q. J. Duan, S. H. Ge and C. Y. Wang, Water uptake, ionic conductivity and swelling properties of anion-exchange membrane, J. Power Sources, 2013, 243, 773–778 CrossRef CAS.
- Y. S. Li, T. S. Zhao and W. W. Yang, Measurements of water uptake and transport properties in anion-exchange membranes, Int. J. Hydrogen Energy, 2010, 35(11), 5656–5665 CrossRef CAS.
- J. Peng, et al., Effect of CO absorption on ion and water mobility in an anion exchange membrane, J. Power Sources, 2018, 380, 64–75 CrossRef CAS.
- K. N. Grew, X. M. Ren and D. Chu, Effects of Temperature and Carbon Dioxide on Anion Exchange Membrane Conductivity, Electrochem. Solid-State Lett., 2011, 14(12), B127–B131 CrossRef CAS.
- K. N. Grew and W. K. S. Chiu, A Dusty Fluid Model for Predicting Hydroxyl Anion Conductivity in Alkaline Anion Exchange Membranes, J. Electrochem. Soc., 2010, 157(3), B327–B337 CrossRef CAS.
- F. H. Sweeton, R. E. Mesmer and C. F. Baes, Acidity Measurements at Elevated Temperatures. VII. Dissociation of Water, J. Solution Chem., 1974, 3(3), 191–214 CrossRef CAS.
- R. N. Roy, et al., The Dissociation-Constants of Carbonic-Acid in Seawater at Salinities 5 to 45 and Temperatures 0-Degrees-C to 45-Degrees-C, Mar. Chem., 1993, 44(2–4), 249–267 CrossRef CAS.
- K. G. Schulz, et al., Determination of the rate constants for the carbon dioxide to bicarbonate inter-conversion in pH-buffered seawater systems, Mar. Chem., 2006, 100(1–2), 53–65 CrossRef CAS.
- E. N. Fuller, P. D. Schettle and J. C. Giddings, A New Method for Prediction of Binary Gas-Phase Diffusion Coeffecients, Ind. Eng. Chem., 1966, 58(5), 19–27 CrossRef.
- A. Z. Weber and J. Newman, Coupled thermal and water management in polymer electrolyte fuel cells, J. Electrochem. Soc., 2006, 153(12), A2205–A2214 CrossRef CAS.
- H. Vogt, Heat-Transfer at Gas Evolving Electrodes, Electrochim. Acta, 1978, 23(10), 1019–1022 CrossRef CAS.
- H. Vogt, Heat transfer in boiling and mass transfer in gas evolution at electrodes – The analogy and its limits, Int. J. Heat Mass Transfer, 2013, 59, 191–197 CrossRef CAS.
- L. M. Baumgartner, et al., Narrow Pressure Stability Window of Gas Diffusion Electrodes Limits the Scale-Up of CO Electrolyzers, ACS Sustainable Chem. Eng., 2022, 10(14), 4683–4693 CrossRef CAS PubMed.
- O. Romiluyi, et al., Membrane–electrode assembly design parameters for optimal CO2 reduction, Electrochem. Sci. Adv., 2022, 3(1), e2100186 CrossRef.
- M. R. Gerhardt, et al., Method-Practices and Pitfalls in Voltage Breakdown Analysis of Electrochemical Energy-Conversion Systems, J. Electrochem. Soc., 2021, 168(7), 074503 CrossRef CAS.
- D. H. Won, et al., Achieving tolerant CO2 electro-reduction catalyst in real water matrix, Appl. Catal., B, 2019, 258, 117961 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ey00190g |
| This journal is © The Royal Society of Chemistry 2025 |







