Energy-saving scheduling for multiple water intake pumping stations in water treatment plants based on personalized federated deep reinforcement learning

Abstract

Urban water treatment plants are among the largest energy consumers in municipal infrastructure, imposing significant economic burdens on their operators. This study employs a data-driven personalized federated learning-based multi-agent attention deep reinforcement learning (PFL-MAADRL) algorithm to address the intake scheduling problem of three water intake pumping stations in urban water treatment plants. Personalized federated learning (PFL) is combined with long short-term memory (LSTM) modeling to create environment models for water plants, focusing on energy consumption, reservoir levels, and mainline pressure. The average accuracies of PFL-based LSTM (PFL-LSTM) models are 0.012, 0.002, and 0.002 higher than those of the LSTM model in the three water plants. Evaluation metrics were established to quantify the effectiveness of each pumping station's energy-efficient scheduling, considering constraints such as reservoir water levels and mainline pressure. The results indicate that the proposed algorithm performs robustly under uncertainties, achieving a maximum energy consumption reduction of 10.6% compared to other benchmark methods.

---

Water impact

Urban water treatment plants are among the largest energy consumers within municipal infrastructure, imposing significant economic burdens on water treatment plant operators. In this study, an algorithm based on personalized federated learning and multi-agent attention deep reinforcement learning (PFL-MAADRL) is employed to address the intake scheduling problem of multiple water intake pumping stations (MWIPSs) in urban water treatment plants. The results indicate that the proposed algorithm demonstrates robust performance against uncertainties and achieves a maximum energy consumption reduction of 10.6% compared to other benchmark methods.

1. Introduction

Urban water treatment plants account for 65% of the total operating costs in urban infrastructure as they are the primary energy consumers.¹ The main sources of this energy consumption are water intake pumping stations (WIPSs) and water supply pumping stations within these plants. Insufficient water pressure in water distribution networks (WDNs) leads to unmet water demands,² whereas excessive or fluctuating water pressure can accelerate the deterioration of WDNs. Aging WDNs are particularly vulnerable to physical defects such as pipe breaks, cracks, and leaks, which can compromise the operational safety of the water supply system.^3,4 Furthermore, maintaining reservoir levels within the designated range is crucial to ensuring that the water supply meets demand.⁵ Consequently, water utilities should adopt efficient methods to optimize operational strategies for the water supply system. This optimization aims to reduce energy consumption while enhancing the reliability and safety of WDN operations.⁶

Numerous methods have been developed to optimize WIPSs in water treatment plants, addressing the significant energy consumption associated with these systems, such as harmony search (HS),⁶ bi-objective optimization (BOO),⁷ particle swarm optimization (PSO),⁸ ant colony optimization (ACO),⁸ and enhanced cooperative distributed model predictive control (EC-DMPC).⁹ For instance, the HS method regulated the opening of pressure-reducing valves in the WDN to reduce overpressure at network nodes, achieving a leakage recovery rate of approximately 45%, although energy savings were not investigated.⁶ Conversely, the BOO method designs real-time pressure control regulators for distribution networks, balancing performance and cost.⁷ Combining PSO and ACO algorithms for WDNs has led to optimal operation scheduling of pressure valves, resulting in a 32.6% improvement in the average reliability index and over a 31% reduction in the average leakage rate.⁸ Additionally, an EC-DMPC strategy maintains uniform water supply pressure near the lower limit, ensuring consistent customer pressure despite changes in water demand, thereby reducing both leakage and energy consumption.⁹ Despite significant progress, some limitations remain. Firstly, when applied to complex problems in multiple waterworks, existing optimization algorithms for controlling pipe network pressure, reservoir level, and energy consumption in a WDN often fall into local optima, resulting in suboptimal solutions.^6–9 Secondly, the high computational complexity of these algorithms often consumes large amounts of computational resources.^6–8 Thirdly, the inconsistent quality of the solutions produced by these algorithms can lead to less robust results, further limiting their effectiveness in practical applications.⁹ Finally, these methods rely on centralized control, which cannot effectively coordinate the operations of multiple pump stations, resulting in poor overall optimization, particularly in terms of information sharing and collaboration. Additionally, the varying data structures, quality, and types between different pump stations and water plants make it difficult for traditional methods to handle this heterogeneous data, thereby limiting the algorithm's application across different devices and environments.^6–9

Compared to traditional research methods, learning-based optimization methods for WDNs offer distinct advantages by eliminating the need for uncertain parameters or explicit system models. Reinforcement learning (RL)^10,11 and deep reinforcement learning (DRL)^12–14 are prominent examples. Particularly, DRL has captivated researchers due to its superior representational capacity and its ability to make informed decisions under uncertainty.^15,16 For instance, a model-free RL-based approach has been used to control pressure in the water supply network, effectively reducing pressure within the WDN.¹⁵ However, this approach did not address WDN withdrawals and reservoir levels, nor did it study energy savings. A knowledge-assisted approximate strategy-based optimization method was used to optimize pumping unit scheduling, satisfying pressure constraints under time-varying water demand.¹⁶ Although the optimal policy derived from RL maps the current network state to pump actions without future water demand information, it does not consider the reservoir level storage function in the operational optimization of WDNs.^15,16 And the spatiotemporal combination of rewards in high-dimensional discrete actions limits the applicability of these methods for efficient scheduling of MWIPSs in water treatment plants. Additionally, the data structures, quality, and types between pump stations often vary, making it difficult for RL algorithms to directly handle these heterogeneous data. And when dealing with multi-agent collaboration tasks, RL methods perform poorly and cannot effectively promote cooperation among multiple agents, leading to suboptimal decisions.^15,16

The aim of this study is to investigate the optimization of energy consumption of MWIPSs under the uncertainty of water supply, considering constraints such as reservoir levels, mainline pressure, and pressure variation values. A data-driven personalized federated learning-based multi-agent attention deep reinforcement learning (PFL-MAADRL) control method was proposed. This approach utilizes the personalized federated learning (PFL) technique to facilitate the sharing and learning of information among different intake pumping stations, thereby enhancing the accuracy of the overall environmental model. In the pump station scheduling problem, employing multi-agent attention deep reinforcement learning (MAADRL) to establish an environment model proves effective in tackling complex and dynamic scheduling scenarios. By leveraging adaptive learning among agents, the system can optimize scheduling strategies, thereby enhancing overall efficiency. Unlike traditional physical models, which are designed for simple and stable systems, these models face difficulties in managing complex interactions and dynamic changes. In contrast, the multi-agent model, through agent collaboration and self-learning, is capable of adapting to evolving conditions and optimizing multiple scheduling objectives, thus improving the system's flexibility and responsiveness to unforeseen events. Concurrently, by employing MAADRL, each intake pumping station acts as an agent that interacts with the environment, learns, and optimizes its scheduling strategy, ultimately minimizing the energy consumption of the entire system.

2. Materials and methods

2.1 Experimental setup

In the data preprocessing process, we used linear interpolation to fill missing data, ensuring the continuity of the dataset. For outliers and anomalies, we employed visualization and statistical methods (such as standard deviation) for detection and replaced obviously unreasonable values with the mean, median, or linear interpolation. Through these steps, we effectively improved the data quality, laying a solid foundation for the accuracy and robustness of the subsequent model. Due to the rarity and difficulty in accurately modeling extreme operating conditions, such as pump failures, we focus on an ideal operational scenario in the model, where the pump station operates under optimal conditions. Actual operational data from the Suzhou Water Supply Company in China was used for the experiments. Specifically, data from 1 November 2020 to 30 April 2021 for Baiyangwan WIPS (WIPS 1), Xujiang WIPS (WIPS 2), and Xiangcheng WIPS (WIPS 3) were utilized. In the experiment, data from 1 November 2020 to 28 February 2021 were used to train all DRL agents, while data from 1 March 2021 to 30 April 2021 were used for performance testing. The training process was conducted on a laptop with an Intel Core™ i5-8300HQ CPU@2.30GHz and 24GB RAM. The proposed algorithm was implemented using Python 3.8. To enhance clarity, Table S1† lists the abbreviations in alphabetical order, and Table S2† describes the parameters used in this paper. The main experimental parameters are listed in Table S3.†

To facilitate performance comparisons, five benchmark methods for dynamically co-regulating water intake were included. The details are as follows: rules 1 and 2: to achieve better performance in dynamically co-regulating the water intake Q_i,t (m³ h⁻¹), two rule-based (RB) baseline methods were adopted. In the RB scheme, adjustments to water withdrawals were made by imposing constraints on the range of mainline pressures. Specifically, the following rules were applied: if: p_i,t ≥ p^max_i − ϕ_i , then: Q_i,t = Q_i,t−1 − ε_i. Elif: p_i,t ≤ p^min_i + ϕ_i , then: Q_i,t = Q_i,t−1 + ε_i, otherwise, Q_i,t = Q_i,t−1. In these rules, ϕ_i = 0.03 MPa, 1 ≤ i ≤ n. Two distinct RB schemes were considered, as indicated in Table S4;† MAAC: the MAAC algorithm (multi-actor-attention-critic¹⁷); greedy: this scheme makes decisions at each time slot based only on current information and optimizes the objective function for the current time slot while adhering to the constraints; DQN: this scheme controls each WIPS independently using the DQN method (i.e., Deep Q-Network¹⁸); manual scheduling: the manual scheduling scheme primarily relies on the experience and intuition of water plant engineers to make scheduling decisions.

Four key performance metrics were defined to comprehensively evaluate the MWIPS scheduling algorithm's performance. The average energy consumption per slot for each WIPS (AEC in kW h), the average pressure violation per slot for each WIPS (APV in MPa), and the average pressure variation violation per slot for each WIPS (APVV in MPa) are defined in eqn (S10)–(S12).† Additionally, the average reservoir level violation per slot for each WIPS (ALV in m) is defined in eqn (S13).† These metrics provide a detailed assessment of the algorithm's effectiveness in managing water intake and maintaining system stability. To demonstrate the accuracy of the proposed personalized federated learning-based long short-term memory (PFL-LSTM) models, mean relative error (MRE) was used as a performance metric, which is defined as , where ŷ_i denotes the actual value, y_i denotes the predicted value and n denotes the number of samples.

2.2 System model and problem formulation

The MWIPS system consists of three WIPSs, each containing five components: a water resource, WIPS, a mainline, a water purification process, and a reservoir. The scheduling period is set to one hour, dividing a day into 24 time slots, denoted as 1 ≤ t ≤ T (h), where T = 24 (h).

2.2.1 System model. There are N WIPSs in the system model. For each WIPS i, its water intake Q_i,t can be adjusted and should be kept within the suitable range of [Q^min_i, Q^max_i] (m³ h⁻¹) as follows:

Q^min_i ≤ Q_i,t ≤ Q^max_i, 1 ≤ i ≤ N, ∀t, (1)

In eqn (1), Q^max_i (m³ h⁻¹) and Q^min_i (m³ h⁻¹) denote the upper limit and lower limit of a suitable range of water intake for WIPS i, respectively. ∀t denotes any time slots.

The reservoir acts as a buffer for the system, storing excess water when the water supply is insufficient or demand surges, helping to balance the system load and prevent water supply interruptions. During periods of lower demand, the reservoir water level rises, ensuring a reliable water supply during peak demand periods. To prevent water shortages or spills, it is necessary to maintain the reservoir's water level within a reasonable range. l_i,t (m) represents the reservoir level of WIPS i at slot t.

l^min_i ≤ l_i,t ≤ l^max_i, ∀t, (2)

In eqn (2), l^max_i (m) and l^min_i (m) denote the upper limit and lower limit of the reservoir level of WIPS i, respectively.

The water level in the reservoir at the end of each time slot for WIPS i is influenced by various factors. These factors include the water level in the reservoir at the end of the previous time slot for each WIPS and the supplied water volume at time slot t for WIPS i (denoted as w_i,t (m³ h⁻¹)). It should be noted that these factors are indirectly related to the mainline pressure, represented as p_i,t (MPa). Therefore, l_i,t can be expressed as eqn (3).

l_i,t = Ω_t(l_i,t−1, Q_i,t, p_i,t, w_i,t), ∀t, (3)

In actual operation, the design of the mainline pressure for the WIPS is determined based on engineering requirements and equipment performance. Therefore, ensuring that the mainline pressure remains within a reasonable range is necessary. Furthermore, excessive fluctuations in mainline pressure can harm the mainline's service life, safety, and reliability. Thus, the mainline pressure p_i,t should be maintained within a reasonable range, and the change in mainline pressure between adjacent time slots should be limited by a value denoted as p^max_v (MPa) in eqn (5):

p^min_i ≤ p_i,t ≤ p^max_i, ∀t, (4)

|p_i,t − p_i,t−1| ≤ p^max_v, ∀t, (5)

In eqn (4), p^max_i (MPa) and p^min_i (MPa) represent the upper limit and lower limit of the mainline pressure for WIPS i, respectively. p_i,t denotes the mainline pressure of WIPS i at time slot t, which is directly influenced by Q_i,t and p_i,t−1 (MPa), and indirectly affected by l_i,t. Therefore, p_i,t can be described by eqn (6).

p_i,t = Θ_t(p_i,t−1, Q_{i, t}, l_i,t), ∀t, (6)

2.2.2 Energy consumption minimization problem. When scheduling water withdrawals, it is crucial to ensure that the operational constraints (eqn (1)–(6)) are met. Φ_i,t(l_i,t, p_i,t, w_i,t, Q_i,t) represent the energy consumption of the MWIPS at time slot t. Based on this, the optimization problem was formulated as follows:where E represents an expectation operator that considers the randomness of a system parameter, which is the supplied water demand w_i,t. To be specific, by incorporating the water supply distribution through direct use of historical data, the multi-pump station model can more authentically represent real situations and mitigate the risks of relying on inaccurate assumptions or uncertain estimates. This method allows us to better capture the trends and variability in water demand, which is vital for optimizing pump scheduling and energy efficiency. The decision variables are denoted as Q_{i,t|1≤i≤n} (m³ h⁻¹), representing the water intake of the WIPS i.

However, there are several challenges in solving the optimization problem P1. Firstly, there are temporally-coupled constraints, including eqn (3), (5) and (6). For instance, in eqn (3), the reservoir level l_i,t at the end of time slot t depends on the reservoir level at the end of the previous time slot t − 1. Secondly, uncertainty in the supplied water demand w_i,t complicates the problem. Thirdly, it is difficult to obtain accurate and explicit model parameters such as Ω_t (·) (m), Θ_t (·) (MPa), and Φ_i,t (·) (kW h). Given these challenges, traditional model-based methods are inadequate for addressing them. Therefore, the problem was reformulated as a Markov game and an efficient data-driven algorithm was proposed to solve it.

2.2.3 Markov game model and problem reformulation. Considering above challenges, a PFL-MAADRL-based scheduling algorithm was established to minimize the energy consumption of MWIPSs. Specifically, P1 was reformulate as a Markov game,¹⁹ which included: the set of states S; the action sets available to agent i{A_i}_i∈N, and the joint action set A = A₁ × …A_N; the state transition function T: S × A₁…A_N ⇒ Π(S), defining the probability distribution of the next state based on the current state and actions of all agents; R_i: S × A₁…A_N ⇒ R, providing the reward for each agent.

In this paper, each agent i(1 ≤ i ≤ N) represents a water withdrawal controller, and the environment encompasses all interactions with the agents. The objective of each agent is to maximize the sum of discounted rewards obtained in the future, given the state s_t ∈ S and action a_t = (a_1,t, …, a_N,t), i.e., 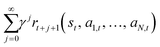. The components of the Markov Game model proposed in this paper are defined as follows.

Environment state S: for WIPS i, agent i takes action a_i,t based on local observations o_i,t to satisfy the constraints of reservoir level l_i,t and mainline pressure p_i,t. Additionally, there exists a relationship between the reservoir level l_i,t and the water supply w_i,t. Hence, the water supply w_i,t should be included as part of the global state s_t. Based on this analysis, the local observation for agent i at time slot t is designed as (t′, l_i,t, p_i,t, w_i,t), where t′ (h) denotes the time slot index within a day, i.e., when τ = 1 h, t′ = mod(t, 24). Considering the local observations of all agents at time slot t, then: o_t = (o_1,t, …, o_N,t). For simplicity, the global state s_t is chosen to be o_t.

Action: to facilitate the training of agents related to WIPS i, the action of agent i is defined as a_i,t = β_i,t, i.e., β_i,t = {−400, −300, −200, −100, 0, 100, 200, 300, 400}, 1 ≤ i ≤ N, where β_i,t (m³ h⁻¹) denotes the action of agent i related to WIPS i and indicates the water intake adjustment value. Note that to ensure the new water intake is a valid value, the following rule is adopted, i.e., max(Q_i,t−1 + β_i,t, Q^min_i) ≤ Q_i,t ≤ min(Q^max_i, Q_i,t−1 + β_i,t), 1 ≤ i ≤ N. For simplicity, the joint action of all agents can be written as a_t = (β_1,t, …, β_N,t).

Reward function: when the environment state transitions from s_t−1 to s_t due to the combined action of a_t−1, a reward r_t is provided by the environment. Our objective is to minimize the total energy consumption of WIPSs while adhering to constraints related to reservoir levels and mainline pressures. The reward function comprises penalties for energy consumption, violations of reservoir level boundaries, violations of mainline pressure at time slot t, and deviations in mainline pressure differences, which are defined in eqn (S1)–(S4).† Taking four parts into consideration, the reward of each agent $i$ can be designed as in eqn (S5).† In eqn (S5),†α_i,1 (in kW h m⁻¹), α_i,2 (in kW h MPa⁻¹), and α_i,3 (in kW h MPa⁻¹) are positive weight coefficients, respectively.

2.3 PFL-MAADRL algorithm for energy scheduling of MWIPSs

2.3.1 Localized training of WIPS agents and PFL algorithm. Localized training of each WIPS agent within the MWIPS system is essential for optimizing water management. This process customizes learning to the specific conditions and data of each WIPS. Key factors influencing the water drawn Q_i,t, at the end of time slot t, include the previous main pipeline pressure p_i,t−1, the reservoir level l_i,t−1 (m), and the energy consumption Φ_i,t−1. To address the unknowns at time slot t (main pipeline pressure p_i,t+1 (MPa), reservoir level l_i,t+1 (m), and energy consumption Φ_i,t+1 (kW h)), this paper employs a long short-term memory (LSTM)²⁰ network, which can process time-series data and mitigate the gradient vanishing problem. The LSTM network, consisting of two hidden layers, predicts the central pipeline pressure, reservoir level, and energy consumption. Inputs include current time slot data such as central pipeline pressure, reservoir level, water supply, and pumping. The outputs provide predicted values for the next time slot. This approach allows for the development of an effective strategy for water withdrawal by accurately forecasting the necessary parameters for future time slots.

Data from different water plants may exhibit significant variations in value ranges and distributions. Specifically, WIPS 1 variable ranges may be larger, and the challenges it faces often include larger fluctuations, different water sources, and more complex environmental conditions, while WIPS 2 variable ranges are smaller, with more consistent water sources and more stable environmental changes. These differences in data consistency and distribution make it difficult for traditional centralized training methods to address the diverse needs of these agents, especially in terms of privacy protection and communication efficiency. Therefore, a method that uses PFL²¹ is proposed to facilitate information sharing and learning between different water intake pumping stations, thereby improving the accuracy of the overall environmental model, as shown in Algorithm S1.† As is shown in lines 1–3 of the algorithm, the inputs and outputs are first defined, and the global personalized model parameters are initialized. During each round of federated learning (FL), denoted as t, a subset S_t is selected from all the clients to participate in the current round of training. The function ClientUpdate, depicted in lines 11–19, is then invoked to obtain the local model parameter w_local and the personalized model parameter w_personalc in parallel for each client. Subsequently, the local model parameters within the subset are aggregated, and the global model parameters are updated. This is achieved using the function Aggregate, as depicted in lines 20–25, resulting in the updated global model parameters w_global as shown in lines 3–10. Finally, the local fine-tuning process corresponds to the ClientUpdate function in Algorithm S1.†

2.3.2 PFL-MAADRL based energy scheduling algorithm for MWIPSs. To solve the Markov game formulated in section 2.2.3, a PFL-MAADRL based scheduling algorithm for MWIPSs was proposed, which employs the multi-agent-actor-critic (MAAC) method¹⁷ and PFL algorithm.²¹ Additionally, to implement effective training among different pump station agents, the attention mechanism is employed, which helps the current agent understand the contributions of other agents when calculating its own action value function. Since MAAC offers stronger scalability and supports discrete action spaces, it is used in this paper to train the DRL agents. The framework of the PFL-MAADRL-based MWIPS scheduling algorithm is shown in Fig. 1.

Fig. 1 The framework of the PFL-MAADRL-based MWIPS scheduling algorithm.

In the MWIPS system, the personalization models were used as the system's environment models. To efficiently train MWIPS DRL agents, the MAAC algorithm that merges an attention mechanism with a soft actor-critic was employed. The algorithm exhibits excellent performance compared to other MADRL algorithms. The paper's emphasis is on MWIPSs that necessitate coordination among several agents. This coordination facilitates task decomposition and boosts the scheduling algorithms' efficiency. The objective is to minimize energy consumption in the MWIPS system by controlling water withdrawal.

In order to realize cooperative actions among agents, an attention mechanism is introduced.²² This mechanism calculates the current agent's state-action value function by considering the contributions of other agents. In addition, to promote exploration during training, the state-action values are supplemented with entropy rewards when updating both the actor network and the critic network. Specifically, the critic network is updated by employing the joint loss function outlined in eqn (S6).†

In eqn (S6),†D denotes the experience replay buffer, in which past system transitions (i.e., a tuple (o, a, õ, r)) are stored. y_i is given as shown in eqn (S7).† In eqn (S7),† the evaluation parameters of the target actor network for each agent can be denoted by [small theta, Greek, macron]_i, and −φ log π_{[small theta, Greek, macron]i}(ã_i|õ_i) is related to entropy of π_{[small theta, Greek, macron]i}(ã_i|õ_i) and maintaining a balance between maximizing entropy and maximizing the reward function depends on φ. Then, the weight parameter of the actor network is updated according to the policy gradient method. Specifically, the policy gradient is calculated as shown in eqn (S8).† In eqn (S8),† the ϱ_i(o_i, a_i) is given in eqn (S9).† In eqn (S9),† the set of agents except i is denoted by \i. Here, can be viewed as baselines, which can indicate whether the current action will result in an increase in the expected return.

The training process for MWIPS DRL agents is shown in Algorithm S2.† At each time slot t, each WIPS agent i interacts with the MWIPS scheduling environment to determine the optimal action a_i,t. The algorithm's inputs and outputs are defined in lines 1 and 2, and the environment and parameters are initialized in lines 3–7. Before each episode Y starts, the environment is reset, and each WIPS agent i receives an initial observation state o_i,1 (lines 8 and 9). During the interaction, each agent accumulates experience transitions (o_t, a_t, o_t+1, r_t+1), which are stored in an experience replay buffer D following a first-in-first-out principle (lines 10–13). During training, a batch of experience data is randomly sampled from D to train the agent's neural network model (lines 14–18). The experience replay method accelerates training and improves learning by reusing stored data. The actor and critic networks are updated (lines 19 and 20), followed by updating the target networks' weight parameters (line 21).

As outlined in Algorithm S3,† once training is complete, the learned policies can be tested in practice. The proposed algorithm facilitates real-time decision making based on the current state of the MWIPS system without requiring future water demand forecasts. Additionally, the algorithm's computational complexity is minimal, relying only on the forward propagation of deep neural networks.

3. Results and discussion

3.1 Algorithm convergence process

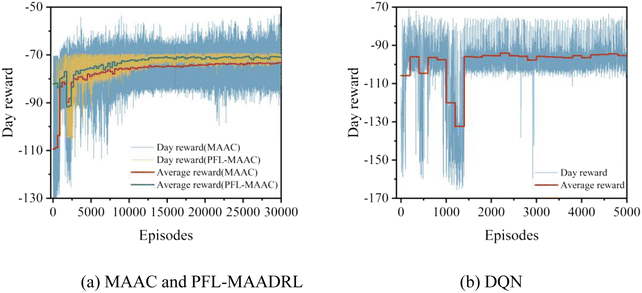
The convergence processes of the proposed PFL-MAADRL algorithm, the MAAC algorithm, and the DQN algorithm are illustrated in Fig. 2. It can be observed that the reward curve under the DQN-based scheme stabilizes within 2000 episodes, whereas both the proposed algorithm and the MAAC algorithm require 10 000 episodes. This disparity arises because DQN learns an independent policy for each WIPS,¹⁸ while the proposed algorithm and the MAAC algorithm learn coordinated scheduling policies, necessitating a greater number of exploration episodes. The convergence reward of the proposed algorithm and MAAC is greater than that of DQN due to the entropy term in the algorithm, which makes it more efficient in exploring the policy space.²² Moreover, the reward curves exhibit slight fluctuations due to uncertainties in the exploration process and parameter settings. Compared to the MAAC algorithm, the daily reward curve of PFL-MAADRL is smoother, indicating better stability and convergence. Both algorithms initially rise and then stabilize, demonstrating good convergence. The average reward of PFL-MAADRL is higher than that of MAAC, suggesting it may offer more stable performance in similar scenarios. This is because the proposed algorithm combines PFL with MAADRL, using PFL to train the environment model in DRL, and a more accurate environment model facilitates the DRL agents to learn a more optimal strategy.

Fig. 2 Algorithm convergence curves. (a) MAAC and PFL-MADRL, (b) DQN.

3.2 PFL-LSTM model evaluation

As shown in Table 1, the performance of different models is compared. Specifically, the prediction accuracies of energy consumption, liquid level, and pressure of the PFL-LSTM model are improved compared to those of the LSTM model across the three WIPSs. Furthermore, the average prediction accuracies of energy consumption, reservoir level, and mainline's pressure of PFL-LSTM are higher than those of LSTM by 0.012, 0.002, and 0.002, respectively.

Table 1 Performance comparisons under different models

Schemes	WIPS 1			WIPS 2			WIPS 3				Average
	Energy	Level	Pressure	Energy	Level	Pressure	Energy	Level	Energy	Level	Energy	Level	Energy	Level
LSTM	0.064	0.022	0.052	0.047	0.024	0.015	0.060	0.014	0.060	0.014	0.060	0.014	0.060	0.014
PF-LSTM	0.047	0.025	0.049	0.033	0.017	0.013	0.056	0.013	0.056	0.013	0.056	0.013	0.056	0.013

---

In this paper, each WIPS represents a client. Each client has its own private local dataset, limiting their ability to train effective local models due to data scarcity. To overcome this limitation, FL is employed to obtain better-performing local models for WIPSs. However, traditional joint learning's global models may not perform well on individual WIPS due to heterogeneous local data distributions. PFL addresses the challenges of data heterogeneity and personalized scenarios by customizing global models to meet the specific needs of each WIPS.²³ PFL-LSTM enables multiple WIPS to share their data, utilizing more diverse datasets for training to create models tailored to their unique requirements. This approach enhances the generalization ability and accuracy of the models within the MAADRL environment. Moreover, improving the model accuracy assists the multi-agent system in learning more effective strategies, thereby boosting the performance of the MAADRL algorithm.

3.3 Algorithm effectiveness

The proposed algorithm for each WIPS in the MWIPS achieves lower APVV, ensuring that trunk pressure variations remain within acceptable ranges for most time intervals. Additionally, the APV of the proposed algorithm reaches 0, indicating that trunk pressure remains within a safe range for all time intervals while achieving the lowest AEC. Table 2 compares the performance of the proposed algorithm in the MWIPS system with various other schemes. It is worth noting that while the proposed algorithm is highly effective in maintaining the reservoir level within the desired range, occasional violations can still occur. These violations are similar to the findings of Wei et al.,²⁴ who experienced a similar overrun in their study. However, their effects are usually manageable and can be effectively minimized. Through continuous exploration, feedback mechanisms, security constraints, training processes, and algorithm optimization, DRL systems can effectively reduce the probability of violations and mitigate their impact.

Table 2 Performance comparisons under different schemes

Schemes	WIPS 1				WIPS 2				WIPS 3
	AEC (kW h)	APV (MPa)	APVV (MPa)	ALV (m)	AEC (kW h)	APV (MPa)	APVV (MPa)	ALV (m)	AEC (kW h)	APV (MPa)	APVV (MPa)	ALV (m)
Manual scheduling	969.6	0	0	2.8 × 10^−3	1271.6	0	1.46 × 10^−5	0	1296.8	0	0	0
Rule-1	892.4	0	0	0	1361.2	0	0	5.3 × 10^−5	1304.0	1.0 × 10^−4	9.5 × 10^−4	0
Rule-2	886.2	0	0	0	1360.8	0	0	5.3 × 10^−5	1302.4	6.3 × 10^−4	4.6 × 10^−4	0
MAAC	666.7	0	0	0	1287.5	0	0	1.0 × 10^−4	1299.0	1.3 × 10^−3	8.2 × 10^−5	0
Greedy	654.8	0	0	2.6 × 10^−2	1207.9	0	0	1.1 × 10^−6	1456.8	0	0	0
DQN	665.6	1.8 × 10^−4	3.4 × 10^−4	0	1293.9	0	0	1.8 × 10^−4	1402.1	3.9 × 10^−2	1.7 × 10^−4	0
Proposed	633.2	0	0	1.5 × 10^−4	1259.2	0	0	1.2 × 10^−4	1291.3	0	1.9 × 10^−4	1.5 × 10^−5

---

Compared with rule-1, rule-2, the MAAC algorithm, the greedy algorithm, the DQN algorithm, and the manual scheduling, the proposed algorithm can save 10.4%, 10.6%, 2.2%, 4.1%, 5.3% and 10.0% of energy consumption, respectively. This is because the proposed algorithm can intelligently select the most energy-efficient water withdrawal methods under different operating conditions. Fig. 3 and 4(a)–(d) and S1(a)–(d)† describe the performance details among all schemes for MWIPSs. The proposed algorithm ensures compliance with mainline pressure and reservoir level constraints while reducing the overall energy consumption of the MWIPS system. Compared with rule-1, rule-2, the greedy algorithm, the DQN algorithm, and the manual scheduling, the proposed algorithm utilizes the attention mechanism, enabling agents to focus on the most relevant information from both the environment and the actions of other agents. By selectively attending to critical data, the algorithm enhances the coordination between agents, leading to more optimal decision-making, reduced energy consumption, and better compliance with system constraints, thus enhancing the overall performance and robustness of the system in dynamic and uncertain environments. The main difference between the proposed algorithm and the MAAC method is the introduction of the PFL mechanism.²³ Specifically, by integrating PFL with MAAC, the knowledge of WIPS agents can be shared without compromising user privacy or data security. This addresses the issue of poor model prediction accuracy due to data heterogeneity. More accurate models can help the MAADRL algorithm select the optimal policy, thereby improving the generalization ability and accuracy of the system.

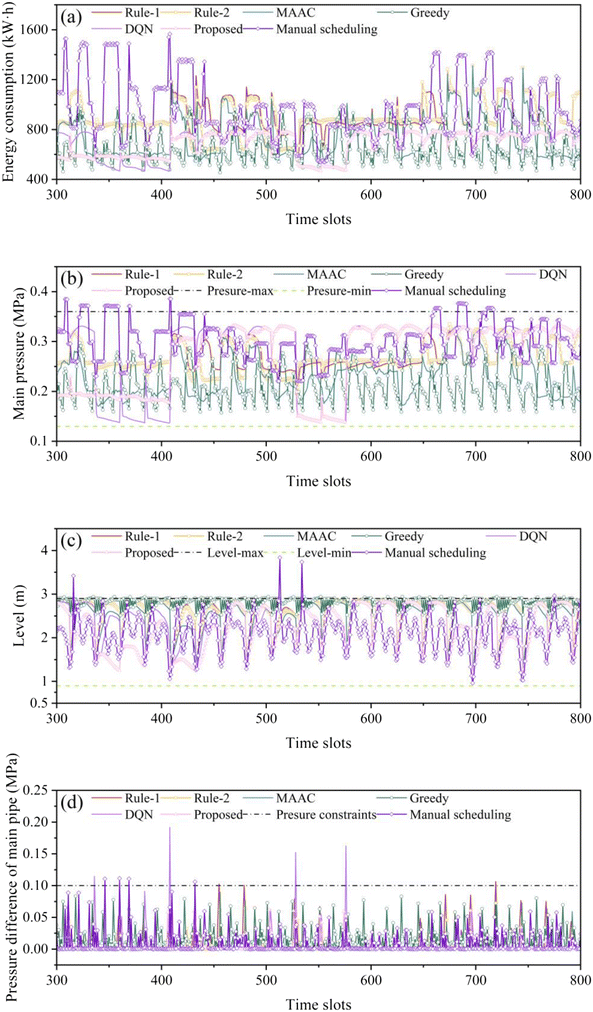Fig. 3 Performance details among all schemes for WIPS 1. (a) Energy consumption, (b) main pressure, (c) level, and (d) pressure difference of the main pipe.

Fig. 4 Performance details among all schemes for WIPS 2. (a) Energy consumption, (b) main pressure, (c) level, and (d) pressure difference of the main pipe.

3.4 Algorithm robustness

In section 3.2, the proposed model is built based on historical data rather than an actual water plant model, which inevitably introduces some degree of error. We assume that the predictions for reservoir water levels, pipeline pressures, and energy consumption accurately replicate the actual environment. However, in real-world scenarios, discrepancies may exist between predicted and actual values in the MWIPS environment. Therefore, to address these errors and uncertainties, it is necessary to evaluate the ability of the proposed algorithm to handle these discrepancies and ensure its robustness. To simulate errors, a disturbance term to the output of each PFL-LSTM model was introduced, representing a certain percentage of the output value (e.g., 2%, 4%, or 6%). For comparison, the relevant metrics (AEC, ALV, APV, and APVV) of the three WIPSs in the MWIPS system were averaged. The proposed algorithm demonstrated the lowest average AEC among all the schemes. Additionally, the deviations in average ALV, APV, and APVV were minimal, as shown in Fig. S2(a)–(d).† In conclusion, the proposed algorithms exhibit strong robustness against model uncertainty in the MWIPS environment. In contrast, K-means clustering methods²⁵ are highly sensitive to the initial placement of centroids, while linear model regression²⁶ is influenced by linearity assumptions, outliers, and multicollinearity. Furthermore, both techniques face significant challenges when applied to complex problems, primarily due to high computational and model complexities.^25,26

The algorithm solves the cooperative competition problem in multi-agent systems through centralized training and decentralized execution.²⁷ During centralized training, the algorithm uses global information to optimize the strategies of an individual agent, and enables each agent to selectively focus on the critical information of other agents through the attention mechanism,¹⁷ thereby enhancing the accuracy of value function estimation. In the execution phase, the agents operate independently. This feature provides the proposed algorithm with substantial advantages in practical applications.

4. Conclusions

This paper presents data-driven PFL-LSTM models and incorporates the MAADRL methodology for scheduling intake pumping stations in drinking water treatment plants. The experiment adheres to constraints on reservoir levels and mainline pressure variations, aiming to optimize the intake volume for efficient energy use within the MWIPS system. The optimization problem is reformulated as a cooperative Markov game, addressing challenges such as parameter uncertainty, temporal coupling constraints, and the absence of an explicit system dynamics model. Results demonstrate the effectiveness of the proposed algorithm, which enhances the flexibility of water withdrawal decisions and leads to significant energy savings. Specifically, the proposed algorithm reduces the overall energy consumption of MWIPSs by up to 10.6% compared to other benchmark methods. These findings underscore the importance of dynamically regulating individual WIPS intakes within the MWIPS system. Future work will focus on handling more agents and more complex systems, particularly optimizing collaboration and interactions between agents.

Data availability

All data included in this study are available upon request by contact with the corresponding author.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 52170001).

References

1. W. Chen, T. Tao, A. Zhou, L. Zhang, L. Liao, X. Wu, K. Yang, C. Li, T. C. Zhang and Z. J. J. o. C. P. Li, Genetic optimization toward operation of water intake-supply pump stations system, J. Cleaner Prod., 2021, 279, 123573.
2. E. Creaco, A. Campisano, N. Fontana, G. Marini, P. Page and T. J. W. r. Walski, Real time control of water distribution networks: A state-of-the-art review, Water Res., 2019, 161, 517–530.
3. M. Odhiambo, V. Viñas, E. Sokolova and T. J. J. E. S. W. R. Pettersson, Technology, Health risks due to intrusion into the drinking water distribution network: hydraulic modelling and quantitative microbial risk assessment, Environ. Sci.: Water Res. Technol., 2023, 9(6), 1701–1716.
4. M. Hannachi, A. Ketata, M. Sinagra, C. Aricò, T. Tucciarelli and Z. J. E. C. Driss, Management, A novel pressure regulation system based on Banki hydro turbine for energy recovery under in-range and out-range discharge conditions, Energy Convers. Manage., 2021, 243, 114417.
5. X. Zhuan and X. J. I. T. o. C. S. T. Xia, Development of efficient model predictive control strategy for cost-optimal operation of a water pumping station, IEEE Trans. Control Syst. Technol., 2012, 21(4), 1449–1454.
6. F. De Paola, M. Giugni and D. J. W. r. m. Portolano, Pressure management through optimal location and setting of valves in water distribution networks using a music-inspired approach, Water Resour. Manag., 2017, 31, 1517–1533.
7. G. Galuppini, E. Creaco and L. J. C. E. P. Magni, Bi-objective optimisation based tuning of pressure control algorithms for water distribution networks, Control Eng. Pract., 2020, 104, 104632.
8. M. Dini and A. J. W. R. M. Asadi, Optimal operational scheduling of available partially closed valves for pressure management in water distribution networks, Water Resour. Manag., 2020, 34, 2571–2583.
9. Y. Zhang, Y. Zheng and S. J. J. Li, Enhancing cooperative distributed model predictive control for the water distribution networks pressure optimization, J. Process Control, 2019, 84, 70–88.
10. A. M. Kintsakis, F. E. Psomopoulos and P. A. J. E. A. o. A. I. Mitkas, Reinforcement learning based scheduling in a workflow management system, Eng. Appl. Artif. Intell., 2019, 81, 94–106.
11. T. M. Moerland, J. Broekens, A. Plaat and C. M. J. F. Jonker, Model-based reinforcement learning: A survey, Found. Trends Mach. Learn., 2023, 16(1), 1–118.
12. A. Mathew, A. Roy and J. J. I. S. J. Mathew, Intelligent residential energy management system using deep reinforcement learning, IEEE Syst. J, 2020, 14(4), 5362–5372.
13. S. E. Li, Deep reinforcement learning, in Reinforcement learning for sequential decision and optimal control, Springer, 2023, pp. 365–402.
14. L. Yu, W. Xie, D. Xie, Y. Zou, D. Zhang, Z. Sun, L. Zhang, Y. Zhang and T. J. I. I. o. T. J. Jiang, Deep reinforcement learning for smart home energy management, IEEE Internet Things J., 2019, 7(4), 2751–2762.
15. T. C. Mosetlhe, Y. Hamam, S. Du, E. Monacelli and A. A. J. W. Yusuff, Towards model-free pressure control in water distribution networks, Water, 2020, 12(10), 2697.
16. J. Xu, H. Wang, J. Rao and J. J. S. C. Wang, Zone scheduling optimization of pumps in water distribution networks with deep reinforcement learning and knowledge-assisted learning, Soft Comput., 2021, 25, 14757–14767.
17. S. Iqbal and F. Sha, in Actor-attention-critic for multi-agent reinforcement learning, International conference on machine learning, PMLR, 2019, pp. 2961–2970.
18. V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland and G. J. n. Ostrovski, Human-level control through deep reinforcement learning, Nature, 2015, 518(7540), 529–533.
19. M. L. Littman, Markov games as a framework for multi-agent reinforcement learning, in Machine learning proceedings 1994, Elsevier, 1994, pp. 157–163.
20. S. Hochreiter and J. J. N. Schmidhuber, Long short-term memory, Neural Comput., 1997, 9(8), 1735–1780.
21. A. Z. Tan, H. Yu, L. Cui and Q. Yang, Towards personalized federated learning, IEEE Trans. Neural Netw. Learn. Syst., 2022, 34(12), 9587–9603.
22. D. Cao, J. Zhao, W. Hu, F. Ding, Q. Huang, Z. Chen and F. J. I. T. o. S. G. Blaabjerg, Data-driven multi-agent deep reinforcement learning for distribution system decentralized voltage control with high penetration of PVs, IEEE Trans. Smart Grid, 2021, 12(5), 4137–4150.
23. A. Z. Tan, H. Yu, L. Cui and Q. Yang, Towards personalized federated learning, IEEE Trans. Neural Netw. Learn. Syst., 2022, 34(12), 9587–9603.
24. T. Wei, Y. Wang and Q. Zhu, Deep reinforcement learning for building HVAC control, Proceedings of the 54th annual design automation conference 2017, 2017, pp. 1–6.
25. H. Guo, X. Liu and Q. J. A. W. I. Zhang, Identifying daily water consumption patterns based on K-means Clustering, Agglomerative Hierarchical Clustering, and Spectral Clustering algorithms, Aqua Water Infrastruct. Ecosyst. Soc., 2024, 73(5), 870–887.
26. G. Bonvin, S. Demassey and A. J. O. Lodi, Pump scheduling in drinking water distribution networks with an LP/NLP-based branch and bound, Optim. Eng., 2021, 1–39.
27. R. Lowe, Y. I. Wu, A. Tamar, J. Harb, O. Pieter Abbeel and I. J. A. Mordatch, Multi-agent actor-critic for mixed cooperative-competitive environments, Advances in neural information processing systems, 2017, vol. 30.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ew00685b

---