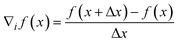Identification of dissipation pathways for pharmaceuticals in soils – a modelling approach†
Received
13th December 2024
, Accepted 4th January 2025
First published on 16th January 2025
Abstract
Concentrations of pollutants like pharmaceuticals in soils typically decrease over time, though it often remains unclear whether this dissipation is caused by the transformation of the pollutant or a decreasing extractability. We developed a mathematical model that (1) explores the plausibility of different dissipation pathways, and (2) allows the quantification of concentration differences between aqueous soil extracts and soil solution. The model considers soil particles as uniform spheres, kinetic sorption towards an equilibrium (Freundlich model), and two dissipation pathways, i.e. irreversible transformation and mineralization (following 1st order kinetics) as well as the formation of non-extractable residues via intraparticle diffusion. Applying the model to 19 published datasets (eight pharmaceuticals, three soils) showed that intraparticle diffusion accounts for approximately two thirds of all simulated mass fluxes. Reversible formation of non-extractable residues could play a major role for dissipation, while irreversible transformation and mineralization cannot be excluded either based on the available datasets. The difference between concentrations in aqueous extracts and soil solution quantified by the model is below typical model and measurement uncertainties for most of the investigated pharmaceuticals. Larger differences might be linked to a positive ionic charge of the pollutant. The model helps in disentangling different dissipation pathways in soils and optimizing experiments elucidating the long-term fate of pollutants in soils.
Environmental significance
Antimicrobial resistance (AMR) poses a severe threat to public health and spreads, among others, also in soils that are subjected to inputs of antibiotic agents and other pharmaceuticals when fertilized with manure or irrigated with treated or untreated wastewater, which might (co-)select AMR. In order to assess the risk of AMR selection and development, it is crucial to quantify the bioavailable and bioaccessible antibiotic concentration over time and space. However, measuring this concentration in soils is challenging due to small pore water volumes and potential biases in soil extraction procedures. Using published data from soil incubation and batch experiments with various antibiotics, this study develops and applies a process-based mathematical model to quantify the extraction bias, evaluate the different dissipation pathways of antibiotics in soils and estimate the bioavailable antibiotic concentration. These results, combined with knowledge on microbial dynamics and AMR formation, provide a comprehensive assessment of the actual environmental risk posed by antibiotics in soils.
|
Introduction
Most of the thousands of chemical compounds we produce and use end up in soils or sediments, either through direct inputs, atmospheric deposition, flooding, irrigation or application of fertilizers or waste materials.1,2 Observed concentrations of pollutants in soils typically decline over time following their input, a phenomenon that is termed “dissipation”.3,4 However, the mere observation of decreasing concentrations does not allow to distinguish between different processes that lead to a removal from the measurable fraction.3,5,6 It thus often remains unclear whether the compound's dissipation is due to actual removal processes like degradation and mineralization, or due to sorption and other sequestration processes that lead to a decrease in the compound's accessibility. As a result, pollutants may still persist in soil but, technically, cannot be observed anymore with the currently available extraction methods and instruments.
Common extraction methods to measure pollutant concentrations in soils in the laboratory distinguish between easily extractable and residual fractions.7,8 Nevertheless, any extraction method necessarily interferes with the quantity it aims to observe. Lesueur et al. 2008 showed that different extraction methods lead to different results.9 While the dilution effect of changing the liquid-to-solid ratio in the soil during extraction can principally be factored out, this correction is complicated by the fact that a change in the liquid to solid ratio leads to a shift in the equilibrium distribution of the pollutant in the soil in favour of the aqueous phase. This potential shift in equilibrium and the potentially resulting extraction bias have hardly been studied systematically.10–14 Since the fraction of pollutants dissolved in the aqueous phase is commonly regarded as the most mobile and biologically effective fraction, a bias in the estimates of aqueous phase concentrations hampers the assessment of risks associated with the occurrence of pollutants in soils.15 One example is the comparison of concentrations of antibiotics in aqueous extracts of soils with minimum inhibitory concentrations (MICs) and minimum selective concentrations (MSCs) determined in laboratory incubation experiments in which microorganisms are exposed to antibiotics that are dissolved in an aqueous growth medium at well-defined concentrations.16,17
A process-based model could be able to simulate the extraction process, explore the extraction bias and either allow to correct for it or provide justification to neglect it. Some existing modelling approaches link sorption directly to physical processes under steady-state conditions, but are not designed to simulate time series that reflect the kinetics.18,19 Existing dynamic models are able to simulate observed sorption time series, but are either not able to consider multiple conceptual substance fractions in agricultural soil differing in binding strength and accessibility (easily extractable – EAS, residual – RES, non-extractable – NER and the fraction resulting from transformation and mineralization – TM)20–22 or are based on simple first-order kinetics without considering physical processes.13,23,24 However, intraparticle diffusion was previously proposed as an important mechanism in sorption.25 Hence, a model that can simulate multiple pollutant fractions differing in binding strength extractability and accessibility over time based on physical processes is still missing.
Therefore, the overarching objective of this study is to develop a mathematical model based on published data for antibiotics and other pharmaceuticals extracted from soils over time that distinguishes different dissipation pathways of pollutants in soils and quantifies their kinetics. The model explores pollutant sorption via intraparticle diffusion as a possible dissipation pathway in addition to transformation and formation of non-extractable residues. Since the model reflects conceptually the actual chemical fate processes and not, technically, the extraction steps, it helps to simulate undisturbed processes in comparison to simulated extraction fractions to quantify the discrepancy in the aqueous concentration introduced by the extraction method (extraction bias). Hence, by applying the model to measured extraction data on antibiotics in different soils this study aims to (1) identify and quantify the processes that lead to antibiotic dissipation in soil, and (2) quantify the extraction bias that occurs if the easily extracted pollutant concentration is considered equal to the actual dissolved concentration.
Methods
General procedure
In this study, the conceptual understanding of sorption, sequestration and transformation of pharmaceuticals in soils has been translated into respective mathematical models that are each based on a system of ordinary differential equations representing the physico-chemical processes that drive the substance fate in soils. Available data in the literature on sequential soil extractions of pharmaceuticals were used to identify relevant processes that allow a meaningful representation of the observations by comparing different model structures derived by including or excluding potential sorption and dissipation pathways. Model parameter values, e.g. kinetic rate constants, were deduced by fitting the model structures to the extraction data during the calibration procedure. A local and a global sensitivity analysis were run to quantify the impact of changes in parameter values on the model outcome. Mass flux rates were simulated to identify the main processes governing the fate of the pharmaceuticals.
Based on the model development and quantification, simulations were run to identify the extraction bias that might be induced by shifts in the liquid-to-solid ratio during soil extraction in the laboratory.
Underlying data
In total, 19 datasets of time series of extractions of eight pharmaceuticals from natural soils from Germany or Mexico from Sittig et al. 2012, Dalkmann et al. 2014 and Förster et al. 2009 (ref. 12–14) (Table 1) were used for this study. Confidence intervals of time series were not available for these datasets. However, the average relative standard deviation of replicate measurements was ∼50% for Dalkmann et al. 2014 and ∼20% for Förster et al. 2009. No standard deviations were provided in Sittig et al. 2012. For each of the datasets, natural soils (0–30 cm depth) had been collected from the Mezquital Valley, north of Mexico City (Dalkmann) or from Merzenhausen and Kaldenkirchen in western Germany (Sittig and Förster). The investigated soils cover a large range of soil properties like clay content or organic matter content (Table 2), and developed under humid temperate climate conditions12,14 or tropical steppe climate.13 Since all soils were used as cropland, the variation of soil pH was only moderate ranging from slightly alkaline to slightly acidic (Table 2). The general extraction procedure is briefly outlined here, more details can be found in the references of the datasets. While Förster et al. 2009 and Dalkmann et al. 2014 extracted soils that were incubated in the dark with water spiked with pollutants under constant temperature and moisture in the laboratory over 150 days13 or 215 days,14 the experiments by Sittig et al. 2012 were implemented in an end-over-end-shaker with a soil suspension for 60 days. In all experiments, at least an easily extractable fraction (EAS, following a mild extraction procedure with 10 mM CaCl2) and a residual fraction (RES, from an extraction step with methanol, acetonitrile and phosphoric acid, partly combined with high temperature in a microwave oven) of the substances have been extracted and chemically analysed for a period of 60–215 days for 6–10 time points.
Table 1 Chemical properties of substances for which time series datasets on soil extraction are available
| Substance |
Molecular weight [g mol−1] |
pKa |
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW KOW |
Investigated by |
| Bezafibrate |
362 (ref. 26) |
3.6 (ref. 27) |
3.97 (ref. 27) |
Dalkmann et al.,13 2014 |
| Carbamazepine |
236 (ref. 26) |
13.9 (ref. 27) |
2.77 (ref. 27) |
Dalkmann et al.,13 2014 |
| Ciprofloxacin |
331 (ref. 26) |
6.1, 8.6 (ref. 28) |
0.28 (ref. 29) |
Dalkmann et al.,13 2014 |
| Diclofenac |
296 (ref. 26) |
4.2 (ref. 27) |
4.06 (ref. 27) |
Dalkmann et al.,13 2014 |
| Naproxen |
230 (ref. 26) |
4.2 (ref. 30) |
0.33 (ref. 31) |
Dalkmann et al.,13 2014 |
| Sulfadiazine |
250 (ref. 26) |
2.5, 6.5 (ref. 32) |
−0.07 (ref. 33) |
Sittig et al.,12 2012, Förster et al.,14 2009 |
| Sulfamethoxazole |
253 (ref. 26) |
1.7, 5.6 (ref. 34) |
0.89 (ref. 33) |
Dalkmann et al.,13 2014 |
| Trimethoprim |
290 (ref. 26) |
7.2 (ref. 35) |
0.91 (ref. 29) |
Dalkmann et al.,13 2014 |
Table 2 Properties of the natural soils used in the extraction experiments
| Soil |
pH |
OC [%] |
Sand [%] |
Silt [%] |
Clay [%] |
Duration of experiment [day] |
Reference |
| Leptosol, Vertisol, Phaeozem; Mezquital Valley, Mexico |
6.8–7.5 |
0.95–2.8 |
6.7–41 |
40–47 |
12–54 |
150 |
Dalkmann et al.13 2014 |
| Silty loam; Merzenhausen, Germany |
7.0 |
0.97 |
4.3 |
82.9 |
12.8 |
60 |
Sittig et al.12 2012 |
| Luvisol; Merzenhausen, Germany |
6.3 |
1.2 |
6 |
78 |
16 |
215 |
Förster et al.14 2009 |
| Cambisol; Kaldenkirchen, Germany |
6.0 |
1 |
75 |
22 |
3 |
215 |
Förster et al.14 2009 |
For 6 out of the 19 datasets, also the non-extractable residues could be quantified because the authors were able to work with radioactively-labelled compounds,12,14 and for 3 datasets transformation products of the pharmaceuticals were determined. The dataset from Förster et al. 2009 (ref. 14) contains concentration data on two transformation products, 4-hydroxysulfadiazine (OH-SDZ) and N-acetylsulfadiazine (Ac-SDZ).
Conceptual model
In the conceptual model, the soil matrix is assumed to be a homogeneously mixed compartment (in analogy to batch conditions of the underlying lab experiments) that consists of an aqueous and a solid phase. The solid phase is conceptualized as spherical particles of homogenous size and material, covered with at least a film of water. In order to account for the different extraction fractions of the investigated pharmaceuticals, the particles are conceptually discretized into different shells Si. In general, the pharmaceuticals are assumed to distribute between the different phases and particle shells by considering (equilibrium) Freundlich sorption, intraparticle diffusion processes as well as transformation and mineralization. More details on the processes are given below. In relation to the data gained from the available extraction experiments, the water phase and the outermost shell S1 are considered to correspond to the EAS fraction while all inner shells correspond either to the RES fraction or, towards the centre of the particle, the fraction of non-extractable residues (NER).
The following processes that link the pharmaceutical fate in and between the different fractions are considered in the conceptual model (equations are given below): sorption equilibrium between the compound concentration in the aqueous phase and the outermost shell of the particles is assumed to follow the Freundlich model. Transfer of the compound between these two phases is thus following the gradient towards Freundlich sorption equilibrium. Intraparticle diffusion determines the exchange of the compound between all inner shells of the particle, i.e. the EAS, the shells corresponding to the RES and the inner-most NER fractions. Although the amount of NER technically describes the amount of pollutant that cannot be extracted by common extraction methods, the NER-formation is assumed to be potentially fully reversible. An alternative model structure with irreversible NER formation was tested to check the plausibility of fully reversible NER formation. The transformation and mineralization pool (TM) represents the substance fraction resulting from biotic transformation from the EAS fraction following first order kinetics. Sittig et al. 2012 (ref. 12) excluded other, i.e. abiotic, degradation pathways based on the observation of radiolabelled sulfadiazine.
Model equations
Mass balances.
The basic condition for all model simulations here that represent conditions in a closed system is the mass balance. Hence the total mass of the pharmaceutical is given by:| | | mtot = (CEAS + CRES + CNER + CTM) × Mtot | (1) |
where mtot [M] is the total mass of the compound, while CEAS [M M−1], CRES [M M−1], CNER [M M−1] and CTM [M M−1] are the compound concentrations relative to the total soil mass Mtot in the EAS, RES, NER and TM fraction, respectively. The total mass of EAS comprises the compound fraction that is dissolved in the aqueous phase and the compound fraction in the outermost shell of the particles:| | | mEAS = CW,aq × Vaq + S1 × MS1 | (2) |
where CW,aq [ML−3] is the concentration in the aqueous soil phase (porewater) per volume of water, S1 [M M−1] is the content of the compound in the outermost shell S1 per mass of sorbent, Vaq [L3] is the porewater volume and MS1 [M] is the mass of shell S1. The concentration in the EAS fraction (CEAS [M M−1]) related to the total soil bulk mass is given as:| | 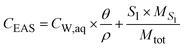 | (3) |
where θ [L3 L−3] is the volumetric water content and ρ [ML−3] is the dry soil bulk density. The volume and mass of all shells are defined as equal based on the assumption that all particles are homogeneous, i.e. have a constant density throughout the particle. Hence, the mass of an individual shell is defined as:| | 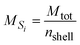 | (4) |
where MSi [M] is the mass of any shell and nshell [−] is the total number of shells. Inserted in eqn (3), this leads to:| | 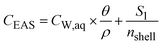 | (5) |
since all concentration data from the literature are given in mass of compound per mass dry bulk soil [M M−1], CW in [M M−1] is defined, for consistency reasons, as:| | 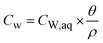 | (6) |
and used in all equations following from here on.
The concentrations of the RES-fraction, CRES [M M−1], and the NER fraction, CNER [M M−1], are defined as the average mass of the compound that has been distributed into all shells defined as RES or NER, respectively, in relation to the total dry bulk soil mass:
| | 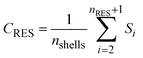 | (7) |
| |  | (8) |
where
nRES [−] and
nNER [−] are the numbers of shells that are assigned to RES and NER, respectively. The numbers of shells that correspond to the RES and the NER fraction is not fixed in the model structure but is derived from the fitting results, conceptually, a characteristic of the soil, the extraction procedure and the compound, in combination.
Initial conditions.
For setting the initial conditions of the differential equations, the total concentration of the pharmaceutical was calculated based on the first observations of EAS and RES. These first observations were taken at t = 0.24d. Hence the respective masses at t = 0d were extrapolated. The initial masses of EAS and RES were then distributed among the different phases/shells according to the following three assumptions:
(1) The initial distribution of mass between Cw and S1 is ambiguous, as both phases are represented by the EAS-fraction. Hence, the mass distribution between these phases is assumed to be approximately even. In the context of sorption, this leads to the Freundlich sorption equilibrium according to eqn (9).
(2) The concentration of all inner shells that are assigned to RES is assumed to be scaled by an empirical, dimensionless gradient factor g, which is determined during calibration:
(3) NER and, if applicable, TM are assumed to be zero.
Initialization of parameter values
Each parameter was initially defined by a prior distribution function based on all knowledge to start the calibration procedure of fitting the model to the available data and deriving optimal parameter values. By this, the empirical distribution of the parameter values resembles the prior distribution of the parameters (Table S1†). Hence, the parameter values are not limited to an arbitrary range, as the continuous prior distribution function can be chosen to cover all physically possible values.
To sample from these prior distributions, normalized parameter values were drawn from a uniform distribution between zero and one.
| | 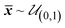 | (22) |
where
![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif)
is the normalized location vector in the parameter space and
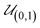
is the uniform distribution ranging from zero to one. The absolute parameter value is defined as the inverse cumulative probability density function of the respective parameter:
| | xi = Φ−1i(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) i) i) | (23) |
where
xi is the absolute value of the respective parameter that is used for the model simulation,
Φ−1i is the inverse cumulative probability density function of the respective parameter and
i is the parameter index.
Model calibration
Model equations were fitted to the 19 sets of extraction time series to gain a set of optimum model parameter values for each combination of pharmaceutical compound and soil. The datasets from Dalkmann et al. 2014 contain information about sterile and non-sterile conditions (except the ciprofloxacin dataset) under otherwise identical conditions, and thus a calibration in two steps was applied. The datasets under sterile conditions were used for calibration of all parameters except the rate constant for transformation and mineralization kTM which is, conceptually, set to zero. Based on these calibration results, the six corresponding datasets under non-sterile conditions were evaluated by fixing the derived parameter values from the datasets under sterile conditions, and calibrating kTM. These six datasets were excluded from the sensitivity analysis since all parameters except kTM are fixed. For all other datasets which have all been derived from experiments under non-sterile conditions, all parameters including kTM were used for calibration simultaneously.
The root-mean-square error (RMSE) between the observed and simulated values was defined as the objective function for minimizing the deviation between data and model outcomes.
| | 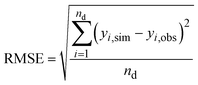 | (24) |
where
nd is the number of data points,
yi,obs is the respective observed datapoint,
yi,sim is the simulated value and
i is the datapoint index. Data points for different fractions (EAS, RES) were considered as data points from the same data series. The simulated values were created by solving the differential equations numerically. The RMSE was minimized using the
surrogateopt algorithm in MATLAB. The algorithm relies on a surrogate model based on a radial basis function to evaluate promising points in the parameter space faster than the process-based model. For model comparison and comparison between extraction experiments, the normalized root mean square error (NRMSE) was used:
| | 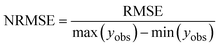 | (25) |
Alternative model structures
The reference model structure represents one possible explanation for transfer pathways and sorption processes but needs to be compared to potential alternative model structures that might explain the underlying experimental data equally well or even better. Thus, two alternative model structures were tested in the frame of evaluating model uncertainty: (1) irreversible NER-formation from RES and (2) reversible NER-formation from RES. Details of these alternative models are described in the ESI.† In addition, existing model approaches described in the literature were also applied to the available extraction data, if suitable, and respective results compared to the developed reference model.12,23,36
Sensitivity analysis
A model is considered sensitive to parameters that have the strongest effect on the simulation results, in this case, the RMSE between observed and simulated pollutant concentrations in the different soil phases. Sensitivity analyses, which determine the sensitivity of the model to its parameters, can be categorized as local and global. Local sensitivity determines the sensitivity of a model only for a specific location in the parameter space while the global sensitivity analysis determines the mean sensitivity over the whole parameter space.
In cases where models contain multiple parameters, the sensitivity of the models towards individual parameters often varies strongly. Parameters to which the model is sensitive are considered active parameters.
To account for global sensitivity, Constantine et al. 2014 (ref. 37) proposed the active subspace method.37 Constantine et al. 2014 (ref. 37) defined an active subspace as the eigenvectors of the matrix E:37
| | E = ∫∇f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) ⊗ f( ) ⊗ f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) q( ) q(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) )dx )dx | (26) |
⊗ is the matrix product,
q is the probability density function of the normalized parameters
![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif)
, and
f is the objective function. The integration is performed by the Monte-Carlo-method:
38| | 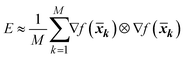 | (27) |
M is the number of samples and is set to 10
4 and
![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) k
k are independently drawn normalized parameter vectors.
The global sensitivity was assessed by the metric of Constantine and Diaz:39
| | 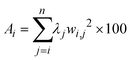 | (28) |
where
Ai is the activity score for parameter
i,
j is the eigenvector index,
n is the number of eigenvalues (equal to the number of parameters),
λj is the
j-th eigenvalue and
wi,j is the value for parameter
i in the
j-th eigenvector of the matrix
E. The activity score is the square of the unit of the observation. Therefore, in this work, the square root of the activity score was used. To increase readability, the activity score is scaled to a range of 0 to 100.
The most common challenge in this approach is to reliably determine ∇f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ).40 In this case, f(
).40 In this case, f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) is not an observation, but a simulation by the model. Hence, f(
) is not an observation, but a simulation by the model. Hence, f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) is noise-free. Therefore, the finite-difference method poses a possibility to determine ∇f(
) is noise-free. Therefore, the finite-difference method poses a possibility to determine ∇f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ):
):
| | 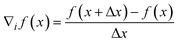 | (29) |
In addition to the global sensitivity analysis a local sensitivity analysis was added around the fitted parameters. All calculations were implemented in MATLAB.
41
Uncertainty analysis
The bootstrapping algorithm was used to determine the uncertainty of the calibration.42 Efron and Tibshirani (1997) described bootstrapping as a smoothed version of cross-variance.43 It is a method that involves multiple sub-datasets which are created by slight perturbations of the original dataset by resampling with replacement (bootstrap-samples). All resulting bootstrap-datasets were used for fitting, leading to different parameter sets for each bootstrap-sample. The resulting parameter sets formed a posterior distribution that were used as a measure of uncertainty for the determined parameter values (e.g., 95% confidence interval).
Model application: estimation of the extraction bias
For the determination of the extraction bias, the pollutant concentration in the aqueous phase (CW) was simulated with the parameters determined by the model calibration. All datasets describe extraction experiments for sorption to a clean soil and dissipation. Therefore, after spiking the soil with the respective pollutant, the pollutant mass in the soil water decreases over time (Fig. 1). With the beginning of the extraction step, the ratio of water to soil mass in the soil sample is increased. CW,aq (concentration per volume of water) is thus decreased by the same factor due to dilution. The simulation was then continued with the new soil to solution ratio for the typical duration of the extraction time (24 h). During this time, desorption takes place due to the deviation from the sorption equilibrium after the addition of the mild aqueous extractant. Hence, the simulation showed a sudden increase in pollutant mass in the water phase to return to the equilibrium concentration ratio between solids and liquid phase.
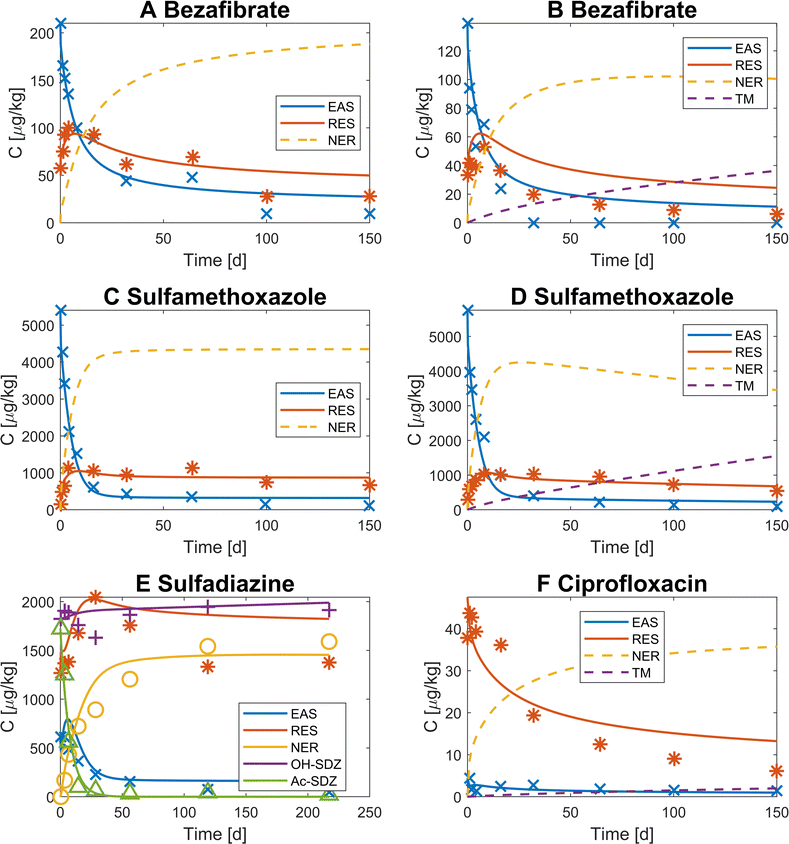 |
| | Fig. 1 Observed (markers) and simulated (lines) concentrations under sterile (A and C) and non-sterile conditions (B and D–F) for different pollutants in the easily extractable fraction EAS (blue), the residual fraction RES (red), the non-extractable fraction NER (yellow) and the transformed and mineralized fraction TM of the pollutant (purple). In sub-figure (E), the concentration of the transformation product of sulfadiazine, Ac-SDZ, is indicated in green. Dashed lines indicate simulation results for the substance fractions for which no data were available (in general TM and/or NER). | |
The extraction bias was calculated by simulating individual extractions at all time points sampled. Due to the shift in sorption equilibrium, the observed concentration values for the EAS fraction overestimate the pollutant mass in the water phase. This leads to an extraction bias, quantified as the NRMSE between the simulated pollutant concentration in the water phase and the simulated extracted concentration (Table S4†). Only observed time points were considered for the NRMSE. The correlation between calibrated parameter values and the extraction bias was tested using the two-sided Pearson and Spearman correlation coefficients as well as Kendall's τ.
Results and discussion
After calibration of parameters, the reference model structure describes the datasets reasonably well according to the indicators for goodness of fit (NRMSE < 0.3) and the visual agreement between model simulations and data (Fig. 1). Differences between datasets under sterile conditions (Fig. 1A and C) and non-sterile conditions (Fig. 1B and D) are small. The model quality of this reference model is comparable to the reference model by Zarfl et al. 2009 (ref. 23) (no significant difference between the NRMSEs, t-test, p = 0.29). Other published dynamic compartment models were not considered for comparison, because they do not account for all pollutant fractions included in the datasets used for our analysis (EAS, RES, NER and TM).12,36
Including the formation of TM under non-sterile conditions in the model structure leads to a different projected dynamic despite fixed parameter values for the formation of EAS, RES and NER. Remobilization of NER might become relevant over longer timescales in favour of the dissipation and actual removal from the soil by the formation of TM as indicated by a decrease of the simulated NER fraction (Fig. 1B and D). Remobilization is not reflected in the data and simulations for all compounds, e.g. sulfadiazine and ciprofloxacin, both under non-sterile conditions, over the observed timescale for which the simulated NER fraction reaches a plateau (Fig. 1E and F), suggesting that the reversibility of NER formation is a substance-specific behaviour if, in contrast to our assumption that NER was fully reversible, substance sequestration in soils is partially irreversible,18 simulations longer than considered here might lead to an overestimation of long-term remobilization.
In the case of bezafibrate, the parameters from the dataset under sterile conditions lead to a slight overestimation of EAS and RES for the non-sterile dataset that could not be compensated by the formation of TM. This might be caused by an overestimation of the initial conditions and hence of the total mass of pharmaceutical in this case. E.g. an overestimation of 10% (within the experimental error) can cause a substantial overestimation of total mass in the system. In cases where a tailing of the dissipation process is observed (due to a “balance” in long-term sequestration and desorption), the model was able to simulate this effect (Fig. 1A, C and D). Dissipation leads to a decrease in the observed pollutant mass in the EAS and RES fraction of all investigated compounds by an average of 60% by the end of the experiment (60–220 days). The NER and TM fractions increase analogously with the decrease in EAS and RES through dissipation. The relevance of the three main processes – Freundlich sorption, transformation and mineralization as well as intraparticle-diffusion – differs substantially between substances and presence or absence of microbial activity (see Table 3). For the first 40 days, Freundlich sorption and intraparticle diffusion contribute almost equally to the total average mass flux, while transformation and mineralization play only a minor role in the non-sterile datasets (set to zero for the sterile datasets). The mass fluxes of the respective processes were normalized to the number of elements within a process (e.g. shells in the particle, soil water, TM pool, etc.) to factor out an overestimation of the respective mass flux by transitions within the same process (e.g. diffusion between multiple shells). The relevance of Freundlich sorption decreases over time in favour of diffusion. Intraparticle diffusion is generally much slower to equilibrate due to the high number of particle shells. Therefore, its relative relevance is higher in later stages of the experiment, although total mass fluxes are orders of magnitude lower in these later stages of the experiment. Unlike sorption the formation of TM is irreversible. Hence, it only ceases when all pollutant mass is transformed and/or mineralized. Due to the low availability of pollutant mass in the water phase, this process is very slow. This leads to higher relative mass fluxes of TM in later stages of the experiment when sorption processes are close to equilibrium. The relevance of transformation and mineralization might be underestimated, since any amount of pollutant might be part of the Freundlich sorption and intraparticle diffusion process multiple times but can only once undergo the transition to the TM pool.
Table 3 Relative mass fluxes of the respective processes normalized to the number of elements within that process and normalized to the reference soil mass of one kilogram (mean value, ranges in the line below). Only those pollutants are listed for which the average mass flux in the first forty days exceeds one percent of the total mass in the soil
| Simulation time |
0–40 days |
40–80 days |
| Sorption [%] |
TM [%] |
Diffusion [%] |
Mass flux [μg per day] |
Sorption [%] |
TM [%] |
Diffusion [%] |
Mass flux [μg per day] |
| Bezafibrate non-sterile |
72 |
6 |
22 |
4.5 |
20 |
10 |
70 |
0.2 |
| 69–74 |
3–13 |
17–25 |
3.8–5.6 |
4–32 |
7–11 |
60–89 |
0.1–0.2 |
| Bezafibrate sterile |
66 |
0 |
34 |
6.1 |
33 |
0 |
67 |
0.7 |
| 50–75 |
|
25–50 |
4–8.4 |
23–57 |
|
43–77 |
0.6–1 |
| Ciprofloxacin non-sterile |
0.3 |
0 |
100 |
0.2 |
1 |
0 |
99 |
0.07 |
| 0–9 |
0–0.1 |
91–100 |
0.1–1.6 |
0–22 |
0–0.2 |
78–100 |
0.04–0.1 |
| Diclofenac non-sterile |
13 |
5 |
80 |
23.5 |
1 |
3 |
96 |
0.04 |
| 8–19 |
1–11 |
78–89 |
9.2–31.5 |
0–1 |
1–6 |
94–98 |
0.01–0.4 |
| Diclofenac sterile |
7 |
0 |
93 |
160 |
17 |
0 |
83 |
0 |
| 0–28 |
|
72–100 |
50–200 |
0–95 |
|
5–100 |
0–0.5 |
| Naproxen non-sterile |
78 |
10 |
12 |
86 |
67 |
17 |
16 |
30 |
| 77–78 |
10–11 |
12–13 |
82–94 |
67–67 |
17–18 |
16–16 |
30–33 |
| Naproxen sterile |
81 |
0 |
19 |
70 |
68 |
0 |
32 |
25 |
| 25–84 |
|
16–75 |
26–160 |
54–76 |
|
24–46 |
18–34 |
| Sulfamethoxazole non-sterile |
49 |
1 |
50 |
303 |
4 |
13 |
83 |
4 |
| 48–50 |
0–2 |
49–51 |
291–320 |
2–15 |
0–14 |
77–86 |
2–7 |
| Sulfamethoxazole sterile |
52 |
0 |
48 |
297 |
14 |
0 |
86 |
2 |
| 3–62 |
|
38–97 |
257–500 |
6–65 |
|
35–94 |
0–4 |
The role of the kinetic sorption processes in relation to their equilibrium state changes during the course of the experiment. Therefore, the simulated aqueous compound concentration (Cw) and the compound concentration averaged across all particle shells are compared to their respective equilibrium (Fig. 2). Please note that the sorption equilibrium (dashed lines in Fig. 2) changes gradually due to the irreversible formation of TM, which reduces the total available mass of pollutant over time and thus the absolute equilibrium concentrations. In the beginning of the experiment, concentrations differ substantially from the sorption equilibrium.
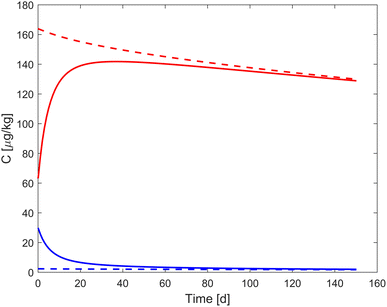 |
| | Fig. 2 Simulation of bezafibrate concentrations in the aqueous phase (CW, blue) and averaged across all particle shells (red) in a non-sterile soil. Dashed lines indicate the equilibrium concentrations, based on the Freundlich-model, while solid lines indicate the simulation results with the calibrated model. | |
In the example shown in Fig. 2, the concentrations approach equilibrium of Freundlich sorption in the first half of the experiment. After this, sorption processes between the outer shell and the aqueous phase are almost in equilibrium and their sorption kinetics play only a minor role. The time required to reach Freundlich sorption equilibrium differs substantially between pharmaceuticals. Fast sorbing pharmaceuticals equilibrate almost instantly (e.g. trimethoprim, carbamazepine).
Estimation of the extraction bias
Based on the estimated extraction bias, the investigated pharmaceuticals can be divided into substances with high extraction bias (NRMSEextract ≥ 0.47) and those with low extraction bias (NRMSEextract ≤ 0.28) (see Fig. 3 for comparison). The categorization of a substance as having a “high extraction bias” corresponds to an overestimation of the soil water concentration of more than 40%. The substances with high extraction bias include ciprofloxacin, trimethoprim and carbamazepine. Ciprofloxacin and trimethoprim are the only pharmaceuticals in the analysed dataset which have a positive charge at soil pH (Table S3†), so that cation exchange is a possible sorption process.44–46 Cation exchange with Ca2+ added with the CaCl2 extraction solution is a possible explanation for fast desorption that causes a high extraction bias. A previous study identified a correlation between sorption of trimethoprim and ciprofloxacin and cation exchange capacity.44 Carbamazepine is the only substance with a neutral charge at soil pH, which is a possible reason for fast desorption that has also been described by other studies, especially from carbon rich substrate.47,48
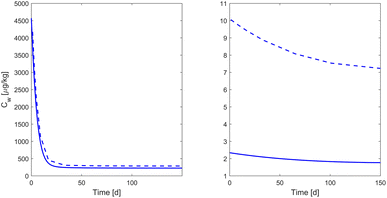 |
| | Fig. 3 Exemplary visualization of the simulated sulfamethoxazole (left) and trimethoprim (right) concentration under sterilized conditions in soil water (Cw) without extraction (solid blue) and as it would be observed in the extracted fraction (dashed blue). | |
Most calibrated parameters show little to no correlation to the extraction bias. Only the Freundlich exponent m shows a significant correlation (Table S2†). The correlation for the Freundlich exponent m is highest for the Pearson coefficient and much lower and not significant for Spearman and Kendall's τ. Kendall's τ is less susceptible to extreme values.49 Hence, the correlation shown by the Pearson coefficient might be mostly based on the more extreme values for pharmaceuticals with high extraction bias.
Sensitivity and uncertainty analysis
Unlike a local sensitivity, the global sensitivity is a property of the model. It depends on the chosen prior parameter distribution but not on the calibrated parameter values. Since some parameter distributions are compound-specific, the sensitivity is not necessarily equal for all compounds, but is averaged over compounds that are simulated with the same combination of model and data source (Tables S5–S7†). For the model used for the sterile datasets from Dalkmann et al. 2014,13 the RES and NER fractions are most sensitive to the apparent diffusivity D, since diffusion affects these fractions directly. EAS, which is only directly affected by Freundlich sorption, is most sensitive towards the Freundlich sorption rate parameter α and the Freundlich parameters Kf and m. Overall, out of all sorption parameters, the model is most sensitive to m, which can be explained by its exponential effect. Kf is the least sensitive sorption parameter, which is most likely outperformed by m, since both parameters describe the Freundlich equilibrium. EAS is, unlike all other fractions, moderately sensitive to the scaling factor β.
Unlike the sensitivity analysis for the model applied to the data from Dalkmann et al. 2014,13 the sensitivity analysis for the model applied to the data from Sittig et al. 2012 (ref. 12) considers both dissipation pathways (TM and NER) (Table S6†). In this case, the mass fractions are most sensitive to the rate constant for transformation and mineralization kTM. The sensitivity is highest for Cw and TM that are directly affected by the rate constant kTM, and propagates to the other pollutant fractions. EAS and RES are most sensitive to the Freundlich sorption rate constant α and the Freundlich parameters Kf and m, due to Freundlich sorption affecting these quantities directly. NER is most sensitive to the apparent diffusivity D, which is the only parameter that controls the formation of NER. Unlike the rate constant kTM, the sensitivity does not propagate to the other pollutant fractions. Most likely, this is caused by the availability of data about the NER fraction. This means that the amount of NER is fixed, while the amount of TM can only be estimated by the mass balance.
The sensitivity analysis for the model applied to the data of Förster et al. 2009 (ref. 14) is, in general, similar to the sensitivity results for the model related to the data from Sittig et al. 2012 (ref. 12) (Table S7†). Nevertheless, unlike all other datasets, transformation was observed in this dataset, so results regarding TM might be more reliable. In contrast to the sensitivity for the data from Sittig et al. 2012,12 NER and RES are less sensitive to kTM. This might be caused by additional information in the data on the transformation products, which is only the case in the datasets from Förster et al. 2009 (ref. 14) EAS is more sensitive towards the parameters describing transformation between OH-SDZ and Ac-SDZ than Freundlich sorption. Unlike for the other datasets, no quantity was sensitive to the apparent diffusivity D. Most likely, the kinetics of the formation of NER is more sensitive to the number of shells assigned to NER (see eqn (7) and (8)) than to the diffusive process described by D.
The confidence intervals of the determined parameters are relatively small for established processes like Freundlich sorption kinetic and equilibrium, while the confidence interval of the apparent diffusivity D is much larger, since the exact nature of the diffusion process is less clear and might be more simplified than the Freundlich sorption (Tables S8–S10†).
Characterization of dissipation
Depending on the shell distribution, either the NER- or TM-dissipation pathway is dominant when both pathways are considered. The exact amount of NER and TM is known for the data from Sittig et al. 2012 (ref. 12) and Förster et al. 2009,14 where NER was quantified experimentally (see Fig. S2 and S3†). However, the dataset from Dalkmann et al. 2014 (ref. 13) does not contain NER or TM data. Therefore, the shell distribution cannot be fitted in the same way as for the other two datasets. In the case where both, sterile and non-sterile, datasets were available, it was possible to determine the parameter kTM for transformation and mineralization from the comparison of these two cases, assuming no transformation and mineralization under sterile conditions. In the case of ciprofloxacin, only data taken under non-sterile conditions was available. The model showed similarly good fits when considering the NER-pathway or the TM-pathway (see Fig. 4). This indicates that it is in general not possible to distinguish between NER and TM solely by applying the different model structures to extraction data without any knowledge about potential degradation products or inclusion of a sterile treatment.
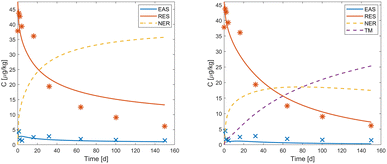 |
| | Fig. 4 Observed (markers) and simulated (lines) values of EAS (blue), RES (red), NER (yellow, dashed) and TM (purple, dashed) of ciprofloxacin. The left tile shows the NER-focused scenario. The right tile shows the TM-focused scenario. Note that the right tile necessarily indicates a better fit of the model to the data due to an additional parameter (kTM) in the model structure available for calibration. | |
Conclusions
The assessment of environmental risks associated with pollutants requires the estimation of “bioaccessible”, “bioavailable” and mobile pollutants fractions in soils, which change over time, based on sound conceptual models. In this study, the abstraction of the soil as homogeneous spherical particles is one of several options to conceptualize the soil's solid phase. Diffusion to the centre of the particle as described in this model concept might, in reality, be reflected in similar mechanisms that cause hysteresis. E.g., if pollutant mass diffused into the outer half (radius-wise) of the particle only and the apparent diffusivity was a quarter of the fitted value (due to the quadratic nature of diffusion over distance), the modelled observations would look similar, assuming that the number of, now smaller shells, stays the same. These mechanisms are indistinguishable from the chosen mechanisms from a modelling perspective. A differentiation between transformation and mineralization on the one hand and NER formation on the other hand requires either the complete experimental quantification of transformation products or the quantification of NER formation e.g. by means of isotope-labelled compounds, experiments under sterile and non-sterile conditions or longer observation times to observe possible desorption. Otherwise, the model cannot differentiate between these processes. Extended observation periods may also be considered to test the reversibility of NER formation. If the isolated determination of the individual simulated processes in experiments were possible, the uncertainties for the structure and parameters of the model could be decreased.
The estimated extraction bias was negligibly small for most of the pharmaceuticals that were investigated in the datasets we used. Hence, simple extractions with aqueous solutions allow a reasonable assessment of “bioaccessible”, “bioavailable” or biologically effective concentrations of pharmaceuticals. The cases for which the estimation of “bioaccessible”, “bioavailable” or “bioeffective” concentrations based on “mild”, aqueous extracts might be challenging can probably be identified in advance based on the chemical properties of the observed compounds (i.e. ionic charge).
Data availability
No new data was created in this study. The used MATLAB-Code is available at: https://www.github.com/Sigma-Librae/IPDSM.
Author contributions
M. B., J. S. and C. Z. designed the research. M. B. created the model, performed analysis, and visualized graphics. C. Z., J. S. and B. J. H. substantially contributed to the interpretation of results. M. B. outlined the manuscript and all co-authors revised the work carefully. All authors have read and agreed to the published version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Research Unit “Pollutant – Antibiotic Resistance–Pathogen Interactions in a Changing Wastewater Irrigation System” (PARES, FOR 5095), funded by the German Research Foundation (DFG, Project no. 431531292). We also acknowledge fiancial support from the Open Access Publishing Fund of the University of Tübingen. We thank Peter Grathwohl for his comments and insights.
References
- J. I. Nieto-Juárez, R. A. Torres-Palma, A. M. Botero-Coy and F. Hernández, Pharmaceuticals and environmental risk assessment in municipal wastewater treatment plants and rivers from Peru, Environ. Int., 2021, 155, 106674 CrossRef PubMed.
- B. Gworek, M. Kijeńska, J. Wrzosek and M. Graniewska, Pharmaceuticals in the soil and plant environment: a review, Water, Air, Soil Pollut., 2021, 232, 145 CrossRef CAS.
- R. Kodešová, M. Kočárek, A. Klement, O. Golovko, O. Koba, M. Fér, A. Nikodem, L. Vondráčková, O. Jakšík and R. Grabic, An analysis of the dissipation of pharmaceuticals under thirteen different soil conditions, Sci. Total Environ., 2016, 544, 369–381 CrossRef PubMed.
- M. Cycoń, A. Mrozik and Z. Piotrowska-Seget, Antibiotics in the soil environment—degradation and their impact on microbial activity and diversity, Front. Microbiol., 2019, 10, 338 CrossRef PubMed.
- P. A. Blackwell, P. Kay and A. B. A. Boxall, The dissipation and transport of veterinary antibiotics in a sandy loam soil, Chemosphere, 2007, 67, 292–299 CrossRef CAS PubMed.
- E. Pose-Juan, M. J. Sánchez-Martín, E. Herrero-Hernández and M. S. Rodríguez-Cruz, Application of mesotrione at different doses in an amended soil: Dissipation and effect on the soil microbial biomass and activity, Sci. Total Environ., 2015, 536, 31–38 CrossRef CAS PubMed.
- I. Rosendahl, J. Siemens, J. Groeneweg, E. Linzbach, V. Laabs, C. Herrmann, H. Vereecken and W. Amelung, Dissipation and sequestration of the veterinary antibiotic sulfadiazine and its metabolites under field conditions, Environ. Sci. Technol., 2011, 45, 5216–5222 CrossRef CAS PubMed.
- T. Müller, I. Rosendahl, A. Focks, J. Siemens, J. Klasmeier and M. Matthies, Short-term extractability of sulfadiazine after application to soils, Environ. Pollut., 2013, 172, 180–185 CrossRef PubMed.
- C. Lesueur, M. Gartner, A. Mentler and M. Fuerhacker, Comparison of four extraction methods for the analysis of 24 pesticides in soil samples with gas chromatography–mass spectrometry and liquid chromatography–ion trap–mass spectrometry, Talanta, 2008, 75, 284–293 CrossRef CAS PubMed.
- L. Cáceres-Jensen, J. Rodríguez-Becerra, C. Garrido, M. Escudey, L. Barrientos, J. Parra-Rivero, V. Domínguez-Vera and B. Loch-Arellano, Study of Sorption Kinetics and Sorption–Desorption Models to Assess the Transport Mechanisms of 2,4-Dichlorophenoxyacetic Acid on Volcanic Soils, Int. J. Environ. Res. Public Health, 2021, 18, 6264 CrossRef PubMed.
- R. Đurović-Pejčev, S. Radmanović, Z. P. Tomić, L. Kaluđerović and T. Đorđević, Characterization of the clomazone sorption process in four agricultural soils using different kinetic models, Environ. Sci.:Processes Impacts, 2023, 25, 542–553 RSC.
- S. Sittig, R. Kasteel, J. Groeneweg and H. Vereecken, Long-term sorption and sequestration dynamics of the antibiotic sulfadiazine: A batch study, J. Environ. Qual., 2012, 41, 1497–1506 CrossRef CAS PubMed.
- P. Dalkmann, C. Siebe, W. Amelung, M. Schloter and J. Siemens, Does long-term irrigation with untreated wastewater accelerate the dissipation of pharmaceuticals in soil?, Environ. Sci. Technol., 2014, 48, 4963–4970 CrossRef CAS PubMed.
- M. Förster, V. Laabs, M. Lamshöft, J. Groeneweg, S. Zühlke, M. Spiteller, M. Krauss, M. Kaupenjohann and W. Amelung, Sequestration of manure-applied sulfadiazine residues in soils, Environ. Sci. Technol., 2009, 43, 1824–1830 CrossRef PubMed.
- J. Menz, J. Müller, O. Olsson and K. Kümmerer, Bioavailability of antibiotics at soil–water interfaces: A comparison of measured activities and equilibrium partitioning estimates, Environ. Sci. Technol., 2018, 52, 6555–6564 CrossRef CAS PubMed.
- I. C. Stanton, A. K. Murray, L. Zhang, J. Snape and W. H. Gaze, Evolution of antibiotic resistance at low antibiotic concentrations including selection below the minimal selective concentration, Commun. Biol., 2020, 3, 1–11 CrossRef PubMed.
- D. Schuster, K. Axtmann, N. Holstein, C. Felder, A. Voigt, H. Färber, P. Ciorba, C. Szekat, A. Schallenberg, M. Böckmann, C. Zarfl, C. Neidhöfer, K. Smalla, M. Exner and G. Bierbaum, Antibiotic concentrations in raw hospital wastewater surpass minimal selective and minimum inhibitory concentrations of resistant Acinetobacter baylyi strains, Environ. Microbiol., 2022, 24, 5721–5733 CrossRef CAS PubMed.
- M. Sander, Y. Lu and J. J. Pignatello, A Thermodynamically Based Method to Quantify True Sorption Hysteresis, J. Environ. Qual., 2005, 34, 1063–1072 CrossRef CAS PubMed.
- M. Sander and J. J. Pignatello, Sorption irreversibility of 1,4-dichlorobenzene in two natural organic matter–rich geosorbents, Environ. Toxicol. Chem., 2009, 28, 447–457 CrossRef CAS PubMed.
- A. Wehrhan, T. Streck, J. Groeneweg, H. Vereecken and R. Kasteel, Long-Term Sorption and Desorption of Sulfadiazine in Soil: Experiments and Modeling, J. Environ. Qual., 2010, 39, 654–666 CrossRef CAS PubMed.
- K. Brimo, P. Garnier, S. Sun, J.-L. Bertrand-Krajewski, A. Cébron and S. Ouvrard, Using a Bayesian approach to improve and calibrate a dynamic model of polycyclic aromatic hydrocarbons degradation in an industrial contaminated soil, Environ. Pollut., 2016, 215, 27–37 CrossRef CAS PubMed.
- G. Lashermes, Y. Zhang, S. Houot, J. P. Steyer, D. Patureau, E. Barriuso and P. Garnier, Simulation of Organic Matter and Pollutant Evolution during Composting: The COP-Compost Model, J. Environ. Qual., 2013, 42, 361–372 CrossRef CAS PubMed.
- C. Zarfl, J. Klasmeier and M. Matthies, A conceptual model describing the fate of sulfadiazine and its metabolites observed in manure-amended soils, Chemosphere, 2009, 77, 720–726 CrossRef CAS PubMed.
- A. Berez, F. Ayari, N. Abidi, G. Schäfer and M. Trabelsi-Ayadi, Adsorption-desorption processes of azo dye on natural bentonite: batch experiments and modelling, Clay Miner., 2014, 49, 747–763 CrossRef.
- J. J. Pignatello and B. Xing, Mechanisms of Slow Sorption of Organic Chemicals to Natural Particles, Environ. Sci. Technol., 1996, 30, 1–11 CrossRef CAS.
-
PubChem, PubChem, https://pubchem.ncbi.nlm.nih.gov/, accessed 9 August 2023.
- K. Styszko, J. Szczurowski, N. Czuma, D. Makowska, M. Kistler and Ł. Uruski, Adsorptive removal of pharmaceuticals and personal care products from aqueous solutions by chemically treated fly ash, Int. J. Environ. Sci. Technol., 2018, 15, 493–506 CrossRef CAS.
- P. C. Sharma, A. Jain, S. Jain, R. Pahwa and M. S. Yar, Ciprofloxacin: review on developments in synthetic, analytical, and medicinal aspects, J. Enzyme Inhib. Med. Chem., 2010, 25, 577–589 CrossRef CAS PubMed.
- B. Halling-Sørensen, H.-C. H. Lützhøft, H. R. Andersen and F. Ingerslev, Environmental risk assessment of antibiotics: comparison of mecillinam, trimethoprim and ciprofloxacin, J. Antimicrob. Chemother., 2000, 46, 53–58 CrossRef.
- M. Röhricht, J. Krisam, U. Weise, U. R. Kraus and R.-A. Düring, Elimination of carbamazepine, diclofenac and naproxen from treated wastewater by nanofiltration, Clean:Soil, Air, Water, 2009, 37, 638–641 Search PubMed.
- F. Barbato, G. Caliendo, M. I. La Rotonda, C. Silipo, G. Toraldo and A. Vittoria, Distribution coefficients by curve fitting: Application to ionogenic nonsteroidal antiinflammatory drugs, Quant. Struct.-Act. Relat., 1986, 5, 88–95 CrossRef CAS.
- K. P. de Amorim, L. L. Romualdo and L. S. Andrade, Performance and kinetic-mechanistic aspects in the electrochemical degradation of sulfadiazine on boron-doped diamond electrode, J. Braz. Chem. Soc., 2014, 25, 1484–1492 CAS.
- S. G. Machatha and S. H. Yalkowsky, Comparison of the octanol/water partition coefficients calculated by ClogP®, ACDlogP and KowWin® to experimentally determined values, Int. J. Pharm., 2005, 294, 185–192 CrossRef CAS PubMed.
- H. Lucida, J. E. Parkin and V. B. Sunderland, Kinetic study of the reaction of sulfamethoxazole and glucose under acidic conditions: I. Effect of pH and temperature, Int. J. Pharm., 2000, 202, 47–62 CrossRef CAS PubMed.
- O. Mikes and S. Trapp, Acute toxicity of the dissociating veterinary antibiotics trimethoprim to willow trees at varying pH, Bull. Environ. Contam. Toxicol., 2010, 85, 556–561 CrossRef CAS PubMed.
- A. Wehrhan, R. Kasteel, J. Simunek, J. Groeneweg and H. Vereecken, Transport of sulfadiazine in soil columns—experiments and modelling approaches, J. Contam. Hydrol., 2007, 89, 107–135 CrossRef CAS PubMed.
- P. G. Constantine, E. Dow and Q. Wang, Active subspace methods in theory and practice: Applications to Kriging surfaces, SIAM J. Sci. Comput., 2014, 36, A1500–A1524 CrossRef.
- P. G. Constantine, C. Kent and T. Bui-Thanh, Accelerating Markov chain Monte Carlo with active subspaces, SIAM J. Sci. Comput., 2016, 38, A2779–A2805 CrossRef.
- P. G. Constantine and P. Diaz, Global sensitivity metrics from active subspaces, Reliab. Eng. Syst. Saf., 2017, 162, 1–13 CrossRef.
- D. Erdal and O. A. Cirpka, Global sensitivity analysis and adaptive stochastic sampling of a subsurface-flow model using active subspaces, Hydrol. Earth Syst. Sci., 2019, 23, 3787–3805 CrossRef.
-
MATLAB, 9.12.0.1884302 (R2022a), The MathWorks Inc., Natick, Massachusetts, 2022 Search PubMed.
-
B. Efron, in Breakthroughs in Statistics: Methodology and Distribution, ed. S. Kotz and N. L. Johnson, Springer, New York, NY, 1992, pp. 569–593 Search PubMed.
- B. Efron and R. Tibshirani, Improvements on cross-validation: The 632+ bootstrap method, J. Am. Stat. Assoc., 1997, 92, 548–560 Search PubMed.
- L. Rodríguez-López, V. Santás-Miguel, R. Cela-Dablanca, A. Núñez-Delgado, E. Álvarez-Rodríguez, P. Pérez-Rodríguez and M. Arias-Estévez, Ciprofloxacin and trimethoprim adsorption/desorption in agricultural soils, Int. J. Environ. Res. Public Health, 2022, 19, 8426 CrossRef PubMed.
- F.-J. Peng, G.-G. Ying, Y.-S. Liu, H.-C. Su and L.-Y. He, Joint antibacterial activity of soil-adsorbed antibiotics trimethoprim and sulfamethazine, Sci. Total Environ., 2015, 506–507, 58–65 CrossRef CAS PubMed.
- A. Pasket, H. Zhang, Y. Wang, M. Krzmarzick, J. E. Gustafson and S. Deng, Clay content played a key role governing sorption of ciprofloxacin in soil, Front. Soil Sci., 2022, 2, 814924 CrossRef.
- P. Oleszczuk, B. Pan and B. Xing, Adsorption and desorption of oxytetracycline and carbamazepine by multiwalled carbon nanotubes, Environ. Sci. Technol., 2009, 43, 9167–9173 CrossRef CAS PubMed.
- X. Ji, J. K. Challis, J. Cantin, A. S. Cardenas Perez, Y. Gong, J. P. Giesy and M. Brinkmann, A novel passive sampling and sequential extraction approach to investigate desorption kinetics of emerging organic contaminants at the sediment−water interface, Water Res., 2022, 217, 118455 CrossRef CAS PubMed.
- M. B. Abdullah, On a robust correlation coefficient, J. R. Stat. Soc., 1990, 39, 455–460 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Jan
Siemens
b,
Benjamin Justus
Heyde
*a,
Jan
Siemens
b,
Benjamin Justus
Heyde
 c and
Christiane
Zarfl
a
c and
Christiane
Zarfl
a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW
KOW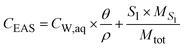
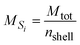
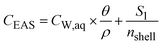
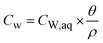
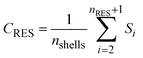




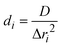





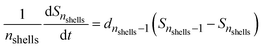

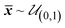
![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) is the normalized location vector in the parameter space and
is the normalized location vector in the parameter space and 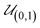 is the uniform distribution ranging from zero to one. The absolute parameter value is defined as the inverse cumulative probability density function of the respective parameter:
is the uniform distribution ranging from zero to one. The absolute parameter value is defined as the inverse cumulative probability density function of the respective parameter:![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) i)
i)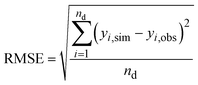
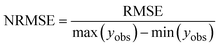
![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) ⊗ f(
) ⊗ f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) q(
) q(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) )dx
)dx![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) , and f is the objective function. The integration is performed by the Monte-Carlo-method:38
, and f is the objective function. The integration is performed by the Monte-Carlo-method:38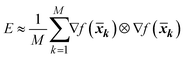
![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) k are independently drawn normalized parameter vectors.
k are independently drawn normalized parameter vectors.
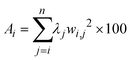
![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ).40 In this case, f(
).40 In this case, f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) is not an observation, but a simulation by the model. Hence, f(
) is not an observation, but a simulation by the model. Hence, f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ) is noise-free. Therefore, the finite-difference method poses a possibility to determine ∇f(
) is noise-free. Therefore, the finite-difference method poses a possibility to determine ∇f(![[x with combining macron]](https://www.rsc.org/images/entities/b_i_char_0078_0304.gif) ):
):