 Open Access Article
Open Access ArticleSilicone wristbands for assessing personal chemical exposures: impacts of movement on chemical uptake rates†
Joshua D.
Miller
a,
Nicholas J.
Herkert
b,
Heather M.
Stapleton
 b and
Heileen
Hsu-Kim
b and
Heileen
Hsu-Kim
 *a
*a
aDuke University, Department of Civil & Environmental Engineering, Box 90287, Durham, NC 27708, USA. E-mail: hsukim@duke.edu; Tel: +1(919)-660-5109
bDuke University, Nicholas School of the Environment, Box 90328, Durham, NC 27708, USA
First published on 28th January 2025
Abstract
Silicone wristbands are utilized as personal passive sampling devices for exposure assessments of semi-volatile organic compounds (SVOCs). While research demonstrates that accumulation of SVOCs on the wristbands correlates with internal dose for many different chemical classes, the mechanisms of accumulation remain poorly understood. Multiple factors such as movement of the individual lead to variable mass transfer conditions at the sampler interface. The objective of this study was to investigate the effect of air flow velocity across the wristband surface on SVOC uptake rates and to evaluate if enhanced rates vary between compounds with a range physicochemical properties. Experiments were conducted in a residential home where wristbands were either held in static conditions or attached to an end-over-end rotator at different speeds for a four week period. We measured the uptake of 17 different SVOCs that are commonly detected in indoor environments and compared their accumulation rates as a function of the rotating velocity. For wristbands moving at tangential speeds of 0.05, 0.5, and 1.1 m s−1 (relevant for a walking pace), the motion enhanced uptake rates by 1.2 ± 0.2, 3.2 ± 0.6, and 4.3 ± 0.8 times the respective rates for the static controls. This enhancement is consistent with gas phase diffusion-controlled mass transfer theory at the wristband interface. Moreover, the enhancement of uptake positively correlated with octanol–air partition coefficients log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA (R = 0.6; p < 0.02) of the chemicals and negatively correlated with diffusivity (R = 0.5; p < 0.05). In a comparison with worn wristband studies, the ratio of uptakes rates for worn relative to rotating wristbands correlated with SVOC properties (R = 0.85 for log
KOA (R = 0.6; p < 0.02) of the chemicals and negatively correlated with diffusivity (R = 0.5; p < 0.05). In a comparison with worn wristband studies, the ratio of uptakes rates for worn relative to rotating wristbands correlated with SVOC properties (R = 0.85 for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA). For SVOCs with log
KOA). For SVOCs with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA > 9, uptake rates on worn wristbands greatly exceeded (by a factor of 10 to 104) the respective rates in this rotator experiment. These results suggest that a mass transfer mechanism based solely on gas–solid partitioning under variations in air velocity cannot fully explain uptake on worn wristbands. Instead, the results implicate additional processes such as particle phase deposition, direct contact with certain materials, and excretion from skin as pathways of accumulation on the wristband sampler and personal exposure.
KOA > 9, uptake rates on worn wristbands greatly exceeded (by a factor of 10 to 104) the respective rates in this rotator experiment. These results suggest that a mass transfer mechanism based solely on gas–solid partitioning under variations in air velocity cannot fully explain uptake on worn wristbands. Instead, the results implicate additional processes such as particle phase deposition, direct contact with certain materials, and excretion from skin as pathways of accumulation on the wristband sampler and personal exposure.
Environmental significanceSilicone wristbands are utilized as wearable personal exposure tools due to their ease of implementation and for their ability to predict internal dosage after exposure to semi-volatile organic chemicals. Although these wristbands are utilized for environmental health research, the reasons why the wristband data correlate with biomarkers of internal exposure remain uncertain. This study quantified how individual movements and increased air flow over the wristband sampler enhance chemical uptake rates on the wristband. While this enhancement effect depends on physicochemical properties of the SVOC, movement and air flow does not fully explain observed uptake rates in worn wristbands. These insights highlight the need to consider other factors such as contact with suspended particles and SVOC-enriched surfaces for controlling personal exposures to these chemicals. |
1. Introduction
Semi-volatile organic compounds (SVOCs) are widespread in indoor built environments. These chemicals are derived from additives in synthetic materials, personal care products, combustion processes and off-gassing from other household items. SVOCs fall into a variety of chemical classes such as polycyclic aromatic hydrocarbons (PAHs), plasticizers, flame retardants, and pesticides, among others.1,2 These molecules can volatilize into the gas phase or partition into aerosol particles to varying degrees, depending on the environmental conditions. Exposures to some of these SVOCs are a major concern given that people spend the overwhelming majority of daily hours indoors3 and some of these chemicals are known to adversely affect human health.4,5 A key step towards understanding overall health risks posed by SVOCs is to assess the magnitude of exposure to vulnerable individuals.Exposure assessments for SVOCs can involve a multitude of strategies. Analysis of biomarkers of exposure (e.g., target chemicals in urine, serum, breast milk, hair) are common for evaluating an individual's overall exposure and internal dose, which is most relevant to health.6 However, collection of biological samples can be challenging, particularly from remote or vulnerable populations (e.g., children) and might not offer insights into long term exposures or sources of the chemicals. Alternatives to analysis of exposure biomarkers include collection of ambient environmental samples such as air and dust as well as personal sampling devices like handwipes and wearable passive samplers.6 In particular, polydimethylsiloxane (i.e., silicone) wristbands, first introduced in 2014, are a type of wearable passive sampler that has shown promise for measuring personal exposures to SVOCs.7 The main advantages of these wristbands relative to other sampling strategies are their lower cost, the ability to sample multiple micro-environments experienced by the individual, and the ability to capture and retain a wide range of SVOCs.6,7 The efficacy of silicone wristbands as personal exposure devices is supported by research demonstrating that concentrations of SVOCs (e.g., organophosphate esters – OPEs, brominated flame retardants, pesticides) on the wristband significantly correlate with the concentrations of the same chemical or metabolite in the wearer's urine or serum.8–12 Additionally, studies suggests that wristbands can capture multiple exposure routes, namely dermal contact and inhalation of SVOCs.9,13–15 Wristband devices are also much less invasive to the participant than biospecimen collection and they maintain the chemical in its original form. In contrast, exposure assessments based on biomarker sampling sometimes rely on measurements of metabolites which may not be specific to one SVOC (e.g., metabolites of PAHs and some OPEs), while other SVOCs have no specific metabolite or biomarker of exposure identified (e.g., di(2-ethylhexyl)terephthalate (DEHTP) and many PAHs).6,16,17
With the growing body of research suggesting that silicone wristbands could be a device to evaluate internal dose for SVOCs, the factors affecting chemical uptake on the wristbands and why uptake rates correlate with internal dose remain to be elucidated. Previous studies with other types of wearable passive samplers have attempted to extrapolate environmental levels (e.g., atmospheric concentrations) from measured values on the wristband,18–20 similar to the approach used for passive air samplers. Though unlike air samplers,21 silicone wristbands are unshielded surfaces for which the wearer's movement, deposition of particles, and direct contact of the sampler with skin, clothing and other surfaces are not controlled. For instance, factors such as individual movements and increased air flow speed over the wristband from such movements (e.g., sitting versus walking/running) would increase chemical accumulation rates if gas phase uptake was the major mode of uptake.22,23 Uptake rates are also influenced by other factors such as increased particle concentration in the immediate vicinity of the wearer24–27 and direct contact of the wristband with SVOC-enriched surfaces.6,28 The relative importance of each of these factors is unclear. Given that SVOC uptake on worn silicone wristbands may be an indicator of internal dose, an improved understanding of the factors influencing SVOC uptake rates on silicone wristbands can provide insight into the relative importance of these pathways for personal exposures.
The goal of this study was to quantify the relevance of one of these factors, air flow speed caused by movement, on mass accumulation rates of SVOCs on silicone wristbands, and to evaluate if the effect of speed varies with physicochemical properties of the SVOCs. Wristbands were placed in a common room space of a residential home for 4 weeks and were exposed to different air flow velocities by attaching them to rotating end-over-end mixers. The influence of rotating velocity on uptake rates was assessed for a variety of SVOCs often detected in residential settings. A mass transfer model was then employed to determine if gas phase transport at a diffusion boundary layer can explain these enhanced uptake rates. The results were also compared to previously published measurements in worn wristbands to understand if airflow velocity can explain the range of measured SVOC uptake rates on worn wristbands in human exposure assessment studies.
2. Methods
2.1 Materials
Commercially-purchased polydimethylsiloxane (or ‘silicone’) wristbands were cleaned via two 24 hour cycles of Soxhlet extraction. The first cycle used a mixture of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hexane
1 hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl acetate and the second involved a mixture of 1
ethyl acetate and the second involved a mixture of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl acetate. Afterward, wristbands were dried in a vacuum oven, wrapped in aluminum foil (pre-cleaned by baking overnight at 450 °C) and stored in glass jars until use in the uptake experiments. Equipment components that were used to hold the wristbands during the uptake experiment, including detachable clamps for the rotators and ring stands, were wrapped in pre-cleaned aluminum foil.
ethyl acetate. Afterward, wristbands were dried in a vacuum oven, wrapped in aluminum foil (pre-cleaned by baking overnight at 450 °C) and stored in glass jars until use in the uptake experiments. Equipment components that were used to hold the wristbands during the uptake experiment, including detachable clamps for the rotators and ring stands, were wrapped in pre-cleaned aluminum foil.
2.2 Experimental design
The impact of air velocity on the partitioning rate of SVOCs to the wristbands was evaluated by attaching clean wristbands to 3 end-over-end rotators (depicted in Fig. 1). Twelve wristbands were placed on each rotator. Another set of ‘static’ wristbands were suspended onto horizontal arms of a standard laboratory ring stand. The wristbands were then placed on tables in a carpeted and sparingly occupied common room space of a residential home constructed in 1995 and located in central North Carolina (USA). The rotators were set at different rotating speeds: 5, 50 and 85 rpm. With the measured radii of rotation at the exposed ends of the wristbands (Fig. 1), these rotating speeds corresponded to tangential velocities of 0.05, 0.5, and 1.1 m s−1, respectively. This range of speeds was selected based on the minimum and maximum rotation rates that could be consistently established on the rotator devices for the experimental duration. We also note that 1.1 m s−1 represents a slow walking pace, while 0.05 and 0.5 m s−1 would bracket the average speed over a cumulative day of standard activities such as walking, sleeping, and sitting.Wristbands were collected at multiple time points: t = 0, 8, 16 and 28 days. For each sampling event, triplicate wristbands were detached from the holder, and a 0.7 g section (approximately 3 cm) was cut from the wristband section corresponding to the distal end from the point of attachment to the rotator clamps (i.e., wristband sections that were not touching adjacent wristbands). Each wristband piece was wrapped in pre-baked foil, placed in a plastic specimen bag, and stored in the freezer (−20 °C) until further analysis.
2.3 Chemical analysis
The wristband sections were analyzed for a suite of SVOCs that included brominated diphenyl ethers, organophosphates, polycyclic aromatic hydrocarbons (PAHs), polychlorinated biphenyls (PCBs), pesticides, phthalates, per- and polyfluoroalkyl substances (PFAS) and a few chemicals associated with personal care products. Wristband extraction for SVOCs is described in detail elsewhere.10–12,29 A list of all analytes can be found in ESI Table S1.†For the analysis of all target chemicals except for PFAS, a ∼0.7 g segment of the wristband was weighed and placed in extraction vials with 100 μL of internal standard solution (Table S2†). A 10 mL aliquot of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hexane
1 hexane![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acetone was dispensed into the sample vial, the mixture was sonicated for 15 min, and then the extraction solution was decanted. This process was repeated twice more, and all supernatant extracts were combined. The extracts were evaporated under a gentle nitrogen flow to a final volume of 0.75 mL and reconstituted in high purity hexane.
acetone was dispensed into the sample vial, the mixture was sonicated for 15 min, and then the extraction solution was decanted. This process was repeated twice more, and all supernatant extracts were combined. The extracts were evaporated under a gentle nitrogen flow to a final volume of 0.75 mL and reconstituted in high purity hexane.
PFAS precursor analytes were extracted via previously published methods.30 Briefly, separate wristband sections cut from the most distal ends of the remaining wristband (∼0.35 g from each of the two ends) were weighed in a vial and spiked with 50 μL of internal standard. The sections were extracted by adding 7 mL of ethyl acetate, sonicating for 15 minutes, and then decanting the liquid into a separate vial. This sonication process with ethyl acetate was repeated twice more and the extracts were combined. The extracts were evaporated to ∼0.75 mL under a gentle nitrogen flow and reconstituted in high purity ethyl acetate. Just prior to instrumental analysis, all extracts (both hexane and ethyl acetate) were spiked with respective recovery standards (Table S2†) and filtered using a 2 mL glass syringe and 0.45 μm nylon filters.
The hexane extracts were analyzed for organophosphates, brominated diphenyl ethers, PAHs, PCBs, phthalates, and pesticides (Table S1†) using a Q Exactive GC (QE-GC) hybrid quadrupole-Orbitrap GC-MS/MS system (Thermo Scientific™). The QE-GC was equipped with a Thermo Scientific™ TraceGOLD TG-5HT GC column capillary column (30 m × 0.25 mm ID, 0.25 μm film thicknesses) with helium as the carrier gas flowing at 1.3 mL min−1. The programmable temperature vaporizer (PTV) inlet was operated in split injection mode with a 1 μL injection and a split ratio of 10. The GC oven temperature program was 80 °C for 2 min, 80 to 250 °C ramping at 20 °C per min, 250 to 260C ramping at 1.5 °C per min, 260 to 300 at 25 °C per min with a 12 min hold at 300 °C, 300 to 320 °C ramping at 25 °C per min, and final hold at 320 °C for 15 min (total run time 46 min). The transfer line and ion source were held at 300 °C for the duration of the batch run. Samples were run in full scan mode with a scan range of 70–1050 m/z at 70 eV and quantified using the Tracefinder software.
The ethyl acetate extracts were analyzed for volatile PFAS compounds (Table S1†) using an Exactive GC Orbitrap MS system (Thermo Scientific™) operated in the full-scan positive chemical ionization (PCI) mode with a scan range from 325 to 620 m/z. The MS transfer line and ion source were set at 250 °C. Methane was the reagent gas and set to flow at 1.5 mL min−1. Injections were conducted on a split/splitless (S/SL) inlet with an isothermal hold at 250 °C. The S/SL was operated in splitless w/surge mode with a surge pressure set at 100 kPa for 1 min. The carrier flow was set at 1.5 mL min−1, the split flow set at 50 mL min−1, and the splitless time set at 1 min. The Trace 1310 GC was equipped with an Agilent J&W DB-WAX GC capillary column (30 m × 0.25 mm ID, 0.25 μm film thicknesses). The GC oven temperature program was 50 °C for 1 min, 50 to 150 °C ramping at 10 °C per min, 150 to 250 °C ramping at 25 °C per min, and held at 250 °C for 15 min.
Digital microscope images were also collected for 28 day wristbands. Please see ESI Text 2† for further details.
2.4 Quality assurance and control (QA/QC)
Field blanks (non-deployed wristbands) and lab blanks (hexane) were processed with every batch of wristbands to assess background levels. All samples were blank subtracted with the average response across all blanks for each analyte. Method detection limits (MDLs) were calculated as three times the standard deviation of the blanks. All analytes were quantified with a seven-point calibration curve. Isotopically labelled standards recoveries ranged from 73 ± 8% (d10-phenanthrene) to 109 ± 12% (dDEP) across all standards evaluated. Summary recovery values can be found in the ESI (Table S3†). Target analyte values were corrected for recoveries. Prior to sample analysis, the QE-GC was tuned and calibrated to ensure maximum mass accuracy (<0.5 ppm). The tune was examined after the sample batch run to ensure no significant sensitivity loss had occurred during analysis. Additionally, a quality control (QC) mixture was injected periodically within the batch run to monitor stability across all m/z values of interest during the run. The QC mixture consisted of ∼160 analytes, including PCBs, PBDEs, PAHs, pesticides, and OPEs.2.5 Data analysis
The concentrations of SVOCs in the wristband sampler xs (ng g−1) were monitored with exposure time t. For the targeted SVOC species that were quantifiable and observed to increase in wristband concentration with time (17 chemicals total, Table S1†), we modeled chemical partitioning into the passive sampler as a balance between uptake and elimination from the sampler:31 | (1) |
With the initial condition that xs is zero at t = 0, the integration of eqn (1) yields:
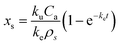 | (2) |
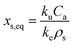 | (3) |
 | (4) |
For each chemical, a non-linear least squares regression algorithm with JMP statistical software was used to fit eqn (4) to experimentally measured values of xs in wristbands held under constant tangential velocity of the rotator or static conditions. If detectable levels of a chemical were observed at the initial time point (relevant to lilial, nonylphenol, and 4-tert-octylphenol), then the mean of initial concentration values was subtracted from values of xs at subsequent time points prior to the model regression of eqn (4) to the data. The adjustable parameters for the regression model fits were xs,eq and ke, and initial guesses for these parameters in the regression algorithm were xs,eq = 800 ng g−1 and ke = 0.05 d−1. These values were chosen as an order of magnitude approximation of xs,eq and ke based on the chosen time frame and range of observed concentration values. The optimization algorithm was set to run for 6000 iterations.
The product xs,eq × ke represents the initial uptake rate at early time points (i.e., as t → 0) and, according to eqn (3), depends on the air concentration Ca and the uptake rate constant ku. Gaseous concentrations were not monitored in this study. However, assuming that the wristbands held in static and rotating conditions were exposed to the same air concentration Ca, the increased uptake rate constant for tangential velocity v relative to the static condition can be expressed as a speed enhancement factor (SEF), analogous to the concept of “wind enhancement factor” presented in Zhang et al. (2013):33
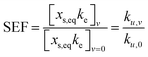 | (5) |
The SEF values for each chemical were compared to its physicochemical properties via linear regression using JMP statistical software. R2 and statistical significance were calculated assuming Pearson correlation. Physicochemical properties included in the analysis were molecular weight (MW), molar volume, boiling point, vapor pressure, and octanol–air partition coefficient KOA (Table S4†). These values were obtained from the U.S. EPA comptox dashboard using the OPERA model predicted value. The OPERA model did not provide predictions of molar volume; therefore, we used the ACD/Labs model predicted values.34–36 The gas phase diffusivity of each chemical was calculated based on MW and molar volume values, according to Fuller et al. (1966)37 (Table S4†).
3. Results and discussion
3.1 Accumulation of SVOCs on wristbands with time and rotator speed
Of the 126 targeted analytes (ESI Table S1†), 34 were detected in the wristbands; however, for our data analyses, we restricted the analytes to the 19 that were detected at all non-zero time points. These 19 chemicals ranged in physical–chemical properties (Table S4;†e.g., log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA from 4.2 to 11.7). Two of the chemicals, 2-(perfluorooctyl)ethanol and 2-(perfluorodecyl)ethanol, were excluded from data analyses due to poor model fit with eqn (4). These compounds have low KOA values relative to other detected chemicals (Table S4†), suggesting low affinity to the silicone wristbands and an uptake mechanism that was not represented by eqn (4). Subsequent data analyses were therefore restricted to 17 analytes for which we observed consistent increase in wristband concentrations (ng of chemical per gram of wristband) with time of exposure. These chemicals included 4 phthalates, 6 organophosphate esters, two polyfluorinated compounds, 1 PAH (anthracene), and other substituted aromatic compounds (i.e., alkylphenols and lilial). Most of these compounds are additives for common household products (e.g., building materials, furnishings, personal care products) with the exception of anthracene, a combustion byproduct.
KOA from 4.2 to 11.7). Two of the chemicals, 2-(perfluorooctyl)ethanol and 2-(perfluorodecyl)ethanol, were excluded from data analyses due to poor model fit with eqn (4). These compounds have low KOA values relative to other detected chemicals (Table S4†), suggesting low affinity to the silicone wristbands and an uptake mechanism that was not represented by eqn (4). Subsequent data analyses were therefore restricted to 17 analytes for which we observed consistent increase in wristband concentrations (ng of chemical per gram of wristband) with time of exposure. These chemicals included 4 phthalates, 6 organophosphate esters, two polyfluorinated compounds, 1 PAH (anthracene), and other substituted aromatic compounds (i.e., alkylphenols and lilial). Most of these compounds are additives for common household products (e.g., building materials, furnishings, personal care products) with the exception of anthracene, a combustion byproduct.
During the experiment, the partitioning kinetics of these 17 chemicals in the silicone occurred at different apparent stages of uptake (i.e., linear, curvilinear, and equilibrium stages), as shown in Fig. 2 and S1.† For instance, the mass uptake of tris(2-chloroisopropyl)phosphate (TCPP1) in the wristband (Fig. 2A) increased linearly with time for both static and rotating wristbands. Furthermore, the rate of TCPP1 mass accumulation increased with tangential velocity of the rotator. In contrast, the uptake of 4-tert-octylphenol (4tOP) and lilial were observed as curvilinear with respect to time (Fig. 2B and C). Lilial appeared to reach equilibrium in less than 28 days for the faster moving wristbands (0.5 and 1.1 m s−1). Accumulation of other targeted SVOC species demonstrated similar spectrum of uptake trends (Fig. S1†).
 | ||
| Fig. 2 Observed wristband concentrations (symbols) and model fit (lines; eqn (4)) for the accumulation of three different chemicals in wristbands held static or rotating at different tangential velocities of the rotator. (A) Tris(2-chloroisopropyl)phosphate (TCPP1), (B) 4-tert-octylphenol (4tOP), and (C) lilial (3-(4-tert-butylphenyl)-2-methylpropanal). Chemical structure of each chemical is shown in the top left corner. Wristband concentrations of other chemicals are shown in ESI Fig. S1.† | ||
3.2 Effect of tangential air velocity on uptake rate
SVOC mass uptake rates were faster for rotating wristbands than for wristbands held static. The speed enhancement factor (SEF), which is the uptake rate constant for a wristband at velocity v normalized to the static control, increased with velocity for all 17 chemicals. Average SEF values (±1 standard deviation) were 1.2 ± 0.2, 3.2 ± 0.6, and 4.3 ± 0.8 for velocities at 0.05, 0.5, and 1.1 m s−1, respectively. These values are consistent with a previous study33 that tested uptake of polychlorinated biphenyls (PCBs) onto a passive air sampler comprising XAD resin.33 The enhancement factor for PCB accumulation rate on the sampler was 3.3 ± 0.2 for wind speeds of approximately 0.4 m s−1 at the XAD surface inside the cover screen of the sampler. Likewise in a different study with polyurethane foam passive samplers,38 wind velocity at ∼1 m s−1 resulted in speed enhancement factors of approximately 4 and depended on the PCB congener. However, we note that chemical transport and uptake on a porous air sampler (i.e., foam) would not necessarily follow similar wind enhancement trends as those for a smooth surface such as the silicone wristband.As noted above, the uptake rates depended on the magnitude of the velocity. In fact, the SEF values varied between the 17 SVOCs and appeared to have a non-linear relationship with v (Fig. 3A). With the values of v and 1.27 cm width of the wristband, we calculated Reynold's number (Re) to be 930 or less at all speeds, suggesting conditions of laminar boundary layer flow over the wristband surface.39 Thus, if the uptake of each chemical was controlled by mass transfer on the gas side of the air–wristband interface, then the velocity would influence mass transfer by thinning the interfacial diffusion boundary layer. While we cannot completely rule out some turbulence in the flow field, the rotational movement would have the same effect on the boundary layer. In the laminar flow scenario, the uptake rate constant can be expressed as the following:
 | (6) |
While movement of the wristband alters chemical uptake rates due to changes in the air-side resistance (i.e., the diffusion layer thickness) at the wristband interface, we also observed that variations in velocity had a greater effect on certain chemicals. In other words, the slope of the linear regressions of SEF vs. v0.5 (Fig. 3B) ranged from 2 to 5.5 (m s−1)−0.5. We hypothesized that this variation is due to differences in properties of each compound and thus examined the correlation in the slope values (i.e., the derivative of SEF with respect to v0.5) with physical–chemical parameters of the SVOCs (Fig. 4).
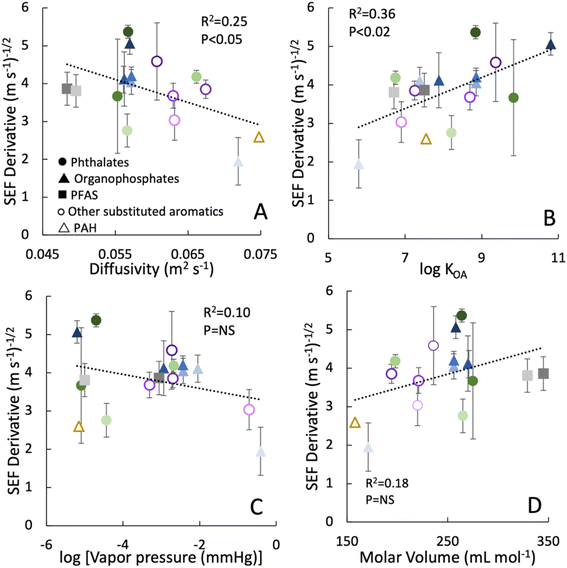 | ||
| Fig. 4 Derivative of the speed enhancement factor (SEF) with respect to v0.5 for 17 chemicals plotted as a function of their physical properties: (A) gas phase diffusivity D (m2 s−1) calculated according to Fuller et al. (1966);37; (B) octanol–air partition coefficient KOA; (C) vapor pressure at 25 °C, (D) molar volume (mL mol−1). The SEF derivative corresponds to the slope of linear regressions shown in Fig. 3B. Error bars correspond to the standard error of the regression. | ||
Assuming a scenario of mass transport in a stagnant fluid, the uptake rate constant for a static wristband can be expressed as:
 | (7) |
Substituting eqn (6) and (7) for ku,v and ku,0 into eqn (5) suggests that the slope of SEF vs. v0.5 should have a positive relationship with the diffusivity in air, D, if gas-phase diffusion was the primary factor controlling uptake rates. Yet, a plot of this slope value with D yielded a reverse relationship and a negative correlation (Fig. 4A). Moreover, these SEF derivative values correlated positively with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA of the SVOCs (Fig. 4B). Correlations of these SEF derivative values with other properties such as vapor pressure, molar volume, molecular weight, and were not significant (Fig. 4C, D and S2†).
KOA of the SVOCs (Fig. 4B). Correlations of these SEF derivative values with other properties such as vapor pressure, molar volume, molecular weight, and were not significant (Fig. 4C, D and S2†).
One explanation for the trends observed in Fig. 4 is that with an increase in tangential velocity, the rate-limiting mass transfer step shifted from an air-side uptake regime to a sampler-side uptake regime. Chemical uptake rates are controlled by mass transfer across two distinct boundary layers (air and solid phases) at the wristband interface, and the enhanced air speed compressed the air-side boundary layer without altering the sampler-side.32 Although air-side resistance is often assumed to be the limiting step, this is not always the case,21,33,41 especially for samplers experiencing increased air flow speeds.33 With a sampler-side transport regime, the uptake rate is proportional to the SVOC diffusivity in the silicone and the silicone–air partition coefficient KSA.31 Given that KSA values are proportional to KOA values18,41 and the 5 orders of magnitude range of KOA values for the 17 chemicals in our study, the correlation observed between the SEF derivatives with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA suggests that chemical affinity for the silicone, and not diffusivity in the silicone, was another factor influencing uptake rates. In other words, chemicals with relatively high KOA values would have lower mass transfer resistance across the sampler side boundary layer. Thus, any changes to the air-side resistance for the high KOA chemicals would yield greater impacts for overall observed uptake rates. The data in Fig. 4b indicate that the speed enhancement effect with increased velocity (i.e., the SEF derivative) is approximately double for chemicals with log
KOA suggests that chemical affinity for the silicone, and not diffusivity in the silicone, was another factor influencing uptake rates. In other words, chemicals with relatively high KOA values would have lower mass transfer resistance across the sampler side boundary layer. Thus, any changes to the air-side resistance for the high KOA chemicals would yield greater impacts for overall observed uptake rates. The data in Fig. 4b indicate that the speed enhancement effect with increased velocity (i.e., the SEF derivative) is approximately double for chemicals with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA ∼11 compared to the enhanced effect for chemicals with log
KOA ∼11 compared to the enhanced effect for chemicals with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA ∼6. The correlation between SEF and log
KOA ∼6. The correlation between SEF and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA is stronger with increasing velocity (Fig. S3†), further supporting the importance of sampler-side transport at high air flow velocity.
KOA is stronger with increasing velocity (Fig. S3†), further supporting the importance of sampler-side transport at high air flow velocity.
A second explanation for the trends shown in Fig. 4 is that particle accumulation on the wristbands increased with increasing wristband velocity. SVOCs with higher KOA values and lower diffusivities are more likely to be in the aerosol particle phase rather than the gas phase. Thus, an increase in particle accumulation on the moving wristbands would result in greater enhancement of chemical uptake with increasing velocity. The wristband lacks a cover screen, which are common for gas phase passive sampling devices; as such, the bare surface of the wristband is apt to particle accumulation.21 Likewise in other passive air sampling studies,42,43 sampling rates were reported to increase with the MW of SVOC, and this trend was also attributed to particle deposition on the sampler surface.42,43 This could indicate that increasing movement speed not only increases the rate of uptake of gas-phase chemicals via diffusion but also intensifies additional processes involving particle uptake such as inertial impaction and interception.44 Microscope images collected for the 28 day samples suggest there may be increased attachment of large particles for the fastest moving (85 rpm) sampler (Fig. S4†). With these various factors to explain the enhanced uptake rates caused by air movement, the calculation of air concentrations of chemicals from worn wristband data is difficult to estimate. However, we emphasize this calculation is not essential for the purpose of wristband passive samplers, which is to estimate internal exposure.
3.3 Comparison to worn wristband studies
The results of the rotator experiments suggest that when an individual wears a silicone wristband, the increased air flow speed over the wristbands would alter rates of SVOC uptake. To understand if such an increase could explain SVOC measurements observed in wristbands worn by people, we compared chemical uptake rates in worn wristbands to the uptake rates in wristbands attached to the rotators. Using data from ten different studies,10–12,29,45–50 we calculated a ratio of chemical uptake rates in worn wristbands and in wristbands set at the fastest rotator velocity 1.1 m s−1 (a slow walking speed). This ratio is referred here as the worn enhancement factor (WEF): | (8) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) worn is the median (or geometric mean) of the wristband concentration for a chemical reported from a wristband study that involved participants wearing the silicone wristbands for tworn = 5, 6 or 7 days; and
worn is the median (or geometric mean) of the wristband concentration for a chemical reported from a wristband study that involved participants wearing the silicone wristbands for tworn = 5, 6 or 7 days; and ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) rotator is the average concentration of that same chemical in wristbands moving on the rotator at v = 1.1 m s−1 for trotator = 8 days.
rotator is the average concentration of that same chemical in wristbands moving on the rotator at v = 1.1 m s−1 for trotator = 8 days.
The calculated WEF values spanned several orders of magnitude for different chemicals (Fig. 5). We note that this ratio does not control for differences in exposure concentrations between the rotator experiment and worn wristband studies in which exposure levels depend on the presence of additive materials and household products that emit SVOCs to the ambient air, the presence of particles that accumulate on the samplers, and direct contact with surfaces for worn wristbands. Differences between study exposure environments can help explain the wide range of WEF values for a single chemical. For example, WEF values for TCPP1 were 10−0.77 to 10−0.022. Likewise, for DEHA WEF values ranged from 102.4 to 103.9. This range, typically within one or two orders of magnitude for each chemical, could be explained by variations in ambient concentrations of the SVOC and the abundance of emission sources.
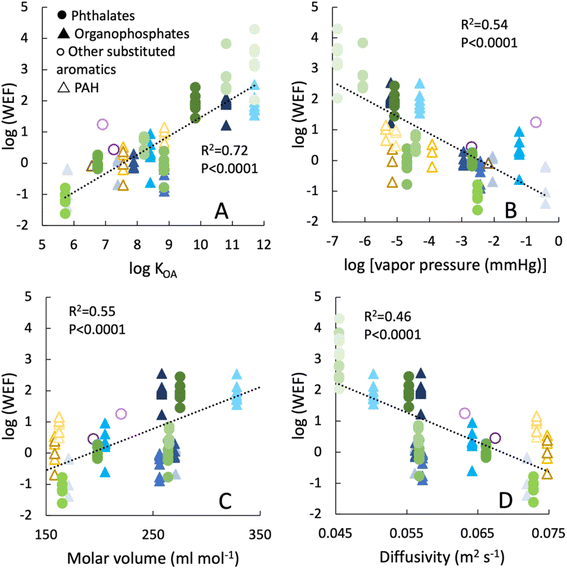 | ||
| Fig. 5 Worn enhancement factors (WEF), defined as the ratio of SVOC accumulation rates on worn wristbands relative to the rotating wristbands that were moving at the fastest velocity (1.1 m s−1) for 8 days. Worn wristband data were obtained from prior studies. WEF values are plotted as a function of various SVOC physicochemical properties: (A) octanol–air partition coefficient KOA; (B) vapor pressure at 25 °C; (C) molar volume; (D) diffusivity (m2 s−1) of the chemical in air calculated according to Fuller et al. (1966).37 | ||
Despite the range of WEF values for a single chemical, we observed a much broader range of WEF values in a comparison across all SVOCs. These WEF values correlated on a log–log scale with physical–chemical properties such as KOA and vapor pressure (Fig. 5 and S5†). For SVOCs with higher vapor pressures, higher diffusivity in air, lower molar volumes, and lower KOA values, the WEF ratios were close to 1 (i.e., log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) WEF ∼ 0). These results suggest that uptake via gas phase partitioning to the silicone is likely the main factor influencing uptake rates. Further they indicate that movements by the individuals, in addition to ambient concentrations could contribute to the variation of uptake rates of such chemicals.
WEF ∼ 0). These results suggest that uptake via gas phase partitioning to the silicone is likely the main factor influencing uptake rates. Further they indicate that movements by the individuals, in addition to ambient concentrations could contribute to the variation of uptake rates of such chemicals.
In contrast, for SVOCs with higher KOA values, higher molar volumes, lower diffusivity in air, and lower vapor pressures, the WEF values were in the range of 10 to 104. In other words, uptake rates on worn wristbands for these chemicals were orders of magnitude above the rates observed in this rotator experiment. These large WEF values suggest that the processes contributing to SVOC uptake in worn wristbands are distinct from wristbands in the rotator experiment in which gas phase mass transfer explained changes in SVOC uptake with velocity. The fastest rotator speed tested (1.1 m s−1) is a slow walking pace, yet it is much faster than the movement speed of an average person over the course of several days that would include periods of stillness (e.g., sitting, sleeping). Differences in ambient SVOC concentrations should depend on the availability of emission sources for these chemicals rather than chemical traits. Thus, the correlations in Fig. 5 suggest that when an individual wears the wristband, the accumulation of the chemicals with the large WEF values (10 to 104) involves additional processes that include deposition of SVOC-enriched particles and mass transfer of chemicals between surfaces (including attached particles) and the silicone. These process are enhanced by the observed increase in particle concentration in the immediate vicinity of the wearer (i.e., the personal cloud effect24–27) or could be the result of direct contact with fabrics and other surfaces. These findings are consistent with conclusions from other studies which also indicate that wristbands capture distinct chemical profiles, potentially influenced by movement and contact with surfaces and clothing.13,15,51
3.4 Implications for environmental exposure monitoring
The results of this study demonstrate that SVOC accumulation onto silicone wristbands increases with increasing movement and speed. To our best knowledge, these data are the first to indicate that the magnitude of enhancement by an individual's movement is a factor of 5 at most. This study also suggests that with increasing wristband movement, gas phase diffusion at the air-sampler boundary becomes less important for SVOC uptake relative to other processes such as particle accumulation and SVOC partitioning and transport in the PDMS phase. Thus, with increasing movement, there is a disproportionate increase in uptake of higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA chemicals.
KOA chemicals.
This study also showed that the degree to which movement speed affects SVOC uptake rate depends on the physicochemical properties of the SVOC. For chemicals that are generally associated with solids (i.e., SVOCs with high KOA, low vapor pressure), uptake rates were greatly enhanced by an increase in velocity, while the uptakes rates of gaseous SVOCs were comparatively less affected by the increased velocity. Furthermore, for the chemicals more likely to be particle-bound (e.g., KOA > 109), uptake rates in worn wristband studies were 10 to 104-fold greater than uptake rates in the rotating wristbands. Therefore, it is unlikely that gas phase diffusion is the only factor contributing to SVOC accumulation on worn silicone wristbands, especially for compounds with higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA.
KOA.
A limitation of this study is that we did not measure ambient air or dust particle concentrations of the SVOCs and other ambient conditions such as temparature and humidity. Such information of the sampling environment would then facilitate the quantification of sampling rates of the wristbands, mass transfer coefficients, and direct comparisons to other studies involving passive air sampling. Likewise, the addition of performance reference compounds to the wristbands for measurement of release rate during the experiment could have helped constrain parameters of the transport model. We did not include this aspect in the study design due to unknown risks of exposing home occupants to potentially harmful chemicals.
Regardless of these limitations, precise knowledge of gas phase sampling rates of worn wristbands may not be essential for the intended purpose of these samplers. Silicone wristbands should not be used to calculate air concentrations of chemicals. Instead, the wrisbands are designed to be personal exposure samplers for chemicals with multiple pathyways of exposure to individuals. This purpose is underscored by human exposure studies involving epidemiologically relevant exposures and demonstrating significant correlations between wristband measurements and corresponding biomarkers in urine and blood for chemicals that include both gas phase and particle-bound SVOCs.8–12 Thus, while the mechanisms of uptake are complex, the wristband sampler can be useful in assessing personal exposure to a variety of SVOCs.
Overall, the results revealed key insights that can assist environmental exposure researchers who utilize silicone wristbands for chemical exposure assessments. Additional knowledge of individual body movements and/or activity levels could be useful to fully parameterize mass transfer models for chemical uptake on wristbands. However, a mechanistic model of uptake may not be necessary given that concentration data from worn wristband studies correlate with biomarkers of internal dosage, as noted above. In fact, dermal absorption of SVOCs could follow mechanisms analogous to uptake on the wristbands. Thus, individual movements could also increase dermal absorption rates. The magnitude of this impact may be similar to the speed enhancement factors observed for the rotating wristbands.
Finally, multiple modes of SVOC uptake on wristbands means that there are multiple modes of exposure. Analysis of ambient air concentrations in one or multiple locations provides a limited picture of the human exposure potential and could underestimate other exposure pathways involving surfaces or suspended particles enriched with these chemicals (e.g., dermal contact, ingestion, inhalation). This study suggests that thresholds could be established with physicochemical properties such as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA as a way to group SVOCs according to their dominant uptake mode and exposure pathway. Such insight would enable a better understanding of the exposure data offered by personal passive sampling devices such as silicone wristbands.
KOA as a way to group SVOCs according to their dominant uptake mode and exposure pathway. Such insight would enable a better understanding of the exposure data offered by personal passive sampling devices such as silicone wristbands.
Data availability
Data for this article, including the measured SVOC concentration values and model fitting parameters, are available at the Duke University Digital Research Data Repository https://doi.org/10.7924/r4tm7f33j.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This study was supported by the U.S. Department of Housing and Urban Development (NCHHU0062-21). The study was also supported by the National Institute of Environmental Health Sciences through the Duke University Superfund Research Center (P42ES010356) and the Duke Environmental Analysis Laboratory Hub (U2CES030851) within the Human Health Exposure Analysis Resource. We thank Zhiheng Hao for her assistance with the experimental setup for this study. We also thank Lijia Gao for contributing her artwork to the ToC figure.References
- C. J. Weschler and W. W. Nazaroff, Semivolatile organic compounds in indoor environments, Atmos. Environ., 2008, 42(40), 9018–9040, DOI:10.1016/j.atmosenv.2008.09.052.
- R. E. Dodson, D. E. Camann, R. Morello-Frosch, J. G. Brody and R. A. Rudel, Semivolatile organic compounds in homes: strategies for efficient and systematic exposure measurement based on empirical and theoretical factors, Environ. Sci. Technol., 2015, 49(1), 113–122, DOI:10.1021/es502988r.
- J. Saini, M. Dutta and G. Marques, A comprehensive review on indoor air quality monitoring systems for enhanced public health, Sustainable Environ. Res., 2020, 30(1), 6, DOI:10.1186/s42834-020-0047-y.
- A. S. Young, J. G. Allen, U. J. Kim, S. Seller, T. F. Webster, K. Kannan and D. M. Ceballos, Phthalate and organophosphate plasticizers in nail polish: evaluation of labels and ingredients, Environ. Sci. Technol., 2018, 52(21), 12841–12850, DOI:10.1021/acs.est.8b04495.
- K.-H. Kim, S. A. Jahan, E. Kabir and R. J. C. Brown, A review of airborne polycyclic aromatic hydrocarbons (PAHs) and their human health effects, Environ. Int., 2013, 60, 71–80, DOI:10.1016/j.envint.2013.07.019.
- S. M. Samon, S. C. Hammel, H. M. Stapleton and K. A. Anderson, Silicone wristbands as personal passive sampling devices: current knowledge, recommendations for use, and future directions, Environ. Int., 2022, 169, 107339, DOI:10.1016/j.envint.2022.107339.
- S. G. O'Connell, L. D. Kind and K. A. Anderson, Silicone wristbands as personal passive samplers, Environ. Sci. Technol., 2014, 48(6), 3327–3335, DOI:10.1021/es405022f.
- S. C. Hammel, K. Hoffman, T. F. Webster, K. A. Anderson and H. M. Stapleton, Measuring personal exposure to organophosphate flame retardants using silicone wristbands and hand wipes, Environ. Sci. Technol., 2016, 50(8), 4483–4491, DOI:10.1021/acs.est.6b00030.
- S. C. Hammel, A. L. Phillips, K. Hoffman and H. M. Stapleton, Evaluating the use of silicone wristbands to measure personal exposure to brominated flame retardants, Environ. Sci. Technol., 2018, 52(20), 11875–11885, DOI:10.1021/acs.est.8b03755.
- S. C. Hammel, K. Hoffman, A. L. Phillips, J. L. Levasseur, A. M. Lorenzo, T. F. Webster and H. M. Stapleton, Comparing the use of silicone wristbands, hand wipes, and dust to evaluate children's exposure to flame retardants and plasticizers, Environ. Sci. Technol., 2020, 54(7), 4484–4494, DOI:10.1021/acs.est.9b07909.
- J. L. Levasseur, K. Hoffman, N. J. Herkert, E. Cooper, D. Hay and H. M. Stapleton, Characterizing firefighter’s exposure to over 130 SVOCs using silicone wristbands: a pilot study comparing on-duty and off-duty exposures, Sci. Total Environ., 2022, 834, 155237, DOI:10.1016/j.scitotenv.2022.155237.
- C. F. Wise, S. C. Hammel, N. Herkert, J. Ma, A. Motsinger-Reif, H. M. Stapleton and M. Breen, Comparative exposure assessment using silicone passive samplers indicates that domestic dogs are sentinels to support human health research, Environ. Sci. Technol., 2020, 54(12), 7409–7419, DOI:10.1021/acs.est.9b06605.
- S. R. Wang, K. A. Romanak, W. A. Stubbings, V. H. Arrandale, M. Hendryx, M. L. Diamond, A. Salamova and M. Venier, Silicone wristbands integrate dermal and inhalation exposures to semi-volatile organic compounds (SVOCs), Environ. Int., 2019, 132, 105104, DOI:10.1016/j.envint.2019.105104.
- Y. Hong, C. Y. Chen, C. C. Wu, L. J. Bao and E. Y. Zeng, A novel personal passive sampler for collecting gaseous phthalates, Environ. Sci. Technol., 2021, 55(23), 15961–15968, DOI:10.1021/acs.est.1c06611.
- L. V. Nguyen, M. L. Diamond, S. Kalenge, T. L. Kirkham, D. L. Holness and V. H. Arrandale, Occupational exposure of Canadian nail salon workers to plasticizers including phthalates and organophosphate esters, Environ. Sci. Technol., 2022, 56(5), 3193–3203 CrossRef CAS PubMed.
- L. L. Aylward, S. M. Hays, R. Smolders, H. M. Koch, J. Cocker, K. Jones, N. Warren, L. Levy and R. Bevan, Sources of variability in biomarker concentrations, J. Toxicol. Environ. Health B Crit. Rev., 2014, 17(1), 45–61, DOI:10.1080/10937404.2013.864250.
- F. Lessmann, A. Schütze, T. Weiss, A. Langsch, R. Otter, T. Brüning and H. M. Koch, Metabolism and urinary excretion kinetics of di(2-ethylhexyl) terephthalate (DEHTP) in three male volunteers after oral dosage, Arch. Toxicol., 2016, 90(7), 1659–1667, DOI:10.1007/s00204-016-1715-x.
- P. C. Tromp, H. Beeltje, J. O. Okeme, R. Vermeulen, A. Pronk and M. L. Diamond, Calibration of polydimethylsiloxane and polyurethane foam passive air samplers for measuring semi volatile organic compounds using a novel exposure chamber design, Chemosphere, 2019, 227, 435–443, DOI:10.1016/j.chemosphere.2019.04.043.
- J. O. Okeme, L. V. Nguyen, M. Lorenzo, S. Dhal, Y. Pico, V. H. Arrandale and M. L. Diamond, Polydimethylsiloxane (silicone rubber) brooch as a personal passive air sampler for semi-volatile organic compounds, Chemosphere, 2018, 208, 1002–1007, DOI:10.1016/j.chemosphere.2018.05.196.
- M. Frederiksen, H. V. Andersen, S. L. Ovesen, K. Vorkamp, S. C. Hammel and L. E. Knudsen, Silicone wristbands as personal passive samplers of exposure to polychlorinated biphenyls in contaminated buildings, Environ. Int., 2022, 167, 107397, DOI:10.1016/j.envint.2022.107397.
- F. Wania and C. Shunthirasingham, Passive air sampling for semi-volatile organic chemicals, Environ Sci-Proc Imp, 2020, 22(10), 1925–2002, 10.1039/d0em00194e.
- J. Dalton, Experimental essays, on the constitution of mixed gases; on the force of steam or vapour from water and other liquids in different temperatures, both in a Torricellian vacuum and in air; on evaporation; and on the expansion of gases by heat, Mem. Literary Philos. Soc. Manchester, 1798, 5(2), 535–602 Search PubMed.
- C. Rohwer, Evaporation from Free Water Surfaces, United States Department of Agriculture, Economic Research Service, 1931, https://EconPapers.repec.org/RePEc:ags:uerstb:163103 Search PubMed.
- M. Brauer, R. D. Hirtle, A. C. Hall and T. R. Yip, Monitoring personal fine particle exposure with a particle counter, J. Exposure Sci. Environ. Epidemiol., 1999, 9(3), 228–236 CrossRef CAS PubMed.
- L. Wallace, Indoor particles: a review, J. Air Waste Manage. Assoc., 1996, 46(2), 98–126 CrossRef CAS PubMed.
- L. Wallace, R. Williams, A. Rea and C. Croghan, Continuous weeklong measurements of personal exposures and indoor concentrations of fine particles for 37 health-impaired North Carolina residents for up to four seasons, Atmos. Environ., 2006, 40(3), 399–414, DOI:10.1016/j.atmosenv.2005.08.042.
- D. Licina, Y. Tian and W. W. Nazaroff, Emission rates and the personal cloud effect associated with particle release from the perihuman environment, Indoor Air, 2017, 27(4), 791–802 CrossRef CAS PubMed.
- M. Wacławik, W. Rodzaj and B. Wielgomas, Silicone wristbands in exposure assessment: analytical considerations and comparison with other approaches, Int. J. Environ. Res. Public Health, 2022, 19(4), 1935 CrossRef PubMed.
- A. Reddam, G. Tait, N. Herkert, S. C. Hammel, H. M. Stapleton and D. C. Volz, Longer commutes are associated with increased human exposure to tris(1,3-dichloro-2-propyl) phosphate, Environ. Int., 2020, 136, 105499, DOI:10.1016/j.envint.2020.105499.
- T. Hoxie, S. Zhang, N. J. Herkert, R. A. Bauer, Y. Guo, A. Bhattacharya, C. C. Carignan, K. Hoffman, C. P. Higgins and H. M. Stapleton, Silicone wristbands as a personal passive sampler to evaluate ambient exposure to volatile and non-volatile PFASs, Environ. Sci. Technol., 2023, 58(37), 16316–16326, DOI:10.1021/acs.est.4c05707.
- M. E. Bartkow, K. Booij, K. E. Kennedy, J. F. Muller and D. W. Hawker, Passive air sampling theory for semivolatile organic compounds, Chemosphere, 2005, 60(2), 170–176, DOI:10.1016/j.chemosphere.2004.12.033.
- M. Shoeib and T. Harner, Characterization and comparison of three passive air samplers for persistent organic pollutants, Environ. Sci. Technol., 2002, 36(19), 4142–4151, DOI:10.1021/es020635t.
- X. M. Zhang, T. N. Brown, A. Ansari, B. Yeun, K. Kitaoka, A. Kondo, Y. D. Lei and F. Wania, Effect of wind on the chemical uptake kinetics of a passive air sampler, Environ. Sci. Technol., 2013, 47(14), 7868–7875, DOI:10.1021/es401486f.
- EPA, U. CompTox Chemicals Dashboard, https://www.epa.gov/comptox-tools/comptox-chemicals-dashboard-resource-hub, accessed 6 November, 2023 Search PubMed.
- K. Mansouri, C. M. Grulke, R. S. Judson and A. J. Williams, OPERA models for predicting physicochemical properties and environmental fate endpoints, J. Cheminform., 2018, 10(1), 10, DOI:10.1186/s13321-018-0263-1.
- A. J. Williams, C. M. Grulke, J. Edwards, A. D. McEachran, K. Mansouri, N. C. Baker, G. Patlewicz, I. Shah, J. F. Wambaugh, R. S. Judson and A. M. Richard, The CompTox chemistry dashboard: a community data resource for environmental chemistry, J. Cheminform., 2017, 9(1), 61, DOI:10.1186/s13321-017-0247-6.
- E. N. Fuller, P. D. Schettler and J. C. Giddings, New method for prediction of binary gas-phase diffusion coefficients, Ind. Eng. Chem., 1966, 58(5), 18–27, DOI:10.1021/ie50677a007.
- L. Tuduri, T. Harner and H. Hung, Polyurethane foam (PUF) disks passive air samplers: wind effect on sampling rates, Environ. Pollut., 2006, 144(2), 377–383, DOI:10.1016/j.envpol.2005.12.047.
- B. Munson; D. Young and T. Okiishi, Fundamentals of Fluid Mechanics, 2002 Search PubMed.
- T. K. Sherwood; R. L. Pigford and C. R. Wilke, Mass Transfer, New York, McGraw-Hill, 1975 Search PubMed.
- X. M. Zhang, M. Tsurukawa, T. Nakano, Y. D. Lei and F. Wania, Sampling medium side resistance to uptake of semivolatile organic compounds in passive air samplers, Environ. Sci. Technol., 2011, 45(24), 10509–10515, DOI:10.1021/es2032373.
- S. Hazrati and S. Harrad, Calibration of polyurethane foam (PUF) disk passive air samplers for quantitative measurement of polychlorinated biphenyls (PCBs) and polybrominated diphenyl ethers (PBDEs): factors influencing sampling rates, Chemosphere, 2007, 67(3), 448–455, DOI:10.1016/j.chemosphere.2006.09.091.
- C. Chaemfa, J. L. Barber, C. Moeckel, T. Gocht, T. Harner, I. Holoubek, J. Klanova and K. C. Jones, Field calibration of polyurethane foam disk passive air samplers for PBDEs, J. Environ. Monit., 2009, 11(10), 1859–1865, 10.1039/b903152a.
- N. Yamamoto, M. Hikono, H. Koyama, K. Kumagai, M. Fujii and Y. Yanagisawa, A passive sampler for airborne coarse particles, J. Aerosol Sci., 2006, 37(11), 1442–1454 CrossRef CAS.
- S. Samon, N. Herkert, A. Ghassabian, H. Liu, S. C. Hammel, L. Trasande, H. M. Stapleton and K. Hoffman, Measuring semi-volatile organic compound exposures during pregnancy using silicone wristbands, Chemosphere, 2023, 339, 139778, DOI:10.1016/j.chemosphere.2023.139778.
- K. Hoffman, J. L. Levasseur, S. Zhang, D. Hay, N. J. Herkert and H. M. Stapleton, Monitoring human exposure to organophosphate esters: comparing silicone wristbands with spot urine samples as predictors of internal dose, Environ. Sci. Technol. Lett., 2021, 8(9), 805–810, DOI:10.1021/acs.estlett.1c00629.
- C. D. Kassotis, N. J. Herkert, S. C. Hammel, K. Hoffman, Q. Y. Xia, S. W. Kullman, J. A. Sosa and H. M. Stapleton, Thyroid receptor antagonism of chemicals extracted from personal silicone wristbands within a papillary thyroid cancer pilot study, Environ. Sci. Technol., 2020, 54(23), 15296–15312, DOI:10.1021/acs.est.0c05972.
- A. S. Young, N. Herkert, H. M. Stapleton, J. G. Cedeño Laurent, E. R. Jones, P. MacNaughton, B. A. Coull, T. James-Todd, R. Hauser and M. L. Luna, et al., Chemical contaminant exposures assessed using silicone wristbands among occupants in office buildings in the USA, UK, China, and India, Environ. Int., 2021, 156, 106727, DOI:10.1016/j.envint.2021.106727.
- B. T. Doherty, S. L. McRitchie, W. W. Pathmasiri, D. A. Stewart, D. Kirchner, K. A. Anderson, J. Gui, J. C. Madan, A. G. Hoen and S. J. Sumner, et al., Chemical exposures assessed via silicone wristbands and endogenous plasma metabolomics during pregnancy, J. Exposure Sci. Environ. Epidemiol., 2022, 32(2), 259–267, DOI:10.1038/s41370-021-00394-6.
- K. A. Romanak, S. Wang, W. A. Stubbings, M. Hendryx, M. Venier and A. Salamova, Analysis of brominated and chlorinated flame retardants, organophosphate esters, and polycyclic aromatic hydrocarbons in silicone wristbands used as personal passive samplers, J. Chromatogr., A, 2019, 1588, 41–47, DOI:10.1016/j.chroma.2018.12.041.
- J. P. Koelmel, E. Z. Lin, A. Nichols, P. Guo, Y. Zhou, G. Pollitt and K. J. Head, Shoulders, knees, and toes: placement of wearable passive samplers alters exposure profiles observed, Environ. Sci. Technol., 2021, 55(6), 3796–3806 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: List of targeted chemical analytes; time- and velocity-dependent accumulation of chemicals on wristbands; additional correlations of SEF values with chemical properties; light microscopy images of silicone wristbands after their deployment for 28 days. See DOI: https://doi.org/10.1039/d4em00440j |
| This journal is © The Royal Society of Chemistry 2025 |


