From lab to reality: how non-AM1.5 conditions shape the future of perovskite and organic solar cells

Abstract

The power conversion efficiencies (PCEs) of perovskite and organic photovoltaic (PV) devices under AM1.5 standard test conditions have improved rapidly, but their real-world energy yield remains poorly characterised. This study explores the competitiveness of emerging PV technologies compared to silicon-based PVs by integrating device-specific performance data into energy yield models using historical climate datasets from locations around the world. Our analysis demonstrates that favourable temperature coefficients and spectral responses allow perovskite and organic PVs to achieve higher energy yields in certain climates than their AM1.5 ratings would predict. Indeed, the changes in performance due to real world operation is similar in magnitude to the incremental improvement in record cell efficiencies under AM1.5 conditions. These advantages narrow performance gaps or even achieve parity with silicon PVs in some specific climate regions, and our findings indicate that, in certain equatorial regions, perovskite PVs can already achieve near parity with silicon PVs under real operating conditions by narrowing the STC gap from about 4.8% to 1.5%. Our findings underscore the critical need for comprehensive non-AM1.5 characterisation to improve energy yield predictions, optimise device design for real-world conditions, and enhance the competitiveness of emerging PV technologies.

---

Broader context

Solar energy is widely recognised as indispensable for mitigating climate change, with the PV industry historically led by silicon-based technologies. However, next-generation PVs based on organics and perovskites are steadily gaining traction, both in research and near-commercial phases. Notably, most device characterisation remains confined to the AM1.5 standard, an approach that fails to capture the broad array of real-world operating conditions—particularly high temperatures, varied spectral outputs, and low-irradiance environments. By systematically quantifying the combined effects of irradiance, temperature, and spectral mismatch, this study demonstrates how advanced emerging PVs can significantly narrow the performance gap with established silicon modules under realistic environmental conditions. In regions characterised by intense heat or prolonged cloud cover, these emerging PV materials, benefiting from favourable temperature coefficients, enhanced spectral responses and low irradiance performance, can yield outputs that closely approach expectations based on AM1.5 for silicon. Beyond underscoring the necessity of more comprehensive performance data, these findings highlight pathways for technology optimisation. They further offer incentives for researchers to consider the broader advantages of alternative PV architecture—advantages that may be critical for accelerating the pace of global decarbonisation.

1 Introduction

The performance of photovoltaic (PV) devices with perovskite or organic absorbing materials has advanced rapidly since their invention and are close to commercialisation. Much of the ongoing development of these emerging PV technologies has used measurements of power conversion efficiency (PCE) under AM1.5 conditions to quantify performance and enable like-for-like comparison with competing PV technologies. AM1.5 defines a distribution of power per wavelength of incident light and intensity (1000 W m⁻²) which is a reasonable annual average for the continental United States, at a temperature of 25 °C. Inevitably, the AM1.5 measurement standard is somewhat arbitrary and often not representative of actual operating conditions, particularly in a global context.¹ Hence, further information is required to make accurate predictions of energy production under real conditions.

Standards for commercial solar PVs have evolved to address these limitations. For example, the IEC 61853-1 test standard published by the International Electrotechnical Commission (IEC) measures the performance of PV modules at temperatures between 15 °C and 75 °C and irradiances from 100 W m⁻² to 1100 W m⁻²,³ providing a more comprehensive basis for energy yield predictions. These expanded measurements are essential for estimating energy yield (i.e., kWh produced per rated power production under AM1.5, kWpeak) more accurately, which is necessary for determining the economic viability – or ‘bankability’ – of solar installations. Notably, such assessments reveal performance challenges for market-leading silicon PV technologies, which tend to exhibit reduced efficiency at low irradiances and high temperatures.⁴

To further illustrate these performance challenges, Fig. 1(a) visualises the extent to which commercial silicon modules lose efficiency when operating outside nominal conditions using the De Soto single-diode model,⁵ discussed further in Section 3. In this example, the silicon module experiences over a 20% relative efficiency loss at high operating temperatures and approximately a 10% loss under low irradiance conditions, emphasising how sensitive commercial silicon technology is to real-world operating conditions. To contextualise these losses in practical settings, Fig. 1(b) and (c) present the density distributions of real operating conditions for silicon PV modules in California City and London in 2019, respectively. These datasets highlight the significant variation in irradiance and cell temperature profiles across different geographic regions. The AM1.5 STC and IEC 61853-1 matrix points are also marked in the figures to demonstrate the deviation between actual PV operation and standard test points. In California, the operating conditions frequently align with higher irradiances and temperatures, where silicon modules experience efficiency losses due to thermal effects, while in London, lower irradiance conditions dominate, where again silicon modules operate less efficiently.

Fig. 1 (a) Normalised PCE of commercial silicon PVs² under different irradiance and temperature conditions, (b) density of real operation conditions of silicon PVs in California 2019 and (c) London 2019.

These intrinsic limitations of silicon PVs may represent opportunities for emerging technologies, such as perovskite and organic PVs, to contribute to future renewable energy generation. Although limited, initial studies on non-AM1.5 performance of these technologies suggest that their intrinsic properties may address some of silicon PVs' deficiencies. In the case of organic PVs, some architectures have shown increasing short-circuit current with rising temperature⁶ and improved efficiency under low irradiance,⁷ with performance varying across different climatic conditions.⁸ These distinct behaviours have prompted researchers to develop new energy generation models for organic PVs under realistic operating conditions based on silicon PVs⁸ or machine learning,⁹ though these models remain architecture- and composition-specific. Likewise, it has been shown that perovskite PV devices have a different temperature dependence of PCE as compared to silicon PVs,¹⁰ to an extent that varies with composition¹¹ and architecture.¹² Furthermore, the irradiance dependence of PCE also differs, influenced by material composition and device structure.¹³ These unique characteristics have been integrated into energy prediction models to estimate the potential performance of perovskite PV systems under various climatic conditions and installation strategies.^10,14,15

Overall, it is evident that the PCEs of both organic and perovskite PV devices exhibit significant variation under different light and temperature conditions, distinguishing them from silicon PVs. However, these variations are influenced by the specific composition and architecture of the devices, leading to both opportunities and uncertainties regarding their competitiveness in different locations. Crucially, the well-documented AM1.5 performance may not be a reliable predictor of real-world performance due to the limited characterisation of non-AM1.5 behaviour in emerging PV technologies.

The objective of this paper is to quantify how real-world performance differences influence the competitiveness of a range of perovskite and organic PVs compared to silicon counterparts. We curate a broad dataset of organic and perovskite PV devices reported in the literature and use these data in an energy yield model utilising historical climate data to assess the impact of temperature, irradiance, and spectral effects on efficiency. These models are then combined to predict efficiency under realistic conditions worldwide for competing PV technologies.

Our analysis reveals that favourable temperature, irradiance, and spectral responses narrow the performance gap between perovskite and organic PV devices and silicon counterparts compared to what is expected from PCE measurements under standard AM1.5 conditions. Lower temperature coefficients give emerging PV technologies a relative advantage in warm climates, while a stronger response at shorter wavelengths makes them more resilient to cloud cover. In some locations, a specific perovskite PV is predicted to achieve parity with silicon despite a 4.8% performance deficit under AM1.5 conditions. Similarly, the organic PV significantly reduces its performance gap with silicon compared to AM1.5 conditions in nearly all locations below 50° latitude. These findings underscore an opportunity for the emerging PV community to quantify and improve real-world competitiveness by characterising performance beyond AM1.5 conditions. Without this characterisation, significant uncertainty remains regarding the real-world viability of emerging PV technologies. Indeed, we show that the wide range of reported non AM1.5 performances is significant compared to incremental improvements in record PCE achieved under standardised AM1.5 test conditions.

2 Yield model

A range of yield models have been proposed for predicting the performance of different PV systems including mathematical models,^16,17 empirical models^18,19 and diode models.^20–22 Among these are models that involve fitting to operational data, usually with an underlying assumption that the PV device is silicon, such as PVMAPS²³ or some single diode models.²⁴ However, such models are not designed for emerging PV technologies which have distinct, diverse operational characteristics shown later. Other models developed specifically for emerging PV devices often lack interoperability across different technologies. To address these challenges, we developed a simplified yield model using separation of variables to describe the temperature and irradiance dependence of PCE using separate linear relationships. We introduce two dimensionless parameters: the normalised temperature coefficient, T_coe, and the irradiance factor, f_I. The normalised temperature coefficient, defined in eqn (1), captures the slope of the device's temperature dependence relative to its performance at 25 °C:where T is the cell temperature and PCE(25 °C) denotes the efficiency measured at the reference temperature of 25 °C. Next, the irradiance factor, f_I, given in eqn (2), accounts for how the efficiency evolves with changing irradiance levels:where I is the irradiance, PCE(I) is the PCE at irradiance level of I W m⁻² and PCE (1000 W m⁻²) is the device efficiency at a reference irradiance level of 1000 W m⁻².

Within the model, we utilise historical meteorological data (wind speed, irradiance and air temperature) at hourly resolution from the National Solar Radiation Database (NSRDB),²⁵ along with spectral data computed using the Fast All-Sky Radiation Model for Solar Applications with Narrowband Irradiances on Tilted Surfaces (FARMS-NIT) model for the site of interest. Solar panels are assumed to be ground mounted and have a fixed optimum tilt angle provided by PVGIS.²⁶ A previous study by Peters et al. primarily focused on silicon-based and cadmium telluride (CdTe) PV technologies using satellite-derived irradiance data to predict global PV performance.²⁷ However, the meteorological data in the referenced model are derived from satellite data with a daily temporal resolution, as opposed to hourly as here, and the spectral correction is calculated using the SMART clear-sky model, thereby neglecting the significant impacts of clouds and aerosols on the spectrum.²⁸ These simplifications lead to inaccuracies in PV power generation predictions, which are highly sensitive to dynamic weather conditions. In contrast, our model employs satellite meteorological data with an hourly temporal resolution and utilises the FARMS-NIT model, which accurately captures spectral conditions under both clear and cloudy scenarios, for spectral mismatch calculations. Furthermore, our study significantly expands upon previous research by systematically integrating device-specific performance characteristics into predictive energy yield models — including temperature coefficients, irradiance dependencies, and spectral responses—for perovskite and organic PV technologies.

The Plane of Array (POA) irradiance determines the incident solar radiation on a tilted PV panel surface,²⁹ and can be obtained using various approaches, including transposition models that convert global horizontal irradiance (GHI) to POA irradiance, direct measurements using sensors or computational models accounting for atmospheric parameters. Transposition models typically split POA irradiance into beam, diffuse, and reflected components, with widely used methods including the isotropic model,³⁰ Perez model,³¹ and the HDKR model (Hay, Davies, Klucher, and Reindl).³² Although the isotropic model is more accurate under clear-sky conditions, it underestimates strong forward scattering from clouds or aerosols, making it less reliable under cloudy conditions.³³ The performance of the empirical models (Perez and HDKR) is sensitive to local atmospheric and surface conditions and the direction of the sun and PV, potentially limiting their broader applicability.³⁴

The POA irradiance used in our model was directly integrated from the spectral data computed using the FARMS-NIT model which accounts for both clear and cloudy conditions. FARMS-NIT is an advanced radiative transfer model developed at the National Renewable Energy Laboratory (NREL) to compute solar radiances in narrow-wavelength and integrates them over tilted PV panels to determine POA irradiances.^28,35 Under clear skies, it employs the Simple Model of the Atmospheric Radiative Transfer of Sunshine (SMARTS)³⁶ and solves the radiative transfer equation using single-scattering approximations. For cloudy conditions, FARMS-NIT incorporates cloud reflectance and a bidirectional transmittance distribution function from precomputed lookup tables generated by the LibRadtran model using a 32-stream Discrete Ordinates Radiative Transfer (DISORT) scheme.³⁷ Validation studies show that FARMS-NIT achieves higher accuracy than TMYSPEC when evaluated against both surface observations and state-of-the-art radiative transfer models, while offering significantly improved computational efficiency.³⁴

Finally, all data points with an irradiance of 0 W m⁻² were filtered out for the purposes of this study. The cell temperature T_cell(t) of the PV was calculated with eqn (3) using hourly data for irradiance I(t), air temperature T_ambient(t) and Ross coefficients k_w(t) from Bristow et al.^38,39 The relationship is expressed as:

T_cell(t) = T_ambient(t) + k_w(t) × I(t) (3)

where k_w(t) captures the wind-dependent heat transfer. Because the wind speed–Ross coefficient and irradiance–PCE relationships were extracted from figures in the literature, linear interpolation was employed to ensure continuity between discrete data points. Next, the temperature factor f_T(t) is defined in eqn (4), where T_coe denotes the normalized temperature coefficient described earlier:

f_T(t) = (T_cell(t) − 25) × T_coe (4)

Finally, the energy generation P at each time step t at a specific location could thus be calculated using eqn (5):

P_max is the rated capacity of the defined solar farm and f_T(t), f_I(t) and f_S(t) represent the temperature-, irradiance- and spectral mismatch dependent factors, respectively. The equation for spectral mismatch factor f_S(t) is introduced and examined later in Section 6. In this way, the model evaluates each component at hourly intervals (indexed by t) to capture the time-resolved behaviour of PV power generation under varying meteorological conditions.

3 Temperature dependence

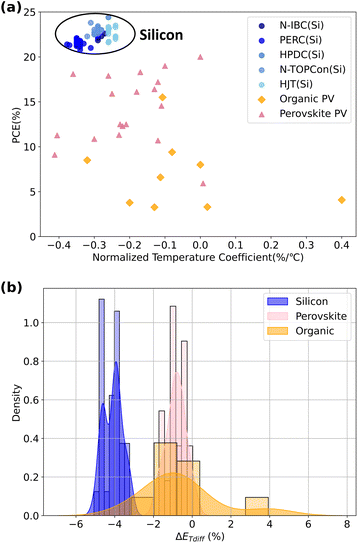
To assess the current state of understanding and measurement of the temperature dependence of PCE in organic and perovskite PVs, we conducted a systematic literature review. Using the Web of Science database, we searched for papers published within the past decade using topic search terms “temperature dependence/effect”, “temperature coefficient”, “PCE”, “organic photovoltaics/solar cell”, “perovskite photovoltaic/solar cell”, “yield”, or “outdoor test.” Each paper was reviewed and included in our analysis if it reported the temperature dependence of PCE in either indoor or outdoor settings, with indoor measurements conducted using an AM1.5 G solar simulator. We excluded studies that reported temperature coefficients under varying irradiance conditions in outdoor tests but retained three^11,40,41 as they reported temperature coefficients at fixed irradiance levels. This approach to outdoor PV data minimises the influence of irradiance and spectral variations on the PCE temperature coefficient. To maximise the size of the dataset, we included PV devices of all sizes, though we addressed the impact of cell size later in our analysis. We excluded data for devices with PCE below 3% under standard test conditions (STC, defined as an AM1.5 spectrum at 1000 W m⁻² and a cell temperature of 25 °C), as our focus is on state-of-the-art PV technologies. Additionally, we excluded studies that included only modelled data. The total dataset comprises nine organic and nineteen perovskite PVs, the full details are provided in the ESI.†

These emerging PV devices were compared against data from a range of commercial silicon PV panels. In total, 61 different types of commercial silicon solar panels from 31 manufacturers, released within the past three years, were included in the analysis, with performance metrics sourced directly from product datasheets. To provide insight into how the construction of silicon PV devices influences performance, we selected modules featuring Interdigitated Back Contact (N-IBC) technology, Passivated Emitter and Rear Contact (PERC) technology, Tunnel Oxide Passivated Contact (N-TOPCon) technology, High-Performance and Hybrid Passivated Dual-Junction Cells (HPDC), and Heterojunction (HJT) solar cells, where available.

Fig. 2 shows the normalised temperature coefficient for PCE, T_coe and PCE under STCs for each PV device in our dataset. The data for silicon PVs exhibit a tight clustering of temperature coefficients indicative of a mature technology. A zoomed-in view of the distribution of the silicon clusters is shown in Fig. S1 in the ESI.† Within the silicon dataset, there are 5 discernible clusters which largely relate to variations in passivation techniques.⁴² Effective passivation can enhance open-circuit voltage (V_oc) and result in a lower T_coe, as the success of HJT cells is largely attributed to the effective a-Si passivation.^43,44 Despite these variations, all silicon panels consistently demonstrate a negative T_coe, typically ranging from −0.38% °C⁻¹ to −0.24% °C⁻¹. Technological advancements in silicon PVs have clearly improved both PCE and T_coe. However, within silicon PVs of the same technological generation, a higher PCE does not necessarily correlate with a less negative T_coe.

Fig. 2 (a) Temperature coefficient and PCE measured at 25 °C for different reported PV technologies and (b) histogram (bars) with accompanying kernel density estimation (curves) of E_Tdiff predicted for California City (2019) for populations of PVs in the dataset.

By contrast, the PCE and T_coe of perovskite PVs exhibit considerable variability. Generally, the PCE under STCs for perovskites is lower than that of silicon, while their T_coe tend to be more positive. Previous studies have found that the T_coe of perovskites is closely related to the device structure and the composition of the active layer for a variety of reasons. In part, the T_coe for perovskites has been attributed to their wide band gap as well as the increase in the bandgap with increasing temperature.^12,45,46 Device-specific architecture is also argued to play a role, with compositions and architecture that improve carrier extraction reducing temperature sensitivity.^12,47 However, the overall picture remains unclear and is further complicated by the presence of reversible and non-reversible degradation in present devices.¹³ A detailed correlation analysis between band-gap values and these performance metrics across our device dataset is performed in the ESI, Fig. S3–S6.† The analysis demonstrates that no significant relationship exists between the band-gap and the temperature coefficient or low irradiance performance of the investigated PV devices.

Moving on to consider organic PVs, it is observed that the PCEs under STCs are generally lower than those of both silicon and perovskite PVs. As with perovskite PVs, the T_coe for organic PVs is generally more positive than for silicon and covers a wide range, indeed stretching as high as 0.4% °C⁻¹ for DIBSQ : PC70BM.⁴⁸ Present understanding for this range in temperature performance has some similarity to that for perovskite PVs. First, several studies have indicated that the temperature characteristics of organic PVs are influenced by the active materials used.^49,50 The chosen architecture is also important, since the hole-extraction has been shown to influence T_coe⁵¹ via improved charge extraction.⁴⁸ More generally, it is suggested that increased phonon–electron coupling at higher temperatures leads to more positive short-circuit current with temperature, leading to a less negative T_coe.⁴¹

However, our intention here is not to dwell on the reasons for these variations in T_coe for perovskite and organic PVs, rather it is to quantify the influence these variations have on energy production under realistic conditions. Our goal is to quantify the importance of differing temperature behaviour in the competitiveness of the devices, and contextualise how important temperature coefficients are with respect to AM1.5 performance.

Hence we used the energy yield model described above to predict the annual energy production of a 5 MW solar farm comprised of PV devices within the dataset shown in Fig. 2(a) for the year 2019. We selected California City in the US (a city roughly 100 miles north of Los Angeles) for our analysis as California has a large installed capacity of PVs and so is representative of the locations where ground mount solar farms may be installed. Our approach was to predict the annual yield for a PV installation not including temperature dependence of PCE (i.e., assuming T_coe = 0), E_woT, and again including the temperature dependence of the PCE (i.e., T_coe as reported in Fig. 2(a)), and E_wT. We then calculated E_Tdiff = E_wT − E_woT to quantify the impact of T_coe on energy production. Note that here we did not include the irradiance or spectral dependence of PCE (discussed later) in these calculations to avoid complicating the analysis. We present yield calculations including all of these effects simultaneously to quantify their relative importance later in the paper.

Fig. 2(b) shows histograms of E_Tdiff as well as kernel density estimation of the same (i.e., a smoothed estimate of the probability distribution of a random variable) for the populations of PV technologies in the dataset. It can be seen that the distribution of silicon PV datapoints (blue) are negative, meaning it is predicted that silicon PV devices would lose efficiency relative to that measured at STC due to the effect of temperature. This is in contrast to less negative, and indeed sometimes positive, E_Tdiff for perovskite (pink) and organic (orange) PV devices. The more negative values for silicon compared to organic and perovskite PVs represents a relative gain in performance for organic and perovskite PVs to silicon PVs due to the effect of temperature.

We quantified these relative performance changes of PV populations by measuring the peak positions of their kernel density estimates: E_Tdiff = −3.9% for silicon, −0.6% for perovskite, and −0.8% for organics. These results indicate a 3.3% energy gain for perovskite PVs and a 3.1% energy gain for organic PVs when compared to silicon. While there is some variation in behaviour, the distributions suggest that the temperature-dependent characteristics of perovskite and organic PVs typically enhance their real-world energy generation beyond what is predicted by PCE measurements under STCs. We note that the relative change in energy generation due to beneficial temperature coefficients is similar to the incremental increases in record PCE under STCs.⁵² For example, even when one takes a long period of 5 years, the world record PCE for perovskite research cells increased by a relative 4.7% and organic PVs by a relative 9.7%. This, we argue, is a compelling reason for increased focus on PV testing under realistic operating conditions to maximise their potential before reaching the market, particularly given the intrinsic negative T_coe of silicon PVs.

4 Irradiance dependence

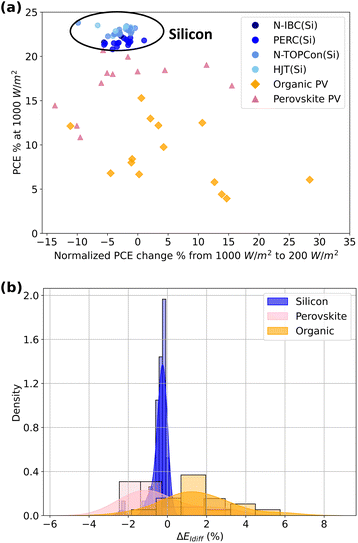
We established the state-of-the-art in the measurement of irradiance dependence of PCE for organic and perovskite PVs by conducting a topic search using the database Web of Science including the terms “irradiance dependence/effect”, “light/sun intensity”, “low light”, “PCE”, “silicon/c-si photovoltaics/solar cell”, “organic photovoltaics/solar cell”, “perovskite photovoltaic/solar cell”, “0.1sun to 1sun” or “AM1.5.” As before, we only included studies published in the last decade and with AM1.5 efficiencies of more than 3%. As our focus is the prediction of performance in outdoor settings, changing the spectrum whilst keeping the irradiance the same can lead to changes in the current–voltage curve,⁵³ we only include studies using a solar simulator with class A spectral mismatch (i.e., AM1.5 spectral shape). However, we note that even a class A spectral mismatch is not a zero error reproduction of the AM1.5 spectrum,⁵⁴ and spectral mismatch of this class can cause measurement errors exceeding 10%, particularly given the varying spectral response ranges of different PV technologies.⁵⁵ However, given this is the best widely available measurement standard, we proceed with knowledge of the degree of uncertainty. Finally, we exclude data from outdoor tests, as these studies did not control temperature, leading to potential inaccuracies in assessing irradiance dependence.

Following this process, our curated dataset included 12 perovskite and 14 organic PV devices. We highlight that our search methodology only yielded two eligible non-fullerene acceptor OPVs^56,57 with the remaining records comprising fullerene-based acceptors, highlighting the need for further studies on more recent materials. For each device in our dataset, we quantified the change in efficiency between irradiance levels of 1000 W m⁻² and 200 W m⁻² (i.e., Δ_η = η(1000 W m⁻²) − η(200 W m⁻²)) using linear extrapolation between datapoints if necessary. We selected 200 W m⁻² as a reference point since most commercial silicon PV datasheets (44 of the 61 in our dataset) report irradiance dependence measurements down to this level. These data are shown in Fig. 3 as a function of the PCE under STC (i.e., η(1000 W m⁻²)), while the complete dataset is provided in the ESI.†

Fig. 3 (a) Difference in PCE measured at 1000 and 200 W m⁻² for different reported PV technologies and (b) histogram (bars) with accompanying kernel density estimation (curves) of E_Idiff predicted for California City (2019) for populations of PVs in the dataset.

Fig. 3(a) shows that the PCEs for both perovskite and organic PVs have a wide range behaviour when irradiance changes, with Δ_η varying from −15% to 15% and beyond, and further, that these values of Δ_η are uncorrelated with PCE under STCs. This is in contrast with silicon PVs, which has a smaller grouping of irradiance dependence behaviours from Δ_η = −10% to 0%, albeit again with no correlation with PCE under STCs. A zoomed-in view of the silicon distribution is shown in Fig. S2 in the ESI.† In general, we observe that organic and perovskite PVs show relatively better performance under low-light conditions compared to silicon, mirroring findings under other thin-film PV conditions.⁵⁸ A significant factor that contributes to the low light performance of perovskite PVs is the active layer thickness, since thicker layers both increase absorption and reduce interface recombination,⁵⁹ while for organic PVs, the improved performance at low light levels is ascribed to lower recombination rates and lower charge carrier densities.^60–62

Taking the same approach as before, we contextualised the impact of varying Δ_η on annual energy yield by predicting the average energy yield for a 5 MW solar farm in California City using historical meteorological data for 2019. We calculated the average energy yield for each PV technology without irradiance dependence of PCE, E_woI, and again with irradiance dependence of PCE, E_wI, shown in Fig. 3(b). We then plot the difference of these values E_Idiff = E_wI– E_woI which represents the predicted difference in annual yield for each PV technology because of the irradiance dependence of PCE. We exclude the variation of PCE with temperature and incident spectrum in this calculation to simplify the analysis here, but return to look at their combined effect later in the paper.

As expected, we observed a negative E_Idiff with a narrow distribution due to the consistent lower efficiency of silicon under low light conditions. Comparing this population to that of perovskite and organic PVs, while we saw slight changes in peak position compared to silicon, the most significant difference was the much broader distribution of energy yields for the emerging PVs. The full width at half maximum of the perovskite PV distribution peak was 3.2%, while for the organic PV it was 4%, both of which are comparable to the incremental increase in record efficiencies under AM1.5 conditions. Furthermore, it is important to note that our analysis considers only the aggregated energy yield of a PV farm and does not account for energy demand variations throughout the day. Renewable energy generated during periods of high demand, such as early evening when irradiance is low, has a greater impact on reducing greenhouse gas emissions. This highlights additional opportunities for emerging PV technologies with positive Δ_η to distinguish themselves from silicon-based systems.⁶³

5 Spectral mismatch

Here we consider the influence of the differing spectral response of perovskite and organic PVs on their efficiency under realistic conditions. The spectrum of sunlight under real operating conditions is influenced by geographical location and season via the intervening air mass (AM), as well as concentrations of atmospheric water vapour, particulate matter, and others, all of which may cause deviation from the AM1.5 standard.^67,68 Thus to calculate the impact of varying input spectra on power output, one must consider both the spectrum under real conditions, E and the spectral response of the PV device in question, S_r, i.e., the ratio of the current generated to the power incident on the solar cell as a function of wavelength. Fig. 4 shows the normalised S_r for PV devices with different absorber layers. The narrow bandgap of silicon allows for better response to wavelengths in the infra-red, while emerging PVs with a wider band gap have a peak response in the visible region,⁶⁹ however we note that the S_r of emerging PV technologies can be tuned with the device architecture, composition, and molecular structure, as the non-fullerene acceptor (NFA) organic device⁶⁶ has a smaller band gap than the small molecule organic device.⁴¹ By contrast, the spectral response of commercial silicon PVs can be influenced by different passivation technologies, however, the effect is relatively minor.

Fig. 4 Normalised spectral responses of different PVs.^{10,41,64–66}

When the real spectrum deviates from the AM1.5 standard, a spectral mismatch factor (SPMM) must be introduced to correct predictions of power output,⁷⁰ calculated using eqn (6):⁷¹

Here λ represents the wavelength, E_ref denotes the AM1.5 reference spectrum, E represents the spectrum under real conditions, and S_r signifies the spectral response of the selected PV device. In this way, the predicted PV output under real conditions is obtained by multiplying SPMM (f_S) by the predicted output for the same intensity of light with an AM1.5 spectral shape.

Many PV modelling tools either do not include the impact of spectral effects on PV performance or rely on simplified models that approximate spectral mismatch by considering only a few atmospheric variables.⁷² For instance, the Sandia model accounts only for AM,⁷³ while the CREST and First Solar models incorporate AM along with an additional variable.^74,75 More complex models, those by Duck and Fell and Caballero et al.,^76,77 consider multiple factors including AM, precipitable water (PW), and sky clearness or aerosol optical thickness. However, the application of these models is limited, as they generally rely on standardised spectral response data for conventional PV technologies, which have not yet been proven suitable for emerging PVs with different spectral irradiance characteristics.

The Simple Model of the Atmospheric Radiative Transfer of Sunshine (SMARTS) has been a widely used spectral model for several decades,⁷⁸ though it is limited to clear sky conditions. To address this limitation, NREL developed the FARMS-NIT model.^28,35 This model is capable of computing real-time spectral data under both clear and cloudy conditions. FARMS-NIT offers greater accuracy than the TMYSPEC model and is more efficient than many other existing models. Furthermore, the FARMS-NIT model allows for the analysis of PV systems at any selected location, time and angles. In the context of emerging PVs, the S_r and external quantum efficiency (EQE) are interchangeable metrics, and though their EQE is commonly reported,^54,55 the spectral mismatch these technologies experience under real-world conditions has been seldom explored.

Here we examine the effect of considering only the spectral mismatch on the energy yield of emerging PV technologies using real-time spectral data from the FARMS-NIT model, the spectral response of different PV technologies, and eqn (6) to evaluate the spectral mismatch of different PVs in selected locations and time periods. Our goal was to enable comparison of SPMM for different PV technologies in California City, Lisbon and London as having a range of different latitudes and irradiances, and time periods, including over the course of a year and over a day.

The calculated monthly and hourly average values of SPMM for these locations are shown in Fig. 5. First, we observe that emerging PV technologies, except NFA organic PV, and silicon PV exhibit opposite seasonal trends in their spectral mismatch behaviour. Specifically, in summer months, increased short-wavelength irradiance (i.e., blue light) enhances the performance of wide-bandgap devices such as perovskite and organic PVs, while simultaneously reducing the relative efficiency of silicon PVs.^64,79,80 Since the NFA organic PV has a relatively small band gap, its spectral response is close to that of commercial silicon, and SPMM shows a similar trend. On an hourly scale, the SPMM for emerging PV technologies typically has a peak around solar noon, when the spectrum is most blue-shifted, whereas the SPMM for silicon devices reaches a minimum at this time. Notably, in high-latitude cities such as London and Lisbon during summer, early morning and late evening conditions are frequently affected by persistent low-level cloud cover. These clouds induce additional Mie scattering and absorb infrared wavelengths, further blue-shifting the incident spectrum. As a result, organic small molecule PV devices in these locations can exhibit average SPMM values exceeding 1.35 during early morning hours.

Fig. 5 (a), (c) and (e) show the monthly average spectral mismatch factor for London, California and Lisbon, respectively, during 2019 for various PV technologies. (b), (d) and (f) show the corresponding hourly average spectral mismatch factor for the same locations.

Then examining the influence of latitudes, we observe that higher latitudes lead to larger deviations from AM1.5 as expected, reaching over 20% in the case of London in some instances. Additionally, it is important to note that SPMM also significantly increases during periods of high solar zenith angle, particularly at the start and end of the day. This temporal variation is critical because these are typically periods when electricity demand peaks while renewable energy generation from solar PV is inherently reduced. Efficient renewable generation during these periods is therefore particularly valuable for balancing grid supply and demand.⁸¹ Moving on to consider the difference between PV technologies, we observe that commercial silicon has SPMM factors close to 1 in all locations, times of day, and times of the year. By contrast, the SPMM of perovskite and organic small molecule devices can be in excess of 1.2, particularly at high latitudes. This demonstrates that simple models which ignore SPMM are less suitable for the analysis of these emerging PV technologies, and highlights the necessity of characterising the SPMM of emerging PV technologies to enable accurate yield prediction. These data also reveal a performance opportunity: emerging PV devices will perform better than expected based on AM1.5 characterisation alone in high-zenith angle situations. For example, a mono-Si PV device in London is predicted to have an annual yield 1.94% greater than that expected based on AM1.5 behaviour alone, while the small molecule organic PV device considered here is predicted to have an annual yield 7.17% higher than predicted under AM1.5 conditions. Our analysis suggests that cloud-modified spectral conditions, rather than air mass effects alone,⁸² are the dominant driver of enhanced spectral mismatch for some emerging PVs at high latitudes. Although large zenith angles generally increase Rayleigh scattering and reduce blue light availability,⁸³ they also amplify the impact of cloud-induced spectral shifts. This mechanism explains why wide-bandgap PV devices maintain high SPMM values in cloudy, high-latitude environments such as London. We highlight that again the changes in predicted real world power output due to SPMM effects in emerging PVs are quantitatively similar to incremental increases in AM1.5 record efficiency over a period of years.

An important mechanism affecting PV performance, beyond the temperature, irradiance, and spectral mismatch factors discussed earlier, is optical reflection at device interfaces. For instance, silicon-based PV cells can experience significant reflection losses, with approximately 30% of incident solar radiation reflected at the cell surface and around an additional 4% reflected at the air–glass interface of the PV modules.⁸⁴ These reflection losses notably reduce the achievable power output of silicon PV cells, prompting widespread application of anti-reflection (AR) coatings both on the glass covers and the silicon cells themselves in commercial modules.⁸⁵

Emerging PV technologies, including organic and perovskite PVs, similarly suffer from interface reflection losses and limited active-layer absorption. However, mitigation strategies are being explored, for example, in perovskite PVs various optical engineering techniques such as AR coatings, light trapping, light scattering, photon recycling, and plasmonic enhancements are being developed to maximise photon absorption.⁴³ Wang et al. demonstrated that porous and mesoporous silica nanoparticle-based dual-layer AR coatings effectively increased the transmittance of glass substrates from about 90% to around 95%, significantly improving the PCE of perovskite PVs.⁸⁶ Optical management strategies for organics also include the use of metallic nanoparticles, sub-wavelength gratings, blazed gratings, biomimetic moth-eye structures, and microcavities,⁸⁷ which can increase peak absorption rates to over 95%.⁸⁸

It is important to acknowledge explicitly that the analysis presented here did not incorporate the effects of varying incident angles and reflection losses between different PV technologies. Nevertheless, given that the primary focus of our work is to evaluate temperature, irradiance, and spectral mismatch impacts, the potential bias introduced by omitting angular and reflection-related effects is expected to be small within the scope of the current study. Future work could benefit from incorporating detailed optical modelling, taking into account angular and reflection-dependent behaviour to further improve prediction accuracy.

6 Global variation of effective efficiency for different PV technologies

Having considered the individual impacts of temperature, irradiance, and spectral mismatch on the power output of emerging PV devices at a single location, we now examine their combined effect on a global scale. A key characteristic of the dataset discussed above is that while the temperature dependence may be reported for one device, its irradiance dependence may not be, and vice versa. To address this, we selected a representative PV device for each technology, prioritising those with the most comprehensive data on spectral, irradiance, and temperature effects.

For silicon-based PVs, we selected Canadian Solar's N-TOPCon module due to its strong performance, with a PCE of 23.3% under STCs and a temperature coefficient of T_coe = −0.29%°C⁻¹. However, as its datasheet does not provide spectral response data, we adopted the spectral response reported by Jang et al.⁶⁵ Moreover, because the datasheet only specifies performance at five discrete irradiance levels (1000, 800, 600, 400, and 200 W m⁻²), the five-parameter De Soto single-diode model⁵ was used to predict the actual output of the silicon PV module under different irradiance and temperature conditions. For perovskite PVs, we utilised data from Jošt et al.,¹⁰ which reports a PCE of 18.5% under STCs and a T_coe = −0.17%°C⁻¹. For organic PVs, we selected modules from Heliatek for simulation,⁸⁹ with a PCE of 8% under STCs and a T_coe = 0%°C⁻¹. As the datasheet for the chosen organic PV lacked spectral response information, we used the spectral response of the small-molecule organic PV reported by Burlingame et al.⁴¹ Both organic and perovskite PVs were typical within the context of our larger dataset, though we highlight the results of earlier sections which show the impact of the broad distribution of behaviours observed. These data should therefore only be taken as a prediction of yield for specific device compositions and architecture.

Meteorological and spectral data for 2019 were sourced from the NSRDB, with a spatial resolution of 3° latitude and longitude. The yield model described earlier was employed to calculate the annual energy output of each PV technology, incorporating temperature dependence, irradiance dependence, and spectral mismatch effects E_wT,I,S and not incorporating them E_woT,I,S. Data gaps for adjacent geographic locations were estimated using linear interpolation. Our analysis is limited to where satellite data are available, which excludes latitudes outside the range of −60° to 60° and parts of southern South America, Ireland, northern England, and central Russia. The real efficiency (PCE_real) of the PVs is calculated as follows:

where PCE_STC is the efficiency recorded at STCs.

Fig. 6 shows the predicted effective efficiency of silicon, perovskite, and organic PV exemplars across the world in 2019. Red areas indicate regions where the effective efficiency is lower than the STCs, while blue areas indicate higher effective efficiency. For silicon PVs, the absolute effective efficiency can be up to 2% lower (8% relative) than its efficiency under AM1.5 STC, primarily due to performance losses at high temperatures. Spectral mismatch also contributes a geographic variation of efficiency, with substantial efficiency gains in high-altitude regions.

Fig. 6 (a) Predicted PCE_real compared to PCE_STC for silicon PVs across the world in 2019, (b) the corresponding map for perovskite PVs and (c) for organic PVs.

The global distribution of effective efficiency for the selected perovskite and organic PV exemplars differs significantly from that of silicon PVs, as shown in Fig. 6(b) and (c), respectively. This difference is primarily due to their smaller temperature coefficients and favourable spectral responses. Under cloudy conditions, the relative irradiance at wavelengths below 700 nm increases (where these devices perform well) compared to AM1.5, while there is a relative decrease at wavelengths above 1200 nm.⁹⁰ However, it is important to note that the clear-sky spectrum from the NSRDB may overestimate irradiance below 500 nm and underestimate it above 500 nm, as noted by Kinsey et al. and Pelland and Gueymard^72,91 which could amplify the gains observed for emerging PV technologies in our analysis.

Despite this caveat, we can observe that the efficiency of different PV technologies is highly regional, highlighting that a “one size fits all” approach is not exploiting the full range of performances available to different PV technologies. This is demonstrated by the perovskite PV device almost achieving parity with silicon PVs in some equatorial locations as shown in Fig. 7, despite a 4.8% lower efficiency under STCs. Depending on specific climatic conditions, the gap can drop from as high as 5.5% under STC down to roughly 1.5% in certain equatorial or tropical locales. This improvement underscores the beneficial interplay of less negative temperature coefficients and optimised spectral response in warm, humid, or cloudy environments. The organic PV exhibits a 15.3% deficit relative to silicon under STC, sometimes extending to 16.5% in select regions, yet this shortfall is reduced to around 12% over a large portion of the globe. Although it is insufficient to achieve parity, it nonetheless highlights the importance of low (or zero) temperature coefficients and robust absorption at shorter wavelengths in enhancing organic PVs' field performance. These effects are especially pronounced in climates characterised by consistently high temperatures or diffuse-light conditions, both of which enhance the proportion of blue light in the spectrum.

Fig. 7 The comparison of PCE_real gap across the world in 2019 between silicon and (a) perovskite PVs and (b) organic PVs.

These findings make clear that exclusive reliance on AM1.5 data overlooks essential real-world behaviours that dictate actual energy yield. While silicon remains the industry standard, it can lose a considerable share of its rated output in hot, humid, or frequently overcast locations. Perovskite and organic PVs, however, often reclaim a portion of the nominal gap observed at STC by leveraging more favourable thermal properties and stronger responses to lower irradiances or altered spectral distributions.

7 Conclusions

This study presents a comprehensive analysis of the real-world performance potential of perovskite and organic PV technologies in comparison to silicon PVs. Our dataset incorporates all available state-of-the-art perovskite and organic PV devices from the literature with complete environmental response characterisation. While several entries originate from earlier generations (e.g., fullerene-based organic PVs), these datasets provide essential baselines, particularly given the current absence of systematic temperature and irradiance response data for more recent, high-efficiency devices. Importantly, we find no consistent correlation between improvements in AM1.5 PCE and better real-world performance under non-standard conditions. This disconnect underscores a central concern: the prevailing focus on AM1.5 metrics alone is insufficient to guide the optimisation and evaluation of emerging PV technologies. Our population-based approach, comprising 22 organic and 29 perovskite PV datasets (detailed in ESI Table 1†), enables robust insights into the diversity of behaviours across technologies and highlights the pressing need to reform device evaluation frameworks.

Photovoltaic devices based on perovskite and organic materials exhibit distinct temperature and spectral responses compared to silicon PVs, with the potential to achieve higher energy yields under real-world conditions as compared to AM1.5 standard testing conditions. This study quantified these differences by integrating state-of-the-art PV device characteristics from the literature into energy yield models incorporating historical climate data from diverse global locations. The results show that favourable temperature coefficients and spectral sensitivities enable perovskite and organic PV devices to exhibit narrow, or even close, performance gaps with silicon PVs in certain climates, despite significantly lower efficiencies under AM1.5 conditions. The findings highlight that reliance on AM1.5 measurements introduces uncertainty in predicting real-world energy generation for emerging PV technologies. Comprehensive characterisation across varying environmental conditions is therefore essential to improve energy yield predictions and reduce the risks associated with technology development and large-scale deployment. However, while the wide range of temperature- and irradiance-dependent behaviours in perovskite and organic PVs presents a risk to future development, it also represents an opportunity, since these characteristics can be exploited to improve real-world competitiveness. Further work is encouraged to expand non-AM1.5 performance measurements and to explore strategies that leverage these unique properties to differentiate emerging PV technologies from established silicon counterparts.

Data availability

This study was carried out using publicly available data from the National Solar Radiation Database (NSRDB) developed and maintained by the National Renewable Energy Laboratory (NREL) at https://www.nsrdb.nrel.gov/.

Author contributions

Z. Z. – software, investigation, visualisation, validation, writing (original draft), writing (review and editing). A. C. – validation, writing (review and editing). R. M. – supervision, writing (review and editing), conceptualisation. C. G. – supervision, conceptualisation, project administration, funding acquisition, writing (original draft), writing (review and editing).

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

We sincerely acknowledge the Durham Engineering Doctoral Studentship funding provided by Durham University.

Notes and references

1. International Electrotechnical Commission (IEC), Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approval—Part 1-1: Special Requirements for Testing of Crystalline Silicon Photovoltaic (PV) Modules (IEC 61215-1-1:2021), 2021, available online: https://webstore.iec.ch/en/publication/61346, accessed on 15 March 2025.
2. CSI Solar, CS-Datasheet-TOPBiHiKu7-TOPCon_CS7N-TB-AG_v1.62_EN, https://www.static.csisolar.com, 2022, Accessed: 24 March 2024.
3. International Electrotechnical Commission (IEC), Photovoltaic (PV) Module Performance Testing and Energy Rating—Part 1: Irradiance and Temperature Performance Measurements and Power Rating (IEC 61853-1:2011), 2011, available online: https://webstore.iec.ch/en/publication/6035, accessed on 15 March 2025.
4. E. Cuce, P. M. Cuce and T. Bali, Appl. Energy, 2013, 111, 374–382.
5. W. De Soto, S. A. Klein and W. A. Beckman, Sol. Energy, 2006, 80, 78–88.
6. A. Dolara, S. Leva, G. Manzolini, R. Simonetti and I. Trattenero, Energies, 2022, 15, 1620.
7. O. Cardozo, S. Farooq, A. Stingl and N. Fraidenraich, Sol. Energy, 2019, 190, 543–548.
8. A. M. Gracia-Amillo, G. Bardizza, E. Salis, T. Huld and E. D. Dunlop, Renewable Sustainable Energy Rev., 2018, 93, 76–89.
9. T. W. David, G. A. Soares, N. Bristow, D. Bagnis and J. Kettle, Prog. Photovolt.: Res. Appl., 2021, 29, 1274–1284.
10. M. Jošt, B. Lipovšek, B. Glažar, A. Al-Ashouri, K. Brecl, G. Matič, A. Magomedov, V. Getautis, M. Topič and S. Albrecht, Adv. Energy Mater., 2020, 10, 2000454.
11. V. Stoichkov, N. Bristow, J. Troughton, F. De Rossi, T. Watson and J. Kettle, Sol. Energy, 2018, 170, 549–556.
12. T. Moot, J. B. Patel, G. McAndrews, E. J. Wolf, D. Morales, I. E. Gould, B. A. Rosales, C. C. Boyd, L. M. Wheeler and P. A. Parilla, et al., ACS Energy Lett., 2021, 6, 2038–2047.
13. W. Tress, K. Domanski, B. Carlsen, A. Agarwalla, E. A. Alharbi, M. Graetzel and A. Hagfeldt, Nat. Energy, 2019, 4, 568–574.
14. P. Lopez-Varo, M. Amara, S. Cacovich, A. Julien, A. Yaiche, M. Jouhari, J. Rousset, P. Schulz, J.-F. Guillemoles and J.-B. Puel, Sustainable Energy Fuels, 2021, 5, 5523–5534.
15. B. Lipovšek, M. Jošt, Š. Tomšič and M. Topič, Sol. Energy Mater. Sol. Cells, 2022, 234, 111421.
16. S. Williams, T. R. Betts, P. Vorasayan, R. Gottschalg and D. Infield, Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, 2005., 2005, pp. 1607–1610.
17. N. Blair, M. Mehos, C. Christensen and C. Cameron, Modeling Photovoltaic and Concentrating Solar Power Trough Performance, Cost, and Financing with the Solar Advisor Model, National Renewable Energy lab.(Nrel), Golden, Co (united states) Technical Report, 2008.
18. B. Kroposki, W. Marion, D. L. King, W. E. Boyson and J. Kratochvil, Conference Record of the Twenty-Eighth IEEE Photovoltaic Specialists Conference-2000 (Cat. No. 00CH37036), 2000, pp. 1407–1411.
19. D. Petreus, I. Ciocan and C. Farcas, 2008 31st International Spring Seminar on Electronics Technology, 2008, pp. 598–603.
20. S. R. Wenham, M. A. Green, M. E. Watt, R. Corkish and A. Sproul, Applied Photovoltaics, Routledge, 2013.
21. Y. T. Tan, D. S. Kirschen and N. Jenkins, IEEE Trans. Energy Convers., 2004, 19, 748–755.
22. A. Mermoud and T. Lejeune, 25th European Photovoltaic Solar Energy Conference, 2010, pp. 6–10.
23. T. Huld, Sol. Energy, 2017, 142, 171–181.
24. W. De Soto, S. Klein and W. Beckman, Sol. Energy, 2006, 80, 78–88.
25. M. Sengupta, Y. Xie, A. Lopez, A. Habte, G. Maclaurin and J. Shelby, Renewable Sustainable Energy Rev., 2018, 89, 51–60.
26. T. Huld, R. Müller and A. Gambardella, Sol. Energy, 2012, 86, 1803–1815.
27. I. M. Peters and T. Buonassisi, Joule, 2018, 2, 1160–1170.
28. Y. Xie, M. Sengupta and C. Wang, Sol. Energy, 2019, 188, 799–812.
29. M. Lave, W. Hayes, A. Pohl and C. W. Hansen, IEEE J. Photovolt., 2015, 5, 597–606.
30. B. Y. Liu and R. C. Jordan, Sol. Energy, 1960, 4, 1–19.
31. R. Perez, P. Ineichen, R. Seals, J. Michalsky and R. Stewart, Sol. Energy, 1990, 44, 271–289.
32. D. T. Reindl, W. A. Beckman and J. A. Duffie, Sol. Energy, 1990, 45, 9–17.
33. Y. Xie, P. Yang, G. W. Kattawar, P. Minnis and Y. X. Hu, J. Geophys. Res.:Atmos., 2009, 114, D11203.
34. Y. Xie, M. Sengupta and M. Dooraghi, Sol. Energy, 2018, 165, 55–64.
35. Y. Xie and M. Sengupta, Sol. Energy, 2018, 174, 691–702.
36. C. Gueymard et al., SMARTS2: a simple model of the atmospheric radiative transfer of sunshine: algorithms and performance assessment, Florida Solar Energy Center Cocoa, FL, 1995, vol. 1.
37. K. Stamnes, S.-C. Tsay, W. Wiscombe and K. Jayaweera, Appl. Opt., 1988, 27, 2502–2509.
38. R. Ross Jr, 12th Photovoltaic Specialists Conference, 1976, pp. 801–806.
39. N. Bristow and J. Kettle, Sol. Energy Mater. Sol. Cells, 2018, 175, 52–59.
40. S. Pescetelli, A. Agresti, G. Viskadouros, S. Razza, K. Rogdakis, I. Kalogerakis, E. Spiliarotis, E. Leonardi, P. Mariani and L. Sorbello, et al., Nat. Energy, 2022, 7, 597–607.
41. Q. Burlingame, G. Zanotti, L. Ciammaruchi, E. A. Katz and S. R. Forrest, Org. Electron., 2017, 41, 274–279.
42. Y. Chen, D. Chen, C. Liu, Z. Wang, Y. Zou, Y. He, Y. Wang, L. Yuan, J. Gong and W. Lin, et al., Prog. Photovolt.: Res. Appl., 2019, 27, 827–834.
43. L. Wang, Y. Tang, S. Zhang, F. Wang and J. Wang, Sol. Energy, 2022, 238, 258–263.
44. X. Fan, M. Rabelo, Y. Hu, M. Q. Khokhar, Y. Kim and J. Yi, Trans. Electr. Electron. Mater., 2023, 24, 123–131.
45. A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pérez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 11755.
46. M. I. Dar, G. Jacopin, S. Meloni, A. Mattoni, N. Arora, A. Boziki, S. M. Zakeeruddin, U. Rothlisberger and M. Grätzel, Sci. Adv., 2016, 2, e1601156.
47. X. Zhang, Y. Guan, Y. Zhang, W. Yu, C. Wu, J. Han, Y. Zhang, C. Chen, S. Zheng and L. Xiao, Adv. Opt. Mater., 2022, 10, 2201598.
48. G. Chen, C. Si, Z. Tang, K. Guo, T. Wang, J. Zhang and B. Wei, Synth. Met., 2016, 222, 293–298.
49. D. Chirvase, Z. Chiguvare, M. Knipper, J. Parisi, V. Dyakonov and J. C. Hummelen, J. Appl. Phys., 2003, 93, 3376–3383.
50. W. Bagienski and M. Gupta, Sol. Energy Mater. Sol. Cells, 2011, 95, 933–941.
51. D. Lee, J. Kim, G. Park, H. W. Bae, M. An and J. Y. Kim, Polymers, 2020, 12, 992.
52. National Renewable Energy Laboratory, Best Research-Cell Efficiency Chart, 2024, https://www.nrel.gov/pv/cell-efficiency.html, Accessed: 2024-08-05.
53. B. H. Hamadani and M. B. Campanelli, IEEE J. Photovolt., 2020, 10, 1119–1125.
54. T. Song, D. J. Friedman and N. Kopidakis, Adv. Energy Mater., 2021, 11, 2100728.
55. S. Ye, B. Chen, Y. Cheng, M. Feng, H. Rao, Y. M. Lam and T. C. Sum, J. Phys. Chem. Lett., 2020, 11, 3782–3788.
56. U. Kräling, P. Gebhardt, M. Kaiser and D. Philipp, Ratio, 2022, 9, 58–1.
57. X. Liu, X. Liu, Z. Xia, Y. Ji, D. Zhang, Y. Cheng, X. Liu, J. Yuan, X. Yang and W. Huang, Mater. Today Energy, 2024, 101614.
58. X. He, J. Chen, X. Ren, L. Zhang, Y. Liu, J. Feng, J. Fang, K. Zhao and S. Liu, Adv. Mater., 2021, 33, 2100770.
59. T. Du, W. Xu, S. Xu, S. R. Ratnasingham, C.-T. Lin, J. Kim, J. Briscoe, M. A. McLachlan and J. R. Durrant, J. Mater. Chem. C, 2020, 8, 12648–12655.
60. L. Wu, H. Zang, Y.-C. Hsiao, X. Zhang and B. Hu, Appl. Phys. Lett., 2014, 104, 153903.
61. K.-K. Chong, P. P. Khlyabich, K.-J. Hong, M. Reyes-Martinez, B. P. Rand and Y.-L. Loo, Appl. Energy, 2016, 180, 516–523.
62. V. K. Wong, C. Zhang, Z. Zhang, M. Hao, Y. Zhou and S. K. So, Mater. Today Energy, 2023, 101347.
63. C. Williams, H. Michaels, A. F. Crossland, Z. Zhang, N. Shirshova, R. C. MacKenzie, H. Sun, J. Kettle, M. Freitag and C. Groves, Energy Environ. Sci., 2023, 16, 4650–4659.
64. D. Dirnberger, G. Blackburn, B. Müller and C. Reise, Sol. Energy Mater. Sol. Cells, 2015, 132, 431–442.
65. H. Jang, S. Lee, H. Lee, D. Choi, H. Song, J. Jeong, J. W. Sohn, D. Kim, H.-S. Lee and Y. Choe, et al., Process Integr. Optim. Sustain., 2024, 1–9.
66. Y. Chen, Y. Zheng, Y. Jiang, H. Fan and X. Zhu, J. Am. Chem. Soc., 2021, 143, 4281–4289.
67. G. S. Kinsey, Sol. Energy, 2021, 217, 49–57.
68. T. Mambrini, A. M. Dubois, C. Longeaud, J. Badosa, M. Haeffelin, L. Prieur and V. Radivoniuk, EPJ Photovoltaics, 2015, 6, 60701.
69. S. M. Ahsan and H. A. Khan, IET Renew. Power Gener., 2019, 13, 1920–1926.
70. M. F. Khaleda, B. Vengadaesvaran and N. Rahim, Energy Mater., 2021, 525–566.
71. K. Emery, C. Osterwald, T. Cannon, D. Myers, J. Burdick, T. Glatfelter, W. Czubatyj and J. Yang, Proc. 18th IEEE PV Spec. Conf, 1985.
72. S. Pelland and C. A. Gueymard, IEEE J. Photovolt., 2022, 12, 1361–1368.
73. D. L. King, J. A. Kratochvil and W. E. Boyson, Photovoltaic Array Performance Model, Citeseer, 2004, vol. 8.
74. T. Betts, D. Infield and R. Gottschalg, 19th European Photovoltaic Solar Energy Conference, 2004.
75. M. Lee and A. Panchula, 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), 2016, pp. 1351–1356.
76. B. C. Duck and C. J. Fell, 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC), 2016, pp. 2647–2652.
77. J. Caballero, E. Fernández, M. Theristis, F. Almonacid and G. Nofuentes, IEEE J. Photovolt., 2018, 8, 552–558.
78. C. A. Gueymard, Energy, 2005, 30, 1551–1576.
79. R. Daxini, R. Wilson and Y. Wu, Energy Rep., 2025, 13, 759–769.
80. K. Takeguchi, K. Nakayama, J. Chantana, Y. Kawano, T. Nishimura, Y. Hishikawa and T. Minemoto, Sol. Energy, 2021, 214, 1–10.
81. A. Crossland, K. Scoles, A. Wang, C. Groves and S. Sun, Energies, 2020, 13, 2799.
82. Y. Nakada, H. Takahashi, K. Ichida, T. Minemoto and H. Takakura, Curr. Appl. Phys, 2010, 10, S261–S264.
83. M. Sevillano-Bendezú, M. Khenkin, G. Nofuentes, J. De la Casa, C. Ulbrich and J. Töfflinger, Sol. Energy, 2023, 259, 174–187.
84. A. M. Oni, A. S. Mohsin, M. M. Rahman and M. B. H. Bhuian, Energy Rep., 2024, 11, 3345–3366.
85. A. M. Law, L. O. Jones and J. M. Walls, Sol. Energy, 2023, 261, 85–95.
86. Y. Wang, H. Wang, M. Chen, P. Wang, Y. Mao, W. Han, T. Wang and D. Liu, Sci. China Mater., 2020, 64, 789–797.
87. H. Ren, J.-D. Chen, Y.-F. Zhang, J.-L. Zhang, W.-S. Chen, Y.-Q. Li and J.-X. Tang, Sci. Adv., 2024, 10, eadp9439.
88. B. Chen, Z. Yu, A. Onno, Z. Yu, S. Chen, J. Wang, Z. C. Holman and J. Huang, Sci. Adv., 2022, 8, eadd0377.
89. Heliatek, Datasheet HeliaSol 436-2000, https://www.heliatek.com, 2023, Accessed: 24 March 2024.
90. T. Ishii, K. Otani, T. Takashima and Y. Xue, Prog. Photovolt.: Res. Appl., 2013, 21, 481–489.
91. G. S. Kinsey, N. C. Riedel-Lyngskær, A.-A. Miguel, M. Boyd, M. Braga, C. Shou, R. R. Cordero, B. C. Duck, C. J. Fell and S. Feron, et al., Renewable Energy, 2022, 196, 995–1016.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5el00096c

---